Virtual Coupling in Railways: A Comprehensive Review
Abstract
1. Introduction
2. Review Methodology and Publications Overview
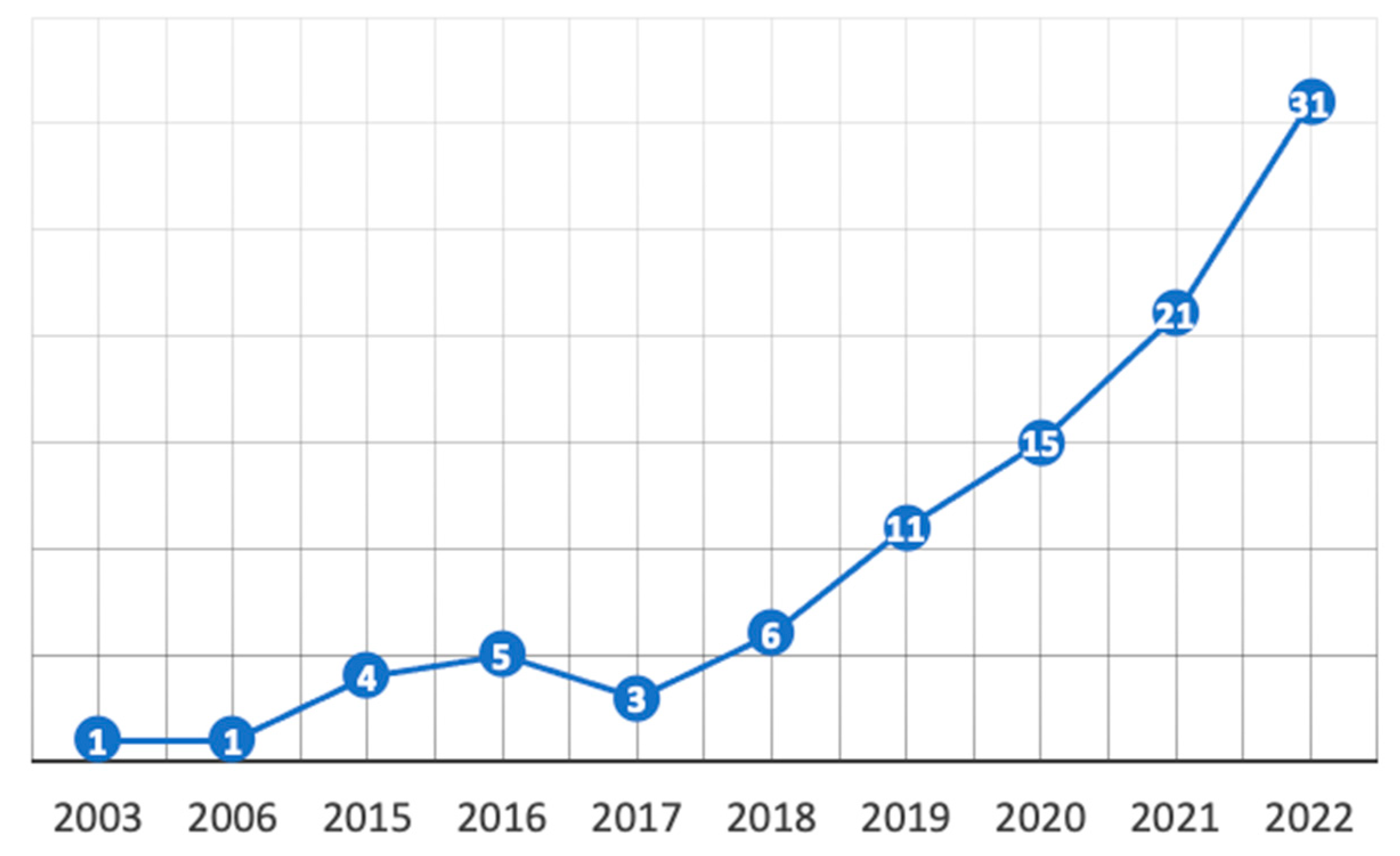
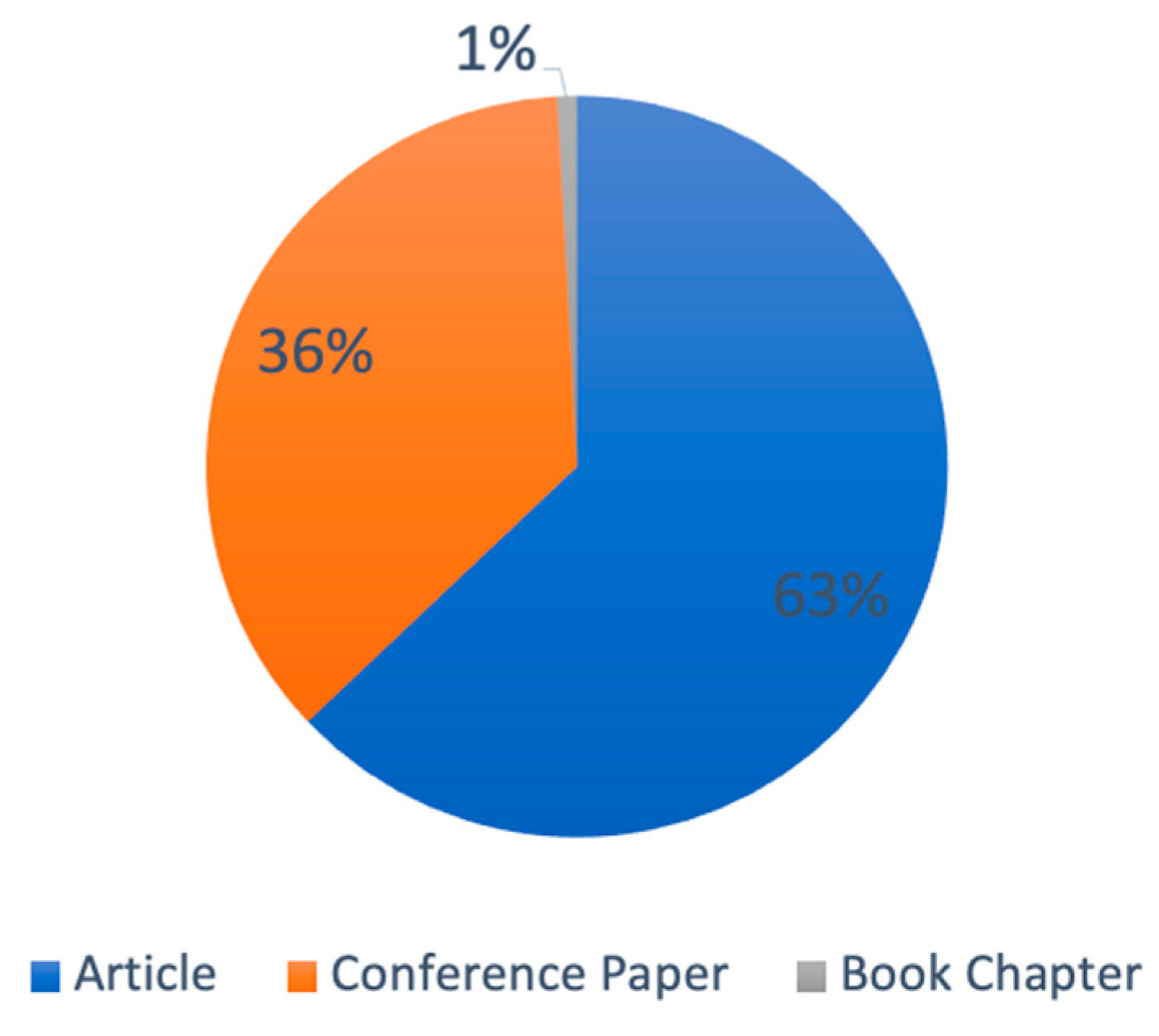
2.1. Literature Review Methodology
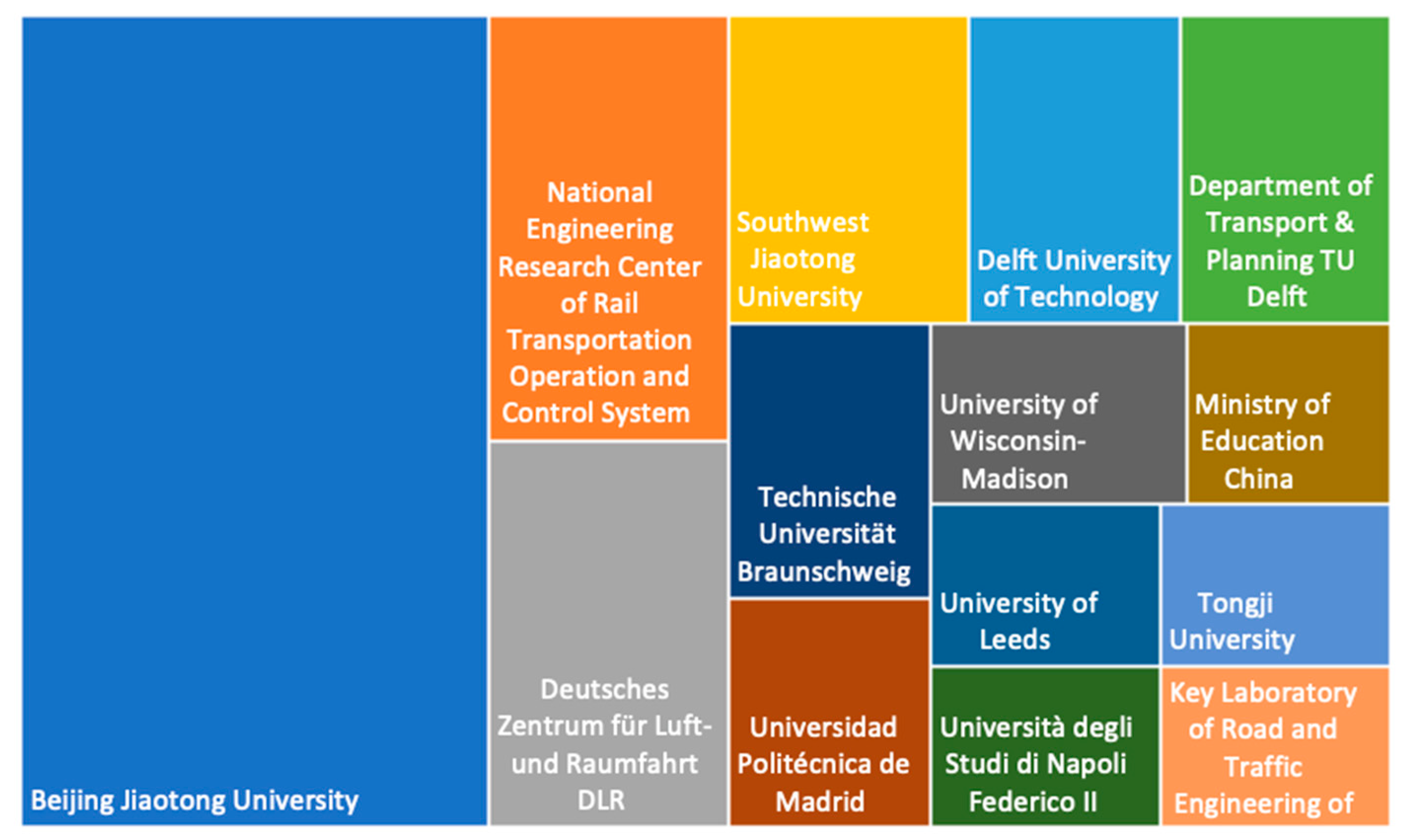
2.2. General Publications Overview
3. Terminology and Definitions
| Moving block system (MBS) | Signaling and train management system based on moving blocks. |
| Fixed block system (FBS) | Signaling and train management system based on fixed blocks. |
| Trainset | Single vehicle or group of mechanically coupled railway vehicles with at least one power unit. |
| Consist | A trainset, i.e., a train formation. A consist is defined as a single vehicle or group of vehicles that are not separated during normal operation and have a specific traction and braking capability. |
| Virtual coupling (VC) | Evolution of the moving block concept based on the relative braking distance. |
| Virtually coupled train set (VCTS) | A group of separate trains that are virtually connected and behave as unique coupled trains. A VCTS is defined by two or more consists, which are not connected mechanically. |
| Convoy | A VCTS, i.e., a platoon of trains. |
| Platoon | A group of physically uncoupled vehicles that behave as a single vehicle. |
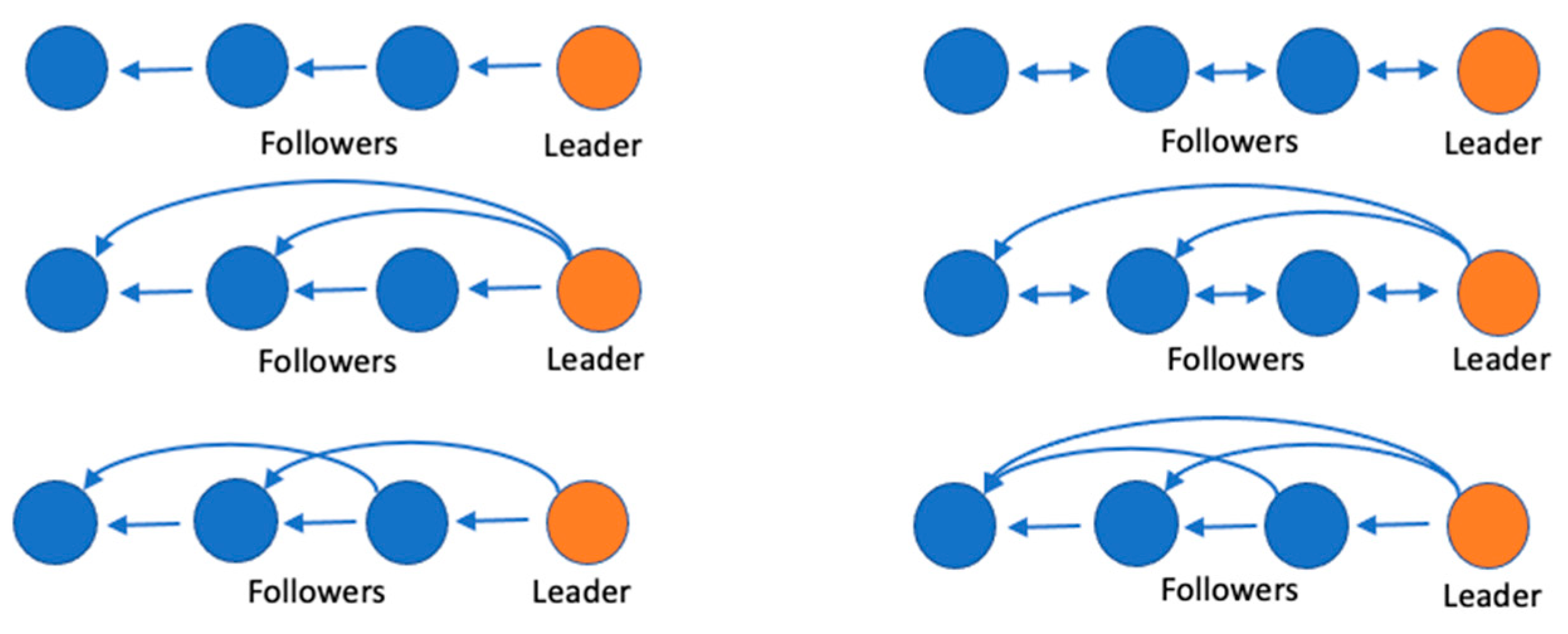
| Leader | In a VCTS, the first train in the convoy. |
| Followers | In a VCTS, all the trains of a convoy except for the first train. |
| Train positioning (TP) | This refers to the information generated by a function external to the VC, which mainly provides the distance traveled (or absolute position) and speed measurement with an appropriate level of safety integrity to support the functions of the VC. |
| Communication-Based Train Control (CBTC) | Moving block train control system associated with the IEEE 1474 standard. |
| European Rail Traffic Management System (ERTMS) | EU initiative for managing railway lines through interoperability among different rail networks. Currently, it officially specifies three basic levels of operation with an increasing level of technological complexity, from fixed block-based Level 1 (L1) to moving block-based Level 3 (L3). |
| European Train Control System (ETCS) | Railway controller in the ERTMS. |
| Chinese Train Control System (CTCS) | Railway controller developed in the People’s Republic of China. It is based on four basic levels of increasing technological complexity, from the fixed block-based Level 1 (L1) to the moving block-based Level 4 (L4). |
| Information Technology (IT) | Hardware and software systems that allow for the management and exchange of data. |
| Railway company | In railway-liberalized countries, railway companies are classified into two main groups: railway operators and infrastructure managers. A railway operator (also known as a railway undertaking in the European regulation) is a type of railway company that offers passenger and/or freight services, whereas an infrastructure manager is a type of railway company that owns the infrastructure and acts as its administrator. |
4. Background and Concept of VC
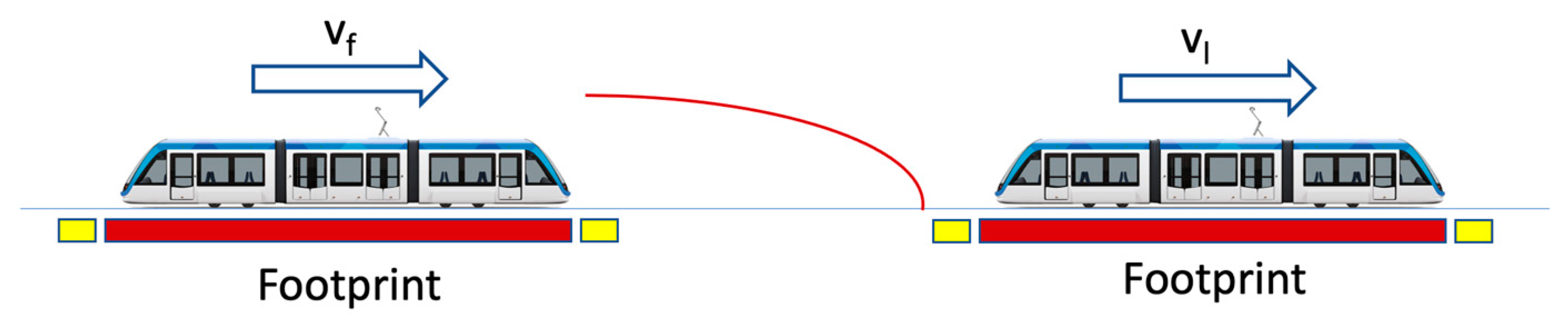
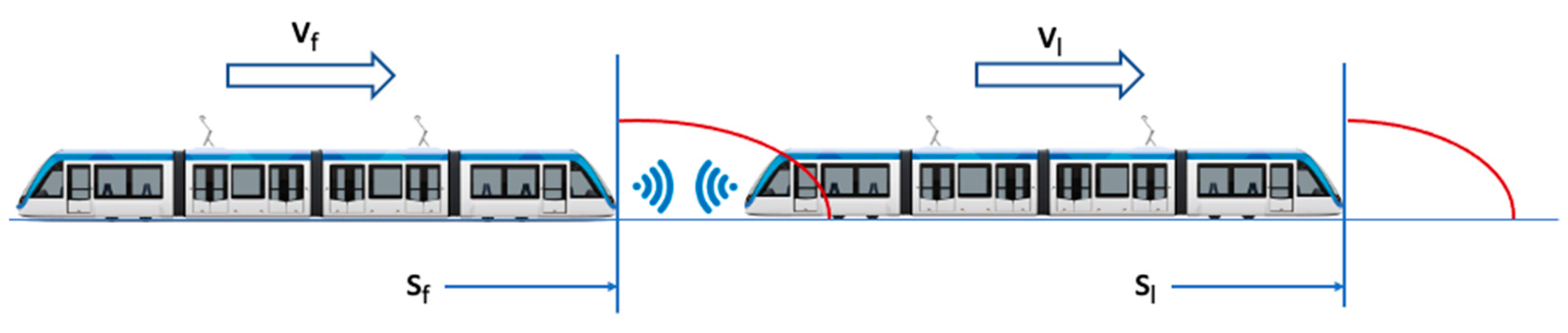
4.1. Railway Virtual Coupling System Concept
4.2. Virtual Coupling System Evolution and Development
5. Research in the Field of Virtual Coupling
5.1. Methodology Used for the Identification of the Most Important Research Topics
- Cluster 1: virtual coupling, train operation, train control systems, communications, moving block, and transport management.
- Cluster 2: model predictive control, cooperative control, robust control, consensus-based control, optimal control, stochastic control, vehicle-following models, adaptive control, intelligent control, distributed control, and sliding mode control.
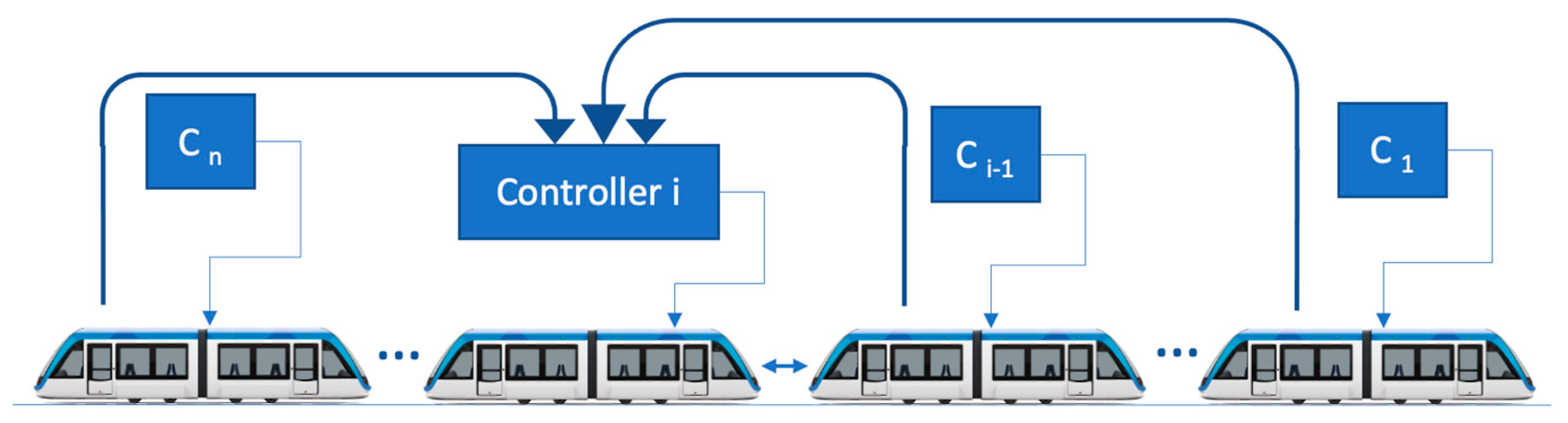
5.2. Control Architectures
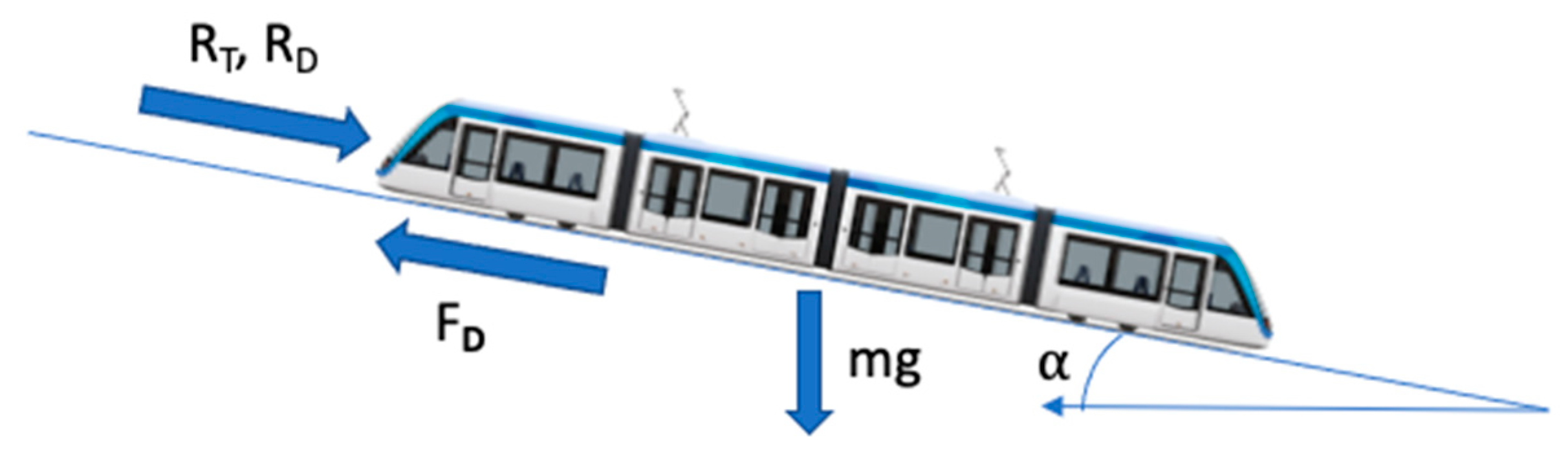
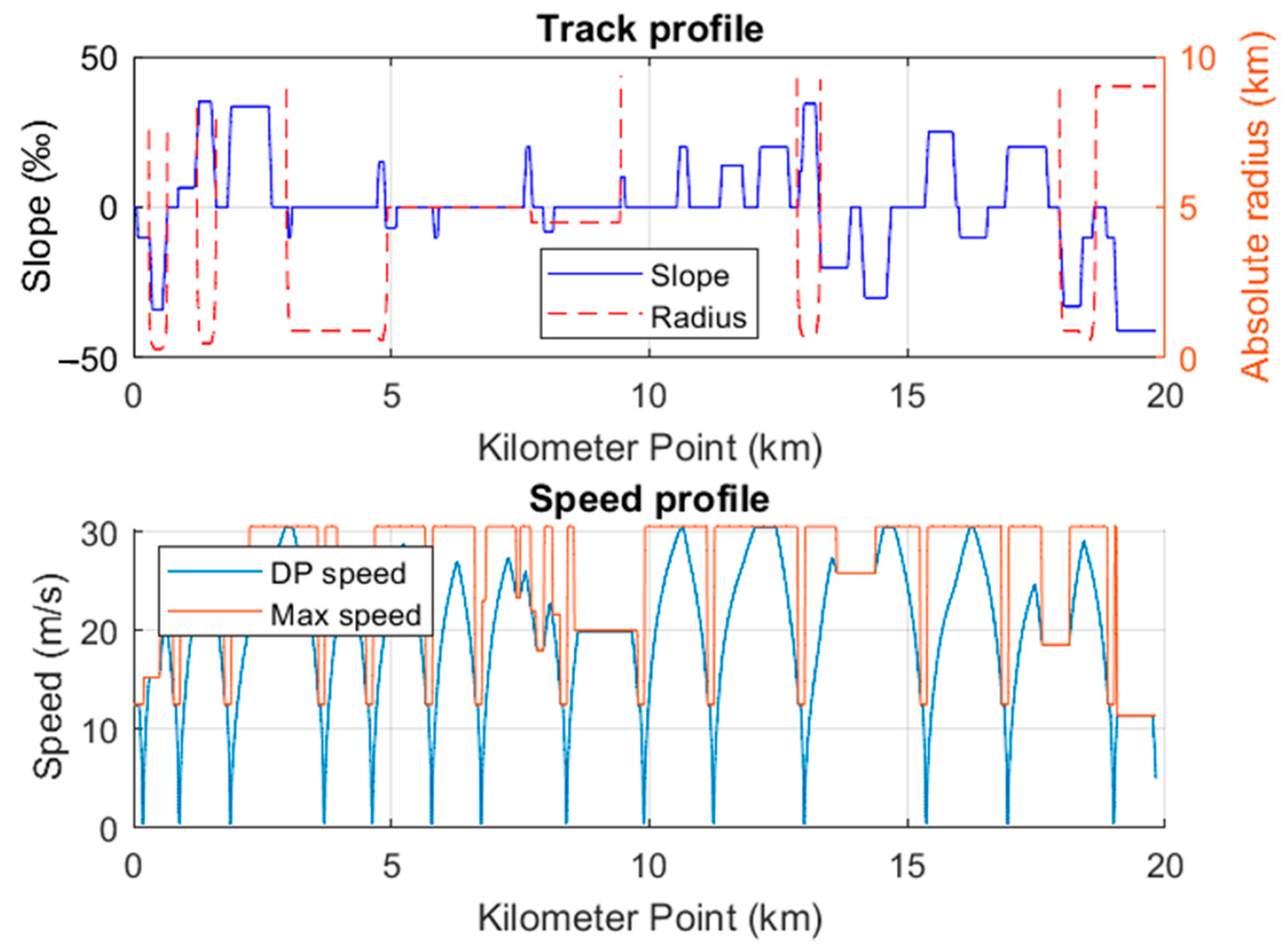
5.3. Dynamic Model
5.4. Control Methods Used in Virtual Coupling
5.4.1. Vehicle-Following Models
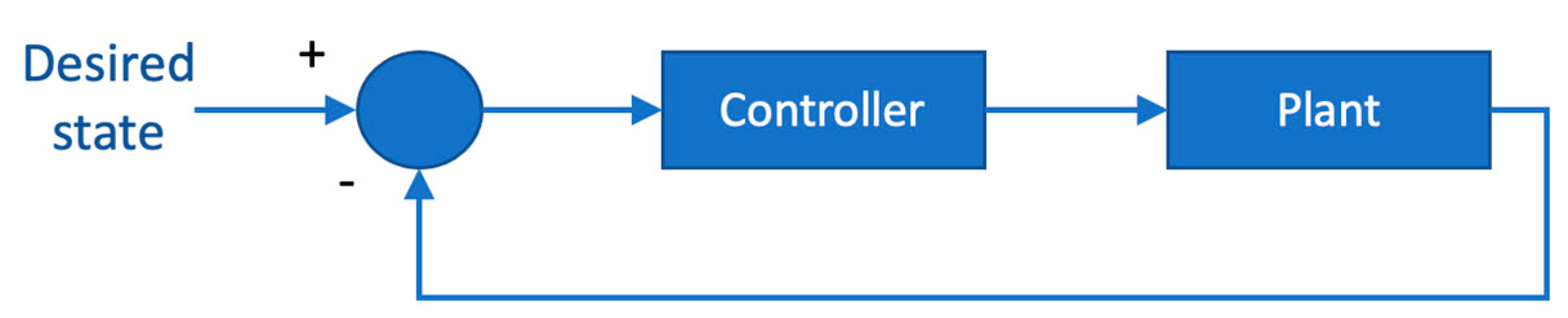
5.4.2. Feedback Controllers
5.4.3. Consensus-Based Control (CBC)
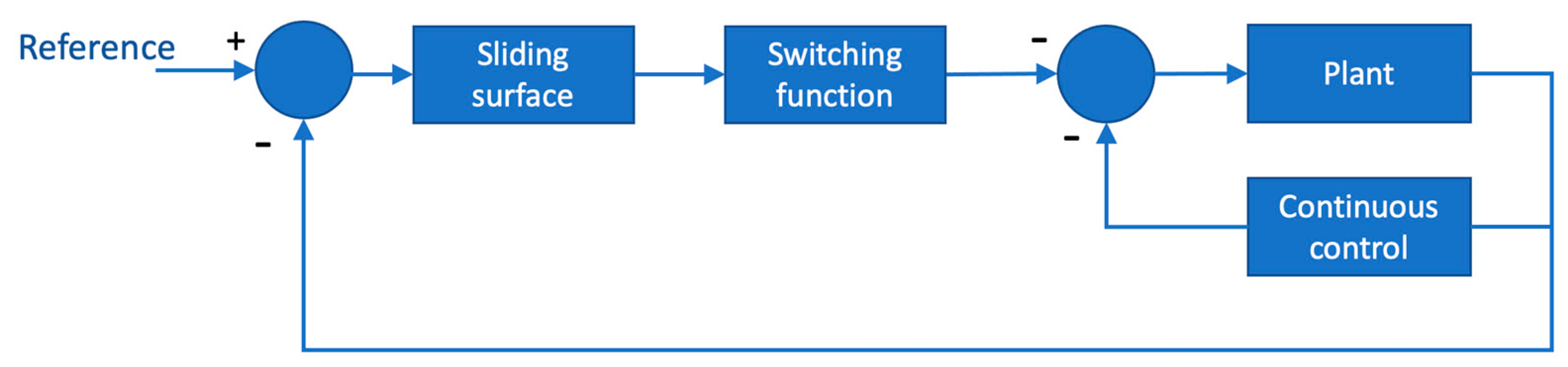
5.4.4. Sliding Mode Control
5.4.5. Optimization and Optimal Control
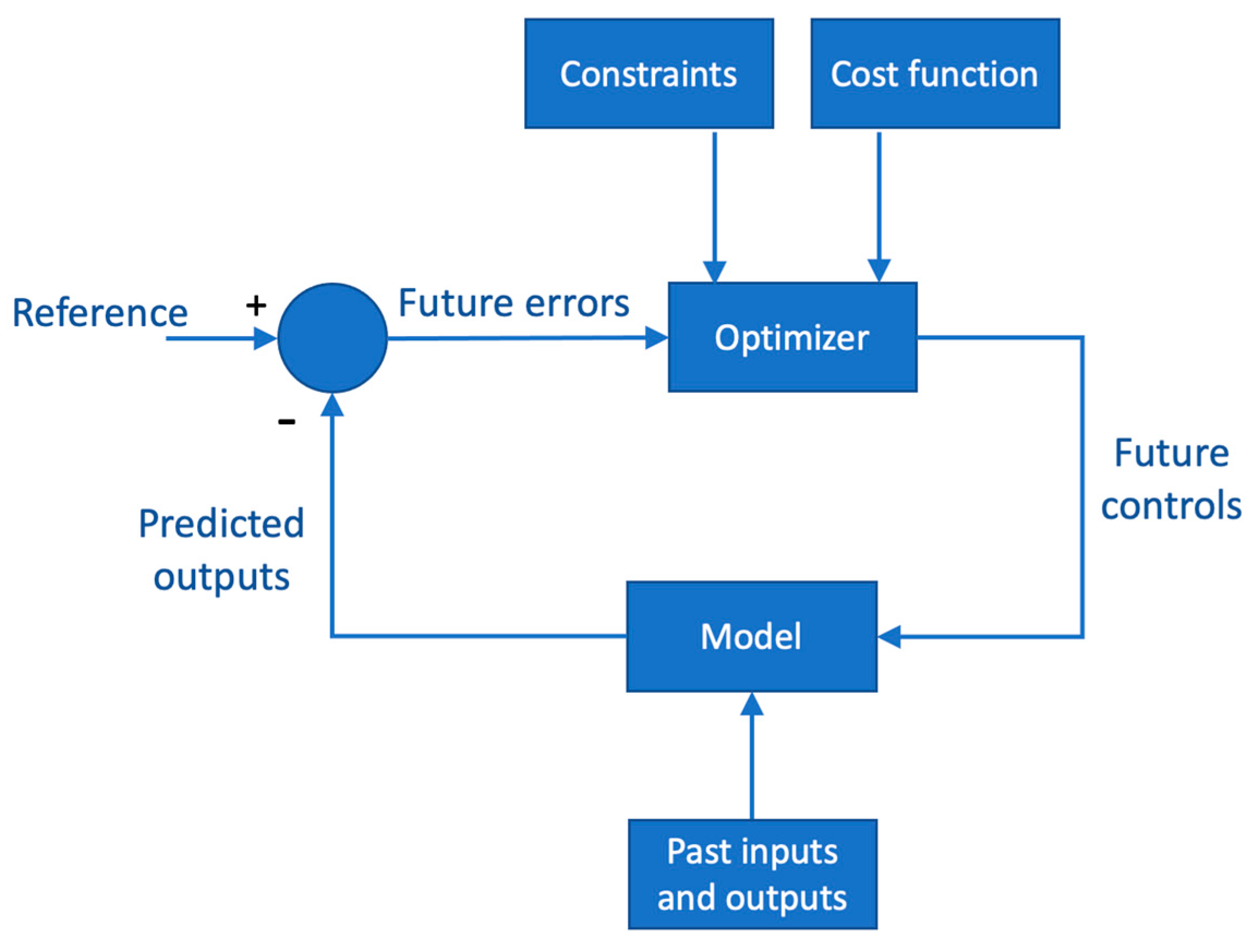
5.4.6. Model Predictive Control
5.4.7. Robust Model Predictive Control
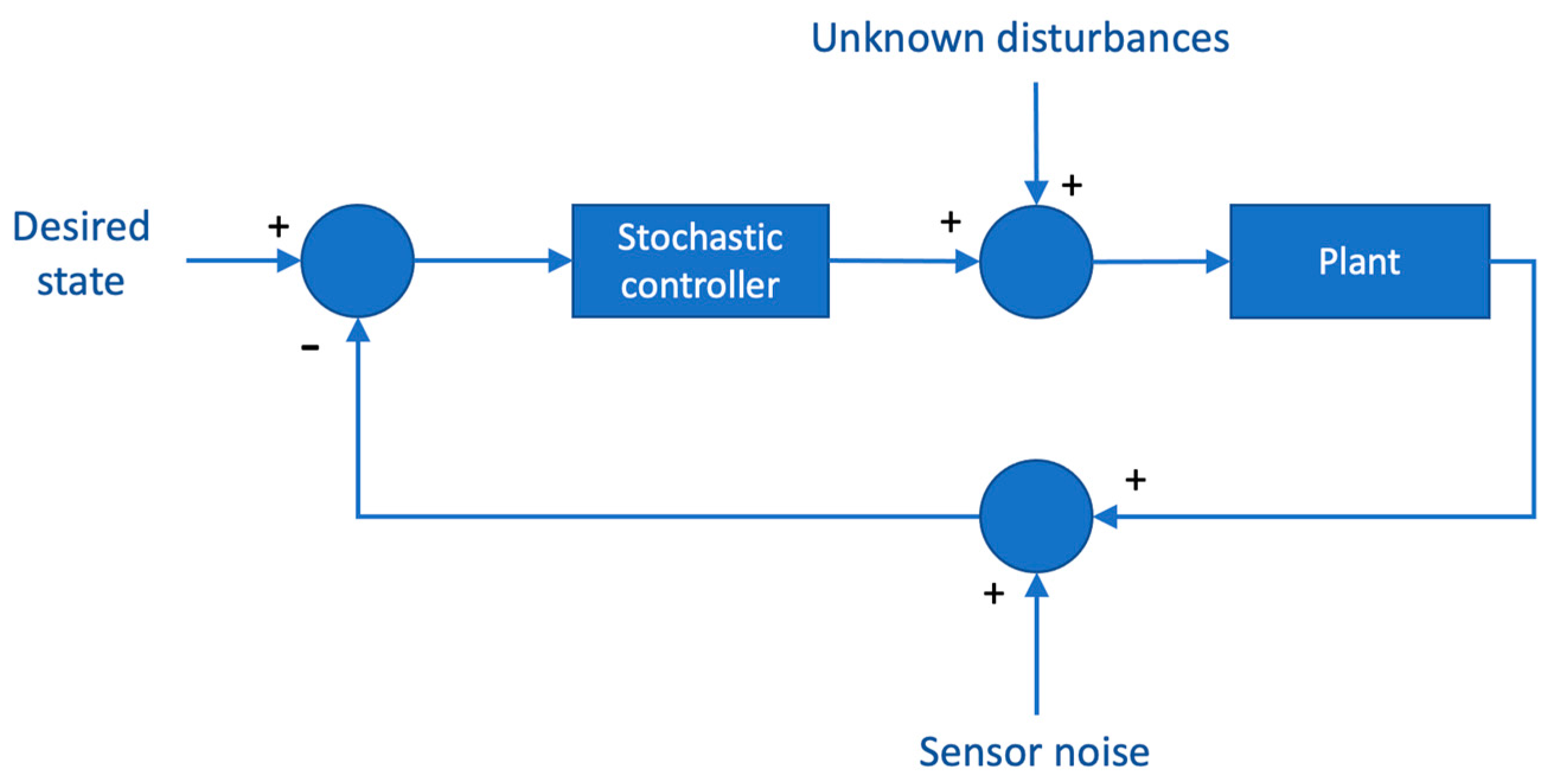
5.4.8. Stochastic Control
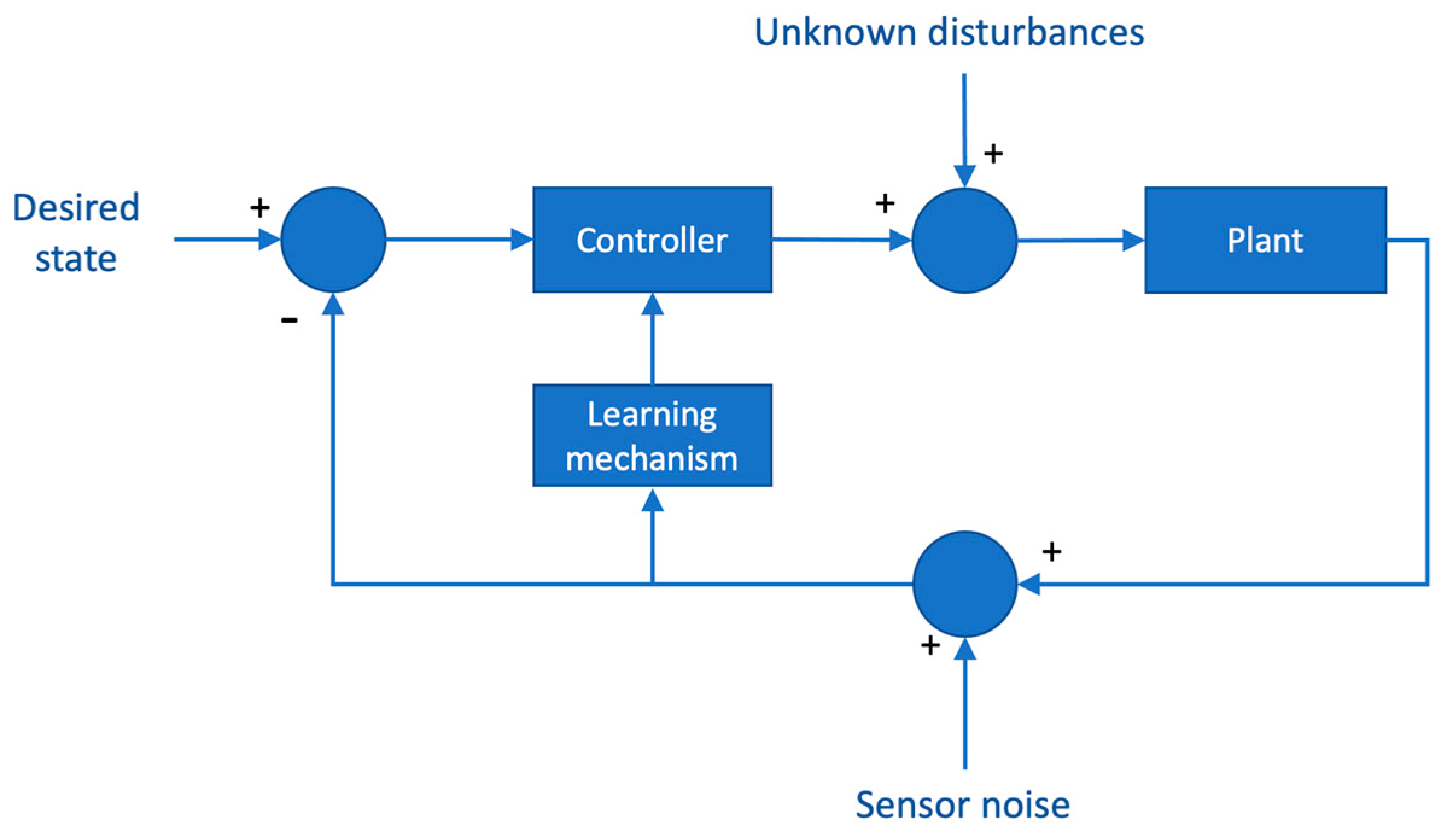
5.4.9. Intelligent Control
5.4.10. Critical Comparisons of VC Control Techniques
5.5. Communication Solutions
6. Future Research
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- EU Transport in Figures: Statistical Pocketbook; European Commission: Luxembourg, 2021.
- IEEE. IEEE 1474.1-2004 Standard for Communications-Based Train Control (CBTC). Performance and Functional Requirements. 2004. Available online: https://standards.ieee.org/ieee/1474.1/3552/ (accessed on 20 February 2023).
- Furness, N.; van Houten, H.; Bartholomeus, M.; Arenas, L. ERTMS Level 3: The Game-Changer; IRSE: London, UK, 2017. [Google Scholar]
- Wu, Q.; Ge, X.; Zhu, S.; Cole, C.; Spiryagin, M. Physical coupling and decoupling of railway trains at cruising speeds: Train control and dynamics. Int. J. Rail Transp. 2023, 1–16. [Google Scholar] [CrossRef]
- Nold, M.; Corman, F. Dynamic train unit coupling and decoupling at cruising speed: Systematic classification, operational potentials, and research agenda. J. Rail Transp. Plan. Manag. 2021, 18, 100241. [Google Scholar] [CrossRef]
- Nold, M. Coupling assistance device for coupling and uncoupling rail vehicles during travel. German Patent DE102018009589B3, 2019. [Google Scholar]
- Quaglietta, E.; Wang, M.; Goverde, R. A multi-state train-following model for the analysis of virtual coupling railway operations. J. Rail Transp. Plan. Manag. 2020, 15, 100195. [Google Scholar] [CrossRef]
- X2Rail-3. Advanced Signalling, Automation and Communication System (IP2 and IP5)—Prototyping the Future by Means of Capacity Increase, Autonomy and Flexible Communication. Cordis Database. Available online: https://cordis.europa.eu/project/id/826141 (accessed on 7 October 2022).
- Schumann, T. Increase of capacity on the shinkansen high-speed line using virtual coupling. Int. J. Transp. Dev. Integr. 2017, 1, 666–676. [Google Scholar] [CrossRef]
- Quaglietta, E.; Spartalis, P.; Wang, M.; Goverde, R.M.; van Koningsbruggen, P. Modelling and analysis of Virtual Coupling with dynamic safety margin considering risk factors in railway operations. J. Rail Transp. Plan. Manag. 2022, 22, 100313. [Google Scholar] [CrossRef]
- Scopus. Available online: https://www.scopus.com/home.uri (accessed on 24 June 2022).
- WoS, Web Os Science. Available online: https://clarivate.com/products/scientific-and-academic-research/research-discovery-and-workflow-solutions/webofscience-platform/ (accessed on 21 April 2023).
- Google Scholar. Available online: https://scholar.google.es/ (accessed on 21 April 2023).
- ResearchGate. Available online: https://www.researchgate.net/ (accessed on 21 April 2023).
- IEEE Xplore. Available online: https://ieeexplore.ieee.org/Xplore/home.jsp (accessed on 26 April 2023).
- Inciteful. Available online: https://inciteful.xyz/ (accessed on 21 April 2023).
- Cao, Y.; Wen, J.; Ma, L. Tracking and collision avoidance of virtual coupling train control system. Futur. Gener. Comput. Syst. 2021, 120, 76–90. [Google Scholar] [CrossRef]
- Felez, J.; Kim, Y.; Borrelli, F. A model predictive control approach for virtual coupling in railways. IEEE Trans. Intell. Transp. Syst. 2019, 20, 2728–2739. [Google Scholar] [CrossRef]
- Di Meo, C.; Di Vaio, M.; Flammini, F.; Nardone, R.; Santini, S.; Vittorini, V. ERTMS/ETCS virtual coupling: Proof of concept and numerical analysis. IEEE Trans. Intell. Transp. Syst. 2019, 21, 2545–2556. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Y.; Su, S.; Xun, J.; Tang, T. An analytical optimal control approach for virtually coupled high-speed trains with local and string stability. Transp. Res. Part C: Emerg. Technol. 2021, 125, 102886. [Google Scholar] [CrossRef]
- Ning, B. Absolute braking and relative distance braking—Train operation control modes in moving block systems. WIT Trans. Built Environ. 1998, 34, 991–1001. [Google Scholar]
- Williams, C. The next ETCS level? In Proceedings of the 2016 IEEE International Conference on Intelligent Rail Transportation (ICIRT), Birmingham, UK, 23–25 August 2016; pp. 75–79. [Google Scholar] [CrossRef]
- Winter, J.; Lehner, A.; Polisky, E. Electronic Coupling of Next Generation Trains. In Proceedings of the Third International Conference on Railway Technology: Research, Development and Maintenance, Cagliari, Italy, 5–8 April 2016. [Google Scholar] [CrossRef]
- Mitchell, I. ERTMS Level 4, Train Convoys or Virtual Coupling. IRSE News. 2016. Available online: https://webinfo.uk/webdocssl/irse-kbase/ref-viewer.aspx?Refno=1882928268&document=ITC%20Report%2039%20Train%20convoys%20and%20virtual%20coupling.pdf (accessed on 7 October 2022).
- Bock, U.; Varchmin, J.U. Enhancement of the Occupancy of Railroads Using Virtually Coupled Train Formations. In Proceedings of the World Congress on Railway Research (WCRR), Tokyo, Japan, 16–20 November 1999. [Google Scholar]
- Bock, U.; Bikker, G. Design and development of a future freight train concept—Virtually coupled train formations. IFAC Proc. Vol. 2000, 33, 395–400. [Google Scholar] [CrossRef]
- Braun, I.; Konig, S.; Schnieder, E. Concepts on a future railway management system. In Proceedings of the 8th World Congress on Intelligent Transport Systems, Sydney, Australia, 30 September–4 October 2001. [Google Scholar]
- Konig, S.; Schnieder, E. Modeling and simulation of an operation concept for future rail traffic. In Proceedings of the 2001 IEEE Intelligent Transportation Systems. Proceedings (Cat. No.01TH8585), Oakland, CA, USA, 25–29 August 2001; pp. 808–812. [Google Scholar] [CrossRef]
- König, S.; Braun, I.; Schnieder, E. Decentralized management and operations control concept for railway freight transport services by multi agent systems. IFAC Proc. Vol. 2003, 36, 317–322. [Google Scholar] [CrossRef]
- Henke, C.; Tichy, M.; Schneider, T.; Böcker, J.; Schäfer, W. Organization and control of autonomous railway convoys. In Proceedings of the 9th International Symposium on Advanced Vehicle Control, Kobe, Japan, 6–9 October 2008. [Google Scholar]
- Ständer, T.; Drewes, J.; Braun, D.-W.I.; Schnieder, D.-I.D.H.E. Operational and safety concepts for railway operation with virtual train-sets. IFAC Proc. Vol. 2006, 39, 261–266. [Google Scholar] [CrossRef]
- Shift2Rail. The Rail Joint Undertaking. 2015. Available online: https://projects.shift2rail.org/ (accessed on 4 January 2023).
- Shift2Rail. Shift2Rail Strategic Master Plan. 2015. Available online: https://rail-research.europa.eu/wp-content/uploads/2016/03/S2R-JU-GB_Decision-N-4-2015-on-the-adoption-of-the-S2R-Master-Plan.pdf (accessed on 4 January 2023).
- Goikoetxea, J. Roadmap towards the wireless virtual coupling of trains. Commun. Technol. Veh. 2016, 3–9. [Google Scholar] [CrossRef]
- Europe’s Rail. Europe’s Rail Join Undertaking. 2023. Available online: https://rail-research.europa.eu/ (accessed on 30 April 2023).
- National Key R&D Program of China. Available online: https://chinainnovationfunding.eu/national-key-rd-programmes/ (accessed on 27 December 2022).
- NSFC. National Natural Science Foundation of China. 2023. Available online: https://www.nsfc.gov.cn/english/site_1/index.html (accessed on 19 January 2023).
- MOVINGRAIL. Moving Block and Virtual Coupling New Generations of RAIL Signalling. 2020. Available online: https://movingrail.eu/ (accessed on 27 December 2022).
- Stickel, S.; Schenker, M.; Dittus, H.; Unterhuber, P.; Canesi, S.; Riquier, V.; Ayuso, F.P.; Berbineau, M.; Goikoetxea, J. Technical feasibility analysis and introduction strategy of the virtually coupled train set concept. Sci. Rep. 2022, 12, 4248. [Google Scholar] [CrossRef] [PubMed]
- Aoun, J.; Quaglietta, E.; Goverde, R.M.P. Investigating market potentials and operational scenarios of virtual coupling railway signaling. Transp. Res. Rec. J. Transp. Res. Board 2020, 2674, 799–812. [Google Scholar] [CrossRef]
- Aoun, J.; Quaglietta, E.; Goverde, R.M.; Scheidt, M.; Blumenfeld, M.; Jack, A.; Redfern, B. A hybrid delphi-AHP multi-criteria analysis of moving block and virtual coupling railway signalling. Transp. Res. Part C Emerg. Technol. 2021, 129, 103250. [Google Scholar] [CrossRef]
- Aoun, J.; Quaglietta, E.; Goverde, R.M. Roadmap development for the deployment of virtual coupling in railway signalling. Technol. Forecast. Soc. Chang. 2023, 189, 122263. [Google Scholar] [CrossRef]
- SCOTT. Secure Connected Trustable Things. 2017. Available online: https://scottproject.eu/domains/rail/ (accessed on 25 January 2023).
- InSecTT. Intelligent Secure Trustable Things. 2021. Available online: https://www.insectt.eu/ (accessed on 30 April 2023).
- Vaquero-Serrano, M.A.; Felez, J. A decentralized robust control approach for virtually coupled train sets. Comput. Civ. Infrastruct. Eng. 2023, 1–20. [Google Scholar] [CrossRef]
- VOSviewer. Available online: https://www.vosviewer.com/features/highlights (accessed on 21 April 2023).
- MOVINGRAIL. Deliverables. 2020. Available online: https://movingrail.eu/public-information/deliverables (accessed on 10 January 2023).
- UIC. FRMCS—Future Railway Mobile Communication System. 2023. Available online: https://uic.org/rail-system/frmcs/ (accessed on 18 January 2023).
- Liu, Y.; Liu, R.; Wei, C.; Xun, J.; Tang, T. Distributed model predictive control strategy for constrained high-speed virtually coupled train set. IEEE Trans. Veh. Technol. 2021, 71, 171–183. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Y.; Su, S.; Xun, J.; Tang, T. Control strategy for stable formation of high-speed virtually coupled trains with disturbances and delays. Comput. Civ. Infrastruct. Eng. 2022, 38. [Google Scholar] [CrossRef]
- Zhao, H.; Dai, X.; Zhang, Q.; Ding, J. Robust event-triggered model predictive control for multiple high-speed trains with switching topologies. IEEE Trans. Veh. Technol. 2020, 69, 4700–4710. [Google Scholar] [CrossRef]
- Luo, X.; Tang, T.; Liu, H.; Zhang, L.; Li, K. An adaptive model predictive control system for virtual coupling in metros. Actuators 2021, 10, 178. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, C.; Tang, T. A virtually coupled metro train platoon control approach based on model predictive control. IEEE Access 2021, 9, 56354–56363. [Google Scholar] [CrossRef]
- Chai, S.; Yin, J.; D’ariano, A.; Samà, M.; Tang, T. Scheduling of coupled train platoons for metro networks: A passenger demand-oriented approach. Transp. Res. Rec. J. Transp. Res. Board 2022, 2677, 1671–1689. [Google Scholar] [CrossRef]
- Felez, J.; Vaquero-Serrano, M.A.; Sanz, J.D.D. A robust model predictive control for virtual coupling in train sets. Actuators 2022, 11, 372. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, C.; Bao, F.; Zhang, L.; Xiao, X. The safety braking protection model of virtually coupled train platoon in subway. In Proceedings of the 2020 10th Institute of Electrical and Electronics Engineers International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER), Xi’an, China, 10–14 October 2020; IEEE: Piscataway Township, NJ, USA, 2020; pp. 401–406. [Google Scholar] [CrossRef]
- Borges, R.M.; Quaglietta, E. Assessing hyperloop transport capacity under moving-block and virtual coupling operations. IEEE Trans. Intell. Transp. Syst. 2021, 23, 12612–12621. [Google Scholar] [CrossRef]
- Su, S.; She, J.; Li, K.; Wang, X.; Zhou, Y. A nonlinear safety equilibrium spacing-based model predictive control for virtually coupled train set over gradient terrains. IEEE Trans. Transp. Electrification 2021, 8, 2810–2824. [Google Scholar] [CrossRef]
- Guanetti, J.; Kim, Y.; Borrelli, F. Control of connected and automated vehicles: State of the art and future challenges. Annu. Rev. Control 2018, 45, 18–40. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, S.E.; Li, K.; Borrelli, F.; Hedrick, J.K. Distributed model predictive control for heterogeneous vehicle platoons under unidirectional topologies. IEEE Trans. Control Syst. Technol. 2016, 25, 899–910. [Google Scholar] [CrossRef]
- Turri, V.; Kim, Y.; Guanetti, J.; Johansson, K.H.; Borrelli, F. A model predictive controller for non-cooperative eco-platooning. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; IEEE: Piscataway Township, NJ, USA; pp. 2309–2314. [Google Scholar] [CrossRef]
- Brackstone, M.; McDonald, M. Car-following: A historical review. Transp. Res. Part F Traffic Psychol. Behav. 1999, 2, 181–196. [Google Scholar] [CrossRef]
- Turri, V.; Besselink, B.; Johansson, K.H. Cooperative look-ahead control for fuel-efficient and safe heavy-duty vehicle platooning. IEEE Trans. Control Syst. Technol. 2016, 25, 12–28. [Google Scholar] [CrossRef]
- Li, S.E.; Zheng, Y.; Li, K.; Wang, J. An overview of vehicular platoon control under the four-component framework. IEEE Intell. Veh. Symp. 2015, 286–291. [Google Scholar] [CrossRef]
- Feng, S.; Zhang, Y.; Li, S.E.; Cao, Z.; Liu, H.X.; Li, L. String stability for vehicular platoon control: Definitions and analysis methods. Annu. Rev. Control 2019, 47, 81–97. [Google Scholar] [CrossRef]
- Wang, M.; Daamen, W.; Hoogendoorn, S.P.; van Arem, B. Rolling horizon control framework for driver assistance systems. Part I: Mathematical formulation and non-cooperative systems. Transp. Res. Part C Emerg. Technol. 2014, 40, 271–289. [Google Scholar] [CrossRef]
- Wang, M.; Daamen, W.; Hoogendoorn, S.P.; van Arem, B. Rolling horizon control framework for driver assistance systems. Part II: Cooperative sensing and cooperative control. Transp. Res. Part C Emerg. Technol. 2014, 40, 290–311. [Google Scholar] [CrossRef]
- Yang, Y.; Yan, F. Research on train dynamic coupling strategy based on distributed model predictive control. J. Physics Conf. Ser. 2022, 2183, 12029. [Google Scholar] [CrossRef]
- Bai, W.; Dong, H.; Lu, J.; Li, Y. Event-triggering communication based distributed coordinated control of multiple high-speed trains. IEEE Trans. Veh. Technol. 2021, 70, 8556–8566. [Google Scholar] [CrossRef]
- Chu, K.-C. Decentralized control of high-speed vehicular strings. Transp. Sci. 1974, 8, 361–384. [Google Scholar] [CrossRef]
- Wu, Q.; Spiryagin, M.; Cole, C. Longitudinal train dynamics: An overview. Veh. Syst. Dyn. 2016, 54, 1688–1714. [Google Scholar] [CrossRef]
- Niu, J.; Sui, Y.; Yu, Q.; Cao, X.; Yuan, Y. Aerodynamics of railway train/tunnel system: A review of recent research. Energy Built Environ. 2020, 1, 351–375. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, T.; Hemida, H.; Chen, Z.; Liu, H. Numerical simulation of the aerodynamic characteristics of double unit train. Eng. Appl. Comput. Fluid Mech. 2020, 14, 910–922. [Google Scholar] [CrossRef]
- Gillani, S.A.; Panikulam, V.P.; Sadasivan, S.; Yaoping, Z. CFD analysis of aerodynamic drag effects on vacuum tube trains. J. Appl. Fluid Mech. 2019, 12, 303–309. [Google Scholar] [CrossRef]
- Carrarini, A. Coupled multibody-aerodynamic simulation of high-speed trains manoeuvres. Pamm 2003, 2, 114–115. [Google Scholar] [CrossRef]
- Niu, J.-Q.; Zhou, D.; Liu, T.-H.; Liang, X.-F. Numerical simulation of aerodynamic performance of a couple multiple units high-speed train. Veh. Syst. Dyn. 2017, 55, 681–703. [Google Scholar] [CrossRef]
- Huo, X.; Liu, T.; Chen, Z.; Li, W.; Gao, H.; Wang, S. Comparative analysis of the aerodynamic characteristics on double-unit trains formed by different types of high-speed train. J. Wind. Eng. Ind. Aerodyn. 2021, 217, 104757. [Google Scholar] [CrossRef]
- Guo, Z.-J.; Liu, T.-H.; Chen, Z.-W.; Xie, T.-Z.; Jiang, Z.-H. Comparative numerical analysis of the slipstream caused by single and double unit trains. J. Wind. Eng. Ind. Aerodyn. 2018, 172, 395–408. [Google Scholar] [CrossRef]
- Watkins, S.; Vino, G. The effect of vehicle spacing on the aerodynamics of a representative car shape. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1232–1239. [Google Scholar] [CrossRef]
- Wilhelmi, H.; Thieme, T.; Henning, A.; Wagner, C. Aerodynamic investigations of the effects of virtual coupling on two next generation trains. In New Results in Numerical and Experimental Fluid Mechanics XI; Springer: Cham, Switzerland, 2017; pp. 695–704. [Google Scholar] [CrossRef]
- Fadhel, S.; Fromont, S. Quantification of the aerodynamic gain on two virtually coupled modular trains. Int. J. Comput. Methods Exp. Meas. 2022, 10, 372–384. [Google Scholar] [CrossRef]
- Wu, Q.; Ge, X.; Han, Q.-L.; Wang, B.; Wu, H.; Cole, C.; Spiryagin, M. Dynamics and control simulation of railway virtual coupling. Veh. Syst. Dyn. 2022, 1–25. [Google Scholar] [CrossRef]
- Wu, Q.; Ge, X.; Cole, C.; Spiryagin, M. Car and train platoon simulations. J. Vib. Control 2022, 107754632211401. [Google Scholar] [CrossRef]
- Wu, Q.; Ge, X.; Cole, C.; Spiryagin, M. A Method for High Fidelity Simulations of Railway Virtual Coupling. In Proceedings of the 2022 Joint Rail Conference, Virtual, Online, 20–21 April 2022. [Google Scholar] [CrossRef]
- Soto, M.G.; Adeli, H. Recent advances in control algorithms for smart structures and machines. Expert Syst. 2017, 34, e12205. [Google Scholar] [CrossRef]
- Yin, J.; Tang, T.; Yang, L.; Xun, J.; Huang, Y.; Gao, Z. Research and development of automatic train operation for railway transportation systems: A survey. Transp. Res. Part C Emerg. Technol. 2017, 85, 548–572. [Google Scholar] [CrossRef]
- Xun, J.; Li, Y.; Liu, R.; Li, Y.; Liu, Y. A survey on control methods for virtual coupling in railway operation. IEEE Open J. Intell. Transp. Syst. 2022, 3, 838–855. [Google Scholar] [CrossRef]
- Wu, Q.; Ge, X.; Han, Q.-L.; Liu, Y. Railway virtual coupling: A survey of emerging control techniques. IEEE Trans. Intell. Veh. 2023, 1–17. [Google Scholar] [CrossRef]
- Ahmed, H.U.; Huang, Y.; Lu, P. A review of car-following models and modeling tools for human and autonomous-ready driving behaviors in micro-simulation. Smart Cities 2021, 4, 314–335. [Google Scholar] [CrossRef]
- Saidi, S.; Koutsopoulos, H.N.; Wilson, N.H.; Zhao, J. Train following model for urban rail transit performance analysis. Transp. Res. Part C Emerg. Technol. 2023, 148, 104037. [Google Scholar] [CrossRef]
- Qianqian, Z.; Hongwei, W. A Multi-train cooperative control method of urban railway transportation based on artificial potential field. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; 2019; pp. 1350–1355. [Google Scholar] [CrossRef]
- Cao, Y.; Wen, J.; Hobiny, A.; Li, P.; Wen, T. Parameter-varying artificial potential field control of virtual coupling system with nonlinear dynamics. Fractals 2022, 30, 990. [Google Scholar] [CrossRef]
- Pan, J.; Peng, Q.; Zhan, S.; Bai, J. Multiscenario-based train headway analysis under virtual coupling system. J. Adv. Transp. 2021, 2021, 5642709. [Google Scholar] [CrossRef]
- Su, S.; She, J.; Wang, D.; Gong, S.; Zhou, Y. A stabilized virtual coupling scheme for a train set with heterogeneous braking dynamics capability. Transp. Res. Part C Emerg. Technol. 2023, 146, 103947. [Google Scholar] [CrossRef]
- Szkopiński, J.; Kochan, A. Maximization of energy efficiency by synchronizing the speed of trains on a moving block system. Energies 2023, 16, 1764. [Google Scholar] [CrossRef]
- Cao, Y.; Yang, Y.; Ma, L.; Wen, J. Research on virtual coupled train control method based on GPC & VAPF. Chin. J. Electron. 2022, 31, 897–905. [Google Scholar] [CrossRef]
- Flammini, F.; Marrone, S.; Nardone, R.; Vittorini, V. Compositional modeling of railway Virtual Coupling with Stochastic Activity Networks. Form. Asp. Comput. 2021, 33, 989–1007. [Google Scholar] [CrossRef]
- Havaei, P.; Sandidzadeh, M.A. Intelligent-PID controller design for speed track in automatic train operation system with heuristic algorithms. J. Rail Transp. Plan. Manag. 2022, 22, 100321. [Google Scholar] [CrossRef]
- Pickering, J.E.; Davies, J.; Burnham, K.J. Development of model prototype to investigate closer running autonomous train operation: Seamless interchangeability. In Proceedings of the 2019 23rd International Conference on System Theory, Control and Computing (ICSTCC), Sinaia, Romania, 9–11 October 2019; pp. 572–579. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Li, K.; Gao, Z. Robust sampled-data cruise control scheduling of high speed train. Transp. Res. Part C Emerg. Technol. 2014, 46, 274–283. [Google Scholar] [CrossRef]
- Wang, B.; Yang, D.; Zhang, X.; Jia, X. Constraint-force driven control design for rail vehicle virtual coupling. J. Vib. Control 2021, 28, 551–563. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, D.; Zhang, W.; Huang, J. Optimal robust constraints-following control for rail vehicle virtual coupling. J. Vib. Control 2022, 29, 1352–1365. [Google Scholar] [CrossRef]
- Qiu, C.; Chen, T.; Lu, S.; Wang, H. A safety-oriented dynamic moving block train control system based on train-to-train communication. IEEE Intell. Transp. Syst. Mag. 2021, 14, 175–187. [Google Scholar] [CrossRef]
- Gulzar, M.M.; Rizvi, S.T.H.; Javed, M.Y.; Munir, U.; Asif, H. Multi-agent cooperative control consensus: A comparative review. Electronics 2018, 7, 22. [Google Scholar] [CrossRef]
- Liu, L.; Wang, P.; Zhang, B.; Wei, W. Coordinated Control Method of Virtually Coupled Train Formation Based on Multi Agent System. In Advances in Smart Vehicular Technology, Transportation, Communication and Applications; VTCA 2018. Smart Innovation, Systems and Technologies; Ni, S., Wu, T.Y., Chang, T.H., Pan, J.S., Jain, L., Eds.; Springer: Cham, Switzerland, 2019; Volume 129. [Google Scholar] [CrossRef]
- Liu, L.; Wang, P.; Wei, W.; Li, Q.; Zhang, B. Intelligent dispatching and coordinated control method at railway stations for virtually coupled train sets. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, L.; Liu, J.; Shi, J. Carrying capacity calculation method of regional rail transit line based on flexible train formation. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Muniandi, G. Blockchain-enabled virtual coupling of automatic train operation fitted mainline trains for railway traffic conflict control. IET Intell. Transp. Syst. 2020, 14, 611–619. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, H.; Wang, H.; Wang, X.; Dong, H. Cooperative multi-scenario departure control for virtual coupling trains: A fixed-time approach. IEEE Trans. Veh. Technol. 2021, 70, 8545–8555. [Google Scholar] [CrossRef]
- Zhang, J. Simulation-based schedule optimization for virtual coupling-enabled rail transit services with multiagent technique. J. Adv. Transp. 2023, 2023, 1–21. [Google Scholar] [CrossRef]
- He, R.; Zhang, Y. Safe distance model and improved consensus control algorithm for virtual coupling of high-speed train. In Proceedings of the Sixth International Conference on Traffic Engineering and Transportation System (ICTETS 2022), Guangzhou, China, 2 February 2023. [Google Scholar] [CrossRef]
- Sun, N.; Zhang, Y. A distributed adaptive cruise control method for virtually coupled train formation. In Proceedings of the Sixth International Conference on Traffic Engineering and Transportation System (ICTETS 2022), Guangzhou, China, 2 February 2023; Zhou, J., Sheng, J., Eds.; SPIE: Bellingham, WA, USA, 2023; p. 87. [Google Scholar] [CrossRef]
- Bauso, D.; Fecarotti, C.; Khaleghi, A. Cooperative control and stability analysis for virtual coupling of rail vehicles. Control Eng. Pract. 2023, 133, 105452. [Google Scholar] [CrossRef]
- Gambhire, S.J.; Kishore, D.R.; Londhe, P.S.; Pawar, S.N. Review of sliding mode based control techniques for control system applications. Int. J. Dyn. Control 2020, 9, 363–378. [Google Scholar] [CrossRef]
- Wang, D.; Cao, Y. Adaptive Finite-Time Sliding Mode Control of Virtually Coupled Train Set with State Constraints. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 1778–1783. [Google Scholar] [CrossRef]
- Park, J.; Lee, B.-H.; Eun, Y. Virtual coupling of railway vehicles: Gap reference for merge and separation, robust control, and position measurement. IEEE Trans. Intell. Transp. Syst. 2020, 23, 1085–1096. [Google Scholar] [CrossRef]
- Liu, Y.; Ou, D.; Yang, Y.; Dong, D. A method for maintaining virtually coupled states of train convoys. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 237, 243–252. [Google Scholar] [CrossRef]
- Lin, J.; Ni, M.; Liang, H. High-speed train cooperative control based on fractional-order sliding mode adaptive algorithm. Railw. Sci. 2023; ahead-of-print. [Google Scholar] [CrossRef]
- Cheng, F.; Su, S.; Tang, T.; Wang, W. Optimization of the coupling operation for train platoon in the junction area. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 2405–2410. [Google Scholar] [CrossRef]
- Chen, F.; Tang, T.; Su, S.; Meng, J. Optimization on the dynamic train coupling process in high-speed railway. Chin. J. Electron. 2023. Available online: https://cje.ejournal.org.cn/article/doi/10.23919/cje.2022.00.189 (accessed on 18 January 2023).
- Gallo, F.; Di Febbraro, A.; Giglio, D.; Sacco, N. Planning and optimization of passenger railway services with virtually coupled trains. In Proceedings of the 2021 7th International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Heraklion, Greece, 16–17 June 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Gallo, F.; Di Febbraro, A.; Giglio, D.; Sacco, N. A mathematical programming model for the management of carriages in virtually coupled trains. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Gallo, F.; Di Febbraro, A.; Giglio, D.; Sacco, N. Global Sensitivity Analysis for the evaluation of the effects of uncertainty of transport demand and passenger behavior on planning railway services with variable train composition. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 2298–2305. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, Y.; Zhu, W. Robust cooperative train trajectory optimization with stochastic delays under virtual coupling. IET Intell. Transp. Syst. 2023. [Google Scholar] [CrossRef]
- Tian, D.; Li, J.; Zhou, J.; Duan, X.; Sheng, Z.; Zhao, D.; Hao, W.; Long, K. A Linear Quadratic Gaussian Optimal Control Approach for Train Platoon Formation. In Proceedings of the 2021 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 15–17 October 2021; pp. 116–121. [Google Scholar] [CrossRef]
- Wang, Q.; Chai, M.; Liu, H.; Tang, T. Optimized control of virtual coupling at junctions: A cooperative game-based approach. Actuators 2021, 10, 207. [Google Scholar] [CrossRef]
- Wang, Q.; Chai, M.; Wang, H.; Chen, L.; Lv, J. Train operation strategy optimization of virtual coupling: A cooperative game based approach. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 3933–3938. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, Y. Research on virtual coupling railway safety protection based on track prediction. In Proceedings of the Sixth International Conference on Traffic Engineering and Transportation System (ICTETS 2022), Guangzhou, China, 23–25 September 2022; Zhou, J., Sheng, J., Eds.; SPIE: Bellingham, WA, USA, 2023; p. 5. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; James, P.; Roggenbach, M.; Tian, D. A train protection logic based on topological manifolds for virtual coupling. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11930–11945. [Google Scholar] [CrossRef]
- Wu, Q.; Li, Y.; Dan, P. Optimization of urban rail transit station spacing for minimizing passenger travel time. J. Rail Transp. Plan. Manag. 2022, 22, 100317. [Google Scholar] [CrossRef]
- Borrelli, F.; Bemporad, A.; Morari, M. Predictive Control for Linear and Hybrid Systems, 1st ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Mayne, D.Q.; Rawlings, J.B.; Rao, C.V.; Scokaert, P.O.M. Constrained model predictive control: Stability and optimality. Automatica 2000, 36, 789–814. [Google Scholar] [CrossRef]
- Lan, J.; Zhao, D. Min-max model predictive vehicle platooning with communication delay. IEEE Trans. Veh. Technol. 2020, 69, 12570–12584. [Google Scholar] [CrossRef]
- Cavone, G.; van den Boom, T.; Blenkers, L.; Dotoli, M.; Seatzu, C.; De Schutter, B. An MPC-based rescheduling algorithm for disruptions and disturbances in large-scale railway networks. IEEE Trans. Autom. Sci. Eng. 2020, 19, 99–112. [Google Scholar] [CrossRef]
- Tong, Y.; Xu, W.; Dotoli, M.; Cavone, G. An integrated model predictive control method for the rescheduling of metro traffic with backup trains. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; IEEE: Piscataway Township, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Yang, Y.; Ou, D.; Liu, Y.; Dong, D. Transition Control of Virtual Coupling Train Formation Based on Model Predictive Control. In Proceedings of the 5th International Conference on Electrical Engineering and Information Technologies for Rail Transportation (EITRT) 2021; EITRT 2021. Lecture Notes in Electrical Engineering; Qin, Y., Jia, L., Liang, J., Liu, Z., Diao, L., An, M., Eds.; Springer: Singapore, 2022; Volume 868. [Google Scholar] [CrossRef]
- Su, H.; Chai, M.; Chen, L.; Lv, J. Deep learning-based model predictive control for virtual coupling railways operation. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 3490–3495. [Google Scholar] [CrossRef]
- She, J.; Li, K.; Yuan, L.; Zhou, Y.; Su, S. Cruising control approach for virtually coupled train set based on model predictive control. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, M.; Xun, J.; Liu, Y. A coordinated collision mitigation approach for virtual coupling trains by using model predictive control. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Chai, M.; Su, H.; Liu, H. Long short-term memory-based model predictive control for virtual coupling in railways. Wirel. Commun. Mob. Comput. 2022, 2022, 1859709. [Google Scholar] [CrossRef]
- Luo, X.; Liu, H.; Zhang, L.; Xun, J. A model predictive control based inter-station driving strategy for virtual coupling trains in railway system. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 3927–3932. [Google Scholar] [CrossRef]
- Xun, J.; Yin, J.; Liu, R.; Liu, F.; Zhou, Y.; Tang, T. Cooperative control of high-speed trains for headway regulation: A self-triggered model predictive control based approach. Transp. Res. Part C Emerg. Technol. 2019, 102, 106–120. [Google Scholar] [CrossRef]
- Milenković, M.S.; Bojović, N.J.; Švadlenka, L.; Melichar, V. A stochastic model predictive control to heterogeneous rail freight car fleet sizing problem. Transp. Res. Part E Logist. Transp. Rev. 2015, 82, 162–198. [Google Scholar] [CrossRef]
- Bemporad, A.; Morari, M. Robust model predictive control: A survey. In Robustness in identification and control; Springer: London, UK, 1999; pp. 207–226. [Google Scholar] [CrossRef]
- Zeilinger, M.N.; Raimondo, D.M.; Domahidi, A.; Morari, M.; Jones, C.N. On real-time robust model predictive control. Automatica 2014, 50, 683–694. [Google Scholar] [CrossRef]
- Löfberg, J. Automatic robust convex programming. Optim. Methods Softw. 2012, 27, 115–129. [Google Scholar] [CrossRef]
- Lorenzen, M.; Cannon, M.; Allgöwer, F. Robust MPC with recursive model update. Automatica 2019, 103, 461–471. [Google Scholar] [CrossRef]
- Li, G.; Zou, J.; Ma, W.; Lan, M. Research on virtual coupling technology in rail transit train collision protection. Transp. Saf. Environ. 2023. [Google Scholar] [CrossRef]
- Xun, J.; Chen, M.; Liu, Y.; Liu, F. An overspeed protection mechanism for virtual coupling in railway. IEEE Access 2020, 8, 187400–187410. [Google Scholar] [CrossRef]
- Liu, W.; Shangguan, W.; Song, H.; Pan, J. A virtual coupling operation strategy based on state transition considering special case. In Proceedings of the 2022 China Automation Congress (CAC), Xiamen, China, 25–27 November 2022; IEEE: Piscataway Township, NJ, USA, 2022; pp. 5772–5777. [Google Scholar] [CrossRef]
- Lucia, S.; Engell, S. Potential and limitations of multi-stage nonlinear model predictive control. IFAC-PapersOnLine 2015, 48, 1015–1020. [Google Scholar] [CrossRef]
- Richards, A.; How, J. Robust stable model predictive control with constraint tightening. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; IEEE: Piscataway Township, NJ, USA, 2006; p. 6. [Google Scholar] [CrossRef]
- Subramanian, S.; Abdelsalam, Y.; Lucia, S.; Engell, S. Robust tube-enhanced multi-stage NMPC with stability guarantees. IEEE Control Syst. Lett. 2021, 6, 1112–1117. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Shan, J.; Lanzon, A.; Petersen, I.R. Robust cooperative control of networked train platoons: A negative-imaginary systems’ perspective. IEEE Trans. Control Netw. Syst. 2021, 8, 1743–1753. [Google Scholar] [CrossRef]
- Heirung, T.A.N.; Paulson, J.A.; O’leary, J.; Mesbah, A. Stochastic model predictive control—How does it work? Comput. Chem. Eng. 2018, 114, 158–170. [Google Scholar] [CrossRef]
- Brüdigam, T.; Jacumet, R.; Wollherr, D.; Leibold, M. Safe stochastic model predictive control. In Proceedings of the IEEE 2022 Conference on Decision and Contro, Cancún, Mexico, 6–9 December 2022. [Google Scholar]
- Mesbah, A. Stochastic model predictive control with active uncertainty learning: A Survey on dual control. Annu. Rev. Control 2018, 45, 107–117. [Google Scholar] [CrossRef]
- Shen, X.; Boyd, S. Incremental proximal multi-forecast model predictive control. arXiv 2021. [Google Scholar] [CrossRef]
- Ma, Y.; Li, C.; Wang, S. Multi-objective energy management strategy for fuel cell hybrid electric vehicle based on stochastic model predictive control. ISA Trans. 2022, 131, 178–196. [Google Scholar] [CrossRef]
- Tang, H.; Wang, Q.; Feng, X. Robust stochastic control for high-speed trains with nonlinearity, parametric uncertainty, and multiple time-varying delays. IEEE Trans. Intell. Transp. Syst. 2017, 19, 1027–1037. [Google Scholar] [CrossRef]
- Song, H.; Shen, T.; Wang, W. Train-centric communication-based close proximity driving train movement authority system. IEEE Intell. Transp. Syst. Mag. 2018, 10, 22–34. [Google Scholar] [CrossRef]
- Bujarbaruah, M.; Zhang, X.; Rosolia, U.; Borrelli, F. Adaptive MPC for iterative tasks. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2022; IEEE: Piscataway Township, NJ, USA, 2018; pp. 6322–6327. [Google Scholar] [CrossRef]
- Rosolia, U.; Borrelli, F. Learning model predictive control for iterative tasks: A computationally efficient approach for linear system. IFAC-PapersOnLine 2017, 50, 3142–3147. [Google Scholar] [CrossRef]
- Zhu, E.L.; Sturz, Y.R.; Rosolia, U.; Borrelli, F. Trajectory optimization for nonlinear multi-agent systems using decentralized learning model predictive control. In Proceedings of the 2020 59th IEEE Conference on Decision and Control (CDC), Jeju, South Korea, 14–18 December 2020; IEEE: Piscataway Township, NJ, USA, 2020; pp. 6198–6203. [Google Scholar] [CrossRef]
- Scianca, N.; Rosolia, U.; Borrelli, F. Learning Model Predictive Control for Periodic Repetitive Tasks. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; IEEE: Piscataway Township, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Rosolia, U.; Borrelli, F. Learning model predictive control for iterative tasks. A data-driven control framework. IEEE Trans. Autom. Control 2017, 63, 1883–1896. [Google Scholar] [CrossRef]
- Rosolia, U.; Zhang, X.; Borrelli, F. A Stochastic MPC approach with application to iterative learning. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; IEEE: Piscataway Township, NJ, USA, 2018; pp. 5152–5157. [Google Scholar] [CrossRef]
- Rosolia, U.; Zhang, X.; Borrelli, F. Data-driven predictive control for autonomous systems. Annu. Rev. Control Robot. Auton. Syst. 2018, 1, 259–286. [Google Scholar] [CrossRef]
- Rosolia, U.; Borrelli, F. Minimum time learning model predictive control. Int. J. Robust Nonlinear Control 2020, 31, 8830–8854. [Google Scholar] [CrossRef]
- Rosolia, U.; Zhang, X.; Borrelli, F. Robust learning model-predictive control for linear systems performing iterative tasks. IEEE Trans. Autom. Control 2021, 67, 856–869. [Google Scholar] [CrossRef]
- Zhang, K.; Shi, Y. Adaptive model predictive control for a class of constrained linear systems with parametric uncertainties. Automatica 2020, 117, 108974. [Google Scholar] [CrossRef]
- Bujarbaruah, M.; Zhang, X.; Tanaskovic, M.; Borrelli, F. Adaptive stochastic MPC under time-varying uncertainty. IEEE Trans. Autom. Control 2020, 66, 2840–2845. [Google Scholar] [CrossRef]
- Wang, X.; Huang, D.; Xing, H. A Train cooperative operation optimization method based on improved reinforcement learning algorithm. In Proceedings of the 4th International Conference on Industrial Artificial Intelligence (IAI), Shenyang, China, 24–27 August 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Y.; Huang, D.; Zhu, L.; Lu, Z.; He, Y. A train cooperative operation optimization method considering passenger comfort based on reinforcement learning. In Proceedings of the 2022 IEEE 11th Data Driven Control and Learning Systems Conference (DDCLS), Chengdu, China, 3–5 August 2022; pp. 368–373. [Google Scholar] [CrossRef]
- Liu, H.; Yang, L.; Yang, H. Cooperative optimal control of the following operation of high-speed trains. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17744–17755. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Q.; Lin, S.; Cui, D.; Luo, C.; Zhu, L.; Wang, X.; Tang, T. A reinforcement learning empowered cooperative control approach for IIoT-based virtually coupled train sets. IEEE Trans. Ind. Informatics 2020, 17, 4935–4945. [Google Scholar] [CrossRef]
- Jia, Y.; Huang, D.; Li, X. Tracking control of two virtually coupled trains via prescribed performance control method. In Proceedings of the 2022 IEEE 11th Data Driven Control and Learning Systems Conference (DDCLS), Chengdu, China, 3–5 August 2022; pp. 268–273. [Google Scholar] [CrossRef]
- Du, Z.; Wu, H.; Yang, Z.; Wen, X. Research on intelligent formation operation performance of straddle-type rapid transit vehicles in heterogeneous operating environment. Mechanika 2023, 29, 59–66. [Google Scholar] [CrossRef]
- Yong, Z.; Sirui, Z. Typical train virtual coupling scenario modeling and analysis of train control system based on vehicle-vehicle communication. In Proceedings of the 2020 IEEE 6th International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 July 2020; pp. 143–148. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, F.; Wang, L. Optimization of train operation planning with full-length and short-turn routes of virtual coupling trains. Appl. Sci. 2022, 12, 7935. [Google Scholar] [CrossRef]
- Hao, A.Z.; Yan, B.F.; Niu, C.R. A Key Step to Virtual Coupling. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Su, S.; Liu, W.; Zhu, Q.; Li, R.; Tang, T.; Lv, J. A cooperative collision-avoidance control methodology for virtual coupling trains. Accid. Anal. Prev. 2022, 173, 106703. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Wang, H.; Li, Z.; Zhang, Q. A novel approach for estimating performance of IIoT-based virtual control train sets under DoS attacks. Secur. Commun. Networks 2022, 2022, 1781757. [Google Scholar] [CrossRef]
- Basile, G.; Lui, D.G.; Petrillo, A.; Santini, S. Deep deterministic policy gradient-based virtual coupling control for high-speed train convoys. In Proceedings of the 2022 IEEE International Conference on Networking, Sensing and Control (ICNSC), Shanghai, China, 15–18 December 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Ludicke, D.; Lehner, A. Train communication networks and prospects. IEEE Commun. Mag. 2019, 57, 39–43. [Google Scholar] [CrossRef]
- Moreno, J.; Riera, J.M.; de Haro, L.; Rodriguez, C. A survey on future railway radio communications services: Challenges and opportunities. IEEE Commun. Mag. 2015, 53, 62–68. [Google Scholar] [CrossRef]
- Hu, J.; Liu, G.; Li, Y.; Ma, Z.; Wang, W.; Liang, C.; Yu, F.R.; Fan, P. Off-network communications for future railway mobile communication systems: Challenges and opportunities. IEEE Commun. Mag. 2022, 60, 64–70. [Google Scholar] [CrossRef]
- Unterhuber, P.; Pfletschinger, S.; Sand, S.; Soliman, M.; Jost, T.; Arriola, A.; Val, I.; Cruces, C.; Moreno, J.; García-Nieto, J.P.; et al. A survey of channel measurements and models for current and future railway communication systems. Mob. Inf. Syst. 2016, 2016, 1–14. [Google Scholar] [CrossRef]
- Unterhuber, P.; Lehner, A.; Müller, F.D.P. Measurement and analysis of ITS-G5 in railway environments. In Communication Technologies for Vehicles; Springer: Cham, Switzerland, 2016; Volume 9669, pp. 62–73. [Google Scholar] [CrossRef]
- Gomez, A.A.; Mozo, E.; Bernado, L.; Zelenbaba, S.; Zemen, T.; Parrilla, F.; Alberdi, A. Performance analysis of ITS-G5 for smart train composition coupling. In Proceedings of the 2018 16th International Conference on Intelligent Transportation Systems Telecommunications (ITST); 2018; pp. 1–7. [Google Scholar] [CrossRef]
- Le, H.Q.; Lehner, A.; Sand, S. Performance analysis of ITS-G5 for dynamic train coupling application. In Communication Technologies for Vehicles; Springer: Cham, Switzerland, 2015; pp. 129–140. [Google Scholar] [CrossRef]
- Yang, K.; Berbineau, M.; Ghys, J.-P.; Cocheril, Y.; Seetharamdoo, D. Propagation measurements with regional train at 60 GHz for virtual coupling application. In Proceedings of the 2017 11th European Conference on Antennas and Propagation (EUCAP), Paris, France, 19–24 March 2017. [Google Scholar] [CrossRef]
- Unterhuber, P.; Sand, S.; Fiebig, U.; Siebler, B. Path loss models for train-to-train communications in typical high speed railway environments. IET Microw. Antennas Propag. 2018, 12, 492–500. [Google Scholar] [CrossRef]
- Zeller, P.; Siebler, B.; Lehner, A.; Sand, S. Relative train localization for cooperative maneuvers using GNSS pseudoranges and geometric track information. In Proceedings of the 2015 International Conference on Location and GNSS (ICL-GNSS), Gothenburg, Sweden, 22–24 June 2015; IEEE: Piscataway Township, NJ, USA, 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Lichtblau, J.; Scheiner, B.; Michler, F.; Graebner, M.; Sanftl, B.; Weigel, R.; Koelpin, A. Novel approach for virtual coupling of trains using different modulation and coding schemes. In Proceedings of the 2018 International Conference on Intelligent Rail Transportation (ICIRT), Singapore, 12–14 December 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Parise, R.; Dittus, H.; Winter, J.; Lehner, A. Reasoning functional requirements for virtually coupled train sets: Communication. IEEE Commun. Mag. 2019, 57, 12–17. [Google Scholar] [CrossRef]
- Trzuskowsky, A.; Wehr, M.; Abel, D. Virtual coupling: A cooperative and collaborative autonomous navigation application. In Proceedings of the 29th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016; pp. 1096–1102. [Google Scholar] [CrossRef]
- Song, H.; Schnieder, E. Development and evaluation procedure of the train-centric communication-based system. IEEE Trans. Veh. Technol. 2018, 68, 2035–2043. [Google Scholar] [CrossRef]
- Song, H.; Wu, W.; Dong, H.; Schnieder, E. Propagation and safety analysis of the train-to-train communication system. IET Microw. Antennas Propag. 2019, 13, 2324–2329. [Google Scholar] [CrossRef]
- Verma, S.; Ghazel, M.; Berbineau, M. Model-based dependability evaluation of a Wireless Communication System in a Virtually Coupled Train Set. IFAC-PapersOnLine 2021, 54, 179–186. [Google Scholar] [CrossRef]
- Ma, S.; Bu, B.; Wang, H. A virtual coupling approach based on event-triggering control for CBTC systems under jamming attacks. In Proceedings of the 2020 IEEE 92nd Vehicular Technology Conference (VTC2020-Fall), Victoria, BC, Canada, 18 November–16 December 2020; pp. 1–6. [Google Scholar]
- Kadkhodayi, F.; Mohammad-Ali-Nezhad, S.; Ghasemi, R. A wideband beam shaping reflector antenna using model predictive control. Int. J. RF Microw. Comput. Eng. 2020, 30, e22220. [Google Scholar] [CrossRef]
- Mujica, G.; Henche, J.; Portilla, J. Internet of Things in the railway domain: Edge sensing system based on solid-state LIDAR and fuzzy clustering for virtual coupling. IEEE Access 2021, 9, 68093–68107. [Google Scholar] [CrossRef]
- Li, Z.; Adeli, H. Control methodologies for vibration control of smart civil and mechanical structures. Expert Syst. 2018, 35, e12354. [Google Scholar] [CrossRef]
- Soto, M.G.; Adeli, H. Multi-agent replicator controller for sustainable vibration control of smart structures. J. Vibroengineering 2017, 19, 4300–4322. [Google Scholar] [CrossRef]
- Hormozabad, S.J.; Soto, M.G.; Adeli, H. Integrating structural control, health monitoring, and energy harvesting for smart cities. Expert Syst. 2021, 38, e12845. [Google Scholar] [CrossRef]
- Kour, R.; Patwardhan, A.; Thaduri, A.; Karim, R. A review on cybersecurity in railways. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2022, 237, 3–20. [Google Scholar] [CrossRef]
- Tang, R.; De Donato, L.; Besinović, N.; Flammini, F.; Goverde, R.M.; Lin, Z.; Liu, R.; Tang, T.; Vittorini, V.; Wang, Z. A literature review of Artificial Intelligence applications in railway systems. Transp. Res. Part C: Emerg. Technol. 2022, 140, 103679. [Google Scholar] [CrossRef]
- Basile, G.; Napoletano, E.; Petrillo, A.; Santini, S. Roadmap and challenges for reinforcement learning control in railway virtual coupling. Discov. Artif. Intell. 2022, 2, 27. [Google Scholar] [CrossRef]






| Type of Rolling Stock | M (kg) | Length (m) | Power (kW) | A (N) | B (N/(m/s)) | C (N/(m/s)2) |
|---|---|---|---|---|---|---|
| LRV | 39,000 | 35 | 480 | 570 | 50 | 1.8 |
| Metro | 115,000 | 60 | 1500 | 1200 | 130 | 3.1 |
| Commuter | 170,000 | 85 | 2000 | 1400 | 164 | 4.2 |
| Main line | 240,000 | 160 | 4000 | 1800 | 65 | 4.9 |
| High speed | 360,000 | 200 | 7600 | 2700 | 100 | 7.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Felez, J.; Vaquero-Serrano, M.A. Virtual Coupling in Railways: A Comprehensive Review. Machines 2023, 11, 521. https://doi.org/10.3390/machines11050521
Felez J, Vaquero-Serrano MA. Virtual Coupling in Railways: A Comprehensive Review. Machines. 2023; 11(5):521. https://doi.org/10.3390/machines11050521
Chicago/Turabian StyleFelez, Jesus, and Miguel Angel Vaquero-Serrano. 2023. "Virtual Coupling in Railways: A Comprehensive Review" Machines 11, no. 5: 521. https://doi.org/10.3390/machines11050521
APA StyleFelez, J., & Vaquero-Serrano, M. A. (2023). Virtual Coupling in Railways: A Comprehensive Review. Machines, 11(5), 521. https://doi.org/10.3390/machines11050521







