Vibration Modeling and Analysis of a Flexible 3-PRR Planar Parallel Manipulator Based on Transfer Matrix Method for Multibody System
Abstract
1. Introduction
2. Introduction of the Linear MSTMM
State Vector, Transfer Matrix, and Transfer Equation
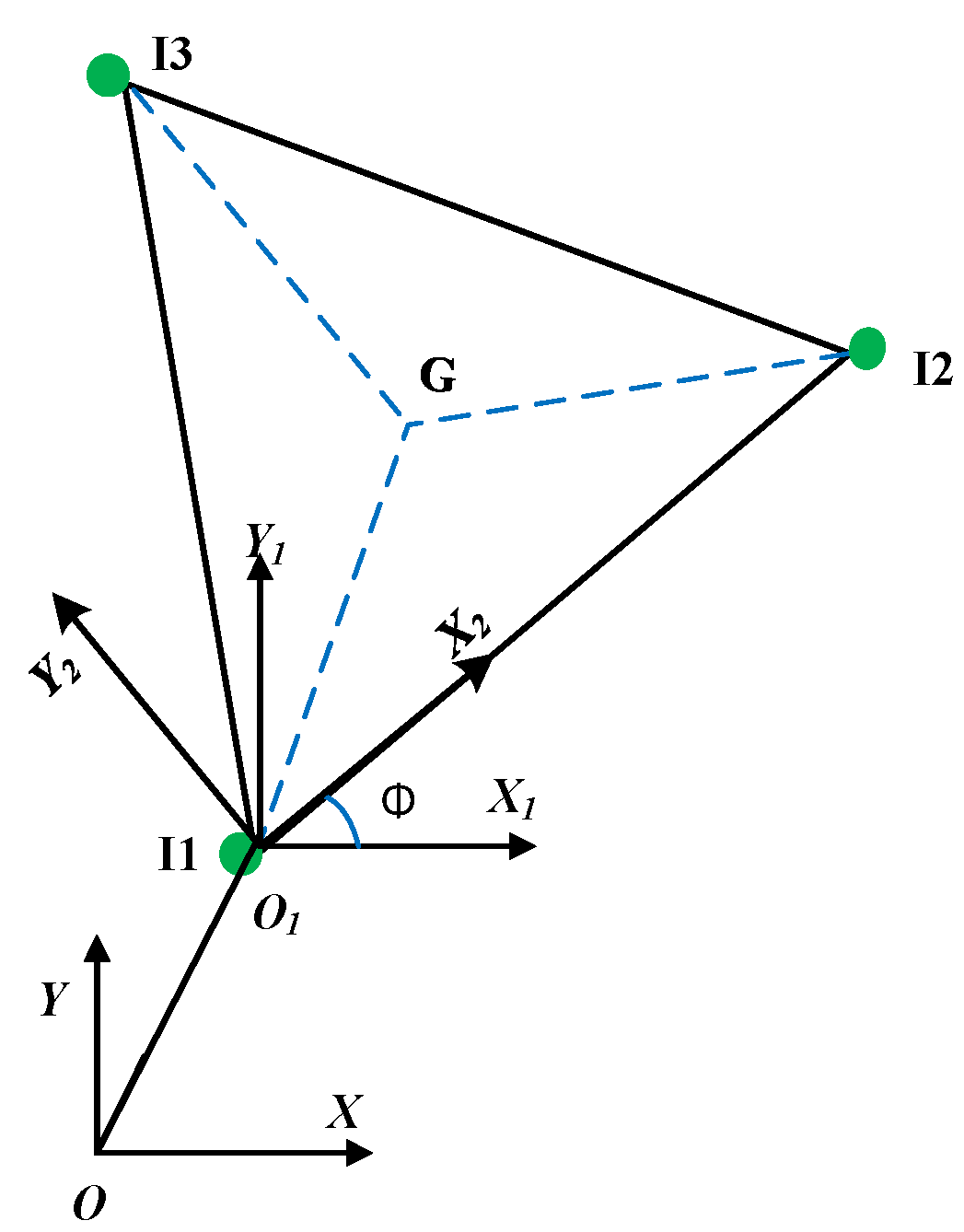
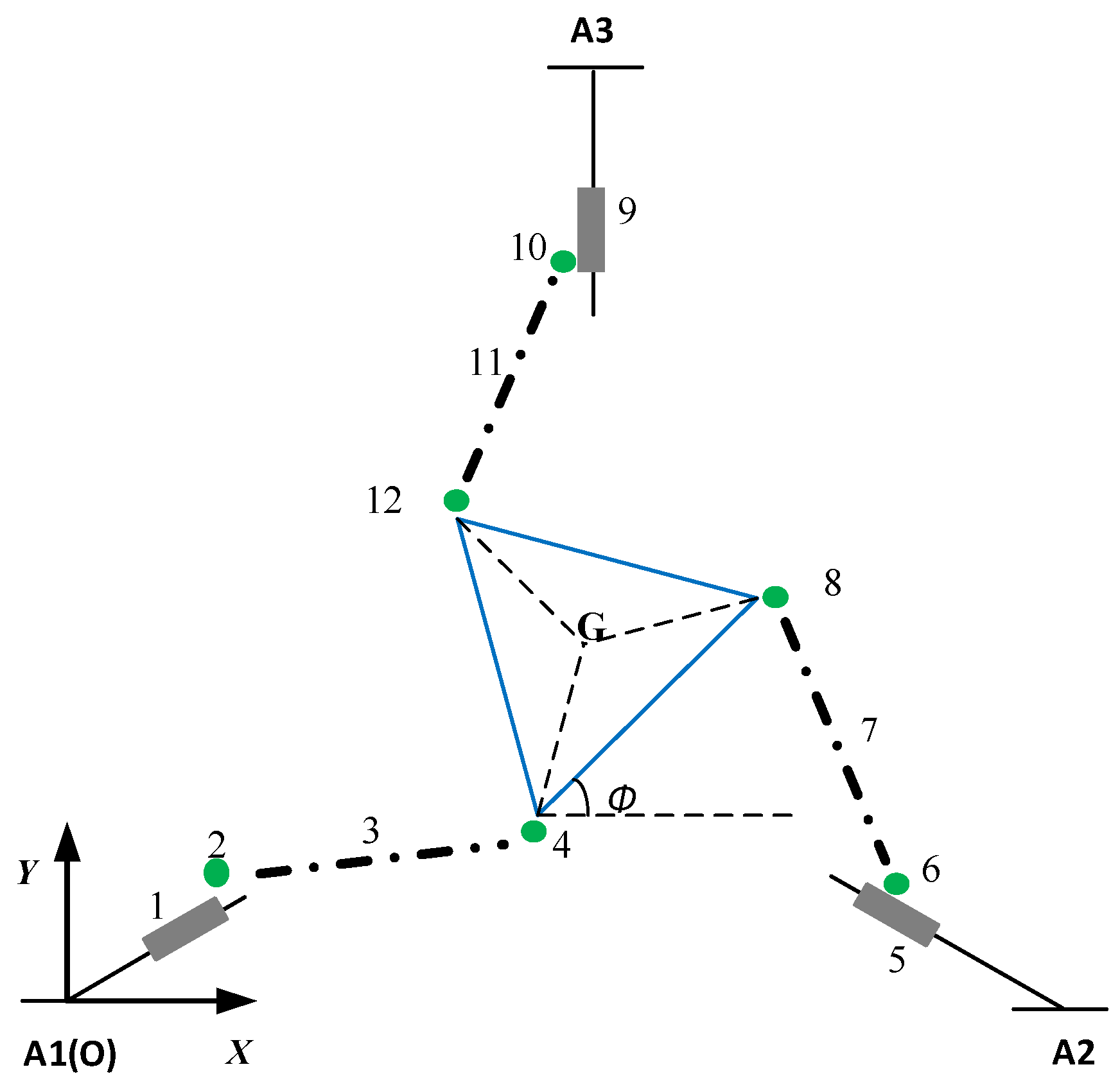
3. Dynamic Model of the Flexible 3-PRR PPM
3.1. Transfer Matrix of the Mobile Platform
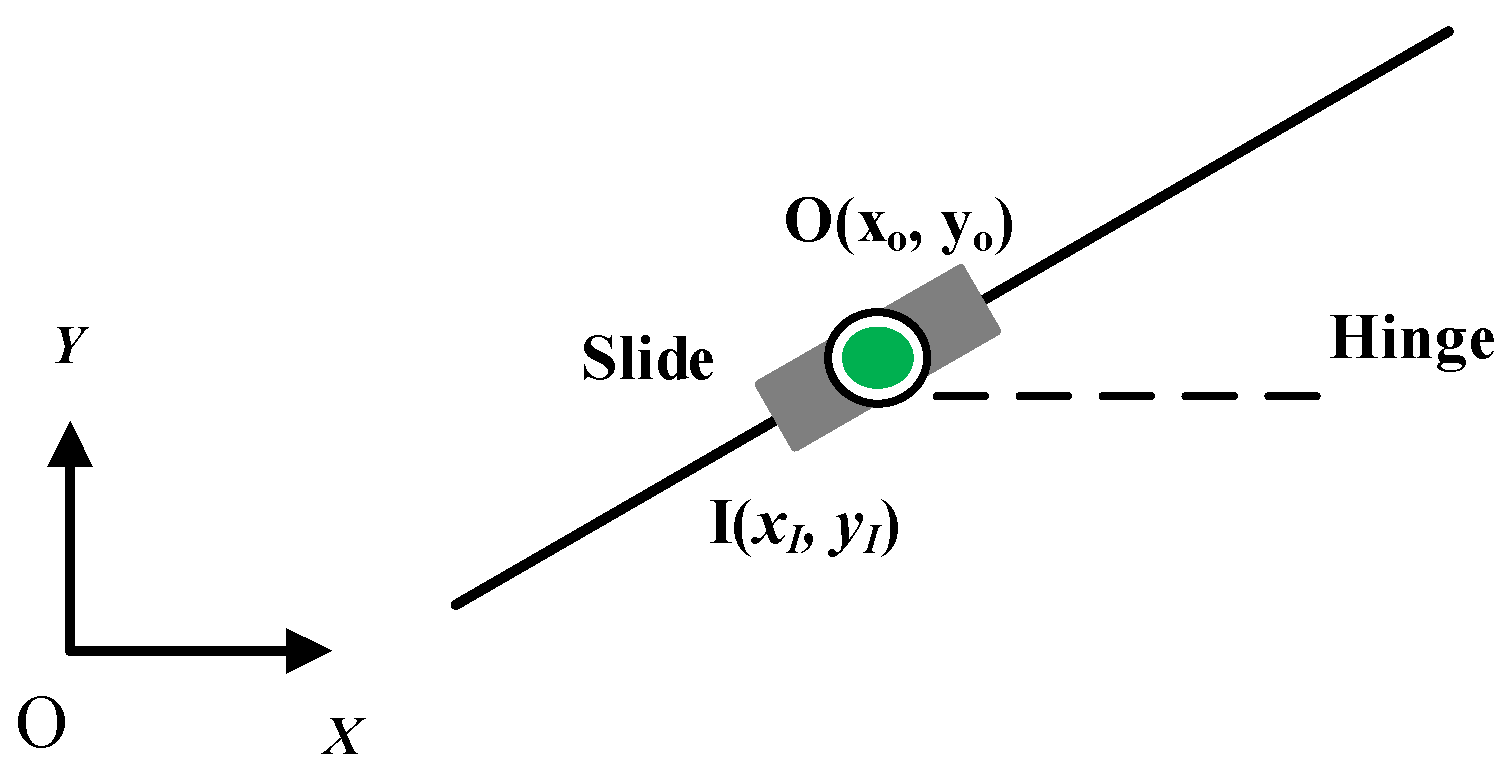
3.2. Transfer Matrix of the Slider
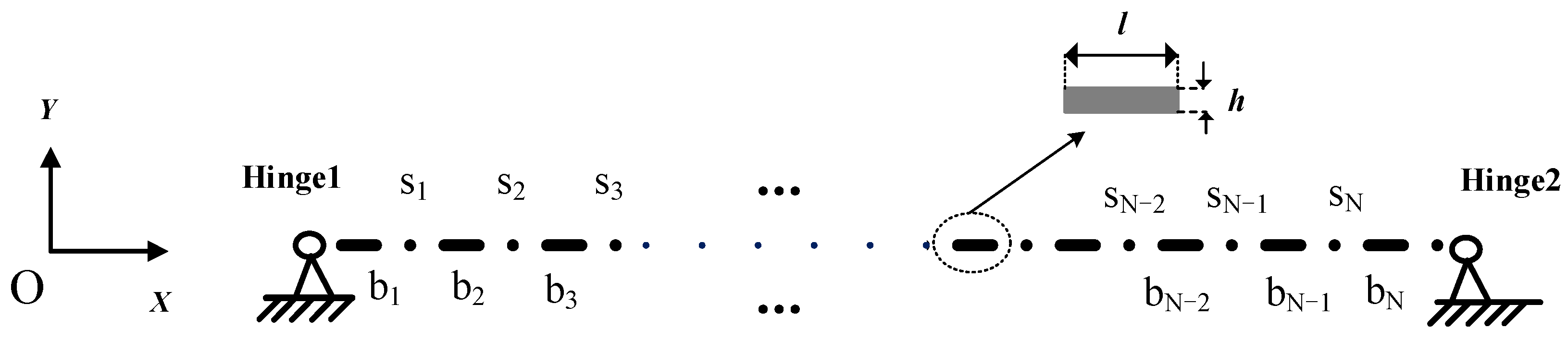
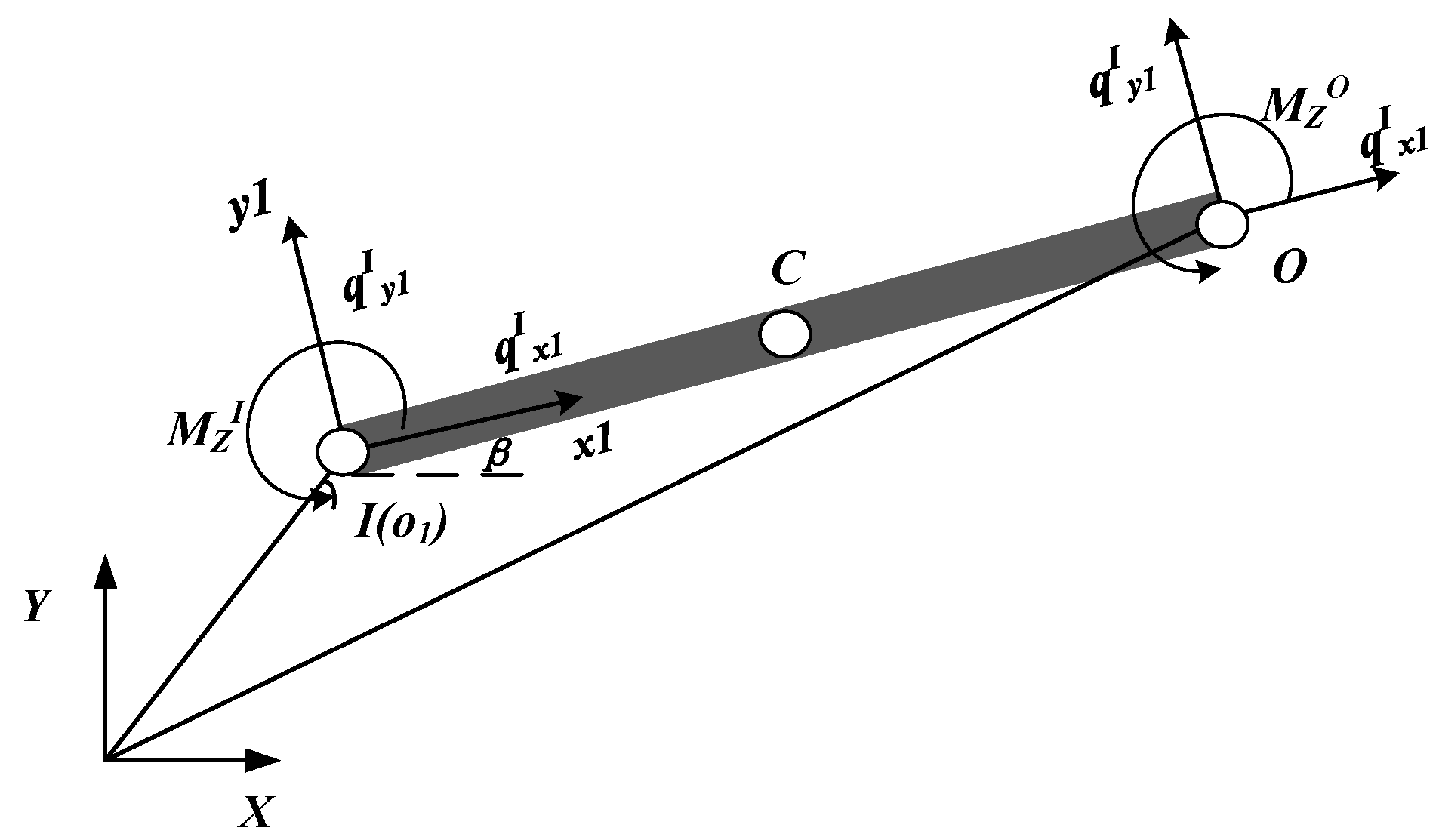
3.3. Transfer Matrix of the Flexible Link
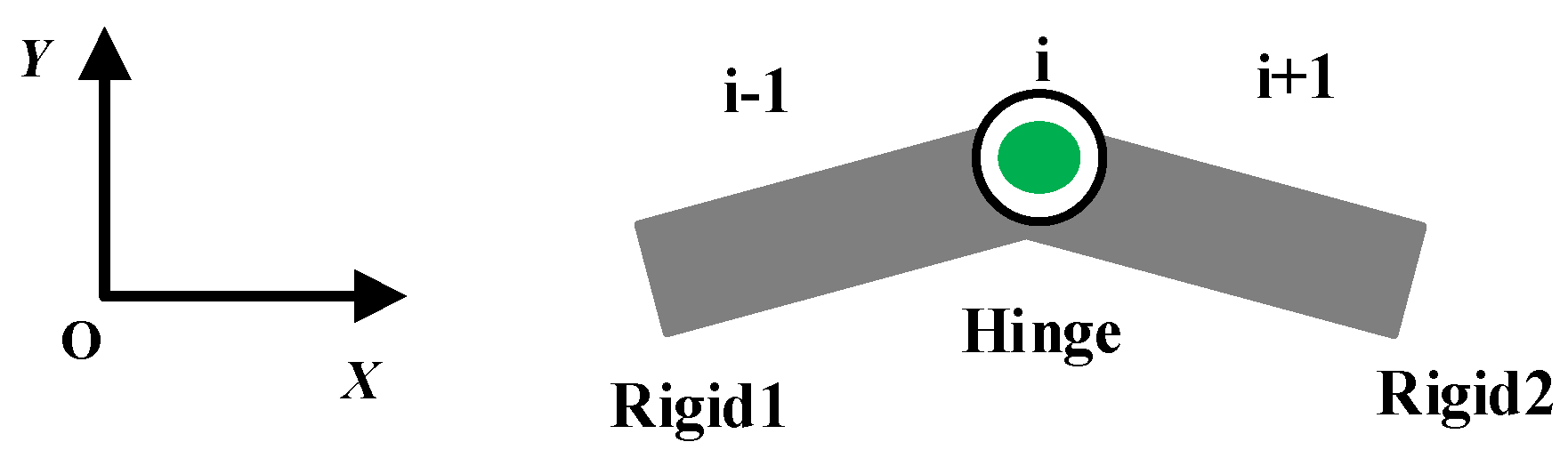
3.3.1. Transfer Matrix of the Elastic Hinge
3.3.2. Transfer Matrix of the Rigid Element
3.4. Transfer Matrix of the Smooth Hinge
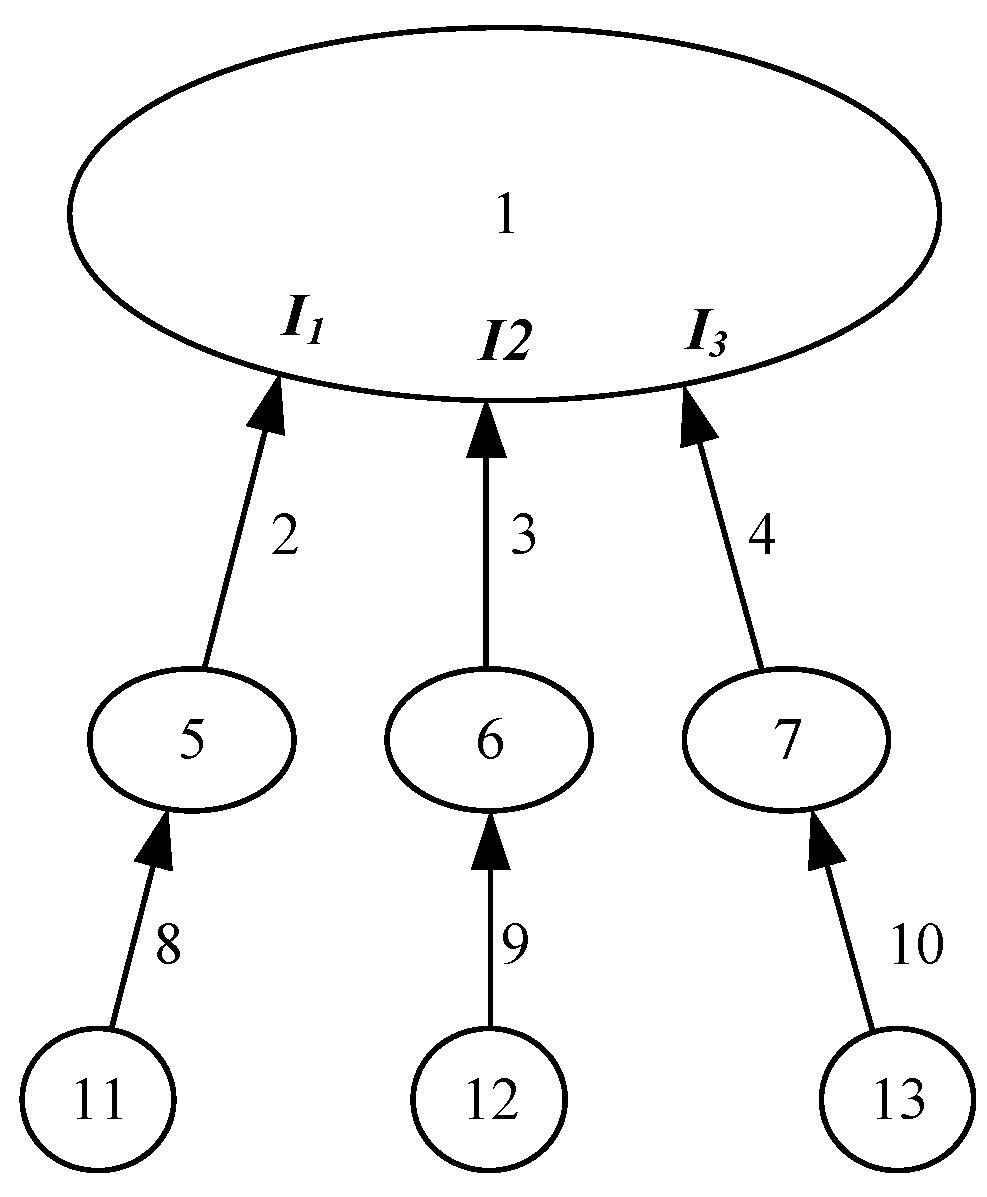
3.5. Overall System Transfer Equation
3.6. Vibration Characteristics
3.6.1. Vibration Characteristics of Flexible Link
3.6.2. Vibration Characteristics of the Flexible Parallel Manipulator
4. Numerical Simulation and Discussion
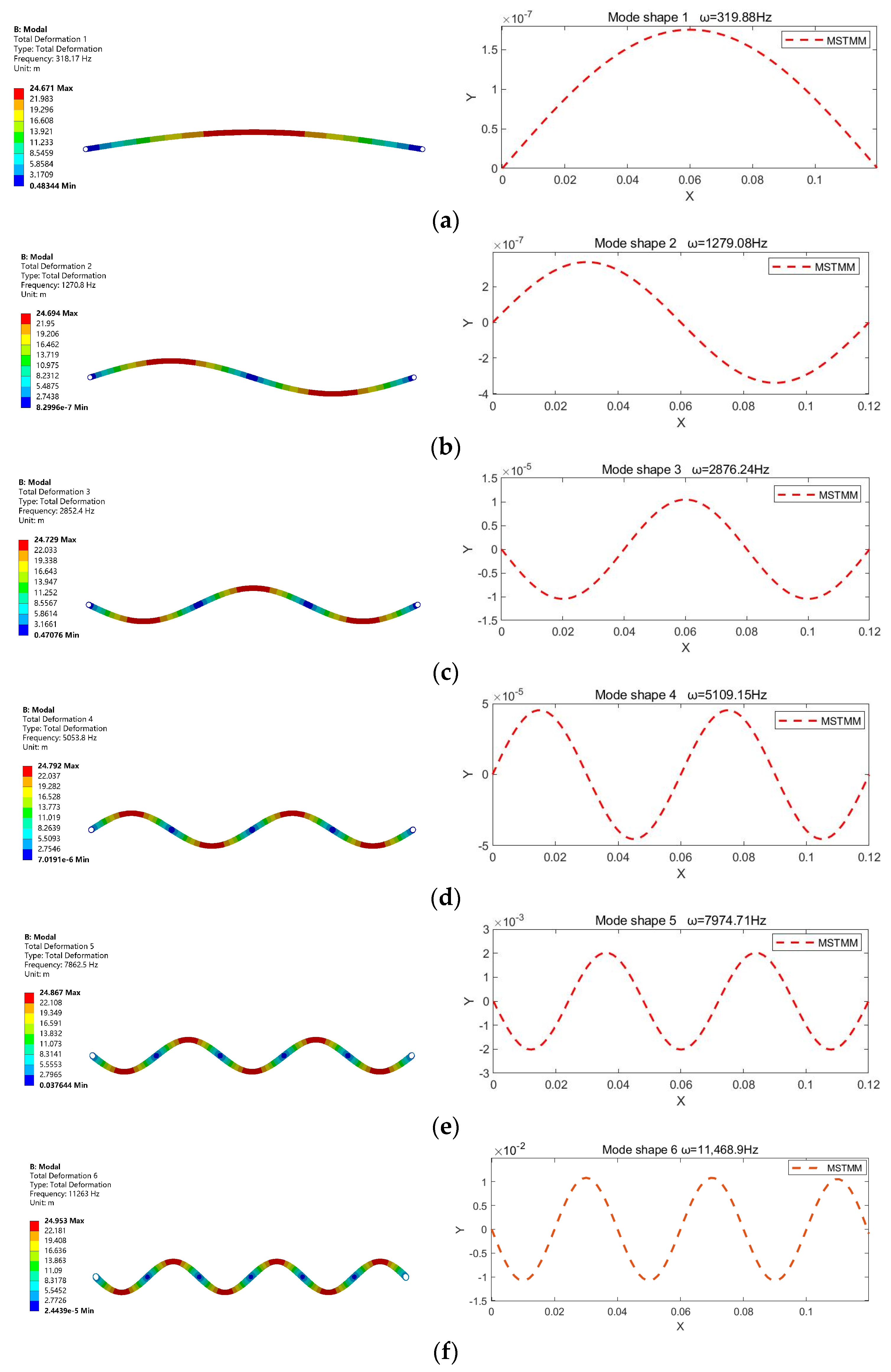
4.1. In-Plane Vibration of Flexible Link
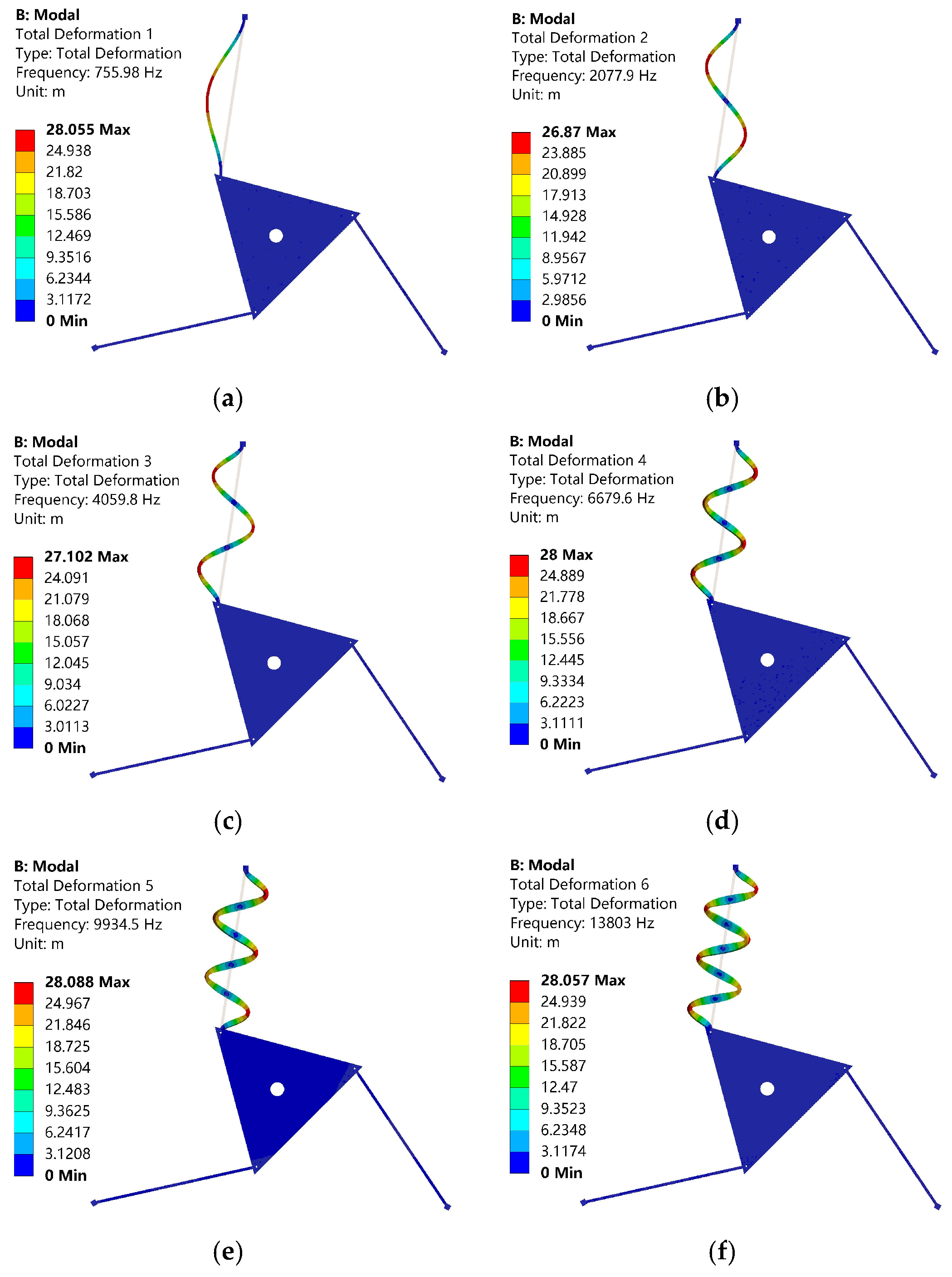
4.2. In-Plane Vibration of the Flexible 3-PRR PPM
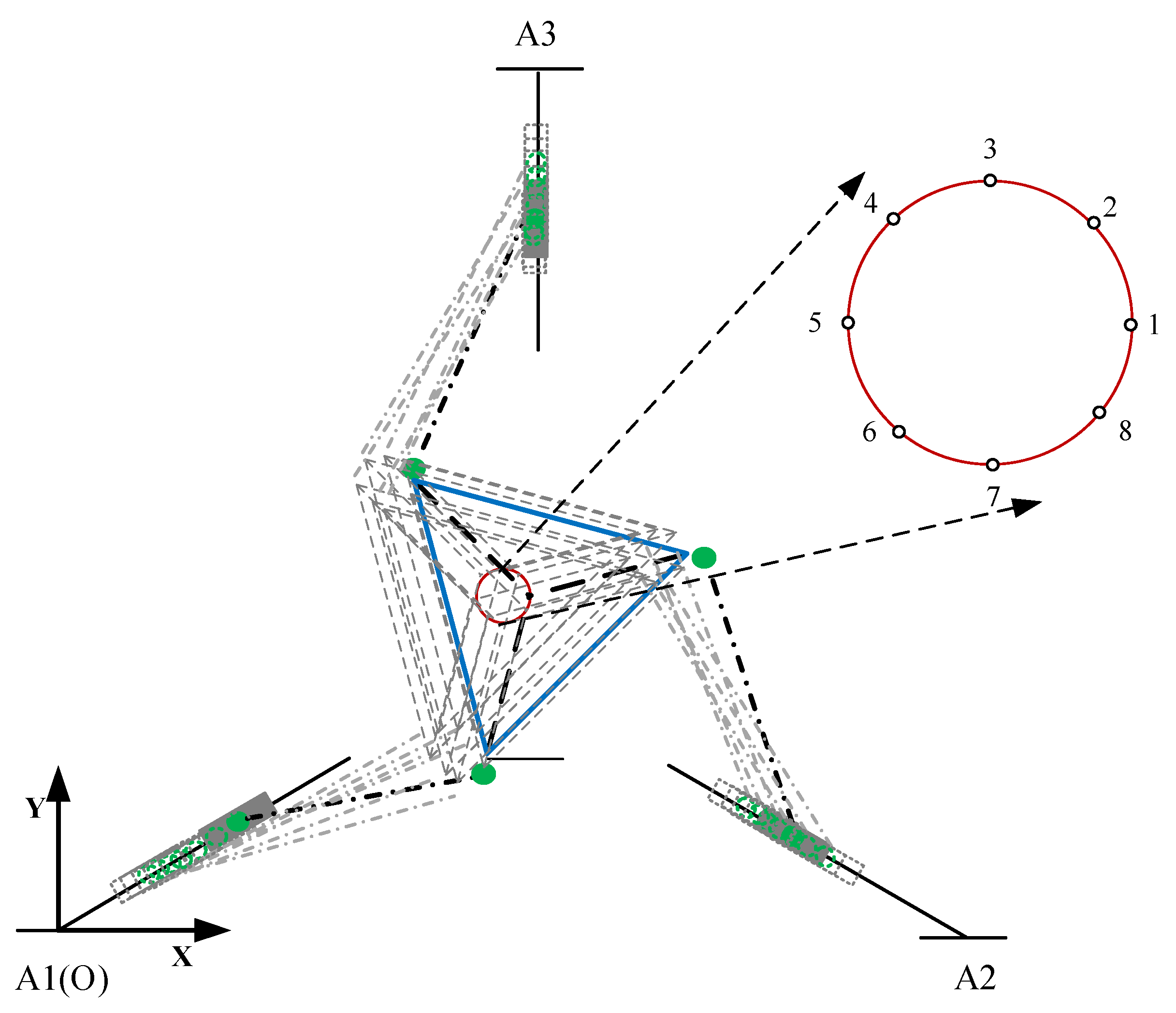
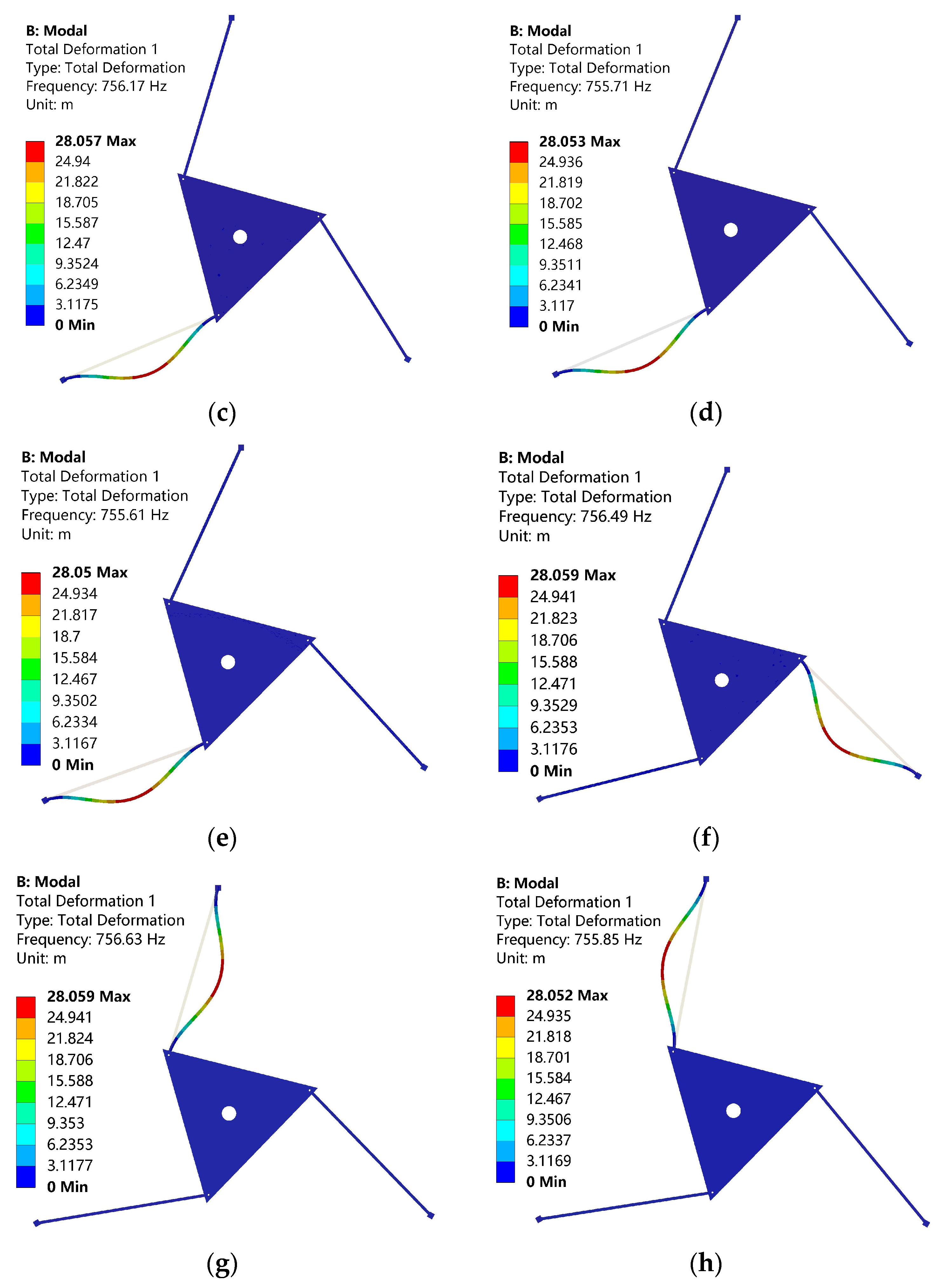
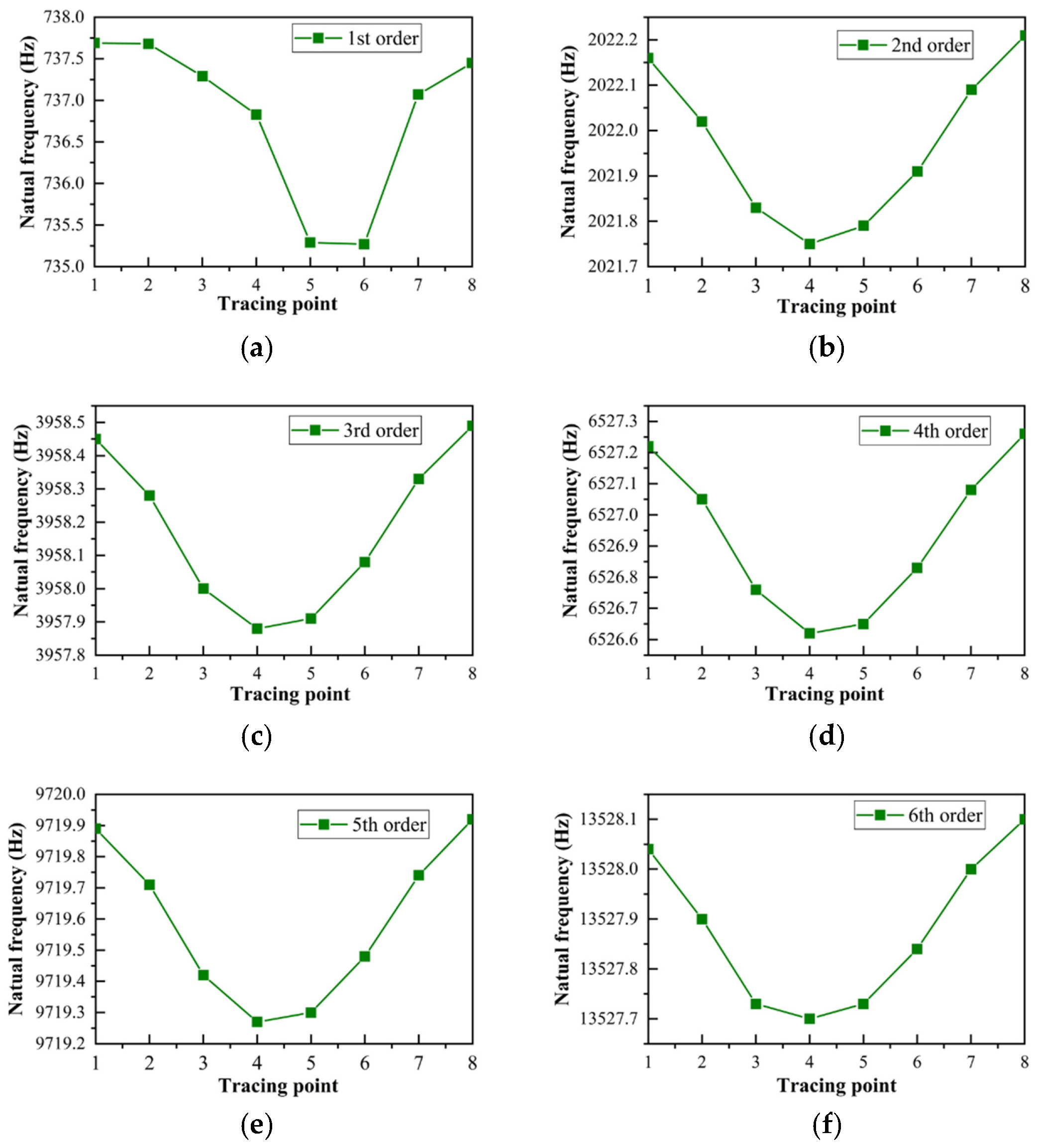
4.3. Analysis of the Vibration Characteristics of the Flexible Parallel Manipulator under a Specific Trajectory
5. Conclusions
- (1)
- There is no need for formulating and solving the global dynamics equations;
- (2)
- Even for complex multibody systems, the overall transfer equations are always of low order, with high computational efficiency and computational accuracy;
- (3)
- The principle is simple and efficient and can be easily extended to model and analyze other parallel manipulators containing flexible components.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Abo-Shanab, R.F. Dynamic modeling of parallel manipulators based on Lagrange–D’Alembert formulation and Jacobian/Hessian matrices. Multibody Syst. Dyn. 2020, 48, 403–426. [Google Scholar] [CrossRef]
- Lu, H.J.; Rui, X.T.; Ma, Z.Y. Hybrid multibody system method for the dynamic analysis of an ultra-precision fly-cutting machine tool. Int. J. Mech. Syst. Dyn. 2022, 2, 290–307. [Google Scholar] [CrossRef]
- Zhang, J.; Bi, L.; Wu, W.R. Reinforcement Learning-Based Parallel Approach Control of Micro-Assembly Manipulators. In Proceedings of the 2022 14th International Conference on Computer and Automation Engineering (ICCAE), Brisbane, QLD, Australia, 25–27 March 2022; pp. 25–30. [Google Scholar]
- Alamdari, A.; Krovi, V. Design and analysis of a cable-driven articulated rehabilitation system for gait training. J. Mech. Robot 2016, 8, 051018. [Google Scholar] [CrossRef]
- He, W.; Ouyang, Y.; Hong, J. Vibration control of a flexible robotic manipulator in the presence of input deadzone. IEEE. T. Ind Inform. 2016, 13, 48–59. [Google Scholar] [CrossRef]
- Wang, D.; Cao, H.; Yang, Y. Dynamic modeling and vibration analysis of cracked rotor-bearing system based on rigid body element method. Mech. Syst. Signal. Process 2023, 191, 110152. [Google Scholar] [CrossRef]
- Li, Y.B.; Wang, Z.S.; Chen, C.Q. Dynamic accuracy analysis of a 5PSS/UPU parallel mechanism based on rigid-flexible coupled modeling. Chin. J. Mech. Eng. 2022, 35, 33. [Google Scholar] [CrossRef]
- Zhang, X.P.; Mills, J.K.; Cleghorn, W.L. Vibration control of elasto dynamic response of a 3-PRR flexible parallel manipulator using PZT transducers. Robotica 2008, 26, 655–665. [Google Scholar] [CrossRef]
- Gao, H.J.; He, W.; Zhou, C. Neural network control of a two-link flexible robotic manipulator using assumed mode method. IEEE. T. Ind. Inform 2018, 15, 755–765. [Google Scholar] [CrossRef]
- Piras, G.; Cleghorn, W.L.; Mills, J.K. Dynamic finite-element analysis of a planar high-speed, high-precision parallel manipulator with flexible links. Mech. Mach. Theory 2005, 40, 849–862. [Google Scholar] [CrossRef]
- Li, Z.; Kota, S. Dynamic analysis of compliant mechanisms. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Montreal, QC, Canada, 29 September–2 October 2002; Volume 5, pp. 43–50. [Google Scholar]
- Wang, X.Y.; Mills, J.K. FEM dynamic model for active vibration control of flexible linkages and its application to a planar parallel manipulator. Appl. Acoust. 2005, 66, 1151–1161. [Google Scholar] [CrossRef]
- Mahboubkhah, M.; Nategh, M.J.; Esmaeilzadeh Khadem, S. A comprehensive study on the free vibration of machine tools’ hexapod table. Int. J. Adv. Manuf. Tech. 2009, 40, 1239–1251. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, S.; Cheng, C. Study on modeling and dynamic performance of a planar flexible parallel manipulator based on finite element method. Math. Biosci. Eng. 2023, 20, 807–836. [Google Scholar] [CrossRef]
- Karamanli, A.; Eltaher, M.A.; Thai, S. Transient dynamics of 2D-FG porous microplates under moving loads using higher order finite element model. Eng. Struct. 2023, 278, 115566. [Google Scholar] [CrossRef]
- Chang, C.W.; Chen, Y.N.; Chang, H.C. Biomechanical comparison of different screw-included angles in crossing screw fixation for transverse patellar fracture in level walking: A quasi-dynamic finite element study. J. Orthop. Surg. Res. 2023, 18, 5. [Google Scholar] [CrossRef]
- Al-Zahrani, M.A.; Asiri, S.A.; Ahmed, K.I. Free Vibration Analysis of 2D Functionally Graded Strip Beam using Finite Element Method. J. Appl. Comput. Mech. 2022, 8, 1422–1430. [Google Scholar]
- Rui, X.T.; Wang, X.; Zhou, Q.B. Transfer matrix method for multibody systems (Rui method) and its applications. Sci. China. Technol. Sci. 2019, 62, 712–720. [Google Scholar] [CrossRef]
- Rui, X.T.; Wang, G.; Lu, Y. Transfer matrix method for linear multibody system. Multibody Syst. Dyn. 2008, 19, 179–207. [Google Scholar] [CrossRef]
- Rui, X.T.; U, O. Advances in transfer matrix method for multibody system dynamics. Adv. Mech. Eng. 2012, 42, 4. [Google Scholar]
- Rui, X.T.; Zhang, J.; Zhou, Q. Automatic deduction theorem of overall transfer equation of multibody system. Adv. Mech. Eng. 2014, 6, 378047. [Google Scholar] [CrossRef]
- Rong, B. Efficient dynamics analysis of large-deformation flexible beams by using the absolute nodal coordinate transfer matrix method. Multibody Syst. Dyn. 2014, 32, 535–549. [Google Scholar] [CrossRef]
- Bestle, D.; Abbas, L.; Rui, X.T. Recursive eigenvalue search algorithm for transfer matrix method of linear flexible multibody systems. Multibody Syst. Dyn. 2014, 32, 429–444. [Google Scholar] [CrossRef]
- Chen, G.L.; Rui, X.T.; Abbas, L.K. A novel method for the dynamic modeling of Stewart parallel mechanism. Mech. Mach. Theory 2018, 126, 397–412. [Google Scholar] [CrossRef]
- Rong, B.; Rui, X.T.; Tao, L. Discrete time transfer matrix method for launch dynamics modeling and cosimulation of self-propelled artillery system. J. Appl. Mech. 2013, 80, 011008. [Google Scholar] [CrossRef]
- Chen, D.Y.; Abbas, L.K.; Wang, G.P. The application of transfer matrix method for multibody systems in the dynamics of sail mounted hydroplanes system. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Quebec City, QC, Canada, 26–29 August 2018; pp. 1–9. [Google Scholar]
- Chen, D.Y.; Abbas, L.K.; Rui, X.T. Dynamic modeling of sail mounted hydroplanes system-part I: Modal characteristics from a transfer matrix method. Ocean Eng. 2017, 130, 629–644. [Google Scholar]
- Rong, B.; Rui, X.T.; Tao, L. Theoretical modeling and numerical solution methods for flexible multibody system dynamics. Nonlinear. Dyn. 2019, 98, 1519–1553. [Google Scholar] [CrossRef]
- Rui, X.T.; Zhang, J.S.; Wang, X. Multibody system transfer matrix method: The past, the present, and the future. Int. J. Mech. Sci. 2022, 2, 3–26. [Google Scholar] [CrossRef]
- Wang, X.Y.; Mills, J.K. Dynamic modeling of a flexible-link planar parallel platform using a substructuring approach. Mech. Mach. Theory 2006, 41, 671–687. [Google Scholar] [CrossRef]
- Si, G.N.; Chu, M.Q.; Zhang, Z.; Zhang, X.P. Integrating dynamics into design and motion optimization of a 3-PRR planar parallel manipulator with discrete time transfer matrix method. Math. Probl. Eng. 2020, 2020, 2761508. [Google Scholar] [CrossRef]
- Si, G.N.; Chen, F.H.; Zhang, X.P. Comparison of the Dynamic Performance of Planar 3-DOF Parallel Manipulators. Machines 2022, 10, 233. [Google Scholar] [CrossRef]
- Lu, H.J.; Rui, X.T.; Zhang, X.P. A computationally efficient modeling method for the vibration analyses of two-dimensional system structures using reduced transfer matrix method for multibody system. J. Sound Vib. 2021, 502, 116096. [Google Scholar] [CrossRef]



| Symbols | Unit | Parameters |
|---|---|---|
| [m] | Length of flexible link | |
| - | Number of split segments of flexible link | |
| [Pa] | Young’s modulus of flexible link | |
| [m] | Cross section parameters | |
| = 2740 | [kg/m3] | Density of flexible link |
| = | [kg.m2] | The inertia of the links |
| Mode | ||||||
|---|---|---|---|---|---|---|
| MSTMM | 319.88 | 1279.08 | 2876.24 | 5109.15 | 7974.71 | 11,468.9 |
| FEM | 318.17 | 1270.8 | 2852.4 | 5053.8 | 7862.5 | 11,263 |
| Error(%) | 0.57 | 0.64 | 0.82 | 1.08 | 1.41 | 1.79 |
| Symbols | Unit | Parameters |
|---|---|---|
| [m] | Length of flexible link | |
| - | Number of split segments of flexible link | |
| [m] | Side of mobile platform | |
| [kg] | Mass of slider | |
| [Pa] | Young’s modulus of flexible link | |
| [kg] | Mass of mobile platform | |
| [m] | Cross section parameters | |
| [Pa] | Young’s modulus of the mobile platform and slide | |
| [deg] | Orientation of the platform | |
| = 2740 | [kg/m3] | Density of flexible link |
| = 7850 | [kg/m3] | Density of mobile platform and slide |
| = | [kg.m2] | Inertia of the links |
| [kg.m2] | The inertia of the mobile platform |
| Mode | ||||||
|---|---|---|---|---|---|---|
| MSTMM | 737.69 | 2022.16 | 3958.45 | 6527.22 | 9719.89 | 13,528.04 |
| FEM | 755.98 | 2077.9 | 4059.8 | 6679.6 | 9934.5 | 13,803 |
| Error(%) | 2.42 | 2.68 | 2.49 | 2.28 | 2.16 | 1.99 |
| Point | ||||||
|---|---|---|---|---|---|---|
| 1 | 737.69 | 2022.16 | 3958.45 | 6527.22 | 9719.89 | 13,528.04 |
| 2 | 737.68 | 2022.02 | 3958.28 | 6527.05 | 9719.71 | 13,527.90 |
| 3 | 737.29 | 2021.83 | 3958.00 | 6526.76 | 9719.42 | 13,527.73 |
| 4 | 736.83 | 2021.75 | 3957.88 | 6526.62 | 9719.27 | 13,527.70 |
| 5 | 735.29 | 2021.79 | 3957.91 | 6526.65 | 9719.30 | 13,527.73 |
| 6 | 735.27 | 2021.91 | 3958.08 | 6526.83 | 9719.48 | 13,527.84 |
| 7 | 737.07 | 2022.09 | 3958.33 | 6527.08 | 9719.74 | 13,528.00 |
| 8 | 737.45 | 2022.21 | 3958.49 | 6527.26 | 9719.92 | 13,528.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Si, G.; Li, W.; Lu, H.; Zhang, Z.; Zhang, X. Vibration Modeling and Analysis of a Flexible 3-PRR Planar Parallel Manipulator Based on Transfer Matrix Method for Multibody System. Machines 2023, 11, 505. https://doi.org/10.3390/machines11050505
Si G, Li W, Lu H, Zhang Z, Zhang X. Vibration Modeling and Analysis of a Flexible 3-PRR Planar Parallel Manipulator Based on Transfer Matrix Method for Multibody System. Machines. 2023; 11(5):505. https://doi.org/10.3390/machines11050505
Chicago/Turabian StyleSi, Guoning, Wenkai Li, Hanjing Lu, Zhuo Zhang, and Xuping Zhang. 2023. "Vibration Modeling and Analysis of a Flexible 3-PRR Planar Parallel Manipulator Based on Transfer Matrix Method for Multibody System" Machines 11, no. 5: 505. https://doi.org/10.3390/machines11050505
APA StyleSi, G., Li, W., Lu, H., Zhang, Z., & Zhang, X. (2023). Vibration Modeling and Analysis of a Flexible 3-PRR Planar Parallel Manipulator Based on Transfer Matrix Method for Multibody System. Machines, 11(5), 505. https://doi.org/10.3390/machines11050505






