Characterization of Microscopic Damage Evolution of Functional Groove in Cageless Bearings

Abstract

Bearings with partial function grooves as cageless bearings related to magnetic floating bearing protection have characteristics, such as fast offsetting of the impact force caused by rotor fall, and they gradually become important parts of ultra clean and cryogenic transportation systems. However, the functional failure mechanism of the bearing, which is caused by functional groove wear, is not clear. Therefore, this paper establishes a force–motion intrinsic model of particles inside the functional groove, which is based on the discrete element method, which it itself combined with the functional groove damage evolution trend analysis. Then, a hyper-quadratic surface model of inter-particle contact is established to simulate the time-varying friction coefficient of the functional groove by combining particles of different sizes to form particle clusters. Additionally, as the boundary condition, EDEM is used to solve the contact motion state of rolling element rolling through the functional groove for one week to obtain the overlap between particles and contact force change law. The results show that the wide side of the functional groove wears more seriously than the narrow side, and the rolling element leaves the functional groove with more impact than when it enters the functional groove, and the functional groove wears more seriously. In this paper, through the study of local functional groove wear of cageless ball bearing, we propose to characterize the damage extension of functional groove by using the number of particle fracture and motion trend in discrete element method, and this study provides theoretical guidance for the design of cageless bearings.

1. Introduction

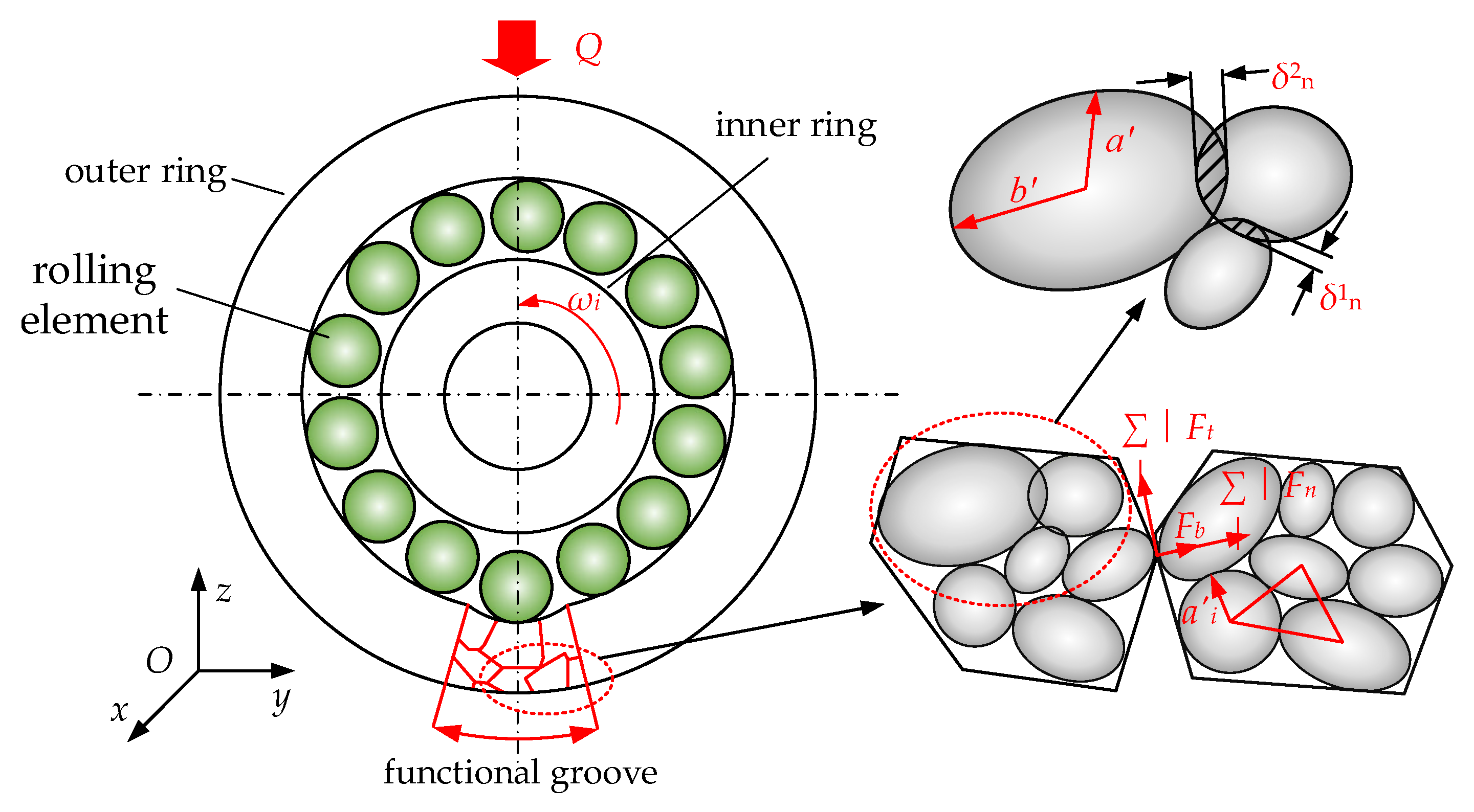
As the core part of the magnetic floating bearing, the outer ring of the cageless protection bearing often adopts the local functional groove to keep the rolling element automatically discrete because it often rotates at high speed to make the local functional groove wear, so it is especially important to explore its wear texture [1,2].

The damage caused by the rolling element, passing through the local function groove, is typical of rolling contact fatigue (RCF). During the operation of the bearing, the structure of the local function groove is so small that, once minor wear occurs, it will affect the automatic dispersion of the rolling element. The failure caused by RCF has a very complex mechanism. Lian established a thermo-mechanical phase change finite element method to quantitatively predict the formation process of thermally induced white-etched layer (WEL) on the track surface [3]. Yan conducted a systematic analysis of rolling–sliding contact fatigue (RSCF) failure of AISI 9310 gear steel, studying the evolution of fatigue life, microstructure and crystal orientation, as well as changes in microhardness and residual stress distribution [4]. Areitioaurtena investigated the effect of induction hardening residual stresses on rolling contact fatigue life using the Dang Van multi-axial criterion, confirming the importance of including residual stress profiles in fatigue life assessment [5]. Ren characterized and reconstructed the three-dimensional geometric structure of RCF cracks based on experimental statistics. The results show that the initial microcrack growth rate is highest for the tilt angle of 15–30 degrees, and the three-dimensional superposition of the I + II + Ill fracture mode is considered to predict the expansion path of RCF cracks more accurately and reveal the crack expansion mechanism at the contact surface and subsurface, respectively [6]. Usually, most scholars use the finite element method for bearing wear, but due to the special structure of functional groove, this method can only study the wear and crack expansion of the surface layer of functional groove, but it cannot obtain the internal changes of bearing steel material when the functional groove wears. In order to obtain the evolution of functional groove surface morphology expansion, the article uses the discrete element method to study the frictional wear process of bearing outer raceway surface, and the functional groove expansion process is described by inter-particle fracture trend, which can not only quantitatively study the macroscopic wear of functional groove, but also analyze the kinetics of functional groove particle fracture expansion from the microscopic ontological model of material.

In past studies, multi-scale modeling has been gradually applied in the field of bearing wear studies. Li used scanning electron microscopy and laser three-dimensional microimaging measurements to determine the friction coefficients and wear amounts of sliding bearings under different operating conditions to examine the wear surfaces of bearings [7]. Zhang performed a microscopic analysis of the spalling and found a large number of drop pits and microcracks of different sizes on the surface of the damage zone. The process of spalling formation of cylindrical roller bearings was inferred from the cross-sectional topography of the damaged area on the bearings [8]. Few scholars have studied the wear muscle from the bearing itself. Machado, a French scholar, established a discrete element model of the inner and outer rings of the bearing in a two-dimensional simulation. In the model, in addition to the rolling element and cage equivalent into particles, the inner and outer rings of the bearing are also discrete and enter into a combination of particles with viscosity, and the relationship between the dynamic mechanical state of the bearing and the electrical signal is simulated by introducing the electrical and mechanical coupling method. The lubrication state of the bearing is predicted to improve the bearing life [9,10,11].

The macroscopic wear behavior depends both on the physical properties of the microscopic particles and on their interactions. The EDEM method, first proposed by Cundall and Strack, is an ideal method for dealing with these interparticle contact configurations, which allows the use of a large number of discrete elements to describe the physical state of the system. This method uses a soft-sphere particle model in which the particles are squeezed and collided to produce a certain amount of overlap, which in turn calculates the interparticle contact forces. Various inter-particle contact models are proposed by quantifying the particle force–velocity–displacement interactions. Lu modified the extended solution of Maugis’ Johnson-Kendall-Roberts (JKR) theory of adhesive contact for exact spherical contact by defining the interface adhesion energy on the actual spherical contact area, rather than on its projection plane [12]. Lu reviewed advances in non-spherical particle modeling, implementation, and algorithms for effective detection of contact and determination of contact parameters [13]. Most of the structures under study are irregular, and the traditional calculation of spherical particles does not accurately describe the properties of the material [14,15,16]. M. Acevedo characterized the morphology of the deposit based on the aspect ratio and the feed rate of the particles. The discrete element method, based on spherical polygons, was then validated with experimental results. Experimental and numerical results are given for particle alignment and stress distribution in faceted granular fillers deposited in small-scale two-dimensional silos [17]. Donev proposed an algorithm applied to systems of hard ellipsoids and ellipsoids [18]. Unlike other microscopic research methods, the discrete element method conducts the study of inter-particle contact states by building an inter-particle intrinsic structure model. Chen proposed a fine-scale mechanics-based intrinsic structure model for linear viscoelastic particle-reinforced composites based on the time–domain homogenization method. The effective intrinsic constitutive model of the composite was derived after decomposing the particle contact deformation into the volume part and the bias part. The effects of particle volume fraction, strain rate, and elastic–viscous parameters on the effective viscoelastic behavior and creep properties of the composites were investigated [19]. Song proposed a new intrinsic model for magneto-rheological polished fluids (MRPFs) using the hexagonal compact stacking structure of magneto-rheological fluids (MRFs) for predicting field-related properties, such as yield shear stress [20]. Since particle media have complex properties different from those of continuous media, hydrostatics does not completely describe the particle states and the study of particle motion is necessary. Mando and Rosendahl have reviewed the existing methods for dealing with the motion of nonspherical particles at high Reynolds numbers in the Euler-Lagrange method for dispersed flows [21]. Wachem derived a new framework for computing the rotation matrix of particles using unit quaternion transform vectors and tensors [22].

The field of application for the discrete element method has also been extended from the initial geotechnical field to the mechanical field and is widely used in wear and tear. Yin ensemble finite element and discrete element method to simulate and analyze the wear of ball mill hoist, the simulation results predict the wear distribution of the hoist and provide a theoretical basis for the subsequent reduction of the hoist wear [23]. Chen used the discrete element method to simulate pin-disk wear tests to predict the sliding wear of individual iron ore particles, and the contact model in the discrete element was used to simulate the interaction between particles and geometry [24]. Some scholars used the bonding model in the discrete element method to disperse the continuum to predict the wear of the continuum. Nguyen, a Dutch scholar, used the discrete element method to numerically simulate the wear and fragmentation of agglomerates in a diffusion blender and distinguished the wear and fragmentation behavior of agglomerates by comparing the amount of agglomerate shrinkage due to bond breakage with the amount of agglomerate shrinkage calculated on a particle-by-particle basis [25]. Luo used a homemade experimental device to measure the discrete element parameters of ellipsoidal pellets and analyzed the effect of different roasting temperatures and equivalent diameters on the discrete element parameters of pellet ores, in addition to measuring and extracting the wear rate and movement velocity of different pellets inside the drum [26]. Luo used discrete element phase numerical simulation to study the evolution of tool wear during cutting of high-temperature alloys and established a discrete element model of tool-chip wear behavior based on boundary conditions. Predicted and Analyzed values of the number of micro-crack were evaluated, and the number of separated particles and wear rate of ceramic tools by discrete element simulation was determined [27]. Fang proposes a method for predicting the wear evolution of structural boundaries based on the discrete element method, which represents the worn structural boundaries by spherical boundary units and reduces the computational effort of discrete element simulation by transforming the contact detection between structural boundaries and particles into contact detection between spherical boundary units and particles [28]. Zhang established a mechanical model of the wear body surface based on the discrete element method, and Zhang used discrete element software to establish the step, convexity, and scale arrangement structure of the wear surface and its abrasive wear system. Through qualitative analysis of abrasive grain morphology, contact bond field, and contact force chain, light injuries and shedding of abrasive wear behavior were observed. This study provides a new approach to abrasive wear on non-smooth surfaces [29,30].

In summary, EDEM models are widely used in modern development applications, but fewer scholars have applied the discrete element method in the study of bearing wear. In the process of calculating inter-particle contact, although many scholars have conducted a lot of research on non-spherical particles in order to conform to the natural matter model, they do not pay too much attention to the influence of contact surface shape on the contact model. In this paper, in order to construct its macroscopic stress tensor intrinsic structure model more accurately, the reflectance of the microstructural changes of the granular medium and the trend of inter-particle motion were determined. In analyzing the functional groove particle contact model, a super secondary contact surface for inter-particle contact was established. Since RCF-induced failures have very complex mechanisms, high stress, heat, phase change, etc., they can have an impact on the service life of the bearing. This paper analyzes the rolling contact fatigue of bearings from a microscopic point-of-view to better explain the mechanism of functional groove damage extension, and it provides a theoretical basis for subsequent damage extension studies of functional groove surfaces.

2. Methods

The functional groove of the outer ring of a cageless ball bearing generates local stress changes after being subjected to the external load generated by the passing of the rolling element, which macroscopically leads to the dynamic frictional wear response of the functional groove edge. In order to characterize the mesoscopic surface morphological expansion of the functional groove edge after damage, an EDM model of the functional groove is established, as shown in Figure 1. The geometrical characteristics of the machined functional groove edges are complex, and the edges are micronized in order to analyze the mesoscopic local fracture behavior of the functional groove edges more reliably and accurately. The discrete element method (DEM) is used to simulate the functional groove of the bearing outer ring as a cluster of rough particles with irregular geometric characteristics. There exist vertex–vertex, vertex–face, vertex–edge, edge–edge, and face–face contacts between these rough particles in the form shown in Figure 1. Each cluster of rough particles is composed of clusters of non-spherical particles. In order to keep each particle in each rough particle cluster as a rigid body, the particles in the cluster are constrained to be in elastic linear contact with each particle, having three degrees of freedom, and the total number of degrees of freedom in the rough particle cluster is equal to 3n. n is the total number of particles in a cluster, and the more the number of particles in the cluster, the more accurately the shape and roughness of the functional groove boundary can be represented.

2.1. Functional Groove Edge Particle Cluster Intrinsic Structure Model

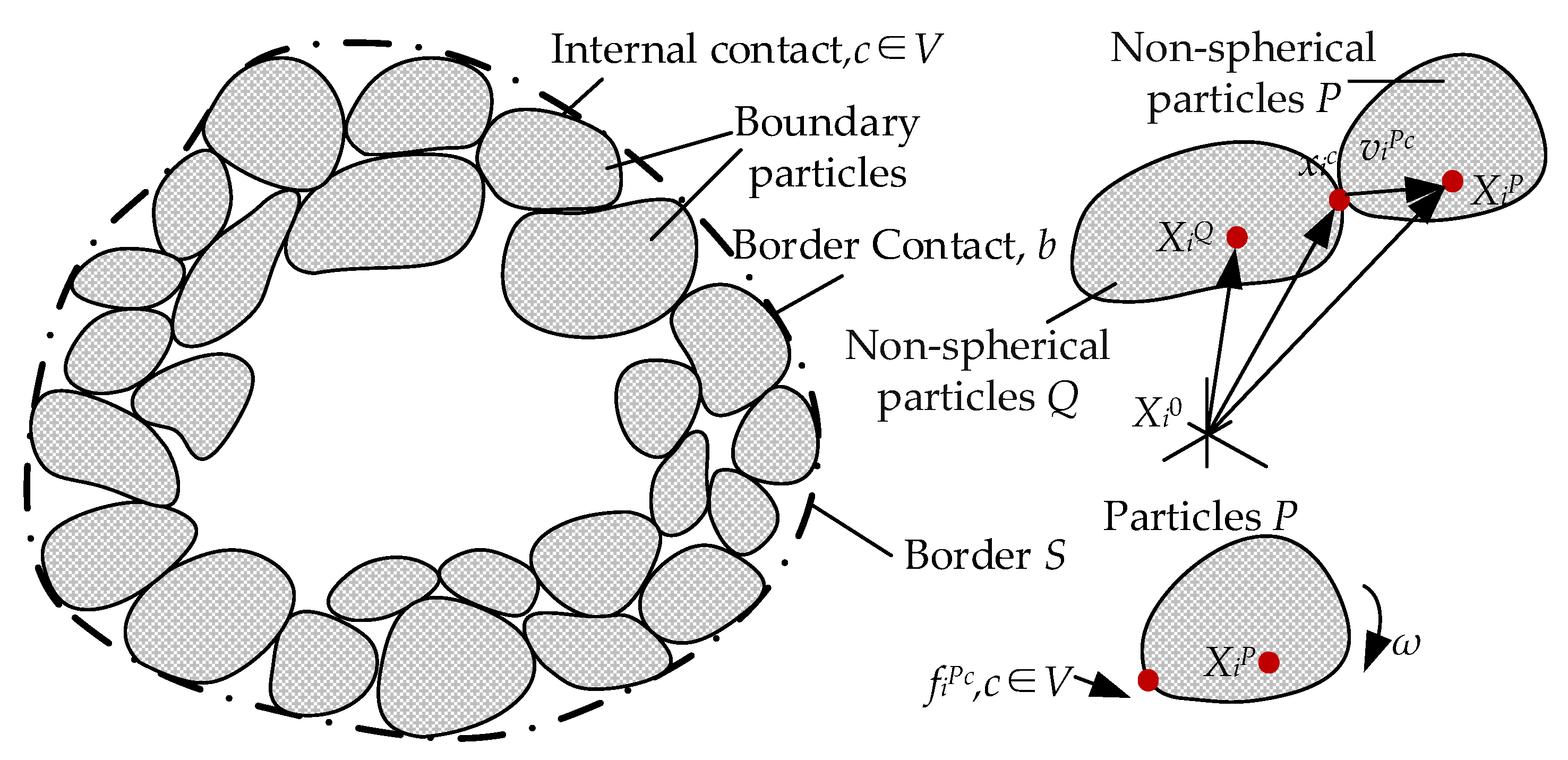
2.1.1. Analysis of the Motion of Particles at the Edge of the Functional Groove

Newton’s second law and the relationship between force-displacement are usually used for the calculation of the discrete element method, and the total contact force acting on the particle cluster is given according to Newton’s second law, and the force-displacement is used to find the contact force, leading to the motion of individual particles. Bearings with functional grooves are subjected to different total forces due to the different contact states with the wide and narrow sides when the rolling element rolls through the functional grooves, resulting in different motion states for each particle. Figure 2 shows the motion trends of the particle clusters in the wide and narrow wear areas.

To describe the general motion of the non-spherical particle, a Cartesian coordinate system is used, as shown in Figure 2b. W = <X^W,Y^W,Z^W> is the inertial coordinate system of the particle, and B = <X^B,Y^B,Z^B> is the coordinate system of the motion of the particle. The coordinate system of the particle is parallel to the axis of the inertial coordinate system at the center of the particle. The article introduces the kinematic system parameter Euler coefficients, whose purpose is to describe the tendency of the motion of non-spherical particles. The motion orientation of the particle directly affects the amount of rotation and translation of the particle, and the inertial and kinematic systems of the particle are interconverted by the coordinate transformation matrix A.

$$L^W={\mathit{A}}^T{L}^B,$$

(1)

The conversion matrix A can be expressed as:

$$\mathit{A}=\left[\begin{array}{ccc}{x}^2+y^2-z^2-w^2& 2(yz+xw)& 2(yw-xz)\\ 2(yz-xw)& x^2-y^2+z^2-w^2& 2(zw+xy)\\ 2(yw+xz)& 2(zw-xy)& x^2-y^2-z^2+w^2\end{array}\right],$$

(2)

The parameters x, y, z, and w are Euler parameters, which are related and must satisfy the following constraints:

$$x^2+y^2+z^2+w^2=1,$$

(3)

As shown in Figure 2a, the motion of the particle cluster at the edge of the functional groove is analyzed in order to analyze the intrinsic model of the wear region at the edge of the functional groove and to study its fracture expansion trend. The functional groove edge is subjected to the frictional and drag forces generated by the rolling element passing by, and the rough particle cluster produces translation and rotation in the world space, as shown in Figure 2b, and the kinematic equations of the rough particle cluster are established as follows:

$$\left\{\begin{array}{l}{\rho }_i{V}_i\frac{d^2{\mathbf{r}}_i}{d{t}^2}={\displaystyle \sum _{j=1}^{N_i}({\mathbf{F}}_{ij}^n}+{\mathbf{F}}_{ij}^{\tau })\\ J_i\frac{d^2{\omega }_i}{dt}={\displaystyle \sum _{j=1}^{N_i}{\mathbf{M}}_{ij}}\end{array}\right.,$$

(4)

where ρ_i and V_i are the particle density and volume of the ith particle. r_i, ω_i, and J_i are the position radius vector, rotational speed, and rotational inertia of the ith particle, respectively. ${\mathbf{F}}_{ij}^n$ and ${\mathbf{F}}_{ij}^{\tau }$ are the normal and tangential forces of particle i and j contact. ${\mathbf{M}}_i=p_{ij}\left(\frac{\left({\mathbf{r}}_j-r_i\right)}{{\mathbf{r}}_{ij}}{\mathbf{F}}_{ij}\right)+{\mathbf{K}}_{ij}$ is the moment of the particle cluster.

The rotational inertia is located along the z-axis axis of the non-spherical particles in the functional groove, at the center of the cluster of rough particles in the functional groove. Since the functional groove rough particle cluster is composed of different non-spherical particles, the rotational inertia of the rough particle cluster is composed of the rotational inertia of all non-spherical particles in the cluster, and the rotational inertia of each non-spherical particle is calculated, as shown in Equation (5).

$$J_i=\frac{1}{5}{m}_i(a^2+b^2),$$

(5)

a and b are the long and short radii of the non-spherical particles in the x–y plane, respectively. J_i is the rotational inertia of the particle. p_ij is the distance from the center of the i-th particle to the contact point of the ith particle with the j-th particle. r_j and r_i are the radius vectors of the ith particle and the jth particle to the contact point, respectively. r_ij is the distance between i and j. K_i is the resistance to the relative rotation of elements i and j.

The velocity of the particle cluster is changing in real time, and in order to obtain the velocity model of the particle cluster, the expansion trend of the rough particles at the edge of the functional groove is updated in real time, where the kinetic components, such as the moment and rotation velocity of the rough particles, are freely transformed between the world coordinate system and the body coordinate system. In the motion coordinate system, the angular acceleration of the functional groove rough particle cluster can be expressed as:

$$\left\{\begin{array}{l}{\dot{\omega }}_x^B=\frac{M_x^B}{I_{xx}}+\left(\frac{I_{yy}-I_{zz}}{I_{xx}}\right){\omega }_y^B{\omega }_z^B\\ {\dot{\omega }}_y^B=\frac{M_y^B}{I_{yy}}+\left(\frac{I_{zz}-I_{xx}}{I_{yy}}\right){\omega }_x^B{\omega }_z^B\\ {\dot{\omega }}_z^B=\frac{M_z^B}{I_{zz}}+\left(\frac{I_{xx}-I_{yy}}{I_{zz}}\right){\omega }_x^B{\omega }_y^B\end{array}\right.,$$

(6)

where I_xx, I_yy, and I_zz are the rotational moments of inertia at the three individual coordinate axes. The Euler equations are expressed in the particle frame with the main moments of inertia as:

$$I_{xx}=I_{yy}=\frac{\left(1+{\lambda }^2\right)m{a}^2}{5},I_{zz}=\frac{2m{a}^2}{5},$$

(7)

m is the mass of the rough particle cluster with aspect ratio λ = b/a and λ > 1.

After t moments, the velocity of the rough particle in the inertial coordinate system under the action of external force F and moment M is calculated. Then, at t + 1 moments, the velocity of the rough particle in the functional groove is updated as:

$$v_W^{n+1}=v_W^n+\frac{{\displaystyle \sum F}\Delta t}{{\displaystyle \sum M}},$$

(8)

2.1.2. Development of a Particle Contact Instantiation Model for Functional Groove Edges during Wear

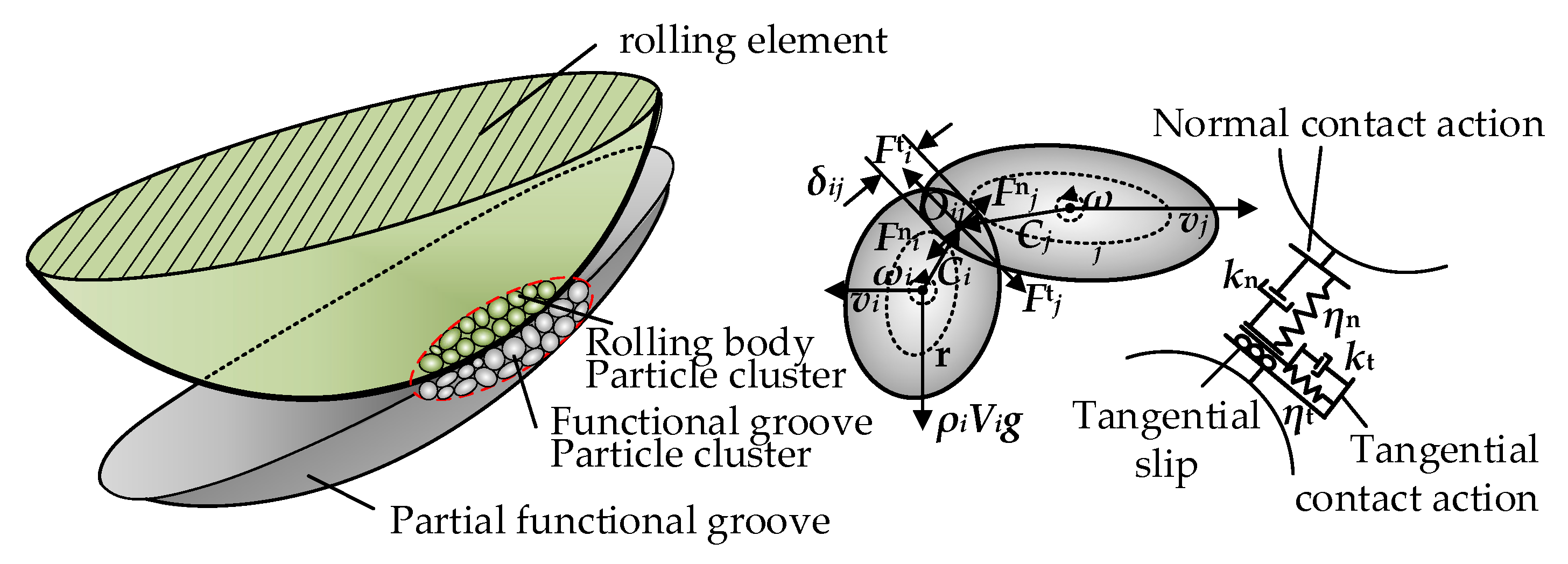
In order to analyze the macroscopic wear of the functional groove, an intrinsic model of the particles at the edge of the functional groove is established to analyze the local stresses in the particle clusters. The friction and viscosity between the mesoscopic particles of the functional groove are the two main factors controlling the particle behavior. When the rolling element rolls over the edge of the functional groove, the viscous response of the particles is generated by the coexistence of frictional and viscous stresses in order to establish the relationship between the macroscopic view of the edge of the functional groove at the moment of wear. The particle–particle and particle–boundary interaction models are first established, as shown in Figure 3. Equation (9) establishes the stress tensor function of the unitary body under a uniform stress field.

$${\overline{\sigma }}_{ij}=\frac{1}{V}{\displaystyle \underset{V}{\oint }{\sigma }_{ij}dV},$$

(9)

$${\overline{\sigma }}_{ij}=\frac{1}{V}\left[{\displaystyle \underset{S}{\oint }{x}_i{p}_{i}dS}+{\displaystyle \underset{V}{\oint }{\rho }_i{x}_i(g_i-a_i)dV}\right],$$

(10)

where p_i denotes the uniform force on the cell boundary S. ρ_i denotes the volume force in the cell volume V. a_i denotes the acceleration obtained in the x_i direction. N(x) is the normal unit vector at the boundary surface located at point x, pointing to a positive value inside the rough particle cell. The force equilibrium condition inside the rough particle cluster cell is ${\sigma }_{ij}-\rho g_i=\rho a_i$, and the boundary condition can be expressed as ${\sigma }_{ij}{n}_i(\mathit{x})=p{x}_i$.

For the system of rough particle cluster with volume V and closed surface (S = ∂V) at the outer boundary shown in Figure 3, the distributed forces on the boundary are concentrated as the concentrated forces at the discrete points of the boundary, so ${\displaystyle \underset{S}{\oint }{x}_i{p}_{i}dS}={\displaystyle \sum _{\beta \in S}{x}_i^{\beta }{F}_j^{\beta }}$. $F_j^{\beta }$ is the boundary force acting at the point β with coordinates $x_i^{\beta }$. The discrete form of Equation (9) can be obtained as:

$${\overline{\sigma }}_{ij}=-\frac{1}{V}\left[{\displaystyle \sum _{\beta \in S}{x}_i^{\beta }}{F}_i^{\beta }+{\displaystyle \sum _{\beta \in V}{\displaystyle \oint \rho }{x}_i}(g_i-a_i)d{V}^P\right],$$

(11)

where V^P is the volume of non-spherical particles, and the volume density g within the non-spherical particles is uniformly distributed. The position of the center of mass of the non-spherical particles P can be obtained.

$${\displaystyle \underset{V^P}{\oint }\rho }{x}_i{g}_{i}d{V}^p=X_i^P{G}_i^P=X_i^P{A}_j^P+R_{ij}^P,$$

(12)

$$A_j^P={\displaystyle \underset{V^P}{\oint }\rho }{a}_{j}d{V}^p,$$

(13)

$$R_{ij}^P={\omega }_i^P{\omega }_j^P{J}_{ij}^P-{\omega }_i^P{\omega }_i^P{J}_{ij}^P+{\phi }_{ij}{\dot{\omega }}_i^P{J}_{ij}^P,$$

(14)

where $G_i^P={\displaystyle \oint \rho g_i}d{V}^p$ is the volume force of the non-spherical particle P. The acceleration and angular acceleration of any point x on the particle are ${\mathit{\omega }}^{\mathit{P}}$ and ${\dot{\mathit{\omega }}}^{\mathit{P}}$. The distance of the point x from the center of mass is $\mathit{r}=\mathit{x}-{\mathit{X}}^p$, and its acceleration is $\mathit{a}={\mathit{a}}^p+\mathit{X}{\mathit{\omega }}^p\times {\mathit{\omega }}^p\times \mathit{r}+{\dot{\mathit{\omega }}}^p\times \mathit{r}$. a^P is the acceleration at the center of mass. $J_{ij}^P$ is caused by the rotational inertia $J_{ij}^P={\displaystyle \underset{V^P}{\oint }\rho }{r}_i{r}_{j}d{V}^p$. ${\phi }_{ij}$ is the displacement tensor.

Within the cluster of rough particles, interparticle contact interaction occurs, resulting in deformation of the particles of the rough cluster at the edge of the functional groove, when the following mechanical properties are satisfied:

$${\displaystyle \sum _{c\in P}{F}_i^{Pc}}+{\displaystyle \sum _{c\in P}{F}_{adh}^{Pc}}+G_i^P=A_i^P,$$

(15)

The fine expression of the stress tensor for rough particles can be obtained by bringing Equations (12)–(14) into Equation (15).

$${\overline{\sigma }}_{ij}=-\frac{1}{V}\left[{\displaystyle \sum _{P\in V}{\displaystyle \sum _{c\in P}{v}_i^{Pc}(F_i^{Pc}}}+F_{adh}^{Pc})+{\displaystyle \sum _{P\in V}({\omega }_i^P{\omega }_j^P{J}_{ij}^P-{\omega }_i^P{\omega }_i^P{J}_{ij}^P+{\phi }_{ij}{\dot{\omega }}_i^P{J}_{ij}^P)}\right],$$

(16)

2.2. Establishment of the Contact Model of the Non-Spherical Particles on the Edge of a Functional Groove

When the functional groove particle cluster is subjected to the total force of the rolling element rolling over, a certain amount of deformation is generated. The deformation of individual particles is small compared to the deformation of particle clusters, and, in order to study the contact deformation of particle clusters, the deformation of individual particles is first analyzed. This deformation depends mainly on the motion of the particles as rigid bodies, leading to a mutual overlapping behavior of the contact points of the particle motion instead of the individual deformation. The magnitude of the overlap δ is directly determined by the contact force, and the overlap of individual particles is small relative to the particle size, but the effect of the deformation due to the superposition of the overall particle overlap in the whole particle cluster on the particle motion, as well as on the fracture, cannot be ignored.

In order to simulate the edge of the functional groove of the outer ring of the bearing more realistically, the rough particles at the edge of the functional groove are discretized into irregular polyhedral clusters, and the spherical Hertzian contact theory is improved to establish a hyper-quadratic surface unit polyhedral contact model when the rolling element passes through the edge of the functional groove, as shown in Figure 4, with non-spherical particles for contact analysis, and each non-spherical inter-particle contact is modeled with the normal spring and damper and the tangential spring damper slider assembly.

2.2.1. Normal Forces

When the interaction of hyper-quadratic surface units, resulting from particle collisions, the normal contact force of non-spherical particles is mainly composed of elastic and viscous forces. We use the nonlinear normal force model proposed by Tsuji to describe the relationship between two non-spherical particles, and the normal force F_n can be expressed as:

$$F_n=K_n{\delta }_n^{3/2}\mathit{n}-{\eta }_n{\mathit{v}}_n+F_{adh},$$

(17)

K_n and η_n represent the stiffness and damping coefficients. Δ_n denotes the normal overlap between two non-spherical particles. N is the unit vector from the collision center to the center of the non-spherical particle. V is the normal component of velocity. F_adh is the adhesion force between two non-spherical particles.

$$K_n=\frac{4}{3}{E}^{\ast }{\left(R^{\ast }\right)}^{1/2},$$

(18)

$${\eta }_n=\alpha (m{K_n}^{1/2}{\delta }_n^{1/4}),$$

(19)

$${\delta }_n=\frac{2{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{1}{\sqrt{1-e^2{\sin }^2\varphi }}d\varphi }}{\pi \sqrt[3]{\frac{2E}{\pi (1-e^2)}}\sqrt{(1-e^2)}}\sqrt[3]{\frac{1}{8}{\left(\frac{3}{E^{\ast }}\right)}^2{F_n}^2{K}_{\mathrm{mean}}},$$

(20)

where, $E^{\ast }=\frac{E_1{E}_2}{E_1(1-{\nu }_2^2)+E_2(1-{\nu }_1^2)}$, $R^{\ast }=\frac{R_1{R}_2}{R_1+R_2}$. E, υ, and R are the elastic modulus of the non-spherical particle material, Poisson’s ratio, and the radius of curvature at the contact point. m is the mass of a non-spherical particle. α is the correction coefficient allowing particle energy dissipation, 0 < α < 1. e is the eccentricity of the contact surface. K_mean is the average radius of curvature of the contact surface.

When the rolling element passes through the functional groove, the curvature radius R of the contact point of the particles at the edge of the functional groove changes with the change in the contact form of the polyhedron. If the local curvature K = K_mean, the curvature radius R of any contact of non-spherical particles can be obtained.

$$R=\frac{1}{K}=\frac{1}{K_{mean}}=\frac{2{\left|\nabla F\right|}^2}{\nabla F^{T}H(F)\nabla F-{\left|\nabla F\right|}^2(F_{XX}+F_{YY}+F_{ZZ})},$$

(21)

The adhesion between non-spherical particles is related to the contact surface energy of particles. According to the DMT model, the adhesion between relatively small particles is calculated by using van der Waals forces.

$$F_{adh}=2\pi R^{\ast }({\gamma }_1+{\gamma }_1-{\gamma }_{12})\mathit{n},$$

(22)

$$\frac{3E^{\ast }{a}^3}{4R^{\ast }}=P+2\pi R^{\ast }({\gamma }_1+{\gamma }_2-{\gamma }_{12}),$$

(23)

γ₁ and γ₂ are the surface energy of two non-spherical particles in a vacuum alone, and γ₁₂ is the surface energy of two non-spherical particles in contact. a is the contact radius, and P is the external load.

2.2.2. Tangential Forces

When a non-spherical particle moves in the direction perpendicular to the contact normal, the tangential contact force is only related to the friction force, and its magnitude will change according to the size of the contact area.

$$F_t=\left\{\begin{array}{ll}-k_t{\delta }_t-{\eta }_t{v}_s& \mathrm{if}\left|F_t\right|<{\mu }_f\left|F_n\right|,\\ -{\mu }_f(P+2\pi R^{\ast }({\gamma }_1+{\gamma }_2-{\gamma }_{12}))\mathit{t}& \mathrm{otherwise},\end{array}\right.,$$

(24)

η_t is the tangential damping coefficient, and δ_t is the tangential overlap between two non-spherical particles. vs- and μ_f are the slip velocity and the friction coefficient. t is opposite to the direction of slip.

$${\eta }_t=\alpha \sqrt{m{K}_t}{\delta }_t^{1/4},$$

(25)

$$K_t=8\sqrt{R^{\ast }{\delta }_n}{G}^{\ast },$$

(26)

$${\delta }_t=\frac{2{\displaystyle \underset{0}{\overset{\pi /2}{\int }}\frac{1}{\sqrt{1-e^2{\sin }^2\varphi }}d\varphi }}{\pi \sqrt[3]{\frac{2E}{\pi (1-e^2)}}}\sqrt[3]{\frac{1}{8}{\left(\frac{3}{E^{\ast }}\right)}^2{F_t}^2{K}_{\mathrm{mean}}},$$

(27)

K_t is the tangential stiffness coefficient, and $G^{\ast }$ is the shear modulus of the contact particle. $G^{\ast }$ = $K^{\ast }$.

The slip of the contact becomes more complicated in the presence of adhesive interactions between the particles, with the existence of positive and negative pressure regions.

2.3. Fracture and Failure Prediction of Non-Spherical Particles with Functional Groove Edges

Bonding between the two particles due to contact, here, can become the formation of the connection bond in the process of bearing operation. The particles are subjected to the external force generated when the rolling element squeezes the surface of the functional groove, and the particles on the surface of the functional groove transform the external force into the internal force of the internal particle contact and transfer it to each layer on the particle level [31]. The change in the amount of overlap generated between the particles leads to a change in the contact force, and the area of contact and the magnitude of the contact force directly affects the change in the interparticle bonding force. When the particles are subjected to an external force, the particles produce a certain speed of motion, and, as the particles continue to move, the external force that causes the particles to move reaches a certain value. The bond between the particles breaks, and the bonding force between the particles is less than the external force applied at this time. When the number of fractured particles increases to a certain degree, the surface of the functional groove is damaged until the functional groove fails. Establish the relationship equation between the number of bearing outer raceway particle layers and the amount of particle shedding as:

$$y=\left\{\begin{array}{cc}12.776x+63.224& 1\le x\le 2\\ -5.167x+99.11& x>2\end{array}\right.$$

(28)

where y is the amount of particle shedding, and x is the number of outer raceway particle layers.

Since the outer raceway wear studied in this paper is characterized by particle shedding, there is a relationship between particle shedding and outer raceway wear. Therefore, there is a relationship between the amount of particle shedding and the amount of outer raceway wear, and there is a relationship between the number of particle shedding layers and the depth of functional groove wear. Combining the size and density of the outer raceway particles with the relationship between the particle shedding amount and the number of particle shedding layers described in Equation (12), the outer raceway failure model can be obtained as follows:

$$W=\left\{\begin{array}{cc}4.527h+0.672& 0<h\le 0.06\\ -1.831h+1.054& h>0.06\end{array}\right.$$

(29)

where W is the outer raceway wear amount; h is the outer raceway wear depth.

According to the relationship between the outer raceway wear amount and the wear depth given in Equation (13), the maximum wear depth can be calculated as 0.5756 mm, and then the total wear amount of the outer raceway is 9.397 mg, according to the integration of Equation (13).

In order to analyze the fracture of non-spherical particles at the edge of the functional groove, the flow chart for calculating the distribution of the particle shedding quantity, according to the theoretical analysis conducted in the previous section, is shown in Figure 5.

3. Discrete Element Simulation and Experimental Analysis

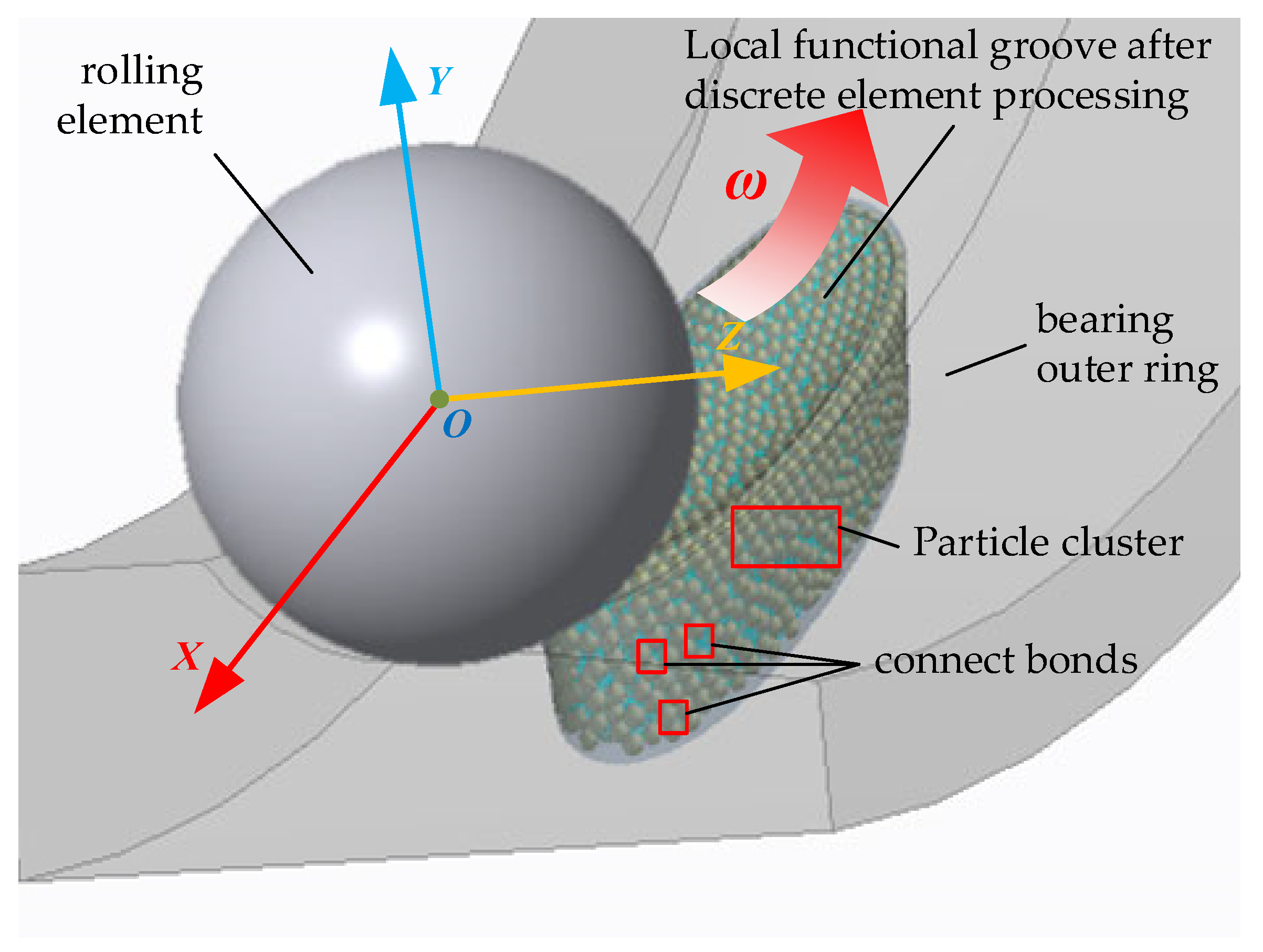
In order to investigate the motion and contact state of the functional groove particles during the process of rolling the body over the functional groove, and to further study the wear trend of the functional groove edge surface, EDEM software was used to simulate the functional groove particles, as shown in Figure 6. In order to facilitate the calculation, spherical particles with a diameter of 0.02 mm were selected to fill the functional groove, and only the functional groove part was discrete, while the particles were combined to simulate different shapes of particle clusters, which could observe the state of the functional groove particles more clearly. Firstly, the three-dimensional model of the bearing drawn by the three-dimensional modeling software is imported into the software EDEM as a solid, and the parameters of the bearing rings and rolling elements are set according to the basic parameters of the cageless bearing in

Table 1. Basic parameters of the cageless ball bearing.

Parameter	Value of Number
Inner diameter Di/mm	30
Outside diameter Do/mm	55
Width W/mm	13
Pitch circle diameter dm/mm	42.5
Inner ring groove diameter di/mm	39.325
Inner ring groove radius of curvature ri/mm	3.38
Outer ring groove diameter do/mm	45.675
Outer ring groove radius of curvature ro/mm	3.38
Diameter of rolling element Dw/mm	6.35
Number of rolling elements	14
Contact angle	15

and the material setting parameters in

Table 2. Material simulation parameters.

Material Simulation Parameters	Inner and Outer Ring (Bearing Steel)	Rolling Elements (Si3N4)
Intensity ρ/(kg/mm3)	7.81 × 10−6	3.12 × 10−6
Elastic modulus E/MPa	2.07 × 105	3.1 × 105
Poisson ratio	0.3	0.29
Collision recovery factor	0.56	0.45
Static friction coefficient	0.08
Rolling friction coefficient	0.05

, respectively.

The article studies the change trend of the functional groove particle contact intrinsic model when the rolling element passes through one turn of the functional groove. When the rolling element enters the functional groove, the mass center of the rolling element moves downward and detaches from the inner ring, and, instantly, the forces generated by the motion of the rolling element’s revolution, rotation, and slip act on the functional groove, resulting in the change in the contact force on the edge of the functional groove particle. Additionally, the velocity of the particle changes instantly. The velocity change in the contact particle when the rolling element rolls through the functional groove is shown in Figure 7, and the kinetic energy momentum diagram of the functional groove contact particle is shown in Figure 8.

From Figure 7a, it can be seen that, when the rolling element just enters the functional groove, the particle velocity of the functional groove is surged by the impact of the rolling element, and the velocity growth slows down at point A. Because the functional groove has the function of slowing down the speed of the rolling element, when the particle velocity increases to the maximum value, the particle velocity is affected by the decrease in the rolling element velocity, and there is a trend of slowing down. When the rolling element is at point B, it is about to leave the functional groove, and the particle velocity increases faster at the functional groove due to the impact of the end of the functional groove on the rolling element. The velocity in the X-axis direction in Figure 7b shows a decreasing trend when the rolling element completely enters the center of the functional groove, which is related to the decrease in the rotational speed of the rolling element here. 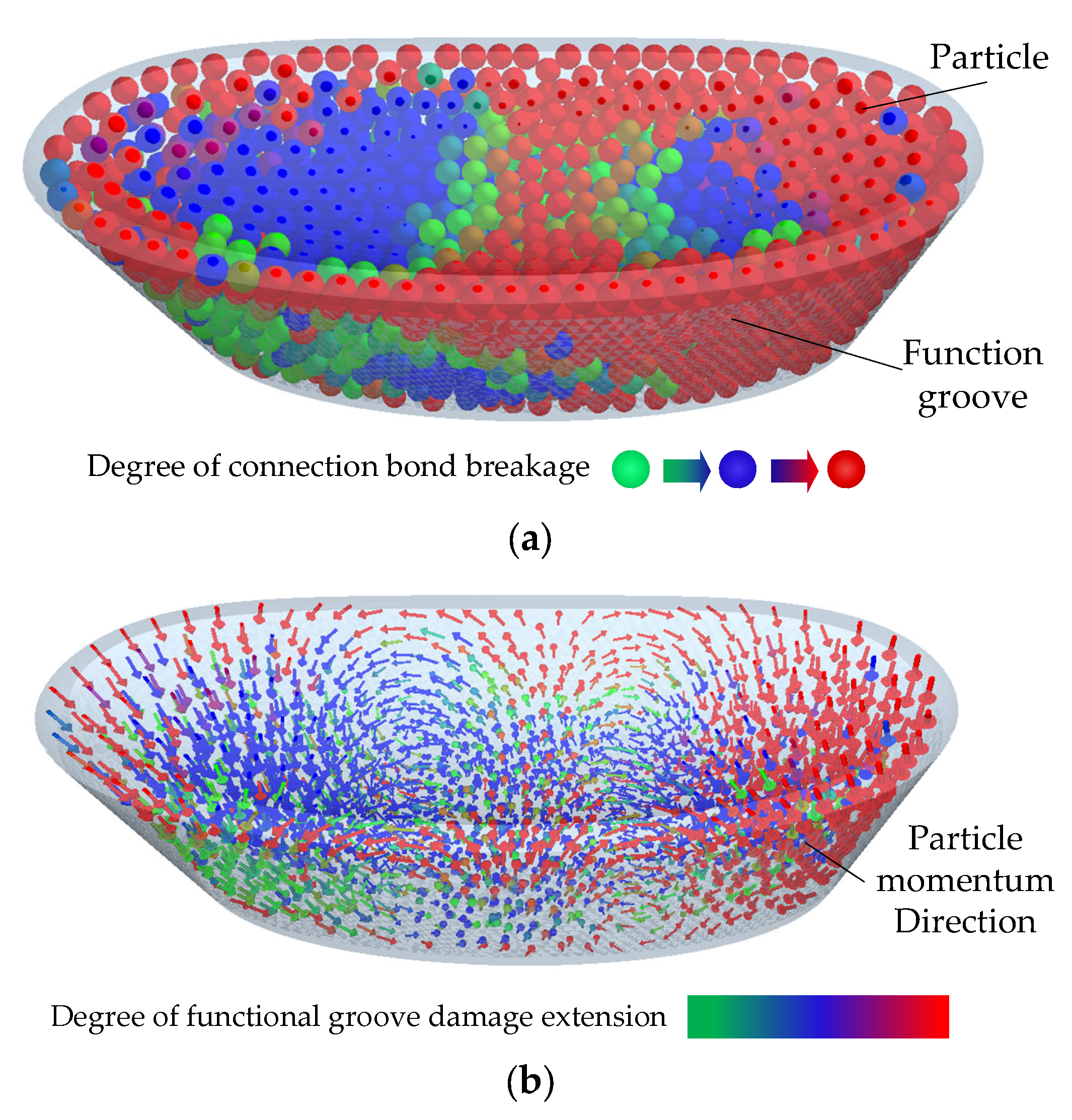Figure 8 shows that the particles at the edge of the functional groove have a serious tendency to expand outward, and the bonds connecting the particles at the end of the functional groove and the particles at the narrow edge are more likely to break. This is due to the fact that the rolling element is subjected to gravity and end impact force, and the rolling element acts more on the narrow edge.

When the rolling element rolls over the functional groove for one turn, the stress variation diagram of the functional groove is shown in Figure 8, and the contact force and contact moment diagrams between the functional groove particles in different axes are shown in Figure 9 and Figure 10.

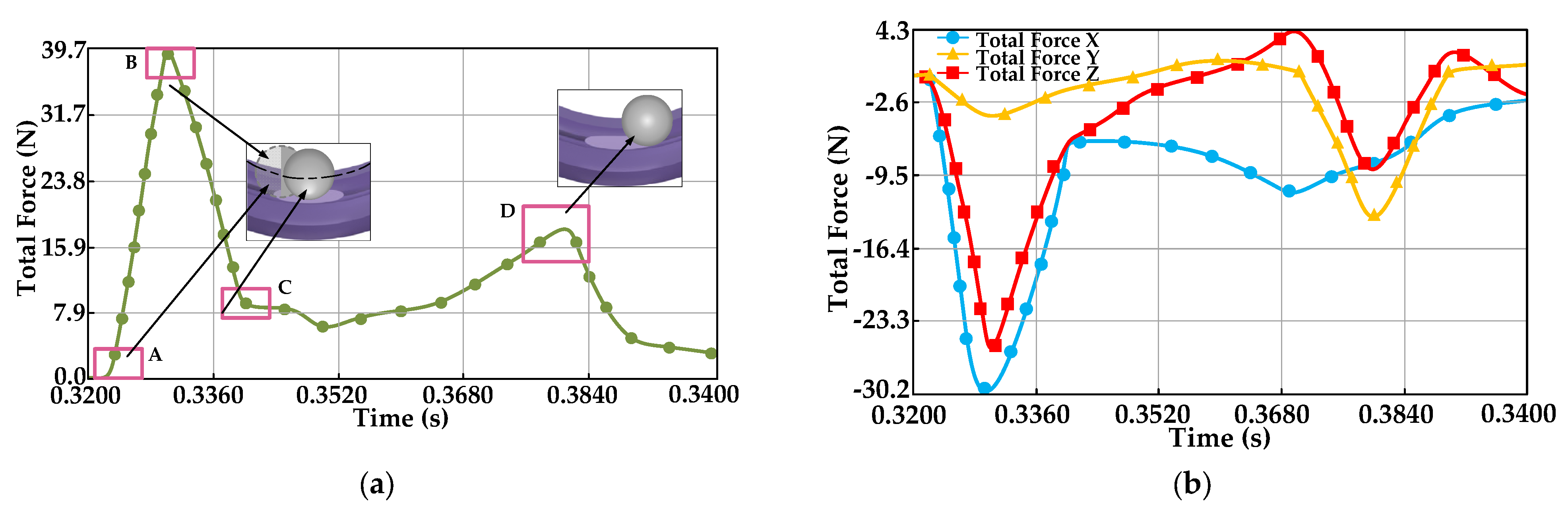
As can be seen from Figure 9, when the rolling element enters the functional groove, the contact stress gradually increases, which is caused by the change in the rolling element contact point. With the complete entry into the functional groove, the contact stress is not fluctuated much by change. When the rolling element leaves the functional groove, the contact stress decreases, although the impact force will have some effect on the contact stress, but the effect is small.

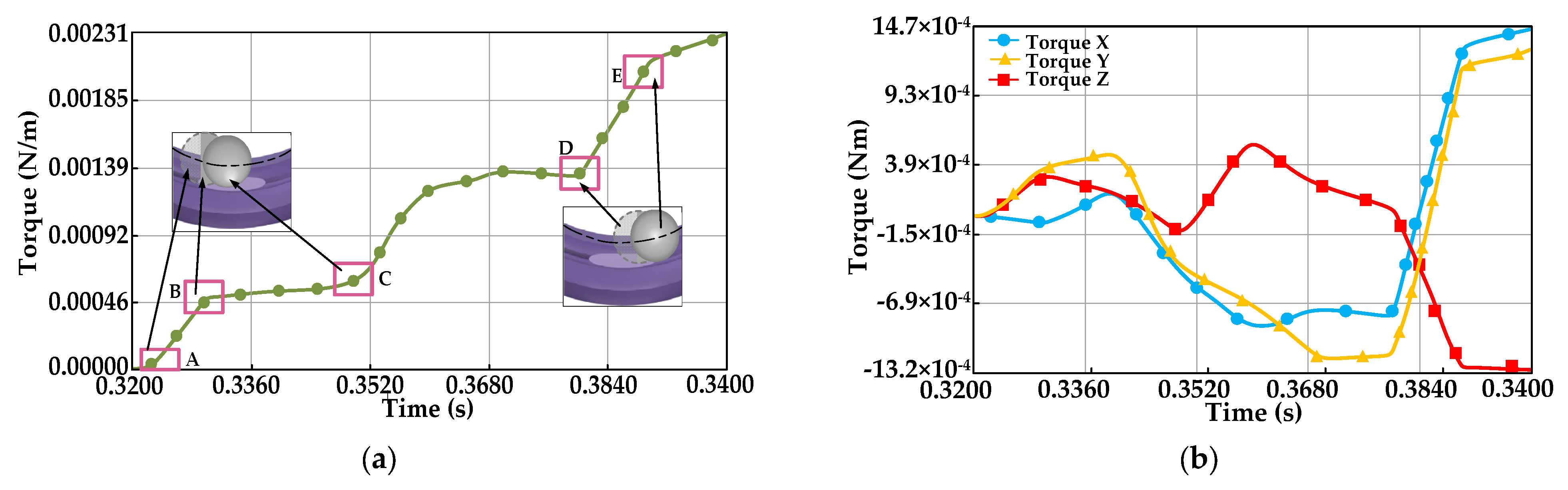
As can be seen from Figure 10, points A–B–C depict the complete process when the rolling element enters the functional groove, at which time the total contact force of the functional groove particles first increases and then decreases and changes sharply. This is due to the fact that, when the rolling element first enters the functional groove, the rolling element changes from a one-point contact to a three-point contact. When it enters completely, it changes to two-point contact, and the change in contact point makes the contact force change sharply. The force in the X–Y–Z three axis direction stays in negative value, which is related to the contact angle between the rolling element and the outer ring, and this change trend is consistent with the direction of the force on the outer ring of the bearing. The inter-particle moment in Figure 11 shows a gradual increase in a step. This indicates that the inter-particle connection bonds are broken when the particles are subjected to the friction and dragging force of the rolling element. Some of them are attracted, so as to be connected by other particles, and the particle clusters are continuously updated. There is a decreasing trend of the moment in the Z-direction, which is caused by the micro-sliding of the rolling element here and the certain vibration of the rolling element along the axial direction.

After obtaining the external force between the particles, the internal force between the particles is calculated, and the amount of overlap between the particles and the inter-particle force is obtained, as shown in Figure 12, Figure 13 and Figure 14.

When the rolling element squeezes the functional groove, the overlap amount of the particle cluster is shown in Figure 12. The normal overlap decreases and then increases as the rolling element enters and leaves the functional groove. This is due to the fact that, when the rolling element enters and leaves the functional groove, the contact point increases and then decreases, and the elastic force is dispersed. The particle entering the functional groove is instantaneously subjected to a huge elastic force. When leaving the functional groove, with the gradual entry due to the special structure of the functional groove, the end of the functional groove produces a certain resistance to the rolling element. The normal overlap of these two points is the largest. When the rolling element rolls over the functional groove, the tangential overlap amount has been in a growing trend, and the growth rate is fast when entering and gradually stabilized.

As shown in Figure 13, the normal force of the functional groove particle grows steadily when the rolling element rolls over the functional groove, and the growth rate slows down at point A. On the X and Y axes, the normal force is always negative, indicating that the direction of the force is along the opposite direction of the X and Y axes, which is consistent with the rolling element motion. On the Z-axis, the normal force is positive, indicating that the direction of the force is in line with the direction of the Z-axis, and the rolling element squeezes toward the narrow edge.

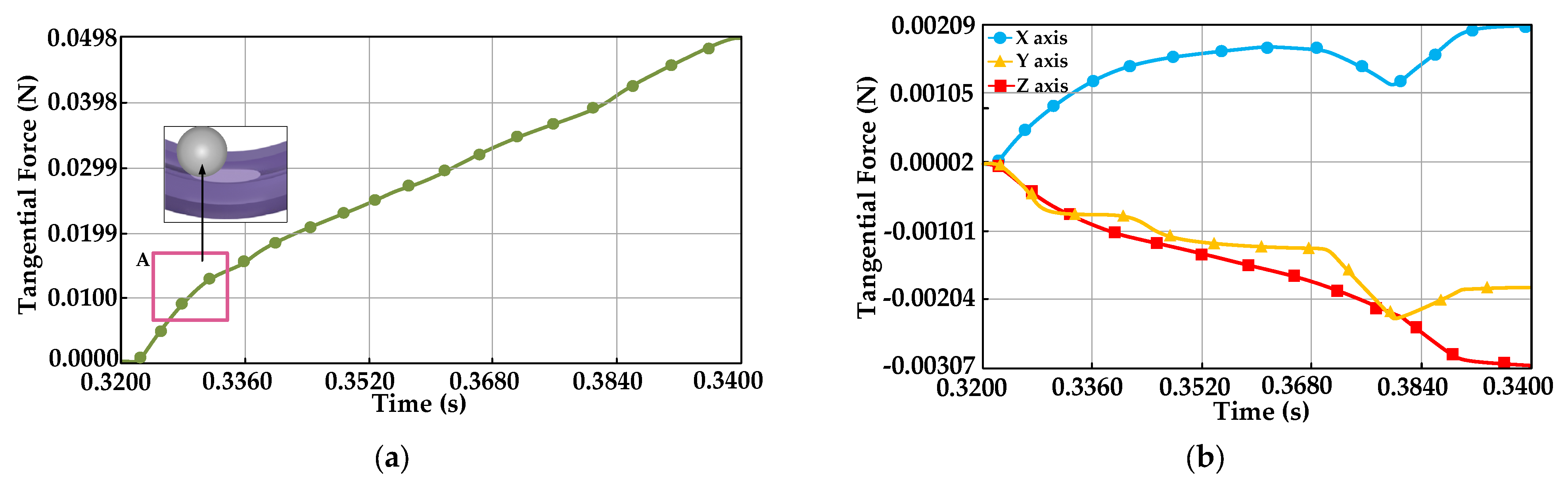
As shown in Figure 14, when the rolling element rolls over the functional groove, the tangential force of the functional groove particle grows in the same trend as the normal force, and the growth rate slows down at point A. On the Y and Z axes, the normal force is always negative, indicating that the direction of the force is along the opposite direction of the Y and Z axes. On the X-axis, the normal force is positive, indicating that the direction of the force is in the same direction as the X-axis, and the functional groove produces a certain impact wear on the rolling element due to its special shape.

When the rolling element rolls over the functional groove, the connection bond between particles breaks is shown in Figure 15, and, when the rolling element enters the functional groove, the functional groove breaks under the external force generated by the instant impact of the rolling element. When completely into the functional groove, the bonding force between the connection keys plays a certain role, and the external force between the particles and their own internal force reaches a certain balance and tends to stabilize, and it slowly breaks.

The mechanical properties of the particles, as well as the dynamic response of the rolling element during the complete cycle of the rolling element passing through the functional groove, respond to the motion of the rolling element. The micro-sliding and slipping of the rolling element have a great impact on the wear of the bearing, and the functional groove is more prone to wear when the rolling element enters and leaves. The motion of the particles and the number of fractured bonds respond to the trend of functional groove damage expansion, and the narrow side has a more severe wear trend than the wide side due to the presence of the bearing contact angle.

The wear test was carried out on the T10-60 type bearing testing machine at 6000 r/min speed and radial loading of 1000 N, 1500 N, and 2000 N until the bearing failed, respectively, for the ball bearing without cage. This is shown in Figure 16 for the T10-60 type bearing testing machine.

Table 3. Basic parameters of cageless ball bearing.

Specimen Number	Radial Load/N	Mass before Wear/g	Mass after Wear/g	Wear Quality/mg
1	1000	97.4966	90.5166	6.98
2	1000	97.8781	89.8881	7.46
3	1000	97.7901	89.8001	7.99
4	1000	97.0384	89.9684	7.07
5	1500	97.0379	89.9579	7.08
6	1500	97.7477	89.5377	8.21
7	1500	97.1867	88.9167	8.27
8	1500	97.2204	88.7904	8.43
9	2000	97.6552	88.2852	9.37
10	2000	97.6569	89.0769	8.58
11	2000	97.0451	88.2251	8.82
12	2000	97.6655	88.6555	9.01

shows the wear amount of outer raceway of the ball bearing without cage under different radial loads.

The experimental results show that, with the increase in radial load, the wear of the outer race becomes gradually larger. The wear study of the outer raceway of the bearing calculated in the theoretical part was carried out at an inner ring speed of 6000 r/min and a radial load of 2000 N. Therefore, comparing the obtained theoretical value with the test value of test piece 9–12, the error between the theoretical wear amount of 9.397 mg and the average test wear amount of 8.945 mg is 4.81%, which is within the error allowed. The reasons for the error are:

(1)

The particle size set in the theoretical analysis is larger than some of the wear particles in the test, so the test value of the wear amount is small.

(2)

Some of the test wear off of the tiny bearing steel material is attached to the outer race of the bearing, and, when cleaning, the worn specimen did not clean off, so the test value of wear is small.

4. Discussion

In this paper, the wear principle of the local functional groove of the cageless bearing is studied by EDEM method. By analyzing the contact between the particles, the equations of motion of the particles to obtain the functional groove particles are established, and the velocity model of the particle cluster is obtained. According to the force motion relationship of particles, the particle–particle and particle–boundary interaction models are established, and the intrinsic model of functional groove particles is obtained. Based on the results of the theoretical analysis, the EDEM simulation conditions were established and solved to obtain the particle motion and force when the rolling element rolls over the functional groove for one week. The results show that the functional groove is more prone to wear during the entry and exit phases of the rolling element, and the tendency of damage extension is heavier when leaving due to impact friction. Due to the special structure of the functional groove and the contact angle, the narrow side of the functional groove is more strongly affected by the sliding and collision of the rolling element than the wide side, and it is more prone to wear.

Although these studies reveal important findings, there are still some limitations. The article only solves for the inter-particle forces and overlap when the rolling element rolls through one turn of the functional groove, which can reduce the amount of operations and analyze the motion trend of microscopic particles under the action of external forces in more detail. However, this does not consider the macroscopic impact of multiple rolling elements superimposed on the functional groove. In the next step of research, it is necessary to convert from microscopic wear to macroscopic wear trend. In the calculation of inter-particle contact, the Hertz contact theory was not used in order to simulate the process more realistically, but the hyper-quadratic surface was created according to the change in external conditions. However, in the EDEM simulation, different spherical particles were combined into particle clusters of different shapes to achieve the simulation of the special structure of the bearing and the friction characteristics of the material, but they were not completely accurate. The next step will be to study the shape of particles and analyze the effect of different particle shapes on the accuracy of wear simulation. The results show that the inter-particle connecting bonds break more when the rolling element first enters the functional groove, and the broken bonds break less as the rolling element enters the functional groove completely, which may be the effect of entanglement of the two parts of particles on the motion state of the particles in the functional groove after discrete performance, which needs further study.

The article reveals the failure mechanism of the functional groove based on the EDEM method, explores the formation of cracks on the surface of functional groove, provides a theoretical basis for the study of damage extension morphology on the surface of functional groove, and explores the transfer model of external force between particles inside functional groove based on fracture mechanics theory to improve the study of micro-macro wear of functional groove.

5. Conclusions

The following conclusions were obtained from the study of microscopic wear mechanisms in local functional grooves:

• Based on the material properties of the bearing and the structure of the functional groove, a discrete unit model of the functional groove was established, and the functional groove was discrete into a particle system composed of irregular particle groups.
• The super quadratic surface of the particle cluster contact of the functional groove is established, and the discrete element method contact model is improved. Coordinate transformation of the inertial system and the motion system of the particles was carried out to obtain the equations of motion of the functional groove particles, by which the particle cluster velocity model was established and the motion trend of the rough particles at the edge of the functional groove was obtained. Based on the force–motion relationship of the particles, the particle–particle and particle–boundary interaction models were established, and the intrinsic model of the functional groove particles was constructed in this way.
• The EDEM simulation model was established, and the solution results show that, due to the end impact wear effect, the expansion tendency of the end of the functional groove is more serious than other parts, and due to the special structure of the functional groove and the existence of the contact angle, the narrow side of the functional groove is more strongly affected by the sliding and collision of the rolling element than the wide side, which is more likely to lead to failure.

The study of the internal particle motion trend and fracture of the functional groove can provide a theoretical basis for the rolling contact fatigue mechanism of the bearing and also provide a theoretical basis for the condition detection of the bearing operation, reducing the failure of the machine and equipment and economic loss due to the bearing failure. In future research, we will consider the change in functional groove response due to rolling element motion migration, continuously improve the research of rolling contact fatigue failure of bearings, and provide more accurate failure prediction models for machines.