A Wearable Upper Limb Exoskeleton for Intuitive Teleoperation of Anthropomorphic Manipulators
Abstract
1. Introduction
- We present a complete solution for measuring precisely upper limb posture with a wearable exoskeleton device. Compared with existing works in [19,20,21,22], our exoskeleton can be steadily fixed on the torso by the curved back frame and carrying system, which provides self-alignment capabilities and guarantees measurement accuracy.
- We seek to make a balance between the complexity and human-machine compatibility of the device. A spherical scissor mechanism is proposed for the exoskeleton shoulder to maximize the device’s range of motion without making the system bulky. The overall mass of the device is only 4.8 kg, which is lighter than most existing similar devices.
- We provide both joint space and task space control strategies for performing teleoperation of anthropomorphic manipulators with the exoskeleton device. The flexible control strategies allow the exoskeleton to adapt to different types of slave devices and application requirements.
2. Design and Implementation
2.1. Upper Limb Motions and Modeling
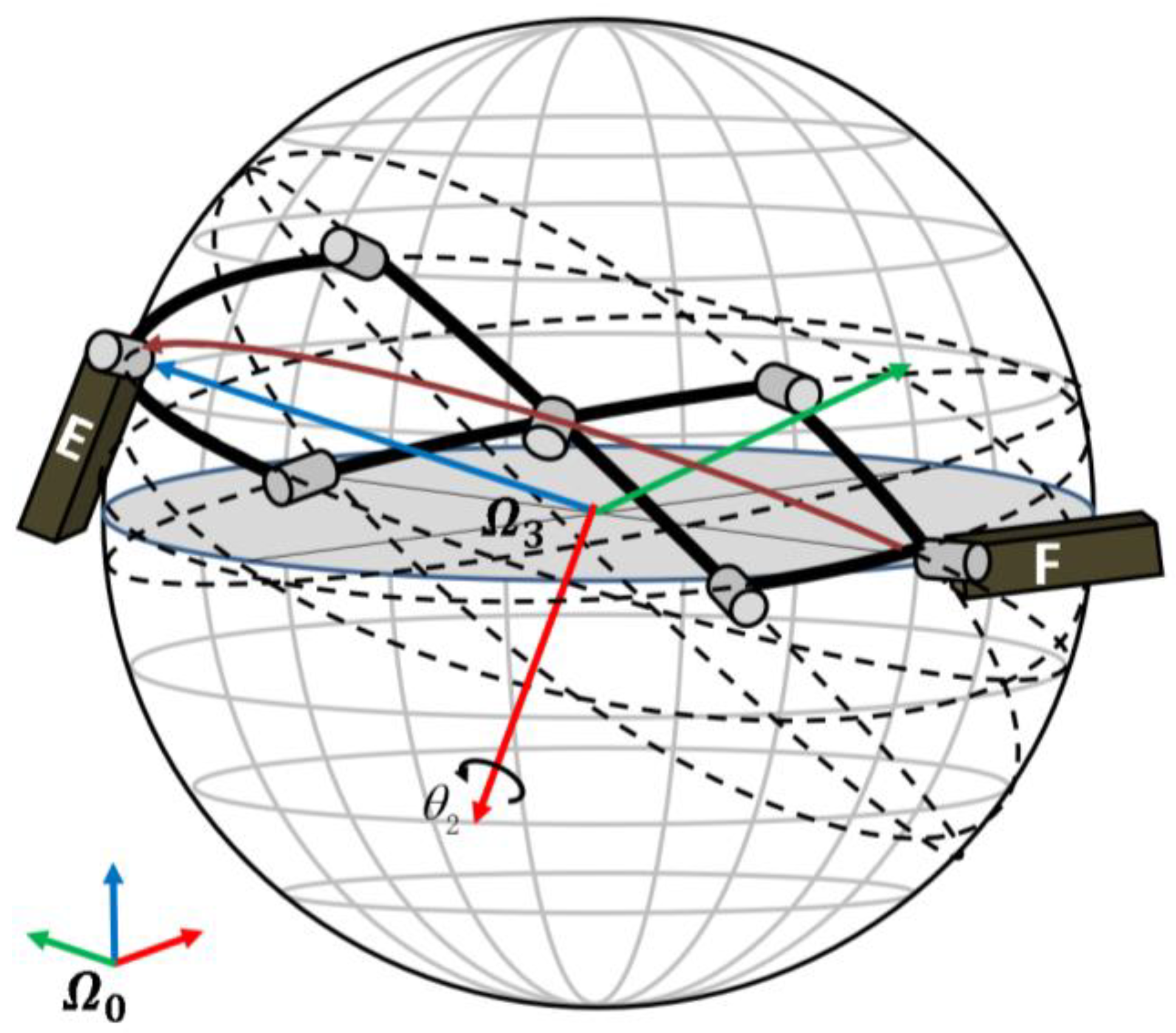
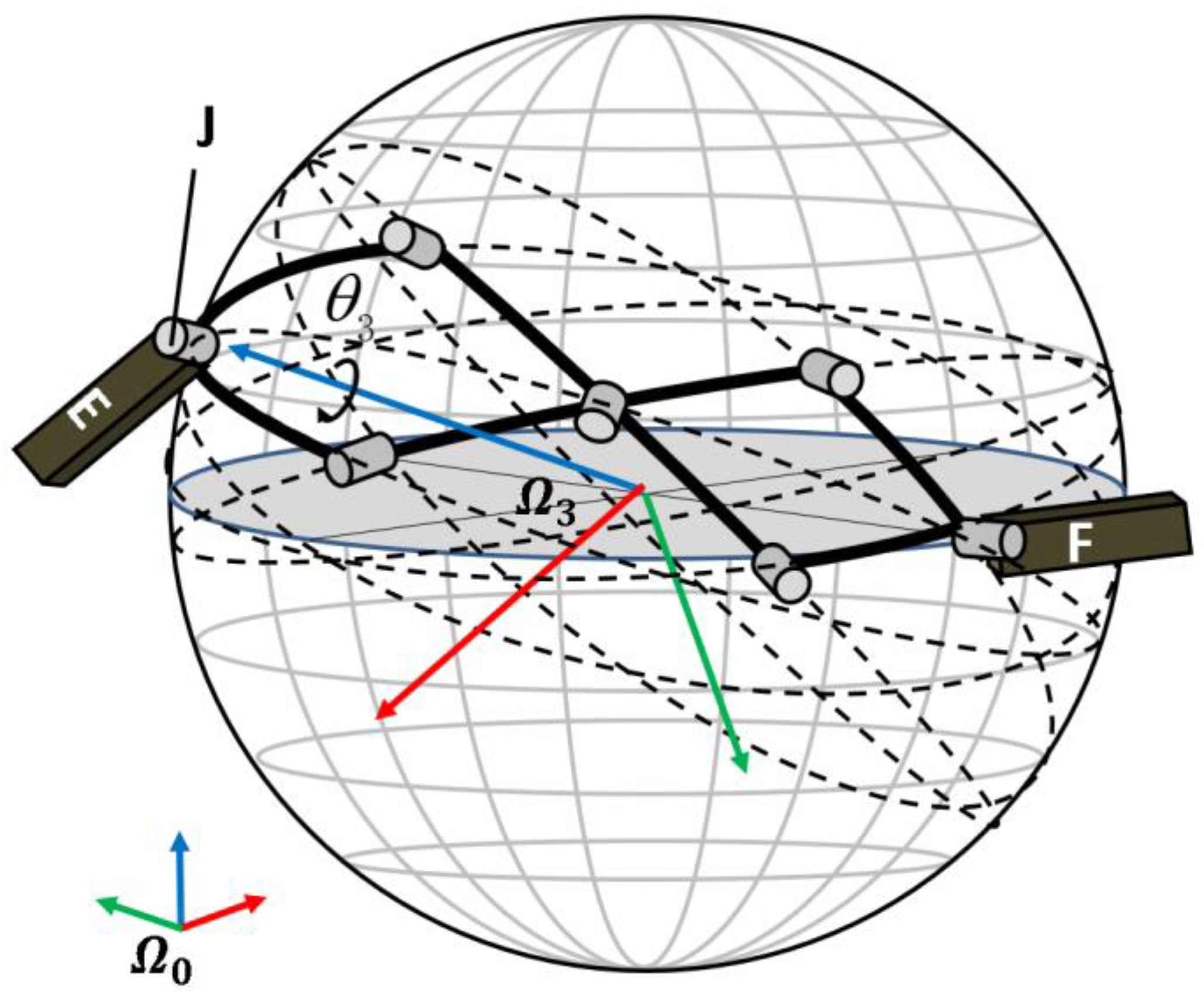
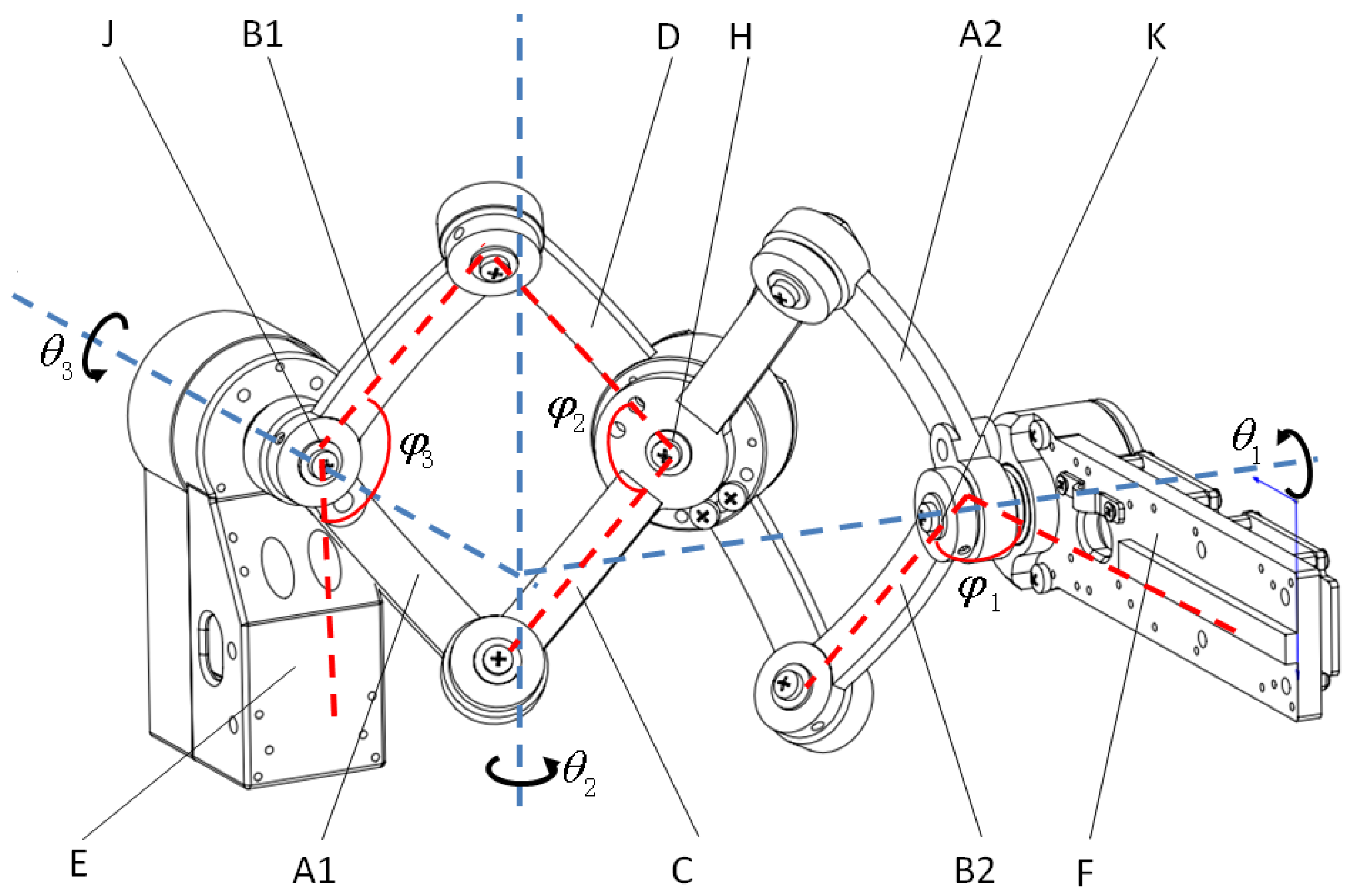
2.2. Shoulder Mechanism
2.3. Shoulder Pose Estimation
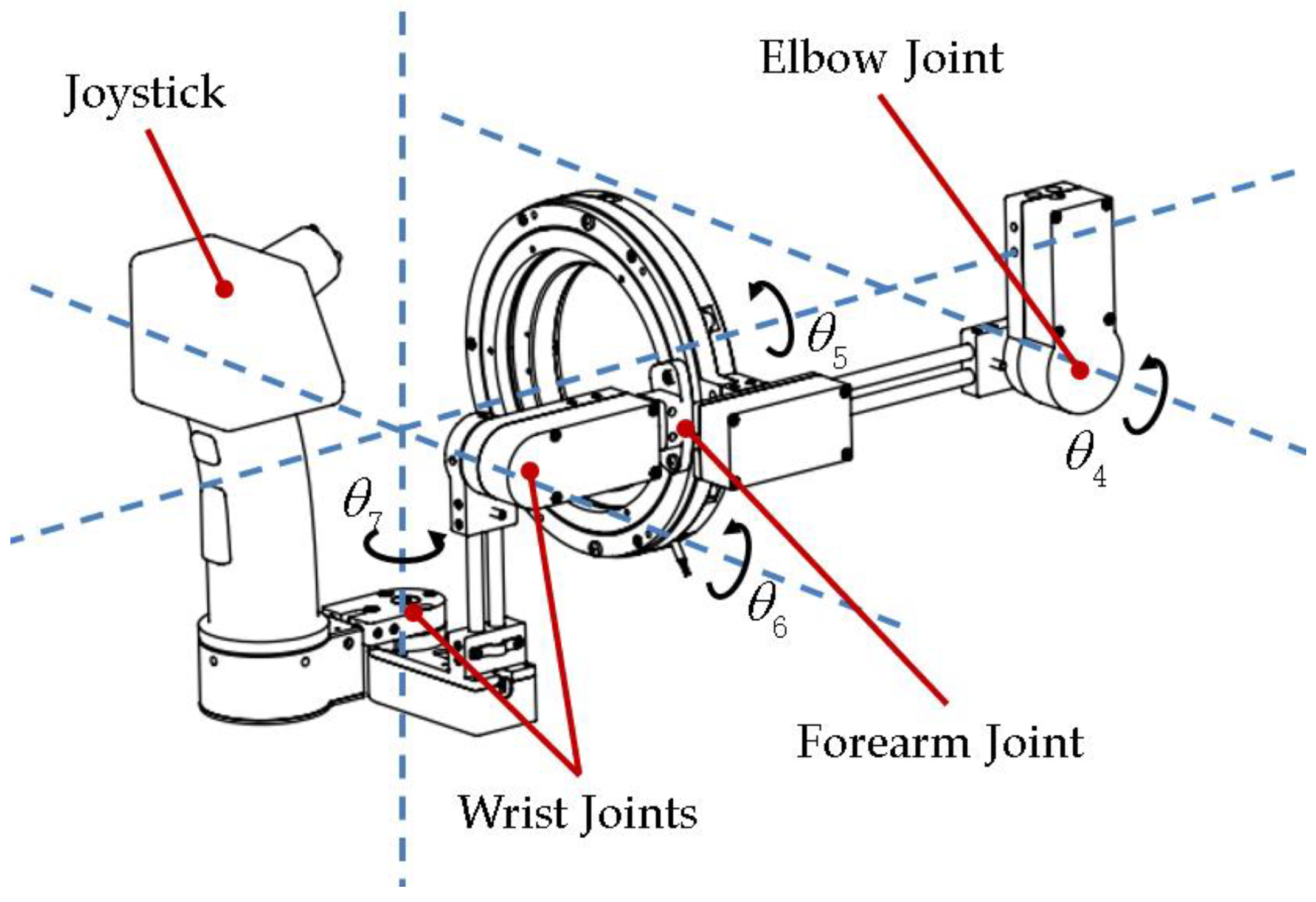
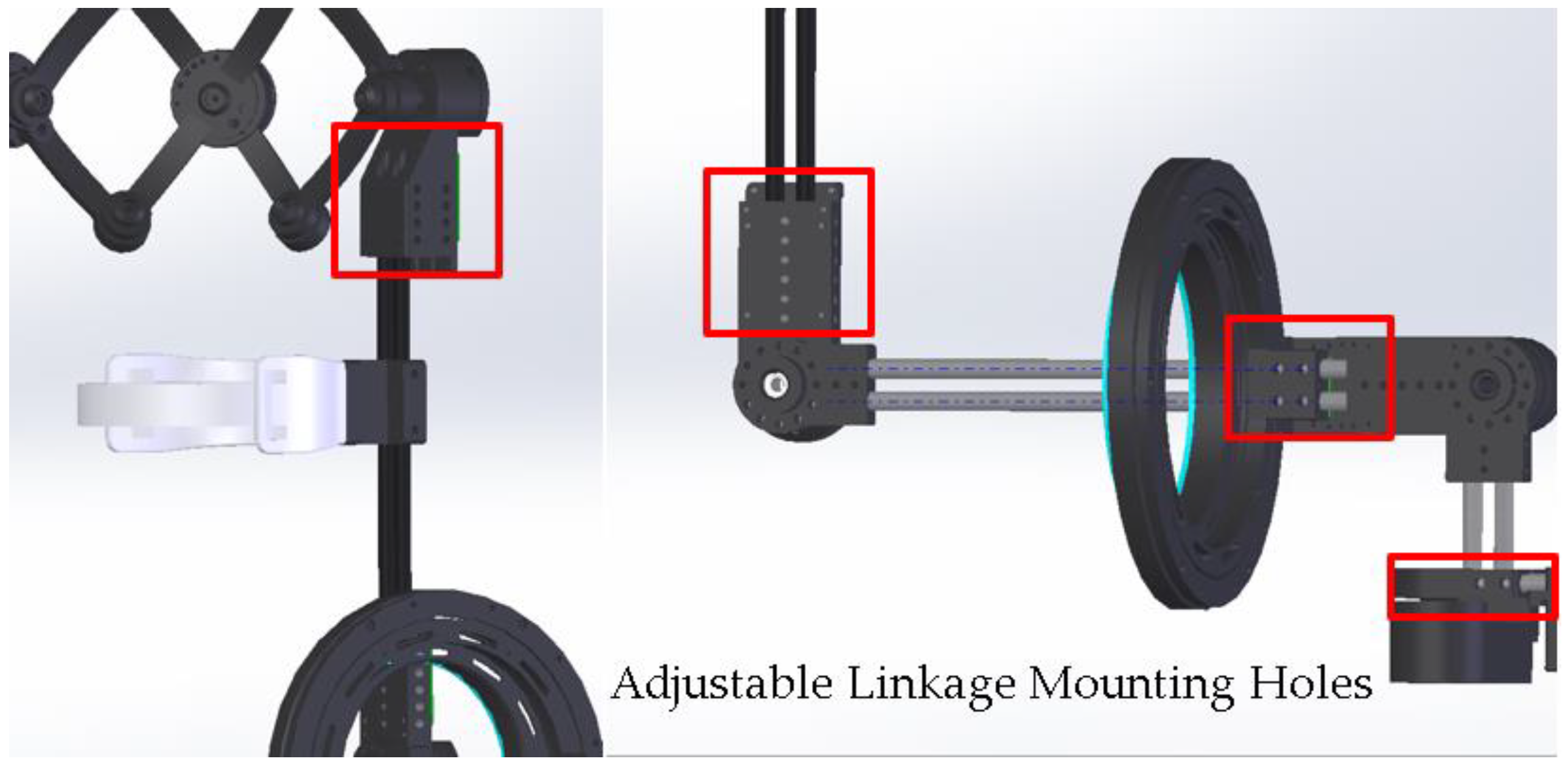
2.4. Position-Orientation Decoupled Wrist Mechanism
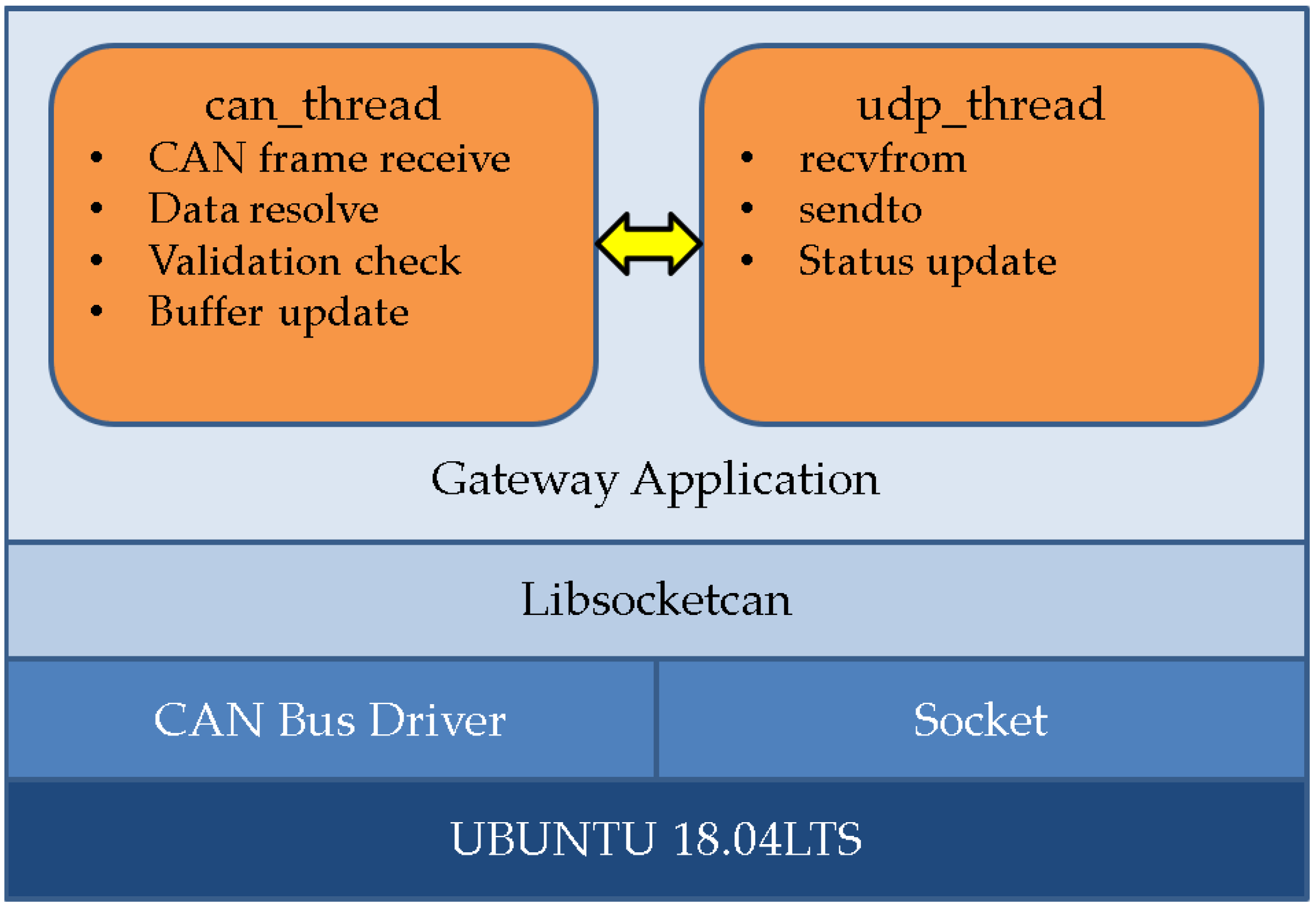
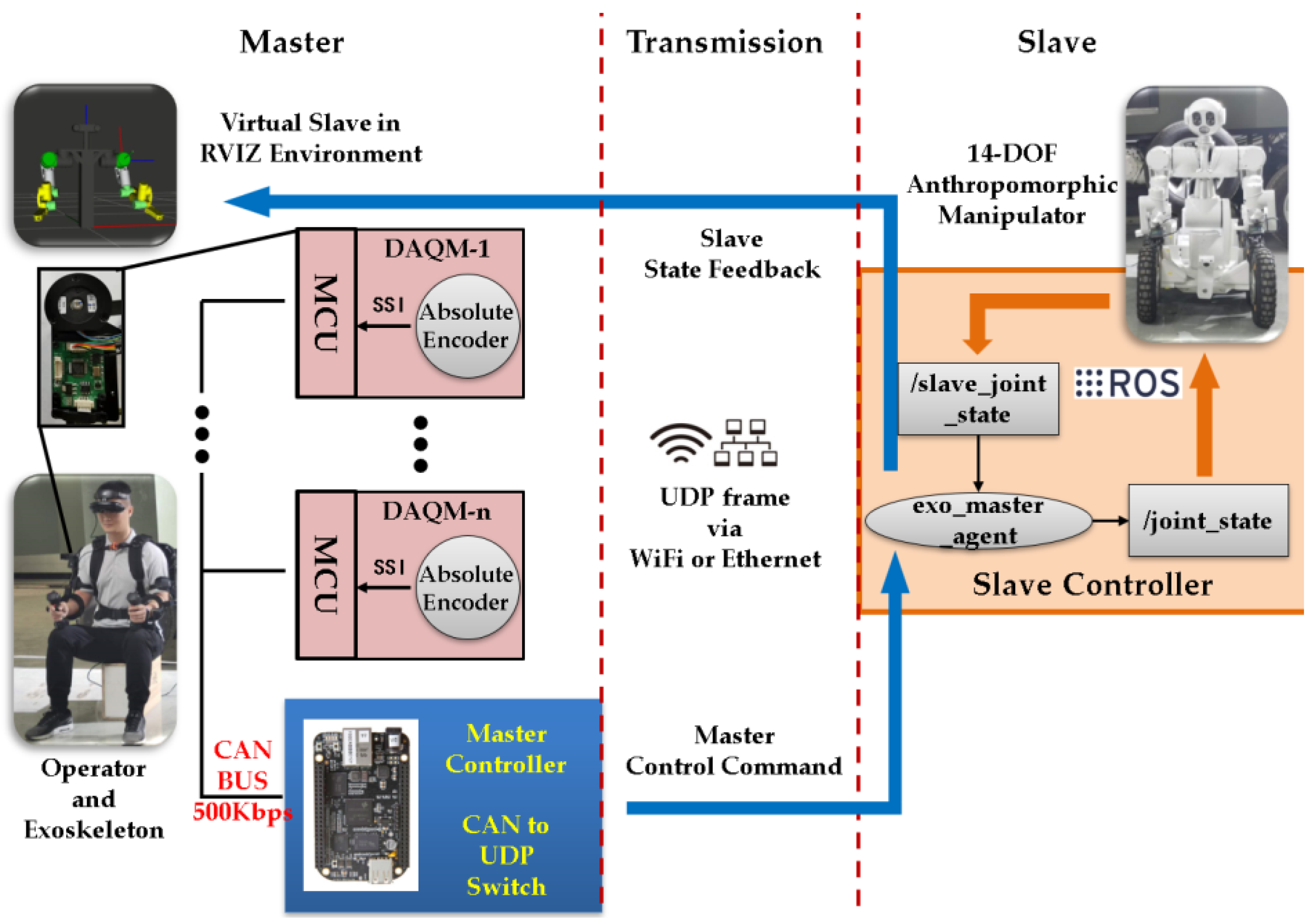
2.5. Data Acquisition and Transmission
2.6. Implementation Details of a Prototype
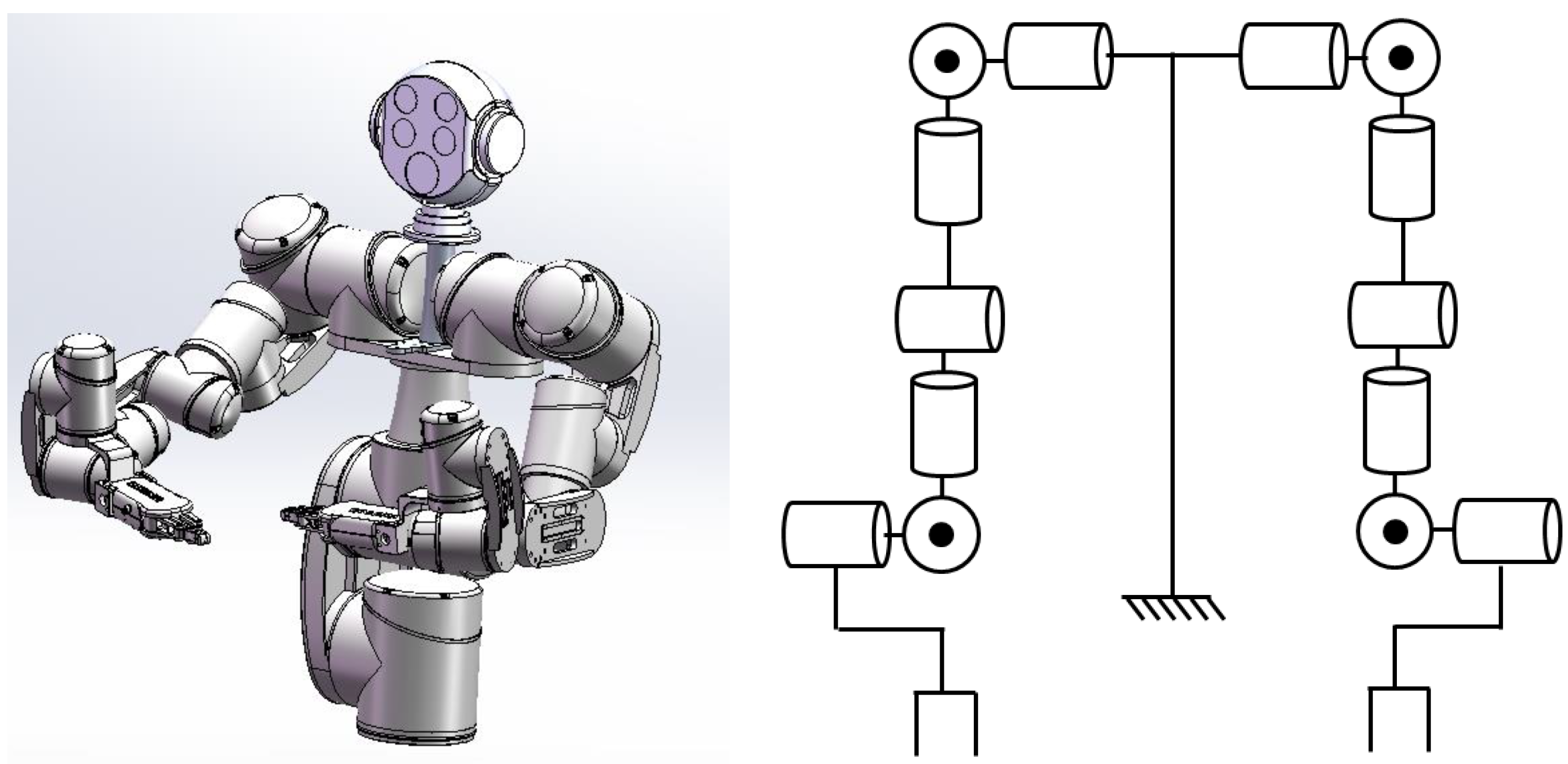
3. Motion Mapping to the Anthropomorphic Manipulators
3.1. Joint Space Mapping
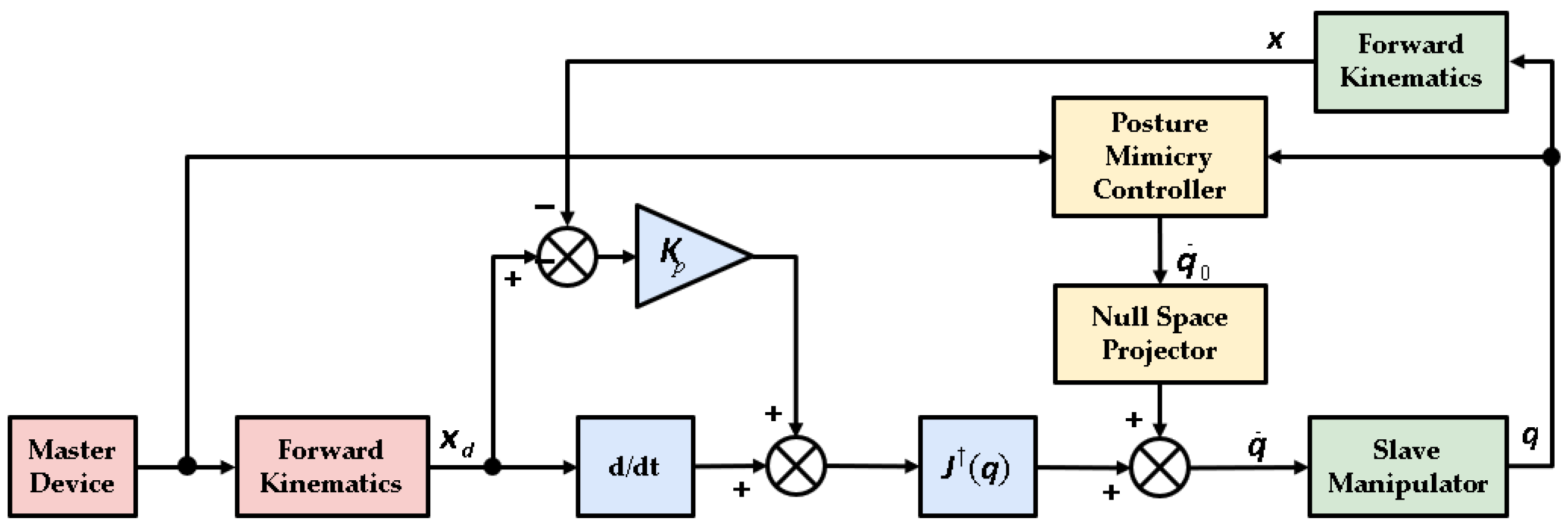
3.2. Task Space Mapping
4. Experiments
4.1. Experimental Setup
4.2. Range of Motion Evaluation
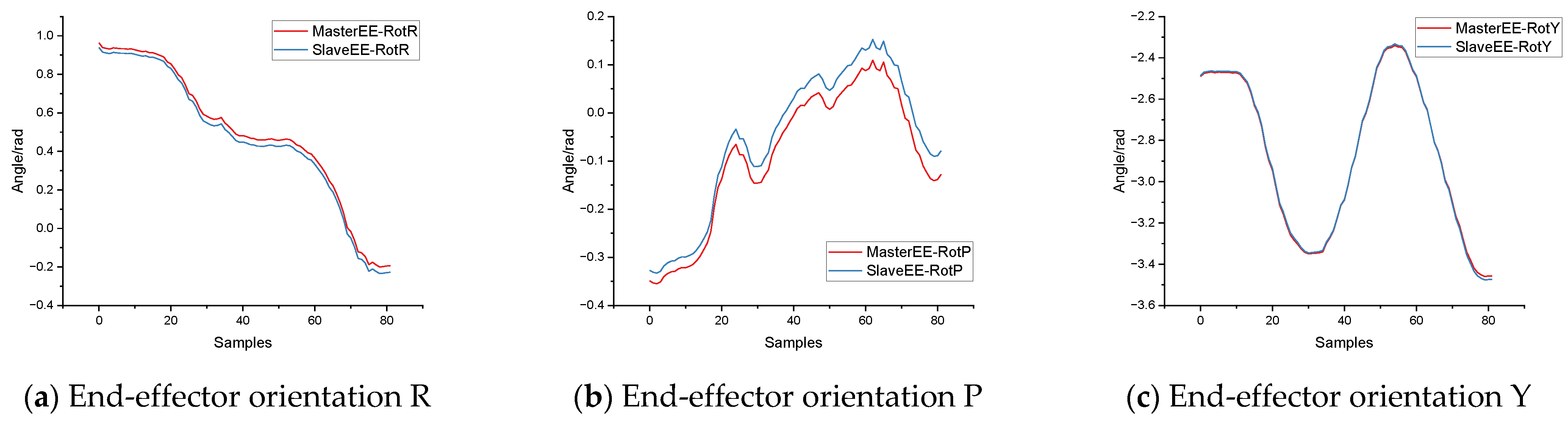
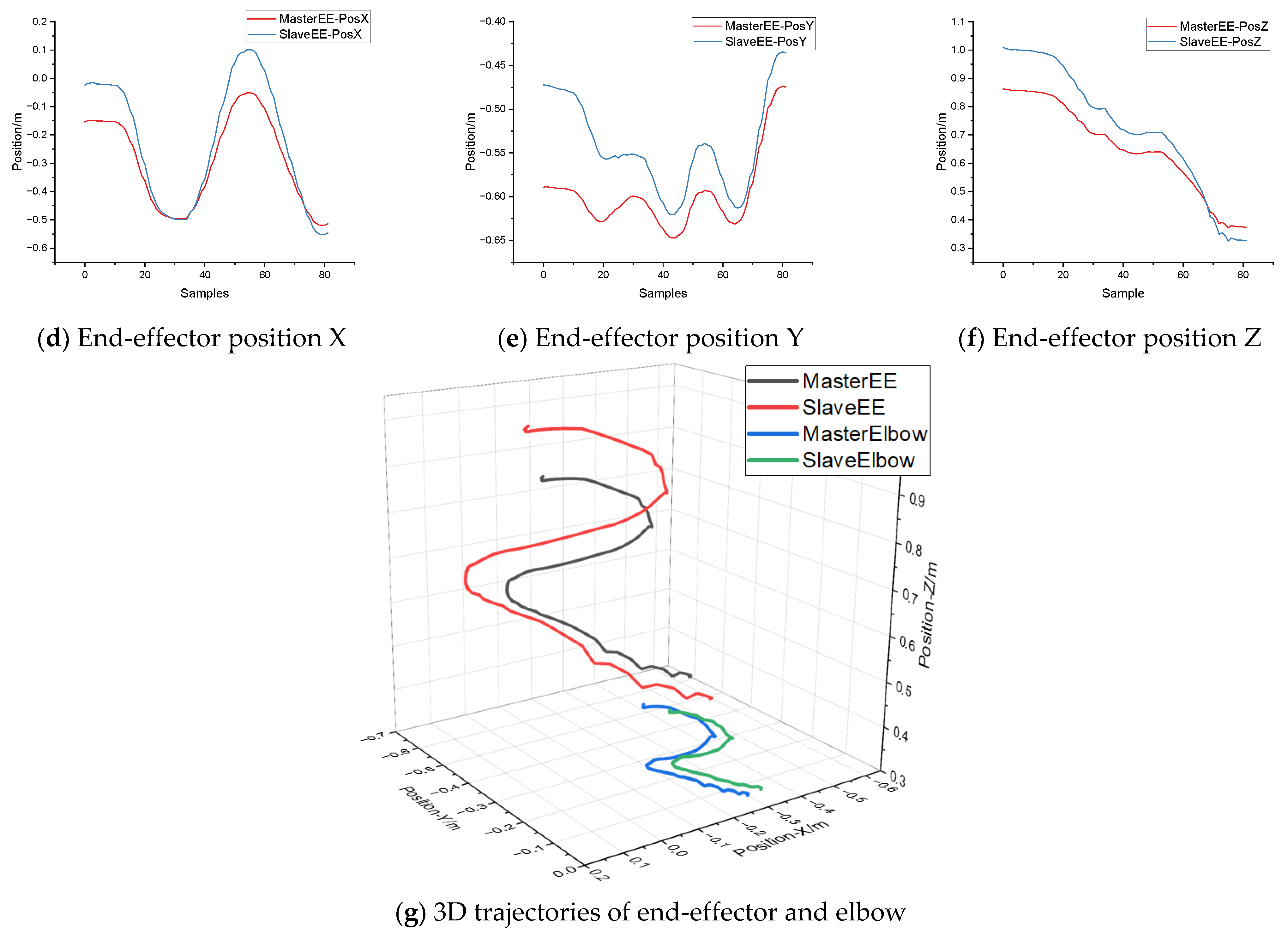
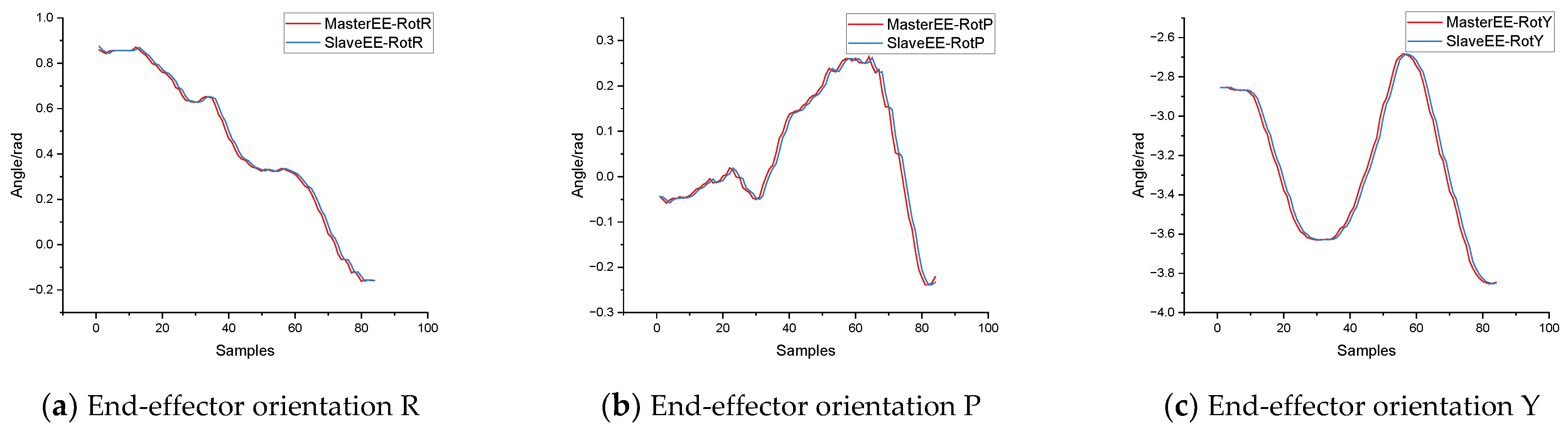
4.3. Precision and Dynamic Performance Evaluation
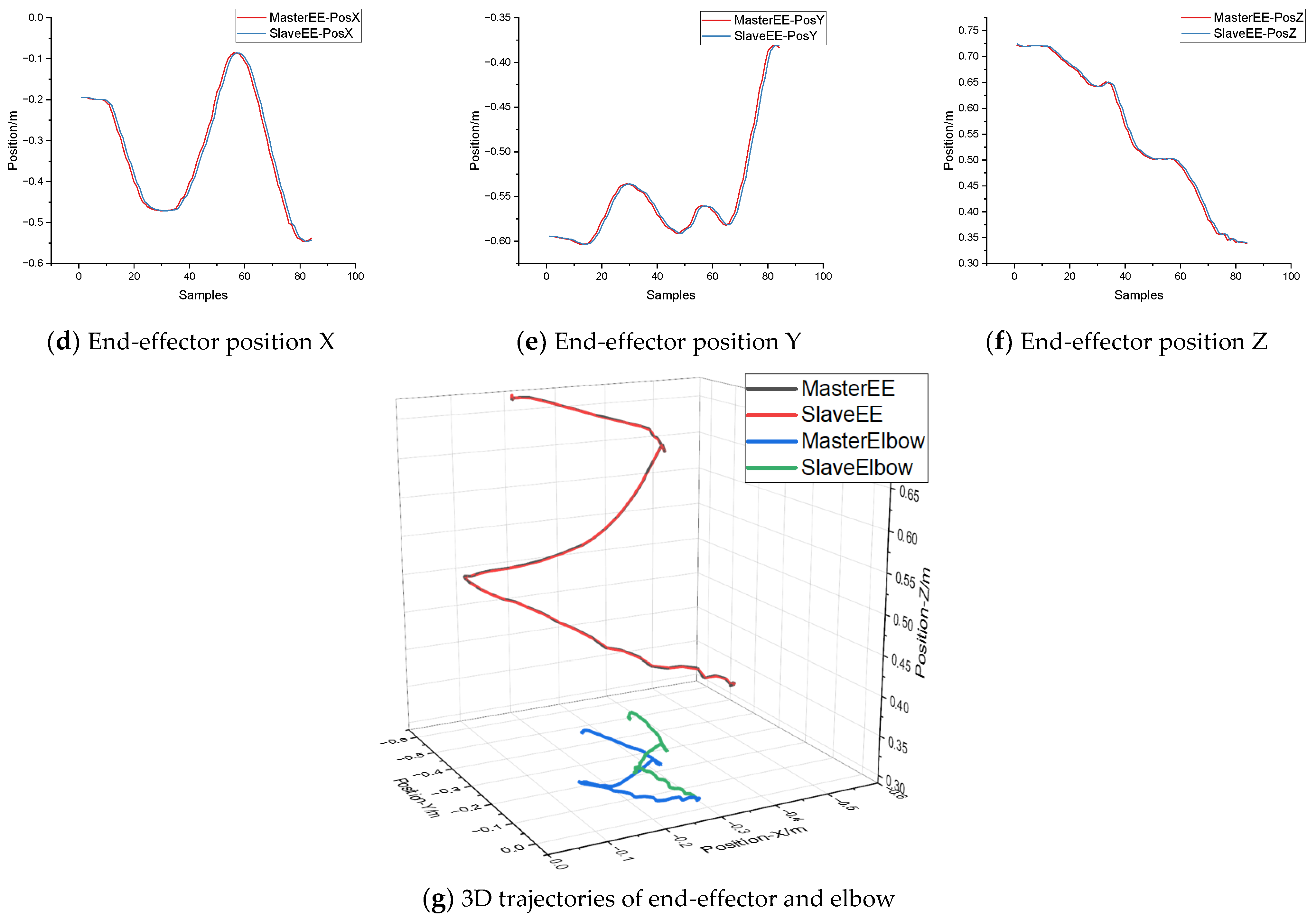
4.4. Task Demonstrations on a Real Anthropomorphic Manipulator
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Caiza, G.; Garcia, C.A.; Naranjo, J.E.; Garcia, M.V. Flexible Robotic Teleoperation Architecture for Intelligent Oil Fields. Heliyon 2020, 6, e03833. [Google Scholar] [CrossRef] [PubMed]
- Conte, D.; Leamy, S.; Furukawa, T. Design and Map-Based Teleoperation of a Robot for Disinfection of COVID-19 in Complex Indoor Environments. In Proceedings of the 2020 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Abu Dhabi, United Arab Emirates, 4–6 November 2020; pp. 276–282. [Google Scholar]
- Guo, J.; Ye, L.; Liu, H.; Wang, X.; Liang, L.; Liang, B. Safety-Oriented Teleoperation of a Dual-Arm Mobile Manipulation Robot. In Intelligent Robotics and Applications, Proceedings of the 15th International Conference, ICIRA 2022, Harbin, China, 1–3 August 2022; Liu, H., Yin, Z., Liu, L., Jiang, L., Gu, G., Wu, X., Ren, W., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 780–792. [Google Scholar]
- Liu, G.; Geng, X.; Liu, L.; Wang, Y. Haptic Based Teleoperation with Master-Slave Motion Mapping and Haptic Rendering for Space Exploration. Chin. J. Aeronaut. 2019, 32, 723–736. [Google Scholar] [CrossRef]
- Nawab, A.; Chintamani, K.; Ellis, D.; Auner, G.; Pandya, A. Joystick Mapped Augmented Reality Cues for End-Effector Controlled Tele-Operated Robots. In Proceedings of the 2007 IEEE Virtual Reality Conference, Charlotte, NC, USA, 10–14 March 2007; pp. 263–266. [Google Scholar]
- Cornejo, J.; Denegri, E.; Vasquez, K.; Ramos, O.E. Real-Time Joystick Teleoperation of the Sawyer Robot Using a Numerical Approach. In Proceedings of the 2018 IEEE ANDESCON, Cali, Colombia, 22–24 August 2018; pp. 1–3. [Google Scholar]
- Silva, A.J.; Ramirez, O.A.D.; Vega, V.P.; Oliver, J.P.O. PHANToM OMNI Haptic Device: Kinematic and Manipulability. In Proceedings of the 2009 Electronics, Robotics and Automotive Mechanics Conference (CERMA), Cuernavaca, Mexico, 22–25 September 2009; pp. 193–198. [Google Scholar]
- Tobergte, A.; Helmer, P.; Hagn, U.; Rouiller, P.; Thielmann, S.; Grange, S.; Albu-Schäffer, A.; Conti, F.; Hirzinger, G. The Sigma.7 Haptic Interface for MiroSurge: A New Bi-Manual Surgical Console. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 3023–3030. [Google Scholar]
- Núñez, M.L.; Dajles, D.; Siles, F. Teleoperation of a Humanoid Robot Using an Optical Motion Capture System. In Proceedings of the 2018 IEEE International Work Conference on Bioinspired Intelligence (IWOBI), San Carlos, Costa Rica, 18–20 July 2018; pp. 1–8. [Google Scholar]
- Vongchumyen, C.; Bamrung, C.; Kamintra, W.; Watcharapupong, A. Teleoperation of Humanoid Robot by Motion Capturing Using KINECT. In Proceedings of the 2018 International Conference on Engineering, Applied Sciences, and Technology (ICEAST), Phuket, Thailand, 4–7 July 2018; pp. 1–4. [Google Scholar]
- Vasiljevic, G.; Jagodin, N.; Kovacic, Z. Kinect-Based Robot Teleoperation by Velocities Control in the Joint/Cartesian Frames. IFAC Proc. Vol. 2012, 45, 805–810. [Google Scholar] [CrossRef]
- Miller, N.; Jenkins, O.C.; Kallmann, M.; Mataric, M.J. Motion Capture from Inertial Sensing for Untethered Humanoid Teleoperation. In Proceedings of the 4th IEEE/RAS International Conference on Humanoid Robots, Santa Monica, CA, USA, 28–30 November 2004; Volume 2, pp. 547–565. [Google Scholar]
- Park, S.; Jung, Y.; Bae, J. An Interactive and Intuitive Control Interface for a Tele-Operated Robot (AVATAR) System. Mechatronics 2018, 55, 54–62. [Google Scholar] [CrossRef]
- Proietti, T.; Crocher, V.; Roby-Brami, A.; Jarrassé, N. Upper-Limb Robotic Exoskeletons for Neurorehabilitation: A Review on Control Strategies. IEEE Rev. Biomed. Eng. 2016, 9, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Esposito, D.; Centracchio, J.; Andreozzi, E.; Savino, S.; Gargiulo, G.D.; Naik, G.R.; Bifulco, P. Design of a 3D-Printed Hand Exoskeleton Based on Force-Myography Control for Assistance and Rehabilitation. Machines 2022, 10, 57. [Google Scholar] [CrossRef]
- Zuccon, G.; Bottin, M.; Ceccarelli, M.; Rosati, G. Design and Performance of an Elbow Assisting Mechanism. Machines 2020, 8, 68. [Google Scholar] [CrossRef]
- Geonea, I.; Copilusi, C.; Dumitru, N.; Margine, A.; Ciurezu, L.; Rosca, A.S. A New Exoskeleton Robot for Human Motion Assistance. In Proceedings of the 2022 IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 19–21 May 2022; pp. 1–6. [Google Scholar]
- Bai, S.; Islam, M.R.; Hansen, K.; Nørgaard, J.; Chen, C.-Y.; Yang, G. A Semi-Active Upper-Body Exoskeleton for Motion Assistance. In Wearable Robotics: Challenges and Trends, Proceedings of the 5th International Symposium on Wearable Robotics, WeRob2020, and of WearRAcon Europe 2020, 13–16 October 2020; Moreno, J.C., Masood, J., Schneider, U., Maufroy, C., Pons, J.L., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 301–305. [Google Scholar]
- Planthaber, S.; Mallwitz, M.; Kirchner, E.A. Immersive Robot Control in Virtual Reality to Command Robots in Space Missions. JSEA 2018, 11, 341–347. [Google Scholar] [CrossRef]
- Maekawa, A.; Takahashi, S.; Saraiji, M.Y.; Wakisaka, S.; Iwata, H.; Inami, M. Naviarm: Augmenting the Learning of Motor Skills Using a Backpack-Type Robotic Arm System. In Proceedings of the 10th Augmented Human International Conference 2019, Reims, France, 11–12 March 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 1–8. [Google Scholar]
- Barnaby, G.; Roudaut, A. Mantis: A Scalable, Lightweight and Accessible Architecture to Build Multiform Force Feedback Systems. In Proceedings of the 32nd Annual ACM Symposium on User Interface Software and Technology, New Orleans, LA, USA, 20–23 October 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 937–948. [Google Scholar]
- Lee, C.-H.; Choi, J.; Lee, H.; Kim, J.; Lee, K.; Bang, Y. Exoskeletal Master Device for Dual Arm Robot Teaching. Mechatronics 2017, 43, 76–85. [Google Scholar] [CrossRef]
- Holzbaur, K.R.S.; Murray, W.M.; Delp, S.L. A Model of the Upper Extremity for Simulating Musculoskeletal Surgery and Analyzing Neuromuscular Control. Ann. Biomed. Eng. 2005, 33, 829–840. [Google Scholar] [CrossRef] [PubMed]
- Roderick, S.; Liszka, M.; Carignan, C.; Roderick, S.; Liszka, M.; Carignan, C. Design of an Arm Exoskeleton with Scapula Motion for Shoulder Rehabilitation. In Proceedings of the ICAR ’05, 12th International Conference on Advanced Robotics, Seattle, WA, USA, 18–20 July 2005; pp. 524–531. [Google Scholar]
- Clinicalgate.com Upper Limb—General Description. Available online: https://clinicalgate.com/upper-limb-2/ (accessed on 1 March 2023).
- Boone, D.C.; Azen, S.P. Normal Range of Motion of Joints in Male Subjects. J. Bone Jt. Surg. Am. 1979, 61, 756–759. [Google Scholar] [CrossRef]
- Lo, H.S.; Xie, S.S.Q. Optimization of a Redundant 4R Robot for a Shoulder Exoskeleton. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, 9–12 July 2013; pp. 798–803. [Google Scholar]
- Castro, M.N.; Rasmussen, J.; Andersen, M.S.; Bai, S. A Compact 3-DOF Shoulder Mechanism Constructed with Scissors Linkages for Exoskeleton Applications. Mech. Mach. Theory 2019, 132, 264–278. [Google Scholar] [CrossRef]
- Li, R.; Liu, Z.; Mi, W.; Bai, S.; Zhang, J. Design and Kinematic Analysis of a Novel Wire-Driven Spherical Scissors Mechanism. In Recent Advances in Mechanisms, Transmissions and Applications; Wang, D., Petuya, V., Chen, Y., Yu, S., Eds.; Springer: Singapore, 2020; pp. 192–200. [Google Scholar]
- Balser, F.; Desai, R.; Ekizoglou, A.; Bai, S. A Novel Passive Shoulder Exoskeleton Designed with Variable Stiffness Mechanism. IEEE Robot. Autom. Lett. 2022, 7, 2748–2754. [Google Scholar] [CrossRef]
- Matsui, K.; Tachibana, T.; Nobuhara, K.; Uchiyama, Y. Translational Movement within the Glenohumeral Joint at Different Rotation Velocities as Seen by Cine MRI. J. Exp. Orthop. 2018, 5, 7. [Google Scholar] [CrossRef] [PubMed]
- Bischoff, R.; Kurth, J.; Schreiber, G.; Koeppe, R.; Albu-Schaeffer, A.; Beyer, A.; Eiberger, O.; Haddadin, S.; Stemmer, A.; Grunwald, G.; et al. The KUKA-DLR Lightweight Robot Arm—A New Reference Platform for Robotics Research and Manufacturing. In Proceedings of the ISR 2010 (41st International Symposium on Robotics) and ROBOTIK 2010 (6th German Conference on Robotics), Munich, Germany, 7–9 June 2010; pp. 1–8. [Google Scholar]
- Bäuml, B.; Hammer, T.; Wagner, R.; Birbach, O.; Gumpert, T.; Zhi, F.; Hillenbrand, U.; Beer, S.; Friedl, W.; Butterfass, J. Agile Justin: An Upgraded Member of DLR’s Family of Lightweight and Torque Controlled Humanoids. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 2562–2563. [Google Scholar]
- Perry, J.C.; Trimble, S.; Machado, L.G.C.; Schroeder, J.S.; Belloso, A.; Rodriguez-de-Pablo, C.; Keller, T. Design of a Spring-Assisted Exoskeleton Module for Wrist and Hand Rehabilitation. In Proceedings of the 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 594–597. [Google Scholar]
- Perry, J.C.; Rosen, J.; Burns, S. Upper-Limb Powered Exoskeleton Design. IEEE/ASME Trans. Mechatron. 2007, 12, 408–417. [Google Scholar] [CrossRef]
- Di Natale, M.; Zeng, H.; Giusto, P.; Ghosal, A. Understanding and Using the Controller Area Network Communication Protocol: Theory and Practice; Springer: New York, NY, USA, 2012; ISBN 978-1-4614-0313-5. [Google Scholar]
- CAN in Automation Designing a CAN Network. Available online: https://www.can-cia.org/can-knowledge/can/design-can-network/ (accessed on 27 February 2023).
- Kleine-Budde, M. SocketCAN—The Official CAN API of the Linux Kernel; Hambach Castle: Neustadt, Germany, 2012; Volume 5, pp. 17–22. [Google Scholar]
- Wang, J.; Li, Y.; Zhao, X. Inverse Kinematics and Control of a 7-DOF Redundant Manipulator Based on the Closed-Loop Algorithm. Int. J. Adv. Robot. Syst. 2010, 7, 37. [Google Scholar] [CrossRef]
- Corke, P. Robotics, Vision and Control; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Rueden, C.T.; Schindelin, J.; Hiner, M.C.; DeZonia, B.E.; Walter, A.E.; Arena, E.T.; Eliceiri, K.W. ImageJ2: ImageJ for the next Generation of Scientific Image Data. BMC Bioinform. 2017, 18, 529. [Google Scholar] [CrossRef] [PubMed]

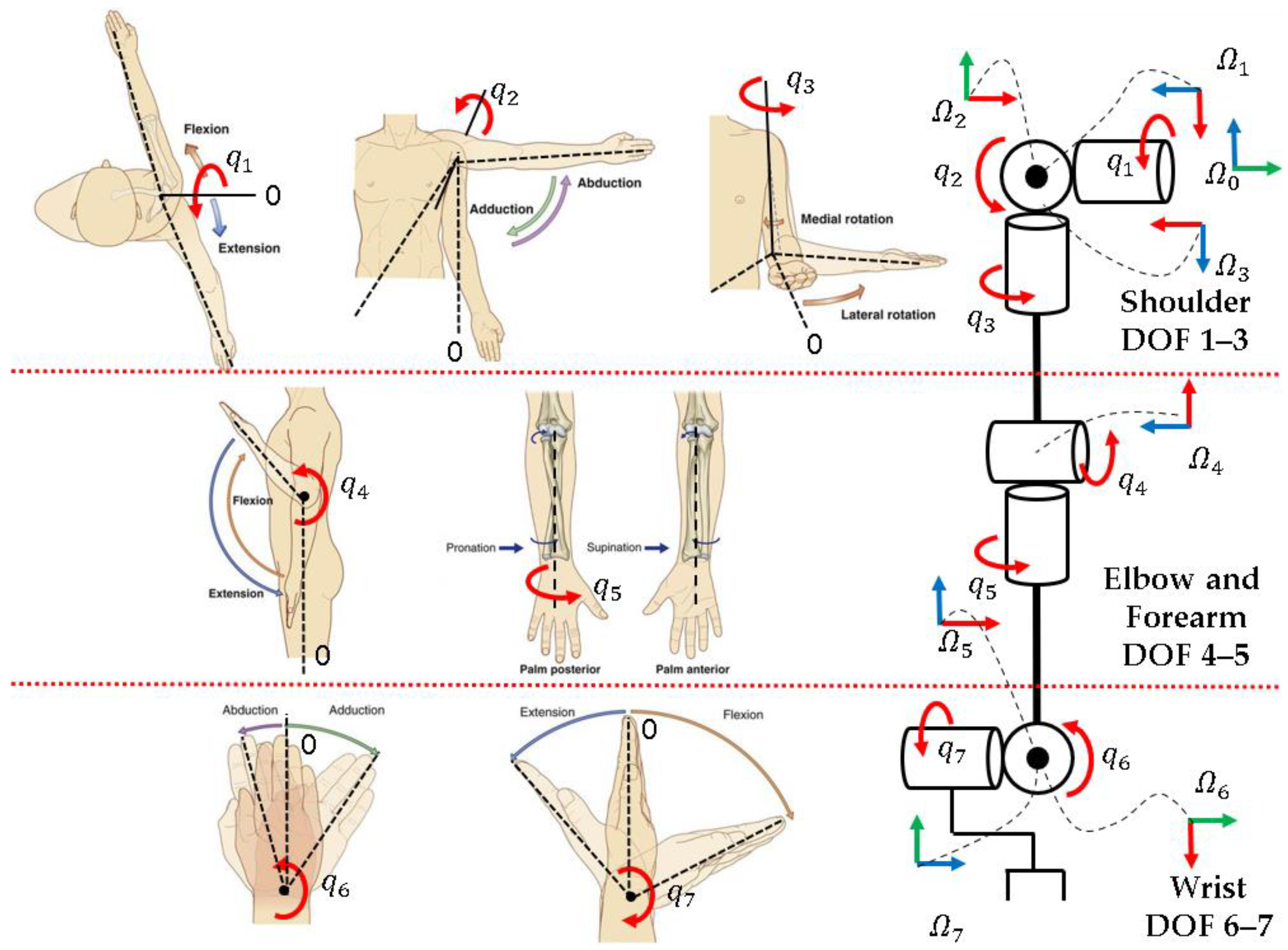
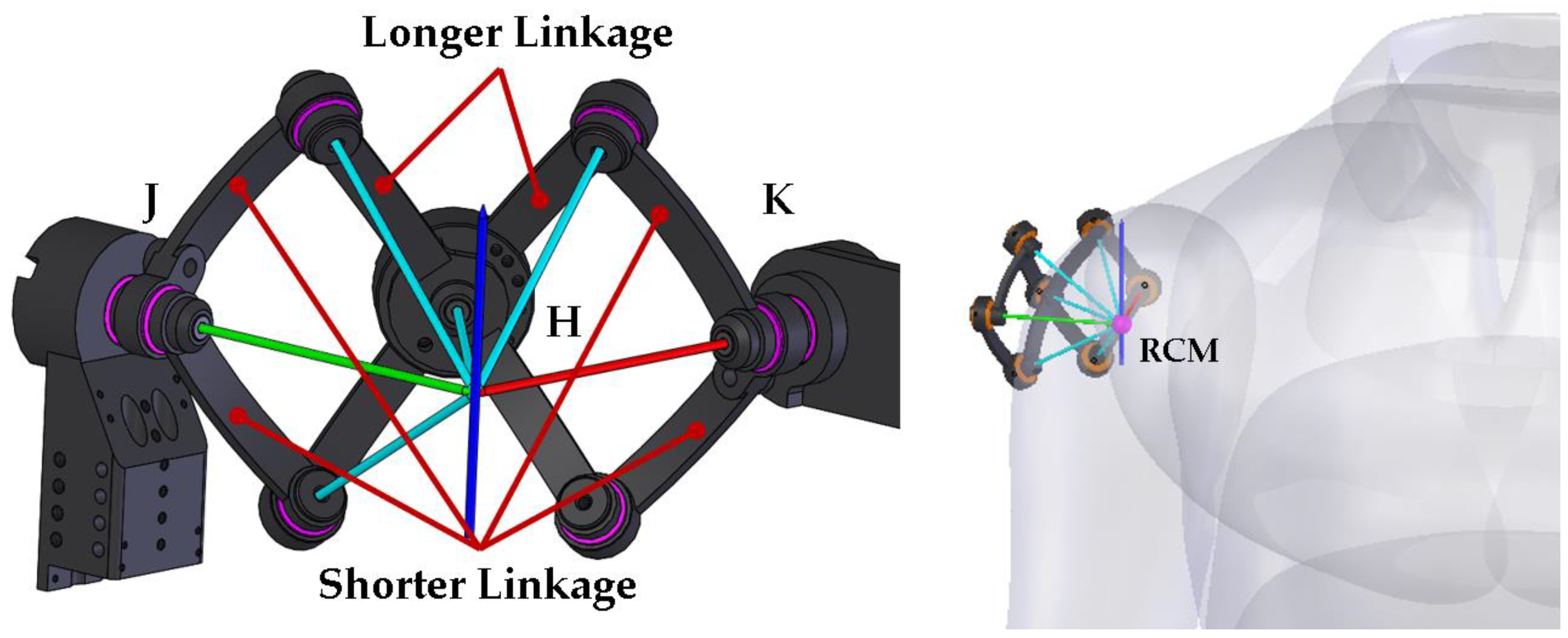

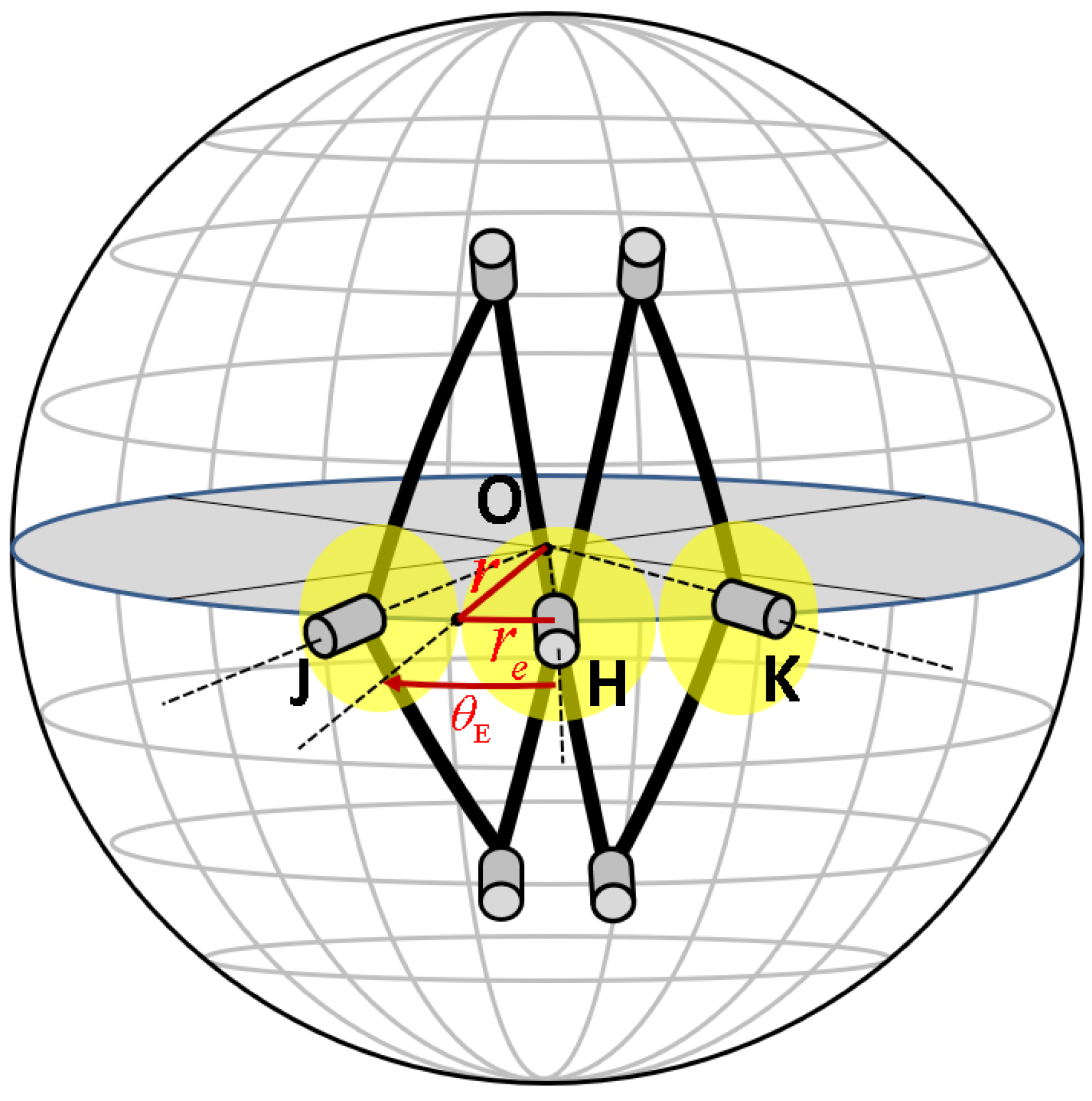

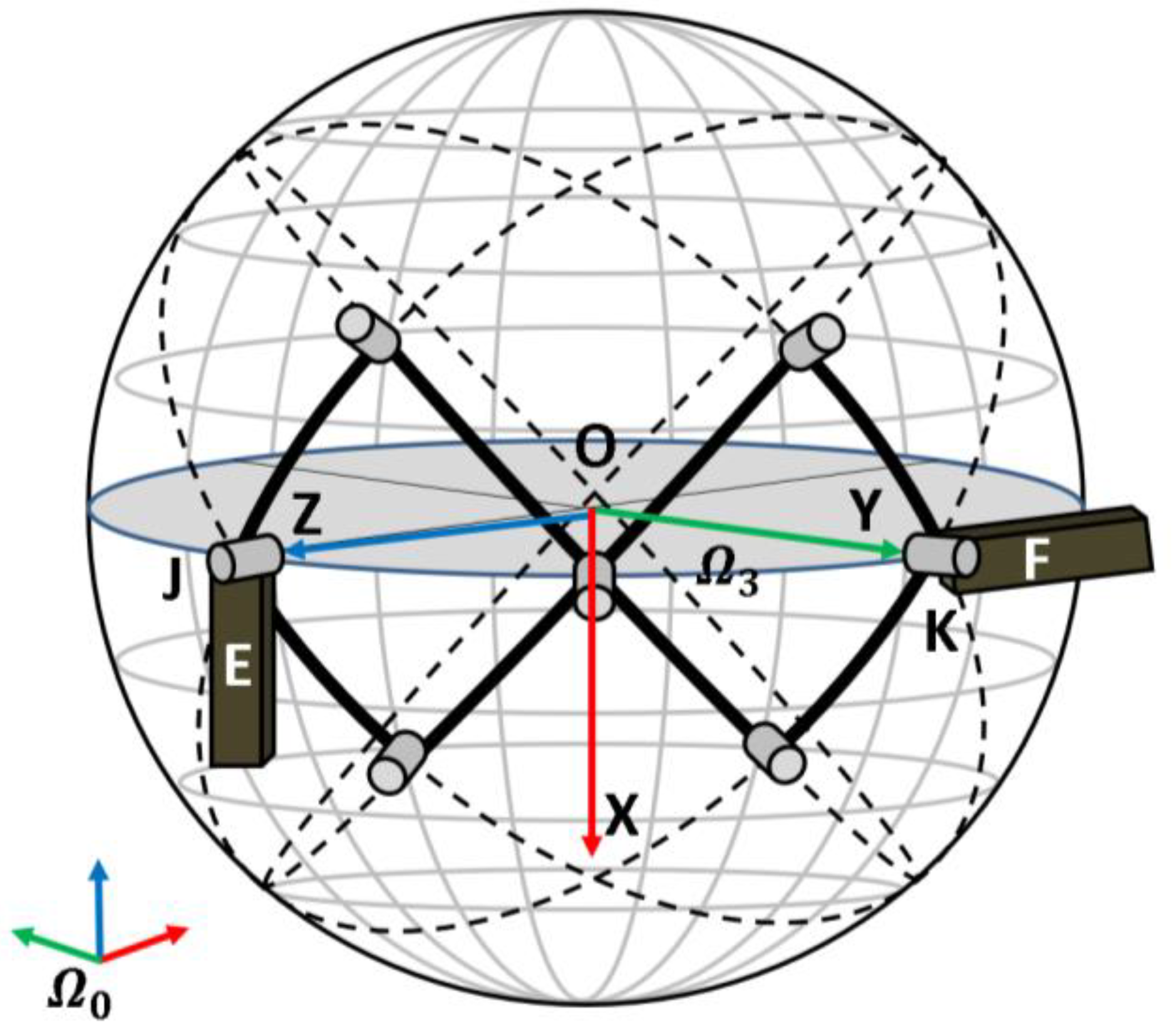





| Motion | Normal Range (deg) |
|---|---|
| Shoulder Flexion/Extension | 158/53 |
| Shoulder Abduction/Adduction | 170/0 |
| Shoulder Medial/Lateral | 70/90 |
| Elbow Flexion/Extension | 146/0 |
| Forearm pronation/supination | 71/84 |
| Wrist Abduction/Adduction | 19/33 |
| Wrist Flexion/Extension | 73/71 |
| Joint Index | Master | Slave | ||||||
|---|---|---|---|---|---|---|---|---|
| i | ||||||||
| 1 | 0 | 0.19 | 0 | 0.235 | ||||
| 2 | 0 | 0 | 0 | 0 | ||||
| 3 | 0 | 0.245 | 0 | 0.265 | ||||
| 4 | 0 | 0 | 0 | 0 | ||||
| 5 | 0 | −0.25 | 0 | −0.272 | ||||
| 6 | 0 | 0 | 0 | 0 | ||||
| 7 | 0 | 0 | 0 | 0 | ||||
| EE | 0 | 0 | 0.04 | 0 | 0 | 0 | 0.168 | 0 |
| Motions | With Exoskeleton (deg) | Without Exoskeleton (deg) | Coverage (%) |
|---|---|---|---|
| Shoulder Flexion/Extension | 168/30 | 173/30 | 97/100 |
| Shoulder Abduction/Adduction | 85/32 | 139/36 | 61/89 |
| Shoulder Medial/Lateral | 47/47 | 62/47 | 76/100 |
| Elbow Flexion/Extension | 127/0 | 127/0 | 100/- |
| Forearm pronation/supination | 90/81 | 90/85 | 100/95 |
| Wrist Abduction/Adduction | 34/55 | 34/55 | 100/100 |
| Wrist Flexion/Extension | 62/35 | 62/45 | 100/78 |
| Control Strategy | Task 1 | Task 2 |
|---|---|---|
| Joint space control | 80% | 40% |
| Task space control | 60% | 90% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Yang, T.; Yang, Y.; Yu, P. A Wearable Upper Limb Exoskeleton for Intuitive Teleoperation of Anthropomorphic Manipulators. Machines 2023, 11, 441. https://doi.org/10.3390/machines11040441
Zhao L, Yang T, Yang Y, Yu P. A Wearable Upper Limb Exoskeleton for Intuitive Teleoperation of Anthropomorphic Manipulators. Machines. 2023; 11(4):441. https://doi.org/10.3390/machines11040441
Chicago/Turabian StyleZhao, Liang, Tie Yang, Yang Yang, and Peng Yu. 2023. "A Wearable Upper Limb Exoskeleton for Intuitive Teleoperation of Anthropomorphic Manipulators" Machines 11, no. 4: 441. https://doi.org/10.3390/machines11040441
APA StyleZhao, L., Yang, T., Yang, Y., & Yu, P. (2023). A Wearable Upper Limb Exoskeleton for Intuitive Teleoperation of Anthropomorphic Manipulators. Machines, 11(4), 441. https://doi.org/10.3390/machines11040441





