Abstract
This paper presents the design of a new control scheme for a group of omnidirectional robots in a multi-robot system operating in an environment with obstacles. The control scheme uses a decision agent based on discrete-time Markov chains and takes into account the state of the system, obstacle positions, and geometries to manipulate targets, providing robustness against measurement uncertainties. The decision process is dynamic, with state information updating at each time step and tasks being executed based on the hierarchy determined by quadratic hierarchical programming. The system’s stability in the mean-square sense is analyzed through the study of a closed-loop stochastic system, and the effectiveness of the proposed control scheme is demonstrated through numerical simulations, including a comparative analysis with a finite-state machine decision agent.
1. Introduction
The demand for advanced technology has increased due to the growing popularity of multi-robot systems in industry and warehouses for logistics tasks. These systems are essential for performing tasks that cannot be handled by a single robot, and are more cost-effective and durable than specialised robots [1]. This makes them ideal for use in flexible manufacturing cells or automated warehouses [2,3,4]. However, the current challenge is to effectively manipulate objects with mobile robots in large warehouses. Non-inertial multi-robot systems offer a solution to this problem, as they can operate in a much larger workspace than inertial robots. Among mobile robots, holonomic robots have proven to be effective in performing manipulation tasks in various applications, such as material handling, warehouse management, and assembly line production. These robots have high flexibility and manoeuvrability as they can move in any direction and orientation. However, the design and control of such robots can be challenging, requiring careful consideration of the robot’s dynamics and control algorithms to ensure safe and effective manipulation of objects [5]. Despite this advantage, there is still a need to enable them to manipulate a wider range of object types with specific end effectors [6,7]. Further research is needed to improve the efficiency of these systems and to overcome any challenges that may arise during their deployment.
Manipulation by caging refers to a method of controlling groups of robots to interact with and manipulate objects in the environment [8]. This method is based on the idea of surrounding and holding an object with the action of multiple robots. This approach offers several advantages over traditional manipulation methods, such as increased stability, robustness to external disturbances, and the ability to manipulate objects with complex shapes and textures. To achieve this type of manipulation, it is often necessary to break it down into simpler behaviours. These behaviours may include establishing and maintaining contact between the manipulators and the object, moving the object to a desired position, and releasing the object. In this paper, we focus on a manipulation scheme that is capable of manipulating regular cylindrical objects rather than those with complex shapes. Although complex figures may require more sophisticated manipulation techniques, regular shaped objects are more common in warehouse environments and can be manipulated efficiently using simple grasping and manipulation strategies. In addition, the perception and localization required for the manipulation task are simplified because regular objects are easier to recognize and track in the environment. Therefore, our decision to focus on regular shaped objects is motivated by the practical considerations of warehouse applications. Nevertheless, the proposed manipulation scheme can be extended to handle more complex shapes by incorporating additional perception and planning capabilities.
Transition processes are useful for coordinating cooperative behaviour in a multi-robot system. Specifically, the transition process is a sequence of specific behaviours, whose fulfilment in the correct order contributes to the performance of a specific task autonomously. In a multi-robot system, the autonomy of the transition process is attained by integrating a decision agent that manages the transition between the behaviours executed by each robot during the process [9,10]. In Ref. [11], a solution is proposed to integrate a transition agent using flags to change the system behaviour. This behaviour consists of task sequences, moving groups of robots between work areas, but relies heavily on sensor precision due to error dependence [12,13,14]. Additionally, the described solution increases the complexity of working with groups of tasks. From here, the problem of the phase transition arises, which has been worked on in Ref. [15], where a kinematic controller capable of handling several conflicting tasks in a multi-robot system is proposed; this proposal considers the performance of both cooperative tasks as well as individual tasks. In Ref. [16], a task set is proposed for object handling and transportation. The method utilizes internal distances between robots to form relatively rigid formations, ignoring clamping methods. The transition process is managed by a state machine, the transition agent, which changes the state based on a metric determined by the designer. In consequence, the system’s reliability depends on the operator’s knowledge and the sensitivity of the sensors. Regarding the task transition planning, the authors in Ref. [17] focus on the task planning aspect of home service robotics, where sequences of actions are generated to complete tasks based on high-level and low-level actions. However, unlike classical planning methods, task planning in the home environment is fraught with uncertainty and change, which requires consideration of human–robot interactions. In addition, this paper discusses the challenges and current approaches to accomplish the task under uncertain and incomplete information. In Ref. [18], a dynamic control for mobile robots with an integrated manipulator is presented. This work proposes a robust controller that ensures finite-time convergence of the error in the presence of parametric uncertainties. The work integrates a finite-state machine (FSM) with transitions of predetermined lapses. This type of FSM works only under the premise that the predetermined transition time is greater than the convergence time of the system.
Our proposed scheme focuses on transitions as events in a probability space and utilizes measurements to adjust the probability measure of each event to formulate a stochastic control system. Stochastic systems are well-suited for scenarios where the phenomenon under investigation is influenced by unpredictable factors. They have been applied in the field of multi-robot systems, resulting in innovative navigation approaches in stochastic environments (such as wind currents and flexible patterns) [19,20]. In Ref. [21], the authors analyse network applications and information processing, where access to information depends heavily on human interaction. To enhance this, a medium access control based on stochastic models is proposed to improve the management of information flow. In Ref. [22], a Markov chain-based methodology is proposed to define system behaviour subject to random forces. Additionally, in Ref. [23], the authors present a control design for stochastic perturbations using observer-based output feedback with a Markov chain and the invariant ellipsoid approach.
Following this line of research, it is necessary to find useful qualities to analytically evaluate a stochastic system. In our proposal, stability in the mean-square sense was adopted. This stability notion is a deeply studied quality of the behaviour of stochastic differential systems, which is used to demonstrate the desired properties of such systems [24,25]. In Ref. [26], the mean square lemma is analysed. It shows, through system causality, that having a bound on the mathematical expectation of the state, output, or stochastic phenomenon is sufficient to prove mean-square stability of the entire closed-loop system [27].
The main contribution of this paper is the development of a novel decision agent, represented by a discrete-time Markov chain (DTMC), which ensures the stability of a comprehensive manipulation scheme. This scheme uses information from the environment and a group of robots to execute a set of behaviours that achieve the goals of the manipulation task [28]. Furthermore, our proposal is robust to uncertainties that may occur during the manipulation, keeping the desired behaviour according only to the actual conditions of the task, which makes it more reliable and applicable to real-world scenarios. Additionally, a stability analysis of the manipulation scheme is presented, demonstrating that the mathematical distribution of the DTMC is dependent on the error of the robot task and the resulting closed-loop system is stable in a mean-square sense, thereby confirming the stability of the manipulation scheme.
The paper is organized as follows. Section 2 presents the methodology of the proposed manipulation scheme. Section 3 describes the equations of motion of the multi-robot system. Section 4 details the tasks that the multi-robot system can perform. Then, Section 5 shows how to deal with tasks simultaneously with hierarchical quadratic programming (HQP). Section 6 explains how the tasks are grouped in a space defined as “action phases”. Section 7 describes the construction of a Markov chain with a state-measure-dependent distribution. Section 8 shows simulations that support the operation of the complete scheme, demonstrating that the proposed DTMC decision agent provides significant improvement in performance when compared with a FSM agent. Finally, the conclusions of the work and future work based on the results of this research are presented in Section 9.
2. Manipulation Scheme
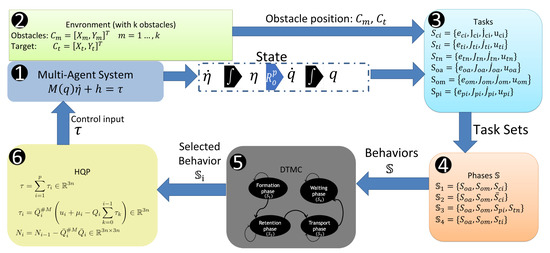
The methodology involved in constructing the manipulation scheme consists of six process blocks: Robot, Environment, Tasks, Phases, DTMC, and finally HQP. The blocks are connected as shown in Figure 1. In the Robot block, the dynamic model of the multi-robot system is found, from which the state of all the agents in the system is obtained. In the environment block all the information of the workspace and the assignment of objectives of the scheme are defined, such as the position and size of the obstacles, the selection of the objective, and the desired position of the objective. The Tasks block obtains the values of the tasks available to the multi-robot system in the form of errors, whose minimization represents the fulfilment of the task. The tasks are computed with the information of the environment and robots, which includes both cooperative and individual tasks. In the Phases block, tasks are grouped into distinct phases, defining the necessary behaviour for the robot to perform the target manipulation process. The DTMC process block has a transition agent, represented by a DTMC, which selects a Phase based on the completion of the previous one, as it uses a state-measured probability distribution. Finally, the HQP block generates a control input to the multi-robot system that seeks the fulfillment of the tasks contained in the selected phase simultaneously.
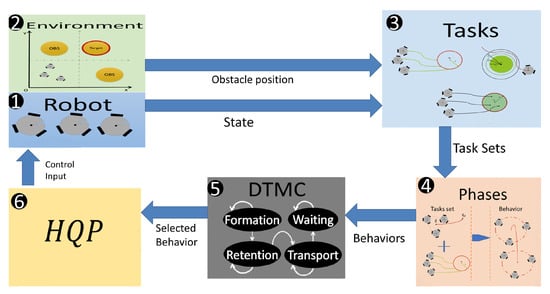
Figure 1.
The Manipulation scheme involves six interconnected blocks: 1. Robots, representing the omnidirectional robots; 2. Environment, the operational space for the robots; 3. Tasks, the specific goals to be achieved by the robots; 4. Phases, the stages involved in the manipulation scheme; 5. DTMC, which utilizes a discrete-time Markov chain; and 6. HQP, which computes the control of the robots to carry out simultaneous tasks.
In the context of modelling our decision agent, it is important to choose a suitable mathematical model that can maintain consistent performance despite potential uncertainties. While conventional DTMC and FSM are common mathematical models for discrete systems, modelling decision agents requires selecting a model that can effectively address robustness to unexpected events and consider its limitations. Our focus is on DTMC as it has been shown to be effective in handling uncertainties and randomness [23,29]. On the other hand, FSM, which relies on deterministic rules, is limited in its ability to model probabilistic behaviour [15,18], and constructing an accurate FSM-based decision agent can be complex and requires specialized knowledge of the system. Despite this, the proposed manipulation scheme has the disadvantage of requiring a simultaneous transition of the behaviour of each of its agents. Therefore, without reconsidering a more specialised Markov chain, it is currently not possible to implement it in a decentralised manipulation scheme.
We implement this scheme in a simulation study by considering a group of Festo Robotinos. We chose these robots since they represent a versatile and powerful mobile robot platform suitable for a wide range of applications, including material handling, warehouse management, and research [30]. The Robotino’s omniwheels provide smooth and accurate motion, enabling precise positioning for object manipulation.
3. Dynamic Model
For implementing the scheme, the Robot block represents a group of n omnidirectional robots, with its dynamic model. The notation used in the scheme is presented in Table 1. The position and orientation of this group of robots is represented by , where is the position and orientation of the mobile frame attached to the centre of the i-th robot, with respect to the inertial frame O. Let us define the rotation matrix as
then, for a total representation of the system, it is defined
which is the block-diagonal matrix that relates the frame P to the frame O. To determine the velocities of each of the n robots in the P frame, we introduce the space with defined as
where is the transpose of the rotation matrix from frame P to O at orientation , and is the velocity of the i-th robot in the O frame.

Table 1.
Common variables used.
These robots have an omnidirectional configuration that is achieved with three holonomic wheels coupled equidistant around the main body [5]. In order to better understand the mathematical representation of the robot, the variables used in (4) are described in Table 1. The robot seen in Figure 2 is represented mathematically by
where the matrix E encodes the wheel configuration and represents the holonomic wheel projection as
where b is the distance between the robot centroid and the wheel, and is the radius of the wheel i.
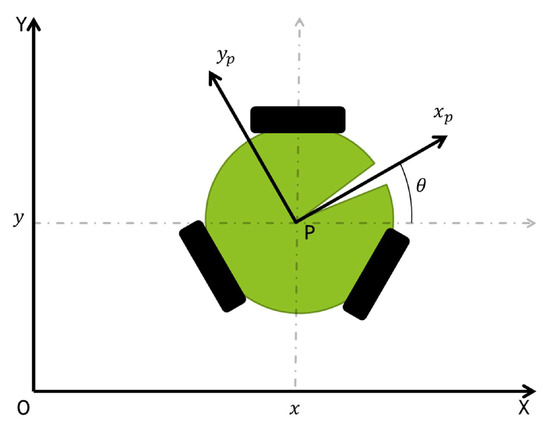
Figure 2.
Omni-wheeled robot representation.
A compound system is defined to represent the dynamic behaviour of a group of robots,
4. Multi-Robot Tasks
Manipulation by caging is a complex task that requires coordination and precision among various simpler tasks. To perform this type of manipulation, a set of individual tasks is designed and executed in a specific sequence. These tasks are often geometric or kinematic in nature and are used to guide and control the motion of objects towards a desired location. The success of manipulation by caging is dependent on the proper execution of these smaller tasks, which can include tasks such as grasping, positioning, and releasing. The combination of these individual tasks results in a smooth and accurate final outcome. In accordance with (6), the presence of obstacles in the workspace is taken into account to formulate the available tasks for the robot to perform the manipulation. These tasks are modelled through the application of inequality or equality constraints in a quadratic programming framework. Each task is characterized by an error function, the optimization of which serves to minimize the error and thereby indicate successful task completion.
4.1. Equality Tasks
We consider equality tasks to be those tasks that are active at all times. We refer to regulation and geometric formation tasks. Tasks can be assigned to individual agents or multiple agents working in coordination. The equality tasks used here are described below.
4.1.1. Geometric Shape Formation
A geometric shape formation task, such as maintaining a circular formation with vehicles, is demonstrated in Figure 3. In this particular case, the task limits the feasible displacements of each robot over the circumference.
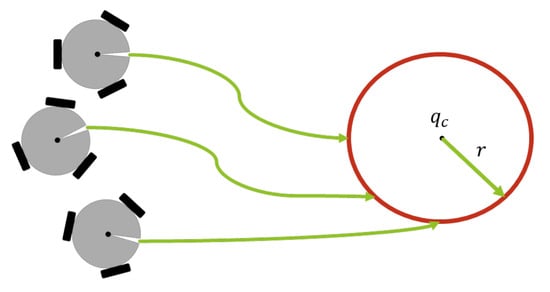
Figure 3.
Geometric shape formation.
This is a local task function because each vehicle reaches the perimeter of a given circumference without the need to know the location of other team members. The error function of the task is defined as
where r is the radius and is the centre of the circle. The circular task error function is described as , where its time-derivative is . The task Jacobian is calculated as:
and the double time derivative is computed as where is defined as:
4.1.2. Regulation Task
Individual
In order to reach an individual target, as can be seen in Figure 4, the error function is defined as
where is the desired state of the system, which also implies a desired position and orientation for each of the robots. The time derivative of (10) is , with since it is a regulation task. Then, the task Jacobian becomes
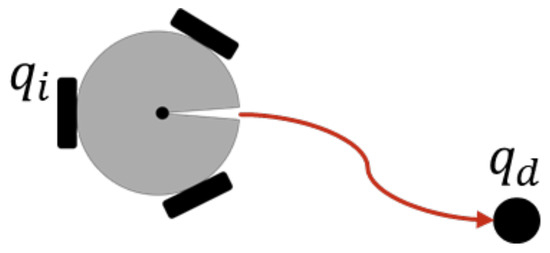
Figure 4.
Individual regulation task.
Since is constant, its time derivative becomes .
Cooperative
This task is designed to reach a target as a group while the vehicles can keep a desired formation, see Figure 5. It consists in regulating the centroid of the formation towards a desired object. The centroid of the formation is , where
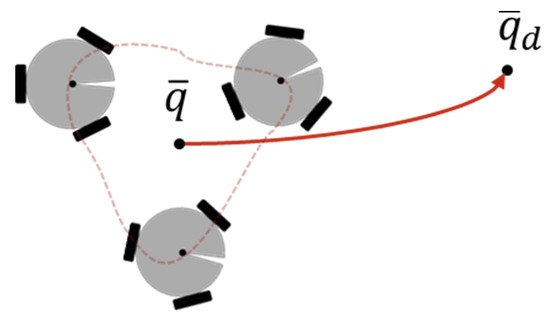
Figure 5.
Cooperative regulation task.
Then, the error function becomes
It is straightforward to adapt the task error for tracking purposes if the target is a time-varying function: , where the task Jacobian of n agents is given by
Since is constant, its time derivative becomes .
4.2. Inequality Tasks
The proposed function to control the inequality tasks is a combination of an inequality and an activation function. The activation function, , determines if the task is activated, based on the distance between the i-th robot and the target (obstacle, robot, or formation), . The activation function has a range of and is defined as:
where is a weight, is the activation distance, and is the distance between the ith robot and the target. The function has a smooth transition and is used for obstacle avoidance, collision avoidance, and geometric permissible region, where the value of is negative.
4.3. Obstacle Avoidance
Avoidance tasks are at the top of the hierarchy of task stacks. They are essential for proper navigation within a workspace populated by inert objects and robots. They prevent robots from being damaged by accidental encounters in their defined tasks. In addition, geometric formation tasks can be constructed with less processing, since it is not necessary to precisely calculate the position of each robot, but it is enough to define the centroid of the formation.
When the robot approaches the obstacles, the corresponding inequality constraint is activated, as shown in Figure 6. In particular, each obstacle is embedded within a spherical shell of radii and , with . Thus, the obstacle avoidance task is defined as
where is the distance from a centre point of the i-th robot , to the nearest point over the j-th obstacle . Assuming that is constant, the time derivative of (16) becomes where the task Jacobian is given by
where is the linear velocity Jacobian and with
also, the time derivative of (18) is:
which is needed to construct in order to compute the double time derivative of (16), where the time derivative Jacobian becomes
since is constant, its time derivative becomes .
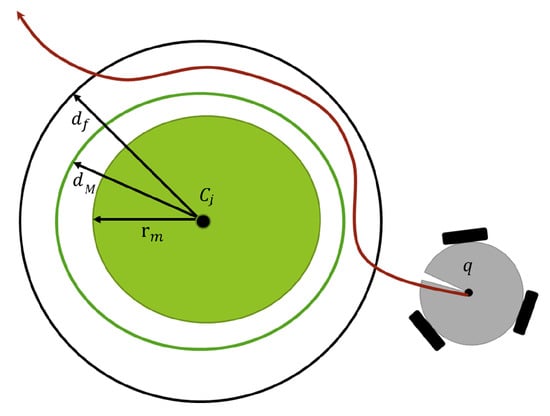
Figure 6.
Obstacle avoidance task.
4.4. Collision Avoidance
Because the group of robots shares the same workspace, it is necessary to consider the evasion of the robots among themselves, as can be seen in Figure 7.
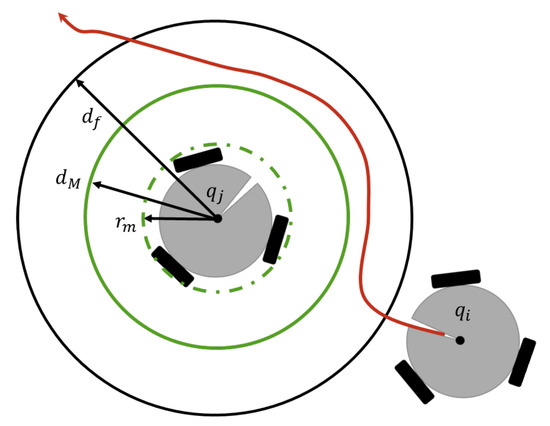
Figure 7.
Collision avoidance task.
The collision avoidance task, , is obtained in the same way as the obstacle avoidance, with the difference that is considered as the position of the robot j, which implies that becomes
If and then has the form
Since is constant, its time derivative becomes .
4.5. Geometric Permissible Region
In this task, the allowable navigation area represents the interior of a circle, as shown in Figure 8, where the robots must remain. Then, the structure of the task error and its Jacobian are the same as in (7)–(9). However, we will consider it as an inequality task:
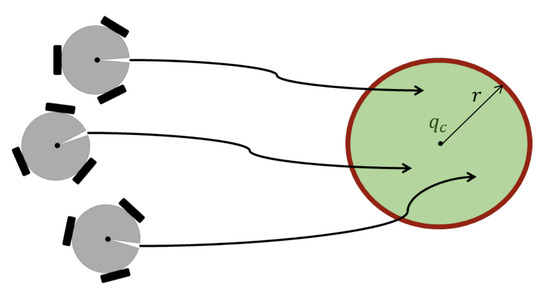
Figure 8.
Geometric permissible region.
5. Hierarchical Quadratic Programming
HQP is capable of handling multiple hierarchical objectives while ensuring that kinematic and dynamic constraints are satisfied, and provides a computationally efficient solution by decomposing the problem into a hierarchy of sub-problems and solving them iteratively. This allows us to ensure that the robot’s motion satisfies all the constraints, while dealing with multiple objectives at different levels of the hierarchy.
A group of the tasks described in Section 4 can be performed simultaneously by the multi-robot system in each of the phases of the scheme, so HQP is used to find a control input , applied in (6), which fulfils all the tasks included in a phase. The main characteristic of HQP is that lower priority tasks cannot affect higher priority tasks by solving a quadratic programming cascade with slack variables. The main idea is to find a control signal that obeys a set of p tasks to be executed simultaneously, as shown in the Algorithm 1.
Consider the double integrator system and as a PD control law , which is needed for HQP of the tasks defined in Section 4 [18]. The tasks are considered an error function of the form
We assume that (26) is twice differentiable with respect to time
From (6) and (27), we obtain
where and is the task’s drift. The task-based inverse dynamic is obtained by solving for in (28) as follows:
is the weighted generalized inversion of , and u is the auxiliary vector of control inputs. To overcome possible conflicts among the tasks, the hierarchy between them is imposed such that (29) becomes:
where , , and . Notice that belongs to the null space of .
| Algorithm 1 Task phase |
Get with (2) Get with (6) Indicate the order of the tasks: Get task Jacobians: Get time derivative task Jacobians: Get with (30) Get with (6) |
6. Action Phases
Each phase requires specific behaviour in the robots. Depending on the task, the robots can work as a team or individually. However, they are always reacting to their environment for obstacle and collision avoidance tasks.
The action phase is a set of tasks introduced in the HQP block to be fulfilled in a defined hierarchy. Each Action phase considers the sets of task errors, task projector Jacobians, the time derivative from the projector Jacobians, and a set of auxiliary control inputs that asymptotically minimize each error of the Action Phase. The i phase of action is arranged in the group . For the purpose of this paper, four phases of action are considered, presented in Table 2,

Table 2.
Tasks to accomplish in each phase.
The evaluation of whether tasks are fulfilled is measured through the error generated by each task. A task is considered accomplished when its error remains in a neighbourhood close to zero. Likewise, a phase is considered to be reached when the errors of all its tasks are fulfilled. It is considered a state composed of the errors generated in the phase,
This state exists in a normed space of the phase whose vector norm provides us with substantial information about the development of the task at each time step. A norm is proposed in order to have an analytical perception of the behaviour of the vector in a scalar way, even when the dimension of the vector changes between the existing phases in the totality of the process.
7. Discrete-Time Markov Decision Agent
Definition 1
(Probabilistic space). Let Ω be a space with a family of subsets (in this paper it is considered as the set ), such that any subset is closed under accounting complements, unions, and intersections. A family of subsets possessing these properties is known as a algebra. If a probability measure P is defined on the σ-algebra , then the triple is called a Probability space and the sets in are called random events.
Definition 2
(Markov condition). Consider a probability space from Definition 1 . Let E be a finite or countable set of states and a sequence of random variables. The process is said to satisfy the Markov condition if for all integer and all that belongs to E, it holds:
Definition 3
(Distribution by state measure). Let E be a countable set. Each is called a state and I is called a state space. We say that a subset , where , is a measure on E∀. We work with a probability space from Definition 1, a random event Ξ that takes values of and a random event with values in E. Then, it is said that α defines a distribution by state measure if it satisfies the condition:
Definition 4
(Mean-square stability). Let , if for every , there exist such that for all whenever then it is said that X is stable in mean-square sense [31].
The Markov chain is a discrete-time stochastic process in which a random variable that takes values of changes over time. Its main characteristic is that it complies with the Definition 2 [22]. The measurement of the phase for the system comes from the error vector of (32). Likewise, the norm is proposed as a decision agent to affect the transition matrix. A bounded exponential function is generated to provide information about the tasks in each phase and ensure that the task has been completed before each transition. This function depends on ,
Notice the non-negative nature of the vector norm and the exponential envelope of the function . A new transition matrix is defined, where the probability of task development is based on relevant state measurement information for each element,
where , is the nominal probability, m is the number of states in the system, and T is the current instant of the system. This obeys the requirement of a transition matrix where the sum of the elements of each row is 1. After finding , it is balanced with the complement probability, forcing with (36), this of State 1 is considerably small, the measurement of State 2 is the complement and therefore takes higher values.
Theorem 1.
Let a decision agent be represented by a probabilistic space and fulfil the Markov condition with distribution by state measure as Definition 3. Then is stable in mean-square sense according to Definition 4.
Sketch of the Proof.
Once the decision agent, represented by a Markov chain, selects a phase , we obtain an error and therefore the computation of a control , which is applied to the robot to minimize that error. Since measures the phase error , it will change as the error converges to zero. Given the from (35), there is a direct proportion relationship with , if the error takes values close to 0 then in phase is close to 0, ensuring the existence of . Since there are a limited number of transitions from the current state, according to Definition 3, exists in every moment and implies that is less than or equal to the number of possible transitions that exist in each phase. Then and from Definition 4 always exist, which implies that the proposed decision agent is stable in the least-squares sense. □
The manipulation scheme is considered a stochastic system when it operates in a closed loop since the random variable of the decision agent is being fed back. Therefore, it is important to demonstrate the stability of the system with stochastic tools. The stability presented in the decision agent ensures that the stability in the mean-squares sense is preserved in the rest of the processes thanks to the causality of the events in the whole manipulation scheme.
8. Simulation Results
To test the validity of the proposed manipulation scheme, which is described in Figure 9, numerical simulation results are presented. The simulator was programmed in Python3, on a computer equipped with an Intel® Core™ i7-8565U CPU @ 1.80 GHz and 8 GB RAM. The Markov chain’s transition probability is set at a 0.01 second sampling time, affecting the duration of each phase. Each phase is expected to last 1500 steps with this transition probability design. This means that the probability of staying in phase is , which implies that the initial transition probability is . Wheeled robots with a mass of m = 1 kg, an inertia tensor of kgm, as well as an inertia tensor of the wheels of the wheeled robot of kgm, and a radius of m, are considered. There are obstacles at and with a radius of m.
8.1. Phase 1: Formation Phase
The robots are directed from their starting position to the border with the target (), where strict avoidance of the obstacles and collision between them is important (). Therefore the task Phase is designed as
where is the radius of the robots and is the security distance of the obstacles, which indicates that is more important than . The resulting trajectory is seen in Figure 10.
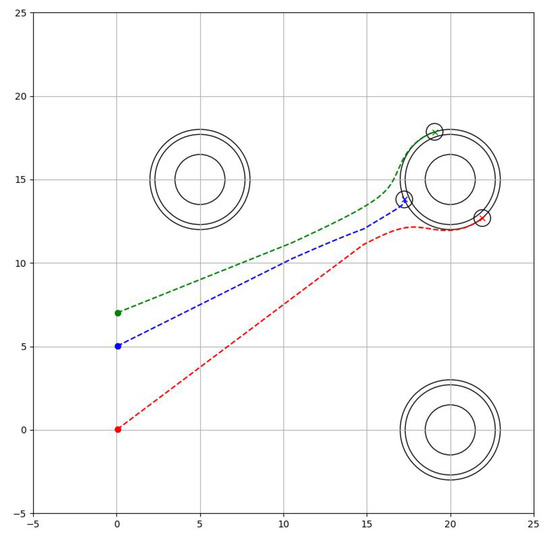
Figure 10.
Formation phase.
8.2. Phase 2: Grip Phase
The robots must ensure that the object they are going to hold is kept in the centroid of the formation, therefore, they must avoid the target space without separating from it, while separating equally from each other. The task to accomplish is practically the same as the first phase, however, they need to take a greater distance to avoid collisions between the robots. Then
where is the distance needed in order to form a circumscribed triangle towards the objective as seen in Figure 11.
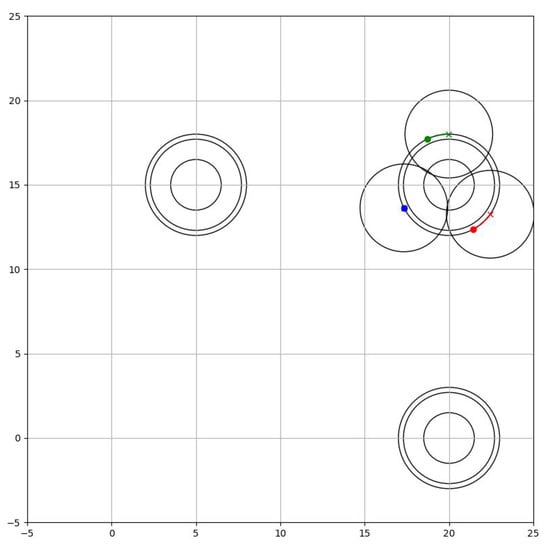
Figure 11.
Grip Phase.
8.3. Phase 3: Manipulation Phase
Robots must maintain the desired permissible space in the formation while avoiding obstacles on the stage. The task is completed when they move the object, that is, the centroid of the formation to the desired position. Thus, the task phase becomes
The behaviour can be seen in Figure 12.
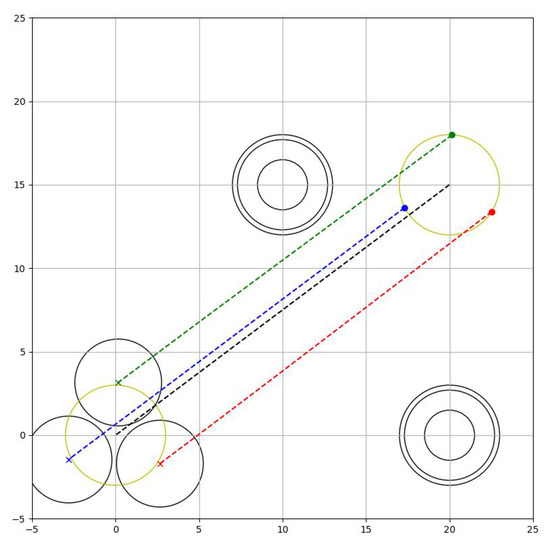
Figure 12.
Manipulation Phase.
Notice that the formation can avoid also the target to move since it is logically considered an obstacle.
8.4. Phase 4: Waiting Phase
Once the robots have moved the target to the desired location, they separate from it and head towards a pre-defined obstacle-free position, in order to finish the job or wait for a new target. The task phase becomes
The behaviour can be seen in Figure 13.
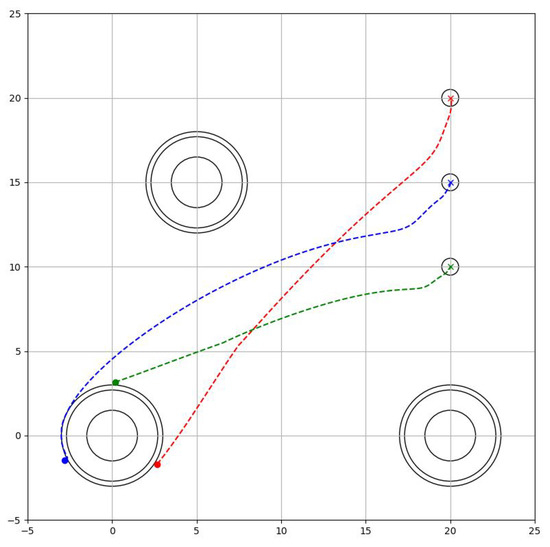
Figure 13.
Waiting Phase.
Notice that in all the tasks one of the priorities is that the robots strictly avoid the obstacles, therefore it would be a task of greater importance in all the phases. Although the tasks of lower priority are projected into the null space of the stricter tasks, they find a close solution for each of the tasks.
8.5. Variance Value and Phase Measure
The closed-loop system becomes a differential stochastic system. Therefore, the stability analysis of the system has to consider tools applied in stochastic formulations.
The function , defined in (35) and based on the error within phase , serves as the applied measure. The system exhibits robustness against uncertainty in measurement, as evidenced by the recurrent activation of obstacle and collision avoidance tasks in Figure 14, without immediate transition until the error persists and the transition probability increases. This is in contrast to other schemes where the transition occurs as soon as a flag is crossed, leading to transition even in the presence of false positives arising from uncertainty in sensor measurement.
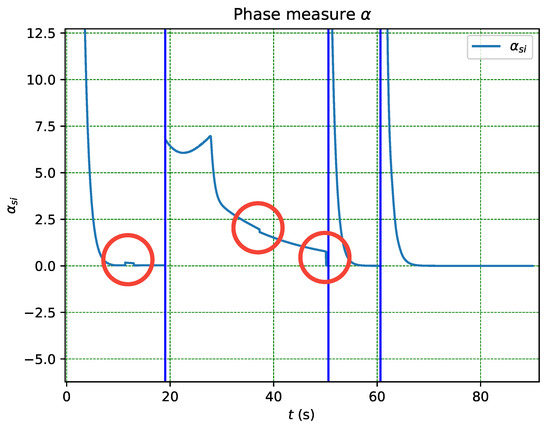
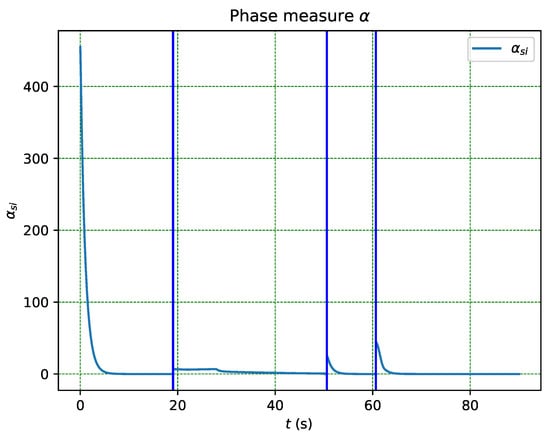

Figure 14.
Close up of the Measure from Figure 15.

Figure 15.
Measure given by each phase.
Due to the behaviour of the distribution in each phase, the variance of each phase starts at zero and tends towards the next state until a transition occurs, as shown in Figure 16. The variance in a finite-state Markov chain is always bounded since there are a limited number of transitions from the current state. Thus, the validation of Theorem 1 is shown in Figure 16.
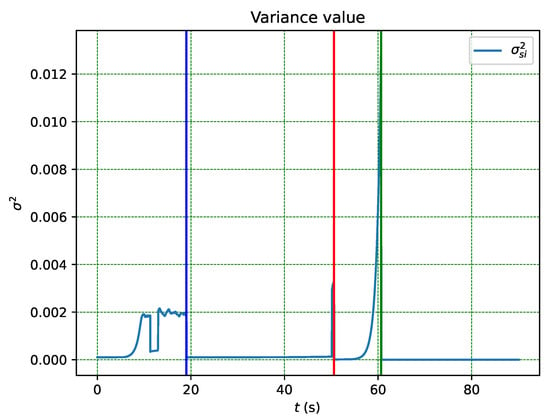
Figure 16.
Variance given in each phase.
8.6. Comparison of DTMC and FSM in the Presence of Unexpected Failures
Figure 17 compares the DTMC and FSM decision agents for the same manipulation task in the case of unexpected failures that lead to the loss of partial state information and therefore the error in the measure of of the system. The experience in the use of the system indicates that a flag error limit of is necessary for the correct functioning of the FSM while DTMC does not need such information. The failures occur between and .
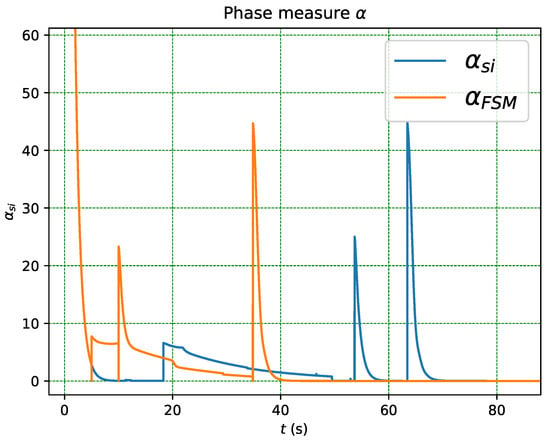
Figure 17.
Comparison between DTMC and FSM decision agents.
The DTMC-based decision agent is able to recover from the failure and continues to make the correct decision, while the FSM-based decision agent is unable to recover and continues to make the incorrect decision. Note that at t = 5, due to the unexpected transition, the FSM decision agent can no longer satisfy the behaviour in the first phase, which implies that the following behaviours can no longer be satisfied. This highlights the advantage of using DTMC-based decision agents, as they are more robust and can handle unexpected failures better than FSM-based agents.
9. Conclusions
This paper presents a manipulation scheme for robots to transport objects in a workspace with obstacles. The novel decision agent proposed in this paper is the main contribution, as it guarantees the stability of the scheme and offers an effective and efficient solution for object manipulation in complex workspaces. The proposed decision agent is model-free, relying solely on errors of tasks in each phase, which are dependent on workspace information. Distribution by state measurement provides robustness against intermittent event measurement and unexpected behaviours, as demonstrated in simulation results comparing the DTMC agent with a FSM. The proposed approach reduces the required expertise during implementation, as the decision agent handles most of the complexity. The stability of the scheme was evaluated using mean-square analysis, with the variance being constrained at all times. The scheme demonstrated the ability to change the phase autonomously as the error approached zero, indicating its efficacy in ensuring stability. Future work includes developing auxiliary controls to enhance the robustness against parametric uncertainty and disturbances from contact forces.
Author Contributions
D.A.-J. proposed the manipulation scheme, theorem of the decision agent, contributed to the algorithm design, and generated the simulation results. A.S.-O. proposed the Multi-Robot system application, worked on the control law used in the scheme, and provided the contextual concepts for the theorem of the manipulation scheme. H.A. worked on the mean-square stability proof and definitions related to the proposed scheme and on the design of the Markov Chain decision Agent. All the authors discussed the proposed approach, and results, and reviewed and approved the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is available under request to the corresponding author.
Acknowledgments
The authors acknowledge the support from Conacyt-Mexico, CINVESTAV and UACAM.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DTMC | Discrete-Time Markov Chain |
| HQP | Hierarchical Quadratic Programming |
| FSM | Finite-State Machine |
References
- Ebel, H.; Eberhard, P. Non-Prehensile Cooperative Object Transportation with Omnidirectional Mobile Robots: Organization, Control, Simulation, and Experimentation. In Proceedings of the 2021 International Symposium on Multi-Robot and Multi-Agent Systems (MRS), Cambridge, UK, 4–5 November 2021; pp. 1–10. [Google Scholar] [CrossRef]
- Simões, M.A.C.; da Silva, R.M.; Nogueira, T. A Dataset Schema for Cooperative Learning from Demonstration in Multi-robot Systems. J. Intell. Robot. Syst. 2020, 99, 589–608. [Google Scholar] [CrossRef]
- Lin, S.; Liu, A.; Wang, J.; Kong, X. A Review of Path-Planning Approaches for Multiple Mobile Robots. Machines 2022, 10, 773. [Google Scholar] [CrossRef]
- Ordaz-Rivas, E.; Rodriguez-Liñan, A.; Torres-Treviño, L. Flock of Robots with Self-Cooperation for Prey-Predator Task. J. Intell. Robot. Syst. 2021, 101, 39. [Google Scholar] [CrossRef]
- Saenz, J.; Bugarin, E.; Santibañez, V. Kinematic and Dynamic Modeling of a 4-Wheel Omnidirectional Mobile Robot Considering Actuator Dynamics. Congreso Internacional de Robótica y Computación. 2015, pp. 115–121. Available online: https://posgrado.lapaz.tecnm.mx/CIRC2015/CIRC2015.pdf (accessed on 18 March 2023).
- Li, R.; Qiao, H. A Survey of Methods and Strategies for High-Precision Robotic Grasping and Assembly Tasks—Some New Trends. IEEE/ASME Trans. Mechatronics 2019, 24, 2718–2732. [Google Scholar] [CrossRef]
- Juang, C.F.; Lu, C.H.; Huang, C.A. Navigation of Three Cooperative Object-Transportation Robots Using a Multistage Evolutionary Fuzzy Control Approach. IEEE Trans. Cybern. 2022, 52, 3606–3619. [Google Scholar] [CrossRef] [PubMed]
- Dai, Y.; Kim, Y.G.; Lee, D.H.; Lee, S. Symmetric caging formation for convex polygon object transportation by multiple mobile robots. In Proceedings of the 2015 IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Busan, Republic of Korea, 7–11 July 2015; pp. 595–600, ISSN: 2159-6255. [Google Scholar] [CrossRef]
- Yazıcıoğlu, Y.; Bhat, R.; Aksaray, D. Distributed Planning for Serving Cooperative Tasks with Time Windows: A Game Theoretic Approach. J. Intell. Robot. Syst. 2021, 103, 27. [Google Scholar] [CrossRef]
- Chandarana, M.; Hughes, D.; Lewis, M.; Sycara, K.; Scherer, S. Planning and Monitoring Multi-Job Type Swarm Search and Service Missions. J. Intell. Robot. Syst. 2021, 101, 44. [Google Scholar] [CrossRef]
- Yang, H.; Sun, L.; Li, X. A Multi-Agent Navigation Controller for Sequential Tasks Performing. In Proceedings of the 2017 IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Honolulu, HI, USA, 31 July–4 August 2017; pp. 1680–1684. [Google Scholar] [CrossRef]
- Wu, H.; Yan, W.; Xu, Z.; Li, S.; Cheng, T.; Zhou, X. Multimodal Prediction-Based Robot Abnormal Movement Identification Under Variable Time-length Experiences. J. Intell. Robot. Syst. 2021, 104, 8. [Google Scholar] [CrossRef]
- Luo, S.; Wu, H.; Duan, S.; Lin, Y.; Rojas, J. Endowing Robots with Longer-term Autonomy by Recovering from External Disturbances in Manipulation Through Grounded Anomaly Classification and Recovery Policies. J. Intell. Robot. Syst. 2021, 101, 51. [Google Scholar] [CrossRef]
- Shen, L.; Mao, P.; Fang, Q.; Wang, J. A Trajectory Tracking Approach for Aerial Manipulators Using Nonsingular Global Fast Terminal Sliding Mode and an RBF Neural Network. Machines 2022, 10, 1021. [Google Scholar] [CrossRef]
- Pérez-Villeda, H.M.; Arechavaleta, G.; Morales-Díaz, A. Multi-vehicle coordination based on hierarchical quadratic programming. Control. Eng. Pract. 2020, 94, 104206. [Google Scholar] [CrossRef]
- Koung, D.; Kermorgant, O.; Fantoni, I.; Belouaer, L. Cooperative Multi-Robot Object Transportation System Based on Hierarchical Quadratic Programming. IEEE Robot. Autom. Lett. 2021, 6, 6466–6472. [Google Scholar] [CrossRef]
- Li, H.; Ding, X. Adaptive and intelligent robot task planning for home service: A review. Eng. Appl. Artif. Intell. 2023, 117, 105618. [Google Scholar] [CrossRef]
- Obregón-Flores, J.; Arechavaleta, G.; Becerra, H.M.; Morales-Díaz, A. Predefined-Time Robust Hierarchical Inverse Dynamics on Torque-Controlled Redundant Manipulators. IEEE Trans. Robot. 2021, 37, 962–978. [Google Scholar] [CrossRef]
- Alam, T.; Rahman, M.M.; Carrillo, P.; Bobadilla, L.; Rapp, B. Stochastic Multi-Robot Patrolling with Limited Visibility. J. Intell. Robot. Syst. 2020, 97, 411–429. [Google Scholar] [CrossRef]
- Mirzaei, F.; Pouyan, A.A.; Biglari, M. Automatic Controller Code Generation for Swarm Robotics Using Probabilistic Timed Supervisory Control Theory (ptSCT). J. Intell. Robot. Syst. 2020, 100, 729–750. [Google Scholar] [CrossRef]
- Nguyen, V.; Kim, O.T.T.; Pham, C.; Oo, T.Z.; Tran, N.H.; Hong, C.S.; Huh, E.N. A Survey on Adaptive Multi-Channel MAC Protocols in VANETs Using Markov Models. IEEE Access 2018, 6, 16493–16514. [Google Scholar] [CrossRef]
- Meyn, S.P.; Tweedie, R.L. Markov Chains and Stochastic Stability; Springer London: London, UK, 1993. [Google Scholar] [CrossRef]
- Poznyak, A.S.; Alazki, H.; Soliman, H.M. Invariant-set design of observer-based robust control for power systems under stochastic topology and parameters changes. Int. J. Electr. Power Energy Syst. 2021, 131, 107112. [Google Scholar] [CrossRef]
- Yang, Y.; Xi, X.; Miao, S.; Wu, J. Event-triggered output feedback containment control for a class of stochastic nonlinear multi-agent systems. Appl. Math. Comput. 2022, 418, 126817. [Google Scholar] [CrossRef]
- Han, Y.; Zhou, S. Novel Criteria of Stochastic Stability for Discrete-Time Markovian Jump Singular Systems via Supermartingale Approach. IEEE Trans. Autom. Control 2022, 67, 6940–6947. [Google Scholar] [CrossRef]
- Qi, T.; Chen, J.; Su, W.; Fu, M. Control Under Stochastic Multiplicative Uncertainties: Part I, Fundamental Conditions of Stabilizability. IEEE Trans. Autom. Control 2017, 62, 1269–1284. [Google Scholar] [CrossRef]
- Long, S.; Zhong, S. Mean-square exponential stability for a class of discrete-time nonlinear singular Markovian jump systems with time-varying delay. J. Frankl. Inst. 2014, 351, 4688–4723. [Google Scholar] [CrossRef]
- Francelino, E.; Pereira, M.; Inoue, R.; Terra, M.; Siqueira, A.; Nogueira, S. Markov System with Self-Aligning Joint Constraint to Estimate Attitude and Joint Angles between Two Consecutive Segments. J. Intell. Robot. Syst. 2022, 104, 43. [Google Scholar] [CrossRef]
- Cao, X.; Jain, P.; Goodrich, M.A. Adapted Metrics for Measuring Competency and Resilience for Autonomous Robot Systems in Discrete Time Markov Chains. In Proceedings of the 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Prague, Czech Republic, 9–12 October 2022; pp. 71–76. [Google Scholar] [CrossRef]
- Ralph-Christoph, W.; Bellenberg, M.; Schwarzenberger, D. Festo’s Robotino User Guide; Manual Order No.:KG 544305; FESTO: Esslingen, Germany, 2009. [Google Scholar]
- Lang, A.; Petersson, A.; Thalhammer, A. Mean-square stability analysis of approximations of stochastic differential equations in infinite dimensions. BIT Numer. Math. 2017, 57, 963–990. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).