1. Introduction
A compliant mechanism (CM) is a device that employs the deformation of its compliant elements to transform or transmit loads and motions. One of the significant benefits of CMs is their ability to reduce costs and improve performance by minimizing the number of parts required, shortening assembly times, simplifying manufacturing processes, and decreasing wear, friction, and noise. These advantages make CMs widely used in different applications, such as compliant assembly systems, vibratory bowl feeders, and high-precision manipulators.
Recently, CMs have drawn much attention from researchers, and have been used in precision position systems, metrology instruments, MEMS/NEMS devices and other fields.
For precision position systems, Schitter [
1] presented a novel design of a scanning unit for atomic force microscopy (AFM). Kim [
2] designed a new AFM with a 2D plane CM for the establishment of a standard technique of nano-length measurement. Minh [
3] designed a decoupled 6-DOF compliant parallel mechanism.
For metrology instrumentation, Khalid [
4] applied a CM in 3D coordinate measurement. Jin [
5] and Hao [
6] used CMs as force/moment sensors. Hansen [
7] and Gao [
8] designed displacement/acceleration sensors with CMs. For bio-medical/health devices, Sung [
9] designed an ankle rehabilitation with CMs. Chen [
10] applied CMs to a body-gravity compensation device. Awtar [
11] presented a new minimally invasive surgical tool design paradigm that enables enhanced dexterity.
For MEMS/NEMS devices, Liew [
12] designed a bulk-micromachined CMOS micro-mirror. In [
13,
14], Olfatnia applied electrostatic comb-drive actuators to drive a large-range dual-axis micro-stage. Aten [
15] presented a self-reconfiguring metamorphic nanoinjector for injection into mouse zygotes. For compliant space mechanisms, Fowler [
16] studied compliant space mechanisms applied to a frontier and a space-pointing mechanism. Throughout all the CMs in these applications, most of them use plate-shape compliant elements which mainly provide deformation in a plane. In this paper, compliant elements that can provide deformation in three-dimensional space will be used. Thalman [
17] proposed an approach to design Flexure Pivot time bases.
The main challenge in CM application and analysis is the modeling of compliant element deformation. Accurate modeling of CMs is consistently desired to provide quick insight into the effect of material properties, displacements, geometrical parameters, and loads on the performance characteristics of CMs. The key issue in accurate modeling is how to describe the coordinates of any point on the compliant rod. There are many emerging modeling methods [
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31] for compliant elements.
For free-body diagram methods [
18,
19,
20,
21], Mldha [
18] proposed parametric deflection approximations for end-loaded, large-deflection beams in 1995. Awtar [
19,
20] used the standard double-parallelogram flexure module in analyzing XY flexure mechanisms. Hao [
21] proposed multi-beam modules in a nonlinear analysis of spatial compliant parallel mechanisms.
For energy methods [
22,
23], Sen [
22] used a closed-form nonlinear model when analyzing the constraint characteristics of symmetric spatial beams. In [
23], Awter proposed the nonlinear strain energy formulation for two-dimensional beam flexures.
For numerical solutions [
24,
25,
26,
27,
28,
29,
30,
31], the elliptical integration method is commonly used to address large geometrical nonlinearity [
24]. Saxena and Kramer [
25] solved these equations with numerical integration using Gauss–Chebyshev quadrature formula. Howell et al. [
26] first proposed the pseudo-rigid body method (PRBM), which can help simplify the design and analysis of compliant mechanisms. Pietro [
27] used the pseudo-rigid body method to synthesize a sub-optimal lumped compliance solution. More recently, other PRBM with prismatic (P) joints [
28] was proposed to incorporate the elastic extension effect and even the effects from shearing deflection and cross-section changes for Timoshenko beams. With the Cosserat rod model widely used in computer graphics, some researchers [
29,
30] have tried to apply it to robotics. Weak-form Cosserat rod models can be formulated and solved using a finite-element [
31], finite-difference, or discrete-differential geometry approach, and will be used in this study.
In the above studies, the exact solution of the compliant rod requires a huge amount of computation. This is not conducive to real-time precise control of CMs. How to balance the contradiction between accuracy and calculation amount is another challenge in compliant rod modeling. Therefore, this paper will combine neural networks to simplify the mapping relationship between the input and output variables of CMs, and discuss the modeling and kinematics analysis of the novel compliant mechanism.
The rest of this paper is organized as follows.
Section 2 introduces the novel compliant mechanism and its structure.
Section 3 introduces the theoretical models used in analyzing compliant rods, and discusses the mobility of the novel mechanism. In
Section 4, the mechanism is simplified to a rigid model, and kinematic variables are calculated based on the simplified model. Next, the singularity is discussed with force analysis, and the workspace without singularity positions. Finally, a prototype is manufactured and used to verify the mobility analysis and simplified model.
3. Theoretical Model
In this section, three methods will be introduced to analyze the mechanism’s movement characteristics. At first, the Cosserat rod model will be applied to the analysis of the compliant rod. The relationship between force and deformation of a compliant rod will be investigated with the Cosserat rod model and Lagrangian dynamics equation. Next, the relationship will be trained as a neural network, and the neural network will be used to calculate the mechanism’s kinematics. To solve a large number of nonlinear equations in the mechanism’s kinematics, a chaos-enhanced accelerated particle swarm optimization method will be used.
3.1. Method 1: Cosserat Rod Model
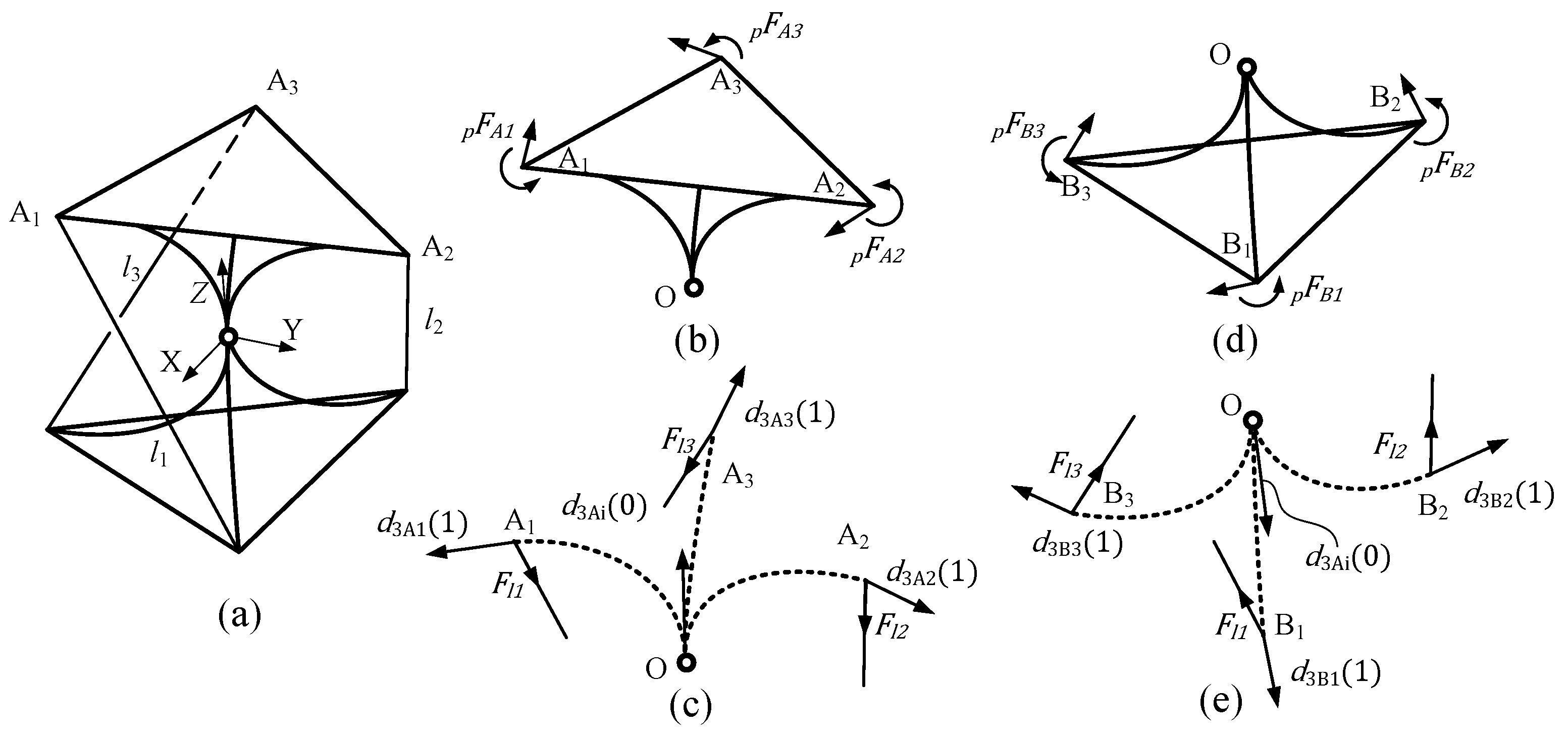
This section provides a brief introduction to the Cosserat rod model of elastic rods. An elastic rod can be visualized as a long thin deformable body. If a rod’s length is much greater than its radius, the rod’s continuous configuration can be characterized by the centerline
r(
w) = {
rx(
w),
ry(
w),
rz(
w)}
T, where
r(
w) assigns a position in space to each line parameter value
w ∈ [0, 1]. An orthonormal frame with basis vectors {
d1(
w),
d2(
w),
d3(
w)} is attached to every point on the curve, such that
d1 and
d2 span the plane of the rod’s cross-section, and
d3 is the normal to the cross-section (as shown in
Figure 3).
To relate the directions
di to the reference frame, quaternions are chosen as a representation of rotation. Quaternions can be present as a quadruple
q = {
q1,
q2,
q3,
q4}
T with
qi ∈
R. Only unit quaternions represent pure rotations, thus the
qi is not independent but coupled by the constraint ‖
q‖ = 1. The directions
di in terms of the quaternion
q are given by:
For elastic rods, the potential energy consists of three parts, namely the energy versus the stretch deformation, energy
Vb of the bending deformation, and energy
Vt of the torsional deformation. However, the bending deformation and torsional deformation are similar in expression, and can be integrated to
Vb,t. The three energies are given as:
where
Ks =
Esπrr2 is the stretching stiffness;
Es is the stretch modulus; the
ûk conform to the intrinsic bending and torsion of the rod;
Kk is the stiffness tensor (
K1 =
K2 = 0.25
Eπrr2,
K3 = 0.5
Gπrr2);
E is the Young’s modulus governing the bending resistance;
G is the shear modulus governing the torsional resistance; and
rr is the radius of the rod’s cross-section.
The dynamic equilibrium configuration of an elastic rod is characterized as a critical point of the Lagrangian. Details can be found in Goldstein [
32].
where the
gi∈{
rx,
ry,
rz,
q1,
q2,
q3,
q4} are coordinates and
Fe are external forces and torques;
T and
V = vs. +
Vb +
Vt are the kinetic energy and the potential energy of the system;
D is the total dissipation energy;
γt is the translational internal friction coefficient;
γr is the rotational internal friction coefficient;
Cp and
Cq are holonomic constraints;
λ and
μ are Lagrangian multipliers;
Bk and
Bk0 are a constant skew-symmetric matrix;
r’ is the tangent vector at point
r;
′ is the derivative of
r′.
3.2. Method 2: Back-Propagation Neural Network
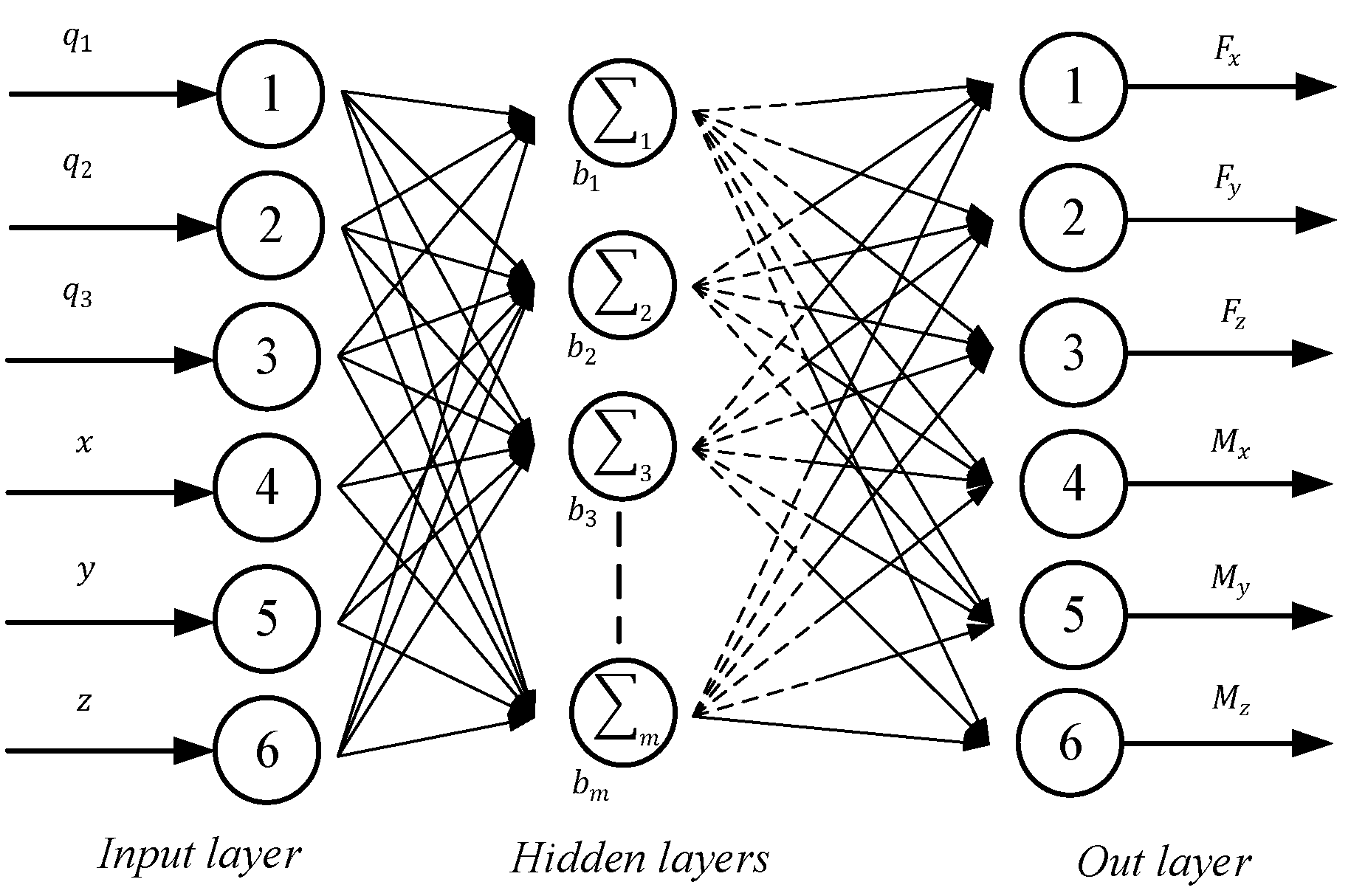
The back-propagation (BP) network is a widely used multi-layer feed-forward network with error inverse propagation. It is generated using the BP algorithm, which is a type of supervised learning algorithm. The BP algorithm continuously calculates the network’s weights and the error’s trend in the direction that minimizes the error. By doing so, it gradually reduces the error until the sum of squares of errors is minimal. The weights and the error’s trend are positively correlated with the network’s errors and are transmitted in reverse to every layer. The BP network can learn and store numerous input–output mapping relationships without a mathematical expression. It can be used to map the relationship between forces and the position and direction at a compliant rod’s end.
A BP network consists of an input layer, an output layer, and multiple hidden layers. In this study, positions and quaternions of a compliant rod are taken as the input layer, and the forces at the rod’s end are taken as the output layer. This BP network’s structure is shown in
Figure 4, and can replace the function
Ff in Equation (6). To train the neural network, 6.4 × 10
7 sets of data are calculated and used as the samples.
3.3. Method 3: Chaos-Enhanced Accelerated Particle Swarm Optimization Method
Kennedy and Eberhart developed the standard Particle Swarm Optimization (PSO) in 1995. Extensive studies have demonstrated that PSO is highly efficient for optimizing many problems. However, for highly multimodal problems, it may suffer from premature convergence. The standard PSO uses
g (the current global best) and
x (the individual best) to increase the diversity in quality solutions. To simplify the algorithm and accelerate convergence, the global best can be used exclusively. In 2008, accelerated particle swarm optimization (APSO) [
33] was proposed, which generates the velocity vector using a simpler formula.
where
rrandom is drawn from
N (0,1).
During each iteration, the particle’s position is updated by
The randomization term
αr allows the system to escape local optima, and
r can be solved by a probability distribution. Typically, a value of
β ranging from 0.2 to 0.7 is adequate for most situations. Another enhancement to APSO involves reducing randomness as iterations progress. This can be achieved using the follow function:
where 0 <
δ < 1 is an annealing-like parameter whose value can be taken as 0.7 to 0.9 for most applications;
t is the
t-th iteration.
There is no requirement to maintain a constant value of
β in standard APSO. However, a varying
β may provide advantages and lead to faster convergence of the algorithm. Since all chaotic maps are normalized, a chaos-enhanced APSO (known as chaotic APSO) uses the chaotic map to tune the parameter
β. In [
34], after comparing various chaotic APSO variants, the sinusoidal map is deemed the best chaotic APSO, and is expressed as follows:
3.4. Numerical Computation
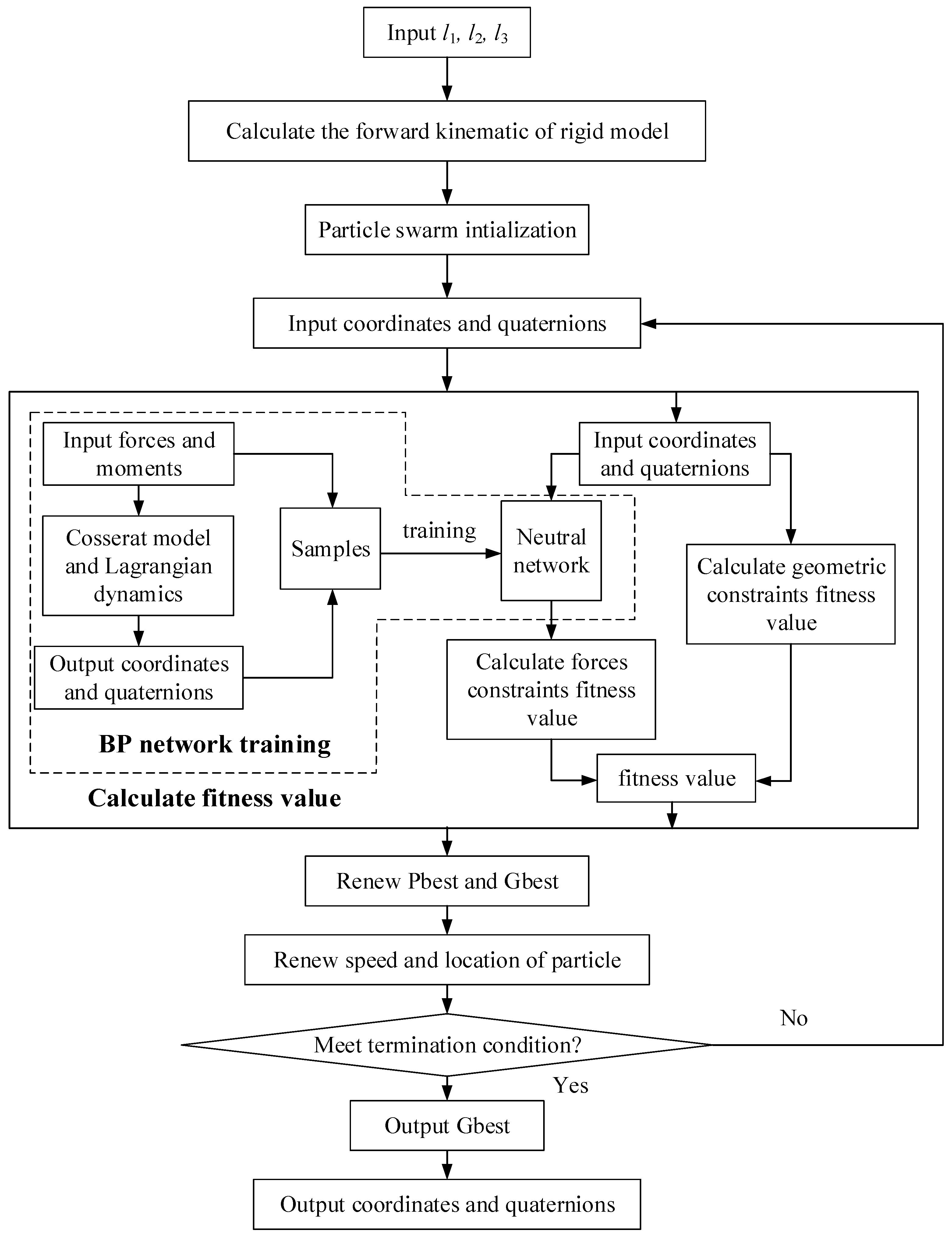
In this section, all these three methods will be integrated. There are two steps in this integration. The first is to analyze a single compliant rod with the Cosserat rod model and BP network. The second is to build the compliant mechanism’s kinematical model.
The purpose of the first step is to establish the relationship between forces, positions and quaternion of a compliant rod. First, the rod will be simplified to a Cosserat rod model. By solving the Lagrange dynamic equations, the rod’s position and quaternion can be calculated under forces. In addition, all the material parameters for the compliant rod are shown in
Table 1. To facilitate the solution of the motion’s equations, the rod is discretized into elements. First, the centerline of the rod is expressed as a chain of
N nodes
ri,
i ∈ [1,
N]. The centerline elements
ri+1 −
ri may differ in size. The orientations of the centerline elements are represented by quaternions q
j,
j ∈ [1,
N − 1], as illustrated in
Figure 2. The discrete spatial derivative
ri′ of the centerline and q
j′ are obtained as
Next, a large number of the rod’s positions and quaternions can be calculated as samples in the training BP network. Taking the positions and quaternions as the input parameters and the forces and moments as the output parameters, the BP network is trained with 10 hidden neurons and the Levenberg–Marquardt algorithm.
The second step is to build the compliant mechanism’s kinematical model. The model is introduced in
Section 2.2. However, as it is hard to solve these equations with an analytical solution, the chaos-enhanced accelerated particle swarm optimization method is used here. As shown in
Figure 5, the numerical computation can be separated into serval steps:
(a) taking the mechanism as a rigid mechanism, the position and quaternions can be calculated. The result can be taken as the initial value. Next, all particle swarms can be initialed.
(b) calculating the fitness value.
(c) renewing the Pbest, Gbest and particles’ speed and location.
(d) judging the termination condition. If the Gbest meets the termination condition, output the Gbest; if not, come back to step (a).
3.5. Results and Summary
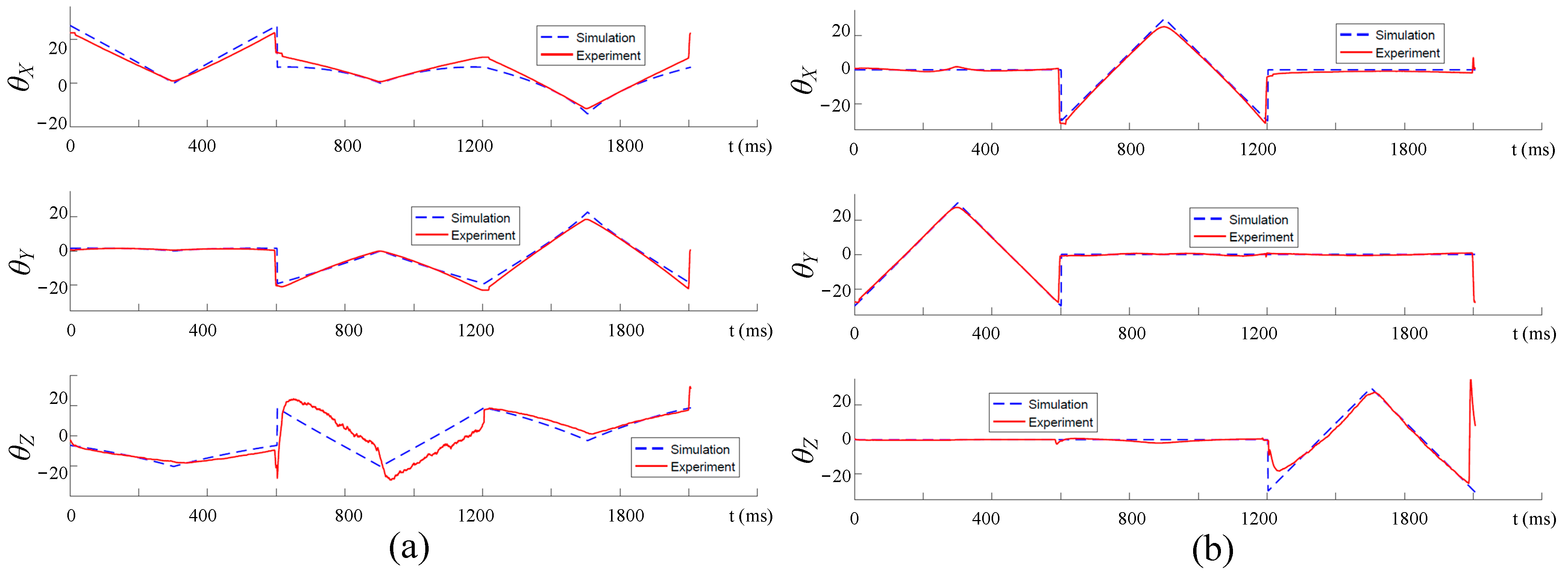
For numerical computation, the radii of the moving platform and base platform is set as 65 mm. The range of the driven cable’s length is set to be 65 mm–185 mm. To reduce the calculation amount and ensure the result’s reliability, 124 sets inputs are chosen randomly from the range of the driven cable’s length.
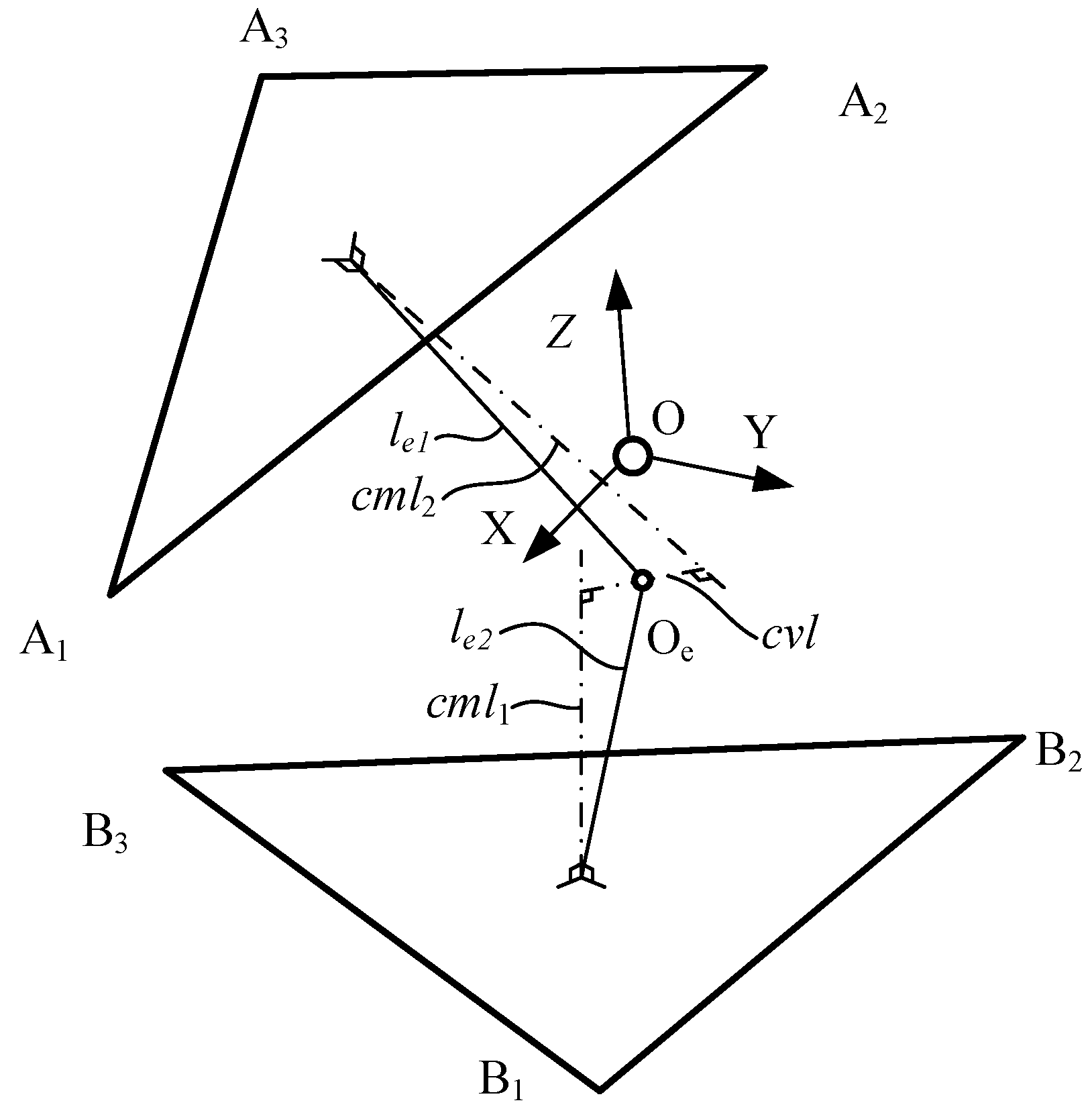
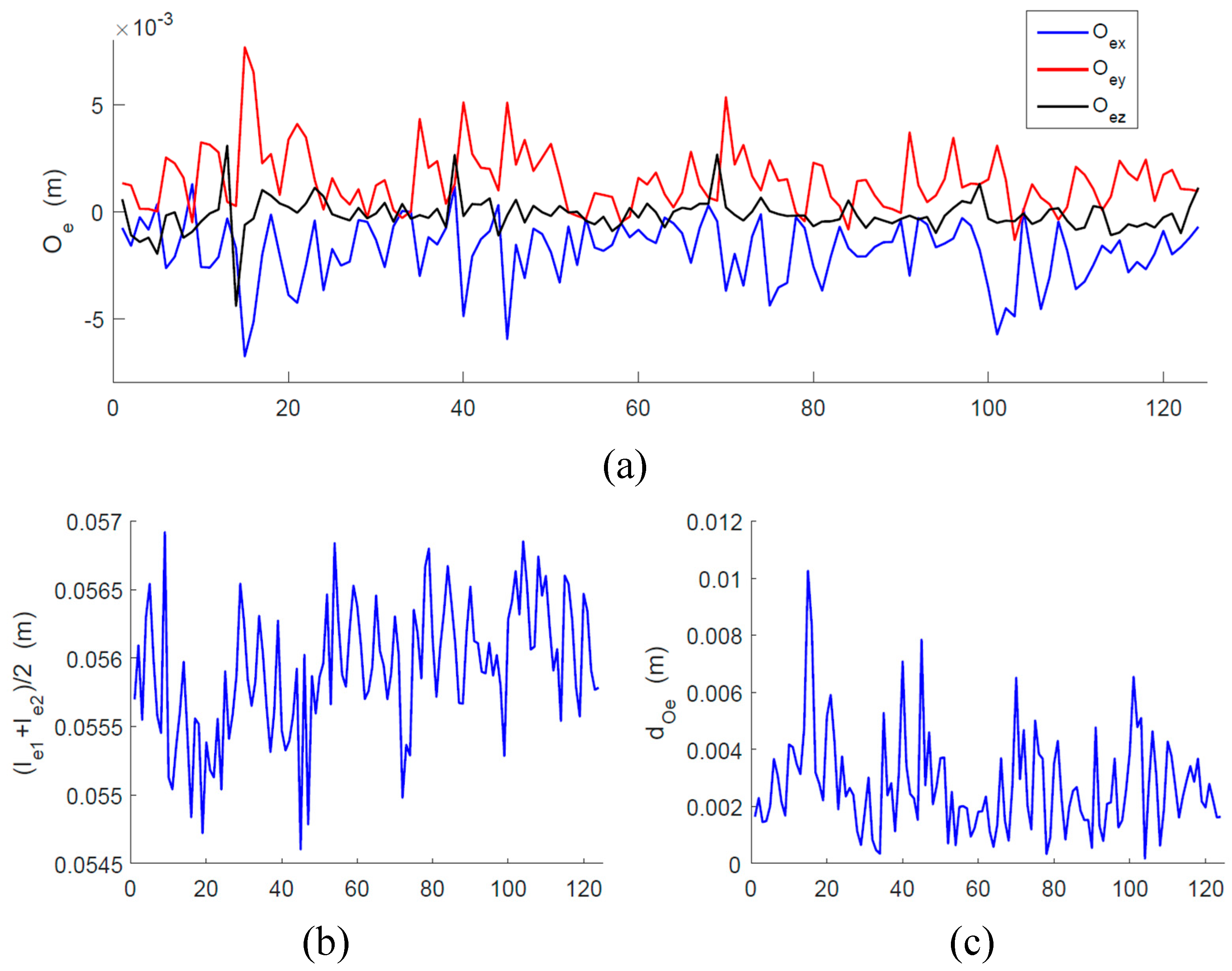
Next, all these positions will be analyzed. The relative motion between a moving platform and base platform will be investigated. According to the moving platform and base platform positions, the relative rotating center (RRC) and the relative rotating radius (RRR) will be defined here. As shown in
Figure 6,
cml1 is the normal line of the moving platform via the moving platform’s center point O
A, the same as
cml2 to base platform. Next, the common vertical line of
cml1 and
cml2 could be found, and the middle point of common vertical line is set as O
e. Point O
e is approximately seen as the relative rotational center. Next, the distance between O
e and the moving platform’s center point O
A is approximately seen as its relative rotational radii
le1, the same as
le2 to the base platform. The mean of
le1 and
le2 are seen as the mechanism’s RRR.
According to the position results, a set of RRC and RRR can be calculated. The results are shown in
Figure 7. From
Figure 7c, the RRC is close to the origin point O, and the mean distance is 2.7 mm. On the other hand, the RRR ranges from 54 mm to 57 mm, and the mean is 56 mm. It is obvious that 2.7 is far less than 56 mm, which means that origin point O could be taken as the mechanism’s RRC. In addition, the RRR can be seen as a constant. A constant rotate radius and a fixed rotational center means that the moving platform and base platform move along a spherical surface. In summary, the moving platform has three spatial rotational degrees of freedom.
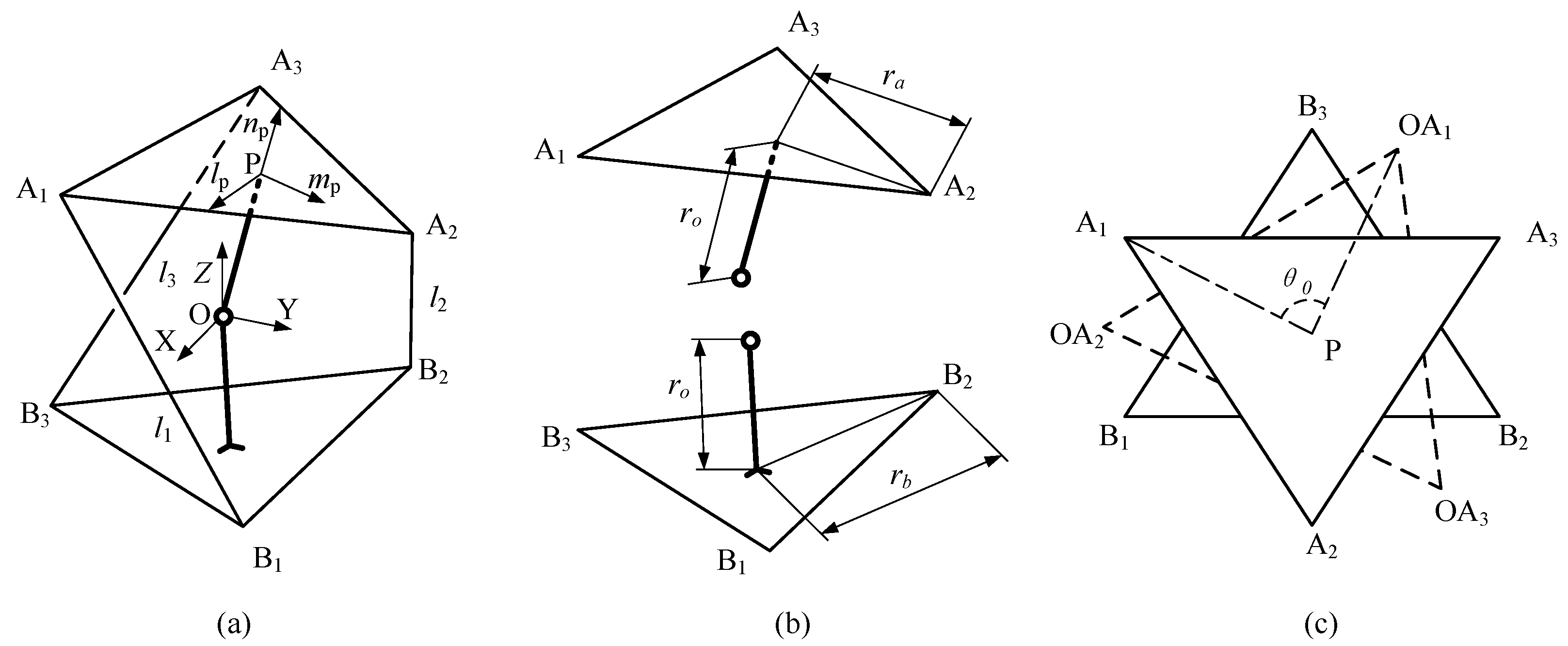
4. Kinematics Analysis of 3R Parallel Compliant Mechanism
From the conclusion in
Section 3.5, the novel compliant mechanism is a device whose moving platform can rotate around the center point in any direction. Thus, it can be considered to be a rigid parallel mechanism with three rotational degrees of freedom. As shown in Fig.8, three flexural limbs are replaced by a spatial ball hinge at a center point. On the other hand, the driven cable can only bear the tension. That means the cable can just drive the moving platform rotate counterclockwise along the
Z-axis. To drive the moving platform to rotate clockwise at the initial position, there must be a pre-rotation at the initial position. As shown in
Figure 8c, the position OA
1OA
2OA
3 is the moving platform in assembly-complete state without pre-rotation. Next, a pre-rotation is applied to the mechanism. Then, the mechanism reaches the initial position A
1A
2A
3 with a counterclockwise degree
θ0.
4.1. Direct Kinematics
The direct kinematics analysis of a parallel mechanism aims to calculate moving platform attitude angles and positions according to given joint variables. For the novel mechanism, the three driven cables’ lengths
li (
I = 1, 2, 3) are joint variables, and the three attitude angles are the moving platform’s pose. In this study, Z-Y-X Euler angles are applied to express the moving platform’s pose, as the sensor in the experiment used it. The Z-Y-X Euler angles mean that the moving platform rotates
θz degrees along the Z-axis of the fixed frame first, acquiring a new frame X′Y′Z′. Then, the moving platform rotates
θy degrees along the Y′-axis of the new frame X′Y′Z′, acquiring another new frame X″Y″Z″. After that, the moving platform rotates
θx degrees along X″-axis of the new frame X″Y″Z″. Next, the rotation matrix of the moving platform can be expressed as follows.
where
Ci and
Si represent cos(
θi) and sin(
θi), and
i = x, y, z.
At the initial position, the vertexes’ coordinates of the moving platform and base platform can be expressed as follows.
Then, the vertexes’ coordinate of the moving platform at any position can be written as follows.
According to the given driven cables’ lengths
li, forward kinematics equations can be obtained.
By solving Equation (19), three Euler angles can be obtained.
4.2. Inverse Kinematics
The inverse kinematics of the novel mechanism aims to solve the three driven cable’s lengths according to a given moving platform pose. According to Equations (16)–(19), the inverse kinematics can be solved.
4.3. Results and Summary
A mechanism is driven by actuators to move. When a mechanism experiences changes in its kinematical or dynamic performance at certain positions, it may become stuck in dead-point positions, lose balance stability, or alter its degree of freedom. Consequently, the mechanism cannot transfer movements or be controlled properly. These positions are known as singularities. In the case of a novel mechanism, the movement of the moving platform depends on compliant rods and driven cables. Thus, the mechanism will only encounter singularity positions when the deformation of the compliant rods disappears or the tension in the driven cables disappears.
4.3.1. Compliant Rods’ Deformation Disappearance
Compliant rods’ deformation includes bending, stretching, and twisting. In this mechanism, the compliant rods mainly bear radial forces, so stretching will not be discussed here. The key points are bending and twisting deformation. When rod bending disappears, rods will recover to become straight rods. However, whatever position the moving platform is in, the compliant rod will always bend. As a result, the rod bending will not disappear.
For rod twisting deformation, when the mechanism is at initial position, there is a pre-rotation along the
Z-axis. When the twisting deformation disappeared, the mechanism’s pre-rotation will disappear. Thus, when the moving platform’s rotation angle along the Z-axis clockwise is bigger than
θ0, the mechanism is in singularity positions.
4.3.2. Driven Cables’ Tension Disappearance
Considering that cables only can bear tension, when the driven cables’ tension disappears, the moving platform will lose the control along with the power from driven cables. Thus, the mechanism is in a singularity position.
When the three driven cables’ length are given, the position and quaternion can be calculated according to
Section 4.1. Next, the forces at the rods’ ends can be calculated from
Section 3.1, and the driven cable’s force
Fli can be obtained too.
When the directions of cables’ force were reverse to vector
, the mechanism is in singularity positions.
4.4. Workspace
In this section, the parasitic motion workspace and the reachability of the novel mechanism are obtained based on forward position analysis and singularity analysis. The key points in analyzing the workspace are the mechanism’s kinematical constraints and singularity. The kinematical constraints include action range and physical joint range.
The actuator’s range limits the mechanism’s workspace. Because of the actuator’s physical structure, its range is usually between a minimum value and a maximum value. The corresponding actuator’s constraint condition can be expressed as follows:
Physical joints also limit the mechanism’s range of motion. As mentioned in
Section 3.5, the compliant rods are equivalently replaced by a ball hinge joint. However, a ball hinge joint’s range is limited by its physical structure. For this mechanism, the moving platform and base platform have the same structure size, so the maximum angle between these two platforms is 90 degrees. Thus, the angle between the moving platform’s normal and
Z-axis should be less then 90 degrees. According to the rotation matrix, this constraint can be present as
According to
Section 4.3, the mechanism has two kinds of singularity position. The first depends on the pre-rotation angle. When the prototype is manufactured, the pre-rotation angle
θ0 is set as 60 degrees. The second singularity position is related to the mechanism’s forward kinematic and force analysis in
Section 2.2.
Figure 9a shows the mechanism’s workspace with singularity positions. The blue plane is the border of the pre-rotation angle, and the green parts are the positions of that mechanism’s driven cable without tension. After excluding singularities, the mechanism’s final workspace is shown in
Figure 9b.