Comparison of Linear Regression and Artificial Neural Network Models for the Dimensional Control of the Welded Stamped Steel Arms
Abstract
1. Introduction
2. Materials and Methods
2.1. Linear Regression
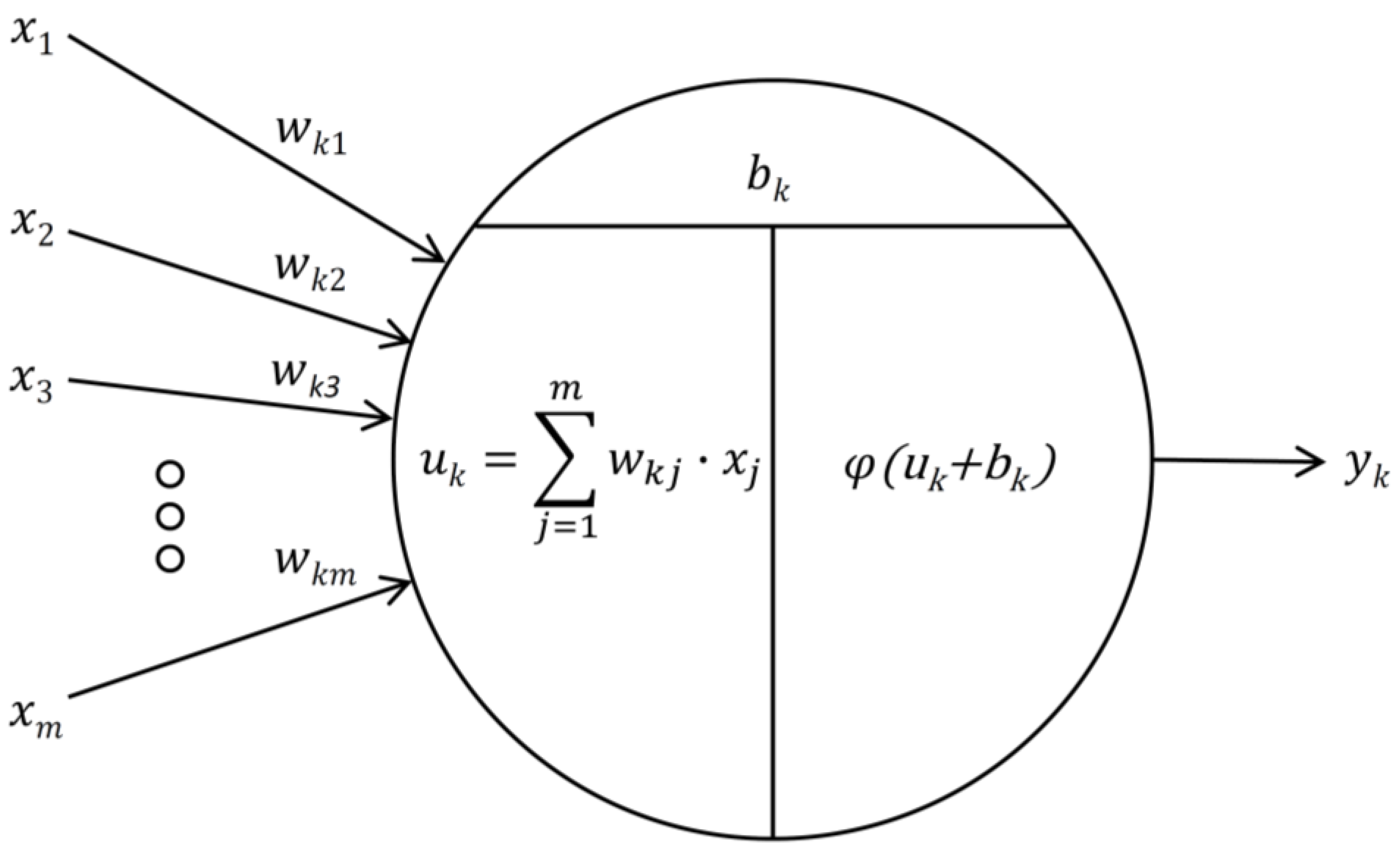
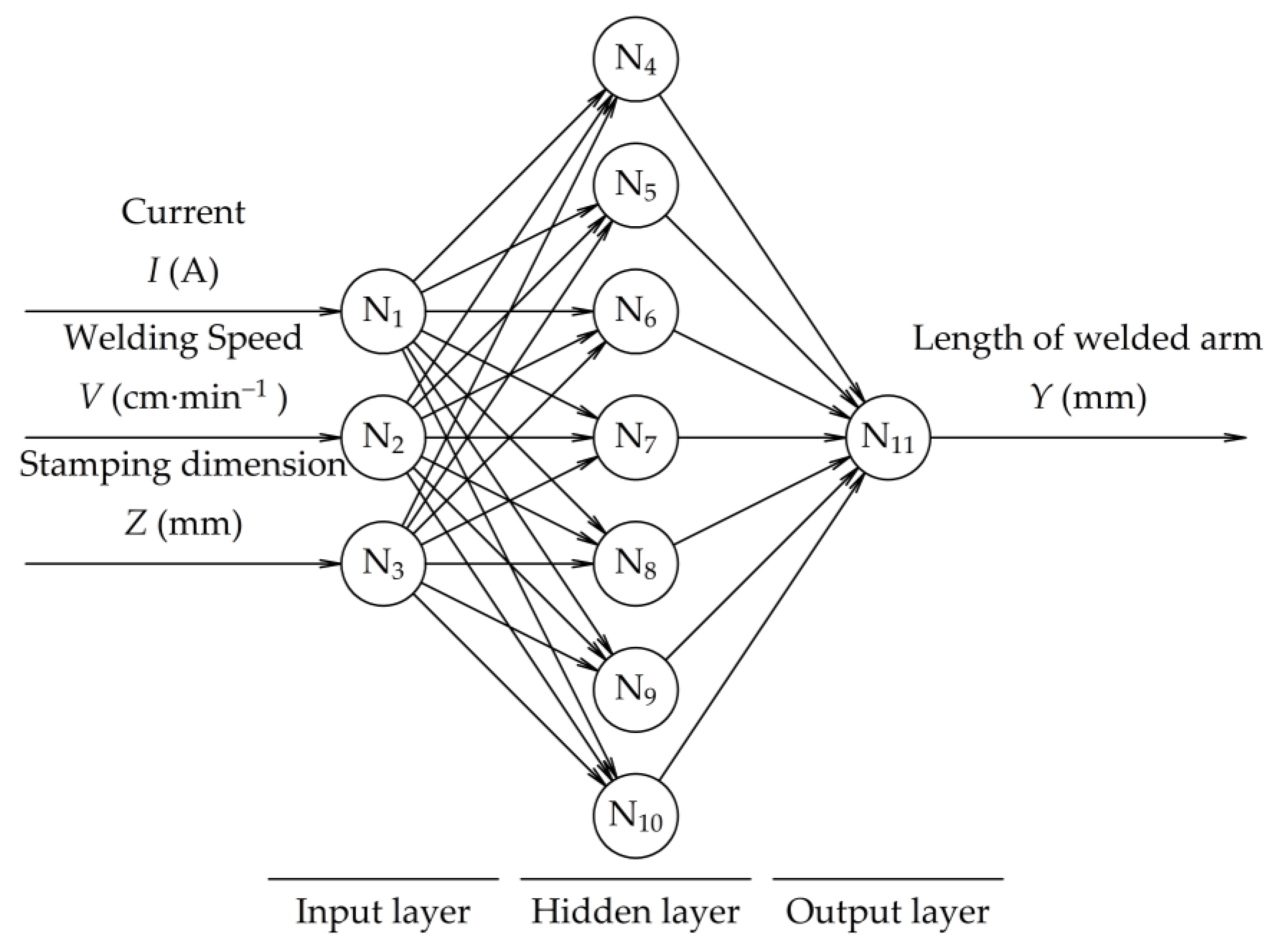
2.2. Artificial Neural Networks
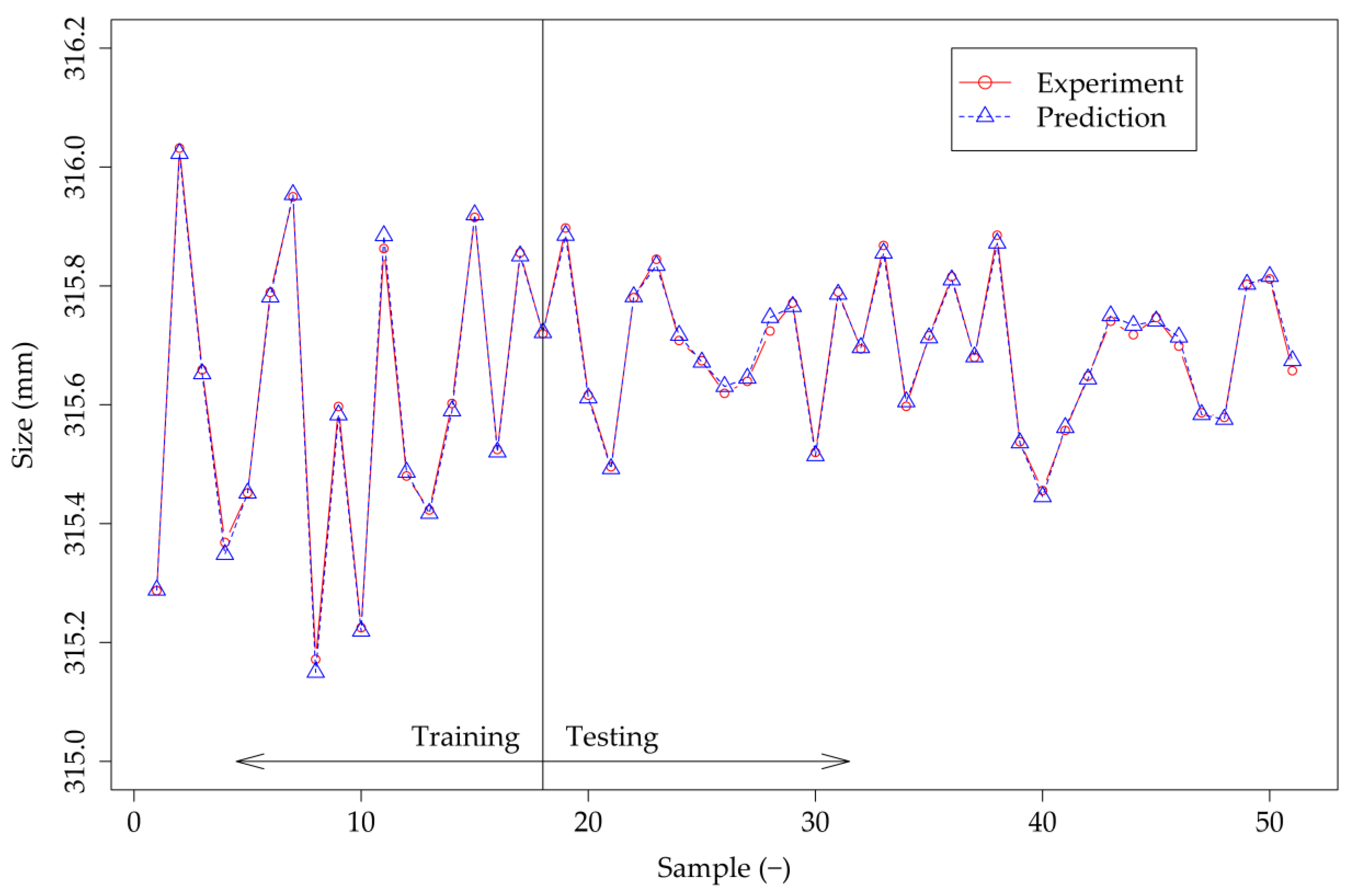
3. Results and Discussion
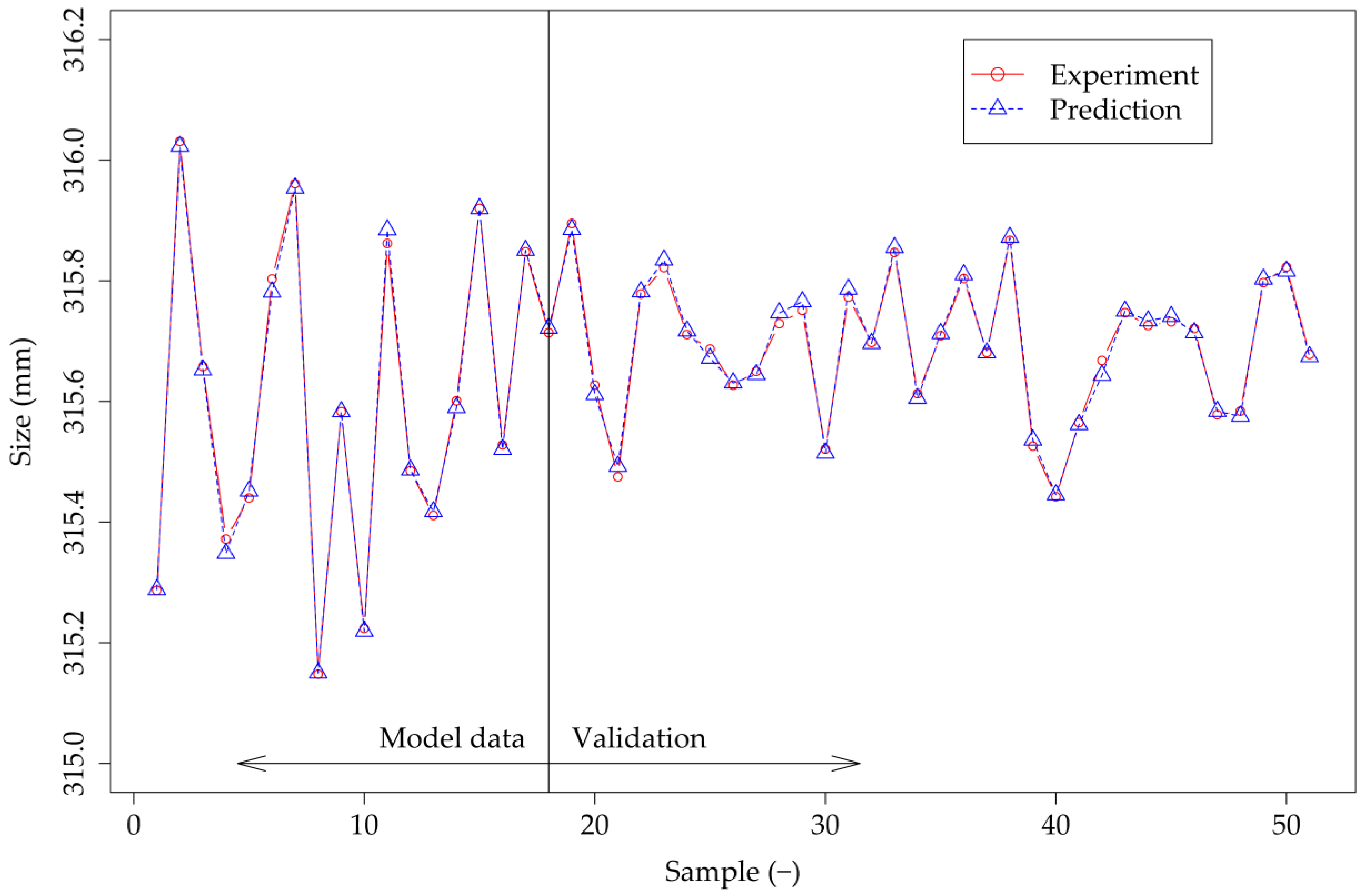
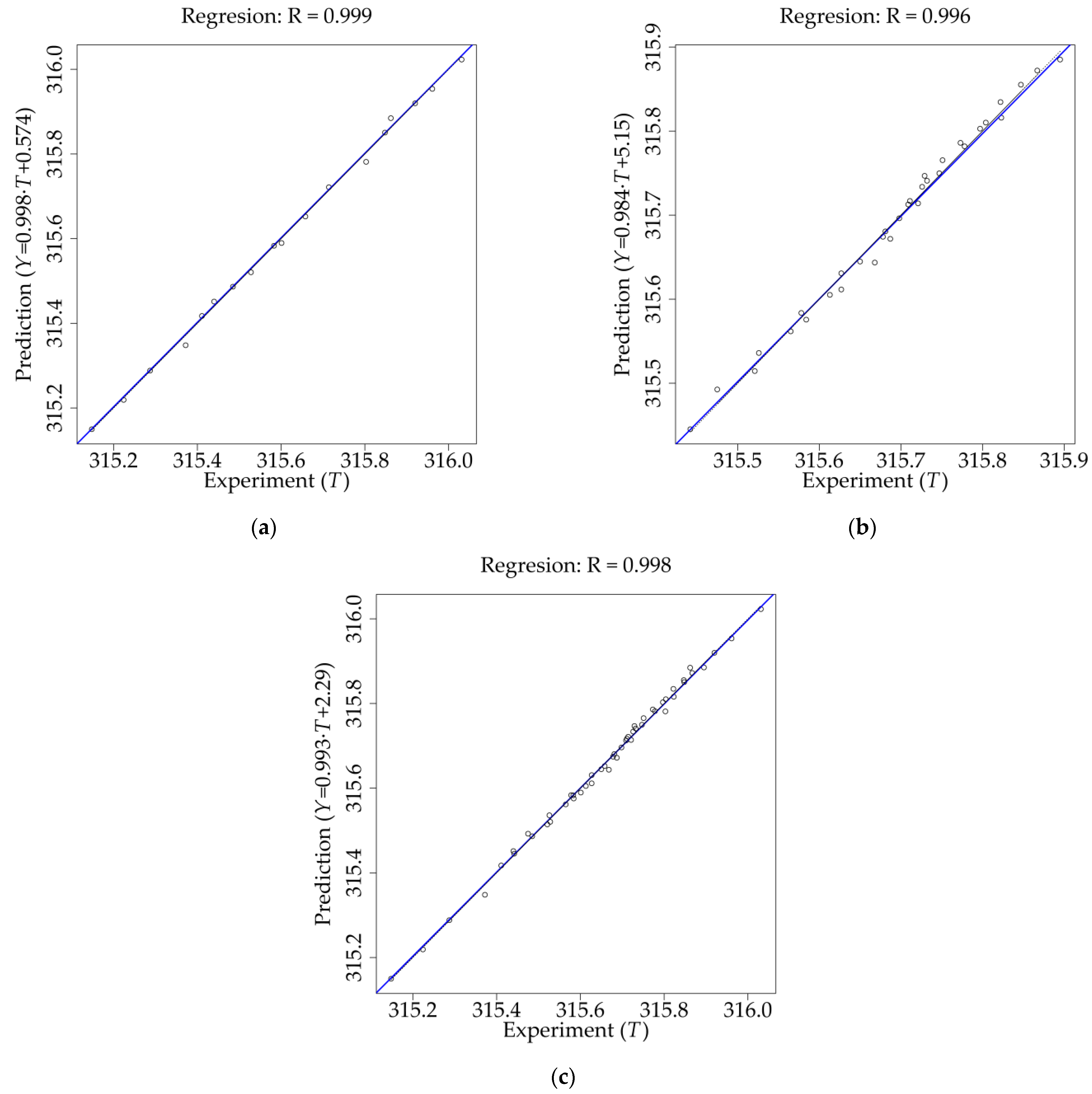
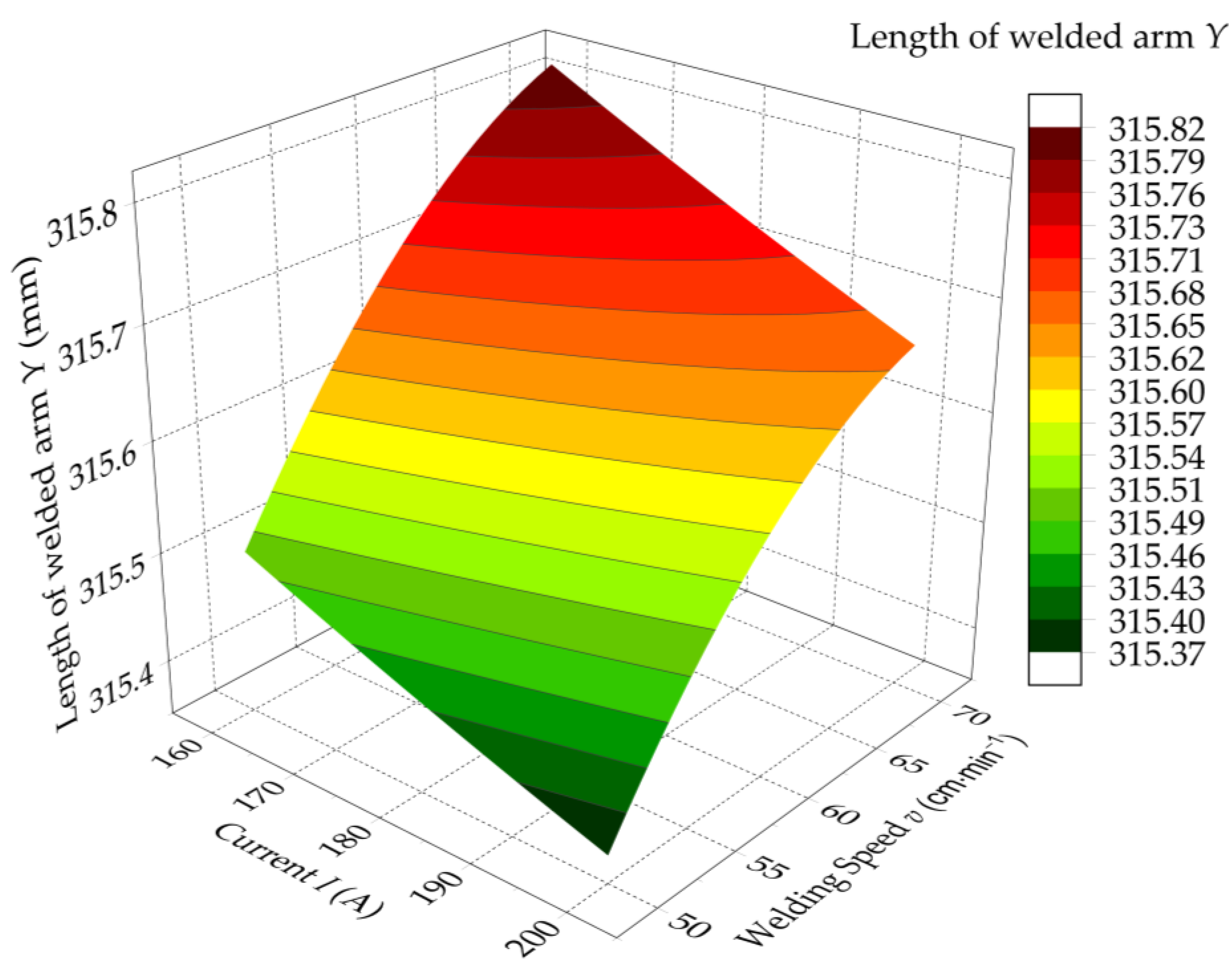
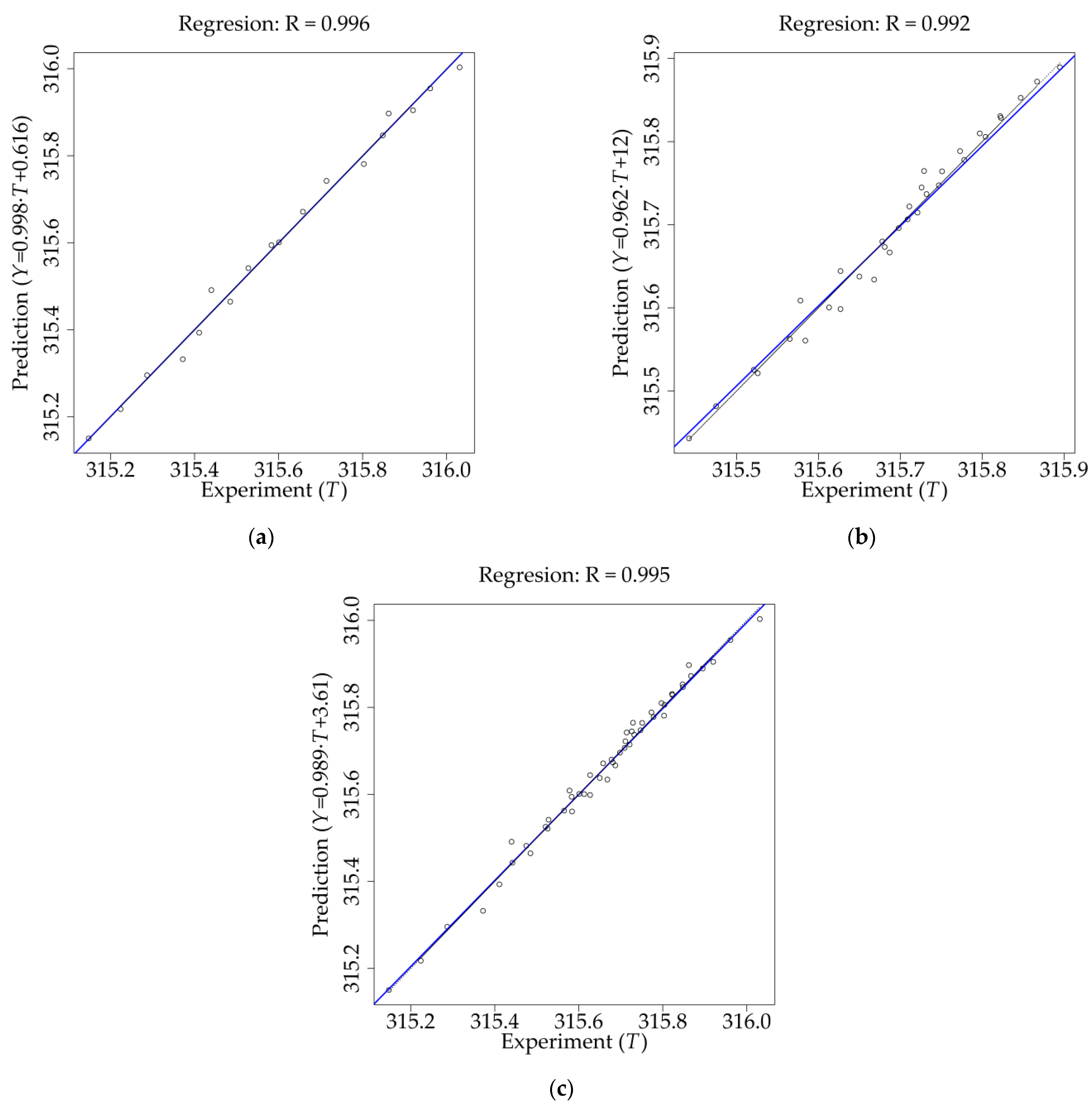
3.1. LR Results
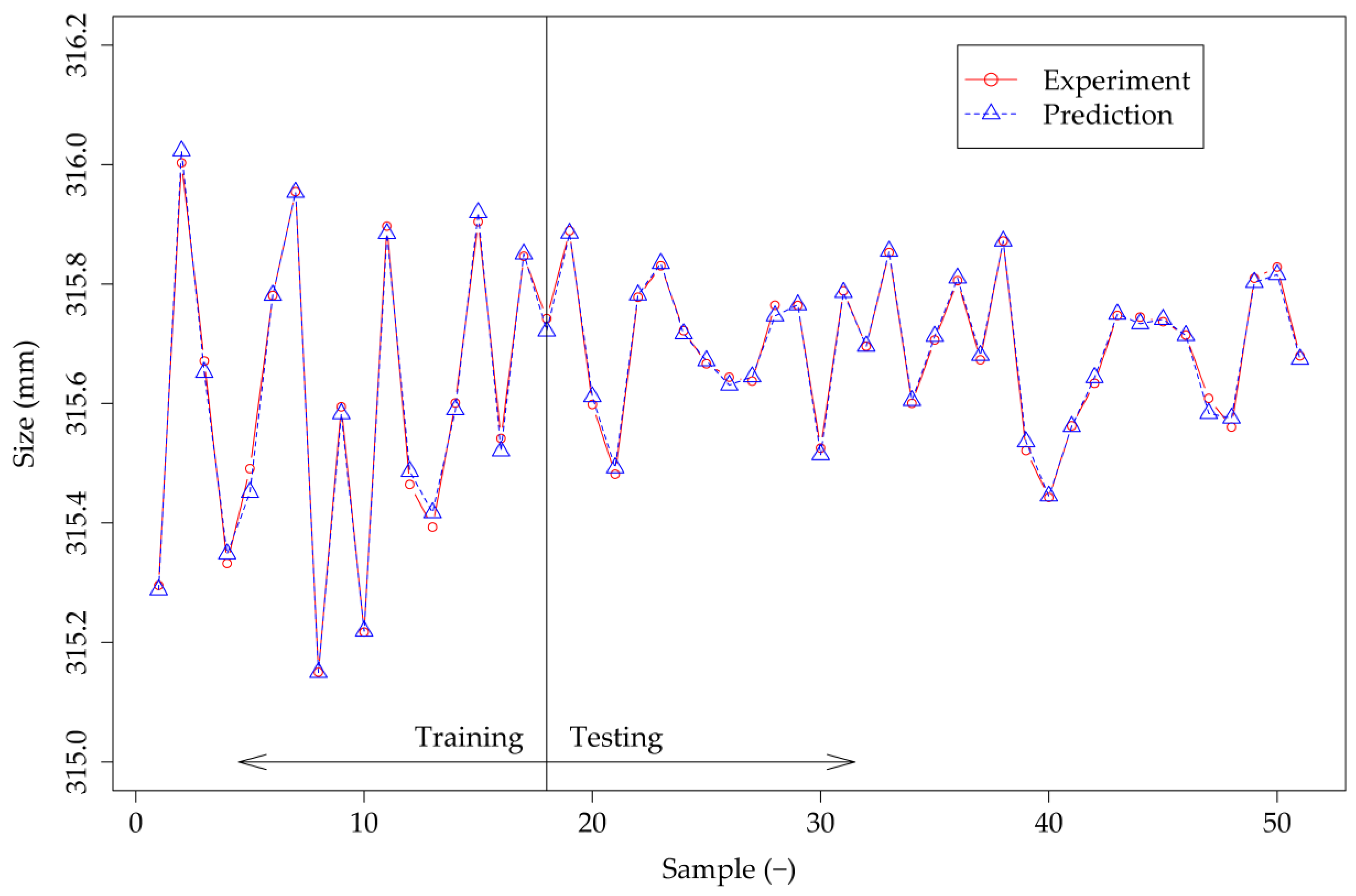
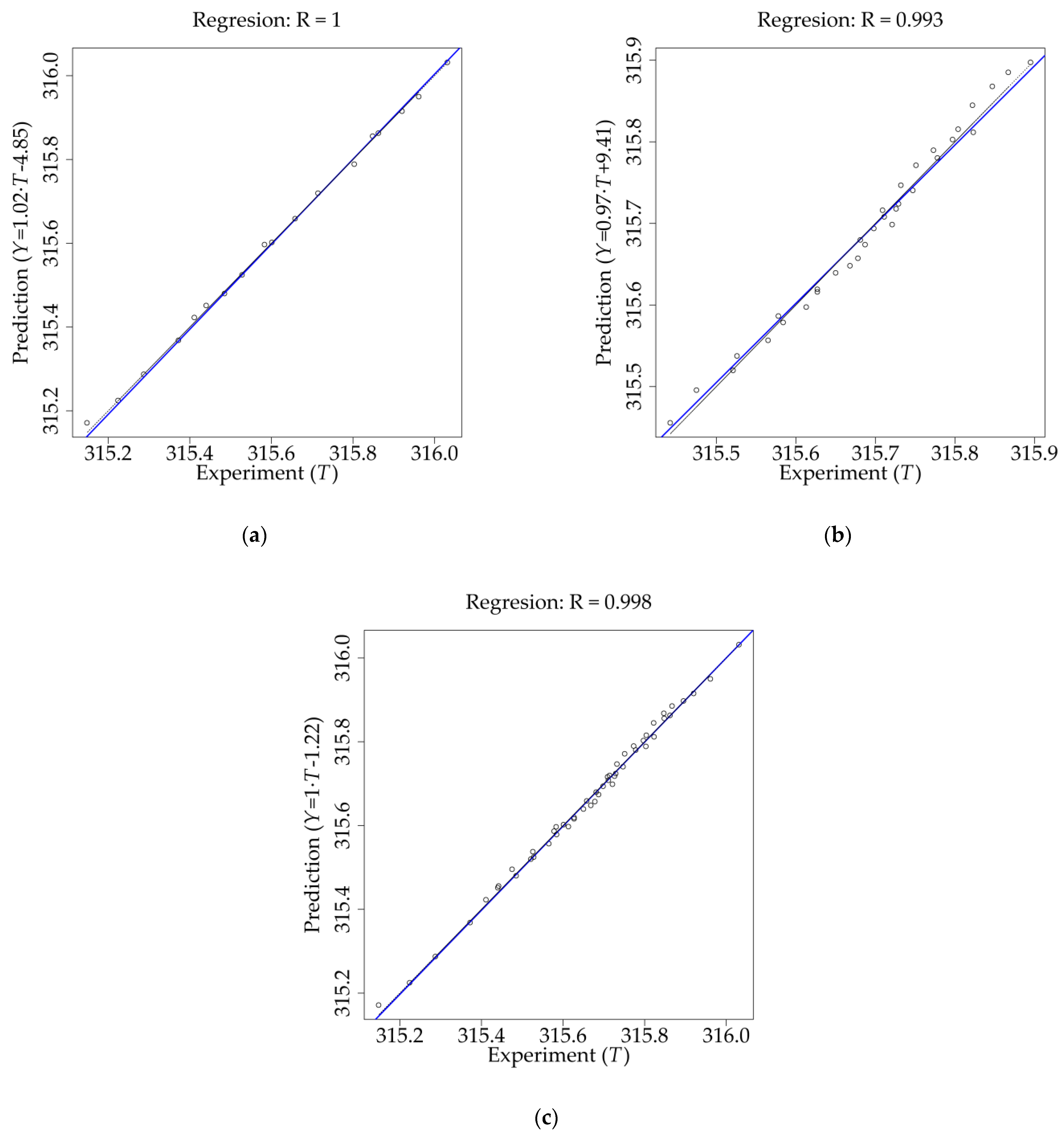
3.2. ANN Results
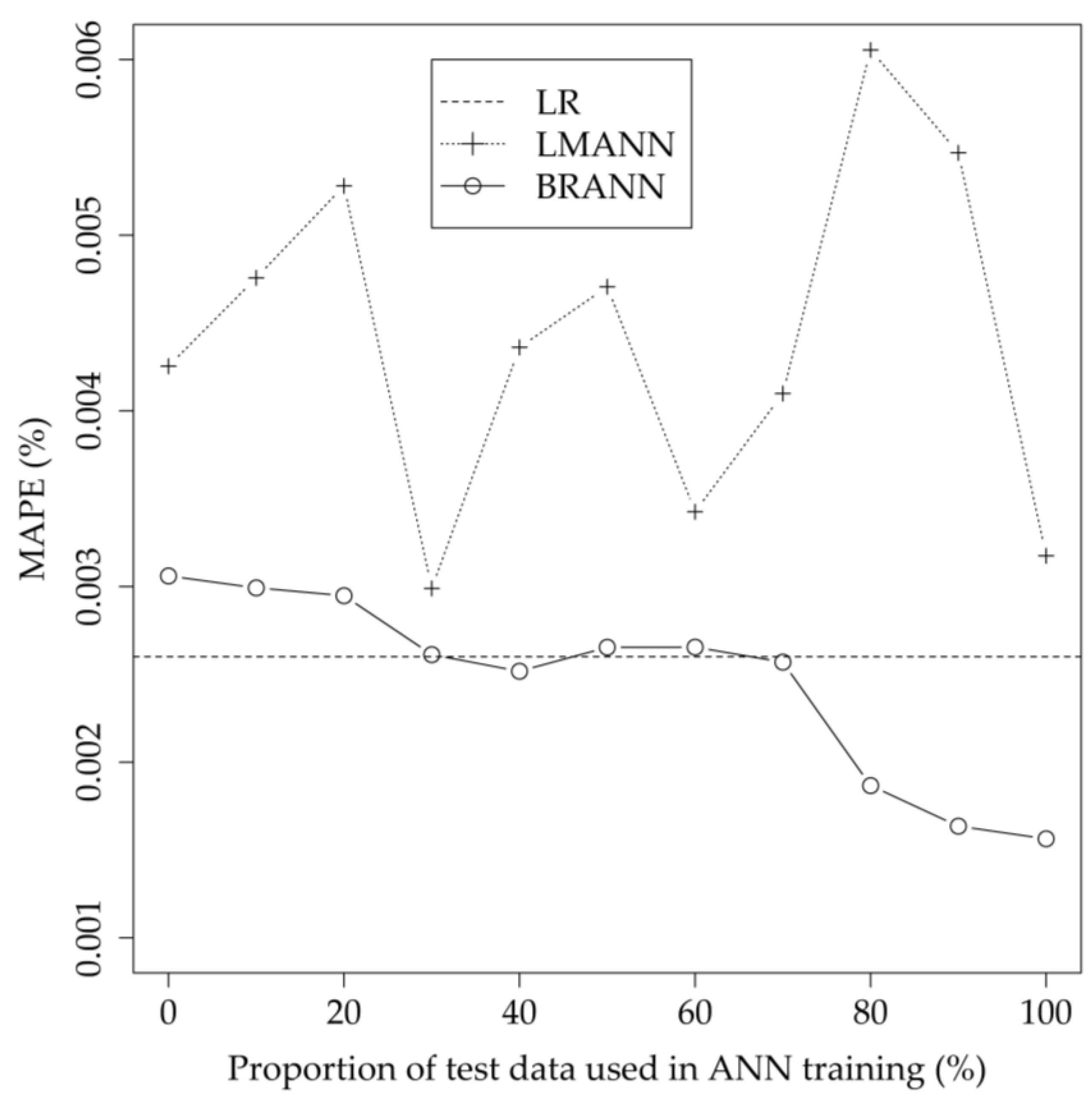
3.3. Perfrormance Comparison for the LR Model and ANN Models
4. Conclusions
- Neural networks can be trained on reduced number of samples of data based on a design of experiment methodology.
- The new derived Equations (7) and (10) can be used to predict the resulting dimension directly from the input operating parameters within the considered interval.
- It was observed that linear regression had the lowest MAPE when training the ANN using DOE data. Despite the low number of training data, the neural network with Bayesian regularized back propagation algorithm achieved comparable results.
- MAPE for ANN with Levenberg–Marquardt back-propagation algorithm fluctuated around a value of 4 × 10−3%, which is greater than that for LR.
- MAPE for ANN with Bayesian regularized back-propagation algorithm trained on DOE data was at the MAPE level of 3 × 10−3%. However, the accuracy of the model increased with the increase of the training dataset up to the level of 1.6 × 10−3%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ozcelik, S.; Moore, K. Modeling, Sensing and Control of Gas Metal Arc Welding; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Cary, H.B. Arc Welding Automation; Marcel Dekker: New York, NY, USA, 1995. [Google Scholar]
- Omar, M.A. The Automotive Body Manufacturing Systems and Processes; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Zong, R.; Chen, J.; Wu, C. A comparison of TIG-MIG hybrid welding with conventional MIG welding in the behaviors of arc, droplet and weld pool. J. Mater. Process. Technol. 2019, 270, 345–355. [Google Scholar] [CrossRef]
- Noga, P.; Tuz, L.; Żaba, K.; Zwoliński, A. Analysis of Microstructure and Mechanical Properties of AlSi11 after Chip Recycling, Co-Extrusion, and Arc Welding. Materials 2021, 14, 3124. [Google Scholar] [CrossRef] [PubMed]
- Tuz, L.; Kąc, S.; Sierakowski, D. Technology of electron beam welding of 10CrMo9-10 steel with the specific quality requirements. Manuf. Lett. 2023, 35, 53–57. [Google Scholar] [CrossRef]
- Weman, K.; Gunnar, L. MIG Welding Guide; Woodhead Publishing: Cambridge, England, 2006. [Google Scholar]
- Sun, Z.; Yu, X. Prediction of welding residual stress and distortion in multi-layer butt-welded 22SiMn2TiB steel with LTT filling metal. J. Mater. Res. Technol. 2022, 18, 3564–3580. [Google Scholar] [CrossRef]
- Liang, W.; Murakawa, H. Predicting welding distortion in a panel structure with longitudinal stiffeners using inherent deformations obtained by inverse analysis method. Sci. World J. 2014, 2014, 601417. [Google Scholar] [CrossRef]
- Heinze, C.; Schwenk, C.; Rethmeier, M. The effect of tack welding on numerically calculated welding-induced distortion. J. Mater. Process. Technol. 2012, 212, 308–314. [Google Scholar] [CrossRef]
- Luo, M.; Hu, R.; Li, Q.; Huang, A.; Pang, S. Physical understanding of keyhole and weld pool dynamics in laser welding under different water pressures. Int. J. Heat Mass Transf. 2019, 137, 328–336. [Google Scholar] [CrossRef]
- Guu, A.; Rokhlin, S. Arc weld process control using radiographic sensing. Mater. Eval. 1992, 50, 1344–1348. [Google Scholar]
- Han, Y.; Fan, J.; Yang, X. A structured light vision sensor for on-line weld bead measurement and weld quality inspection. Int. J. Adv. Manuf. Tech. 2019, 106, 2065–2078. [Google Scholar] [CrossRef]
- Huang, N.; Zhang, J.; Zhang, T.; Zheng, X.; Yan, Z. Control of Welding Speed and Current in Machine–Human Cooperative Welding Processes. Crystals 2022, 12, 235. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Zhang, Y. Dynamic Neuro-Fuzzy-Based Human Intelligence Modeling and Control in GTAW. IEEE Trans. Autom. Sci. Eng. 2015, 12, 324–335. [Google Scholar] [CrossRef]
- Chandrasekhar, N.; Vasudevan, M.; Bhaduri, A.K.; Jayakumar, T. Intelligent modeling for estimating weld bead width and depth of penetration from infra-red thermal images of the weld pool. J. Intell. Manuf. 2013, 26, 59–71. [Google Scholar] [CrossRef]
- Guzmán, L.G.; Hammett, P.C. A Tolerance Adjustment Process for Dimensional Validation of Stamping Parts and Welded Assemblies; International Body Engineering Conference & Exposition; Society of Automotive Engineers (SAE): Warrendale, PA, USA, 2003. [Google Scholar]
- Lee, D.; Kwon, K.E.; Lee, J.; Jee, H.; Yim, H.; Cho, S.W.; Shin, J.-G.; Lee, G. Tolerance Analysis Considering Weld Distortion by Use of Pregenerated Database. J. Manuf. Sci. Eng. 2009, 131. [Google Scholar] [CrossRef]
- Michaleris, P.; DeBiccari, A. Prediction of welding distortion. Weld. J. Includ. Weld. Res. Suppl. 1997, 76, 172s. [Google Scholar]
- Reisgen, U.; Sharma, R.; Christ, M.; Mann, S. Method development of statistical modeling for the description of welding fume emissions in gas metal arc welding using transient process characteristics. Weld. World 2020, 64, 1497–1502. [Google Scholar] [CrossRef]
- Mallieswaran, K.; Padmanabhan, R.; Balasubramanian, V. Friction stir welding parameters optimization for tailored welded blank sheets of AA1100 with AA6061 dissimilar alloy using response surface methodology. Adv. Mater. Process. Technol. 2018, 4, 142–157. [Google Scholar] [CrossRef]
- Artinov, A.; Karkhin, V.; Bachmann, M.; Rethmeier, M. Mathematical modeling of the geometrical differences between the weld end crater and the steady-state weld pool. J. Laser Appl. 2020, 32, 022024. [Google Scholar] [CrossRef]
- Daunys, M.; Dundulis, R.; Kilikevičius, S.; Česnavičius, R. Analytical investigation and numerical simulation of the stress–strain state in mechanically heterogeneous welded joints with a single-V butt weld. Eng. Fail. Anal. 2016, 62, 232–241. [Google Scholar] [CrossRef]
- Nasiri, M.B.; Enzinger, N. An analytical solution for temperature distribution in fillet arc welding based on an adaptive function. Weld. World 2018, 63, 409–419. [Google Scholar] [CrossRef]
- Reisgen, U.; Schleser, M.; Mokrov, O.; Ahmed, E. Optimization of laser welding of DP/TRIP steel sheets using statistical approach. Opt. Laser Technol. 2012, 44, 255–262. [Google Scholar] [CrossRef]
- Mikno, Z.; Grzesik, B.; Stępień, M. The investigation on the ideal spot weld numerical model in resistance welding. Int. J. Adv. Manuf. Tech. 2020, 111, 895–907. [Google Scholar] [CrossRef]
- Mohanty, U.K.; Sharma, A.; Abe, Y.; Fujimoto, T.; Nakatani, M.; Kitagawa, A.; Tanaka, M.; Suga, T. Thermal modelling of alternating current square waveform arc welding. Case Stud. Therm. Eng. 2021, 25, 100885. [Google Scholar] [CrossRef]
- Abdelhafeez Hassan, A.; Küçüktürk, G.; Yazgin, H.V.; Gürün, H.; Kaya, D. Selection of Constitutive Material Model for the Finite Element Simulation of Pressure-Assisted Single-Point Incremental Forming. Machines 2022, 10, 941. [Google Scholar] [CrossRef]
- Kim, J.-J.; Bae, M.; Hong, M.-P.; Kim, Y.-S. Finite Element Analysis on Welding-Induced Distortion of Automotive Rear Chassis Component. Metals 2022, 12, 287. [Google Scholar] [CrossRef]
- Amirsalari, B.; Golabi, S.I. Finite element analysis, prediction, and optimization of residual stresses in multi-pass arc welding with experimental evaluation. J. Strain. Anal. Eng. Des. 2022, 57, 305–320. [Google Scholar] [CrossRef]
- Ma, B.; Meng, D.; Gu, X.; Ma, X.; Zhang, D.; Zhang, Q. Integration process of stamping and welding for DP600 advanced high strength steel sheets. Procedia Manuf. 2018, 15, 684–692. [Google Scholar] [CrossRef]
- Kang, W.; Cheon, S.S. Analysis of coupled residual stresses in stamping and welding processes by finite element methods. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2012, 226, 884–897. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Zaccaria, V.; Kyprianidis, K. Aircraft Engine Performance Monitoring and Diagnostics Based on Deep Convolutional Neural Networks. Machines 2021, 9, 337. [Google Scholar] [CrossRef]
- Fahle, S.; Prinz, C.; Kuhlenkötter, B. Systematic review on machine learning (ML) methods for manufacturing processes—Identifying artificial intelligence (AI) methods for field application. Procedia CIRP 2020, 93, 413–418. [Google Scholar] [CrossRef]
- Hamedi, M.; Shariatpanahi, M.; Mansourzadeh, A. Optimizing spot welding parameters in a sheet metal assembly by neural networks and genetic algorithm. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2007, 221, 1175–1184. [Google Scholar] [CrossRef]
- Kadnár, M.; Káčer, P.; Harničárová, M.; Valíček, J.; Gombár, M.; Kušnerová, M.; Tóth, F.; Boržan, M.; Rusnák, J. Prediction Model of the Resulting Dimensions of Welded Stamped Parts. Materials 2021, 14, 3062. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Artificial neural networks in renewable energy systems applications: A review. Renew. Sustain. Energy Rev. 2001, 5, 373–401. [Google Scholar] [CrossRef]
- Ozgoren, M.; Bilgili, M.; Sahin, B. Estimation of global solar radiation using ANN over Turkey. Expert Syst. Appl. 2012, 39, 5043–5051. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Bilgili, M.; Sahin, B. Comparative analysis of regression and artificial neural network models for wind speed prediction. Meteorol. Atmos. Phys. 2010, 109, 61–72. [Google Scholar] [CrossRef]
- Nele, L.; Mattera, G.; Vozza, M. Deep Neural Networks for Defects Detection in Gas Metal Arc Welding. Appl. Sci. 2022, 12, 3615. [Google Scholar] [CrossRef]
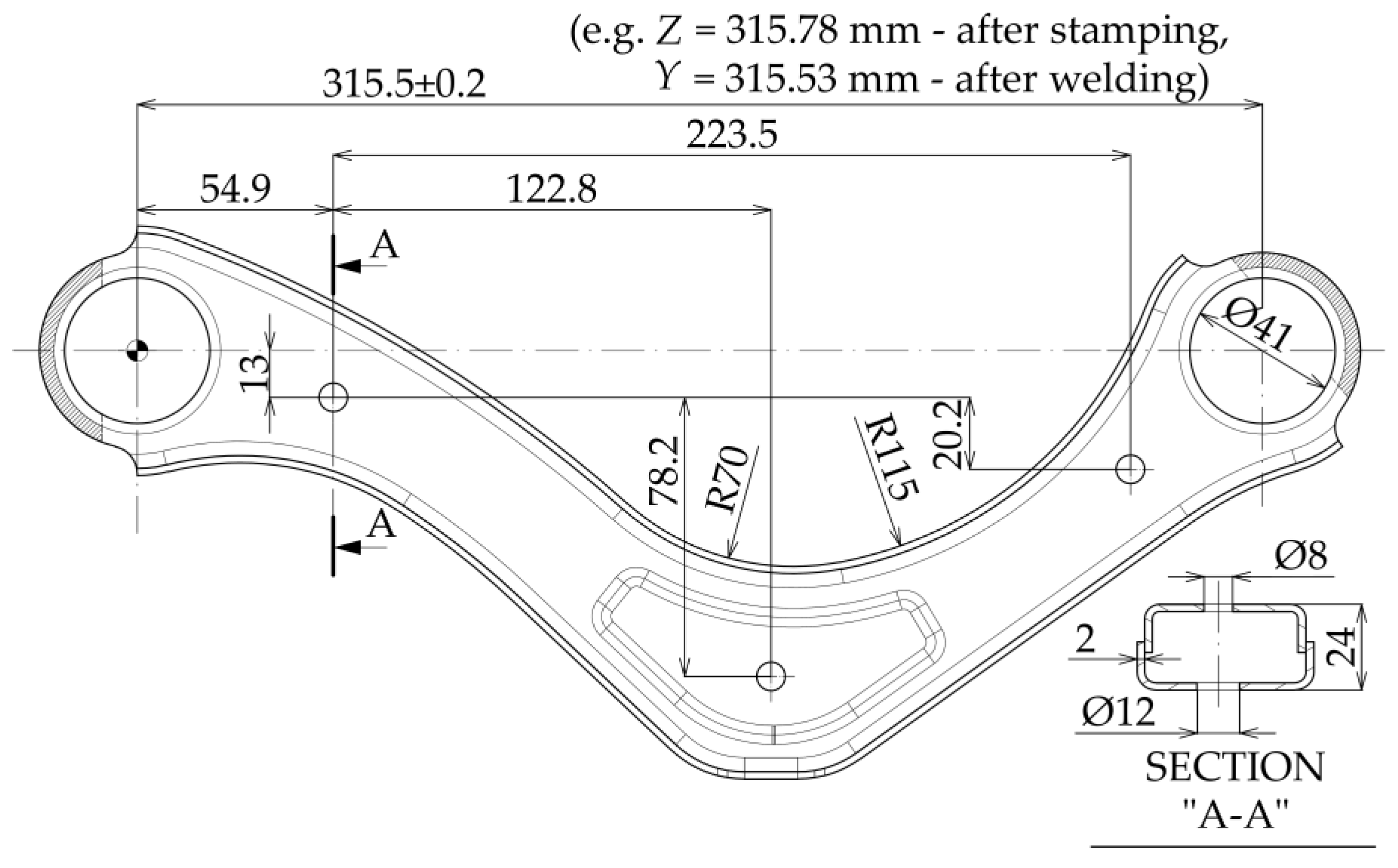
| Tested Material | Chemical Composition (Weight %) | Mechanical Properties | ||
|---|---|---|---|---|
| SGAFC590DP (2 mm thickness) | C | 0.071 | Yield Strength (MPa) | 405 |
| Si | 0.183 | |||
| Mn | 1.895 | Ultimate Tensile Strength (MPa) | 643 | |
| P | 0.018 | |||
| S | 0.004 | Elongation (%) | 28 | |
| Parameter | Parameter Type | Marking | Value | Unit |
|---|---|---|---|---|
| Welding speed | Variable | v | 50–70 | cm·min−1 |
| Current | I | 160–200 | A | |
| Gas dosing | Automatic | - | >18 | l·min−1 |
| Wire dosing | - | 344–480 | cm·min−1 | |
| Voltage | U | 17.4–19 | V | |
| Shielding welding gas | Constant | Ar | - | - |
| Technology | MIG | - | - | |
| Wire-type | KISWEL KC-25M | - | - | |
| Wire-diameter | d | 1.2 | mm | |
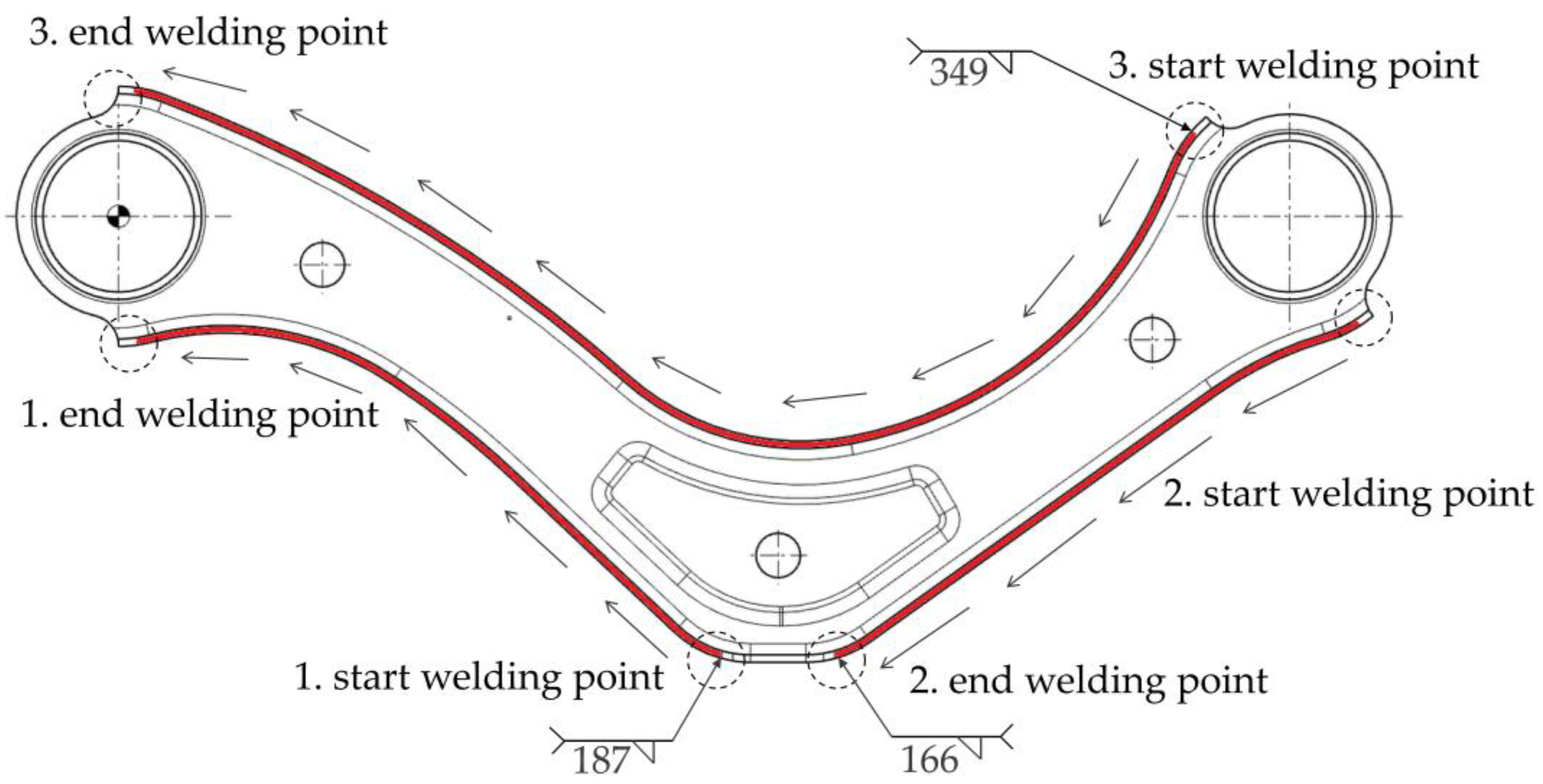
| Location and order of welds | - | - | ||
| Clamping parts | - | - |
| n | nE | I | v | Z | Y |
|---|---|---|---|---|---|
| 1 | 18 | 160 | 50 | 316.22 | 315.714 |
| 2 | 3 | 180 | 50 | 316.22 | 315.658 |
| 3 | 9 | 200 | 50 | 316.22 | 315.583 |
| 4 | 15 | 160 | 60 | 316.22 | 315.920 |
| 5 | 17 | 180 | 60 | 316.22 | 315.848 |
| 6 | 6 | 200 | 60 | 316.22 | 315.803 |
| 7 | 2 | 160 | 70 | 316.22 | 316.031 |
| 8 | 7 | 180 | 70 | 316.22 | 315.961 |
| 9 | 11 | 200 | 70 | 316.22 | 315.862 |
| 10 | 1 | 160 | 50 | 315.78 | 315.287 |
| 11 | 10 | 180 | 50 | 315.78 | 315.224 |
| 12 | 8 | 200 | 50 | 315.78 | 315.148 |
| 13 | 12 | 160 | 60 | 315.78 | 315.485 |
| 14 | 13 | 180 | 60 | 315.78 | 315.411 |
| 15 | 4 | 200 | 60 | 315.78 | 315.372 |
| 16 | 14 | 160 | 70 | 315.78 | 315.601 |
| 17 | 16 | 180 | 70 | 315.78 | 315.528 |
| 18 | 5 | 200 | 70 | 315.78 | 315.440 |
| n | nE | I | v | Z | Y |
|---|---|---|---|---|---|
| 1 | 29 | 160 | 50 | 316.08 | 315.578 |
| 2 | 12 | 180 | 50 | 316.08 | 315.521 |
| 3 | 22 | 200 | 50 | 316.08 | 315.442 |
| 4 | 8 | 160 | 52 | 316.08 | 315.627 |
| 5 | 23 | 180 | 52 | 316.08 | 315.565 |
| 6 | 3 | 200 | 52 | 316.08 | 315.475 |
| 7 | 33 | 160 | 54 | 316.08 | 315.678 |
| 8 | 16 | 180 | 54 | 316.08 | 315.613 |
| 9 | 21 | 200 | 54 | 316.08 | 315.526 |
| 10 | 28 | 160 | 56 | 316.08 | 315.721 |
| 11 | 9 | 180 | 56 | 316.08 | 315.650 |
| 12 | 30 | 200 | 56 | 316.08 | 315.584 |
| 13 | 25 | 160 | 58 | 316.08 | 315.747 |
| 14 | 19 | 180 | 58 | 316.08 | 315.681 |
| 15 | 2 | 200 | 58 | 316.08 | 315.627 |
| 16 | 4 | 160 | 60 | 316.08 | 315.778 |
| 17 | 17 | 180 | 60 | 316.08 | 315.709 |
| 18 | 24 | 200 | 60 | 316.08 | 315.668 |
| 19 | 18 | 160 | 62 | 316.08 | 315.804 |
| 20 | 27 | 180 | 62 | 316.08 | 315.732 |
| 21 | 7 | 200 | 62 | 316.08 | 315.687 |
| 22 | 5 | 160 | 64 | 316.08 | 315.822 |
| 23 | 11 | 180 | 64 | 316.08 | 315.751 |
| 24 | 14 | 200 | 64 | 316.08 | 315.698 |
| 25 | 15 | 160 | 66 | 316.08 | 315.847 |
| 26 | 13 | 180 | 66 | 316.08 | 315.773 |
| 27 | 6 | 200 | 66 | 316.08 | 315.711 |
| 28 | 20 | 160 | 68 | 316.08 | 315.867 |
| 29 | 31 | 180 | 68 | 316.08 | 315.797 |
| 30 | 26 | 200 | 68 | 316.08 | 315.726 |
| 31 | 1 | 160 | 70 | 316.08 | 315.895 |
| 32 | 32 | 180 | 70 | 316.08 | 315.823 |
| 33 | 10 | 200 | 70 | 316.08 | 315.729 |
| ANN | Learning Algorithm | ANN Structure | Hidden Layer Activation Function | Output Layer Activation Function |
|---|---|---|---|---|
| LMANN | Levenberg–Marquardt BP | 3-7-1 | Logistic Sigmoid | Linear Transfer |
| BRANN | Bayesian Regularization BP | Hyperbolic Tangent |
| i | W1i | W2i | W3i | bi |
|---|---|---|---|---|
| 1 | 0.349 | −0.031 | 0.186 | 0.542 |
| 2 | 0.304 | 0.076 | −1.208 | 0.105 |
| 3 | 1.063 | −0.120 | −2.101 | 0.951 |
| 4 | 0.143 | −2.427 | −0.737 | 0.559 |
| 5 | −0.424 | −1.071 | −0.479 | 0.022 |
| 6 | −0.518 | −1.564 | −0.630 | −0.128 |
| 7 | −0.652 | 0.192 | 1.294 | −0.109 |
| i | W1i | W2i | W3i | bi |
|---|---|---|---|---|
| 1 | 0.139 | 0.894 | 0.020 | 0.449 |
| 2 | −0.117 | −0.032 | 0.284 | −0.054 |
| 3 | −0.090 | −0.003 | 0.231 | −0.078 |
| 4 | 0.109 | 0.020 | −0.249 | 0.073 |
| 5 | −0.113 | −0.016 | 0.243 | −0.059 |
| 6 | −0.116 | −0.034 | 0.254 | −0.096 |
| 7 | 0.125 | 0.026 | −0.271 | 0.080 |
| Dataset | R | RMSE | MAPE (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| LR | LMANN | BRANN | LR | LMANN | BRANN | LR | LMANN | BRANN | |
| Training | 0.999 | 0.996 | 1.000 | 0.011 | 0.022 | 0.009 | 0.003 | 0.006 | 0.002 |
| Testing | 0.996 | 0.992 | 0.993 | 0.010 | 0.015 | 0.013 | 0.003 | 0.003 | 0.004 |
| All data | 0.998 | 0.995 | 0.998 | 0.010 | 0.018 | 0.012 | 0.003 | 0.004 | 0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kadnár, M.; Káčer, P.; Harničárová, M.; Valíček, J.; Tóth, F.; Bujna, M.; Kušnerová, M.; Mikuš, R.; Boržan, M. Comparison of Linear Regression and Artificial Neural Network Models for the Dimensional Control of the Welded Stamped Steel Arms. Machines 2023, 11, 376. https://doi.org/10.3390/machines11030376
Kadnár M, Káčer P, Harničárová M, Valíček J, Tóth F, Bujna M, Kušnerová M, Mikuš R, Boržan M. Comparison of Linear Regression and Artificial Neural Network Models for the Dimensional Control of the Welded Stamped Steel Arms. Machines. 2023; 11(3):376. https://doi.org/10.3390/machines11030376
Chicago/Turabian StyleKadnár, Milan, Peter Káčer, Marta Harničárová, Jan Valíček, František Tóth, Marián Bujna, Milena Kušnerová, Rastislav Mikuš, and Marian Boržan. 2023. "Comparison of Linear Regression and Artificial Neural Network Models for the Dimensional Control of the Welded Stamped Steel Arms" Machines 11, no. 3: 376. https://doi.org/10.3390/machines11030376
APA StyleKadnár, M., Káčer, P., Harničárová, M., Valíček, J., Tóth, F., Bujna, M., Kušnerová, M., Mikuš, R., & Boržan, M. (2023). Comparison of Linear Regression and Artificial Neural Network Models for the Dimensional Control of the Welded Stamped Steel Arms. Machines, 11(3), 376. https://doi.org/10.3390/machines11030376










