Experimental Determination and Calculation of the Wire Drawing Force in Monolithic Dies on Straight-Line Drawing Machines
Abstract
1. Introduction
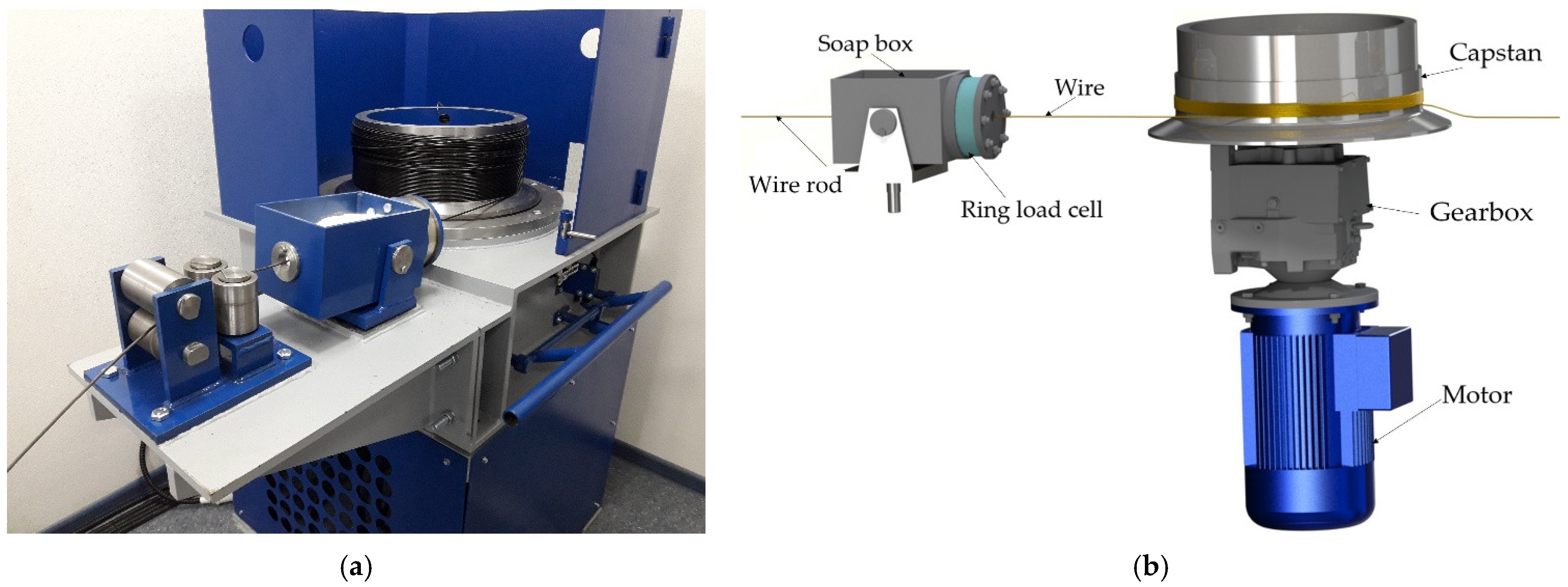
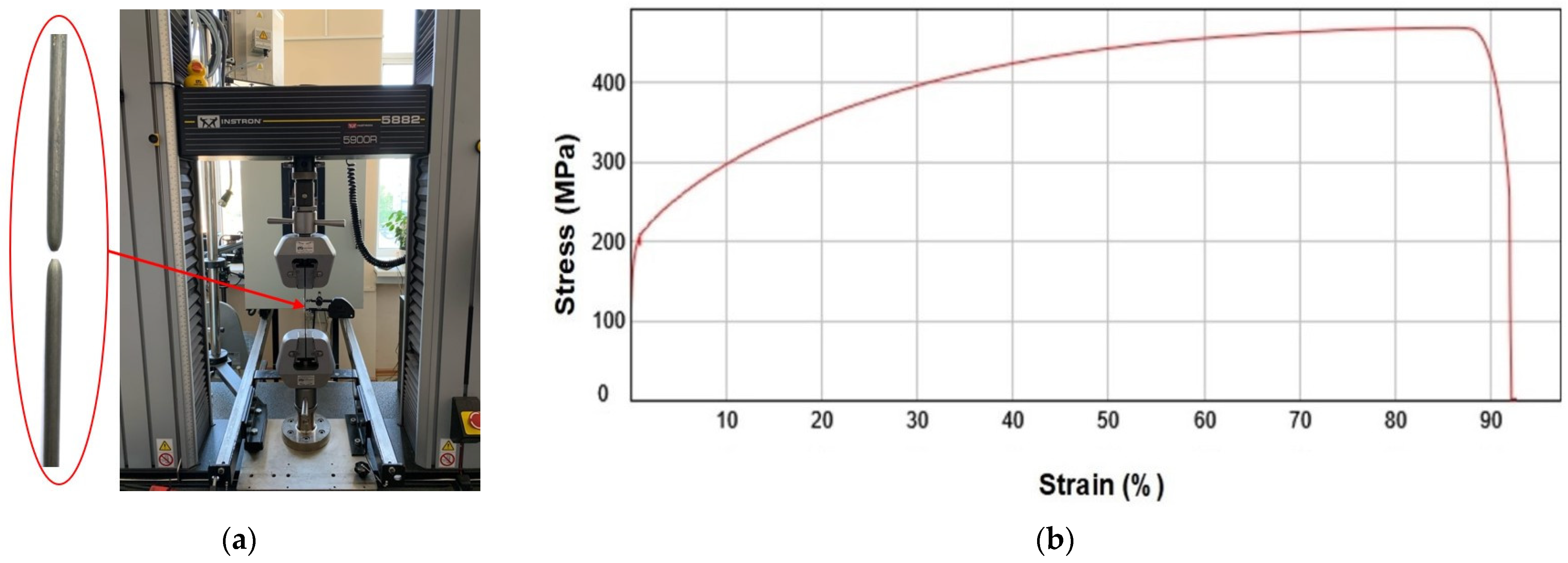
2. Materials and Methods
3. Results and Discussion
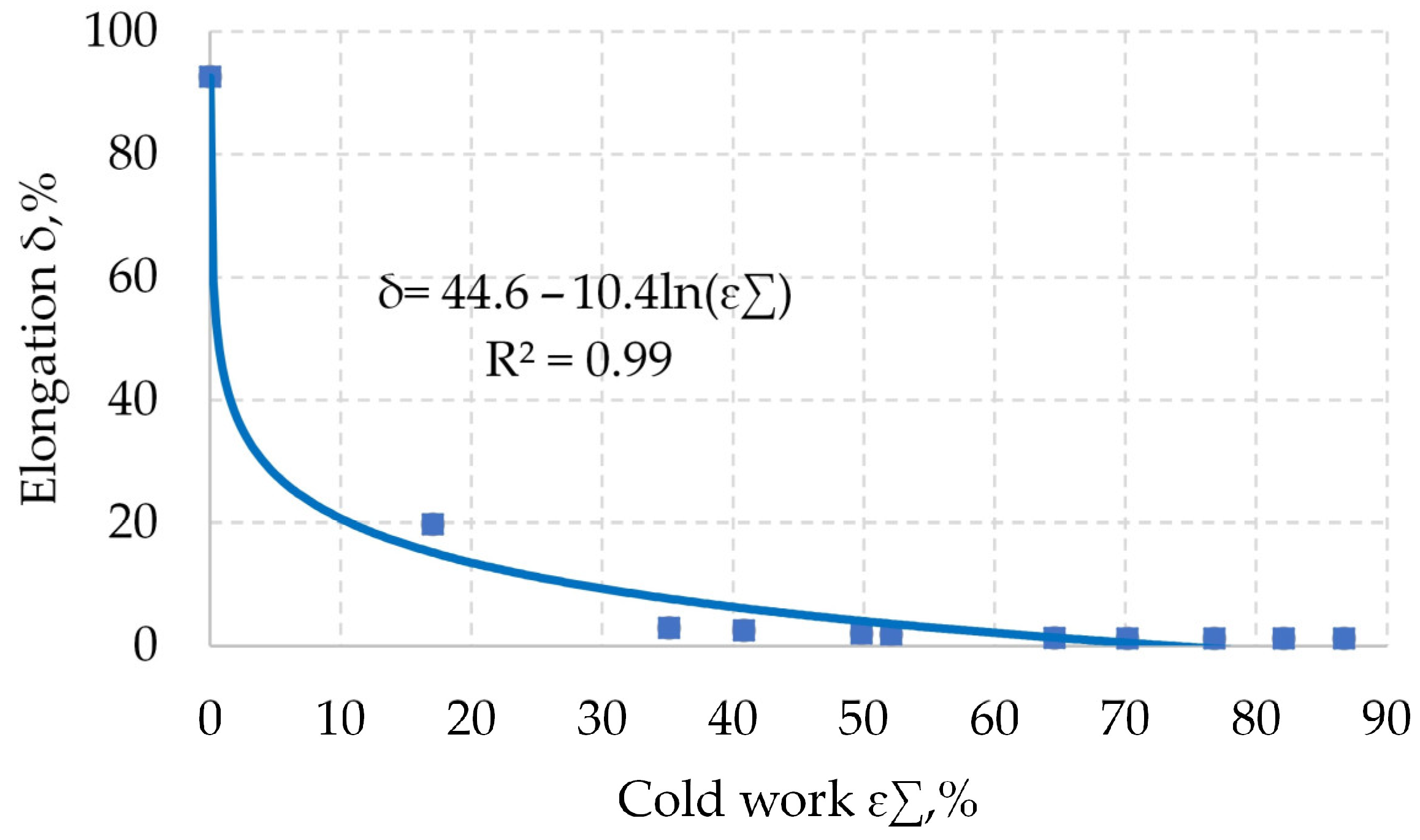
3.1. Effects of Cold Working on the Mechanical Properties of the NP2 Nickel
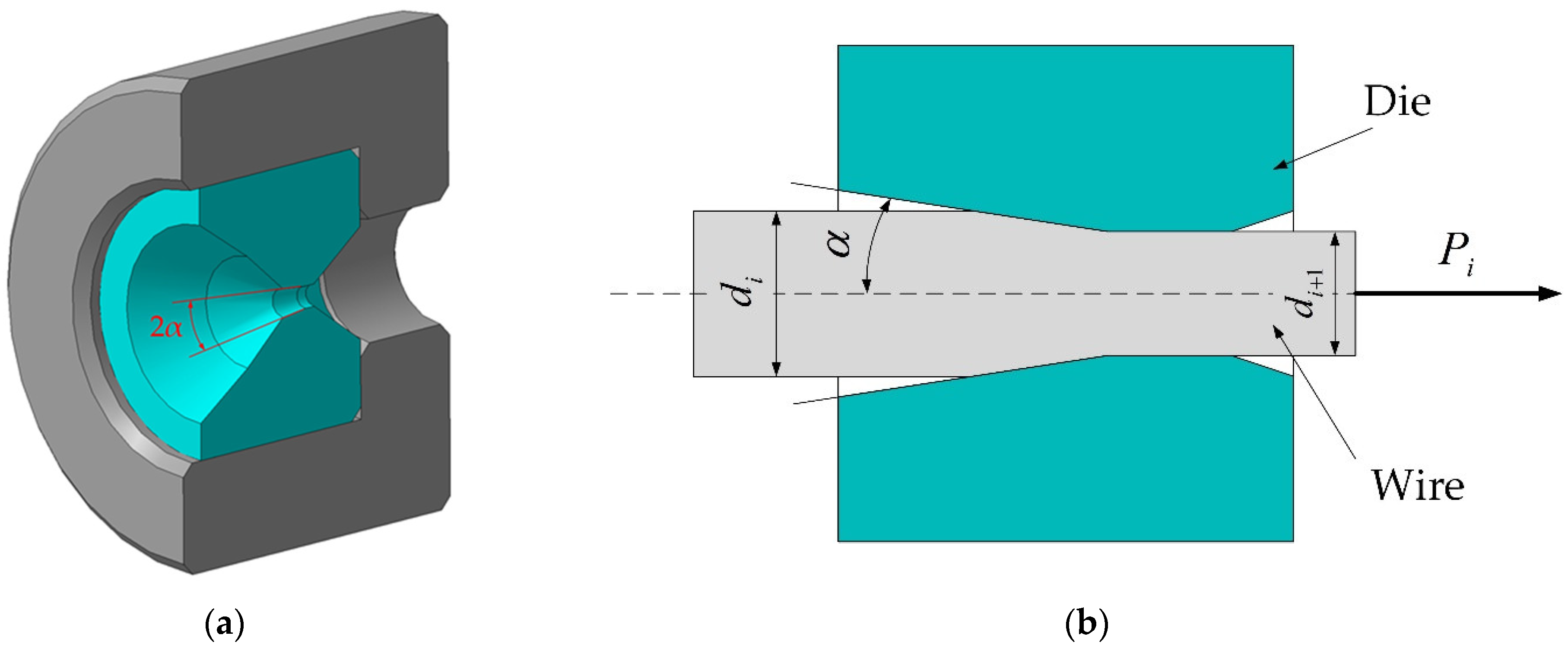
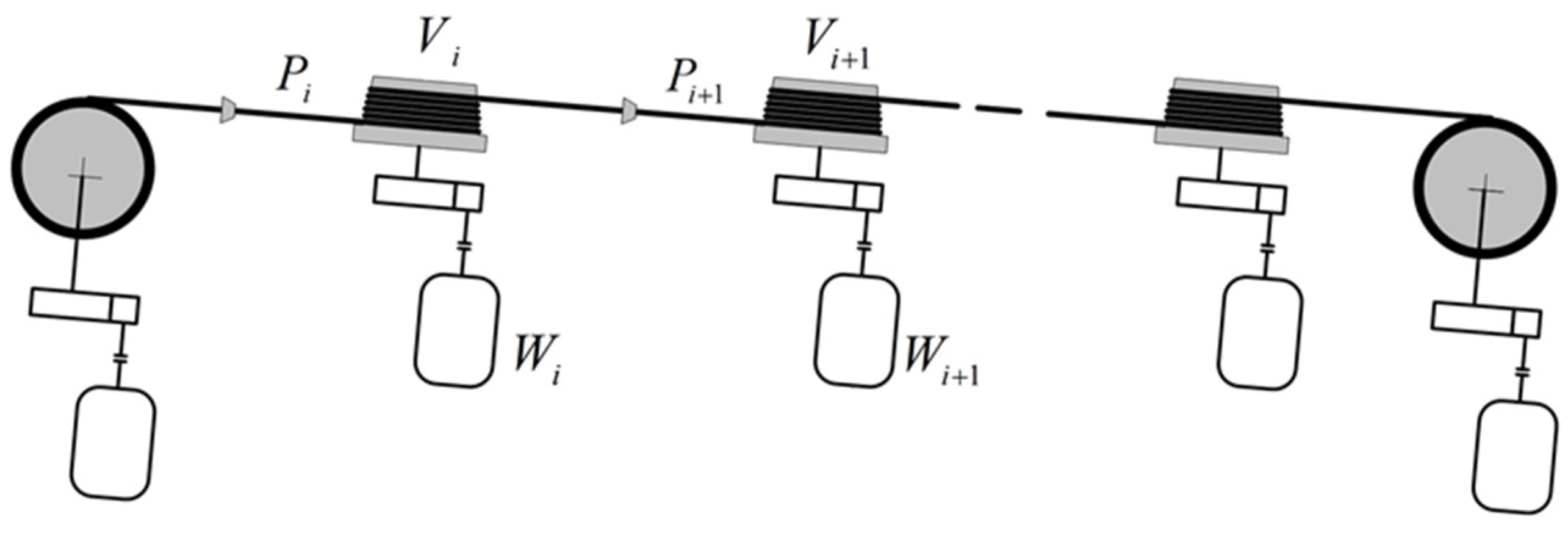
3.2. Mathematical Modeling for the Wire Drawing Process
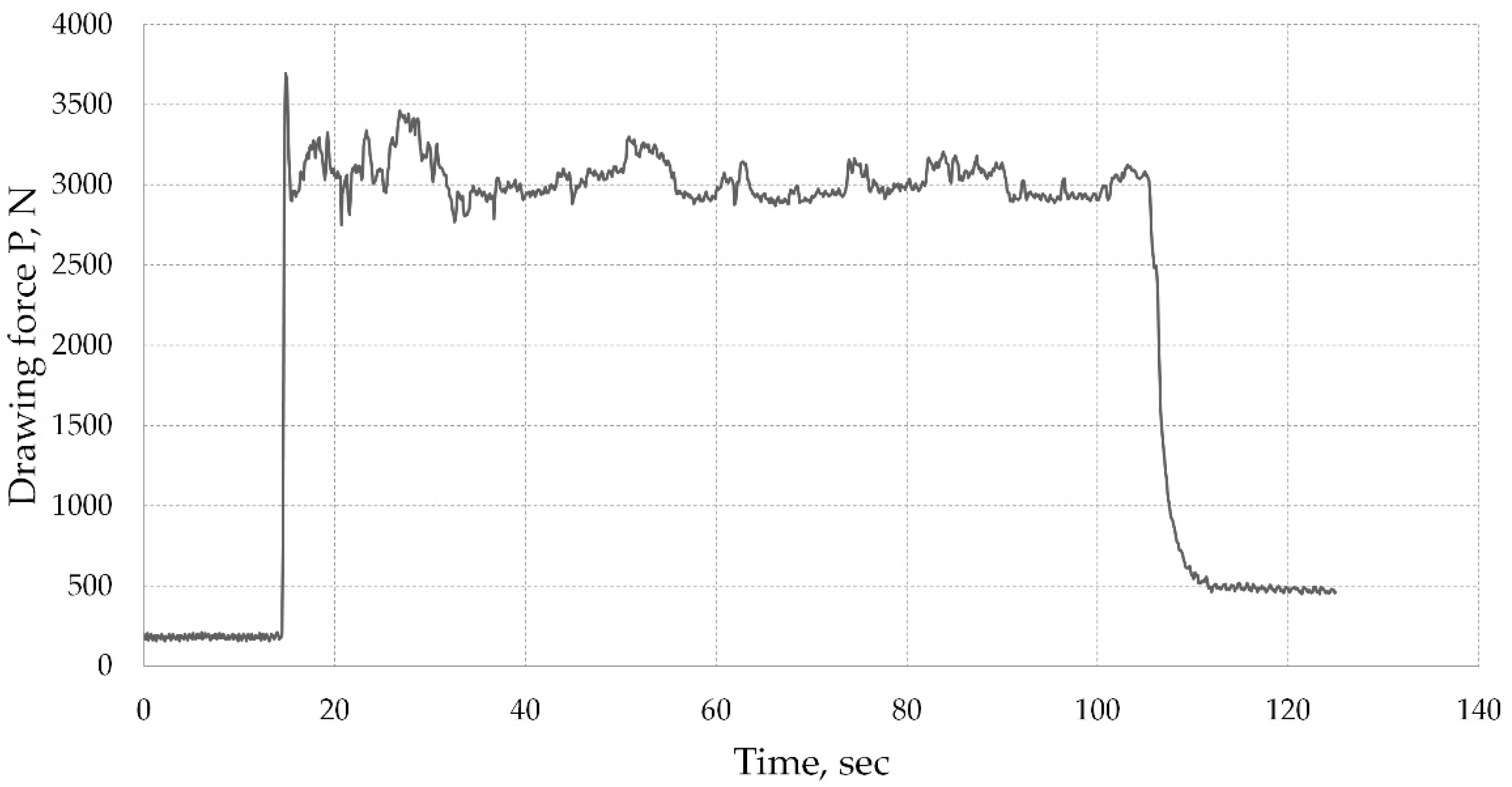
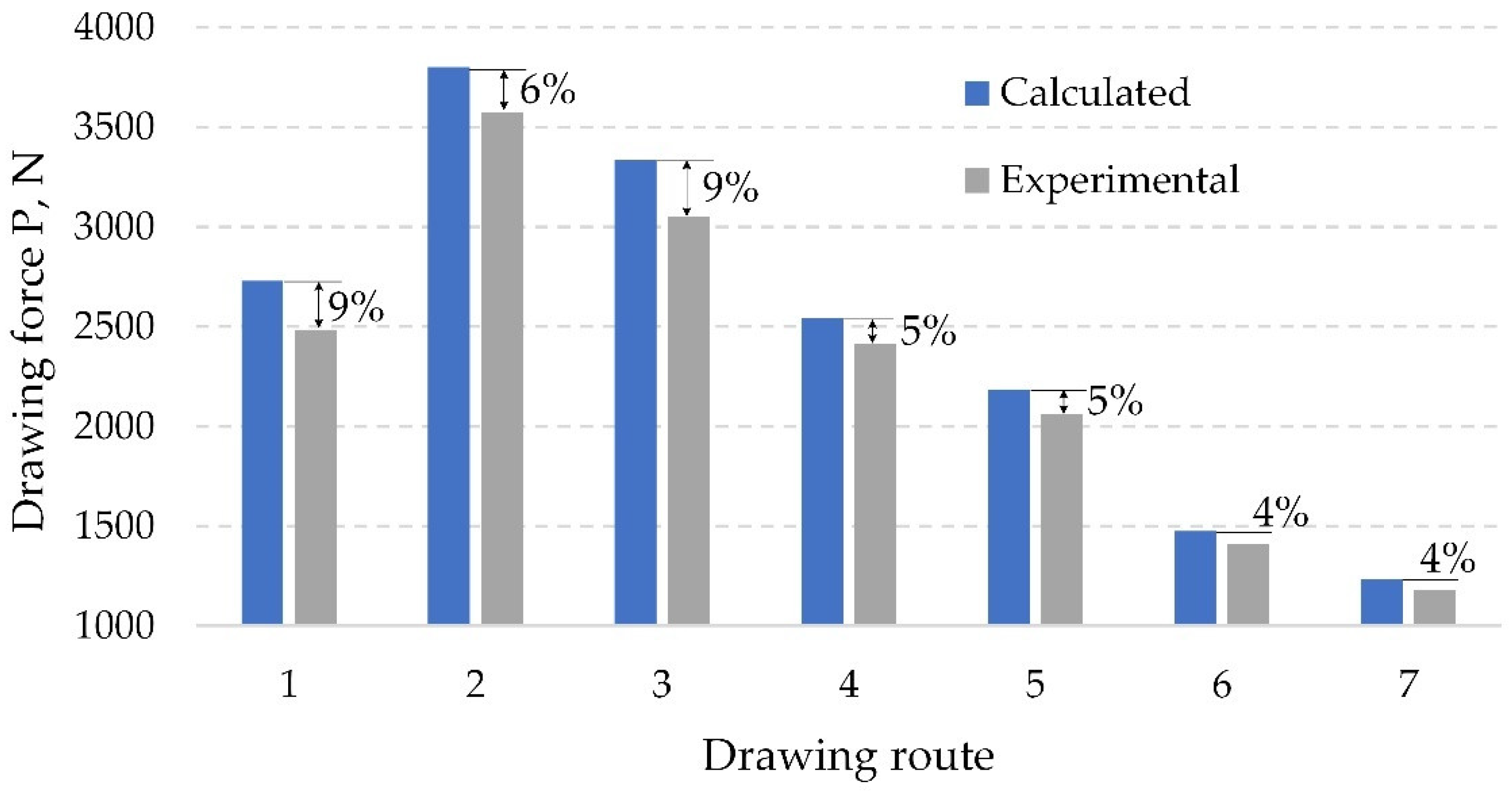
3.3. Verification of the Convergence of the Calculated and Experimental Drawing Forces of Nickel NP2
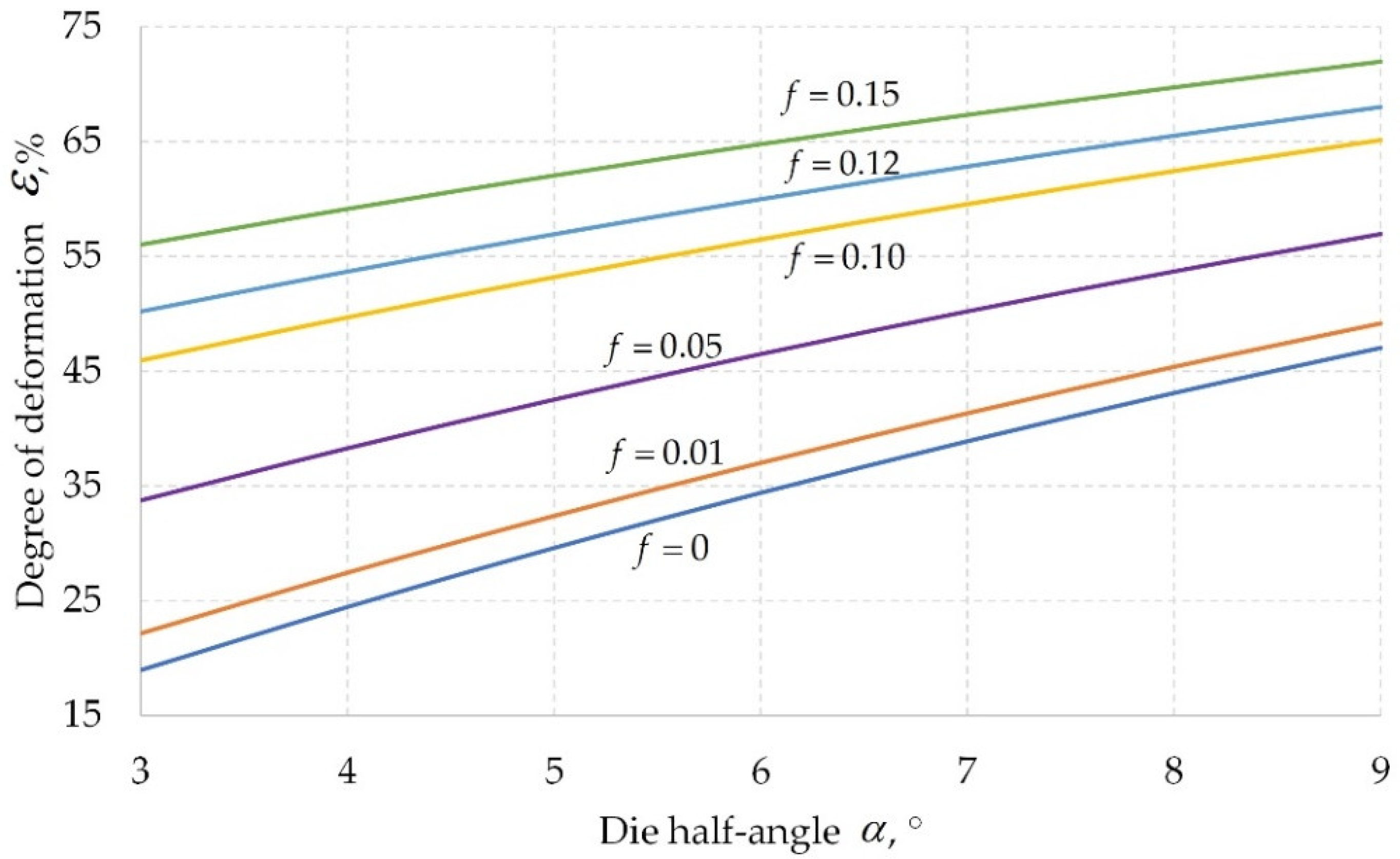
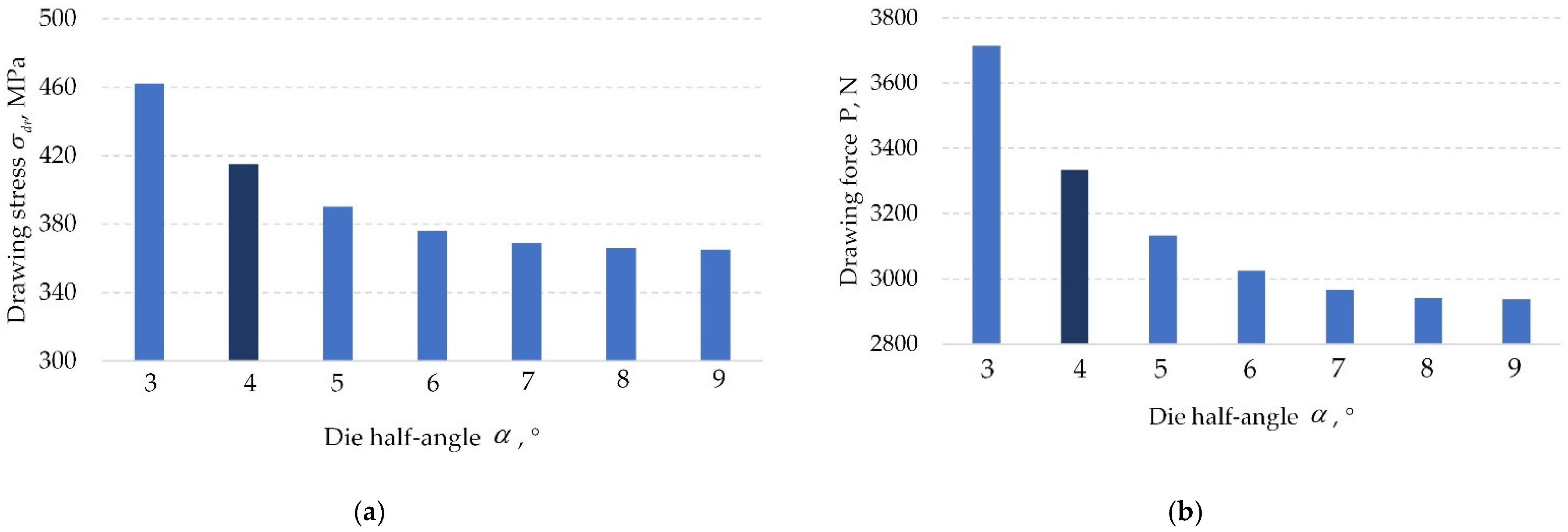
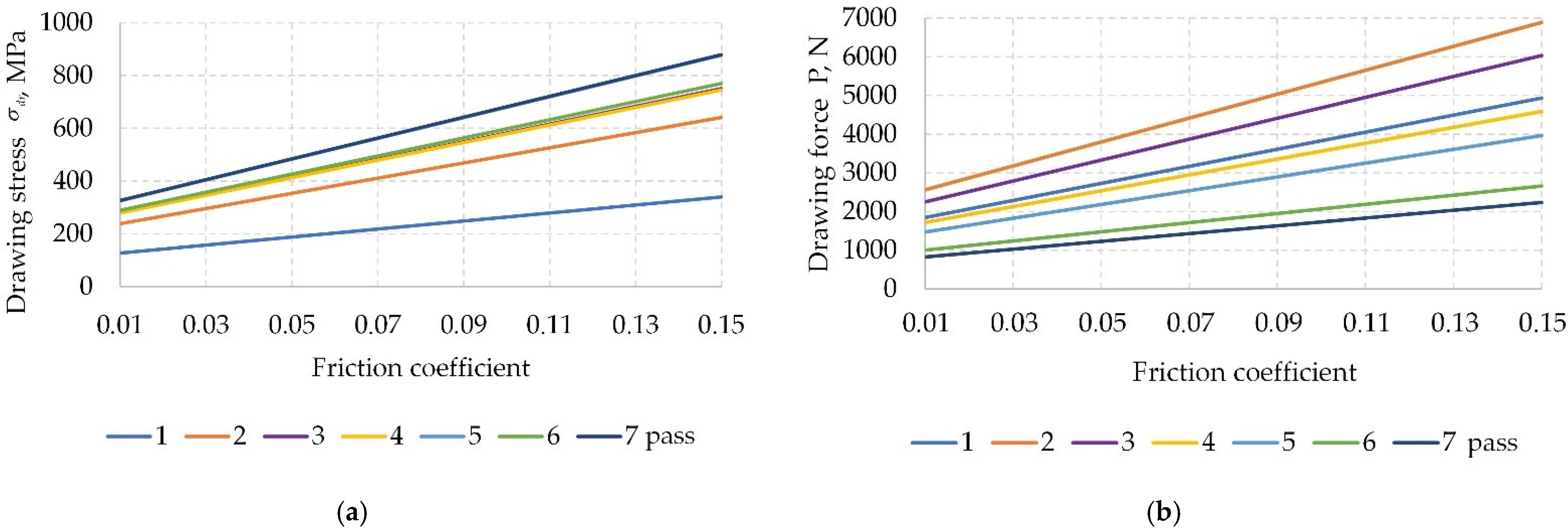
3.4. Analytical Studies of the Influence of the Coefficient of Friction and Die Half-Angle on the Energy-Power Parameters of Drawing Wire from Nickel NP2
4. Conclusions
- -
- Allows us to evaluate the uniformity of deformation over the wire section, depending on the technological parameters of the deformation zone, namely, the die half-angle, the friction coefficient, and the degree of deformation. To select the technological parameters of the deformation zone, which ensure uniform deformation over the wire cross-section, a nomogram was compiled;
- -
- The calculation of the drawing stress is carried out for multiple straight-line drawing machines, taking into account the hardening of the alloy, depending on the cold work. For nickel NP2, the equations of hardening during wire drawing are obtained. Using nickel NP2 as an example, a method for obtaining dependences of tensile strength and yield strength on cold work is shown, using which equations can be obtained for other alloys;
- -
- When checking the adequacy of the mathematical model, it was revealed that in the calculations, it is necessary to more accurately indicate the values of the friction coefficient. The influence of the friction coefficient on the drawing stress and the drawing force is significant. A change in the friction coefficient by 0.02 leads to an increase in the drawing stress and drawing force by 20%;
- -
- The program compiled on the basis of the presented mathematical model is a very convenient and efficient assistant in the calculation and design of wire drawing routes on multiple straight drawing machines. The program allows us to calculate the drawing stress, drawing force, tensile strength and yield strength of the alloy after wire drawing, safety factor, and drawing power;
- -
- In the future, experimental studies should be carried out on a laboratory drawing machine to determine the effect on the energy-power parameters of the drawing process of the values of technological parameters entered into the program as constant real values, such as the friction coefficient, the die half-angle, drawing speed and back tension. This will improve the accuracy of the developed mathematical model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sheu, J.-J.; Ho, C.-J.; Yu, C.-H.; Kao, C.-Y. High-Order Groove-Shape Curve Roll Design for Aluminum Alloy 7075 Wire Rolling. Metals 2022, 12, 1071. [Google Scholar] [CrossRef]
- Radionov, A.A.; Petukhova, O.I.; Erdakov, I.N.; Karandaev, A.S.; Loginov, B.M.; Khramshin, V.R. Developing an Automated System to Control the Rolled Product Section for a Wire Rod Mill with Multi-Roll Passes. J. Manuf. Mater. Process. 2022, 6, 88. [Google Scholar] [CrossRef]
- Hwang, J.-K. Effect of Cambered and Oval-Grooved Roll on the Strain Distribution During the Flat Rolling Process of a Wire. Processes 2020, 8, 876. [Google Scholar] [CrossRef]
- Čapek, J.; Kadeřávek, L.; Pinc, J.; Kopeček, J.; Klimša, L. Influence of the Microstructure of the Initial Material on the Zn Wires Prepared by Direct Extrusion with a Huge Extrusion Ratio. Metals 2021, 11, 787. [Google Scholar] [CrossRef]
- Langelandsvik, G.; Grandcolas, M.; Skorpen, K.G.; Furu, T.; Akselsen, O.M.; Roven, H.J. Development of Al-TiC Wire Feedstock for Additive Manufacturing by Metal Screw Extrusion. Metals 2020, 10, 1485. [Google Scholar] [CrossRef]
- Nienaber, M.; Yi, S.; Kainer, K.U.; Letzig, D.; Bohlen, J. On the Direct Extrusion of Magnesium Wires from Mg-Al-Zn Series Alloys. Metals 2020, 10, 1208. [Google Scholar] [CrossRef]
- Rodríguez-González, P.; Ruiz-Navas, E.M.; Gordo, E. Effect of Heat Treatment Prior to Direct Hot-Extrusion Processing of Al–Cu–Li Alloy. Metals 2022, 12, 1046. [Google Scholar] [CrossRef]
- Faizov, S.; Sarafanov, A.; Erdakov, I.; Gromov, D.; Svistun, A.; Glebov, L.; Bykov, V.; Bryk, A.; Radionova, L. On the Direct Extrusion of Solder Wire from 52In-48Sn Alloy. Machines 2021, 9, 93. [Google Scholar] [CrossRef]
- Kucharska, M.; Wiewiórowska, S.; Michalczyk, J.; Gontarz, A. The Influence of the Drawing Process on the Mechanical Properties of TRIP Steel Wires with 0.4% C Content. Materials 2020, 13, 5769. [Google Scholar] [CrossRef]
- Suliga, M.; Wartacz, R.; Hawryluk, M.; Kostrzewa, J. The Effect of Drawing in Conventional and Hydrodynamic Dies on Structure and Corrosion Resistance of Hot-Dip Galvanized Zinc Coatings on Medium-Carbon Steel Wire. Materials 2022, 15, 6728. [Google Scholar] [CrossRef]
- Wang, L.; Yu, Y.; Zhang, P.; Yang, J. Influence of Lanthanum-Doped Tungsten Wire Drawing Process on Microstructure and Properties. Materials 2022, 15, 4979. [Google Scholar] [CrossRef]
- Toribio, J.; González, B.; Matos, J.-C. Analysis of Fatigue Crack Paths in Cold Drawn Pearlitic Steel. Materials 2015, 8, 7439–7446. [Google Scholar] [CrossRef]
- Lezhnev, S.; Panin, E.; Volokitina, I. Research of Combined Process ‘Rolling-Pressing’ Influence on the Microstructure and Mechanical Properties of Aluminium. In Advanced Materials Research; Trans Tech Publications, Ltd.: Bäch, Switzerland, 2013; Volume 814, pp. 68–75. [Google Scholar] [CrossRef]
- Naizabekov, A.; Volokitina, I.; Volokitin, A.; Panin, E. Structure and Mechanical Properties of Steel in the Process “Pressing–Drawing”. J. Mater. Eng. Perform. 2019, 28, 1762–1771. [Google Scholar] [CrossRef]
- Volokitina, I.; Vasilyeva, N.; Fediuk, R.; Kolesnikov, A. Hardening of Bimetallic Wires from Secondary Materials Used in the Construction of Power Lines. Materials 2022, 15, 3975. [Google Scholar] [CrossRef]
- Jung, J.Y.; An, K.S.; Park, P.Y.; Nam, W.J. Correlation between Microstructures and Ductility Parameters of Cold Drawn Hyper-Eutectoid Steel Wires with Different Drawing Strains and Post-Deformation Annealing Conditions. Metals 2021, 11, 178. [Google Scholar] [CrossRef]
- Stolyarov, A.; Polyakova, M.; Atangulova, G.; Alexandrov, S. Effect of Die Angle and Frictional Conditions on Fine Grain Layer Generation in Multipass Drawing of High Carbon Steel Wire. Metals 2020, 10, 1462. [Google Scholar] [CrossRef]
- Radionova, L.V.; Sarafanov, A.E.; Siverin, O.O. Roller Drawing of Simple Profiles from Hard-to-Form Alloys. Mater. Sci. Forum 2022, 1052, 364–369. [Google Scholar] [CrossRef]
- Santana Martinez, G.A.; Qian, W.-L.; Kabayama, L.K.; Prisco, U. Effect of Process Parameters in Copper-Wire Drawing. Metals 2020, 10, 105. [Google Scholar] [CrossRef]
- Pilarczyk, J.W.; Nitkiewicz, Z.; Kucharska, B.; Małecki, T. Analysis of Textures of Wires Drawn in Pressure and Roller Dies with ODF. In Materials Science Forum; Trans Tech Publications, Ltd.: Bäch, Switzerland, 2005; Volume 495–497, pp. 865–870. [Google Scholar] [CrossRef]
- Radionova, L.V.; Gromov, D.V.; Svistun, A.S.; Lisovskiy, R.A.; Faizov, S.R.; Glebov, L.A.; Zaramenskikh, S.E.; Bykov, V.A.; Erdakov, I.N. Mathematical Modeling of Heating and Strain Aging of Steel during High-Speed Wire Drawing. Metals 2022, 12, 1472. [Google Scholar] [CrossRef]
- Jung, J.Y.; An, K.S.; Park, P.Y.; Nam, W.J. Effects of Wire Drawing and Annealing Conditions on Torsional Ductility of Cold Drawn and Annealed Hyper-Eutectoid Steel Wires. Metals 2020, 10, 1043. [Google Scholar] [CrossRef]
- Rodríguez-Alabanda, Ó.; Romero, P.E.; Molero, E.; Guerrero-Vaca, G. Analysis, Validation and Optimization of the Multi-Stage Sequential Wiredrawing Process of EN AW-1370 Aluminium. Metals 2019, 9, 1021. [Google Scholar] [CrossRef]
- Radionova, L.V.; Lisovsky, R.A.; Lezin, V.D. Theory of Energy Conservation as the Basis for the Design of Wire Drawing. In Lecture Notes in Mechanical Engineering, Proceedings of the 6th International Conference on Industrial Engineering (ICIE 2020), ICIE 2021, Sochi, Russia, 18–20 May 2020; Radionov, A.A., Gasiyarov, V.R., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Ioana Monica Sas-Boca, Marius Tintelecan, Mariana Pop, Dana-Adriana Iluţiu-Varvara, Adriana Maria Mihu, The Wire Drawing Process Simulation and the Optimization of Geometry Dies. Procedia Eng. 2017, 181, 187–192. [CrossRef]
- Larsson, J.; Karlsson, P.; Ekengren, J.; Pejryd, L. Enhanced Cooling Design in Wire Drawing Tooling Using Additive Manufacturing. In Industrializing Additive Manufacturing: AMPA 2020; Meboldt, M., Klahn, C., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Karandaev, A.S.; Gasiyarov, V.R.; Radionov, A.A.; Loginov, B.M. Development of Digital Models of Interconnected Electrical Profiles for Rolling–Drawing Wire Mills. Machines 2021, 9, 54. [Google Scholar] [CrossRef]
- Radionova, L.V.; Shirokov, V.V.; Faizov, S.R.; Zhludov, M.A. Studies of Influence of Process Parameters on the Strain Rate at High-Speed Wire Drawing. Mater. Sci. Forum 2019, 946, 832–838. [Google Scholar] [CrossRef]
- Li, L.; Huang, H.; Zhao, F.; Zou, X.; Mendis, G.P.; Luan, X.; Liu, Z.; Sutherland, J.W. Modeling and Analysis of the Process Energy for Cylindrical Drawing. ASME J. Manuf. Sci. Eng. 2019, 141, 021001. [Google Scholar] [CrossRef]
- Radionova, L.V.; Lisovskiy, R.A.; Svistun, A.S.; Gromov, D.V.; Erdakov, I.N. FEM Simulation Analysis of Wire Drawing Process at Different Angles Dies on Straight-Line Drawing Machines. In Lecture Notes in Mechanical Engineering, Proceedings of the 8th International Conference on Industrial Engineering, ICIE 2022, Sochi, Russia, 16–20 May 2022; Radionov, A.A., Gasiyarov, V.R., Eds.; Springer: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Kharitonov, V.A.; Usanov, M.Y. Evaluation of Efficiency of Methods for Drawing Round Wire with Large Diameters. Chernye Met. 2021, 3, 28–33. [Google Scholar] [CrossRef]
- Tasevski, G.; Angjushev, K.; Petereski, Z.; Shishkovski, D. Experimental measurement of system dynamics between two stages of wire drawing machine. Arch. Mech. Eng. 2015, 62, 61–72. [Google Scholar] [CrossRef]
- Hemeda, S.G.; Aboukarima, A.M.; Minyawi, M. Developing a logging unit for measuring and recording power data using Arduino board. Misr. J. Agric. Eng. 2017, 34, 2053–2072. [Google Scholar] [CrossRef]
- Hwang, J.-K. Impact of Die Radius in a Streamlined Die during Wire Drawing. Appl. Sci. 2021, 11, 3922. [Google Scholar] [CrossRef]
- Perlin, I.L.; Ermanok, M.Z. Theory of Drawing; Metallurgy: Moscow, Russia, 1971; 447p. [Google Scholar]
- Lange, K. (Ed.) Drawing and Ironing. In Handbook of Metalforming; McGraw-Hill Book Company: New York, NY, USA, 1985; pp. 14–27. [Google Scholar]
- Kharitonov, V.A.; Zyuzin, V.I.; Radionova, L.V.; Rol’shchikov, L.D. New technological lubricants for steel wire drawing. Cmaль 2001, 12, 49–50. [Google Scholar]
- Radionova, L.V.; Lisovskiy, R.; Svistun, A.; Erdakov, I. Change in Mechanical Properties During Drawing of Wire from Ni 99.6. In Materials Science Forum; Trans Tech Publications, Ltd.: Bäch, Switzerland, 2022. [Google Scholar] [CrossRef]
- Radionova, L.V. Kharitonov VA Designing resource-saving technologies for the production of high-strength carbon wire based on modeling. In Monograph/V; MSTU: Magnitogorsk, Russia, 2008; 171p. [Google Scholar]
- Shetty, S.; Nilsson, L. An evaluation of simple techniques to model the variation in strain hardening behavior of steel. Struct. Multidisc. Optim. 2017, 55, 945–957. [Google Scholar] [CrossRef]
- Radionov, A.A. Automated Electric Drive of Mills for the Production of Steel Wire; Magnitogorsk State Technical University: Magnitogorsk, Russia, 2007; 311p. [Google Scholar]
- Martinez, G.A.S.; Santos, E.F.D.; Kabayama, L.K.; Guidi, E.S.; Silva, F.D.A. Influences of Different Die Bearing Geometries on the Wire-Drawing Process. Metals 2019, 9, 1089. [Google Scholar] [CrossRef]
- Tintelecan, M.; Sas-Boca, I.M.; Iluţiu-Varvara, D.-A. The Influence of the Dies Geometry on the Drawing Force for Steel Wires. Procedia Eng. 2017, 181, 193–199. [Google Scholar] [CrossRef]
- Majzoobi, G.; Saniee, F.F.; Aghili, A. An investigation into the effect of redundant shear deformation in bar drawing. J. Mater. Process. Technol. 2008, 201, 133–137. [Google Scholar] [CrossRef]
- Radionova, L.V.; Lisovskii, R.A. Study of deformation and contact heating of wire during the high-speed drawing process in a monolithic die. Ferrous Metallurgy. Bull. Sci. Tech. Econ. Inf. 2022, 78, 784–792. (In Russian) [Google Scholar] [CrossRef]

| Ni + Co | Fe | C | Si | Mn | S | P | Cu | As | Pb | Mg |
|---|---|---|---|---|---|---|---|---|---|---|
| min | less | |||||||||
| 99.5 | 0.1 | 0.1 | 0.15 | 0.05 | 0.005 | 0.002 | 0.1 | 0.002 | 0.002 | 0.1 |
| Drawing Route | |||||||
|---|---|---|---|---|---|---|---|
| Wire rod | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 4.94 | 4.30 | 3.70 | 3.20 | 2.80 | 2.40 | 2.10 | 1.80 |
| Alloy Grade | Tensile Strength UST | Yield Strength 0.2 US |
|---|---|---|
| NP2 | ||
| OK Autrod 4043 | ||
| C10 (steel) | ||
| C67 (steel) |
| Initial Data | |||||||
|---|---|---|---|---|---|---|---|
| Wire rod Ø, mm | 4.94 | ||||||
| Wire Ø, mm | 1.80 | ||||||
| ), MPa | 469 | ||||||
| ), MPa | 174 | ||||||
| Calculation Results | |||||||
| Drawing route (No. pass) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Wire Ø, mm | 4.30 | 3.70 | 3.20 | 2.80 | 2.40 | 2.10 | 1.80 |
| Degree of deformation , % | 24.23 | 25.96 | 25.20 | 23.44 | 26.53 | 23.44 | 26.53 |
| Cold work , % | 24.23 | 43.90 | 58.04 | 67.87 | 76.40 | 81.93 | 86.72 |
| Drawing ratio | 1.32 | 1.35 | 1.34 | 1.31 | 1.36 | 1.31 | 1.36 |
| ), MPa | 619 | 717 | 788 | 837 | 880 | 907 | 931 |
| ), MPa | 514 | 689 | 767 | 797 | 808 | 808 | 802 |
| Die half-angle α, ° | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| Friction coefficient f | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 | 0.05 |
| Drawing stress , MPa | 188 | 354 | 415 | 413 | 483 | 426 | 484 |
| Safety factor γ | 3.3 | 2.0 | 1.9 | 2.0 | 1.8 | 2.1 | 1.9 |
| Wire cross-sectional area , mm2 | 14.51 | 10.75 | 8.04 | 6.15 | 4.52 | 3.46 | 2.54 |
| Drawing force P, N | 2730 | 3802 | 3333 | 2541 | 2185 | 1476 | 1232 |
| Drawing speed V, m/min | 20 | 27 | 36 | 47 | 64 | 84 | 114 |
| Drawing power W, kW | 0.91 | 1.71 | 2.01 | 2.00 | 2.34 | 2.06 | 2.34 |
| Drawing Route (No. Pass) | Wire Ø, mm | ||||
|---|---|---|---|---|---|
| Min | Max | Average | Standard Deviation | ||
| Wire rod | 4.94 | - | - | - | - |
| 1 | 4.30 | 2453 | 2816 | 2484 | 129 |
| 2 | 3.70 | 3499 | 3956 | 3573 | 150 |
| 3 | 3.20 | 2750 | 3650 | 3050 | 139 |
| 4 | 2.80 | 2293 | 2786 | 2414 | 116 |
| 5 | 2.40 | 1918 | 2274 | 2065 | 89 |
| 6 | 2.10 | 1358 | 1536 | 1410 | 62 |
| 7 | 1.80 | 1152 | 1285 | 1182 | 57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radionova, L.V.; Gromov, D.V.; Lisovskiy, R.A.; Erdakov, I.N. Experimental Determination and Calculation of the Wire Drawing Force in Monolithic Dies on Straight-Line Drawing Machines. Machines 2023, 11, 252. https://doi.org/10.3390/machines11020252
Radionova LV, Gromov DV, Lisovskiy RA, Erdakov IN. Experimental Determination and Calculation of the Wire Drawing Force in Monolithic Dies on Straight-Line Drawing Machines. Machines. 2023; 11(2):252. https://doi.org/10.3390/machines11020252
Chicago/Turabian StyleRadionova, Liudmila V., Dmitry V. Gromov, Roman A. Lisovskiy, and Ivan N. Erdakov. 2023. "Experimental Determination and Calculation of the Wire Drawing Force in Monolithic Dies on Straight-Line Drawing Machines" Machines 11, no. 2: 252. https://doi.org/10.3390/machines11020252
APA StyleRadionova, L. V., Gromov, D. V., Lisovskiy, R. A., & Erdakov, I. N. (2023). Experimental Determination and Calculation of the Wire Drawing Force in Monolithic Dies on Straight-Line Drawing Machines. Machines, 11(2), 252. https://doi.org/10.3390/machines11020252







