Abstract
In this paper, a numerical experimental study about coupled vibration and natural frequency of thin-walled beams with an arbitrary closed cross-section is presented. A new thin-walled beam dynamic transfer matrix method, named TDTMM, is presented in the frequency domain for the thin-walled beam, which expands the advantages of the general dynamic transfer matrix method (GDTMM). The theory takes into account the influence of warping effect, that is, both the bimoment B and the rate of twist of the beam are considered, and the TDTMM is derived by solving the governing differential equations of motion for coupled bending and torsional vibration of the thin-walled beam. Finally, two numerical examples and one experimental example are given and compared with the GDTMM and the finite element method (FEM) results to validate the developed theory.
1. Introduction
Thin-walled beams are now widely used in industrial products, such as automobile and aerospace products. These structures are often subjected to dynamic loads such as vibration and wind loading. Thus, it is important to study their dynamic behaviors and accurately assess the dynamic characteristics of thin-walled beams. The thin-walled beam theory was first established by Vlasov [1]. and Timoshenko [2]. Many researchers have studied the vibration behaviors for flexural and torsional vibration of thin-walled beams while considering the shear center and the centroid of the cross-section coincident [3,4,5,6,7,8,9]. Generally, for the thin-walled beams, the shear center and the centroid of the cross-section is not coincident. Thus, the vibration behaviors for such beams should be investigated in detail.
According to the symmetry of the cross-section, the coupled vibrations are divided into doubly coupled vibration and triply coupled vibration. When the section of thin-walled beam is symmetrical about the Y axis, its vibration coupling is double. Many scholars have carried out in-depth research based on the doubly coupled vibration problem of thin-walled beams. The exact determination of coupled bending and torsion vibration behaviors of uniform asymmetric beams’ effect was developed by Dokumaci [10]. However, the warping effects were neglected. Bishop et al. [11] extended Dokumaci’s theory to allow for warping and investigated the coupled vibration of thin-walled beams having a plane of symmetry. Later, Laakso et al. [12] studied the free flexural vibration of symmetric beams with inertia-induced cross-section deformations and presented a correction of beam modal properties by modifying its modal stiffness and mass. Additionally, an exact element approach is developed to analyze the dynamic behavior of thin-walled lipped channel members based on the generalized beam theory of Bebiano [13]. The above works of the literature are related to the doubly coupled vibration of thin-walled beams. Compared with doubly coupled vibration, not much research has been conducted about triply coupled vibration where the cross-sectional shape of the beam is arbitrary. Yaman [14] investigated the forced, triply coupled vibration of open cross-section channels by the wave analysis method. Similarly, Arpaci et al. [15] studied the triply coupled vibration of open cross-section thin-walled beams including rotary inertia effects. In addition, some progress has been made in the numerical experimental study of thin-walled beams with doubly unsymmetrical open cross-sections, which involve scholars such as Ambrosini et al. [16] and Zhou et al. [17]. In addition, the triply flexural–torsional coupled vibration of axially loaded thin-walled beams with open cross-sections is presented by Kim et al. [18] and Borbon et al. [19], while Prokic [20] investigated the effect of the bimoment on natural frequencies of unsymmetrical open cross-sections. As for the closed cross-section, to the authors’ knowledge, few attempts have been made to analyze the problem of triply coupled vibration of thin-walled beams with arbitrary closed cross-sections, that is, most researchers have neglected the deformational influence of warping shear stress in relation to that of the Bredt’s shear stress [21]. The analysis of the free vibration of anisotropic thin-walled closed cross-section beams was developed by Armanios et al. [22] and Kim et al. [23]. However, the effect of warping shear stress has not received enough consideration. Bastawrous et al. [24] studied the coupled bending and torsional vibration of the wind turbine blades by the assumed modes method but ignored the warping effect. In Ref. [25], Tesar researched the static and dynamic behavior of thin-walled box beams through the FETM method, the accuracy of the theoretical approach being validated via the comparison of theoretical and experimental values.
The purpose of this paper is twofold. First is to establish the inherent relationship between the properties of the cross-section and the beam’s dynamic behaviors. As most commercial software (ANSYS, ABAQUS, Hypermesh et al.) is based on finite element method (FEM) analysis, it is difficult to achieve that [26,27]. The dynamic transfer matrix method [28] for vibration of thin-walled beams filled with shear-sensitive material was presented by Bozdogan and Ozturk, but the coupling between flexural and torsional vibration was ignored. The transfer matrix method (TMM) is an efficient and computerized method which is extensively used in the static analysis of solid beams or space frame structures [29]. In order to extend the application of TMM in dynamic analysis of thin-walled beams, a new thin-walled beam dynamic transfer matrix method, named TDTMM, is presented in this paper. The second purpose is to reflect the effect of warping on the natural frequencies of thin-walled beams with arbitrary closed cross-sections.
Finally, two numerical examples and one experimental example of coupled vibration are presented to verify the accuracy of the TDTMM. The numerical results obtained by TDTMM are compared with those obtained by the general dynamic transfer matrix method (GDTMM) with the warping effect being ignored and the FEM using Hypermesh with shell elements. In addition, by comparing experimental results with those of TDTMM and FEM, the rationality of using the FEM as a comparison reference and the validity of the TDTMM are verified.
2. Basics of the Theoretical and Mathematical Model
2.1. Equations of Motion
As shown in Figure 1, the right-hand orthogonal coordinate system (xyz) and the s-coordinate system along the midline of the cross-section are used to describe the details of the cross-section, where C- and S- points are the centroid and the shear center, respectively. Thus, the displacements of arbitrary point P on the midline of the cross-section can be represented by the longitudinal displacement and the tangential displacement .
where t is a time variable; both the displacement components (u0(x, t), v0(x, t), w0(x, t)) and the rotation components (θx(x, t), θy(x, t), θz(x, t) and φ(x, t)) are time dependent. Ys and Zs are the shear center coordinates with respect to the centroid coordinate system; h(s) represents the perpendicular distance from the shear center to the tangential direction of the point P.
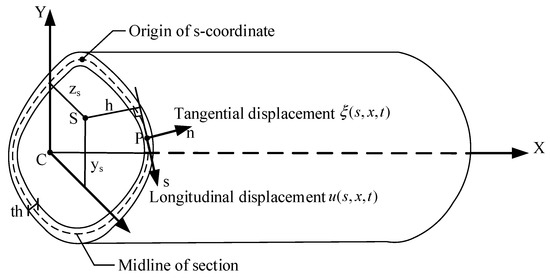
Figure 1.
Element geometry of the beam and the details of the cross-section.
The positive convention of forces and moments is indicated in Figure 2, in which the bimoment is independent of the coordinate system [30].
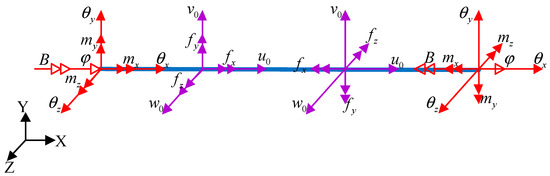
Figure 2.
The positive convention for the forces and moments of the beam.
According to Figure 2, the seven stress resultants (axial force fx, shear forces fy and fz, bending moments my and mz, twisting moment mx and bimoment B) of thin-walled beams with arbitrary closed cross-sections can be expressed as Equation (3), and the explicit derivation process form displacement field to stress field is introduced by Zhong et al. [29]. In the aforementioned and the following relations, superscript primes and dots denote the derivatives with respect to axial position x and time t, respectively.
where
The sectorial coordinate and the torsional function Ψ can be defined as follows:
where denotes the cross-sectional area of the beam bounded by the midline contour.
Stress resultants of the GDTMM can be expressed as Equation (6). Comparing the stress resultants of TDTMM and GDTMM, the difference is obvious. In the GDTMM, the shear correction coefficient k is introduced and exists as a constant term, but the rate of twist and the bimoment B are not considered. In order to study the effect of warping on the natural frequencies of thin-walled beams, it is necessary to compare the GDTMM and TDTMM, and the numerical examples in the following article consider these two methods, respectively.
The total twisting moment with respect to the shear center in the x-direction, which is reported in [29], consists of two parts: (i) the twisting moment of free torsion mfx; (ii) the twisting moment of restrained torsion mwx.
As shown in Figure 3, the equilibrium diagrams for an infinitesimal thin-walled beam segment in the xy- and xz-planes and the x-direction are described, respectively. The equilibrium equations can be expressed as:
where Jy and Jz are the mass moments of inertia of the beam about the centroid principal axes; Jx is the polar mass moment of inertia about the x-axis; is the mass per unit length; and is the material density.
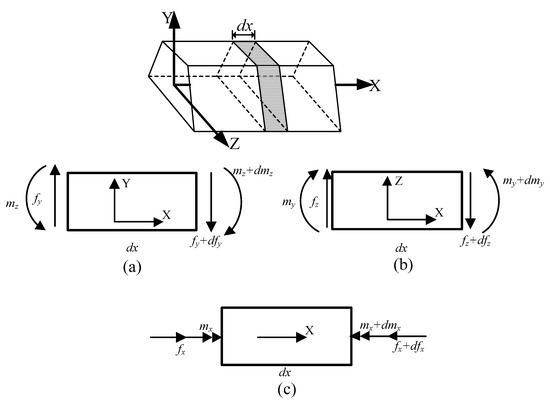
Figure 3.
The equilibrium diagrams of forces and moments for an infinitesimal beam segment in the xy- (a) and xz-planes (b) and the x-direction (c).
The mass moments of inertia Jx, Jy and Jz can be obtained by converting the area moments of inertia Ip, Iy and Iz.
in which , and denote the radius of gyration with respect to the x-, y- and z-axes.
Then, equations of motion can be found by substituting Equations (3) and (10) into Equation (9). The equation of flexural vibration about the xy-plane is:
It will be seen that the transverse displacement v0(x, t) is coupled with w0(x, t) and the angle of twist θx(x, t).
Similarly, the remaining two equations about flexural vibration of the xz-plane and the torsional vibration are:
In light of Equations (3) and (4), it is important to note that the relationship among , and can be written as follows:
where the specific expressions of are given in Appendix A(1). Substituting Equations (14)–(17) into Equations (11)–(13), the equations of motion for triply coupled vibration are obtained, and the specific expressions are given in Appendix A(2).
2.2. Free Vibration
For a free vibration analysis, it is known that every point of the beam will move in a sinusoidal form, i.e., the motion in a complex notion can be described as:
where , and are the amplitudes of the sinusoidal varying displacements and rotation, and is the circular frequency.
Substituting Equation (18) into equations of motion A2 from Appendix A(2), and assuming that , and for amplitudes, the three equations of motion can be simplified as:
The equations can be expressed in a matrix form as:
in which the symbolic variables of matrix, , and , are expressed in Appendix A(3).
Setting the determinant of the linear system equal to zero yields an ordinary polynomial of the 12th order with respect to r, as:
where the coefficients of polynomial, , are given in Appendix A(4).
Upon defining a new variable , the polynomial can be written as:
Using the method adopted by Bishop et al. [11], it may be shown that all six roots of Equation (22) are real, nonzero and nonequal, and three of them positive and the others negative. So, the twelve roots of Equation (21) can be expressed in the form:
where and .
Therefore, the general solution of , and can be written as follows:
where , and are three sets of undetermined constants.
Substituting the general solutions of , and into Equation (14) could yield the relations among the , and as follows:
in which .
2.3. Axial Vibration
The first equation in stress resultants of Equation (3), describing axial force, is uncoupled with the rest of the system. Therefore, the axial vibration can be analyzed separately. Substituting Equation (3) into Equation (4), the equation of motion about axial vibration can be expressed as:
Similarly, the sinusoidal variation of u0 with circular frequency ω is assumed as:
Substituting Equation (24) into Equation (23), the axial vibration equation of motion becomes:
The general solution of linear ordinary differential Equation (25) can be written in the following form:
where are undetermined constants, while coefficient is:
2.4. Dynamic Transfer Matrix Formulation
Different from the general solid beam, both the bimoment and the rate of twist are taken into account in this paper. Therefore, the state vector of thin-walled beam consists of two parts: (i) the displacement field vector, i.e., ; (ii) the stress field vector, i.e., . Thus, the state vector of thin-walled beam with respect to amplitude is defined as:
In light of Equation (6), we can convert it to an equation of amplitude and frequency.
where represents the integral of x.
The total twisting moment with respect to the shear center in the x-direction, which is reported in [29], consists of two parts: (i) the twisting moment of free torsion mfx; (ii) the twisting moment of restrained torsion mwx.
with mwx = B’.
According to Equations (28) and (29), the bimoment B can be written as following:
Then, the B amplitude of the bimoment can be expressed in the following form:
In light of Equation (3), the amplitude of ϕ can be expressed as:
Similarly, the amplitudes and of and can be obtained by solving the linear equation of Equation (3).
With , , .
Finally, by combining the above equations about amplitude, these fourteen linear, homogeneous equations may be written in a matrix form.
where the coefficient vector C contains the fourteen constants and H is a 14 × 14 nonsymmetric matrix with respect to x, given by:
Let . Substituting it into Equation (34) gives:
The coefficient vector can be determined from the above equation to yield.
Substituting Equation (35) into Equation (34) gives:
Then, let . Substituting it into Equation (36) gives:
where l is the length of the thin-walled beam.
SL and SR are the state vectors of the left and right side of the thin-walled beam, respectively. Therefore, the dynamic transfer matrix that relates the state vector on the left side to the right side of the beam is expressed as matrix multiplication H(l)H(0)−1.
3. Boundary Conditions
In this chapter, the free vibration of thin-walled beams with three cases of boundary conditions will be considered, that is, fixed beams, cantilever beams and free beams. As the boundary conditions are homogeneous, half of the variables of the state vector of each boundary end are zeroes, and the others are unknowns. Both the left and the right sides of the beam are the boundary ends whose boundary state vector is divided into two parts: the boundary displacement field Sdb and the boundary stress field Sfb. The explicit forms are given as follows.
As shown in Table 1, the explicit values of boundary conditions for warping with respect to three different categories (completely free, fully restrained or partially restrained) are listed, separately.

Table 1.
Boundary conditions (B and Ψ) for warping.
So, for fixed beams where both ends are clamped (C-C boundary conditions),
where and are the boundary displacement fields of the two ends.
For cantilever beams clamped at the left side of the beam and free at the right side of the beam (C-F boundary conditions),
And for free beams where both two ends are free (F-F boundary conditions),
where and are the boundary stress fields of two ends.
Substituting the boundary conditions into Equation (34) may yield the coupling equations of the free vibration, which can be written in a matrix form:
where contains the seven nonzero values and M(ω), which is obtained from dynamic transfer matrix is a 7 × 7 matrix. The natural frequencies ω are obtained under the condition that a nontrivial solution of Equation (37) exists, i.e., the determinant of M(ω) is set to zero.
4. Accuracy Verification and Numerical Examples
Two examples of general analysis are adopted to verify the above theoretical considerations of TDTMM on dynamic analysis of thin-walled beam, and the results are compared with those for the same beam obtained by the finite element analysis of shell elements (S-FEM) and the GDTMM. The S-FEM analysis results are obtained through the program Hypermesh with four nodes’ 3D shell elements (shell63), while the TDTMM and GDTMM analysis results are obtained through the program MATLAB code. All beams have the same properties, that is, elastic modulus (E) is equal to 210 GPa and Poisson’s ratio (v) equal to 0.3.
4.1. Example 1
A thin-walled uniform beam with an arbitrary cross-section shown in Figure 4 is considered in the first example. The length of the beam is 1000 mm, and the cross-section has the same thickness (th = 5 mm). The FE model of the beams with three constraints are also shown in Figure 4. Meanwhile, the properties of the cross-section are listed in Table 2.
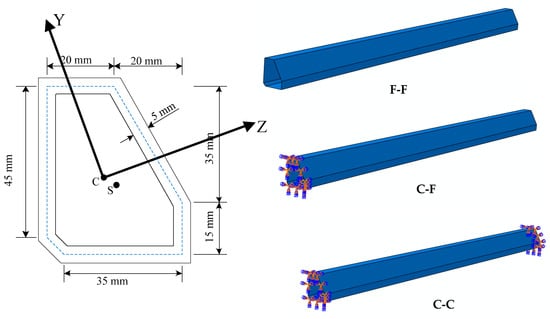
Figure 4.
Beam numerical example 1.

Table 2.
Property details of the example 1.
The first five natural frequencies (Hz) with various boundary conditions (C-C, C-F and F-F) calculated by TDTMM are shown in Table 3, together with the results of the same beam obtained by GDTMM and S-FEM. In the S-FEM analysis, the detailed model of the single beam has 6432 nodes and 6400 elements.

Table 3.
Natural frequencies (Hz) for the beam of example 1 with three boundary conditions (C-C, C-F, F-F) obtained by TDTMM, GDTMM and S-FEM.
Comparison is made between the errors of the first five frequencies between TDTMM and S-FEM, and those between GDTMM and S-FEM, as shown in Table 4. The maximum error of natural frequency between GDTMM and S-FEM may reach 8.77% in the case of the F-F boundary condition, while the maximum error between TDTMM and S-FEM is only −3.41%. The minus indicates that frequencies obtained with TMM analysis are lower than the S-FEM analysis. In addition, the first five errors between TMM (TDTMM and GDTMM) and S-FEM under different boundary conditions are plotted together in Figure 5. It can be seen that the errors between TDTMM and S-FEM fluctuate more smoothly. Therefore, it is necessary to consider the warping effect of the thin-walled beam for the dynamic analysis, and TDTMM proposed in this paper is more suitable for thin-walled beam vibration calculation.

Table 4.
The error of natural frequencies between TMM (TDTMM and GDTMM) and S-FEM analyses in example 1.
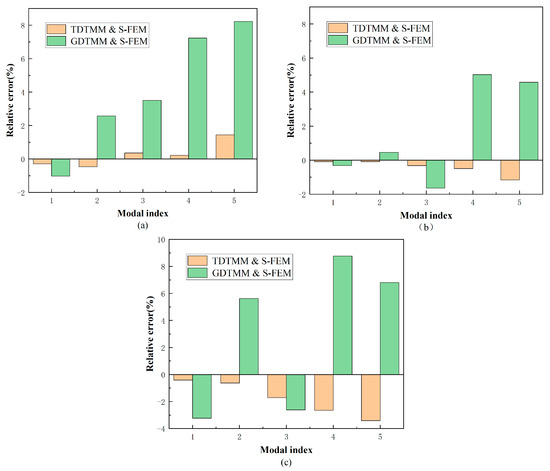
Figure 5.
The plot of relative error on natural frequencies versus modal index for example 1 under different boundary conditions: (a) C-C; (b) C-F; (c) F-F.
4.2. Example 2
As shown in Figure 6, this is the case of a uniform thin-walled beam with a rectangular cross-section, that is, ys = 0 and zs = 0. The length of the beam is 1000 mm, and the cross-section has the same thickness (th = 3 mm). The FE model of the rectangular cross-section beams with three constraints are also shown in Figure 6. The properties of the cross-section are given in Table 5.
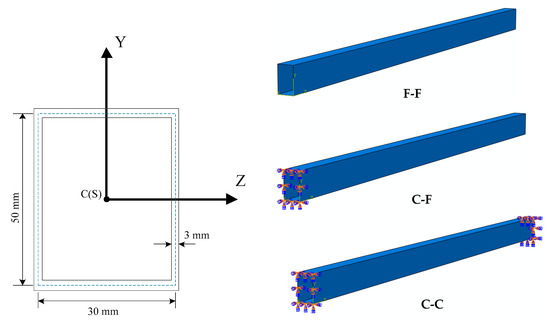
Figure 6.
Beam numerical example 2.

Table 5.
Property details of example 2.
Similarly, the first five natural frequencies of the beam are given in Table 6 for three boundary conditions (C-C, C-F and F-F) by TDTMM, GDTMM and S-FEM analyses, respectively. In the S-FEM analysis, the detailed model of the thin-walled beam has 6432 nodes and 6400 elements.

Table 6.
Natural frequencies (Hz) for the beam of example 2 with three boundary conditions (C-C, C-F, F-F) obtained by TDTMM, GDTMM and S-FEM.
As can be obviously seen from Table 7, TDTMM demonstrates advantages for the analysis of the dynamic behavior of the thin-walled beam considering the first five frequencies between TDTMM and S-FEM and those between GDTMM and S-FEM. The maximum error of natural frequency between GDTMM and S-FEM may reach 9.84% in the case of the C-C boundary condition, while the maximum error between TDTMM and S-FEM is only 4.95%. Moreover, as in example 1, the error between TDTMM and S-FEM are smaller, as shown in Figure 7. As example 2 is concerned with a rectangular cross-section, the centerline of the cross-section is warping free, and the resulting deviations of the TDTMM and GDTMM in example 2 are smaller than those in example 1, but the application of thin-walled beam theory and the consideration of the secondary shear stress make the calculation results more accurate. In general, combining with examples 1 and 2, the method proposed in this paper greatly improved the calculation accuracy of the vibration behaviors of thin-walled beam with rectangular or arbitrary cross-sections.

Table 7.
The error of natural frequencies between TMM (TDTMM and GDTMM) and S-FEM analyses in example 2.
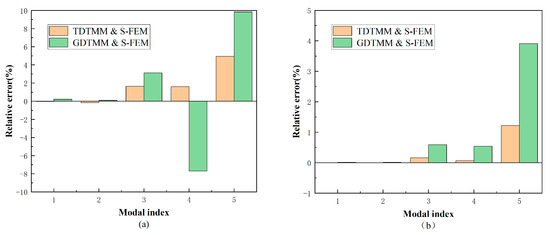
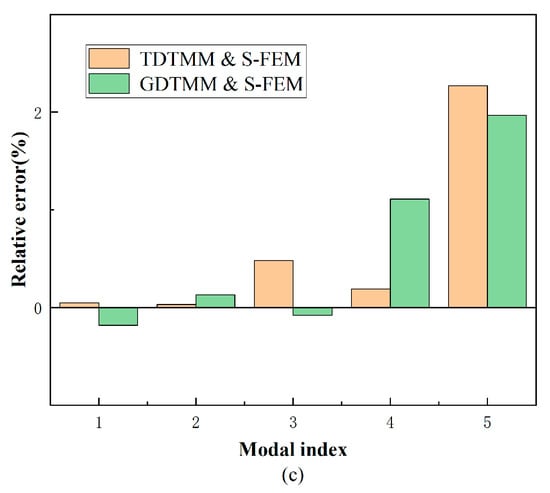
Figure 7.
The plot of relative error on natural frequencies versus modal index for example 2 under different boundary conditions: (a) C-C; (b) C-F; (c) F-F.
5. Experimental Model
5.1. Case Study
As the S-FEM analysis is an approximate calculation method, comparing the results obtained by TMM with S-FEM analysis may lead to an undefined problem, as the S-FEM analysis is an approximate calculation method. As pointed out in Section 1, experimental evidence about thin-walled beams with arbitrary cross-sections are rather scarce in the literature. Therefore, taking into account the controversial point discussed in this paper and to further verify the theory of TDTMM, a series of free vibration tests were carried out on thin-walled beams with an arbitrary cross-section in this section.
Beams with the cross-section shown in Figure 8 were tested. The lengths of the beam are 1000 mm, 1052 mm and 995 mm, respectively, corresponding to the boundary conditions of C-C, C-F and F-F, and the cross-sections have the same thickness (th = 1.5 mm). The properties of the cross-sections are given in Table 8.
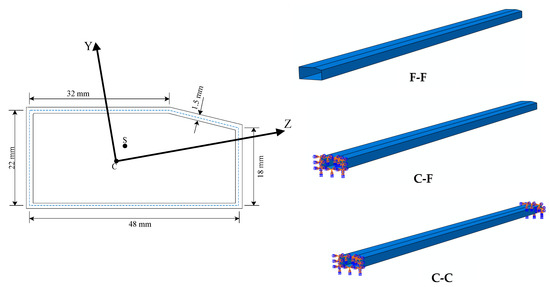
Figure 8.
Beam cross-section used in the test.

Table 8.
Property details of the beam considered in the experimental model.
5.2. Experimental Setup and Instrumentation
Two accelerometers, B and K4524, were used to measure the dynamic response of the thin-walled beams. The LMS SCANDAS Mobile was used to collect the experimental data. The experimental signals collected by the LMS SCANDAS Mobile were recorded and processed by the computer through the LMS Test Lab. Aimed at the clear and accurate modes, the beams were excited by a hammer blow PCB086D05 at different positions. The experimental setup of the F-F boundary condition is shown in Figure 9.

Figure 9.
Experimental setup and instrumentation.
5.3. Dynamic Response
The peak-picking method [31]. was used to carry out the system identification and determination of natural frequencies. Figure 10 shows the dynamic response with various boundary conditions for TDTMM, GDTMM and Test. In addition, the first five natural frequencies of the beams are given in Table 9 for various boundary conditions (C-C, C-F and F-F) by TDTMM, S-FEM and Test, respectively.
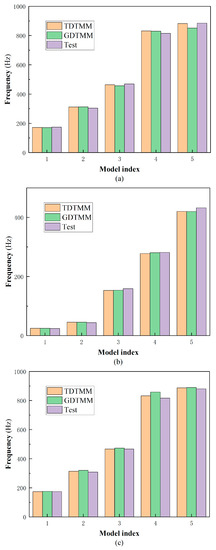
Figure 10.
Dynamic response with various boundary conditions for TDTMM, GDTMM and Test: (a) C-C; (b) C-F; (c) F-F.

Table 9.
Natural frequencies (Hz) of the beams of the experimental models for three boundary conditions (C-C, C-F, F-F) obtained by TDTMM, GDTMM and Test.
As listed in Table 10, it is important to note that the error between the experimental results and those obtained with the TDTMM are lower than 5% in all cases. Moreover, the maximum error between S-FEM and the experimental result is about 5%, so it is reasonable to compare the S-FEM results in the previous section.

Table 10.
The error of natural frequencies between TDTMM, S-FEM and test results of experimental models.
6. Conclusions
In this paper, the new thin-walled beam dynamic transfer matrix method, named TDTMM, is presented in the frequency domain for thin-walled beams with an arbitrary closed single-cell cross-section. The theory takes into account the influence of warping effect, that is, both the bimoment B and the rate of twist ϕ(x) of the beam are considered based on the Vlasov’s beam theory and Kollbrunner-Hajdin assumption. In this paper, the relationship between the cross-section’s properties and the dynamic behavior of the beam is established, which allows us to quickly predict the dynamic behaviors of the beam. In addition, this theory enables the analysis of practical space structure problems using joint coupling matrix in conjunction with coordinate transformation matrix [29,32]. Moreover, the proposed theory can also be used for solid beams in which coupling between bending and torsion occurs. Two numerical examples and one experimental example were considered to illustrate the theory. The comparison with GDTMM, S-FEM and experiment results proved that the TDTMM analysis proposed in this paper has good accuracy and practicality.
Author Contributions
Conceptualization, T.X., J.Y., H.Z. and M.S; methodology, H.Z., J.Y. and M.S.; software, J.Y. and H.Z.; validation, H.Z., J.Y. and M.S.; formal analysis, H.Z., J.Y. and M.S.; investigation, H.Z., J.Y. and M.S.; resources, T.X.; data curation, H.Z., J.Y. and M.S.; writing—original draft preparation, H.Z., J.Y. and M.S.; writing—review and editing, J.Y., T.X. and F.G.; visualization, H.Z., J.Y. and M.S.; supervision, T.X.; project administration, T.X.; funding acquisition, T.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the “Research and development of energy-saving and environment-friendly high-performance nonpneumatic tire” and ”Development and industrialization of high-performance nonpneumatic tires and their special polyurethane materials”, grant numbers X220091TL220 and 2120001007947.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available upon request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
(1) In light of Equations (3) and (6), the linear equations with respect to , , and are as follows:
and the can be obtained by solving the above linear equations. That is:
and so:
where
(2) Substituting Equations (14)–(17) into Equations (11)–(13), the specific equations of motion for triply coupled vibration are obtained.
(3) Let , , , , , . The equations of motion A2 can be written as:
where , , , , , , , , , , , , , , , , , , , , , , , , , , .
(4) The coefficients of polynomial
where det[ ] is determinant of the matrix.
Appendix B
The H is a 14 × 14 matrix, as:
where
in which
References
- Vlasov, V.Z. Thin-walled elastic beams. PST Cat. 1959, 428. [Google Scholar]
- Timoshenko, S.P. Theory of bending, torsion and buckling of thin-walled members of open cross section. J. Frankl. Inst. 1945, 239, 343–361. [Google Scholar] [CrossRef]
- Kim, Y.Y.; Kim, J.H. Thin-walled closed box beam element for static and dynamic analysis. Int. J. Numer. Methods Eng. 1999, 45, 473–490. [Google Scholar] [CrossRef]
- Song, O.; Librescu, L. Free vibration of anisotropic composite thin-walled beams of closed cross-section contour. J. Sound Vib. 1993, 167, 129–147. [Google Scholar] [CrossRef]
- Maalawi, K.Y. Dynamic Optimization of Functionally Graded Thin-Walled Box Beams. Int. J. Struct. Stab. Dyn. 2017, 17, 1750109. [Google Scholar] [CrossRef]
- Qin, H.; Liu, Z.; Liu, Y.; Zhong, H. An object-oriented MATLAB toolbox for automotive body conceptual design using distributed parallel optimization. Adv. Eng. Softw. 2017, 106, 19–32. [Google Scholar] [CrossRef]
- Yadav, A.; Panda, S.K.; Dey, T. Non-linear dynamic instability analysis of thin-walled stiffener beam subjected to uniform harmonic in-plane loading. J. Sound Vib. 2017, 408, 383–399. [Google Scholar] [CrossRef]
- Wu, Q.; Gao, H.; Zhang, Y.; Chen, L. Dynamical analysis of a thin-walled rectangular plate with preload force. J. Vibroengineering 2017, 19, 5735–5745. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, Y.; Li, Y.; Hao, P.; Zhao, Y.; Wang, B. Free Vibration Analysis of Beam-Type Structures Based on Novel Reduced-Order Model. AIAA J. 2017, 55, 3143–3152. [Google Scholar] [CrossRef]
- Dokumaci, E. An exact solution for coupled bending and torsion vibrations of uniform beams having single cross-sectional symmetry. J. Sound Vib. 1987, 119, 443–449. [Google Scholar] [CrossRef]
- Bishop, R.; Cannon, S.; Miao, S. On coupled bending and torsional vibration of uniform beams. J. Sound Vib. 1989, 131, 457–464. [Google Scholar] [CrossRef]
- Laakso, A.; Romanoff, J.; Niemelä, A.; Remes, H.; Avi, E. Free vibration by length-scale separation and inertia-induced interaction–application to large thin-walled structures. Mech. Adv. Mater. Struct. 2022, 1–15. [Google Scholar] [CrossRef]
- Bebiano, R.; Eisenberger, M.; Camotim, D.; Gonçalves, R. GBT-Based Vibration Analysis Using the Exact Element Method. Int. J. Struct. Stab. Dyn. 2018, 18, 1850068. [Google Scholar] [CrossRef]
- Yaman, Y. Vibrations of open-section channels: A coupled flexural and torsional wave analysis. J. Sound Vib. 1997, 204, 131–158. [Google Scholar] [CrossRef]
- Arpaci, A.; Bozdag, S.; Sunbuloglu, E. Triply coupled vibrations of thin-walled open cross-section beams including rotary inertia effects. J. Sound Vib. 2003, 260, 889–900. [Google Scholar] [CrossRef]
- Ambrosini, D. On free vibration of nonsymmetrical thin-walled beams. Thin-Walled Struct. 2009, 47, 629–636. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, S.; Li, F.; Zhu, Y. Coupled bending and torsional vibrations of non-uniform thin-walled beams by the transfer differential transform method and experiments. Thin-Walled Struct. 2018, 127, 373–388. [Google Scholar] [CrossRef]
- Kim, N.-I.; Fu, C.C.; Kim, M.-Y. Stiffness matrices for flexural–torsional/lateral buckling and vibration analysis of thin-walled beam. J. Sound Vib. 2007, 299, 739–756. [Google Scholar] [CrossRef]
- De Borbon, F.; Mirasso, A.; Ambrosini, D. A beam element for coupled torsional-flexural vibration of doubly unsymmetrical thin walled beams axially loaded. Comput. Struct. 2011, 89, 1406–1416. [Google Scholar] [CrossRef]
- Prokić, A.; Mandić, R.; Vojnić-Purčar, M. An improved analysis of free torsional vibration of axially loaded thin-walled beams with point-symmetric open cross-section. Appl. Math. Model. 2016, 40, 10199–10209. [Google Scholar] [CrossRef]
- Massonnet, C. A new approach (including shear lag) to elementary mechanics of materials. Int. J. Solids Struct. 1983, 19, 33–54. [Google Scholar] [CrossRef]
- Armanios, E.A.; Badir, A.M. Free vibration analysis of anisotropic thin-walled closed-section beams. AIAA J. 1995, 33, 1905–1910. [Google Scholar] [CrossRef]
- Kim, N.-I.; Lee, J. Improved formulation for spatial free vibration of thin-walled Al/Al2O3 FG sandwich beams with non-symmetric open, single- and double-cell sections. Compos. Struct. 2017, 178, 162–185. [Google Scholar] [CrossRef]
- Bastawrous, M.V.; El-Badawy, A.A. A Study on Coupled Bending and Torsional Vibrations of Wind Turbine Blades. Adv. Mater. Res. 2012, 622–623, 1236–1242. [Google Scholar]
- Tesar, A. The effect of diaphragms on distortion vibration of thin-walled box beams. Comput. Struct. 1998, 66, 499–507. [Google Scholar] [CrossRef]
- Kim, Y.Y.; Kim, Y. A one-dimensional theory of thin-walled curved rectangular box beams under torsion and out-of-plane bending. Int. J. Numer. Methods Eng. 2002, 53, 1675–1693. [Google Scholar] [CrossRef]
- Kenny, S.; Pegg, N.; Taheri, F. Dynamic elastic buckling of a slender beam with geometric imperfections subject to an axial impulse. Finite Elem. Anal. Des. 2000, 35, 227–246. [Google Scholar] [CrossRef]
- Li, J.; Shen, R.; Hua, H.; Jin, X. Coupled bending and torsional vibration of axially loaded thin-walled Timoshenko beams. Int. J. Mech. Sci. 2004, 46, 299–320. [Google Scholar] [CrossRef]
- Zhong, H.; Liu, Z.; Qin, H.; Liu, Y. Static analysis of thin-walled space frame structures with arbitrary closed cross-sections using transfer matrix method. Thin-Walled Struct. 2018, 123, 255–269. [Google Scholar] [CrossRef]
- Kollbrunner, C.F.; Hajdin, N. Stäbe Mit Undeformierbaren Querschnitten; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice and Application; John Wiley & Sons: New York, NY, USA, 2009. [Google Scholar]
- Zhong, H.; Xu, T.; Yang, J.; Sun, M.; Gao, F. Optimization Design of Automotive Body Stiffness Using a Boundary Hybrid Genetic Algorithm. Machines 2022, 10, 1171. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).