An Error-Pursuing Adaptive Uncertainty Analysis Method Based on Bayesian Support Vector Regression

Abstract

The Bayesian support vector regression (BSVR) metamodel is widely used in various engineering fields to analyze the uncertainty arising from uncertain parameters. However, the accuracy of the BSVR metamodel based on the traditional one-shot sampling method fails to meet the requirements of the uncertainty analysis of complex systems. To this end, an error-pursing adaptive uncertainty analysis method based on the BSVR metamodel is presented by combining a new adaptive sampling scheme. This new sampling scheme was improved by a new error-pursuing active learning function that is named, herein, adjusted mean square error (AMSE), which guides the adaptive sampling of the BSVR metamodel’s design of experiments (DoE). During the sampling process, AMSE combines mean square error and leave-one-out cross-validation error to estimate the prediction error of the metamodel in the entire design space. Stepwise refinement of the metamodel was achieved by placing the sampled regions at locations with large prediction errors. Six benchmark analytical functions featuring different dimensions were used to validate the proposed method. The effectiveness of the method was then further illustrated by a more realistic application of an overhung rotor system.

1. Introduction

In practical problems, the presence of uncertainty factors seriously affects the performance of engineering systems. Therefore, quantifying these uncertainties and fully considering the impact of them on aspects such as system security assessment, optimal design, and usage maintenance is essential [1]. Uncertainty analysis aims to quantify the uncertainties in engineering system outputs that are propagated from uncertain inputs [2], which usually consist of the following three aspects: (a) the calculation of the statistical moments of the stochastic response [3,4], (b) the probability density function of the response [5,6], and (c) the probability of exceeding an acceptable threshold (reliability analysis) [7,8,9].

Recently, uncertainty analysis methods based on Bayesian support vector regression (BSVR) have gained widespread attention [10,11]. BSVR is a special support vector regression (SVR) model that is derived from the Bayesian inference framework. Law and Kwok [12] applied MacKay’s Bayesian framework to SVR in the weight space. Gao et al. [13] derived an evidence and error bar approximation for SVR based on the approach proposed by Sollich [14]. Chu et al. [15] proposed the soft insensitive loss function (SILF) to address the inaccuracies in evidence evaluation and inference that were brought on by the unsmoothed loss function, which further enriches the diversity of BSVR models. Compared with other metamodel methods, the BSVR model based on the structural risk minimization principle features better generalization ability and shows superior performance in dealing with non-linear problems and avoiding overfitting.

An accurate BSVR metamodel is the basis for uncertainty analysis, while the accuracy of the metamodel highly depends on the number and quality of training samples. For uncertainty analysis tasks in real engineering, numerical computational models are usually complex, which means that training sample points are costly to obtain. Therefore, the only way to obtain a high-precision BSVR metamodel for uncertainty analysis is to improve the quality of the training samples. 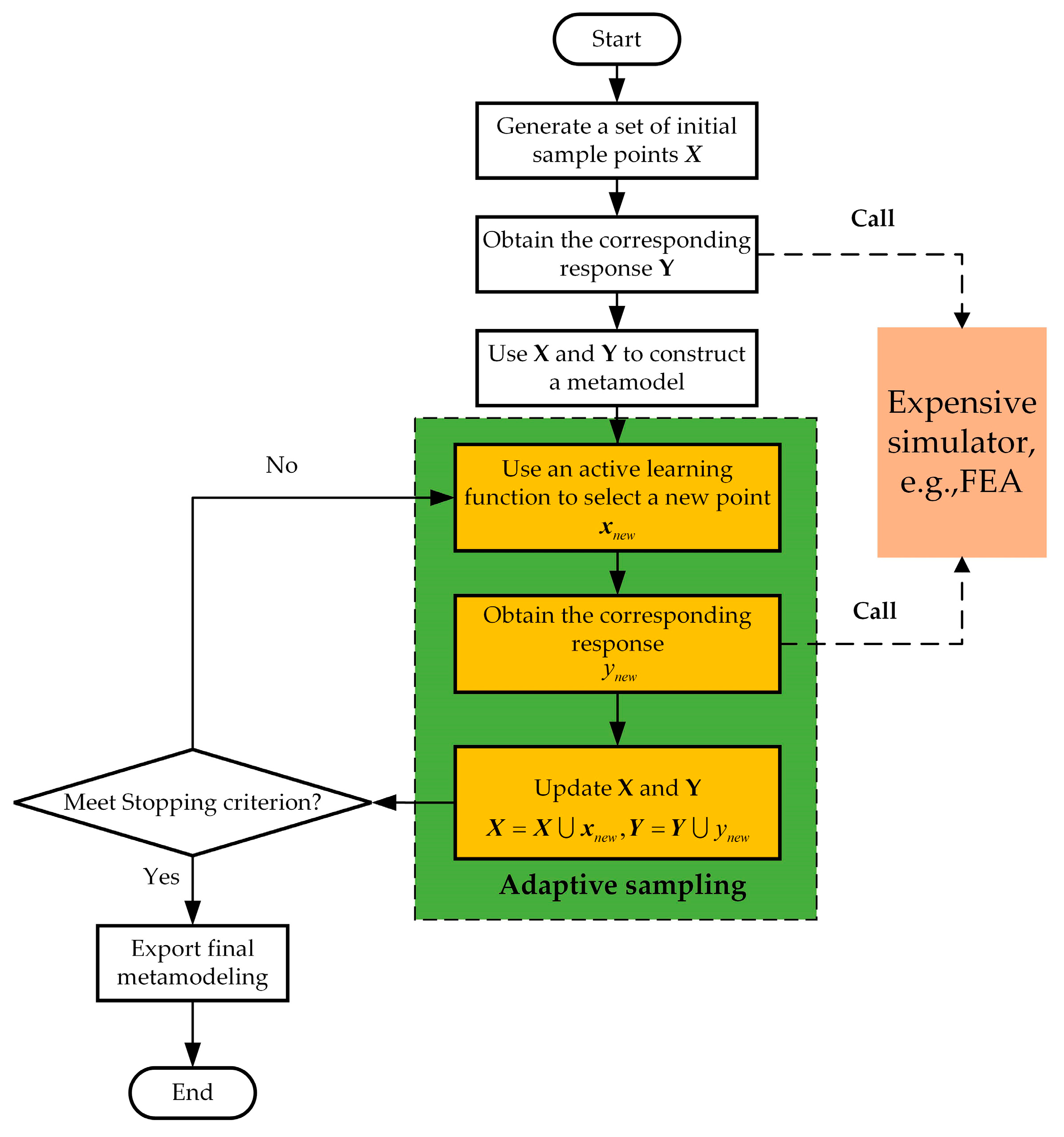The traditional one-shot sampling method determines the sample size and number of points in one stage [16], which fails to meet the requirement of constructing a high-precision metamodel using as few sample points as possible. The challenge of appropriate training sample selection has led to the development of various adaptive sampling schemes. These schemes start with an initial design of experiments (DoE) with a minimal sample set, and then the most informative or important sample points are sequentially added to the DoE by the active learning function. The steps for improving the metamodel by utilizing the adaptive sampling schemes are illustrated in detail in Figure 1.

From Figure 1, it can be observed that the most crucial factor during the adaptive sampling process is the active learning function. In general, active learning functions require a point-wise local prediction error or confidence interval to guide the operation [17,18], i.e., active learning functions all feature error-pursuit properties. The active learning function focuses on determining the prediction error information of the unsampled points. Note that the actual prediction error is unknown a priori. Therefore, the actual unsampled prediction error is generally estimated by the mean square error (also known as the prediction variance), the cross-validation error, and the local gradient information. Only the mean square error and cross-validation error are discussed here.

Most of the mean square error-based active learning functions are deeply combined with the Gaussian process (GP) model. Thanks to the assumption of a Gaussian process, BSVR can provide information about the mean square error at the unsampled points. The active learning function based on mean square error considers that regions with a significant mean square error of the metamodel may have larger prediction errors. Shewry and Wynn [19] proposed the maximum entropy (ME) criterion that selects new points by maximizing the determinant of the correlation matrix in the Bayesian framework. In the maximizing the mean square error (MMSE) method proposed by Jin et al. [20], new sample points were selected by maximizing the mean square error. Interestingly, Jin et al. [20] pointed out that the MMSE criterion is equivalent to the one-by-one ME criterion. It is worth noting that the above sampling method utilizes the property that the GP model follows the stationary assumption, which causes the value of the covariance matrix (mean square error) to depend only on the relative distance between the sample points. Lin et al. [21] pointed out that the stationary assumption is inappropriate in adaptive experimental designs, because the correlation between two points does not depend only on the relative distance.

Active learning functions based on cross-validation errors usually focus excessively on local exploration and, thus, often require the introduction of distance constraints [22]. However, without sufficient a priori knowledge, the choice of distance constraint usually has a large uncertainty. In the SFCVT learning function proposed by Aute [23], the Euclidean distance between the sampled and unsampled points was used. The CV-Voronoi learning function proposed by Xu [24] selects the unsampled point in the Voronoi cell that is farthest from the sampled point. Jiang [25] used the average minimum distance between sampled and unsampled points as the distance constraint. Jiang [26] and Roy [27], on the other hand, used the maximin distance criterion, i.e., the maximum value of the minimum distance between sampled and unsampled points was chosen as the distance constraint. However, without sufficient a priori knowledge, the choice of distance constraint usually has a significant uncertainty.

In general, the above active learning functions have the following drawbacks:

(1) Local error information is not considered;

(2) Clustering problems exist.

To address the above problems, in this paper, a new error-pursing active learning function, named, herein, adjusted mean square error (AMSE), was designed to improve the adaptive sampling process. In fact, AMSE can combine the mean square error and LOO cross-validation error to evaluate the prediction error information of unsampled points. It introduces local error information through the LOO cross-validation error, which results in a significant advantage for AMSE when dealing with non-linear problems. Moreover, the global exploration property of the mean square error can effectively avoid the clustering problem.

Finally, in order to implement uncertain analysis, the error-pursing adaptive uncertain analysis method based on BSVR was present by integrating the adaptive sampling scheme with the new error-pursing AMSE. Additionally, six benchmark analytical functions, featuring different dimensions and a more realistic application of an overhung rotor system, were selected to validate the proposed algorithm.

The rest of the paper is organized as follows. Section 2 briefly reviews Bayesian support vector regression based on Bayesian inference. Then, the proposed adaptive sampling scheme based on AMSE and the new error-pursuing adaptive uncertainty analysis method are introduced in Section 3. In Section 4, the performance and properties of the proposed method are explored using several analytic mathematical examples and are compared with other methods. In Section 5, the proposed method is applied to rotor system uncertainty analysis to validate the advantages of the proposed method further. Finally, conclusions are given.

2. The Bayesian Support Vector Regression Method

In this section, the basic theories of the Bayesian support vector regression (BSVR) proposed by Chu [15] and Cheng [16] are briefly introduced.

2.1. Bayesian Inference Framework

For a regression problem with a given training sample $\mathit{D}=\{\mathit{X},\mathit{Y}\}$, the mapping relationship between the inputs and outputs can be expressed as:

$$y_i=\widehat{g}({\mathit{x}}_i)+{\delta }_i i=1,2,\dots ,N$$

(1)

where $\widehat{g}(\mathit{x})$ is the regression model, and ${\delta }_i$is the additive noise with the independent identical distribution.

The regression aims to use the training sample D to obtain a specific formula for $\widehat{g}(\mathit{x})$. In the framework of Bayesian inference, this problem can be transformed by solving for the maximum posterior of $\widehat{g}(\mathit{x})$:

$$P(\mathit{G}|\mathit{D})=\frac{P(\mathit{D}|\mathit{G})P(\mathit{G})}{P(\mathit{D})}$$

(2)

where $\mathit{G}={[\widehat{g}({\mathit{x}}_1),\widehat{g}({\mathit{x}}_2),\dots ,\widehat{g}({\mathit{x}}_N)]}^T$, $P(\mathit{D}|\mathit{G})$ is the likelihood function, $P(\mathit{G})$ is the prior probability, and $P(\mathit{D})$ is the marginal likelihood, which can usually be assumed to be a constant.

2.2. Prior Probability

Unlike the traditional SVR problem, where $\widehat{g}(\mathit{x})$ is considered as a series of hyperplane equations, BSVR assumes $\widehat{g}(\mathit{x})$ as a stationary Gaussian process with a mean function of zero and a covariance function of $k(\mathit{X},{\mathit{X}}^{\prime })$, i.e., $\widehat{g}(\mathit{x})~GP(0,k(\mathit{X},{\mathit{X}}^{\prime }))$. The Gaussian covariance function is used in this study and illustrated as follows:

$$k({\mathit{x}}_i,{\mathit{x}}_j)=\exp (-{\displaystyle \sum _{l=1}^d{\theta }_l{(x_i^l-x_j^l)}^2}) i,j=1,2,\dots ,N$$

(3)

where $\mathit{\theta }={\left[{\theta }_1,\dots ,{\theta }_d\right]}^T$ is the parameter to be determined for the covariance function, and $x^l$ denotes the $l-\mathrm{th}$ element of the input vector $\mathit{x}$.

With these assumptions, the expression of the prior probability can be derived as follows:

$$P(\mathit{G})=\frac{1}{z_{\mathit{G}}}\exp \left(-\frac{1}{2}{\mathit{G}}^T{\mathit{K}}^{-1}\mathit{G}\right)$$

(4)

where $z_{\mathit{G}}={(2\pi )}^{\frac{n}{2}}\cdot \sqrt{\left|\mathit{K}\right|}$, K is the covariance matrix of training samples with entry $K_{ij}=k({\mathit{x}}_i,{\mathit{x}}_j)$.

2.3. Likelihood Function

The likelihood function $P(\mathit{D}|\mathit{G})$ is essentially a model of noise [15]. In the previous description, the noise ${\delta }_i$ is assumed to obey an independent identical distribution, and then $P(\mathit{D}|\mathit{G})$ can be expressed as:

$$P(\mathit{D}|\mathit{G})=\prod _{i=1}^{n}P\left(y_i-f\left({\mathit{x}}_i\right)\right)=\prod _{i=1}^{n}P\left({\delta }_i\right)\propto \exp \left(C\cdot \sum _{i=1}^n\ell \left(y_i-f\left({\mathit{x}}_i\right)\right)\right)$$

(5)

2.4. Posterior Probability

By substituting Equations (4) and (5) into Equation (2), the expression of the posterior probability can be obtained as follows:

$$P(\mathit{G}|\mathit{D})=\frac{1}{z}\exp (-h(\mathit{G}))$$

(6)

where $z={\displaystyle \int \exp (-h(\mathit{G}))} d\mathit{G}$, and $h(\mathit{G})=C{\displaystyle \sum _{i=1}^N\ell (y_i-\widehat{g}({\mathit{x}}_i))}+\frac{1}{2}{\mathit{G}}^T{\mathit{K}}^{-1}\mathit{G}$.

Thus, the maximum a posteriori probability of $\widehat{g}(\mathit{x})$ can be expressed as:

$$\underset{G}{\min }{\displaystyle \sum _{i=1}^{N}C\cdot \ell (y_i-\widehat{g}({\mathit{x}}_i))}+\frac{1}{2}{\mathit{G}}^T{\mathit{K}}^{-1}\mathit{G}$$

(7)

where C is the regularization coefficient, and $\ell (\cdot )$ denotes the loss function. The $\epsilon$-insensitive squared loss function is used here, while any other type of loss function, such as those introduced in [16], can also be used:

$$\ell (\delta )=\left\{\begin{array}{l}0 , if\left|\delta \right|\le \epsilon \\ \frac{1}{2}{(|\delta |-\epsilon )}^2, otherwise\end{array}\right\}$$

(8)

2.5. Bayesian Support Vector Regression

It can be observed from Equations (3), (7), and (8), and that the hyperparameters in the BSVR model mainly come from the covariance function, the regularization coefficient, and the loss function, i.e., $\mathit{\eta }=[C,\epsilon ,\mathit{\theta }]$. Similarly to solving the regression model, the optimal model hyperparameters can be obtained using Bayes’ theorem, which is not repeated here, and the specific derivation process is described in [16].

After obtaining the model hyperparameters, the BSVR model can be obtained by solving Equation (7). It is worth noting that Equation (7) is a convex quadratic optimization problem, which can be conveniently solved by using the Lagrangian algorithm.

Unlike the traditional SVR model, the BSVR model built following the Gaussian process provides the error measure of this predicted response along with the mean squared error information of the sample points, which is the area of interest in this paper. The predicted response and the mean squared error information of the BSVR can be expressed as:

$$\widehat{\mu }(\mathit{x})=\mathit{k}(\mathit{x},\mathit{X})(\mathit{\alpha }-{\mathit{\alpha }}^{*})={\displaystyle \sum _{j=1}^m({\alpha }_j-{\alpha }_j{}^{*})}\mathit{k}(\mathit{x},{\mathit{x}}_j)$$

(9)

$${\widehat{\Sigma }}^2(\mathit{x})=k(\mathit{x},\mathit{x})-{\mathit{k}}_m(\mathit{x},{\mathit{x}}_m){({\mathit{K}}_m+{\mathit{I}}_m/C)}^{-1}{\mathit{K}}_m({\mathit{x}}_m,\mathit{x})$$

(10)

where $\mathit{k}(\mathit{x},\mathit{X})={\left[k\left({\mathit{x}}_1,\mathit{x}\right),\dots ,k\left({\mathit{x}}_N,\mathit{x}\right)\right]}^{\mathrm{T}}$ represents the covariance matrix between the predicted and training samples, which can be calculated according to Equation (3), and ${\alpha }_i,{\alpha }_i^{*}$ are Lagrange multipliers. The training samples with ${\alpha }_i-{\alpha }_i^{*}\ne 0,i=1,2,\dots ,m$ are support vectors, and ${\mathit{K}}_m,{\mathit{k}}_m$ are the subsets of $\mathit{K},\mathit{k}$, respectively.

3. A New Error-Pursuing Adaptive Uncertainty Analysis Method

In this section, after reviewing some often-used error-pursing active learning functions, the new function named AMSE was designed to improve the adaptive sampling process. Finally, the algorithm steps and flowchart of the proposed error-pursing adaptive uncertainty analysis method based on BSVR and the AMSE-based adaptive sampling scheme are presented.

3.1. Some Frequrntly Used Error-Pursing Active Learning Functions

Based on the above mean squared error information, various error-pursuing active learning functions have been proposed in the past decades, among which the properties of some frequently used active learning functions, such as MMSE, MEI, and CV-Voronoi, are compared and described as follows.

To facilitate the formulation, the following assumptions are introduced:

• All sample points in the adaptive sampling process are divided into an initial experimental design S_I and a candidate sample set S_C;
• The initial DoE is assumed to be S_I = $\{{\mathit{X}}_I,{\mathit{Y}}_I\}=\{(x_I^1,y_I^1),\dots ,(x_I^N,y_I^N)\}$, where ${\mathit{X}}_I$ is obtained by sampling in the design space of the input variable x according to a certain distribution law, ${\mathit{Y}}_I$ is the response of ${\mathit{X}}_I$ on the real model $y(\cdot )$, and $(x_I^N,y_I^N)$ is the N-th set of sample points in the initial experimental design S_D;
• The candidate sample set is assumed to be S_C = {${\mathit{X}}_C$} $=\{{\mathit{x}}_C^1,\dots ,{\mathit{x}}_C^P\}$. Similarly to ${\mathit{X}}_I$, ${\mathit{X}}_C$ is obtained by sampling in the design space of the input variable x. It is worth noting that the candidate sample set S_C does not contain model response values.

In the maximizing the mean square error (MMSE) learning function proposed by Jin et al. [20], the MMSE selected new sample points by maximizing the mean square error. The employment of the MMSE method in BSVR can be expressed as:

$$MMSE({\mathit{x}}_{new})=\arg \max {\sum }^2({\mathit{x}}_{\mathit{C}})$$

(11)

As can be seen from Equation (11), it is clear that the mean square error depends on the relative distance between sample points and fails to characterize the prediction error information of the candidate sample points, which can lead to sampling in inappropriate regions.

To address this problem, Lam [28] introduced the error information of the candidate sample points and proposed a modified expected improvement (referred to here as MEI) learning function with the following expression:

$$MEI({\mathit{x}}_{new})=\arg \max \{{\left(\widehat{\mu }({\mathit{x}}_{\mathit{C}})-y_{\mathit{I}}{}^{*}\right)}^2+{\hat{\mathsf{\Sigma }}}^2({\mathit{x}}_{\mathit{C}})\}$$

(12)

where $y_{\mathit{I}}{}^{*}$ is the true model response of the nearest initial sample point ${\mathit{x}}_I^{*}$ to the candidate sample ${\mathit{x}}_{\mathit{C}}$, and $\widehat{\mu }({\mathit{x}}_{\mathit{C}})$ is the predicted response of the candidate sample. By comparing Equations (11) and (12), it can be found that the MEI assumes the true response of the candidate sample as the response of the closest initial sample and introduces the prediction error information of the candidate sample by solving for the deviation between the predicted response and the true response. However, this assumption is sensitive to the number of initial samples and the degree of nonlinearity of the true model. A case for a highly non-linear situation is illustrated in Figure 2. It is clear that the distance between the initial sample points and the candidate sample points is small, but the gap between the corresponding true models’ responses is huge. In this case, the error information of the calculated candidate samples is not reliable.

It is noteworthy that the error measurement provided by the BSVR model, i.e., the mean square error, is used in both MMSE and MEI.

As another manifestation of model error, the cross-validation error, is also frequently used in active learning functions, such as the cross-validation-Voronoi (CV-Voronoi) method proposed by Xu [24], which uses the Voronoi diagram to divide the candidate samples into a set of Voronoi cells according to the initial DoE and assumes that the same sample points in the Voronoi cell have the same error behavior. The error information of each Voronoi cell is obtained by the leave-one-out (LOO) cross-validation approach. The specific expression of CV-Voronoi is as follows:

$$\begin{array}{l}\mathrm{Find} {\mathit{x}}_{new}=\arg \max \left\{C_{sensitive}\right\}\\ s.t.\left|\right|{\mathit{x}}_{new}-{\mathit{x}}_I|{|}_2=\max \{\left|\right|{\mathit{x}}_C^{sensitive}-{\mathit{x}}_I^{sensitive}\left|\right|\}\end{array}$$

(13)

From Equation (13), it is shown that CV-Voronoi adds a distance constraint to prevent the clustering of new sample points based on local exploration; however, this distance constraint may lead to the selection of sample points located at the junction of different Voronoi cells, and the error description of this point will be biased, as is shown in Figure 3. Figure 3 shows the Voronoi cells divided using the initial DoE, and the black dots are the error information of different Voronoi cells; the larger the dots, the larger the error. The red triangles indicate the new points selected using the distance constraint.

3.2. The Proposed New Error-Pursuing Active Learning Function

To address the above-mentioned issues, a new error-pursuing active learning function called adjusted mean square error (AMSE) was designed. The AMSE active learning function can be expressed by the following formula:

$${\mathit{x}}_{new}=\underset{x\in {\mathit{S}}_C}{\arg \max }({\sum }^2(\mathit{x})+e_{LOO}(\mathit{x}))$$

(14)

where ${\sum }^2(\mathit{x})$ is the predictive variance of the Bayesian support vector regression, which can be calculated from Equation (10), and $e_{LOO}(\mathit{x})$ is the leave-one-out (LOO) cross-validation error.

For the initial training sample points, the LOO cross-validation method was used to calculate $e_{LOO}$, which is easy to implement and can estimate metamodel errors [21]:

$$e_i^{LOO}={(y({\mathit{x}}_i)-{\widehat{y}}_{D/x_i}({\mathit{x}}_i))}^2,{\mathit{x}}_i\in {\mathit{S}}_I$$

(15)

where ${\mathit{S}}_I$ is the initial set of training sample points, $y({\mathit{x}}_i)$ denotes the true response at point ${\mathit{x}}_i$, and ${\widehat{y}}_{D/x_i}({\mathit{x}}_i)$ represents the predicted response at the point of the metamodel constructed with all initial training sample points except for point ${\mathit{x}}_i$.

For the error information $e^{LOO}$ of the candidate sample point, since the true response of the point is unknown, its error information cannot be calculated directly using Equation (15). Currently, there are two main types of methods used to solve this problem; one is to use the LOO error information of the initial sample point to establish an error prediction metamodel, through which the LOO error information of the candidate sample point is predicted [23]. Being limited by the number of initial sample points, this method often cannot obtain a better error prediction effect, which will further affect the efficacy of subsequent model adaptations. The other method assumes that the error information of the points in the adjacent region is similar [29], which is influenced by the initial sample points to a lesser extent than the first assumption; moreover, with the addition of sample points, the assumed error information will gradually approximate the true error information of the points. Thus, the prediction error information at the candidate sample points can be expressed as:

$$e^{LOO}({\mathit{x}}_j)=e^{LOO}({\mathit{x}}_i)={(y({\mathit{x}}_i)-{\widehat{y}}_{D/x_i}({\mathit{x}}_i))}^2,{\mathit{x}}_j\in {\mathit{S}}_C,{\mathit{x}}_i\in {\mathit{S}}_I$$

(16)

where $x_j$ is the nearest candidate sample point to the initial sample point $x_i$. Equation (14) can therefore be rewritten as:

$${\mathit{x}}_{new}=\underset{x\in {\mathit{S}}_P}{\arg \max }(\frac{{\sum }^2(\mathit{x})}{{\sum }_{\max }^2}+\frac{e^{LOO}(\mathit{x})}{e_{\max }^{LOO}})$$

(17)

where ${\sum }_{\max }^2=\underset{x\in {\mathit{S}}_C}{\max }({\sum }^2(x))\mathrm{and}{e}_{\max }^{LOO}=\underset{x\in {\mathit{S}}_C}{\max }(e^{LOO}(\mathit{x}))$. From Equation (17), it can be seen that this active learning function consists of two parts. The first term is responsible for global exploration, and the second term is responsible for local exploration. The local exploration aims to develop regions with large nonlinearity or variability, while the global exploration tends to select points with large prediction variance, with the combination of the two effectively characterizing the prediction error information of the metamodel during the construction process. The implementation steps of the proposed AMSE active learning function are summarized as follows:

Step 1: Calculate the LOO cross-validation error for the training samples.

Step 2: Calculate the mean square error for the candidate samples.

Step 3: Calculate the leave-one-out cross-validation error for the candidate samples.

Step 4: Select new sample points by maximizing the adjusted mean square error.

3.3. Example Illustration

The advantage of the proposed method for prediction error characterization is illustrated using a one-dimensional test function with the following expression:

$$y=3{(1-x)}^2{e}^{(-x^2)}-(2x-10x^3)e^{-x^2}-\frac{1}{3}e(-{(x+1)}^2), x~U[-8,8]$$

(18)

The initial DoE is composed by averaging five sample points in the range of the x values and calculating the corresponding response values. The BSVR metamodel is then built based on the initial DoE. The prediction error of the metamodel is characterized by solving for the absolute error between the metamodel and the real model, and the corresponding error bars are derived, as is shown in Figure 4.

As can be seen from Figure 4, the true model has multiple local optima on the interval [−4, 4], while the other regions tend to be flat. The metamodel built by the initial DoE has a large deviation from the true model, and the prediction errors are mainly concentrated in the non-linear region.

In this test example, 15 samples were selected from the same candidate sample set using MEI, CV-Voronoi, MMSE, and AMSE methods; then, the BSVR metamodel was constructed based on these samples, as is shown in Figure 5.

As can be seen in Figure 5, CV-Voronoi and MEI tended to oversample regions with large errors and ignore other regions, which leads to a good approximation in the non-linear region and shows a large deviation in the rest of the region. More importantly, CV-Voronoi suffered from clustering problems in the second non-linear region; MMSE selected sample points that were evenly distributed throughout the sampling area, which indicates that MMSE does not guide the sample points to be placed in regions with large errors. It is worth noting that the proposed AMSE can determine the regions with large model prediction errors well and reasonably avoid the clustering problem by using global exploration. It can also be seen that the metamodel constructed based on AMSE has the best approximation.

3.4. Algorithm Summary

The flowchart of the proposed new adaptive uncertainty analysis method is depicted in Figure 6 with 7 steps as summarized below:

Step 1: Initialization of the algorithm. In this step, the initial DoE sample size is set as 10N [30]. N is the number of input variables, the candidate sample size is fixed at 10,000, and the stopping criterion is set as the maximum number of sample points to be added.

Step 2: Generation of the initial sample set S_I and the candidate sample set S_C. In this study, the Latin hypercube sampling method in UQLab [31] is used to select a certain number of S_I and S_C that satisfy the corresponding distribution law.

Step 3: Construction of the BSVR model. The BSVR model is constructed using the initial DoE in step 2, and the initial values of the hyperparameters $\mathit{\eta }=[C,\epsilon ,\mathit{\theta }]$ in the model are set to ${10}^5$, ${10}^{-5}$, and 1. To obtain the best hyperparameters, a wide optimization range is set, namely,$[{10}^5,{10}^{10}]$ for C, $[{10}^{-7},{10}^{-2}]$ for $\epsilon$, and $[{10}^{-5},{10}^2]$ for $\mathit{\theta }$.

Step 4: Selection of samples using AMSE to enrich the DoE. New sample points are selected from the candidate sample set S_C in each iteration with the active learning function AMSE.

Step 5: Update the DoE. Call the true model to calculate the response value $y_{New}$ at the new point $x_{New}$, and update the initial DoE; let ${\mathit{S}}_I={\mathit{S}}_I\cup {\mathit{x}}_{new},{\mathit{Y}}_I={\mathit{Y}}_I\cup y_{new}$.

Step 6: End of iterative process. If the stopping criterion is satisfied, the final BSVR model is exported, and the uncertainty analysis is based on the final BSVR metamodel; otherwise, return to step 3.

Step 7: Uncertainty analysis. Once the final BSVR metamodel is obtained, uncertainty analysis can be performed by combining the BSVR metamodel with Monte Carlo simulation (MCS) to obtain the uncertainty analysis results of interest.

4. Numerical Examples

In this section, the proposed new error-pursing adaptive uncertainty analysis method based on BSVR, AMSE, and MCS was applied to the uncertainty analysis of six numerical cases to investigate the effect of various stochastic parameters on the model’s response. These six numerical examples were specially selected to have different performances, such as multi-response modes, high dimensionality, highly nonlinearity, etc. The specific functional behaviors and expressions are shown in

Table 1. Six benchmark test functions.

Test Function	Expression	Performance
P1	$\begin{array}{l}y=3{(1-x_1)}^2\cdot \exp (a)-10(\frac{x_1}{5}-x_1^3-x_2^5)\cdot \exp (b)-\frac{1}{3}\exp (c)\\ a=-{x_1}^2-{(x_2+1)}^2,b=-x_1^2-x_2^2,c=-{(x_1+1)}^2-x_2^2\end{array}$	low-dimensional with non-linear multimodal
P2	$y=\cos (\sqrt{{(x_1-3)}^2+{(x_2-2)}^2})$	low-dimensional with non-linear multimodal
P3	$y=0.5+\sin (\frac{\sqrt{{(x_1^2+x_2^2)}^2}}{1+0.1{(x_1^2+x_2^2)}^2})$	low-dimensional with non-linear multimodal
P4	$y=(30+x_1\sin x_1)(4+e^{-x_2^2})$	low-dimensional with non-linear multimodal
P5	$y=\frac{1}{1+x_1^2+\dots +x_4^2}$	medium dimension with nonlinearity
P6	$y=-20\exp (-0.2\sqrt{0.1\cdot {\displaystyle \sum _{i=1}^8{x}_i^2}})-\exp (0.1\cdot {\displaystyle \sum _{i=1}^8\cos (2\pi x_i)})+20$	high dimension with nonlinearity

. For simplicity, these cases are denoted as P1–P6.

To simulate the different distribution laws of the random parameters in the uncertainty analysis problem, three cases were designed in which the random parameters obeyed uniform, normal, and log-normal distributions, and here, only the random variables were considered to be independent of each other.

Table 2. Statistical information of the random variables.

Test Function	Number of Variables	Distribution	Parameter 1	Parameter 2
P1	2	Uniform	−4	4
P2	2	Uniform	−5	5
P3	2	Lognormal	0.5	0.25
P4	2	Normal	5	2
P5	4	Normal	0.5	0.25
P6	8	Normal	0.5	0.25

provides the distribution laws corresponding to the random parameters obeyed by these examples.

In this study, the proposed AMSE method was compared with the MMSE [20], MEI [28], and CV-Voronoi [24] methods. The statistical moment information of the response is a crucial indicator in uncertainty analysis, which reflects the probabilistic information of the response and the statistical laws of the change in the system’s characteristics. Therefore, the calculation of the first fourth-order statistical moments of the uncertainty response was regarded here as the main content of the uncertainty analysis.

To assess the accuracy performance of different adaptive sampling methods in the uncertainty analysis, the relative error index was used, and the reference value for each order of statistical moments was the result of ${10}^5$ Monte Carlo simulations. The relative error of the calculated results can be expressed as:

$${ϵ}_{{\widehat{\beta }}_i}=\frac{\left|{\widehat{\beta }}_i-{\widehat{\beta }}_i^{MCS}\right|}{{\widehat{\beta }}_i^{MCS}}\times 100\% i=1,\dots ,4$$

(19)

where ${\widehat{\beta }}_i^{MCS}$ denotes the statistical moments of each order calculated by the MCS, and ${\widehat{\beta }}_i$ denotes the statistical moments of each order calculated by the adaptive algorithm.

All adaptive sampling algorithms started with the same number of initial experimental designs (10N). The maximum number of additional sample points was used as the stopping criterion and kept the same stopping criterion for the same dimensional problem. The sampling configurations of the six test functions are shown in

Table 3. The sampling configurations for the six test functions.

Test Function	Initial Samples	Enriched Samples	Candidate Samples	Test Samples
P1	20	100	10,000	50,000
P2	20	100	10,000	50,000
P3	20	100	10,000	50,000
P4	20	100	10,000	50,000
P5	40	200	10,000	50,000
P6	80	300	10,000	50,000

. In each iteration of the adaptive sampling algorithm, each adaptive sampling method selects a new point from the same pool of candidate samples and uses the same test samples to evaluate the approximation accuracy. It is worth noting that the initial candidate and test samples of the same test function obeyed the same probability density function, and the samples’ generation and the MCS calculation were conducted using UQLab [31].

Test Results and Discussion

In this section, a general comparison between the AMSE and the other three adaptive sampling methods is presented.

Table 4. Results of mean.

Test Function	MEI	CV-Voronoi	MMSE	AMSE
P1	5.2933	7.0123	8.4442	0.2401
P2	1.1367	0.4463	0.3191	0.7125
P3	0.1077	3.1987	0.0873	0.4698
P4	0.0088	0.0202	0.0718	0.0936
P5	0.0843	0.0539	0.0232	0.0099
P6	0.1704	0.1654	0.2119	0.0935

,

Table 5. Results of standard deviation.

Test Function	MEI	CV-Voronoi	MMSE	AMSE
P1	0.0385	0.3849	5.0166	0.0989
P2	0.0733	0.0302	0.0070	0.0076
P3	0.0662	2.7603	0.1313	0.4936
P4	0.4897	0.0362	0.7148	0.5214
P5	0.6369	1.3097	0.0032	0.0647
P6	2.6664	3.7448	3.4027	3.0182

,

Table 6. Results of skewness.

Test Function	MEI	CV-Voronoi	MMSE	AMSE
P1	6.63228	11.54111	32.05191	1.17126
P2	0.35682	2.39839	1.10245	0.07698
P3	2.50817	69.03483	1.46564	0.44338
P4	1.47453	0.74755	12.66128	0.47580
P5	2.13077	0.37482	0.10402	0.27997
P6	14.84989	12.55071	22.71276	0.02850

and

Table 7. Results of kurtosis.

Test Function	MEI	CV-Voronoi	MMSE	AMSE
P1	2.84158	14.56858	30.11551	0.64745
P2	0.07045	0.10046	0.00992	0.0129
P3	0.25142	6.32713	1.11854	0.04331
P4	9.6449	4.61977	5.7637	0.10787
P5	2.56813	1.65662	0.42069	0.33926
P6	12.11533	0.13212	26.65362	0.14522

show the results of the first four orders of statistical moments computed by different adaptive sampling methods, and the data in the tables show the relative errors between the computed results of different adaptive sampling algorithms and the MCS simulation results. Note that the data in bold indicates the smallest relative error.

From Table 4 and Table 5, it can be seen that all adaptive sampling algorithms showed better accuracy in calculating the lower-order statistical moments, and the relative errors of all adaptive sampling algorithms were kept below 5%, except for the test function P1, which fully demonstrates the advantages of the adaptive agent model in the field of uncertainty analysis. It is worth noting that the relative error of the AMSE method was also lower than 5% when dealing with case P1.

As can be seen from Table 6 and Table 7, the proposed AMSE method showed a far smaller error in the calculation of higher-order statistical moments than the other methods, especially in examples P6 and P1. In example P5, the MMSE method gave the best results, but both the AMSE and CV-Voronoi showed comparable accuracy. Significantly, CV-Voronoi performed much worse than the other methods in calculating the skewness values; for example, in P3, which indicates that the CV-Voronoi method picked inappropriate sample points in the model adaptation process.

When dealing with high-dimensional, non-linear problems (i.e., test function P6), the skewness and kurtosis calculations of the MMSE were much worse than the other methods. Following the previous discussion, this is mainly because the MMSE method considers only mean square error information when selecting new sample points, making the distribution of the selected sample points in the design space have a tendency to be “space-filling”.

To further explore the characteristics of the proposed method, the convergence curves of different methods were plotted.

Figure 7 shows the results of the convergence curves of the first fourth-order statistical moments of the P1 test function obtained by different adaptive sampling algorithms. It can be seen that the MMSE method, which did not consider the local errors at the sampling points, performed the worst in all cases. The error of the CV-Voronoi method showed a steadily decreasing trend when calculating the lower-order statistical moments, but it had a significant error jump in the latter part of the adaptive process when calculating the higher-order statistical moments. The MEI and the proposed AMSE method had comparable convergence rates, but the final accuracy performance of the AMSE was better than that of the MEI. It is worth noting that all adaptive sampling methods showed good convergence trends in computing low-order statistical moments, and it is clear from combining Table 1, Table 2, Table 3 and Table 4 that all methods performed much better at computing low-order statistical moments than high-order statistical moments in terms of accuracy. Therefore, only the convergence curves of higher-order statistics are plotted in the subsequent examples.

As can be seen from Figure 8, the MMSE method showed the best convergence speed in calculating the statistical moments of skewness of the uncertainty response. It significantly reduced the relative error once 20 sample points were added. Still, its final convergence accuracy was worse than the other methods, because it did not consider the local error information of the sample points. When calculating kurtosis, all methods had comparable convergence speeds.

Figure 9 shows the convergence curve of test function P3, and it can be seen that the convergence speed and final accuracy of CV-Voronoi were the worst, and its relative error showed an abnormal rising trend after adding the 85th sample point, which indicates that the CV-Voronoi method selected unsuitable sample points when dealing with test function P3.

It can be observed from Figure 10 that all the methods showed large error fluctuations in the test function P4, with the MMSE showing the most drastic relative error change, while the AMSE showed a good convergence trend after adding 70 sample points.

As can be seen from Figure 11, the AMSE and CV-Voronoi were better than other methods for problems of medium dimensionality. Both the MEI and MMSE showed a sudden increase in error when adding the 70th sample and a sudden decrease in error when adding the 150th sample; this sudden change in model performance indicates that both methods significantly reduced/increased the amount of information obtained from the sample by adding a new sample, thus reflecting that MEI and MMSE are not good judges of the amount of information in each candidate sample point when dealing with this problem.

As shown in Figure 12, the relative errors of AMSE and CV-Voronoi method gradually decrease as the sample points increase in the face of the high-dimensional and highly non-linear problems (P6). While CV-Voronoi exhibited large error fluctuations at the beginning of the model adaptation, and AMSE performed more smoothly and had the best final accuracy. It is worth noting that MMSE and MEI had better accuracy performance when a small number of sample points were added, but with the addition of sample points, they did not make the accuracy decrease steadily; instead, the accuracy performance became worse and worse in the continuous fluctuation, which shows that MMSE and MEI do not deal with highly non-linear problems well.

Altogether, the proposed AMSE method showed the best accuracy and convergence rate when dealing with the uncertainty analysis of high-dimensional test functions; when dealing with low and medium-dimensional test functions, the AMSE provided superior accuracy and comparable convergence rates.

5. The Overhung Rotor System as an Engineering Example

To further verify the effectiveness of the proposed method, it was applied to the uncertainty analysis of an overhung rotor system to calculate the first four orders of statistical moment information of the system’s peak response past the first-order critical speed under the action of random parameters.

The overhung rotor system has flexible support at both ends, where the flexible rotor shaft is 1.5 m long and 0.05 m in diameter; it is shown in Figure 13. The thickness and diameter of the rigid disc are denoted as T and D, respectively. Bearings 1 and 2 are reduced to two anisotropic linear spring damping coefficients with the same characteristics and are located at the leftmost and 2/3 of the span of the rotating shaft, in that order. In this study, only the main bearing characteristics were considered, and the characteristic coefficients $K_{mn}$ and $C_{mn}$ ($m=1,2$ is the bearing number; $n=x,y$ is the direction of the main bearing characteristics) were used to represent the stiffness and damping coefficients, respectively. In addition, the material parameters involved in the rotor shaft and the stiffness disc, such as the modulus of elasticity, Poisson’s ratio, and density, were denoted by E, $\mu$, and $\rho$, respectively. The rotor’s transient startup stochastic dynamics equation can be expressed as [32]:

$$\mathit{M}(\mathit{X})\ddot{\mathit{\delta }}(\mathit{X},t)+[\mathit{C}(\mathit{X})+\dot{\theta }(t)\mathit{G}(\mathit{X})]\dot{\mathit{\delta }}(\mathit{X},t)+\mathit{K}(\mathit{X})\mathit{\delta }(\mathit{X},t)=\mathit{F}(\mathit{X},t)$$

(20)

$$\theta (t)=a{t}^2+bt+c$$

(21)

where M, C, G, and K are the mass, damping, gyroscopic, and stiffness matrices of the rotor system, respectively; $\dot{\theta }(t)$ and $\theta (t)$ are the rotor angular velocity and rotor angular displacement, respectively; a is the rotor starting acceleration; b and c are the rotor angular velocity and angular displacement at $t=0$, respectively; F is the synchronous unbalance force vector caused by the rigid disc unbalance; $\mathit{\delta }$ is the unknown global displacement vector; and $\mathit{X}={\left[X_1,X_2,\cdots ,X_N\right]}^{\mathrm{T}}$ is a random vector consisting of N random input variables. Solving Equations (20) and (21) yields an expression for the corresponding random response quantity:

$$\mathit{\delta }(\mathit{X},t)=\left\{\begin{array}{c}\mathit{\delta }|\begin{array}{c}\mathit{M}\ddot{\mathit{\delta }}+(\mathit{C}+\dot{\theta }\mathit{G})\dot{\mathit{\delta }}+\mathit{K}\mathit{\delta }=\mathit{F}\\ \mathit{X}\in f_X(\mathit{x})\end{array}\end{array}\right\}$$

(22)

where $f_X(x)$ is the joint probability density function of the random variable X. Here, only the random variables are considered to be independent of each other, and each random variable is subject to a normal distribution. Their specific parameters are shown in

Table 8. Statistical information on the random variables.

Variable	Means	Standard Deviation
Elastic Modulus $E/P_a$	$2.11\times {10}^{11}$	$2.11\times {10}^{10}$
Poisson’s ratio $\mu$	$0.30$	$0.03$
Density $\rho /(\mathrm{kg}\cdot {\mathrm{m}}^{-3})$	$7810$	$781$
Disc diameter $D/m$	$0.250$	$0.025$
Disc thickness $T/m$	$0.040$	$0.004$
x-direction stiffness of bearing 1 $k_{1x}/(N\cdot {\mathrm{m}}^{-1})$	$1\times {10}^7$	$1\times {10}^6$
x-direction stiffness of bearing 2 $k_{2x}/(N\cdot {\mathrm{m}}^{-1})$	$1\times {10}^7$	$1\times {10}^6$
x-direction damping for bearing 1 $c_{1x}/[(N\cdot S)\cdot {\mathrm{m}}^{-1}]$	$4\times {10}^5$	$4\times {10}^6$
x-direction damping for bearing 2 $c_{2x}/[(N\cdot S)\cdot {\mathrm{m}}^{-1}]$	$4\times {10}^5$	$4\times {10}^6$
Imbalance $f/(\mathrm{kg}\cdot \mathrm{m})$	$1\times {10}^{-3}$	$1\times {10}^{-4}$

.

The number of initial experimental designs was set to 100 (10N), with the stopping criterion set to the maximum number of sample points added (400), among which the MCS (sample size of ${10}^5$) was used as the reference result for the calculation of the statistical moments of each order. The relative errors of different adaptive sampling algorithms for calculating the first-four statistical moments are given in

Table 9. Relative error of different methods.

	MEI	CV-Voronoi	MMSE	AMSE
Mean	0.8403	0.1896	0.1571	0.141
Standard Deviation	1.9916	1.1159	1.1782	0.1922
Skewness	9.2566	3.2339	5.0594	0.5524
Kurtosis	13.9278	12.4339	11.49696	1.4485

. Note that the data in bold indicates the smallest relative error.

From Table 9, it can be seen that, after reaching the stopping criterion, the best prediction was achieved using the AMSE method, which had the smallest relative error for the first fourth-order moments; the CV-Voronoi and MMSE methods showed comparable prediction accuracy in the face of low-order moments, but poor performance in the face of high-order moments; the MEI method performed the worst in the calculation of all statistical moments. It is worth noting that the relative errors of the AMSE method were much smaller than the other methods in calculating the kurtosis and skewness indicators, thus showing good prediction ability for higher-order statistical moments.

As can be seen in Figure 14, the MEI, CV-Voronoi, and MMSE methods all showed a good trend of decreasing error when faced with skewness and kurtosis metrics predictions until 150 sample points were added; however, there was a sudden increase in error during subsequent sampling. This sudden change in the performance of the model indicates that the amount of information obtained from the sample by the sampling method was significantly reduced by adding a new sample, which indicates to some extent that the MEI, CV-Voronoi, and MMSE methods did not discriminate the error information of the sample points well in the face of a high-dimensional, strongly non-linear rotor system. The proposed AMSE method, on the other hand, showed a good convergence trend, and the relative errors of both skewness and kurtosis prediction results steadily decreased with the addition of sample points.

Overall, the proposed AMSE method had a better advantage in the analysis of statistical moments in the face of random responses and had the best accuracy performance and comparable convergence speed compared to other adaptive sampling algorithms.

6. Conclusions

In this paper, an error-pursuing adaptive method based on BSVR was proposed for efficient and accurate uncertainty analysis. This adaptive method was improved by a new error-pursuing active learning function named AMSE, which guided the adaptive sampling of the BSVR metamodel’s DoE. To address the deficiency of the mean square error in characterizing the prediction error information of sample points, the AMSE active learning function adjusts the mean square error using the leave-one-out (LOO) cross-validation error, and the adjusted prediction variance information depends not only on the relative distance between sample points, but also on their errors.

To verify the effectiveness of this uncertainty analysis method, six numerical examples with different dimensions were investigated, and the results were compared in detail with other frequently used error-pursing active learning functions, such as the MMSE, MEI, and CV-Voronoi. The results showed that the proposed method had better accuracy and comparable convergence speed, in addition to exhibiting better prediction of the higher-order statistical moments. Furthermore, a single-disk cantilever rotor system was studied, which was subject to 10 uncertainties. This application was used to demonstrate the computational efficiency of the method when applied to the rotor system. It was shown that the method had a significant accuracy advantage with the inclusion of the same sample points.

Overall, the proposed AMSE error-pursing active learning function performed better in terms of accuracy and convergence speed than others. Moreover, an adaptive metamodel constructed based on this method shows promising applications in the field of uncertainty analysis.