Abstract
This paper deals with the formation control problem without collisions for second-order multi-agent systems. We propose a control strategy which consists of a bounded attractive component to ensure convergence to a specific geometrical pattern and a complementary repulsive component to guarantee collision-free rearrangement. For convergence purposes, it is assumed that the communication graph contains at least a directed spanning tree. The avoidance complementary component is formed by applying repulsive vector fields with unstable focus structure. Using the well-known input-to-state stability property a control law for second-order agents is derived in a constructive manner starting from the first-order case. We consider that every agent is able to detect the presence of any other agent in the surrounding area and also can measure and share both position and velocity with his predefined set of neighbours. The resulting control law ensures the convergence to the desired geometrical pattern without collisions during the transient behaviour, as well as bounded velocities and accelerations. Numerical simulations are provided to show the performance and effectiveness of the proposed strategy.
1. Introduction
Multi-agent systems have received much attention in the last decades because of their wide range of potential applications in situations where a single agent could not be effective enough, e.g., exploration, surveillance and rescue tasks, among others [1,2,3,4,5]. In order to design versatile systems that can achieve the mentioned tasks, a number of different issues have been studied in this research area: for example, consensus, trajectory tracking, formation control, coordination, synchronization and so forth [6,7,8,9,10]. In formation control, a group of agents is meant to be driven to a prescribed spatial pattern. Depending on the constraints imposed in the ability to measure or share information with other agents, those geometrical patterns could be reached up to translation, rotation, scaling or a combination of them. In terms of the sensing capability and interaction among agents, previous results in formation control algorithms can be divided into three main categories: position-, displacement- and distance-based schemes [7]. In position-based control strategies, agents usually are able to determine their absolute position with respect to a global reference frame. Communication among agents is not strictly necessary, but the whole performance can be enhanced if coordination is regarded. As a result, the desired patterns are reached with proper scale and orientation [11,12,13]. Displacement-based control schemes require the agents to measure relative positions of their neighbouring agents with respect to a local frame attached to each agent which has to be aligned with the global reference frame. Communication among agents needs to include at least a spanning tree, and the desired formation is specified by a set of relative displacements among agents. Under this approach, the resulting formation is invariant up to translation [10,14]. Distance-based strategies treat the desired formation as a set of inter-agent distances which can be expressed in local coordinates where the local frames are not necessarily aligned with respect to the global frame. Interactions among agents must be enhanced in order to ensure the agents converge to the correct formation by using rigidity, angle rigidity or signed area approaches [15,16,17,18]. The aforementioned results have been developed by regarding a number of mathematical models, such as single or double integrator, unicycle-type robots, high-order linear agents, as well as a variety of constraints as intermittent communication, time delay, input saturation, quantization and digitization, among others [18,19,20,21,22,23].
One important issue that arises independently of the control objective and approach for solving the formation control problem is to guarantee that collisions will not occur among agents. Different schemes have been proposed for multi-agent systems regarding several mathematical models, communication topology and agents’ capabilities to either receive or transmit information and sensing equipment. In the same way, there are different works regarding collisions between agents or collisions against obstacles, in [24,25,26,27,28,29,30,31,32,33,34].
A common approach to avoid collisions is based on the use of repulsive vector fields designed as the negative gradient of an artificial potential function. The main advantage of this approach is the simplicity in the design process, but it can lead to undesired equilibrium points where the agents could get stuck [25,26]. A immediate remedy to guarantee that the agents can escape from unwanted local minima is to add a controlled perturbation to the overall control input [26]. In [28,29], velocity information was used to modify the avoidance functions in order to be more energy-efficient and to generate faster and smoother trajectories. Many strategies under this approach have been designed in such a way that the repulsive vector fields grow indefinitely as the distance between agents tends to zero. This results in high magnitude control inputs that might be unrealistic for physical agents to achieve. Furthermore, if physical dimensions of agents are taken into account, collisions could eventually occur. Therefore, modified potential functions are proposed to comply with a minimum safety distance between any pair of agents and bounded control input magnitude in [26,32]. A recent work proposed the use of the rotation matrix to modify the vector fields depending on the relative position of the agent with respect to obstacles [30]. In contrast, in [33], the shape of obstacles are taken into account to guarantee motion without collisions. However, both algorithms were developed for nonholonomic vehicles. An alternative strategy to the collision avoidance problem was formulated in [27], where the agents are labelled according to a priority level which provide solution to the conflicts between agents. The priority in this scheme varies for leader and followers. An interesting strategy was proposed in [34], where an adaptive control component was used to ensure free-collision convergence. A novel approach was reported in [31], in which barrier functions are applied to ensure input and velocity constraints and collision avoidance requirements.
In [35], a collision avoidance algorithm based on reactive repulsive vector fields was proposed. This work was proposed to solve the formation control problem without collisions for first-order agents by applying repulsive vector fields with unstable focus structure. This technique, first reported in [36], considers that there exists an unstable focus centred at the position of any other robot or obstacle. This mechanism is activated when agents are near enough to each other. The repulsive vector fields are turned on/off in a discontinuous manner which could provoke the appearance of chattering phenomenon. Finite-time convergence to the desired formation, as well as finite-time for solving the conflicts between agents, were achieved. Unlike many previous works, the repulsive vector fields proposed in [36] cannot be derived as the gradient of any potential function. Then, in [37], the switching control strategy was modified by using continuous switching functions to ensure a smooth transition between the components of the control law and conditions to guarantee asymptotic convergence to the desired formation were derived. It is important to notice that the convergence component is bounded by considering saturation, while the collision avoidance component is, by definition, bounded. This results in a bounded control algorithm. Moreover, this strategy has been shown to be effective in real-time experiments [38]. Additionally, in [37], a detailed analysis of the repulsive vector fields leads to minimum gain parameters such that the collision avoidance is guaranteed.
In this paper, we propose a solution to the formation control problem without collisions for second-order agents by generalizing the algorithm in [35]. Regarding the second-order agents as a cascade of two single integrators, we apply the mentioned control law to first integrator in order to ensure asymptotic stability of the position error. Then, taking the velocity as a virtual control, we find the expression of acceleration signal which are, indeed, the control input. A cascaded system approach is utilized to show that the interconnected systems is globally asymptotically stable. We consider that every agent is equipped to measure the relative position and velocity of a predefined set of neighbours. For convergence purposes, it is assumed that the communication among agents contains, at least, a spanning tree. Even more, each agent is able to detect the presence of any agent in the surrounding area and share both position and velocity with agents into their sensing region. The convergence component of the algorithm is bounded by a saturating function while the repulsive vector fields are smoothly activated/deactivated. The resulting control law ensures the convergence to the desired geometrical pattern without collisions during the transient behaviour and bounded velocities and control inputs. The use of repulsive vector fields with unstable focus structure provides a relatively simple tool to avoid undesired equilibrium points. Moreover, the algorithm can be scaled in case that agents were added or removed with the only requirement of existing a spanning tree in the nominal communication scheme.
The remainder of this paper is organized as follows. In Section 2, some basic concepts about graph theory and some definitions are reviewed. We state, in detail, the problem and the control objective in Section 3. Our main results are provided in Section 4 and the corresponding simulation results to validate the performance of the proposed strategy are presented in Section 5. Finally, in Section 6, we list some conclusions and perspectives of our future work in this research line.
2. Preliminaries
In this section, we provide some concepts and definitions that will be useful throughout the rest of the paper.
2.1. Graph Theory
The communication among a set of agents is described by a formation graph , which consists of a set of vertices corresponding to each agent and a set of edges , which denotes the agent receive information about ; the agent is called the parent node and is, respectively, the child node; finally, is a set of constant vectors that represent the relative desired position of agent with respect to its neighbours. A formation graph is undirected if implies that . That is, the communication is bidirectional. On the other hand, a formation graph is said to be directed if implies that . If a formation graph is neither directed nor undirected, it is called mixed. There exists a path between the vertices and if there is a sequence of edges for some . A directed tree is a directed graph in which every node has exactly one parent, except for one single node, called the root. The root has no parent and has a directed path to every other node. A directed spanning tree of a directed graph G is a directed tree involving every node in G. The Laplacian matrix associated with a formation graph G is given by
where is the degree matrix defined as , is the number of edges directed to , and is the adjacency matrix of G defined as follows
2.2. Saturating and Switching Functions
Definition 1.
Let be the set of the saturating functions which is composed of all the real functions which satisfy the following conditions
- ;
- for some ;
- , ;
- .
Then, it is said is a saturating function parameterized by r.
Definition 2.
Let Ψ be the set of smooth switching functions which is composed of functions satisfying the next properties
- if ;
- if ;
- if ;
- .
where .
2.3. Input-to-State Stability
Definition 3.
The system
is said to be input-to-state stable (ISS) if there exist a class function β and a class function γ, such that for any initial state and any bounded input , the solution exists for all and satisfies
Lemma 1 ([39]).
Let be a continuously differentiable function such that
, where , are class functions, ρ is a class function and is a continuous positive definite function on . Then, the system (1) is input-to-state stable with .
3. Problem Statement
Consider the set consisting of N mobile agents at the plane. The position coordinates of every robot are specified by , . The agent is modelled by the double integrator
where and represent the velocity and acceleration along the X and Y axes, respectively. We assume that robot can sense continuously. The relative position and velocity of a specific subset of robots are determined by the corresponding formation graph G. Therefore, the desired position of robot is defined as
where is the cardinality of and , defines the geometrical pattern to be reached. In addition, we assume that each agent is able to detect and measure the relative position and velocity of any other agent within a circle of radius D. This region is called the sensing region and is assumed to be the same for all robots. The set of agents into the sensing region is denoted as . Analogously, the collision region is defined by a radius d, which is the smallest allowed distance between any pair of agents. If some agents get closer than this value, it is considered that they collide with each other because of their physical dimensions.
3.1. Control Objective
The control goal is to design distributed controllers , , such that:
- (i)
- The agents reach the desired relative positions, that is,
- (ii)
- There are no collisions among agents. Even more, the agents remain at some predefined distance d from each other, that is, , , ;
- (iii)
- Once the agents achieve the desired formation, the geometrical pattern does not move from its current location any more, i. e., , .
3.2. Position Error Dynamics
Define the position error for each agent as the difference between the current and the desired position,
Then, the position error dynamics is given by
Given (7), the last equation can be written in terms of velocities. The whole system in vector form is
where is the Laplacian matrix, is the identity matrix, ⊗ denotes the Kronecker product, , and
4. Control Design
In this section, we solve the formation control problem without collisions in two stages. First, we propose a control law attending only the convergence issue. Then, we propose a complementary reactive control component which prevent agents from collisions.
4.1. Formation Control Strategy
In order to design a control law to achieve the aforementioned objective, we start by recalling the control law in ([37] Thm. 1), which was proposed for first-order agents and consists of a bounded control input
which applied to (7a). The closed-loop system in vector form takes the form
where , and . Indeed, it was proven that the error trajectories in (15) coverge to zero, implying that the agents reach their desired formation. Keeping this in mind and in view of (12), we can add and subtract the right-hand term of (15) into (12). Then, grouping conveniently, we have
where we have defined an auxiliary variable as
whose dynamics is given by
Using (12),
Theorem 1.
Proof.
First, we show that the subsystem (16) is ISS with as input. Then, if we have
In vector form, it becomes
Since every agent defines its desired position with respect to, at least, another agent, the matrix . If there exists a directed spanning tree in the communication graph, the Laplacian matrix has exactly one zero eigenvalue, say . This implies , while the rest of the eigenvalues have positive real parts, that is, , . Then, we can ensure that
Now, to prove asymptotic stability, consider the eigenvector associated to the zero eigenvalue, which has a value of Then, , which implies that in the equilibrium, the components are all equal, i.e., . Due to the properties of saturation functions, . On the other hand, there exists a left eigenvector such that and , [40]. In other words, there exists a linear combination of the position errors in such a way that
with coefficients not all equal to zero. Finally,
implies that , which means that only the trivial solution can identically ensure . Then, is asymptotically stable. Moreover, as the Lyapunov function candidate (22) is strictly increasing and radially unbounded, the origin is globally asymptotically stable (GAS). Now, we allow . Using the same Lyapunov candidate function, we get
The last expression can be written as
or, bounding the last right-hand term,
with . Then, according to Lemma 1, (16) is ISS with . Finally, by direct application of the control law (20), (19) becomes
which is not only GAS, but also globally exponentially stable. Recalling Lemma 2, a cascaded composition of an ISS subsystem as (16) and a GAS subsystem as (32) result in another GAS system. This implies that and the auxiliary variable as . As a consequence, from (17), we also notice that as . In summary, this implies that the agents reach the desired geometrical pattern and the whole formation remains stationary after achieving the formation goal. This concludes the proof. □
Once the formation control problem has been solved, it is of interest to implement the control law in each agent. Then, rewriting (20) in terms of the position and velocity errors, we have
where
The implementation of this control law in each agent is
4.2. Formation Control Strategy with Collision Avoidance
In order to enhance the applicability of the control law proposed in the previous subsection, we now take into account the possibility of collisions to occur while the rearrangement of agents. Following the same reasoning, we start from a control law designed for first-order agents inspired in the one reported in [37], given as
where are smooth distance-based switching functions which satisfy that for and for . This allows us to turn on/off the collision avoidance mechanism. is the distance between the i-th and the j-th agents. For designing this control law, every agent considers that there exists an unstable focus structure centred at the position of any other agent which ensures that the agents repel each other. The repulsive vector fields, which are given by the second right-hand term in (36), are designed by taking into consideration the relative positions between any pair of robots, when they are in their sensing regions. The relative position variables are defined as
Clearly, if an agent does not detect any other agents into its sensing region, the repulsive component is not necessary. In this case, the repulsive component should be turned off, i.e., if the agents are far enough from each other, the second right-hand term in (36) vanishes. This implies that, in vector form, the control law reduces to the one applied in (15). In [41], it was shown that (36) and a gain , properly selected, solve the problem for first-order agents. It is also proved that, even if the repulsive vector fields are applied when the agents are at a distance D, the agents could get closer, but never at a distance smaller than d. Once the agents leave their sensing regions, their reactive components are deactivated and they proceed with their motion to the respective desired locations.
4.3. Reduced System
In the design of a collision avoidance complementary control law for second-order agents, we start by considering a reduced system consisting of two first-order agents with bidirectional communication between them. The closed-loop system for this reduced set, is given in (40) by applying (36), where we denote the distance simply by .
is the matrix which provides the unstable focus behaviour.
We can assume without loss of generality that every agent has the same range of measurement, then , and (40) becomes
Remark 1.
It is worthwhile to point out that a well-defined desired geometric pattern is such that the distance among the agents is larger that the minimum one, that is, at the desired formation, no conflicts between agents exist. Then, at the origin of (41), the second right-hand term vanishes.
Then, following the same procedure applied in the previous subsection, and adding and subtracting the right-hand side of (41) to (12), we have
where
and a new auxiliary variable is defined as
whose dynamics is given by
If the control input is selected as
the -subsystem reduces to
Then, once that the control law (46) is applied, the cascaded system (42)–(47) could be analysed as in Theorem 1. Since the -subsystem is clearly GAS, it remains to show that -subsystem is ISS, which can be done by using the stability theory for perturbed systems. Indeed, if we let , (42) can be focused as (15) perturbed by the term . As mentioned in Remark 1, this term is a vanishing perturbation at the desired formation.
4.4. General System
If we consider a set of N first-order agents along with the formation control strategy (36), the closed-loop system (42), in vector form, can be expressed as
where F is defined as in (39). The matrix , which depends on the distance between every pair of agents and models the conflicts among agents, is described by
Remark 2.
As it was assumed, every robot is able to detect other robots in a certain radius, which ensure the matrix Ω is a symmetric Laplacian-like matrix if only the agents in conflict are regarded.
The position error dynamics (12) in combination with (48) is
where
and a general auxiliary variable was defined as
Since the time derivative of the auxiliary variable is
the control input could be selected as
which implies that the dynamics of the auxiliary variable becomes
Now, we are ready to state our main result.
Theorem 2.
Consider the system (50) and (55), and assume that the communication graph contains at least a directed spanning tree. Then, using the control law (54), the set of agents reaches the desired geometrical pattern without collisions. Once the desired formation is achieved, the whole pattern does not move from its current position. Even more, the agents remains for all time at a distance greater than or equal to a predefined bound d.
Proof.
As mentioned before, the second right-hand term vanishes when the agents are far enough from each other, including when they reach the desired formation; that is, . Then, regarding (51), we have
with . Equation (56) could be considered as (15) perturbed by the term , which is fully described in (51) and could be bounded as in (57). According to [39], since vanishes at the origin of the error dynamics, if the parameters are selected properly, the system is still GAS. In [41], it has been shown that (56) is GAS when applying (36) and conditions in the selection of parameters and were derived. If we let and recall the same Lyapunov function candidate (22), we have
where and . Then, (50) is ISS, which, along with (55), implies that the cascaded system remains GAS even when the complementary control component is applied. As a conclusion, the formation control problem with collision avoidance is solved satisfying the control objective stated above. □
5. Simulations
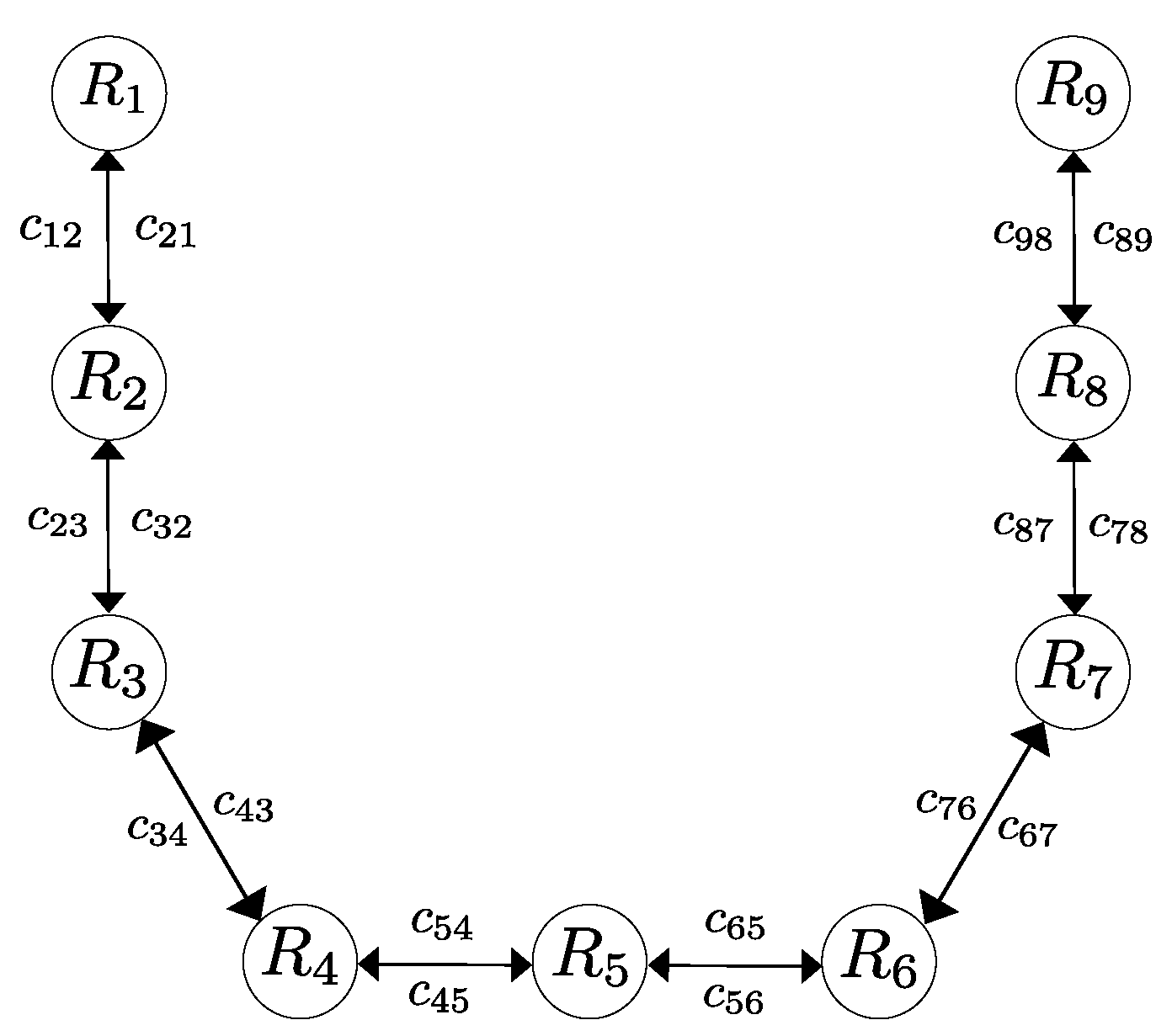
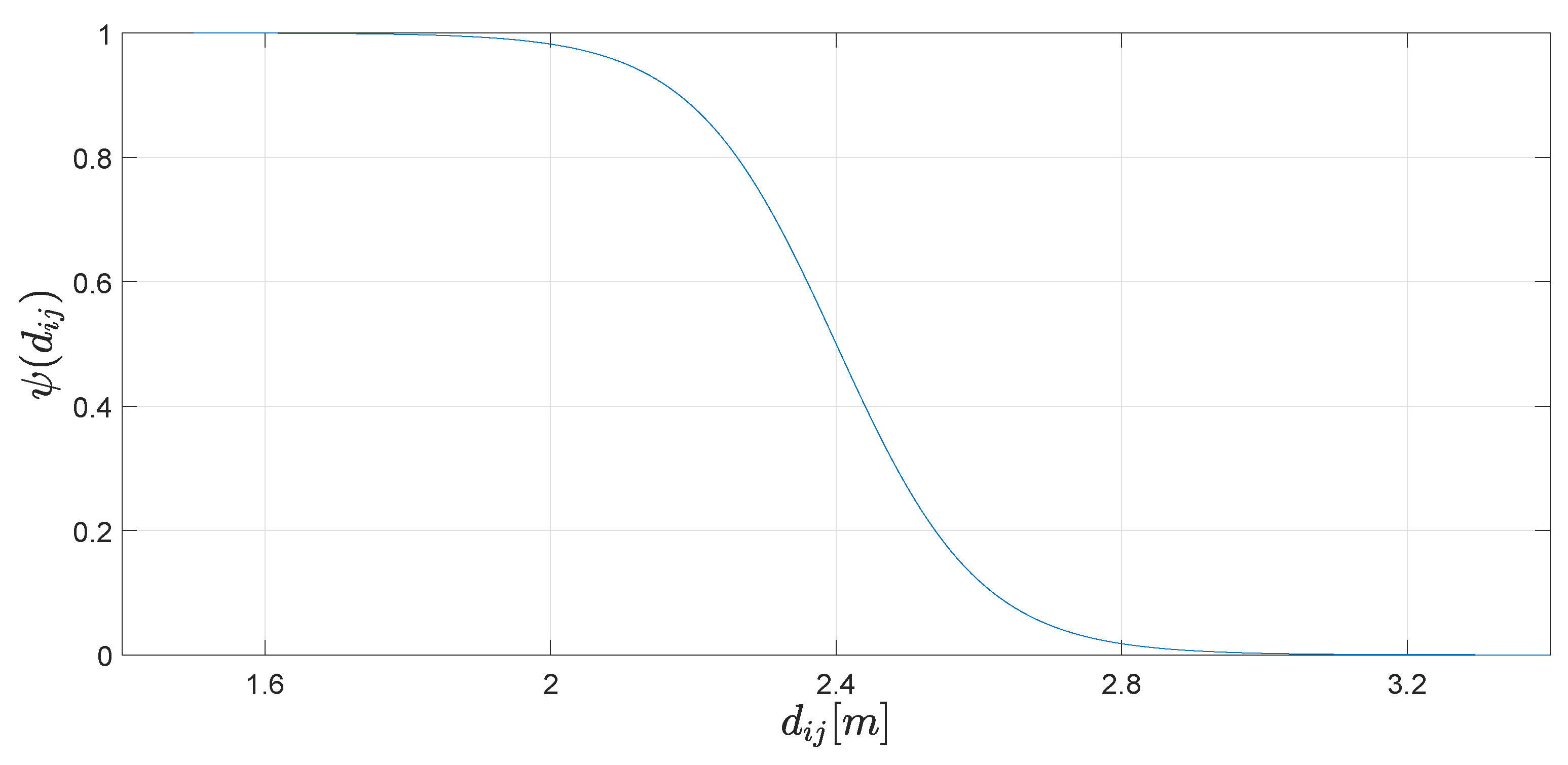
In this section, we present the results of a series of simulations carried out to show and evaluate the performance of the proposed control strategy. To illustrate the effectiveness of the control law, we study a system composed of nine agents whose objective is to reach a sequence of desired geometrical patterns which are shown in Figure 1, Figure 2, Figure 3 and Figure 4 where the communication links are shown as well. The parameters used for this example are , and , and the sensing and collision radius were and , respectively, i.e., the minimum allowed distance between any pair of agents is 2 m and each agent is able to detect any another robots within a range of 2.8 m. The switching function that enables the repulsive vector fields is given by
with and . This exhibits the behaviour depicted in Figure 5 and gives a good approximation to the properties of the switching functions defined previously. The minimum distance between agents one they reach the desired formations is about 3.5 m. This distance ensures these patterns are reachable. The parameters of the simulation are summarized in Table 1.
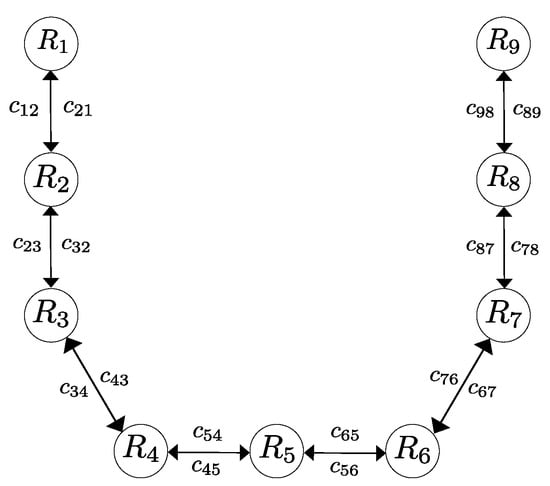
Figure 1.
First desired formation.
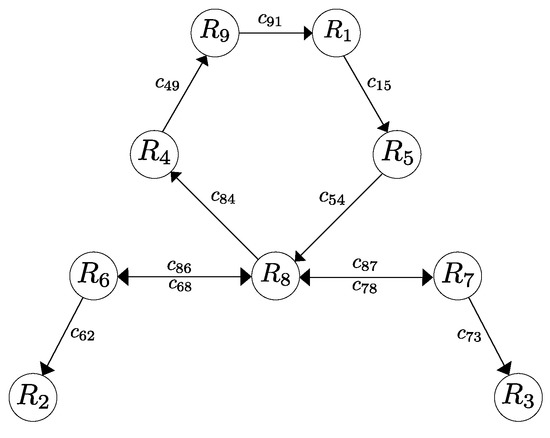
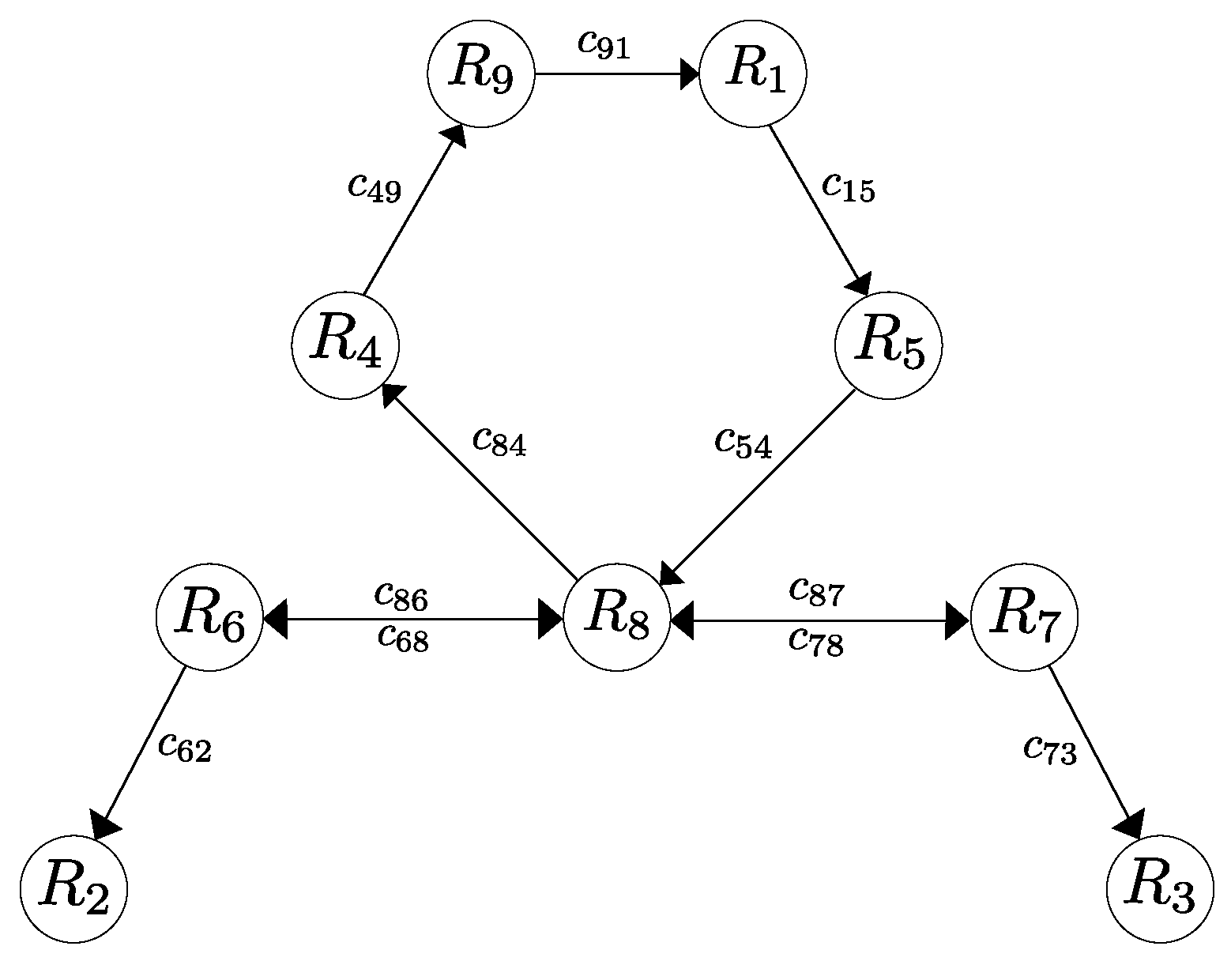
Figure 2.
Second desired formation.
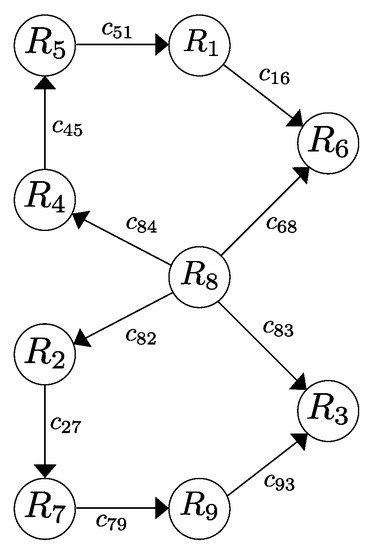
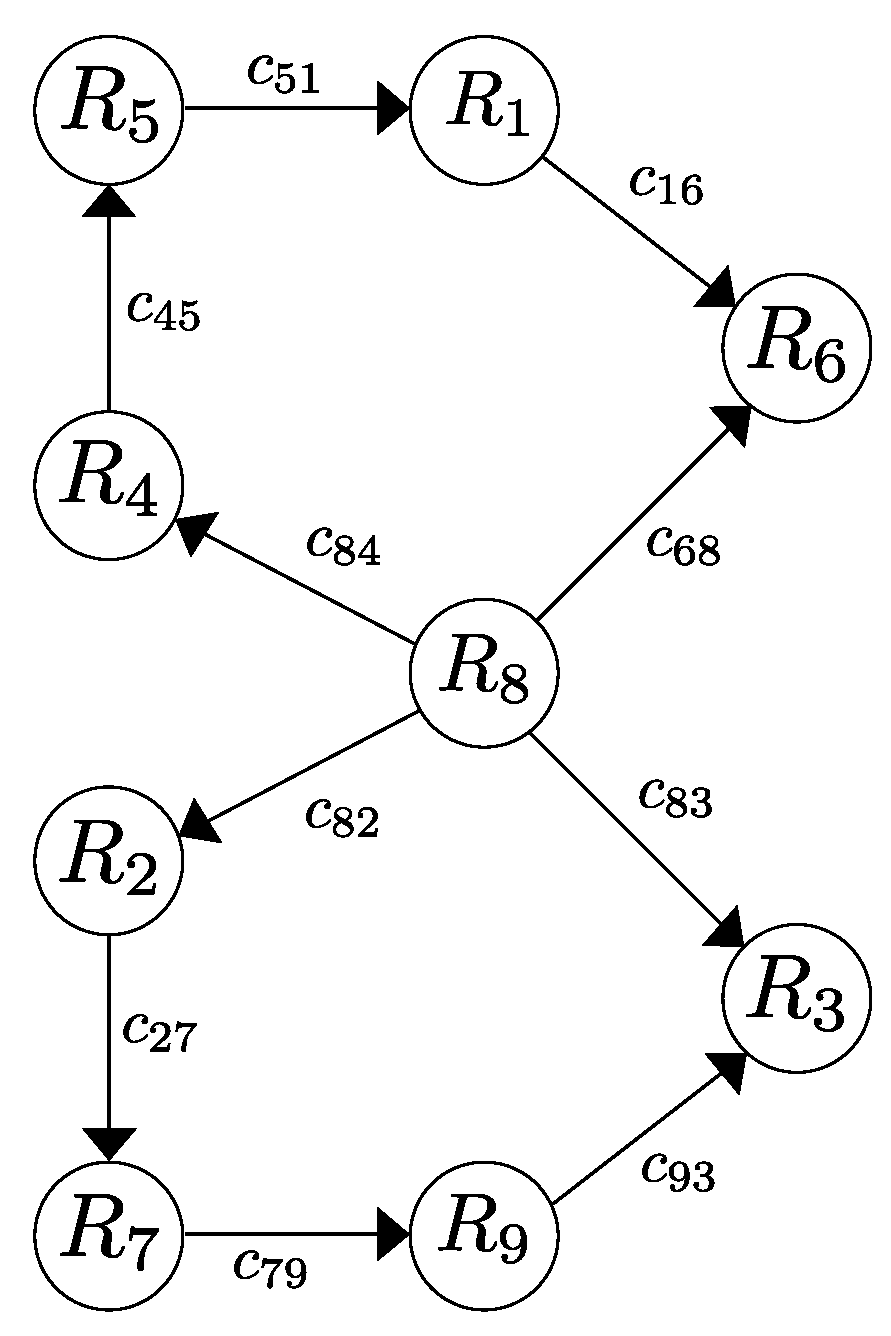
Figure 3.
Third desired formation.
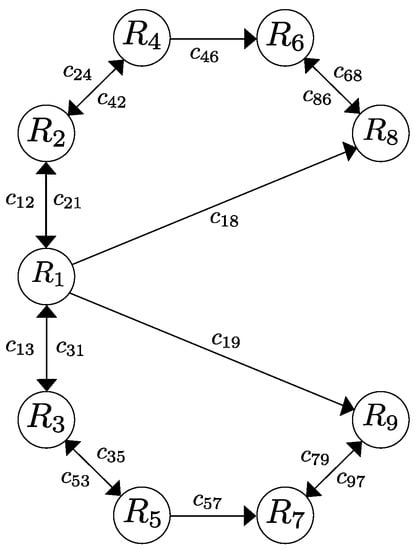
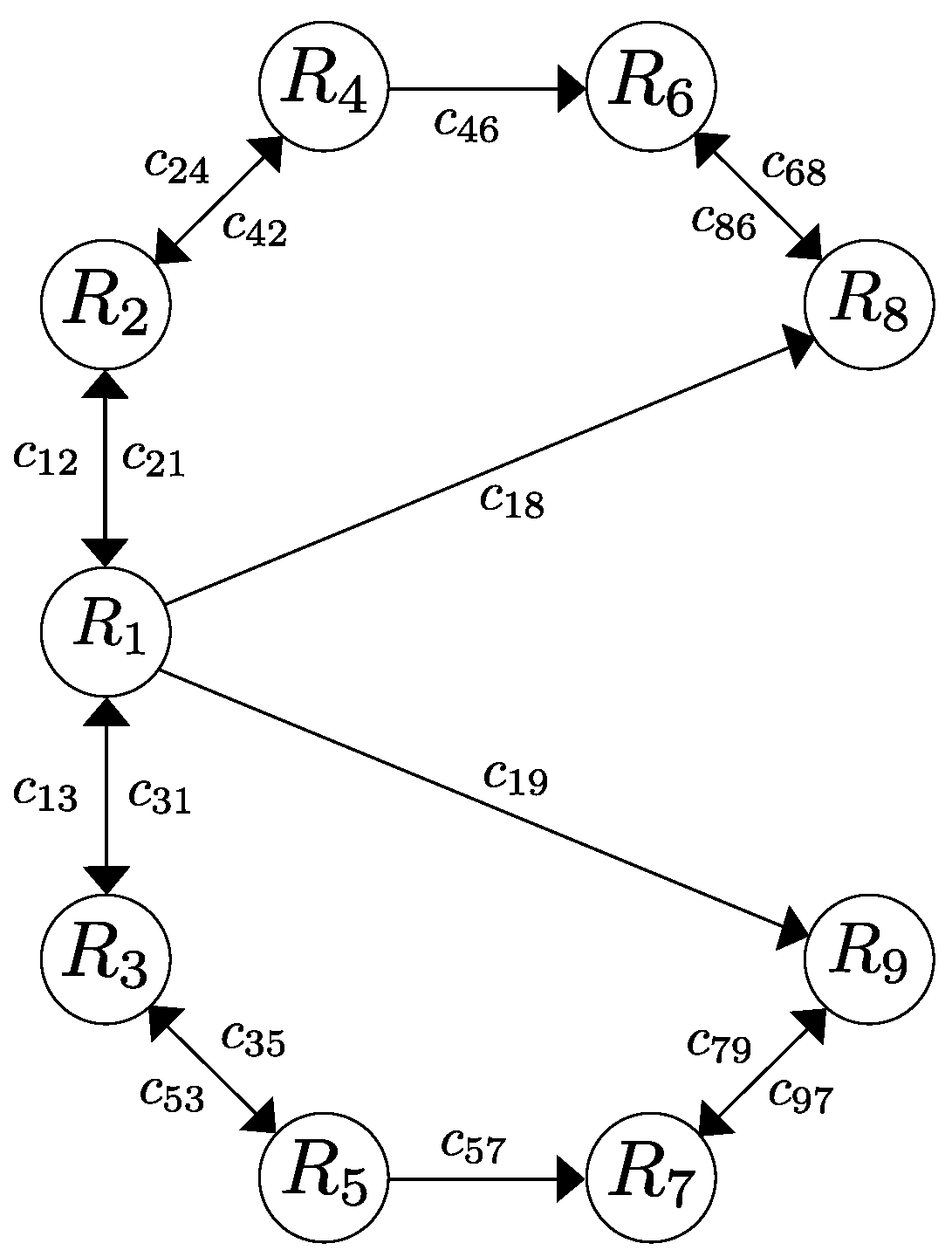
Figure 4.
Fourth desired formation.
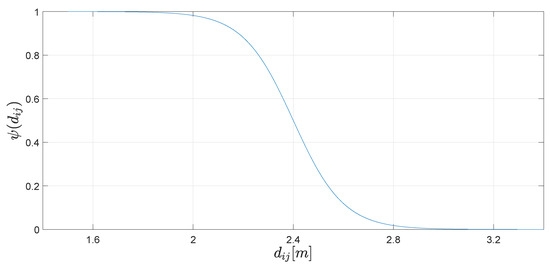
Figure 5.
Switching function to turn on/off the repulsive vector fields. A function which satisfy conditions given in Section 2, with the same behaviour, could also be used instead of the proposed one.

Table 1.
General parameters used for simulation.
5.1. Desired Formations
For this simulation, the nine agents are initially located at , , , , , , , and , all with zero velocity.
The desired formations are parametrized by a scale factor metersm such that the set of constant vectors that specify the first pattern are , , , , , , and .
The second desired pattern is defined by the vectors , , , , , , , , , and .
In the same way, the third formation to be formed is given by , , , , , , , , and . It is important to notice that, in this case, the communication is reduced to contain a directed spanning tree rooted in robot . Moreover, we consider in this case that the robot is not able to apply the repulsive vector fields, i. e., the agent remains stationary while the rest of them get in formation with respect to it.
Finally, the last desired configuration is determined by , , , , , , , , , , , , , , and .
5.2. Simulation Results and Discussions
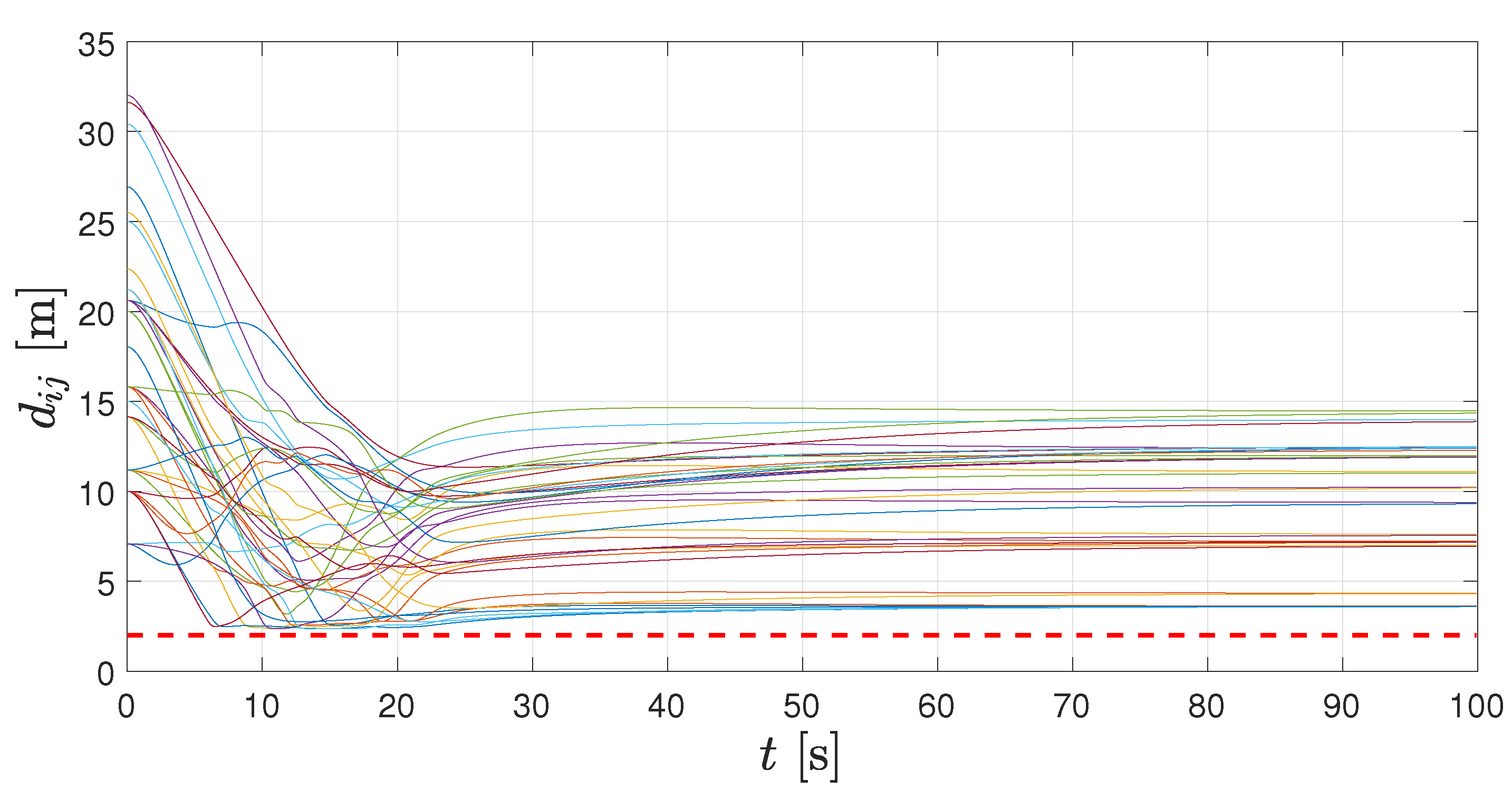
In Figure 6, Figure 7 and Figure 8, we show the results up to the first 100 s of simulation. In Figure 6, the distances among any pair of agents are depicted. There, a horizontal dashed line represents the minimum allowed distance between them. Clearly, no pair of robot get closer than this predefined bound and, even more, the conflict among agents are solved after about 30 s.
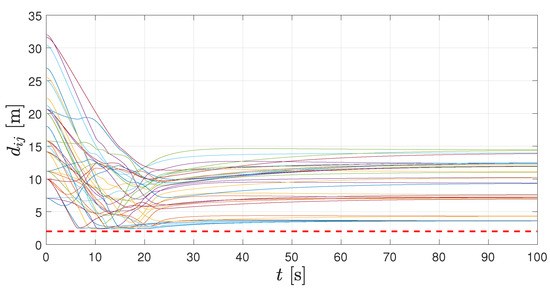
Figure 6.
Distancesbetween any pair of agents from 0 [s] to 100 [s]. The dashed line indicates the minimum allowed distance.
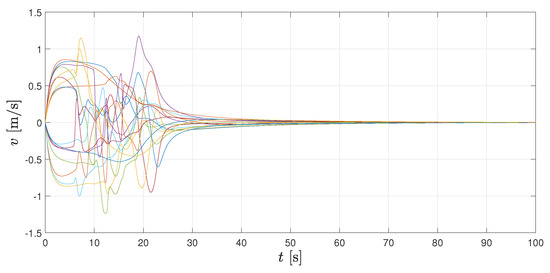
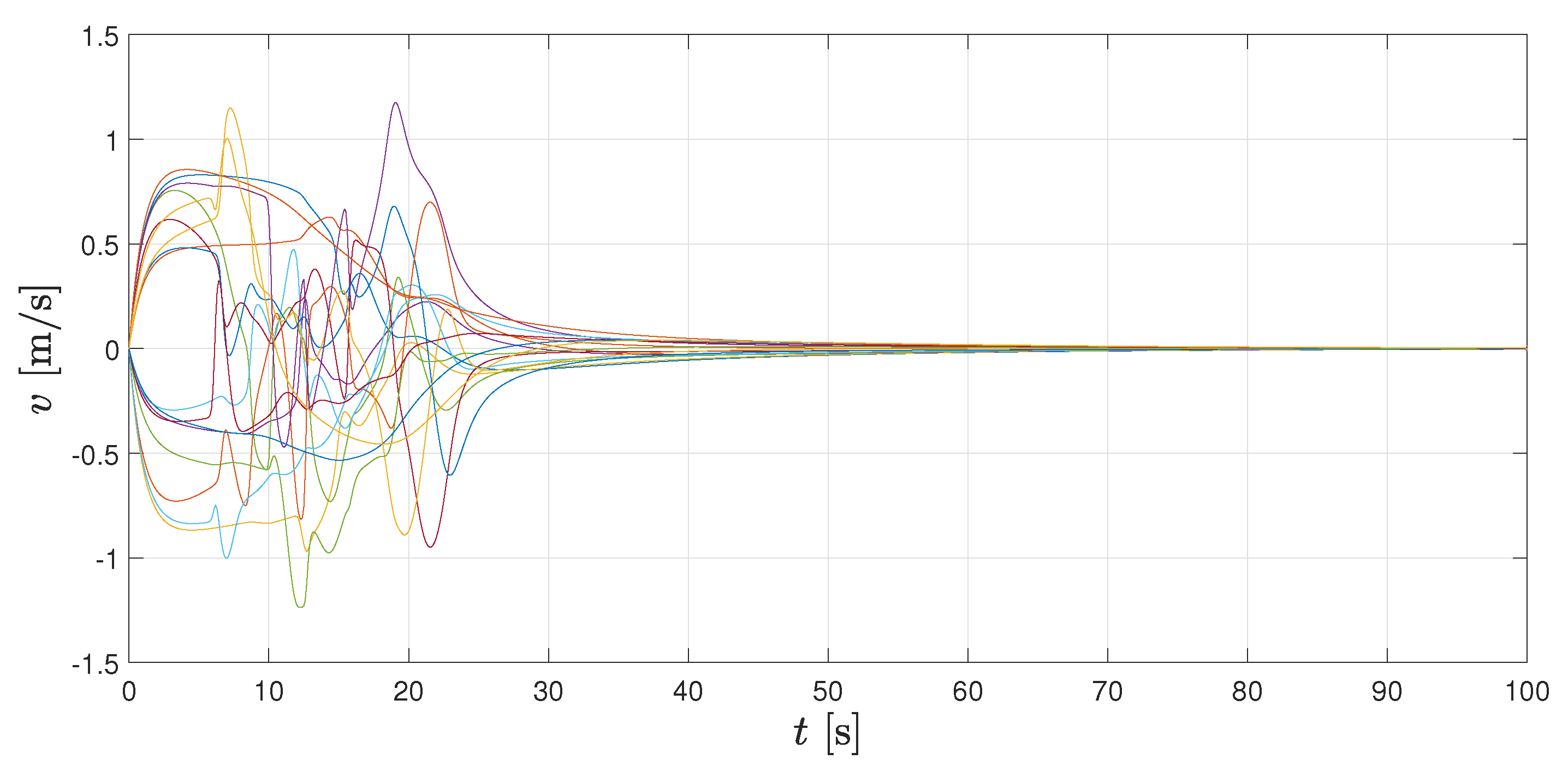
Figure 7.
Velocities from 0 [s] to 100 [s].
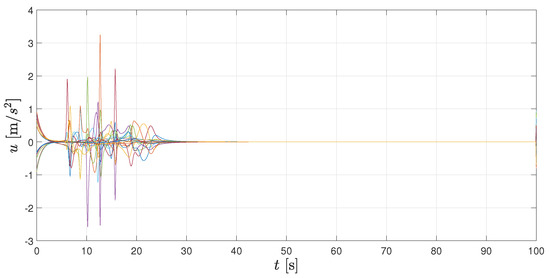
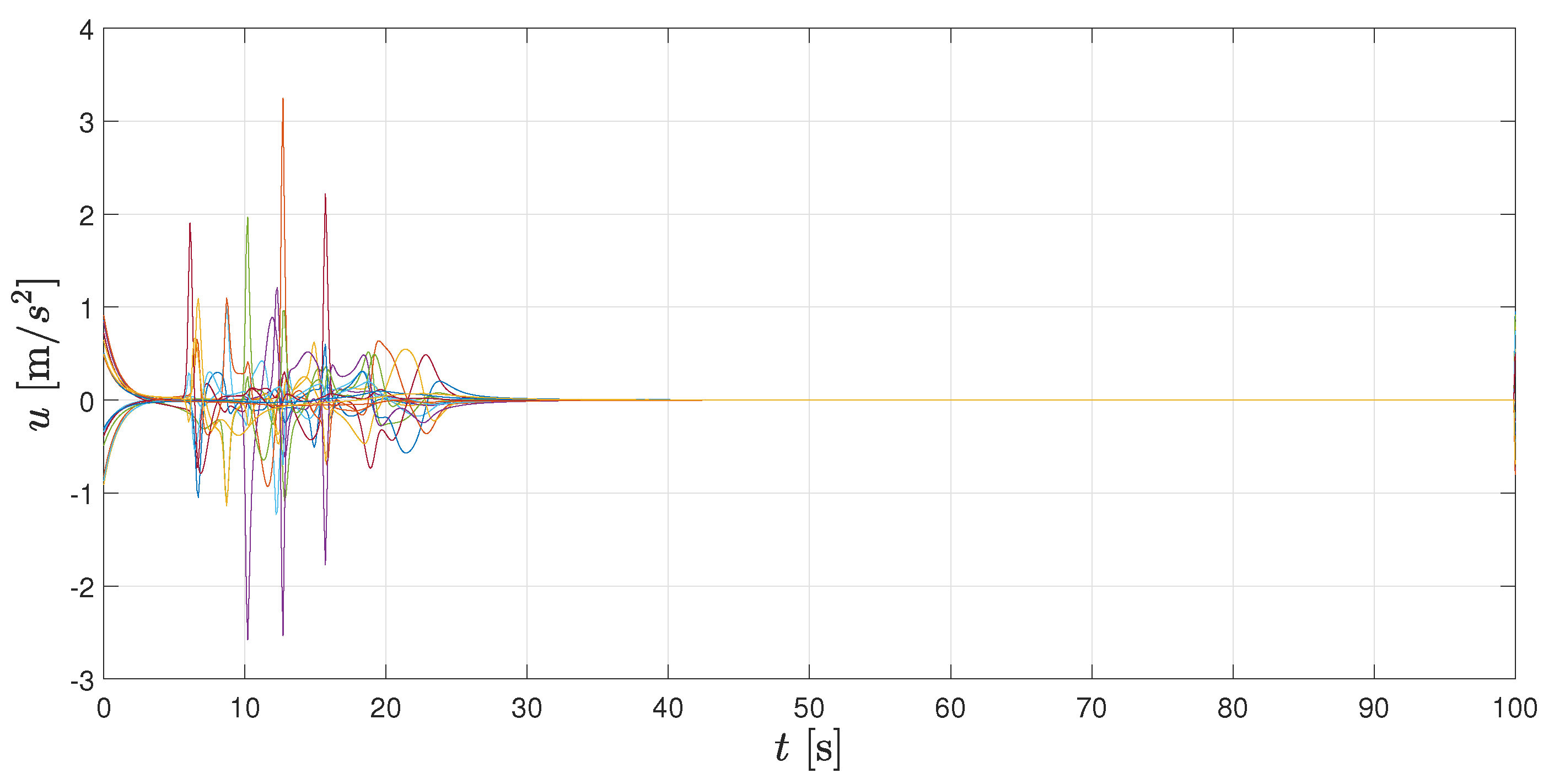
Figure 8.
Control inputs from 0 [s] to 100 [s].
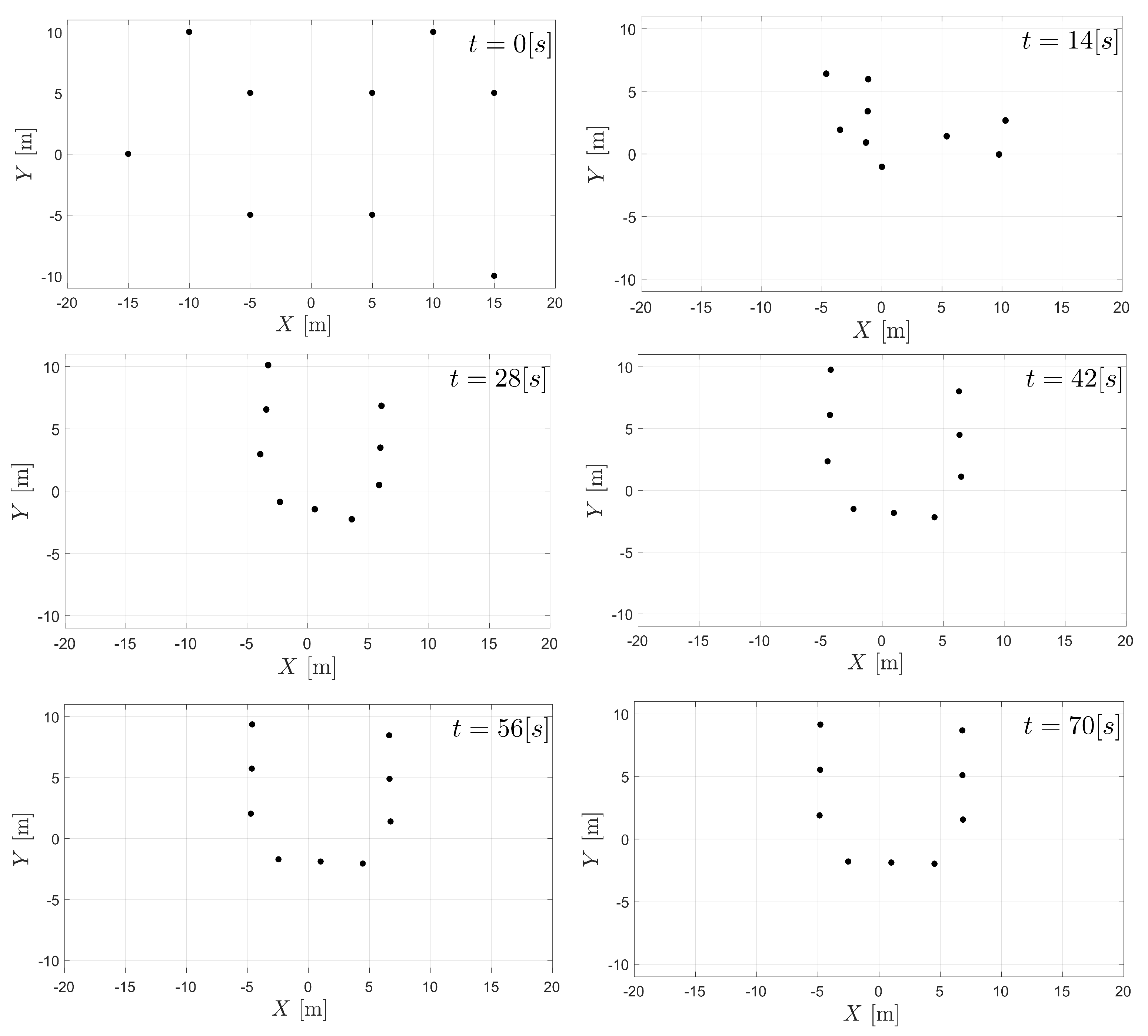
Additionally, in Figure 7 and Figure 8, velocity and control signals are illustrated, respectively. As it can be seen, velocities tend to zero, which implies that the whole formation stays at its current location once the geometrical pattern is reached. Both velocities and accelerations remain bounded during the transient period. Figure 9 shows the spatial configuration of agents at different times, which helps to illustrate the convergence to the desired formation.
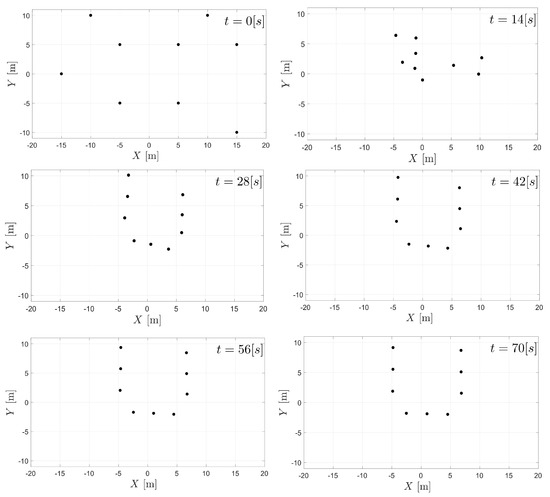
Figure 9.
Spatial distribution of agents at some specific times.
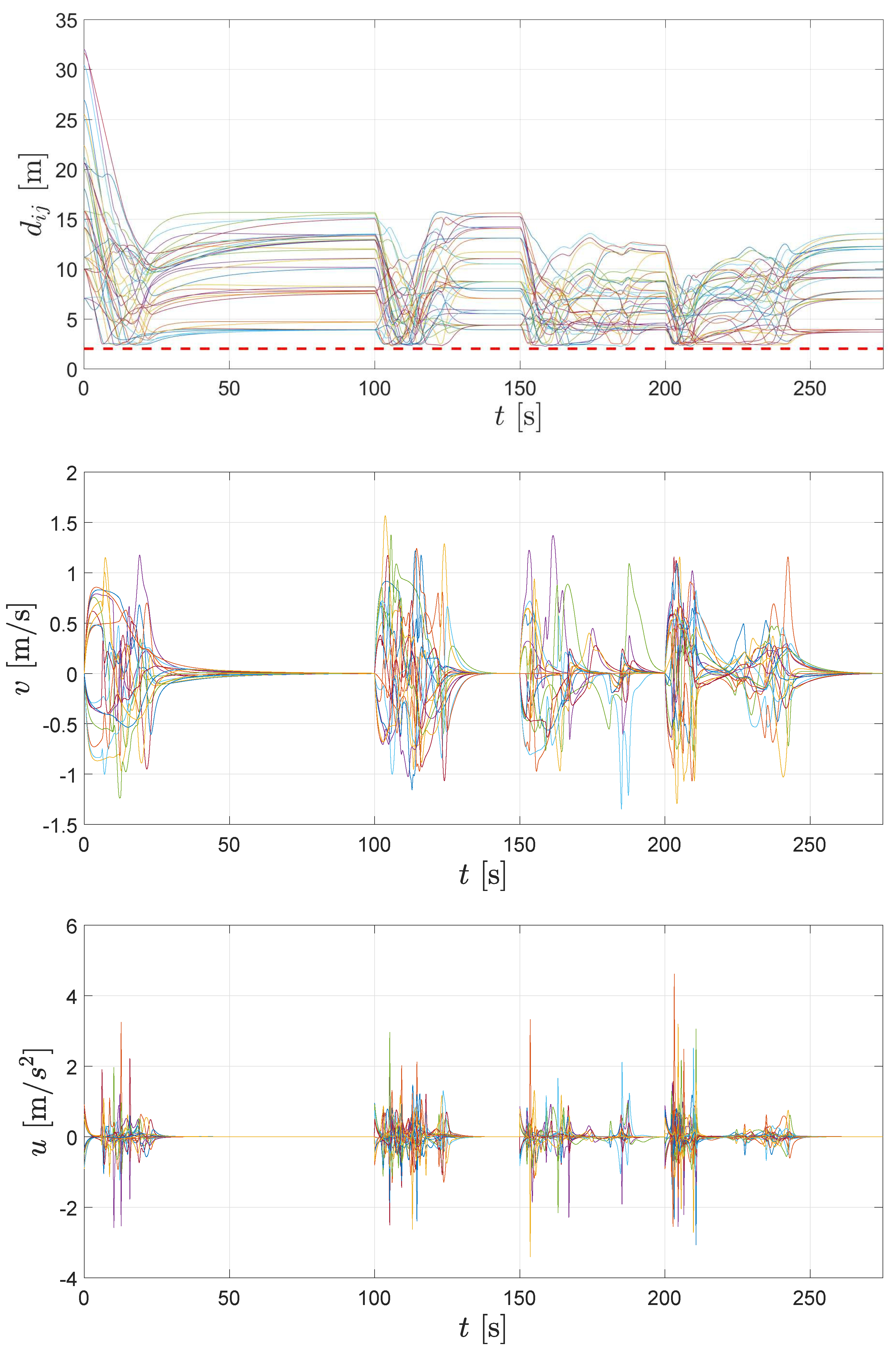
In Figure 10, distances between agents, velocities and accelerations are depicted for the whole simulation time. Details about time evolution can be appreciated more clearly in the video attached as Supplementary Materials.
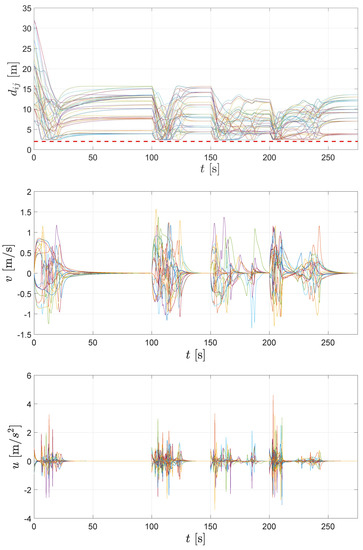
Figure 10.
Distancesbetween an pair of agents, velocities and control inputs for whole simulation.
6. Conclusions
In this paper, we proposed a strategy for solving the formation control problem without collisions for second-order multi-agent systems. The control law is the result of a generalization from a strategy which has been proved to solve the similar problem for first-order systems. The main characteristics of the proposed design are preserved: the unstable focus structure in the collision avoidance mechanism and the absence of undesired equilibria. In this work, we assume that every agent in the set is able to determine and share both position and velocity, and that each of them can apply repulsive vector fields to repel others to avoid collision. The notion of input to state stability is applied to show convergence to the desired formation by using the approach of cascaded subsystems. As a future work, performance of this methodology under constraints in the communication at position and/or velocity level, the effect of time delay, intermittent communication and the non-cooperative case could be studied.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/machines11020208/s1, Video S1: Real-time animation of agents’ positions of the numerical example.
Author Contributions
Conceptualization, J.F.F.-R. and E.A.-B.; methodology, All authors; software, J.F.F.-R.; formal analysis, J.F.F.-R. and E.A.-B.; writing—original draft preparation, All authors; writing—review and editing, J.F.F.-R.; All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CONACYT through the project A1-S-31628.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ISS | Input-to-State Stable |
| GAS | Globally Asymptotically Stable |
References
- Ku, S.Y.; Nejat, G.; Benhabib, B. Wilderness Search for Lost Persons Using a Multimodal Aerial-Terrestrial Robot Team. Robotics 2022, 11, 64. [Google Scholar] [CrossRef]
- Nordin, M.H.; Sharma, S.; Khan, A.; Gianni, M.; Rajendran, S.; Sutton, R. Collaborative Unmanned Vehicles for Inspection, Maintenance, and Repairs of Offshore Wind Turbines. Drones 2022, 6, 137. [Google Scholar] [CrossRef]
- Sharma, M.; Gupta, A.; Gupta, S.K.; Alsamhi, S.H.; Shvetsov, A.V. Survey on Unmanned Aerial Vehicle for Mars Exploration: Deployment Use Case. Drones 2022, 6, 4. [Google Scholar] [CrossRef]
- Xie, J.; Liu, C.C. Multi-agent systems and their applications. J. Int. Counc. Electr. Eng. 2017, 7, 188–197. [Google Scholar] [CrossRef]
- Roldán-Gómez, J.J.; González-Gironda, E.; Barrientos, A. A Survey on Robotic Technologies for Forest Firefighting: Applying Drone Swarms to Improve Firefighters’ Efficiency and Safety. Appl. Sci. 2021, 11, 363. [Google Scholar] [CrossRef]
- Mondal, A.; Bhowmick, C.; Behera, L.; Jamshidi, M. Trajectory Tracking by Multiple Agents in Formation With Collision Avoidance and Connectivity Assurance. IEEE Syst. J. 2018, 12, 2449–2460. [Google Scholar] [CrossRef]
- Oh, K.K.; Park, M.C.; Ahn, H.S. A survey of multi-agent formation control. Automatica 2015, 53, 424–440. [Google Scholar] [CrossRef]
- Wu, S.; Pu, Z.; Yi, J.; Sun, J.; Xiong, T.; Qiu, T. Adaptive Flocking of Multi-Agent Systems with Uncertain Nonlinear Dynamics and Unknown Disturbances Using Neural Networks*. In Proceedings of the 2020 IEEE 16th International Conference on Automation Science and Engineering (CASE), Hong Kong, China, 20–21 August 2020; pp. 1090–1095. [Google Scholar] [CrossRef]
- Young, Z.; La, H.M. Consensus, cooperative learning, and flocking for multiagent predator avoidance. Int. J. Adv. Robot. Syst. 2020, 17, 1729881420960342. [Google Scholar] [CrossRef]
- Briñón-Arranz, L.; Seuret, A.; Canudas-de Wit, C. Cooperative Control Design for Time-Varying Formations of Multi-Agent Systems. IEEE Trans. Autom. Control 2014, 59, 2283–2288. [Google Scholar] [CrossRef]
- Ren, W.; Atkins, E. Distributed multi-vehicle coordinated control via local information exchange. Int. J. Robust Nonlinear Control 2007, 17, 1002–1033. [Google Scholar] [CrossRef]
- Dong, W.; Farrell, J.A. Cooperative Control of Multiple Nonholonomic Mobile Agents. IEEE Trans. Autom. Control 2008, 53, 1434–1448. [Google Scholar] [CrossRef]
- Do, K.; Pan, J. Nonlinear formation control of unicycle-type mobile robots. Robot. Auton. Syst. 2007, 55, 191–204. [Google Scholar] [CrossRef]
- Wen, G.; Duan, Z.; Ren, W.; Chen, G. Distributed consensus of multi-agent systems with general linear node dynamics and intermittent communications. Int. J. Robust Nonlinear Control 2014, 24, 2438–2457. [Google Scholar] [CrossRef]
- Anderson, B.D.O.; Sun, Z.; Sugie, T.; Azuma, S.; Sakurama, K. Distance-based rigid formation control with signed area constraints. In Proceedings of the 2017 IEEE 56th Annual Conference on Decision and Control (CDC), Melbourne, VIC, Australia, 12–15 December 2017; pp. 2830–2835. [Google Scholar] [CrossRef]
- Hernandez-Martinez, E.G.; Ferreira-Vazquez, E.D.; Fernandez-Anaya, G.; Flores-Godoy, J.J. Formation Tracking of Heterogeneous Mobile Agents Using Distance and Area Constraints. Complexity 2017, 2017, 13. [Google Scholar] [CrossRef]
- Mehdifar, F.; Bechlioulis, C.P.; Hashemzadeh, F.; Baradarannia, M. Prescribed performance distance-based formation control of Multi-Agent Systems. Automatica 2020, 119, 109086. [Google Scholar] [CrossRef]
- Chan, N.P.K.; Jayawardhana, B.; de Marina, H.G. Angle-Constrained Formation Control for Circular Mobile Robots. IEEE Control Syst. Lett. 2021, 5, 109–114. [Google Scholar] [CrossRef]
- Sadowska, A.; Kostić, D.; van de Wouw, N.; Huijberts, H.; Nijmeijer, H. Distributed formation control of unicycle robots. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 1564–1569. [Google Scholar] [CrossRef]
- Onuoha, O.; Tnunay, H.; Wang, C.; Ding, Z. Fully distributed affine formation control of general linear systems with uncertainty. J. Frankl. Inst. 2020, 357, 12143–12162. [Google Scholar] [CrossRef]
- Dang, A.D.; La, H.; Nguyen, T.; Horn, J. Distributed Formation Control for Autonomous Robots in Dynamic Environments. arXiv 2017, arXiv:1705.02017. [Google Scholar]
- Fathian, K.; Summers, T.H.; Gans, N.R. Robust Distributed Formation Control of Agents with Higher-Order Dynamics. IEEE Control Syst. Lett. 2018, 2, 495–500. [Google Scholar] [CrossRef]
- Di Ferdinando, M.; Bianchi, D.; Di Gennaro, S.; Pepe, P. On the Robust Quantized Sampled–Data Leaderless Consensus Tracking of Nonlinear Multi–Agent Systems. In Proceedings of the 2021 60th IEEE Conference on Decision and Control (CDC), Austin, TX, USA, 13–17 December 2021; pp. 3263–3268. [Google Scholar] [CrossRef]
- Rodríguez-Seda, E.; Tang, C.; Spong, M.; Stipanović, D. Trajectory tracking with collision avoidance for nonholonomic vehicles with acceleration constraints and limited sensing. Int. J. Robot. Res. 2014, 33, 1569–1592. [Google Scholar] [CrossRef]
- Rodríguez-Seda, E.J. Decentralized trajectory tracking with collision avoidance control for teams of unmanned vehicles with constant speed. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 1216–1223. [Google Scholar] [CrossRef]
- Rodriguez-Seda, E.J.; Stipanović, D.M.; Spong, M.W. Guaranteed Collision Avoidance for Autonomous Systems with Acceleration Constraints and Sensing Uncertainties. J. Optim. Theory Appl. 2016, 168, 1014–1038. [Google Scholar] [CrossRef]
- Dai, Y.; Kim, Y.; Wee, S.; Lee, D.; Lee, S. A switching formation strategy for obstacle avoidance of a multi-robot system based on robot priority model. ISA Trans. 2015, 56, 123–134. [Google Scholar] [CrossRef]
- Rodríguez-Seda, E.J.; Stipanović, D.M. Cooperative Avoidance Control With Velocity-Based Detection Regions. IEEE Control Syst. Lett. 2020, 4, 432–437. [Google Scholar] [CrossRef]
- Zhang, W.; Rodriguez-Seda, E.J.; Deka, S.A.; Amrouche, M.; Zhou, D.; Stipanović, D.M.; Leitmann, G. Avoidance Control with Relative Velocity Information for Lagrangian Dynamics. J. Intell. & Robot. Syst. 2020, 99, 229–244. [Google Scholar] [CrossRef]
- Wang, M.; Geng, Z.; Peng, X. Measurement-Based method for nonholonomic mobile vehicles with obstacle avoidance. J. Frankl. Inst. 2020, 357, 7761–7778. [Google Scholar] [CrossRef]
- Fu, J.; Wen, G.; Yu, X.; Wu, Z.G. Distributed Formation Navigation of Constrained Second-Order Multiagent Systems With Collision Avoidance and Connectivity Maintenance. IEEE Trans. Cybern. 2022, 52, 2149–2162. [Google Scholar] [CrossRef]
- Zhang, W.; Stipanović, D.M.; Zhou, D. Motion information based avoidance control for 3-D multi-agent systems. J. Frankl. Inst. 2021, 358, 9621–9652. [Google Scholar] [CrossRef]
- Haraldsen, A.; Wiig, M.S.; Pettersen, K.Y. Reactive Collision Avoidance for Nonholonomic Vehicles in Dynamic Environments with Obstacles of Arbitrary Shape. IFAC-PapersOnLine 2021, 54, 155–160. [Google Scholar] [CrossRef]
- Shi, Q.; Li, T.; Li, J.; Chen, C.P.; Xiao, Y.; Shan, Q. Adaptive leader-following formation control with collision avoidance for a class of second-order nonlinear multi-agent systems. Neurocomputing 2019, 350, 282–290. [Google Scholar] [CrossRef]
- Flores-Resendiz, J.F.; Aranda-Bricaire, E.; González-Sierra, J.; Santiaguillo-Salinas, J. Finite-Time Formation Control without Collisions for Multiagent Systems with Communication Graphs Composed of Cyclic Paths. Math. Probl. Eng. 2015, 2015, 948086. [Google Scholar] [CrossRef]
- Hernandez-Martinez, E.; Aranda-Bricaire, E. Collision Avoidance in Formation Control using Discontinuous Vector Fields. IFAC Proc. Vol. 2013, 46, 797–802. [Google Scholar] [CrossRef]
- Flores-Resendiz, J.F.; Aranda-Bricaire, E. A General Solution to the Formation Control Problem Without Collisions for First-Order Multi-Agent Systems. Robotica 2020, 38, 1123–1137. [Google Scholar] [CrossRef]
- Flores-Resendiz, J.; Meza-Herrera, J.; Aranda-Bricaire, E. Formation control with collision avoidance for first-order multi-agent systems: Experimental results. IFAC-PapersOnLine 2019, 52, 127–132. [Google Scholar] [CrossRef]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice-Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Ren, W.; Beard, R. Distributed Consensus in Multi-Vehicle Cooperative Control: Theory and Applications; Springer: London, UK, 2008. [Google Scholar]
- Flores-Resendiz, J.F.; Aviles, D.; Aranda-Bricaire, E. Formation Control with Collision Avoidance for First-Order Multi-Agent Systems using Bounded Vector Fields. In Memorias del Congreso Nacional de Control Automático; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1–6. ISSN 2594-2492. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).