Research on PID Controller of Excavator Electro-Hydraulic System Based on Improved Differential Evolution
Abstract
:1. Introduction
2. System Structure
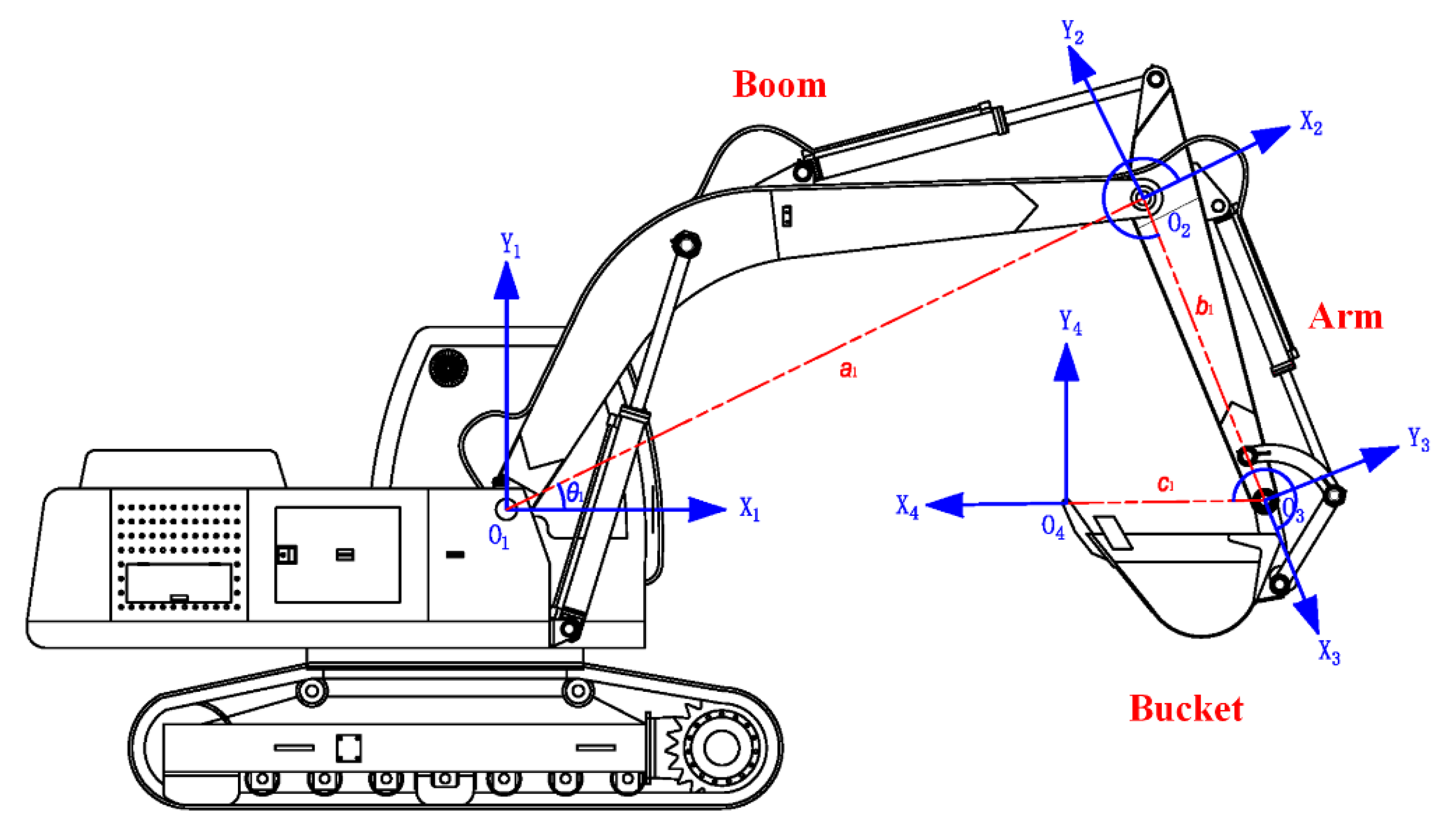
2.1. Kinematics of the Electronic-Hydraulic System for the 23t Excavator
2.2. System Control Objective
3. Control System Design
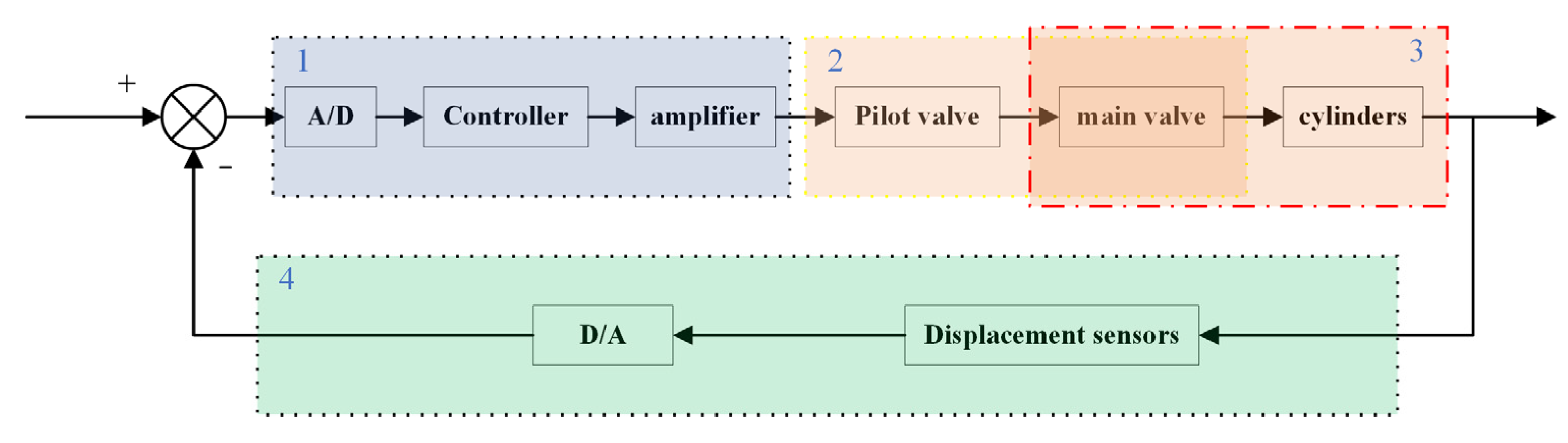
3.1. PID Control System Description
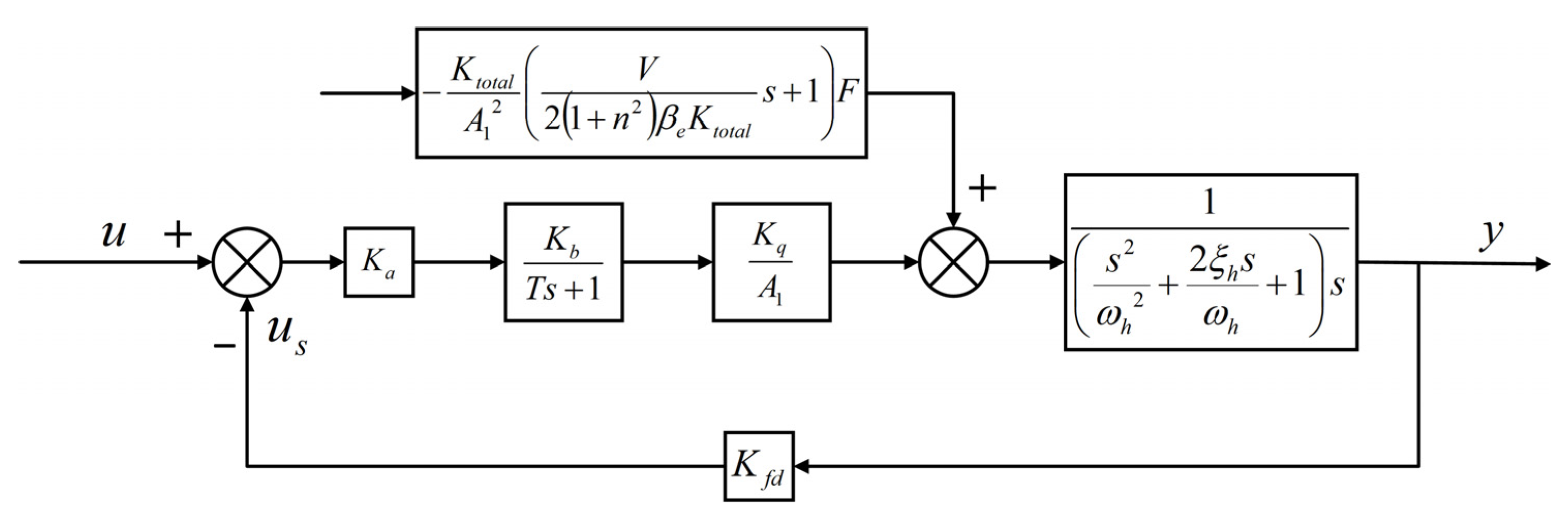
3.2. Electro-Proportional System Formulation
3.2.1. Proportional Gain Stage
3.2.2. Electro-Hydraulic Proportional Stage
3.2.3. Valve-Controlled Cylinder Stage
3.2.4. Feedback Stage
4. SDE and IDE Algorithm
4.1. SDE
- Initialization: During initialization, a random original population is generated within the value range of the solution. The initialization of DE can be given as:where denotes any individual; and represent the upper and lower limits of the search interval, respectively; is the size of population; and denotes the dimension of problem.
- Mutation: During mutation, the mutation vector will be generated for each target vector at any generation as:where denotes the scaling factor, and are randomly selected from the population and are different from each other. According to Storn’s suggestion, the initial value of is 0.5, and the values vary from 0.5 to 1.
- Crossover: After mutation (Figure 7), an intermediate vector , called the test vector, will be generated from target vector and the mutation vector using a crossover coefficient as:Figure 7. The process of crossover operation.
- Selection: When the mutation and crossover are finished, the next generation will be produced based on the fitness functions ( and ) of the target vector and test vector. This operation can be expressed as:
4.2. IDE
- (1)
- Scaling factor self-adaptation
- (2)
- Crossover probability self-adaption
4.3. Comparison of SDE and IDE
4.3.1. Objective Function and Fitness Value
4.3.2. The Steps for Optimization of PID Parameters
- Step 1. Randomly generate original population xg, which is composed of individuals.
- Step 2. Scaling factor and fitness value of everyone will be calculated according to Equations (24), (25), and (27).
- Step 3. Calculate and generate mutation vector and fitness of everyone according to Equation (21).
- Step 4. Calculate and generate crossover probability and test vector by Equations (26) and (22). Update the fitness value of everyone.
- Step 5. Generate new population and update the fitness value to execute the next iteration.
- Step 6. Repeat steps (3)–(5) until the iteration number is to the limits and stop the algorithm.
4.3.3. Simulation Results
5. Experiments
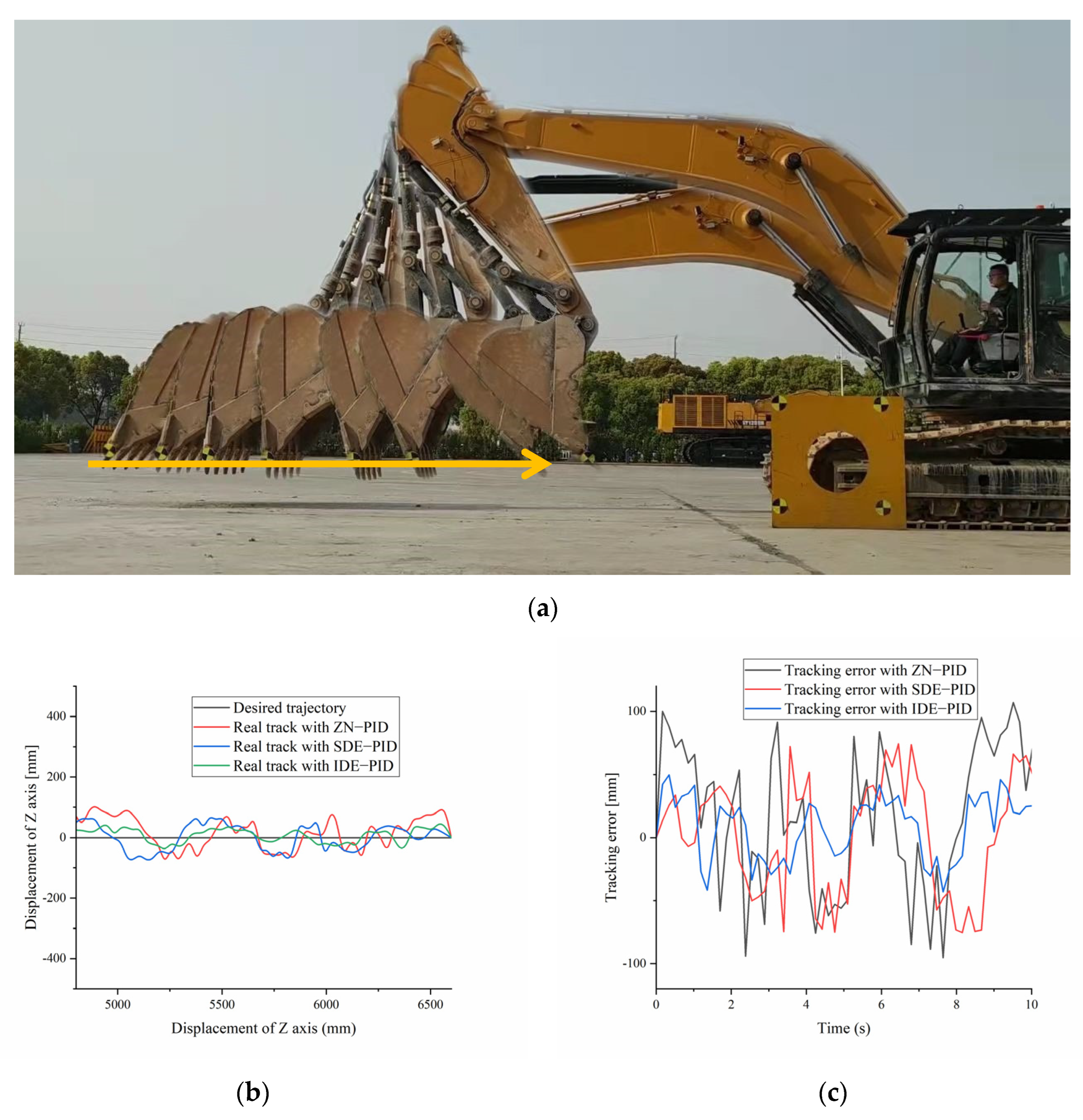
5.1. Experiment Platform
5.2. Experiments Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, J.; Jin, M.; Choi, W.; Lee, J. Discrete time delay control for hydraulic excavator motion control with terminal sliding mode control. Mechatronics 2019, 60, 15–25. [Google Scholar] [CrossRef]
- Shi, J.; Quan, L.; Zhang, X.; Xiong, X. Electro-hydraulic velocity and position control based on independent metering valve control in mobile construction equipment. Autom. Constr. 2018, 94, 73–84. [Google Scholar] [CrossRef]
- Park, J.; Cho, D.; Kim, S.; Kim, Y.B.; Kim, P.Y.; Kim, H.J. Utilizing online learning based on echo-state networks for the control of a hydraulic excavator. Mechatronics 2014, 24, 986–1000. [Google Scholar] [CrossRef]
- Wang, D.; Lin, X.; Zhang, Y. Fuzzy logic control for a parallel hybrid hydraulic excavator using genetic algorithm. Autom. Constr. 2011, 20, 581–587. [Google Scholar] [CrossRef]
- Won, D.; Kim, W.; Tomizuka, M. High Gain Observer Based Integral Sliding Mode Control for Position Tracking of Electro-hydraulic Servo Systems. IEEE/ASME Trans. Mechatron. 2017, 22, 2695–2704. [Google Scholar] [CrossRef]
- Le Hanh, D.; Ahn, K.K.; Kha, N.B.; Jo, W.K. Trajectory control of electro-hydraulic excavator using fuzzy self tuning algorithm with neural network. J. Mech. Sci. Technol. 2009, 23, 149–160. [Google Scholar] [CrossRef]
- Khalil, H.M.; El-Bardini, M. Implementation of speed controller for rotary hydraulic motor based on LS-SVM. Expert Syst. Appl. 2011, 38, 14249–14256. [Google Scholar] [CrossRef]
- Duan, H.; Liu, S.; Wang, D.; Yu, X. Design and realization of hybrid ACO-based PID and LuGre friction compensation controller for three degree-of-freedom high precision flight simulator. Simul. Model. Pract. Theory 2009, 17, 1160–1169. [Google Scholar] [CrossRef]
- Ye, Y.; Yin, C.B.; Gong, Y.; Zhou, J.J. Position control of nonlinear hydraulic system using an improved PSO based PID controller. Mech. Syst. Signal Process. 2017, 83, 241–259. [Google Scholar] [CrossRef]
- Song, H.; Li, G.; Li, Z.; Xiong, X. Trajectory Control Strategy and System Modeling of Load-Sensitive Hydraulic Excavator. Machines 2023, 11, 10. [Google Scholar] [CrossRef]
- Feng, H.; Yin, C.B.; Weng, W.W.; Ma, W.; Zhou, J.J.; Jia, W.H.; Zhang, Z.L. Robotic excavator trajectory control using an improved GA based PID controller. Mech. Syst. Signal Process. 2018, 105, 153–168. [Google Scholar] [CrossRef]
- Lee, C.S.; Bae, J.; Hong, D. Contour control for leveling work with robotic excavator. Int. J. Precis. Eng. Manuf. 2013, 14, 2055–2060. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution: A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces; Technical Report TR-95-012; International Computer Science Institute: Berkeley, CA, USA, 2005. [Google Scholar]
- Mohanty, B.; Panda, S.; Hota, P.K. Controller parameters tuning of differential evolution algorithm and its application to load frequency control of multi-source power system. Int. J. Electr. Power Energy Syst. 2014, 54, 77–85. [Google Scholar] [CrossRef]
- Küçükoğlu, İ.; Öztürk, N. A differential evolution approach for the vehicle routing problem with backhauls and time windows. J. Adv. Transp. 2014, 48, 942–956. [Google Scholar] [CrossRef]
- Pant, M.; Zaheer, H.; Garcia-Hernandez, L.; Abraham, A. Differential evolution: A review of more than two decades of research. Eng. Appl. Artif. Intell. 2020, 90, 103479. [Google Scholar]
- Zhao, Z.; Yang, J.; Hu, Z.; Che, H. A differential evolution algorithm with self-adaptive strategy and control parameters based on symmetric Latin hypercube design for unconstrained optimization problems. Eur. J. Oper. Res. 2016, 250, 30–45. [Google Scholar]
- Ghosh, A.; Das, S.; Chowdhury, A.; Giri, R. An improved differential evolution algorithm with fitness-based adaptation of the control parameters. Inf. Sci. 2011, 181, 3749–3765. [Google Scholar]
- Wang, H.; Rahnamayan, S.; Sun, H.; Omran, M.G. Gaussian Bare-Bones Differential Evolution. IEEE Trans. Cybern. 2013, 43, 634–647. [Google Scholar] [CrossRef]
- Meng, Z.; Pan, J.S.; Kong, L. Parameters with Adaptive Learning Mechanism (PALM) for the enhancement of Differential Evolution. Knowl. Based Syst. 2018, 141, 92–112. [Google Scholar] [CrossRef]
- Zamuda, A.; Brest, J. Self-adaptive control parameters? randomization frequency and propagations in differential evolution. Swarm Evol. Comput. 2015, 25, 72–99. [Google Scholar] [CrossRef]
- Hou, Y.-Y. Design and implementation of EP-based PID controller for chaos synchronization of Rikitake circuit systems. ISA Trans. 2017, 70, 260–268. [Google Scholar] [CrossRef] [PubMed]
- Vasiliu, N.; Vasiliu, D.; Călinoiu, C.; Puhalschi, R. Simulation of Fluid Power Systems with Simcenter Amesim; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Nguyen, T.H.; Do, T.C.; Nguyen, V.H.; Ahn, K.K. High Tracking Control for a New Independent Metering Valve System Using Velocity-Load Feedforward and Position Feedback Methods. Appl. Sci. 2022, 12, 9827. [Google Scholar] [CrossRef]
- Heybroek, K.; Sahlman, M. A hydraulic hybrid excavator based on multi-chamber cylinders and secondary control—Design and experimental validation. Int. J. Fluid Power 2018, 19, 91–105. [Google Scholar] [CrossRef]
- Qu, S.; Fassbender, D.; Vacca, A.; Busquets, E. A high-efficient solution for electro-hydraulic actuators with energy regeneration capability—ScienceDirect. Energy 2020, 216, 119291. [Google Scholar] [CrossRef]
- Lin, T.; Wang, Q.; Hu, B.; Gong, W. Research on the energy regeneration systems for hybrid hydraulic excavators. Autom. Constr. 2010, 19, 1016–1026. [Google Scholar] [CrossRef]
- Xu, J.; Yoon, H.S. A review on mechanical and hydraulic system modeling of excavator manipulator system. J. Constr. Eng. 2016, 2016, 9409370. [Google Scholar] [CrossRef]
- Ronkkonen, J.; Kukkonen, S.; Price, K.V. Real-parameter optimization with differential evolution. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Edinburgh, UK, 2–5 September 2005; Volume 1, pp. 506–513. [Google Scholar]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem Definitions and Evaluation Criteria for the CEC 2005 Special Session on Real-Parameter Optimization. Nat. Comput. 2005, 2005, 341–357. [Google Scholar]








| Symbol | Parameters | SDE | IDE |
|---|---|---|---|
| Number of individuals | 50 | 50 | |
| Mutation scaling factor | 0.9 | unfixed | |
| Crossover probability | 0.8 | unfixed | |
| Dimension of issue | 3 | 3 | |
| Maximum number of iterations | 100 | 100 | |
| Weight 1 | 0.999 | 0.999 | |
| Weight 2 | 0.001 | 0.001 | |
| Weight 3 | 2 | 2 | |
| Search range of | [0, 20] | [0, 20] | |
| Search range of | [0, 10] | [0, 10] | |
| Search range of | [0, 10] | [0, 10] |
| Tuning Method | Rise Time (s) | Settling Time (s) | Number of Iterations | Best J |
|---|---|---|---|---|
| ZN | 1.55 | 3.27 | / | / |
| SDE | 1.17 | 2.37 | 81 | 2.35 |
| IDE | 0.93 | 1.84 | 57 | 1.74 |
| Sensors | Type | Main Parameters |
|---|---|---|
| DSP controller | 283H | 32-bit, duty cycle < 1 ms |
| DAQ card | NI USB 6215 | 16-bit, 8AI/2AO, 4DI/4DO |
| Displacement sensor | WDS-2500 | Scale 0–2500 mm, 0.2 accuracy class |
| Pressure sensor | 625 T4-16-Z23 | Scale 0–400 bar, 0.2% FS accuracy |
| USB-CAN | USBCAN-Ⅱ PRO | 32-bit CPU |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, W.; Ma, S.; Qiao, W.; Cao, D.; Yin, C. Research on PID Controller of Excavator Electro-Hydraulic System Based on Improved Differential Evolution. Machines 2023, 11, 143. https://doi.org/10.3390/machines11020143
Ma W, Ma S, Qiao W, Cao D, Yin C. Research on PID Controller of Excavator Electro-Hydraulic System Based on Improved Differential Evolution. Machines. 2023; 11(2):143. https://doi.org/10.3390/machines11020143
Chicago/Turabian StyleMa, Wei, Shoulei Ma, Wenhua Qiao, Donghui Cao, and Chenbo Yin. 2023. "Research on PID Controller of Excavator Electro-Hydraulic System Based on Improved Differential Evolution" Machines 11, no. 2: 143. https://doi.org/10.3390/machines11020143
APA StyleMa, W., Ma, S., Qiao, W., Cao, D., & Yin, C. (2023). Research on PID Controller of Excavator Electro-Hydraulic System Based on Improved Differential Evolution. Machines, 11(2), 143. https://doi.org/10.3390/machines11020143








