Design and Experiments of Electro-Hydrostatic Actuator for Wheel-Legged Robot with Fast Force Control Response
Abstract
1. Introduction
2. System Description and Model
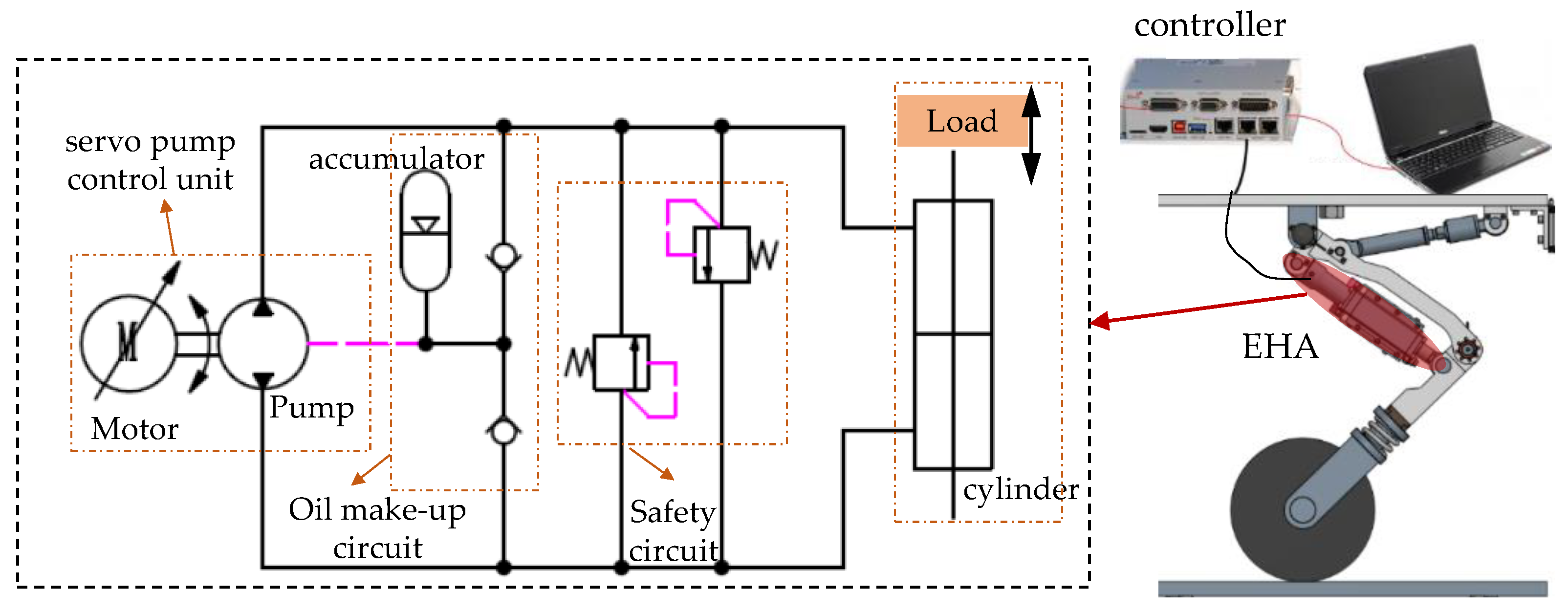
2.1. System Description
2.2. EHA Modeling
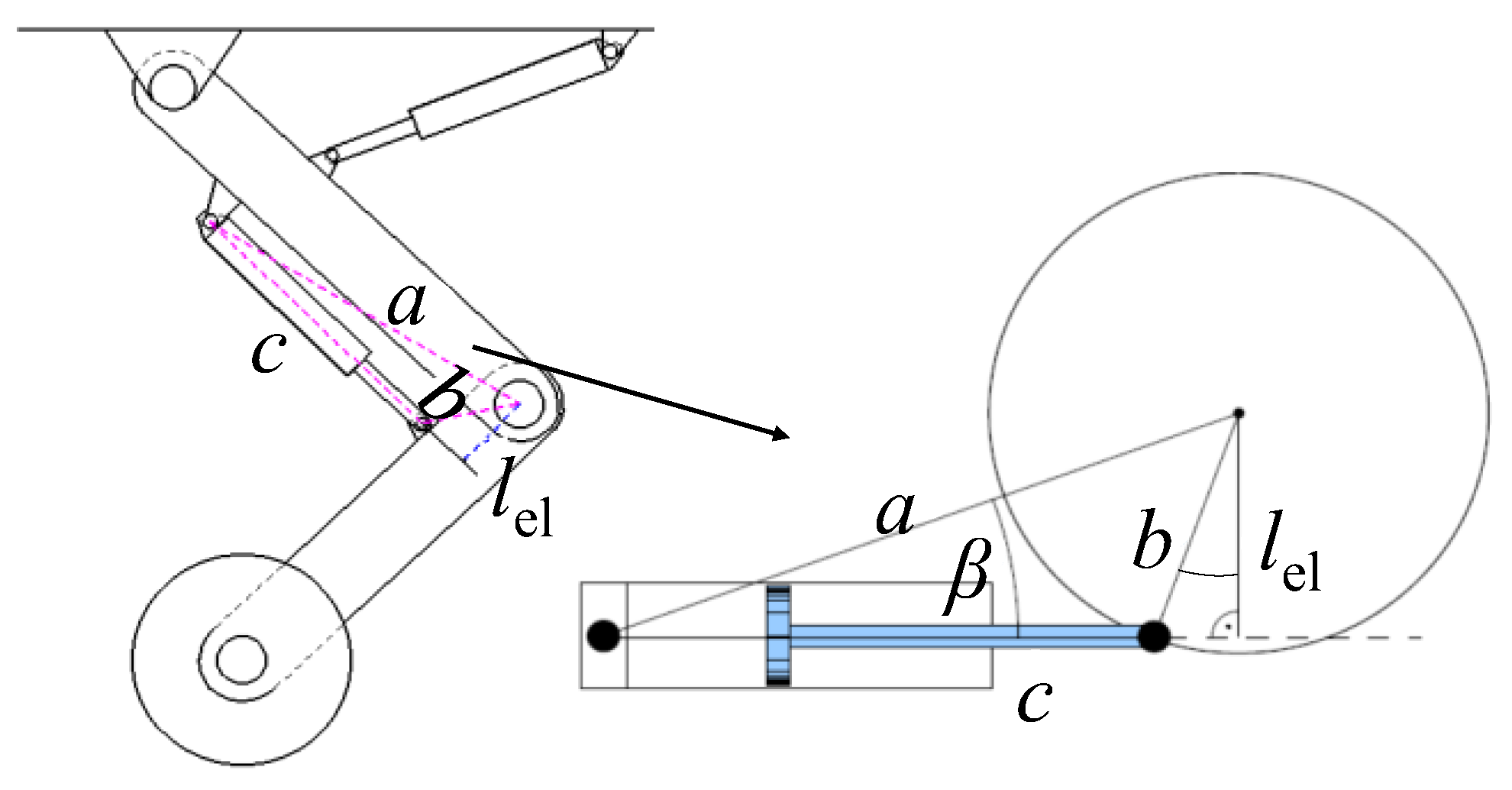
2.3. Knee Joint with EHA Modeling
3. Design of EHA
3.1. Mechanical Design
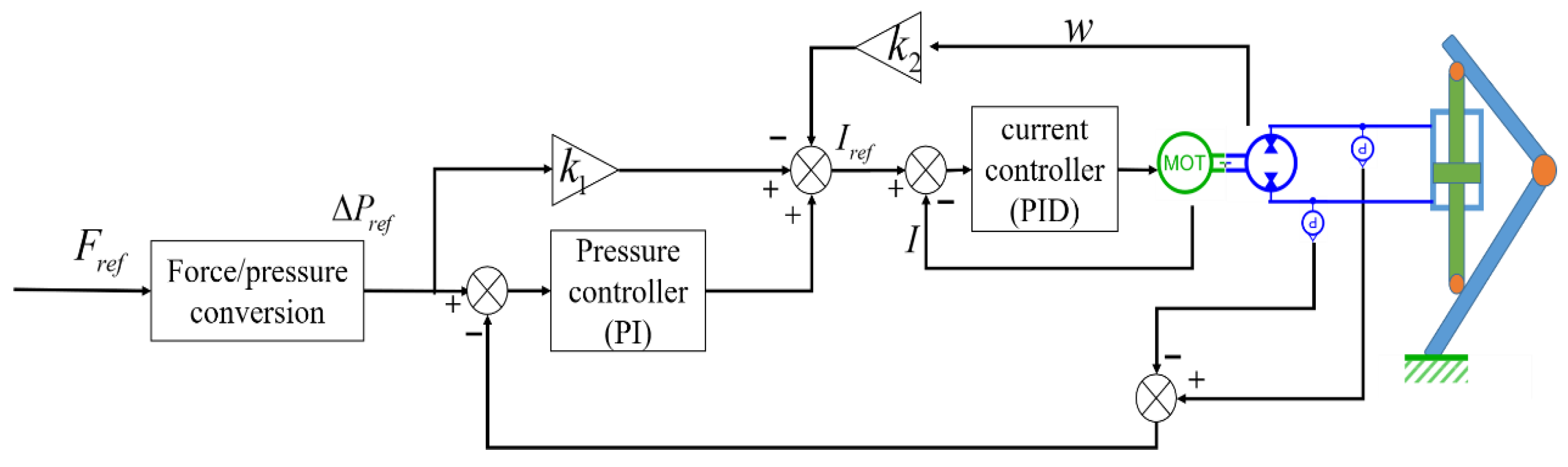
3.2. Controller Design
- A.
- Pressure controller design
- B.
- Position controller design
4. Parameter Identification
4.1. Experimental Set Up
4.2. Open-Loop Experiments and Parameter Identification
- a.
- Locking the piston tests
- b.
- Connecting two ports of hydraulic cylinder test
5. Simulation and Experimental Results
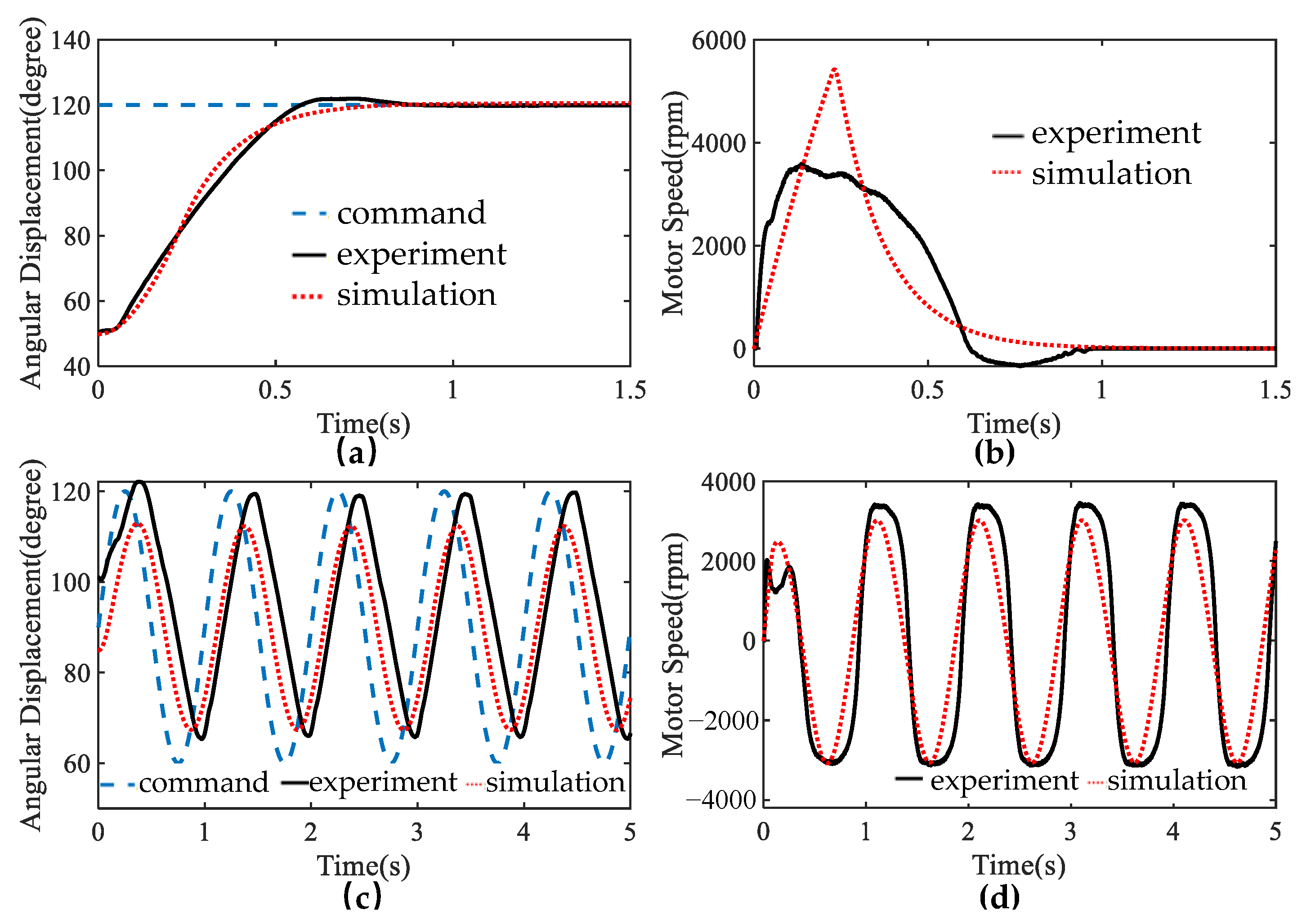
5.1. Pressure Tracking Performance
5.2. Position Tracking Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, Y.S.; Jung, G.P.; Kim, H.; Cho, K.J.; Chu, C.N. Wheel transformer: A wheel-leg hybrid robot with passive transformable wheels. IEEE Trans. Robot. 2014, 30, 1487–1498. [Google Scholar] [CrossRef]
- Du, W.; Fnadi, M.; Benamar, F. Rolling based locomotion on rough terrain for a wheeled quadruped using centroidal dynamics. Mech. Mach. Theory 2020, 153, 103984. [Google Scholar] [CrossRef]
- Liu, D.; Wang, J.; Wang, S. Coordinated motion control and event-based obstacle-crossing for four wheel-leg independent motor-driven robotic system. Mechatronics 2022, 81, 102697. [Google Scholar] [CrossRef]
- Bjelonic, M.; Sankar, P.K.; Bellicoso, C.D.; Vallery, H.; Hutter, M. Rolling in the deep–hybrid locomotion for wheeled-legged robots using online trajectory optimization. IEEE Robot. Autom. Lett. 2020, 5, 3626–3633. [Google Scholar] [CrossRef]
- Kashiri, N.; Baccelliere, L.; Muratore, L.; Laurenzi, A.; Ren, Z.; Hoffman, E.M.; Kamedula, M.; Rigano, G.F.; Malzahn, J.; Cordasco, S.; et al. CENTAURO: A hybrid locomotion and high-power resilient manipulation platform. IEEE Robot. Autom. Lett. 2019, 4, 1595–1602. [Google Scholar] [CrossRef]
- Suzumura, A.; Fujimoto, Y. Real-time motion generation and control systems for high wheel-legged robot mobility. IEEE Trans. Ind. Electron. 2013, 61, 3648–3659. [Google Scholar] [CrossRef]
- Li, X.; Zhou, H.; Zhang, S.; Feng, H.; Fu, Y. WLR-II, a hose-less hydraulic wheel-legged robot. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; pp. 4339–4346. [Google Scholar]
- Wong, C.Y.; Turker, K.; Sharf, I.; Beckman, B. Posture Reconfiguration and Navigation Maneuvers on a Wheel-Legged Hydraulic Robot. In Field and Service Robotics, Proceedings of the 9th International Conference on Field and Service Robotics FSR, Brisbane, Australia, 9–11 December 2013; Springer: Berlin, Germany, 2013. [Google Scholar]
- Tamburrino, F.; Graziosi, S.; Bordegoni, M. The influence of slicing parameters on the multi-material adhesion mechanisms of FDM printed parts: An exploratory study. Virtual Phys. Prototyp. 2019, 14, 316–332. [Google Scholar] [CrossRef]
- Stano, G.; Ovy, S.M.A.; Percoco, G.; Zhang, R.Y.; Lu, H.B.; Tadesse, Y. Additive Manufacturing for Bioinspired Structures: Experimental Study to Improve the Multimaterial Adhesion between Soft and Stiff Materials. 3D Print. Addit. Manuf. 2023; ahead of print. [Google Scholar] [CrossRef]
- Lussenburg, K.; Sakes, A.; Breedveld, P. Design of non-assembly mechanisms: A state-of-the-art review. Addit. Manuf. 2021, 39, 101846. [Google Scholar] [CrossRef]
- Tsagarakis, N.G.; Caldwell, D.G.; Negrello, F.; Choi, W.; Baccelliere, L.; Loc, V.G.; Noorden, J.; Muratore, L.; Margan, A.; Cardellino, A.; et al. Walk-man: A high-performance humanoid platform for realistic environments. J. Field Robot. 2017, 34, 1225–1259. [Google Scholar] [CrossRef]
- Hutter, M.; Gehring, C.; Höpflinger, M.A.; Blösch, M.; Siegwart, R. Toward combining speed, efficiency, versatility, and robustness in an autonomous quadruped. IEEE Trans. Robot. 2014, 30, 1427–1440. [Google Scholar] [CrossRef]
- Wensing, P.M.; Wang, A.; Seok, S.; Otten, D.; Lang, J.; Kim, S. Proprioceptive actuator design in the MIT cheetah: Impact mitigation and high-bandwidth physical interaction for dynamic legged robots. IEEE Trans. Robot. 2017, 33, 509–522. [Google Scholar] [CrossRef]
- Rus, D.; Tolley, M.T. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef]
- Wang, Z.; Torigoe, Y.; Hirai, S. A prestressed soft gripper: Design, modeling, fabrication, and tests for food handling. IEEE Robot. Autom. Lett. 2017, 2, 1909–1916. [Google Scholar] [CrossRef]
- Lee, Y.H.; Lee, Y.H.; Lee, H.; Kang, H.; Lee, J.H.; Phan, L.T.; Jin, S.; Kim, Y.B.; Seok, D.-Y.; Lee, S.Y.; et al. Development of a quadruped robot system with torque-controllable modular actuator unit. IEEE Trans. Ind. Electron. 2020, 68, 7263–7273. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Huang, H.; Pan, M. A review of high-speed electro-hydrostatic actuator pumps in aerospace applications: Challenges and solutions. J. Mech. Des. 2019, 141, 050801. [Google Scholar] [CrossRef]
- Chao, Q.; Zhang, J.; Xu, B.; Chen, Y.; Ge, Y. Spline design for the cylinder block within a high-speed electro-hydrostatic actuator pump of aircraft. Meccanica 2019, 53, 395–411. [Google Scholar] [CrossRef]
- Shang, Y.; Li, X.; Qian, H.; Wu, S.; Pan, Q.; Huang, L.; Jiao, Z. A novel electro hydrostatic actuator system with energy recovery module for more electric aircraft. IEEE Trans. Ind. Electron. 2019, 67, 2991–2999. [Google Scholar] [CrossRef]
- Habibi, S.; Goldenberg, A. Design of a new high-performance electrohydraulic actuator. IEEE ASME Trans. Mechatron. 2000, 5, 158–164. [Google Scholar] [CrossRef]
- Bobrow, J.E.; Desai, J. Modeling and Analysis of a High-Torque, Hydrostatic Actuator for robotic Applications. In Experimental Robotics I, Proceedings of the First International Symposium Montreal, Montreal, QC, Canada, 9–21 June 1989; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Kaminaga, H.; Ono, J.; Nakashima, Y.; Nakamura, Y. Development of back drivable hydraulic joint mechanism for knee joint of humanoid robots. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009. [Google Scholar]
- Neubauer, B.; Durfee, W. Preliminary design and engineering evaluation of a hydraulic ankle–foot orthosis. J. Med. Devices 2016, 10, 041002. [Google Scholar] [CrossRef]
- Ko, T.; Murotani, K.; Yamamoto, K.; Nakamura, Y. Whole-body compliant motion by sensor integration of an EHA-Driven humanoid hydra. Int. J. Hum. Robot. 2021, 18, 2150002. [Google Scholar] [CrossRef]
- Komagata, M.; Imashiro, Y.; Yamamoto, K.; Nakamura, Y. Preferred oil and ceramics options for EHA drive systems and computed torque control of an EHA-Driven Robot manipulator. In Proceedings of the 2021 30th IEEE International Conference on Robot & Human Interactive Communication (RO-MAN), Vancouver, BC, Canada, 8–12 August 2021; pp. 540–545. [Google Scholar]
- Lee, T.; Lee, D.; Song, B.; Baek, Y.S. Design and control of a polycentric knee exoskeleton using an electro-hydraulic actuator. Sensors 2019, 20, 211. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Liu, X.; Wang, J.; Karimi, H.R. Robust H∞ sliding mode control with pole placement for a fluid power electrohydraulic actuator (EHA) system. Int. J. Adv. Manuf. Technol. 2014, 73, 1095–1104. [Google Scholar] [CrossRef]







| Feature | Value | Unit |
|---|---|---|
| Weight | 3.694 | |
| Length | 290 | |
| Width | 170 | |
| Height | 70 |
| EHA of Robots | Force-to-Weight Ratio |
|---|---|
| This article | 2518 |
| Hydra | 1424 |
| Kaleido | 1500~2000 |
| Variable | Value | Unit |
|---|---|---|
| 0.13 | ||
| 0.003 | ||
| 0.00498 | ||
| 0.16 | ||
| 0.2537 | ||
| 2.0084 × 10−15 | ||
| 0.69 | ||
| 900 | ||
| 1.2535 × 10−5 | ||
| 1.2535 × 10−5 | ||
| 3.1337 × 10−5 | ||
| 9400 | ||
| 320.8 | mm | |
| 46.2 | mm | |
| 280 | mm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Zhou, J.; Ma, S.; Du, S.; Liu, H.; Han, L. Design and Experiments of Electro-Hydrostatic Actuator for Wheel-Legged Robot with Fast Force Control Response. Machines 2023, 11, 685. https://doi.org/10.3390/machines11070685
Zhao H, Zhou J, Ma S, Du S, Liu H, Han L. Design and Experiments of Electro-Hydrostatic Actuator for Wheel-Legged Robot with Fast Force Control Response. Machines. 2023; 11(7):685. https://doi.org/10.3390/machines11070685
Chicago/Turabian StyleZhao, Huipeng, Junjie Zhou, Sanxi Ma, Shanxiao Du, Hui Liu, and Lijin Han. 2023. "Design and Experiments of Electro-Hydrostatic Actuator for Wheel-Legged Robot with Fast Force Control Response" Machines 11, no. 7: 685. https://doi.org/10.3390/machines11070685
APA StyleZhao, H., Zhou, J., Ma, S., Du, S., Liu, H., & Han, L. (2023). Design and Experiments of Electro-Hydrostatic Actuator for Wheel-Legged Robot with Fast Force Control Response. Machines, 11(7), 685. https://doi.org/10.3390/machines11070685







