Research on a Method of Robot Grinding Force Tracking and Compensation Based on Deep Genetic Algorithm
Abstract
1. Introduction
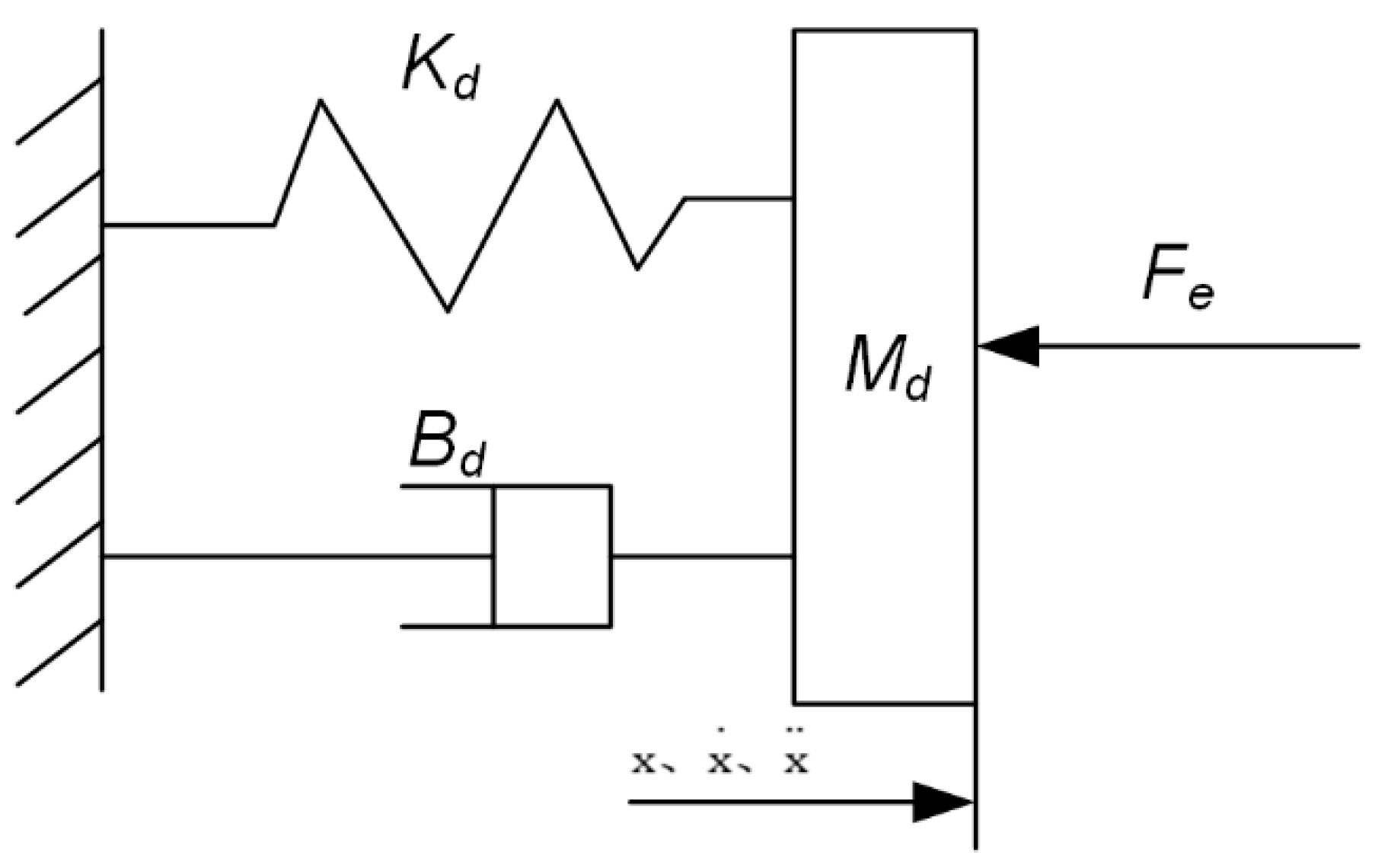
2. Robot Grinding Force Impedance Control Model
3. Grinding Force-Tracking Compensation Algorithm
3.1. Grinding Trajectory Based on 3D Model and Environmental Parameters
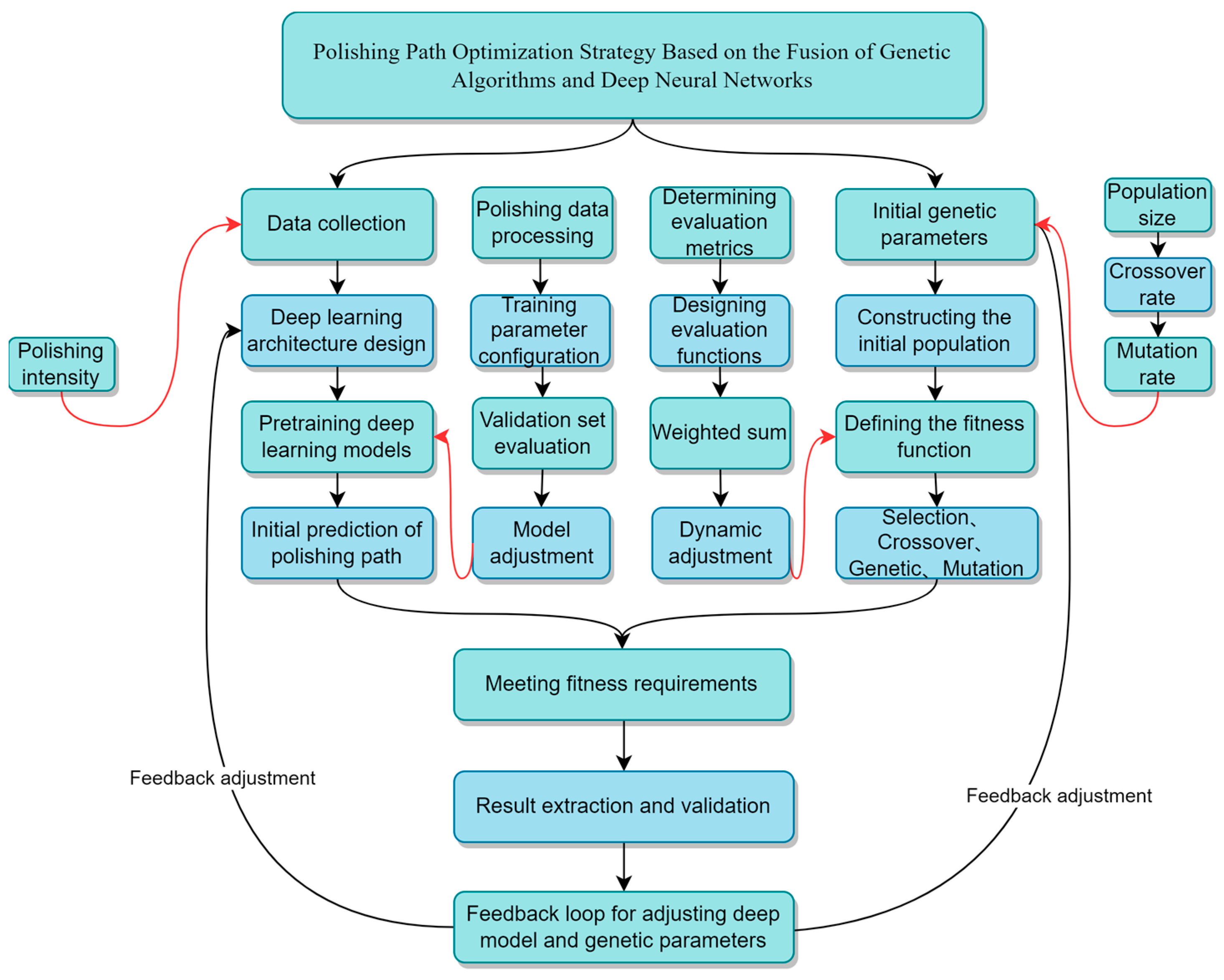
3.2. Optimizing Grinding Trajectory Based on Deep Genetic Algorithm
- (1)
- Data Collection: Initially, it is necessary to gather extensive data on polishing tasks (polishing forces).
- (2)
- Deep Learning Model Design and Training: Considering the time dynamics during the polishing process, such as factors related to changes in polishing force over time, recurrent neural networks and DNNs are chosen as the core architecture.
- (3)
- Initial Prediction of the Polishing Path: Utilizing the trained deep learning model, input the current polishing task parameters and the polishing trajectory estimated based on the workpiece’s three-dimensional model and environmental parameters to obtain an initial prediction of the polishing path. This prediction takes into account the workpiece’s shape, physical characteristics, and the expected quality of polishing.
- (4)
- Initial Setting of Genetic Algorithm Parameters: Determine the initial parameters for the genetic algorithm, which include the scale of the population, the rate of crossover, the rate of mutation, and the upper limit of iterations.
- (5)
- Construction of the Initial Population: Based on the initial polishing path provided by the deep learning model, construct the initial population for the genetic algorithm. Each individual represents a potential solution for the polishing path, with the initial population containing the paths predicted by the deep model and random variations introduced on this basis.
- (6)
- Definition of Fitness Function: The fitness function serves as the standard for evaluating the quality of each individual and should reflect the actual requirements of the polishing task. It can be based on several factors, including the stability of the polishing process, the quality of polishing, and the time taken to complete the task.
- (7)
- Genetic Algorithm Iteration:
- Selection: Based on the fitness function, select the best-performing individuals from the current population for breeding.
- Crossover: Chosen individuals produce offspring through genetic exchange, mimicking reproduction in nature.
- Mutation: Randomly alter parts of certain offspring’s genes to increase population diversity.
- Evaluation: After the new-generation population emerges, reassess it using the fitness function.
- (8)
- Termination Condition Assessment: The algorithm concludes if it reaches the preset maximum number of iterations, or if the best individual in the population achieves a fitness level that meets task requirements. If the maximum iterations are reached without attaining a satisfactory result, the algorithm will return the best solution found thus far. Additionally, an alert or error message will be generated to inform the user of the suboptimal conclusion. The user can then consider adjusting the algorithm’s parameters or adopting alternative strategies for improved outcomes in subsequent runs.
- (9)
- Result Extraction and Verification: Identify the individual with the highest fitness from the final population as the optimal polishing path. Then, implement this path in actual polishing tasks, gather feedback data, and verify the path’s effectiveness.
- (10)
- Feedback Loop: Adjust the parameters of the deep learning model and genetic algorithm based on feedback from actual polishing results. Through continuous feedback loops, the model will constantly learn and improve, enhancing its adaptability and predictive accuracy for future polishing tasks.
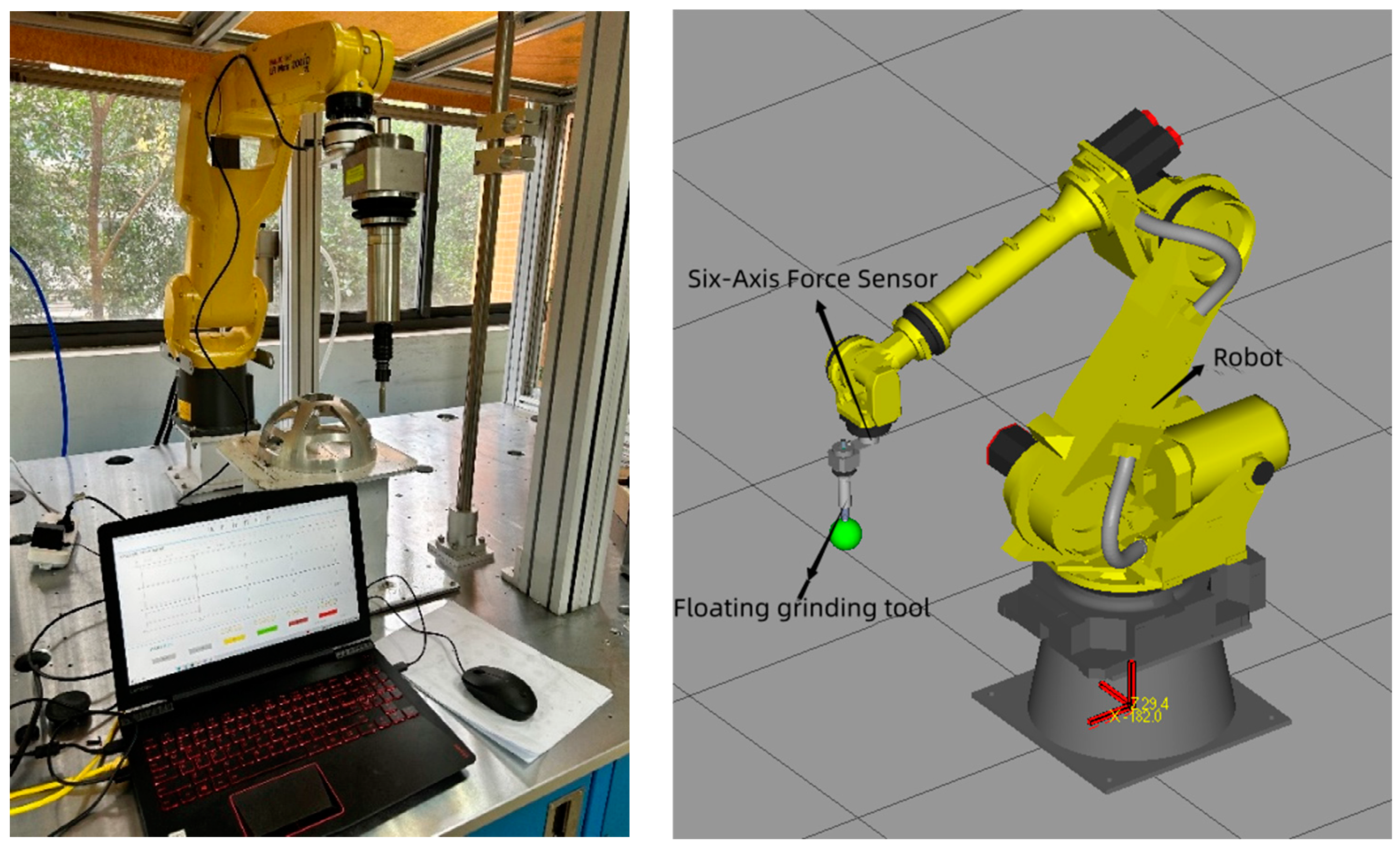
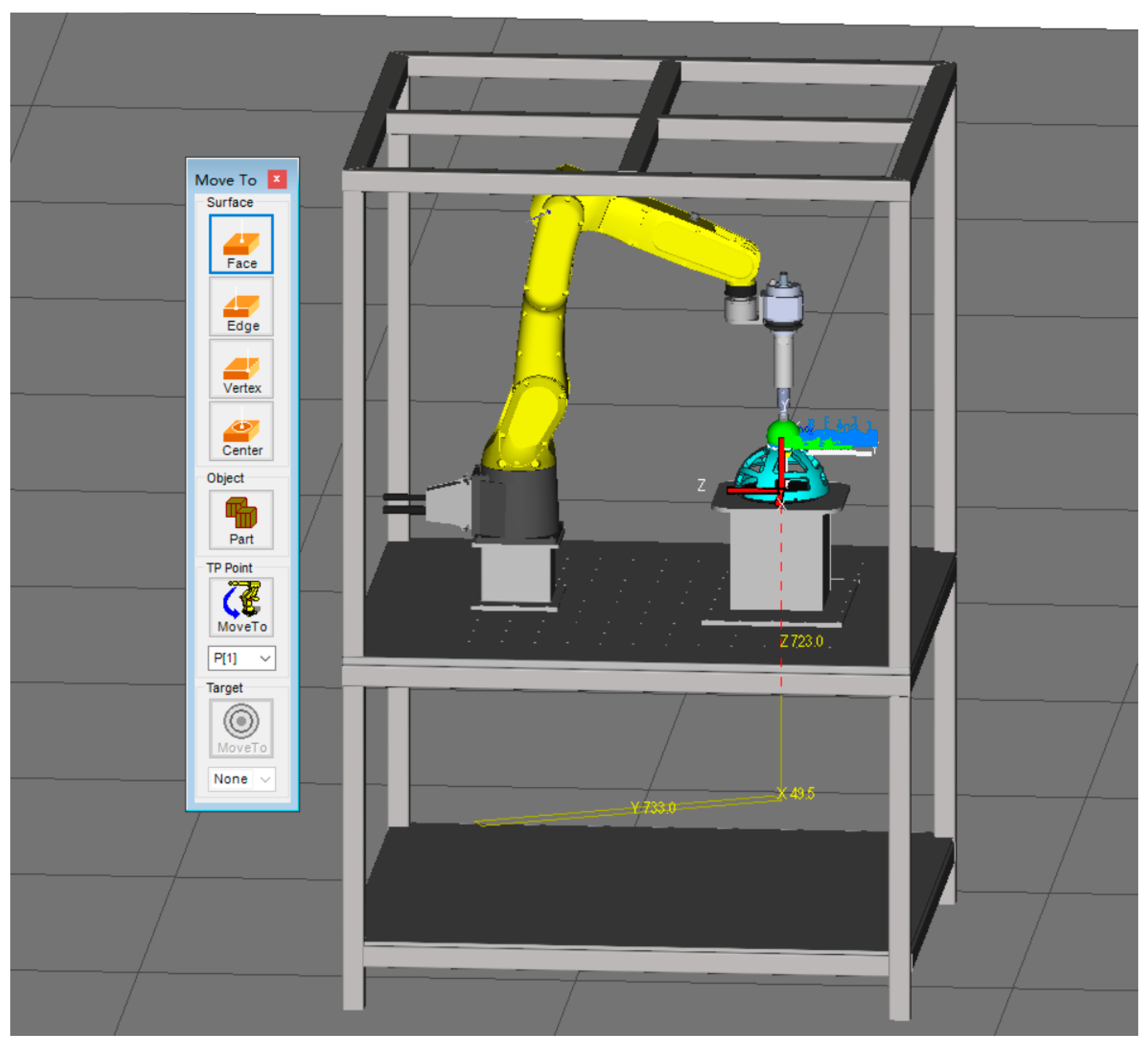
4. Flexible Grinding Experiment
5. Conclusions
- (1)
- Addressing the challenge of under-grinding and over-grinding in the grinding process of complex-shaped casting workpieces, this paper presents research on optimizing the grinding trajectory using force-sensing information. It also introduces a novel force-tracking control strategy aimed at enhancing the accuracy of contact force tracking during the grinding process.
- (2)
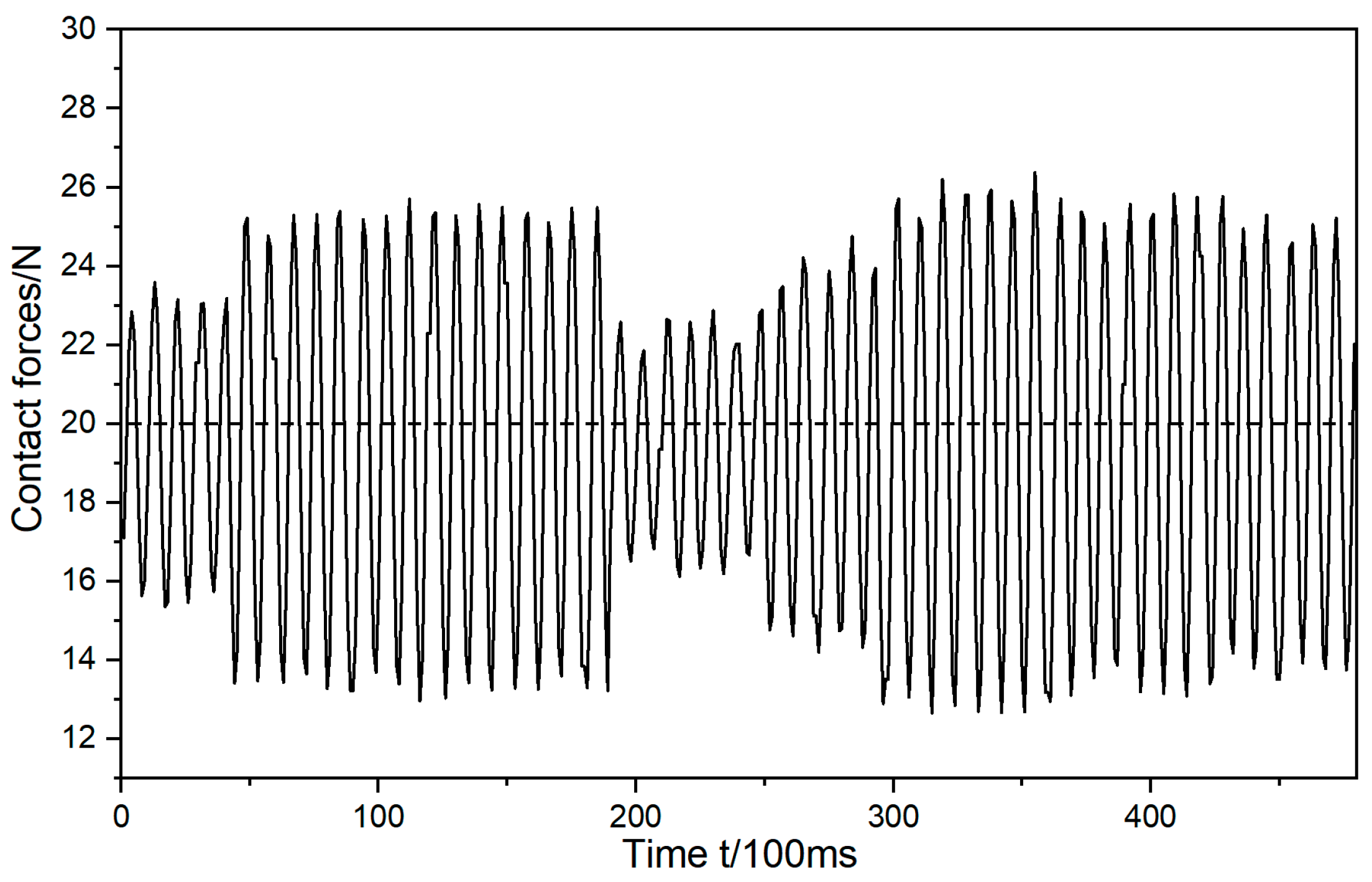
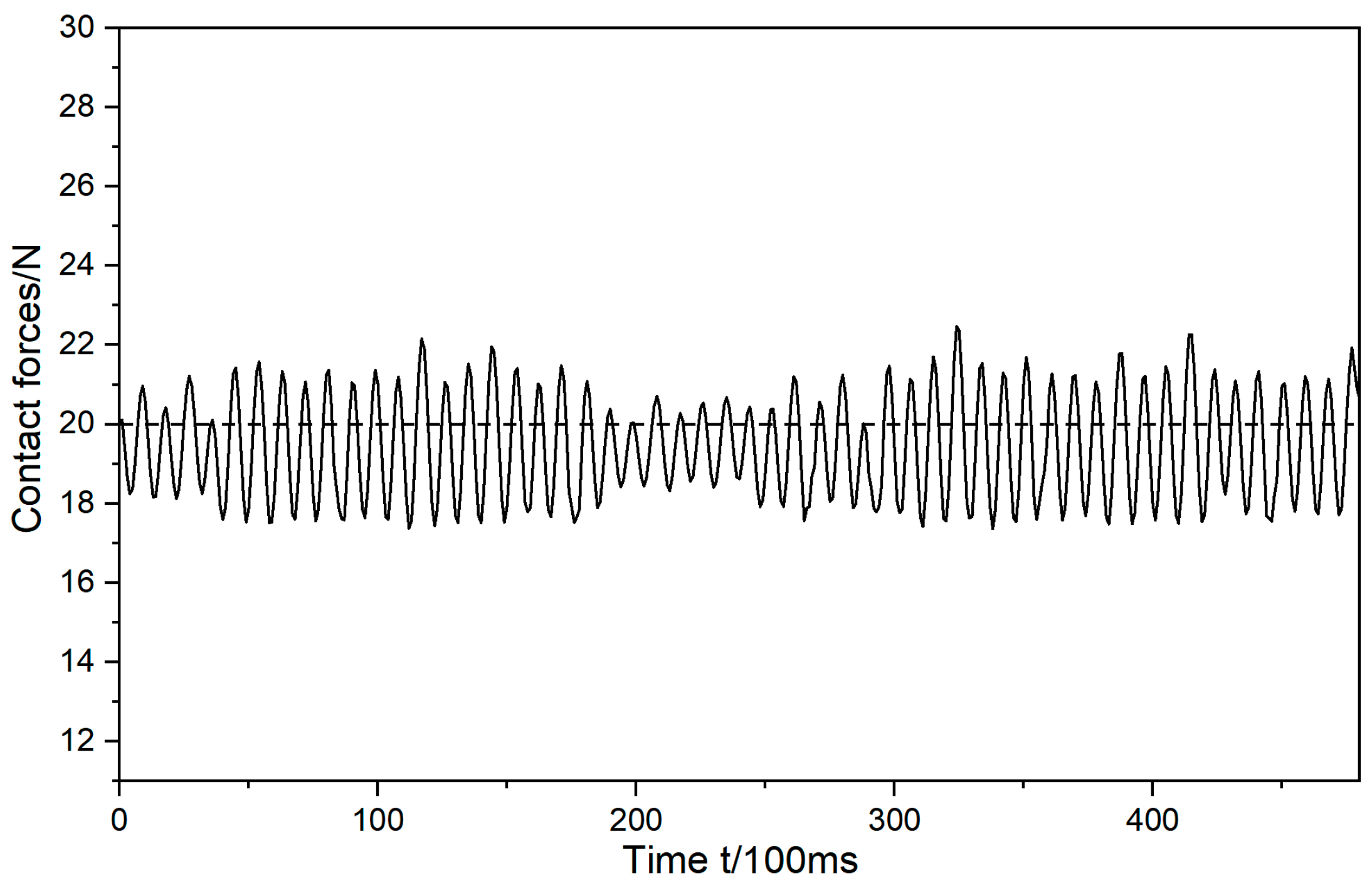
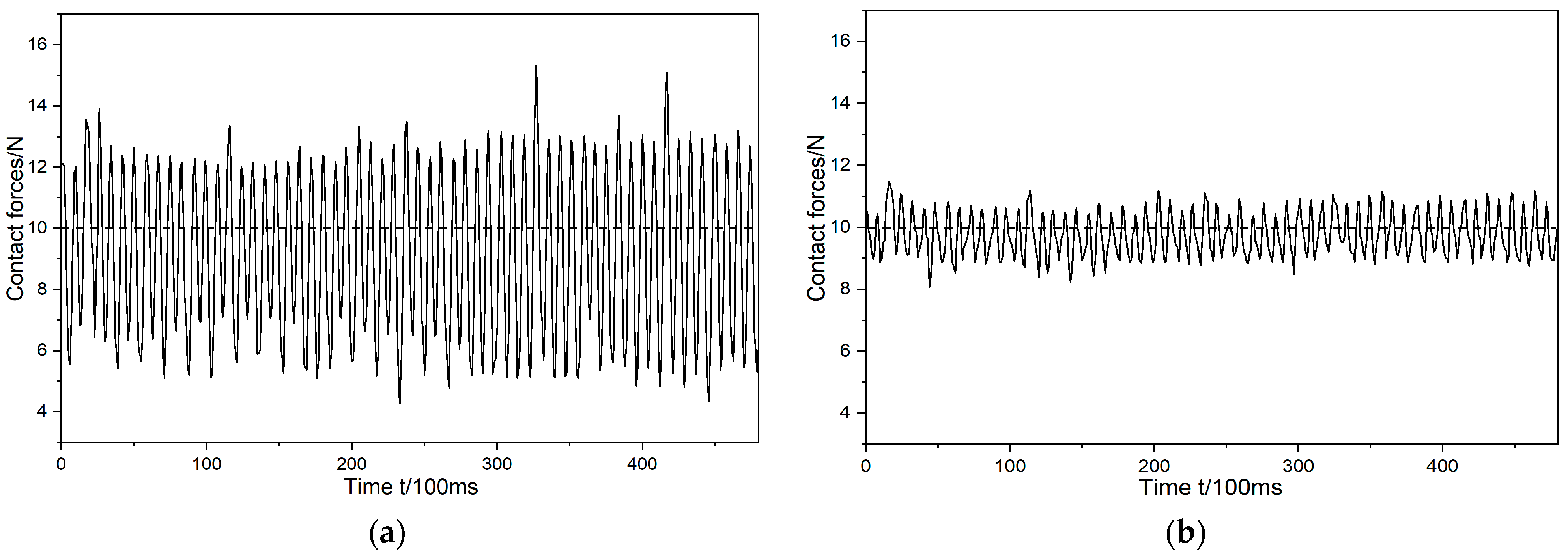
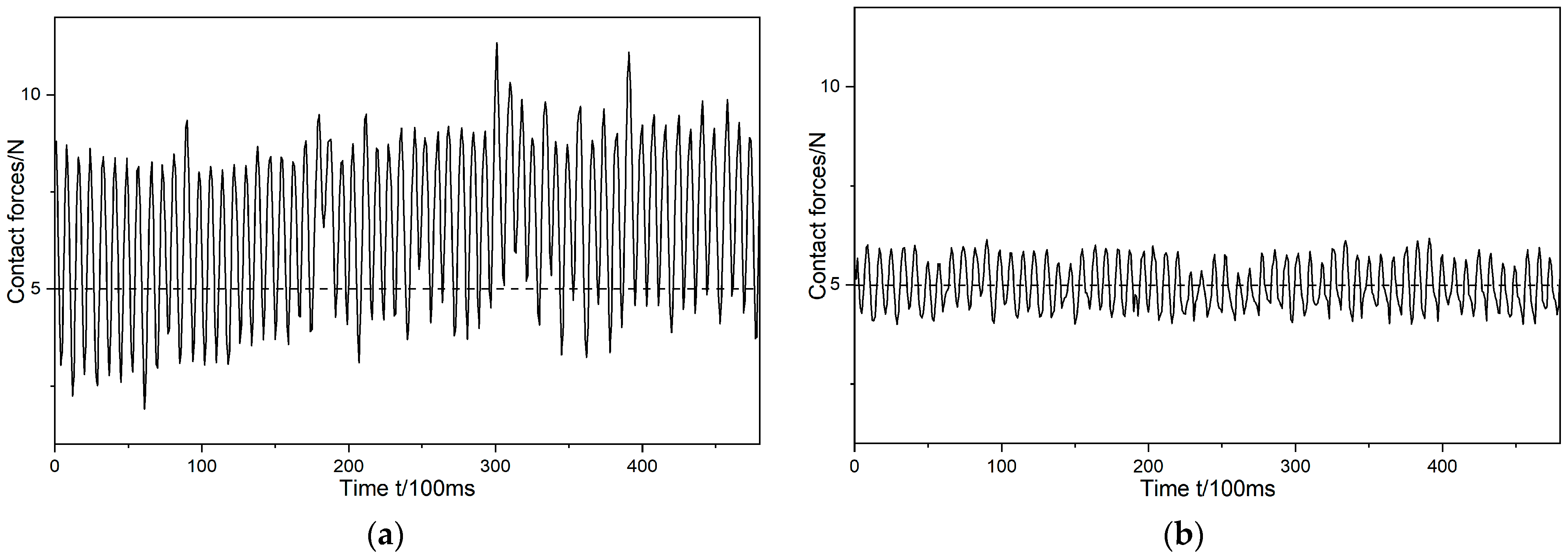
- This paper commences with an analytical study of the impedance control model. Building upon this impedance control framework, it presents research on a grinding trajectory adaptive generation method that combines the three-dimensional model of the workpiece, impedance control, and environmental parameter estimation. This paper then introduces the use of a deep genetic algorithm to compensate for contact force errors resulting from positional discrepancies. This optimization of the grinding trajectory is followed by the presentation of experimental research that led to the achievement of stable control of the grinding normal force at the expected contact force of 20 N, maintaining a level of around 20 ± 2.5 N. This marks a significant 68% reduction in grinding normal force compared to the teaching trajectory grinding. The entire grinding process demonstrates relative stability, with roughness reduced to approximately 2.2 μm, representing a 47% improvement in roughness accuracy over the teaching trajectory grinding. Furthermore, surface quality across various parts exhibits uniformity, contributing to enhanced accuracy of contact force tracking.
- (3)
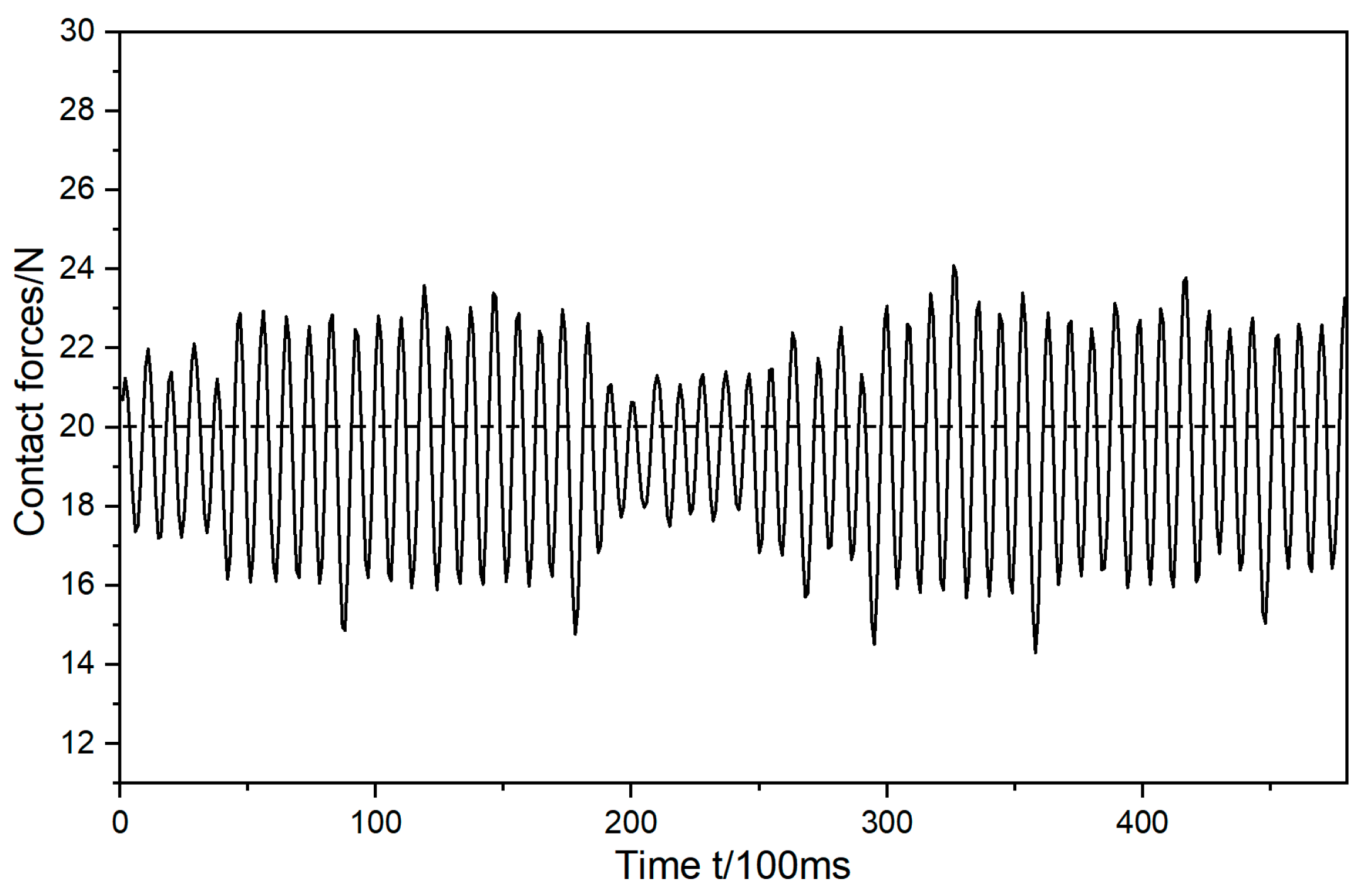
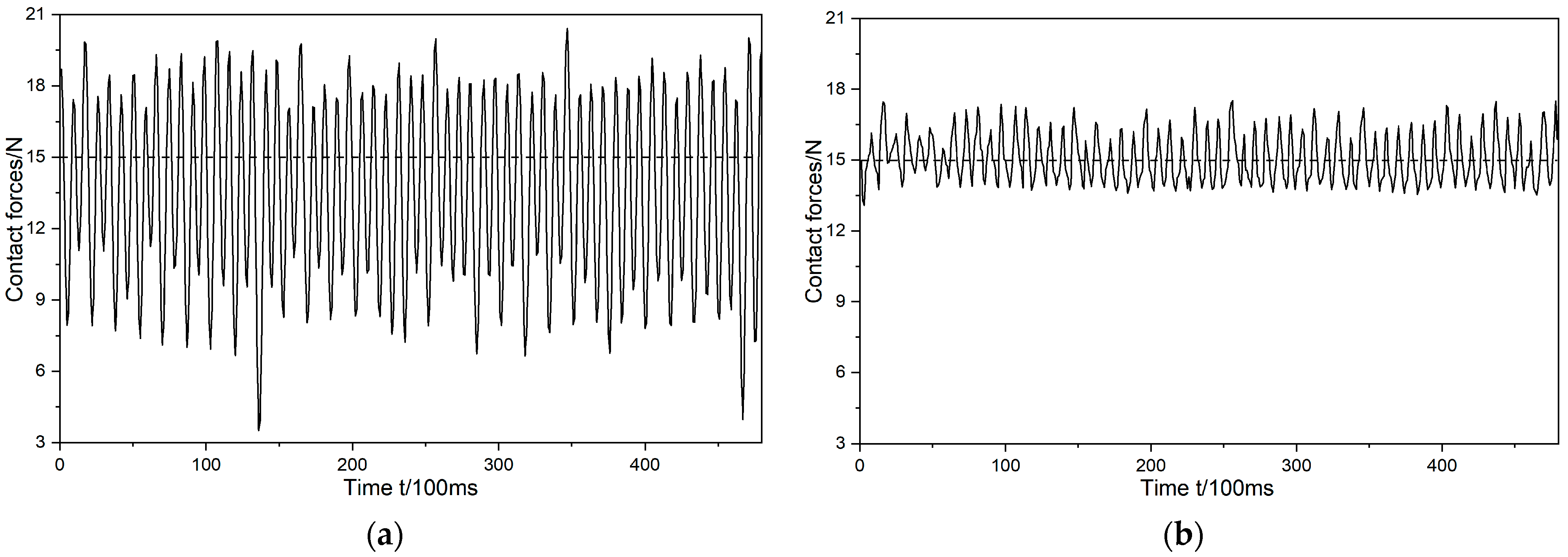
- This paper presents a comprehensive analytical study of the technological characteristics of irregularly shaped castings and establishes a dedicated experimental platform for validation. In the experiments, conducted under expected normal forces of 5 N, 10 N, and 15 N, the normal force during grinding was consistently stabilized at 5 ± 1 N, 10 ± 1.5 N, and 15 ± 2 N, respectively. These results represent reductions of 71.4%, 70%, and 75% compared to the teaching trajectory grinding, thereby ensuring process stability. Following the grinding process, the workpiece surfaces exhibit remarkable smoothness, with roughness values under the three different conditions decreasing significantly from 17.5 μm, 17.1 μm, and 18.7 μm to 1.5 μm, 1.6 μm, and 1.4 μm, respectively. These improvements represent substantial enhancements of 76%, 73%, and 78% compared to the teaching trajectory grinding roughness values of 6.3 μm, 6.0 μm, and 6.6 μm. The uniformity and consistency of the post-grinding surfaces not only fully meet the roughness criteria for complex curved workpieces but also underscore the efficacy of the method in precisely controlling contact forces in robotic contact-oriented tasks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ott, C.; Mukherjee, R.; Nakamura, Y. A hybrid system framework for unified impedance and admittance control. J. Intell. Robot. Syst. 2015, 78, 359–375. [Google Scholar] [CrossRef]
- Yang, R.; Yang, C.; Chen, M.; Na, J. Adaptive impedance control of robot manipulators based on Q-learning and disturbance observer. Syst. Sci. Control Eng. 2017, 5, 287–300. [Google Scholar] [CrossRef]
- Roveda, L.; Pallucca, G.; Pedrocchi, N.; Braghin, F.; Tosatti, L.M. Iterative learning procedure with reinforcement for high-accuracy force tracking in robotized tasks. IEEE Trans. Ind. Inform. 2017, 14, 1753–1763. [Google Scholar] [CrossRef]
- Kronander, K.; Billard, A. Stability Considerations for Variable Impedance Control. IEEE Trans. Robot. 2017, 32, 1298–1305. [Google Scholar] [CrossRef]
- Sharifi, M.; Behzadipour, S.; Vossoughi, G. Nonlinear model reference adaptive impedance control for human-robot interactions. Control Eng. Pract. 2014, 32, 9–27. [Google Scholar] [CrossRef]
- Braun, D.; Howard, M.; Vijayakumar, S. Optimal variable stiffness control: Formulation and application to explosive movement tasks. Auton. Robot. 2012, 33, 237–253. [Google Scholar] [CrossRef]
- Dong, Y.; Ren, B. UDE-Based Variable Impedance Control of Uncertain Robot Systems. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 2487–2498. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, J.C.; Min, X. Impedance Control and Parameter Optimization of Surface Polishing Robot Based on Reinforcement Learning. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2023, 237, 216–228. [Google Scholar] [CrossRef]
- Dai, S.; Liu, S.; Ji, W.; Li, S. Vibration Suppression in Macro–Micro Grinding System of Aeroengine Blade Based on Impedance Compensation Prediction Control Strategy. Int. J. Adv. Manuf. Technol. 2023, 125, 793–807. [Google Scholar] [CrossRef]
- Mallapragada, V.; Erol, D.; Sarkar, N. A New Method of Force Control for Unknown Environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–13 October 2006; pp. 4509–4514. [Google Scholar]
- Calanca, A.; Fiorini, P. Understanding environment-adaptive force control of series elastic actuators. IEEE/AsME Trans. Mechatron. 2018, 23, 413–423. [Google Scholar] [CrossRef]
- Lee, K.; Buss, M. Force tracking impedance control with variable target stiffness. IFAC Proc. Vol. 2008, 41, 6751–6756. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, C.; Fan, W. Robotic Magnetorheological Finishing Technology Based on Constant Polishing Force Control. Appl. Sci. 2022, 12, 3737. [Google Scholar] [CrossRef]
- Zhou, H.; Ma, S.; Wang, G.; Deng, Y.; Liu, Z. A hybrid control strategy for grinding and polishing robot based on adaptive impedance control. Adv. Mech. Eng. 2021, 13, 168781402110040. [Google Scholar] [CrossRef]
- Fateh, M.M.; Azargoshasb, S. Discrete adaptive fuzzy control for asymptotic tracking of robotic manipulators. Nonlinear Dyn. 2014, 78, 2195–2204. [Google Scholar] [CrossRef]
- Fateh, S.; Fateh, M.M. Adaptive Fuzzy Control of Robot Manipulators with Asymptotic Tracking Performance. J. Control Autom. Electr. Syst. 2020, 31, 52–61. [Google Scholar] [CrossRef]
- Lakshminarayanan, S.; Kana, S.; Mohan, D.M.; Manyar, O.M.; Then, D.; Campolo, D. An adaptive framework for robotic polishing based on impedance control. Int. J. Adv. Manuf. Technol. 2021, 112, 401–417. [Google Scholar] [CrossRef]
- Young, S.; Rose, D.; Karnowski, T.; Lim, S.; Patton, R. Optimizing Deep Learning Hyper-Parameters through an Evolutionary Algorithm. In Proceedings of the Workshop on Machine Learning in High-Performance Computing Environments, Austin, TX, USA, 15–20 November 2015; pp. 4:1–18. [Google Scholar]
- Lamos-Sweeney, J. Deep Learning Using Genetic Algorithms. Master’s Thesis, Department of Rochester Institute of Technology, New York, NY, USA, 2012. [Google Scholar]
- Lander, S. An Evolutionary Method for Training Auto Encoders for Deep Learning Networks. Master’s Thesis, Department of Computer Science, Missouri University, Columbia, MO, USA, 2014. [Google Scholar]
- Shao, L.; Liu, L.; Li, X. Feature Learning for Image Classification via Multi-Objective Genetic Programming. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 1359–1371. [Google Scholar] [CrossRef]
- Roveda, L.; Pedrocchi, N.; Tosatti, L.M. Exploiting impedance shaping approaches to overcome force overshoots in delicate interaction tasks. Int. J. Adv. Robot. Syst. 2016, 13, 1729881416662771. [Google Scholar] [CrossRef]
- Liang, X.; Zhao, H.; Li, X.; Ding, H. Force tracking impedance control with unknown environment via an iterative learning algorithm. Sci. China-Inf. Sci. 2019, 62, 050215. [Google Scholar] [CrossRef]
- Beltran-Hernandez, C.C.; Petit, D.; Ramirez-Alpizar, I.G.; Nishi, T.; Kikuchi, S.; Matsubara, T. Learning Force Control for Contact-Rich Manipulation Tasks With Rigid Position-Controlled Robots. IEEE Robot. Autom. Lett. 2020, 5, 5709–5716. [Google Scholar] [CrossRef]
- Deisenroth, M.P.; Fox, D.; Rasmussen, C.E. Gaussian Processes for Data-Efficient Learning in Robotics and Control. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 408–423. [Google Scholar] [CrossRef] [PubMed]
- Isela, B.; Fernando, R. A Dynamic-compensation Approach to Impedance Control of Robot Manipulators. J. Intell. Robot. Syst. 2011, 63, 51–73. [Google Scholar]
- Tsuji, T.; Tanaka, Y. On-line learning of robot arm impedance using neural networks. Robot. Auton. Syst. 2005, 52, 257–271. [Google Scholar] [CrossRef]
- Chen, S.; Wang, Z.; Chakraborty, A.; Klecka, M.; Saunders, G.; Wen, J. Robotic Deep Rolling With Iterative Learning Motion and Force Control. IEEE Robot. Autom. Lett. 2020, 5, 5581–5588. [Google Scholar] [CrossRef]
- Izadbakhsh, A.; Khorashadizadeh, S.; Ghandali, S. Robust adaptive impedance control of robot manipulators using Szász–Mirakyan operator as universal approximator. ISA Trans. 2020, 106, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Nazmara, G.; Fateh, M.M.; Ahmadi, S.M. A model-reference impedance control of robot manipulators using an adaptive fuzzy uncertainty estimator. Int. J. Comput. Intell. Syst. 2018, 11, 979–990. [Google Scholar] [CrossRef]
- Sohail, A. Genetic algorithms in the fields of artificial intelligence and data sciences. Ann. Data Sci. 2023, 10, 1007–1018. [Google Scholar] [CrossRef]
- Khatri, K.C.A.; Shah, K.B.; Logeshwaran, J.; Shrestha, A. Genetic algorithm based techno-economic optimization of an isolated hybrid energy system. CRF 2023, 8, 1447–1450. [Google Scholar]
- Gu, Z.; Lu, W.; Fan, Y.; Gao, Y. Automated simplified structural modeling method for megatall buildings based on genetic algorithm. J. Build. Eng. 2023, 77, 107485. [Google Scholar] [CrossRef]
- Pan, Y.; Yang, Y.; Liu, H.; Li, W. UAVs and mobile sensors trajectories optimization with deep learning trained by genetic algorithm towards data collection scenario. Mob. Netw. Appl. 2023, 28, 808–823. [Google Scholar] [CrossRef]
- Ayan, E. Genetic Algorithm-Based Hyperparameter Optimization for Convolutional Neural Networks in the Classification of Crop Pests. Arab. J. Sci. Eng. 2023, 8, 1–15. [Google Scholar] [CrossRef]
- Voronkov, A.D.; Diane, S.A.K. Continuous Genetic Algorithm for Grasping an Object of a Priori Unknown Shape by a Robotic Manipulator. Russ. Technol. J. 2023, 11, 18–30. [Google Scholar] [CrossRef]
- Sehgal, A.; La, H.; Louis, S.; Nguyen, H. Deep reinforcement learning using genetic algorithm for parameter optimization. In Proceedings of the 2019 Third IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 25–27 February 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 596–601. [Google Scholar]
- Lee, S.; Kim, J.; Kang, H.; Kang, D.-Y.; Park, J. Genetic algorithm based deep learning neural network structure and hyperparameter optimization. Appl. Sci. 2021, 11, 744. [Google Scholar] [CrossRef]
- Wang, L.C.; Chen, C.C.; Hsu, C.C. Applying machine learning and GA for process parameter optimization in car steering wheel manufacturing. Int. J. Adv. Manuf. Technol. 2022, 122, 4389–4403. [Google Scholar] [CrossRef]
- Qie, X.; Kang, C.; Zong, G.; Chen, S. Trajectory planning and simulation study of redundant robotic arm for upper limb rehabilitation based on back propagation neural network and genetic algorithm. Sensors 2022, 22, 4071. [Google Scholar] [CrossRef]
- Rajasimman, M.A.V.; Manoharan, R.K.; Subramani, N.; Aridoss, M.; Galety, M.G. Robust facial expression recognition using an evolutionary algorithm with a deep learning model. Appl. Sci. 2022, 13, 468. [Google Scholar] [CrossRef]
- Moussafir, M.; Chaibi, H.; Saadane, R.; Chehri, A.; Rharras, A.E.; Jeon, G. Design of efficient techniques for tomato leaf disease detection using genetic algorithm-based and deep neural networks. Plant Soil 2022, 479, 251–266. [Google Scholar] [CrossRef]
- Mishra, V.; Kane, L. A survey of designing convolutional neural network using evolutionary algorithms. Artif. Intell. Rev. 2023, 56, 5095–5132. [Google Scholar] [CrossRef]
- Kotyrba, M.; Volna, E.; Habiballa, H.; Czyz, J. The Influence of Genetic Algorithms on Learning Possibilities of Artificial Neural Networks. Computers 2022, 11, 70. [Google Scholar] [CrossRef]
- Erden, C. Genetic algorithm-based hyperparameter optimization of deep learning models for PM2.5 time-series prediction. Int. J. Environ. Sci. Technol. 2023, 20, 2959–2982. [Google Scholar] [CrossRef]
- Tameswar, K.; Suddul, G.; Dookhitram, K. A hybrid deep learning approach with genetic and coral reefs metaheuristics for enhanced defect detection in software. Int. J. Inf. Manag. Data Insights 2022, 2, 100105. [Google Scholar] [CrossRef]
- Ji, H.; Wang, M.; Sun, M.; Liu, Q. Neural network classifier based on genetic algorithm image segmentation of subject robot optimisation system. Int. J. Grid Util. Comput. 2021, 12, 369–379. [Google Scholar] [CrossRef]





| Working Condition | Contour Analysis Image | Surface Roughness Trend Graph |
|---|---|---|
| Unpolished workpiece surface | 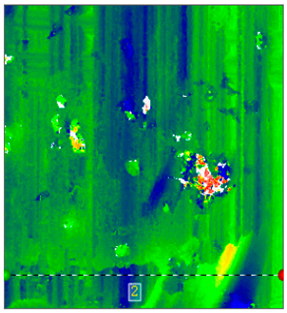 | 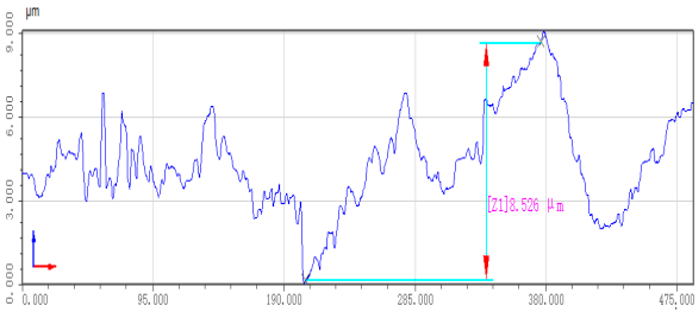 |
| Robot teaching trajectory grinding |  | 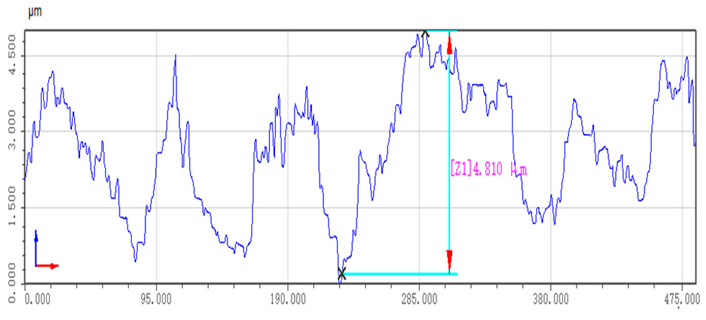 |
| Estimating grinding trajectory based on environmental parameters |  | 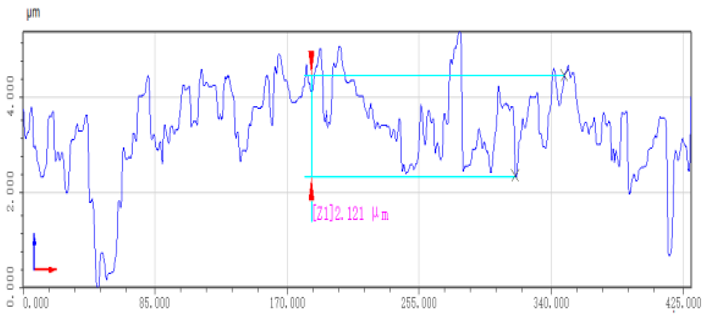 |
| Working Condition | Contour Analysis Image | Surface Roughness Trend Graph |
|---|---|---|
| Workpiece surface after optimization by deep genetic algorithm | 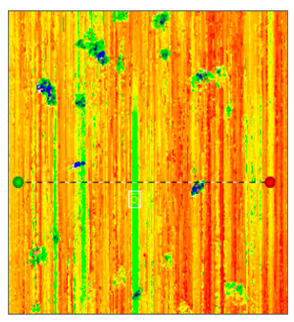 |  |
| Working Condition | Contour Analysis Image | Surface Roughness Trend Graph |
|---|---|---|
| Unpolished workpiece |  | 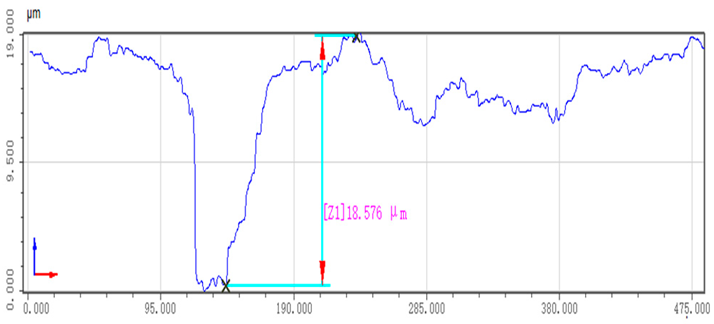 |
| Teaching trajectory grinding | 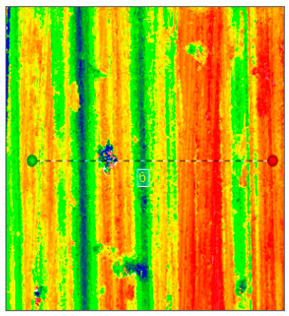 | 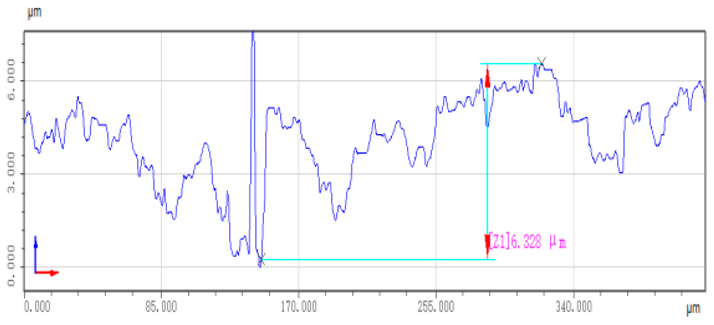 |
| Optimization of grinding trajectories | 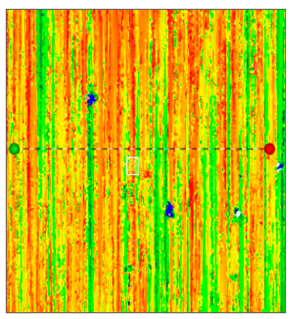 | 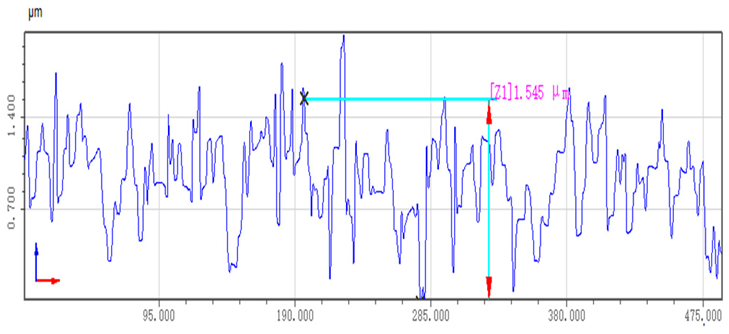 |
| Working Condition | Contour Analysis Image | Surface Roughness Trend Graph |
|---|---|---|
| Unpolished workpiece surface | 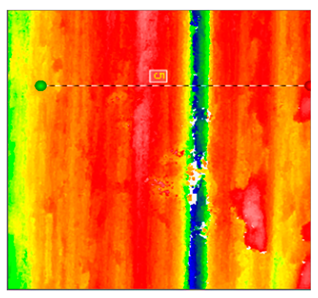 | 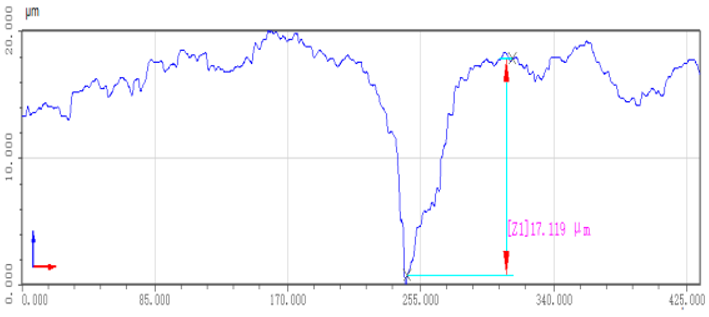 |
| Robot teaching trajectory grinding | 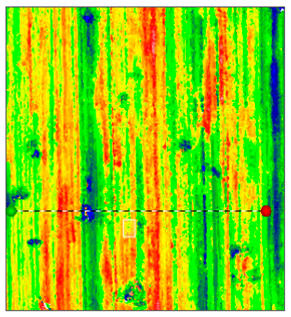 |  |
| Optimization of grinding trajectories | 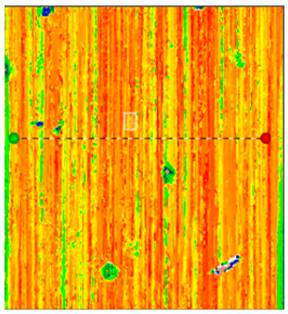 | 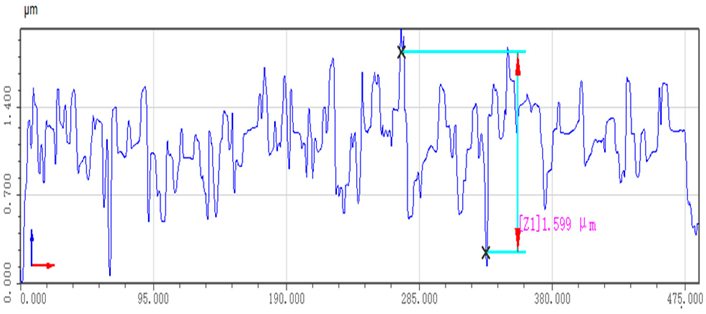 |
| Working Condition | Contour Analysis Image | Surface Roughness Trend Graph |
|---|---|---|
| Unpolished workpiece surface |  | 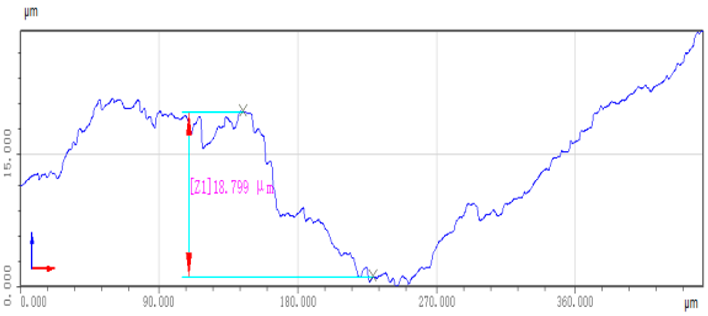 |
| Teaching trajectory grinding |  |  |
| Optimization of grinding trajectories |  |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, M.; Zhou, C.; Lv, Z.; Zheng, L.; Feng, W.; Wu, T.; Zhang, X. Research on a Method of Robot Grinding Force Tracking and Compensation Based on Deep Genetic Algorithm. Machines 2023, 11, 1075. https://doi.org/10.3390/machines11121075
Meng M, Zhou C, Lv Z, Zheng L, Feng W, Wu T, Zhang X. Research on a Method of Robot Grinding Force Tracking and Compensation Based on Deep Genetic Algorithm. Machines. 2023; 11(12):1075. https://doi.org/10.3390/machines11121075
Chicago/Turabian StyleMeng, Minghui, Chuande Zhou, Zhongliang Lv, Lingbo Zheng, Wei Feng, Ting Wu, and Xuewei Zhang. 2023. "Research on a Method of Robot Grinding Force Tracking and Compensation Based on Deep Genetic Algorithm" Machines 11, no. 12: 1075. https://doi.org/10.3390/machines11121075
APA StyleMeng, M., Zhou, C., Lv, Z., Zheng, L., Feng, W., Wu, T., & Zhang, X. (2023). Research on a Method of Robot Grinding Force Tracking and Compensation Based on Deep Genetic Algorithm. Machines, 11(12), 1075. https://doi.org/10.3390/machines11121075






