Precision Face Milling of Maraging Steel 350: An Experimental Investigation and Optimization Using Different Machine Learning Techniques
Abstract
:1. Introduction
- An experimental investigation of the effect of face milling parameters on responses, including surface roughness, power consumption, cutting temperature, and material removal rate, to provide an understanding of the inherent machining challenges;
- A comparative study of five different machine learning models to predict machining responses. The ML approaches examined are SVM, K-KNN, ANN, random forest, and XGBoost;
- Additionally, multi-objective optimization of process parameters using different weighting methods and the genetic algorithm (GA) was conducted for precision face milling of maraging steel 350.
2. Materials Preparation and Methodology
3. Result and Discussion
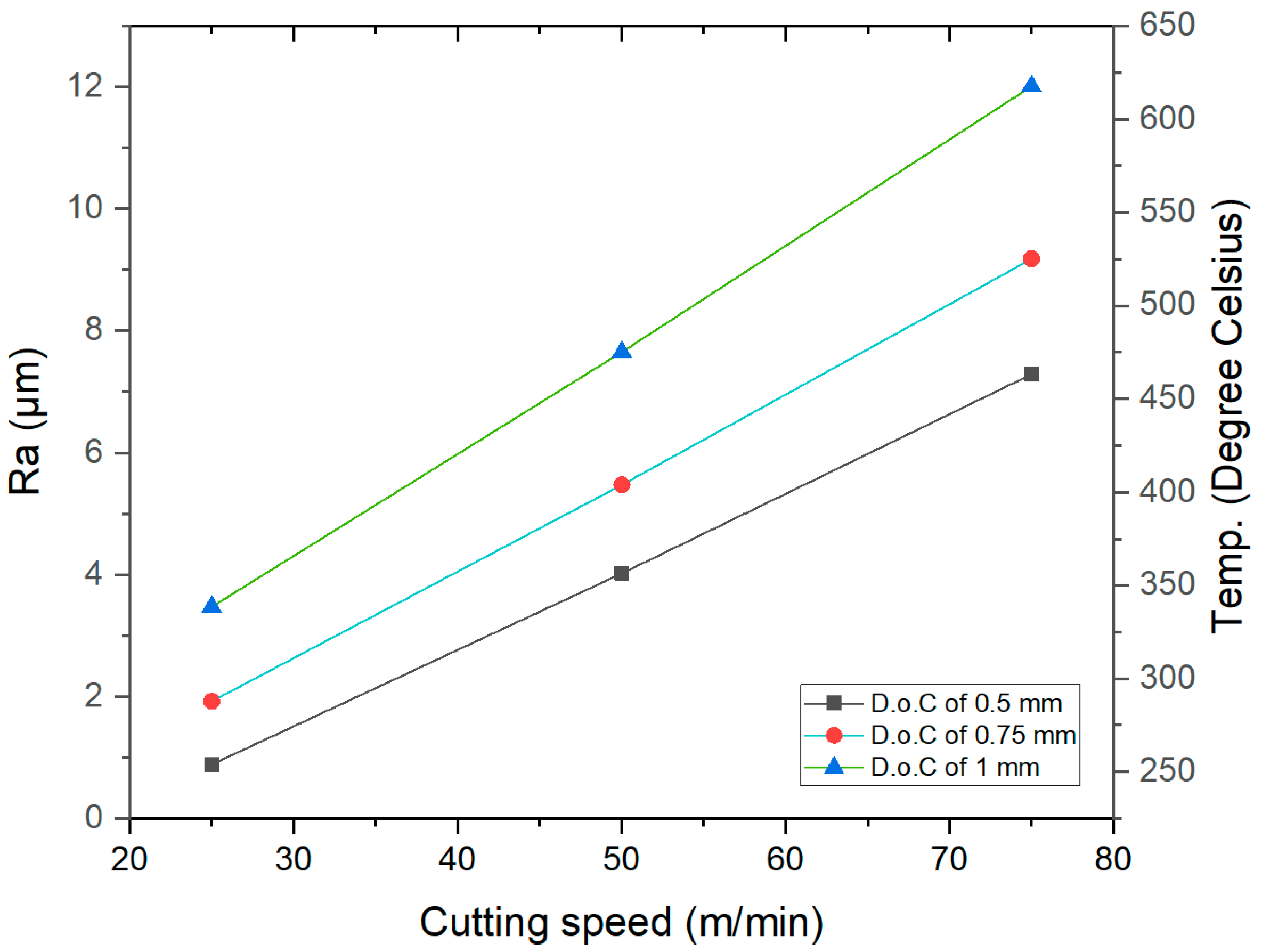
3.1. Effect of Process Parameters on Surface Quality
3.2. Effect of Process Parameters on Cutting Temperature
3.3. Effect of Process Parameters on MRR and Power Consumption
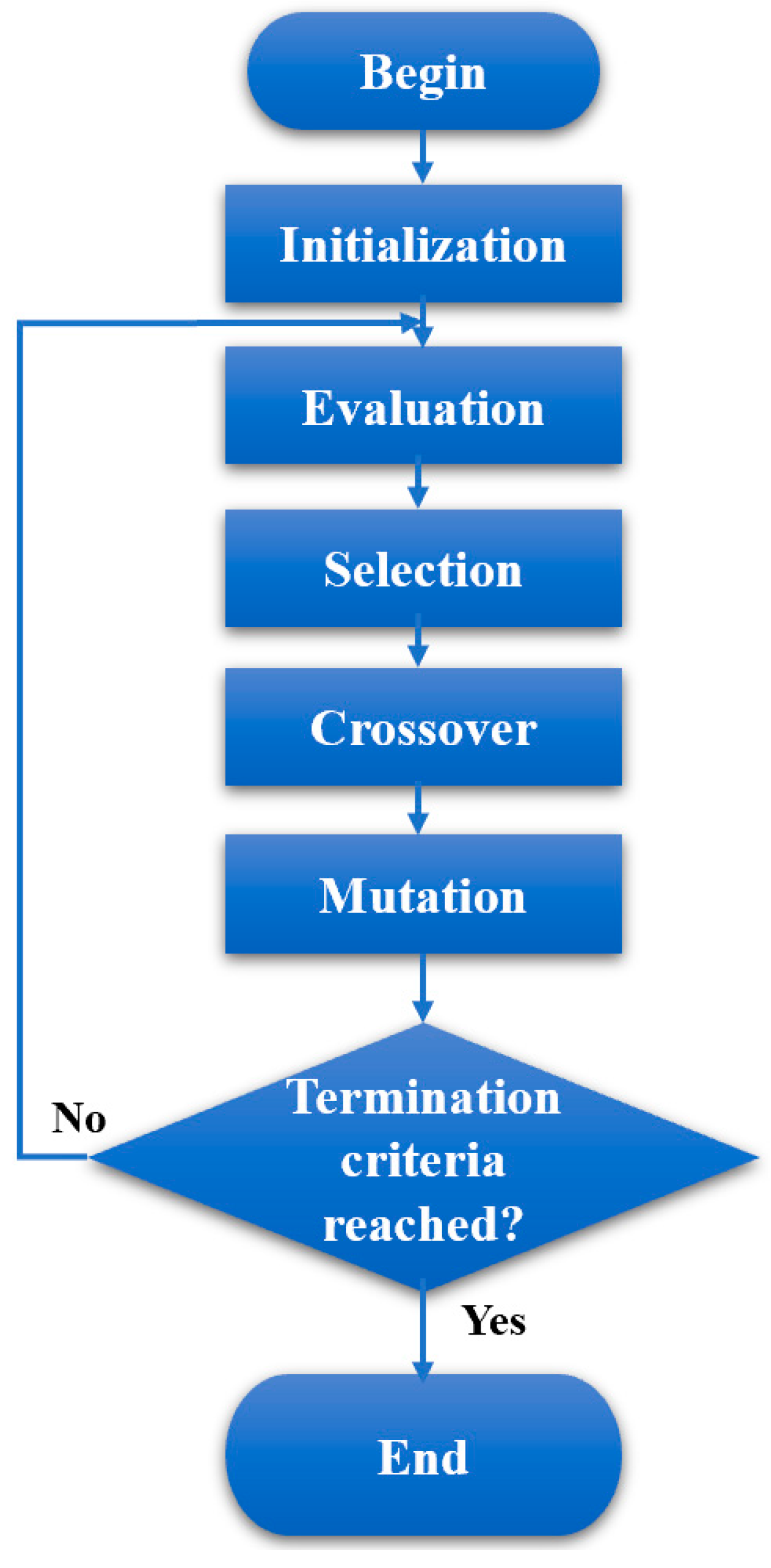
4. ML Algorithms Adopted
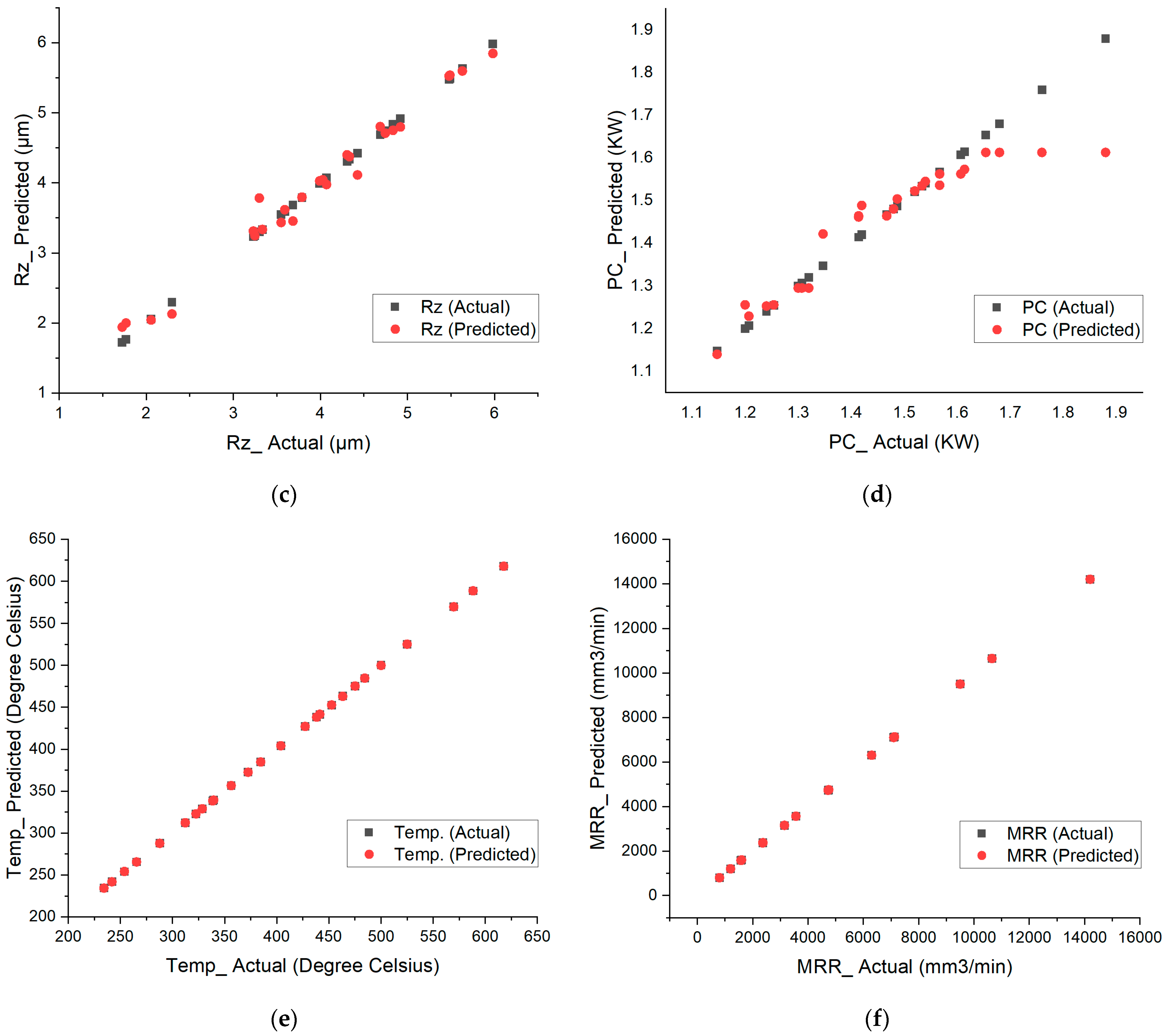
5. Comparative Results of ML Algorithms
6. Optimal XGBoost Prediction of Responses
7. Multi-Objective Optimization of Process Parameters
8. Conclusions
- The intricate interplay between cutting speed and feed rate has been identified as a pivotal factor influencing surface finish. A 50 m/min cutting speed threshold was recognized, beyond which surface roughness escalated due to heightened friction and temperature;
- Increasing the cutting speed led to a proportional rise in cutting temperature. These insights underline the need for strategic control of speed to mitigate thermal effects, optimizing tool longevity and surface integrity;
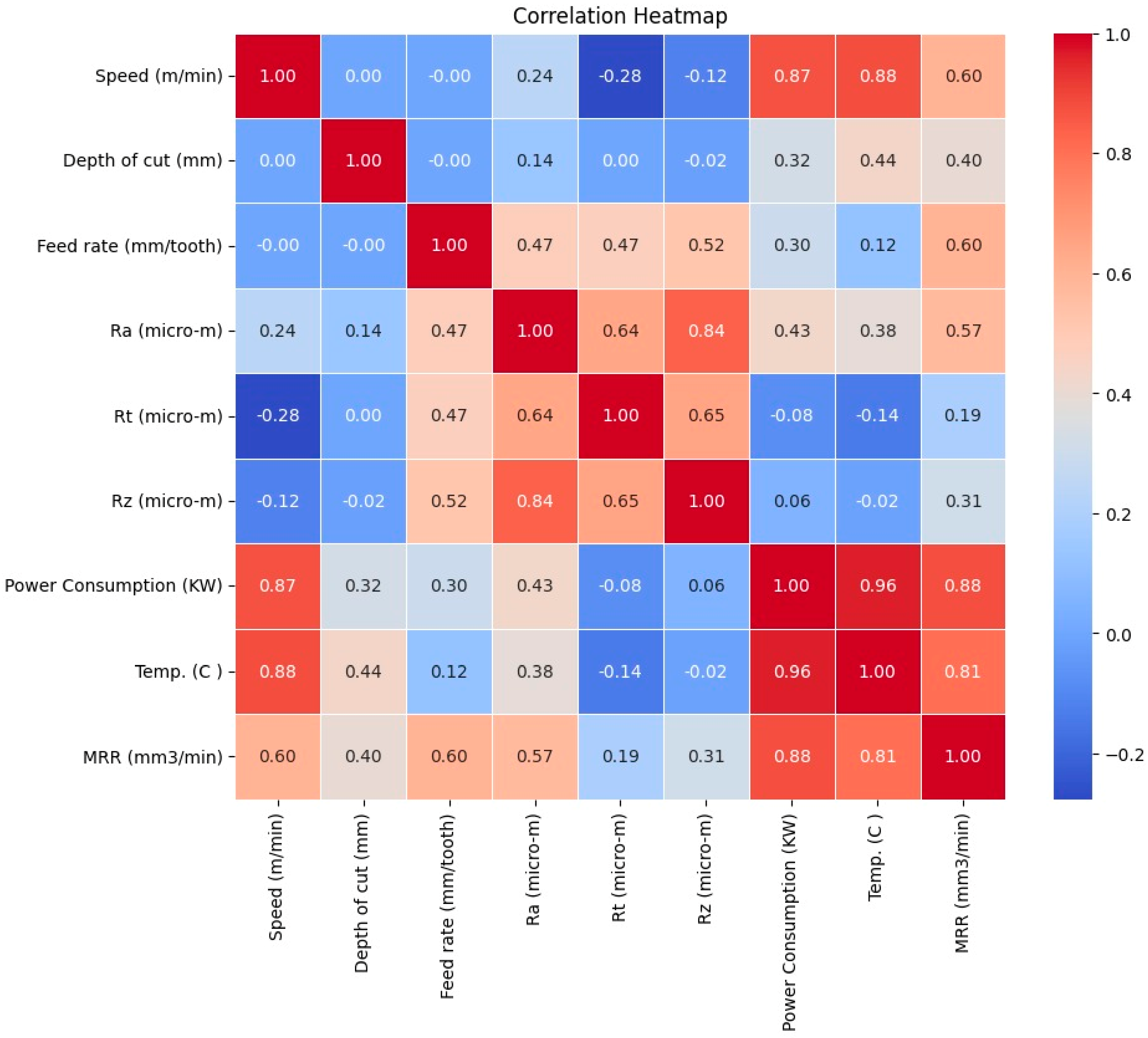
- The relationship between power consumption and MRR in terms of cutting speed, D.o.C, and feed rate was established. This relationship provides a foundational understanding for balancing operational efficiency with energy consumption;
- Among the evaluated machine learning models, XGBoost demonstrated superior performance, validating its aptitude for modeling complex, non-linear relationships inherent in machining processes. Its predictive accuracy stood at a commendable 98%;
- The employment of the genetic algorithm (GA) in optimizing XGBoost’s hyperparameters further refined the model’s predictive power. The optimization balanced multiple objectives, ensuring holistic performance improvement;
- A comparative analysis of equal weights and AHP-based weights emphasized the consistency in optimization outcomes, underscoring the model’s robustness and adaptability to diverse weighting scenarios.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pardal, J.; Tavares, S.; Terra, V.; Da Silva, M.; Dos Santos, D. Modeling of precipitation hardening during the aging and overaging of 18Ni–Co–Mo–Ti maraging 300 steel. J. Alloys Compd. 2005, 393, 109–113. [Google Scholar] [CrossRef]
- Chandraker, S. Taguchi analysis on cutting force and surface roughness in turning MDN350 steel. Mater. Today Proc. 2015, 2, 3388–3393. [Google Scholar]
- Jägle, E.A.; Choi, P.-P.; Van Humbeeck, J.; Raabe, D. Precipitation and austenite reversion behavior of a maraging steel produced by selective laser melting. J. Mater. Res. 2014, 29, 2072–2079. [Google Scholar] [CrossRef]
- Casalino, G.; Campanelli, S.; Contuzzi, N.; Ludovico, A. Experimental investigation and statistical optimisation of the selective laser melting process of a maraging steel. Opt. Laser Technol. 2015, 65, 151–158. [Google Scholar] [CrossRef]
- Fortunato, A.; Lulaj, A.; Melkote, S.; Liverani, E.; Ascari, A.; Umbrello, D. Milling of maraging steel components produced by selective laser melting. Int. J. Adv. Manuf. Technol. 2018, 94, 1895–1902. [Google Scholar] [CrossRef]
- Santhanakumar, M.; Adalarasan, R.; Siddharth, S.; Velayudham, A. An investigation on surface finish and flank wear in hard machining of solution treated and aged 18% Ni maraging steel. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 2071–2084. [Google Scholar] [CrossRef]
- Stachurski, W.; Sawicki, J.; Wójcik, R.; Nadolny, K. Influence of application of hybrid MQL-CCA method of applying coolant during hob cutter sharpening on cutting blade surface condition. J. Clean. Prod. 2018, 171, 892–910. [Google Scholar] [CrossRef]
- Benedicto, E.; Carou, D.; Rubio, E. Technical, economic and environmental review of the lubrication/cooling systems used in machining processes. Procedia Eng. 2017, 184, 99–116. [Google Scholar] [CrossRef]
- Sharma, V.S.; Singh, G.; Sørby, K. A review on minimum quantity lubrication for machining processes. Mater. Manuf. Process. 2015, 30, 935–953. [Google Scholar] [CrossRef]
- Tomaz, Í.V.; Pardal, J.M.; Fonseca, M.C. Influence of minimum quantity lubrication in the surface quality of milled maraging steel. Int. J. Adv. Manuf. Technol. 2019, 104, 4301–4311. [Google Scholar] [CrossRef]
- Helmy, M.O.; El-Hofy, M.; El-Hofy, H. Effect of cutting fluid delivery method on ultrasonic assisted edge trimming of multidirectional CFRP composites at different machining conditions. Procedia CIRP 2018, 68, 450–455. [Google Scholar] [CrossRef]
- Helmy, M.O.; El-Hofy, M.; El-Hofy, H. Influence of process parameters on the ultrasonic assisted edge trimming of aerospace CFRP laminates using MQL. Int. J. Mach. Mach. Mater. 2020, 22, 349–373. [Google Scholar] [CrossRef]
- Beake, B.; Ning, L.; Gey, C.; Veldhuis, S.; Kornberg, A.; Weaver, A.; Khanna, M.; Fox-Rabinovich, G. Wear performance of different PVD coatings during hard wet end milling of H13 tool steel. Surf. Coat. Technol. 2015, 279, 118–125. [Google Scholar] [CrossRef]
- Mo, J.; Zhu, M.; Leyland, A.; Matthews, A. Impact wear and abrasion resistance of CrN, AlCrN and AlTiN PVD coatings. Surf. Coat. Technol. 2013, 215, 170–177. [Google Scholar] [CrossRef]
- Mo, J.; Zhu, M. Sliding tribological behaviors of PVD CrN and AlCrN coatings against Si3N4 ceramic and pure titanium. Wear 2009, 267, 874–881. [Google Scholar] [CrossRef]
- Varghese, V.; Akhil, K.; Ramesh, M.; Chakradhar, D. Investigation on the performance of AlCrN and AlTiN coated cemented carbide inserts during end milling of maraging steel under dry, wet and cryogenic environments. J. Manuf. Process. 2019, 43, 136–144. [Google Scholar] [CrossRef]
- Lou, S.; Jiang, X.; Sun, W.; Zeng, W.; Pagani, L.; Scott, P. Characterisation methods for powder bed fusion processed surface topography. Precis. Eng. 2019, 57, 1–15. [Google Scholar] [CrossRef]
- Promoppatum, P.; Yao, S.-C. Analytical evaluation of defect generation for selective laser melting of metals. Int. J. Adv. Manuf. Technol. 2019, 103, 1185–1198. [Google Scholar] [CrossRef]
- Bai, Y.; Yang, Y.; Xiao, Z.; Wang, D. Selective laser melting of maraging steel: Mechanical properties development and its application in mold. Rapid Prototyp. J. 2018, 24, 623–629. [Google Scholar] [CrossRef]
- Mercelis, P.; Kruth, J.P. Residual stresses in selective laser sintering and selective laser melting. Rapid Prototyp. J. 2006, 12, 254–265. [Google Scholar] [CrossRef]
- Withers, P.J.; Bhadeshia, H. Residual stress. Part 1–measurement techniques. Mater. Sci. Technol. 2001, 17, 355–365. [Google Scholar] [CrossRef]
- Bhardwaj, T.; Shukla, M. Effect of laser scanning strategies on texture, physical and mechanical properties of laser sintered maraging steel. Mater. Sci. Eng. A 2018, 734, 102–109. [Google Scholar] [CrossRef]
- Tamura, S.; Ezura, A.; Matsumura, T. Cutting Force in Peripheral Milling of Additively Manufactured Maraging Steel. Int. J. Autom. Technol. 2022, 16, 897–905. [Google Scholar] [CrossRef]
- Oliveira, A.; Jardini, A.; Del Conte, E. Effects of cutting parameters on roughness and residual stress of maraging steel specimens produced by additive manufacturing. Int. J. Adv. Manuf. Technol. 2020, 111, 2449–2459. [Google Scholar] [CrossRef]
- Abbas, A.T.; Sharma, N.; Alsuhaibani, Z.A.; Sharma, A.; Farooq, I.; Elkaseer, A. Multi-Objective Optimization of AISI P20 Mold Steel Machining in Dry Conditions Using Machine Learning—TOPSIS Approach. Machines 2023, 11, 748. [Google Scholar] [CrossRef]
- Abbas, A.T.; Sharma, N.; Al-Bahkali, E.A.; Sharma, V.S.; Farooq, I.; Elkaseer, A. A Machine Learning Perspective to the Investigation of Surface Integrity of Al/SiC/Gr Composite on EDM. J. Manuf. Mater. Process. 2023, 7, 163. [Google Scholar] [CrossRef]
- Chakraborty, D.; Elzarka, H. Advanced machine learning techniques for building performance simulation: A comparative analysis. J. Build. Perform. Simul. 2019, 12, 193–207. [Google Scholar] [CrossRef]
- Abbas, A.T.; Pimenov, D.Y.; Erdakov, I.N.; Mikolajczyk, T.; Soliman, M.S.; El Rayes, M.M. Optimization of cutting conditions using artificial neural networks and the Edgeworth-Pareto method for CNC face-milling operations on high-strength grade-H steel. Int. J. Adv. Manuf. Technol. 2019, 105, 2151–2165. [Google Scholar] [CrossRef]
- Zou, M.; Jiang, W.-G.; Qin, Q.-H.; Liu, Y.-C.; Li, M.-L. Optimized XGBoost model with small dataset for predicting relative density of Ti-6Al-4V parts manufactured by selective laser melting. Materials 2022, 15, 5298. [Google Scholar] [CrossRef]
- Richetti, A.; Machado, A.; Da Silva, M.; Ezugwu, E.; Bonney, J. Influence of the number of inserts for tool life evaluation in face milling of steels. Int. J. Mach. Tools Manuf. 2004, 44, 695–700. [Google Scholar] [CrossRef]
- Kilundu, B.; Dehombreux, P.; Chiementin, X. Tool wear monitoring by machine learning techniques and singular spectrum analysis. Mech. Syst. Signal Process. 2011, 25, 400–415. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D.; Zhao, Q.; Wang, L.; Yin, K. Comparison of random forest, artificial neural networks and support vector machine for intelligent diagnosis of rotating machinery. Trans. Inst. Meas. Control 2018, 40, 2681–2693. [Google Scholar] [CrossRef]
- Prihatno, A.T.; Nurcahyanto, H.; Jang, Y.M. Predictive maintenance of relative humidity using random forest method. In Proceedings of the 2021 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Jeju Island, Republic of Korea, 13–16 April 2021; pp. 497–499. [Google Scholar]
- Zhang, K.; Gu, C.; Zhu, Y.; Chen, S.; Dai, B.; Li, Y.; Shu, X. A novel seepage behavior prediction and lag process identification method for concrete dams using HGWO-XGBoost model. IEEE Access 2021, 9, 23311–23325. [Google Scholar] [CrossRef]
- Lambora, A.; Gupta, K.; Chopra, K. Genetic algorithm—A literature review. In Proceedings of the 2019 International Conference on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 14–16 February 2019; pp. 380–384. [Google Scholar]
- Nayak, B.; Mahapatra, S. Multi-response optimization of WEDM process parameters using the AHP and TOPSIS method. Int. J. Theor. Appl. Res. Mech. Eng. 2013, 2, 109–215. [Google Scholar]
- Saaty, T.L. Decision making with the analytic hierarchy process. Int. J. Serv. Sci. 2008, 1, 83–98. [Google Scholar] [CrossRef]






| Element | Ni | Co | Mo | Ti | Al | Cu | C | Cr | Mn | Fe |
|---|---|---|---|---|---|---|---|---|---|---|
| weight (wt.%) | 18.164 | 12.173 | 4.06 | 2.211 | 0.147 | 0.010 | 0.032 | 0.004 | 0.022 | 63.177 |
| Description | Unit | Value |
|---|---|---|
| Ultimate tensile strength | MPa | 1132 |
| Yield strength | MPa | 1080 |
| Young’s modulus | GPa | 200 |
| Elongation | % | 22.5 |
| Hardness | HRc | 38 |
| Parameters | Unit | Levels | ||
|---|---|---|---|---|
| Cutting Speed | m/min | 20 | 50 | 75 |
| D.o.C | mm | 0.5 | 0.75 | 1.0 |
| Feed per Tooth | mm/tooth | 0.05 | 0.10 | 0.15 |
| Feature | Specification |
|---|---|
| Measurement Range | −20 to 1000 °C |
| Thermal Sensitivity | ≤0.08 °C at 30 °C |
| Set Emissivity for Steel | 0.18 |
| Accuracy | ±2 °C |
| Spectral Range | 8–14 μm |
| Detector type | Micro-bolometer—UFPA384 × 288 pixels |
| Test No. | Speed m/min | D.o.C (mm) | Feed Rate (mm/tooth) | Surface Roughness | Power Consumption (KW) | Temp. (°C) | MRR (mm3/min) | ||
|---|---|---|---|---|---|---|---|---|---|
| Ra (µm) | Rt (µm) | Rz (µm) | |||||||
| 1 | 25 | 0.5 | 0.05 | 0.753 | 8.606 | 4.92 | 1.147 | 234.2 | 800 |
| 2 | 25 | 0.5 | 0.1 | 0.765 | 8.729 | 5.489 | 1.2 | 241.9 | 1575 |
| 3 | 25 | 0.5 | 0.15 | 0.884 | 9.059 | 5.632 | 1.254 | 253.9 | 2375 |
| 4 | 25 | 0.75 | 0.05 | 0.601 | 7.236 | 3.79 | 1.207 | 265.5 | 1200 |
| 5 | 25 | 0.75 | 0.1 | 0.628 | 7.972 | 4.437 | 1.267 | 274.1 | 2363 |
| 6 | 25 | 0.75 | 0.15 | 0.691 | 8.286 | 4.688 | 1.307 | 287.8 | 3563 |
| 7 | 25 | 1 | 0.05 | 0.517 | 5.922 | 3.55 | 1.24 | 312.3 | 1600 |
| 8 | 25 | 1 | 0.1 | 0.543 | 6.972 | 4.029 | 1.3 | 322.5 | 3150 |
| 9 | 25 | 1 | 0.15 | 0.585 | 7.324 | 4.335 | 1.32 | 338.6 | 4750 |
| 10 | 50 | 0.5 | 0.05 | 0.261 | 3.905 | 1.768 | 1.347 | 328.7 | 1575 |
| 11 | 50 | 0.5 | 0.1 | 0.52 | 7.081 | 3.334 | 1.414 | 339.5 | 3150 |
| 12 | 50 | 0.5 | 0.15 | 0.674 | 9.124 | 4.427 | 1.467 | 356.4 | 4750 |
| 13 | 50 | 0.75 | 0.05 | 0.256 | 3.259 | 1.724 | 1.414 | 372.6 | 2363 |
| 14 | 50 | 0.75 | 0.1 | 0.634 | 4.489 | 3.248 | 1.487 | 384.7 | 4725 |
| 15 | 50 | 0.75 | 0.15 | 0.813 | 12.477 | 4.071 | 1.52 | 403.9 | 7125 |
| 16 | 50 | 1 | 0.05 | 0.371 | 3.494 | 2.296 | 1.48 | 438.3 | 3150 |
| 17 | 50 | 1 | 0.1 | 0.592 | 5.201 | 3.231 | 1.534 | 452.6 | 6300 |
| 18 | 50 | 1 | 0.15 | 0.698 | 6.73 | 3.993 | 1.567 | 475.2 | 9500 |
| 19 | 75 | 0.5 | 0.05 | 0.365 | 5.164 | 2.057 | 1.42 | 427.3 | 2375 |
| 20 | 75 | 0.5 | 0.1 | 0.606 | 4.965 | 3.686 | 1.54 | 441.4 | 4750 |
| 21 | 75 | 0.5 | 0.15 | 0.652 | 3.682 | 3.299 | 1.614 | 463.3 | 7100 |
| 22 | 75 | 0.75 | 0.05 | 0.842 | 5.361 | 4.747 | 1.567 | 484.4 | 3563 |
| 23 | 75 | 0.75 | 0.1 | 0.858 | 6.363 | 5.479 | 1.654 | 500.1 | 7125 |
| 24 | 75 | 0.75 | 0.15 | 0.875 | 7.042 | 5.983 | 1.68 | 525.1 | 10,650 |
| 25 | 75 | 1 | 0.05 | 0.886 | 7.763 | 3.592 | 1.607 | 569.8 | 4750 |
| 26 | 75 | 1 | 0.1 | 0.902 | 8.307 | 4.307 | 1.76 | 588.4 | 9500 |
| 27 | 75 | 1 | 0.15 | 0.989 | 8.695 | 4.835 | 1.88 | 617.8 | 14,200 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Speed | 2 | 0.259 | 0.129 | 34.940 | 0.000 | Significant |
| D.o.C | 2 | 0.033 | 0.017 | 4.470 | 0.050 | Not Significant |
| Feed rate | 2 | 0.227 | 0.113 | 30.660 | 0.000 | Significant |
| Speed * D.o.C | 4 | 0.330 | 0.082 | 22.280 | 0.000 | Significant |
| Speed * Feed rate | 4 | 0.109 | 0.027 | 7.370 | 0.009 | Significant |
| D.o.C * Feed rate | 4 | 0.010 | 0.003 | 0.680 | 0.623 | Not Significant |
| Error | 8 | 0.030 | 0.004 | |||
| Total | 26 | 0.997 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Speed | 2 | 241,967 | 120,983 | 255,398.59 | 0.000 | Significant |
| D.o.C | 2 | 59,597 | 29,798 | 62,904.97 | 0.000 | Significant |
| Feed rate | 2 | 4714 | 2357 | 4976.07 | 0.000 | Significant |
| Speed * D.o.C | 4 | 3399 | 850 | 1793.74 | 0.000 | Significant |
| Speed * Feed rate | 4 | 270 | 67 | 142.25 | 0.000 | Significant |
| D.o.C * Feed rate | 4 | 67 | 17 | 35.20 | 0.000 | Significant |
| Error | 8 | 4 | 0 | |||
| Total | 26 | 310,016 |
| Source | DF | Adj SS | Adj MS | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Speed | 2 | 0.677 | 0.339 | 482.270 | 0.000 | Significant |
| D.o.C | 2 | 0.092 | 0.046 | 65.490 | 0.000 | Significant |
| Feed rate | 2 | 0.079 | 0.039 | 56.070 | 0.000 | Significant |
| Speed * D.o.C | 4 | 0.016 | 0.004 | 5.730 | 0.018 | Significant |
| Speed * Feed rate | 4 | 0.009 | 0.002 | 3.190 | 0.076 | Not Significant |
| D.o.C * Feed rate | 4 | 0.002 | 0.000 | 0.540 | 0.711 | Not Significant |
| Error | 8 | 0.006 | 0.001 | |||
| Total | 26 | 0.880 |
| Ra (µm) | Rt (µm) | Rz (µm) | PC (KW) | Temp. (°C) | MRR (mm3/min) | ||
|---|---|---|---|---|---|---|---|
| Actual | 0.902 | 8.307 | 4.307 | 1.76 | 588.4 | 9500 | |
| KNN | Predicted | 0.79 | 6.50 | 4.08 | 1.63 | 505.00 | 7420.00 |
| Percentage Correctness | 0.877827 | 0.782737 | 0.946599 | 0.9275 | 0.85826 | 0.781053 | |
| XGBOOST | Predicted | 0.87 | 8.28 | 4.18 | 1.81 | 596.44 | 9688.08 |
| Percentage Correctness | 0.960451 | 0.996439 | 0.970013 | 0.968806 | 0.986336 | 0.980203 | |
| ANN | Predicted | 0.94 | 5.14 | 4.16 | 1.58 | 13.28 | 13.23 |
| Percentage Correctness | 0.952647 | 0.618528 | 0.966594 | 0.895583 | 0.022562 | 0.001393 | |
| SVR | Predicted | 0.85 | 6.76 | 4.30 | 1.66 | 382.43 | 3565.77 |
| Percentage Correctness | 0.940451 | 0.814061 | 0.997267 | 0.941342 | 0.649956 | 0.375344 | |
| Random Forest | Predicted | 0.83 | 6.88 | 4.36 | 1.70 | 572.75 | 7207.50 |
| Percentage Correctness | 0.922517 | 0.828719 | 0.98671 | 0.963687 | 0.973408 | 0.758684 |
| Hyperparameter Parameter | Optimal Value |
|---|---|
| Maximum Depth | 4 |
| Number of Estimators | 365 |
| Subsample | 0.247020091 |
| Colsample by Tree | 0.829416734 |
| Regularization Alpha | 0.188535466 |
| Regularization Lambda | 0.980953654 |
| Predicted | Actual | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Order | Ra (µm) | Rt (µm) | Rz (µm) | PC (KW) | Temp. (°C) | MRR (mm3/min) | Ra (µm) | Rt (µm) | Rz (µm) | PC (KW) | Temp. (°C) | MRR (mm3/min) |
| 3 | 0.6948 | 8.9826 | 5.5978 | 1.2552 | 254.1231 | 2374.803 | 0.884 | 9.059 | 5.632 | 1.254 | 253.9 | 2375 |
| 1 | 0.5875 | 8.4114 | 4.7987 | 1.1394 | 234.2131 | 799.9993 | 0.753 | 8.606 | 4.92 | 1.147 | 234.2 | 800 |
| 4 | 0.5875 | 7.2322 | 3.7959 | 1.2288 | 265.4778 | 1199.994 | 0.601 | 7.236 | 3.79 | 1.207 | 265.5 | 1200 |
| 8 | 0.6001 | 6.8984 | 4.0436 | 1.2949 | 322.7358 | 3149.850 | 0.543 | 6.972 | 4.029 | 1.3 | 322.5 | 3150 |
| 23 | 0.8302 | 6.2875 | 5.5252 | 1.6128 | 499.8404 | 7125.210 | 0.858 | 6.363 | 5.479 | 1.654 | 500.1 | 7125 |
| 6 | 0.6948 | 8.3705 | 4.8029 | 1.2949 | 287.6072 | 3563.305 | 0.691 | 8.286 | 4.688 | 1.307 | 287.8 | 3563 |
| 18 | 0.657 | 6.8045 | 4.0277 | 1.5357 | 475.1958 | 9500.082 | 0.698 | 6.73 | 3.993 | 1.567 | 475.2 | 9500 |
| 19 | 0.4843 | 4.9828 | 2.0431 | 1.4883 | 427.1518 | 2375.214 | 0.365 | 5.164 | 2.057 | 1.42 | 427.3 | 2375 |
| 26 | 0.8302 | 8.2402 | 4.3994 | 1.6128 | 588.4298 | 9500.226 | 0.902 | 8.307 | 4.307 | 1.76 | 588.4 | 9500 |
| 2 | 0.6684 | 8.8814 | 5.5383 | 1.2552 | 241.824 | 1575.122 | 0.765 | 8.729 | 5.489 | 1.2 | 241.9 | 1575 |
| 27 | 0.8566 | 8.6883 | 4.7501 | 1.6128 | 617.7504 | 14,199.80 | 0.989 | 8.695 | 4.835 | 1.88 | 617.8 | 14,200 |
| 10 | 0.4643 | 4.2384 | 2.0001 | 1.4217 | 328.8993 | 1574.773 | 0.261 | 3.905 | 1.768 | 1.347 | 328.7 | 1575 |
| 22 | 0.7671 | 5.3605 | 4.7104 | 1.5624 | 484.7287 | 3562.817 | 0.842 | 5.361 | 4.747 | 1.567 | 484.4 | 3563 |
| 11 | 0.6001 | 6.9588 | 3.3356 | 1.464 | 339.1916 | 3150.316 | 0.52 | 7.081 | 3.334 | 1.414 | 339.5 | 3150 |
| 15 | 0.657 | 12.0827 | 3.9767 | 1.5223 | 404.0421 | 7124.864 | 0.813 | 12.477 | 4.071 | 1.52 | 403.9 | 7125 |
| 21 | 0.6945 | 4.0596 | 3.7828 | 1.5731 | 462.9821 | 7100.231 | 0.652 | 3.682 | 3.299 | 1.614 | 463.3 | 7100 |
| 9 | 0.6507 | 7.325 | 4.3751 | 1.2949 | 338.3776 | 4750.052 | 0.585 | 7.324 | 4.335 | 1.32 | 338.6 | 4750 |
| 14 | 0.6065 | 4.687 | 3.2458 | 1.5037 | 384.6817 | 4724.958 | 0.634 | 4.489 | 3.248 | 1.487 | 384.7 | 4725 |
| 13 | 0.4643 | 3.3416 | 1.9411 | 1.4614 | 372.3993 | 2363.066 | 0.256 | 3.259 | 1.724 | 1.414 | 372.6 | 2363 |
| 24 | 0.8566 | 7.1392 | 5.8478 | 1.6128 | 525.2257 | 10,649.85 | 0.875 | 7.042 | 5.983 | 1.68 | 525.1 | 10,650 |
| 17 | 0.6065 | 5.2128 | 3.3118 | 1.5347 | 452.7394 | 6299.734 | 0.592 | 5.201 | 3.231 | 1.534 | 452.6 | 6300 |
| 20 | 0.618 | 4.9388 | 3.4556 | 1.5448 | 441.6176 | 4749.693 | 0.606 | 4.965 | 3.686 | 1.54 | 441.4 | 4750 |
| 12 | 0.6507 | 8.9212 | 4.1137 | 1.464 | 356.6009 | 4749.916 | 0.674 | 9.124 | 4.427 | 1.467 | 356.4 | 4750 |
| 16 | 0.4707 | 3.5253 | 2.1291 | 1.4802 | 438.2168 | 3150.195 | 0.371 | 3.494 | 2.296 | 1.48 | 438.3 | 3150 |
| 25 | 0.7671 | 7.7504 | 3.6168 | 1.5624 | 569.7158 | 4749.959 | 0.886 | 7.763 | 3.592 | 1.607 | 569.8 | 4750 |
| 7 | 0.5207 | 5.9012 | 3.4344 | 1.2526 | 312.2711 | 1599.980 | 0.517 | 5.922 | 3.55 | 1.24 | 312.3 | 1600 |
| Scale | Definition | Explanation |
|---|---|---|
| 1 | Equally Important | Indifferent |
| 3 | Weakly Important | Slightly better |
| 5 | Strongly Important | Better |
| 7 | Very Strongly Important | Much better |
| 9 | Extremely Important | Definitely much better |
| 2, 4, 6, 8 | Intermediate value | When compromise needed |
| Criteria | Ra | PC | Temp. | MRR |
|---|---|---|---|---|
| Ra | 1 | 9 | 5 | 5 |
| PC | 1/9 | 1 | 1/7 | 1/5 |
| Temp. | 1/5 | 7 | 1 | 3 |
| MRR | 1/5 | 5 | 1/3 | 1 |
| No. of Criteria | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|
| RI | 0.0 | 0.0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 |
| Criteria | AHP Weights | Equal Weights |
|---|---|---|
| Ra | 0.510369 | 0.25 |
| Power Consumption | 0.037103 | 0.25 |
| Temp | 0.285807 | 0.25 |
| MRR | 0.166721 | 0.25 |
| Optimal Input | Output | ||||||
|---|---|---|---|---|---|---|---|
| Weighting Methods | Speed m/min | D.o.C (mm) | Feed Rate (mm/tooth) | Ra (µm) | PC (KW) | Temp. (°C) | MRR (mm3/min) |
| Equal Weights | 50 | 0.5 | 0.05 | 2.54 | 1.42 | 328.97 | 1608.83 |
| AHP Weights | 50 | 0.5 | 0.15 | 2.58 | 1.35 | 319.92 | 1613.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbas, A.T.; Helmy, M.O.; Al-Abduljabbar, A.A.; Soliman, M.S.; Hasan, A.S.; Elkaseer, A. Precision Face Milling of Maraging Steel 350: An Experimental Investigation and Optimization Using Different Machine Learning Techniques. Machines 2023, 11, 1001. https://doi.org/10.3390/machines11111001
Abbas AT, Helmy MO, Al-Abduljabbar AA, Soliman MS, Hasan AS, Elkaseer A. Precision Face Milling of Maraging Steel 350: An Experimental Investigation and Optimization Using Different Machine Learning Techniques. Machines. 2023; 11(11):1001. https://doi.org/10.3390/machines11111001
Chicago/Turabian StyleAbbas, Adel T., Mohamed O. Helmy, Abdulhamid A. Al-Abduljabbar, Mahmoud S. Soliman, Ali S. Hasan, and Ahmed Elkaseer. 2023. "Precision Face Milling of Maraging Steel 350: An Experimental Investigation and Optimization Using Different Machine Learning Techniques" Machines 11, no. 11: 1001. https://doi.org/10.3390/machines11111001
APA StyleAbbas, A. T., Helmy, M. O., Al-Abduljabbar, A. A., Soliman, M. S., Hasan, A. S., & Elkaseer, A. (2023). Precision Face Milling of Maraging Steel 350: An Experimental Investigation and Optimization Using Different Machine Learning Techniques. Machines, 11(11), 1001. https://doi.org/10.3390/machines11111001








