Correlation between Infill Percentages, Layer Width, and Mechanical Properties in Fused Deposition Modelling of Poly-Lactic Acid 3D Printing
Abstract
:1. Introduction
2. Experimental Design and Methodology
2.1. Response Surface Methodology (RSM)
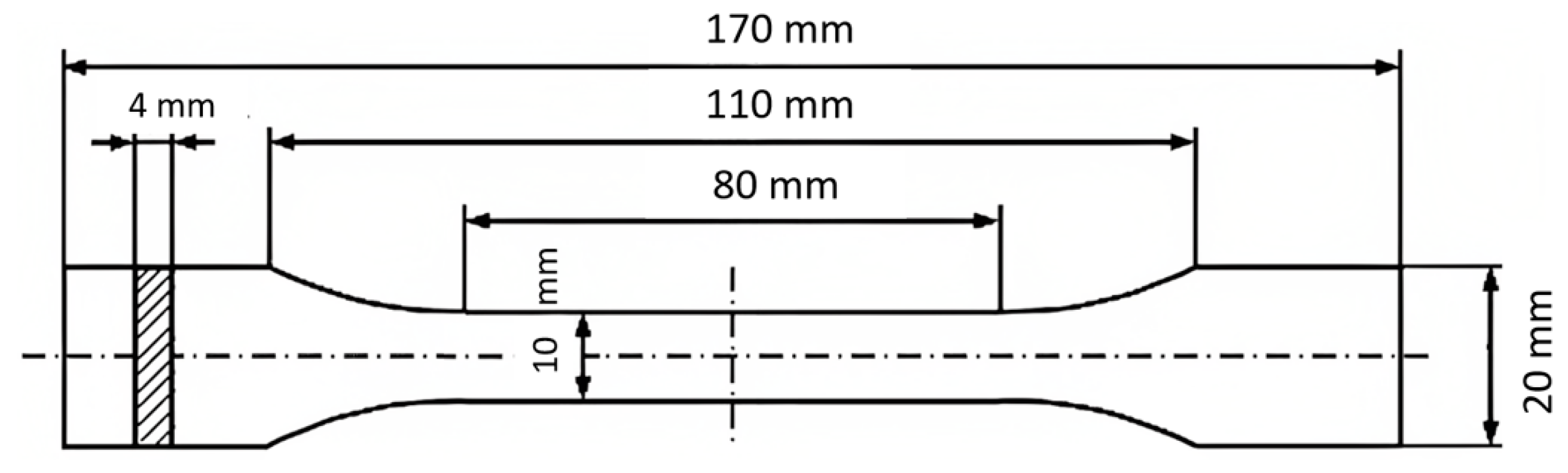
2.2. Material and Dimensional Design Drafting
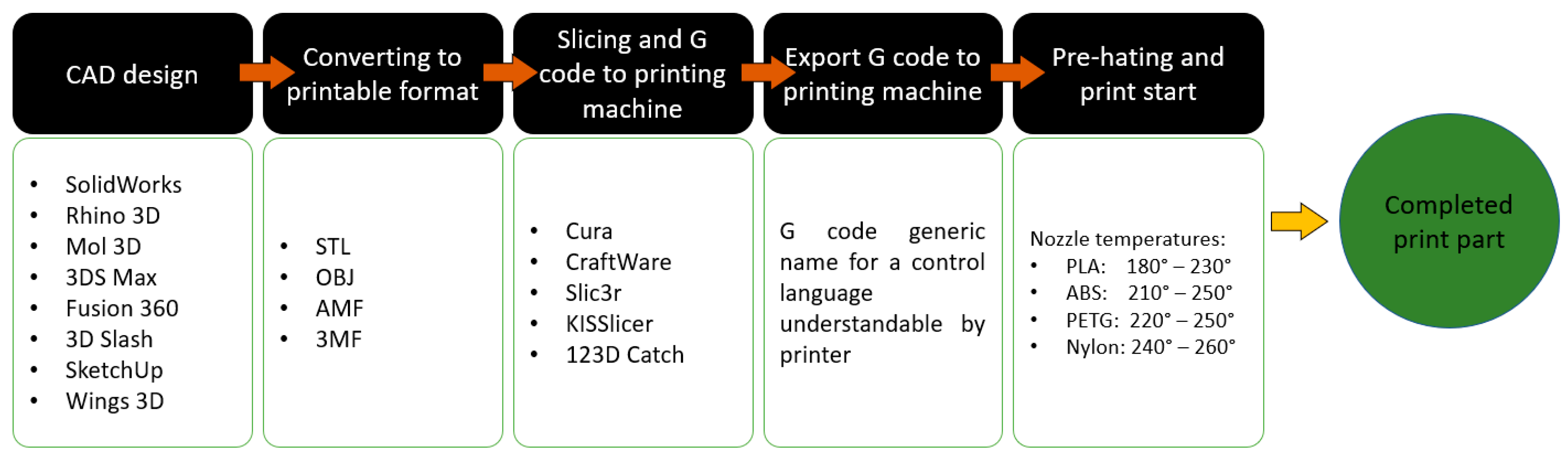
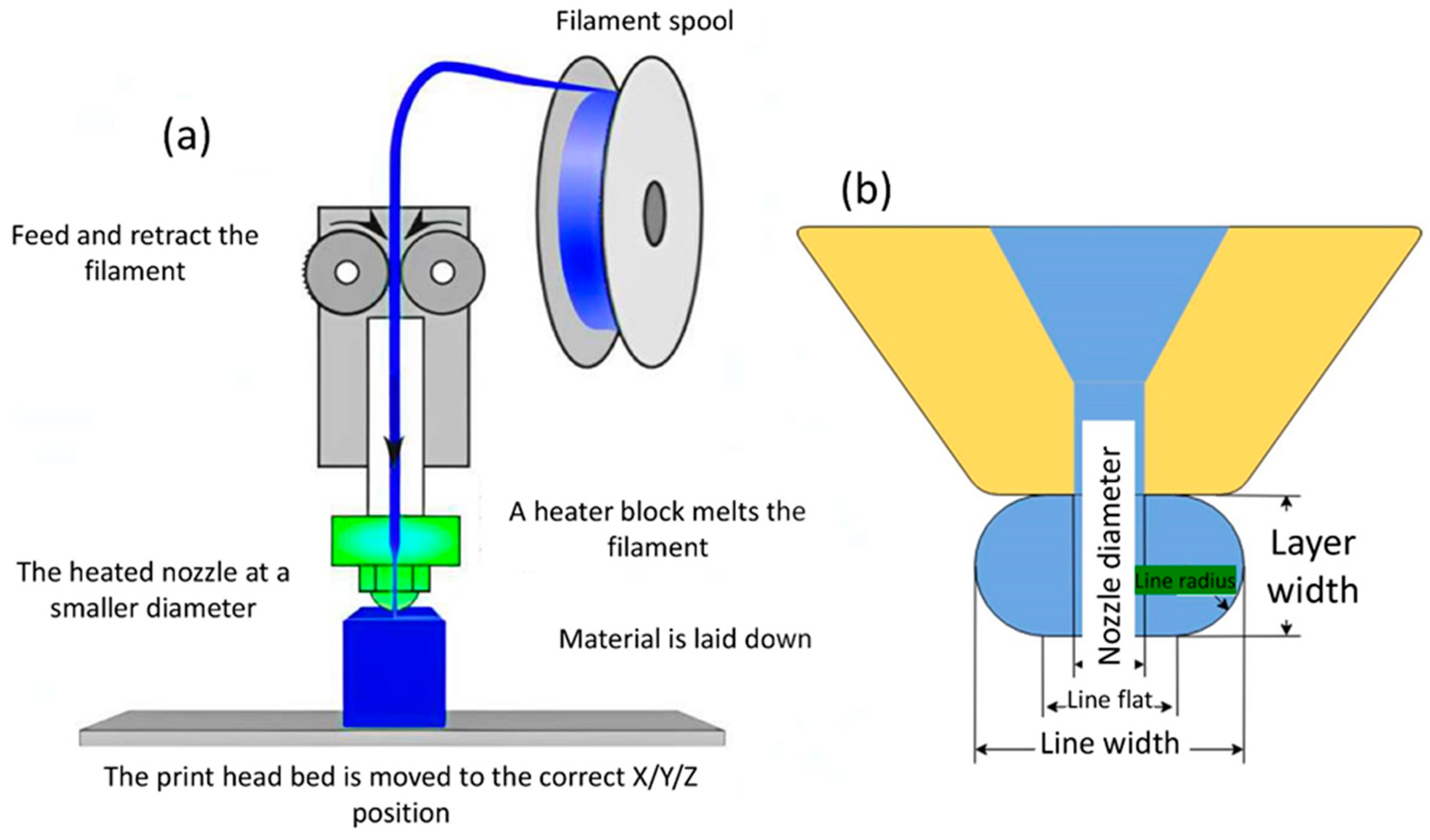
2.3. 3D Printing of the Model
2.4. Tensile Testing
3. Results and Discussion
3.1. Tensile Test Result
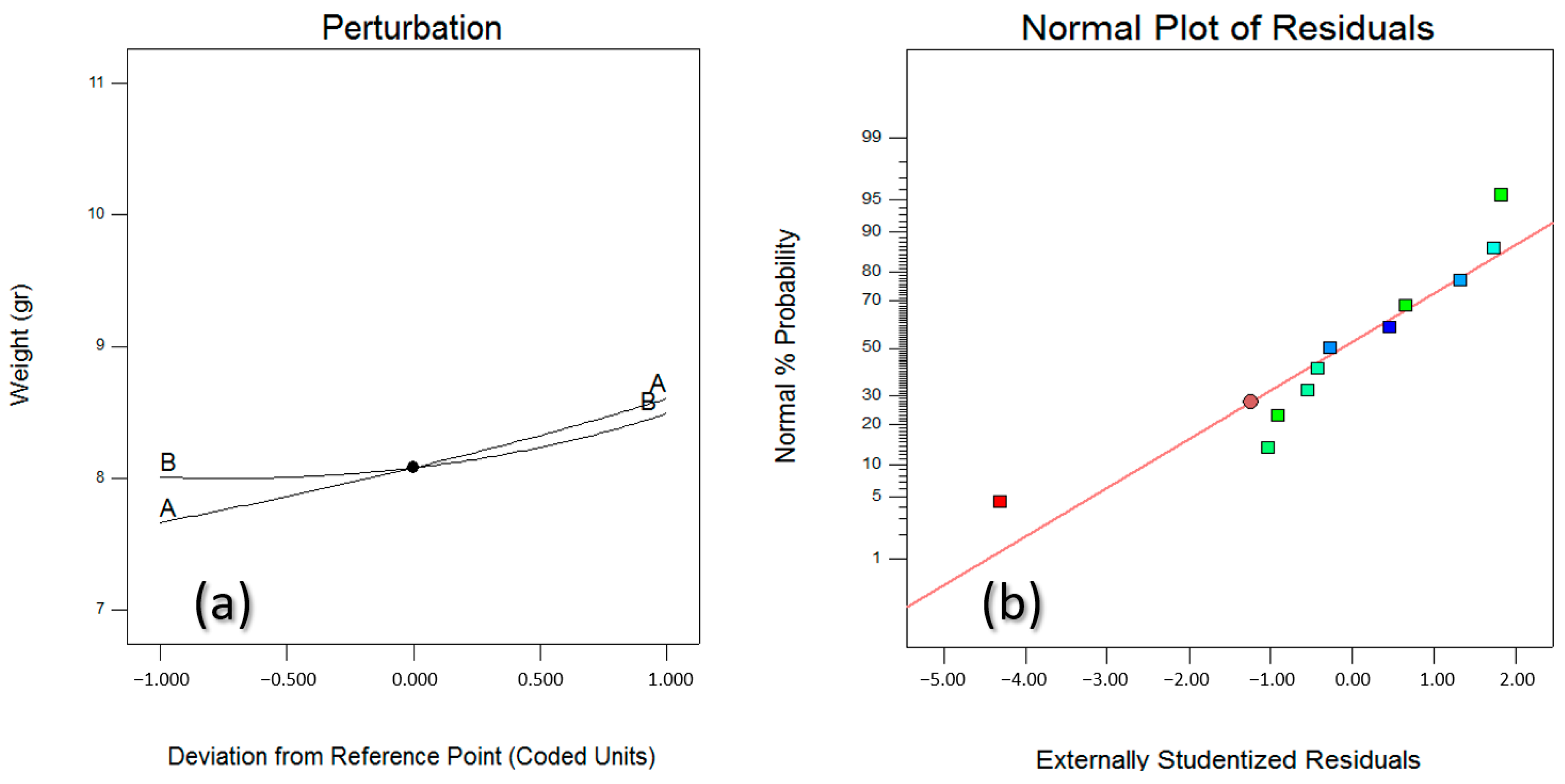
3.2. Weight
3.3. Modulus
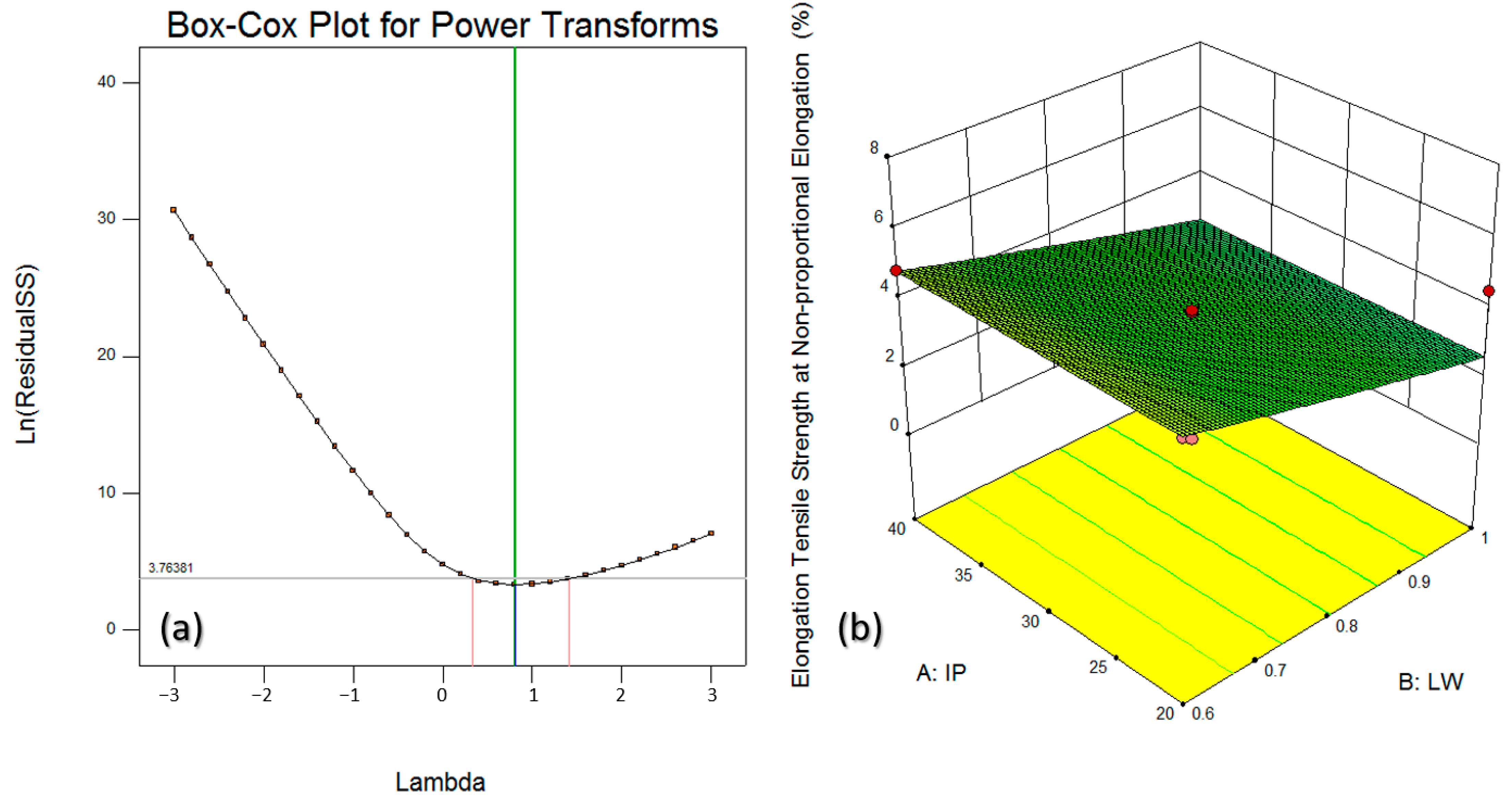
3.4. Elongation Tensile Strength at Non-Proportional Elongation
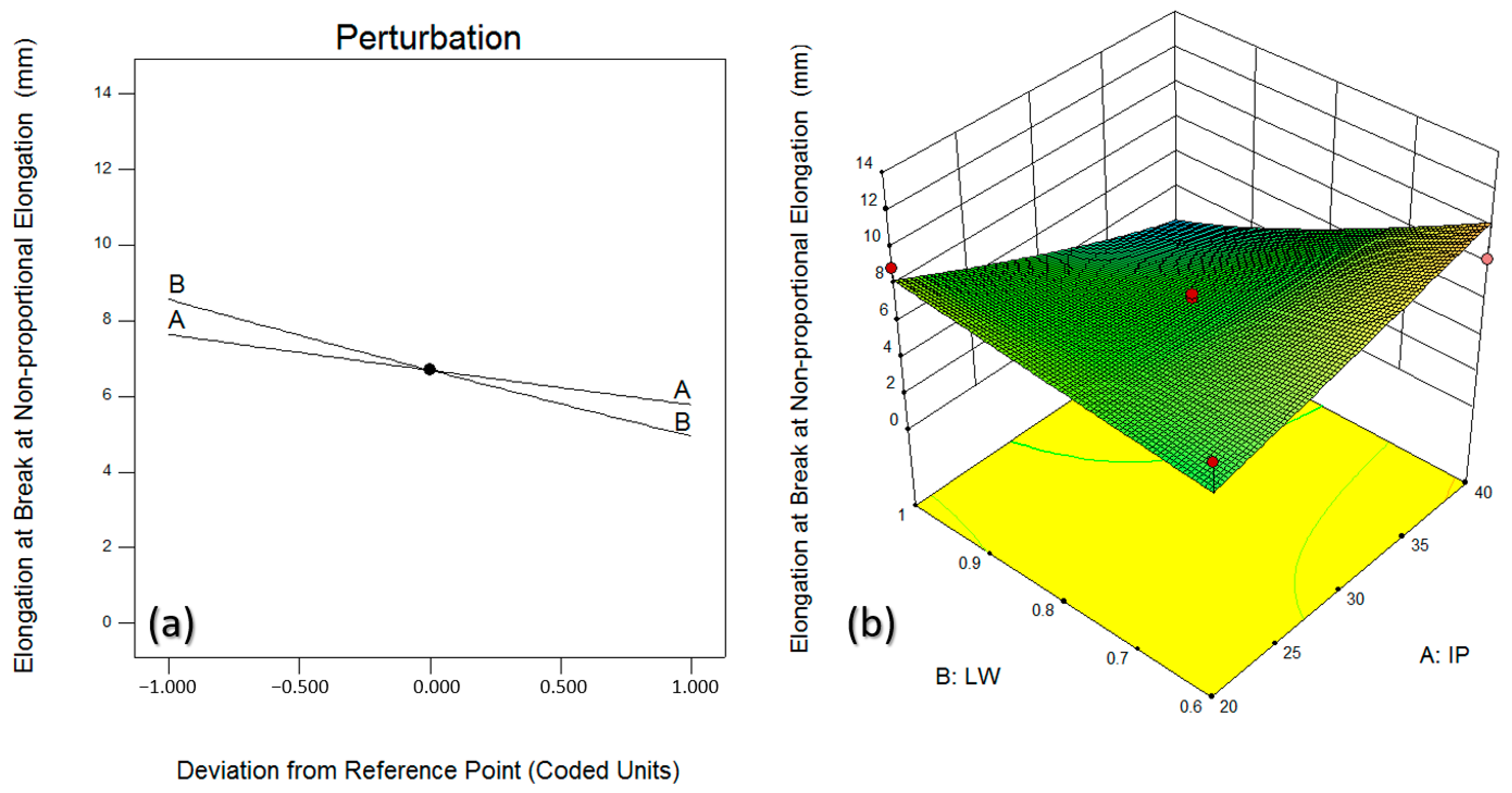
3.5. Elongation at Break at Non-Proportional Elongation
3.6. Tensile Extension at Tensile Strength
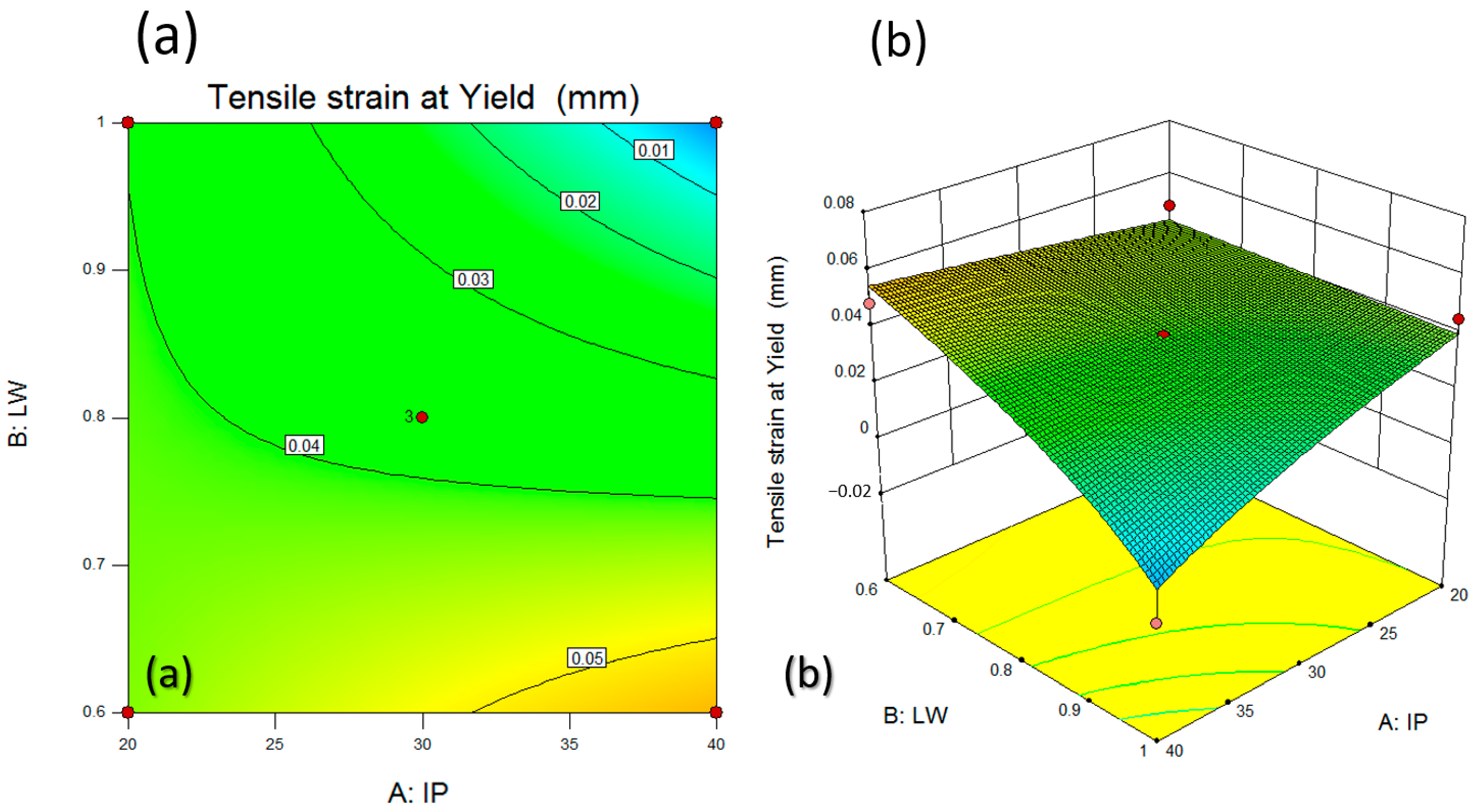
3.7. Tensile Strain at Yield
4. Optimisation
5. Conclusions
- Higher infill percentages lead to increased modulus and stiffness, while thinner layer widths enhance tensile strength and rigidity.
- Response Surface Methodology (RSM) and Box-Cox transformation improved model accuracy and linearity.
- Elongation Tensile Strength at Non-proportional Elongation decreased with higher B-LW and lower A-IP.
- The layer width decreases and the infill percentage increases, the material’s ability to elongate before reaching the point of breakage decreases.
- Increasing B:LW and A:IP led to a reduction in the corresponding responses. This observation implies that higher values of layer width and infill percentage contribute to a decrease in the tensile extension at the point of tensile strength and the material’s strain at yield.
- Featuring a 40% infill percentage and 0.6 mm layer width, emerged as the optimal choice based on the given optimisation criteria and constraints. This particular combination of A:IP and B:LW resulted in a favourable balance of mechanical properties, including modulus, tensile strength, and elongation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mazzanti, V.; Malagutti, L.; Mollica, F. FDM 3D Printing of Polymers Containing Natural Fillers: A Review of their Mechanical Properties. Polymers 2019, 11, 1094. [Google Scholar] [CrossRef] [PubMed]
- Cano-Vicent, A.; Tambuwala, M.M.; Hassan, S.S.; Barh, D.; Aljabali, A.A.A.; Birkett, M.; Arjunan, A.; Serrano-Aroca, Á. Fused deposition modelling: Current status, methodology, applications and future prospects. Addit. Manuf. 2021, 47, 102378. [Google Scholar] [CrossRef]
- Ahmad, M.N.; Ishak, M.R.; Taha, M.M.; Mustapha, F.; Leman, Z. A Review of Natural Fiber-Based Filaments for 3D Printing: Filament Fabrication and Characterization. Materials 2023, 16, 4052. [Google Scholar] [CrossRef] [PubMed]
- Radzuan, N.A.M.; Khalid, N.N.; Foudzi, F.M.; Royan, N.R.R.; Sulong, A.B. Mechanical Analysis of 3D Printed Polyamide Composites under Different Filler Loadings. Polymers 2023, 15, 1846. [Google Scholar] [CrossRef] [PubMed]
- Ehrmann, G.; Ehrmann, A. Investigation of the Shape-Memory Properties of 3D Printed PLA Structures with Different Infills. Polymers 2021, 13, 164. [Google Scholar] [CrossRef]
- Sandanamsamy, L.; Harun, W.S.W.; Ishak, I.; Romlay, F.R.M.; Kadirgama, K.; Ramasamy, D.; Idris, S.R.A.; Tsumori, F. A comprehensive review on fused deposition modelling of polylactic acid. In Progress in Additive Manufacturing; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar] [CrossRef]
- Lyu, Y.; Liu, D.; Guo, R.; Ji, Z.; Wang, X.; Shi, X. Flexibility of Diels-Alder reversible covalent bonds in fused deposition modeling 3D printing: Bonding and de-bonding. Polymer 2023, 266, 125637. [Google Scholar] [CrossRef]
- Sharma, A.; Rai, A. Fused deposition modelling (FDM) based 3D & 4D Printing: A state of art review. Mater. Today Proc. 2022, 62, 367–372. [Google Scholar] [CrossRef]
- Mishra, V.; Negi, S.; Kar, S. FDM-based additive manufacturing of recycled thermoplastics and associated composites. J. Mater. Cycles Waste Manag. 2023, 25, 758–784. [Google Scholar] [CrossRef]
- Rajendran, S.; Palani, G.; Kanakaraj, A.; Shanmugam, V.; Veerasimman, A.; Gądek, S.; Korniejenko, K.; Marimuthu, U. Metal and Polymer Based Composites Manufactured Using Additive Manufacturing—A Brief Review. Polymers 2023, 15, 2564. [Google Scholar] [CrossRef] [PubMed]
- Gibson, I.J.; Ashby, F. The mechanics of three-dimensional cellular materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 382, 43–59. [Google Scholar] [CrossRef]
- Kalita, S.J.; Bose, S.; Hosick, H.L.; Bandyopadhyay, A. Development of controlled porosity polymer-ceramic composite scaffolds via fused deposition modeling. Mater. Sci. Eng. C 2003, 23, 611–620. [Google Scholar] [CrossRef]
- Drummer, D.; Cifuentes-Cuéllar, S.; Rietzel, D. Suitability of PLA/TCP for fused deposition modeling. Rapid Prototyp. J. 2012, 18, 500–507. [Google Scholar] [CrossRef]
- Suzdaltsev, A.; Rakhmanova, O. Special Issue on Metal-Based Composite Materials: Preparation, Structure, Properties and Applications. Appl. Sci. 2023, 13, 4799. [Google Scholar] [CrossRef]
- Mierzwiński, D.; Łach, M.; Gądek, S.; Lin, W.-T.; Tran, D.H.; Korniejenko, K. A brief overview of the use of additive manufacturing of con-create materials in construction. Acta Innov. 2023, 48, 22–37. [Google Scholar] [CrossRef]
- Monaldo, E.; Ricci, M.; Marfia, S. Mechanical properties of 3D printed polylactic acid elements: Experimental and numerical insights. Mech. Mater. 2023, 177, 104551. [Google Scholar] [CrossRef]
- Suteja, T.J.; Soesanti, A. Mechanical Properties of 3D Printed Polylactic Acid Product for Various Infill Design Parameters: A Review. J. Phys. Conf. Ser. 2020, 1569, 042010. [Google Scholar] [CrossRef]
- Scaffaro, R.; Citarrella, M.C.; Gulino, E.F. Opuntia Ficus Indica based green composites for NPK fertilizer controlled release produced by compression molding and fused deposition modeling. Compos. Part A Appl. Sci. Manuf. 2022, 159, 107030. [Google Scholar] [CrossRef]
- Turner, B.N.; Strong, R.; Gold, S.A. A review of melt extrusion additive manufacturing processes: I. Process design and modeling. Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Afsharkohan, M.S.; Dehrooyeh, S.; Sohrabian, M.; Vaseghi, M. Influence of processing parameters tuning and rheological characterization on improvement of mechanical properties and fabrication accuracy of 3D printed models. Rapid Prototyp. J. 2023, 29, 867–881. [Google Scholar] [CrossRef]
- Nakajima, J.; Fayazbakhsh, K.; Teshima, Y. Experimental study on tensile properties of 3D printed flexible kirigami specimens. Addit. Manuf. 2020, 32, 101100. [Google Scholar] [CrossRef]
- Wang, K.; Xie, X.; Wang, J.; Zhao, A.; Peng, Y.; Rao, Y. Effects of infill characteristics and strain rate on the deformation and failure properties of additively manufactured polyamide-based composite structures. Results Phys. 2020, 18, 103346. [Google Scholar] [CrossRef]
- Moradi, M.; Karamimoghadam, M.; Meiabadi, S.; Casalino, G.; Ghaleeh, M.; Baby, B.; Ganapathi, H.; Jose, J.; Abdulla, M.S.; Tallon, P.; et al. Mathematical Modelling of Fused Deposition Modeling (FDM) 3D Printing of Poly Vinyl Alcohol Parts through Statistical Design of Experiments Approach. Mathematics 2023, 11, 3022. [Google Scholar] [CrossRef]
- Rezayat, M.; Karamimoghadam, M.; Yazdi, M.S.; Moradi, M.; Bodaghi, M. Statistical analysis of experimental factors for synthesis of copper oxide and tin oxide for antibacterial applications. Int. J. Adv. Manuf. Technol. 2023, 127, 3017–3030. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Ezati, N.; Sadeghi, P.; Badrossamay, M. Optimization of FDM process parameters for tensile properties of polylactic acid specimens using Taguchi design of experiment method. J. Thermoplast. Compos. Mater. 2022, 35, 2435–2452. [Google Scholar] [CrossRef]
- Jin, M.; Neuber, C.; Schmidt, H.-W. Tailoring polypropylene for extrusion-based additive manufacturing. Addit. Manuf. 2020, 33, 101101. [Google Scholar] [CrossRef]
- Equbal, A.; Sood, A.K.; Equbal, M.I.; Badruddin, I.A.; Khan, Z.A. RSM based investigation of compressive properties of FDM fabricated part. CIRP J. Manuf. Sci. Technol. 2021, 35, 701–714. [Google Scholar] [CrossRef]
- El Magri, A.; El Mabrouk, K.; Vaudreuil, S.; Touhami, M.E. Experimental investigation and optimization of printing parameters of 3D printed polyphenylene sulfide through response surface methodology. J. Appl. Polym. Sci. 2021, 138, 49625. [Google Scholar] [CrossRef]
- Wickramasinghe, S.; Do, T.; Tran, P. FDM-Based 3D Printing of Polymer and Associated Composite: A Review on Mechanical Properties, Defects and Treatments. Polymers 2020, 12, 1529. [Google Scholar] [CrossRef]
- Tanveer, M.Q.; Mishra, G.; Mishra, S.; Sharma, R. Effect of infill pattern and infill density on mechanical behaviour of FDM 3D printed Parts—A current review. Mater. Today Proc. 2022, 62, 100–108. [Google Scholar] [CrossRef]
- Moradi, M.; Karamimoghadam, M.; Meiabadi, S.; Rasool, S.; Casalino, G.; Shamsborhan, M.; Sebastian, P.K.; Poulose, A.; Shaiju, A.; Rezayat, M. Optimizing Layer Thickness and Width for Fused Filament Fabrication of Polyvinyl Alcohol in Three-Dimensional Printing and Support Structures. Machines 2023, 11, 829–844. [Google Scholar] [CrossRef]
- Patel, A.; Taufik, M. Extrusion-Based Technology in Additive Manufacturing: A Comprehensive Review. Arab. J. Sci. Eng. 2022, 140, 2044–2056. [Google Scholar] [CrossRef]
- Krajangsawasdi, N.; Blok, L.G.; Hamerton, I.; Longana, M.L.; Woods, B.K.S.; Ivanov, D.S. Fused Deposition Modelling of Fibre Reinforced Polymer Composites: A Parametric Review. J. Compos. Sci. 2021, 5, 29. [Google Scholar] [CrossRef]
- Moncayo-Matute, F.P.; Vázquez-Silva, E.; Peña-Tapia, P.G.; Torres-Jara, P.B.; Moya-Loaiza, D.P.; Viloria-Ávila, T.J. Finite Element Analysis of Patient-Specific 3D-Printed Cranial Implant Manufactured with PMMA and PEEK: A Mechanical Comparative Study. Polymers 2023, 15, 3620. [Google Scholar] [CrossRef] [PubMed]
- Chalgham, A.; Ehrmann, A.; Wickenkamp, I. Mechanical Properties of FDM Printed PLA Parts before and after Thermal Treatment. Polymers 2021, 13, 1239. [Google Scholar] [CrossRef]
- Portoacă, A.I.; Ripeanu, R.G.; Dini, A.; Tănase, M. Optimization of 3D Printing Parameters for Enhanced Surface Quality and Wear Resistance. Polymers 2023, 15, 3419. [Google Scholar] [CrossRef]
- Pepelnjak, T.; Stojšić, J.; Sevšek, L.; Movrin, D.; Milutinović, M. Influence of Process Parameters on the Characteristics of Additively Manufactured Parts Made from Advanced Biopolymers. Polymers 2023, 15, 716. [Google Scholar] [CrossRef]
- Susmel, L.; Berto, F.; Hu, Z. The Strain energy density to estimate lifetime of notched components subjected to variable amplitude fatigue loading. Frat. Integrità Strutt. 2018, 13, 383–393. [Google Scholar] [CrossRef]
- Pertuz-Comas, A.D.; Díaz, J.G.; Meneses-Duran, O.J.; Niño-Álvarez, N.Y.; León-Becerra, J. Flexural Fatigue in a Polymer Matrix Composite Material Reinforced with Continuous Kevlar Fibers Fabricated by Additive Manufacturing. Polymers 2022, 14, 3586. [Google Scholar] [CrossRef]
- Rezayat, M.; Moradi, M.; Mateo, A. Nanosecond pulsed laser surface processing of AISI 301LN steel: Effect on surface topography and mechanical properties. Int. J. Adv. Manuf. Technol. 2023, 128, 3025–3040. [Google Scholar] [CrossRef]
- Raj, S.A.; Muthukumaran, E.; Jayakrishna, K. A Case Study of 3D Printed PLA and Its Mechanical Properties. Mater. Today Proc. 2018, 5, 11219–11226. [Google Scholar] [CrossRef]
- Travieso-Rodriguez, J.A.; Jerez-Mesa, R.; Llumà, J.; Traver-Ramos, O.; Gomez-Gras, G.; Rovira, J.J.R. Mechanical Properties of 3D-Printing Polylactic Acid Parts subjected to Bending Stress and Fatigue Testing. Materials 2019, 12, 3859. [Google Scholar] [CrossRef] [PubMed]
- ASTM Standards, Standard Test Method for Tensile Properties of Plastics, ASTM International, PA, USA. 2012. Available online: https://www.astm.org/d0638-03.html (accessed on 21 August 2023).
- Woigk, W.; Fuentes, C.A.; Rion, J.; Hegemann, D.; van Vuure, A.W.; Dransfeld, C.; Masania, K. Interface properties and their effect on the mechanical performance of flax fibre thermoplastic composites. Compos. Part A Appl. Sci. Manuf. 2019, 122, 8–17. [Google Scholar] [CrossRef]
- Nelson, K.; Kelly, C.N.; Gall, K. Effect of stress state on the mechanical behavior of 3D printed porous Ti6Al4V scaffolds produced by laser powder bed fusion. Mater. Sci. Eng. B 2022, 286, 116013. [Google Scholar] [CrossRef]
- Shanmugam, V.; Rajendran, D.J.J.; Babu, K.; Rajendran, S.; Veerasimman, A.; Marimuthu, U.; Singh, S.; Das, O.; Neisiany, R.E.; Hedenqvist, M.S.; et al. The mechanical testing and performance analysis of polymer-fibre composites prepared through the additive manufacturing. Polym. Test 2021, 93, 106925. [Google Scholar] [CrossRef]
- Vamshinath, K.; Kumar, N.N.; Kumar, R.T.; Nagaraju, D.S.; Sateesh, N.; Subbaiah, R. Analysis of the effect of the process parameters on the mechanical strength of 3D printed and adhesively bonded PETG single lap joint. Mater. Today Proc. 2022, 62, 4509–4514. [Google Scholar] [CrossRef]
- Dutra, T.A.; Ferreira, R.T.L.; Resende, H.B.; Blinzler, B.J.; Larsson, R. Expanding Puck and Schürmann Inter Fiber Fracture Criterion for Fiber Reinforced Thermoplastic 3D-Printed Composite Materials. Materials 2020, 13, 1653. [Google Scholar] [CrossRef]
- Sheoran, A.J.; Kumar, H. Fused Deposition modeling process parameters optimization and effect on mechanical properties and part quality: Review and reflection on present research. Mater. Today Proc. 2020, 21, 1659–1672. [Google Scholar] [CrossRef]
- Melenka, G.W.; Cheung, B.K.O.; Schofield, J.S.; Dawson, M.R.; Carey, J.P. Evaluation and prediction of the tensile properties of continuous fiber-reinforced 3D printed structures. Compos. Struct. 2016, 153, 866–875. [Google Scholar] [CrossRef]





| Variable | Notation | Unit | −2 | −1 | 0 | 1 | 2 |
|---|---|---|---|---|---|---|---|
| Infill Percentages | IP | % | 10 | 20 | 30 | 40 | 50 |
| Width of layer | W | mm | 0.4 | 0.6 | 0.8 | 1 | 1.2 |
| Input Variables | Output Variables | |||||||
|---|---|---|---|---|---|---|---|---|
| Experiment No. | Infill Percentages (%) | Width of Layer (mm) | Weight (g) | Modulus (Automatic) (GPa) | % Elongation Tensile Strength at Non-Proportional Elongation (Standard) (%) | Elongation at Break at Non-Proportional Elongation (Standard) (mm) | Tensile Extension at Tensile Strength (mm) | Tensile Strain at Yield (Zero Slope) (mm/mm) |
| 1 | 30 | 1.2 | 10.09 | 1.43 | 2.85 | 5.27 | 4.70 | 0.02 |
| 2 | 40 | 0.6 | 8.77 | 1.18 | 4.83 | 8.33 | 7.98 | 0.04 |
| 3 | 30 | 0.4 | 8.03 | 1.10 | 6.94 | 12.05 | 11.45 | 0.06 |
| 4 | 30 | 0.8 | 8.18 | 1.26 | 3.78 | 6.84 | 6.24 | 0.03 |
| 5 | 30 | 0.8 | 8.21 | 1.27 | 3.82 | 7.07 | 6.31 | 0.03 |
| 6 | 10 | 0.8 | 7.25 | 1.10 | 4.91 | 9.10 | 8.11 | 0.04 |
| 7 | 50 | 0.8 | 9.03 | 1.31 | 4.79 | 8.75 | 7.91 | 0.04 |
| 8 | 20 | 0.6 | 7.65 | 1.08 | 4.80 | 8.48 | 7.93 | 0.04 |
| 9 | 20 | 1 | 7.71 | 1.14 | 4.50 | 9.04 | 7.43 | 0.04 |
| 10 | 30 | 0.8 | 8.34 | 1.26 | 0.00 | 0.00 | −4.58 | −0.04 |
| 11 | 40 | 1 | 8.57 | 1.35 | 0.00 | 0.00 | −5.10 | −0.01 |
| Property | Description |
|---|---|
| Molecular Weight | 72.06 g/mol |
| Melting Point | 150–160 °C |
| Glass Transition Temperature | 60–65 °C |
| Density | 1.24–1.26 g/cm3 |
| Refractive Index | 1.33–1.53 |
| Young’s Modulus (GPa) | 2–4 GPa |
| Tensile Strength | 30–60 MPa |
| Elongation at Break | 5–10% |
| Impact Strength | 5–10 kJ/m2 |
| FDM Printing Temperature Range | 190–220 °C |
| Filament Diameter | 1.75 mm or 2.85 mm (common sizes) |
| Printing Bed Temperature Range | 20–60 °C |
| Biodegradability | Biodegradable under proper conditions |
| Output Variables | High-Performing Value | Experiment No. | Low-Performing Value | Experiment No. |
|---|---|---|---|---|
| Modulus (Automatic) (GPa) | 1.43 | 1 | 1.26 | 10 |
| % Elongation Tensile Strength at Non-proportional Elongation (Standard) (%) | 6.94 | 3 | 0.00 | 10 |
| Elongation at Break at Non-proportional Elongation (Standard) (mm) | 12.05 | 3 | 0.00 | 10 |
| Tensile extension at Tensile Strength (mm) | 9.10 | 6 | −4.58 | 10 |
| Tensile strain at Yield (Zero Slope) (mm/mm) | 0.04 | 9 | −0.08 | 10 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 1.796 × 10−6 | 3 | 5.988 × 10−7 | 15.88 | 0.0017 |
| A-IP | 1.252 × 10−6 | 1 | 1.252 × 10−6 | 33.21 | 0.0007 |
| B-LW | 2.887 × 10−7 | 1 | 2.887 × 10−7 | 7.66 | 0.0278 |
| B2 | 2.555 × 10−7 | 1 | 2.555 × 10−7 | 6.78 | 0.0353 |
| Residual | 2.639 × 10−7 | 7 | 3.771 × 10−8 | ||
| Lack of Fit | 2.580 × 10−7 | 5 | 5.159 × 10−8 | 17.24 | 0.0557 |
| Pure Error | 5.986 × 10−9 | 2 | 2.993 × 10−9 | ||
| Cor Total | 2.060 × 10−6 | 10 | |||
| R-Squared = 87.19% | Adj R-Squared = 81.79% | ||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 1.699 × 10−4 | 2 | 8.496 × 10−5 | 21.58 | 0.0006 |
| A-IP | 7.578 × 10−5 | 1 | 7.578 × 10−5 | 19.25 | 0.0023 |
| B-LW | 9.414 × 10−5 | 1 | 9.414 × 10−5 | 23.91 | 0.0012 |
| Residual | 3.149 × 10−5 | 8 | 3.937 × 10−6 | ||
| Lack of Fit | 3.131 × 10−5 | 6 | 5.219 × 10−6 | 58.23 | 0.0170 |
| Pure Error | 1.793 × 10−7 | 2 | 8.963 × 10−8 | ||
| Cor Total | 2.014 × 10−4 | 10 | |||
| R-Squared = 84.36% | Adj R-Squared = 80.46% | ||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 6.31 | 1 | 6.31 | 3.45 | 0.0962 |
| B-LW | 6.31 | 1 | 6.31 | 3.45 | 0.0962 |
| Residual | 16.47 | 9 | 1.83 | ||
| Lack of Fit | 10.66 | 7 | 1.52 | 0.52 | 0.7820 |
| Pure Error | 5.81 | 2 | 2.91 | ||
| Cor Total | 22.78 | 10 | |||
| R-Squared = 27.71% | Adj R-Squared = 19.68% | ||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 24.05 | 3 | 8.02 | 1.76 | 0.2429 |
| A-IP | 3.27 | 1 | 3.27 | 0.72 | 0.4257 |
| B-LW | 12.53 | 1 | 12.53 | 2.74 | 0.1417 |
| AB | 8.26 | 1 | 8.26 | 1.81 | 0.2207 |
| Residual | 31.98 | 7 | 4.57 | ||
| Lack of Fit | 17.10 | 5 | 3.42 | 0.46 | 0.7909 |
| Pure Error | 14.88 | 2 | 7.44 | ||
| Cor Total | 56.03 | 10 | |||
| R-Squared = 42.93% | Adj R-Squared = 18.47% | ||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 9.210 × 106 | 3 | 3.070 × 106 | 3.27 | 0.0889 |
| A-IP | 3.873 × 105 | 1 | 3.873 × 105 | 0.41 | 0.5409 |
| B-LW | 7.821 × 106 | 1 | 7.821 × 106 | 8.34 | 0.0234 |
| AB | 1.002 × 106 | 1 | 1.002 × 106 | 1.07 | 0.3357 |
| Residual | 6.564 × 106 | 7 | 9.377 × 105 | ||
| Lack of Fit | 5.109 × 106 | 5 | 1.022 × 106 | 1.40 | 0.4656 |
| Pure Error | 1.455 × 106 | 2 | 7.277 × 105 | ||
| Cor Total | 1.577 × 107 | 10 | |||
| R-Squared = 58.39% | Adj R-Squared = 40.55% | ||||
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 7.663 × 10−6 | 3 | 2.554 × 10−6 | 2.70 | 0.1259 |
| A-IP | 5.296 × 10−7 | 1 | 5.296 × 10−7 | 0.56 | 0.4786 |
| B-LW | 5.693 × 10−6 | 1 | 5.693 × 10−6 | 6.02 | 0.0439 |
| AB | 1.440 × 10−6 | 1 | 1.440 × 10−6 | 1.52 | 0.2570 |
| Residual | 6.619 × 10−6 | 7 | 9.455 × 10−7 | ||
| Lack of Fit | 4.293 × 10−6 | 5 | 8.587 × 10−7 | 0.74 | 0.6611 |
| Pure Error | 2.325 × 10−6 | 2 | 1.163 × 10−6 | ||
| Cor Total | 1.428 × 10−5 | 10 | |||
| R-Squared = 53.66% | Adj R-Squared = 33.79% | ||||
| Name | Goal | Lower Limit | Upper Limit | Lower Weight | Upper Weight | Importance |
|---|---|---|---|---|---|---|
| A:IF (%) | is in range | 20 | 40 | 1 | 1 | 3 |
| B:LW (mm) | is in range | 0.6 | 1 | 1 | 1 | 3 |
| Weight (g) | minimize | 7.25 | 10.09 | 1 | 1 | 3 |
| Modulus (GPa) | maximize | 1.08 | 1.43 | 1 | 1 | 3 |
| Elongation Tensile Strength at Non-proportional Elongation (%) | maximize | 0 | 6.94 | 1 | 1 | 3 |
| Elongation at Break at Non-proportional Elongation (mm) | maximize | 0 | 12.06 | 1 | 1 | 3 |
| Tensile extension at Tensile Strength (mm) | maximize | −5.109 | 11.45 | 1 | 1 | 3 |
| Tensile strain at Yield (mm/mm) | maximize | −0.01 | 0.06 | 1 | 1 | 3 |
| Number | Input Parameters | Responses | |||||||
|---|---|---|---|---|---|---|---|---|---|
| IP (%) | LW (mm) | Weight (g) | Modulus (GPa) | Elongation Tensile Strength at Non-Proportional Elongation (%) | Elongation at Break at Non-Proportional Elongation (mm) | Tensile Extension at Tensile Strength (mm) | Tensile Strain at Yield (mm/mm) | Desirability | |
| 1 | 40.000 | 0.600 | 8.514 | 1.21 | 4.835 | 10.320 | 8.960 | 0.055 | 0.662 |
| 2 | 39.738 | 0.600 | 8.499 | 1.21 | 4.835 | 10.273 | 8.945 | 0.055 | 0.661 |
| 3 | 40.000 | 0.607 | 8.511 | 1.21 | 4.792 | 10.144 | 8.876 | 0.054 | 0.660 |
| 4 | 20.000 | 0.951 | 7.881 | 1.21 | 2.866 | 8.207 | 6.429 | 0.040 | 0.571 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradi, M.; Rezayat, M.; Rozhbiany, F.A.R.; Meiabadi, S.; Casalino, G.; Shamsborhan, M.; Bijoy, A.; Chakkingal, S.; Lawrence, M.; Mohammed, N.; et al. Correlation between Infill Percentages, Layer Width, and Mechanical Properties in Fused Deposition Modelling of Poly-Lactic Acid 3D Printing. Machines 2023, 11, 950. https://doi.org/10.3390/machines11100950
Moradi M, Rezayat M, Rozhbiany FAR, Meiabadi S, Casalino G, Shamsborhan M, Bijoy A, Chakkingal S, Lawrence M, Mohammed N, et al. Correlation between Infill Percentages, Layer Width, and Mechanical Properties in Fused Deposition Modelling of Poly-Lactic Acid 3D Printing. Machines. 2023; 11(10):950. https://doi.org/10.3390/machines11100950
Chicago/Turabian StyleMoradi, Mahmoud, Mohammad Rezayat, Fakhir Aziz Rasul Rozhbiany, Saleh Meiabadi, Giuseppe Casalino, Mahmoud Shamsborhan, Amar Bijoy, Sidharth Chakkingal, Mathews Lawrence, Nasli Mohammed, and et al. 2023. "Correlation between Infill Percentages, Layer Width, and Mechanical Properties in Fused Deposition Modelling of Poly-Lactic Acid 3D Printing" Machines 11, no. 10: 950. https://doi.org/10.3390/machines11100950
APA StyleMoradi, M., Rezayat, M., Rozhbiany, F. A. R., Meiabadi, S., Casalino, G., Shamsborhan, M., Bijoy, A., Chakkingal, S., Lawrence, M., Mohammed, N., & Karamimoghadam, M. (2023). Correlation between Infill Percentages, Layer Width, and Mechanical Properties in Fused Deposition Modelling of Poly-Lactic Acid 3D Printing. Machines, 11(10), 950. https://doi.org/10.3390/machines11100950








