Abstract
Water heating is a significant part of households’ energy consumption, and tankless gas water heaters (TGWHs) are commonly used. One of the limitations of these devices is the difficulty of keeping hot water temperature setpoints when changes in water flow occur. As these changes are usually unexpected, the controllers typically used in these devices cannot anticipate them, strongly affecting the users’ comfort. Moreover, considerable water and energy waste are associated with the long-time response to cold starts. This work proposes the development of a model predictive control (MPC) to be deployed in low-cost hardware, such that the users’ thermal comfort and water savings can be improved. Matlab/Simulink were used to develop, validate and automatically generate C code for implementing the controller in microcontroller-based systems. Hardware-in-the-loop simulations were performed to evaluate the performance of the MPC algorithm in 8-bit and 32-bit microcontrollers. A 6.8% higher comfort index was obtained using the implementation on the 32-bit microcontroller compared to the current deployments; concerning the 8-bit microcontroller, a 4.2% higher comfort index was achieved. These applications in low-cost hardware highlight that users’ thermal comfort can be successfully enhanced while ensuring operation safety. Additionally, the environmental impact can be significantly reduced by decreasing water and energy consumption in cold starts of TGWHs.
1. Introduction
The energy consumption of buildings includes electric energy for air heating and cooling, lighting and domestic water heating, which account for around 30% of the global energy consumption [1]. In the European Union, the energy required to heat domestic hot water accounts for approximately 15% of the total energy consumption in the residential sector [2]. As the electric efficiency of most buildings can be significantly increased, relevant societal impacts can be obtained by reducing energy consumption [3,4]. Two approaches have been proposed to promote energy savings: (i) by installing more energy-efficient equipment in buildings; or (ii) by managing energy consumption efficiently using sophisticated control strategies in automation systems [3].
Gas instantaneous heating devices are widely used in domestic hot water production [5] and are essential for daily activities such as personal hygiene, cleaning, and bathing. However, one of their limitations is the difficulty of keeping desired hot water temperature setpoints when changes in water flow occur. These changes are usually very fast and unpredictable, severely affecting the users’ perception of comfort. When the user imposes a sudden increase in the hot water flow rate, tankless gas water heaters (TGWHs) are not able to provide such flow, ensuring high-performance temperature control, which results in lower temperatures than the ones desired by users for some (non-negligible) time. This scenario is identified as a temperature undershoot. A similar scenario occurs when a steady flow is followed by a sudden reduction in the requested water flow, and a temperature overshoot occurs [6]. Some of the latest and most advanced TGWHs include feedback controllers with flow and temperature sensors. However, manufacturers currently use control strategies that cannot provide high-performance responses to sudden changes in water temperature for variations in the required flow rate, mainly because it is challenging to deal with inertia, fast water flow changes and nonlinear fluid dynamics [6]. Temperature stabilisation of TGWHs has been pursued by including additional hardware, namely bypass valves, mixing valves and reservoirs working as thermal capacitances [6,7]. The classical feedback controllers, proportional and proportional-integral-derivative (PID), are inappropriate for the temperature control of TGWHs [8]. Some authors propose using advanced control techniques not requiring mathematical modelling, such as fuzzy logic control [9,10] and artificial neural networks [11,12]. In this scope, neuro-fuzzy control was also proposed to overcome the complexity of mathematical problems [13,14]. Classic model predictive control (MPC), adaptive MPC and gain-schedule MPC have also been proposed for water temperature control [5,8,15]. Yuill, Henze and Coward [16,17,18] focused on control strategies for electric water heaters, from classical techniques, such as PID control, to more advanced techniques, such as predictive control. For heat pumps, several studies have focused on predictive control to increase user comfort, improve energy efficiency, and reduce costs and gaseous emissions [19,20,21], while other investigations have focused on researching new refrigerant mixtures and regulating operating parameters [22,23]. Additionally, Garcia and Chua [24] proposed using a hybrid model composed of a gas and electric water heater for fast hot water supply responses while decreasing energy consumption and CO2 emissions. Finally, Bobál et al. [25,26] implemented a Smith predictor control approach for heat exchangers. However, the Smith predictor requires an accurate estimation of models and dead time; moreover, it is susceptible to the linearisation operating point and designed for fixed time delays.
MPC is a promising strategy for the temperature control of buildings because it can predict the dynamic states of processes [6,27]. Included are the optimisation of both the thermal and electric energy supplies [28], minimisation of energy consumption or operating costs [29], optimisation of energy costs of entire buildings [3], and optimisation of temperatures for air-handling units [30] while ensuring thermal comfort. However, MPC requires a significant computational overhead to solve complex and nonlinear problems, such as those found in gas water heaters. Although predictive controllers have already been designed to outperform the combined feedforward–feedback controllers usually implemented in these devices [15,16,31], their use has yet to be established by manufacturers of TGWHs due to the computational and memory resources required by MPC.
Modern microcontrollers can be used to implement complex control algorithms [32]. As the computing capacity of microprocessors increases and electronic control units (ECUs) become more sophisticated, MPC has become feasible even for hard control applications [33]. However, MPC algorithms’ fast and efficient software development relies on automatic code generation for quick code deployment on the selected hardware platforms [34].
Several tools are available to solve MPC problems. First, quadratic programming (QP) solvers, such as qpOASES [35], MOSEK [36], ECOS [37], OSQP [38] and ODYS QP [39], can effectively be used. Second, tools such as CVXGEN [40,41,42,43], FORCES [44], FiOrdOs [45] and QPGEN [46] were developed to optimise the code of quadratic programming solvers. The CasADi [47] tool generates an efficient implementation of nonlinear optimisation problems. Furthermore, tools such as µAO-MPC [48], GRAMPC [49], HPMPC [50] and ACADO [51] also use QP solvers and perform optimised automatic code generation for implementation in hardware. The MultiParametric Toolbox 3.0 [52] generates code for implementation in software, although it is limited to explicit and constrained MPC designs in which online optimisation is not required. The AutoMATiC tool [34] is a code-generation software package for implementing MPC algorithms on microcontrollers with low processing and memory resources. The Matlab/Simulink environment also provides toolboxes for automatic code generation. The Simulink Coder allows the generation and execution of C code from Simulink models. Embedded Coder generates optimised code for embedded systems, enabling hardware-in-the-loop (HIL) simulations.
Recent breakthroughs highlight that automatic code generation is an essential tool to produce highly efficient solvers customised for specific problems, such as those requiring the incorporation of MPC algorithms [53]. The key to overcoming challenges related to devices with limited resources is to employ efficient algorithms with the ability to exploit the computational performance capabilities of target platforms [54].
A preliminary simulation study was recently provided by Ehtiwesh et al. [5] regarding the development of classic and adaptive MPCs to improve the performance of TGWHs in transient regimes. Here, we propose for the first time the development and implementation of predictive control techniques to be embedded into low-cost microcontrollers, ensuring improved users’ thermal comfort and reduced water and energy waste in response to temperature variations. First, we designed a classic MPC and an adaptive MPC, providing improved performances compared to the results achieved by Ehtiwesh et al. [5]. A different TGWH appliance was considered, and improvements were performed to solve implementation problems, namely in the linear model and the successive linearisation approach. Then, the classic MPC controller was implemented in two low-cost microcontrollers using automatic code-generation tools and HIL simulations. The static feedback–feedforward controller was chosen as a benchmark, as TGWH manufacturers commonly use this control technique. Significant improvements were achieved as the controllers were implemented and tested on a real microcontroller with limited features. Finally, a new metric to analyse the users’ comfort is also proposed. The investigation presented in this paper highlights the significance of employing predictive control techniques to enhance the performance of TGWH systems, with a focus on minimising environmental impact and enhancing user comfort. As a result, this study contributes to the potential advancements in domestic water heaters, particularly for residential applications.
2. Methods
2.1. System Modeling
Control strategies were tested using the TGWH Junkers Hydro 4600 F WTD10-4 KME 23 JU, Bosch Thermotechnology, Aveiro, Portugal, commercial and residential instantaneous gas water heater. This non-condensation TGWH model has 22 kW maximum thermal power and 8 L/min and 2.2 L/min maximum and minimum water flow rates, respectively. It implements a thermostatic control strategy embedded in a microcontroller based on the signals of electrical sensors for water flow rate, and inlet and outlet water temperatures. The heating power is defined by the flow of an air–gas mixture, controlled by an electric gas valve and an electric fan for the forced ventilation system. The temperature setpoint is defined by the user in an LCD interface.
2.1.1. Nonlinear Model
The models used here were developed by our research team in previous works [6,7]. The lumped space approach was preferred over distributed analysis to meet the requirements for real-time simulation in HIL and implementation of MPC strategies in computationally limited embedded systems. The mathematical models result from applying physical laws that describe, with minor deviations, the system’s dynamics. Each component is modelled considering a control volume, for which mass and energy conservation equations are established. The heat cell includes the gas combustion burner and energy transfer to the water in the heat exchanger. A semi-empirical model, experimentally validated, has been embraced to incorporate complex combustion processes. A two-way proportional flow control valve was used to incorporate hot water demand, simulating changes in user requests.
The semi-empirical non-linear model for the TGWH heat cell and the model of the user control valve were implemented in MATLAB/Simulink. The system plant was defined as an interconnection of systems, in which the heat cell system is in cascade with the control valve.
For the heat cell, assuming that water and metal are at approximately the same temperature, and fluid density changes are negligible, the outlet water temperature T (°C) can be expressed by defining the energy conservation for a control volume, as in Equation (1). The thermal power (W) is defined by the mixing flow of gas and air. For water, the specific heat cp,w (J/kg°C−1), the density of water (Kg/m3) and the volumetric flow rate (m3/s) were used. C1 is an auxiliary constant that describes the heat capacity of the heat cell, which was experimentally found to be 2218.1 J/°C [55].
The plant model also incorporates time-varying delays, characteristic of thermal processes, that vary significantly, causing severe difficulties in temperature control. A time delay from thermal delivery is defined as a constant input delay, comprising the time since a change in the air–gas mixture occurs until it affects the water temperature within the heat cell. This delay was experimentally determined as 2.9 s [55]. The time delay due to the time it takes the water to travel along the pipes and the heat exchanger (Δt (s)) was defined as a time-varying output delay. This time delay is dependent on the water flow rate, and is expressed by Equation (2),
where (m3/s) is the flow rate, and Ri (m) and L (m) are respectively the radius and length of the circular section pipe.
2.1.2. Linear Model
MPC controllers require a model that describes the main dynamics of the plant system in the operating region [56]. For the control of nonlinear systems, the plant model can be linear or nonlinear; however, the use of a nonlinear model significantly increases the complexity and computational load of the controller. A linear model’s disadvantage is that the model mismatch typically increases with the distance to the linearisation operating point.
A linear model established in our previous work [8] was used, as it requires low computational load and, then, it requires a processing capability that can be provided by low-cost microcontrollers. The model output was defined as the output water temperature (T)’s deviation from the input temperature (Tin), as expressed by Equation (3).
Combining Equations (1) and (3) and assuming that the inlet water temperature is approximately constant (negligible inlet temperature changes were considered for model simplification, as assumed in previous studies [5,8,9,15,57]), the output temperature deviation was defined by Equation (4).
By applying a first-order Taylor series expansion, with operating points , and , and defining new deviation variables for the steady state (, and ), the linear model can be expressed by Equation (6).
The linear model can be expressed as a state–space system, as in Equation (7). This system has one state (x), two inputs (u), thermal power and flow rate, and one output (y), the temperature deviation, as in Equation (8). The state (A), input (B), output (C) and feedthrough (D) matrices are given in Equation (9).
Time delays were included in this state–space model. The linearisation operating point was defined as 5 L/min of flow rate (approximately the average operating flow rate), and 45 °C of setpoint temperature.
2.2. Tools and Methodology
2.2.1. Matlab and Simulink
Matlab/Simulink software (v. 2022a, MathWorks) was used to model, simulate and analyse the developed temperature controllers. The MPC and the adaptive MPC controllers were developed using the Model Predictive Control Toolbox.
2.2.2. Hardware-in-the-Loop Platform
To investigate the performance of the proposed controllers, an HIL platform was established as a virtual test bench [58]. HIL methodologies are state-of-the-art procedures for evaluating embedded systems, aiming to obtain more accurate results closer to the actual scenario and simultaneously shorten the time of the product development process. By simulating actual conditions, or even extreme conditions beyond the physical limits of some of the elements, it is possible to evaluate the performance at reduced costs and time and avoid possible safety problems as with combustion systems.
The HIL simulation process is described (Figure 1). A Simulink model of the controller (feedforward, MPC or adaptive MPC) was created on the host computer. This model was compiled into C code and transferred to the microcontroller. A nonlinear Simulink model of the water heater plant was created on the virtual bench computer. To run the real-time simulation, this model was also compiled in C code and transferred to the DS1104 R&D controller board, which comprises I/O interfaces and a real-time processor connected to a PC. The CLP1104 connector panel was used as the hardware interface between the system virtual plant (implemented on the DS1104 R&D controller board) and the controller (implemented in the microcontroller). The inlet and outlet water temperatures and flow rate values were sent from the plant model as dSPACE analogical output signals and connected to the microcontroller analogue inputs. The controller output was the thermal power, defined as a microcontroller analogical output connected to a dSPACE input. An application was developed in the dSPACE ControlDesk software (v. 6.3, dSPACE) to allow the user–plant interface, namely, to control all experiments and monitor the plant variables.
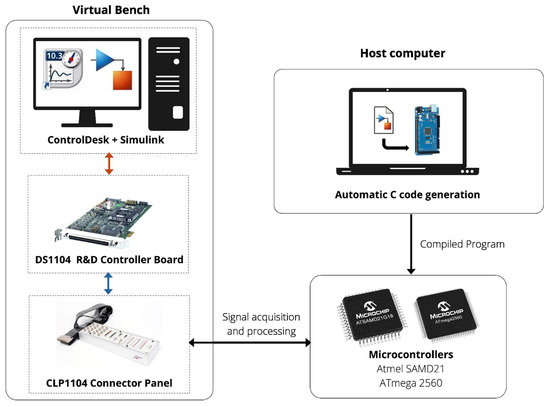
Figure 1.
Schematic of HIL platform used to test the developed controller.
2.2.3. Microcontrollers
The MPC algorithm was embedded into two different low-cost microcontrollers: (i) the Atmel SAMD21 microcontroller using a 32-bit ARM® Cortex®-M0+ processor; (ii) the Atmega2560 microcontroller: a low-power Microchip 8-bit AVR® RISC-based microcontroller. These microcontrollers are popular in a wide range of applications, such as home automation, consumer, metering, and industrial. The Atmega2560 is a more limited microcontroller regarding computational speed and memory and lacks a DAC circuit. Table 1 summarises the most relevant specifications for the analysed microcontrollers.

Table 1.
Comparison of microcontrollers’ main specifications.
2.2.4. Performance Evaluation Metrics
The performance of the controllers was evaluated according to the rise time, settling time, temperature overshoot/undershoot percentage, the integral squared error (ISE), and a comfort index (fcomfort (%)).
If rise and settling times are decreased, less water and energy are wasted, and greater user’s comfort is achieved. In a cold start scenario, it is required to reduce the amount of wasted water until the desired temperature is reached; in a flow change scenario, it is required to reduce the amount of wasted water in response to temperature changes that cause discomfort. The temperature overshoot/undershoot is relevant in flow change scenarios, as they are related to the maximum discomfort during the temperature control operation. For cold start tests, the rise time is defined as the time since the hot water demand starts, measured by the flow rate, until the outlet water temperature reaches 90% of the setpoint temperature. The settling time is defined as the time since the flow rate changes until the outlet water temperature enters and remains within a 2.5% tolerance of the setpoint temperature. The ISE, computed during 60 s as expressed in Equation (10), quantifies the distance between the outlet and setpoint temperatures. This metric was used to quantify the accuracy of the response to a user’s comfort requirement, as it applies a higher penalisation for higher magnitude errors and a lower one for smaller errors, which is similar to human perception of water temperature [17,18].
fcomfort (%) is a comfort index from 0 to 100% proposed by Pärisch [59,60] to quantify the user perception of comfort for each individual event (index i). This comfort index is computed as the ratio between the amount of heat to be delivered to water at a comfortable temperature and the total amount of heat removed from the system during the first 60 s after a disturbance occurs, as in Equation (11). It quantifies the efficiency by relating the fraction of heat employed in unused water and wasted into the drain because the user is uncomfortable with the total heat consumption in the evaluation period.
Both temperature variations and gradients were used to calculate the comfort index, as established in Figure 2, according to a combination of the two criteria proposed by Pärisch [59]. Indeed, variations can be experienced as uncomfortable even within a comfortable temperature range: the perception threshold is gradient-dependent. Water is considered comfortable, denoted by the colour green, when fluctuations are less than 2 °C and simultaneously the gradient is inferior to 0.1 °C/s.

Figure 2.
Comfort criteria adopted: very comfortable (T < 1 (°C)); comfortable (1 ≤ T < 2 (°C) ∧ ΔT < 0.1 (°C/s)); uncomfortable (2 ≤ T < 5 (°C) ∧ 0.1 ≤ ΔT < 0.2 (°C/s)); very uncomfortable (T ≥ 5 (°C) ∨ ΔT ≥ 0.2 (°C/s)).
2.3. Temperature Controllers
Three controllers were implemented using classic MPC, adaptive MPC and feedforward PID control strategies.
2.3.1. Feedforward PID
Manufacturers of TGWHs typically use the feedforward technique combined with feedback control (FFPID). In this control strategy, the feedforward component uses the system’s steady-state behaviour to predict the thermal power required to reach the setpoint temperature, while the feedback component compensates for disturbances and modelling errors. The theoretical thermal power, provided by the feedforward component, was computed considering the measured volumetric water flow rate and the difference between the inlet and setpoint temperatures, as expressed by Equation (12).
The feedback component was implemented with a discrete PID controller, in which the error was computed between the theoretical thermal power, considering the desired temperature, and the effective power, calculated considering the actual output temperature and using Equation (13).
The PID output was added to the theoretical power (feedforward component) to compute the final control action (Figure 3). This controller was implemented in Matlab/Simulink, and the PID parameters were optimised according to the Nelder–Mead simplex algorithm.
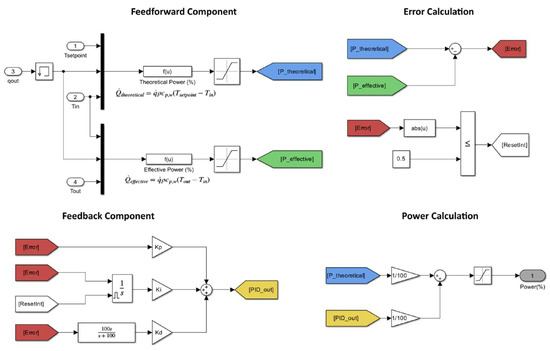
Figure 3.
Simulink block diagram of the FFPID controller.
2.3.2. Model Predictive Control
The MPC controller receives or estimates the current state of the plant and calculates the sequence of control actions that minimises a cost function over the horizon, solving a conditional optimisation problem [56,61]. The cost function, predefined in the Matlab MPC toolbox, was established by Equation (14). This cost function is the sum of four terms, each focusing on a particular aspect of the controller’s performance.
where zk is the sequence of manipulated variables from sample k to k + p − 1, p is the prediction horizon, and Jy, Ju, JΔu and Jε respectively represent the weighting in the cost function for tracking the output variable, tracking the manipulated variables, changing of the manipulated variables and constraint violation.
The MPC controller was designed with three inputs and one output. The controller inputs are: (i) a measured plant output (MO), corresponding to the output water temperature variation; (ii) a measured disturbance (MD) relative to the volumetric flow rate; and (iii) the desired reference. The controller output is the thermal power to be delivered to the plant. Constraints were imposed on the manipulated variable (MV), ranging from 0 to 1 (0–100%). The following MPC parameters were used: sample time Ts = 250 ms, prediction horizon p = 50, control horizon m = 8. Ts = 250 ms was chosen as it is currently the sample time used in the feedback–feedforward controllers implemented by manufacturers of the TGWH used in this study. Because this Ts is a short sample time, high values of control and prediction horizons were required, which increases the computational cost and makes implementing low-cost hardware difficult. Nevertheless, it improves the controller performance, ensuring a faster response and lower temperature overshoots and undershoots. In real-time simulations, these parameters are modified to improve the controller performance regarding required memory and outlet water temperature control. The continuous linear model, described in Section 2.1.2 and linearised for 5 L/min average operating flow rate, was discretised, and the delays were absorbed in the model by converting it into model states.
2.3.3. Adaptive MPC
MPC control can predict future behaviours using a linear time-invariant dynamic model. However, MPC’s performances can degrade over time if the plant is strongly nonlinear or if its characteristics experience significant changes [62]. Adaptive MPC can reduce the impact of this problem by adapting the prediction model to the current operating conditions [63], even if it uses a fixed model structure. Adaptive MPC provides a new linear model at each time interval under updated operating conditions. Therefore, it makes predictions more accurate for the next time interval, unlike the classic MPC, which uses a fixed internal model.
The successive linearisation approach was used to implement the adaptive MPC (Figure 4). Given a set of nonlinear differential and algebraic equations describing the system dynamics, a linear and time-invariant approximation is obtained under a specific operating condition. To avoid the need to perform a numerical linearisation at each step, a new parametrisation (of the matrices from the state–space model) is computed online, and the controller is updated. Successive linearisations allow to combine the accuracy of the nonlinear model with the robustness and ease of implementation of linear models [64]. The adaptive function considers current sensor values for computing the updated state–space linear model through its matrices and considering constant time delays according to the water flow rate measure. In this study, the plant was initially linearised for the minimum flow rate, 2.2 L/min. Since the model must have a fixed size, this flow rate, corresponding to the maximum number of states, allows the states to be absorbed for all operating flow rates. When higher flow rates are required, for example 6 L/min, not all the states will be used, only those required to represent the time delays of the flow rate under study. In addition to the three inputs used in the classic MPC, the model input signal was also required to specify the prediction model. This updated linear prediction model and the nominal operating point were specified as a bus signal for the controller input. The adaptive function was computed at 250 ms sampling time. The cost function used by the adaptive controller is the same as the one used in the classical MPC, Equation (14). The following MPC parameters were established for the adaptive solution: Ts = 250 ms, p = 80 and m = 14. Constraints were also imposed on MV: it was also defined between 0 to 1 (0–100%).
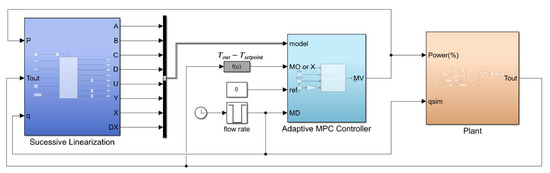
Figure 4.
Simulink model diagram used to implement the adaptive MPC.
3. Results and Discussion
3.1. Simulation Results
FFPID, classic MPC and adaptive MPC controllers were evaluated in three cold start scenarios: 3.65 L/min, 5.10 L/min and 6.55 L/min. Two scenarios expressing maximum water flow rate changes were analysed: from 2.2 L/min to 8 L/min and from 8 L/min to 2.2 L/min.
In the cold start scenarios (Figure 5, Table 2), the rise time and settling time decreased as the flow rate increased, regardless of the control strategy, due to the dynamics and time delays of the system. This pattern highlights that higher comfort indexes are achieved for higher flow rates, which results in higher efficiencies and reduced waste of water and energy throughout the non-comfortable period. A negligible overshoot was observed when the adaptive MPC was used, differently from what was observed when the other controllers were used, highlighting the predictive MPC behaviour. The lowest comfort index was obtained using the FFPID control, whatever the simulated flow rate. The adaptive function allowed higher comfort indexes and lower overshoots, except for the intermediate flow rate of 5.10 L/min, where similar behaviours were observed between predictive controllers. This occurred because the linear solution of the MPC was linearised for a 5 L/mi flow rate, which contains the same delays as the average operating flow rate. Differently, the adaptive control allowed to overcome performance losses related to operating points far from the chosen nominal operating point.
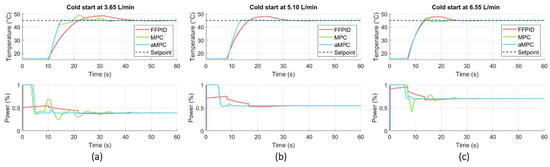
Figure 5.
Cold start simulations results for FFPID, MPC and adaptive MPC (aMPC) controllers for: (a) 3.65 L/min; (b) 5.10 L/min; and (c) 6.55 L/min.

Table 2.
Comparison of simulation results found for cold start using FFPID, linear MPC and adaptive MPC (aMPC) controllers.
In flow change scenarios (Figure 6, Table 3), temperature undershoots and overshoots occurred due to intrinsic system delays, regardless of the control strategy. Concerning the flow rate increasing scenario, the FFPID provided a slightly lower undershoot relative to responses obtained by two predictive control strategies. Shorter settling time was obtained using adaptive MPC compared to both responses obtained by the FFPID and linear MPC controller, which resulted in a higher comfort index found by the adaptive MPC. Indeed, the feedforward–feedback technique showed higher ISE, demonstrating the predictive controller’s superior ability to keep the temperature closer to the setpoint during the 60 s after disturbances. Regarding the flow rate decreasing scenario, the FFPID also achieved a lower overshoot. However, its settling time was about 11 s longer than the one obtained using the linear MPC, which required about 23 s longer than the adaptive MPC. Lower ISE was also observed for adaptive MPC compared to the responses of MPC and FFPID. The classic MPC obtained the lowest comfort index, as its behaviour expressed undesirable oscillations.
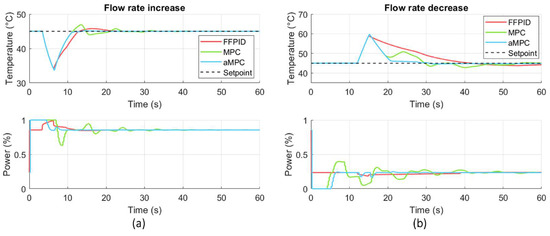
Figure 6.
Simulation results for FFPID, MPC and adaptive MPC (aMPC) controllers for: (a) flow rate increasing scenario; and (b) flow rate decreasing scenario.

Table 3.
Comparison of simulation results found for flow rate changes using FFPID, linear MPC and adaptive MPC (aMPC) controllers.
A progressive improvement of comfort levels from the solution currently used in gas water heaters to the adaptive MPC solution was achieved, as presented in the comfort graphical representation illustrated in Figure 7. Average comfort indexes of 58.7%, 67.9% and 78.2% were obtained for the FFPID, linear MPC and adaptive MPC controllers, respectively. These results highlight that the predictive behaviour of the MPC controller holds the potential to provide high-performance responses related to system delays, ensuring a superior anticipation ability for fast power transitions after changes in the flow rate.
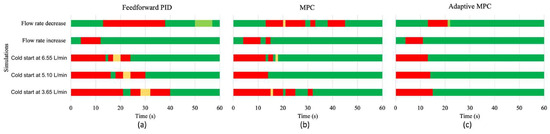
Figure 7.
Graphic representation of comfort using: (a) FFPID; (b) MPC; and (c) adaptive MPC (aMPC) controllers.
The simulation results provide valuable insights into the performance of different control strategies in various scenarios, namely for cold start and flow rate changes. Adopting adaptive MPC control strategies can significantly improve user comfort and energy efficiency (assessed by lower rise time, settling time, and overshoots/undershoots), highlighting its superior predictive behaviour. In some scenarios, the linear MPC presents similar performance, especially when the flow rate is close to the nominal operating point, while FFPID control consistently performs less effectively. Regarding flow rate, higher flow rates generally lead to improved comfort indexes and shorter rise times and settling times, regardless of the control strategy, because of the associated shorter time delays. In summary, these results suggest that by adopting predictive control strategies, more efficient and responsive systems can be achieved, leading to higher comfort and lower environmental impact.
3.2. Embedded Control Results
Implementing the MPC controller on low-cost microcontrollers can be a challenge due to memory and computation time constraints, and to overcome these limitations, optimisation strategies are essential. Results related to the linear optimised MPC solutions for implementation on hardware are reported hereafter, exposing the strategy to implement them. The implementation of the adaptive MPC controller was not possible using automatic code generation due to the high memory requirements. Therefore, the choice of microcontroller depends on the specific requirements of the control system and available computational resources.
The following strategy was used to implement the MPC controller in the Atmel SAMD21 microcontroller: (a) using a suboptimal solution and restricting the number of iterations in the MPC solver improves the controller responses, only requiring a 0.1% increase in the required memory; (b) decreasing the control and prediction horizons improves the controller response while significantly decreasing the memory requirements. The MPC solution optimised for the Atmega2560 microcontroller exceeded its available SRAM memory by 26.8%. Therefore, the strategy was successfully improved as follows: (i) reducing the control and prediction horizons, which have a fundamental impact on SRAM memory; (ii) linearising the plant for the maximum operating flow rate (8 L/min), as this is the flow rate with the shortest delays, and the absorption and conversion to states into system matrices decreases the plant model size.
Table 4 shows the Flash, SRAM memory and MPC parameters, for the Atmel SAMD21 and Atmega2560 microcontrollers. The FFPID controller is relatively light-weight in terms of memory usage on both microcontrollers, as it consumes a small percentage of both Flash and SRAM memory. The MPC controller requires significantly more memory, consuming a higher percentage of Flash and SRAM memory, especially in the Atmega2560 microcontroller, which highlights the inherent complexity of implementing this control strategy in low-cost hardware. Although FFPID is simple and relies on traditional control algorithms, predictive controllers require solving optimisation problems at each control step, which consumes a large amount of resources.

Table 4.
Comparison of memory required to implement the FFPID and MPC controllers in the Atmel SAMD21 and Atmega2560 microcontrollers.
The temperature responses in cold start scenarios (Figure 8) reveal faster responses of the predictive control. Moreover, the predictive controller was also able to provide: lower or equal rise times (Table 5); lower settling times, except for the minimum flow rate scenario (2.2 L/min); lower overshoot, except for 2.2 L/min and 3.65 L/min; and consistent lower ISE and higher comfort indexes (except for 2.2 L/min). Concerning the implementation in the 32-bit microcontroller, the highest comfort difference occurred in the average flow rate, which was approximately 24% higher for MPC. Moreover, a 15% higher comfort index was obtained for the 8-bit microcontroller (when 6.55 L/min is requested).
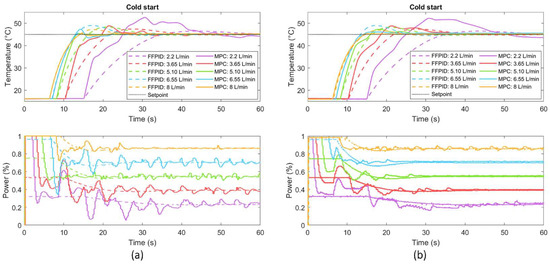
Figure 8.
Cold start HIL simulation results found for different flow rates using FFPID and MPC controllers implemented in: (a) Atmel SAMD21 microcontroller; and (b) Atmega2560 microcontroller.

Table 5.
Comparison of HIL simulation results found for cold start using the FFPID and MPC controllers, implemented in the Atmel SAMD21 and Atmega2560 microcontrollers.
Concerning the flow rate increasing scenario (Figure 9), the MPC controller reached the desired temperature faster than the FFPID controller after disturbances. However, the response improvements obtained with an 8-bit microcontroller are noticeable as the flow rate increase occurred for the linearisation flow rate. Results obtained with the 32-bit microcontroller highlight that, although the MPC controller achieved a settling time 3 s longer than the FFPID controller, it provided a 1% lower undershoot and a 4% higher comfort index, as well as a significantly lower ISE, making it able to provide responses closer to the desired temperatures 60 s after disturbances (Table 6). Regarding the implementation in the 8-bit microcontroller, the settling time decreased by 12 s, which was lowered by 8 s compared to the FFPID. Additionally, the comfort index increased by 5% relative to the one obtained for the 32-bit microcontroller, which is 9% higher than the technique currently used. Significant lower ISE and slightly lower undershoots were achieved for both controllers when the MPC controller was used.
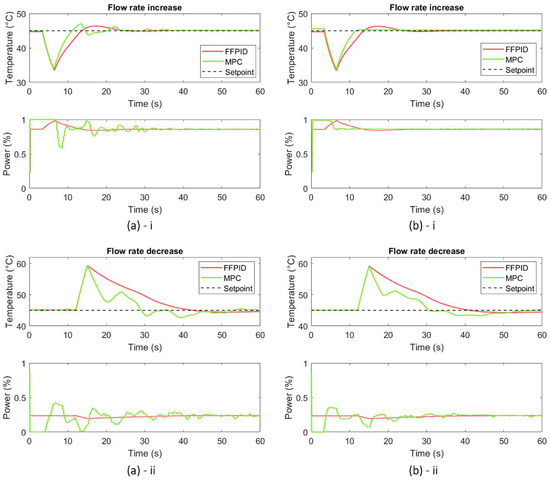
Figure 9.
HIL simulation results found for flow rate changes using FFPID and MPC controllers implemented in: (a) Atmel SAMD21 microcontroller; and (b) Atmega2560 microcontroller. (i—flow rate increase; ii—flow rate decrease).

Table 6.
Comparison of HIL simulation results found for flow rate changes using FFPID and classic MPC controllers, implemented in the Atmel SAMD21 and Atmega2560 microcontrollers.
Concerning the flow rate decreasing scenario (Figure 9), a performance loss was expected using the 8-bit microcontroller, as the flow rate change is performed at the minimum flow rate, the opposite of the limit flow used in plant linearisation. The results show a longer settling time using the predictive controller, about 6 s and 10 s for the 32-bit and 8-bit microcontrollers, respectively (Table 6). However, significantly lower ISE and overshoots were observed using the MPC controller for both types of low-cost hardware. The comfort index obtained in the 32-bit microcontroller was about 0.6% lower using the MPC controller due to its oscillating characteristics. However, the predictive controller presented a comfort index about 4.1% higher when implemented using the 8-bit microcontroller.
A graphical representation of the comfort the user would feel during HIL simulations is presented in Figure 10. The comfort improvement using the MPC controller is noticeable in most HIL simulations, mainly in the cold start scenarios. Using the overall comfort index as the average of the considered events, a 55.4% comfort index for the FFPID controller and 62.2% for the MPC controller were obtained in the 32-bit microcontroller; concerning the 8-bit microcontroller, 55.9% for the FFPID controller and 60.1% for MPC controller were observed. The implementation of the MPC algorithm on the lower-performance hardware made it possible to provide higher user comfort.
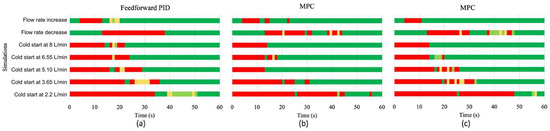
Figure 10.
Graphical representation of comfort using: (a) FFPID; (b) MPC controller implemented in the Atmel SAMD21 microcontroller; and (c) MPC controller implemented in the Atmega2560 microcontroller. Similar results were obtained for the FFPID using both microcontrollers.
4. Conclusions
This work describes the development of predictive temperature control strategies: (i) to reduce the temperature overshoot and undershoot effects of instantaneous water heaters, which usually occur during significant flow rate changes; and (ii) to reduce the rise time in cold start scenarios, such that the amount of wasted water can be reduced. Their performance was analysed both in simulation and HIL environments, in which the predictive controller was successfully embedded into two low-cost microcontrollers, such that it can be incorporated into gas water heaters by manufacturers.
Temperature overshoots and undershoots were not completely eliminated, as the water demand cannot be predicted, and the system is characterised by time delays. Even so, MPC controllers (in particular the adaptive one) were able to provide faster responses to disturbances and lower rise times in cold start scenarios, which result in lower water and energy costs, lower environmental impacts (gaseous emissions) and increased user comfort, as the duration of uncomfortable water exposure is minimised. The classic MPC controller’s performance was dependent on the operating point chosen for plant linearisation, which exhibits a superior performance. The use of successive linearisation at each instant (adaptive MPC) allowed to overcome limitations occurring when operating points are far from the chosen nominal operating point; significantly improved performances over the entire water heater operating range can be obtained. For the lowest flow rate, the performance of MPC was significantly inferior, which demonstrates the significant impact of model mismatch, particularly with time delays, and the advantage of adaptive control.
Although the predictive control requires more computational and memory resources than the FFPID control, the classic MPC controller was successfully embedded into two low-cost microcontrollers, namely 8-bit and 32-bit platforms, using an automatic code-generation tool. Similar conclusions were obtained using both a simulation environment and the HIL simulation environment incorporating these microcontrollers: (1) the predictive controller is able to reduce rise and settling times at cold starts, which can provide a significant reduction of water consumption and energy costs, as well as a relevant increase in the user comfort; (2) the predictive controller is able to provide shorter settling times and higher comfort indexes for sudden changes in water flow rates.
TGWHs have a long service life, up to 20 years, and the degradation of actuators’ performance, along with water flow restriction due to calcium build-up, has a significant impact on the appliance dynamics in the long term. One advantage of adaptive control strategies is the self-adaptation to the deterioration of plant dynamics, which is not achieved with fixed model-based control strategies, such as FFPID or classic MPC.
Future work should be conducted to assess the experimental performance and effectiveness of the developed MPC controller using real water heaters. The proposed predictive control strategy should be incorporated with other water heater control tasks, such as safety features and the control loop for the air–gas mixture; this must be performed in partnership with a TGWH manufacturer. These tests are relevant to analyse the impact of various plant characteristics that can only be considered in a real scenario, such as the time between disturbance events and the disturbance detection performance. Additionally, the adaptive MPC must be successfully embedded into low-cost microcontrollers, as it will most likely provide higher performances than classical MPC controllers. Investigation of the microcontroller requirements can help to define a more suitable hardware for the adaptive embedded implementation. A study that evaluates and compares new advancements in real-time solvers and code-generator tools built explicitly for embedded MPC should also be carried out, considering the control of TGWH. The generic code-generation platform produces excessive redundant code, and more specific and efficient tools must be employed for an optimised implementation.
Author Contributions
Investigation, methodology, software and writing—original draft, C.C. and A.Q.; funding acquisition, conceptualisation, project administration, supervision and writing—review and editing, J.A.F.F., N.M. and M.P.S.d.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Portuguese Foundation for Science and Technology (Projects UIDB/00481/2020 and UIDP/00481/2020) and CENTRO-01-0145 FEDER-022083-Centro Regional Operational Program (Centro2020), through Portugal 2020 and the European Regional Development Fund. The present study was developed under the scope of the Smart Green Homes Project (POCI-01-0247 FEDER-007678). It was also supported by the Centre for Mechanical Technology and Automation (TEMA) and Intelligent Systems Associate Laboratory (LASI).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| aMPC | Adaptive MPC |
| ECU | Electronic control unit |
| FFPID | Feedforward with feedback control |
| HIL | Hardware-in-the-loop |
| ISE | Integral squared error |
| MD | Measured disturbance |
| MO | Measured output |
| MPC | Model predictive control |
| MV | Manipulated variable |
| PID | Proportional-integral-derivative |
| QP | Quadratic programming |
| TGWH | Tankless gas water heaters |
Nomenclature
| A | State matrix |
| B | Input matrix |
| c | Specific heat |
| C | Output matrix |
| C1 | Auxiliar constant |
| D | Feedthrough matrix |
| fcomfort | Comfort index |
| J | Cost function |
| L | Length |
| Thermal power | |
| Volumetric flow rate | |
| R | Radius |
| T | Temperature |
| t | Time |
| u | Input vector |
| x | State vector |
| ρ | Density |
References
- International Energy Agency (IEA). World Energy Outlook 2022; IEA: Paris, France, 2022. [Google Scholar]
- European Statistics-Eurostat. Energy, Transport and Environment Statistics—2020 Edition; Publications Office of the European Union: Luxembourg, 2020; ISBN 978-92-76-20736-8. [Google Scholar]
- Ma, J.; Qin, S.J.; Salsbury, T. Application of Economic MPC to the Energy and Demand Minimization of a Commercial Building. J. Process Control 2014, 24, 1282–1291. [Google Scholar] [CrossRef]
- Rastegarpour, S.; Scattolini, R.; Ferrarini, L. Performance Improvement of an Air-to-Water Heat Pump through Linear Time-Varying MPC with Adaptive COP Predictor. J. Process Control 2021, 99, 69–78. [Google Scholar] [CrossRef]
- Ehtiwesh, I.A.S.; Quintã, A.F.; Ferreira, J.A.F. Predictive Control Strategies for Optimizing Temperature Stability in Instantaneous Hot Water Systems. Sci. Technol. Built Environ. 2021, 27, 679–690. [Google Scholar] [CrossRef]
- Quintã, A.F.; Ferreira, J.A.F.; Ramos, A.; Martins, N.A.D.; Costa, V.A.F. Simulation Models for Tankless Gas Water Heaters. Appl. Therm. Eng. 2019, 148, 944–952. [Google Scholar] [CrossRef]
- Costa, V.; Ferreira, J.; Guilherme, D. Modeling and Simulation of Tankless Gas Water Heaters to Reduce Temperature Overshoots and Undershoots. In Proceedings of the 12th International Conference on Heat Transfer, Fluid Mechanics and Thermodynamics (HEFAT 2016), Online, 8–10 August 2022; HEFAT: Málaga, Spain, 2016; pp. 1404–1409. [Google Scholar]
- Quintã, A.F.; Ehtiwesh, I.; Martins, N.; Ferreira, J.A.F. Gain Scheduling Model Predictive Controller Design for Tankless Gas Water Heaters with Time-Varying Delay. Appl. Therm. Eng. 2022, 213, 118669. [Google Scholar] [CrossRef]
- Wang, L.; Zang, H.; Ning, Y. The Gas Water Heater Control System Design Based on Fuzzy Control. In Proceedings of the 2011 International Conference on Electric Information and Control Engineering, Wuhan, China, 15–17 April 2011; pp. 840–843. [Google Scholar]
- Haissig, C.; Woessner, M. An Adaptive Fuzzy Algorithm for Domestic Hot Water Temperature Control of a Combi-Boiler. HVAC R Res. 2000, 6, 117–134. [Google Scholar] [CrossRef]
- Laurencio-Molina, J.C.; Salazar-Garcia, C. Design of an Artificial Neural Network Controller for a Tankless Water Heater By Using a Low-Profile Embedded System. In Proceedings of the 2018 IEEE International Work Conference on Bioinspired Intelligence (IWOBI), San Carlos, Costa Rica, 18–20 July 2018; pp. 1–9. [Google Scholar]
- Kumar, R.; Vardhan, H.; Bharadwaj, S. Temperature Control System Using Artificial Neural Network. Int. J. Eng. Res. Appl. 2013, 3, 672–675. [Google Scholar]
- Vieira, J.A.; Dias, F.M.; Mota, A.M. Hybrid Neuro-Fuzzy Network-Priori Knowledge Model in Temperature Control of a Gas Water Heater System. In Proceedings of the Fifth International Conference on Hybrid Intelligent Systems (HIS’05), Rio de Janeiro, Brazil, 6–9 November 2005; Volume 2005, pp. 116–121. [Google Scholar]
- Xu, K.; Qiu, X.; Li, X.; Xu, Y. A Dynamic Neuro-Fuzzy Controller for Gas-Fired Water Heater. In Proceedings of the 2008 Fourth International Conference on Natural Computation, Jinan, China, 18–20 October 2008; Volume 7 OP-200, pp. 240–244. [Google Scholar]
- Claquin; Carriere; Rocaries. Modelling and Application of Adaptive Control to a Gas Heater. In Proceedings of the IEEE International Conference on Control and Applications CCA-94, Glasgow, Scotland, 8–12 August 1994; Volume 2, pp. 927–932. [Google Scholar]
- Henze, G.; Yuill, D.; Coward, A. Development of a Model Predictive Controller for Tankless Water Heaters. HVAC R Res. 2009, 15, 3–23. [Google Scholar] [CrossRef]
- Yuill, D. Development of an Accurate Feed-Forward Temperature Control Tankless Water Heater; Pittsburgh, P.A., Morgantown, W.V., Eds.; Building Solutions Incorporated: Dallas, TX, USA, 2008. [Google Scholar]
- Yuill, D.P.; Coward, A.H.; Henze, G.P. Performance Comparison of Control Methods for Tankless Water Heaters. HVAC R Res. 2010, 16, 677–690. [Google Scholar] [CrossRef]
- Jin, X.; Maguire, J.; Christensen, D. Model Predictive Control of Heat Pump Water Heaters for Energy Efficiency. In Proceedings of the ACEEE Summer Study on Energy Efficiency in Buildings, Pacific Grove, CA, USA, 17–22 August 2014; pp. 133–145. [Google Scholar]
- Wanjiru, E.M.; Sichilalu, S.M.; Xia, X. Model Predictive Control of Heat Pump Water Heater-Instantaneous Shower Powered with Integrated Renewable-Grid Energy Systems. Appl. Energy 2017, 204, 1333–1346. [Google Scholar] [CrossRef]
- Tarragona, J.; Fernández, C.; de Gracia, A. Model Predictive Control Applied to a Heating System with PV Panels and Thermal Energy Storage. Energy 2020, 197, 117229. [Google Scholar] [CrossRef]
- Luo, J.; Yang, K.; Zhao, Z.; Chen, G.; Wang, Q. Experimental Investigations on the Performance of a Single-Stage Compound Air-Source Heat Pump Using CO2/R600a in Cold Regions. Appl. Therm. Eng. 2022, 205, 118050. [Google Scholar] [CrossRef]
- Hakkaki-Fard, A.; Aidoun, Z.; Ouzzane, M. Improving Cold Climate Air-Source Heat Pump Performance with Refrigerant Mixtures. Appl. Therm. Eng. 2015, 78, 695–703. [Google Scholar] [CrossRef]
- Garcia, R.F.; Chua, A. An Innovative Control System of a Hybrid Tankless Water Heaters Using LabVIEW. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1109, 012018. [Google Scholar] [CrossRef]
- Bobál, V.; Kubalcik, M.; Dostal, P.; Matejicek, J. Adaptive Predictive Control of Time-Delay Systems. Comput. Math. Appl. 2013, 66, 165–176. [Google Scholar] [CrossRef]
- Holiš, R.; Bobál, V. MATLAB Toolbox for Self-Tuning Predictive Control of Time-Delayed Systems. In Proceedings of the 32nd European Conference on Modelling and Simulation, Wilhelmshaven, Germany, 25 May 2018; Nolle, L., Burger, A., Tholen, C., Werner, J., Eds.; ECMS: Wilhelmshaven, Germany, 2018; pp. 205–211. [Google Scholar]
- Rossiter, J.A. A First Course in Predictive Control, 2nd ed.; Control Series; CRC Press: New York, NY, USA, 2018; ISBN 9781315104126. [Google Scholar]
- Löhr, Y.; Wolf, D.; Pollerberg, C.; Hörsting, A.; Mönnigmann, M. Supervisory Model Predictive Control for Combined Electrical and Thermal Supply with Multiple Sources and Storages. Appl. Energy 2021, 290, 116742. [Google Scholar] [CrossRef]
- Široký, J.; Oldewurtel, F.; Cigler, J.; Prívara, S. Experimental Analysis of Model Predictive Control for an Energy Efficient Building Heating System. Appl. Energy 2011, 88, 3079–3087. [Google Scholar] [CrossRef]
- Bird, M.; Daveau, C.; O’Dwyer, E.; Acha, S.; Shah, N. Real-World Implementation and Cost of a Cloud-Based MPC Retrofit for HVAC Control Systems in Commercial Buildings. Energy Build. 2022, 270, 112269. [Google Scholar] [CrossRef]
- Rodrigues, E.M.G.; Godina, R.; Pouresmaeil, E.; Ferreira, J.R.; Catalão, J.P.S. Domestic Appliances Energy Optimization with Model Predictive Control. Energy Convers. Manag. 2017, 142, 402–413. [Google Scholar] [CrossRef]
- Chaber, P. Implementation of Dynamic Matrix Control Algorithm Using a Microcontroller with Fixed-Point Arithmetic. In Challenges in Automation, Robotics and Measurement Techniques; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 51–61. ISBN 978-3-319-29357-8. [Google Scholar]
- Kaleli, A. Development of the Predictive Based Control of an Autonomous Engine Cooling System for Variable Engine Operating Conditions in SI Engines: Design, Modeling and Real-Time Application. Control Eng. Pract. 2020, 100, 104424. [Google Scholar] [CrossRef]
- Chaber, P.; Lawrynczuk, M. AutoMATiC: Code Generation of Model Predictive Control Algorithms for Microcontrollers. IEEE Trans. Ind. Inform. 2020, 16, 4547–4556. [Google Scholar] [CrossRef]
- Ferreau, H.J.; Kirches, C.; Potschka, A.; Bock, H.G.; Diehl, M. QpOASES: A Parametric Active-Set Algorithm for Quadratic Programming. Math. Program. Comput. 2014, 6, 327–363. [Google Scholar] [CrossRef]
- MOSEK ApS. The MOSEK Optimization Toolbox for MATLAB Manual; MOSEK ApS: Copenhagen, Denmark, 2023. [Google Scholar]
- Domahidi, A.; Chu, E.; Boyd, S. ECOS: An SOCP Solver for Embedded Systems. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 3071–3076. [Google Scholar]
- Stellato, B.; Banjac, G.; Goulart, P.; Bemporad, A.; Boyd, S. OSQP: An Operator Splitting Solver for Quadratic Programs. Math. Program. Comput. 2020, 12, 637–672. [Google Scholar] [CrossRef]
- Cimini, G.; Bernardini, D.; Levijoki, S.; Bemporad, A. Embedded Model Predictive Control With Certified Real-Time Optimization for Synchronous Motors. Trans. Control Syst. Technol. 2021, 29, pp. 893–900. [Google Scholar] [CrossRef]
- Mattingley, J.; Boyd, S. CVXGEN: A Code Generator for Embedded Convex Optimization. Optim. Eng. 2012, 13, 1–27. [Google Scholar] [CrossRef]
- Mattingley, J.; Wang, Y.; Boyd, S. Receding Horizon Control. IEEE Control Syst. 2011, 31, 52–65. [Google Scholar] [CrossRef]
- Kunz, K.; Huck, S.M.; Summers, T.H. Fast Model Predictive Control of Miniature Helicopters. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 1377–1382. [Google Scholar]
- Kufoalor, D.K.M.; Aaker, V.; Johansen, T.A.; Imsland, L.; Eikrem, G.O. Automatically Generated Embedded Model Predictive Control: Moving an Industrial PC-Based MPC to an Embedded Platform. Optim. Control Appl. Methods 2015, 36, 705–727. [Google Scholar] [CrossRef]
- Domahidi, A.; Zgraggen, A.U.; Zeilinger, M.N.; Morari, M.; Jones, C.N. Efficient Interior Point Methods for Multistage Problems Arising in Receding Horizon Control. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 668–674. [Google Scholar]
- Binder, B.J.T.; Kufoalor, D.K.M.; Johansen, T.A. Scalability of QP Solvers for Embedded Model Predictive Control Applied to a Subsea Petroleum Production System. In Proceedings of the 2015 IEEE Conference on Control Applications (CCA), Sydney, Australia, 21–23 September 2015; pp. 1173–1178. [Google Scholar]
- Giselsson, P. Improved Fast Dual Gradient Methods for Embedded Model Predictive Control. IFAC Proc. Vol. 2014, 47, 2303–2309. [Google Scholar] [CrossRef]
- Andersson, J.A.E.; Gillis, J.; Horn, G.; Rawlings, J.B.; Diehl, M. CasADi: A Software Framework for Nonlinear Optimization and Optimal Control. Math. Program. Comput. 2019, 11, 1–36. [Google Scholar] [CrossRef]
- Zometa, P.; Kogel, M.; Findeisen, R. ΜAO-MPC: A Free Code Generation Tool for Embedded Real-Time Linear Model Predictive Control. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 5320–5325. [Google Scholar]
- Englert, T.; Völz, A.; Mesmer, F.; Rhein, S.; Graichen, K. A Software Framework for Embedded Nonlinear Model Predictive Control Using a Gradient-Based Augmented Lagrangian Approach (GRAMPC). Optim. Eng. 2019, 20, 769–809. [Google Scholar] [CrossRef]
- Frison, G.; Sorensen, H.H.B.; Dammann, B.; Jorgensen, J.B. High-Performance Small-Scale Solvers for Linear Model Predictive Control. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 128–133. [Google Scholar]
- Houska, B.; Ferreau, H.J.; Diehl, M. ACADO Toolkit-An Open-Source Framework for Automatic Control and Dynamic Optimization. Optim. Control Appl. Methods 2011, 32, 298–312. [Google Scholar] [CrossRef]
- Herceg, M.; Kvasnica, M.; Jones, C.N.; Morari, M. Multi-Parametric Toolbox 3.0. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 502–510. [Google Scholar]
- Jackson, B.E.; Punnoose, T.; Neamati, D.; Tracy, K.; Jitosho, R.; Manchester, Z. ALTRO-C: A Fast Solver for Conic Model-Predictive Control. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May–5 June 2021; pp. 7357–7364. [Google Scholar]
- Frison, G.; Kufoalor, D.K.M.; Imsland, L.; Jorgensen, J.B. Efficient Implementation of Solvers for Linear Model Predictive Control on Embedded Devices. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA), Antibes/Nice, France, 8-10 October 2014; pp. 1954–1959. [Google Scholar]
- Quintã, A.F.; Oliveira, J.D.; Ferreira, J.A.F.; Costa, V.A.F.; Martins, N. Virtual Test Bench for the Design of Control Strategies for Water Heaters. J. Therm. Sci. Eng. Appl. 2022, 14, 051004. [Google Scholar] [CrossRef]
- Camacho, E.F.; Bordons, C. Model Predictive Control, 2nd ed.; Advanced Textbooks in Control and Signal Processing; Springer: London, UK, 2007; ISBN 978-1-85233-694-3. [Google Scholar]
- Johnson, G.; Beausoleil-Morrison, I. The Calibration and Validation of a Model for Predicting the Performance of Gas-Fired Tankless Water Heaters in Domestic Hot Water Applications. Appl. Energy 2016, 177, 740–750. [Google Scholar] [CrossRef]
- Oliveira, J.D. Development of a Virtual Bench for Simulation and Monitoring of Water Heating Devices. Master’s Thesis, University of Aveiro, Aveiro, Portugal, 2019. [Google Scholar]
- Pärisch, P. Komfortbewertung des Regelverhaltens von Frischwasserstationen Auf Basis von Temperaturgradienten. In Proceedings of the 27. Symposium Thermische Solarenergie, Bad Staffelstein, Germany, 10 May 2017. [Google Scholar]
- Pärisch, P. Comfort Assessment of Tankless Water Heaters: Review and Suggestions. In Proceedings of the International Energy Agency Solar Heating & Cooling Programme (IEA SHC) International Conference on Solar Heating and Cooling for Buildings and Industry, Santiago, Chile, 4–7 November 2019; pp. 1–12. [Google Scholar]
- Oh, T.H.; Kim, J.W.; Son, S.H.; Jeong, D.H.; Lee, J.M. Multi-Strategy Control to Extend the Feasibility Region for Robust Model Predictive Control. J. Process Control 2022, 116, 25–33. [Google Scholar] [CrossRef]
- Kumar, K.; Patwardhan, S.C.; Noronha, S. Development of Adaptive Dual Predictive Control Schemes Based on Wiener–Hammerstein Models. J. Process Control 2022, 119, 68–85. [Google Scholar] [CrossRef]
- Martínez-García, F.; Badawy, G.; Kheradmandi, M.; Down, D.G. Adaptive Predictive Control of a Data Center Cooling Unit. Control Eng. Pract. 2021, 107, 104674. [Google Scholar] [CrossRef]
- Mendis, P.; Wickramasinghe, C.; Narayana, M.; Bayer, C. Adaptive Model Predictive Control with Successive Linearization for Distillate Composition Control in Batch Distillation. In Proceedings of the 2019 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 3–5 July 2019; pp. 366–369. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).