Tip-Over Detection and Avoidance Algorithms as Stabilization Strategy for Small-Footprint and Lightweight Mobile Manipulators
Abstract
1. Introduction
- The center of gravity (COG) of the system is shifted by attaching additional masses as counterweights.
- The tip-over edge is shifted to increase the corresponding lever arm.
2. Literature Review
- either the traveling speed of the mobile platform is reduced/suited, or
- the manipulator takes another position/orientation.
- The mobile manipulator should detect any degree of instability even under dynamic conditions.
- Appropriate and simplified measuring instruments shall be used.
- The mobile manipulator should not abort the tasks currently being executed, thus avoiding wasting time during its operation.
- The motion control should not be manipulated for these purposes; it should only be used to provide target positions and orientation values.
- The motion path should not be predefined, but updated with the corrected repositioning path in real time depending on the stability values calculated by the MHS. The repositioning path must remain close to the original path and the original orientation of the TCP should be maintained.
3. Materials and Methods
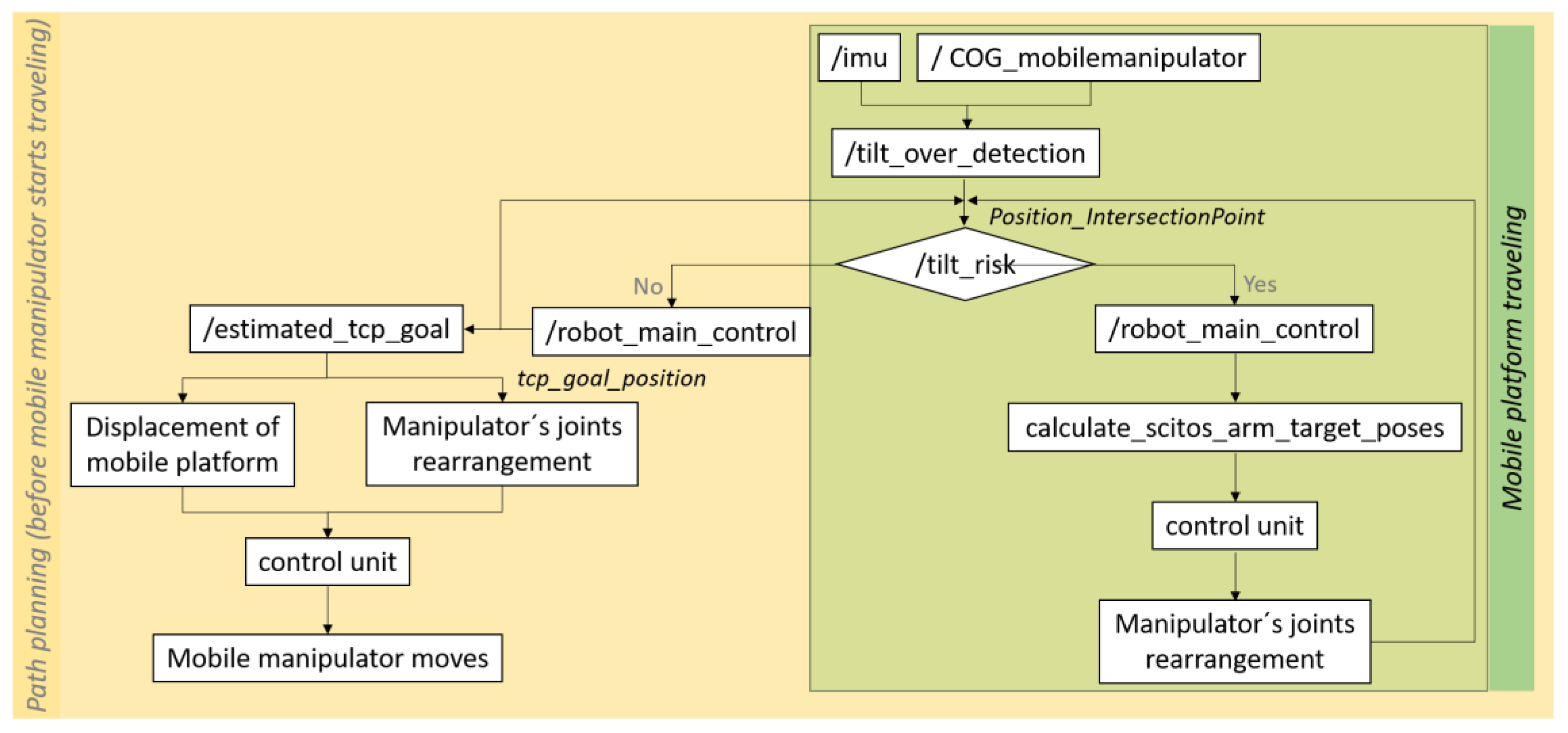
3.1. Tip-Over Detection Algorithm
MHS Algorithm Adaption and Implementation
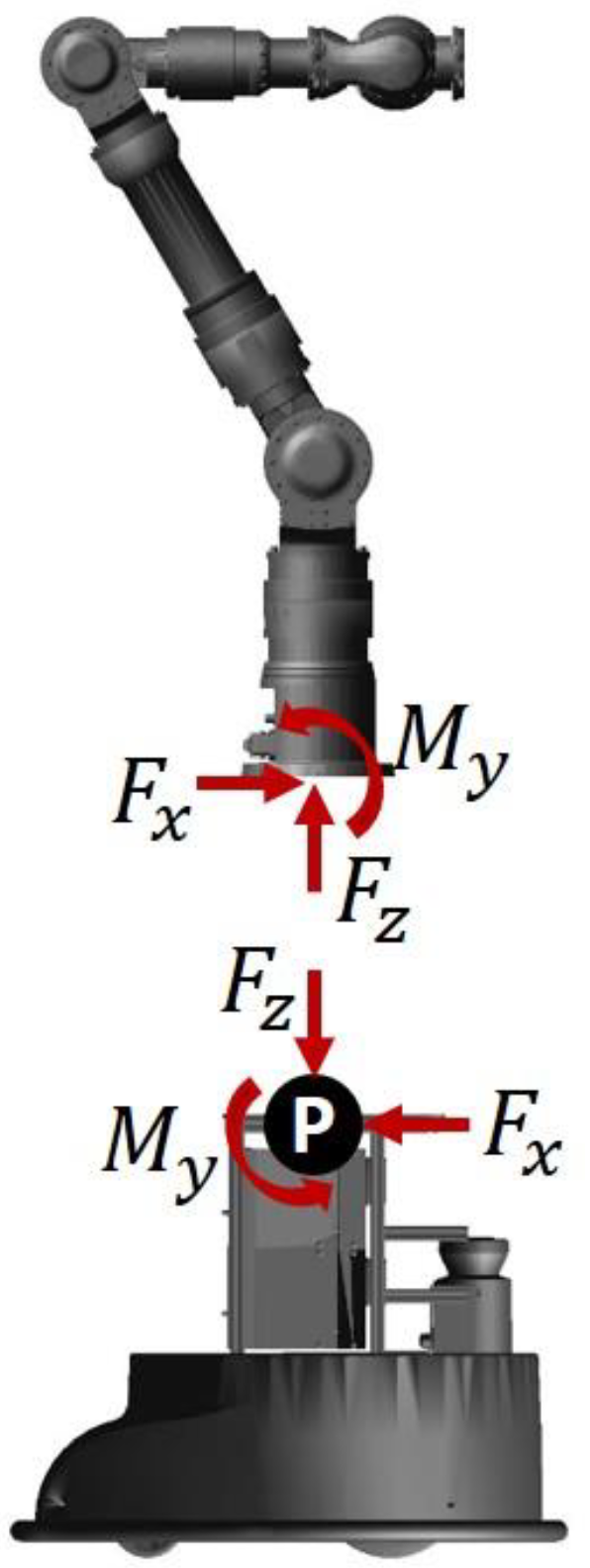
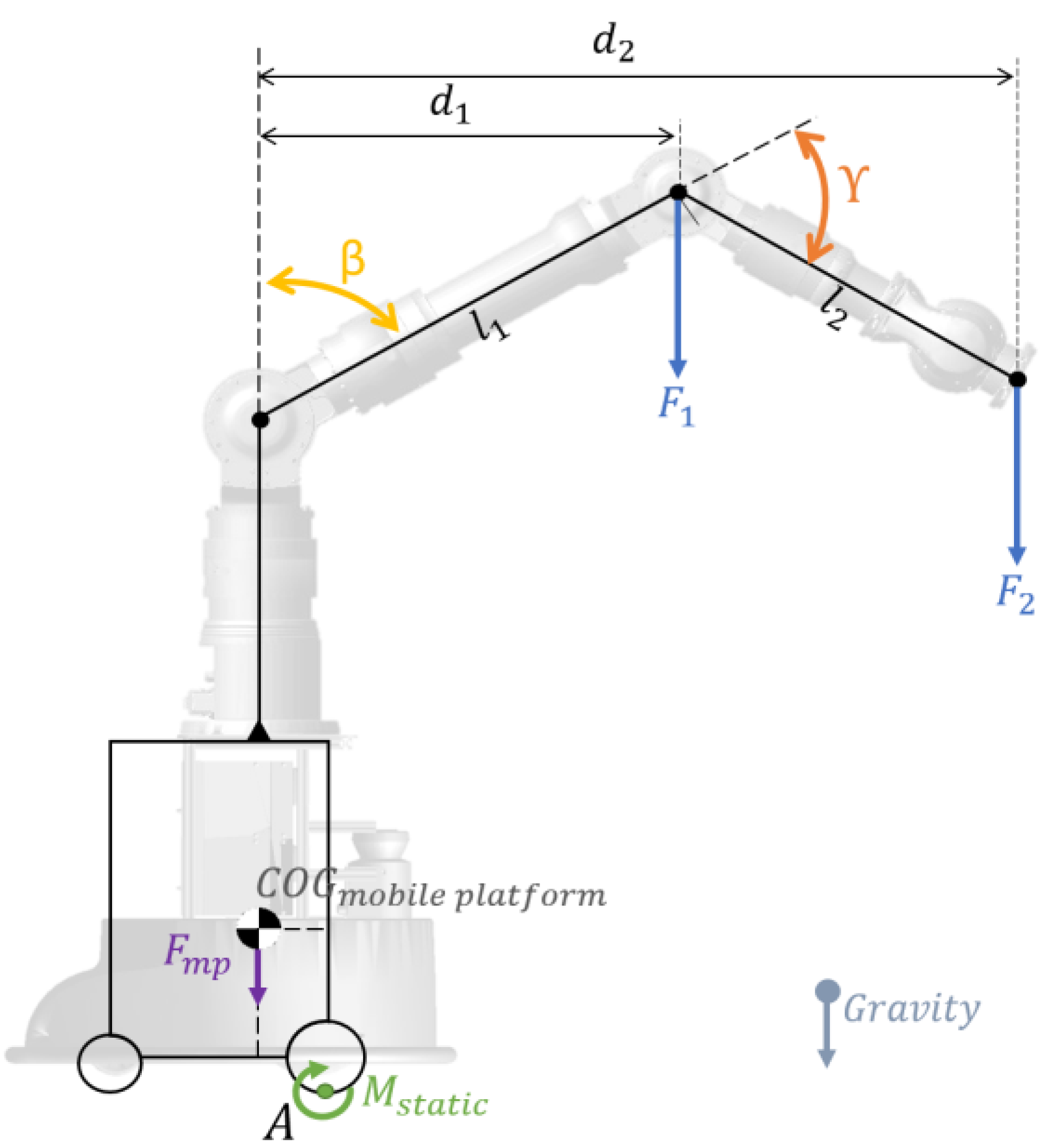
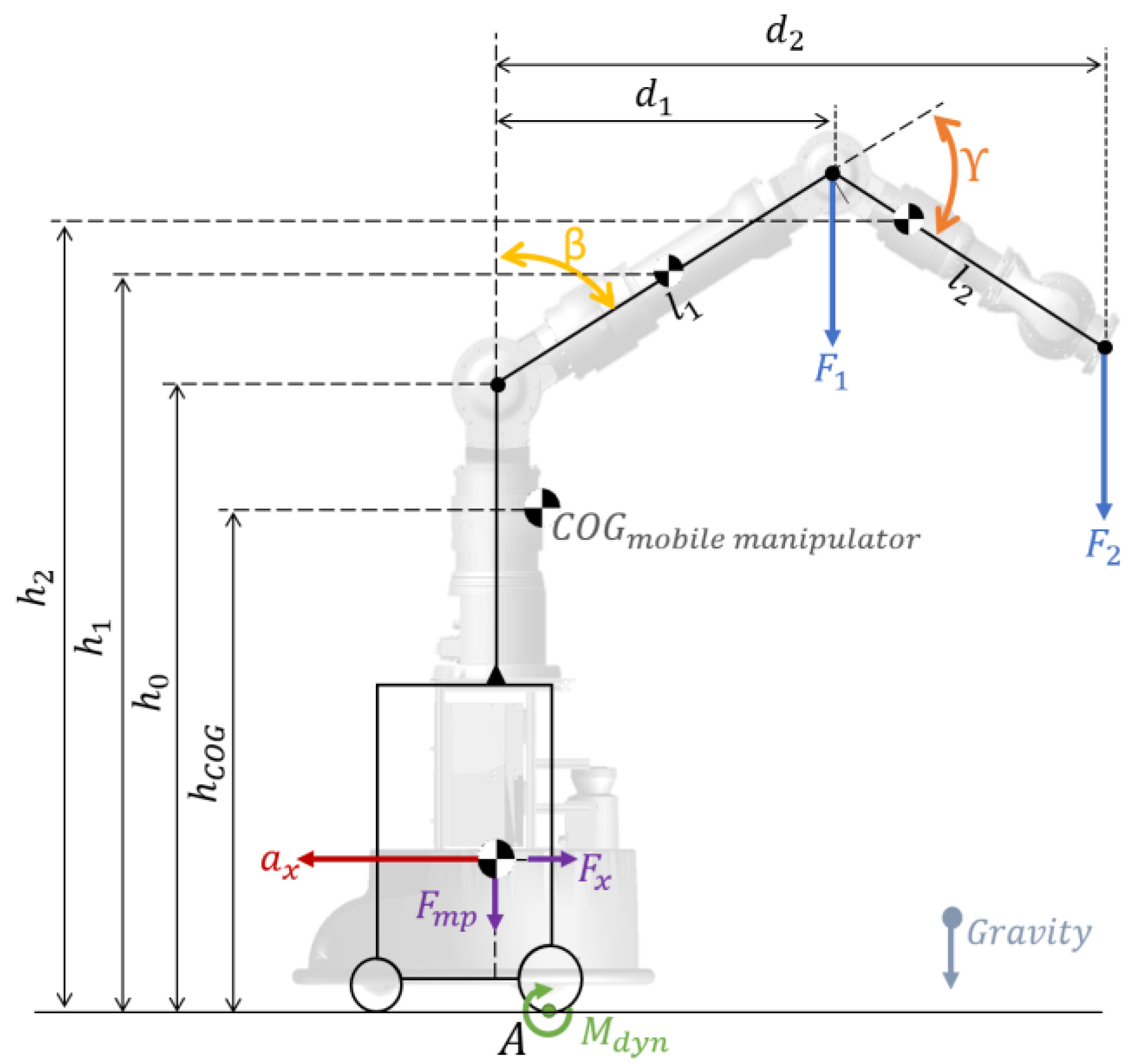
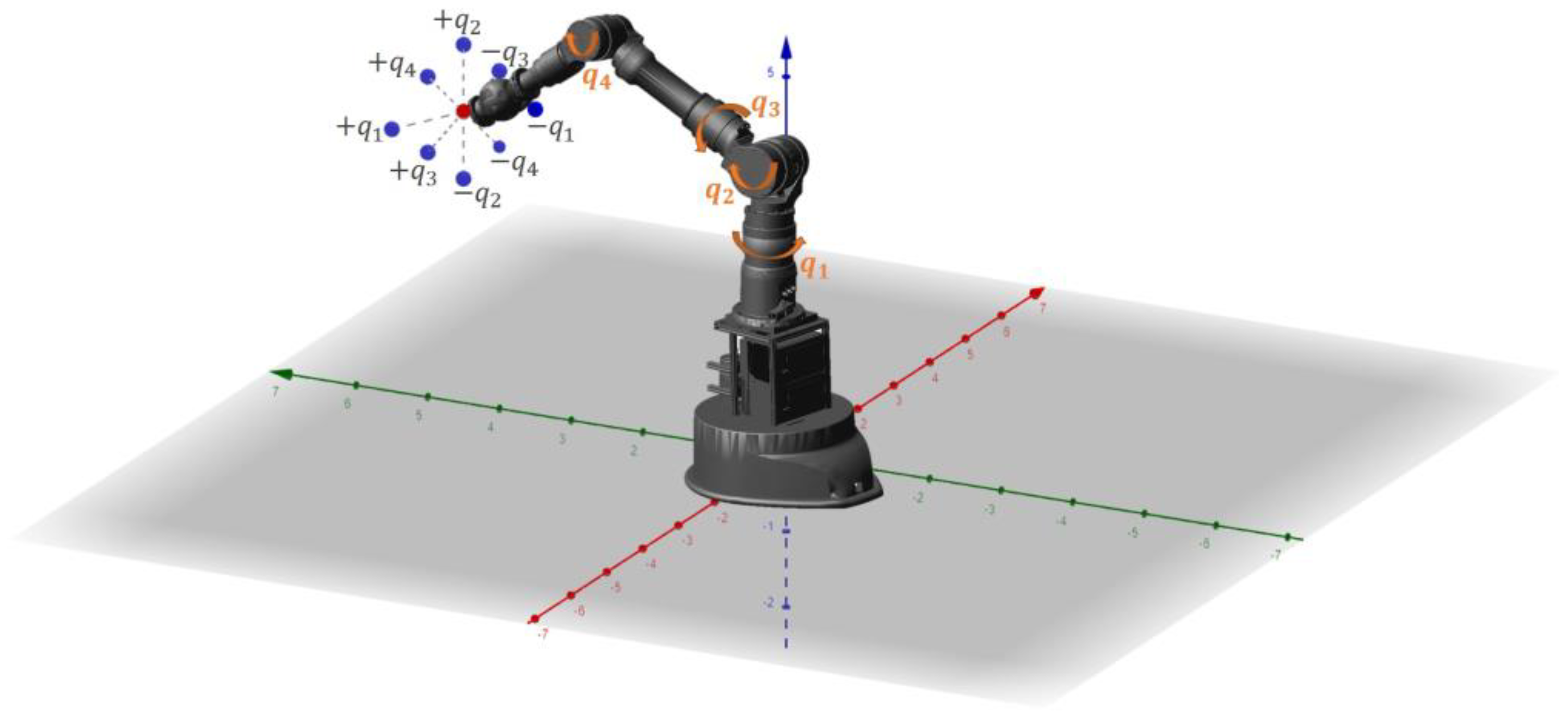
- The COG of the 5th, 6th, and 7th links of the manipulator were vertically aligned close to the rotary axis of its 4th joint so that no extra moments were produced around the 4th joint axis. While the 4th joint was accelerated from this vertical position to the sides, the moment acting on the 4th joint () was continuously calculated using the inertia, , and the angular velocity of the 4th joint axis, , as in (2).
- 2.
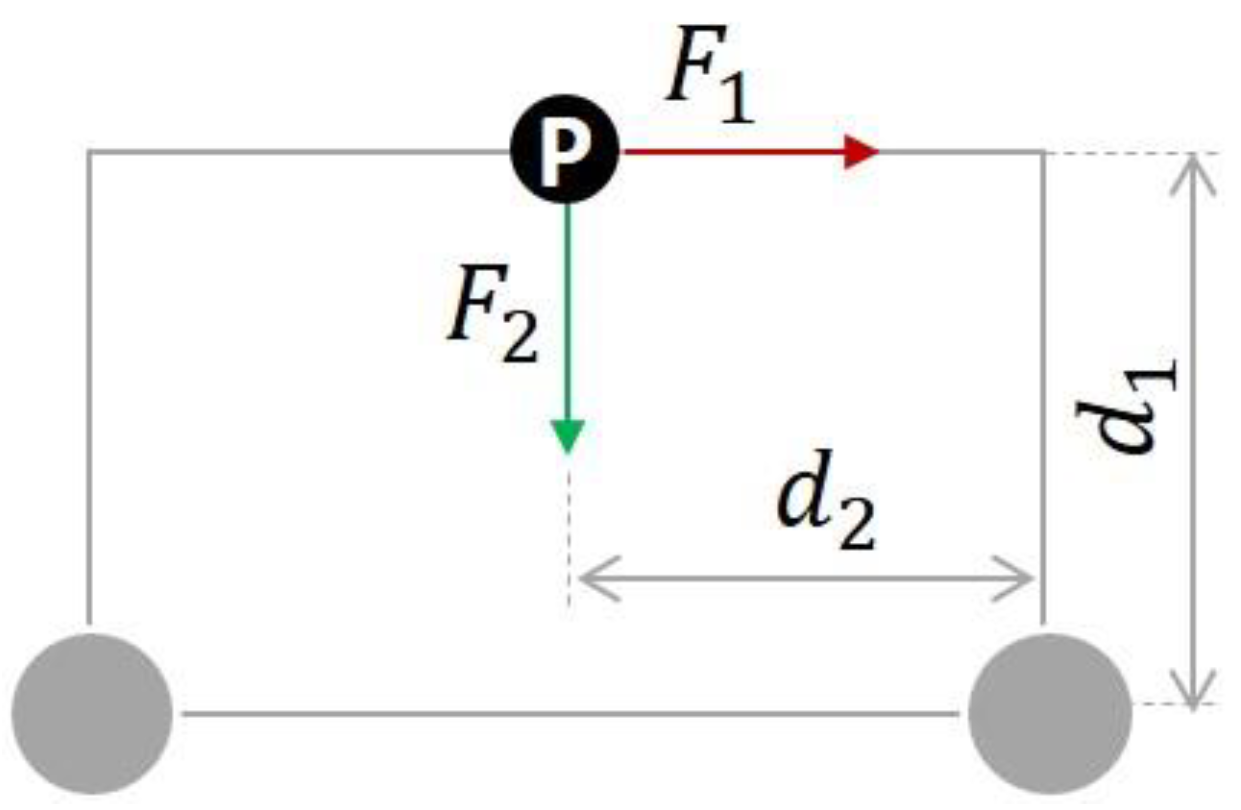
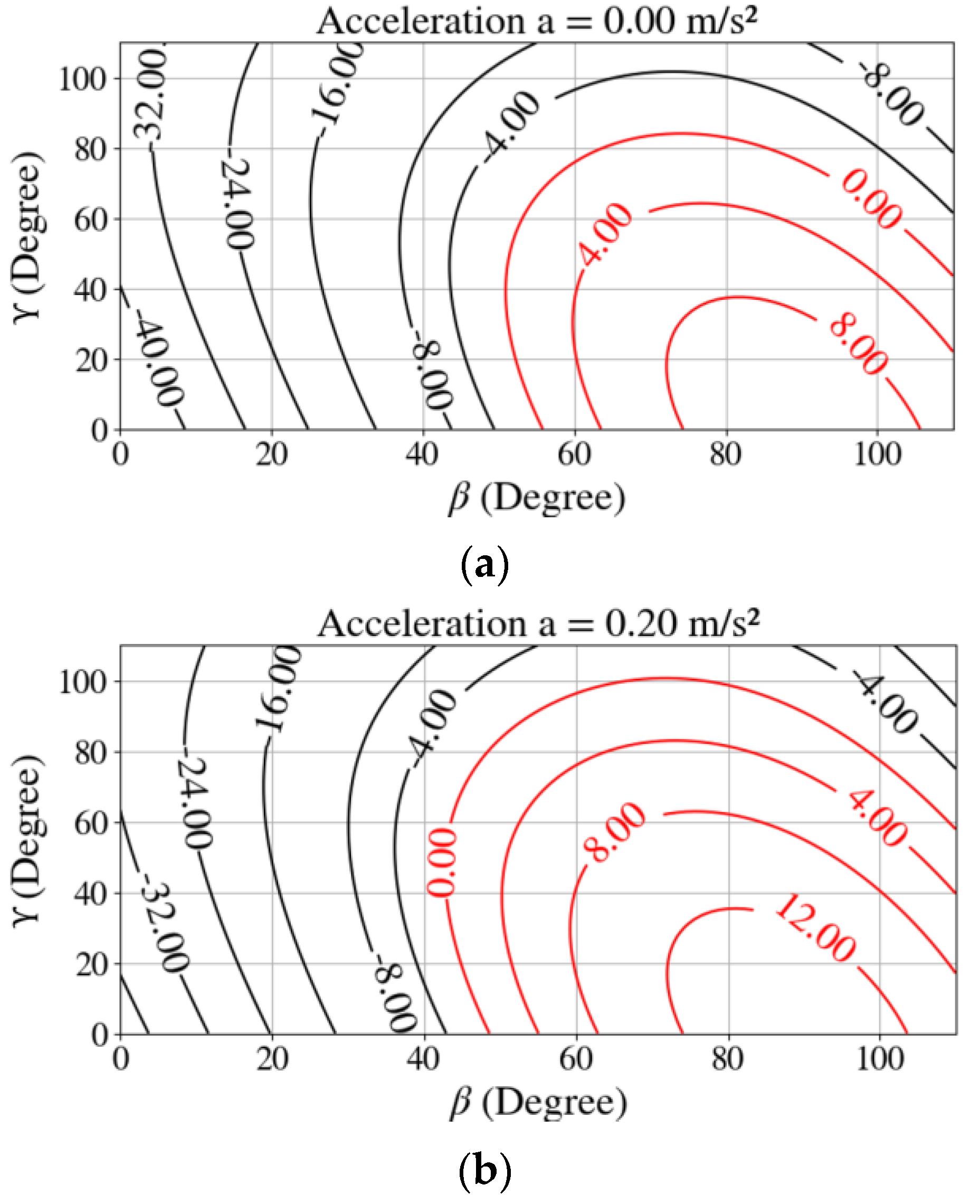
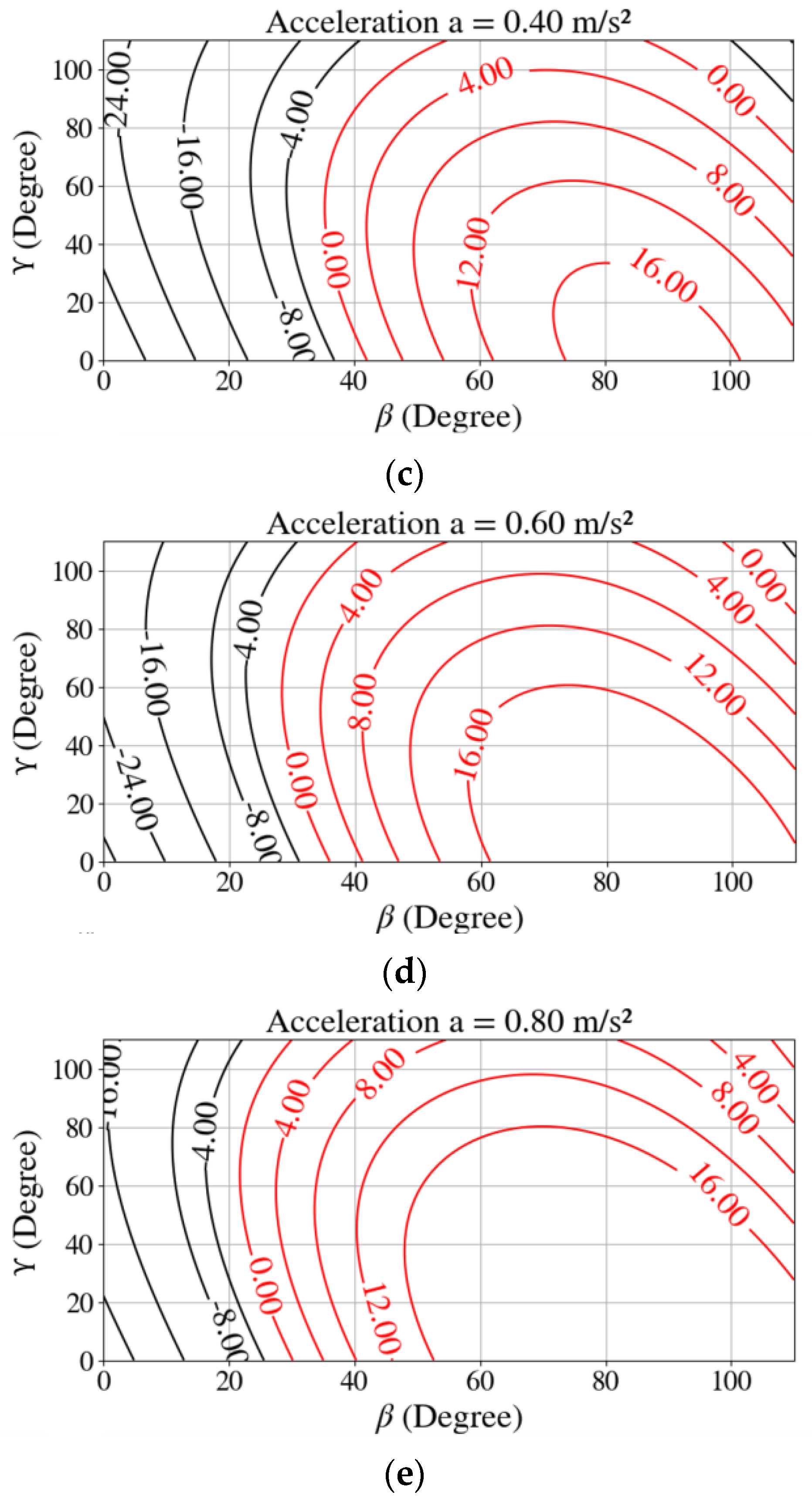
- The manipulator’s arm is set vertically. Now, instead of accelerating its 4th joint (as in scenario 1), the mobile platform is linearly accelerated while the manipulator remains stationary withwhere describes the linear acceleration of the mobile manipulator and defines the position of its COG related to the point P, illustrated in Figure 3.
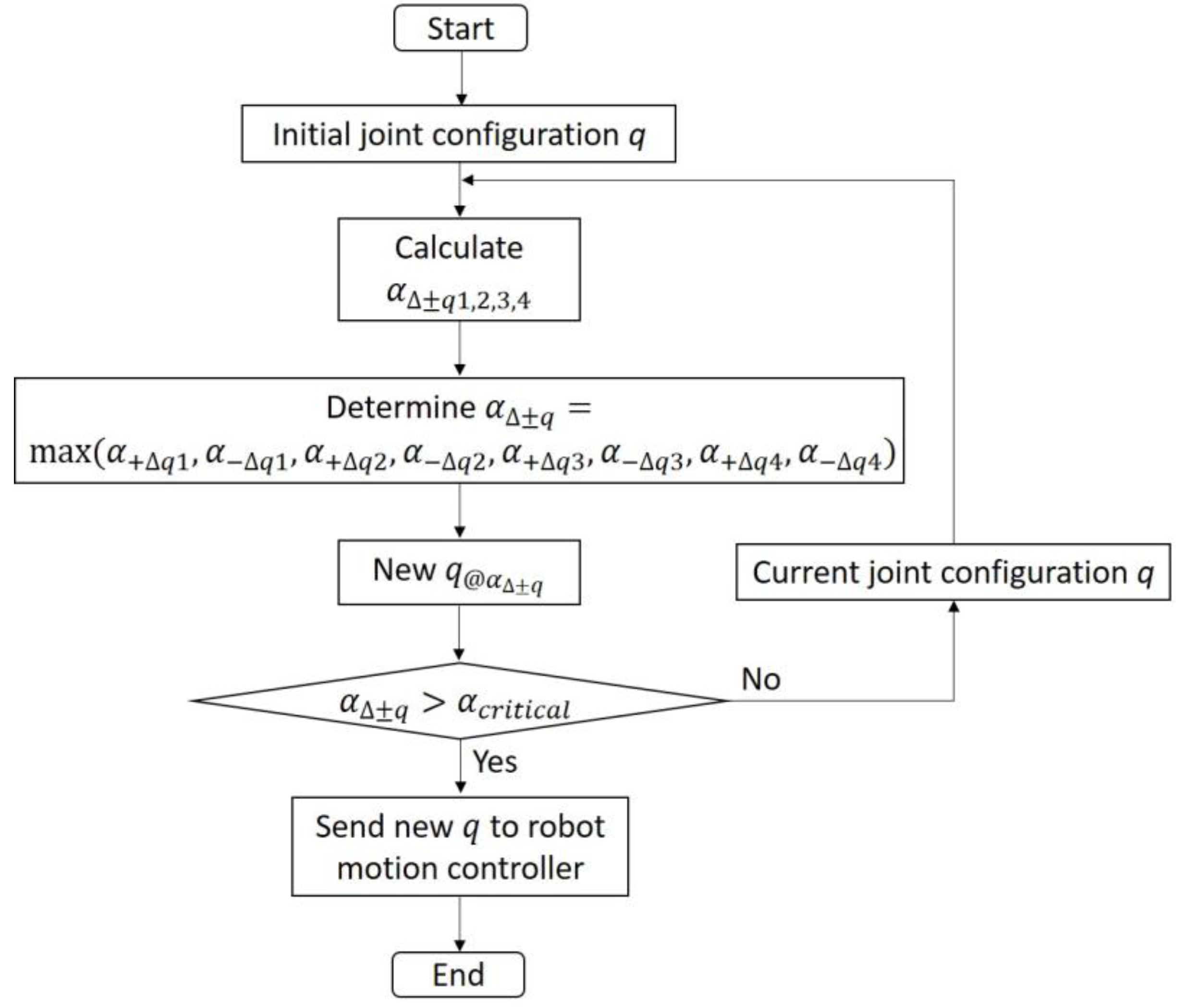
3.2. Tip-Over Avoidance Algorithm
- When one of the subsystems, the base or robotic arm, is stationary, while the other subsystem is moving.
- When the mobile platform and the robot arm move simultaneously.
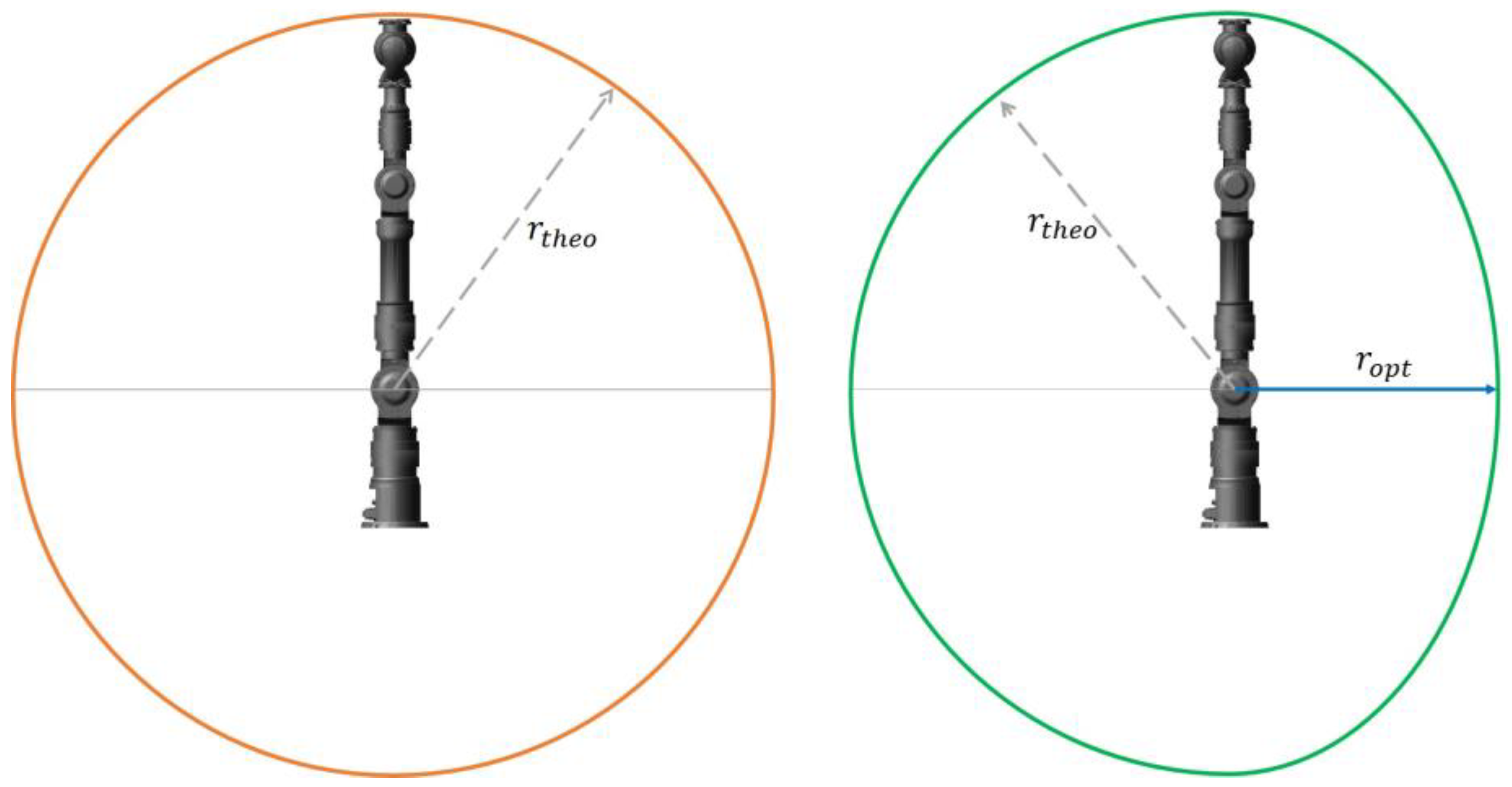
- A noncritical area described by a hemisphere with the maximum radius of the original theoretical workspace, and
- A critical workspace designed as an ellipsoid, since its volume builds the sphere very closely.
- When Γ < 90°, the TPC is located within the critical area, and thus, the ellipsoid should be employed as permitted workspace for the motion planning.
- When Γ > 90°, the TPC is located within the noncritical area; thus, the hemisphere defined by the theoretical local workspace should be employed for the motion planning.
4. Results
- The configuration space was spatially discretized with = 0.1 rad for the manipulator joints to to simplify the implementation of the gradient approach.
- The robot workspace was set as defined in the previous section.
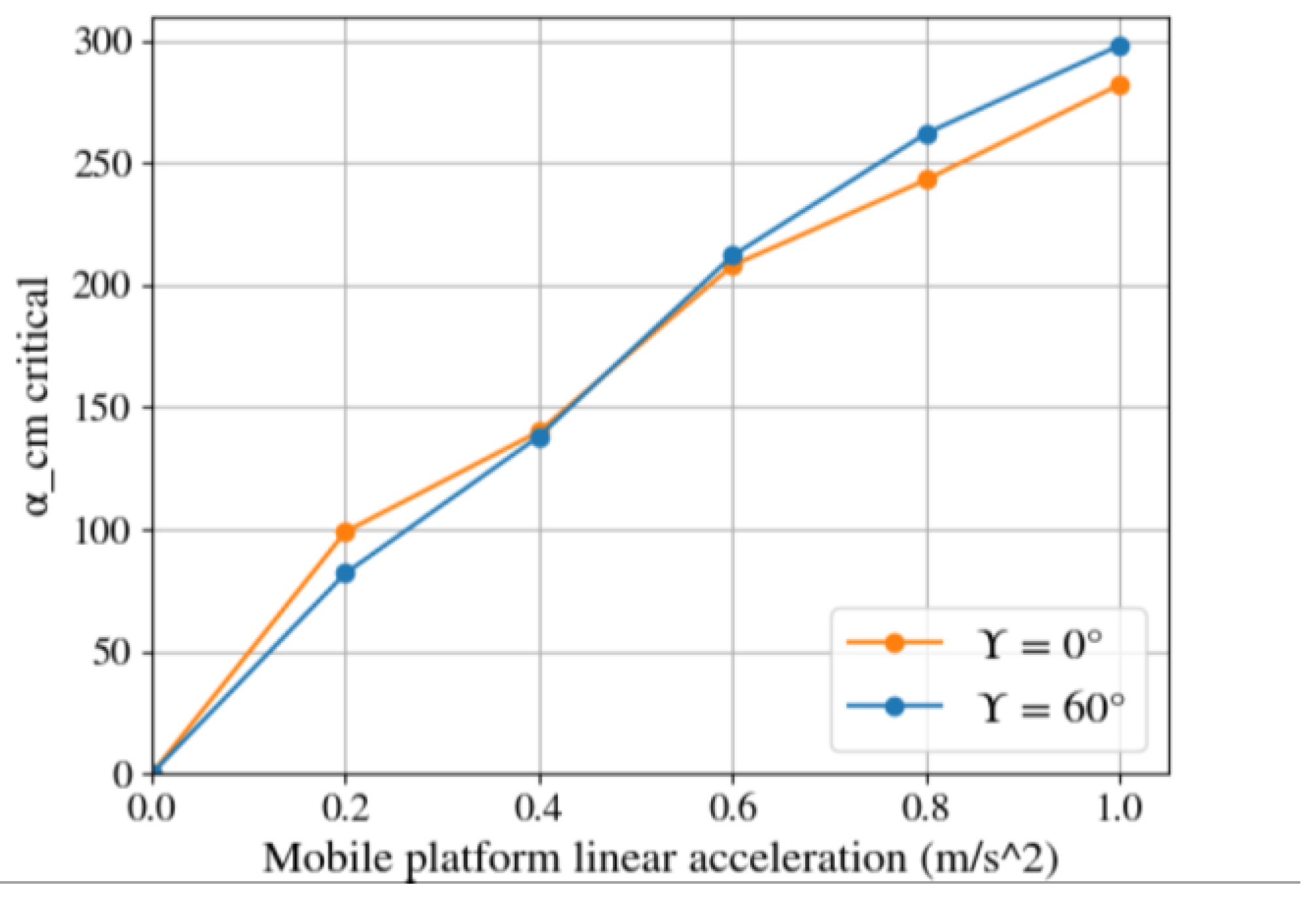
4.1. Evaluation of Workspace Optimization
4.2. Evaluation of Stabilization Strategy by Means of Simulation Sets
- Optimized workspace: The mobile manipulator is capable of deciding if the mobile platform has to be moved to reach the target point without any risk of instability.
- In the case of a repositioning of the robot arm, the initial orientation of the TCP should be maintained.
4.3. Stabilization Strategy Using the Real Mobile Manipulator
5. Discussion
- After receiving a target coordinate, the mobile manipulator independently determines whether the target is located within the predefined reachable and stable workspace or outside it. If the target point is located outside the optimized volume, the mobile platform approaches it.
- When instabilities are detected by the MHS before the mobile platform moves, the robot arm repositions itself to a non-critical position.
- If an instability is caused by accelerations or decelerations, which means that the stability value falls below the predefined threshold value, the robot arm repositions itself without aborting any current tasks. During this repositioning process, the initial orientation of the TPC is maintained.
- The robot arm approaches the target point only after the mobile platform reaches the target location. Thus, by extending the robot arm, it can be guaranteed that the TPC is situated within the stability-optimized workspace.
6. Conclusions
7. Contributions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rey, D.A.; Papadopoulos, E.G. On-line automatic tipover prevention for mobile manipulators. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Grenoble, France, 11 September 1997. [Google Scholar] [CrossRef]
- Tahboub, K.A. Robust control of mobile manipulators. J. Robot. Syst. 1996, 13, 699–708. [Google Scholar] [CrossRef]
- Ding, X.; Liu, Y.; Hou, J.; Ma, Q. Online Dynamic Tip-Over Avoidance for a Wheeled Mobile Manipulator with an Improved Tip-Over Moment Stability Criterion. IEEE Access 2019, 7, 67632–67645. [Google Scholar] [CrossRef]
- Böge, A.; Böge, W. Technische Mechanik: Statik—Reibung—Dynamik—Festigkeitslehre—Fluidmechanik; Springer Vieweg: Wiesbaden, Germany, 2019; Volume 33, ISBN 978-3-658-25724-8. [Google Scholar]
- Ghasempoor, A.; Sepehri, N. Measure of machine stability for moving base manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995. [Google Scholar] [CrossRef]
- Li, Y. Dynamic stability analysis and control for the mobile manipulator. In Proceedings of the IEEE CCECE2002 Canadian Conference on Electrical and Computer Engineering, Winnipeg, MB, Canada, 12–15 May 2002. [Google Scholar] [CrossRef]
- Papadopoulos, E.G.; Rey, D.A. New measure of tipover stability margin for mobile manipulators. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Rey, D.A. Force-angle measure of tipover stability margin for mobile manipulators. Veh. Syst. Dyn. 2000, 33, 29–48. [Google Scholar] [CrossRef] [PubMed]
- Vukobratović, M.; Borovac, B. Zero-Moment Point—Thirty Five Years of its Life. Int. J. Humanoid Robot. 2004, 1, 157–173. [Google Scholar] [CrossRef]
- Sugano, S.; Huang, Q.; Kato, I. Stability criteria in controlling mobile robotic systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS ’93), Yokohama, Japan, 26–30 July 1993. [Google Scholar] [CrossRef]
- Huang, Q.; Sugano, S.; Kato, I. Stability control for a mobile manipulator using a potential method. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS’94), Munich, Germany, 12–16 September 1994. [Google Scholar] [CrossRef]
- Moosavian, S.A.A.; Alipour, K. On the dynamic tip-over stability of wheeled mobile manipulators. Int. J. Robot. Autom. 2007, 22, 322. [Google Scholar] [CrossRef]
- Moosavian, S.A.A.; Alipour, K. Stability evaluation of mobile robotic systems using moment-height measure. In Proceedings of the 2006 IEEE Conference on Robotics, Automation and Mechatronics, Bangkok, Thailand, 1–3 June 2006. [Google Scholar] [CrossRef]
- Moosavian, S.A.A.; Alipour, K. Moment-Height tip-over measure for stability analysis of mobile robotic systems. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006. [Google Scholar] [CrossRef]
- Roan, P.R.; Burmeister, A.; Rahimi, A.; Holz, K.; Hooper, D. Real-world validation of three tipover algorithms for mobile robots. In Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010. [Google Scholar] [CrossRef]
- Huang, Q.; Sugano, S. Manipulator motion planning for stabilizing a mobile-manipulator. In Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots, Pittsburgh, PA, USA, 5–9 August 1995. [Google Scholar] [CrossRef]
- Alipour, K.; Hasanpour, A.; Daemy, P. Comparing two online tip-over avoidance algorithms for mobile manipulators. In Proceedings of the 2014 2nd RSI/ISM International Conference on Robotics and Mechatronics, ICRoM 2014, Tehran, Iran, 15–17 October 2014. [Google Scholar] [CrossRef]
- He, L. Tip-over avoidance algorithm for modular mobile manipulator. In Proceedings of the 2012 First International Conference on Innovative Engineering Systems, ICIES 2012, Alexandria, Egypt, 7–9 December 2012. [Google Scholar] [CrossRef]
- Hatano, M.; Obara, H. Stability evaluation for mobile manipulators using criteria based on reaction. In Proceedings of the SICE 2003 Annual Conference (IEEE Cat. No.03TH8734), Fukui, Japan, 4–6 August 2003. [Google Scholar]
- Furuno, S.; Yamamoto, M.; Mohri, A. Trajectory planning of mobile manipulator with stability considerations. In Proceedings of the IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Taipei, Taiwan, 14–19 September 2003. [Google Scholar] [CrossRef]
- Kim, J.; Chung, W.K.; Youm, Y.; Lee, B.H. Real-time ZMP compensation method using null motion for mobile manipulators. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y. Fuzzy logic self-motion planning and robust adaptive control for tip-over avoidance of redundant mobile modular manipulators. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM, Monterey, CA, USA, 24–28 July 2005. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Y. Real-time tip-over prevention and path following control for redundant nonholonomic mobile modular manipulators via fuzzy and neural-fuzzy approaches. J. Dyn. Syst. Meas. Control. Trans. ASME 2006, 128, 753–764. [Google Scholar] [CrossRef][Green Version]
- Ettorre, C.D.; Stilli, A.; Dwyer, G.; Neves, J.; Tran, M.; Stoyanov, D. Semi-Autonomous Interventional Manipulation using Pneumatically Attachable Flexible Rails. In Proceedings of the 2019 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Macau, China, 3–8 November 2019; IEEE: New York, NY, USA; pp. 1347–1354. [Google Scholar] [CrossRef]
- Ratliff, N.; Zucker, M.; Bagnell, J.; Srinivasa, S. CHOMP: Gradient optimization techniques for efficient motion planning. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; IEEE: New York, NY, USA; pp. 489–494. [Google Scholar] [CrossRef]
- Campana, M.; Lamiraux, F.; Florent, L.; Laumond, J.-P. A gradient-based path optimization method for motion planning. Adv. Robot. 2016, 30, 1126–1144. [Google Scholar] [CrossRef]
- Khatib, O. Real-time obstacle avoidance for manipulators and mobile robots. In Proceedings of the 1985 IEEE International Conference on Robotics and Automation, St. Louis, MO, USA, 25–28 March 1985; pp. 500–505. [Google Scholar] [CrossRef]
- Raj, J.; Raghuwaiya, K.; Sharma, B.; Vanualailai, J. Motion control of a flock of 1—Trailer robots with swarm avoidance. Robotica 2021, 39, 1926–1951. [Google Scholar] [CrossRef]
- Raj, J.; Raghuwaiya, K.S.; Vanualailai, J. Novel Lyapunov-Based Autonomous Controllers for Quadrotors. IEEE Access 2020, 8, 47393–47406. [Google Scholar] [CrossRef]
- MIRA: Concepts. Available online: https://www.mira-project.org/MIRA-doc/ConceptsPage.html (accessed on 16 October 2021).
- STRANDS · GitHub. Available online: https://github.com/strands-project (accessed on 17 October 2021).
- Schunk_Robots—ROS Wiki. Open Robotics. Available online: http://wiki.ros.org/schunk_robots (accessed on 23 October 2021).
- Fraunhofer IPA, GitHub—ipa320/schunk_modular_robotics. Available online: https://github.com/ipa320/schunk_modular_robotics (accessed on 16 October 2021).
- GitHub—ipa320/schunk_robots. Available online: https://github.com/ipa320/schunk_robots (accessed on 23 October 2021).
- Becker, M.; Domnik, N. 3D Volume Modeling of a Mobile Robot as the Basis of a Multi-Body Simulation; Hochschule Karlsruhe University of Applied Science: Karlsruhe, Germany, 2018. (In German) [Google Scholar]
- Spiers, A.; Khan, S.G.; Herrmann, G. Biologically Inspired Control of Humanoid Robot Arms: Robust and Adaptive Approaches; Springer International Publishing: Cham, Switzerland, 2016; ISBN 9783319301600. [Google Scholar]
- Quigley, M.; Gerkey, B.; Smart, W.D. Programming Robots with ROS; O’Reilly Vlg. GmbH & Co.: Seattle, WA, USA, 2015; ISBN 9781449323899. [Google Scholar]
- Möllmann, S. Integration of an Inertial Measurement Unit into the Autonomous Vehicle Platform CampusBot; Hamburg University of Applied Sciences: Karlsruhe, Germany, 2014. (In German) [Google Scholar]
- Featherstone, R. Rigid Body Dynamics Algorithms, 1st ed.; Springer: New York, NY, USA, 2008; ISBN 978-0-387-74314-1. [Google Scholar]
- KDL Wiki|The Orocos Project. Available online: https://www.orocos.org/kdl.html (accessed on 17 October 2021).
- Smits, R. orocos_kdl: KDL::ChainIdSolver_RNE Class Reference. Available online: http://docs.ros.org/en/kinetic/api/orocos_kdl/html/classKDL_1_1ChainIdSolver__RNE.html (accessed on 17 October 2021).
- Company, S.R. Planners Benchmarking Documentation Shadow Robot Company. 2020. Available online: https://buildmedia.readthedocs.org/media/pdf/planners-benchmarking/latest/planners-benchmarking.pdf (accessed on 30 November 2022).
- Moll, M.; Sucan, I.A.; Kavraki, L.E. Benchmarking Motion Planning Algorithms: An Extensible Infrastructure for Analysis and Visualization. IEEE Robot. Autom. Mag. 2015, 22, 96–102. [Google Scholar] [CrossRef]
- GitHub—ros-Controls/ros_controllers: Generic Robotic Controllers to Accompany ros_control. Available online: https://github.com/ros-controls/ros_controllers (accessed on 30 November 2022).
- GitHub—cburbridge/scitos_common. Available online: https://github.com/cburbridge/scitos_common (accessed on 30 November 2022).
- GitHub—Strands-Project/Scitos_drivers: Scitos G5 Drivers that Interface ROS to MIRA. Available online: https://github.com/strands-project/scitos_drivers (accessed on 21 January 2022).
- [1604.04384] The STRANDS Project: Long-Term Autonomy in Everyday Environments. Available online: https://arxiv.org/abs/1604.04384 (accessed on 30 November 2022).
- Navigation/Tutorials/SendingSimpleGoals. Available online: http://library.isr.ist.utl.pt/docs/roswiki/navigation(2f)Tutorials(2f)SendingSimpleGoals.html (accessed on 30 November 2022).


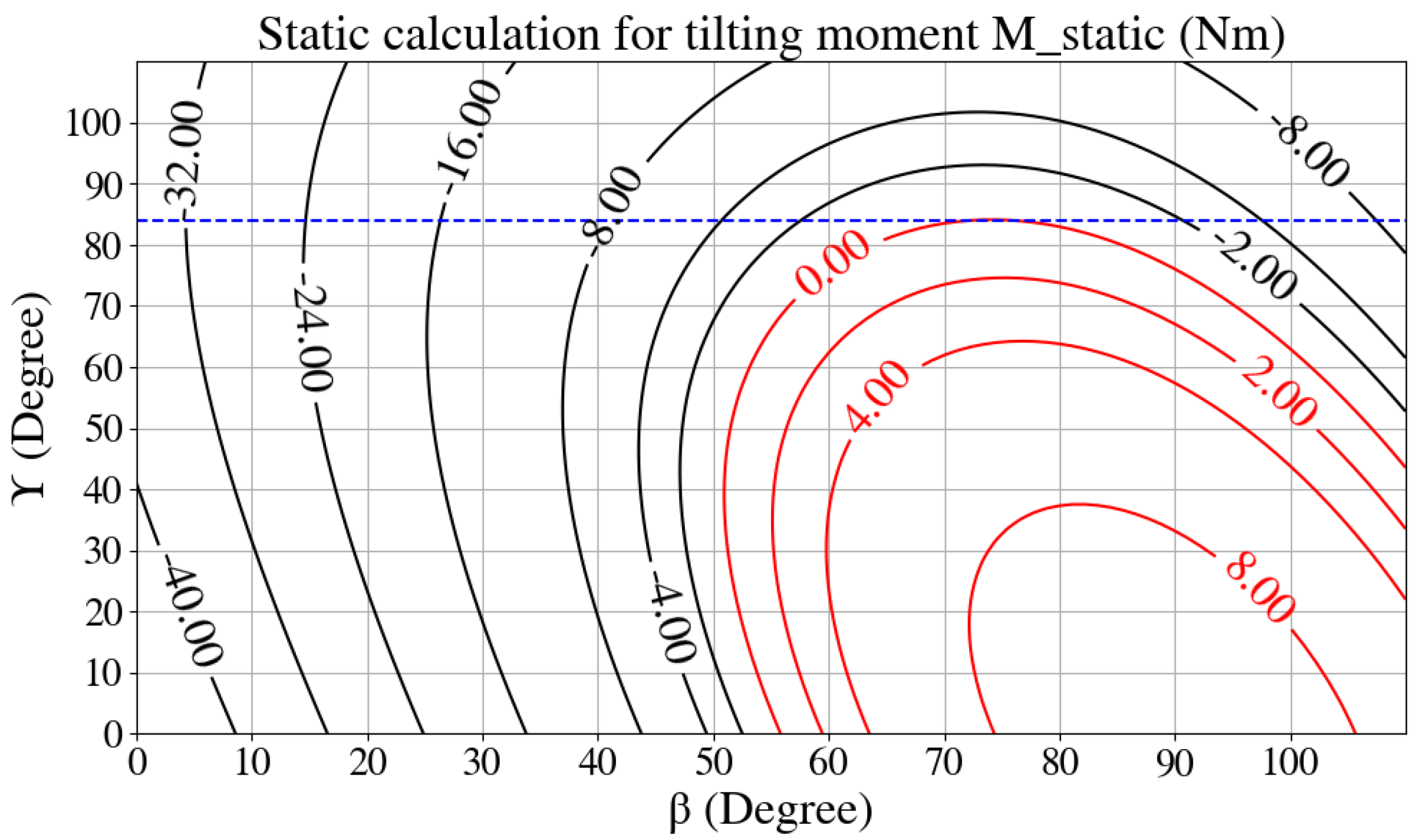
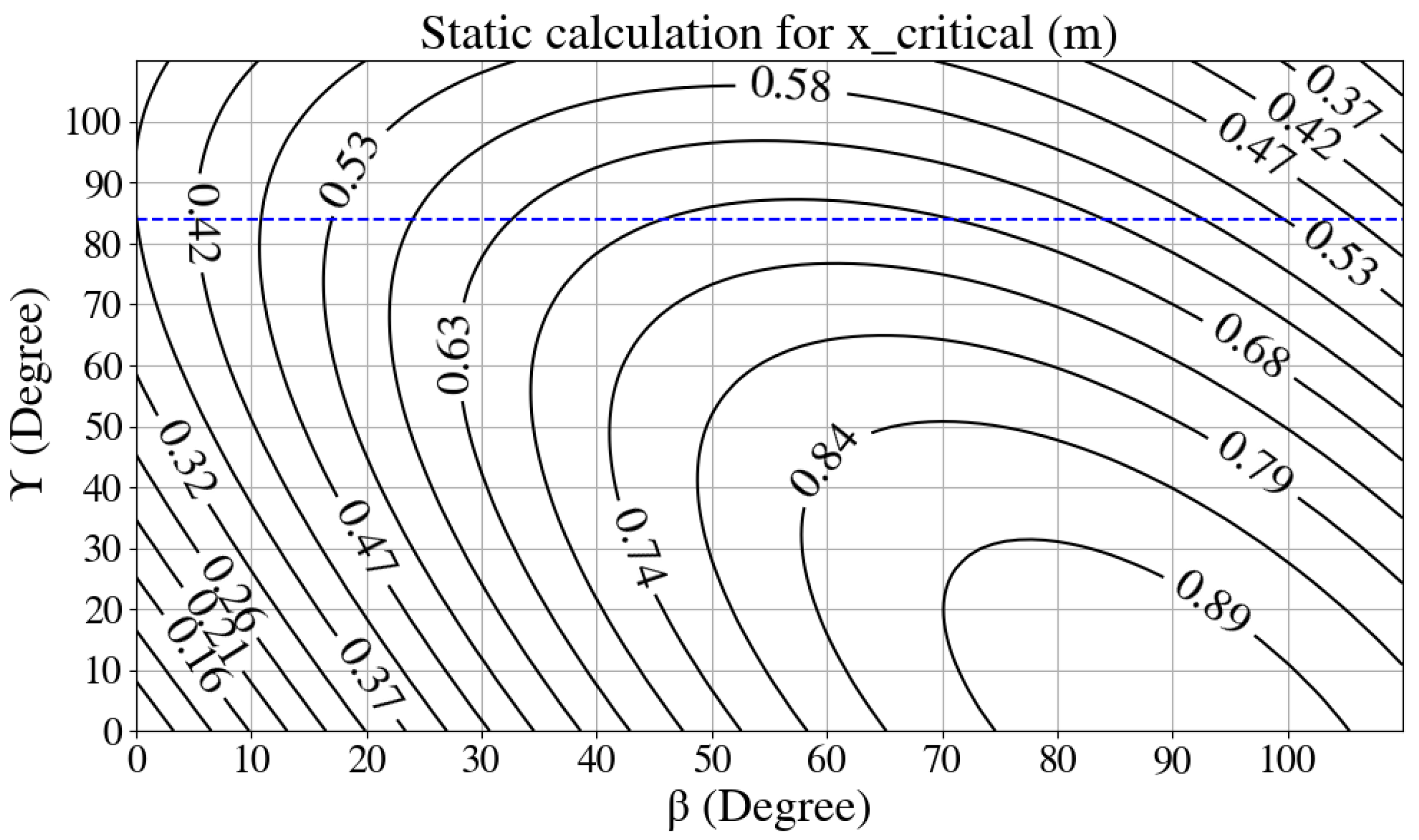

| Analytical | RNEA Using Real Robot |
|---|---|
| 0.49 N·m | 0.49 N·m |
| Force/Torque Components | Analytical | RNEA Using Real Robot |
|---|---|---|
| 8.5 N | 8.5 N | |
| −3.2 N | −3.2 N | |
| 196.0 N | 196.0 N | |
| 1.7 N·m | 1.7 N·m | |
| 5.8 N·m | 5.8 N·m | |
| 0.0 N·m | 0.0 N·m |
| Set 1 | ||
| Initial dynamic tilting stability α = 23  | Without active stabilization The first instability occurred at the time, the robot started to move (at 4 s). The robot tilted slightly over the front wheels. After a brief strong acceleration at 9 s, which was evident from the sudden increase in αcm-3, a deceleration occurred. Consequently, the mobile manipulator completely tipped over from 12 s onwards. | With active stabilization A repositioning was performed before the mobile platform started to move, thus the decisive dynamic tilting stability increased to about αcm-3 = 280. As long as the mobile platform was in motion, several repositioning courses were performed at 7 s, 8 s, 10 s, and 12 s, since the dynamic tilting stability went below the threshold αcm-critical = 250. |
| Set 2 | ||
| Initial dynamic tilting stability α = 17  | Without active stabilization The acceleration process caused the mobile manipulator to tilt over the front edge several times between 10 s and 15 s. From about 15 s, the mobile manipulator tipped completely over the front edge. The acceleration process caused the mobile manipulator to tilt over the front edge several times between 10 s and 15 s. From about 15 s, the mobile manipulator tipped completely over the front edge. | With active stabilization First, before the mobile platform moved forwards, a reposition process took place. The value of the decisive tilting stability αcm-3 increased to just over 250. The mobile platform then started to move. A further stabilization took place at 12 s, increasing αcm-3 by about 500. On the other hand, the αcm-1 fell below the limit value at 16 s. This resulted in a new repositioning for the robot arm. |
| Set 3 | ||
Initial dynamic tilting stability The critical tipping axis was one of the two lateral tipping axes, αcm-1 = 157, representing the critical tilt stability. The critical tipping axis was one of the two lateral tipping axes, αcm-1 = 157, representing the critical tilt stability. | Without active stabilization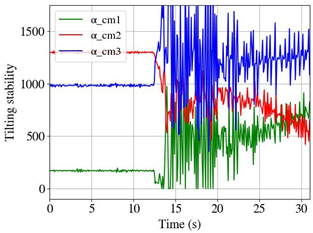 At about 13 s, the entire system tipped over the tilting edge. The bumpers of the mobile platform dragged across the floor, causing a strong noise from 13 s onward. | With active stabilization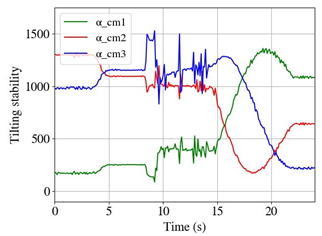 A repositioning occurred at about 4 s. The value for αcm-1 increased thus to about 250. The acceleration process at about 7 s caused a destabilizing effect against the lateral tilting edge. A new reposition was initiated, increasing the value for αcm-1 to about 400. |
| Set 1 | ||
| Initial position and orientation of robot arm  | Dynamic tilting stability value during repositioning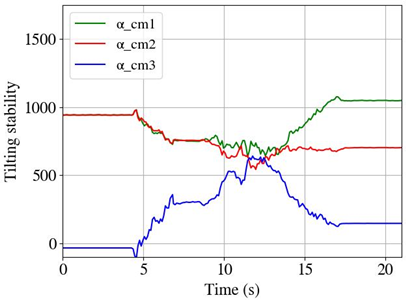 | End position and orientation of robot arm  |
| Between 5 s and 7 s, the robot arm was rearranged to achieve α = 280, before the mobile platform started to move. During the trajectory, no additional repositioning was needed. The mobile manipulator achieved the target point at 16 s. | ||
| Set 2 | ||
| Initial position and orientation of robot arm  | Dynamic tilting stability value during repositioning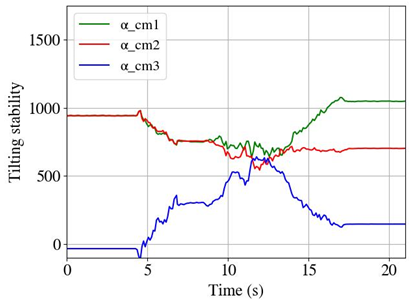 | End position and orientation of robot arm  |
| At 9 s, before the mobile platform started to move, the robot arm was repositioned by arranging joints q1 and q2, thus achieving α = 260. From 11 s to 17 s, the mobile platform kept in motion. At around 11 s, the tilting stability value decreased below α = 250 due to the acceleration of the mobile platform and, as a result, the robot arm repositioned again, keeping this new position until the mobile platform reached the target point at 17 s. | ||
| Set 3 | ||
| Initial position and orientation of robot arm  | Dynamic tilting stability value during repositioning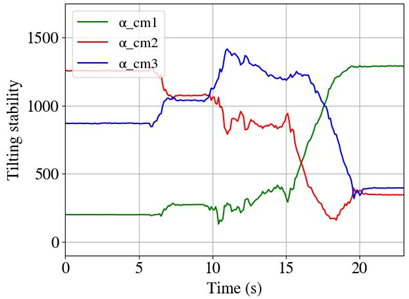 | End position and orientation of robot arm |
| The tilting stability value was improved by a first repositioning at 6 s, rearranging only joints and . One more repositioning was required due to the mobile platform trajectory path, at 11 s. At 15 s, the mobile manipulator reached the target point. | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toledo Fuentes, A.; Kempf, F.; Kipfmüller, M.; Bergmann, T.; J. Prieto, M. Tip-Over Detection and Avoidance Algorithms as Stabilization Strategy for Small-Footprint and Lightweight Mobile Manipulators. Machines 2023, 11, 44. https://doi.org/10.3390/machines11010044
Toledo Fuentes A, Kempf F, Kipfmüller M, Bergmann T, J. Prieto M. Tip-Over Detection and Avoidance Algorithms as Stabilization Strategy for Small-Footprint and Lightweight Mobile Manipulators. Machines. 2023; 11(1):44. https://doi.org/10.3390/machines11010044
Chicago/Turabian StyleToledo Fuentes, Aishe, Franziska Kempf, Martin Kipfmüller, Tobias Bergmann, and Miguel J. Prieto. 2023. "Tip-Over Detection and Avoidance Algorithms as Stabilization Strategy for Small-Footprint and Lightweight Mobile Manipulators" Machines 11, no. 1: 44. https://doi.org/10.3390/machines11010044
APA StyleToledo Fuentes, A., Kempf, F., Kipfmüller, M., Bergmann, T., & J. Prieto, M. (2023). Tip-Over Detection and Avoidance Algorithms as Stabilization Strategy for Small-Footprint and Lightweight Mobile Manipulators. Machines, 11(1), 44. https://doi.org/10.3390/machines11010044







