Optimization of the Bionic Wing Shape of Tidal Turbines Using Multi-Island Genetic Algorithm
Abstract
1. Introduction
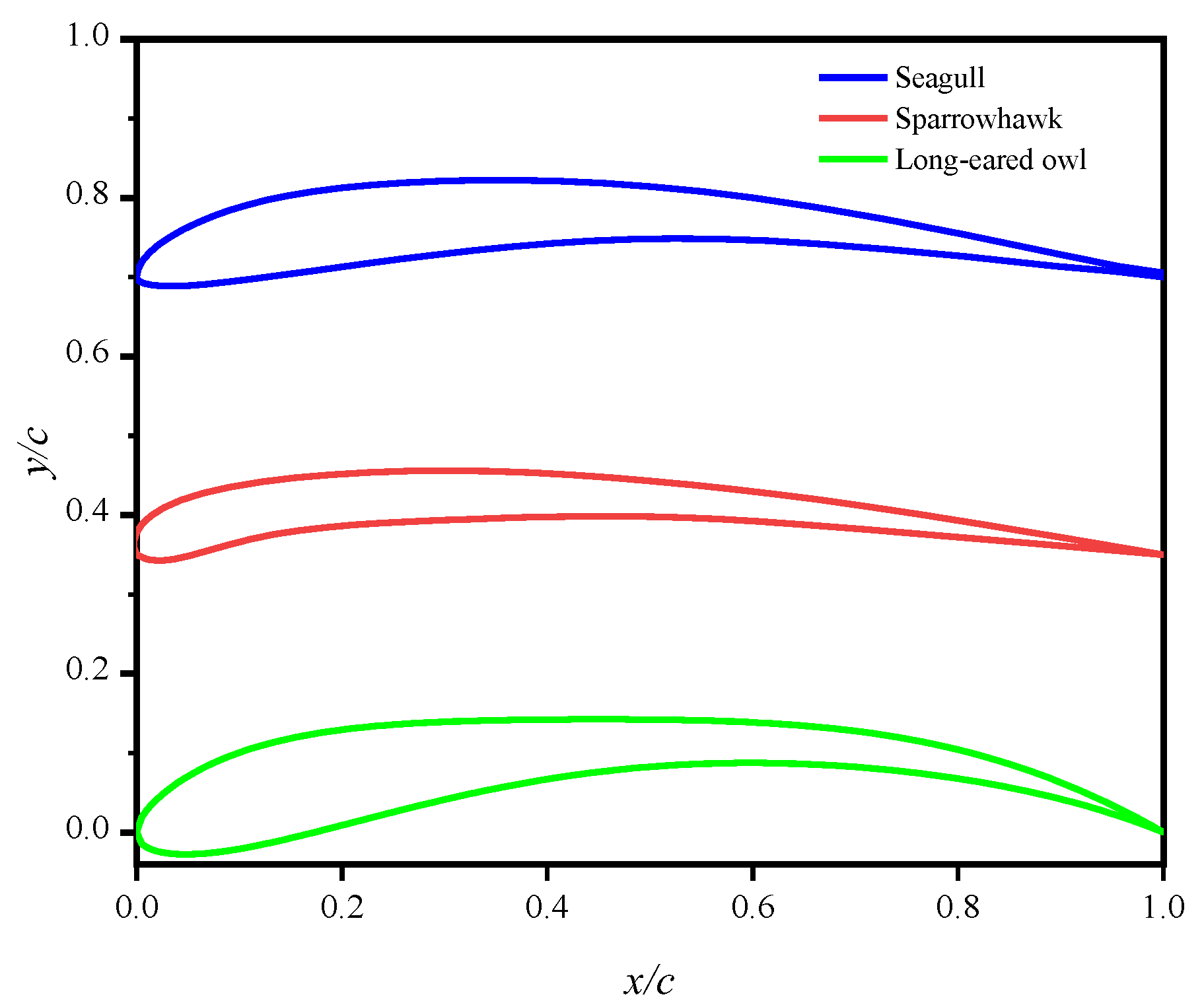
2. Bionic Airfoil Modeling
3. Feasibility Analysis
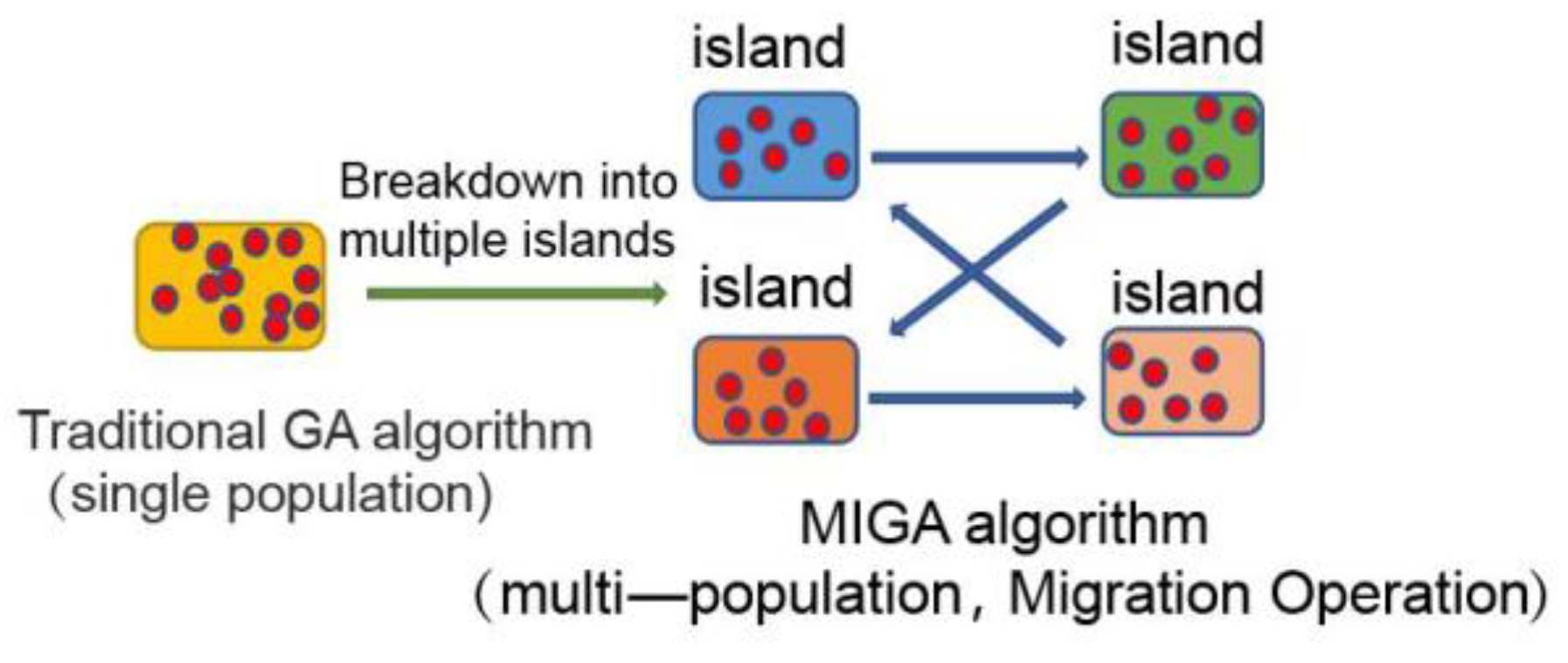
4. Multi-Island Genetic Algorithm
4.1. Introduction to Multi-Island Genetic Algorithm
4.2. Optimization Objectives
- (1)
- Plankton in seawater and seabed particles have considerable influence on turbine blades and high destructive abilities. To satisfy the blade structure and stiffness requirements, its relative thickness should be large.
- (2)
- For turbine blades, satisfying structural requirements is assigned the highest priority. Therefore, the torque coefficient requirement is not a key factor that influences the turbine airfoil optimization process.
- (3)
- The direction and velocity of water flow in the turbine operation is bound by certain constraints. Therefore, fatigue is not considered a key factor that influences the tidal energy of the turbine airfoil.
4.3. Constraints
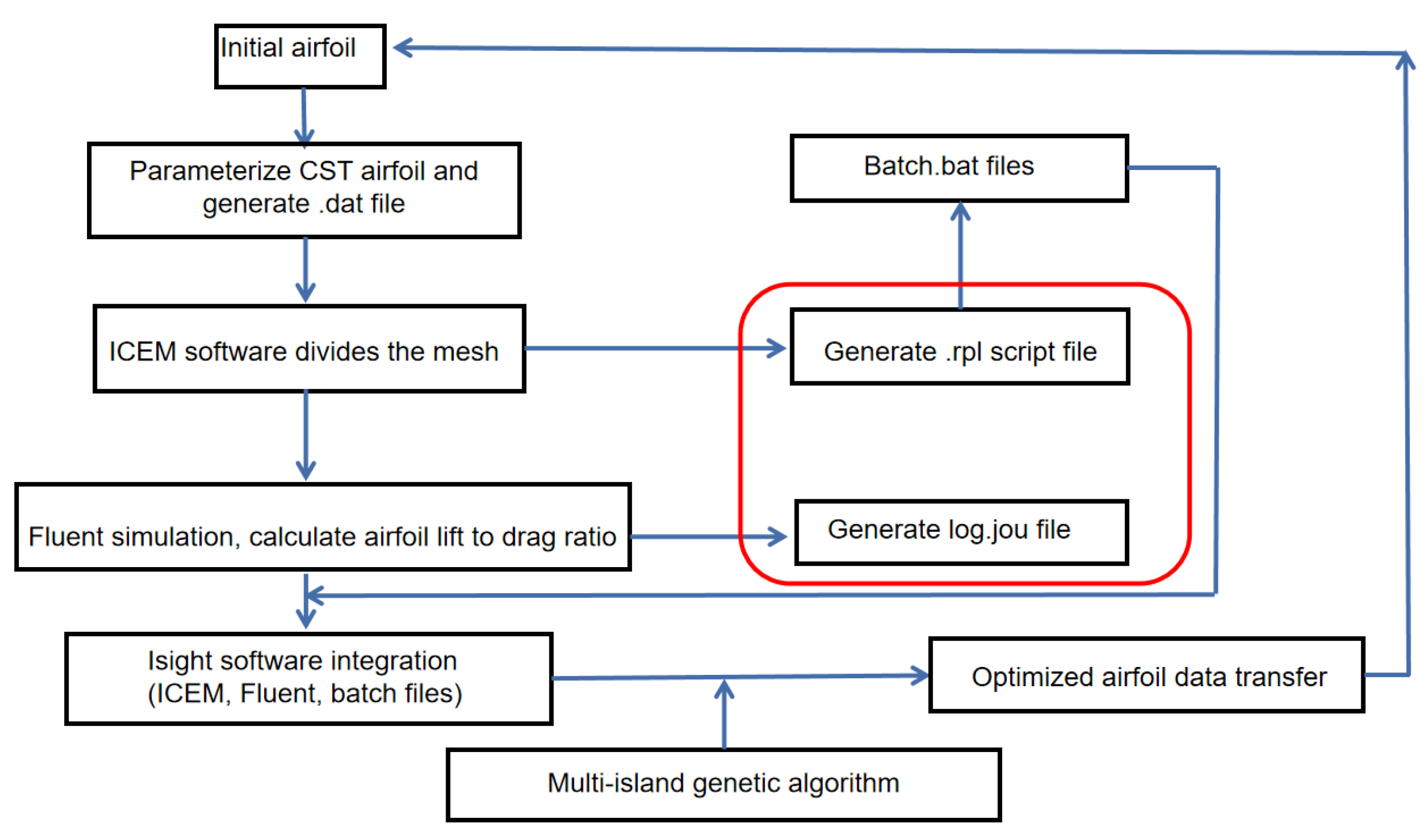
5. Overall Step Design
5.1. Preoperation
5.2. Operation Process
6. Results
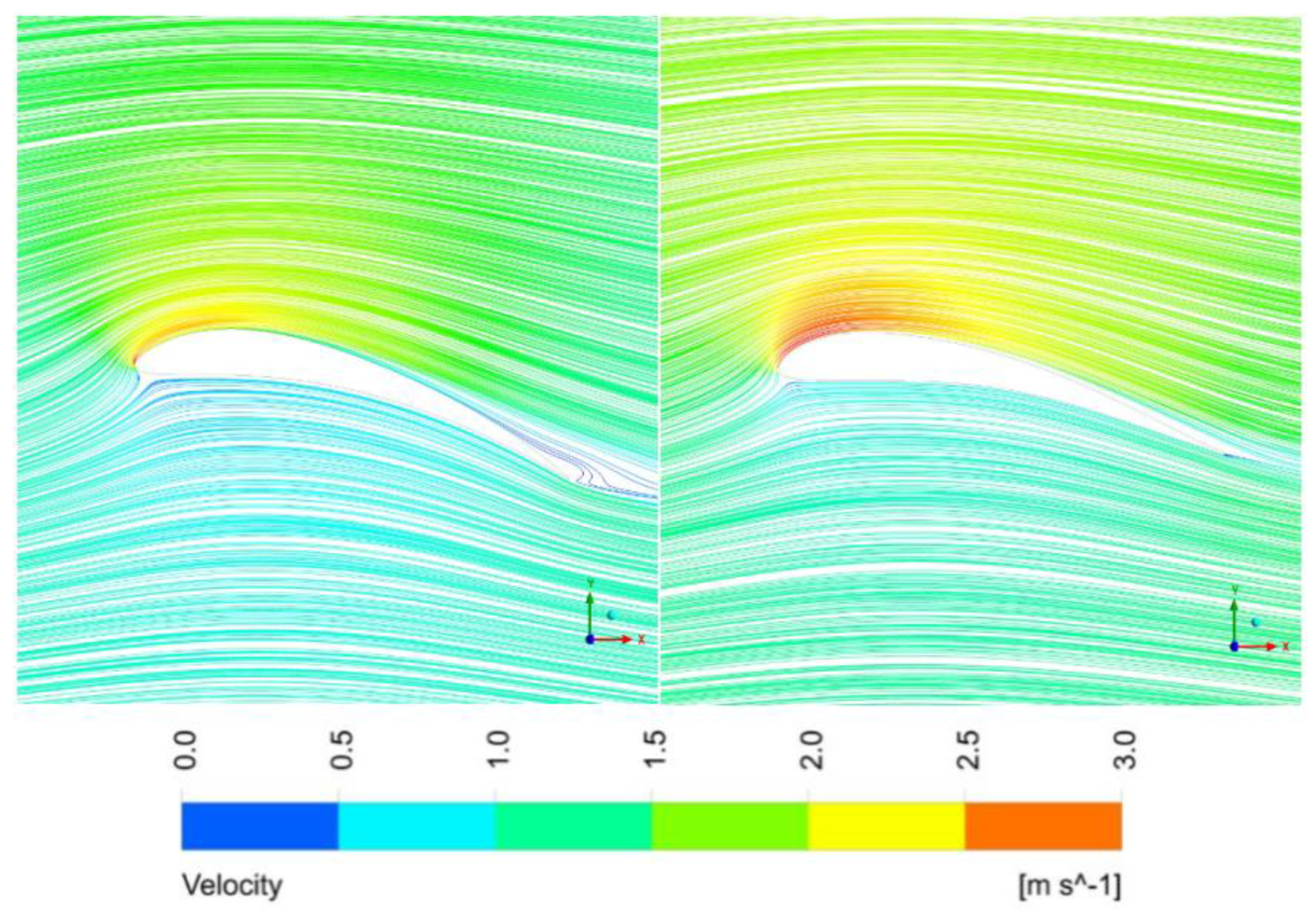
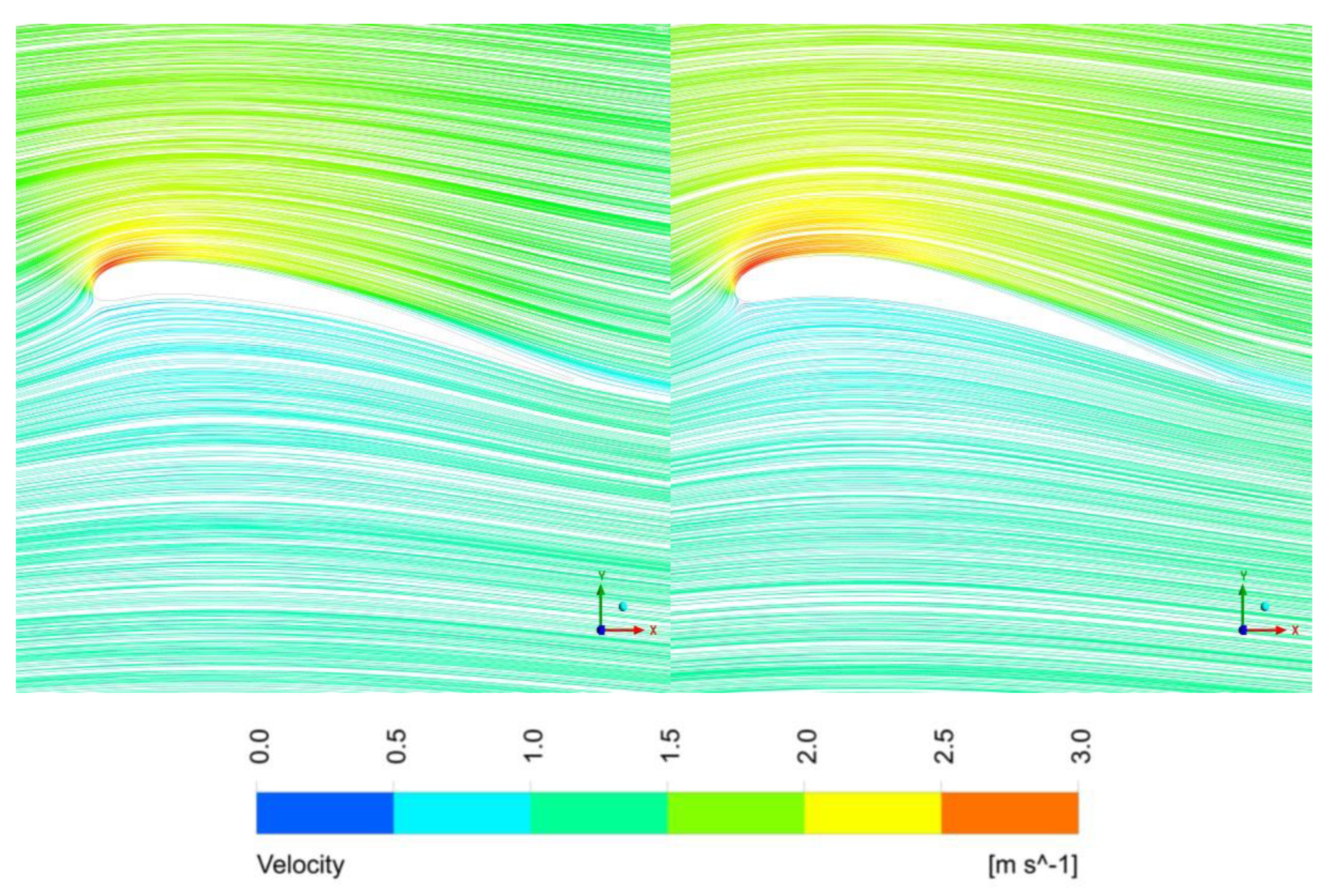
6.1. Comparison of Wing Shape before and after Optimization
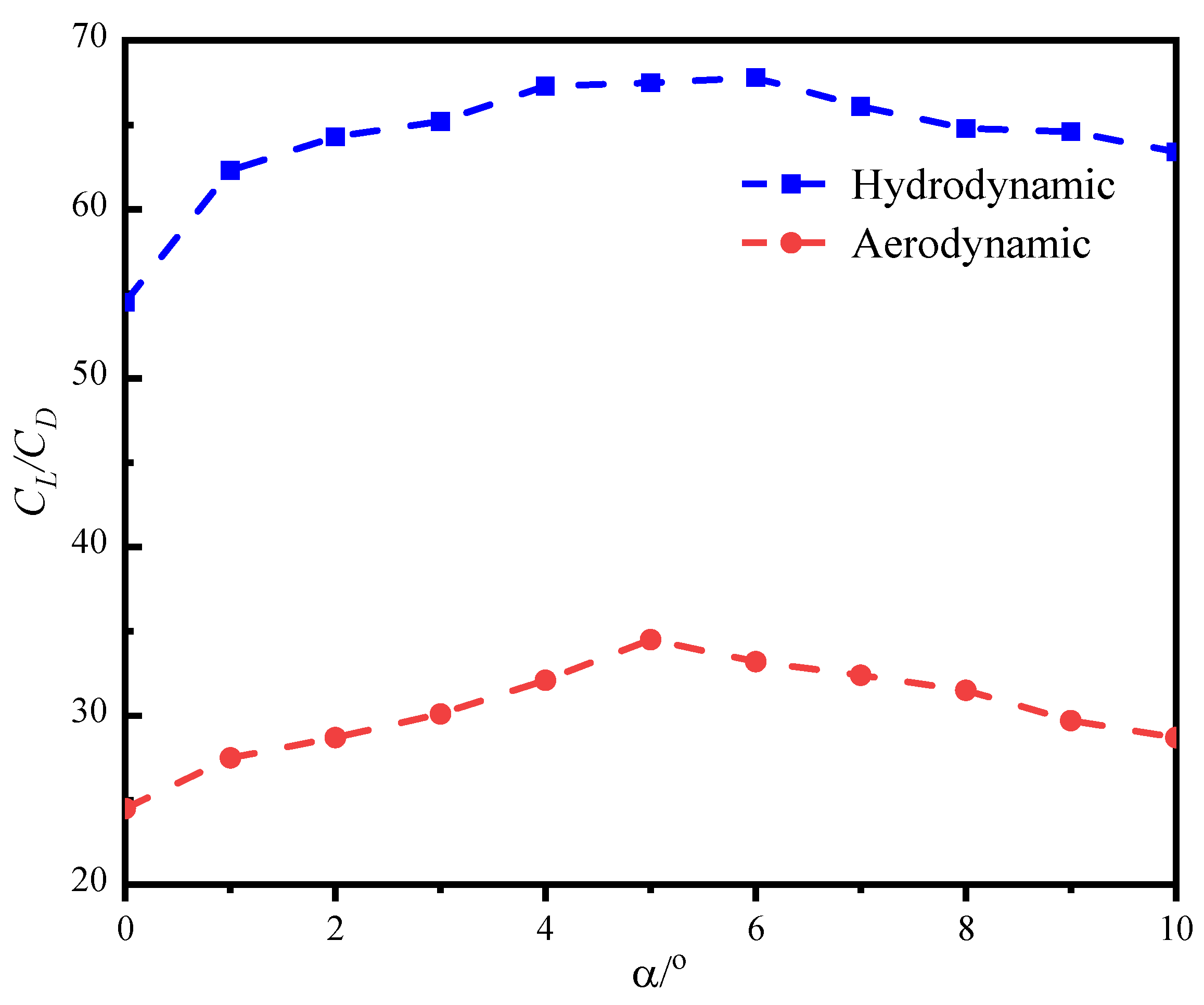
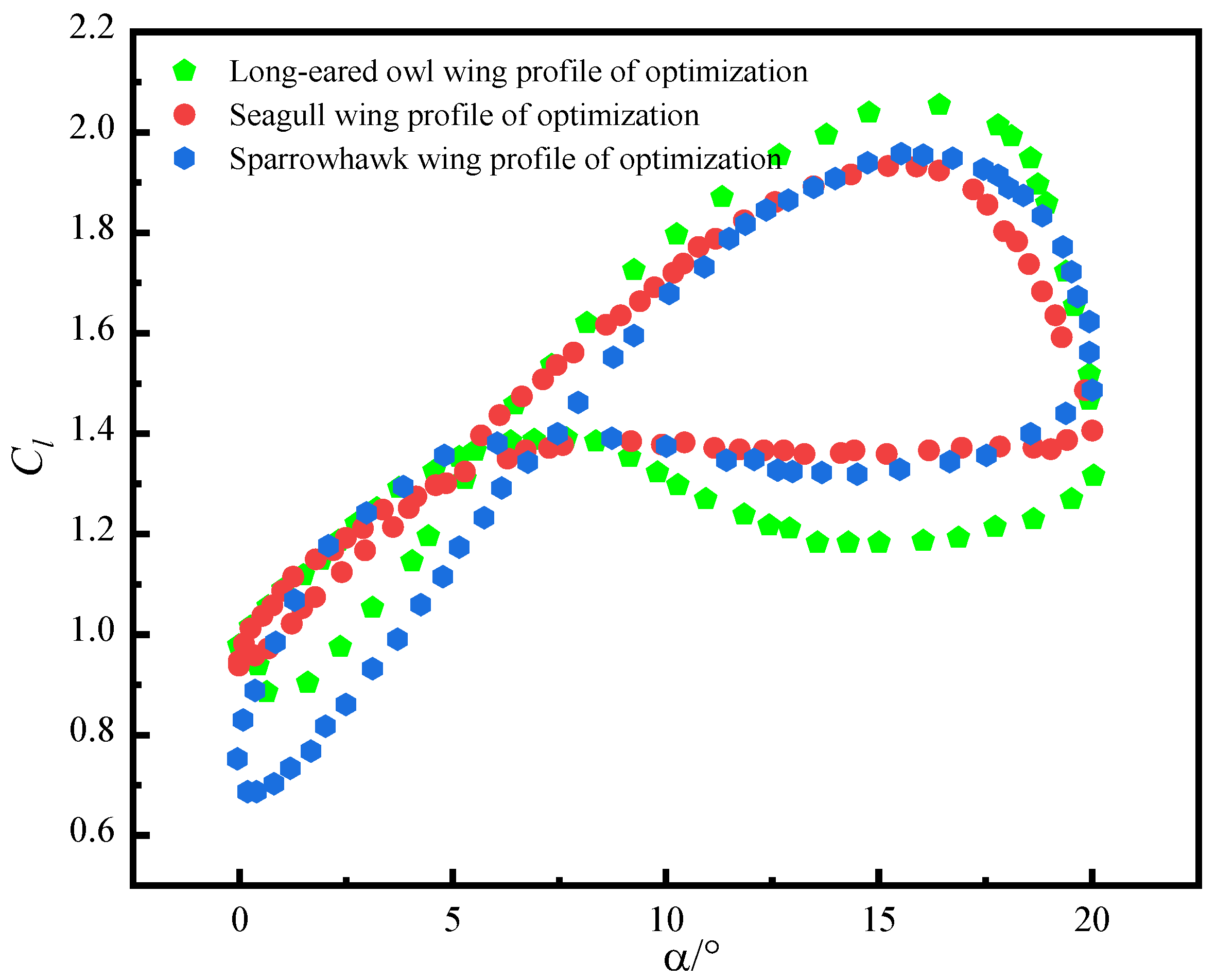
6.2. Comparison of Simulation Results
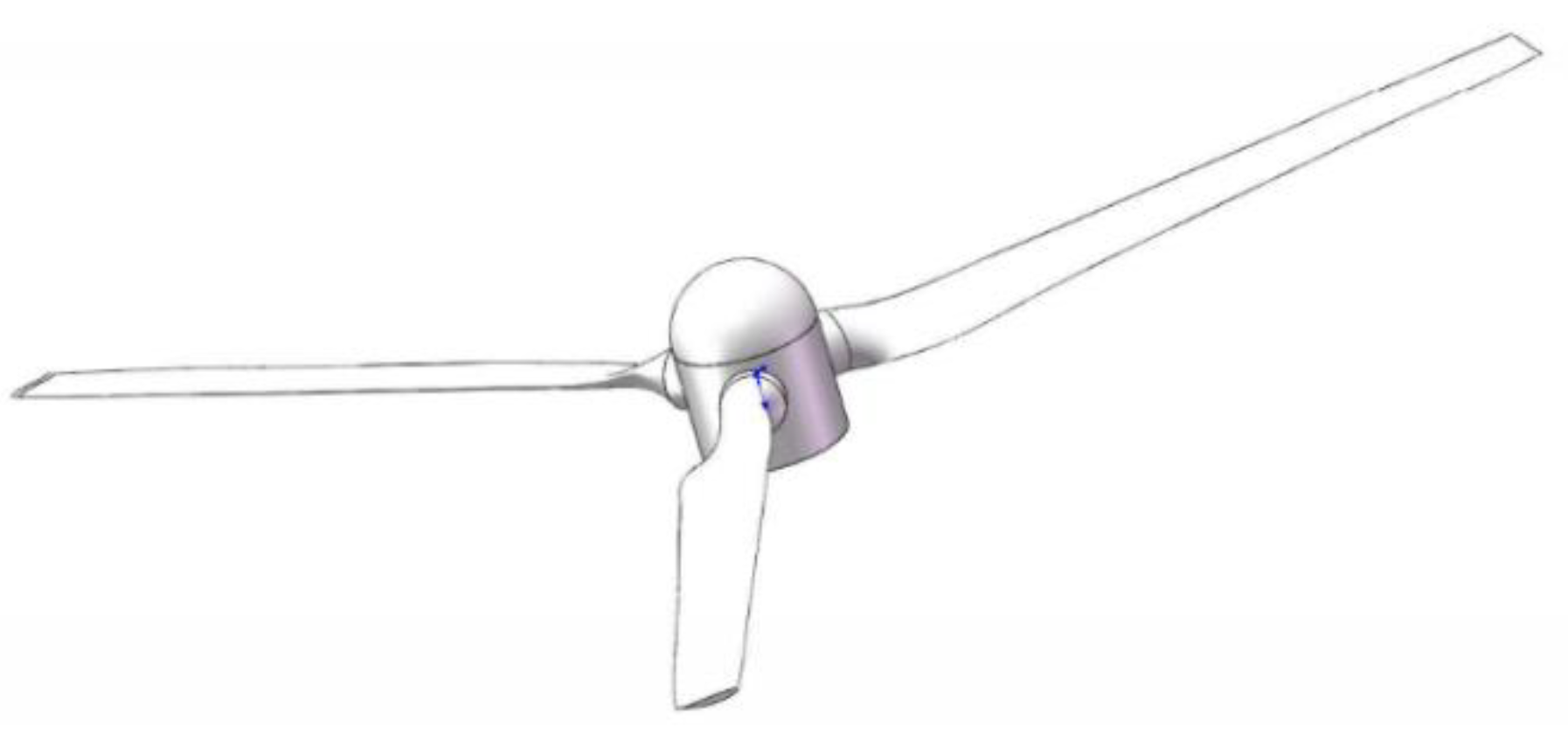
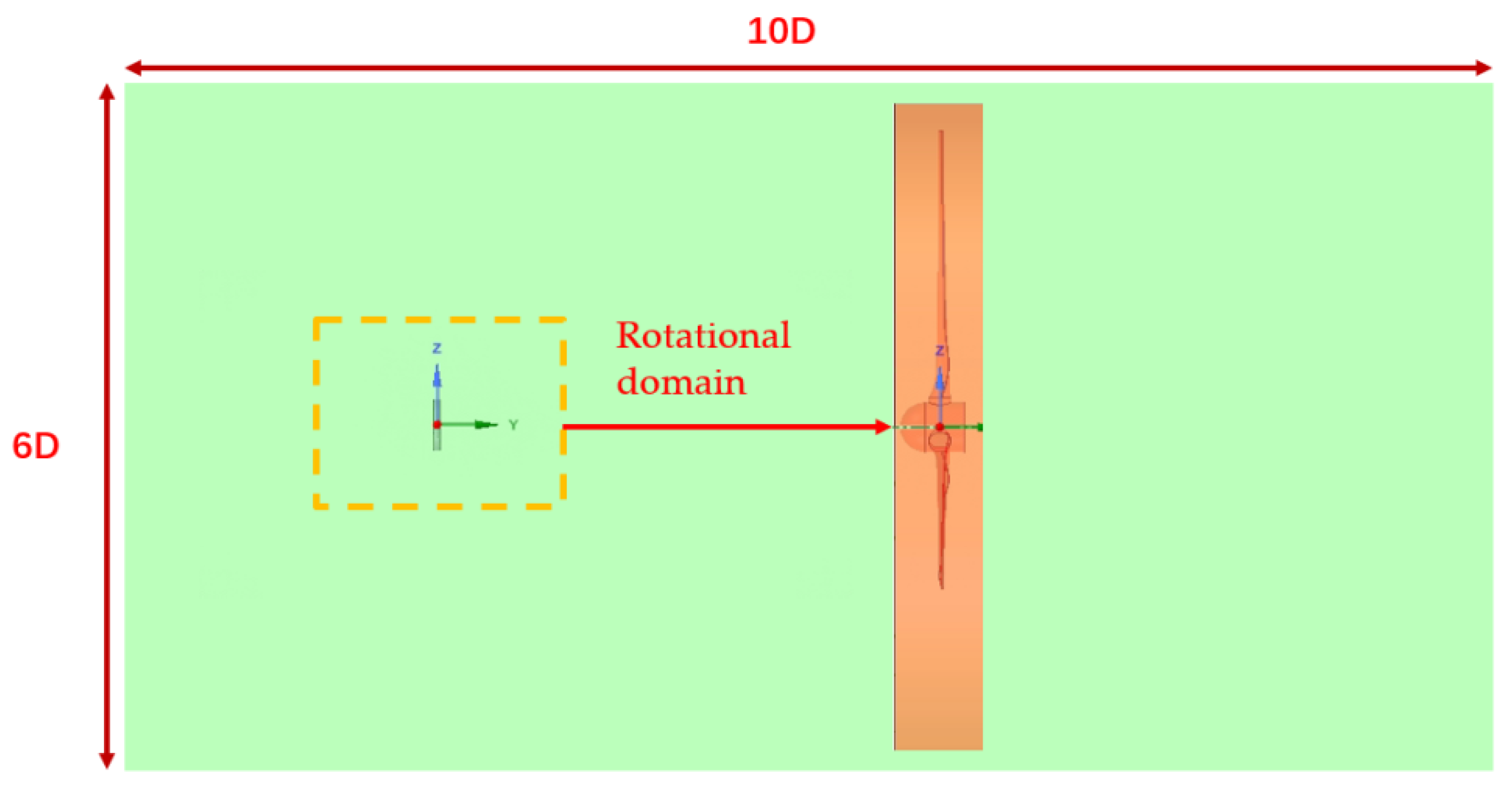
6.3. Application of the Optimized Seagull Wing Profile to a Tidal Turbine
7. Conclusions
- (1)
- The maximum lift–drag ratio was 80.87 at an angle of attack of 6° for the sparrowhawk, 76.82 at an angle of attack of 4° for the seagull, and 68.43 at an angle of attack of 5° for the long-eared owl. The optimized seagull airfoil exhibited a high peak dynamic lift coefficient (1.94), a small dynamic hysteresis loop area, and higher stability than the other two bionic airfoils.
- (2)
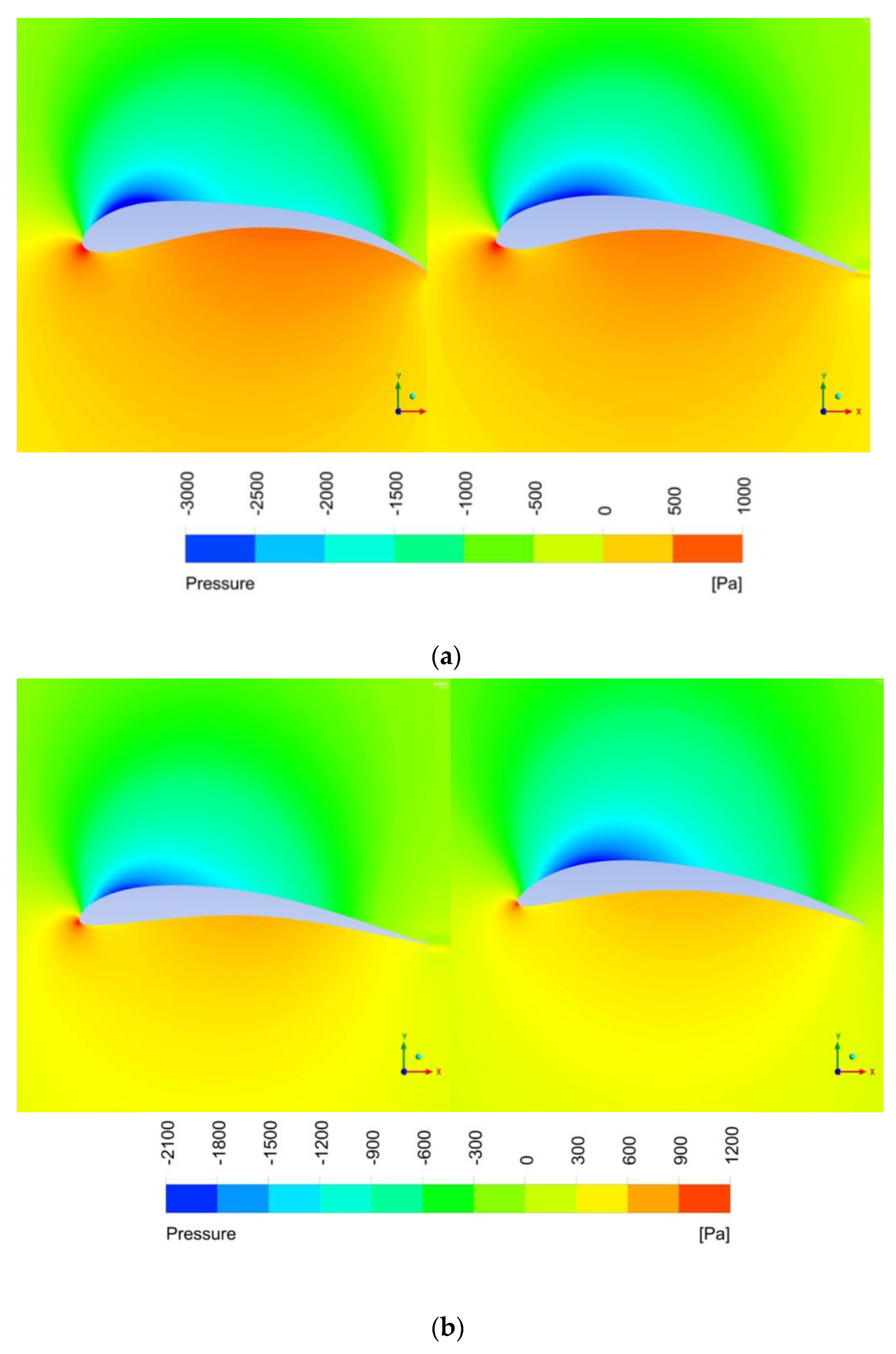
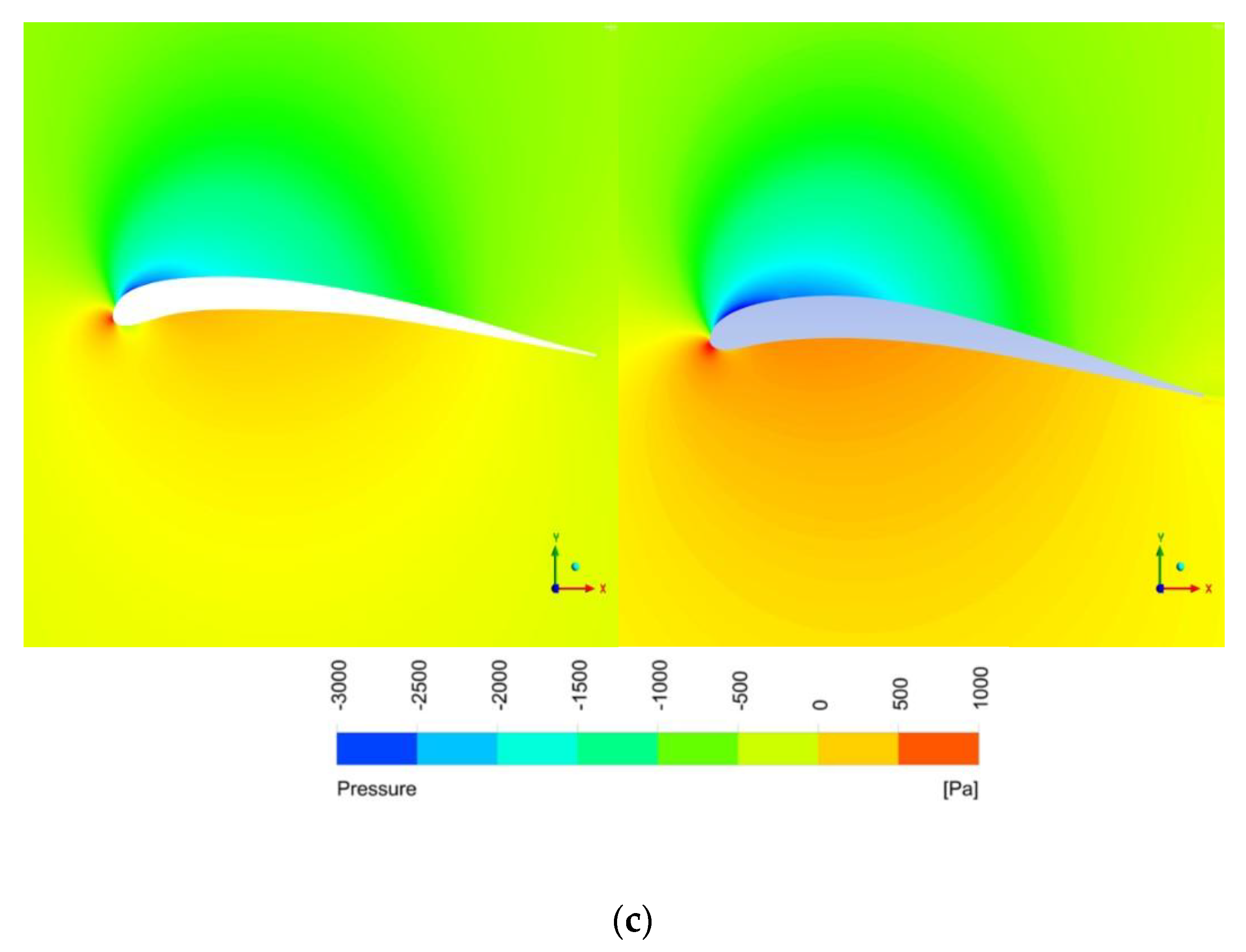
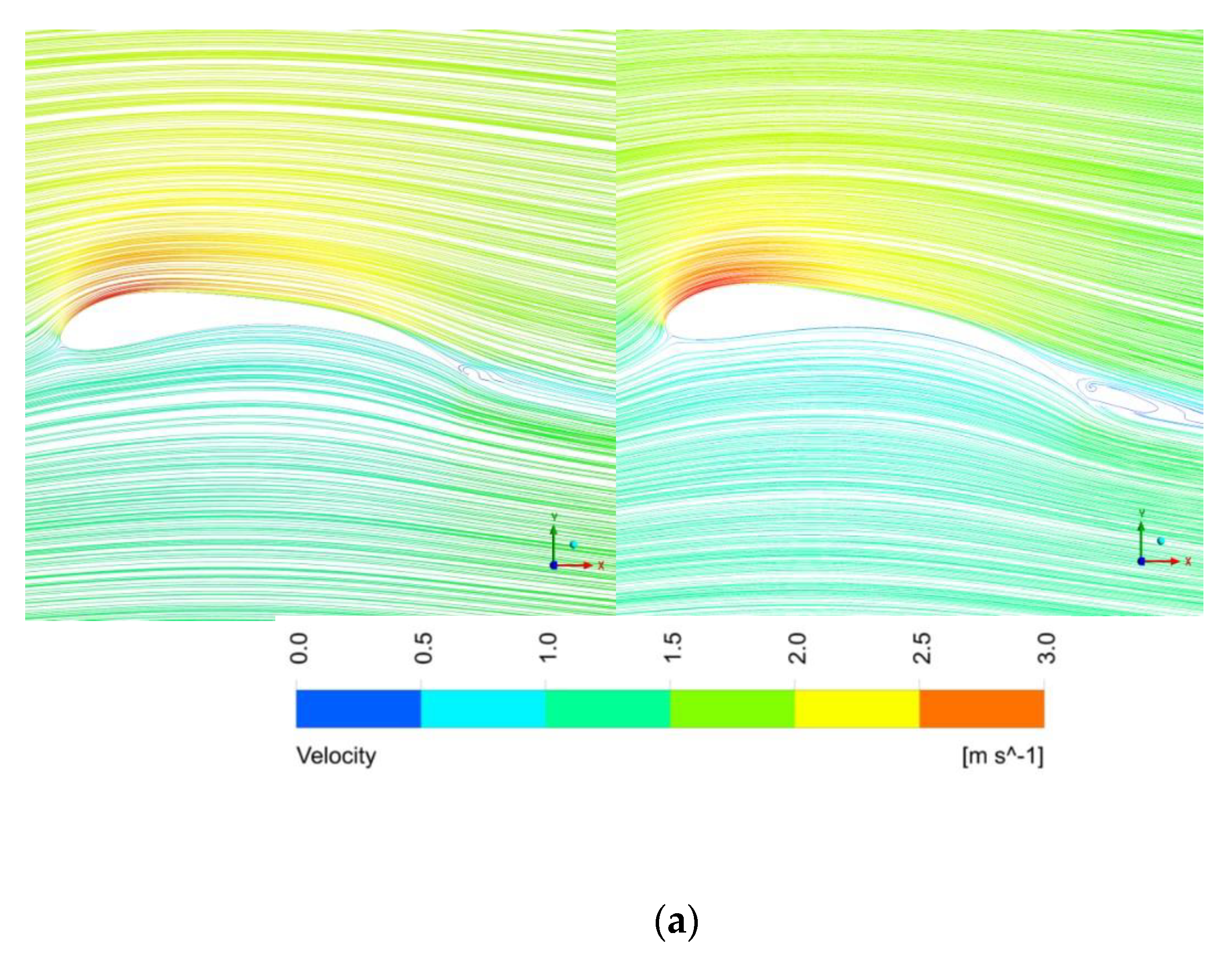
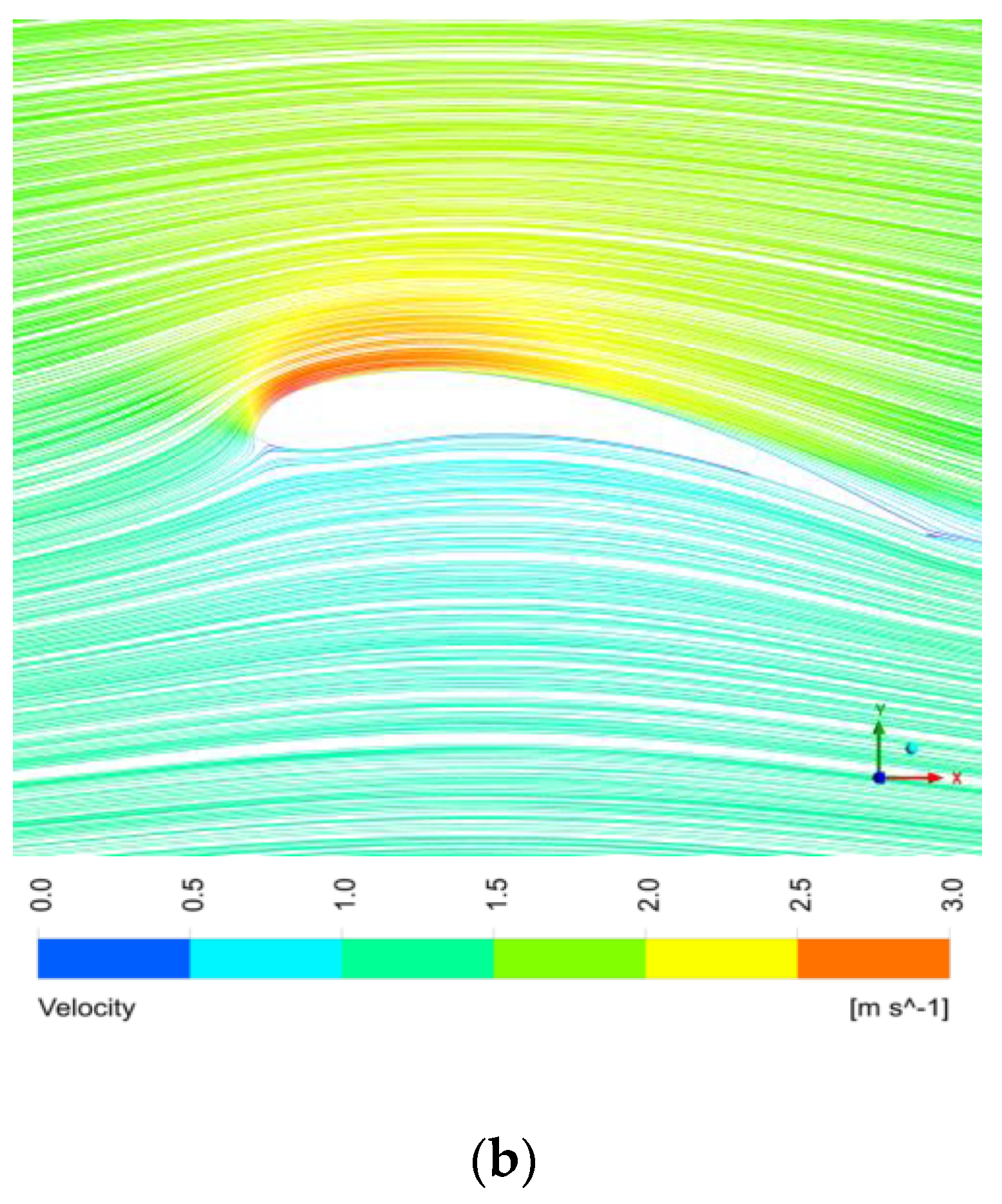
- According to the stress cloud graph and velocity flow line graph obtained after the optimization for the long-eared owl and sparrowhawk airfoil, the flow velocity of water on the upper surface of the airfoil and the suction force on the lower airfoil surface increased when the curvature and thickness of the airfoil increased and the relative maximum curvature and maximum thickness were shifted backward. Consequently, the lift coefficient and the lift–drag coefficient increased.
- (3)
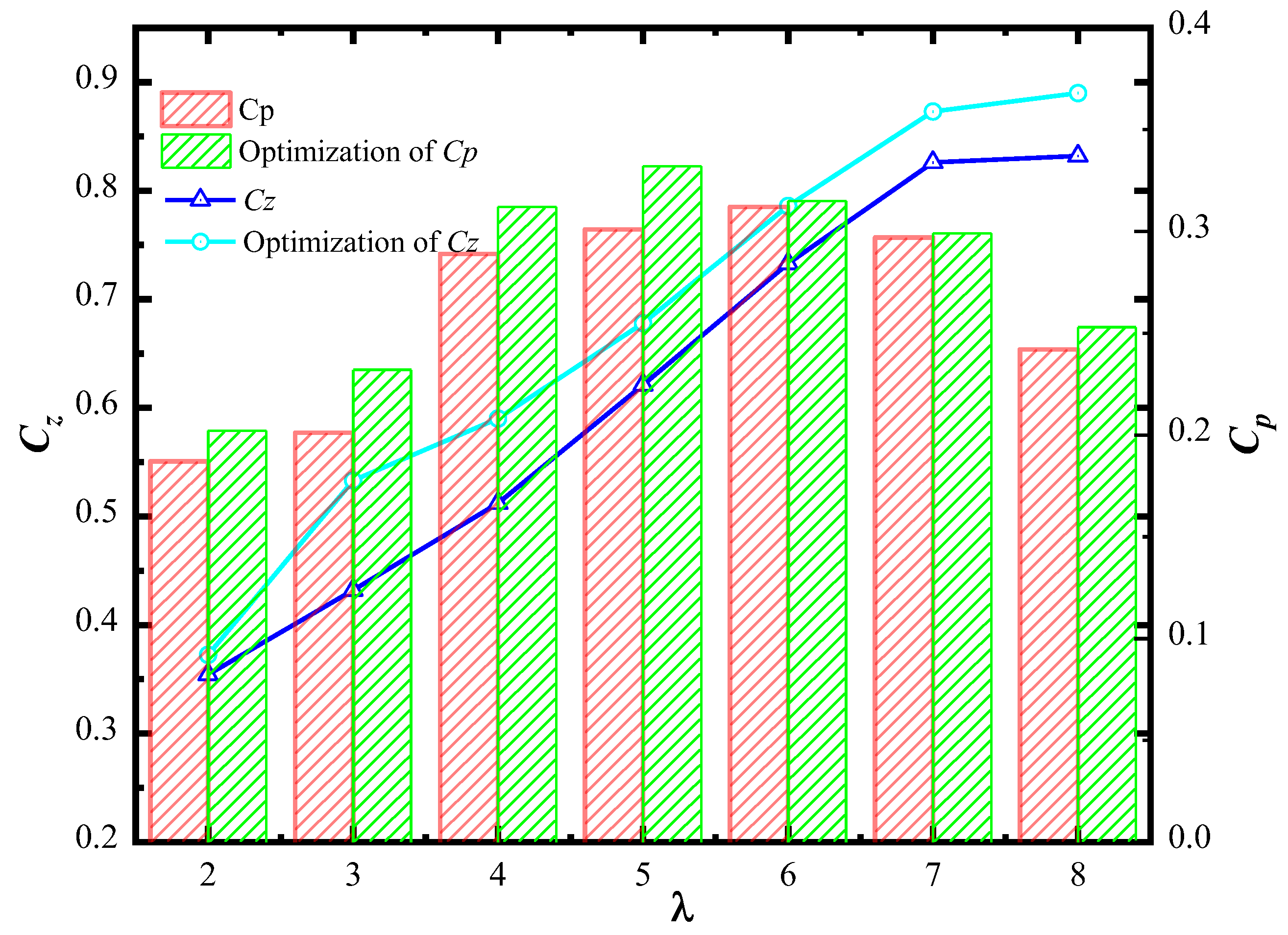
- The tip speed ratio ranged from 2 to 8. When the optimized seagull wing shape was applied to the blade tip of the tidal turbine, the energy gain efficiency of the turbine increased, and the CP coefficient increased by an average of 8.42%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, W.X.; Liu, L.; Wu, H.T.; Chen, Y.L.; Zheng, X.B.; Li, N.Y.; Zhang, Z.Y. Performance analysis and offshore applications of the diffuser augmented tidal turbines. Ships Offshore Struct. 2022, 1, 1–10. [Google Scholar] [CrossRef]
- Wu, H.T.; Cui, L.; Liu, W.X.; Zhang, Z.Y.; Kang, J.C. Performance changes of an engineering ship with one mooring line failure. Eng. Fail. Anal. 2022, 137, 106233. [Google Scholar] [CrossRef]
- Wang, S.Q.; Cui, J.; Ye, R.C.; Chen, Z.F.; Zhang, L. Study of the hydrodynamic performance prediction method for a horizontal axis tidal current turbine with coupled rotation and surging motion. Renew. Energy 2019, 135, 313–325. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Zhao, M.X.; Zheng, Y.; Ji, R.W.; Zhang, Z.; Zang, W. Hydrodynamic analysis of horizontal axis tidal turbine at yawing motion. J. Eng. Thermophys. 2022, 43, 1226–1232. [Google Scholar]
- Tangler, J.L.; Somers, D.M. NREL Airfoil Families for HAWTs; National Renewable Energy Laboratory: Golden, CO, USA, 1995. [Google Scholar]
- Wang, X.C. Study on the Design Theory and Method of the Horizontal Axis Tidal Turbine Hydrofoil Family; Ocean University of China: Qingdao, China, 2017. [Google Scholar]
- Bai, J.Y.; Yang, K.; Li, H.L.; Xu, J.Z. Design of the horizontal axis wind turbine airfoil family. J. Eng. Thermophys. 2010, 31, 589–592. [Google Scholar]
- Yuan, P.; Wang, X.C.; Wang, S.J.; Tang, J.Z.; Si, X.C.; Bian, B.B. Study on optimization of hydrofoil of tidal turbine blade based on genetic algorithm. Period. Ocean Univ. China (Nat. Sci. Ed.) 2018, 48, 125–131. [Google Scholar]
- Grasso, F. Design and optimization of tidal turbine airfoil. J. Aircr. 2012, 49, 636–643. [Google Scholar] [CrossRef]
- Wickramasinghe, U.K.; Carrese, R.; Li, X. Designing Airfoils Using a Reference Point Based Evolutionary Many-Objective Particle Swarm Optimization Algorithm; Evolutionary Computation; IEEE: Barcelona, Spain, 2010. [Google Scholar]
- Timnak, N.; Jahangirian, A. Multi-point optimization of transonic airfoils using an enhanced genetic algorithm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 232, 1347–1360. [Google Scholar] [CrossRef]
- Le-Duc, T.; Nguyen, Q.H. Aerodynamic optimal design for horizontal axis wind turbine airfoil using integrated optimization method. Int. J. Comput. Methods 2019, 16, 1841004. [Google Scholar] [CrossRef]
- Tan, J.Z.; Bian, B.B.; Si, X.C.; Wang, S.J.; Yuan, P. Special hydrofoil optimization design of tidal turbine based on multi-objective genetic algorithm. Period. Ocean Univ. China (Nat. Sci. Ed.) 2020, 50, 127–134. [Google Scholar]
- Liu, T.S.; Kuykendoll, K.; Rhew, R.; Jones, S. Avian airfoil geometry and kinematics. AIAA J. 2006, 44, 954. [Google Scholar] [CrossRef]
- Liao, G.H. Aerodynamic, Acoustic Characteristics of Long-Eared Owl Wing and Its Bionic Application; Jilin University of China: Changchun, China, 2013. [Google Scholar]
- Wang, M.H.; Liu, X.M. Numerical investigation of aerodynamic and acoustic characteristics of bionic airfoils inspired by bird airfoil. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2019, 233, 4004–4016. [Google Scholar] [CrossRef]
- Wu, L.M.; Jiang, Y.X.; Liu, X.M.; Qin, W.X.; Xi, G. Numerical analysis of dynamic stall characteristics of several bionic airfoils. J. Xi’Jiaotong Univ. 2022, 9, 1–9. [Google Scholar] [CrossRef]
- Liu, X.F.; Wang, J.W.; Zhao, J.; Chen, Z.; Zhang, Z.W. Sparrowhawk Wing Bionic Method for Horizontal Axis Wind Turbine Blades. Ningxia Hui Autonomous Region CN105844034B, 12 July 2019. [Google Scholar]
- Liu, Q.Z.; Chen, B.; Wang, L.D.; Su, S.S. Experimental investigation on the hydrodynamics performance of a bionic blade. Renew. Energy Resour. 2018, 36, 611–616. [Google Scholar]
- Wang, L.D.; Wang, L.; Chen, B.; Nagata, S.; Haruki, T. Experimental study on hydrodynamic characteristics of straight blade dynamic effect. Renew. Energy Resour. 2021, 39, 137–142. [Google Scholar]
- Gao, C.; Liu, Q.K.; Jia, Y.Y.; Chen, A.J. Influence of reynolds number on aerodynamic performance of airfoil with vortex generator. J. Vib. Meas. Diagn. 2022, 42, 103–109, 197–198. [Google Scholar]
- Li, D.S.; Li, R.N.; Yang, C.X.; Wang, X.Y.; Yang, R.; Lin, Y.R. Research of the effect on reynolds number on aerodynamic performance of special airfoil for wind turbine. Fluid Mach. 2009, 37, 31–34. [Google Scholar]
- Hayes-Roth, F. Review of “Adaptation in Natural and Artificial Systems by John, H. Holland”; The University of Michigan Press: Ann Arbor, MI, USA, 1975; ACM SIGART Bulletin. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addis on-Wesley: Boston, MA, USA, 1989; pp. 12–23. [Google Scholar]
- Miura, Y.; Kaneko, M.; Hafizur Rahman, M.M.; Watanabe, S. Adaptive routing algorithms and implementation for TESH network. Commun. Netw. 2013, 5, 28236. [Google Scholar] [CrossRef][Green Version]
- Shao, H.M. Research on Airfoil Optimization of Vertical Axis Fan Based on CFD and Genetic Algorithm; East China University of Technology: Shanghai, China, 2021. [Google Scholar]
- Yuan, P.; Wang, X.C.; Wang, S.J.; Tan, J.Z.; Si, X.C.; Bian, B.B. Study on influence of geometric parameters of tidal turbine hydrofoil on its hydrodynamic performance. Acta Energ. Sol. Sin. 2018, 39, 2705–2712. [Google Scholar]
- Bai, J.Y.; Yang, K.; Xu, J.Z. The experimental analysis and optimal design of thin airfoil family for horizontal-axis wind turbines. J. Eng. Thermophys. 2011, 32, 1131–1136. [Google Scholar]
- Zhang, Z.Y.; Wang, X.H.; Liu, W.X.; Ji, R.W.; Guo, G.K. Design and hydrodynamic performance analysis of horizontal axis tidal current turbine. Ship Sci. Technol. 2021, 43, 78–82, 88. [Google Scholar]
- Gharali, K.; Johnson, D.A. Dynamic stall simulation of a pitching airfoil under unsteady freestream velocity. J. Fluids Struct. 2013, 42, 228–244. [Google Scholar] [CrossRef]
- Li, M. Research on Hydrodynamic Characteristics of Hydrofoil in Cascade Based on CST Parameterization; Jiangsu University: Jiangsu, China, 2021. [Google Scholar]
- Chang, L.S.; Zhang, Q.Y.; Guo, X.Y. Airfoil optimization design based on gaussian process regression and genetic algorithm. J. Aerosp. Power 2021, 36, 2306–2316. [Google Scholar]








| Coefficient Name | S1 | S2 | S3 | A1 | A2 | A3 | A4 |
|---|---|---|---|---|---|---|---|
| Long-eared owl | 3.9362 | 0.7705 | 0.8485 | −29.4861 | 66.4565 | −59.8060 | 19.0439 |
| Seagull | 3.8735 | −0.807 | 0.771 | −15.246 | 26.482 | −18.975 | 4.6232 |
| Name | Parameter Setting | Name | Parameter Setting |
|---|---|---|---|
| Subpopulation size | 5 | Mutation probability | 0.01 |
| Number of islands | 10 | Inter-island mobility | 0.01 |
| Evolution algebra | 40 | Migration interval algebra | 5 |
| Crossover probability | 0.99 |
| Name | Thickness (%) | Camber (%) | ||
|---|---|---|---|---|
| Sparrowhawk airfoil | 7.41 | 12.48 | 7.55 | 30.54 |
| Sparrowhawk optimization | 8.40 | 16.73 | 8.37 | 34.36 |
| Seagull airfoil | 8.43 | 14.30 | 6.75 | 38.85 |
| Seagull optimization | 9.99 | 17.30 | 8.24 | 44.30 |
| Long-eared owl airfoil | 10.98 | 12.85 | 10.01 | 40.21 |
| Long-eared owl optimization | 12.61 | 16.10 | 11.37 | 45.10 |
| Name | (CL) Max | Lifting Ratio (%) |
|---|---|---|
| Sparrowhawk airfoil | 1.76 | 7.4% |
| Sparrowhawk optimization | 1.89 | |
| Seagull airfoil | 1.78 | 7.86% |
| Seagull optimization | 1.92 | |
| Long-eared owl airfoil | 1.96 | 3.4% |
| Long-eared owl optimization | 2.03 |
| NO. | r/R | r (mm) | c/R | c (mm) | Twist (°) |
|---|---|---|---|---|---|
| 1 | 0.1 * | 60 | 0.0483 | 29 | 23 |
| 2 | 0.2 | 120 | 0.1117 | 67 | 19 |
| 3 | 0.3 | 180 | 0.1109 | 66.56 | 12.35 |
| 4 | 0.4 | 240 | 0.1045 | 62.72 | 9.96 |
| 5 | 0.5 | 300 | 0.0988 | 59.3 | 8.91 |
| 6 | 0.6 | 360 | 0.0932 | 55.92 | 8 |
| 7 | 0.7 | 420 | 0.0883 | 52.98 | 7.03 |
| 8 | 0.8 | 480 | 0.0857 | 51.44 | 6.12 |
| 9 | 0.9 | 540 | 0.083 | 49.82 | 5.74 |
| 10 | 0.99 | 594 | 0.0733 | 44 | 5.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Wu, B.; Wu, L.; Liu, W.; Liu, L.; Li, N.; Cui, L. Optimization of the Bionic Wing Shape of Tidal Turbines Using Multi-Island Genetic Algorithm. Machines 2023, 11, 43. https://doi.org/10.3390/machines11010043
Zhang Z, Wu B, Wu L, Liu W, Liu L, Li N, Cui L. Optimization of the Bionic Wing Shape of Tidal Turbines Using Multi-Island Genetic Algorithm. Machines. 2023; 11(1):43. https://doi.org/10.3390/machines11010043
Chicago/Turabian StyleZhang, Zhiyang, Bo Wu, Linyan Wu, Weixing Liu, Lei Liu, Ningyu Li, and Lin Cui. 2023. "Optimization of the Bionic Wing Shape of Tidal Turbines Using Multi-Island Genetic Algorithm" Machines 11, no. 1: 43. https://doi.org/10.3390/machines11010043
APA StyleZhang, Z., Wu, B., Wu, L., Liu, W., Liu, L., Li, N., & Cui, L. (2023). Optimization of the Bionic Wing Shape of Tidal Turbines Using Multi-Island Genetic Algorithm. Machines, 11(1), 43. https://doi.org/10.3390/machines11010043







