Film Cooling Performance of a Cylindrical Hole with an Upstream Crescent-Shaped Block in Linear Cascade
Abstract
1. Introduction
2. Geometry Model and Numerical Setup
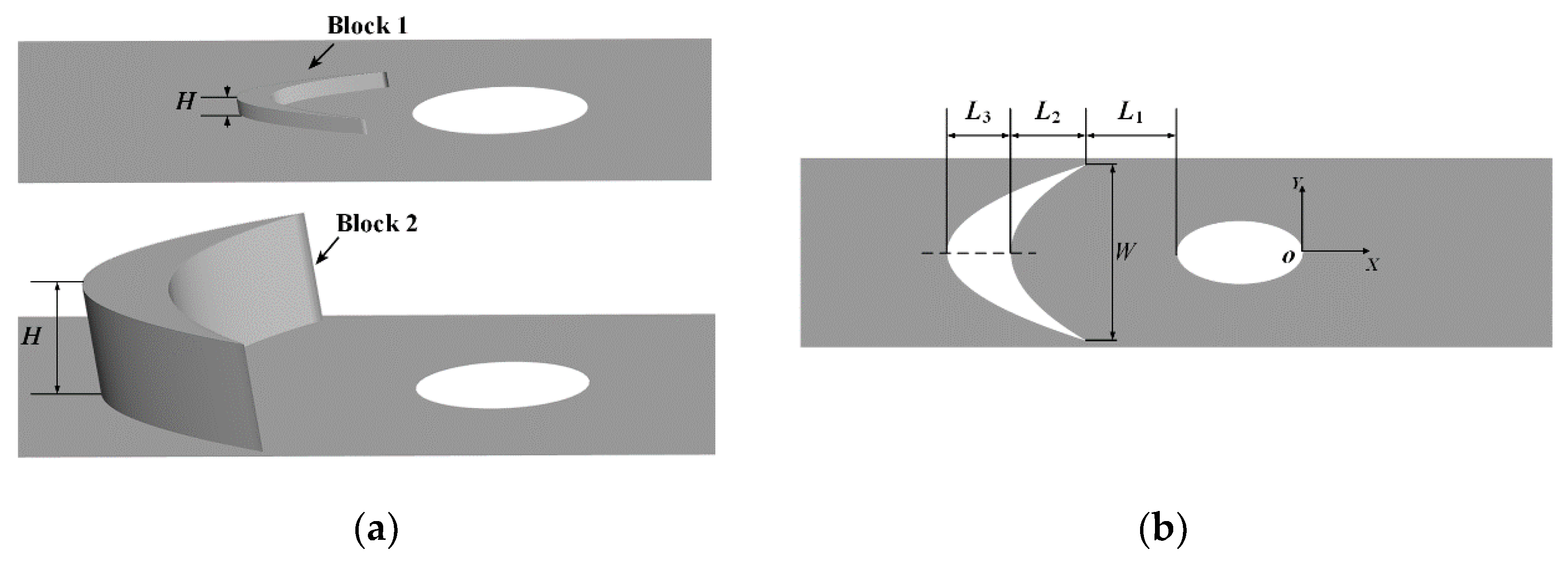
2.1. Linear Cascade Model and Boundary Conditions
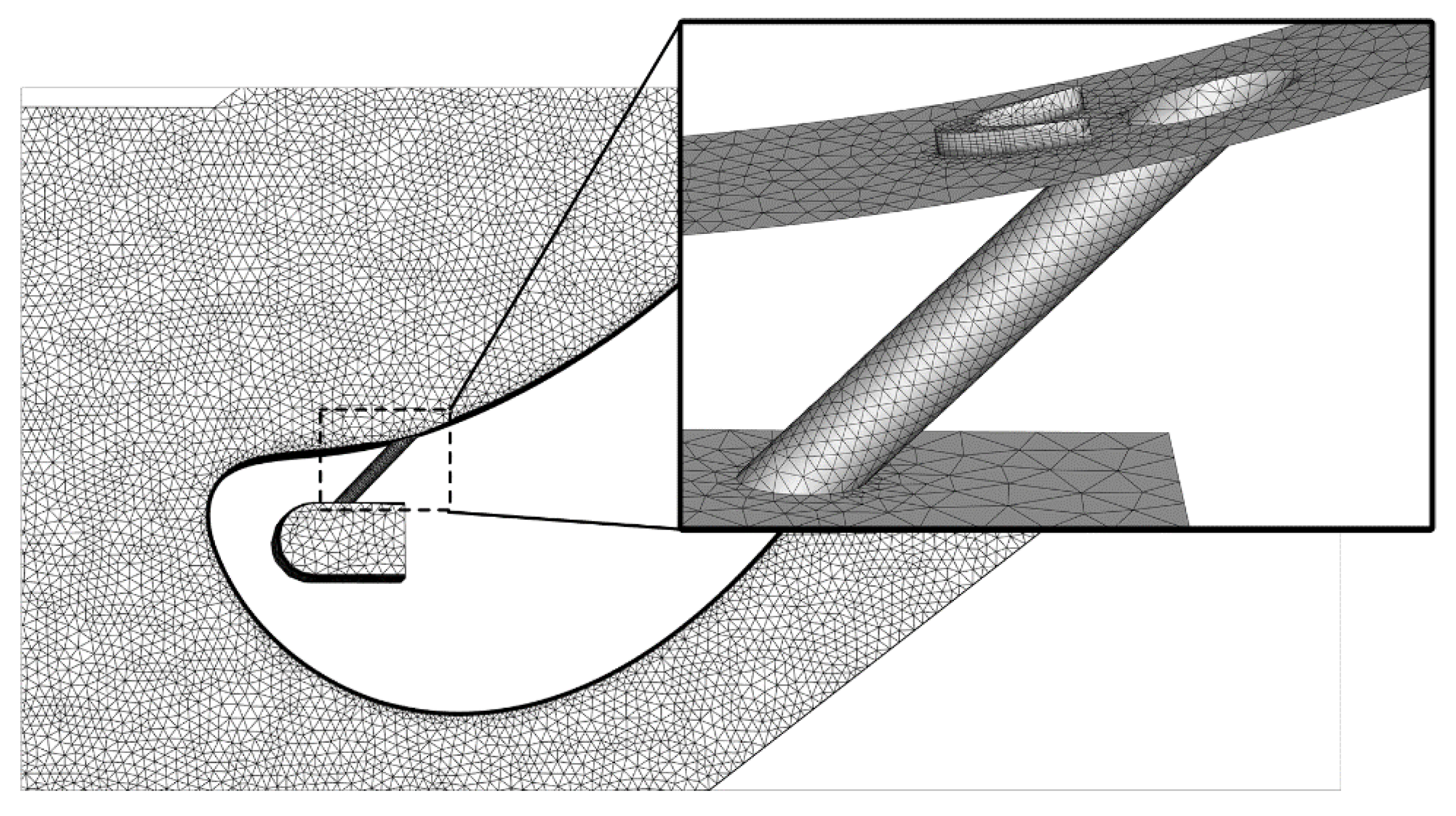
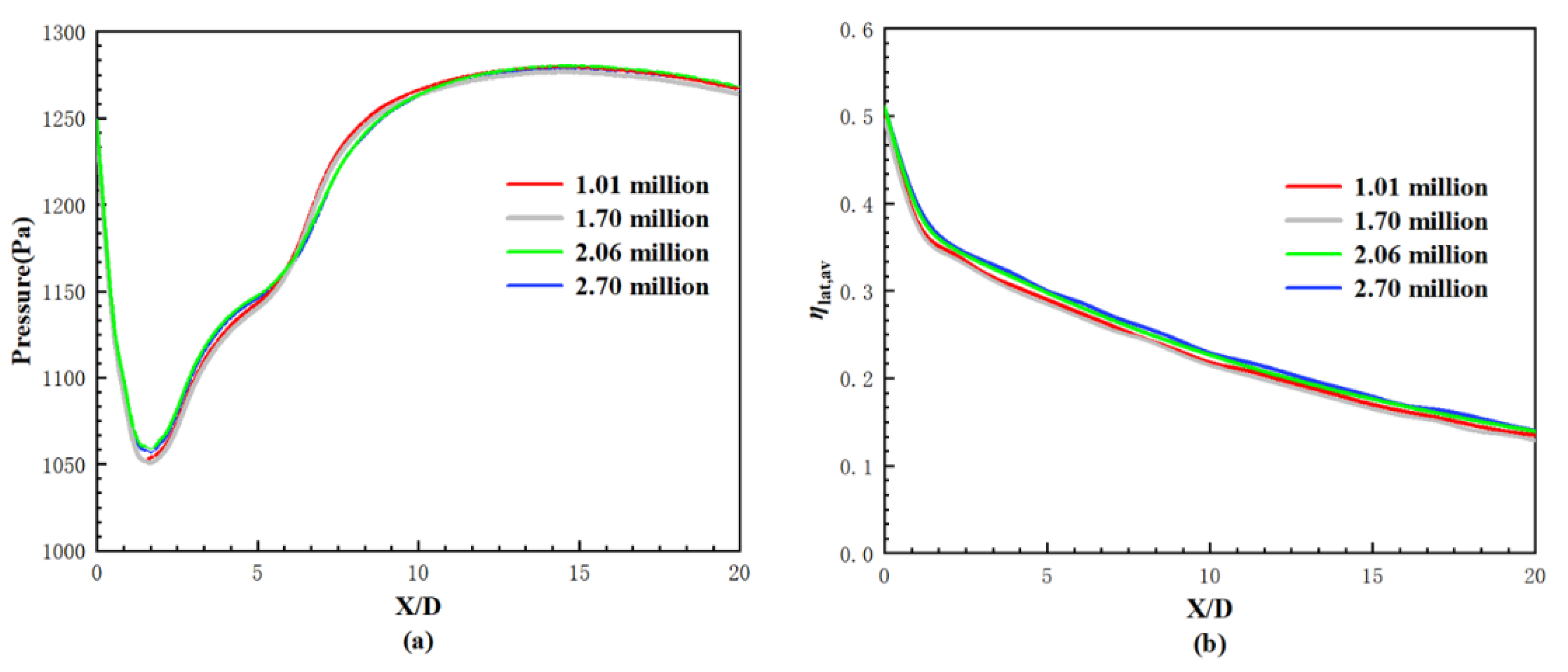
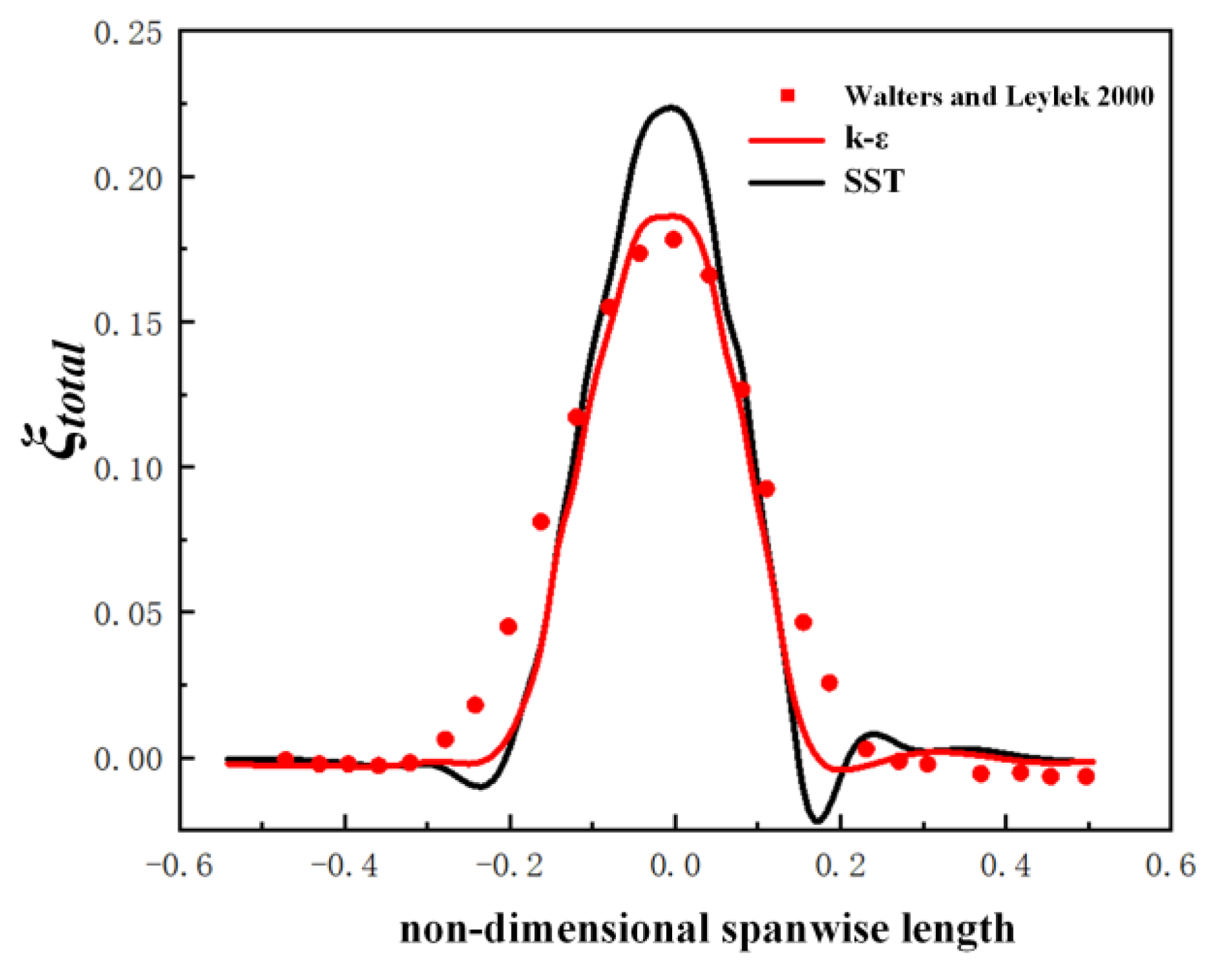
2.2. Computational Mesh and Numerical Method
3. Results and Discussion
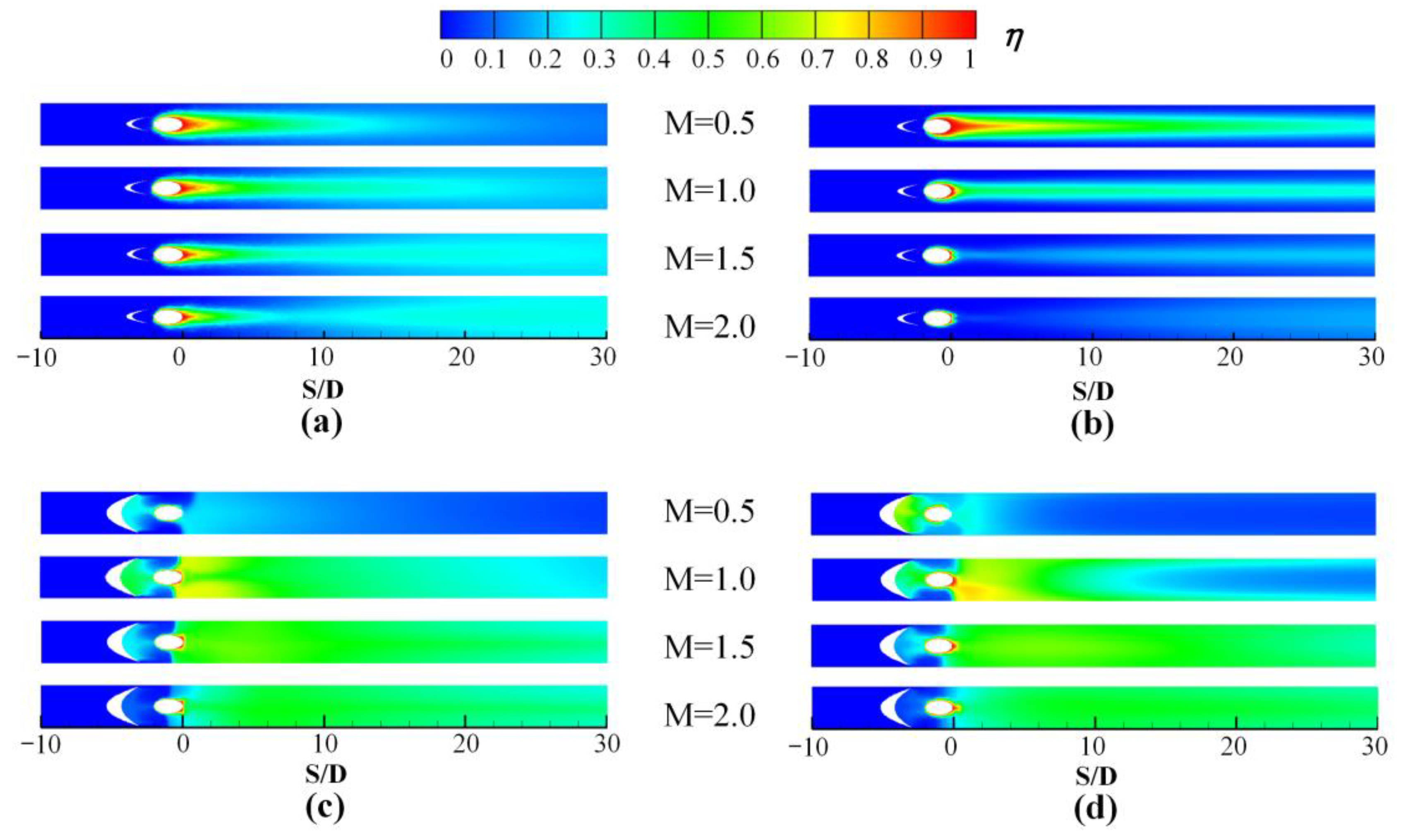
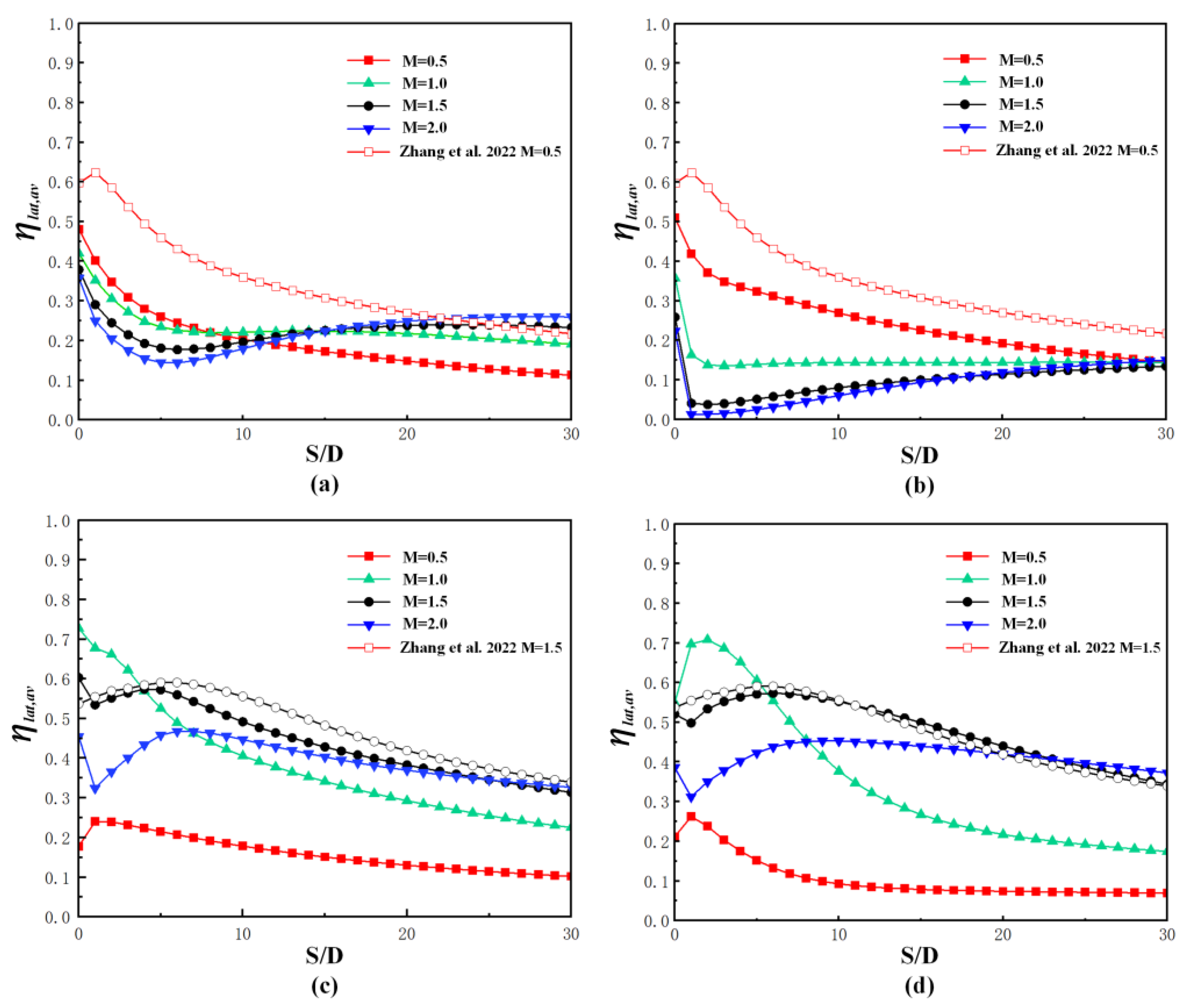
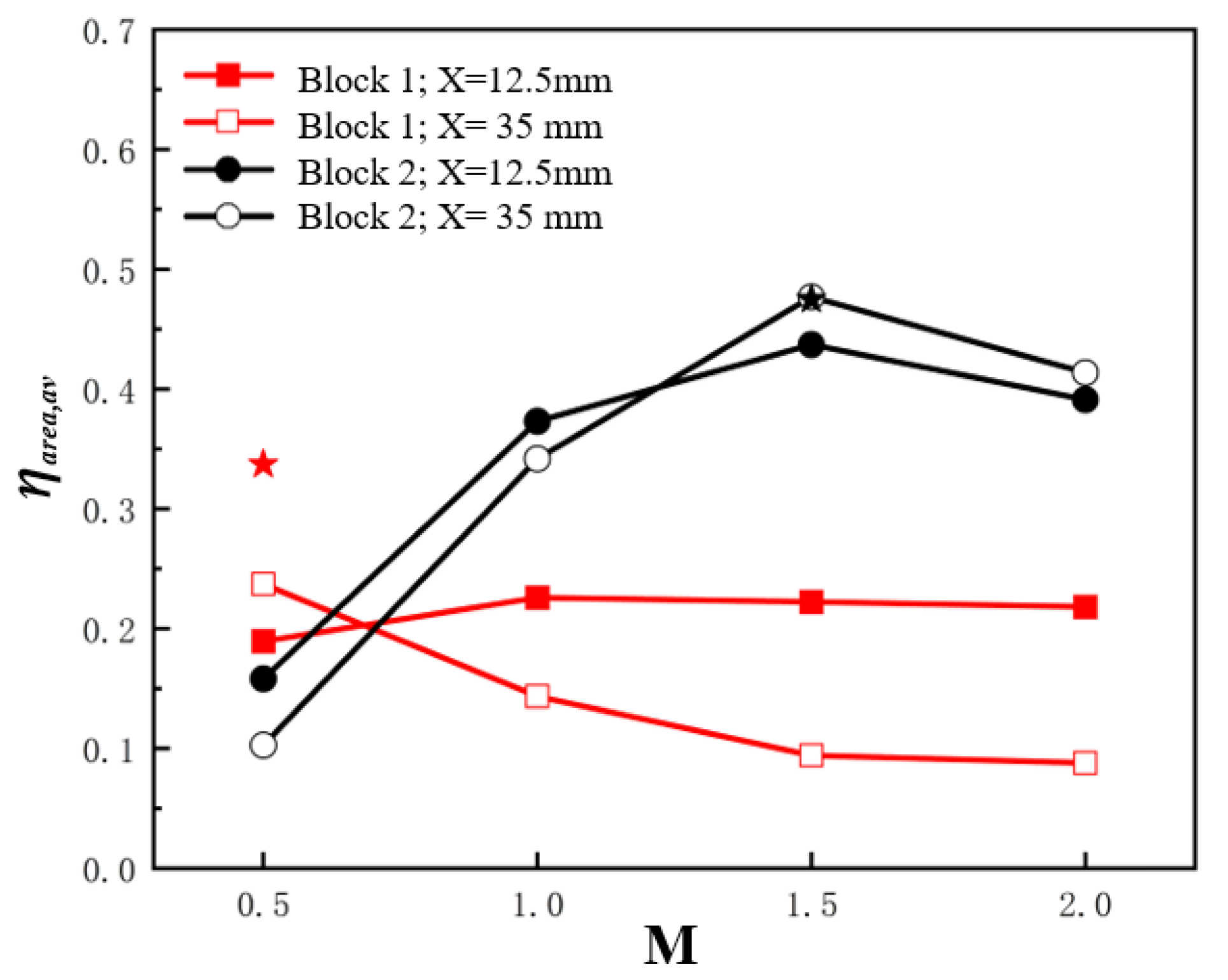
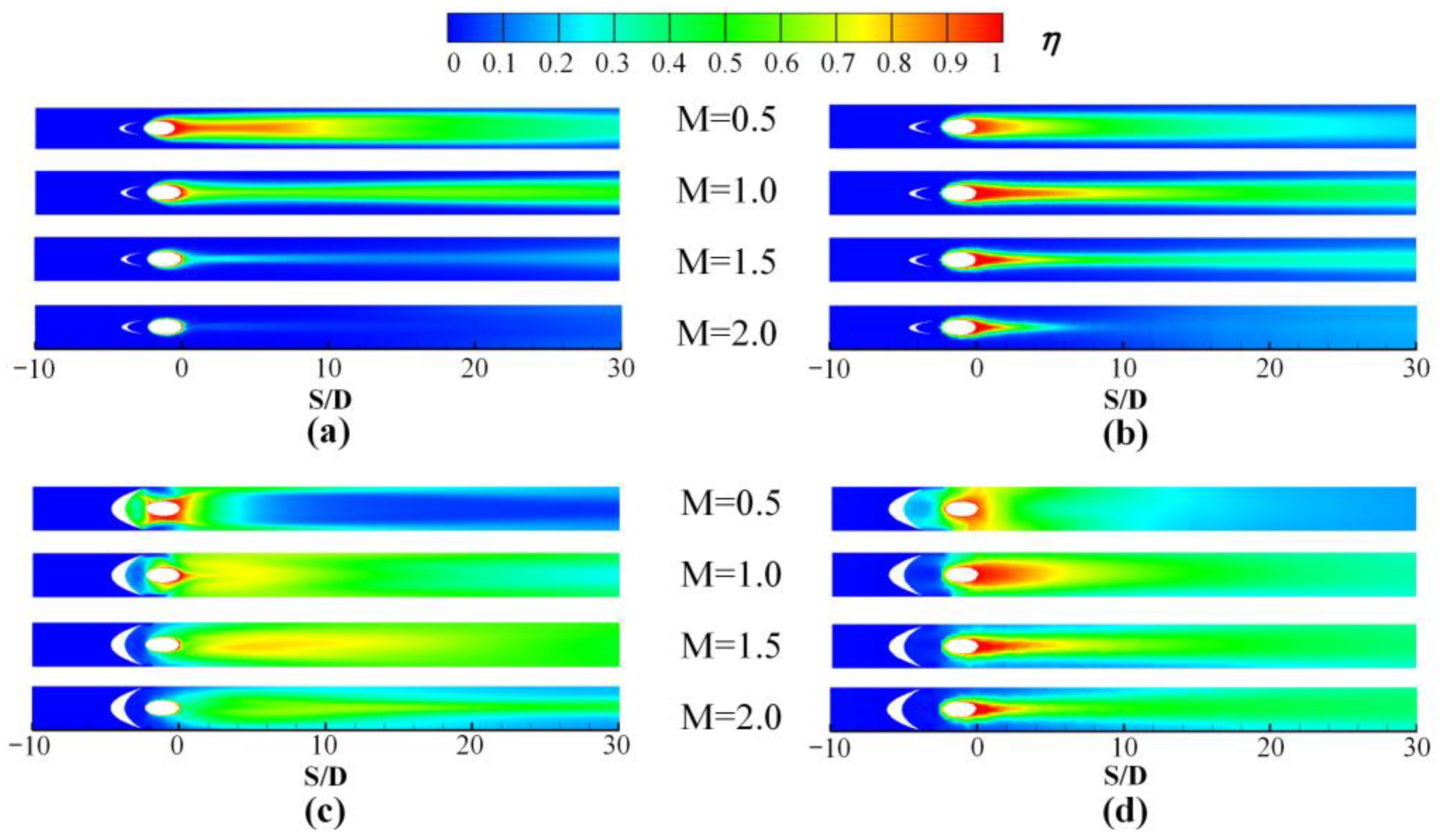
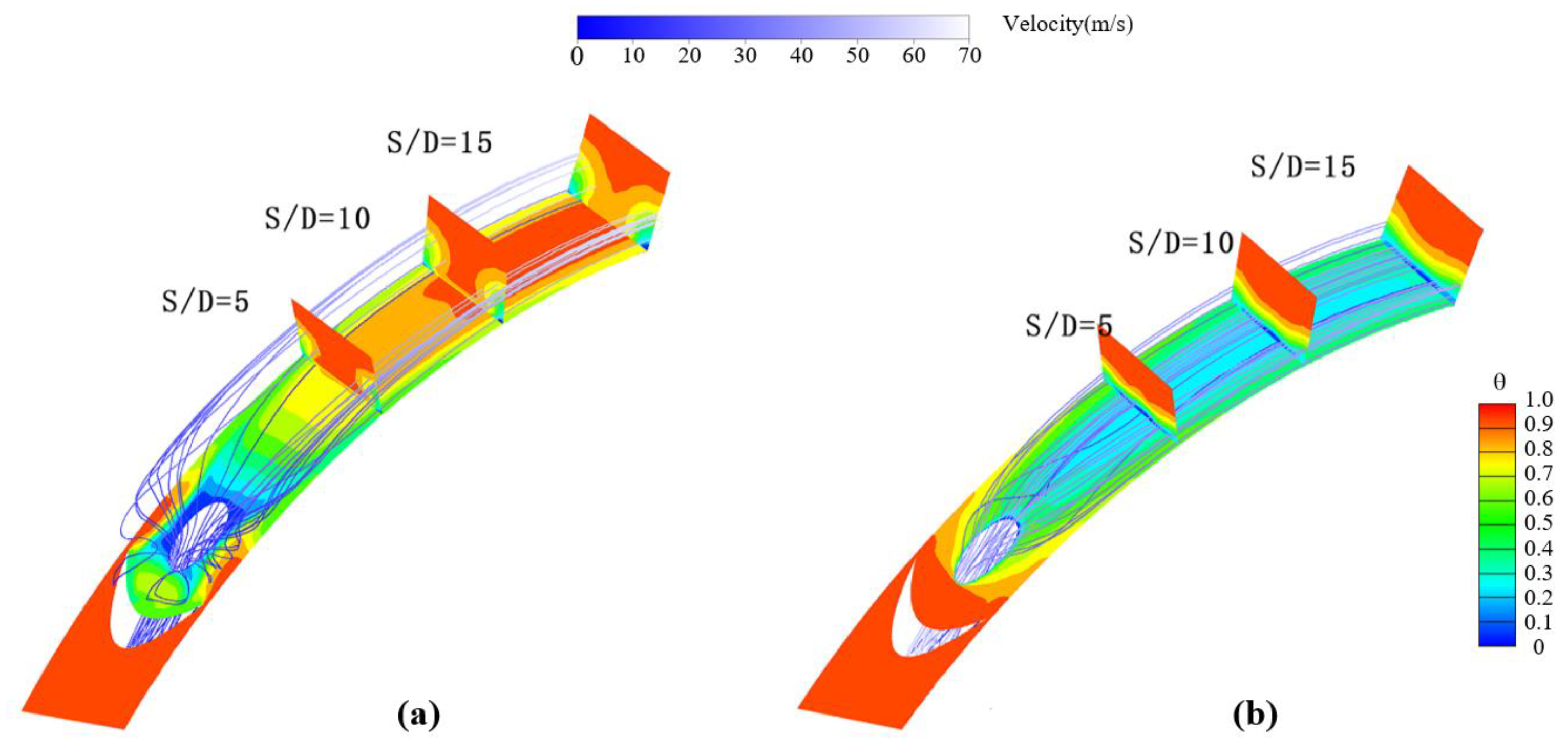
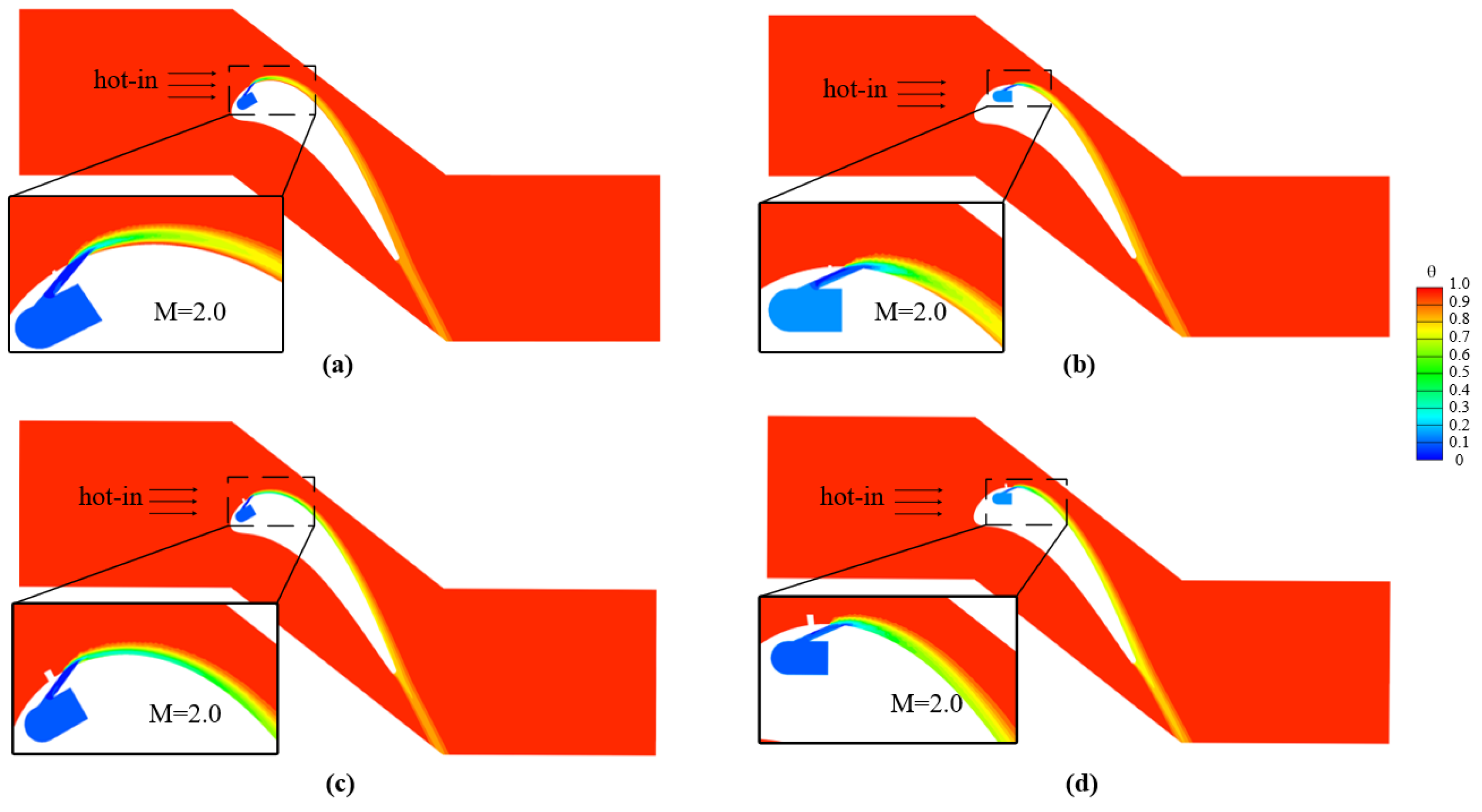
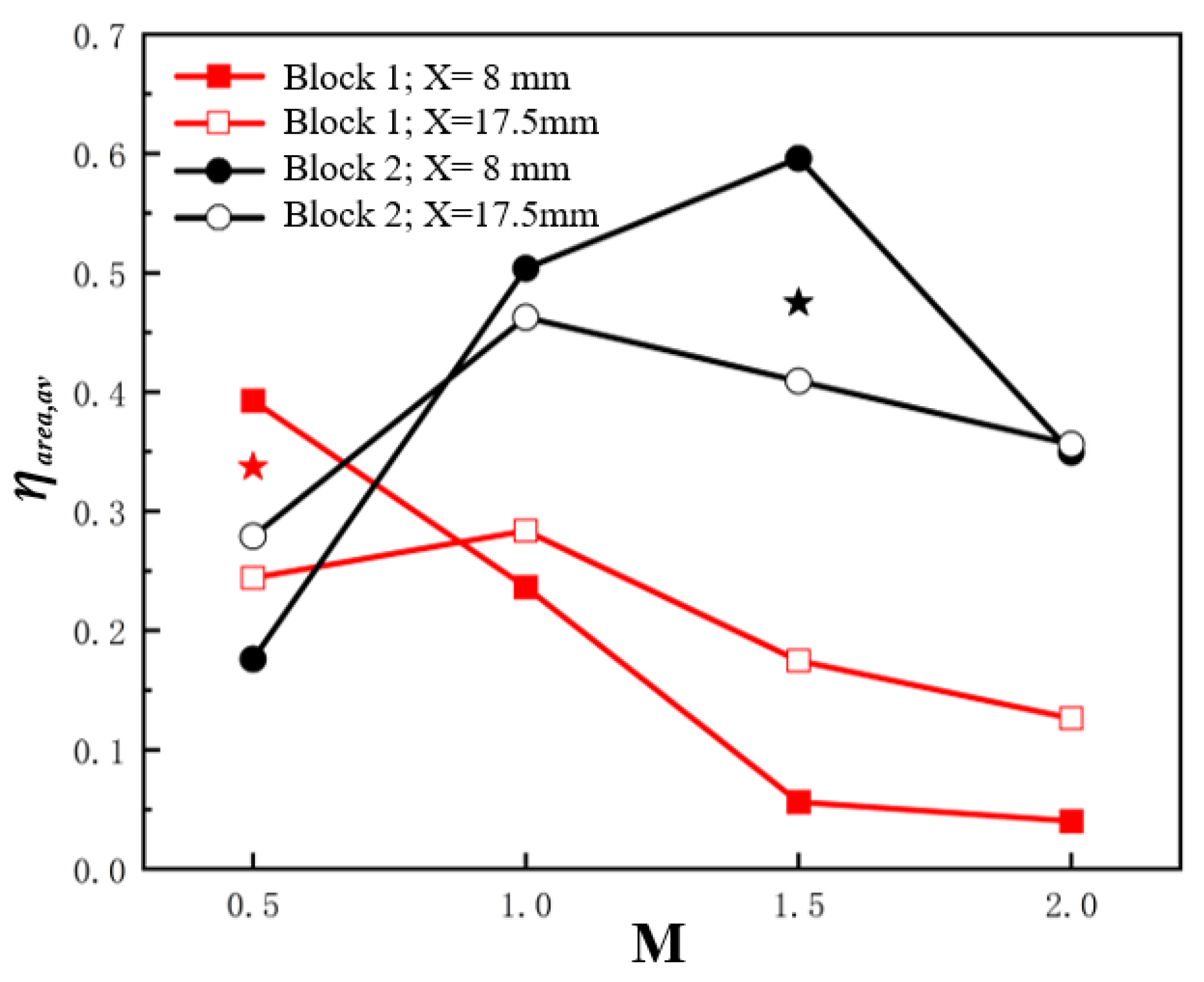
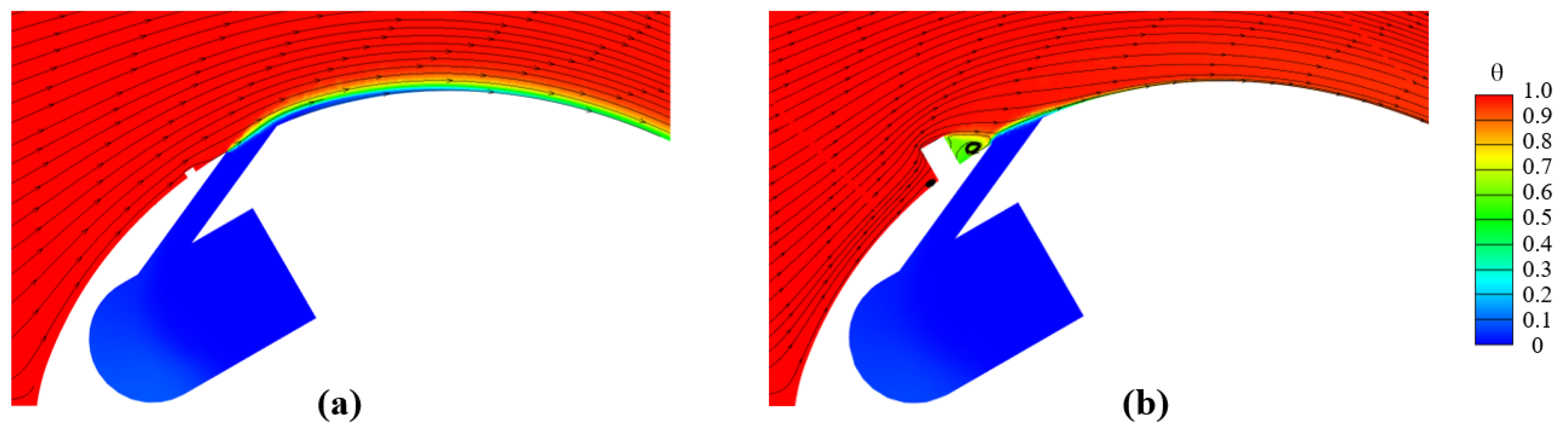
3.1. Film Cooling Performance on the Pressure Side
3.2. Film Cooling Performance on the Suction Side
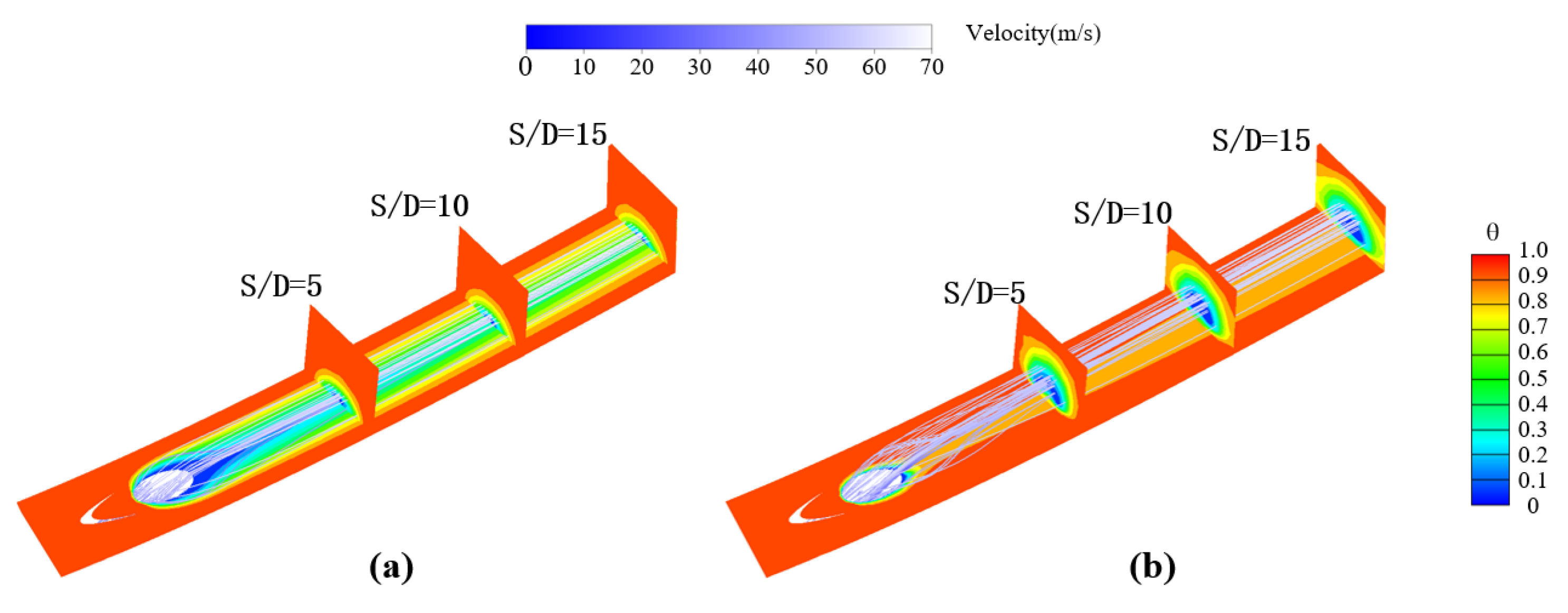
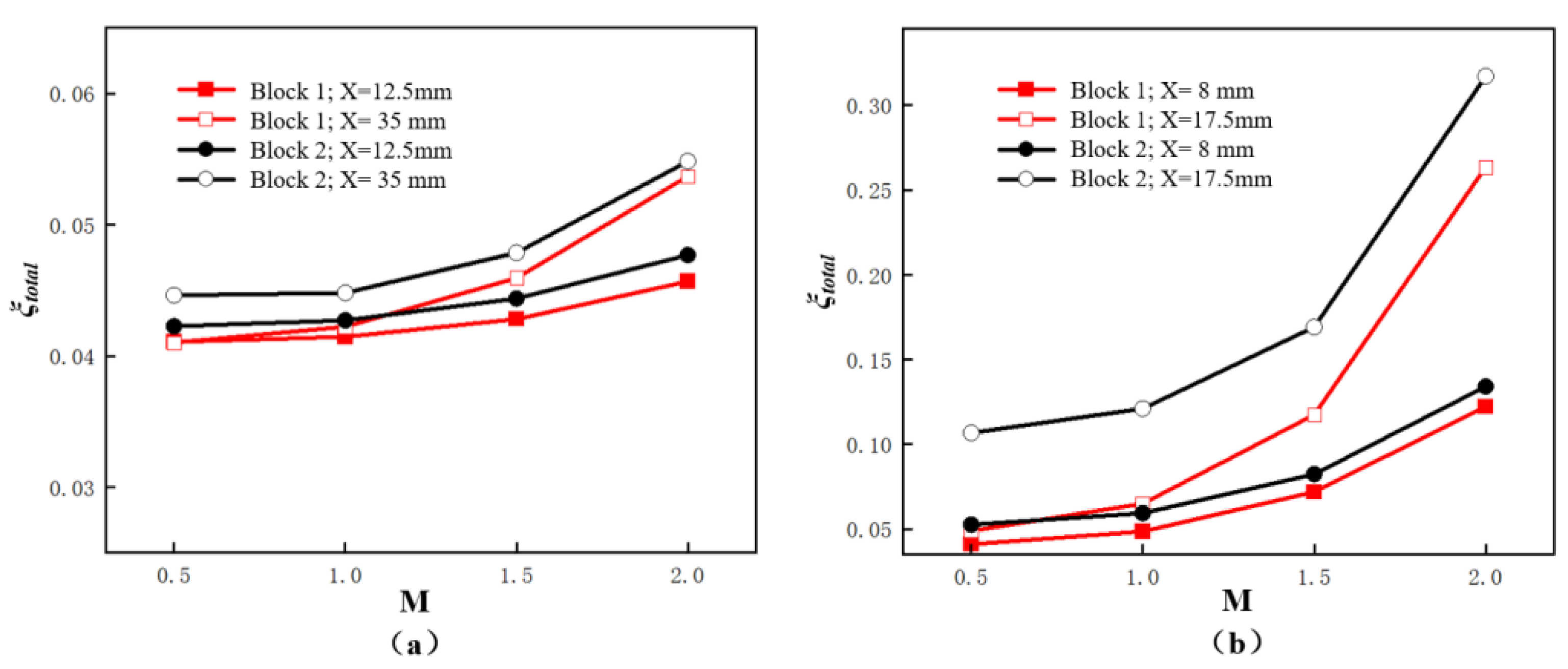
3.3. Aerodynamic Loss
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goldstein, R.J. Film Cooling. Adv. Heat Transf. 1971, 7, 321–379. [Google Scholar]
- Sinha, A.K.; Bogard, D.G.; Crawford, M.E. Film-cooling effectiveness downstream of a single row of holes with variable density ratio. J. Turbomach 1991, 113, 442–449. [Google Scholar] [CrossRef]
- Strzelecki, A.; Gajan, P.; Gricquel, L.; Michel, B. Experimental investigation of the jets in crossflow: Nonswirling flow case. AIAA J. 2012, 47, 1079–1089. [Google Scholar] [CrossRef]
- Pedersen, D.R.; Eckert, E.R.G.; Goldstein, R.J. Film cooling with large density differences between the mainstream and the secondary fluid measured by the heat-mass transfer analogy. J. Heat Transf. 1977, 99, 620–627. [Google Scholar] [CrossRef]
- Mayhew, J.E.; Baughn, J.W.; Byerley, A.R. The effect of freestream turbulence on film cooling adiabatic effectiveness. Int. J. Heat Fluid Flow 2003, 24, 669–679. [Google Scholar] [CrossRef]
- Bons, J.P.; MacArthur, C.D.; Rivir, R.B. The effect of high free-stream turbulence on film cooling effectiveness. J. Turbomach. 1996, 118, 814–825. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Eckert, E.R.G.; Burggraf, F. Effects of hole geometry and density on three-dimensional film cooling. Int. J. Heat Mass Transf. 2015, 17, 595–607. [Google Scholar] [CrossRef]
- Saumweber, C.; Schulz, A. Free-stream effects on the cooling performance of cylindrical and fan-shaped cooling holes. J. Turbomach. 2012, 134, 061007. [Google Scholar] [CrossRef]
- Bunker, R.S. Film cooling effectiveness due to discrete holes within a transverse surface slot. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002; Volume 3. [Google Scholar]
- Lu, Y.P.; Ekkad, S.V. Film cooling measurements for cratered cylindrical inclined holes. J. Turbomach. 2009, 131, 011005. [Google Scholar] [CrossRef]
- Dorrington, J.R.; Bogard, D.G.; Bunker, R.S. Film effectiveness performance for coolant holes embedded in various shallow trench and crater depressions. In Proceedings of the ASME Turbo Expo 2007: Power for Land, Sea, and Air, Montreal, QC, Canada, 14–17 May 2007; Volume 4. [Google Scholar]
- Fric, T.F.; Roshko, A. Vortical structure in the wake of a transverse jet. J. Fluid Mech. 1994, 279, 1–47. [Google Scholar] [CrossRef]
- Kusterer, K.; Bohn, D.; Sugimoto, T.; Tanaka, R. Double-jet ejection of cooling air for improved film cooling. J. Turbomach. 2007, 129, 809–815. [Google Scholar] [CrossRef]
- Kusterer, K.; Elyas, A.; Bohn, D.; Sugimoto, T.; Tanaka, R.; Kazari, M. Film cooling effectiveness comparison between shaped- and double jet cooling holes in a row arrangement. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; Volume 4. [Google Scholar]
- Nasir, H.; Acharya, S.; Ekkad, S. Improved film cooling from cylindrical angled holes with triangular tabs: Effect of tab orientations. Int. J. Heat Fluid Flow 2003, 24, 657–668. [Google Scholar] [CrossRef]
- Na, S.; Shih, T.I.-P. Increasing adiabatic film-cooling effectiveness by using an upstream ramp. J. Heat Transf. 2007, 129, 464–471. [Google Scholar] [CrossRef]
- Kawabata, H.; Funazaki, K.; Nakata, R.; Takahashi, D. Experimental and numerical investigations of effects of flow control devices upon flat-plate film cooling performance. J. Turbomach. 2014, 136, 061021. [Google Scholar] [CrossRef]
- Zhou, W.W.; Hu, H. A novel sand-dune-inspired design for improved film cooling performance. Int. J. Heat Mass Transf. 2017, 110, 908–920. [Google Scholar] [CrossRef]
- An, B.T.; Liu, J.J.; Zhang, C.; Zhou, S.J. Film cooling of cylindrical hole with a downstream short crescent-shaped block. J. Heat Transf. 2013, 135, 031702. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Z. Influence of streamwise position of crescent-shaped block on flat-plate film cooling characteristics. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 499. [Google Scholar] [CrossRef]
- Zhang, C.; Bai, L.C.; Zhang, P.F. Sensitivity analysis of the film-cooling effectiveness of an upstream crescent-shaped vortex generator to geometric parameters. J. Eng. Phys. Thermophys. 2021, 94, 1137–1146. [Google Scholar] [CrossRef]
- Zhang, P.F.; Zhang, C.; Wang, Z. Optimization of crescent-shaped block upstream of the cylindrical hole to enhance film cooling effectiveness using CFD and genetic algorithm. Prog. Comput. Fluid Dyn 2022. Accepted. [Google Scholar]
- Schwarz, S.G.; Goldstein, R.J.; Eckert, E.R.G. The influence of curvature on film cooling performance. J. Turbomach. 1991, 113, 472–478. [Google Scholar] [CrossRef]
- Ligrani, P.; Goodro, M.; Fox, M.; Moon, H.K. Full-coverage film cooling effectiveness and heat transfer coefficients for dense hole arrays at different hole angles, contraction ratios, and blowing ratios. J. Heat Transf. 2013, 135, 031717. [Google Scholar] [CrossRef]
- Kawabata, H.; Funazaki, K.; Suzuki, Y.; Tagawa, H.; Horiuchi, Y. Improvement of turbine vane film cooling performance by double flow-control devices. J. Turbomach. 2016, 138, 111005. [Google Scholar] [CrossRef]
- Zhang, P.F. Investigation on Flow and Cooling Characteristics of Cylindrical Film Cooling Hole with Block. Master’s Thesis, Tianjin University of Technology, Tianjin, China, 2022. [Google Scholar]
- Wang, L.; Luo, J.; Tian, S.; Zhu, H.; Liu, C. Film cooling performance comparison at different positions on blade suction side. J. Aerosp. Power 2017, 32, 1281–1288. [Google Scholar]
- Liu, J.J.; Lin, X.C.; Zhang, X.D.; An, B.T. Investigation on cooling effectiveness and aerodynamic loss of a turbine cascade with film cooling. J. Therm. Sci. 2016, 25, 50–59. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, W.W.; Wang, Z.; Tong, Z.T. Conjugate heat transfer simulation of overall cooling performance for cratered film cooling holes. Machines 2022, 10, 395. [Google Scholar] [CrossRef]
- Walters, D.K.; Leylek, J.H. Impact of film-cooling jets on turbine aerodynamic losses. J. Turbomach. 2000, 122, 537–545. [Google Scholar] [CrossRef]
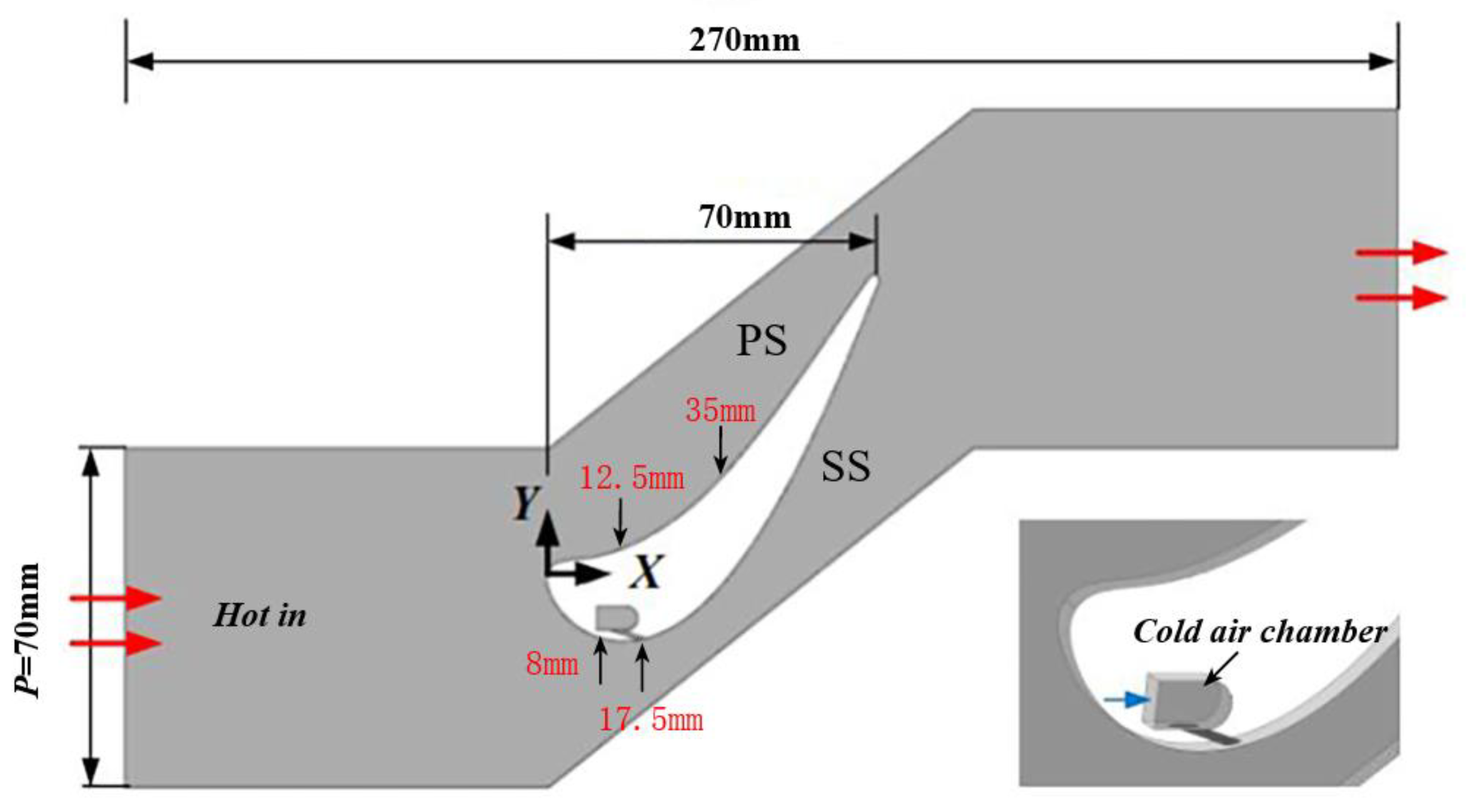
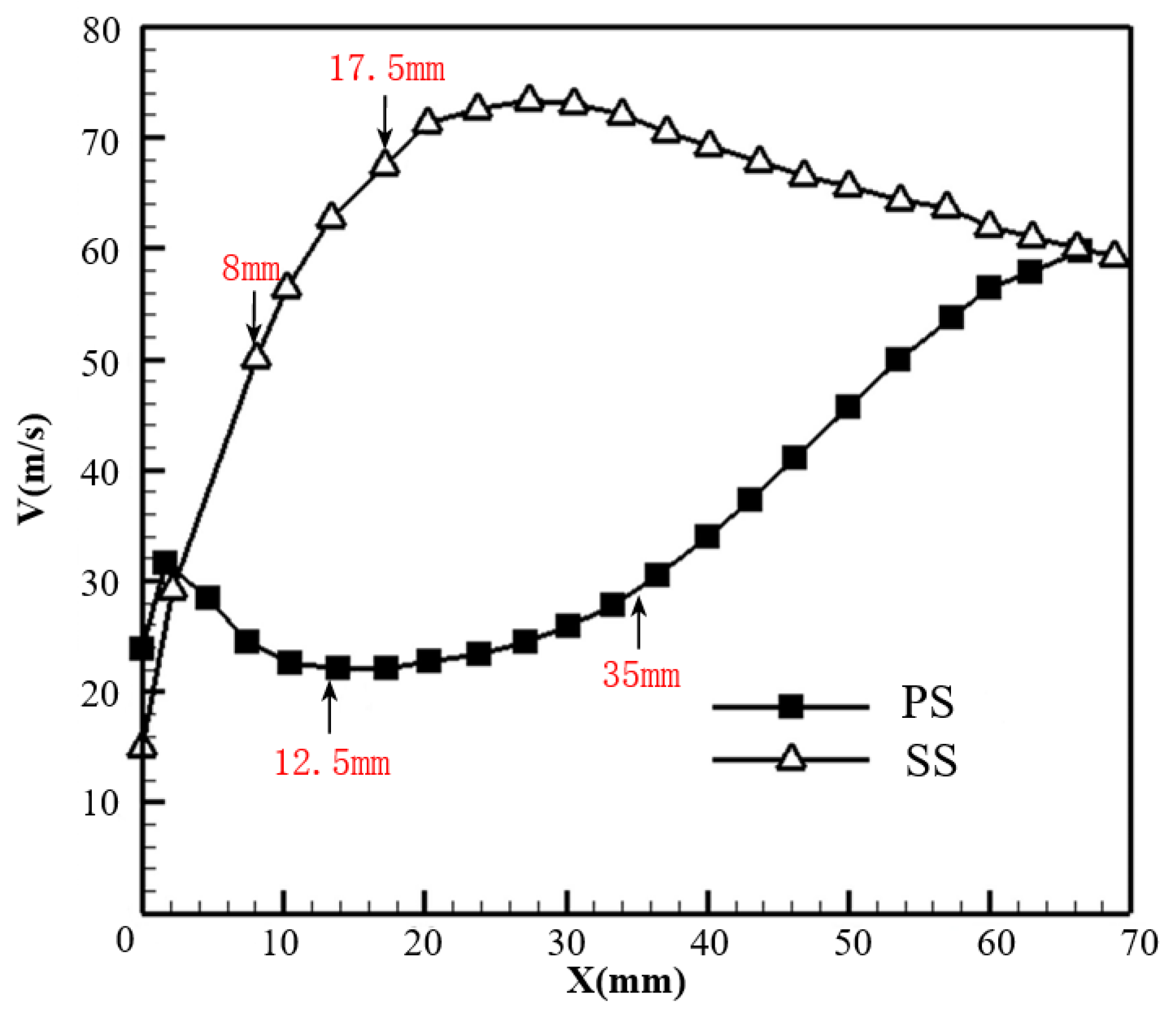



| Hole Location | Local Velocity Vlcoal (m/s) |
|---|---|
| PS, X = 12.5 mm | 22.0 |
| PS, X = 35 mm | 29.3 |
| SS, X = 8 mm | 51.7 |
| SS, X = 17.5 mm | 68.5 |
| Block No. | L1/D | L2/D | L3/D | W/D | H/D |
|---|---|---|---|---|---|
| Block 1 | 0.4 | 1.2 | 0.4 | 1.0 | 0.2 |
| Block 2 | 1.4 | 1.2 | 1.0 | 2.8 | 1.4 |
| Parameter | Mainstream Passage | Coolant Supply Plenum |
|---|---|---|
| Inlet temperature | Tm = 414 K | Tc = 300 K |
| Inlet velocity | Vm = 25 m/s | Vc = M·Vlocal·Ahole/(DR·Ac) |
| Inlet turbulence intensity | 5% | 1% |
| Outlet static pressure | 0.1 MPa | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Dong, J.; Wang, Z.; Zhang, P.; Tong, Z.; Zhang, Y. Film Cooling Performance of a Cylindrical Hole with an Upstream Crescent-Shaped Block in Linear Cascade. Machines 2023, 11, 110. https://doi.org/10.3390/machines11010110
Zhang C, Dong J, Wang Z, Zhang P, Tong Z, Zhang Y. Film Cooling Performance of a Cylindrical Hole with an Upstream Crescent-Shaped Block in Linear Cascade. Machines. 2023; 11(1):110. https://doi.org/10.3390/machines11010110
Chicago/Turabian StyleZhang, Chao, Junhuai Dong, Zhan Wang, Pengfei Zhang, Zhiting Tong, and Yue Zhang. 2023. "Film Cooling Performance of a Cylindrical Hole with an Upstream Crescent-Shaped Block in Linear Cascade" Machines 11, no. 1: 110. https://doi.org/10.3390/machines11010110
APA StyleZhang, C., Dong, J., Wang, Z., Zhang, P., Tong, Z., & Zhang, Y. (2023). Film Cooling Performance of a Cylindrical Hole with an Upstream Crescent-Shaped Block in Linear Cascade. Machines, 11(1), 110. https://doi.org/10.3390/machines11010110







