Abstract
Fault location is one of the main challenges in the distribution network due to its expanse and complexity. Today, with the advent of phasor measurement units (PMU), various techniques for fault location using these devices have been proposed. In this research, distribution network fault location is defined as an optimization problem, and the network fault location is determined by solving it. This is done by combining PMU data before and after the fault with the power system status estimation (PSSE) problem. Two new objective functions are designed to identify the faulty section and fault location based on calculating the voltage difference between the two ends of the grid lines. In the proposed algorithm, the purpose of combining the PMU in the PSSE problem is to estimate the voltage and current quantities at the branch point and the total network nodes after the fault occurs. Branch point quantities are calculated using the PMU and the governing equations of the π line model for each network section, and the faulty section is identified based on a comparison of the resulting values. The advantages of the proposed algorithm include simplicity, step-by-step implementation, efficiency in conditions of different branch specifications, application for various types of faults including short-circuit and series, and its optimal accuracy compared to other methods. Finally, the proposed algorithm has been implemented on the IEEE 123-node distribution feeder and its performance has been evaluated for changes in various factors including fault resistance, type of fault, angle of occurrence of a fault, uncertainty in loading states, and PMU measurement error. The results show the appropriate accuracy of the proposed algorithm showing that it was able to determine the location of the fault with a maximum error of 1.21% at a maximum time of 23.87 s.
1. Introduction
The distribution system has the responsibility of providing subscribers with the energy they need when reducing the frequency and magnitude of power outages. This issue is especially important because fault location is difficult due to the size of these networks and the extent of blackouts in the distribution network, among other parts of the power system [1]. The system reliability index and its efficiency are increased by pinpointing the fault’s precise location in the shortest amount of time and with the greatest degree of accuracy [2,3,4]. A distribution network is always essential due to special circumstances and characteristics such as size, dispersion, load imbalance, and inhomogeneity, as well as the fact that it is the last point of energy delivery to the consumer [5,6,7]. It appears necessary to use a technique or tools that can make decisions quickly and accurately. Since this network experiences the greatest number of blackouts out of the four components of the power system, it is responsible for 80% of all outages. The two main types of distribution network faults are transient faults and permanent faults, with about 80% of transient faults and 20% of permanent faults [8,9,10,11].
Distribution network fault location techniques include impedance methods, traveling wave methods, time domain methods, and intelligent methods. However, each of these techniques has drawbacks. Traveling wave-based methods may face problems such as high sampling frequency, complex structure, and the need for a database [12,13,14,15], and intelligent methods may be problematic due to their complex structure and the need for an accurate and large database [16,17,18,19,20]. Refs. [21,22,23,24,25,26,27] uses an artificial neural network and wavelet transform to extract features for various fault types and is intended to be able to pinpoint the fault’s exact location and the faulty section. The main drawback of this type of method is its dependence on the network structure under study, i.e., in case of a small change in the network structure, new training data must be generated again to train the artificial neural network.
1.1. State of the Art
In a smart grid, the voltage and current of nodes are measured and calculated using phasor measurement units (PMU) and governing circuit laws. These devices can measure the voltage and current of the phasor simultaneously in the electrical network. These devices are located on different buses and send their data to the control center at the same time with an accuracy of less than one microsecond using the global positioning system (GPS) for processing. The optimal placement of this equipment is performed using the governing circuit equations in the network. In distribution lines, due to the short electrical line, micro PMU is used, which is more accurate and can store and analyze data on-site [28,29,30,31,32].
Status estimation means determining system state variables from measurements performed in different parts of the network, and what exists in practice and the general state is to look at the measurements and errors in measuring from a statistical point of view. The governing equations between the measured parameters and the system state variables are determined from the model intended for the system. Then, with additional measurements and support, an optimization problem is developed, and with the proper solution, they get as close as possible to the actual values of the system state variables. Now in problem processing (problem making) and problem-solving, various tricks and methods are presented in the articles and some of them are used in practice as mentioned before, the variables of network state, amplitude, and phase of voltage and current of network buses. The primary reason for performing some processing and optimization tasks in the estimation state is that to start, it is not possible to measure the voltage and current phase of all system buses using the current measuring devices. Although with a new technology, PMU, it is possible to measure the amplitude and phase of voltage and current of the buses with very high accuracy; at present, for economic reasons, it is not possible to install PMUs in all buses of the system. On the other hand, the measuring equipment in the power system has a certain accuracy, which is not very desirable. Therefore, by taking additional measurements of the system by PMUs, the problem could be turned into an optimization problem, and in this way, to achieve the exact amount of system state variables with appropriate accuracy [33,34,35].
1.2. Problematic and Proposed Solution
Today, PMUs are increasingly used in power systems. The reasons that can be mentioned are as follows: (1) PMUs have higher accuracy than traditional measuring devices, although this accuracy is reduced by the transformers used in the PMU. (2) PMUs reduce the effect of deflection time on the measurement performed. (3) They are also used for many other applications such as power system protection, evaluation, control, and stability of systems. (4) Objectives such as identifying the fault topology and detecting and correcting the fault parameters are achieved with the help of PMUs. (5) They increase the accuracy of state estimation and consequently increase the accuracy of estimation of network parameters [36]. To date, there are not many methods for using PMU-based state estimation for fault location. Since the network condition is not normal at the time of the fault, the network parameters can no longer be estimated correctly as normal. One way to apply this technique is to use pre-fault state estimation information. For example, ref. [37] estimated the current and voltage of network nodes after the fault using pre-fault information and the calculation of line voltage drop. The disadvantage of these techniques is that the algorithm has difficulties with large distribution networks and that they are only effective for short-circuit faults rather than series faults. In [38,39], PMUs are used for monitoring and assessing the electrical power quality of the network as well as fault location.
Authors attempt to define the fault location as a matching-based optimization problem today because impedance methods frequently employ iterative algorithms to locate the fault. We can locate the fault with the least amount of iteration by solving the problem. Brahma, S.M. [40] introduces the fault impedance similarity method for fault location in the distribution network. Finding the error involves four steps: First, the voltage is received by the measuring equipment that is installed in some network segments both before and during the fault. The three-phase network impedance matrix is then used to calculate the fault current proportionally to each of these received voltage sags. The relation between the fault current and the fault impedance is then extracted for each type of fault. The similarity between the estimated fault impedances leads to the development of a fault index. In this example, the algorithm uses auxiliary processing to verify the estimated fault impedances. Using a phasor and advanced measuring tools, the suggested method is used to measure the voltage sag. Distributed generation (DG) is frequently modeled as having a constant impedance in a three-phase impedance matrix.
Using the information on the voltage and current at the feeder’s start and other points when a fault occurs, the voltage and voltage sag of each node is calculated in [41]. Assuming that a fault could occur in any section, this method tries to pinpoint the fault current in the damaged section. calculating the voltage sag in the nodes and contrasting it with the measurement device’s recorded value. A fault occurs if these two values are matching, and the location of the fault is determined by the recorded current and voltage. For each node’s simulated fault, the voltage sag’s amplitude and phase are first calculated in [42] and saved in the database. Next, the amplitude and phase of the voltage sag are determined and compared to the database to identify potential fault locations using the fault voltage information as a starting point. Then, using the calculated voltage sag amplitude and phase at the start and end of each potentially flawed section as a guide, the desired locations on the plane are determined, along with the separation between the orthogonal line and straight lines. By selecting a location where the distance along the line orthogonal to the fault is less than the fault location, the main location of the fault can then be identified. The same method is used in [43], but the algorithm is divided into two separate pages: fault location voltage sag phase and amplitude.
Note that so far, little research has been done in the field of fault location based on the optimization problem. Usually, most research based on matching algorithms has been done by comparing measured information such as voltage and current in the network. In this way, the actual fault information is usually compared with the information obtained in the simulation environment, and wherever these two values become the same and their different approaches are zero, the fault location is identified. As they are known, such matching methods will have many defects. It seems a bit far-fetched to be able to model the same real fault in the network in a laboratory environment and compare these two non-homogeneous information items with each other to locate the fault. In practice, the obtained answer will not be valid. Therefore, the best approach will be to compare the information obtained from two different methods on specific data (real or laboratory) so that the obtained answer is valid. A new solution would be to define the objective function based on different approaches, which are presented in this paper. Note that the definition of fault location as an optimization problem in [44,45] is mostly presented for two-terminal transmission lines with objective functions dependent on voltage changes only for short-circuit faults.
1.3. Methodology
One of the drawbacks of the suggested methods is that they depend on the quantity of PMUs in the network, i.e., the more devices in the network, the more nodes are considered in the matching problem. These techniques rely on matching voltage changes for their solutions. The accuracy of the suggested algorithms is consequently decreased, especially in complex distribution networks with heterogeneous structures, as a result of the inability to account for the voltage changes of all of the network nodes involved in the problem as a result of these constraints. In this study, authors try to determine how much the network nodes’ total voltage and current changed before and after the fault. To achieve this, we combine the PSSE problem with the values obtained from the PMU. Additionally, we define two new objective functions that aim to compute the voltage difference between the two-grid line ends and identify the faulty section and fault location. The optimization of the fault location problem depends critically on both the problem’s objective function and the alternative meta-heuristic algorithm used to solve it. The objective function and problem-solving algorithm should be selected in a way that provides the maximum speed and accuracy of fault location because prompt fault resolution is essential, especially in the distribution network. As of now, fault location has been achieved using a variety of algorithms [46,47] with different objective functions, the majority of which are based on comparing simulation data with actual data. The outcomes are only experimental in reality (i.e., comparing two sets of inhomogeneous data).
In this study, the issue is resolved using a genetic algorithm and two new objective functions based on the measurement of pseudo-real data by PMU. The classification of the article is as follows: In Section 2, PSSE-based network visibility before and after the occurrence of the fault is introduced; in Section 3 the general structure of the fault location problem for different types of faults is explained; in Section 4, the simulation results are presented; and Section 5 sets out the conclusions.
2. PSSE-Based Network Visibility Using PMU
PMUs are very powerful and fast devices that enable power network users to fully monitor the network in real time. One of the most important applications of online security analysis in system control centers is power system status estimation, which has improved a lot with the advent of PMUs. The power system consists of generation, transmission, and distribution parts. As shown in Figure 1, the PMU can be used in different parts of the power network and the values measured by them can be transferred to the system control center for network monitoring, analysis, and estimation.
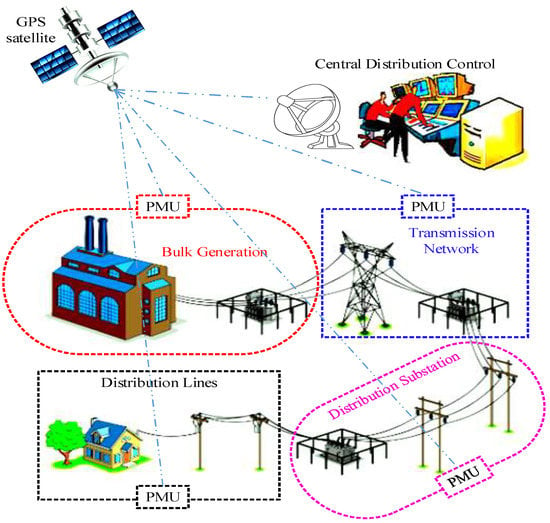
Figure 1.
Power network infrastructure.
Power system status estimation is a process to provide the best estimate of what is happening in the network. This is done in control centers based on real-time measurements and a predetermined system model, in which a set of measured data is collected from the entire power grid and transmitted to the system control centers to the status of the estimation system during static analysis, usually performed by the weighted least square (WLS) method. The governing equations between the measured parameters and the system status variables are determined from the model intended for the system, and then, despite the additional measurements and support available, an optimization problem is formulated, and by solving it properly, they get as close as possible to the actual values of the system status variables. The variables of network status are the amplitude and phase of current and voltage of network buses. Sometimes parameters such as tap changer and transformer phase shift can also be considered as status variables. However, it is not possible to measure the voltage and current phase of all system buses using the current measuring devices, which is the main reason for some processing and optimization issues in status estimation. The new PMU technology makes it possible to measure the amplitude and phase of voltage and current of the buses with very high accuracy, at present for economic reasons, it is not possible to install PMUs in all buses of the system. Nevertheless, the measuring equipment in the power system has a certain accuracy, which is not very desirable. Therefore, the problem could be turned into an optimization problem with additional measurements that are done from the system, and in this way, the exact amount of system status variables can be obtained with appropriate accuracy. The PMU is used in this article to estimate the network parameters as well as to identify and pinpoint the network fault location, which will be discussed below.
2.1. WLS Method to Solve PSSE Problem
The status of a power system refers to the operating conditions of that system, such as loading, voltage, power passing lines, transformers, substations, and so on. Mathematically, all of these variables can be obtained from the magnitude and angle of the voltage and current of the buses. Therefore, in principle, the status of a power system should be defined as a set of magnitudes and angles of voltages and currents. Finally, the purpose of estimating the status in the power system is to find the best estimate of the status variables in such a way that in the power flow model of the power system, the best fit for the measurement data is obtained.
The PSSE mathematical model can be written as Equation (1) based on the mathematical relationships between the measured values and the system status values. Where Z is the vector of the measured variables, x is the vector of the status variables (magnitude and phase of the voltage and current of the buses), h is the vector of the nonlinear functions connecting the status variables to the measured variables, and e is the vector of the measurement error.
Assume that the errors {e1, e2,…, eN} are independent random errors with a Gaussian distribution with a mean of zero. The variance (σi2) of the measurement error ei is an indicator of the degree of certainty of a particular measurement. Large values for variance indicate that the corresponding measurement is not very accurate. Finally, the covariance matrix (R) of the measurement error can be expressed as Equation (2):
In Equation (1), x is an unknown vector that contains definite values (not random). Since the errors of e are random variables, the measured values of Z will also be random. Here Z has a normal distribution with mean h(x) and covariance R. The probability density function Z can be written as Equation (3):
For the static estimation problem, a set of network variables called Z is observed or measured to estimate the x status vector. It makes sense for x values to be estimated in such a way that the probability density function maximizes. The estimated value of x is called the “maximum likelihood estimate”.
Given the exponential characteristic of Equation (3), it is clear that maximizing f(Z) is equivalent to minimizing the quadratic expression in its power according to Equation (4).
An accurate estimate should minimize the squares of the weighted error with accurate measurements. Therefore, the answer to the WLS problem gives the estimated status vector that must be true in the optimization condition of Equation (5):
where H(x) is the Jacobin matrix of the measurement function expressed as Equation (6).
By extending the nonlinear function g(x) to its Taylor series around the status vector, we have Equation (7):
Regardless of the higher degree expressions, a process for extracting the answer to the problem can be obtained by the iterative method called the Gauss-Newton method. So, we will have:
where k is the iteration index and the answer vector of the problem in k iteration.
G(x) is called the gain matrix, which is a sparse, positive, and symmetric matrix from which the visibility of the network can be determined. Network visibility indicates whether the meters installed in the system, in terms of number and location, allow estimating all network status variables.
2.2. Using the PMU in the PSSE Problem before the Fault
This section describes how to use the PMU in the PSSE problem. The phasor representation for a sine quantity such as X can be expressed as Equation (11).
In this case, X(t) shows the signals sampled at time t = τ with X(t) = Xk, where τ is the sampling interval. Using discrete Fourier transform (DFT), phase X(t) is defined as Equation (12).
where N is the number of samples in a base frequency period and θ is the sampling angle corresponding to τ and is expressed as Equation (15).
For most of the measuring and relaying device applications, the typical sampling rate is 12 times the power system frequency. The above-mentioned discrete Fourier transform equation was non-recursive. In practical uses, time-varying phases are calculated using Equation (16) as an iterative equation. Suppose is the phasor obtained from the set of samples x {k = r, r + 1,…, N + r − 1}. In this case, when a new sample is obtained, the new sample set is displayed as x {k= r + 1,…, N + r}. In this case, the updated phasor will be obtained using Equation (16):
whereas requesting two samples at each stage, the recursive calculation method with a moving sampling window is quicker than the non-recursive method. If X(t) has transient changes, the moving window will track amplitude and phase changes with a delay that depends on the sampling time rate.
PMUs, as shown in Figure 2, can measure the amplitude and angle of the bus voltage as well as the current of the lines and transformers connected to the bus. To use PMUs in estimating the status, the PMU bus voltage phasors and the current of the connected lines must be considered in measurement vector Z. Also consider the nonlinear functions of these phasors with the system status variables in the vector h. For this purpose, the relationship between these phasors and system status variables must be extracted. Therefore, according to Figure 3, the relationships between the measured data of PMUs in lines and transformers with status variables through branch current equations of the line π model can be obtained.
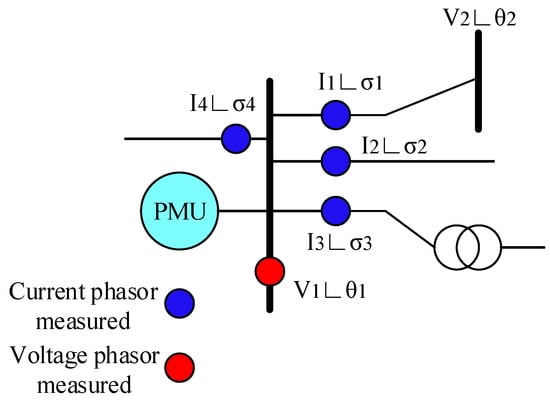
Figure 2.
PMU connected to a bus.
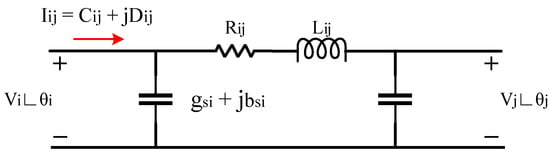
Figure 3.
Model π two inputs of a branch of the power grid.
For the participation of the data measured by PMUs in the Jacobin matrix of H-status estimation, the linearized relations of the branch current equations in terms of amplitude and angle of voltage in the corresponding bus and the end of the connected lines can be considered. Therefore, the Jacobin matrix elements can be defined as Equation (20) to Equation (27).
Thus, the PMU’s contribution to the answer vector and the Jacobin status estimation matrix can be expressed as Equations (28) and (29). Also, for a better understanding of the PSSE problem-solving method, the references are set out below [48,49,50].
2.3. Utilization of Pre-Fault PSSE Information for Fault Location
In this paper, we use pre-fault PSSE information to estimate the voltage and current of network buses after a fault occurs. As can be seen in Figure 4a, using the PSSE, the voltage status of the nodes, the current passing through each branch, and the voltage drop across each line can be determined.
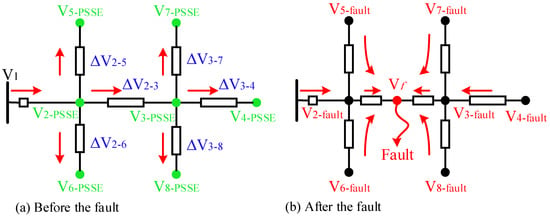
Figure 4.
Network status. (a) Information obtained from the PSSE before the fault, (b) The current direction of each network line after the fault.
Following that, all the currents of various network lines change direction to the point of fault according to Figure 4b, assuming a fault occurs in lines 2–3 of Figure 4a. It will be crucial to locate the problematic area in this case given the size and complexity of the network. When a fault occurs, only the voltage and current at the network’s beginning can be measured, making it challenging to identify the faulty section. In the normal state of the network, it is possible to estimate the voltage and current of network nodes using a variety of techniques. One solution is to use a PMU to measure the current and voltage of various network nodes, allowing for the detection of the faulty section through sporadic measurements throughout the network. The right local to install these devices will be crucial because the cost of these measuring devices prevents their widespread use in the network.
Due to the size of the distribution network, faults could occur in either the main branch or the lateral branches. In this study, the faulty line is located using a combination of data estimated by PSSE and data measured by PMUs. The voltage drop of each network line prior to the fault can also be calculated by PSSE, which allows for the installation of PMUs in each node of the main branch of the network. By doing this, the current flowing through the entire network, including the main and lateral branches, can be estimated, allowing for the identification of the faulty section. As an illustration, Figure 5 depicts the changes in the direction of current flowing through each network line for faults 1, 2, and 3. The faulty line can now be identified if PMUs can be installed in the network’s main branch nodes. Each PMU that is closer to the fault will have a larger value, and each PMU that is farther from the fault will measure less. For example, for fault 3, the fault current measured by PMU3 will have the highest value compared to PMU1 and PMU2. It is possible to identify the problematic area of the network by comparing the PMUs’ data. The voltage drop calculation performed by PSSE prior to the fault can then be used to estimate the end current of each faulty line. As an illustration, Figure 6 depicts a line that is connected to the PMU both before and after the fault. The voltage values V1−PSSE, V2−PSSE, and current I1−PSSE can be estimated in the pre-fault condition by putting the values measured by the PMU in the PSSE problem and using Equation (30) to calculate them after taking into account the line voltage drop (ΔV1−2).
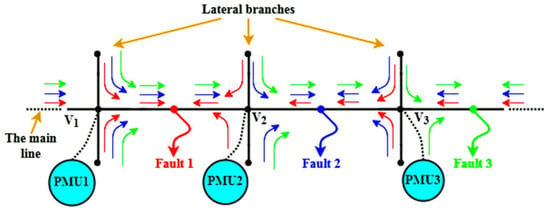
Figure 5.
Changes in the direction of line current in exchange for the location of various faults in the main branch of the network.
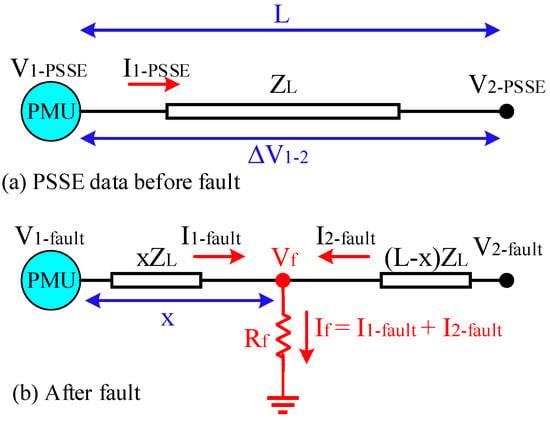
Figure 6.
Voltage and current status of the node connected to the PMU. (a) Before the fault, (b) After the fault.
According to Figure 6b, after the fault, only the values of V1−fault and I1−fault can be measured by the PMU, so at this stage, knowing the amount of voltage drop ΔV1−2, the fault voltage of V2−fault can be calculated from the Equation (31).
Then, through the line transfer matrix, the fault current of I2−fault can be obtained from Equation (32).
As a result, with knowledge of the voltage drop of the lines, the voltage and current changes at the beginning and end of the faulty line can be easily calculated at the time of the fault. In addition, the fault point voltage (Vf) can be calculated depending on the I 1−faultand I2−fault currents through Equations (33) and (34).
Now, by equating Equations (33) and (34), we can estimate the location of fault x by knowing the voltage and current at both ends of the line through Equation (35).
So far, authors have found how to locate faults using PSSE data (prior to the fault) and use the PMU to measure the voltage and current after the fault. The method for finding the faulty section and fault location in the distribution network will be explained in the section that follows.
3. Faulty Section Estimation and Fault Location in the Distribution Network Based on Optimization Problem Solving
Using information from PSSE and PMUs, we try to define the distribution network fault location as an optimization problem in this paper. We then estimate the fault location by resolving the problem. The voltage and current at the start and end of the line are first connected using a feature of the travelling wave model. Figure 7 shows the status of a grid line with the π model.
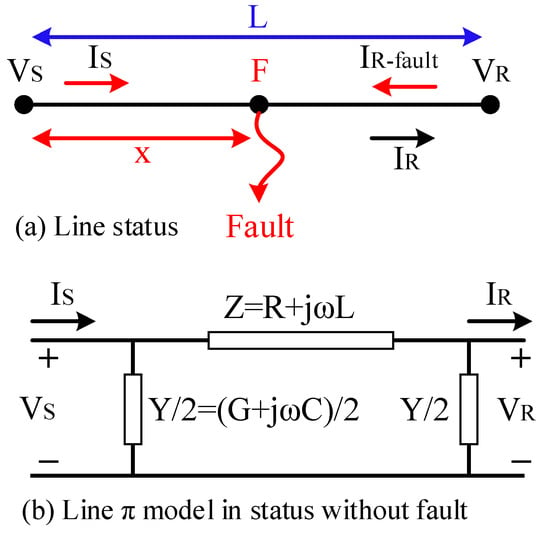
Figure 7.
Information of a sample line.
Equation (36) can be used to describe the relationship between voltage and current at the beginning and end of the line under normal circumstances (without a fault).
where γ = √zy constant or diffusion coefficient, (Zc = √z/y) is the characteristic impedances in ohms and Z and Y are the series impedance and shunt admittance, respectively. With a little algebraic operation, the above steady-state equations can be written in the form of Equation (37):
Now suppose that a fault occurs at point F according to Figure 7a at distance x. In this case, similar to Equations (33) and (34), the fault voltage at the vision of the beginning and end of the line can be calculated through the KVL law according to Equation (38).
According to Equation (38), two indicators M and N are defined, which represent the voltage vision from both sides of the network line. The value of these two indicators is zero in the without fault state and increases suddenly when a fault occurs, which can be used to detect the faulty line. For example, Figure 8 shows a three-line network with four nodes. Suppose a fault occurs here on the LS line (between nodes S, P). According to what has been said, the voltage and current on both sides of each network line must be calculated, and any line whose value at both ends is not the same will be a faulty line. That is, in this case, the symmetric components of voltage and current point P (VP, IP) should be calculated using the voltage and current phasors estimated in nodes R, T, and S, in this case in node R, T approximately with it will be equal to but not equal to what is calculated based on the phasors of node S. By this logic, the voltage of the node and the injection currents from the nodes can be calculated according to Equations (39) and (40).
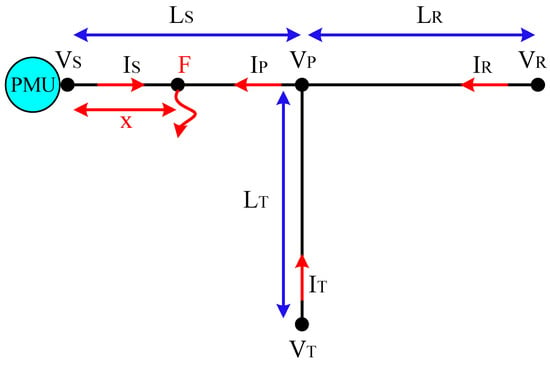
Figure 8.
Sample network of 3 lines.
By considering Equation (41), we can convert Equations (39) and (40) into Equations (42) and (43):
As shown in Equation (44), the difference between the magnitude of the voltage and current without fault state lines is almost zero, and the faulty line will be greater than the specified threshold value. With such a criterion, it is possible to define the identity of the defective distribution network section as an optimization problem that seeks to identify the network line with the greatest voltage or current difference. Therefore, the objective function of the fault location problem can be defined as Equation (45). Where in, L = Number of network lines = 1, …, N, i = Number of network buses = 1,…, M, j = Number of network buses = 1,…, M, I ≠ j.
In the objective function of Equation (45), instead of voltage changes on both sides of the line, it is possible to use changes in the current at both ends of the line, since the absolute value of voltage or current at both ends of the line is used, so in both cases, the changes will be incremental. As is well known, in short-circuit faults the voltage decreases, and in series faults the voltage increases. However, since the absolute value of voltage is used, these changes will be incremental, so the proposed objective function can be used for all types of faults, including short-circuit and series. In this paper, to solve the problem according to the problem space shown in Figure 9, the genetic algorithm is used to find the maximum points.
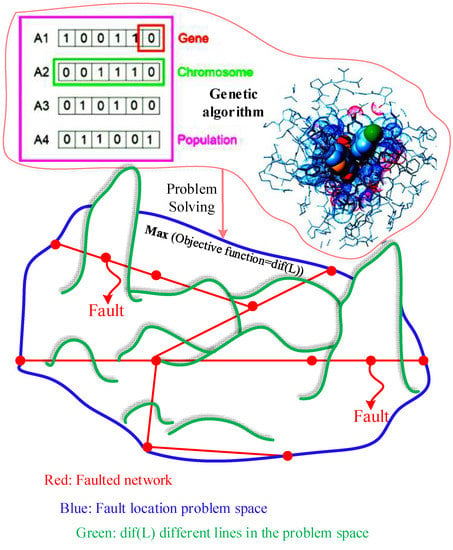
Figure 9.
General space of the fault location problem.
3.1. Fault Location in the Distribution Network for Different Types of Faults
In the previous step, the method of detecting the faulty section was presented. In this section, the method of calculating the fault distance from the beginning of the faulty line for different types of faults will be introduced. In Equation (35), the fault distance x is shown for the information at the beginning and end of the line. Now, Equation (35) can be defined as Equation (46) according to the π model of the network line.
The authors can use the same technique described to identify the faulty section and define a new objective function for fault location since our attempt in this article is to define the fault location as an optimization problem. An objective function for fault location is presented in Equation (47), where the difference between the calculated fault voltage is considered from the perspective of the two sides of the line for the variable x. Here, x = Fault location, F = Fault point, i, j = Nodes at the beginning and end of the faulty line. Equation (47) has two major differences from Equation (45). In Equation (45) the problem variable is the faulty line and in Equation (47) the problem variable is the fault point x. The next difference in Equation (45) is because the current seen from the two ends of the line is inverted (−I) and in the problem, there is a sign (−) so the two values are added together and the value of the objective function will be incremental, but in Equation (47), since the voltage at the fault location must be equal from the point of view of the two sides of the line, the solution to the problem is close to zero.
Equation (47) defines the problem’s objective function as precisely locating the fault between the two faulty buses, Ij. The basis of the work will be that, similar to Figure 10, we will move the length of the fault location between the two buses i, and j, respectively, and at the same time calculate the fault voltage from the point of view of the two buses i, j (i.e., VF→i, VF→j) and repeat this process until the objective function of the problem for x is minimized.
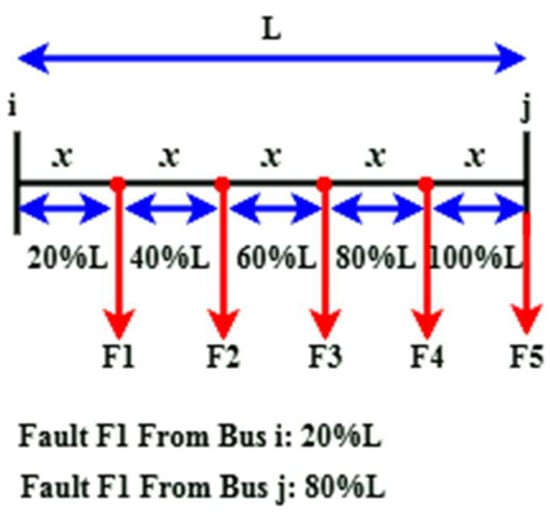
Figure 10.
Fault between two buses i, j.
There are two types of distribution network faults: short-circuit faults and series faults. The calculation of the voltage and current of the fault point depends on the type of fault in the network and will vary depending on the characteristics of each fault. In short-circuit faults, the fault current increases and then the voltage decreases, whereas in series faults, the opposite occurs, i.e., the voltage increases and the current decreases. This section introduces how to calculate the voltage and current of the fault for each type of fault based on the positive, negative, and zero sequence components. Figure 11 shows the different types of faults that will be examined in this article.
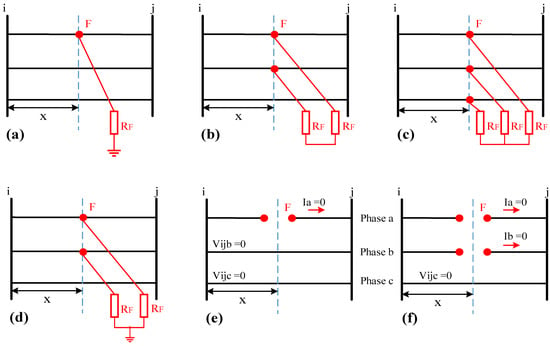
Figure 11.
Types of short-circuit and series faults, (a) single-phase fault to ground, (b) two-phase fault, (c) three-phase fault, (d) two-phase fault to ground, (e) One open conductor, (f) Two open conductors.
3.1.1. Short-Circuit Faults
Figure 11a shows the single-phase short-circuit fault at point F. One of the fault analysis techniques is to use the positive, negative, and zero sequence components of the fault current and voltage. Figure 12 shows the equivalent circuit of symmetrical components for a single-phase fault to ground. In a single-phase fault to ground, there will be all three positive, negative, and zero sequences. In this case, the fault voltage (VF) based on the sequences can be calculated from Equation (48) to Equation (50).
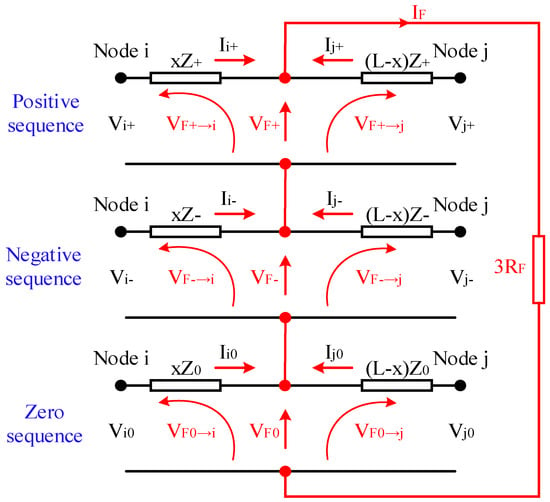
Figure 12.
Equivalent circuit of positive, negative, and zero sequences of single-phase fault to ground.
For two-phase and three-phase faults, the zero-sequence can be omitted, and the fault voltage (VF) can be calculated based on the positive and negative sequences. Therefore, according to Equation (55), we will have:
3.1.2. Series Faults
Series faults are asymmetric faults that can be analyzed through symmetric components. In this type of fault, the faulty phase current is reduced at the beginning of the line and becomes zero at the end of the line. Also, in this type of fault, the voltage of the without fault phases is zero and the voltage of the faulty phase is increased. Figure 13 shows the equivalent circuit of symmetric components for series faults. According to Figure 13, Equation (56) will be established for one open conductor fault and Equation (57) for two open conductors fault.
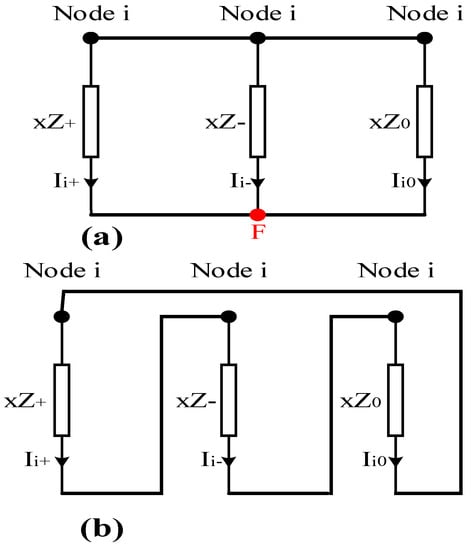
Figure 13.
Equivalent circuit of symmetric components for a fault (a) One open conductor, (b) Two open conductors.
Also note that for series faults, there is no need to solve Equation (47), since the node j side of the information is zero and it is easy to estimate the fault location for this type of fault with Equations (56) and (57). Finally, a flowchart of the steps of the proposed method to solve the fault location problem is shown in Figure 14.
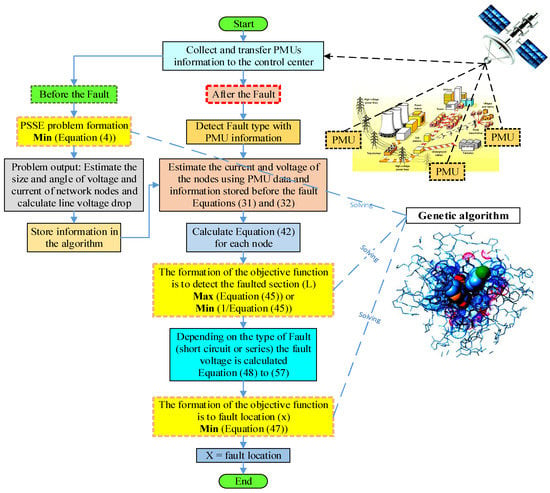
Figure 14.
Flowchart of the steps of the proposed method.
The suggested method has three steps, as shown in Figure 14. Estimating the voltage and current of the network nodes and then the voltage drop across the network lines are the goals of the initial stage, which takes place before the fault occurs. In the second stage, after the fault occurs, the goal is to identify the faulty section using the values of PMUs and using the information from the first stage. In the third stage, the goal is to fault location after identifying the faulty line in the second stage. These three actions are classified as optimization problems, it should be noted. The genetics algorithm (GA) is employed in this paper to resolve the issue and the same conventional techniques are used in the GA algorithm, the accurate details of which are provided in reference [51].
4. Simulation Results
In this paper, a proposed fault location algorithm is implemented on the IEEE 123-node distribution feeder. In this section, the effect of various factors on the accuracy of the proposed algorithm, including the effect of values measured by PMUs, type of fault, angle of occurrence of a fault, and fault resistance will be evaluated. Figure 15 shows the network under study along with the status of DG resources and PMUs installed in the network. At the beginning of the distribution feeder and the connection point of DG sources to the network, it is possible to measure the voltage and current of the nodes. According to the proposed method, PMUs have been installed in a limited number of nodes in the main branches of the network in such a way that the information of the whole network can be estimated with appropriate accuracy. As mentioned in Section 3, our goal is to obtain the line voltage drop before the fault, so that after the fault occurs, by combining the values measured by the PMUs and the voltage drop obtained from the first step, we can estimate the voltage and current of each node after the fault. This depends on how the PMUs are installed on the network, which both improves the accuracy of the estimation and covers the entire network. It should be noted that in reference [8] we have presented a new technique for installing PMUs in the network for fault location. The conventional technique for installing PMUs in the distribution network is to place these devices at the end of the lateral branch of the network, which causes the installation of a large number of these devices in the distribution network. The reference technique [8] is by installing PMUs in the main nodes of the network and using the PSSE problem, in addition to reducing the number of PMUs installed in the network, efforts have been made to obtain the information of the entire network. Therefore, in this article, the technique presented in reference [8] is used to install PMUs in the network. As shown in Figure 15, by measuring the voltage and current at eight nodes, the entire network is covered and the network is divided into eight zones by PMUs. Of course, it should be noted that the more PMUs, the better the accuracy of the method, but their installation will be expensive.
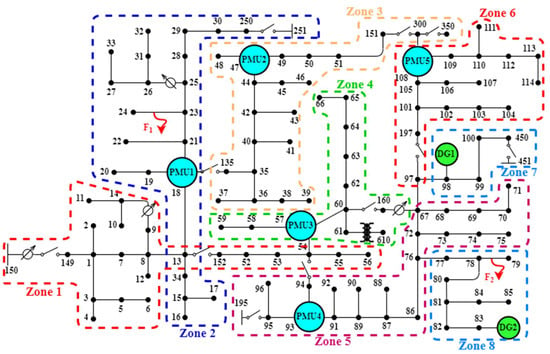
Figure 15.
IEEE 123 Node Test Feeder distribution network with PMU.
The first step in the design is to estimate the voltage and current of the network nodes before the fault occurs. Figure 16a,b show the estimated voltage and current of the network nodes, respectively. Next, according to the voltage information of the network nodes, the voltage drop of each network line can be calculated, which is shown in Figure 16c. One of the main challenges in the distribution network is the detection of the faulty section due to its many branches, and it is more difficult for several faults to occur simultaneously in the network, which makes it difficult to identify the fault points because it is no longer possible to use conventional single-location fault location equations to identify multiple fault locations, as the direction of branch current to the fault location will vary. In this article, we have tried to solve these problems by presenting a new objective function for the fault location problem.
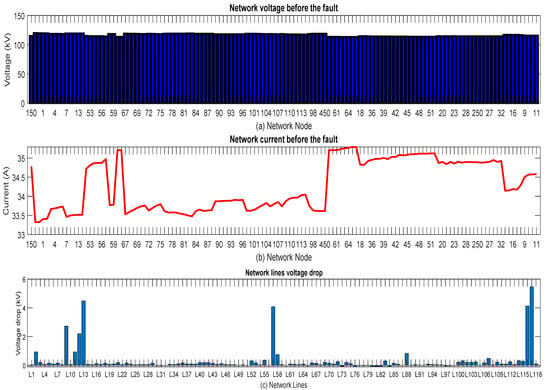
Figure 16.
Voltage and current of network nodes under normal conditions.
Let us suppose that two faults F1 and F2 occur simultaneously in the network. Fault F1 is a single-phase fault ground in Zone 2 between nodes 23 and 24, and fault F2 is a two-phase fault in Zone 8 between nodes 78 and 79. At this stage, the goal is to identify these two points of fault by solving Equation (45) using a genetic algorithm, since in solving optimization problems the goal is to minimize the objective function so Equation (45) can be defined as (1/objective function). Finally, Figure 17 shows the results of the performance of the GA algorithm in solving the fault location problem. As shown in Figure 17, respectively, (a) and (b) the convergence curve of the GA algorithm regarding the best and average solutions, (c) the curve of selection changes and the children created in each generation, (d) and (e) respectively the fitness value and the final convergence of the solutions to the optimal value and the stopping condition and calculation time for all generations, (f) the average distance between the solutions, and (g) the output of the algorithm for all the variables of the algorithm are shown.
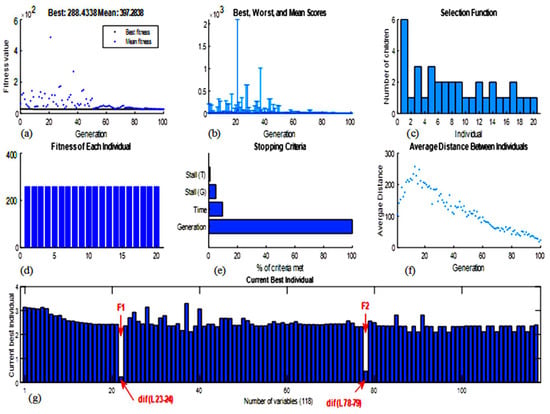
Figure 17.
Results of the performance of the genetic algorithm to identify the fault section.
According to Equation (42) to Equation (44) defined for each line, the voltage seen from both ends of the line without fault is equal, and for the two faulty lines, this voltage difference is not equal because of the current passing through each line. In lines without fault, a certain current passes, and in the faulty line, two currents enter the line from both sides. Therefore, for lines without fault dif (L), Equation (45) will be decreased and for faulty lines dif (L), Equation (45) will be incremental, but from there the goal is to optimize the objective function, so these changes are inverted and the faulty line is it will be a decrease. Figure 17 shows, for faults F1 and F2, the value of dif (L) for the line between nodes 23 and 24 and the line between nodes 78 and 79 has the lowest value, so a fault has occurred in these two lines. After this step, by identifying the faulty line, the exact location of the fault can be identified by solving Equation (47) for the faulty line.
In the following, the performance of the proposed algorithm is evaluated for different types of faults. One method to evaluate the accuracy of the algorithm in estimating the fault location is to use Equation (58) to calculate the percentage error estimation (EE) of the proposed method. Here, xl is the actual location, xe is the estimated location, and L is the length of the line. Table 1 compares the performance results of the proposed algorithm for types of faults with other methods.

Table 1.
Comparison of the results of the proposed method.
According to reference [52], it is suggested to locate faults in the distribution network using network monitoring with PMUs and the presence of DG in the network. In this method, voltage data are collected from the PMU and the fault location is obtained based on the calculation of the equivalent current vector and network impedance matrix. This method depends on the PMUs’ measurements of the network’s nodes and the DG’s connection point; the more of these devices there are in the network, the more accurate the algorithm is. In this scheme, five DGs in nodes 30, 35, 64, 151, 450, and 31 PMUs in nodes 6, 11, 16, 22, 27, 29, 32, 37, 39, 42, 46, 56, 57, 59, 63, 65, 66, 71, 75, 83, 95, 98, 100, 104, 111, 114, 150, 151, 250, 300, and 450 have been used. The maximum estimation error of this method is 3.71%, as shown in Table 1.
Reference [53] suggests an automatic fault location technique based on PMU data. The basis of the work depends on the information before and after the fault and by estimating the load current at the end of the line, using the impedance method, each line is checked in order and if the fault distance (x) is greater than the length of the line, the adjacent line is checked. Therefore, to estimate the load current, PMUs are used at the end of the line, which is installed in nodes 149, 250, 96, 85, 151, 300, and 450, respectively. In this method, the maximum estimation error is 3.85%.
Mixed-integer linear programming is used in reference [54] to pinpoint distribution network faults. By calculating the network impedance matrix, the work in this method is based on calculating the voltage changes of the nodes before and after the fault. Where PMUs are used to collect measured data at the end of the line and form an impedance matrix. Here PMUs are installed in nodes 1, 2, 4, 6, 10, 11, 12, 16, 17, 20, 22, 24, 32, 33, 250, 37, 39, 41, 43, 46, 48, 151, 56, 59, 66, 610, 96, 94, 92, 90, 88, 83, 85, 79, 75, 71, 450, 104, 107, 111, 114, and 300. The maximum estimation error in this method is 1.75%.
By comparing the proposed method with other methods such as references [52,53,54], there are obvious difference in the proposed method. However, in the proposed method, PMUs are installed in the nodes of the main branches of the network, and values measured by PMUs applying to the PSSE problem, the total information of the network nodes can be estimated before and after the fault, so in addition to reducing the number of PMUs in the network, this also allows for the estimation of the total information of the network nodes. As shown in Table 1, the maximum estimation error of the proposed method is 1.21%. In addition, the proposed method can be used for all types of faults (including short-circuit and series faults) because the fault location problem is defined as an optimization problem with a new objective function that will be able to identify the faulty section for different types of faults. The optimization problem is finally solved by a genetic algorithm in the proposed method, allowing it to simultaneously identify multiple fault locations in a maximum of 23.87 s.
Sensitivity Analysis of the Proposed Method
Various factors affect the accuracy of fault location algorithms. As shown in Figure 18a, a fault consists of three important factors: fault resistance, fault angle, and fault location. Here, the purpose of the fault location algorithm is similar to Figure 18b, which estimates the fault distance with the lowest error percentage. In this section, a sensitivity analysis is performed on the performance of the proposed algorithm for various factors including the status of PMUs, fault type, fault resistance, fault occurrence angle, and type of problem-solving algorithm. Let us suppose that in Figure 15, an F2 fault occurs for 60 different types of faults by changing the fault parameters. Table 2 shows the performance accuracy of the proposed algorithm for changes in fault resistance, fault angle, and type of fault. In this table, the EE value is the average value of these errors, as it can be seen that the EE value of the proposed algorithm has increased for high fault resistance, zero-angle fault occurrence, and three-phase faults.
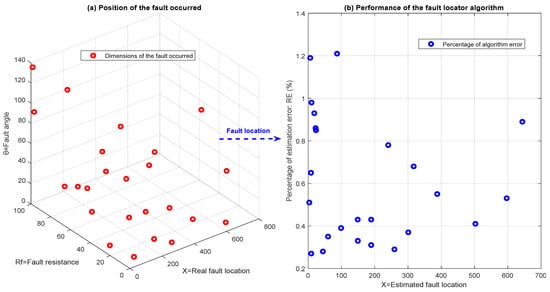
Figure 18.
Dimensions of the fault location problem.

Table 2.
Performance sensitivity analysis of the proposed algorithm for fault parameters.
Another factor influencing the fault location problem is the uncertainty in the network loading states before the fault occurs. Table 3 shows the performance of the proposed algorithm for 10% to 50% network loading states uncertainty. As shown in Table 3, network uncertainty loading states do not have much effect on the accuracy of the algorithm, since the proposed algorithm uses the measured PMU data in the PSSE problem, in practice, the results obtained from the PSSE problem are close to reality and after considering the voltage and current measurement of the nodes connected to the PMU, the changes in the network load can be estimated correctly.

Table 3.
Performance sensitivity analysis of the proposed algorithm for uncertainty in loading states.
Another factor that has a direct impact on the performance of the proposed fault location algorithm is the accuracy of measuring the PMUs installed in the network. Here, assuming a measurement error between 1% and 3%, the average EE value of the proposed algorithm is calculated. Table 4 shows the performance results of the proposed algorithm for PMU measurement error. As shown, the PMU measurement error increases the average EE value. Since the proposed algorithm before and after the fault depends on the measured PMU values, the measurement error will certainly have a direct effect on the accuracy of the fault location algorithm. The next case in Table 5 shows the effect of the number of PMUs installed on the network on the performance of the proposed algorithm. The accuracy of the algorithm decreases with decreasing the number of PMUs, and the accuracy of the algorithm increases with increasing the number of PMUs, which indicates the dependence of the algorithm on PMUs. However, it should be noted that the number of PMUs used in the IEEE 123-node distribution feeder network with the proposed algorithm is much less than other fault location algorithms due to the use of the PSSE problem.

Table 4.
Performance sensitivity analysis of the proposed algorithm for PMU measurement error.

Table 5.
Performance sensitivity analysis of the proposed algorithm for the number of PMUs installed in the network.
Finally, the problem of fault location is defined by solving with different algorithms and its performance is compared with genetic algorithms. Table 6 shows the results of different algorithms. As shown, the accuracy of the genetic algorithm is better than other algorithms, and the only drawback is its computational speed, which, of course, was able to identify the fault location for a 123-bus network in a maximum of 23.87 s, which is a good time.

Table 6.
Performance of different algorithms in solving a fault location problem.
Finally, Figure 19 shows the mean EE value for the various factors presented in Table 2 to Table 6 for comparison. As shown, the greatest impact on the EE value is due to the PMU status in the network and the type of problem-solving algorithm.
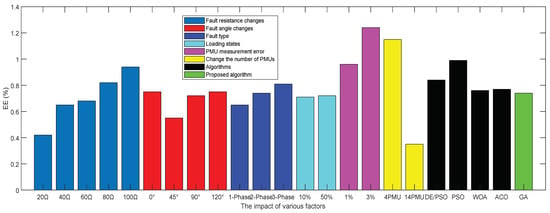
Figure 19.
Mean EE value under the influence of various factors.
In reference [51], a fault location method based on solving the optimization problem is presented, which is clearly different from the proposed method:
- In reference [51], there are weaknesses in the defined objective function, which makes the proposed method not applicable to all types of faults in the distribution network.
- Since in reference [51], the objective function was based on the calculation of voltage changes of all nodes with the impedance matrix method, it is not possible to use it for series faults. In the new article, a new objective function based on current and voltage at the beginning and end of the line is defined so that in addition to reducing the calculations and improving the accuracy of the method, it can be implemented for all types of series and short circuit faults.
- The equations defined for the objective function of reference [51] are more complicated and their implementation will be difficult for large networks. In the new article the equations are based on the feature of the traveling wave model and the relationship between the voltage and current at the beginning and end of the line is defined to simplify calculations. So there is an obvious difference between the equations in the two papers. In addition, the line model considered in the new article has been modified to improve the accuracy of the method.
- In the new article, it is possible to identify several faults simultaneously, but in reference [51], due to the type of the objective function, this is not possible, and the algorithm suffers in this case.
- In the new article, a sensitivity analysis was performed on the proposed method for the types of faults, fault resistance, fault angle, loading states, PMU measurement error, change in the number of PMUs, and algorithms, which did not exist in reference [51].
- Finally, in the new article, there was a maximum time of 23.87 s and an average error of 0.74%, and a maximum error of 1.21%, which was far better than the previous article.
5. Conclusions
In this paper, a new structure for fault location in the distribution network based on optimization problem-solving is presented. The two objective functions were established to identify the faulty area and the location of the fault using voltage variations. Here, the voltage changes across the two ends of each network line were defined as an optimization problem, so that for each line where this difference is maximized, that line will be the faulty line. The important part in this issue, however, is the extraction of voltage values from every node in the network after the fault, which in this design makes use of information collected by the PMU in the PSSE problem prior to the fault, in a way that will allow these values to be extracted by calculating the voltage drop of network lines and the value measured by PMUs. Finally, to evaluate the robustness of the proposed algorithm, a sensitivity analysis for various factors such as fault parameters, the status of PMUs, uncertainty in loading states, and the type of problem-solving algorithm was implemented on the largest IEEE distribution network. The results showed the proper performance of the proposed algorithm so that it was able to identify the fault location with a maximum time of 23.87 s, an average error of 0.74%, and a maximum error of 1.21%.
Author Contributions
Conceptualization, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; methodology, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; software, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; validation, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; formal analysis, investigation, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; resources, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; data curation, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; writing—original draft preparation, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; writing—review and editing, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; visualization, H.K.; supervision, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; project administration, M.D., W.H., H.Z.A.G., A.A.M., A.H., K.M.A. and H.K.; funding acquisition, W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data sources employed for analysis are presented in the text.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| PMU | Phasor Measurement Unit |
| GPS | Global Positioning System |
| GA | Genetic Algorithm |
| WLS | Weighted Least Square |
| KVL | Kirchhoff’s Voltage Law |
| LLS | Linear Least Square |
| MILP | Mixed Integer Linear Programming |
| PSO | Particle Swarm Optimization |
| ACO | Ant Colony Optimization |
| PSSE | Power System Status Estimation |
| DG | Distributed Generation |
| PF | Power Flow |
| DFT | Discrete Fourier Transform |
| F | Fault |
| EE | Error estimation |
| AFL | Automatic Fault Location |
| DE | Differential Evolution |
| WOA | Whale Optimization Algorithm |
| List of symbols | |
| Z | Vector of the measured variables |
| h | Vector of the nonlinear |
| σi2 | Variance |
| f(Z) | Probability density function |
| H(x) | Jacobin matrix |
| k | Iteration index |
| X | Sine quantity |
| θ | The sampling angle |
| Iij | Current between node i and j |
| Dij | Imaginary part of the current Iij |
| Rij | Line resistance between node i and j |
| B | Susceptance |
| ΔV | Line voltage drop |
| x | Location of fault |
| γ | Diffusion coefficient |
| Y | Shunt admittance |
| F | Fault point |
| VF0,+,− | Zero, positive and negative sequence fault voltage |
| x | Vector of the status variables |
| e | Vector of the measurement error |
| R | Covariance matrix |
| J(Z) | Quadratic expression function |
| g(x) | Nonlinear function |
| G(x) | Gain matrix |
| N | The number of samples |
| τ | The sampling interval |
| Cij | Real part of the current Iij |
| Vi | Voltage of node i |
| Lij | Line inductance between node i and j |
| g | Conductance |
| Vf,If | Fault voltage and current |
| ZL | Line impedance L |
| Zc | Characteristic impedances |
| L | Line length |
| Vi→j | Voltage of node i is seen from node j |
| IF0,+,− | Zero, positive and negative sequence fault current |
References
- Apostolopoulos, C.A.; Arsoniadis, C.G.; Georgilakis, P.S.; Nikolaidis, V.C. Evaluating a Fault Location Algorithm for Active Distribution Systems Utilizing Two-Point Synchronized or Unsynchronized Measurements. In Proceedings of the 2021 International Conference on Smart Energy Systems and Technologies (SEST), Vaasa, Finland, 6–8 September 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Okumus, H.; Nuroglu, F.M. A random forest-based approach for fault location detection in distribution systems. Electr. Eng. 2021, 103, 257–264. [Google Scholar] [CrossRef]
- Lin, C.; Gao, W.; Guo, M.-F. Discrete wavelet transform-based triggering method for single-phase earth fault in power distribution systems. IEEE Trans. Power Deliv. 2019, 34, 2058–2068. [Google Scholar] [CrossRef]
- Li, S.; Wang, H.; Song, L.; Wang, P.; Cui, L.; Lin, T. An adaptive data fusion strategy for fault diagnosis based on the convolutional neural network. Measurement 2020, 165, 108122. [Google Scholar] [CrossRef]
- Stolbova, I.; Backhaus, S.; Chertkov, M. Fault-induced delayed voltage recovery in a long inhomogeneous power-distribution feeder. Phys. Rev. E 2015, 91, 022812. [Google Scholar] [CrossRef] [PubMed]
- Das, C.K.; Bass, O.; Kothapalli, G.; Mahmoud, T.S.; Habibi, D. Overview of energy storage systems in distribution networks: Placement, sizing, operation, and power quality. Renew. Sustain. Energy Rev. 2018, 91, 1205–1230. [Google Scholar] [CrossRef]
- Pandakov, K.; Høidalen, H.K.; Marvik, J.I. Misoperation analysis of steady-state and transient methods on earth fault locating in compensated distribution networks. Sustain. Energy Grids Netw. 2018, 15, 34–42. [Google Scholar] [CrossRef]
- Dashtdar, M.; Dashtdar, M. Fault location in the distribution network based on scattered measurement in the network. Energy Syst. 2022, 13, 539–562. [Google Scholar] [CrossRef]
- Mirshekali, H.; Dashti, R.; Keshavarz, A.; Torabi, A.J.; Shaker, H.R. A novel fault location methodology for smart distribution networks. IEEE Trans. Smart Grid 2020, 12, 1277–1288. [Google Scholar] [CrossRef]
- Deng, F.; Zu, Y.; Mao, Y.; Zeng, X.; Li, Z.; Tang, X.; Wang, Y. A method for distribution network line selection and fault location based on a hierarchical fault monitoring and control system. Int. J. Electr. Power Energy Syst. 2020, 123, 106061. [Google Scholar] [CrossRef]
- Fang, J.; Wang, H.; Yang, F.; Wang, Y.; Yin, K.; He, J.; Lin, X. A Data-Driven Fault Location Method in Distribution Network Based on PMU Data. IEEJ Trans. Electr. Electron. Eng. 2022, 17, 325–334. [Google Scholar] [CrossRef]
- Xie, L.; Luo, L.F.; Li, Y.; Zhang, Y.; Cao, Y. A traveling wave-based fault location method employing VMD-TEO for distribution network. IEEE Trans. Power Deliv. 2019, 35, 1987–1998. [Google Scholar] [CrossRef]
- Liang, R.; Fu, G.; Zhu, X.; Xue, X. Fault location based on single terminal travelling wave analysis in radial distribution network. Int. J. Electr. Power Energy Syst. 2015, 66, 160–165. [Google Scholar] [CrossRef]
- Shi, S.; Zhu, B.; Lei, A.; Dong, X. Fault location for radial distribution network via topology and reclosure-generating traveling waves. IEEE Trans. Smart Grid 2019, 10, 6404–6413. [Google Scholar] [CrossRef]
- Zhao, J.; Hou, H.; Gao, Y.; Huang, Y.; Gao, S.; Lou, J. Single-phase ground fault location method for distribution network based on traveling wave time-frequency characteristics. Electr. Power Syst. Res. 2020, 186, 106401. [Google Scholar]
- Majidi, M.; Arabali, A.; Etezadi-Amoli, M. Fault location in distribution networks by compressive sensing. IEEE Trans. Power Deliv. 2014, 30, 1761–1769. [Google Scholar] [CrossRef]
- Perez, R.; Vásquez, C.; Viloria, A. An intelligent strategy for faults location in distribution networks with distributed generation. J. Intell. Fuzzy Syst. 2019, 36, 1627–1637. [Google Scholar] [CrossRef]
- Keshavarz, A.; Dashti, R.; Deljoo, M.; Shaker, H.R. Fault location in distribution networks based on SVM and impedance-based method using online databank generation. Neural Comput. Appl. 2022, 34, 2375–2391. [Google Scholar] [CrossRef]
- Dzafic, I.; Jabr, R.A.; Henselmeyer, S.; Donlagic, T. Fault location in distribution networks through graph marking. IEEE Trans. Smart Grid 2016, 9, 1345–1353. [Google Scholar] [CrossRef]
- Azeroual, M.; Boujoudar, Y.; Bhagat, K.; El Iysaouy, L.; Aljarbouh, A.; Knyazkov, A.; Fayaz, M.; Qureshi, M.S.; Rabbi, F.; EL Markhi, H. Fault location and detection techniques in power distribution systems with distributed generation: Kenitra City (Morocco) as a case study. Electr. Power Syst. Res. 2022, 209, 108026. [Google Scholar] [CrossRef]
- Dashtdar, M.; Esmaeilbeig, M.; Najafi, M.; Bushehri, M.E.N. Fault location in the transmission network using artificial neural network. Autom. Control Comput. Sci. 2020, 54, 39–51. [Google Scholar] [CrossRef]
- Dashtdar, M.; Dashti, R.; Shaker, H.R. Distribution network fault section identification and fault location using artificial neural network. In Proceedings of the 2018 5th International Conference on Electrical and Electronic Engineering (ICEEE), Istanbul, Turkey, 3–5 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 273–278. [Google Scholar]
- Aslan, Y.; Yağan, Y.E. Artificial neural-network-based fault location for power distribution lines using the frequency spectra of fault data. Electr. Eng. 2017, 99, 301–311. [Google Scholar] [CrossRef]
- Adewole, A.C.; Tzoneva, R.; Behardien, S. Distribution network fault section identification and fault location using wavelet entropy and neural networks. Appl. Soft Comput. 2016, 46, 296–306. [Google Scholar] [CrossRef]
- Gholami, M.; Abbaspour, A.; Moeini-Aghtaie, M.; Fotuhi-Firuzabad, M.; Lehtonen, M. Detecting the location of short-circuit faults in active distribution network using PMU-based state estimation. IEEE Trans. Smart Grid 2019, 11, 1396–1406. [Google Scholar] [CrossRef]
- Li, L.; Gao, H.; Cong, W.; Yuan, T. Location method of single line-to-ground faults in low-resistance grounded distribution networks based on ratio of zero-sequence admittance. Int. J. Electr. Power Energy Syst. 2023, 146, 108777. [Google Scholar] [CrossRef]
- Dashtdar, M.; Sarada, K.; Hosseinimoghadam, S.M.S.; Kalyan, C.H.N.S.; Venkateswarlu, A.N.; Goud, B.S.; Reddy, C.H.R.; Belkhier, Y.; Bajaj, M.; Reddy, B.N. Faulted Section Identification and Fault Location in Power Network Based on Histogram Analysis of Three-phase Current and Voltage Modulated. J. Electr. Eng. Technol. 2022, 17, 2631–2647. [Google Scholar] [CrossRef]
- Sheta, A.N.; Abdulsalam, G.M.; Eladl, A.A. Online tracking of fault location in distribution systems based on PMUs data and iterative support detection. Int. J. Electr. Power Energy Syst. 2021, 128, 106793. [Google Scholar] [CrossRef]
- Mirshekali, H.; Dashti, R.; Keshavarz, A.; Shaker, H.R. Machine Learning-Based Fault Location for Smart Distribution Networks Equipped with Micro-PMU. Sensors 2022, 22, 945. [Google Scholar] [CrossRef] [PubMed]
- Khaleghi, A.; Sadegh, M.O.; Ahsaee, M.G. Permanent Fault Location in Distribution System Using Phasor Measurement Units (PMU) in Phase Domain. Int. J. Electr. Comput. Eng. 2018, 8, 2709–2720. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Khodayar, M.E. Graph-based faulted line identification using micro-PMU data in distribution systems. IEEE Trans. Smart Grid 2020, 11, 3982–3992. [Google Scholar] [CrossRef]
- Chen, X.; Jiao, Z. Accurate fault location method of distribution network with limited number of PMUs. In Proceedings of the 2018 China International Conference on Electricity Distribution (CICED), Tianjin, China, 17–19 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1503–1507. [Google Scholar]
- Zanni, L.; Derviškadić, A.; Pignati, M.; Xu, C.; Romano, P.; Cherkaoui, R.; Abur, A.; Paolone, M. PMU-based linear state estimation of lausanne subtransmission network: Experimental validation. Electr. Power Syst. Res. 2020, 189, 106649. [Google Scholar] [CrossRef]
- Li, Q.; Xu, Y.; Ren, C.; Zhao, J. A hybrid data-driven method for online power system dynamic security assessment with incomplete PMU measurements. In Proceedings of the 2019 IEEE Power & Energy Society General Meeting (PESGM), Atlanta, GA, USA, 4–8 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Mishra, B.; Thakur, S.S.; Mallick, S.; Panigrahi, C.K. Optimal Placement of PMU for Fast Robust Power System Dynamic State Estimation using UKF–GBDT Technique. J. Circuits Syst. Comput. 2022, 31, 2250068. [Google Scholar] [CrossRef]
- Zhao, J.; Gómez-Expósito, A.; Netto, M.; Mili, L.; Abur, A.; Terzija, V.; Kamwa, I.; Pal, B.; Singh, A.K.; Qi, J.; et al. Power system dynamic state estimation: Motivations, definitions, methodologies, and future work. IEEE Trans. Power Syst. 2019, 34, 3188–3198. [Google Scholar] [CrossRef]
- Li, J.; Wang, X.; Ren, X.; Zhang, Y.; Zhang, F. Augmented State Estimation Method for Fault Location Based on On-line Parameter Identification of PMU Measurement Data. In Proceedings of the 2018 IEEE 2nd International Electrical and Energy Conference (CIEEC), Beijing, China, 4–6 November 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 105–109. [Google Scholar]
- Mirshekali, H.; Dashti, R.; Handrup, K.; Shaker, H.R. Real Fault Location in a Distribution Network Using Smart Feeder Meter Data. Energies 2021, 14, 3242. [Google Scholar] [CrossRef]
- Di Manno, M.; Varilone, P.; Verde, P.; De Santis, M.; Di Perna, C.; Salemme, M. User friendly smart distributed measurement system for monitoring and assessing the electrical power quality. In Proceedings of the 2015 AEIT International Annual Conference (AEIT), Naples, Italy, 14–16 October 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Brahma, S.M. Fault location in power distribution system with penetration of distributed generation. IEEE Trans. Power Deliv. 2011, 26, 1545–1553. [Google Scholar] [CrossRef]
- De Santis, M.; Noce, C.; Varilone, P.; Verde, P. Analysis of the origin of measured voltage sags in interconnected networks. Electr. Power Syst. Res. 2018, 154, 391–400. [Google Scholar] [CrossRef]
- Kazemi, A.; Mohamed, A.; Shareef, H.; Zayandehroodi, H. A review of power quality monitor placement methods in transmission and distribution systems. Przegląd Elektrotechniczny 2013, 3, 185–188. [Google Scholar]
- Kazemi, A.; Mohamed, A.; Shareef, H.; Zayandehroodi, H. Review of voltage sag source identification methods for power quality diagnosis. Przegląd Elektrotechniczny 2013, 89, 143–146. [Google Scholar]
- Ahmed, A.S.; Attia, M.A.; Hamed, N.M.; Abdelaziz, A.Y. Modern optimization algorithms for fault location estimation in power systems. Eng. Sci. Technol. Int. J. 2017, 20, 1475–1485. [Google Scholar]
- Pereira RA, F.; Da Silva LG, W.; Mantovani JR, S. PMUs optimized allocation using a tabu search algorithm for fault location in electric power distribution system. In Proceedings of the 2004 IEEE/PES Transmision and Distribution Conference and Exposition: Latin America (IEEE Cat. No. 04EX956), Sao Paulo, Brazil, 8–11 November 2004; IEEE: Piscataway, NJ, USA, 2004; pp. 143–148. [Google Scholar]
- Li, Y.; Ye, H.; Chen, Z. Binary particle swarm optimization algorithm with gene translocation for distribution network fault location. In Proceedings of the 2012 Spring Congress on Engineering and Technology, Xi’an, China, 27–30 May 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–4. [Google Scholar]
- Hao, Y.; Wang, Q.; Li, Y.; Song, W. An intelligent algorithm for fault location on VSC-HVDC system. Int. J. Electr. Power Energy Syst. 2018, 94, 116–123. [Google Scholar] [CrossRef]
- Dashtdar, M.; Hosseinimoghadam, S.M.S.; Dashtdar, M. Fault location in the distribution network based on power system status estimation with smart meters data. Int. J. Emerg. Electr. Power Syst. 2021, 22, 129–147. [Google Scholar] [CrossRef]
- Madani, R.; Ashraphijuo, M.; Lavaei, J.; Ross, B. Power system state estimation with a limited number of measurements. In 2016 IEEE 55th Conference on Decision and Control (CDC); IEEE: Las Vegas, NV, USA, 2016. [Google Scholar]
- Bhela, S.; Kekatos, V.; Veeramachaneni, S. Enhancing observability in distribution grids using smart meter data. IEEE Trans. Smart Grid 2017, 9, 5953–5961. [Google Scholar] [CrossRef]
- Dashtdar, M.; Bajaj, M.; Hosseinimoghadam, S.M.S.; Mérshêkáér, H. Fault location in distribution network by solving the optimization problem using genetic algorithm based on the calculating voltage changes. Soft Comput. 2022, 26, 8757–8783. [Google Scholar] [CrossRef]
- Sun, H.; Yi, H.; Zhuo, F.; Du, X.; Yang, G. Precise fault location in distribution networks based on optimal monitor allocation. IEEE Trans. Power Deliv. 2019, 35, 1788–1799. [Google Scholar] [CrossRef]
- Lee, J. Automatic fault location on distribution networks using synchronized voltage phasor measurement units. In ASME Power Conference; American Society of Mechanical Engineers: New York, NY, USA, 2014; Volume 46094, p. V002T14A008. [Google Scholar]
- Alqahtani, M.; Miao, Z.; Fan, L. Mixed integer programming formulation for fault identification based on MicroPMUs. Int. Trans. Electr. Energy Syst. 2021, 31, e12949. [Google Scholar] [CrossRef]
- Zhou, Q.; Zheng, B.; Wang, C.; Zhao, J.; Wang, Y. Fault location for distribution networks with distributed generation sources using a hybrid DE/PSO algorithm. In Proceedings of the 2013 IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–5. [Google Scholar]
- Nashawati, E.; Garcia, R.; Rosenberger, T. Using synchrophasor for fault location identification. In Proceedings of the 2012 65th Annual Conference for Protective Relay Engineers, College Station, TX, USA, 2–5 April 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 14–21. [Google Scholar]
- Ahmed, A.S.; Attia, M.A.; Hamed, N.M.; Abdelaziz, A.Y. Comparison between genetic algorithm and whale optimization algorithm in fault location estimation in power systems. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 631–637. [Google Scholar]
- Chen, L.; Xiao, C.; Li, X.; Wang, Z.; Huo, S. A seismic fault recognition method based on ant colony optimization. J. Appl. Geophys. 2018, 152, 1–8. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).