Abstract
A collision with clearance causes obvious nonlinearity in structures, and dynamic response analysis plays an important role in predicting the mechanical performance of the structure. The general form of the nonlinear dynamic equation of a structure and the clearance modeling method are introduced, and the clearance-caused nonlinear term is expressed by nonlinear impact forces. Different clearance collision models of local nonlinear structures are presented. The relationships between different impact forces and clearances are analyzed by two rigid sphere models. The solution methods of the nonlinear dynamic equation are compared by a vibro-impact response, such as the Newmark-β method combined with the Newton–Raphson method, generalized α method and precise integration method. The single degree of freedom model is adopted to compare the efficiency of the different numerical integration algorithms. Taking the beam structure model as a case study, the accurate nonlinear collision model with clearance is established by using the impact force model with high accuracy, and the accuracy of the model is verified by comparing the reference model with the numerical model.
1. Introduction
Due to a collision with clearance, the vibration of a structure will be significantly aggravated. The accuracy and working efficiency will be reduced [1,2,3]. The nonlinear force generated by the clearance will affect the vibration of the structure [4,5]. It is of critical significance to study the nonlinear characteristics of a collision.
Clearances in structures have gradually attracted attention, and are always represented as a contact force model [6,7,8,9,10,11]. Askari et al. [12] established a nonlinear contact model in a closed form by using multiple sets of spring-damping elements to equal the spherical hinge contact. Considering the changes in contact surfaces, Li et al. [13] established a comprehensive wear prediction method for multi-clearance joint planar mechanical systems and used the improved nonlinear contact force model to evaluate the internal forces of joints. Venanzi et al. [14] introduced a method to evaluate the influence of clearance on the precision of a kinematic pair. Flores et al. [15] made a comprehensive analysis of the continuous contact force model of soft materials in multi-body dynamics. Wang et al. [16] established a contact force model suitable for a spherical hinge by substituting the neutral stiffness coefficient of the Flores model with the nonlinear stiffness coefficient. Tian et al. [17] gave a comprehensive review of analytical, numerical and experimental methods for multi-body mechanical systems with clearances.
The influence of clearances on the dynamic characteristics of structures has been studied widely [18,19,20,21,22,23]. Erkaya et al. [24,25] studied the influence of a clearance hinge on manipulator kinematics and dynamics based on the Lankarani–Nikravesh nonlinear contact force model. By the means of numerical simulation and experiment, the influence of clearance on mechanism vibration and mechanism noise were studied. Flores [26] studied the hinge with clearance, and the results show that the larger the friction is in the collision process, the more obvious the nonlinear behavior of the structure is. At the same time, a lot of numerical simulations and experimental analyses have been carried out on the impact dynamics of the clearance structure, but the representation form of clearance is complex and the calculation is difficult. On this basis, it is necessary to select an appropriate clearance model and efficient dynamic response analysis method to obtain the accurate nonlinear dynamic response of structures with clearance. Alves et al. [27] considered the model based on Hertz contact theory and added a damping term to conduct a comparative study of the contact force model.
Numerical integration methods are adopted to obtain the response of the structure. Liu et al. [28] proposed a new time-domain dynamic Galerkin method, using the shape function to approximate three parameters of dynamic load, kernel function response and measured structural response, and then using the shape function as a weighting function to build a forward model. Fan et al. [29] proposed a dynamic load identification algorithm combining Newmark-β and the self-filtering algorithm, which solved the problem of the large iteration error in the calculation process. Simsek et al. [30] used Newmark-β and the direct iteration method to solve nonlinear motion equations of functionally graded beams. Sun et al. [31] proposed a Wavelet Galerkin scheme-based precise integration time-domain method to decrease the dispersion error.
The fundamental method to solve the clearance problem is to accurately model the structure with nonlinear clearance and accurately describe the dynamic characteristics of the structure with nonlinear clearance. Then, the characteristics of the clearance can be reasonably used to guide the design and manufacture processes. Vibro-impact response analysis of a collision with local clearance can be assessed in three steps:
- Step 1:
- Establish the dynamic equation of the nonlinear structure with local clearance.
- Step 2:
- Select the description method of clearance and the model of nonlinear impact force.
- Step 3:
- Select the solving method of the nonlinear dynamic equations.
In this paper, the method of describing the local clearance, the impact force model and the solving method of the nonlinear dynamic equations are introduced. The accuracy of the response solving by the impact force model and the computational efficiency of the solving method are compared and analyzed through the single degree of freedom model and beam structure model.
2. Vibro-Impact Response Analysis
2.1. Nonlinear Dynamics Equations of Structures with Clearances
The dynamic equation of the structure without collision can be expressed as
where x is the displacement matrix, is the velocity matrix, is the acceleration matrix, M is the mass matrix of the structure, C is the damping matrix, K is the stiffness matrix and F is the external force matrix.
Introducing the impact force into the dynamic equation, we can obtain
where Fn is the contact force matrix. In the dynamic equation of structure with clearance, the contact force vector Fn determines the dynamic features in the process of collision. Different clearance description methods produce different impact force models. It is very important to compare different clearance description methods to select the appropriate impact force model for accurately describing the dynamic characteristics of structures with clearance.
There are many methods to characterize the dynamic characteristics of clearance structures, including the constraint description method and the force description method [32]. The constraint description method is divided into the massless bar method and the spring-damping method, as shown in Figure 1a,b. The responses of these two methods can be obtained by using Equation (1). The massless bar method does not consider the elastic deformation at contact and the clearance is equivalent to a massless rigid bar. This method is calculated simply, but it ignores the problems of elastic deformation and energy loss, so the results are not accurate and can only be used as a reference. The spring-damping method connects the impact points of clearance structures with springs and dampers to characterize their impact behavior. Compared with the massless bar method, this method considers the elastic deformation and energy loss but ignores the energy conversion between colliders.
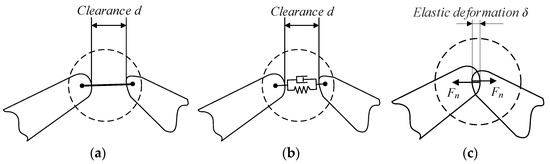
Figure 1.
Description methods of clearance: (a) massless bar method; (b) spring-damping method; (c) force description method.
The force description method mainly uses impact force to represent the collision behavior of structures with clearance after contact, as shown in Figure 1c. The response of this method can be obtained by using Equation (2). The method transforms the geometry constraints into force constraints and simulates the collision of two objects at the contact position when two colliders contact, if the motion state and energy loss simulated by the collision force are consistent with the actual situation. Therefore, the selection of the collision force is the key point of this method. When the two colliders are separated, the collision force is removed and the motion state at the separation time is retained for subsequent analysis and calculation.
The analysis of the three clearance simulation methods shows that, in the massless method and the spring-damping method, the clearance is replaced by equivalent components and the characteristics of the clearance are simulated as much as possible, which is an equivalent method. The force description method is more practical. The impact force between composite structures is a function of the elastic deformation of the contact surface, and the energy loss in the collision process is taken into account. The following focuses on the characterization of the impact force.
2.2. Model of Nonlinear Impact Force
In this section, the characteristics of commonly used contact impact force models are compared to provide a reference for the subsequent selection of appropriate impact force models for nonlinear dynamics calculations. Due to the continuity of several contact force models and the universality of some parameters, the common parameters are explained first, which will not be repeated in the subsequent formula. The parameters of impact force are shown in Table 1.

Table 1.
Parameters of impact force.
- (1)
- Hertz contact force model
The Hertz [33] contact force model is a kind of nonlinear contact force model. The contact deformation of the collision body represented by Hertz is a completely elastic deformation, which is mainly applicable to the quasi-static contact problem of an elastic body. The contact force formula is
For the centripetal collision of two rigid balls, K can be obtained by the following expression
where and are the radius, and are Poisson’s ratio, and are the elastic modulus.
- (2)
- Hunt–Crossley (H-C) contact force model
The Hertz contact force model is widely used and has a good effect on low-speed collisions and uncoordinated contacts. However, the Hertz model does not take into account the energy loss of the collider in the collision process. Therefore, Hunt and Crossley proposed an improved contact collision force model based on Hertz contact theory and considering the damping in the collision process [34], which can be expressed as follows
where b is the damping coefficient, which is determined by the recovery coefficient , and the recovery coefficient is determined by the material parameters. Considering the case of center collision, the relationship between and b can be written as Equation (6)
- (3)
- Lankarani–Nikravesh (L–N) contact force model [35]
Building on the work of Hunt and Crossley, Lankarani and Nikravesh added material damping to the modeling of structures with gaps. It is assumed that material damping is the main cause of energy loss in the process of contact collision, and a new impact force model was established based on the assumption that the relative velocity is low. The model takes into account the material properties and impact velocity. Chen et al. [36] established the normal force and tangential force of the clearance joint based on the Lankarani–Nikravesh contact force model, and studied the influence of the clearance value and crank driving speed on dynamic behavior, including the slider motion response, contact force, crank driving torque, etc. Bifurcation diagrams with different clearance values and different crank driving speeds were also studied. The contact force formula of this model is
where D is the damping coefficient of the collider material, η is the viscous damping factor and is the elastic deformation force in the contact collision process and is consistent with the elastic deformation force in Hertz theory. is the damping force, which constitutes the contact collision process and represents the energy loss behavior of the collider in the processing of the collision.
The energy loss in the collision process can also be obtained by integrating the contact force along the loop of the viscous ring, as shown in Equation (8)
- (4)
- Gonthier contact force model
Gonthier et al. pointed out that the above three collision force models were established based on point contact theory, and would not be applicable if the contact area was larger than the contact body. Therefore, a new viscous damping factor model suitable for a large contact area during a collision was proposed, and the expression of the collision force is as follows [37]
In the formula, can be obtained by the following expression
where χ is the internal damping coefficient, and the dimensionless coefficient d ≈ 1 − ce2.
- (5)
- Flores contact force model [38]
Flores et al. studied the contact collision between an elastic body and a rigid body; they assumed that the energy loss in the collision process was caused by the internal damping of the material and regarded the collision–recovery process as a single degree of freedom dynamic system, and they established another expression of energy loss
where δmax is the maximum elastic deformation; then the internal damping coefficient χ in the collision process can be obtained
Then the Flores impact force model can be obtained
In order to compare and analyze the characteristics of the nonlinear impact force models, a single impact of two rigid balls with different diameters is taken as a case for numerical simulation. It is assumed that the spheres are made of the same material, with elastic modulus E = 207 GPa, Poisson ratio μ = 0.3, initial relative impact velocity = 0.3 m/s, material recovery coefficient ce = 0.5, ball mass m = 0.04 kg, radius R1 = 10 mm for sphere 1 and R2 = 9.9 mm for sphere 2. Each of these values is substituted into the formula in Table 2. The relation between the elastic deformation of the ball and the impact force is shown in Figure 2.

Table 2.
Expressions of different impact force models.
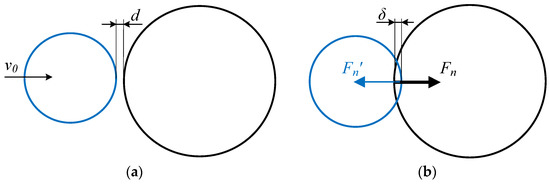
Figure 2.
Schematic diagram of single collision with clearance structure. (a) Before the collision. (b) State of collision.
According to the Figure 3, under the same contact material, initial impact velocity and recovery coefficient, there are viscous rings that appear in the simulation results of all nonlinear impact force models except the Hertz model. The results of the Hunt–Crossley model and the Lankarani–Nikravesh model are close to each other, and the results of the Gonthier model and the Flores model are basically the same. In order to further compare the characteristics of the above nonlinear impact force models, Figure 4 presents the schematic diagram of the relationship between the elastic deformation of the slider and the impact velocity.
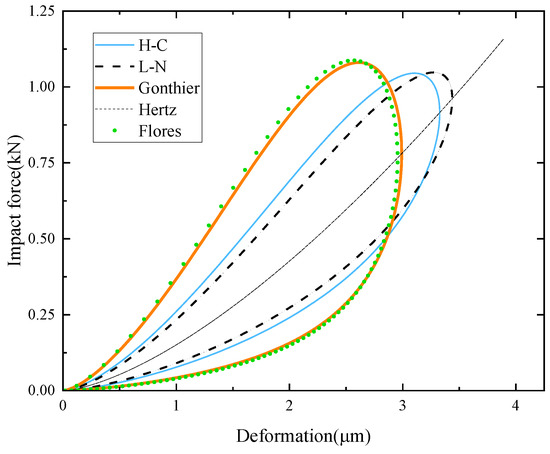
Figure 3.
Diagram of relation between the elastic deformation and the impact force.
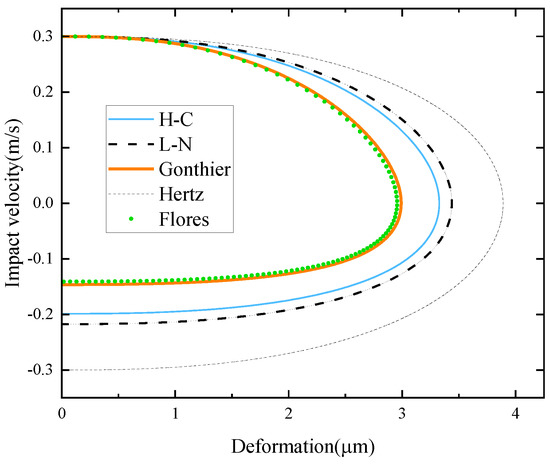
Figure 4.
Diagram of the elastic deformation and the impact velocity.
As can be seen from Figure 4, since energy loss in the collision process is not considered, the separation velocity in the Hertz model does not change and is still 0.3 m/s. The separation velocity of the Hunt–Crossley model and the Lankarani–Nikravesh model is close to 0.2 m/s. The separation velocity of the Gonthier model and the Flores model is 0.15 m/s, which is completely consistent with the recovery coefficient. This indicates that the determination of the damping coefficient in these two models is more accurate than other models.
2.3. Solving Method of Nonlinear Dynamic Equations
When the impact force is expressed as the nonlinear term, many numerical solutions with different accuracies and efficiencies have been developed since most nonlinear dynamic equations do not have analytical solutions. If two of displacement, velocity and acceleration can be found at a given time, the third can be obtained. According to the different assumptions of acceleration and velocity, the multi-step integration method is formed, such as the Newmark-β method [39,40], generalized α method and precise integration method. The theories of several methods are introduced below to provide parameters for the subsequent comparison of these numerical algorithms.
- (1)
- Newmark-β method combined with Newton-Raphson method [41]
Newmark-β directly discretizes the dynamics equation into an algebraic equation through the difference to solve it. The following assumptions are made in the calculation
where is the displacement at tn time, is the velocity at tn time, is the acceleration at tn time, Δt = tn+1 − tn, two parameters γ and β are introduced, and are usually required
To make sure that the computation is unconditionally stable. The calculation formula is further derived below.
The acceleration can be eliminated from Equations (14) and (15), and the velocity expression at tn+1 can be obtained
The acceleration expression at tn+1 can be obtained from Equation (15)
Substitute Equations (14) and (15) into the equation of motion at tn+1
With as an unknown quantity, the equation is sorted out and the following equation is obtained
where:
The displacement was solved by Equation (20), and the result was substituted into Equation (18) to obtain the acceleration at tn+1. Then, the speed at tn+1 could be calculated by using Equation (14). At this point, the motion state at tn+1 has been calculated, and they can be used as the starting values to calculate the motion state at the next moment, and so on.
The above method has high accuracy in the process of solving linear problems, but there is a cumulative error in solving the nonlinear dynamic response. The Newton–Raphson method is introduced to calculate the displacement at tn+1. When there is a nonlinear term in the structure, Equation (21) can be changed to
where fnl is the nonlinear term and xn+1 is taken as the variable. Equation (20) can be written as follows
If the Ψn+1 first-order is continuously differentiable in Equation (23), let the initial approximation obtained by the Newmark-β method be , and the k-th iteration approximation obtained by the Newton–Raphson method be , and Ψn+1 is the Taylor expansion and the higher-order term is dropped
is obtained by calculating xn+1 in Equation (24)
where KT is the tangent stiffness matrix, and the expression is
The above formula can be used to iteratively solve the exact solution at each point in time and control the error
where e is the upper limit of error, and the iteration is stopped after reaching it.
- (2)
- Generalized α method
On the basis of the Newmark method, the generalized α method [42] introduces a new algorithm vector parameter a to obtain the expressions of displacement and velocity
In the above formula, vector a satisfies the following relation
The selection of each parameter is as follows
Compared with Newmark-β, the generalized α method has second-order convergence and better stability.
- (3)
- Precise Adams Multi-step method (precise integration method)
For nonlinear dynamics Equation (2), the precise integration method [43] introduces dual variables
Then the dynamics equation can be written as
where q is the generalized displacement.
The right end term of Equation (32) can be separated into linear and nonlinear parts in form, which can be described as
For the solution of the nonlinear dynamic equation described by Equation (34), Duhamel integration is used to describe
where
The solution on segment [tk, tk+1] can be derived from the above formula
Equation (34) is expressed by Duhamel integration, and introduces and .
In the recursive solution of the above equation, the second term (Duhamel integration term) at the right end is the integral containing the matrix exponential function, and the properties of the matrix exponential function should be fully used in processing.
In the segment t ∈ [tk, tk+1], the nonlinear term f(x, t) is approximated by an m-degree polynomial
where [f0,k, f1,k, … ] denotes the coefficient of the approximate polynomial in section k, and Equation (38) can be expressed as
where
where Φ(η) is the state transfer matrix and Φm(η) can be called the Duhamel integration matrix of external force.
In addition to using the information of the current section [tk, tk+1], we can also use the information of the previous section [tk−2, tk+1], [tk−1, tk] for the polynomial approximation of f(x,t); the most commonly used is the Adams linear multi-step method.
Using tk−2, tk−1 and tk as interpolation points, approximate Lagrange polynomials of f(x,t) are obtained
The unified form of the Adams multi-step method can be derived by substituting the above Equation (42) into Equation (40):
where Φ0(η), …, Φ−m(η) is determined by the Duhamel integration matrix.
3. Nonlinear Dynamic Response Analysis of Structures with Clearance
3.1. Single Degree of Freedom Model
In order to study the difference and effectiveness of the different numerical integration methods for nonlinear dynamic response analysis, the projectile launching system is simplified into a single degree of freedom impact vibration model with bilateral clearances, as shown in Figure 5. In this simplified model, the elastic modulus of the concentrated mass block is 207 GPa, the Poisson ratio is 0.3, the initial relative movement speed is 8 m/s, the material recovery coefficient is 0.9, the mass of the concentrated mass block is m0 = 100 kg and the initial installation clearance is 5 mm.
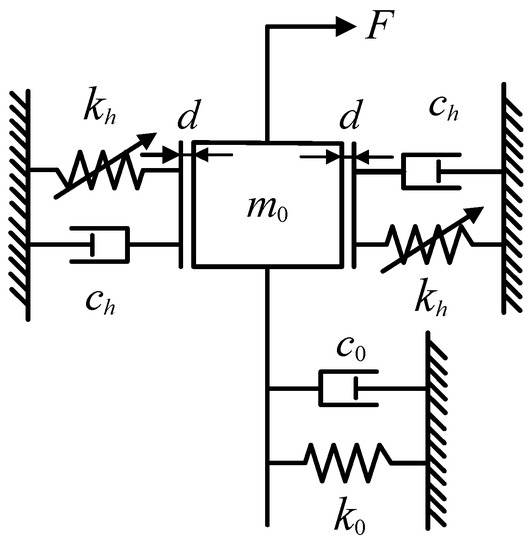
Figure 5.
Impact vibration model of structure with bilateral clearances, where kh is the nonlinear stiffness during collision, k0 is the linear stiffness of the structure, ch is the nonlinear damping during collision, c0 is the linear damping of the structure, d is the initial installation clearance and m0 is the mass block of the concentrated mass.
In this simulation example, the Lankarani–Nikravesh contact force model is used to simulate the collision process between clearance, and the above three numerical integration algorithms are used for the numerical simulation calculation, and the displacement and velocity curves of the slider with time are obtained, respectively. The displacement time curve of the mass block is shown in Figure 6.
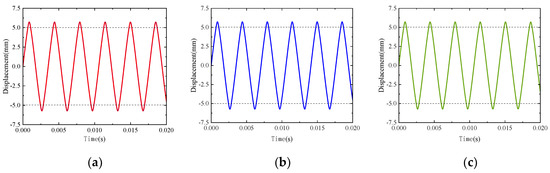
Figure 6.
Displacement time curve of the mass block: (a) Newmark-β method combined with Newton–Raphson method; (b) generalized α method; (c) precise integration method.
As shown in Figure 6, the abilities of the three kinds of numerical integration method to obtain the displacement results are basically identical. When the displacement of the mass block is greater than the initial installation clearance of 5 mm, the mass block collides with the outer wall. The displacement continues to increase until the velocity is equal to zero. The displacement reaches a maximum of about 6 mm, and then the mass moves in the opposite direction. Until the displacement value is less than 5 mm, the mass block is separated from the outer wall. The collision process is over and the free motion state is entered. Outside the black dashed line is the phase of contact and collision between the concentrated mass block and the outer wall. The black dashed line is the free movement stage of the concentrated mass block that is not in collision with the outer wall.
As shown in Figure 7, the results of the mass velocity obtained by the three numerical integration methods are basically the same. According to the corresponding time in the displacement curve, the corresponding motion state of the velocity curve can be found. It can be seen from Figure 7 that in the contact collision stage, the impact force generated by the collision makes the velocity decrease fast. The integral curves of the above three methods for solving the nonlinear vibration response are consistent with the law of motion. In order to further study the computational efficiency of the three integration methods, Table 3 shows the computation time of the different numerical integration algorithms when the simulation time is 0.02 s.
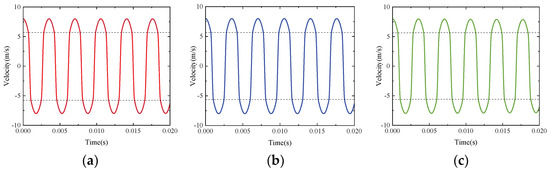
Figure 7.
Time curve of the mass block: (a) Newmark-β method combined with Newton–Raphson method; (b) generalized α method; (c) precise integration method.

Table 3.
The computational efficiency of different numerical integration algorithms at 0.02 s simulation time.
As can be seen from Table 3, the Newmark-β method combined with the Newton–Raphson method has the highest computational efficiency, while the precise integration method has the lowest computational efficiency. The computation time of the precise integration method is 19 times that of the Newmark-β method. Since the model is a single degree of freedom model and the computational burden is small, there is no significant difference in the computational efficiency between the Newmark-β method combined with the Newton–Raphson method and the generalized α method. In conclusion, the Newmark-β method combined with the Newton–Raphson method was planned to be used for numerical integration solution in the subsequent expansion of the multi-degree of freedom problem so as to ensure the computational accuracy and efficiency.
Different impact forces previously studied were substituted into the system, and the Newmark-β method combined with the Newton–Raphson method was used to calculate the displacement response of the system. The results are shown in Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13.
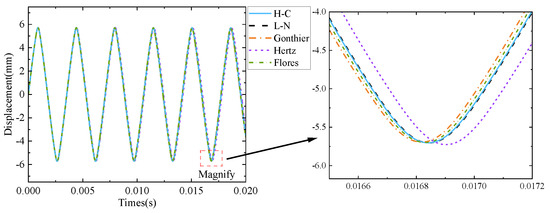
Figure 8.
Displacement response under different impact forces (recovery coefficient is 0.9).
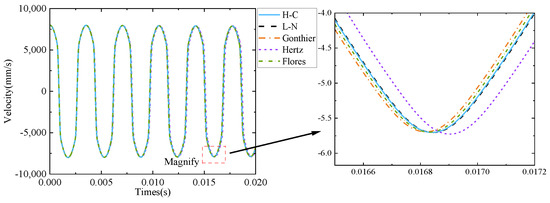
Figure 9.
Velocity response under different impact forces (recovery coefficient is 0.9).
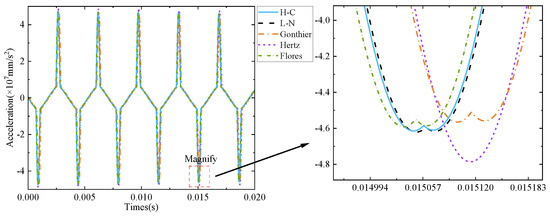
Figure 10.
Acceleration response under different impact forces (recovery coefficient is 0.9).
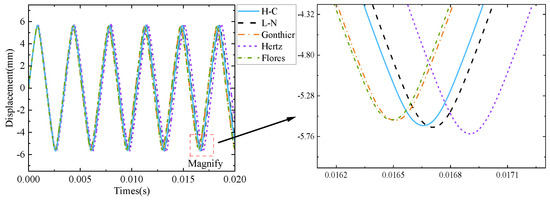
Figure 11.
Displacement response under different impact forces (recovery coefficient is 0.5).
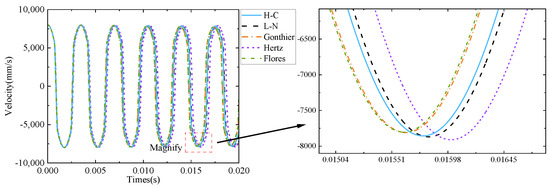
Figure 12.
Velocity response under different impact forces (recovery coefficient is 0.5).
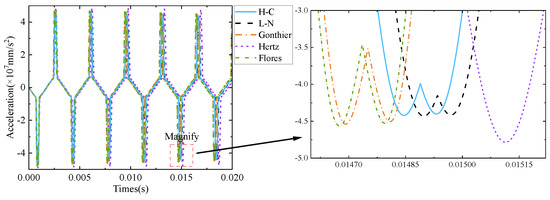
Figure 13.
Acceleration response under different impact forces (recovery coefficient is 0.5).
It can be seen from Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 that the Hertz contact force model has the largest elastic deformation, which is caused by the minimum energy loss in the collision process without considering the energy loss in the Hertz contact force model. Compared with Figure 4, it can be seen that the amount of elastic deformation is positively correlated with the change in velocity in the collision process.
3.2. Multiple Degrees of Freedom Model
In this section, a hollow shaft structure with some nodes containing clearance contact is adopted to compare the above modeling method and numerical integration algorithm. The engineering background is the engine and body of a missile, and its structural schematic diagram is shown in Figure 14. In the figure, the relative distance of the chute has been enlarged for clarity. The top, middle and tail of the hollow shaft are, respectively, provided with two symmetrical slide blocks. The hollow shaft is installed on the chute through the slide block. Only the clearance between the slide block and the chute in the x direction is considered. The geometric dimensions are as follows: hollow shaft with diameter of 190 mm and length of 1000 mm, wall thickness of 5 mm, clearance between chute and slide block of 3 mm, ignoring the influence of gravity. The beam structure finite element model obtained by simplifying the hollow shaft structure is shown in Figure 15.
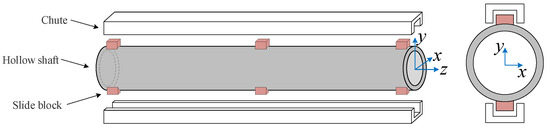
Figure 14.
Hollow shaft structure model with impact clearance.
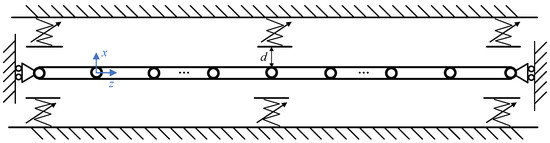
Figure 15.
Beam element modeling.
The beam element is used to simulate the hollow shaft structure, and the contact clearances are added at both ends and the middle joints. When the vibration displacement of the beam element exceeds the clearance d, it is fed back to the beam element in the form of the nonlinear impact force. Structural modeling of the hollow shaft, as the reference model, is established by ABAQUS. The shell element is used for modeling of the hollow shaft, and the solid element is used for the modeling of the joints and chute, as shown in Figure 16. Joints are distributed at both ends and in the middle of the hollow shaft. The material density was 34.41 g/cm3, the elastic modulus was 207 GPa and the Poisson ratio was 0.3. There are 42 nodes in the hollow shaft section and 62 nodes in the axial direction, for a total of 2064 nodes.
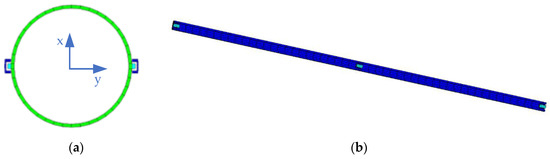
Figure 16.
Finite element model: (a) cutaway view of finite element model; (b) slider distribution position of finite element model.
The equivalent physical parameters of the beam structure were obtained according to the material and structure size of the hollow shaft, and the M, C and K can be calculated by the reference model established by ABAQUS. At the same time, the numerical model by MATLAB and the reference model by ABAQUS were used to analyze the natural characteristics in free–free state. The comparison results of the first three order natural frequencies of the two methods are given, as shown in Table 4. The analysis shows that the first three natural frequencies and modes of vibration based on the numerical method and ABAQUS are basically consistent, thus verifying the correctness of the numerical modal analysis solution program.

Table 4.
Modal frequency analysis results of simplified model.
After mode matching, nonlinear response analysis was carried out. The axial freedom of the hollow shaft structure was constrained and the radial excitation force F = 100 sin(20πt) was applied to each node of the hollow shaft in the same direction. In order to achieve the same constraint effect as the beam structure, all the nodes of the chute were constrained with all degrees of freedom, and only the impact force was considered when the simulated slider was in contact with the rigid surface. At the same time, the axial degrees of freedom were constrained at both ends of the shaft to ensure the vertical collision between the slider and the chute.
Figure 17 shows the vibration response analysis results based on the numerical model and the reference model under sinusoidal excitation. The results of the nonlinear vibration response based on the numerical model and the reference model are consistent as a whole. The main differences are as follows: the amplitude of each rebound after a collision is inconsistent, and the amplitude of the acceleration response is different to some extent. The main reason lies in the inconsistent contact stiffness in the Hertz contact model solved by ABAQUS and MATLAB. The reference model established by ABAQUS has more nodes and is more consistent with the response under actual working conditions. The numerical model established by MATLAB is simplified from the reference model, and the number of nodes is less, which is a relatively idealized structure.
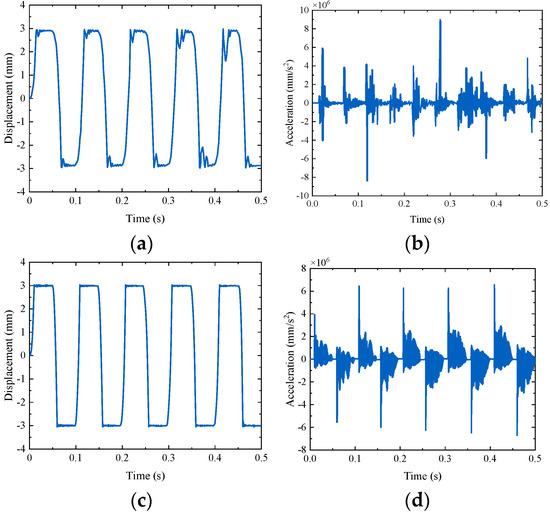
Figure 17.
Dynamic response analysis results of simplified model: (a) displacement in the reference model; (b) acceleration in the reference model; (c) displacement in the numerical model; (d) acceleration in the numerical model.
4. Conclusions
In this paper, the modeling method of a nonlinear structure with clearance and the solution method of the nonlinear vibration response are presented, which are verified by the single degree of freedom model and the beam structure model. The nonlinear term of the nonlinear dynamic equation is exemplified by the impact force model, and the nonlinear characteristics of different collision models are compared. The numerical solution algorithm of the nonlinear dynamic response analysis is studied. The accuracy and computational efficiency of the Newmark-β method combined with the Newton–Raphson method, generalized α method and precise integration method are compared. Under the condition of ensuring the calculation accuracy, the Newmark-β method combined with the Newton–Raphson method has the highest computational efficiency. Then, the results of the numerical model and the reference model of a hollow shaft structure are compared; both the displacement and velocity of the structure are basically the same, and the magnitude of the acceleration response is basically the same, which provides a method for calculating the dynamic response of a nonlinear structure. Other nonlinear impact force models and corresponding nonlinear solution methods will be studied in the subsequent work by building complex structures.
Author Contributions
Conceptualization, D.J.; funding acquisition, D.J.; methodology, Y.T., Q.L. and Y.L.; resources, Y.T.; software, Y.X.; validation, Y.X., Q.L. and Y.L.; writing—original draft, Y.X.; writing—review and editing, Y.T., Q.L., Y.L., D.Z. and D.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 11602112), the Natural Science Research Project of Higher Education in Jiangsu Province (20KJB460003), the QingLan Project, the National Natural Science Foundation of China (52005100), the Natural Science Foundation of Jiangsu Province (BK20190324), the Jiangsu Association for Science and Technology Young Talents Lifting Project (TJ-2022-043), the Fundamental Research Funds for the Central Universities and the Zhishan Youth Scholar Program of SEU (2242021R41169).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that there is no conflict of interest regarding the publication of this paper.
References
- Banerjee, A.; Chanda, A.; Das, R. Historical Origin and Recent Development on Normal Directional Impact Models for Rigid Body Contact Simulation: A Critical Review. Arch. Comput. Methods Eng. 2017, 24, 397–422. [Google Scholar] [CrossRef]
- Li, X.; Yao, Z.; Wu, R. Modeling and analysis of stick-slip motion in a linear piezoelectric ultrasonic motor considering ultrasonic oscillation effect. Int. J. Mech. Sci. 2016, 107, 215–224. [Google Scholar] [CrossRef]
- Paez Chavez, J.; Pavlovskaia, E.; Wiercigroch, M. Bifurcation analysis of a piecewise-linear impact oscillator with drift. Nonlinear Dyn. 2014, 77, 213–227. [Google Scholar] [CrossRef]
- Yaqubi, S.; Dardel, M.; Daniali, H.M.; Ghasemi, M.H. Modeling and control of crank-slider mechanism with multiple clearance joints. Multibody Syst. Dyn. 2016, 36, 143–167. [Google Scholar] [CrossRef]
- Machado, M.; Moreira, P.; Flores, P.; Lankarani, H.M. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mech. Mach. Theory 2012, 53, 99–121. [Google Scholar] [CrossRef]
- Wen, G.; Yin, S.; Xu, H.; Zhang, S.; Lv, Z. Analysis of grazing bifurcation from periodic motion to quasi-periodic motion in impact-damper systems. Chaos Solitons Fractals 2016, 83, 112–118. [Google Scholar] [CrossRef]
- Jiang, H.; Chong, A.S.E.; Ueda, Y.; Wiercigroch, M. Grazing-induced bifurcations bifurcations in impact oscillators with elastic and rigid constraints. Int. J. Mech. Sci. 2017, 127, 204–214. [Google Scholar] [CrossRef]
- Nordmark, A.B.; Piiroinen, P.T. Simulation and stability analysis of impacting systems with complete chattering. Nonlinear Dyn. 2009, 58, 85–106. [Google Scholar] [CrossRef]
- Wagg, D.J. Rising phenomena and the multi-sliding bifurcation in a two-degree of freedom impact oscillator. Chaos Solitons Fractals 2004, 22, 541–548. [Google Scholar] [CrossRef]
- Sharkawy, A.-N.; Mostfa, A.A. Neural networks’ design and training for safe human-robot cooperation. J. King Saud Univ. -Eng. Sci. 2021, 1–15. [Google Scholar]
- Wu, B.; Wu, Y.; Liu, M.; Liu, J.; Jiang, D.; Ma, S.; Yan, B.; Lu, Y. Mechanical Behavior of Human Cancellous Bone in Alveolar Bone under Uniaxial Compression and Creep Tests. Materials 2022, 15, 5912. [Google Scholar] [CrossRef] [PubMed]
- Askari, E. Mathematical models for characterizing non-Hertzian contacts. Appl. Math. Model. 2021, 90, 432–447. [Google Scholar] [CrossRef]
- Li, B.; Wang, M.S.; Gantes, C.J.; Tan, U.X. Modeling and simulation for wear prediction in planar mechanical systems with multiple clearance joints. Nonlinear Dyn. 2022, 108, 887–910. [Google Scholar] [CrossRef]
- Venanzi, S.; Parenti-Castelli, V. A new technique for clearance influence analysis in spatial mechanisms. J. Mech. Des. 2005, 127, 446–455. [Google Scholar] [CrossRef]
- Flores, P.; Machado, M.; Silva, M.T.; Martins, J.M. On the continuous contact force models for soft materials in multibody dynamics. Multibody Syst. Dyn. 2011, 25, 357–375. [Google Scholar] [CrossRef]
- Wang, G.X.; Liu, H.Z.; Deng, P.S. Dynamics Analysis of Spatial Multibody System With Spherical Joint Wear. J. Tribol. Trans. ASME 2015, 137, 021605. [Google Scholar] [CrossRef]
- Tian, Q.; Flores, P.; Lankarani, H.M. A comprehensive survey of the analytical, numerical and experimental methodologies for dynamics of multibody mechanical systems with clearance or imperfect joints. Mech. Mach. Theory 2018, 122, 1–57. [Google Scholar] [CrossRef]
- Koshy, C.S.; Flores, P.; Lankarani, H.M. Study of the effect of contact force model on the dynamic response of mechanical systems with dry clearance joints: Computational and experimental approaches. Nonlinear Dyn. 2013, 73, 325–338. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X.; Chen, Z. Dynamic analysis of a 3-(R) under bar RR parallel mechanism with multiple clearance joints. Mech. Mach. Theory 2014, 78, 105–115. [Google Scholar] [CrossRef]
- Marques, F.; Isaac, F.; Dourado, N.; Flores, P. An enhanced formulation to model spatial revolute joints with radial and axial clearances. Mech. Mach. Theory 2017, 116, 123–144. [Google Scholar] [CrossRef]
- Skrinjar, L.; Slavic, J.; Boltezar, M. A review of continuous contact-force models in multibody dynamics. Int. J. Mech. Sci. 2018, 145, 171–187. [Google Scholar] [CrossRef]
- Ma, J.; Chen, G.; Ji, L.; Qian, L.; Dong, S. A general methodology to establish the contact force model for complex contacting surfaces. Mech. Syst. Signal Process. 2020, 140, 106678. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, L.; Zhao, J.; Hang, X.; Zhou, H. Effective excitation conditions for the intense motion of the ginkgo seed-stem system during mechanical vibration harvesting. Biosyst. Eng. 2022, 215, 239–248. [Google Scholar] [CrossRef]
- Erkaya, S.; Uzmay, I. Experimental investigation of joint clearance effects on the dynamics of a slider-crank mechanism. Multibody Syst. Dyn. 2010, 24, 81–102. [Google Scholar] [CrossRef]
- Erkaya, S.; Uzmay, I. Investigation on effect of joint clearance on dynamics of four-bar mechanism. Nonlinear Dyn. 2009, 58, 179–198. [Google Scholar] [CrossRef]
- Flores, P. A parametric study on the dynamic response of planar multibody systems with multiple clearance joints. Nonlinear Dyn. 2010, 61, 633–653. [Google Scholar] [CrossRef]
- Alves, J.; Peixinho, N.; da Silva, M.T.; Flores, P.; Lankarani, H.M. A comparative study of the viscoelastic constitutive models for frictionless contact interfaces in solids. Mech. Mach. Theory 2015, 85, 172–188. [Google Scholar] [CrossRef]
- Liu, J.; Meng, X.; Jiang, C.; Han, X.; Zhang, D. Time-domain Galerkin method for dynamic load identification. Int. J. Numer. Methods Eng. 2016, 105, 620–640. [Google Scholar] [CrossRef]
- Fan, Y.; Zhao, C.; Yu, H.; Wen, B. Dynamic load identification algorithm based on Newmark-beta and self-filtering. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2020, 234, 96–107. [Google Scholar]
- Simsek, M. Non-linear vibration analysis of a functionally graded Timoshenko beam under action of a moving harmonic load. Compos. Struct. 2010, 92, 2532–2546. [Google Scholar] [CrossRef]
- Sun, G.; Ma, X.; Bai, Z. A Low Dispersion Precise Integration Time Domain Method Based on Wavelet Galerkin Scheme. IEEE Microw. Wirel. Compon. Lett. 2010, 20, 651–653. [Google Scholar] [CrossRef]
- Flores, P.; Ambrosio, J.; Claro, J.C.P.; Lankarani, H.M.; Koshy, C.S. A study on dynamics of mechanical systems including joints with clearance and lubrication. Mech. Mach. Theory 2006, 41, 247–261. [Google Scholar] [CrossRef]
- Guo, Y.; Mi, H.; Habibi, M. Electromechanical energy absorption, resonance frequency, and low-velocity impact analysis of the piezoelectric doubly curved system. Mech. Syst. Signal Process. 2021, 157, 107723. [Google Scholar] [CrossRef]
- Haddadi, A.; Hashtrudi-Zaad, K. Real-Time Identification of Hunt-Crossley Dynamic Models of Contact Environments. IEEE Trans. Robot. 2012, 28, 555–566. [Google Scholar] [CrossRef]
- Ma, J.; Qian, L. Modeling and simulation of planar multibody systems considering multiple revolute clearance joints. Nonlinear Dyn. 2017, 90, 1907–1940. [Google Scholar] [CrossRef]
- Chen, X.; Shuai, J.; Yu, D.; Wang, Q. Dynamics analysis of 2-DOF complex planar mechanical system with joint clearance and flexible links. Nonlinear Dyn. 2018, 93, 1009–1034. [Google Scholar] [CrossRef]
- Li, B.; Wang, S.-M.; Yuan, R.; Xue, X.-Z.; Zhi, C.-J. Dynamic characteristics of planar linear array deployable structure based on scissor-like element with joint clearance using a new mixed contact force model. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2016, 230, 3161–3174. [Google Scholar] [CrossRef]
- Hou, Y.-l.; Deng, Y.-j.; Zeng, D.-X. Dynamic modelling and properties analysis of 3RSR parallel mechanism considering spherical joint clearance and wear. J. Cent. South Univ. 2021, 28, 712–727. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Free and forced vibrations of shear deformable functionally graded porous beams. Int. J. Mech. Sci. 2016, 108, 14–22. [Google Scholar] [CrossRef]
- Arani, A.G.; Kiani, F.; Afshari, H. Free and forced vibration analysis of laminated functionally graded CNT-reinforced composite cylindrical panels. J. Sandw. Struct. Mater. 2021, 23, 255–278. [Google Scholar] [CrossRef]
- Cao, Z.; Fei, Q.; Jiang, D.; Zhu, R.; Jin, H. Sensitivity Analysis of Nonlinear Transient Response Based on Perturbation in the Complex Domain. J. Comput. Nonlinear Dyn. 2021, 16, 011001. [Google Scholar] [CrossRef]
- Erlicher, S.; Bonaventura, L.; Bursi, O.S. The analysis of the Generalized-alpha method for non-linear dynamic problems. Comput. Mech. 2002, 28, 83–104. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Deng, Z.C. An improved precise integration method for nonlinear dynamic system. Mech. Res. Commun. 2003, 30, 33–38. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).