Abstract
In recent decades, quasi-zero stiffness (QZS) vibration isolation systems with nonlinear characteristics have aroused widespread attention and strong research interest due to their enormous potential in low-frequency vibration isolation. This work comprehensively reviews recent research on QZS vibration isolators with a focus on the principle, structural design, and vibration isolation performance of various types of QZS vibration isolators. The negative-stiffness mechanism falls into two categories by different realization methods: passive and active/semi-active negative-stiffness mechanisms. Representative design, performance analysis, and practical application are elaborated for each category. The results show that passive vibration isolation systems have excellent low-frequency vibration isolation performance under specific payload and design parameters, whereas active/semi-active vibration isolation systems can better adapt to different environmental conditions. Finally, the development trends and challenges of QZS vibration isolators are summarized, and the solved and unsolved problems are highlighted. This review aims to give a comprehensive understanding of the QZS vibration isolation mechanism. It also provides guidance on designing new QZS vibration isolators for improving their vibration isolation performance and engineering applicability.
1. Introduction
In recent years, as ultra-precision manufacturing and measurement, aerospace detection, delivery, and weapons/equipment are developing toward being able to work under extreme working conditions or achieve performance limits, low-frequency and ultra-low-frequency vibration isolation are urgently needed, and meanwhile, the structure and performance of vibration isolators also face new challenges. According to linear vibration theory, a linear vibration isolation system can effectively isolate vibration only when the excitation frequency exceeds times the natural frequency of the system [1]. Vibration isolation performance can be improved by reducing the natural frequency of the system, and this can be realized by reducing the stiffness of the system or increasing the payload mass of the system, but the stability of the vibration isolation system will be weakened [1,2]. To overcome the contradiction between the stiffness and static displacement of linear vibration isolators, a nonlinear vibration isolator with quasi-zero stiffness (QZS) has been proposed [3,4]. Such vibration isolators realize the QZS characteristic by combining the positive-stiffness mechanism and the negative-stiffness mechanism. The unique nonlinear characteristics enable them to effectively isolate low-frequency vibrations while providing sufficient load-carrying capacity and maintaining system stability.
Negative stiffness is the key to QZS vibration isolators, which was first proposed by Molyneux [5] in 1957. As the negative-stiffness mechanism itself has no carrying capacity, it will undergo significant deformation under any load [6,7]. That is why the negative-stiffness mechanism is combined with the positive-stiffness mechanism to compensate for the instability caused by negative stiffness in the design. This composite structure is conducive to the formation of a nonlinear force-displacement relationship, thus striking a balance between effective vibration isolation and small static deflection in the linear system. With specific structural parameters, nonlinear characteristics allows the composite structure to possess low-dynamic–high-static-stiffness characteristics.
When designing a QZS vibration isolator, the main idea is to introduce a negative-stiffness mechanism to offset the positive stiffness of elastic elements. This is realized by using passive and active/semi-active negative-stiffness mechanisms. The passive mechanism mainly includes mechanical springs [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33], prebuckled beams [34,35,36,37,38,39], geometrically nonlinear structures [40,41,42,43,44,45,46,47,48,49,50,51,52,53,54], magnetic structures [55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84], bio-inspired structures [85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108], and composite structures [109,110,111,112,113,114,115,116,117,118,119]. Mechanical negative-stiffness mechanisms feature a simple principle but prominent nonlinearity and contact friction, small working range, and limited performance. For magnetic negative-stiffness mechanisms, specially arranged magnets are used to make the non-contact force exhibit the negative-stiffness characteristic, which can be easily controlled. The negative-stiffness characteristic of bionic and composite structures is achieved by designing specific composite materials and structures. Active/semi-active negative-stiffness structures [120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136] can better adapt to different environmental conditions, and the negative-stiffness characteristic of the vibration control force is exhibited based on displacement feedback. With high accuracy of sensors and actuators, the negative-stiffness characteristic will be accurately controllable, so the optimal QZS effect can be obtained theoretically. The realization and application of QZS vibration isolators will be discussed in the following parts of this paper.
Over the past two decades, system and mechanism design of QZS vibration isolators have attracted extensive attention, with abundant results obtained. Therefore, it is significant to systematically summarize these research results. The statistical trend of QZS vibration isolator-related publications published at home and abroad from 2003 to 2022 is presented in Figure 1, reflecting that research in this field is heating up year by year.
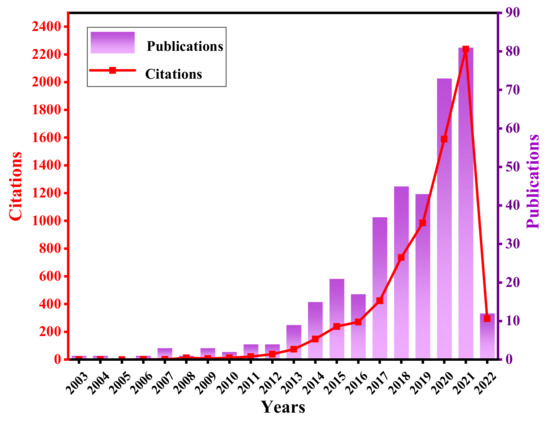
Figure 1.
Trend of QZS vibration isolator-related research at home and abroad in the most recent 20 years from Web of Science.
Nowadays, some emerging QZS isolators have been widely used in the protection of precision equipment and the improvement of product comfort. However, the theoretical system and design principals of QZS vibration isolators are yet to be investigated in detail. This review systematically summarizes, analyzes, and compares the existing research on design principles, structures, applications, and vibration isolation performance from the perspective of mechanics and vibration isolation mechanisms, with the aim of providing insights into the design and development of new QZS vibration isolators. In addition, several potential development directions are introduced, and problems that need to be considered in their applications are emphasized. This paper is mainly divided into five sections. Section 2 overviews the basic principle of QZS vibration isolation, including the concept, realization mode and dynamic characteristics. Section 3 briefly summarizes the basic theories of QZS vibration isolation, proposes the realization route of QZS vibration isolation, and divides the QZS vibration isolation mechanism into two categories based on whether there is control in the system. Section 4 covers QZS vibration isolators with passive negative-stiffness mechanisms. According to the different materials and structures used, negative-stiffness mechanisms fall into six types, including mechanical springs, prebuckled beams, geometrically nonlinear structures, magnetic structures, bio-inspired structures, and composite structures. In Section 5, based on the controller position in the system, the active/semi-active vibration isolators are divided into two categories, and some attempts to introduce active/semi-active control into QZS structures are summarized. Finally, this paper summarizes the development prospects and recommends research directions in this field.
2. Basic Principle of QZS Vibration Isolation: An Overview
2.1. Concept of Quasi-Zero Stiffness
The stiffness is generally defined as the rate of change of the deformation caused by the load on the elastic element, namely, . When the load increases with the increasing deformation, the stiffness is positive; when the load decreases with the increasing deformation, the stiffness is negative; and when the load does not change with the changing deformation, the stiffness is zero. The concept of quasi-zero stiffness (QZS) [137] was proposed by Russian scholar P. M. Alabuzhev in his work in 1989. Generally, the negative-stiffness element is connected in parallel with the positive-stiffness element to achieve quasi-zero stiffness, which also overcomes the instability of the negative-stiffness element [138]. As shown in Figure 2, for springs connected in parallel, the calculation formulas of total force and total stiffness are given by:
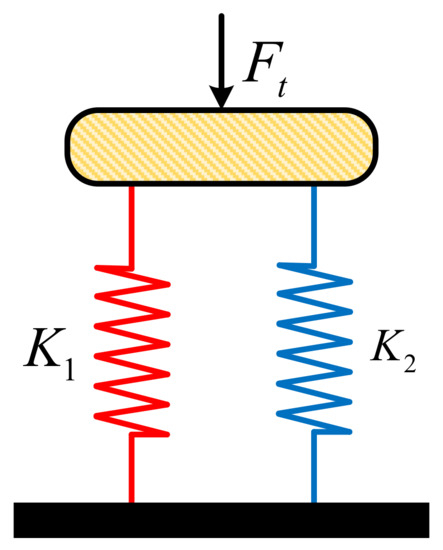
Figure 2.
Schematic diagram of parallel connection of springs.
For a spring mechanism comprising a negative-stiffness spring connected in parallel with a positive-stiffness spring, the quasi-zero stiffness, negative stiffness, or positive stiffness can be realized theoretically by changing the values of and , and the total stiffness is always less than the stiffness of the positive-stiffness element.
2.2. Principle of QZS Vibration Isolator
Figure 3 shows the principle of a quasi-zero stiffness isolator. As can be seen from Figure 3a, in the negative-stiffness region of the negative-stiffness element, the total stiffness of the system after parallel connection is less than that of the positive-stiffness element. Although the total stiffness of the system is reduced, the QZS system has greater load capacity compared with the positive-stiffness element. The total force of the QZS system represented by the solid line is nonlinear, and its stiffness changes with displacement, featuring high static stiffness and low dynamic stiffness. High static stiffness can help maintain sufficient load capacity in static state and prevent large displacement of the system, thus reducing the possibility of overturning of the main structure. Low dynamic stiffness can help effectively isolate low-frequency vibrations. As shown in Figure 3b, the stiffness of the positive-stiffness element is , and a negative-stiffness element with a stiffness of is connected with it in parallel in the neighborhood at the system static equilibrium position 0, so the total stiffness of the system is . or is adjusted to the point , so that when the system suffers micro-amplitude vibrations in the neighborhood of the static equilibrium position , the dynamic stiffness of the system is determined by the joint action of the positive- and negative-stiffness elements, whose value is less than that of the positive-stiffness element. The static stiffness is only determined by the positive stiffness . In this way, the contradiction between low natural frequency and stability is well solved, and the load capacity of the system is ensured.
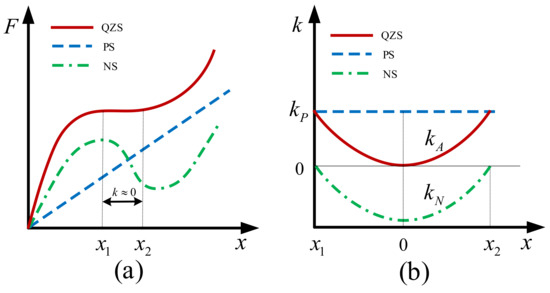
Figure 3.
Principle of QZS vibration isolator: (a) Force-displacement relationship; (b) Stiffness-displacement relationship.
2.3. Vibration Isolation Characteristics of QZS Vibration Isolator
2.3.1. Vibration Transmissibility
As one of the key criteria of vibration isolation, vibration transmissibility can be divided into force transmissibility and displacement transmissibility. The former is defined as the ratio of the amplitude of the force transmitted to the base to the amplitude of the excitation force, and the latter is defined as the ratio of the displacement transmitted to the object of vibration isolation to the excitation displacement [14]. The vibration transmissibility of the system can be obtained from Equation (2):
where is the frequency ratio, and is the damping ratio.
According to Equation (2), when , and decreases with the increasing . Because the frequency ratio of the QZS system is greater than that of the positive-stiffness element, the transmissibility of the system is further reduced. Since decreases with the decreasing natural frequency , increases, which is helpful to suppress the resonance within the system.
The vibration transmissibility of the linear system is related to the frequency ratio and damping ratio of the system, as shown in Figure 4a. If the system is expected to work in the effective vibration isolation region, the frequency ratio needs to exceed . Otherwise, the system will be in the amplification region, especially around the resonance region (). QZS vibration isolators not only overcome the problem of reducing natural frequency by reducing load capacity or increasing deformation when using a single positive-stiffness mechanism in the traditional method, but also enable the system to obtain a lower natural frequency. QZS isolators have the nonlinear force-displacement characteristic, and such non-linearity is valuable to the system compared with linearity in the traditional method. In addition, for the linear vibration isolation system, the force transmission rate and displacement transmission rate are equal quantitatively. However, for the nonlinear vibration isolation system, they are not identical. The expressions of force and displacement transmissibility of the nonlinear system varies, and are related to the degree of non-linearity, damping ratio, and excitation amplitude [36,40]. The force and displacement transfer rate are completely consistent at the high frequency, but at the low frequency, the displacement transfer rate curve has a greater degree of bending than the force transfer rate when the jump frequency is consistent.
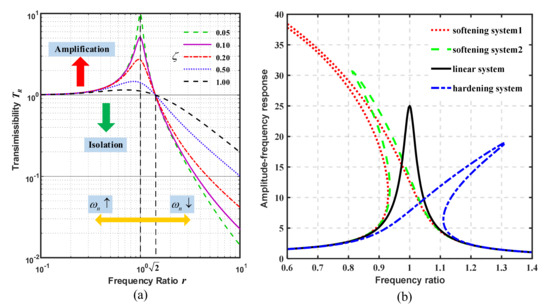
Figure 4.
Response curves: (a) Transmissibility; (b) Amplitude-frequency response.
2.3.2. Amplitude-Frequency Response Curves and Frequency Jump
The nonlinear characteristic leads to the bending of the amplitude-frequency response curves of QZS isolators [139]. As shown in Figure 4b, the softening system curves bends to the left, indicating the resonance frequency decreases but a large response is produced; the response of the hardening systems is smaller but the resonance frequency is higher. Therefore, low-frequency small-amplitude excitation is suitable for softening systems, and high-frequency large-amplitude excitation is suitable for hardening systems. In addition, the amplitude-frequency response curves have two sections, where the jump phenomena are seen. As there are many solutions in the range of jump-up frequencies and jump-down frequencies, jump-up and jump-down phenomena occur. Brennan et al. [140] investigated the jump-up and jump-down phenomena of the Duffing oscillator in detail using the harmonic balance method and disturbance method, and proposed expressions to determine the jump-up and jump-down frequencies of the softening and hardening Duffing oscillators, as well as the conditions for the occurrence of the jump phenomena.
3. Design and Realization of QZS Vibration Isolators
The basic concepts of linear and nonlinear vibration isolation are shown in Figure 5. In the linear vibration isolation system, equivalent mass , damping , and stiffness are constants. Their motion can be described by a linear differential equation:
where is the relative displacement between the block of mass and the base, and and represent their absolute displacement.
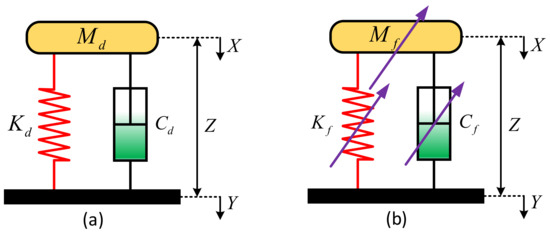
Figure 5.
Schematic diagram of vibration isolation systems: (a) Linear vibration isolation system; (b) Nonlinear vibration isolation system.
The inertia force, damping force, and restoring force in the linear system are directly proportional to the relative acceleration, velocity, and displacement, respectively. However, the linear vibration isolation system cannot effectively isolate low-frequency vibrations, as large vibration isolation bandwidth and high carrying capacity are often incompatible [2]. Ensuring effective vibration isolation in a wide frequency range while maintaining sufficient static load capacity has always been a huge challenge. To reach a balance between the stiffness and static displacement of linear vibration isolation systems, researchers have developed various forms of nonlinear vibration isolators. The dynamic equations of most nonlinear vibration isolation systems can be given by:
where is the nonlinear inertial force, is the nonlinear damping force, and is the nonlinear restoring force.
Different from linear vibration isolation systems, nonlinear vibration isolation systems exhibit excellent characteristics in terms of inertia force and damping force or restoring force. Ref. [3] systematically studied and developed the basic concepts, realization criteria, and basic nonlinear characteristics of nonlinear vibration isolators and concluded that appropriate nonlinearity is conducive to improving the vibration isolation performance of vibration isolators. Therefore, the QZS vibration isolator, as a popular nonlinear vibration isolator, has attracted increasing attention in recent years due to its unique nonlinear characteristics. Researchers have designed various types of QZS vibration isolators with different structural materials. Varying design methods eventually lead to differences in the characteristics of vibration isolators, as shown in Figure 6. Generally, the main design method for QZS vibration isolators is to introduce a negative-stiffness mechanism to counteract the positive stiffness of the elastic element. This is mainly realized by using passive negative-stiffness mechanisms (including mechanical springs, prebuckled beams, geometrically nonlinear structures, magnetic structures, and composite structures) and active negative-stiffness mechanisms (active/semi-active control):
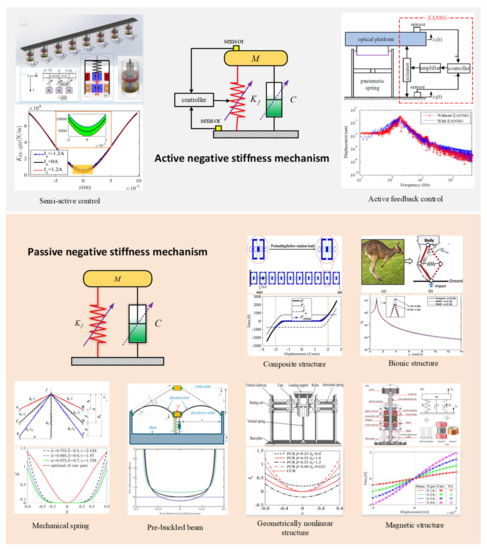
Figure 6.
Overview of QZS vibration isolation systems: realization methods and characteristic differences. Wang and Zhao et al. [127,131] proposed a vibration isolator with active negative-stiffness mechanism. Figures adapted with permission from Ref. [127]. Copyright 2020, copyright Wang, K. Zhao et al. [8,9], Liu et al. [36], Zuo et al. [52] Yuan [77], Dai et al. [85] and Zhou et al. [116,117] used vibration isolators with the proposed six types of passive negative-stiffness mechanisms. Figures adapted with permission from Refs. [9,36,52,77,85,116]. Copyright 2021/2013/2022/2020/2018/2020, copyright Zhao, F./Liu, X./Zuo, S./Yuan, S./Dai, H./Cai, C.
- (1)
- Passive negative-stiffness mechanism: the design of this type of QZS vibration isolator focuses on the balanced matching of restoring force and zero stiffness. How positive- and negative-stiffness mechanisms maintain motion stability was deeply explored first, and then a QZS structure with variable stiffness was proposed. The desired QZS characteristics can be easily obtained by designing different optimal parameter combinations, and improvement design can be carried out according to the requirements for external loads and excitation range. In addition, QZS vibration isolators not only have a vibration isolation frequency bandwidth much larger than the traditional counterparts, but also have a lower transmissivity. Therefore, QZS isolators can be applied to low-frequency large-amplitude excitation or low-frequency small-amplitude excitation and perform better in vibration attenuation efficiency and attenuation range (isolating lower excitation frequencies).
- (2)
- Active negative-stiffness mechanism: multi-source vibrations are ubiquitous in mechanical equipment and building structures. It is often through the introduction of active control to ensure the adaptability and good vibration isolation performance of the vibration isolation system. After in-depth investigation of the actual QZS vibration isolation system, the influence of different physical parameters (excitation frequency, payload mass, or displacement) on the dynamic stiffness of the system can be obtained, and practical needs can be met by introducing appropriate control devices and methods.
Recent developments of QZS vibration isolation systems are presented in Figure 6. Table 1 summarizes some current studies in this field, including application scenarios, negative-stiffness mechanisms, and vibration isolation performance of such systems.

Table 1.
QZS vibration isolators by different realization methods.
Figure 7 shows the whole process of research on QZS vibration isolators from structural design, to model simplification, to verification and application. The good isolation effects of the positive- and negative-stiffness composite structure on low-frequency vibrations provides rich design ideas for the design of QZS vibration isolators. Reasonable simplification is needed for structural design so as to facilitate subsequent design improvement and engineering realization. Static and dynamic analyses based on physical models are employed to explain the composite structure’s vibration isolation mechanism. Finally, the equivalent theoretical model is verified and modified experimentally. In addition, combining the QZS structure with control theory can expand the applications of QZS vibration isolators.
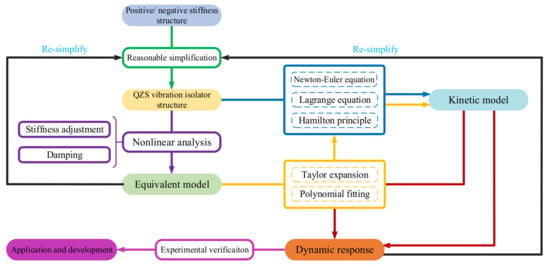
Figure 7.
Process of research on QZS vibration isolation systems: design and analysis.
4. Passive QZS Vibration Isolator
In the decades after Molyneux proposed the three-spring QZS isolator, researchers have proposed many types of passive QZS vibration isolators [3]. The six main types are mechanical springs, prebuckled beams, geometrically nonlinear structures, magnetic structures, bio-inspired structures, and composite structures. Passive QZS vibration isolators are usually designed to solve the vibration problem of a single mass object. In most cases, Equation (4) can be expressed as:
where the variable stiffness is usually realized by the joint action of positive- and negative-stiffness structures. In the actual realization, the stiffness can be adjusted through different geometric layouts. The nonlinear stiffness comes from the nonlinear relationship between the deformation in the working direction of the vibration isolator and the deformation of the elastic element inside.
Generally, to analytically solve the dynamic equation, polynomial curve fitting or Taylor-series expansion is applied to the improved harmonic balance method [141]. The nonlinear restoring force can be written as a polynomial:
where the coefficient is related to the structural parameters. For QZS vibration isolators, the design and adjustment of the negative-stiffness structure is the focus, namely, various coefficients in the restoring force may change with different designed negative-stiffness structures. However, it is important to note that nonlinear damping will inevitably be introduced in the stiffness design, which is usually caused by friction at the joint and is useful to suppress the resonance peak. Therefore, the influence of damping should also be a consideration in the process of dynamic modeling.
4.1. Mechanical Spring
Molyneux proposed a three-spring QZS isolator [5] in 1957, which is regarded as the earliest QZS vibration isolation device, whose negative stiffness is provided by two identical oblique mechanical springs, and positive stiffness by a vertical coil spring. Its dynamic stiffness and carrying capacity can meet the vibration isolation requirements of various isolation equipment. Moreover, the high-static–low-dynamic stiffness of the device opens up a new research direction for low-frequency vibration isolation.
Figure 8 shows the structure and vibration isolation performance of four typical QZS vibration isolators using mechanical springs, which are improved based on the design theory of the three-spring vibration isolator. Some representative applications and experimental prototypes of these QZS isolators are shown in Figure 9. For the purpose of easy manufacture and assemble, rods and different types of springs are usually selected for various designs. According to different improvement forms, mechanical spring negative-stiffness structures can be divided into four types, multi-spring structure, special spring structure, sliding block-rod structure, and origami structure. The restoring force of each isolator structure is provided by multiple linear springs, but their relationship is no longer a simple linear one. The motion displacement of the isolator in the vertical direction is the same, but due to different improvement methods, there are differences in linear spring deformation, and the nonlinear relationship between deformations is finally reflected in the reaction force in the vertical direction.
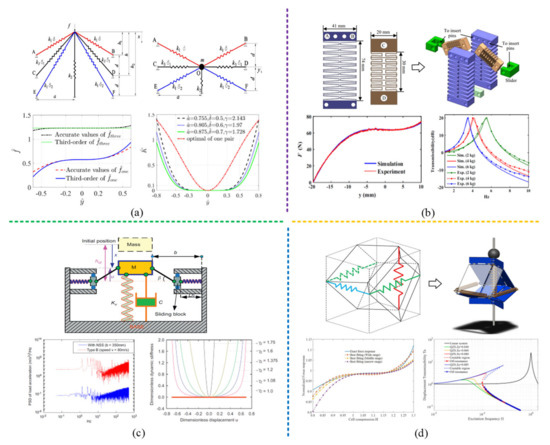
Figure 8.
Structure and vibration isolation performance of four typical mechanical spring QZS vibration isolators: (a) Multi-spring structure proposed by Zhao et al. [8,9,10]; figures adapted with permission from Ref. [9]. Copyright 2021, copyright Zhao, F.; (b) Special spring structure (planar spring) proposed by Lan et al. [21]; figures adapted with permission from Ref. [21]. Copyright 2014, copyright Lan, C.C.; (c) Slider block-guide rod structure proposed by Danh Le et al. [23,24]; figures adapted with permission from Ref. [23]. Copyright 2011, copyright Le, T.D.; (d) Origami structure proposed by Ye et al. [26]; figures adapted with permission from Ref. [26]. Copyright 2022, copyright Ye, K.
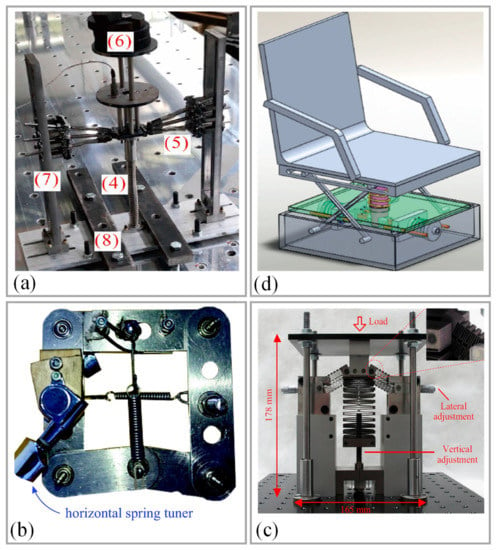
Figure 9.
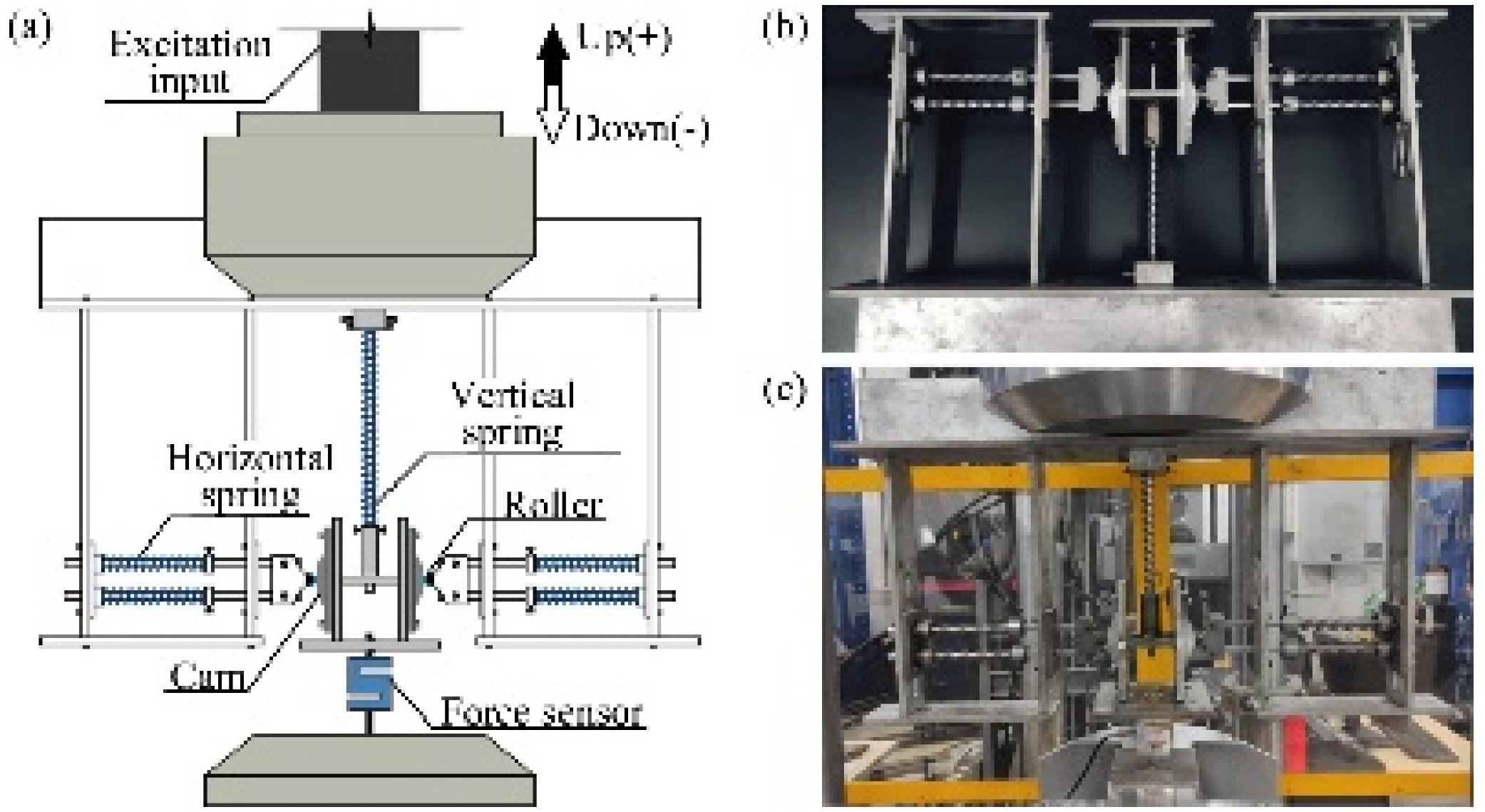
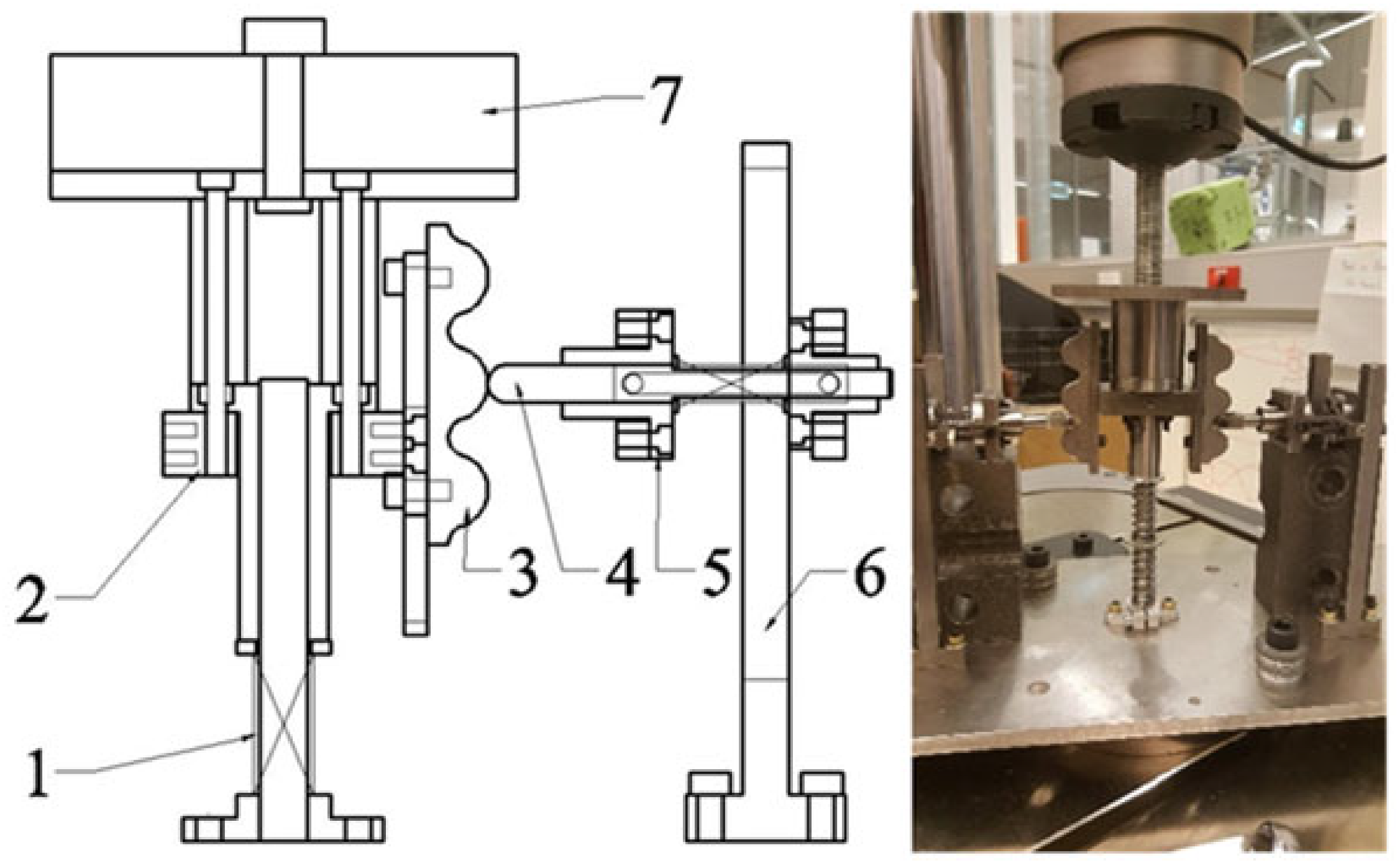
Representative applications and experimental prototypes of QZS vibration isolators using mechanical springs: (a) the experimental prototype of QZS vibration isolator with a multi-spring structure proposed by Zhao et al. [8,9,10]; figure adapted with permission from Ref. [9]. Copyright 2021, copyright Zhao, F.; (4)-the vertical spring to generate positive stiffness, (5)-three pairs of oblique springs to generate negative stiffness, (6)-isolation platform and loaded mass, (7)-supporting frame, (8)-fixture; (b) The mechanically simple quasi-zero stiffness device is designed by Gatti et al. [15,16]; figure adapted with permission from Ref. [16]. Copyright 2021, copyright Shaw, A.D.; (c) The vibration isolator capable of isolating a wide range of loads is proposed by Lan et al. [21]; figure adapted with permission from Ref. [21]. Copyright 2014, copyright Lan, C.C.; (d) The typical QZS vibration isolator with a slider block–guide rod structure proposed by Danh Le et al. [23,24], which is applied to seat suspension of vehicles; figure adapted with permission from Ref. [23]. Copyright 2011, copyright Le, T.D.
Based on the negative-stiffness structures with a pair of oblique springs, Zhao et al. [8,9,10] proposed a multi-spring negative-stiffness structure, which can be designed for different applications by selecting different optimal parameter combinations and has a low transmissivity in a wide frequency range. As shown in Figure 9a, in the vibration isolation device, negative stiffness is provided by three pairs of oblique springs and positive stiffness by one vertical spring. The force-displacement curves of the QZS isolator obtained in the static test had a good correlation with the theoretical results, and the theoretical and experimental results showed that the displacement transmissibility of the proposed multi-spring QZS vibration isolator was much lower than that of the vibration isolator with two oblique springs and that of the linear vibration isolator. Similarly, Xu et al. [11] designed a five-spring QZS vibration isolation system, where four oblique coil springs with the same stiffness provided negative stiffness and one vertical coil spring provided positive stiffness, and each spring was equipped with a guiding device to improve the stability of the system. The results showed that the system could attenuate vibration starting from 0.5 Hz and no resonance peak appeared under the damping effect. In addition, Carrella et al. [12,13] conducted in-depth theoretical analysis of the structure and characteristics of a three-spring QZS vibration isolation system, including static optimization of the optimal stiffness ratio, force transmissibility, and displacement transmissibility. Liu et al. [14] studied a three-spring QZS vibration isolator with a tunable nonlinear inerter, and the results showed that adding inerter elements widened the frequency range of isolation and reduced the peak value of the transmissibility. Gatti et al. [15,16] designed a QZS vibration isolation system using only two springs with rigid links arranged in a specific configuration, which had a good low-frequency vibration isolation effect.
Liu et al. [17] designed a compression bar-type QZS element using a disc spring to provide negative stiffness and built a six-degrees-of-freedom (6-DoF) vibration isolation platform supported by 12 compression bar-type QZS elements. As shown in Figure 9b, the vibration isolation platform comprised a load-carrying platform and four conical columns, and the conical column was composed of three mutually hinged compression bar-type QZS elements. The effects of damping, excitation amplitude, and structural parameters on the dynamic characteristics and force transmissibility of the whole system were analyzed in detail. Compared with the linear vibration isolation system, the resonance frequency of each degree of freedom of the 6-DOF platform was lower, which performed well in isolating multi-directional and low-frequency vibrations. Niu et al. [18], Valeev et al. [19], and Chen et al. [20] respectively designed three types of QZS vibration isolators using disc springs instead of oblique springs, then studied and analyzed the vibration isolation performance of these vibration isolators, and finally obtained beneficial vibration isolation effects. Lan et al. [21] also considered a special spring and developed a QZS vibration isolator with a planar spring as the negative-stiffness mechanism; in this way, arbitrary stiffness could be achieved through varying planar spring designs. The simulation and experimental results verified that the proposed isolator could deal with a payload of 0 ~6 kg and attenuate an external excitation frequency of as low as 2.3 Hz. Liu et al. [22] designed and constructed a QZS vibration isolator prototype with two pairs of transverse groove springs instead of oblique springs as the negative-stiffness mechanism. The experimental results showed that the vibration isolator was able to isolate vibrations at frequencies of 3 Hz and above, and the isolation frequency and peak transmissibility were only 34.52–39.53% and 23.76–45.05% of those of the equivalent linear isolator, as shown in Figure 9c, which is another manifestation of its good vibration isolation performance.
Danh Le et al. [23,24] proposed a typical QZS isolator with a slider block–guide rod structure for application in the vehicle seat, as shown in Figure 9d. Two symmetrical slider block–guide rod structures were installed in the horizontal direction and an additional damper was installed in the vertical direction. The dynamic stiffness value and the QZS region of the device could be adjusted by changing the structural parameters and spring stiffness. The numerical and experimental results showed that this isolator had good vibration isolation performance and anti-resonance phenomenon at excitation frequencies of 0.1~10 Hz, with a reduction of the displacement response of about 67.2%, whereas without using the device, the displacement response could be increased to 268.54%. Liu et al. [25] proposed a QZS vibration isolator with a negative-stiffness mechanism composed of two horizontal springs, two sliding blocks, and two connecting rods; studied the super-harmonic resonance of the isolator; and found that the isolation frequency of the QZS vibration isolator was barely affected by the super-harmonic resonance.
Ye et al. [26] proposed a truss-spring-based stack Miura-ori (TS-SMO) structure inspired by origami and applied it to the QZS vibration isolation system. Using ordinary coil spring sets to replace all the deformable creases in origami structures, different vibration isolation characteristics could be realized through appropriate system parameter design and spring selection. Inspired by the Miura-origami tube, Han et al. [27] and Yang et al. [28] proposed two QZS vibration isolators whose negative stiffness was provided by the origami structure composed of link rods and horizontal springs, which could effectively control low-frequency vibrations.
Ref. [9] compared a multi-spring QZS vibration isolator with a linear vibration isolator and a typical QZS vibration isolator. The results are shown in Figure 10. The traditional QZS vibration isolator exhibited obvious stiffness hardening and frequency jumps, and could work effectively only when the vibration frequency exceeded the jump frequency, as shown in Figure 7. However, the QZS vibration isolator with a multi-spring structure obtained a lower resonance frequency and smaller response peak. At the same time, stiffness hardening was avoided. Obviously, the effective isolation frequency range of the multi-spring QZS vibration isolator was wider. In addition, the time-domain test results showed that the acceleration on the improved platform was reduced compared with the basic acceleration [9]. The frequency domain results showed that the multi-spring QZS vibration isolator could suppress the vibrations over a wide frequency range, especially in the low-frequency band.
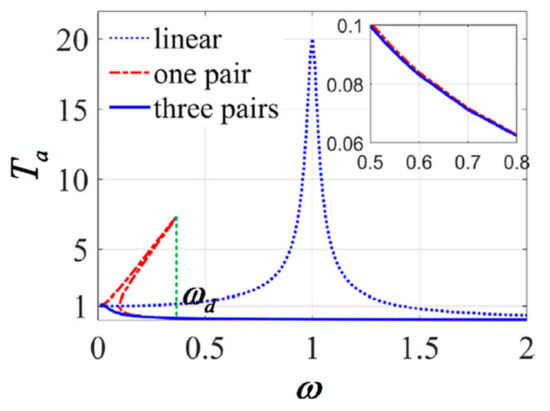
Figure 10.
Comparison of vibration isolation performance of the multi-spring vibration isolator studied by Zhao et al. [9] with that of a linear vibration isolator and a typical QZS vibration isolator. Figure adapted with permission from Ref. [9]. Copyright 2021, copyright Zhao, F.
Besides, it is also an effective way to design and develop a new vibration isolator by combining the existing mechanical spring QZS vibration isolator elements [29]. As shown in Figure 11a, Wang et al. [30] proposed a new vibration isolator with a dual quasi-zero-stiffness (DQZS) mechanism by combining two subordinate QZS mechanisms with a vertical linear spring in parallel. The subordinate mechanism was composed of two oblique springs with exactly the same parameters and a horizontal spring, and provided negative stiffness along the vertical direction through the sleeve-and-link rod. The beginning frequency of vibration isolation was 2.5 Hz, which was about 50% lower than that of the traditional QZS vibration isolator, thus expanding the frequency band of vibration isolation. As shown in Figure 11b, Zhu et al. [31] proposed a 2-DOF (in the horizontal and vertical directions) QZS vibration isolator based on the existing mechanical spring QZS isolator elements, including two QZS vibration isolation units in the orthogonal horizontal directions. Each unit was composed of a pair of oblique linear springs in the horizontal direction and a vertical damper. It was verified theoretically and experimentally that the proposed isolator could decrease the initial isolation frequency to about 0.525 Hz and effectively suppress the system resonance by about 47.775%, indicating that the proposed isolator had relatively good seismic performance under the excitation of seismic waves.
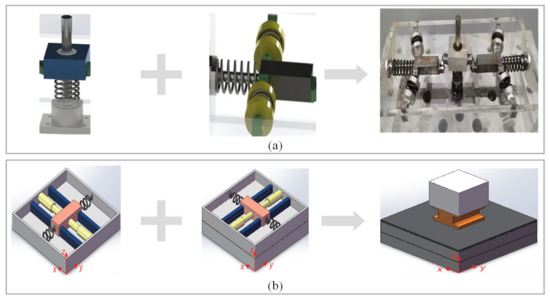
Figure 11.
Development of mechanical springs: the dual QZS vibration isolator proposed by Wang et al. [30] based on the mechanical spring; the 2-DOF QZS vibration isolator proposed by Zhu et al. [31] based on the mechanical spring QZS isolator unit.
In conclusion, using typical QZS vibration isolators with mechanical springs for negative stiffness and modifying the negative-stiffness mechanism with the structures of multi-springs, special springs, sliding block-rods, and origami can improve the isolation performance of different types of isolators to varying degrees. The stiffness-adjusting mechanism of such QZS isolators can be described and summarized as follows: (1) The force-displacement relationship can be expressed as a convex function, and the working range needs to be limited to the positive stiffness interval in order to avoid turning to negative stiffness and triggering instability problems. (2) All these types of structures show the low-dynamic–high-static-stiffness characteristics, which are conducive to suppressing low-frequency vibrations. (3) Using the multi-spring structure to provide negative stiffness helps broaden the low-frequency working range and effectively suppresses the resonance peak. With compact structure and large stiffness coefficient, special springs can significantly improve the working range of vibration isolators, but the design and processing process is cumbersome. QZS vibration isolators with a slider–link rod structure have a relatively wide effective negative-stiffness region, a more stable performance, and easy installation. (4) The parameters related to stiffness and load-carrying capacity can be divided into two categories, namely, design parameters and tunning parameters. The former needs to be completed in the design stage and determined before processing, manufacturing, and assembly. The latter is used to flexibly adjust the stiffness after the vibration isolator is assembled or used.
4.2. Formatting of Mathematical Components
The axially compressed buckled beam is a bistable structure, serving as another negative-stiffness element for the design of QZS vibration isolators as the buckled beam shows negative-stiffness behavior during the transition between the two stable states. The QZS vibration isolator realized by connecting the axially compressed buckled beam with the mechanical spring in parallel is also regarded as an improved three-spring QZS vibration isolator. A simplified model for the dynamic behavior of a prebuckled beam system is presented in Figure 12, and the buckled beam element is simplified as a spring/damper assembly. The buckled beam can be replaced by two compression springs whose spring coefficient is , and the value can be obtained by the following equation [142]:
where is the Young’s modulus of the material, is the area moment of inertia of the beam, and is half the length of the uncompressed beam.
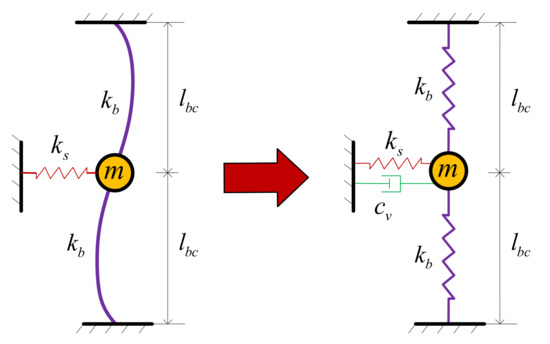
Figure 12.
Simplified model of the buckled beam system.
The beam length is the vertical length of the compressed beam, and the length ratio of the compressed and uncompressed beams is . The two restrained spring elements representing the beams are at a metastable state and must be held at the metastable position by another restrained spring. Assuming that the spring coefficient of the restrained spring is compromised, then there is a damping term . The equivalent mass includes the mass of the beam and one third of the mass of the spring [143].
The response of the system under various excitation frequencies can be measured by system transmissibility. Transmissivity is a transfer function that measures the frequency-related ratio for displacement variation. is the displacement of the beam center and is the input displacement at the bottom of the spring. The transfer function amplitude is given by [144]:
where is the loss factor of the spring material and is the total stiffness of the system, with , depending on the stiffness of the restrained spring and the negative stiffness of the beam.
When the beam is compressed, the deformation coefficient is less than 1, so for the buckled beam, is always negative. When the system is not compressed (), is equal to 1 and increases with the buckling of the beam. Therefore, when the QZS vibration isolation system is in equilibrium, the positive-stiffness spring restricts the beam to the metastable position and provides static stiffness to support the load. Under excitation, the beam oscillates around its metastable state, and the negative stiffness of the beam offsets the positive stiffness of the spring, thus giving quasi-zero stiffness to the system.
After comprehensively investigating the structural behavior of the buckled beam with bistable and negative-stiffness characteristics, Kashdan and Fulcher et al. [34,35] designed a new type of negative-stiffness QZS vibration isolator with buckled beams and established analysis models for the system and buckled beams. The restrained bistable buckled beam with a negative-stiffness feature was designed and fabricated using selective laser sintering (SLS).Three prototypes with single-beam, uncoupled double-beam, and coupled double-beam configurations were designed. The left wall of each system can slide freely to the right to compress the structure. One end of the restrained vertical spring is connected to the rigid frame, and the other end is connected to the center point of the beam. When the beam is subjected to axial compression, the vertical spring restricts it to the metastable state for vibration isolation. A pad is placed between the vertical spring and the rigid frame so that the free length of the spring matches the height of the midpoint of the axially compressed beam.
The equations of nonlinear stiffness and transmissibility of the buckled beam mechanism are derived through static analysis and energy methods:
where is the lateral force, is the vertical displacement at the midpoint of the beam, represents the change in beam length due to compression, is the cross-sectional area of the beam, is the Young’s modulus of the material, and is the free length of the beam.
By adjusting the compression of the buckled beam or the height of the vertical spring, the stiffness and load-carrying capacity can be adjusted, thus producing varying vibration isolation effects. Analytical equation-based prediction and experimental results from the prototypes showed that the resonance frequency and peak transmissivity of the system decreased with the increasing compression of prebuckling. At comparable axial compression levels, the double-beam system reduced the resonance frequency more significantly than the single-beam system, and the coupled double-beam configuration performed better in reducing stiffness and providing greater carrying capacity. However, low-frequency isolation capabilities are sensitive to the high levels of precision required to obtain low levels of system stiffness. The vibration isolation system provides isolation at prespecified threshold levels of force or acceleration.
Taking advantage of the bistable and negative-stiffness characteristics of buckled beams, Liu et al. [36,37] designed a QZS vibration isolator using two oblique Euler buckled beams to provide negative stiffness and one vertical spring to provide positive stiffness, in which both ends of the two buckled beams were hinged, as shown in Figure 13(a). The frequency response curve of the proposed isolator bent to the right, indicating it is a hardening system with a wide and smooth QZS region, as shown in Figure 13(b). The experimental results showed that under the negative stiffness of the Euler buckled beams, the isolator’s natural frequency was reduced from 6.5 Hz to 2.5 Hz, and no obvious peak occurred at the resonance frequency. Similarly, as shown in Figure 14, Huang et al. [38] designed a QZS isolator using four hinged Euler buckled beams to provide negative stiffness and one vertical spring to provide positive stiffness, which reduced the isolator’s natural frequency from 6.1 Hz to 3.9 Hz.
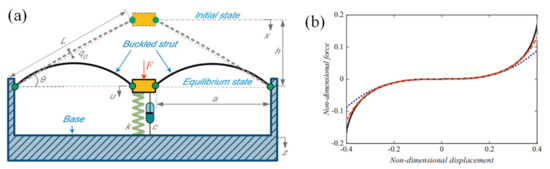
Figure 13.
Ultra-low frequency isolator using Euler buckled beams with hinged-hinged boundary working as negative stiffness corrector: (a) Model diagram; (b) Nondimensional force-displacement of the zero-stiffness system. Figure adapted with permission from Ref. [36]. Copyright 2013, copyright Liu, X.
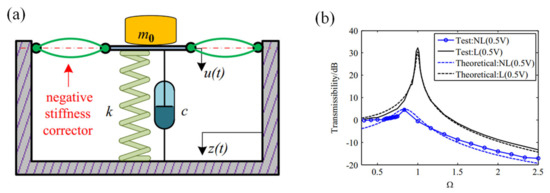
Figure 14.
The nonlinear isolator consisted of a linear isolator and the negative stiffness corrector: (a) Model diagram; (b) The acceleration transmissibility of the linear and nonlinear isolator. Figure adapted with permission from Ref. [38]. Copyright 2014, copyright Huang, X.
Kim et al. [39] proposed a QZS vibration isolator with constant stiffness and damping for application in ultra-precision measurement sensors and constructed a prototype. The proposed isolator is composed of a vertical spring with pre-tightening force and eight transverse leaf springs with nonlinear buckling characteristics. The leaf springs achieved a small change of negative stiffness using the buckling characteristics, giving the isolator a wide and smooth QZS region. The transmissivity curves obtained through prototype experiment and linear model computation are almost consistent.
4.3. Geometrically Nonlinear Structure
When an object moves on a curved surface, its vertical acceleration caused by gravity changes along the curved surface. This is the basis of the generation of negative stiffness. With a curved surface, the geometrically nonlinear structure will facilitate the development of QZS vibration isolators. The most commonly used geometrically nonlinear structure is the cam-roller-spring structure [40,41,42,43]. Zhou et al. [44] developed a geometrically nonlinear system comprising two long cams, four horizontal springs, and four cylindrical rollers, as shown in Figure 15a. They systematically solved the static and dynamic behaviors of the cam-roller-spring configuration. The relationship between vertical deflection and static force of the system is given in dimensionless form:
where , , , , , and are the stiffness of horizontal and vertical springs; and are the radii of rollers and cams; and represents the pre-compression of horizontal springs.
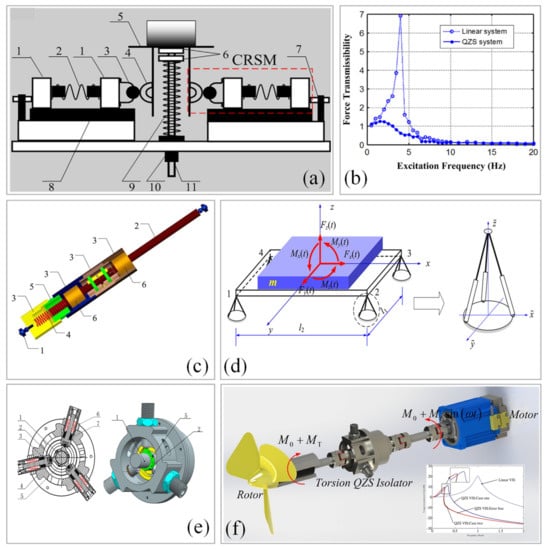
Figure 15.
The cam-roller-spring QZS vibration isolator proposed by Zhou et al. [44,45,46,47]: (a) Single-degree-of-freedom (SDOF) vibration isolator [44]; 1-slider, 2-horizontal spring, 3-roller, 4-semi-circular cam, 5-loading support, 6-vertical adjuster, 7-horizontal adjuster, 8-sliding rail, 9-vertical spring, 10-linear bearing, and 11-sliding rod; (b) Force-displacement characteristic curve; (c) Schematic diagram of the QZS strut [45]; 1-ball joint, 2-rod, 3-sleeve, 4-coil spring, 5-adjuster, 6-linear bearings; (d) 6-DOF vibration isolation platform; (e) Torsional vibration isolator with QZS [46,47]; 1-left shaft connector, 2-cam, 3-disk spring stack, 4-universal wheel, 5-fastening screw, 6-linear bearing, 7-sliding rod; (f) Application in a shaft system. Figures adapted with permission from Refs. [44,45,46]. Copyright 2015/2017/2017, copyright Zhou, J.
The prototype experiment showed that the QZS system started to produce an isolation effect at about 3 Hz and effectively suppressed the resonant amplitude of the system, as shown in Figure 15b. In addition, Zhou et al. [45] proposed a novel cam-roller-spring QZS strut, as shown in Figure 15c. A pyramidal isolator consisting of three QZS struts was assembled to be a mount to symmetrically support a platform, leading to a 6-DOF QZS vibration isolation platform, as shown in Figure 15d. Compared with the linear platform, the 6-DOF QZS platform had broader bandwidth of vibration isolation starting from a lower frequency, and possessed higher isolation effectiveness in the low-frequency range, most importantly, in all six DOFs. Zhou et al. [46,47] also proposed a compact cam-roller-spring QZS vibration isolator to attenuate the transmission of torsional vibration along a shaft system, as shown in Figure 15e,f. A disc spring set was used to support the roller that was in contact with the cam to provide negative stiffness, and then a linear torsion spring was used to provide positive stiffness. Overall, this type of isolator could significantly attenuate torsional vibrations. In addition, Ye et al. [48] also used the QZS vibration isolator with cam-roller mechanism to isolate vibrations in the translational and rotational directions, which achieved good vibration isolation effects.
In other references, the difference of cam-roller-spring structures mainly lies in the cam structural design [49,50,51,52,53] and the number of cams [54]. Their structural design and performance are summarized in Table 2. Such differences in cam structure design, to a certain extent, help expand the negative-stiffness region of the isolator. In particular, with the specially designed cam a wider negative-stiffness region can be obtained, further attenuating low-frequency vibrations, but it also leads to a complex isolator structure, involving many components and the need for a large installation space.

Table 2.
Overview of different types of cam-roller-spring QZS vibration isolators.
4.4. Magnetic Structure
When the magnet leaves the position of equilibrium, the magnetic force difference is produced in the same direction of relative displacement to aid relative motion. The reverse force-displacement characteristic and good stability allows the magnet to be an ideal choice for the development of QZS vibration isolators. Magnetic springs can work alone or together with other positive-stiffness mechanisms (such as coil springs) as magnetic QZS isolators [55,56]. According to the type of magnetic structure, magnetic QZS vibration isolators can be divided into permanent magnet structure, electromagnetic structure, and hybrid magnet structure, as shown in Figure 16. The ring magnet structure is the most commonly used one [57,58,59,60,61,62,63,64,65]. Shan et al. [66] constructed a QZS isolator using a pair of mutually repelling permanent magnets in parallel connection with a pneumatic spring and systematically solved the static and dynamic behavior of the ring magnet structural configuration. The magnetic force between the two ring magnets is given by:
where is the total magnetic permeability between two ring magnets, is the remanence of the permanent magnet, is the relative permeability of the permanent magnet, and is the magnetic permeability of air.
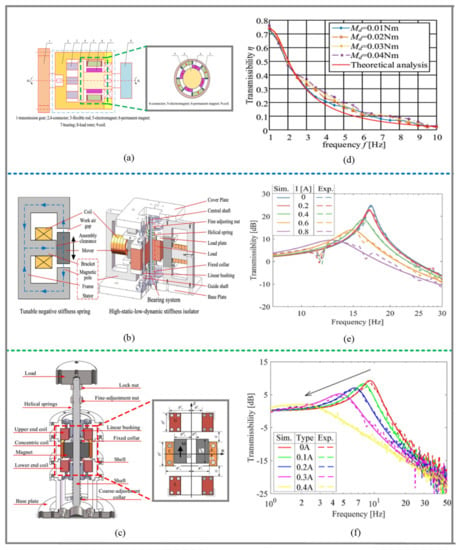
Figure 16.
Structure and vibration isolation performance of three typical magnetic QZS isolators: (a) The permanent magnet structure for suppressing low-frequency torsional vibrations proposed by Xu et al. [59]; figures adapted with permission from Ref. [59]. Copyright 2020, copyright Xu, J.; (b) The electromagnetic structure using Maxwell normal stress proposed by Yuan et al. [75]; figures adapted with permission from Ref. [75]. Copyright 2021, copyright Yuan, S.; (c) The hybrid magnet structure composed of the ring coil and permanent magnet proposed by Yuan et al. [77]; figures adapted with permission from Ref. [77]. Copyright 2020, copyright Yuan, S.; (d–f) show the corresponding transmissivity curves.
The above equation can be used to explore the stiffness-displacement relationship of the ring magnet by optimizing different structural parameters. The experimental results showed that with a payload of 55.4 kg, the resonance frequency was reduced from 3.61 Hz to 2.34 Hz. However, due to the small damping of the pneumatic spring, a large peak transmissibility occurred at the resonance frequency.
Zheng et al. [58] proposed a QZS coupling, where a torsion magnetic spring (TMS) composed of two coaxial ring magnet arrangements in repulsive configuration is employed to produce negative torsion stiffness to counteract the positive stiffness of a rubber spring, as shown in Figure 17 (a). Since the static torque is undertaken by the rubber, which has high stiffness, the QZS coupling can maintain a small static angular displacement when a large driving torque is transmitted through it. The obtained torque transmissibility proves that the QZS coupling can have a good isolation performance in its effective stroke length and also shows how the geometric parameters of the TMS can influence the isolation performance of the coupling, as shown in Figure 17 (d).
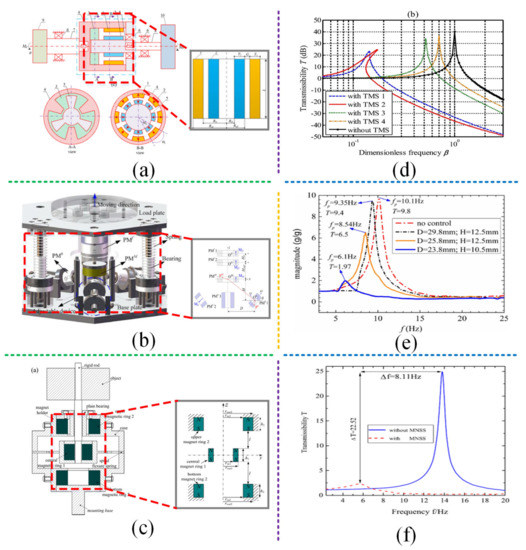
Figure 17.
Annular permanent magnet structure: (a) The torsion magnetic spring structure with a pair of mutually repelling magnetic rings proposed by Zheng et al. [58]; figures adapted with permission from Ref. [58]. Copyright 2018, copyright Zheng, Y.; (b) The magnet structure composed of three moving ring permanent magnets and three fixed ones proposed by Yan et al. [67]; figures adapted with permission from Ref. [67]. Copyright 2018, copyright Yan, B.; (c) The magnet structure composed of three axially magnetized magnetic rings proposed by Dong et al. [70]; figures adapted with permission from Ref. [70]. Copyright 2017, copyright Dong, G.; (d–f) show the corresponding transmissivity curves.
Yan et al. [67] designed a magnet structure composed of three moving-ring permanent magnets and three fixed ones, as shown in Figure 17b. The fixed magnets were assembled separately at the three adjustable devices that were uniformly distributed along the circumference. The magnetic repulsive force and magnetic attractive force effects could be considered in the system at the same time, and the relative position could be adjusted to achieve variable stiffness performance. The results showed that the nonlinear magnetic repulsion softened the spring and thus reduced the jump frequency, as shown in Figure 17e. Yan et al. [68,69] also proposed the concept of nonlinear electromagnetic shunt damping (N-EMSD) to enhance the vibration isolation performance of permanent magnet vibration isolators and investigated the nonlinear mass and damping effect of nonlinear electromagnetic damping.
Dong et al. [70] proposed a magnet structure composed of three axially magnetized ring magnets configured in attraction to produce negative stiffness, as shown in Figure 17c. The spiral flexure spring was embedded in the outer wall of the structure to provide positive stiffness axially. Their combination formed a QZS vibration isolator. The experimental results showed that the resonance frequency of the isolator with magnet structure was reduced from 13.81 Hz to 5.7 Hz, and the vibration transmissibility at the resonance peak was reduced by 22.52 dB, as shown in Figure 17f. In addition, Dong et al. [71] also proposed a geometrically nonlinear damping including a semi-active electromagnetic shunt damping. The vibration isolator could achieve a wide vibration isolation band and low formant. Ref. [72] described the design of a passive low-frequency multi-directional vibration isolator by using a QZS unit using a negative-stiffness magnetic spring, which achieved better low-frequency vibration isolation performance in multiple directions, especially in the vertical direction.
According to other references, the ring magnet structure is also used for multi-degree-of-freedom vibration isolation platforms [73,74]. Zhou et al. [73] constructed a 6-DOF QZS vibration isolation platform using the negative-stiffness mechanism of ring magnets. The platform was effective in almost the whole frequency range under small excitation and large damping, and had obvious advantages over its linear counterpart in all six DOFs. Zheng et al. [74] applied the QZS vibration isolator composed of negative-stiffness ring magnets to a 6-DOF Stewart platform, which exhibited good isolation performance in all six directions.
Yuan et al. [75] proposed an electromagnetic structure using Maxwell normal stress, as shown in Figure 16b. It was composed of a mover, a stator, and a DC coil. The coil was wound around the entire bracket, and the magnetic circuit was in an 8-shaped structure to produce negative stiffness, which could be tuned online via control. The experimental results showed that the QZS vibration isolator with an electromagnetic structure could expand the isolation frequency band. As shown in Figure 16e, the current increased from 0 to 0.8 A, the natural frequency of the system decreased from 17.2 Hz to 13 Hz, and the resonance peak also decreased significantly. In addition, Jiang et al. [76] designed a magnetic-air hybrid quasi-zero stiffness vibration isolation system. The air spring was mounted vertically, and the four electromagnetic springs were mounted horizontally and symmetrically, which were “parallel” to the air spring through the oblique compression rod. The proposed system achieved low-frequency vibration isolation effects for objects with different masses.
Yuan et al. [77] proposed a hybrid magnet structure composed of three annular coils and one annular permanent magnet, as shown in Figure 16c. The permanent magnet was coaxially arranged with three annular coils, and one coil was concentric with the magnet. The coils at both ends attracted the magnet, and the concentric coil repelled the permanent magnet. When relative displacement was generated between the permanent magnet and the concentric coil, negative stiffness was achieved. The negative stiffness produced by the electromagnetic structure had 1% linearity over the whole stroke (±5 mm) and could be adjusted online within the range of ± 2400. The stiffness could be adjusted online linearly by controlling the current in the coil. The experimental results showed that by controlling the current in the coil, the natural frequency was reduced from 10 Hz to 2 Hz, and the resonance peak was significantly reduced, as shown in Figure 16f. In addition, Sun et al. [78,79] proposed a hybrid magnet structure composed of four coaxial coils and four annular permanent magnets, and its stiffness characteristics could be adjusted through the current in the coil. The proposed isolator has the advantages of more compact structure, stronger load capacity, and higher efficiency.
The magnetic levitation structure is also a commonly used design method [80,81]. Robertson et al. [82] proposed a QZS isolator with magnetic levitation, as shown in Figure 18a. They system consisted of two pairs of rare earth magnets and has no mechanical connection between the frame and the floater. Based on the magnetic levitation structure, a 6-DOF QZS vibration isolator was designed, and the magnetic levitation was used as the payload support mechanism. The experimental results showed that the proposed isolator realized the inherent QZS levitation in the vertical direction while providing the static load support force, and there was zero stiffness in the other five DOFs. As shown in Figure 18b–d, the measurement of vibration transmissivity also proved the low resonance frequency achieved in multiple DOFs, which is another manifestation of the good vibration isolation performance of the system. Kamaruzaman et al. [83,84] designed a 6-DOF QZS vibration isolation system with magnetic levitation, which has a special platform supported by four passive magnets to place the payload. Two large magnets attracted each other to compensate for gravity, and four pairs of relatively small magnets repelled each other to reduce stiffness.
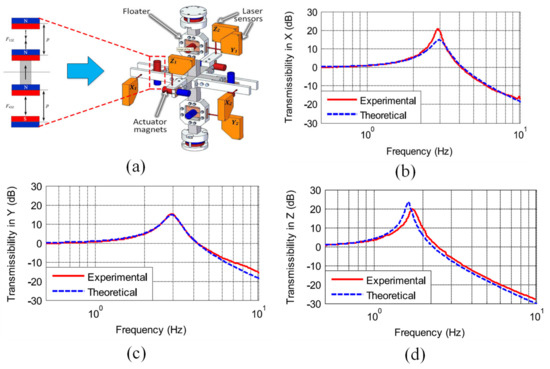
Figure 18.
Robertson et al. [82] proposed a 6-DOF QZS isolator with magnetic levitation: (a) vibration isolator structure; (b–d) show the vibration transmissivity in the X/Y/Z direction, respectively. Figures adapted with permission from Ref. [82]. Copyright 2015, copyright Zhu, T.
4.5. Bio-Inspired Structure
To make continuous and stable movements, such as hopping, running, and tumbling, animals need to withstand the vibration and impact from the ground. Their ability to adjust stiffness flexibly ensures stable movement and protects organs from damage. For example, kangaroos move by hopping, and the hopping speed can be up to 70 km/h [85]. The realization of this fast, smooth, and continuous hopping movement is attributed to the X-shaped structure of their legs. Such a structure can help effectively absorb the strong impact force generated by collision with the ground. Therefore, a type of bionic vibration isolator was designed by imitating the stiffness adjustment of biological structures, and its beneficial nonlinear stiffness has been systematically explored for low-frequency or ultra-low-frequency vibration isolation [86,87,88,89,90,91,92,93,94,95,96,97] to overcome the defects of traditional isolators. Such isolators feature strong adaptability to different payloads and the high-static–low-dynamic stiffness characteristic in a large displacement range.
Due to ease of manufacture and assembly, rods and springs are usually used to simulate bones and muscles. According to different bionic forms, bio-inspired structures fall into three types: limb-like structure, polygonal skeleton structure, and long neck structure, as shown in Figure 19.
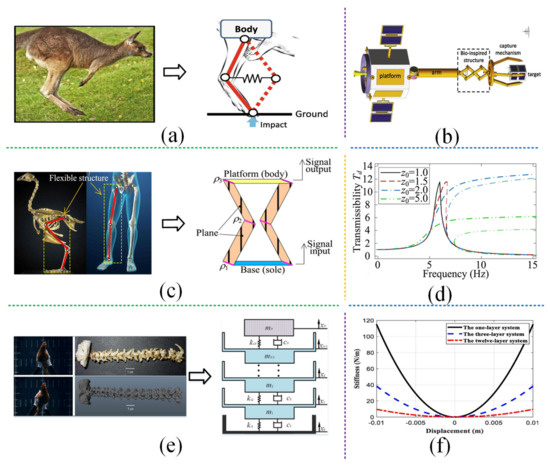
Figure 19.
Three typical bio-inspired structures: (a) The completely symmetrical limb-like structure inspired by kangaroo legs proposed by Dai et al. [85,91,98]; figures adapted with permission from Ref. [85]. Copyright 2018, copyright Dai, H.; (b) The limb-like structure is introduced to suppress the vibration between the satellite arm and the capture mechanism. (c) The polygonal skeleton structure inspired by the biological structure of the legs of bipeds pro-posed by Sun and Ge et al. [99,100,101]; Figures adapted with permission from Ref. [101]. Copyright 2018, copyright Sun, X.; (d) The displacement transmissibility for different excitation amplitudes. (e) The long neck structure imitating a bird’s neck proposed by Deng et al. [103]; figures adapted with permission from Ref. [103]. Copyright 2020, copyright Deng, T.; (f) Stiffness displacement curves.
Inspired by kangaroo legs, Dai et al. [85,91,98] proposed a fully symmetrical limb-like structure with equal rod length to isolate the post-capture vibration of satellite platform subjected to periodic and impulsive forces. As shown in Figure 19a, the limb structure was installed between the arm and the capture mechanism to suppress vibrations. In each basic unit, four rods with equal length formed a diamond, and the horizontal spring connected the two joints. When used in parallel connection, each diamond had equal side length, and the deformation of each spring was the same. Stiffness adjustment could be realized by selecting reasonable rod length, setting an appropriate number of layers, and adjusting the initial assembly angle. The numerical results showed that a smaller rod length was preferred because it could effectively suppress the vibration of the satellite platform and the captured object in terms of velocity and peak acceleration, as shown in Figure 19b. In addition, Wang et al. [89] proposed two limb-like structures (structural constraints). One had unequal and asymmetric rod length, which retained diamond units with unequal element length. The other had unequal and completely symmetrical rod length but no diamond units, and a new parameter called the rod–length ratio was introduced into the structure, considering the difference between rod lengths. When the rod–length ratio exceeded 1, the structure showed better isolation performance due to its smaller dynamic stiffness and greater nonlinear damping effect.
Inspired by the safe landing of cats falling from a high altitude, Ge et al. [99,100] proposed a bio-inspired polygonal skeleton structure. It consisted of two symmetrical bionic legs and a bearing platform (as the spine). Each leg was imitated by a three-rod structure, in which the linear springs were used to imitate the muscle. By adjusting the length of the spine or the distance and angle between the two bionic legs, a wide range of stiffness and load capacity could be realized, which is more convenient than replacing the spring and changing the rod length. Similar to the limb-like structure, the polygonal skeleton structure exhibited the high-static–low-dynamic stiffness characteristic within the effective working range. Using this unique feature, a large-stroke QZS vibration isolator was proposed [99]. In the experimental test of vibration isolation performance, the resonance frequency of the proposed structure was 1.5 Hz. When the excitation frequency was 10 Hz, the acceleration amplitude decreased by 20 dB. Inspired by the biological structure of the legs of bipeds, Sun et al. [101] also proposed a bio-inspired polygonal skeleton structure, as shown in Figure 19 (c). The proposed Origami-Joint Flexible (OJF) structure can effectively protect the isolation object from different types of excitation. For impact excitation, the impact vibration energy decreases rapidly and the response becomes smooth because of the nonlinearity; for long-lasting excitation, the isolation effectiveness is significantly improved in frequency domain due to the adjustable dynamical property, as shown in Figure 19 (d). Inspired by a frog’s M-shaped limbs, Zeng et al. [102] proposed a new polygonal skeleton structure and designed a new QZS vibration isolator with torsion springs, distinguishing them from the existing tension spring structures in the literature.
Inspired by a bird’s neck, Deng et al. [103] designed a multi-layer QZS isolator by imitating the multi-vertebra structure of a bird’s neck, as shown in Figure 19e. The classic three-spring QZS model was selected to imitate each vertebra of the neck. Multiple layers were used to achieve low stiffness and nonlinearity. As shown in Figure 19f, the multi-layer QZS system effectively expanded the effective range of the working stroke. The high-static–low-dynamic-stiffness property during a large stroke could ensure excellent vibration isolation performance, especially for low frequency and ultra-low frequency as well as large-amplitude vibrations. After the numerical calculation of specific parameters, the resonance frequency of the 12-layer system was 0.2502 rad/s and the peak value was 0.02071 m, and the corresponding values of the linear spring were 5.936 rad/s and 0.4935 m, respectively. Moreover, the attenuation effect of the multilayer QZS isolator in a higher-frequency band was also greater than that of linear springs. In addition, Jin and Sun et al. [104,105,106] designed a new QZS vibration isolation system with a multi-layer structure and achieved a good vibration isolation effect.
The bio-inspired QZS isolator was compared with two typical traditional QZS isolators [86], as shown in Figure 20. The traditional ones show obvious stiffness hardening and frequency jump. Only when the vibration frequency exceeded the jump frequency could the QZS vibration isolator work effectively. The bio-inspired isolator obtained a lower resonance frequency and smaller response peak. At the same time, stiffness hardening could also be avoided.
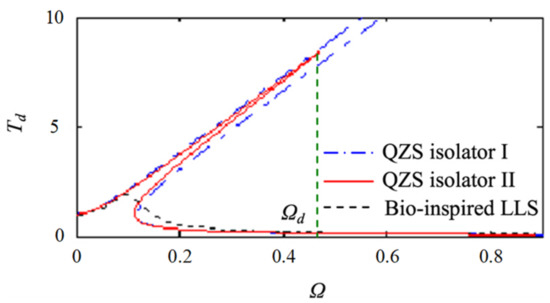
Figure 20.
Comparison of isolation performance between bio-inspired isolator and typical QZS isolators by Wu et al. [86].
It is a common design method to develop new vibration isolators by combining the designed nonlinear elements with the existing structures. Hu et al. [92] combined the bionic limb structure with the Stewart structure and constructed a 6-DOF vibration isolator so as to solve the multi-directional vibration isolation problem. The original actuator of the Stewart platform was replaced by six limb-like structures. The proposed isolator achieved good vibration isolation performance, with reasonable loading capacity and wide vibration isolation bandwidth in all directions. In addition, Ge et al. [95], inspired by the cushioning effect of the felid paws in contact with the ground, developed and systematically studied a novel bio-inspired toe-like structure (TLS) for low-frequency vibration isolation. Chai et al. [96] proposed a novel spring arrangement based on the X-shaped anti-vibration structure with tunable contact mechanism (NXSC), as shown in Figure 21 (a). An enhanced quasi-zero-stiffness (QZS) with large stroke is obtained by tuning contact position between the horizontal springs and vertical fixed rods. The loading capacity of the NXSC structure can be extended by 2–3 times, and the proportion of the QZS zone to the total stroke of the structure can be enhanced by 50% by tuning the contact parameters.Wu et al. [97] studied a 6-DOF isolator theoretically and experimentally. The isolator was based on the Stewart platform configuration and consists of six bionic limbs as legs. Some experimental results were described [97], in which the resonant frequencies in three directions were as low as 2.69 Hz, 0.92 Hz, and 3.81 Hz.
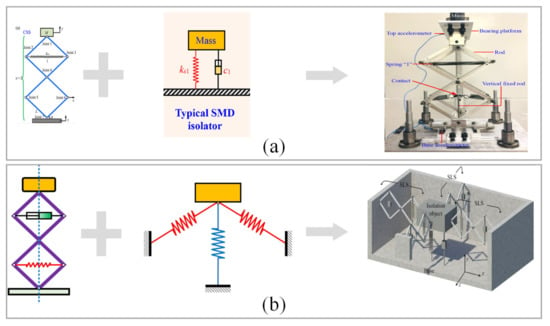
Figure 21.
Development of bio-inspired structures: (a) A novel spring arrangement method based on the X-shaped anti-vibration structure with tunable contact mechanism (NXSC) is proposed by Chai et al. [96]; figures adapted with permission from Ref. [96]; Copyright 2022, copyright Chai, Y.; (b) The three-direction isolator by combining typical three-spring QZS arrangement and X-shaped structure proposed by Jing et al. [108]; figures adapted with permission from Ref. [108]. Copyright 2015, copyright Sun, X.
In other literature, scissor-like bio-inspired structures were adopted [94,107]. Jing et al. [94,107] considered the rod mass and accurately imitated a scissor-like structure. The experimental results showed that 50% (or above) attenuation of the base random impact excitation could be realized at most frequencies. In addition, a new scissor-like structure was used to construct the three-direction isolator [108], as shown in Figure 21b. In the typical three-spring QZS model [25,26,27], the scissor-like structure replaced the oblique spring. The system could realize the QZS vibration control in three directions.
4.6. Composite Structure
Lakes and Drugan et al. [109,110,111,112] conducted a series of studies on composite materials with negative stiffness properties. Innovative composite materials were developed to provide negative volume and the Young’s modulus, and quantitative requirements for the elastic modulus of constituent materials were made to ensure the stability of the composite materials of composite structures. At present, many types of QZS vibration isolators using composite structures have been designed, mainly including honeycomb structure and unit cell structure, as shown in Figure 22. Based on the traditional QZS vibration isolator element or negative-stiffness material, the low-frequency/ultra-low-frequency vibration isolation performance can be realized by designing composite materials/structures.
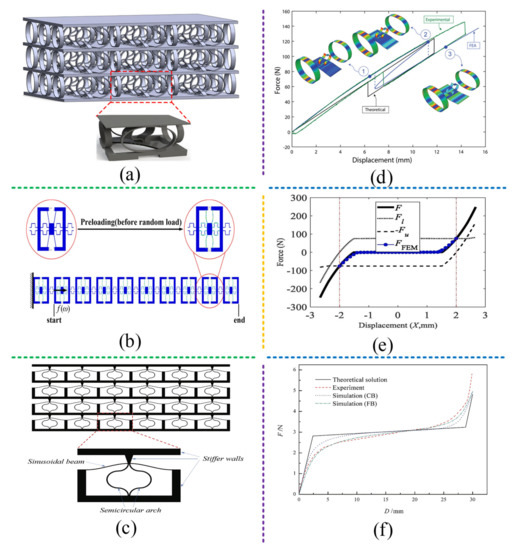
Figure 22.
Composite structures: (a) the honeycomb-like structure proposed by Izard et al. [113]; figures adapted with permission from Ref. [113]. Copyright 2017, copyright Izard, A.G.; (b) The unit cell structure constructed using beams proposed by Zhou et al. [116,117]; figures adapted with permission from Ref. [116]. Copyright 2020, copyright Cai, C.; (c) The unit cell structure using a sinusoidal beams, semicircular arches, and stiffer walls designed by Fan et al. [118]; figures adapted from with permission Ref. [118]. Copyright 2020, copyright Fan, H.; (d–f) show the corresponding stress-displacement curves.
Izard et al. [113] proposed a honeycomb-like QZS vibration isolator using composite materials, as shown in Figure 22a. The structure was designed with the three-spring QZS model as the periodic structural material unit. The customizable combined characteristics of high stiffness, low density, and high energy dissipation were realized by enhancing the natural damping of the main material. Figure 22d presents the force-displacement curve of a single honeycomb-like composite structure during the whole cycle, which is S-shaped. Images of the deformed mesh with Von Mises stress contours at three points in the simulation ((1) along the loading path, (2) immediately before snap-through, and (3) after snap-through) are shown in the insets. Based on the single honeycomb-like structure, the proposed composite material can be designed to be mono-stable or bi-stable, which can be realized by using any constituent material on almost any length scale, without additional specific damping material and a large number of constituent units. In addition, Correa et al. [114] designed conventional honeycomb and hexagonal honeycomb composite structures using negative stiffness beams and fabricated the prototypes by selective laser sintering. The experimental results showed that the honeycomb structure exhibited large positive stiffness. The energy absorbed by the hexagonal honeycomb structure was 64% to 67% of the energy brought by transverse compression, and the shape was fully restorable after compression. Virk et al. [115] constructed a SILICOMB honeycomb structure exhibiting zero Poisson’s ratio-type behavior. The structure was produced using rapid prototyping techniques and PEEK (polyether ether ketone). The quasi-static and closed-loop tests showed that a zero-stiffness region and a negative-stiffness region existed in the force-displacement behavior, and that the structure had the properties of high temperature performance, chemical resistance, and electrical insulation.
Zhou et al. [116,117] designed two types of one-dimensional unit cell (UC) structures using beams. The representative UC was composed of two pairs of folded beams and two pairs of buckled beams connected in parallel, as shown in Figure 22b. The experimental results showed that the negative-stiffness structure (buckled beams) could basically offset the positive stiffness of the folded beams and produce the desired QZS characteristics so that ultra-low local resonance band gaps could be achieved, as shown in Figure 22e. In addition, Fan et al. [118] designed unit cells using a sinusoidal beam, semicircular arches, and stiffer walls, as shown in Figure 22c, in which the sinusoidal beam and semicircular arches were arranged in parallel. The sinusoidal beam showed negative-stiffness characteristics under transverse loads, and the semicircular arches exhibited positive-stiffness characteristics under vertical loads. By using unit cells to form an entire QZS structure, the static stiffness and QZS region for supporting isolated weights can be designed for different applications, as shown in Figure 22f. Ren et al. [119] obtained a new lattice metamaterial structure by adding prefabricated curved beams into multi-dimensional rigid frames. The proposed metamaterial structure was able to undergo multiaxial stress conditions while retaining the negative-stiffness effect and energy absorption characteristics, and had considerable freedom of parametric design, thus having good application prospects.
5. Active/Semi-Active QZS Isolator
Although passive QZS vibration isolators are able to realize vibration suppression in a broad frequency range based on their high-static–low-dynamic-stiffness characteristics, their negative stiffness cannot be easily adjusted, and the best performance can be achieved only under specific payloads and geometric parameters. In addition, the inherent cubic stiffness nonlinearity can lead to strong nonlinear behavior, including multistable, bifurcation, and chaotic responses [124]. Therefore, it is necessary to introduce various control devices and methods to further improve the stability and vibration isolation performance of QZS vibration isolators [120]. Against this background, active/semi-active QZS vibration isolators have become a hot research topic among researchers.
In traditional active/semi-active vibration isolators, additional actuators and sensors are usually connected with them to generate control force and provide feedback signals. Of course, a reasonable control strategy is also needed to better isolate low-frequency vibrations [145,146]. Active/semi-active control also shows the advantage of adapting to varying environmental excitations. Ref. [147] stated that the resulting active/semi-active systems were more complex and consumed more energy than passive systems. Researchers have made innovative attempts to add the controller into the QZS isolation system in order to strengthen the stiffness and damping adjustment effects and thus improve the vibration isolation performance [121,122,123,124,125,126,127,128]. Active/semi-active QZS vibration isolators can be divided into two categories according to the location of the controller, as shown in Figure 23. One has the controller placed outside the isolation system, as shown in Figure 23a, and its dynamic equation can be written as:
where is the nonlinear damping, is the nonlinear stiffness, and represents the control force.
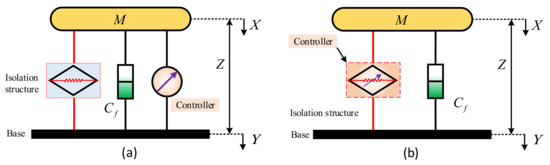
Figure 23.
Schematic diagrams of typical active/semi-active QZS vibration isolation systems: (a) The controller is set outside the isolation structure; (b) the controller is set in the isolation structure.
Danh et al. [129] proposed an active pneumatic QZS vibration isolation system using negative stiffness structures at low excitation frequencies, as shown in Figure 24a. An adaptive intelligent backstepping controller was designed to manage the system operation for high isolation effectiveness. An auxiliary control measure was introduced to eliminate the effect of unpredictable perturbations. Moreover, a radial basis function neural network model was utilized to estimate the optimal gain of the auxiliary control measure. Danh et al. also designed a fuzzy sliding-mode controller to improve the vibration isolation performance of active vibration isolation systems with negative-stiffness structures [130]. Zhao et al. [131] proposed an electromagnetic active-negative-stiffness generator by using nano-resolution laser interferometry sensors to monitor the micro-vibration of the optical platform and integrating precision electromagnetic actuators, as shown in Figure 24b. The relative displacement feedback strategy was utilized to actively generate negative stiffness and counteract the positive stiffness of pneumatic springs, thus producing the high-static–low-dynamic-stiffness property. The experimental results showed that the vertical natural frequency of the optical platform was reduced from 2.00 Hz to 1.37 Hz, the root mean square of displacement was reduced from 1.28 m to 0.69 m, and the root mean square of velocity was reduced from 14.60 m/s to 9.33 m/s, proving that the proposed method could effectively improve the low-frequency isolation performance of the optical platform. Sun et al. [124] proposed a time-delayed active control strategy to improve the performance of a quasi-zero-stiffness vibration isolator (QZS-VI). The schematic structure of the QZS-VI with an active control device is shown in Figure 24 (c), the controlled spring and the time delay are used to form the active control structure. The delayed active control may extend the work range of the isolator without any structural modification. In addition, a bionic adaptive tracking controller was developed for the suspension system of vehicles based on bionic dynamics [132]. Compared with the standard adaptive controller, the proposed method based on bionic dynamics achieved superior vibration isolation performance and lower energy dissipation. Specifically, in the numerical results, the energy input required for bionic adaptive control was 27.1647 W, which was much less than that for standard adaptive control (about 89.4355 W). In addition, other simulation cases further verified that the proposed adaptive controller has higher robustness and effectiveness.
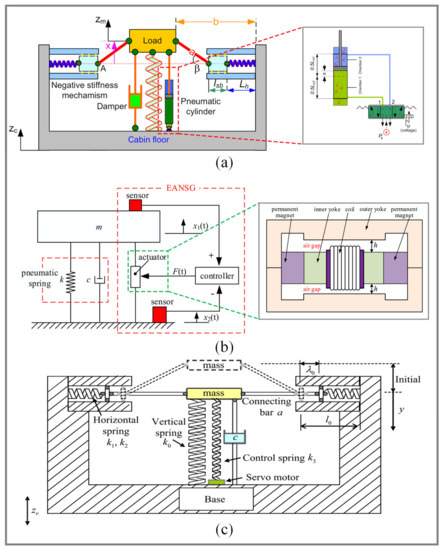
Figure 24.
Active/semi-active QZS vibration isolators with the controller set outside the system: (a) The active pneumatic QZS vibration isolation system for low excitation frequencies proposed by Danh et al. [129]; figures adapted with permission from Ref. [129]. Copyright 2014, copyright Ahn, K.K.; (b) The electromagnetic active-negative-stiffness generator proposed by Zhao et al. [131]. (c) A time-delayed active control strategy to improve the performance of a quasi-zero-stiffness vibration isolator is provided in Ref. [124]. Figures adapted with permission from Ref. [124]. Copyright 2014, copyright Sun, X.
Another type of controller is set in the positive-/negative-stiffness structure, as shown in Figure 23b, and its control equation can be given by:
where and are generated by the internal controller.
Pu et al. [122] proposed a novel compact and contactless multi-layer electromagnetic spring (MES) with tunable negative stiffness, as shown in Figure 25a. The negative stiffness is generated by the electromagnetic force between the coils and the magnets and can be tuned online by controlling the current. The isolator exhibited characteristics of HSLDS, and the transmissibility was tunable by varying the control current. As the magnitude of the control current increased from 0 to 1.2 A, the natural frequency decreased from 8.8 Hz to 2.6 Hz, and the effective isolation frequency band extended from 12.6 Hz to 3.8 Hz. In addition, Kim et al. [133] proposed a 6-DOF active QZS vibration isolation system with a PID feedback control strategy. The uniqueness of the system lies in the voice coil motor (VCM) actuator used in the system, which can generate high driving force. A Halbach magnet array was used for the VCM actuator to generate a maximum force constant. The Halbach magnet array and closed-loop back yoke provided strong magnetic flux density. The experimental results showed that the vibration isolation system effectively attenuated the 6-DOF vibration of the upper plate. When the feedback control was on, the proposed VCM actuator using a Halbach magnet array could improve the energy efficiency of the 6-DOF active QZS vibration isolation system. Chang et al. [134] introduced an electromagnetic active regulation mechanism (ARM) into the traditional QZS vibration isolation system and proposed a semi-active QZS vibration isolator, as shown in Figure 25b. The ARM was composed of an electrically charged coil and a permanent magnet ring. The ability to tune vibration isolation was realized by embedding the electromagnetic ARM in the positive-/negative-stiffness structure. The height and air gap of the ring magnet had a significant impact on the vibration isolation performance of the isolator. Vibrations in the ultra-low-frequency range of 1.9 Hz~4.4 Hz (experimentally verified as 3.86 Hz~4.67 Hz) could be suppressed by adjusting the electromagnetic ARM. Zhao et al. [135] proposed a bio-inspired semi-active vibration isolator with dielectric elastomer-based variable stiffness elements, as shown in Figure 25c. A dielectric elastomer was used as the variable stiffness element, which replaced the linear spring in the bionic limb structure proposed by Dai et al. [85,91,98] for suppressing the vibration transmission between the capture mechanism and the satellite platform. The stiffness of the dielectric elastomer could be controlled by the voltage applied. Its excellent vibration isolation performance was mainly attributed to the geometrical nonlinearity of bionic limb structures and the dielectric elastomer material’s ability to adjust stiffness. The proposed semi-active vibration isolator could meet various application requirements by changing the voltage applied to the elastomer. In addition, even without voltage control, the proposed bionic limb structure with a dielectric elastomer could work effectively as a traditional passive vibration isolator. The simulation results showed that when the voltage for the elastomer was set to 4.0 V, the vibrations of the capture mechanism and the satellite platform under multi-frequency excitation (including 3 Hz and 7 Hz components) were attenuated by 40.5% and 66.4%, respectively. Palomares et al. [136] used two double-acting pneumatic linear actuators instead of oblique springs to realize semi-active QZS isolators with adjustable negative stiffness. The pneumatic spring not only had sufficient stiffness under static conditions, but also could reduce its dynamic stiffness by pressurizing the rear chamber. The experimental results showed that compared with the passive vibration isolation system, the natural frequency of the proposed system was reduced by 58% and vibration attenuation under different excitation frequencies was improved.
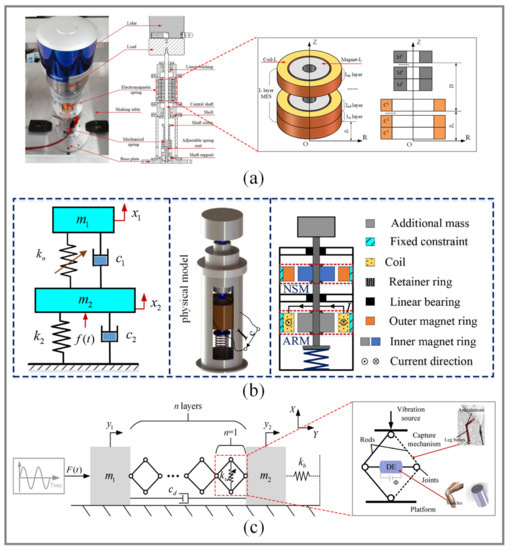
Figure 25.
Active/semi-active QZS vibration isolation system with controller set in the system: (a) A novel compact and contactless multi-layer electromagnetic spring (MES) with tunable negative stiffness is proposed by Pu et al. [122]; Figures adapted with permission from Ref. [122]. Copyright 2019, copyright Pu, H.; (b) The semi-active electromagnetic QZS vibration isolator proposed by Chang et al. [134]; figures adapted with permission from Ref. [134]. Copyright 2022, copyright Chang, Y.; (c) The bio-inspired semi-active QZS vibration isolator with dielectric elastomer-based variable stiffness elements proposed by Zhao et al. [135]; figures adapted with permission from Ref. [135]. Copyright 2020, copyright Zhao, Y.
Semi-active negative-stiffness QZS isolators are able to realize variable stiffness characteristics and deal with the changes in excitation frequency or system parameters. To some extent, they overcome some drawbacks of passive QZS isolators, such as difficult adjustment of negative stiffness, small range of carrying loads, and poor stability. However, as open-loop control systems, they have low control accuracy and cannot effectively compensate for the deviation caused by external interference. Active negative-stiffness QZS isolators with high control accuracy show advantages in producing variable stiffness characteristics and providing better low-frequency vibration isolation performance. However, such active isolators have not been widely applied to vibration isolation systems because they require high-precision sensors and linear actuators to monitor and counteract the low-frequency micro-amplitude vibrations of payload, resulting in high cost and system complexity. In addition, the poor resolution and dynamic range of commercial inertial sensors at low frequencies have also limited the application of active negative-stiffness isolators in vibration isolation systems [148].
6. Conclusions
Quasi-zero stiffness (QZS) vibration isolation is an emerging and effective low-frequency vibration isolation method and has promoted the vigorous development of many research fields. In this review, we paid attention to the recent advances in QZS vibration isolation and exposit the key isolation mechanisms underlying each research partition. A systematic review was presented with an emphasis on passive and active negative-stiffness adjustment mechanisms. At the same time, the realization, application, and vibration isolation effect of QZS vibration isolators under different mechanisms were also introduced and compared. According to the types of negative-stiffness elements, QZS vibration isolators with passive negative-stiffness mechanisms were subdivided into mechanical springs, prebuckled beams, geometrically nonlinear structures, magnetic structures, bio-inspired structures, and composite structures. The design principles, structural realization, and vibration isolation performance of various QZS vibration isolators were introduced one by one. QZS vibration isolators have the high-static–low-dynamic-stiffness characteristics and strong load-carrying capacity, but they are sensitive to load weight and structural parameters and their system adaptability is not strong. In order to improve these conditions, this paper summarized the design principles, control methods, and vibration isolation effects of active/semi-active QZS systems. Generally speaking, such systems exhibit advantages in producing variable stiffness characteristics and providing more stable low-frequency vibration isolation performance under different environmental conditions, but at present, their application is faced with the problems of the high cost and complex structure design of such systems.
So far, domestic and foreign researchers have done abundant research on QZS vibration isolation methods and achieved many remarkable research results. However, some aspects of the existing research still need to be improved and expanded. Some research perspectives are discussed as follows:
- (1)
- Future directions for QZS vibration isolation may involve the optimization of existing structures and vibration isolation mechanisms for broadening the effective vibration isolation frequency band and reducing resonance peak. In particular, further study needs to be done on the modeling and realization of QZS vibration isolation systems. In the modeling process, the commonly used nonlinear degree is the nonlinear stiffness characteristics simulated by the cubic stiffness simulation system. More efforts need to be made in research on high-order stiffness to more accurately understand and predict the dynamic characteristics and vibration isolation effect of the system under high-order stiffness. In addition, most QZS vibration isolators are usually described as a single-degree-of-freedom (SDOF) system ignoring the mass of each component, which greatly affects the equivalent damping and equivalent stiffness of the system. Component mass should be taken as an important factor to further improve the accuracy of the vibration isolator model.
- (2)
- More research on the design and realization of multi-DOF and multi-stage QZS vibration isolation systems is needed. At present, SDOF QZS vibration isolation systems have been studied a lot, but due to the complexity and multidirectionality of excitation in practical engineering, multi-DOF and multistage low-frequency vibration isolation has broader application prospects. By imitating the multi-vertebra structure of a bird’s neck, a multi-stage vibration isolation method has been proposed. Compared with a single QZS system, this method expands the effective range of dynamic displacement and achieves good vibration isolation performance for low- and ultra-low-frequency vibrations. Therefore, the complex nonlinear behavior of these multi-DOF and multi-stage QZS isolators needs to be fully studied.
- (3)
- Composite structures and bio-inspired structures can further improve the vibration isolation performance and promote the diversity of QZS vibration isolators. The composite material has been designed in a special microstructure (unit cell), which has unique dynamic characteristics different from its natural form. Tunable composite materials further expand the application field. In recent years, the development of functional composite materials also provides more possibilities for variable stiffness and damping. In addition, using bio-inspired composite structures can avoid assembly clearance and mechanism wear, and thus reduce production cost and installation space. On the other hand, although composite materials designed in honeycomb structures have been found to be effective in suppressing random and harmonic excitation, and their effectiveness in suppressing impulsive and impact excitation needs to be studied in detail.
- (4)
- The combination of magnetic negative stiffness and intelligent control can further improve the applicability and stability of QZS vibration isolators. Generally, there are many mechanical negative-stiffness structures with an easy fabrication process and a simple working principle, but they have the disadvantages of nonlinearity, prominent contact friction, and limited performance. At present, for magnetic negative stiffness, specially arranged magnets are used to make the non-contact force show the negative-stiffness characteristic. This is a good way to realize QZS vibration isolation. However, more research efforts need to be made in terms of how to improve the volume density, linearity, and working range of magnetic negative-stiffness mechanisms by optimizing magnet structure and array. In addition, the active negative-stiffness mechanism makes the vibration control force show the negative-stiffness characteristic based on displacement feedback. With sufficient accuracy of sensors and actuators, the negative-stiffness characteristics will be accurately controllable, and the best QZS effect can be obtained theoretically. This is also an important research direction in this field. In conclusion, it is recommended to explore the integrated vibration isolators combining non-contact structures with intelligent control in the future.
Author Contributions
Writing—review and editing, Z.M.; project administration, R.Z.; conceptualization and methodology, Q.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (51579242) and the Natural Science Foundation of Hubei Province, China (2018CFB182, the funder is Yang Qingchao), the National Natural Science Foundation of China (51839005, the funder is Zhou Ruiping). The Natural Science Foundation of Hubei Province, China (2022CFB405, the funder is Yang Qingchao).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kim, S.M.; Hong, J.R.; Yoo, H.H. Analysis and design of a torsional vibration isolator for rotating shafts. J. Mech. Sci. Technol. 2019, 33, 4627–4634. [Google Scholar] [CrossRef]
- Wiercigroch, M. Mechanical Vibrations: Theory and Application to Structural Dynamics; John Wiley & Sons Ltd Press: Chichester, UK, 2018; ISBN 978-1-118-90020-8. [Google Scholar] [CrossRef]
- Ibrahim, R.A. Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 2008, 314, 371–452. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Li, J. Negative stiffness devices for vibration isolation applications: A review. Adv. Struct. Eng. 2020, 23, 1739–1755. [Google Scholar] [CrossRef]
- Molyneux, W.G. Supports for Vibration Isolation; Her Majesty’s Stationery Office: London, UK, 1957. [Google Scholar]
- Wang, Y.C.; Lakes, R.S. Extreme stiffness systems due to negative stiffness elements. Am. J. Phys. 2004, 72, 40–50. [Google Scholar] [CrossRef]
- Bažant, Z.; Cedolin, L.; Tabbara, M. New method of analysis for slender columns. ACI Struct. J. 1991, 88, 391–401. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.C.; Ye, K.; Luo, Q. Increase of quasi-zero stiffness region using two pairs of oblique springs. Mech. Syst. Signal Process. 2020, 144, 106975. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.; Ye, K.; Luo, Q. An innovative quasi-zero stiffness isolator with three pairs of oblique springs. Int. J. Mech. Sci. 2021, 192, 106093. [Google Scholar] [CrossRef]
- Zhao, F.; Ji, J.; Luo, Q.; Cao, S.; Chen, L.; Du, W. An improved quasi-zero stiffness isolator with two pairs of oblique springs to increase isolation frequency band. Nonlinear Dyn. 2021, 104, 349–365. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, Y.; Zhou, J.; Lou, J. On the analytical and experimental assessment of the performance of a quasi-zero-stiffness isolator. J. Vib. Control 2014, 20, 2314–2325. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P. Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2007, 301, 678–689. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V., Jr. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Liu, C.; Yu, K.; Liao, B.; Hu, R. Enhanced vibration isolation performance of quasi-zero-stiffness isolator by introducing tunable nonlinear inerter. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105654. [Google Scholar] [CrossRef]
- Gatti, G.; Shaw, A.D.; Gonçalves, P.J.P.; Brennan, M.J. On the detailed design of a quasi-zero stiffness device to assist in the realisation of a translational Lanchester damper. Mech. Syst. Signal Process. 2022, 164, 108258. [Google Scholar] [CrossRef]
- Shaw, A.D.; Gatti, G.; Gonçalves, P.J.P.; Tang, B.; Brennan, M.J. Design and test of an adjustable quasi-zero stiffness device and its use to suspend masses on a multi-modal structure. Mech. Syst. Signal Process. 2021, 152, 107354. [Google Scholar] [CrossRef]
- Liu, Y.; Ji, W.; Gu, H.; Deng, E.; Wang, X.; Song, C. Force transmissibility of a 6-DOF passive quasi-zero stiffness vibration isolation platform. J. Mech. Sci. Technol. 2021, 35, 2313–2324. [Google Scholar] [CrossRef]
- Niu, F.; Meng, L.; Wu, W.; Sun, J.; Zhang, W.; Meng, G.; Rao, Z. Design and analysis of a quasi-zero stiffness isolator using a slotted conical disk spring as negative stiffness structure. J. Vibroeng. 2014, 16, 1769–1785. [Google Scholar]
- Valeev, A.R.; Zotov, A.N.; Kharisov, S.A. Application of disk springs for manufacturing vibration isolators with quasi-zero stiffness. Chem. Petrol. Eng. 2015, 51, 194–200. [Google Scholar] [CrossRef]
- Chen, P.; Zhou, Y. Experiment and Numerical Investigations on a Vertical Isolation System with Quasi-Zero Stiffness Property. In Vibration Engineering for a Sustainable Future; Oberst, S., Halkon, B., Ji, J., Brown, T., Eds.; Springer: Cham, Switzerland, 2021; pp. 255–261. [Google Scholar] [CrossRef]
- Lan, C.C.; Yang, S.A.; Wu, Y.S. Design and experiment of a compact quasi-zero-stiffness isolator capable of a wide range of loads. J. Sound Vib. 2014, 333, 4843–4858. [Google Scholar] [CrossRef]
- Liu, C.; Yu, K. Design and experimental study of a quasi-zero-stiffness vibration isolator incorporating transverse groove springs. Arch. Civ. Mech. Eng. 2020, 20, 67. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. A vibration isolation system in low frequency excitation region using negative stiffness structure for vehicle seat. J. Sound Vib. 2011, 330, 6311–6335. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. Experimental investigation of a vibration isolation system using negative stiffness structure. Int. J. Mech. Sci. 2013, 70, 99–112. [Google Scholar] [CrossRef]
- Liu, C.; Yu, K. Superharmonic resonance of the quasi-zero-stiffness vibration isolator and its effect on the isolation performance. Nonlinear Dyn. 2020, 100, 95–117. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C. An origami inspired quasi-zero stiffness vibration isolator using a novel truss-spring based stack Miura-ori structure. Mech. Syst. Signal Process. 2022, 165, 108383. [Google Scholar] [CrossRef]
- Han, H.; Sorokin, V.; Tang, L.; Cao, D. A nonlinear vibration isolator with quasi-zero-stiffness inspired by Miura-origami tube. Nonlinear Dyn. 2021, 105, 1313–1325. [Google Scholar] [CrossRef]
- Yang, X.; Zheng, J.; Xu, J.; Li, W.; Wang, Y.; Fan, M. Structural design and isolation characteristic analysis of new quasi-zero-stiffness. J. Vib. Eng. Technol. 2020, 8, 47–58. [Google Scholar] [CrossRef]
- Antoniadis, I.; Chronopoulos, D.; Spitas, V.; Koulocheris, D. Hyper-damping properties of a stiff and stable linear oscillator with a negative stiffness element. J. Sound Vib. 2015, 346, 37–52. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Chang, Y.; Ouyang, H.; Xu, D.; Yang, Y. A nonlinear ultra-low-frequency vibration isolator with dual quasi-zero-stiffness mechanism. Nonlinear Dyn. 2020, 101, 755–773. [Google Scholar] [CrossRef]
- Zhu, G.; Liu, J.; Cao, Q.; Cheng, Y.; Lu, Z.; Zhu, Z. A two degree of freedom stable quasi-zero stiffness prototype and its applications in aseismic engineering. Sci. China-Technol. Sci. 2020, 63, 496–505. [Google Scholar] [CrossRef]
- Wu, T.H.; Lan, C.C. A wide-range variable stiffness mechanism for semi-active vibration systems. J. Sound Vib. 2016, 363, 18–32. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H.; Chen, Y.; Gao, P. Beneficial stiffness design of a high-static-low-dynamic-stiffness vibration isolator based on static and dynamic analysis. Int. J. Mech. Sci. 2018, 142, 235–244. [Google Scholar] [CrossRef]
- Kashdan, L.; Seepersad, C.C.; Haberman, M.; Wilson, P.S. Design, fabrication, and evaluation of negative stiffness elements using SLS. Rapid Prototyp. J. 2012, 18, 194–200. [Google Scholar] [CrossRef]
- Fulcher, B.A.; Shahan, D.W.; Haberman, M.R.; Conner Seepersad, C.; Wilson, P.S. Analytical and experimental investigation of buckled beams as negative stiffness elements for passive vibration and shock isolation systems. J. Vib. Acoust.-Trans. ASME. 2014, 136, 031009. [Google Scholar] [CrossRef]
- Liu, X.; Huang, X.; Hua, H. On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector. J. Sound Vib. 2013, 332, 3359–3376. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, Q.; Zhang, Z.; Zhou, X. An experiment investigation on the effect of Coulomb friction on the displacement transmissibility of a quasi-zero stiffness isolator. J. Mech. Sci. Technol. 2019, 33, 121–127. [Google Scholar] [CrossRef]
- Huang, X.; Liu, X.; Sun, J.; Zhang, Z.; Hua, H. Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector: A theoretical and experimental study. J. Sound Vib. 2014, 333, 1132–1148. [Google Scholar] [CrossRef]
- Kim, J.; Jeon, Y.; Um, S.; Park, U.; Kim, K.S.; Kim, S. A novel passive quasi-zero stiffness isolator for ultra-precision measurement systems. Int. J. Precis. Eng. Manuf. 2019, 20, 1573–1580. [Google Scholar] [CrossRef]
- Zou, D.; Liu, G.; Rao, Z.; Tan, T.; Zhang, W.; Liao, W.H. A device capable of customizing nonlinear forces for vibration energy harvesting, vibration isolation, and nonlinear energy sink. Mech. Syst. Signal Process. 2021, 147, 107101. [Google Scholar] [CrossRef]
- Gatti, G. An adjustable device to adaptively realise diverse nonlinear force-displacement characteristics. Mech. Syst. Signal Process. 2022, 180, 109379. [Google Scholar] [CrossRef]
- Sun, M.; Song, G.; Li, Y.; Huang, Z. Effect of negative stiffness mechanism in a vibration isolator with asymmetric and high-static-low-dynamic stiffness. Mech. Syst. Signal Process. 2019, 124, 388–407. [Google Scholar] [CrossRef]
- Liu, Y.; Ji, W.; Xu, L.; Gu, H.; Song, C. Dynamic characteristics of quasi-zero stiffness vibration isolation system for coupled dynamic vibration absorber. Arch. Appl. Mech. 2021, 91, 3799–3818. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, X.; Xu, D.; Bishop, S. Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam–roller–spring mechanisms. J. Sound Vib. 2015, 346, 53–69. [Google Scholar] [CrossRef]
- Zhou, J.; Xiao, Q.; Xu, D.; Ouyang, H.; Li, Y. A novel quasi-zero-stiffness strut and its applications in six-degree-of-freedom vibration isolation platform. J. Sound Vib. 2017, 394, 59–74. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Xu, D. Sensitivity analysis of parametric errors on the performance of a torsion quasi-zero-stiffness vibration isolator. Int. J. Mech. Sci. 2017, 134, 336–346. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, D.; Bishop, S. A torsion quasi-zero stiffness vibration isolator. J. Sound Vib. 2015, 338, 121–133. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C.; Brown, T. A novel integrated quasi-zero stiffness vibration isolator for coupled translational and rotational vibrations. Mech. Syst. Signal Process. 2021, 149, 107340. [Google Scholar] [CrossRef]
- Sun, Y.; Zhou, J.; Thompson, D.; Yuan, T.; Gong, D.; You, T. Design, analysis and experimental validation of high static and low dynamic stiffness mounts based on target force curves. Int. J. Non-Linear Mech. 2020, 126, 103559. [Google Scholar] [CrossRef]
- Yao, Y.; Li, H.; Li, Y.; Wang, X. Analytical and experimental investigation of a high-static-low-dynamic stiffness isolator with cam-roller-spring mechanism. Int. J. Mech. Sci. 2020, 186, 105888. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, L.; Song, C.; Gu, H.; Ji, W. Dynamic characteristics of a quasi-zero stiffness vibration isolator with nonlinear stiffness and damping. Arch. Appl. Mech. 2019, 89, 1743–1759. [Google Scholar] [CrossRef]
- Zuo, S.; Wang, D.; Zhang, Y.; Luo, Q. Design and testing of a parabolic cam-roller quasi-zero-stiffness vibration isolator. Int. J. Mech. Sci. 2022, 220, 107146. [Google Scholar] [CrossRef]
- Li, M.; Cheng, W.; Xie, R. A quasi-zero-stiffness vibration isolator using a cam mechanism with user-defined profile. Int. J. Mech. Sci. 2021, 189, 105938. [Google Scholar] [CrossRef]
- Ye, K.; Ji, J.C.; Brown, T. Design of a quasi-zero stiffness isolation system for supporting different loads. J. Sound Vib. 2020, 471, 115198. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wu, C. A state-of-the-art review on low-frequency nonlinear vibration isolation with electromagnetic mechanisms. Appl. Math. Mech.-Engl. Ed. 2022, 43, 1045–1062. [Google Scholar] [CrossRef]
- Wang, S.; Xin, W.; Ning, Y.; Li, B.; Hu, Y. Design, experiment, and improvement of a quasi-zero-stiffness vibration isolation system. Appl. Sci. 2020, 10, 2273. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Luo, Y.; Yan, B.; Ma, C. Design and experiment of a high-static–low-dynamic stiffness isolator using a negative stiffness magnetic spring. J. Sound Vib. 2016, 360, 31–52. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Luo, Y.; Zhang, Y.; Xie, S. Analytical study of a quasi-zero stiffness coupling using a torsion magnetic spring with negative stiffness. Mech. Syst. Signal Process. 2018, 100, 135–151. [Google Scholar] [CrossRef]
- Xu, J.; Yang, X.; Li, W.; Zheng, J.; Wang, Y.; Fan, M.; Lu, Y. Design of quasi-zero stiffness joint actuator and research on vibration isolation performance. J. Sound Vib. 2020, 479, 115367. [Google Scholar] [CrossRef]
- Xu, D.; Yu, Q.; Zhou, J.; Bishop, S.R. Theoretical and experimental analyses of a nonlinear magnetic vibration isolator with quasi-zero-stiffness characteristic. J. Sound Vib. 2013, 332, 3377–3389. [Google Scholar] [CrossRef]
- Wang, Q.; Zhou, J.; Wang, K.; Xu, D.; Wen, G. Design and experimental study of a compact quasi-zero-stiffness isolator using wave springs. Sci. China-Technol. Sci. 2021, 64, 2255–2271. [Google Scholar] [CrossRef]
- Wu, W.; Chen, X.; Shan, Y. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness. J. Sound Vib. 2014, 333, 2958–2970. [Google Scholar] [CrossRef]
- Yan, B.; Wang, X.; Wang, Z.; Wu, C.; Zhang, W. Enhanced lever-type vibration isolator via electromagnetic shunt damping. Int. J. Mech. Sci. 2022, 218, 107070. [Google Scholar] [CrossRef]
- Yan, B.; Yu, N.; Wang, Z.; Wu, C.; Wang, S.; Zhang, W. Lever-type quasi-zero stiffness vibration isolator with magnetic spring. J. Sound Vib. 2022, 527, 116865. [Google Scholar] [CrossRef]
- Liu, C.; Zhao, R.; Yu, K.; Liao, B. In-plane quasi-zero-stiffness vibration isolator using magnetic interaction and cables: Theoretical and experimental study. Appl. Math. Model. 2021, 96, 497–522. [Google Scholar] [CrossRef]
- Shan, Y.; Wu, W.; Chen, X. Design of a miniaturized pneumatic vibration isolator with high-static-low-dynamic stiffness. J. Vib. Acoust.-Trans. ASME 2015, 137, 045001. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.; Zhao, C.; Wu, C.; Wang, K.; Wang, P. A vari-stiffness nonlinear isolator with magnetic effects: Theoretical modeling and experimental verification. Int. J. Mech. Sci. 2018, 148, 745–755. [Google Scholar] [CrossRef]
- Ma, H.; Yan, B. Nonlinear damping and mass effects of electromagnetic shunt damping for enhanced nonlinear vibration isolation. Mech. Syst. Signal Process. 2021, 146, 107010. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.; Zhang, L.; Zheng, W.; Wang, K.; Wu, C. A bistable vibration isolator with nonlinear electromagnetic shunt damping. Mech. Syst. Signal Process. 2020, 136, 106504. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, X.; Xie, S.; Yan, B.; Luo, Y. Simulated and experimental studies on a high-static-low-dynamic stiffness isolator using magnetic negative stiffness spring. Mech. Syst. Signal Process. 2017, 86, 188–203. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, Y.; Luo, Y.; Xie, S.; Zhang, X. Enhanced isolation performance of a high-static–low-dynamic stiffness isolator with geometric nonlinear damping. Nonlinear Dyn. 2018, 93, 2339–2356. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, X.; Luo, Y.; Zhang, Y.; Xie, S. Analytical study of the low frequency multi-direction isolator with high-static-low-dynamic stiffness struts and spatial pendulum. Mech. Syst. Signal Process. 2018, 110, 521–539. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, K.; Xu, D.; Ouyang, H.; Li, Y. A six degrees-of-freedom vibration isolation platform supported by a hexapod of quasi-zero-stiffness struts. J. Vib. Acoust.-Trans. ASME 2017, 139, 034502. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Q.; Yan, B.; Luo, Y.; Zhang, X. A Stewart isolator with high-static-low-dynamic stiffness struts based on negative stiffness magnetic springs. J. Sound Vib. 2018, 422, 390–408. [Google Scholar] [CrossRef]
- Yuan, S.; Sun, Y.; Wang, M.; Ding, J.; Zhao, J.; Huang, Y.; Yang, X.D. Tunable negative stiffness spring using maxwell normal stress. Int. J. Mech. Sci. 2021, 193, 106127. [Google Scholar] [CrossRef]
- Jiang, Y.; Song, C.; Ding, C.; Xu, B. Design of magnetic-air hybrid quasi-zero stiffness vibration isolation system. J. Sound Vib. 2020, 477, 115346. [Google Scholar] [CrossRef]
- Yuan, S.; Sun, Y.; Zhao, J.; Meng, K.; Wang, M.; Pu, H.; Xie, S. A tunable quasi-zero stiffness isolator based on a linear electromagnetic spring. J. Sound Vib. 2020, 482, 115449. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, J.; Wang, M.; Sun, Y.; Pu, H.; Luo, J.; Yang, Y. High-static–low-dynamic stiffness isolator with tunable electromagnetic mechanism. IEEE-ASME Trans. Mechatron. 2019, 25, 316–326. [Google Scholar] [CrossRef]
- Sun, Y.; Meng, K.; Yuan, S.; Zhao, J.; Xie, R.; Yang, Y.; Pu, H. Modeling electromagnetic force and axial-stiffness for an electromagnetic negative-stiffness spring toward vibration isolation. IEEE Trans. Magn. 2019, 55, 1–10. [Google Scholar] [CrossRef]
- Robertson, W.S.; Kidner, M.R.F.; Cazzolato, B.S.; Zander, A.C. Theoretical design parameters for a quasi-zero stiffness magnetic spring for vibration isolation. J. Sound Vib. 2009, 326, 88–103. [Google Scholar] [CrossRef]
- Li, Q.; Zhu, Y.; Xu, D.; Hu, J.; Min, W.; Pang, L. A negative stiffness vibration isolator using magnetic spring combined with rubber membrane. J. Mech. Sci. Technol. 2013, 27, 813–824. [Google Scholar] [CrossRef]
- Zhu, T.; Cazzolato, B.; Robertson, W.S.; Zander, A. Vibration isolation using six degree-of-freedom quasi-zero stiffness magnetic levitation. J. Sound Vib. 2015, 358, 48–73. [Google Scholar] [CrossRef]
- Kamaruzaman, N.A.; Robertson, W.S.; Ghayesh, M.H.; Cazzolato, B.S.; Zander, A.C. Six degree of freedom quasi-zero stiffness magnetic spring with active control: Theoretical analysis of passive versus active stability for vibration isolation. J. Sound Vib. 2021, 502, 116086. [Google Scholar] [CrossRef]
- Kamaruzaman, N.A.; Robertson, W.S.; Ghayesh, M.H.; Cazzolato, B.S.; Zander, A.C. Vibration Isolation Performance of an LQR-Stabilised Planar Quasi-zero Stiffness Magnetic Levitation System. In Vibration Engineering for a Sustainable Future; Oberst, S., Halkon, B., Ji, J., Brown, T., Eds.; Springer: Cham, Switzerland, 2021; pp. 237–243. [Google Scholar] [CrossRef]
- Dai, H.; Jing, X.; Wang, Y.; Yue, X.; Yuan, J. Post-capture vibration suppression of spacecraft via a bio-inspired isolation system. Mech. Syst. Signal Process. 2018, 105, 214–240. [Google Scholar] [CrossRef]
- Wu, Z.; Jing, X.; Bian, J.; Li, F.; Allen, R. Vibration isolation by exploring bio-inspired structural nonlinearity. Bioinspir. Biomim. 2015, 10, 056015. [Google Scholar] [CrossRef]
- Gatti, G. Optimizing elastic potential energy via geometric nonlinear stiffness. Commun. Nonlinear Sci. Numer. Simul. 2021, 103, 106035. [Google Scholar] [CrossRef]
- Chong, X.; Wu, Z.; Li, F. Vibration isolation properties of the nonlinear X-combined structure with a high-static and low-dynamic stiffness: Theory and experiment. Mech. Syst. Signal Process. 2022, 179, 109352. [Google Scholar] [CrossRef]
- Wang, Y.; Jing, X.; Guo, Y. Nonlinear analysis of a bio-inspired vertically asymmetric isolation system under different structural constraints. Nonlinear Dyn. 2019, 95, 445–464. [Google Scholar] [CrossRef]
- Yan, G.; Zou, H.X.; Wang, S.; Zhao, L.C.; Wu, Z.Y.; Zhang, W.M. Bio-inspired vibration isolation: Methodology and design. Appl. Mech. Rev. 2021, 73, 020801. [Google Scholar] [CrossRef]
- Dai, H.; Jing, X.; Sun, C.; Wang, Y.; Yue, X. Accurate modeling and analysis of a bio-inspired isolation system: With application to on-orbit capture. Mech. Syst. Signal Process. 2018, 109, 111–133. [Google Scholar] [CrossRef]
- Hu, F.; Jing, X. A 6-DOF passive vibration isolator based on Stewart structure with X-shaped legs. Nonlinear Dyn. 2018, 91, 157–185. [Google Scholar] [CrossRef]
- Chai, Y.; Jing, X.; Guo, Y. A compact X-shaped mechanism based 3-DOF anti-vibration unit with enhanced tunable QZS property. Mech. Syst. Signal Process. 2022, 168, 108651. [Google Scholar] [CrossRef]
- Sun, X.; Jing, X. A nonlinear vibration isolator achieving high-static-low-dynamic stiffness and tunable anti-resonance frequency band. Mech. Syst. Signal Process. 2016, 80, 166–188. [Google Scholar] [CrossRef]
- Yan, G.; Zou, H.X.; Wang, S.; Zhao, L.C.; Wu, Z.Y.; Zhang, W.M. Bio-inspired toe-like structure for low-frequency vibration isolation. Mech. Syst. Signal Process. 2022, 162, 108010. [Google Scholar] [CrossRef]
- Chai, Y.; Jing, X.; Chao, X. X-shaped mechanism based enhanced tunable QZS property for passive vibration isolation. Int. J. Mech. Sci. 2022, 218, 107077. [Google Scholar] [CrossRef]
- Wu, Z.; Jing, X.; Sun, B.; Li, F. A 6DOF passive vibration isolator using X-shape supporting structures. J. Sound Vib. 2016, 380, 90–111. [Google Scholar] [CrossRef]
- Dai, H.; Cao, X.; Jing, X.; Wang, X.; Yue, X. Bio-inspired anti-impact manipulator for capturing non-cooperative spacecraft: Theory and experiment. Mech. Syst. Signal Process. 2020, 142, 106785. [Google Scholar] [CrossRef]
- Yan, G.; Zou, H.X.; Wang, S.; Zhao, L.C.; Gao, Q.H.; Tan, T.; Zhang, W.M. Large stroke quasi-zero stiffness vibration isolator using three-link mechanism. J. Sound Vib. 2020, 478, 115344. [Google Scholar] [CrossRef]
- Yan, G.; Wang, S.; Zou, H.; Zhao, L.; Gao, Q.; Zhang, W. Bio-inspired polygonal skeleton structure for vibration isolation: Design, modelling, and experiment. Sci. China-Technol. Sci. 2020, 63, 2617–2630. [Google Scholar] [CrossRef]
- Sun, X.; Xu, J.; Wang, F.; Zhang, S. A novel isolation structure with flexible joints for impact and ultralow-frequency excitations. Int. J. Mech. Sci. 2018, 146, 366–376. [Google Scholar] [CrossRef]
- Zeng, R.; Wen, G.; Zhou, J.; Zhao, G. Limb-inspired bionic quasi-zero stiffness vibration isolator. Acta Mech. Sin. 2021, 37, 1152–1167. [Google Scholar] [CrossRef]
- Deng, T.; Wen, G.; Ding, H.; Lu, Z.Q.; Chen, L.Q. A bio-inspired isolator based on characteristics of quasi-zero stiffness and bird multi-layer neck. Mech. Syst. Signal Process. 2020, 145, 106967. [Google Scholar] [CrossRef]
- Jin, G.; Wang, Z.; Yang, T. Cascaded quasi-zero stiffness nonlinear low-frequency vibration isolator inspired by human spine. Appl. Math. Mech.-Engl. Ed. 2022, 43, 813–824. [Google Scholar] [CrossRef]
- Sun, X.; Qi, Z.; Xu, J. A novel multi-layer isolation structure for transverse stabilization inspired by neck structure. Acta Mech. Sin. 2022, 38, 521543. [Google Scholar] [CrossRef]
- Zeng, R.; Yin, S.; Wen, G.; Zhou, J. A non-smooth quasi-zero-stiffness isolator with displacement constraints. Int. J. Mech. Sci. 2022, 225, 107351. [Google Scholar] [CrossRef]
- Bian, J.; Jing, X. Analysis and design of a novel and compact X-structured vibration isolation mount (X-Mount) with wider quasi-zero-stiffness range. Nonlinear Dyn. 2020, 101, 2195–2222. [Google Scholar] [CrossRef]
- Sun, X.; Jing, X. Multi-direction vibration isolation with quasi-zero stiffness by employing geometrical nonlinearity. Mech. Syst. Signal Process. 2015, 62, 149–163. [Google Scholar] [CrossRef]
- Lakes, R.S. Extreme damping in compliant composites with a negative-stiffness phase. Philos. Mag. Lett. 2001, 81, 95–100. [Google Scholar] [CrossRef]
- Lakes, R.S.; Lee, T.; Bersie, A.; Wang, Y.C. Extreme damping in composite materials with negative-stiffness inclusions. Nature 2001, 410, 565–567. [Google Scholar] [CrossRef]
- Lakes, R.S.; Drugan, W.J. Dramatically stiffer elastic composite materials due to a negative stiffness phase? J. Mech. Phys. Solids 2002, 50, 979–1009. [Google Scholar] [CrossRef]
- Drugan, W.J. Elastic composite materials having a negative stiffness phase can be stable. Phys. Rev. Lett. 2007, 98, 055502. [Google Scholar] [CrossRef]
- Izard, A.G.; Alfonso, R.F.; McKnight, G.; Valdevit, L. Optimal design of a cellular material encompassing negative stiffness elements for unique combinations of stiffness and elastic hysteresis. Mater. Des. 2017, 135, 37–50. [Google Scholar] [CrossRef]
- Correa, D.M.; Klatt, T.; Cortes, S.; Haberman, M.; Kovar, D.; Seepersad, C. Negative stiffness honeycombs for recoverable shock isolation. Rapid Prototyp. J. 2015, 21, 193–200. [Google Scholar] [CrossRef]
- Virk, K.; Monti, A.; Trehard, T.; Marsh, M.; Hazra, K.; Boba, K.; Farrow, I.R. SILICOMB PEEK Kirigami cellular structures: Mechanical response and energy dissipation through zero and negative stiffness. Smart Mater. Struct. 2013, 22, 084014. [Google Scholar] [CrossRef]
- Cai, C.; Zhou, J.; Wu, L.; Wang, K.; Xu, D.; Ouyang, H. Design and numerical validation of quasi-zero-stiffness metamaterials for very low-frequency band gaps. Compos. Struct. 2020, 236, 111862. [Google Scholar] [CrossRef]
- Zhou, J.; Pan, H.; Cai, C.; Xu, D. Tunable ultralow frequency wave attenuations in one-dimensional quasi-zero-stiffness metamaterial. Int. J. Mech. Mater. Des. 2021, 17, 285–300. [Google Scholar] [CrossRef]
- Fan, H.; Yang, L.; Tian, Y.; Wang, Z. Design of metastructures with quasi-zero dynamic stiffness for vibration isolation. Compos. Struct. 2020, 243, 112244. [Google Scholar] [CrossRef]
- Ren, C.; Yang, D.; Qin, H. Mechanical performance of multidirectional buckling-based negative stiffness metamaterials: An analytical and numerical study. Materials 2018, 11, 1078. [Google Scholar] [CrossRef]
- Sun, X.; Xu, J.; Fu, J. The effect and design of time delay in feedback control for a nonlinear isolation system. Mech. Syst. Signal Process. 2017, 87, 206–217. [Google Scholar] [CrossRef]
- Sun, X.; Wang, F.; Xu, J. Dynamics and realization of a feedback-controlled nonlinear isolator with variable time delay. J. Vib. Acoust.-Trans. ASME 2019, 141, 021005. [Google Scholar] [CrossRef]
- Pu, H.; Yuan, S.; Peng, Y.; Meng, K.; Zhao, J.; Xie, R.; Chen, X. Multi-layer electromagnetic spring with tunable negative stiffness for semi-active vibration isolation. Mech. Syst. Signal Process. 2019, 121, 942–960. [Google Scholar] [CrossRef]
- Zhang, F.; Shao, S.; Tian, Z.; Xu, M.; Xie, S. Active-passive hybrid vibration isolation with magnetic negative stiffness isolator based on Maxwell normal stress. Mech. Syst. Signal Process. 2019, 123, 244–263. [Google Scholar] [CrossRef]
- Sun, X.; Xu, J.; Jing, X.; Cheng, L. Beneficial performance of a quasi-zero-stiffness vibration isolator with time-delayed active control. Int. J. Mech. Sci. 2014, 82, 32–40. [Google Scholar] [CrossRef]
- Liu, S.; Feng, L.; Zhao, D.; Shi, X.; Zhang, Y.; Jiang, J.; Chen, L. A real-time controllable electromagnetic vibration isolator based on magnetorheological elastomer with quasi-zero stiffness characteristic. Smart Mater. Struct. 2019, 28, 085037. [Google Scholar] [CrossRef]
- Xu, J.; Sun, X. A multi-directional vibration isolator based on Quasi-Zero-Stiffness structure and time-delayed active control. Int. J. Mech. Sci. 2015, 100, 126–135. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Ouyang, H.; Cheng, L.; Xu, D. A semi-active metamaterial beam with electromagnetic quasi-zero-stiffness resonators for ultralow-frequency band gap tuning. Int. J. Mech. Sci. 2020, 176, 105548. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Cheng, C.; Su, Y. Adaptive control of a vehicle-seat-human coupled model using quasi-zero-stiffness vibration isolator as seat suspension. J. Mech. Sci. Technol. 2018, 32, 2973–2985. [Google Scholar] [CrossRef]
- Ahn, K.K. Active pneumatic vibration isolation system using negative stiffness structures for a vehicle seat. J. Sound Vib. 2014, 333, 1245–1268. [Google Scholar] [CrossRef]
- Le, T.D.; Ahn, K.K. Fuzzy sliding mode controller of a pneumatic active isolating system using negative stiffness structure. J. Mech. Sci. Technol. 2012, 26, 3873–3884. [Google Scholar] [CrossRef]
- Zhao, Y.; Cui, J.; Zhao, J.; Bian, X.; Zou, L. Improving Low Frequency Isolation Performance of Optical Platforms Using Electromagnetic Active-Negative-Stiffness Method. Appl. Sci. 2020, 10, 7342. [Google Scholar] [CrossRef]
- Pan, H.; Jing, X.; Sun, W.; Gao, H. A bioinspired dynamics-based adaptive tracking control for nonlinear suspension systems. IEEE Trans. Control Syst. Technol. 2017, 26, 903–914. [Google Scholar] [CrossRef]
- Kim, M.H.; Kim, H.Y.; Kim, H.C.; Ahn, D.; Gweon, D.G. Design and control of a 6-DOF active vibration isolation system using a Halbach magnet array. IEEE-ASME Trans. Mechatron. 2016, 21, 2185–2196. [Google Scholar] [CrossRef]
- Chang, Y.; Zhou, J.; Wang, K.; Xu, D. Theoretical and experimental investigations on semi-active quasi-zero-stiffness dynamic vibration absorber. Int. J. Mech. Sci. 2022, 214, 106892. [Google Scholar] [CrossRef]
- Zhao, Y.; Meng, G. A bio-inspired semi-active vibration isolator with variable-stiffness dielectric elastomer: Design and modeling. J. Sound Vib. 2020, 485, 115592. [Google Scholar] [CrossRef]
- Palomares, E.; Nieto, A.J.; Morales, A.L.; Chicharro, J.M.; Pintado, P. Numerical and experimental analysis of a vibration isolator equipped with a negative stiffness system. J. Sound Vib. 2018, 414, 31–42. [Google Scholar] [CrossRef]
- Alabuzhev, P.M. Vibration Protection and Measuring Systems with Quasi-Zero Stiffness; CRC Press: Boca Raton, FL, USA, 1989; ISBN 0-89116-811-7. [Google Scholar]
- Tobias, S.A. Design of small isolator units for the suppression of low-frequency vibration. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 1959, 1, 280–292. [Google Scholar] [CrossRef]
- Ravindra, B.; Mallik, A.K. Performance of non-linear vibration isolators under harmonic excitation. J. Sound Vib. 1994, 170, 325–337. [Google Scholar] [CrossRef]
- Brennan, M.J.; Kovacic, I.; Carrella, A.; Waters, T.P. On the jump-up and jump-down frequencies of the Duffing oscillator. J. Sound Vib. 2008, 318, 1250–1261. [Google Scholar] [CrossRef]
- Jiang, G.; Jing, X.; Guo, Y. A novel bio-inspired multi-joint anti-vibration structure and its nonlinear HSLDS properties. Mech. Syst. Signal Process. 2020, 138, 106552. [Google Scholar] [CrossRef]
- Saif, M.T.A. On a tunable bistable MEMS-theory and experiment. J. Microelectromech. Syst. 2000, 9, 157–170. [Google Scholar] [CrossRef]
- Sherman, C.H.; Butler, J.L. Transducers and Arrays for Underwater Sound; Springer: New York, NY, USA, 2007; ISBN 978-0-387-32940-6. [Google Scholar]
- Kashdan, L.B. Evaluation of Negative Stiffness Elements for Enhanced Material Damping Capacity. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2010. Available online: http://hdl.handle.net/2152/ETD-UT-2010-05-1301 (accessed on 1 May 2010).
- Gao, X.; Chen, Q. Nonlinear analysis, design and vibration isolation for a bilinear system with time-delayed cubic velocity feedback. J. Sound Vib. 2014, 333, 1562–1576. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X.; Daley, S.; Li, F. Recent advances in micro-vibration isolation. Mech. Syst. Signal Process. 2015, 56, 55–80. [Google Scholar] [CrossRef]
- Ledezma-Ramírez, D.F.; Tapia-González, P.E.; Ferguson, N.; Brennan, M.; Tang, B. Recent advances in shock vibration isolation: An overview and future possibilities. Appl. Mech. Rev. 2019, 71, 060802. [Google Scholar] [CrossRef]
- Zhao, G.; Ding, B.; Watchi, J.; Deraemaeker, A.; Collette, C. Experimental study on active seismic isolation using interferometric inertial sensors. Mech. Syst. Signal Process. 2020, 145, 106959. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).