Author Contributions
Conceptualization, methodology, software, data analysis, writing-Original draft preparation, W.G.; Writ-ing-review and editing, Experimental analysis, G.W.; Investigation, validation, J.Z.; Investigation, val-idation, Z.F.; Investigation, Supervision, X.L.; Investigation, Supervision, W.W. All authors have read and agreed to the published version of the manuscript.
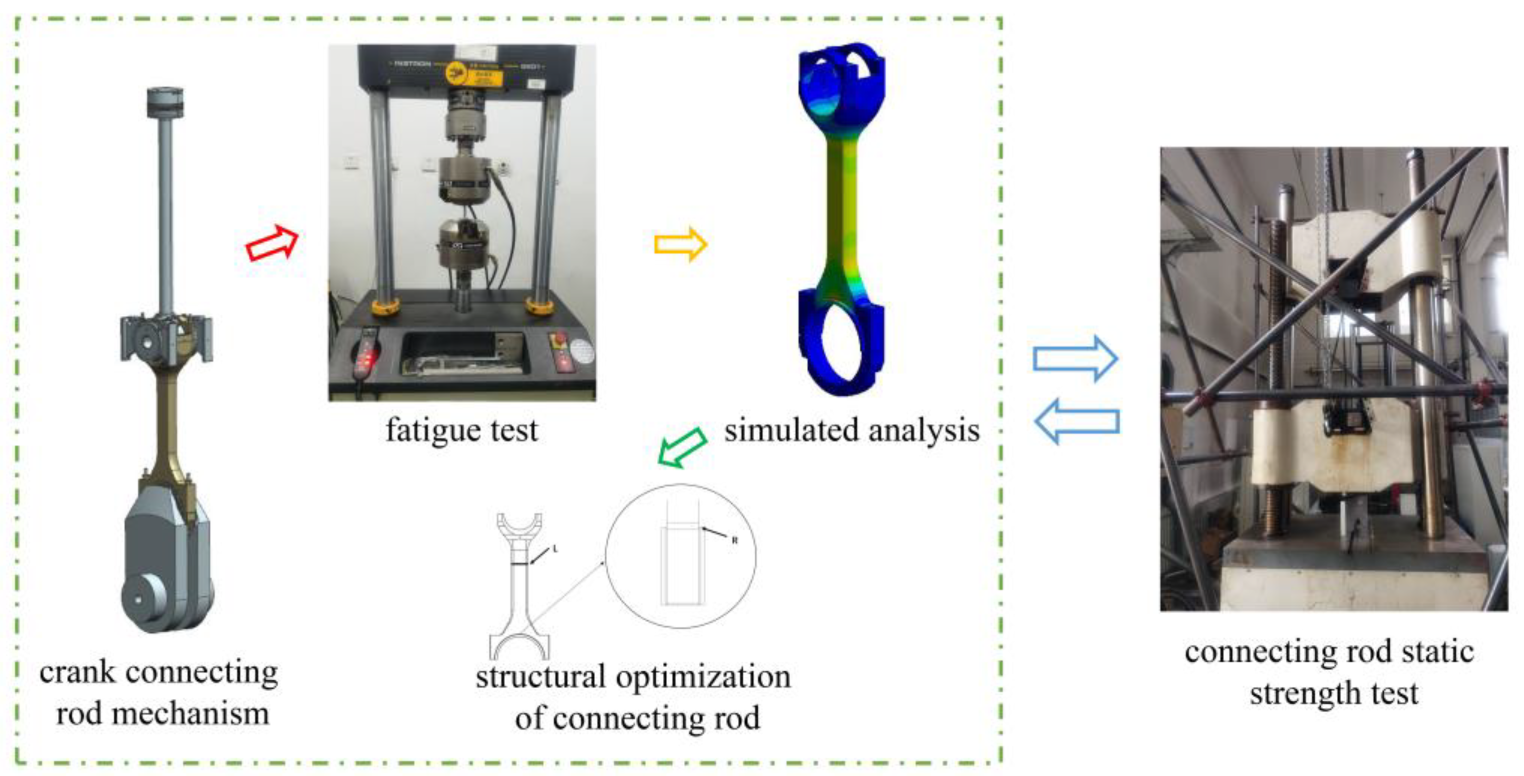
Figure 1.
Overall diagram of structural optimization design and strength test of connecting rod assembly of high-power low-speed diesel engine.
Figure 1.
Overall diagram of structural optimization design and strength test of connecting rod assembly of high-power low-speed diesel engine.
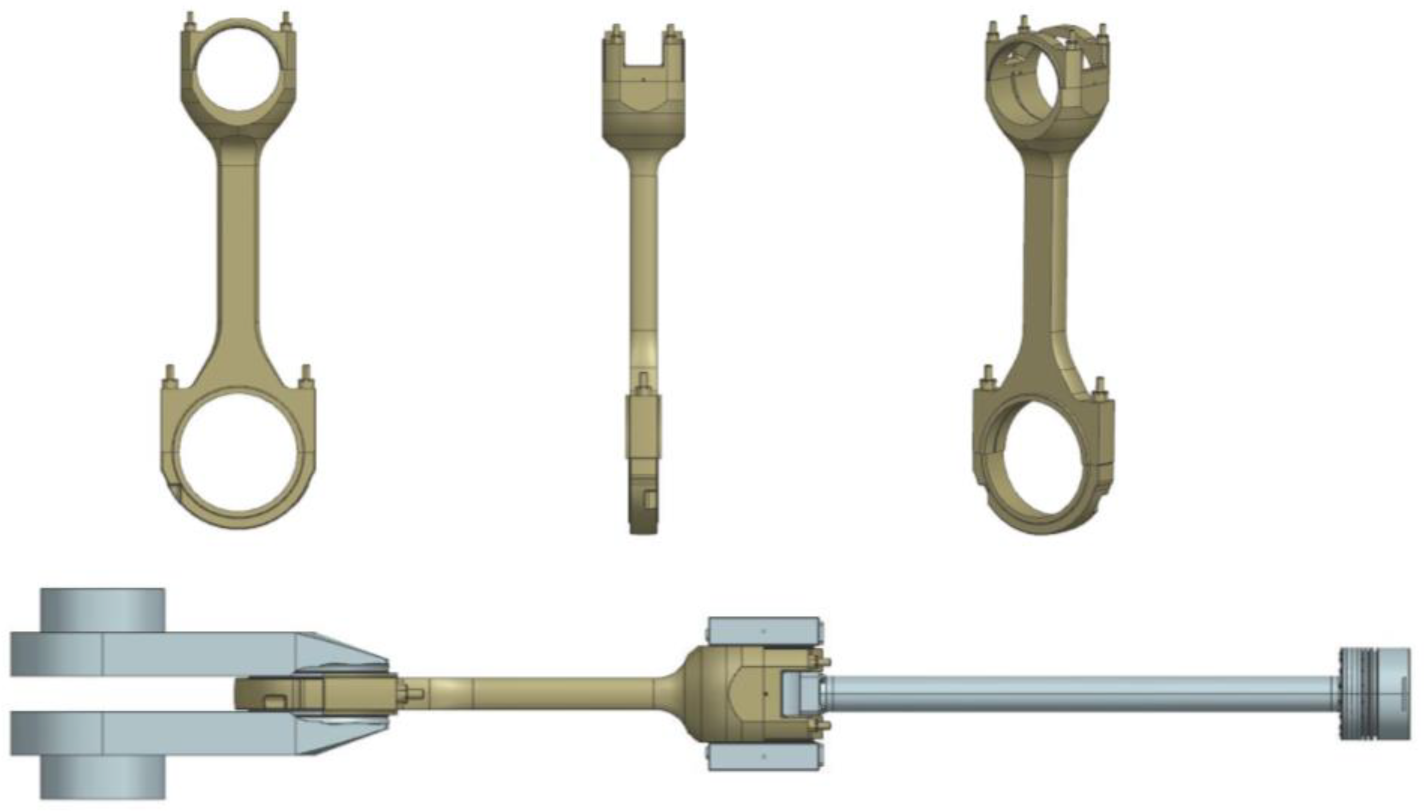
Figure 2.
Crank connecting rod mechanism model.
Figure 2.
Crank connecting rod mechanism model.
Figure 3.
Meshing of connecting rod assembly.
Figure 3.
Meshing of connecting rod assembly.
Figure 4.
Meshing of the rest of the components.
Figure 4.
Meshing of the rest of the components.
Figure 5.
Sample rod for fatigue test.
Figure 5.
Sample rod for fatigue test.
Figure 6.
Electro-hydraulic servo fatigue testing machine.
Figure 6.
Electro-hydraulic servo fatigue testing machine.
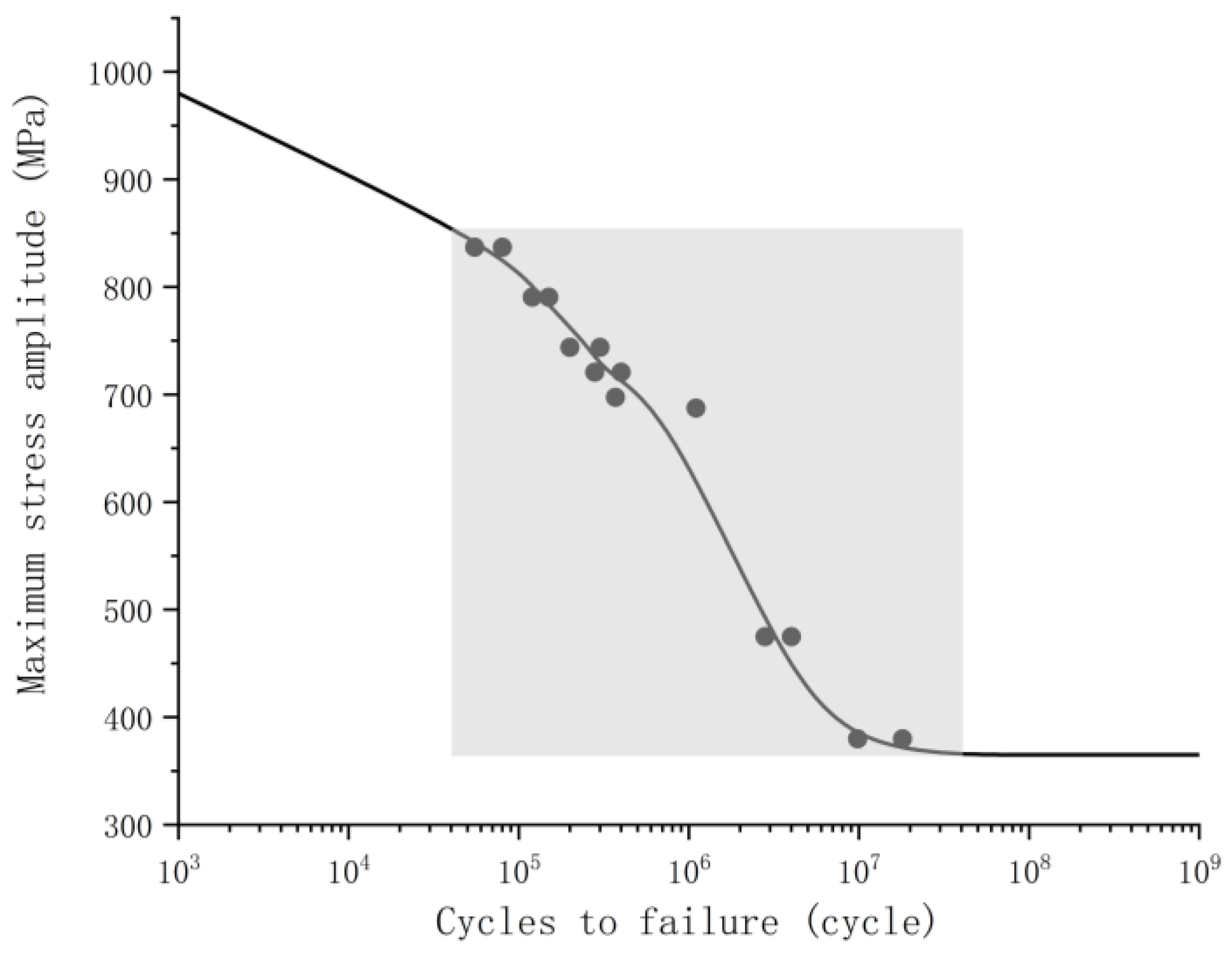
Figure 7.
S-N curve of 42CrMoA.
Figure 7.
S-N curve of 42CrMoA.
Figure 8.
Local magnification of S-N curve.
Figure 8.
Local magnification of S-N curve.
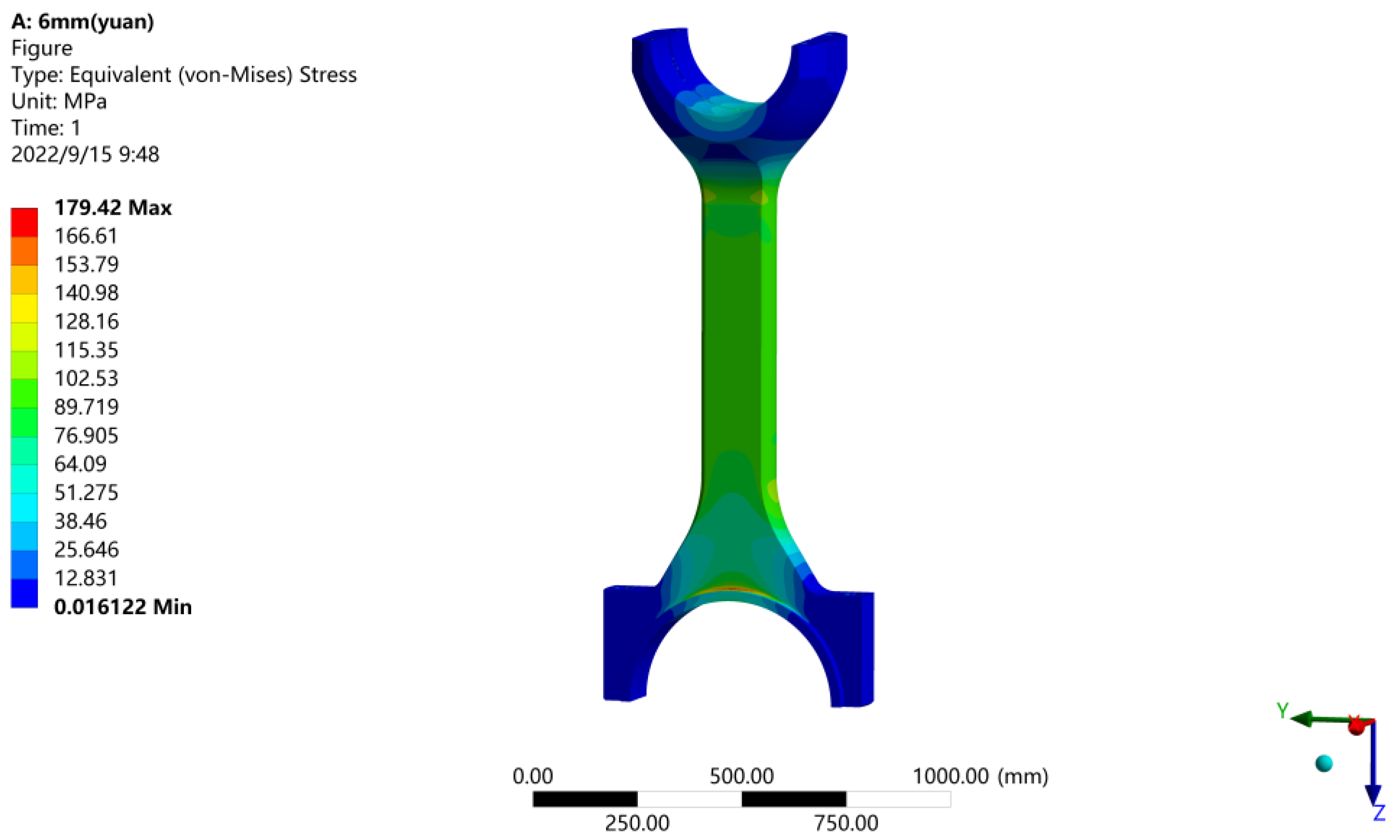
Figure 9.
Stress diagram of the connecting rod assembly.
Figure 9.
Stress diagram of the connecting rod assembly.
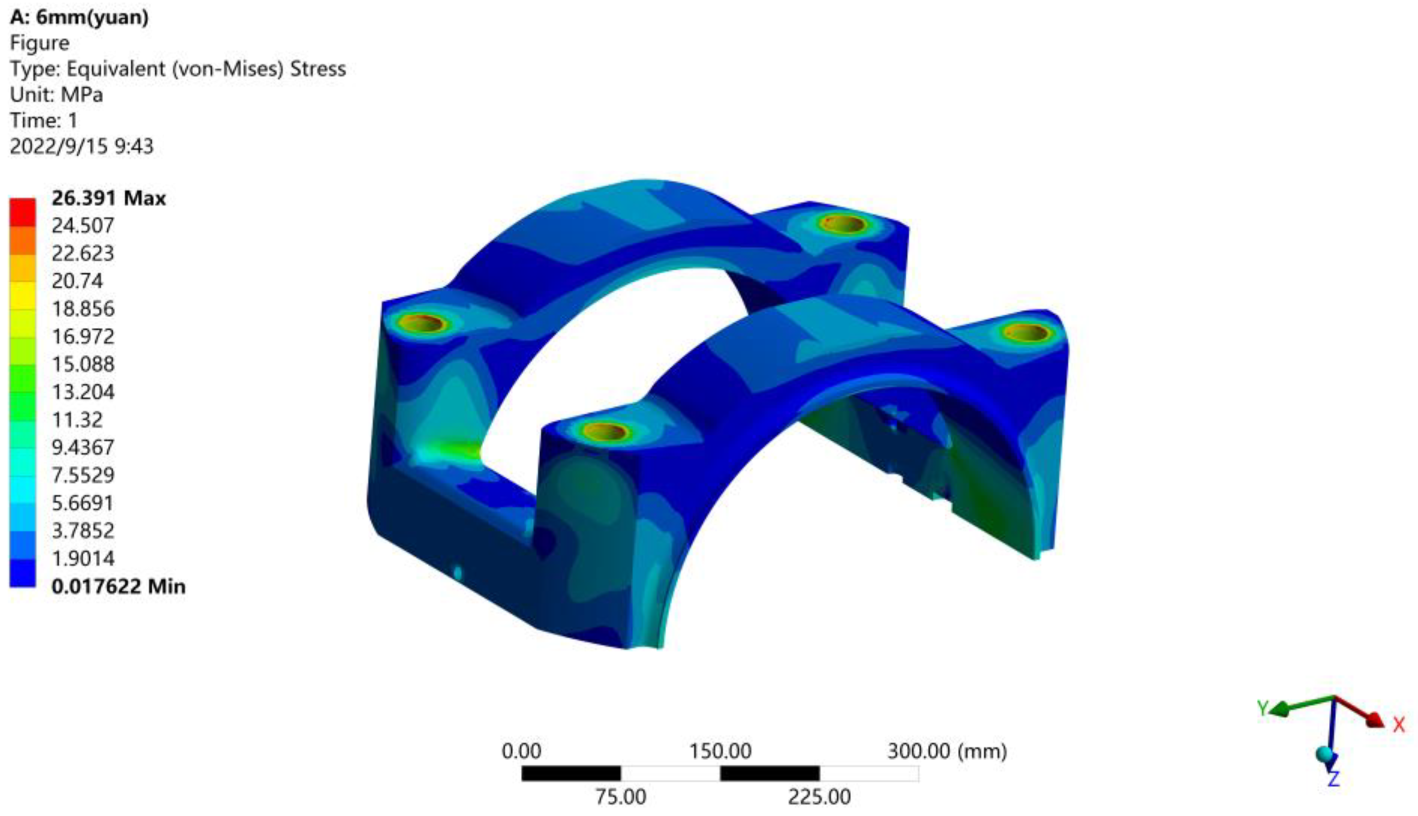
Figure 10.
Stress diagram of small end bearing cover of connecting rod.
Figure 10.
Stress diagram of small end bearing cover of connecting rod.
Figure 11.
Stress diagram of large end bearing cover of connecting rod.
Figure 11.
Stress diagram of large end bearing cover of connecting rod.
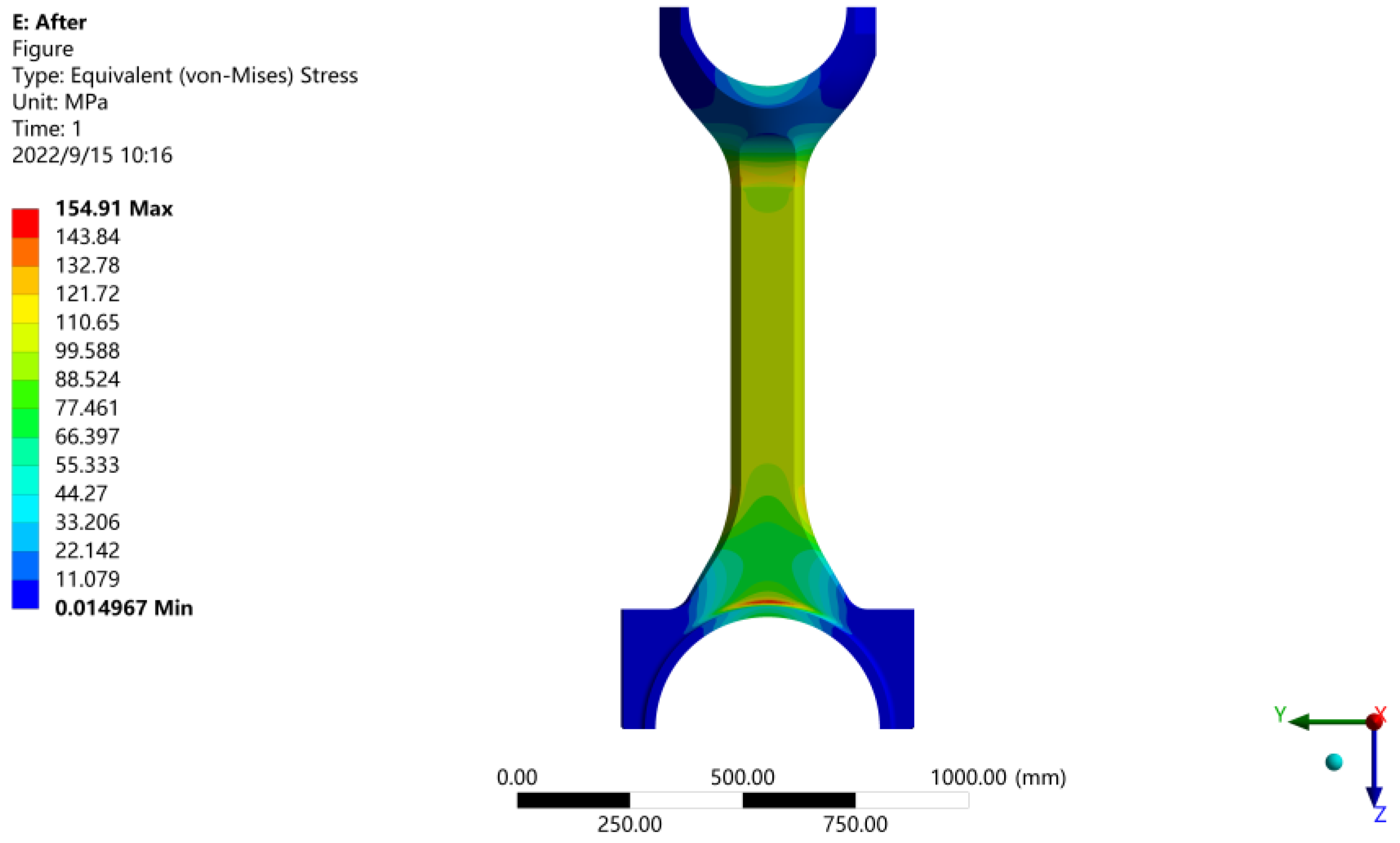
Figure 12.
Stress diagram of connecting rod body.
Figure 12.
Stress diagram of connecting rod body.
Figure 13.
Stress diagram at the large end of the connecting rod body.
Figure 13.
Stress diagram at the large end of the connecting rod body.
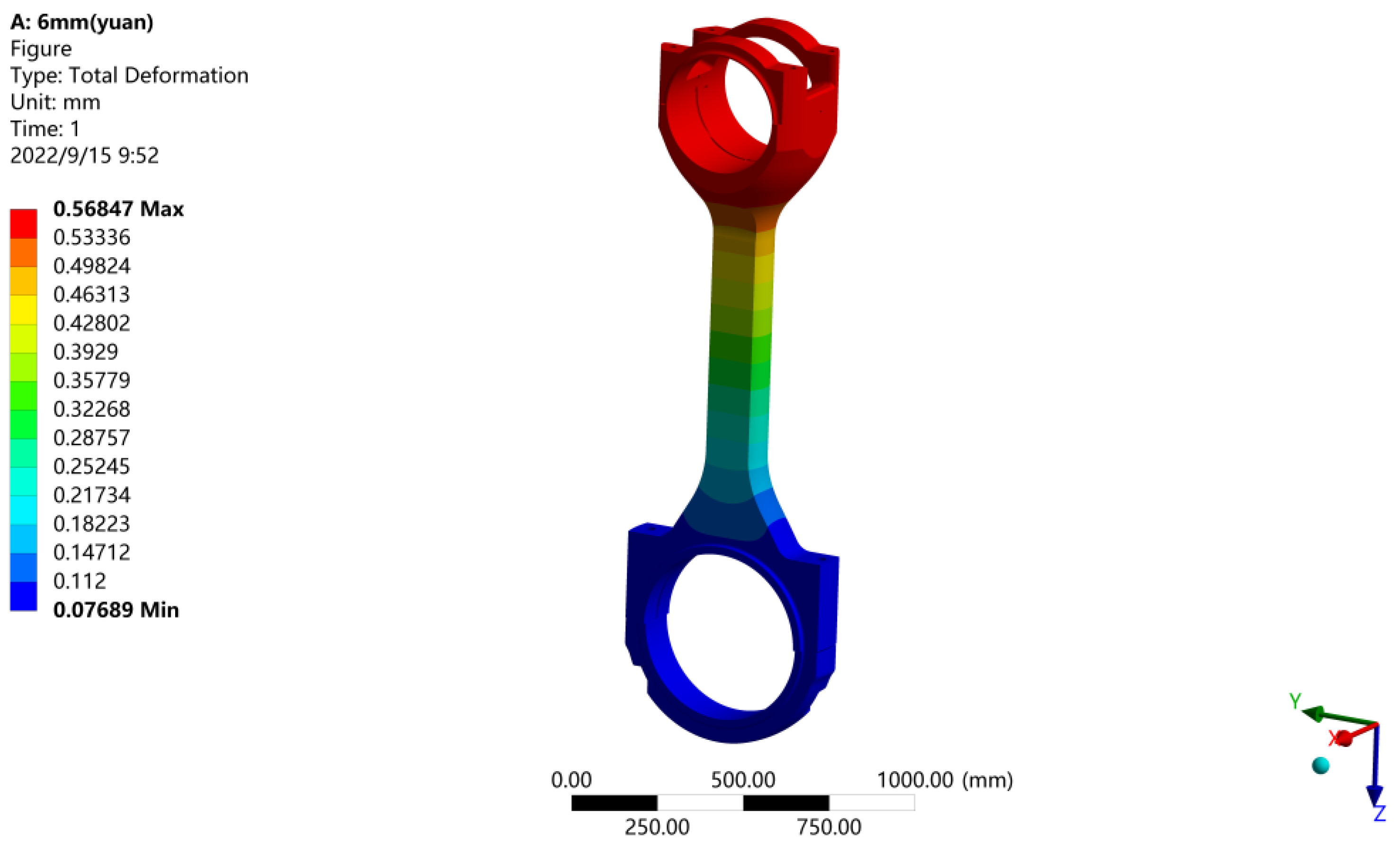
Figure 14.
Deformation diagram of connecting rod.
Figure 14.
Deformation diagram of connecting rod.
Figure 15.
Deformation diagram of connecting rod body.
Figure 15.
Deformation diagram of connecting rod body.
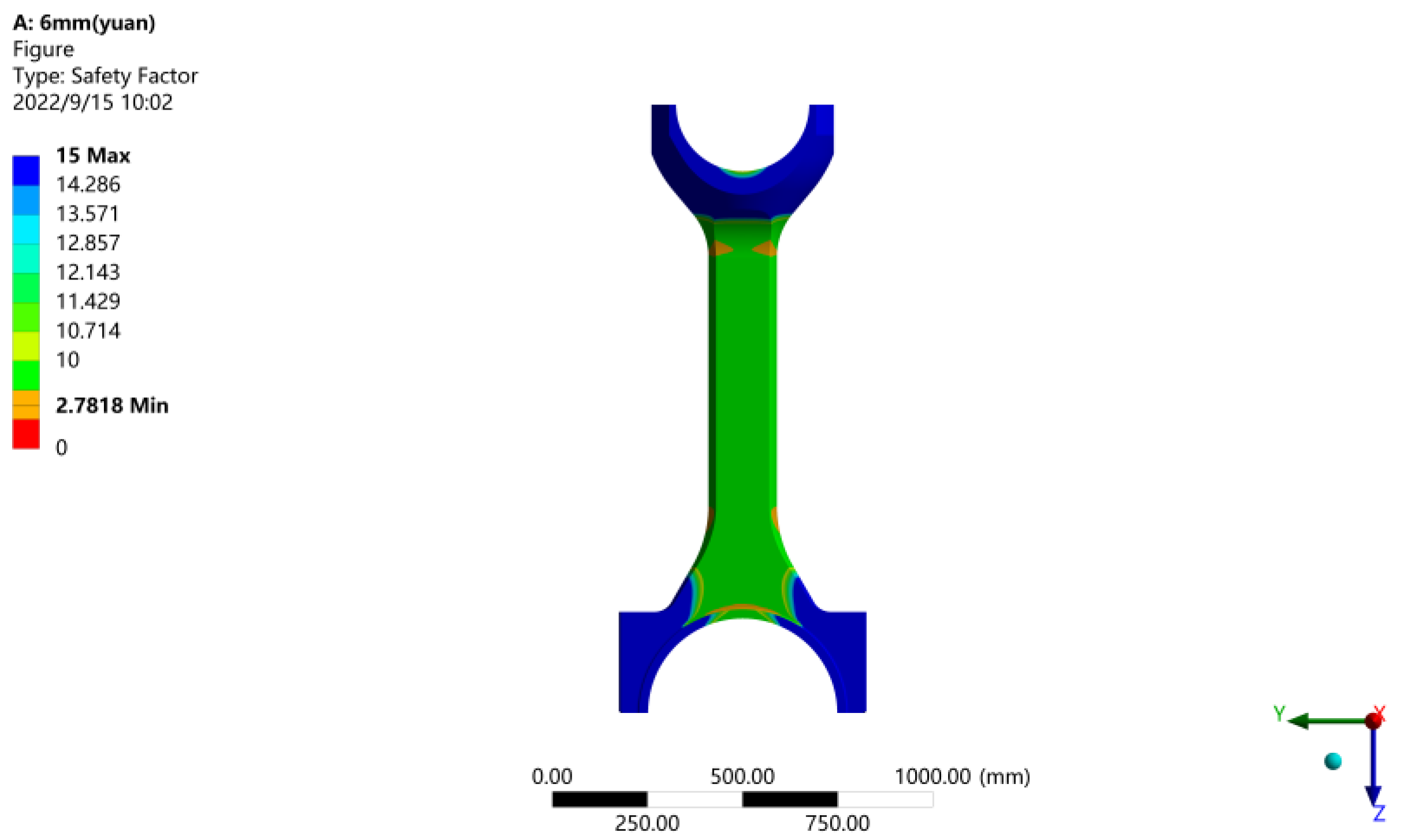
Figure 16.
Safety factor diagram of connecting rod body.
Figure 16.
Safety factor diagram of connecting rod body.
Figure 17.
Schematic diagram of optimization.
Figure 17.
Schematic diagram of optimization.
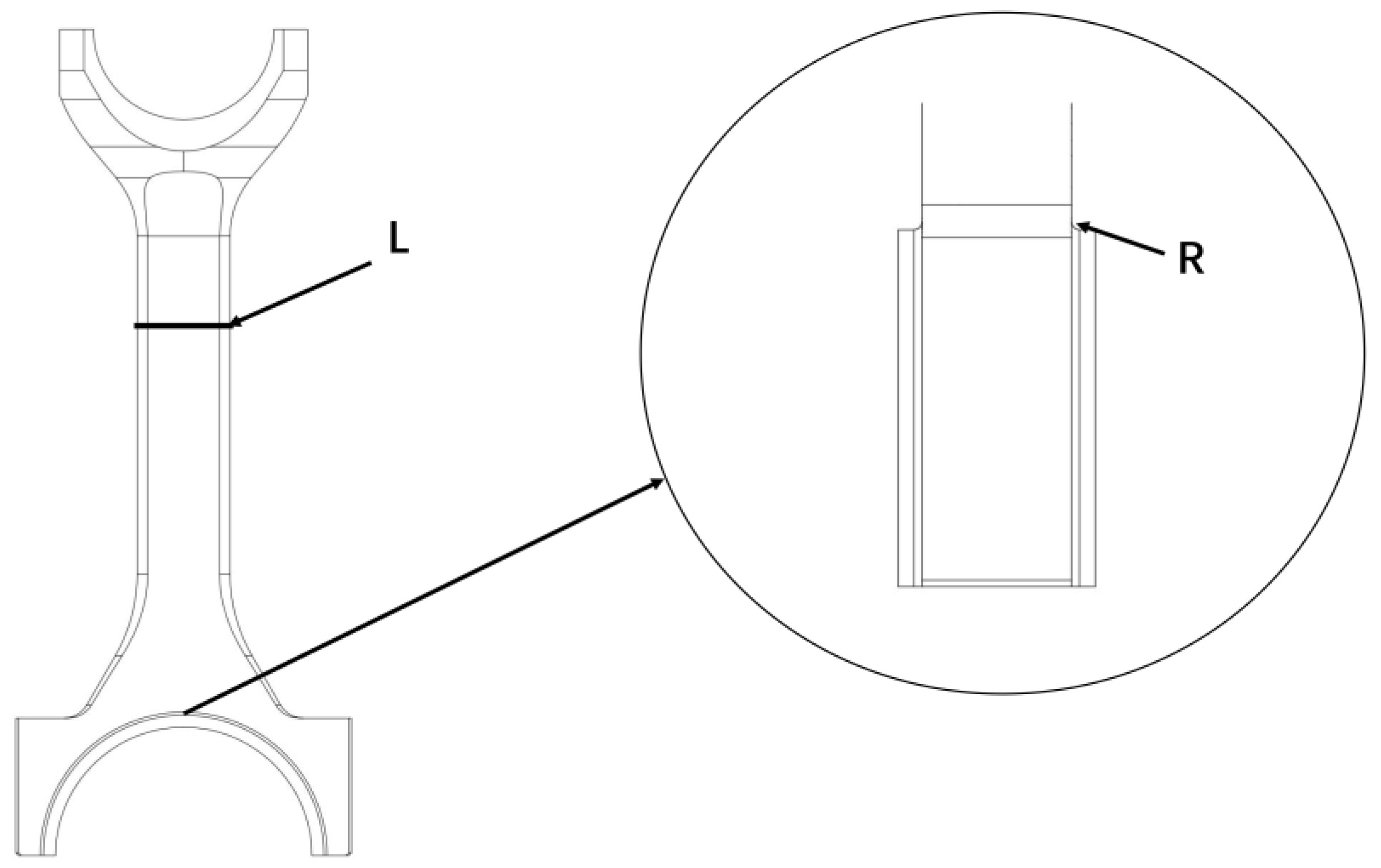
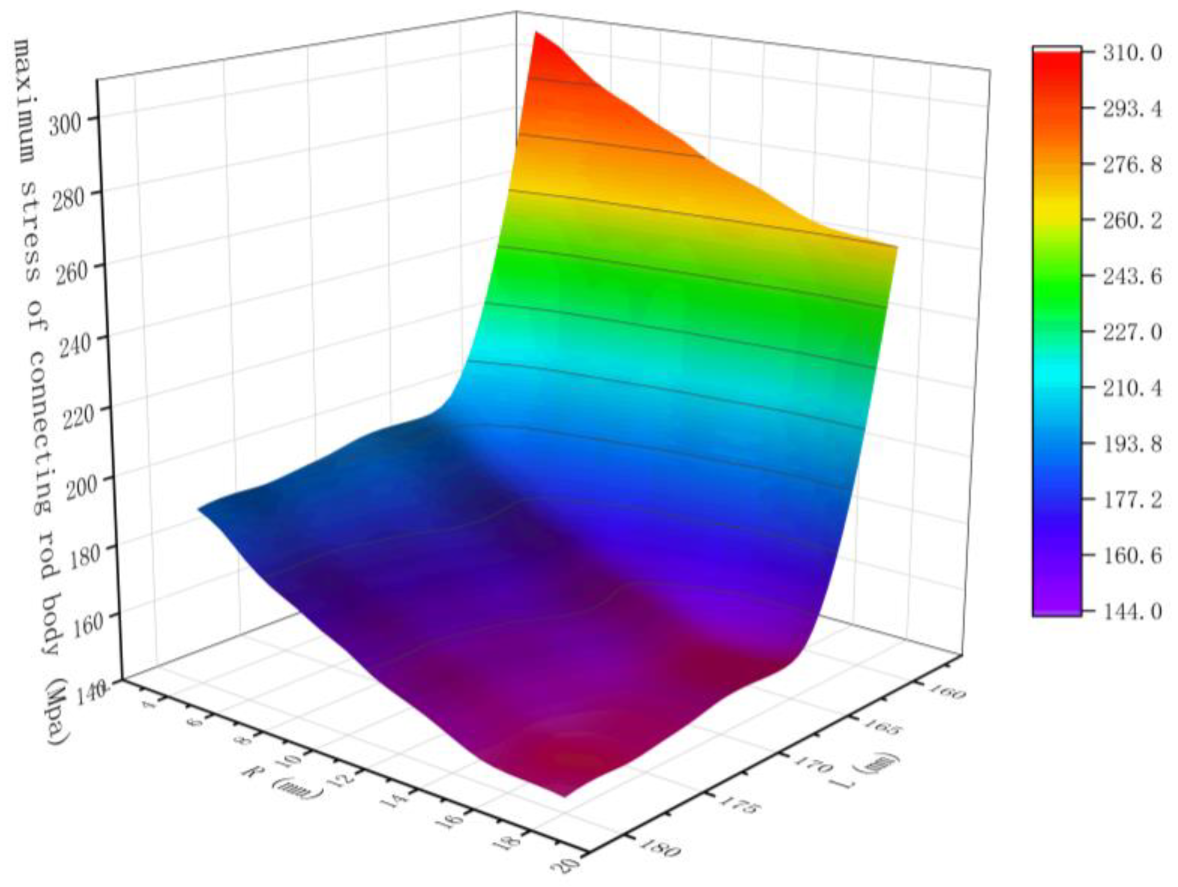
Figure 18.
Relation diagram of R, L, and maximum stress of connecting rod.
Figure 18.
Relation diagram of R, L, and maximum stress of connecting rod.
Figure 19.
Stress diagram of optimized connecting rod body.
Figure 19.
Stress diagram of optimized connecting rod body.
Figure 20.
Safety factor diagram of optimized connecting rod body.
Figure 20.
Safety factor diagram of optimized connecting rod body.
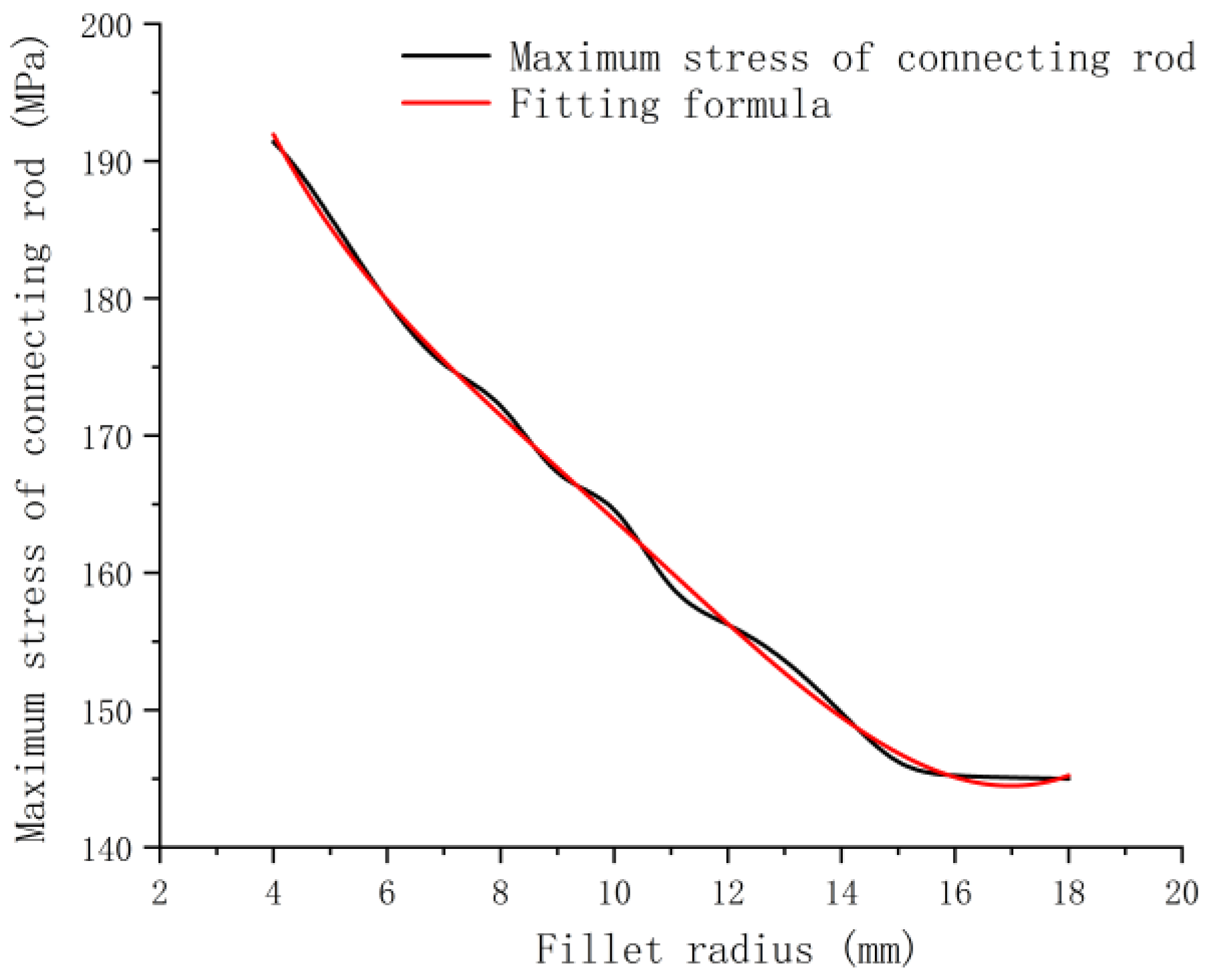
Figure 21.
Comparison between the curve of influence of fillet radius on maximum stress of connecting rod and the formula curve after iteration.
Figure 21.
Comparison between the curve of influence of fillet radius on maximum stress of connecting rod and the formula curve after iteration.
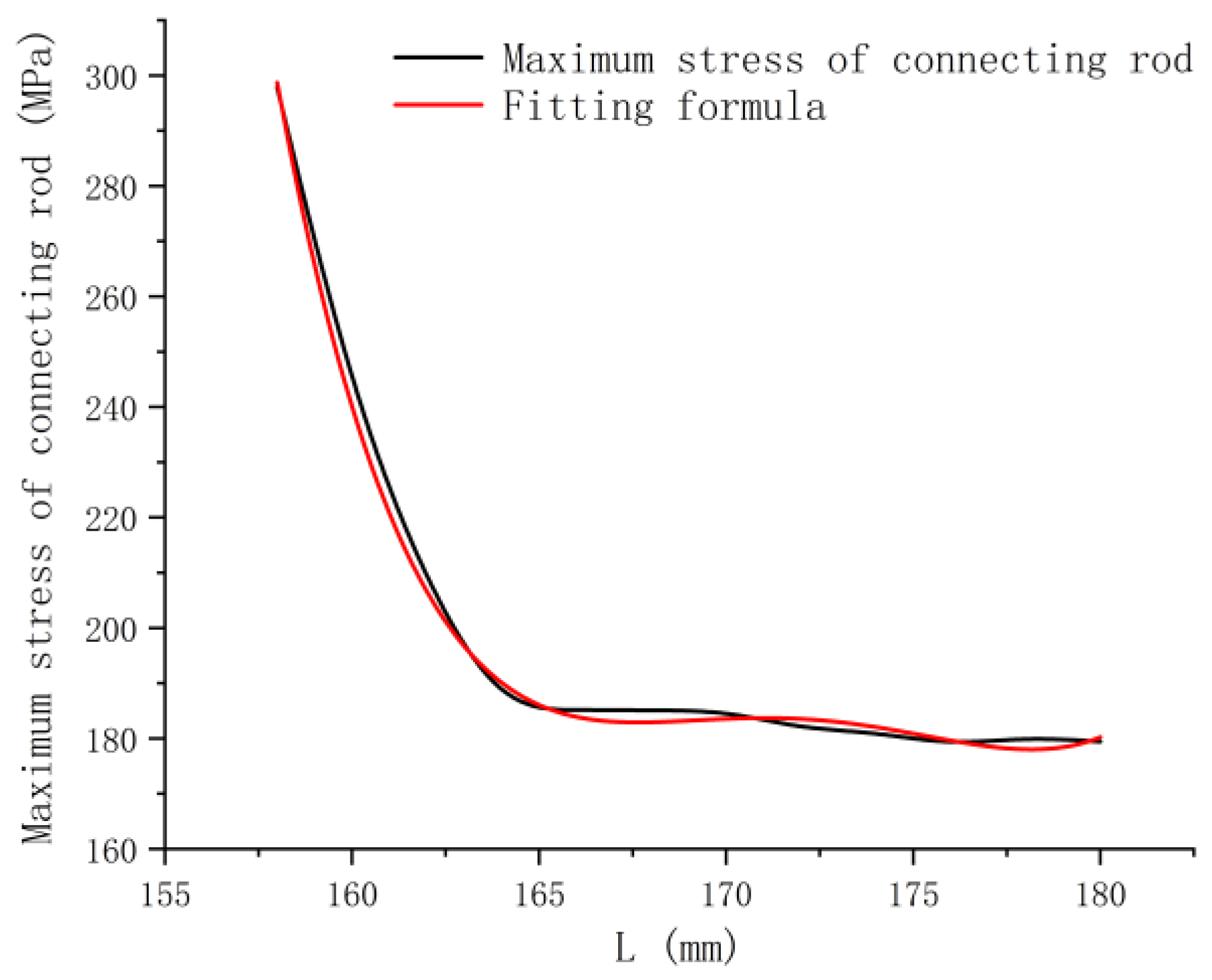
Figure 22.
The influence curve of the long diameter of rod section on the maximum stress of connecting rod is compared with the formula curve after iteration.
Figure 22.
The influence curve of the long diameter of rod section on the maximum stress of connecting rod is compared with the formula curve after iteration.
Figure 23.
Formula coefficient initialization.
Figure 23.
Formula coefficient initialization.
Figure 24.
Corresponding graph of data points and formula surface after iteration.
Figure 24.
Corresponding graph of data points and formula surface after iteration.
Figure 25.
1/4 scale model.
Figure 25.
1/4 scale model.
Figure 26.
WAW-2000 universal testing machine.
Figure 26.
WAW-2000 universal testing machine.
Figure 27.
DH5922D dynamic signal tester.
Figure 27.
DH5922D dynamic signal tester.
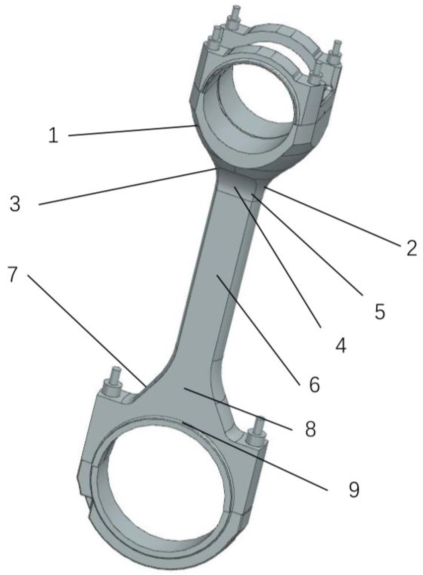
Figure 28.
Pasting position of strain gauge.
Figure 28.
Pasting position of strain gauge.
Figure 29.
Half-bridge connection.
Figure 29.
Half-bridge connection.
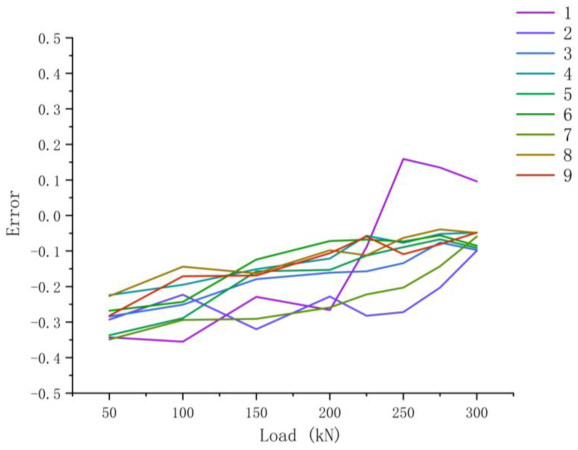
Figure 30.
Error diagram of test and simulation.
Figure 30.
Error diagram of test and simulation.
Table 1.
Main parameters of connecting rod model construction.
Table 1.
Main parameters of connecting rod model construction.
| Name | Value | Name | Value |
|---|
| Cylinder diameter (mm) | 340 | Rated speed (r/min) | 167 |
| Maximum burst pressure (MPa) | 18.94 | Mass of connecting rod (kg) | 525.9 |
| Connecting rod length (mm) | 2137 | Crankshaft radius of gyration (mm) | 800 |
| Connecting rod materials | 42CrMoA | Crank radius-connecting rod length ratio | 0.5 |
Table 2.
Grid independence analysis in simulation calculation of connecting rod assembly.
Table 2.
Grid independence analysis in simulation calculation of connecting rod assembly.
| Connecting Rod Assembly Mesh Size (mm) | Maximum Stress of Connecting Rod Assembly (MPa) |
|---|
| 5 | 179.35 |
| 6 | 179.42 |
| 7 | 182.67 |
| 9 | 197.58 |
| 12 | 205.79 |
| 15 | 237.52 |
Table 3.
Construction of connection relation in simulation calculation of connecting rod assembly.
Table 3.
Construction of connection relation in simulation calculation of connecting rod assembly.
| Connection Relationship Sets Objects | Connected Relation |
|---|
| Piston assembly and crosshead assembly | Friction contact (μ = 0.2) |
| Bushing and crosshead pin | Friction contact (μ = 0.15) |
| Connecting rod large, small end, and rod body | Asperity contact |
| Connecting rod and bolt threads | Bonded contact |
| Connecting rod and bolt head | Friction contact (μ = 0.2) |
| Bearing bush and crankshaft | Friction contact (μ = 0.2) |
Table 4.
Setting of boundary conditions in simulation calculation of connecting rod assembly.
Table 4.
Setting of boundary conditions in simulation calculation of connecting rod assembly.
| Boundary Conditions | Value |
|---|
| Preload of bolt at small end of connecting rod | 21,000 N |
| Preload of bolt at large end of connecting rod | 26,000 N |
| Maximum burst pressure | 18.94 MPa |
| End face of crankshaft | Fixed support |
| Inertia force | See Formulas (1) and (2) |
Table 5.
Safety factors of Kirasu Shveli method.
Table 5.
Safety factors of Kirasu Shveli method.
| Position of Connecting Rod | Minimum Safety Factor Requirements |
|---|
| Connecting rod body | ≥1.5–2.5 |
| Connecting rod large and small end | ≥2.5 |
Table 6.
Comparison of test and simulation results (MPa).
Table 6.
Comparison of test and simulation results (MPa).
| Position of Measuring Point of Connecting Rod | 50 kN | 100 kN | 150 kN | 200 kN | 225 kN | 250 kN | 275 kN | 300 kN |
|---|
| 1 | Test value | 2.35 | 3.84 | 5.36 | 9.31 | 15.12 | 22.42 | 26.93 | 30.87 |
| Simulation value | 3.85 | 6.16 | 6.89 | 12.92 | 16.61 | 19.32 | 23.52 | 26.72 |
| 2 | Test value | 7.42 | 18.05 | 31.52 | 54.36 | 69.72 | 81.28 | 95.73 | 108.34 |
| Simulation value | 10.58 | 23.28 | 46.45 | 70.33 | 97.15 | 111.89 | 137.59 | 154.65 |
| 3 | Test value | 17.63 | 46.94 | 75.26 | 99.15 | 108.67 | 126.67 | 138.91 | 156.73 |
| Simulation value | 25.03 | 63.29 | 92.04 | 118.19 | 130.80 | 146.26 | 150.45 | 173.60 |
| 4 | Test value | 15.63 | 53.13 | 72.64 | 97.76 | 126.61 | 125.03 | 125.48 | 131.37 |
| Simulation value | 20.71 | 65.26 | 85.75 | 111.03 | 134.05 | 135.86 | 132.89 | 139.09 |
| 5 | Test value | 16.13 | 49.36 | 72.48 | 97.39 | 125.95 | 136.05 | 127.89 | 135.91 |
| Simulation value | 25.35 | 69.66 | 86.54 | 115.09 | 142.42 | 148.87 | 140.01 | 151.52 |
| 6 | Test value | 33.06 | 69.48 | 95.28 | 148.39 | 180.36 | 200.07 | 235.49 | 250.63 |
| Simulation value | 45.27 | 91.80 | 108.82 | 160.05 | 193.53 | 216.09 | 247.72 | 271.21 |
| 7 | Test value | 18.65 | 38.74 | 60.83 | 79.13 | 93.81 | 120.57 | 132.71 | 140.89 |
| Simulation value | 28.82 | 55.29 | 85.17 | 105.03 | 120.78 | 157.44 | 175.94 | 156.84 |
| 8 | Test value | 16.84 | 50.49 | 65.56 | 97.97 | 140.13 | 155.94 | 173.94 | 193.75 |
| Simulation value | 23.67 | 57.16 | 80.13 | 108.82 | 157.53 | 166.64 | 179.01 | 204.02 |
| 9 | Test value | 25.43 | 57.48 | 75.93 | 103.57 | 115.91 | 125.10 | 140.51 | 170.89 |
| Simulation value | 35.82 | 68.60 | 92.24 | 116.05 | 122.48 | 140.95 | 152.13 | 179.75 |