Baseline for Split DC Link Design in Three-Phase Three-Level Converters Operating with Unity Power Factor Based on Low-Frequency Partial Voltage Oscillations
Abstract
:1. Introduction
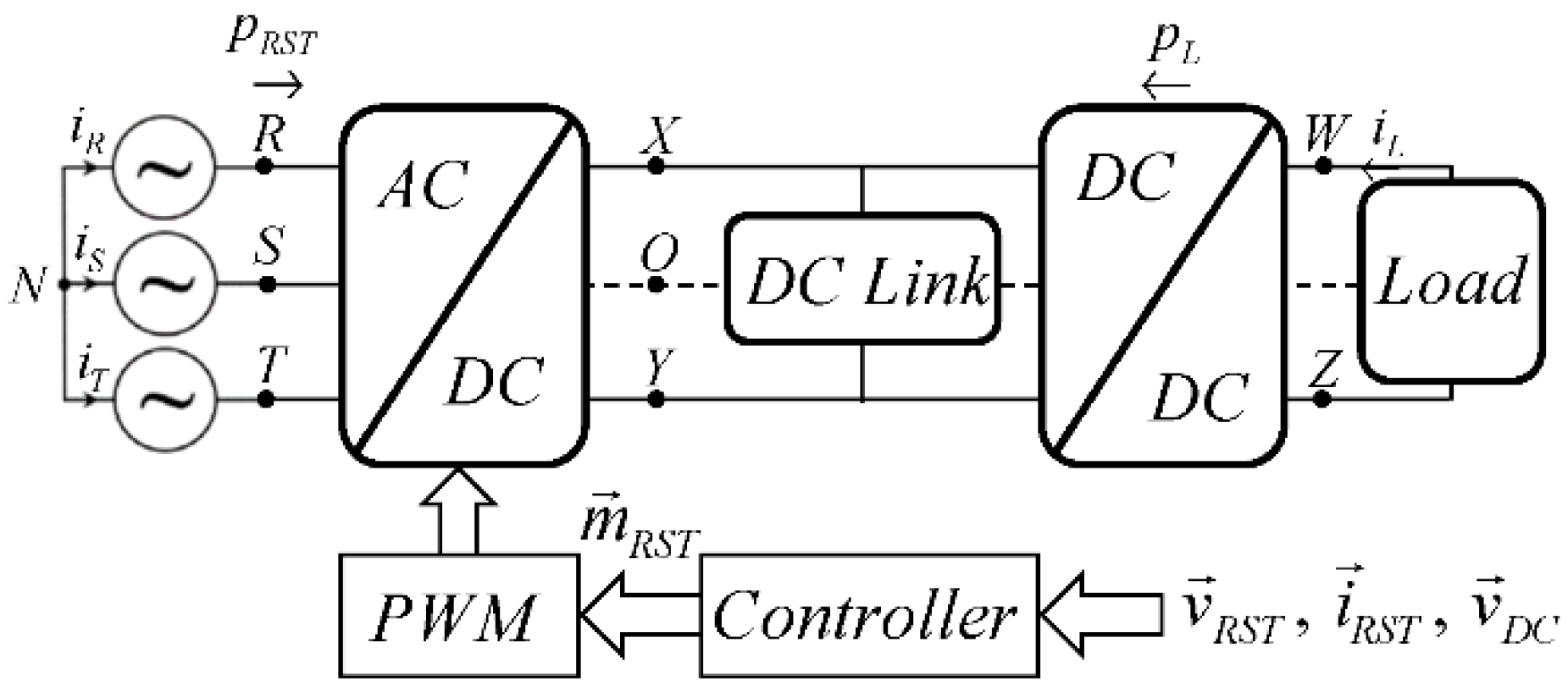
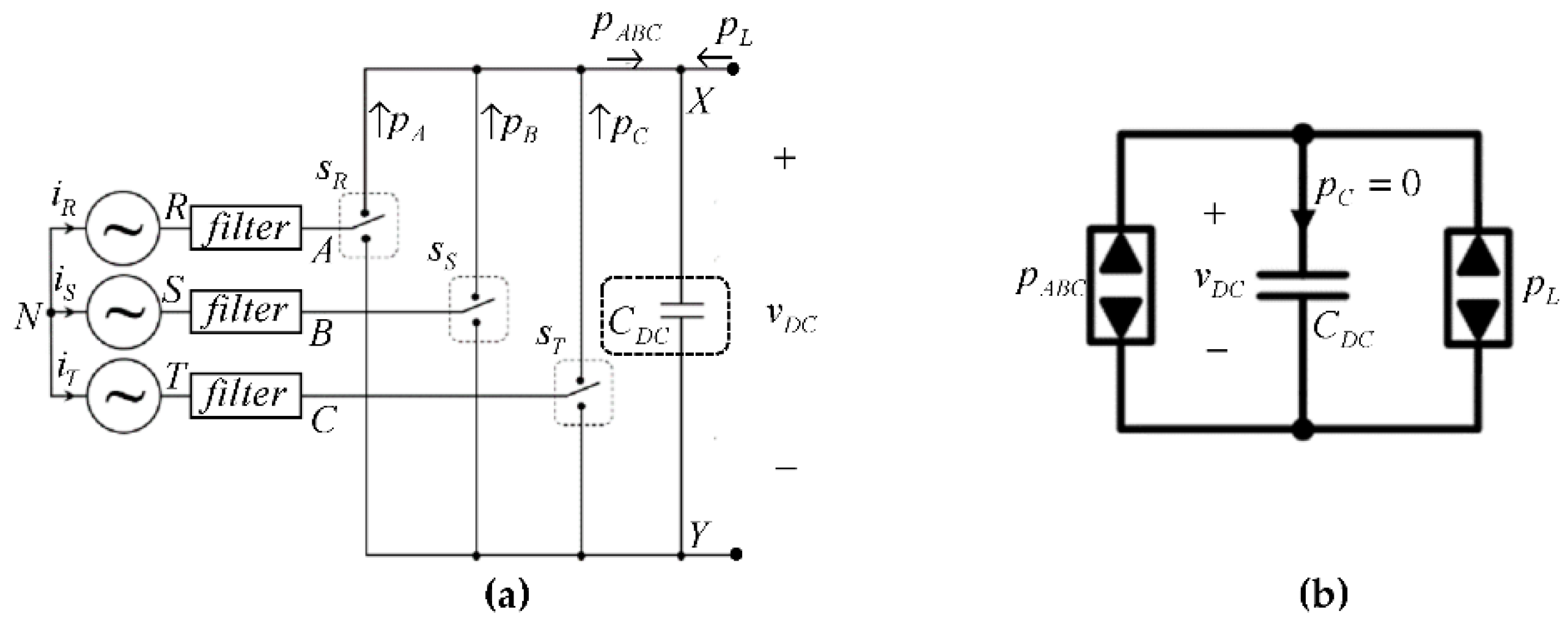
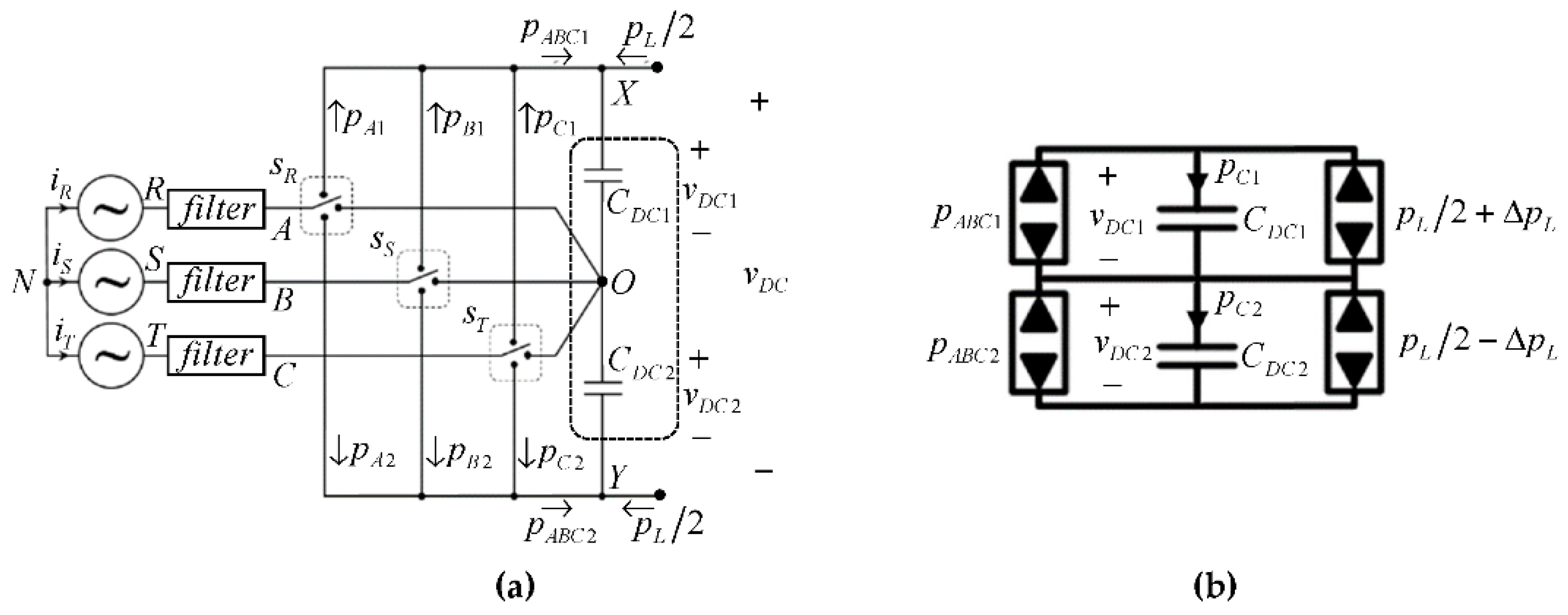
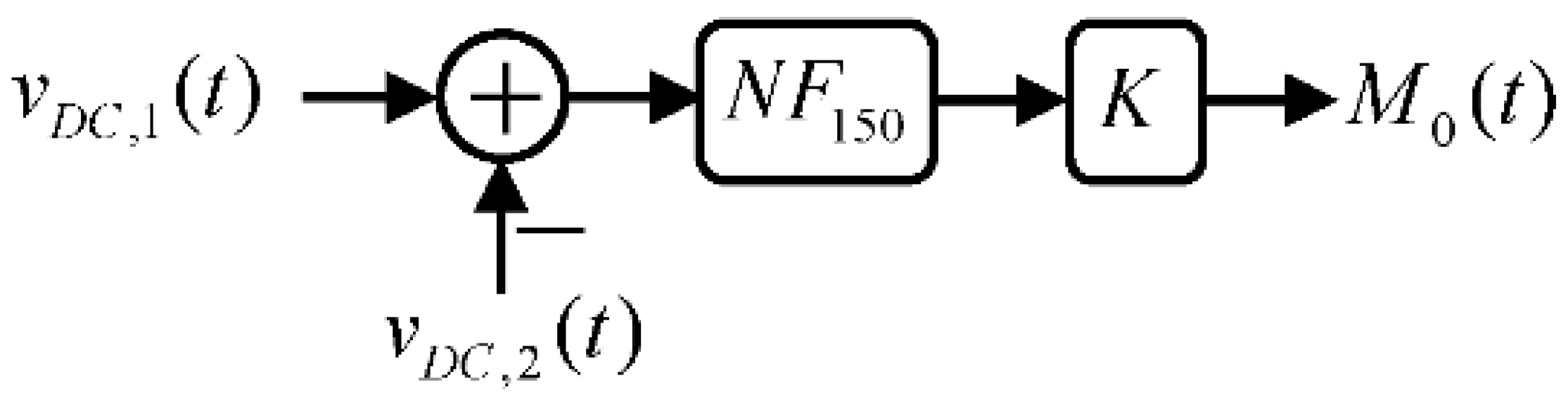
2. Materials and Methods
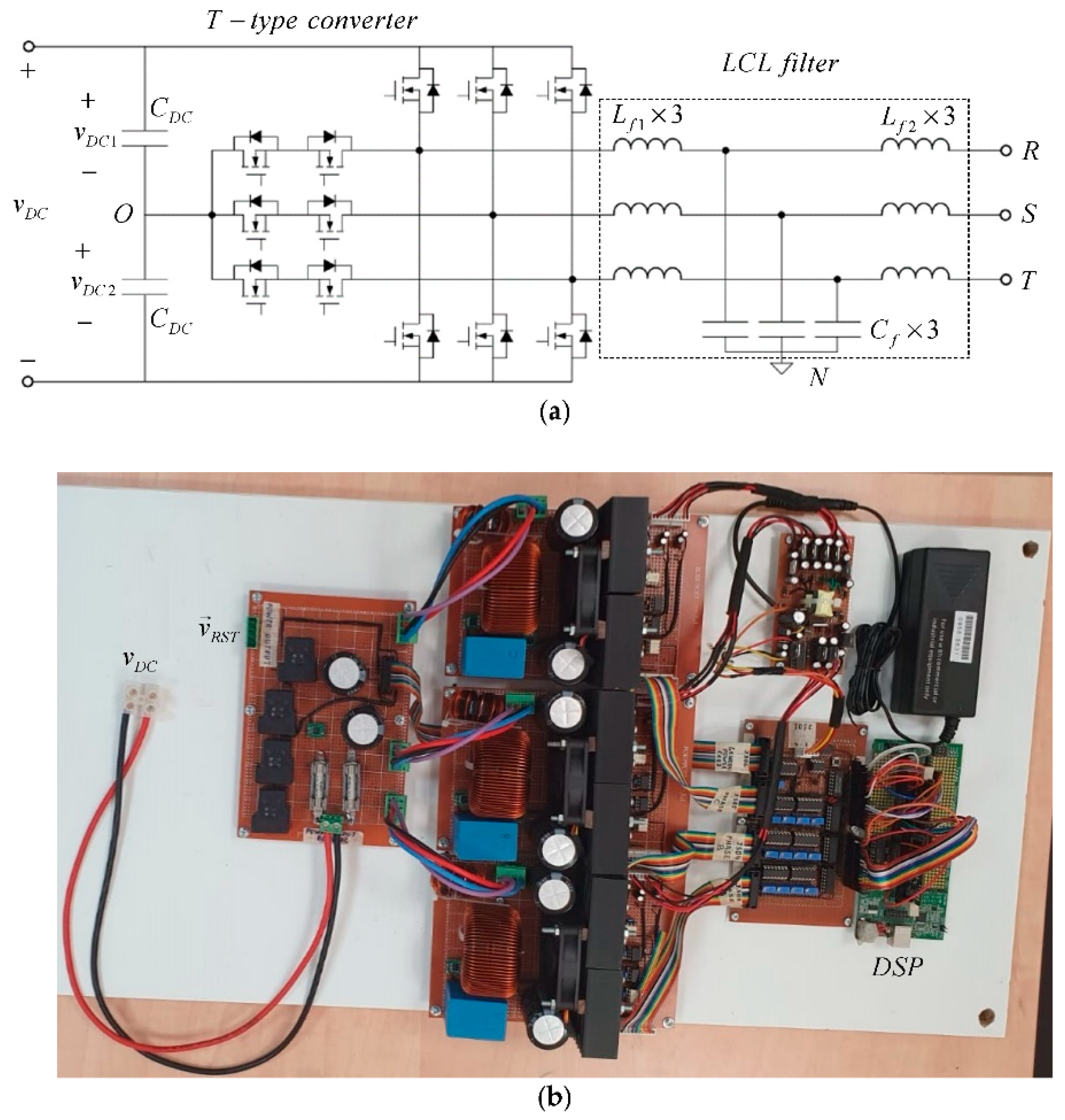
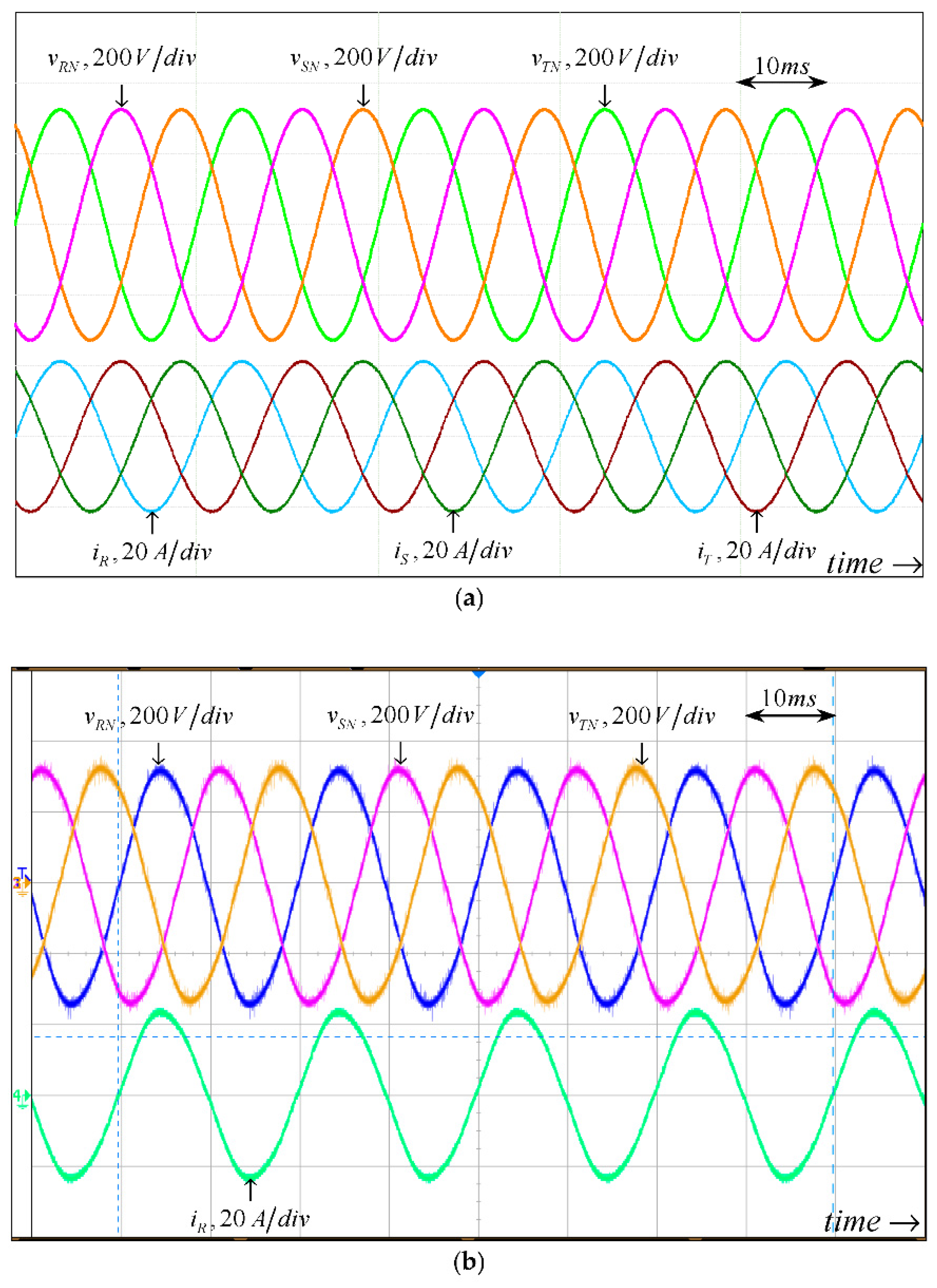
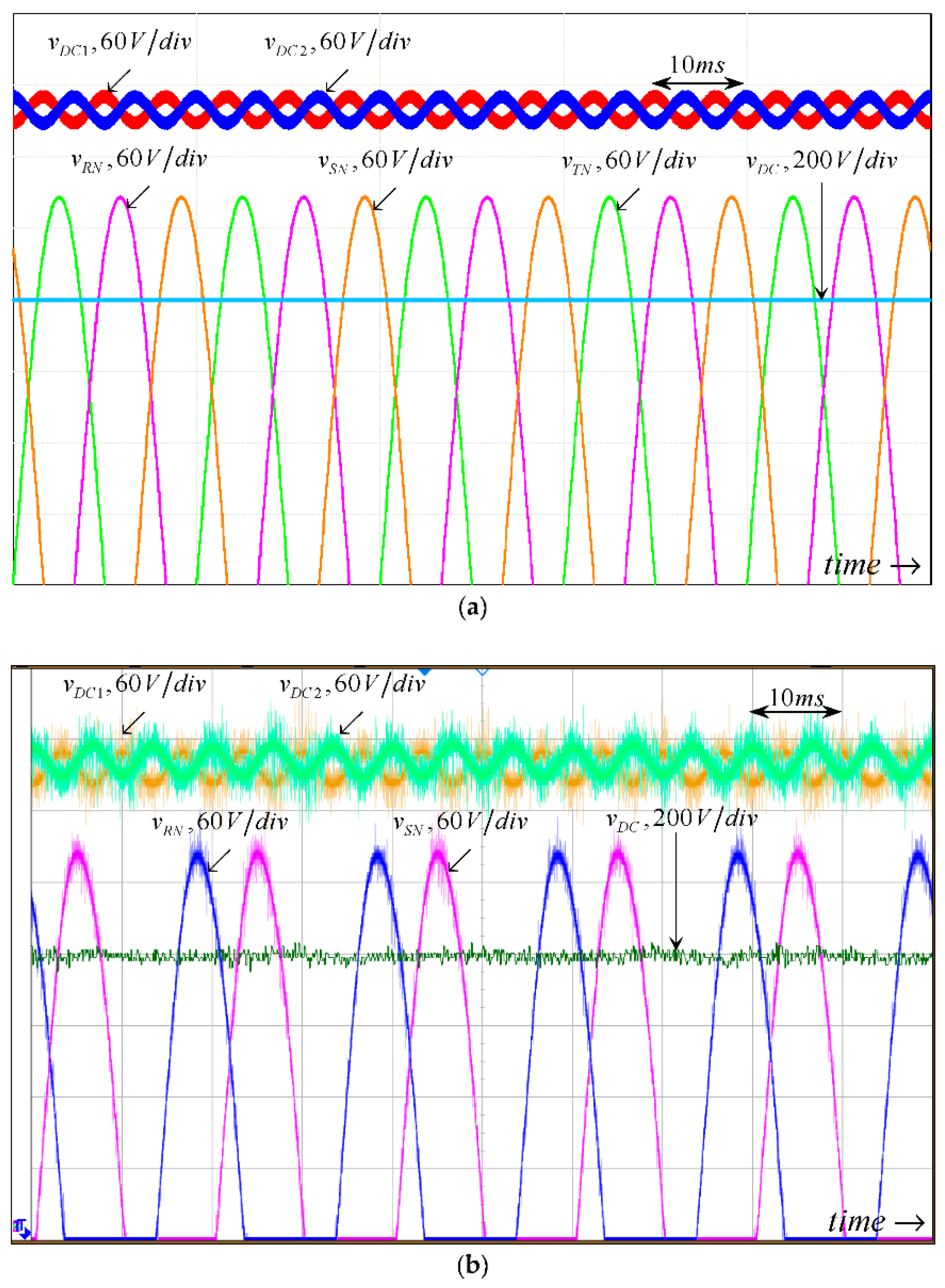
3. Validation
- A.
- Capacitor low-frequency current rating imposed design
- B.
- Capacitor voltage rating imposed design
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bose, B.K. Multi-Level Converters. Electronics 2015, 4, 582–585. [Google Scholar] [CrossRef]
- Franquelo, L.G.; Leonand, J.; Rodriguez, J. The age of multilevel converters arrives. IEEE Ind. Electron. Mag. 2008, 2, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Rodriguez, J.; Lai, J.-S.; Peng, F.Z. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef] [Green Version]
- Norões, M.; Jacobina, C.B.; Carlos, G.A. A new three-phase ac–dc–ac multilevel converter based on cascaded three-leg converters. IEEE Trans. Ind. Appl. 2017, 53, 2210–2221. [Google Scholar]
- Zhou, D.; Zhao, J.; Li, Y. Model-predictive control scheme of five-leg ac–dc–ac converter-fed induction motor drive. IEEE Trans. Ind. Electron. 2016, 63, 4517–4526. [Google Scholar] [CrossRef]
- Lima, M.; Cursino, B.J.; Rocha, N.; Santos, E.C. Ac–dc–ac three-phase converter based on three three-leg converters connected in series. IEEE Trans. Ind. Appl. 2016, 52, 3171–3181. [Google Scholar]
- Filho, S.; Cipriano, O.; de Almeida, B.R.; Souza, D.; Neto, T.R.F. High-frequency isolated AC–DC–AC interleaved converter for power quality applications. IEEE Trans. Ind. Appl. 2018, 54, 4594–4602. [Google Scholar] [CrossRef]
- Norões, M.; Jacobina, C.B.; Freitas, N.B.; Queiroz, A.; Silva, E.R.C. Three-phase four-wire ac–dc–ac multilevel topologies obtained from an interconnection of three-leg converters. IEEE Trans. Ind. Appl. 2018, 54, 4728–4738. [Google Scholar]
- Norões, M.; Jacobina, C.B.; Freitas, N.B.; Alves Vitorino, M. Investigation of three-phase ac–dc–ac multilevel nine-leg converter. IEEE Trans. Ind. Appl. 2016, 52, 4156–4169. [Google Scholar]
- Kaufhold, E.; Meyer, J.; Schegner, P. Measurement-based identification of DC-link capacitance of single-phase power electronic devices for grey-box modelling. IEEE Trans. Power Electron. 2021, 37, 4545–4552. [Google Scholar] [CrossRef]
- Khalil, A.; Ahmed, G.; Lee, D.C. DC-link capacitance estimation in AC/DC/AC PWM converters using voltage injection. IEEE Trans. Ind. Appl. 2008, 44, 1631–1637. [Google Scholar] [CrossRef]
- Divan, D.; Habetler, T.; Lipo, T. PWM techniques for voltage source inverters. In Proceedings of the IEEE Power Electronics Specialists Conference, Charleston, SC, USA, 1 July 1999. [Google Scholar]
- Laszlo, H.; Kumar, M.; Jovanović, M.M. Performance comparison of three-step and six-step PWM in average-current-controlled three-phase six-switch boost PFC rectifier. IEEE Trans. Power. Electron. 2016, 31, 7264–7272. [Google Scholar]
- Lu, Y.; Zhao, Z.; Lu, T.; Yang, S.; Zou, G. An improved DC-link voltage fast control scheme for a PWM rectifier-inverter system. IEEE Trans. Ind. Appl. 2014, 50, 462–473. [Google Scholar]
- Xiong, X.; Zhang, Y.; Wang, J.; Du, H. An improved model predictive control scheme for the PWM rectifier-inverter system based on power-balancing mechanism. IEEE Trans. Ind. Electron. 2016, 63, 5197–5208. [Google Scholar]
- Sahraoui, K.; Gaoui, B. Reconfigurable control of PWM AC-DC-DC converter without redundancy leg supplying an ac motor drive. Period. Polytech. Electr. Eng. Comp. Sci. 2021, 65, 74–81. [Google Scholar] [CrossRef]
- Sitbon, M.; Leppaaho, J.; Suntio, T.; Kuperman, A. Dynamics of photovoltaic-generator-interfacing voltage-controlled buck power stage. IEEE J. Photovolt. 2014, 5, 633–640. [Google Scholar] [CrossRef]
- Iqbal, A.; Lewicki, A.; Morawiec, M. Pulse-width modulation of power electronic DC–AC converter. In High Performance Control of AC Drives with MATLAB®/Simulink, 2nd ed.; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Pu, X.-S.; Nguyen, T.H.; Lee, D.-C.; Lee, K.-B.; Kim, J.-M. Fault diagnosis of DC-link capacitors in three-phase AC/DC PWM converters by online estimation of equivalent series resistance. IEEE Trans. Ind. Electron. 2013, 60, 4118–4127. [Google Scholar] [CrossRef]
- Pu, X.-S.; Nguyen, T.H.; Lee, D.-C.; Lee, S.-G. Identification of DC-link capacitance for single-phase AC/DC PWM converters. J. Pow. Electron. 2010, 10, 270–276. [Google Scholar] [CrossRef] [Green Version]
- Hur, N.; Jung, J.; Nam, K. A fast dynamic DC-link power-balancing scheme for a PWM converter-inverter system. IEEE Trans. Ind. Electron. 2001, 48, 794–803. [Google Scholar]
- Gu, B.-G.; Nam, K. A DC-link capacitor minimization method through direct capacitor current control. IEEE Trans. Ind. Appl. 2006, 42, 573–581. [Google Scholar]
- Malesani, L.; Rossetto, L.; Tenti, P.; Tomasin, P. AC/DC/AC PWM converter with reduced energy storage in the DC link. IEEE Trans. Ind. Appl. 1995, 31, 287–292. [Google Scholar] [CrossRef] [Green Version]
- Stecca, M.; Soeiro, T.B.; Elizondo, L.R.; Bauer, P.; Palensky, P. Comparison of two and three-level DC-AC converters for a 100 kW battery energy storage system. In Proceedings of the IEEE International Symposium on Industrial Electronics, Delft, The Netherlands, 17–19 June 2020; pp. 677–682. [Google Scholar]
- Novak, M.; Sangwongwanich, A.; Blaabjerg, F. Online optimization of zero-sequence voltage injection of PWM strategy for 3L-NPC converters. In Proceedings of the IEEE International Power Electronics Conference, Himeji, Japan, 15–19 May 2022; pp. 2405–2411. [Google Scholar]
- Sangwongwanich, A.; Novak, M.; Sangwongwanich, S.; Blaabjerg, F. Reliability of DC-link capacitors in three-level NPC inverters under different PWM methods. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition, Houston, TX, USA, 20–24 March 2022; pp. 1804–1811. [Google Scholar]
- In, H.-C.; Kim, S.-M.; Lee, K.-B. Design and control of small DC-link capacitor-based three-level inverter with neutral-point voltage balancing. Energies 2018, 11, 1435. [Google Scholar] [CrossRef] [Green Version]
- Zielinski, C.; Stefanczak, B.; Jedrus, K. Phase-independent reactive power compensation based on four-wire power converter in the presence of angular asymmetry between voltage vectors. Energies 2022, 15, 497. [Google Scholar] [CrossRef]
- Cao, D.P.; Song, W.X.; Xi, H.; Chen, G.C.; Chen, C. Research on zero-sequence signal of space-vector modulation for three-level neutral-point-clamped inverter based on vector diagram partition. In Proceedings of the 6th IEEE International Power Electronics and Motion Control Conference, Wuhan, China, 17–20 May 2009; pp. 1435–1439. [Google Scholar]
- Helle, L.; Munk-Nielsen, S.; Enjeti, P. Generalized discontinuous DC-link balancing modulation strategy for three-level inverters. In Proceedings of the Power Conversion Conference, Osaka, Japan, 2–5 April 2002; pp. 359–366. [Google Scholar]
- Song, Q.; Liu, W.; Yu, Q.; Xie, X.; Wang, Z. A neutral-point potential balancing algorithm for three-level NPC inverters using analytically injected zero-sequence voltage. In Proceedings of the IEEE. Applied Power Electronics Conference and Exposition, Miami Beach, FL, USA, 9–13 February 2003; pp. 228–233. [Google Scholar]
- Pou, J.; Zaragoza, J.; Rodriguez, P.; Ceballos, S.; Sala, V.M.; Burgos, R.P.; Boroyevich, D. Fast-processing modulation strategy for the neutral-point-clamped converter with total elimination of low-frequency voltage oscillations in the neutral point. IEEE Trans. Ind. Electron. 2007, 54, 2288–2294. [Google Scholar] [CrossRef]
- Alemi, P.; Jeung, Y.-C.; Lee, D.-C. DC-link capacitance minimization in T-type three-level AC/DC/AC PWM converters. IEEE Trans. Ind. Electron. 2015, 62, 1382–1391. [Google Scholar] [CrossRef]
- Pou, J.; Pindado, R.; Boroyevich, D.; Rodriguez, P. Evaluation of the low-frequency neutral-point voltage oscillations in the three-level inverter. IEEE Trans. Ind. Electron. 2005, 52, 1582–1588. [Google Scholar] [CrossRef]
- Gopalakrishnan, K.S.; Janakiraman, S.; Das, S.; Narayanan, G. Analytical evaluation of DC capacitor RMS current and voltage ripple in neutral-point clamped inverters. Sadhana 2017, 42, 827–839. [Google Scholar] [CrossRef] [Green Version]
- Orfanoudakis, G.I.; Yuratich, M.A.; Sharkh, S.M. Analysis of dc-link capacitor current in three-level neutral point clamped and cascaded H-bridge inverters. IET Pow. Electron. 2013, 6, 1376–1389. [Google Scholar] [CrossRef]
- Beres, R.N.; Wang, X.; Liserre, M.; Blaabjerg, F.; Bak, C.L. A review of passive power filters for three-phase grid-connected voltage-source converters. IEEE J. Emerg. Sel. Top. Pow. Electron. 2016, 4, 54–69. [Google Scholar] [CrossRef] [Green Version]
- Singer, S.; Erickson, R.W. Power-source element and its properties. IEEE Proc. Circ. Dev. Syst. 1994, 141, 220–226. [Google Scholar] [CrossRef]
- Mellinkovsky, M.; Yuhimenko, V.; Zhong, Q.C.; Peretz, M.M.; Kuperman, A. Active DC link capacitance reduction in grid-connected power conversion systems by direct voltage regulation. IEEE Access 2018, 6, 18163–18173. [Google Scholar] [CrossRef]
- Mutovkin, A.; Yuhimenko, V.; Mellinkovsky, M.; Schacham, S.; Kuperman, A. Control of direct voltage regulated active DC-link capacitance reduction circuits to allow plug-and-play operation. IEEE Trans. Ind. Electron. 2019, 66, 6527–6537. [Google Scholar] [CrossRef]
- Available online: https://www.ti.com/lit/ug/tidue53f/tidue53f.pdf (accessed on 28 July 2022).
- Available online: https://product.tdk.com/system/files/dam/doc/product/capacitor/aluminum-electrolytic/snap-in/data_sheet/20/30/db/aec/b43643.pdf (accessed on 28 July 2022).

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Siton, Y.; Yuhimenko, V.; Baimel, D.; Kuperman, A. Baseline for Split DC Link Design in Three-Phase Three-Level Converters Operating with Unity Power Factor Based on Low-Frequency Partial Voltage Oscillations. Machines 2022, 10, 722. https://doi.org/10.3390/machines10090722
Siton Y, Yuhimenko V, Baimel D, Kuperman A. Baseline for Split DC Link Design in Three-Phase Three-Level Converters Operating with Unity Power Factor Based on Low-Frequency Partial Voltage Oscillations. Machines. 2022; 10(9):722. https://doi.org/10.3390/machines10090722
Chicago/Turabian StyleSiton, Yarden, Vladimir Yuhimenko, Dmitry Baimel, and Alon Kuperman. 2022. "Baseline for Split DC Link Design in Three-Phase Three-Level Converters Operating with Unity Power Factor Based on Low-Frequency Partial Voltage Oscillations" Machines 10, no. 9: 722. https://doi.org/10.3390/machines10090722
APA StyleSiton, Y., Yuhimenko, V., Baimel, D., & Kuperman, A. (2022). Baseline for Split DC Link Design in Three-Phase Three-Level Converters Operating with Unity Power Factor Based on Low-Frequency Partial Voltage Oscillations. Machines, 10(9), 722. https://doi.org/10.3390/machines10090722







