An Investigation on Dynamic Characteristics of the Straddle-Type Monorail System under Spatial Alignment
Abstract
1. Introduction
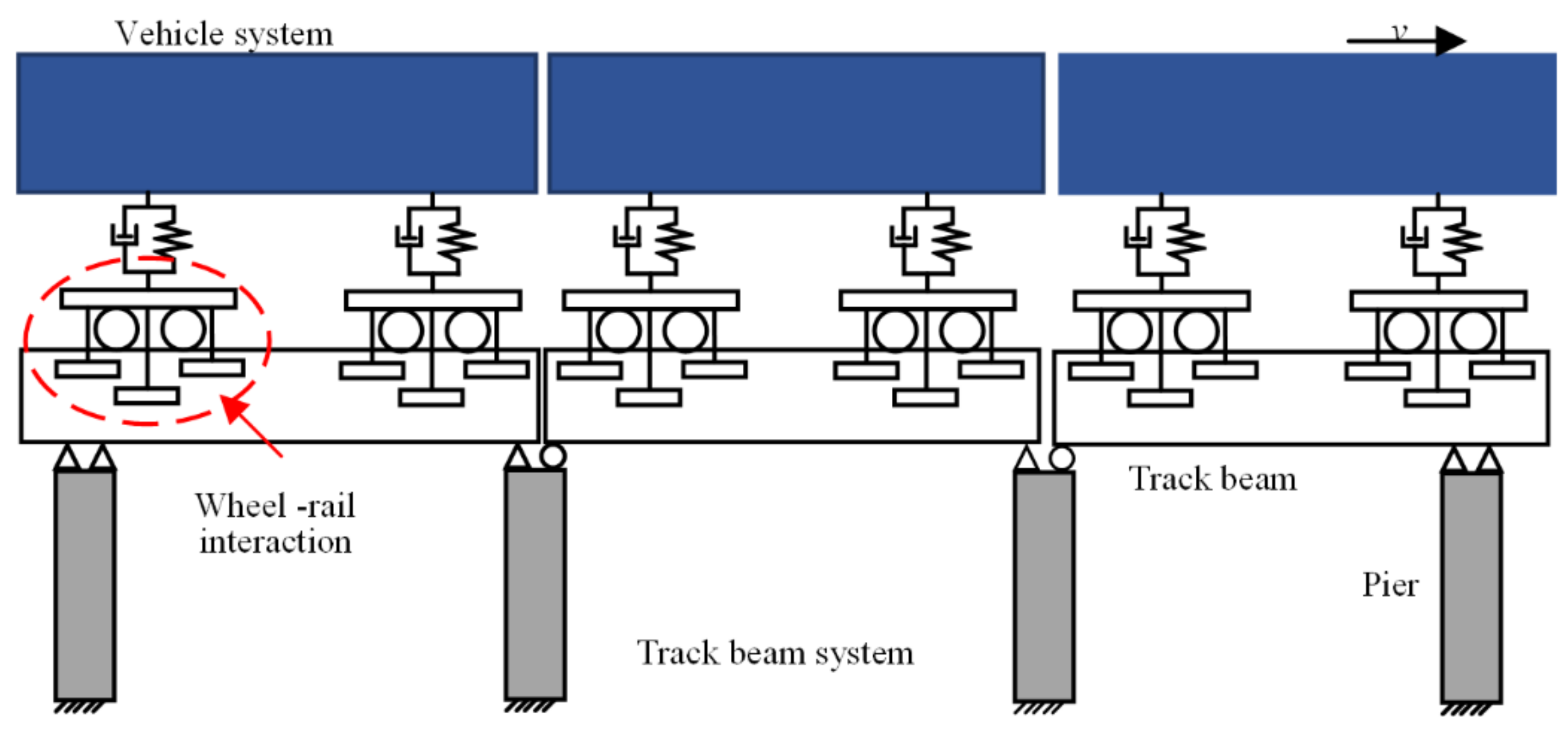
2. Dynamic Model of the Straddle-Type Monorail System
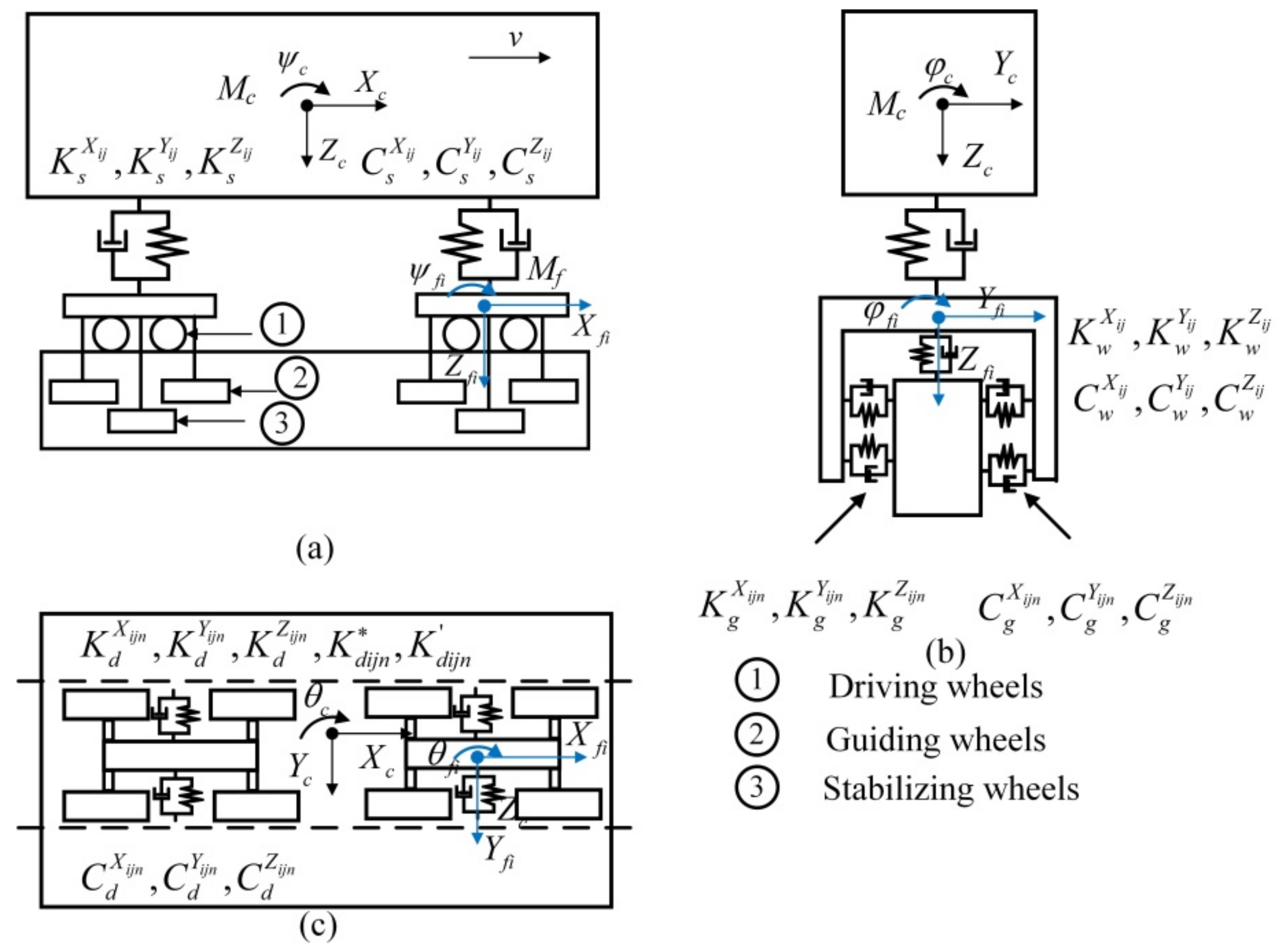
2.1. Vehicle Model
- (1)
- The elastic deformation of the car body and the bogie is not considered, and the car body is symmetrical about the center of mass, left and right and front and rear, that is, the car body and the bogie are symmetrical rigid bodies.
- (2)
- The monorail vehicle moves at a constant speed along the rigid track beam pavement, regardless of the longitudinal dynamic effect, and all tires are in constant contact with the track beam surface;
- (3)
- The structure of the running part is symmetrical and the suspension parameters are equal, the spring characteristic of the suspension system is linear, and the vehicle damping between all suspension systems of the vehicle is calculated as viscous damping.
- (4)
- The rigid bodies of the car body and the bogie are subjected to small displacement vibration at the basic equilibrium position.
- (1)
- The lateral, vertical, roll, pitch, and yaw movement equations of the vehicle body.
- (2)
- The lateral, vertical, roll, pitch, and yaw movement equations of the bogies.
- (3)
- Secondary suspension force.
2.2. Tire Model
- (1)
- The tire movement is a slight vibration, the tire deformation is very small, and the stiffness of all tires is linear in all directions;
- (2)
- Ignore the effects of vertical load changes and tire pressure changes on the stiffness of driving tires;
- (3)
- Consider the radial stiffness and damping, cornering effect and longitudinal slip of the running wheel tire;
- (4)
- Consider the radial stiffness and damping and cornering effects of the guide wheel and stabilizer wheel tire;
- (5)
- Ignoring the camber force and the aligning moment generated by the camber angle.
- (1)
- Tire radial force.
- (2)
- Side force and aligning moment.
- (3)
- Longitudinal slip and head shaking moment.
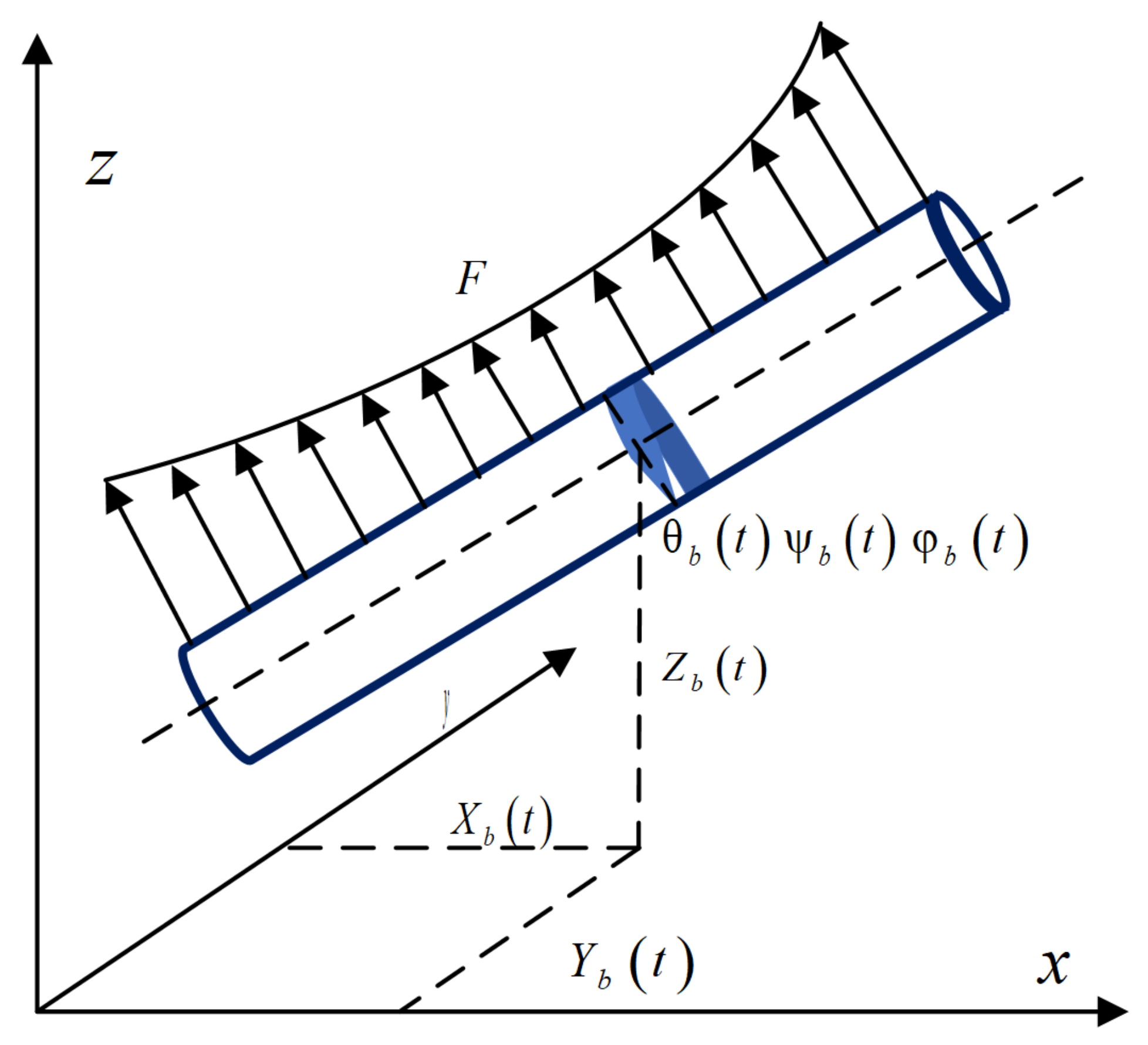
2.3. Track Beam Model
2.4. Vehicle-Track Beam Coupling Model
2.5. Selection of Calculation Parameters of Vehicle-Bridge Coupling System
- (1)
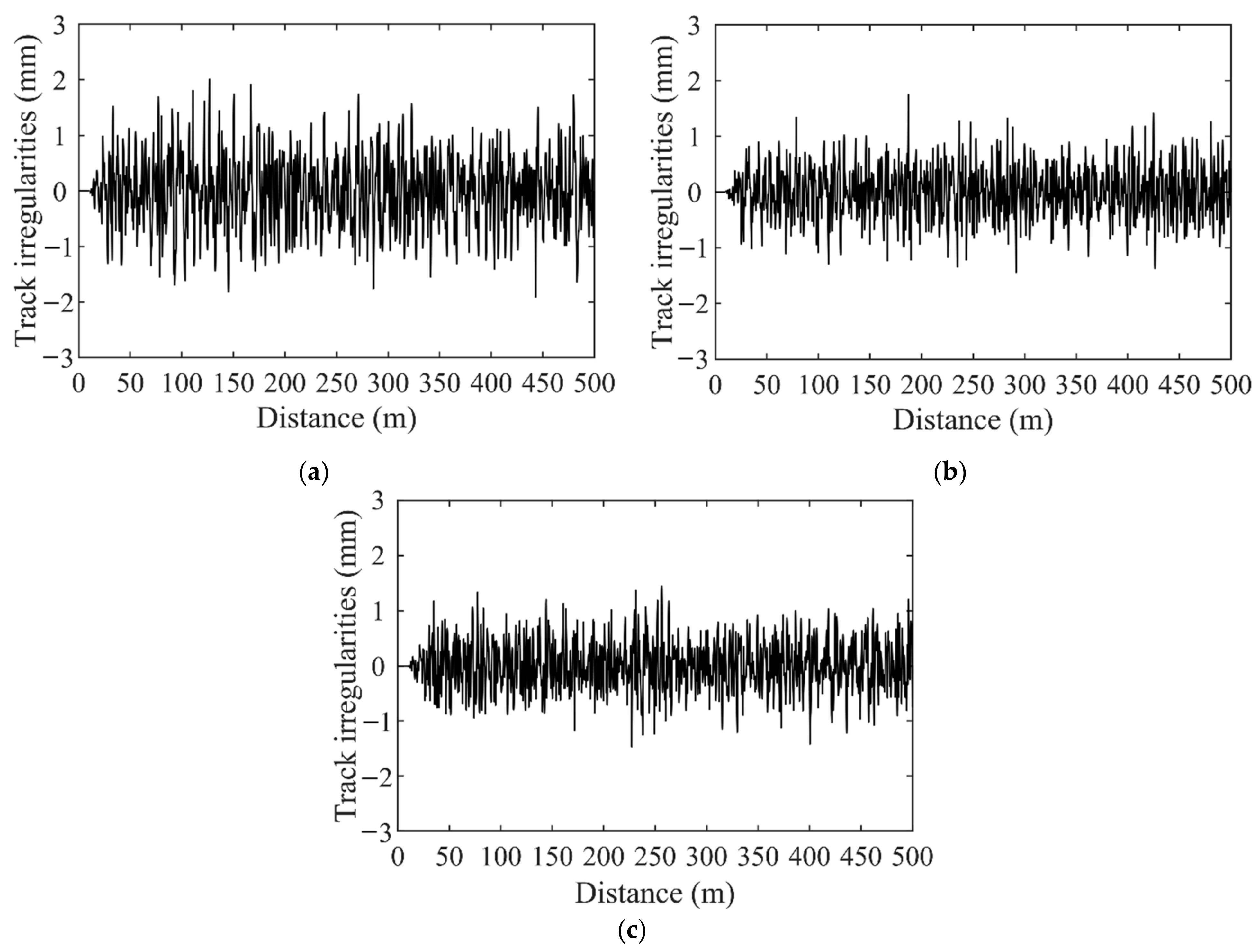
- Track beam irregularities.
- (2)
- Parameter selection of vehicle-track beam system
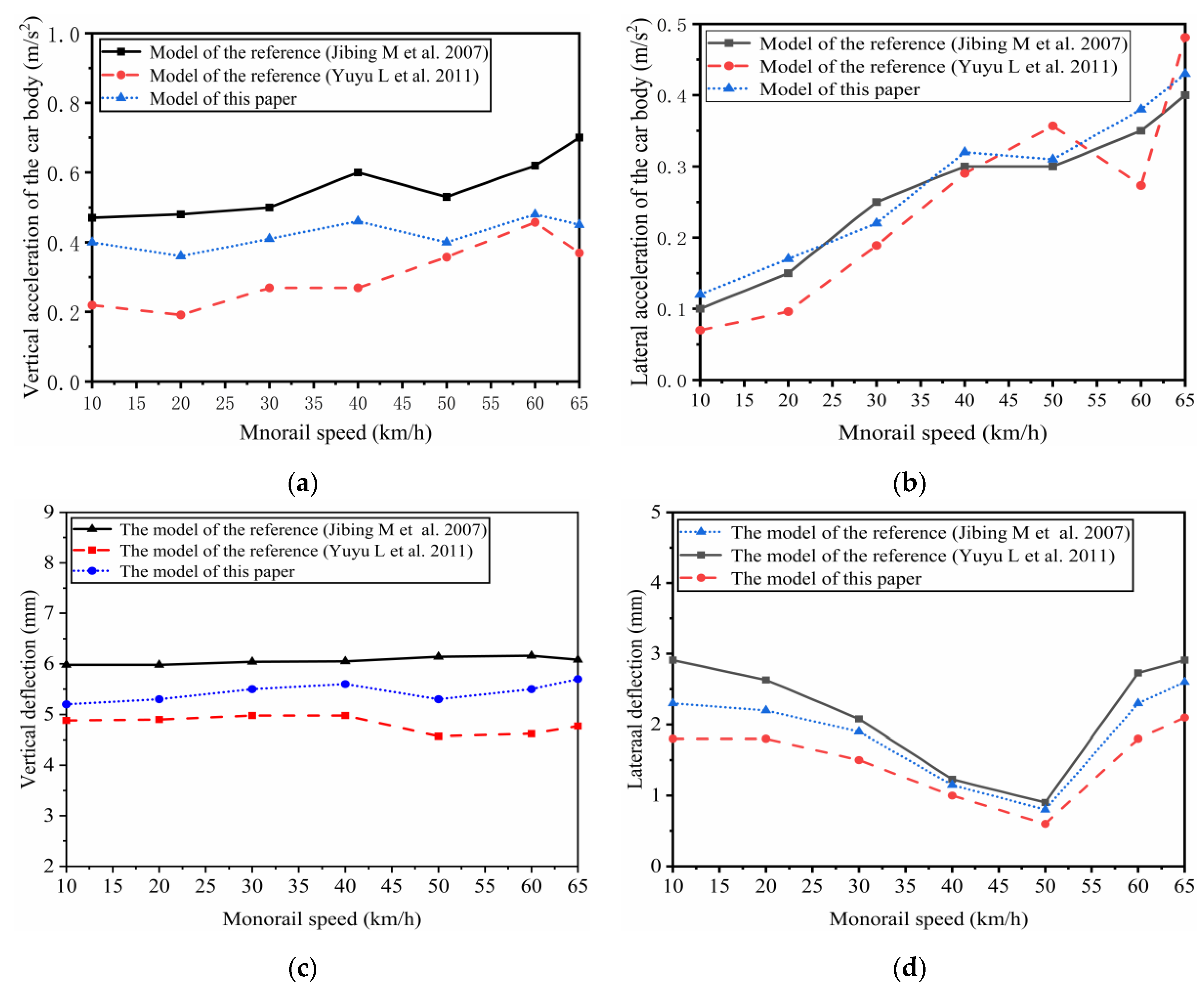
2.6. Model Verification
3. Influence of Spatial Alignment on Dynamic Characteristics of Straddle-Type Monorail System
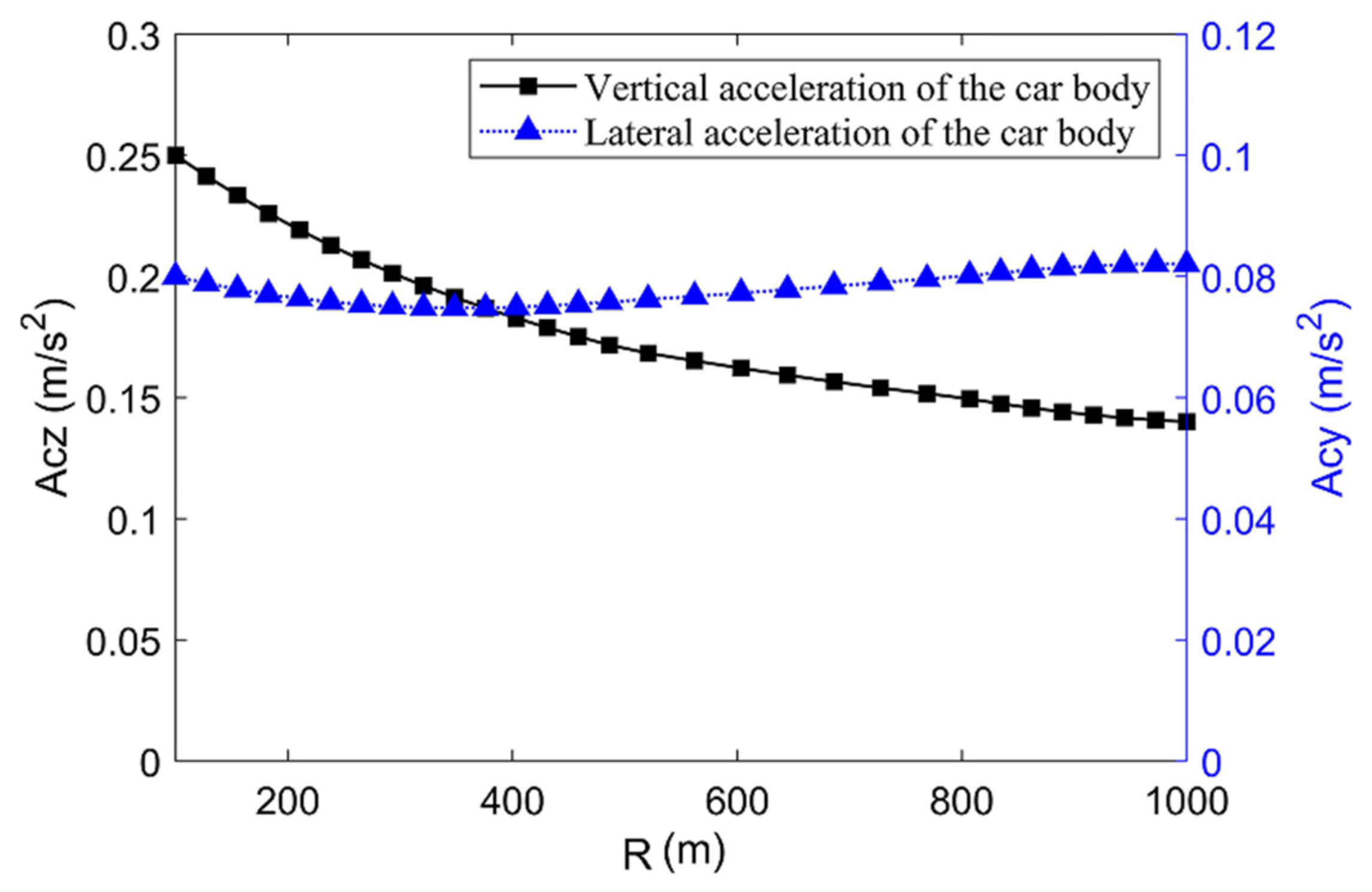
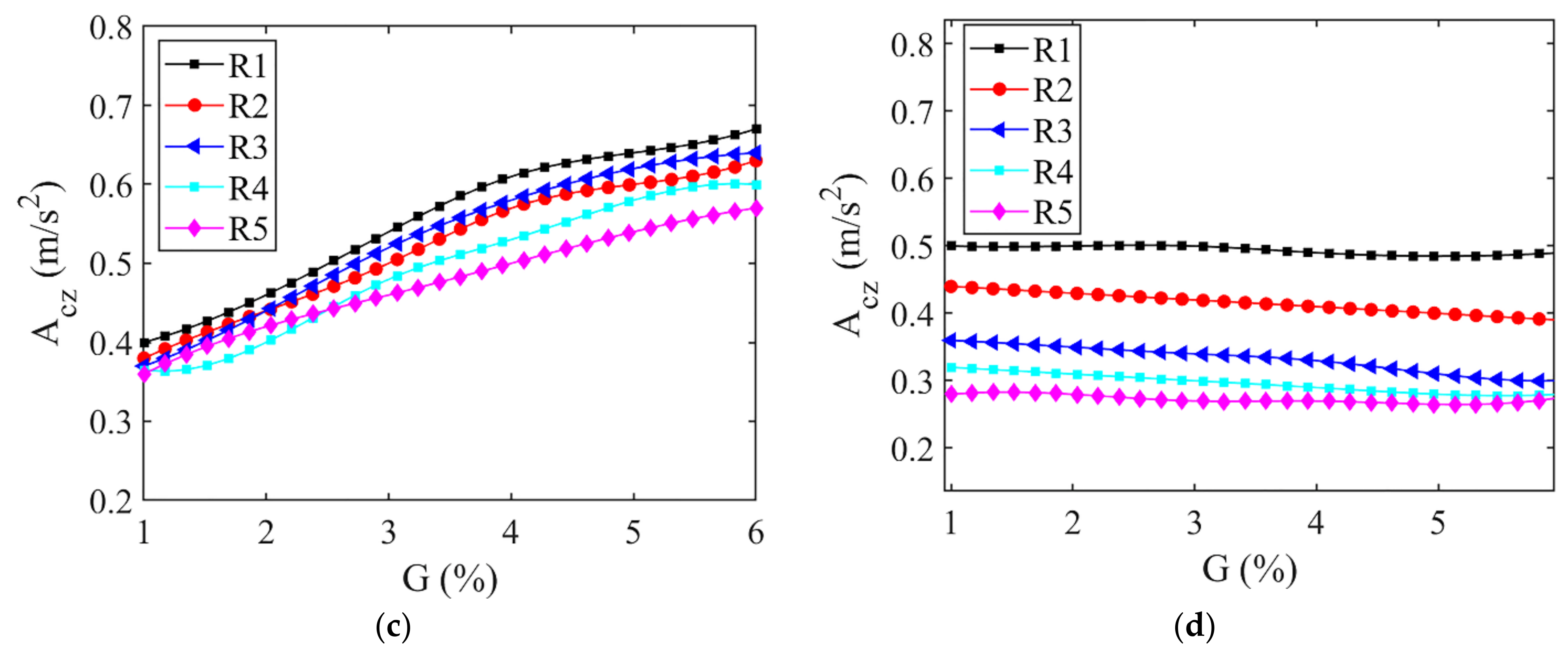
3.1. Influence of Curve Radius on the Dynamic Behaviors of the Straddle-Type Monorail System
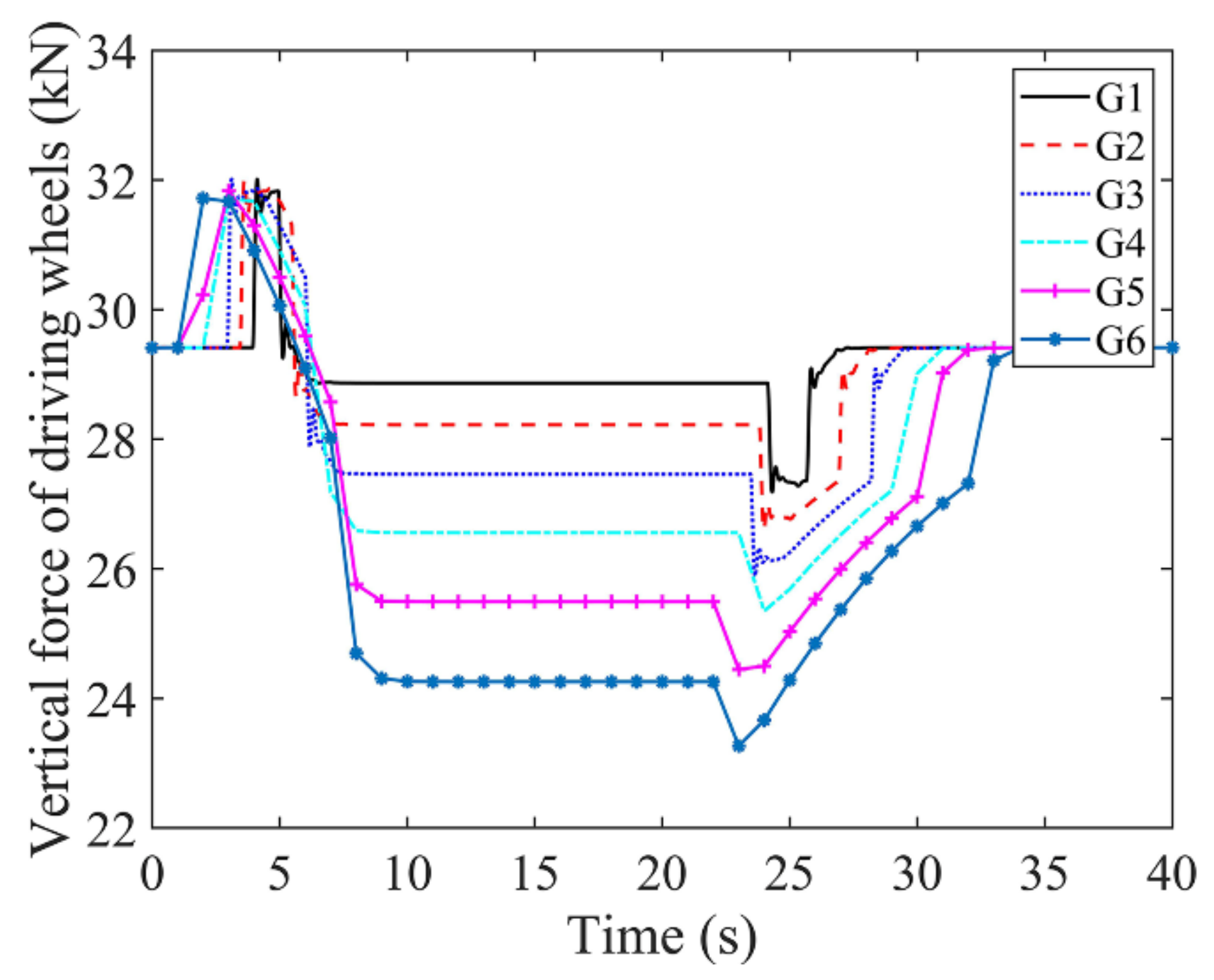
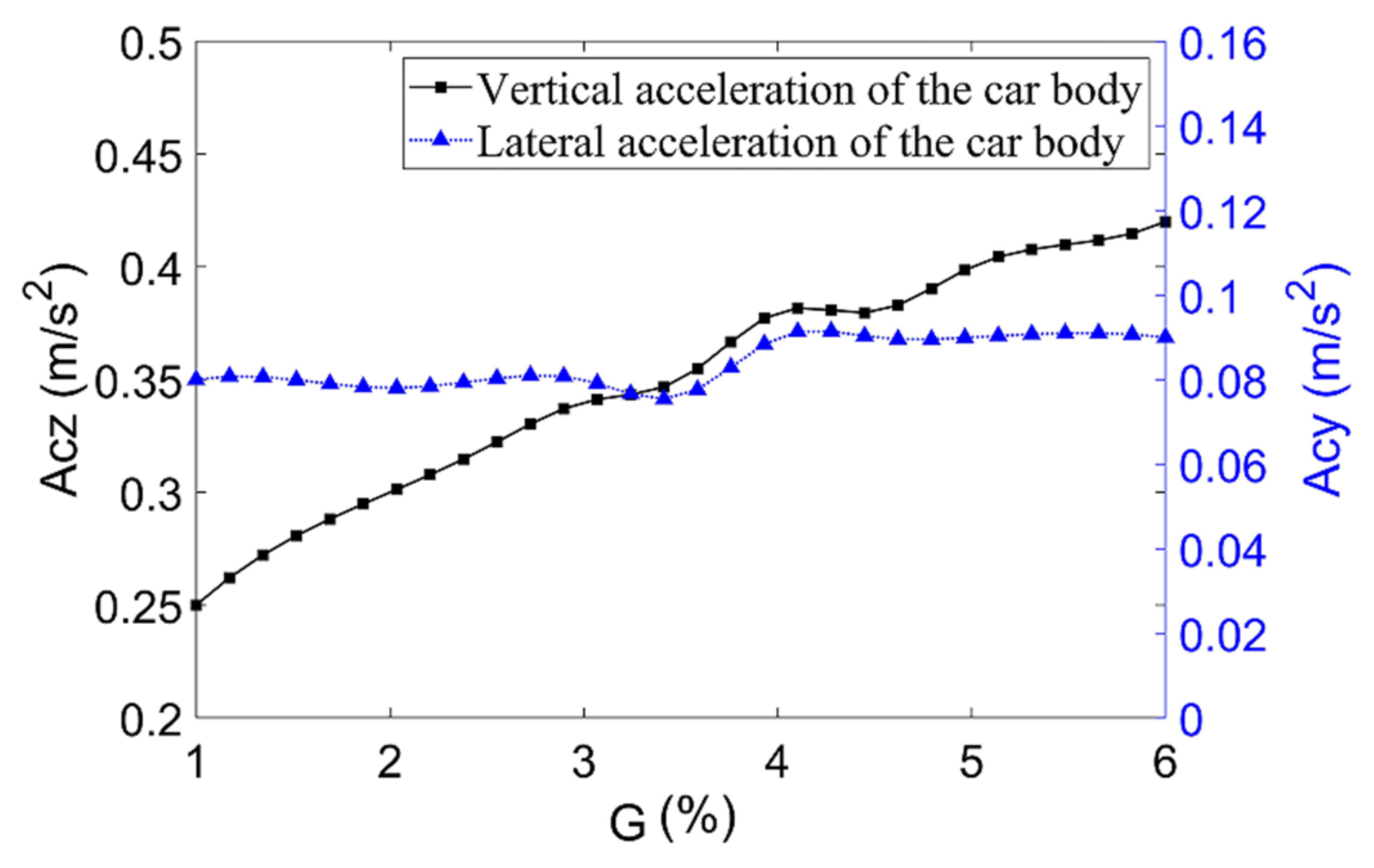
3.2. Influence of the Longitudinal Slope Gradient on the Dynamic Characteristics of the Straddle-Type Monorail System
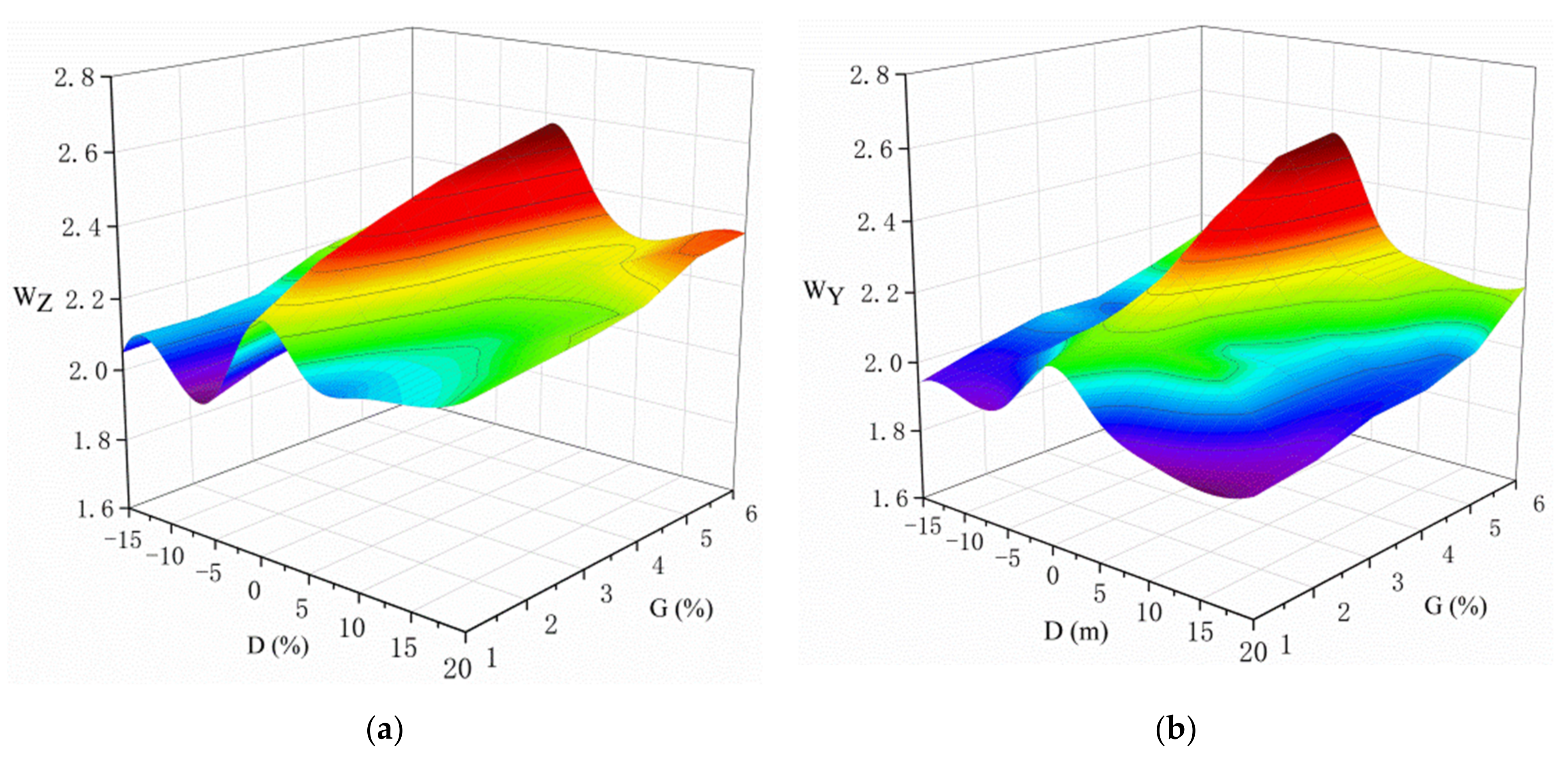
3.3. Dynamic Characteristics of Straddle-Type Monorail System under Compound Conditions of Planar and Vertical Lines
3.4. Influence of the Relative Position Change of the Straight-Slowing Point and the Slope-Changing Point on the Dynamic Characteristics of the Straddle-Type Monorail System
4. Conclusions
- (1)
- A new coupling dynamic model of STM considering the spatial alignment is established by incorporating the shear and torsion deformation of the track flexible beam system and the non-linear characteristics of the vehicle suspension system.
- (2)
- The indexes of running safety and vibration stability of the vehicle decrease with the decrease of curve radius or the increase of longitudinal slope gradient. With the increase in the relative position between the slope-changing point and the straight-slowing point, the dynamic driving safety and vibration stability indexes increase first and then decrease. The maximum value is observed when the straight-slowing points coincide with the slope-changing points. In addition, when the slope-changing point coincides with the transition curve of the track beam, the vibration response of the vehicle is more obvious than that when the straight-slowing points do not coincide with the slope-changing points.
- (3)
- From the viewpoint of dynamical running safety and vibration stability, the slope-changing point should be avoided to coincide with the area of the straight-slowing point. The straight-slowing point and slope-changing point should be located 5–15 m apart to obtain optimized minor dynamic responses of the straddle-type monorail coupling system.
- (4)
- The refined straddle-type monorail-track coupling dynamic analysis model established in this paper comprehensively considers the influence of nonlinear characteristics such as shear and torsional deformation of the track beam. noise problem), the calculation accuracy of the model in this paper is high, which greatly improves the application range of the calculation model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cross-section area of track beam | |
| Half of the lateral span of the driving wheels, guiding wheels and stabilizing | |
| Half of the lateral span of the secondary suspension | |
| Vertical damping of bogie tires | |
| Damping matrix of vehicle system and track beam system | |
| Distance of the slope-changing point relative to the straight-slowing point | |
| Elasticity modulus of track beam | |
| Vertical force of bogie tires | |
| Side force of bogie tires | |
| The longitudinal, lateral and vertical forces acting on the track from the support | |
| Load column vector of the vehicle body, front and rear bogies | |
| Longitudinal slope gradient | |
| Shear modulus of track beam | |
| Height of the vehicle body centre of gravity to the upper surface of the secondary suspension system | |
| Height of the frame centre of gravity to the lower surface of the secondary suspension system | |
| Height of the frame centre of gravity to the surface of the track beam | |
| Height of the frame centre of gravity to the centre of stabilizing wheels | |
| Height of the frame centre of gravity to the centre of guiding wheels | |
| Moment of inertia of track beam section relative to Z-axis and Y-axis | |
| St. venant’s torsional constant of track beam | |
| St. venant’s torsional constant of track beam | |
| Polar moment of inertia of track beam | |
| Mass moment of inertia of vehicle body | |
| Mass moment of inertia of bogies | |
| Spring constant of air spring | |
| Vertical spring constant of bogie tires | |
| Shear correction factors in principal planes of track beam system | |
| Stiffness matrix of vehicle and track beam system | |
| Half of the longitudinal distance between front and rear bogies | |
| Half of bogie wheelbase | |
| Half of guiding wheels wheelbase | |
| Mass of vehicle body and bogies | |
| Aligning moment of bogie tires | |
| Mass matrix of vehicle system and track beam system | |
| Moment (relative longitudinal track axis) that act on the track from the support | |
| The shaking moment generated by cornering force of front and rear bogie driving wheels | |
| Displacement of vehicle system | |
| Velocity of vehicle system | |
| Acceleration of vehicle system | |
| Displacement of track beam system | |
| Velocity of track beam system | |
| Acceleration of track beam system | |
| Curve radius | |
| Coordinates of shear centre relative to centre of gravity in principal central | |
| Lateral and vertical moment of the vehicle body | |
| The roll, pitch and yaw moment of the vehicle body | |
| The lateral and vertical moment of the bogies | |
| The roll, pitch and yaw moment of the bogies | |
| The longitudinal, lateral and vertical moment of the track beam | |
| Shear and torsion moment of the track beam | |
| Dirac delta function | |
| Material density of track beam | |
| The kinetic energy of the STM | |
| The potential energy of the STM | |
| The Rayleigh’s dissipation function | |
| Damping ratio of track beam system | |
| Lowest frequency that corresponds to pinned-pinned vibration mode | |
| The lateral and vertical irregularities | |
| Superelevation angle of the outer rail at the track where the centre of the frame and vehicle is located | |
| Subscripts | |
| Track beam system | |
| Vehicle system | |
| Degree of freedom identifier of the vehicle system | |
| The secondary suspension force | |
| x, y, z direction | |
| The driving wheels, guiding wheels and stabilizing wheels |
Appendix A
References
- Timan, P.E. Why monorail systems provide a great solution for metropolitan areas. Urban Rail Transit 2015, 1, 13–25. [Google Scholar] [CrossRef]
- Goda, K.; Nishigaito, T.; Hiraishi, M.; Iwasaki, K. A curving simulation for a monorail car. In Proceedings of the 2000 ASME/IEEE Joint Railroad Conference, Newark, NY, USA, 6 April 2000; pp. 171–177. [Google Scholar]
- Zhang, J.; Huang, Y.; Fu, L.; Tao, G. Research on the pre-pressure of the steering tire and stabilizing tire of a straddle-type monorail car. Railw. Locomot. Car 2011, 31, 48–52. [Google Scholar]
- Du, Z.; Wang, X. Research on stability simulation for straddle-type monorail vehicle. Railw. Locomot. Car 2009, 29, 56–59. [Google Scholar]
- Gou, H.; Zhou, W.; Yang, C.; Bao, Y.; Pu, Q. Dynamic Response of a Long-Span Concrete-Filled Steel Tube Tied Arch Bridge and the Riding Comfort of Monorail Trains. Appl. Sci. 2018, 8, 650. [Google Scholar] [CrossRef]
- Naeimi, M.; Tatari, M.; Esmaeilzadeh, A.; Mehrali, M. Dynamic interaction of the monorail-bridge system using a combined finite element multibody-based model. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2014, 229, 132–151. [Google Scholar] [CrossRef]
- Naeimi, M.; Tatari, M.; Esmaeilzadeh, A. Dynamic of the Monorail Train Subjected to the Braking on a Straight Guideway Bridge. Arch. Mech. Eng. 2018, 3, 363–375. [Google Scholar] [CrossRef][Green Version]
- Wang, H.; Zhu, E.; Chen, Z. Dynamic Response Analysis of the Straddle-Type Monorail Bridge–Vehicle Coupling System. Urban Rail Transit 2017, 3, 172–181. [Google Scholar] [CrossRef]
- Liu, Y.; Ge, Y.; Yang, Y. Vibration characteristic of coupled system for straddle-type monorail beam and train. J. Traffic Transp. Eng. 2010, 10, 46–53. [Google Scholar]
- Zhang, J. Research on Dynamic of Straddle Monorail Car. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2009. [Google Scholar]
- Ma, J. Research on Structural Static and Dynamic Behaviors of Straddle-Type Monorail Transportation System. Ph.D Thesis, Southwest Jiaotong University, Chengdu, China, 2008. [Google Scholar]
- Kahrobaiyan, M.H.; Asghari, M.; Ahmadian, M.T. A Timoshenko beam element based on the modified couple stress theory. Int. J. Mech. Sci. 2014, 79, 75–83. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Bahrami, A. On size-dependent Timoshenko beam element based on modified couple stress theory. Int. J. Eng. Sci. 2016, 107, 134–148. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, J.; Zhou, S. A micro scale Timoshenko beam model based on strain gradient elasticity theory. Eur. J. Mech. A/Solids 2010, 29, 591–599. [Google Scholar] [CrossRef]
- Ni, Y.; Ye, S.; Song, S. An experimental study on constructing mr secondary suspension for high-speed trains to improve lateral ride comfort. Smart Struct. Syst. 2016, 18, 53–74. [Google Scholar] [CrossRef]
- Liu, Y. Research on Dynamic Interaction of Straddle Type Monorail Vehicle and Track Beam. Ph.D Thesis, Southwest Jiaotong University, Chengdu, China, 2011. [Google Scholar]
- Ma, J.; Pu, Q.; Xia, Z. Experimental research on the Chongqing straddle-type monorail transportation system under dynamic loading. J. Railw. Eng. Soc. 2007, 24, 69–75. [Google Scholar]
- GB 50458:2008; Code for Design of Straddle Monorail Transit. China Building Industry Press: Beijing, China, 2009.




| The Wheels | |||
|---|---|---|---|
| driving wheels | 0.0005 | 0.35 | 3.00 |
| guiding wheels | 0.0006 | 0.50 | 2.80 |
| stabilizing wheels | 0.0006 | 0.50 | 2.60 |
| Serial Number | Calculate Frequency(Hz) | Measured Frequency(Hz) | Mode of Vibration | Error Analysis |
|---|---|---|---|---|
| Z206-25 | 3.670 | 3.882 | first-order lateral bend | −5.46% |
| 7.012 | 7.178 | first-order vertical bend | −2.31% | |
| Y210-40 | 8.545 | 9.180 | first-order lateral bend | −6.9% |
| 4.606 | 4.639 | first-order vertical bend | −0.71% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Lu, H.; Hua, X.; Chen, Q. An Investigation on Dynamic Characteristics of the Straddle-Type Monorail System under Spatial Alignment. Machines 2022, 10, 724. https://doi.org/10.3390/machines10090724
Xu X, Lu H, Hua X, Chen Q. An Investigation on Dynamic Characteristics of the Straddle-Type Monorail System under Spatial Alignment. Machines. 2022; 10(9):724. https://doi.org/10.3390/machines10090724
Chicago/Turabian StyleXu, Xiangyang, Huping Lu, Xia Hua, and Qingke Chen. 2022. "An Investigation on Dynamic Characteristics of the Straddle-Type Monorail System under Spatial Alignment" Machines 10, no. 9: 724. https://doi.org/10.3390/machines10090724
APA StyleXu, X., Lu, H., Hua, X., & Chen, Q. (2022). An Investigation on Dynamic Characteristics of the Straddle-Type Monorail System under Spatial Alignment. Machines, 10(9), 724. https://doi.org/10.3390/machines10090724






