Granular Resistive Force Theory Extension for Saturated Wet Sand Ground
Abstract
:1. Introduction
2. Method and Materials
2.1. STEP 1: Equipment Preparation
2.2. STEP 2: Key Parameter Measurement
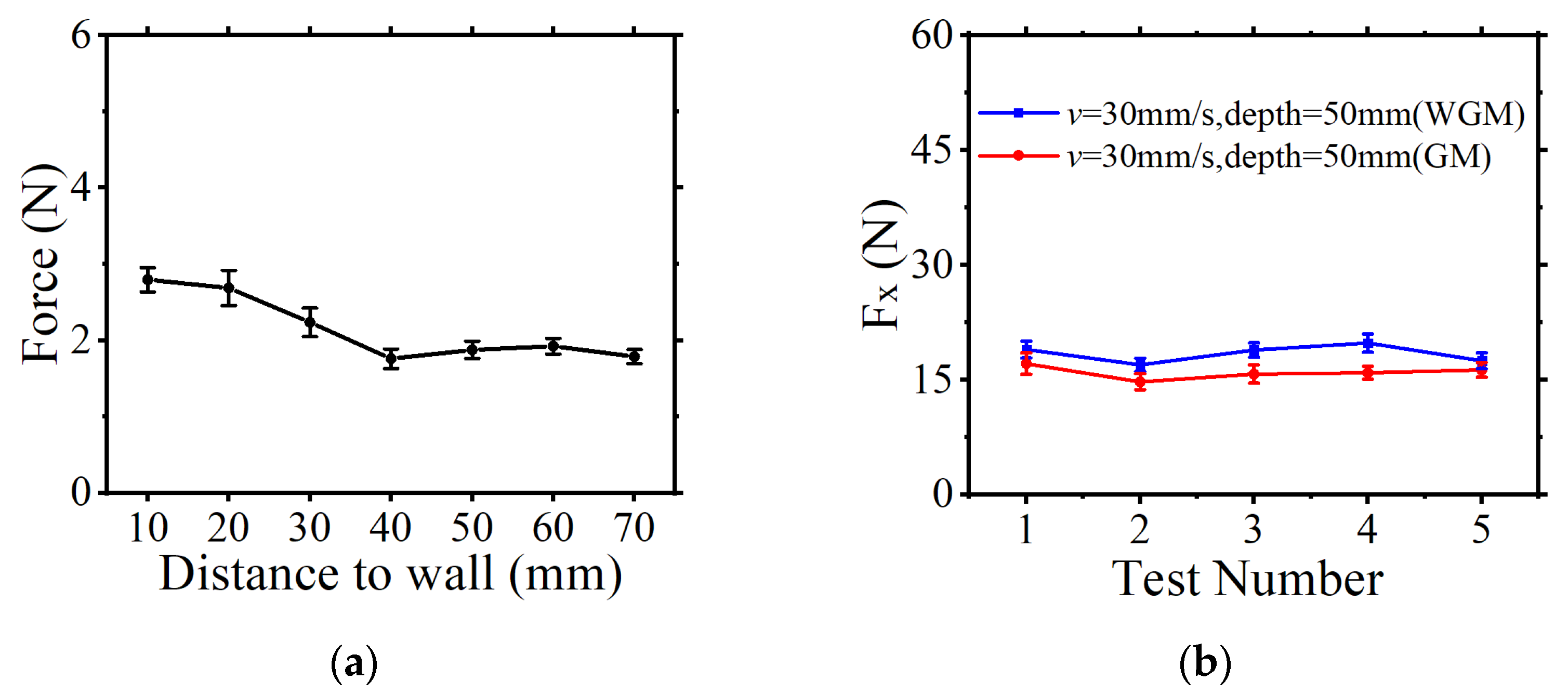
2.3. STEP 3: Two Calibrations for the Test
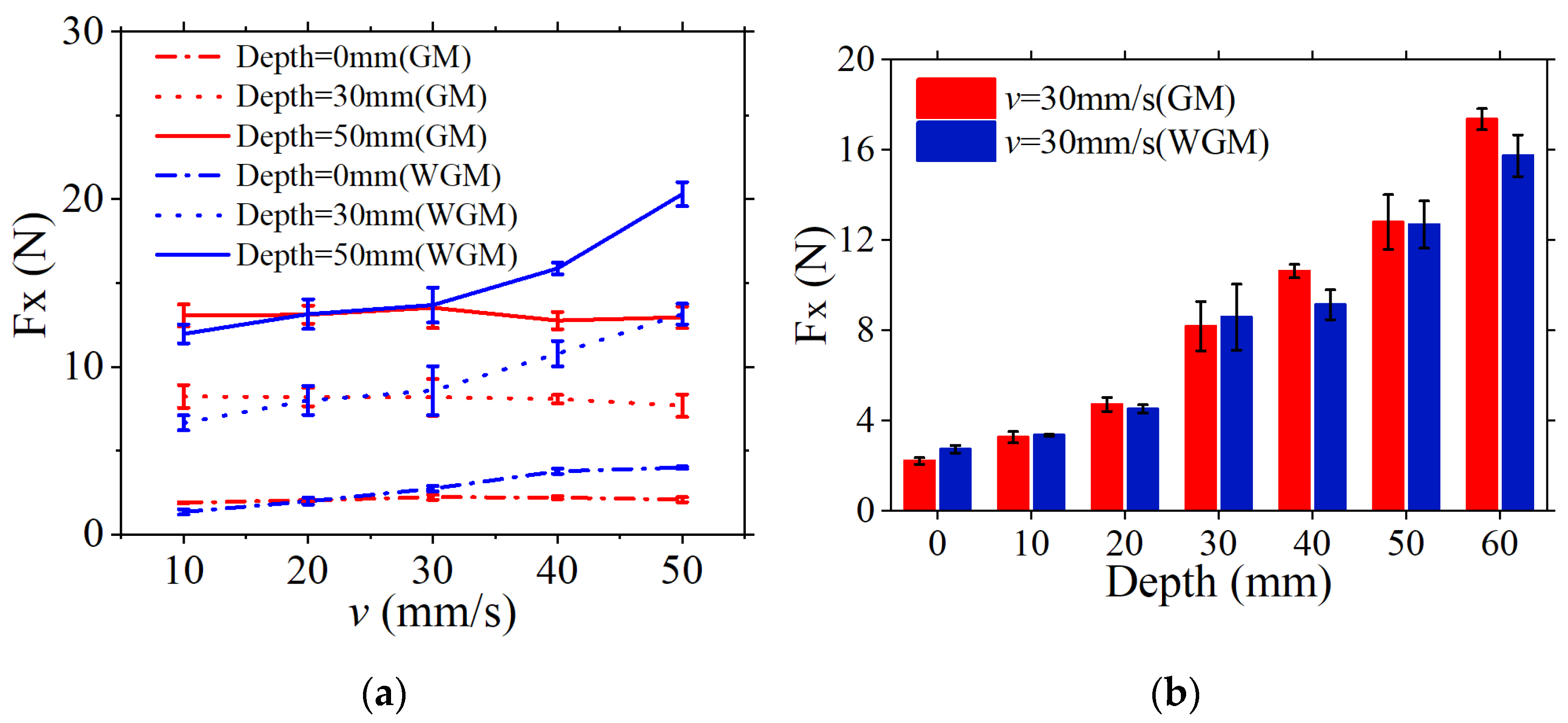
2.4. STEP 4: Tests of the Horizontal Force
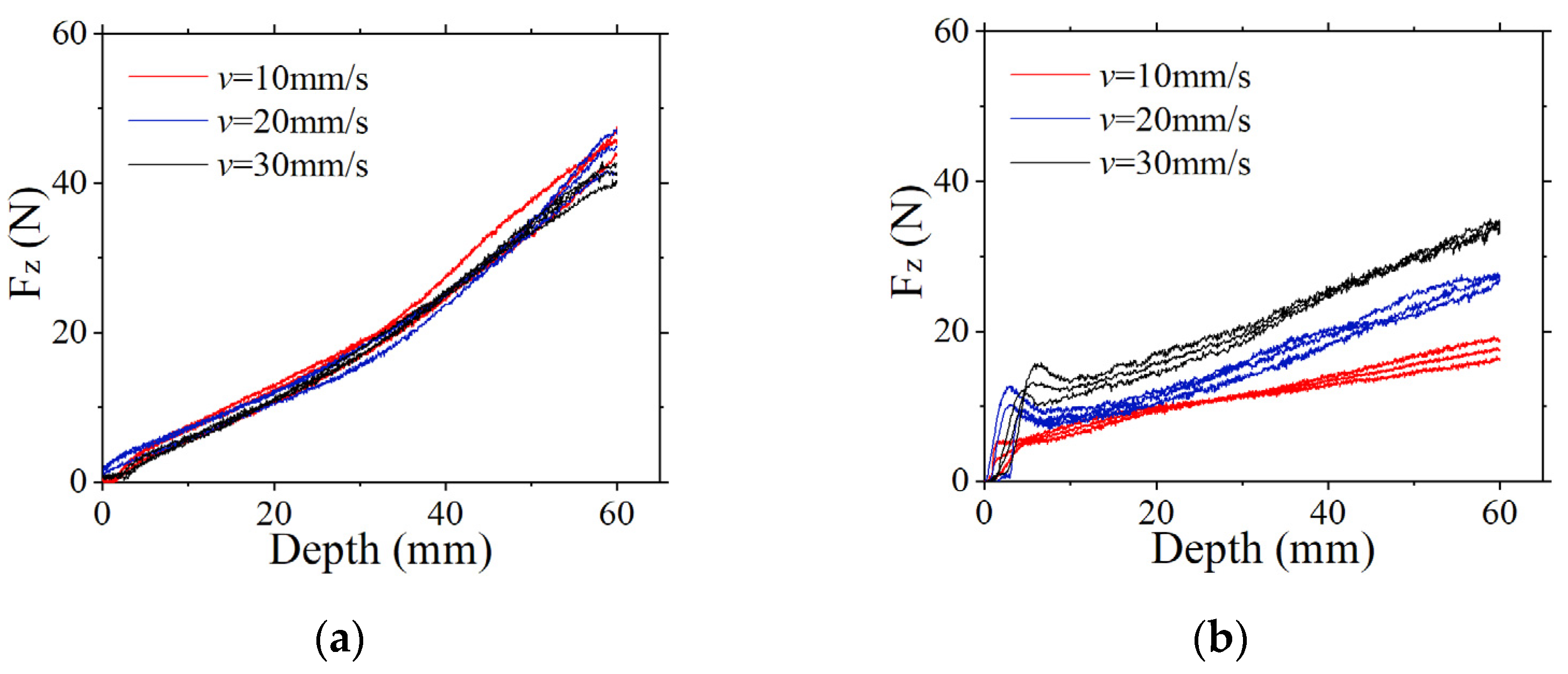
2.5. STEP 5: Tests of the Vertical Force
3. Calculation and Verification of the SGRFT
3.1. SGRFT Method
3.2. Simulation and Validation for Legs in SWGM
4. Experiments
4.1. Test for Propeller-Leg in SWGM
4.2. Setup of the Running Experiment
4.3. Results and Comparison of the Running Experiment
5. Conclusions
- (1)
- The difference in sensitivity to speed was observed by the comparative tests of the leg movement in GM and SWGM. The influence of moving speed on propulsion was much greater in SWGM than in GM. When the speed changes from 10 mm/s to 50 mm/s at the same depth, the change in maximum horizontal force can reach 78.6% in SWGM, but the horizontal force changes in the GM do not exceed 10% under the same measurement conditions.
- (2)
- The SGRFT method was developed by adding the scale factors of velocity coefficient and depth coefficient to RFT. The SGRFT can predict the horizontal propulsion force of legs during low speed (10 mm/s~50 mm/s) motion on the SWGM ground.
- (3)
- The running experiment of the robot equipped with the propeller-leg proved that robotic legs exhibit different force laws on dry GM ground and SWGM ground. The SGRFT can be used as a tool and method to predict the resistive force on the legs of robots working in an amphibious environment.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Arvidson, R.E.; Bell, J.F., III; Bellutta, P.; Cabrol, N.A.; Catalano, J.G.; Cohen, J.; Crumpler, L.S.; Marais, D.J.D.; Estlin, T.A.; Farrand, W.H.; et al. Spirit Mars Rover Mission: Overview and selected results from the northern Home Plate Winter Haven to the side of Scamander crater. J. Geophys. Res. Planets 2010, 115, 64. [Google Scholar] [CrossRef] [Green Version]
- Shrivastava, S.; Karsai, A.; Aydin, Y.O.; Pettinger, R.; Bluethmann, W.; Ambrose, R.O.; Goldman, D.I. Material remodeling and unconventional gaits facilitate locomotion of a robophysical rover over granular terrain. Sci. Robot. 2020, 5, eaba3499. [Google Scholar] [CrossRef] [PubMed]
- Agarwal, S.; Karsai, A.; Goldman, D.I.; Kamrin, K. Surprising simplicity in the modeling of dynamic granular intrusion. Sci. Adv. 2021, 7, eabe0631. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Lewis, K. The Need for and Feasibility of Alternative Ground Robots to Traverse Sandy and Rocky Extraterrestrial Terrain. Adv. Intell. Syst. 2022, 2022, 2100195. [Google Scholar] [CrossRef]
- Brunskill, C.; Patel, N.; Gouache, T.P.; Scott, G.P.; Saaj, C.M.; Matthews, M.; Cui, L. Characterisation of martian soil simulants for the ExoMars rover testbed. J. Terramechanics 2011, 48, 419–438. [Google Scholar] [CrossRef] [Green Version]
- Ding, L.; Gao, H.; Deng, Z.; Song, J.; Liu, Y.; Liu, G.; Iagnemma, K. Foot-terrain interaction mechanics for legged robots: Modeling and experimental validation. Int. J. Robot. Res. 2013, 32, 1585–1606. [Google Scholar] [CrossRef]
- Ding, L.; Huang, L.; Li, S.; Gao, H.; Deng, H.; Li, Y.; Liu, G. Definition and Application of Variable Resistance Coefficient for Wheeled Mobile Robots on Deformable Terrain. IEEE Trans. Robot. 2020, 36, 894–909. [Google Scholar] [CrossRef]
- Maladen, R.D.; Ding, Y.; Umbanhowar, P.B.; Kamor, A.; Goldman, D.I. Mechanical models of sandfish locomotion reveal principles of high performance subsurface sand-swimming. J. R. Soc. Interface 2011, 8, 1332–1345. [Google Scholar] [CrossRef] [Green Version]
- Ding, Y.; Sharpe, S.S.; Masse, A.; Goldman, D.I. Mechanics of Undulatory Swimming in a Frictional Fluid. PLoS Comput. Biol. 2012, 8, e1002810. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Zhang, T.; Goldman, D.I. A Terradynamics of Legged Locomotion on Granular Media. Science 2013, 339, 1408–1412. [Google Scholar] [CrossRef] [Green Version]
- Zhang, T.; Goldman, D.I. The effectiveness of resistive force theory in granular locomotion. Phys. Fluids 2014, 26, 101308. [Google Scholar] [CrossRef] [Green Version]
- Thoesen, A.; McBryan, T.; Green, M.; Mick, D.; Martia, J.; Marvi, H. Revisiting Scaling Laws for Robotic Mobility in Granular Media. IEEE Robot. Autom. Lett. 2020, 5, 1319–1325. [Google Scholar] [CrossRef]
- Marvi, H.; Gong, C.; Gravish, N.; Astley, H.; Travers, M.; Hatton, R.L.; Mendelson, J.R., III; Choset, H.; Hu, D.L.; Goldman, D.I. Sidewinding with minimal slip: Snake and robot ascent of sandy slopes. Science 2014, 346, 224–229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Treers, L.K.; Cao, C.; Stuart, H.S. Granular Resistive Force Theory Implementation for Three-Dimensional Trajectories. IEEE Robot. Autom. Lett. 2021, 6, 1887–1894. [Google Scholar] [CrossRef]
- Huang, L.; Zhu, J.; Yuan, Y.; Yin, Y.; Yin, Y.H. A Dynamic Resistive Force Model for Designing Mobile Robot in Granular Media. IEEE Robot. Autom. Lett. 2022, 7, 5357–5364. [Google Scholar] [CrossRef]
- Naclerio, N.D.; Karsai, A.; Murray-Cooper, M.; Ozkan-Aydin, Y.; Aydin, E.; Goldman, D.I.; Hawkes, E.W. Controlling subterranean forces enables a fast, steerable, burrowing soft robot. Sci. Robot. 2021, 6, eabe2922. [Google Scholar] [CrossRef]
- Ortiz, D.; Gravish, N.; Tolley, M.T. Soft Robot Actuation Strategies for Locomotion in Granular Substrates. IEEE Robot. Autom. Lett. 2019, 4, 2630–2636. [Google Scholar] [CrossRef] [Green Version]
- Li, D.; Huang, S.; Tang, Y.; Marvi, H.; Tao, J.; Aukes, D.M. Compliant Fins for Locomotion in Granular Media. IEEE Robot. Autom. Lett. 2021, 6, 5984–5991. [Google Scholar] [CrossRef]
- Fernandez, J.; Mazumdar, A. Tail-Based Anchoring on Granular Media for Transporting Heavy Payloads. IEEE Robot. Autom. Lett. 2021, 6, 1232–1239. [Google Scholar] [CrossRef]
- Lee, K.; Ryu, S.; Kim, C.; Seo, T. A Compact and Agile Angled-Spoke Wheel-Based Mobile Robot for Uneven and Granular Terrains. IEEE Robot. Autom. Lett. 2022, 7, 1620–1626. [Google Scholar] [CrossRef]
- Sharpe, S.S.; Kuckuk, R.; Goldman, D.I. Controlled preparation of wet granular media reveals limits to lizard burial ability. Phys. Biol. 2015, 12, 046009. [Google Scholar] [CrossRef] [PubMed]
- Gidmark, N.J.; Strother, J.A.; Horton, J.M.; Summers, A.P.; Brainerd, E.L. Locomotory transition from water to sand and its effects on undulatory kinematics in sand lances (Ammodytidae). J. Exp. Biol. 2011, 214, 657–664. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hosoi, A.E.; Goldman, D.I. Beneath Our Feet: Strategies for Locomotion in Granular Media. Annu. Rev. Fluid Mech. 2015, 47, 431–453. [Google Scholar] [CrossRef] [Green Version]
- Jung, S.; Winter, A.G.; Hosoi, A.E. Dynamics of digging in wet soil. Int. J. Non-Linear Mech. 2011, 46, 602–606. [Google Scholar] [CrossRef] [Green Version]
- Winter, A.G.; Deits, R.L.H.; Hosoi, A.E. Localized fluidization burrowing mechanics of Ensis directus. J. Exp. Biol. 2012, 215, 2072–2080. [Google Scholar] [CrossRef] [Green Version]
- Winter, A.G.; Hosoi, A.E. Identification and Evaluation of the Atlantic Razor Clam (Ensis directus) for Biologically Inspired Subsea Burrowing Systems. Integr. Comp. Biol. 2011, 51, 151–157. [Google Scholar] [CrossRef] [Green Version]
- Winter, G.A.G.; Deits, R.L.H.; Dorsch, D.S.; Slocum, A.H.; Hosoi, A.E. Razor clam to RoboClam: Burrowing drag reduction mechanisms and their robotic adaptation. Bioinspiration Biomim. 2014, 9, 036009. [Google Scholar] [CrossRef]
- Ding, Y.; Gravish, N.; Goldman, D.I. Drag Induced Lift in Granular Media. Phys. Rev. Lett. 2011, 106, 028001. [Google Scholar] [CrossRef] [Green Version]
- Michael, M.; Vogel, F.; Peters, B. DEM-FEM coupling simulations of the interactions between a tire tread and granular terrain. Comput. Methods Appl. Mech. Eng. 2015, 289, 227–248. [Google Scholar] [CrossRef]
- Tu, F.; Delbergue, D.; Miao, H.; Klotz, T.; Brochu, M.; Bocher, P.; Levesque, M. A sequential DEM-FEM coupling method for shot peening simulation. Surf. Coat. Technol. 2017, 319, 200–212. [Google Scholar] [CrossRef]
- Mutabaruka, P.; Kamrin, K. Simulation technique for slurries interacting with moving parts and deformable solids with applications. Comput. Part. Mech. 2018, 5, 239–267. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.M.; Wang, G.; Liu, K.X. Design and Optimization of a Multimode Amphibious Robot with Propeller-Leg. IEEE Trans. Robot. 2022, 38, 1–14. [Google Scholar] [CrossRef]
- Hedrick, T.L. Software techniques for two-and three-dimensional kinematic measurements of biological and biomimetic systems. Bioinspiration Biomim. 2008, 3, 034001. [Google Scholar] [CrossRef] [PubMed]
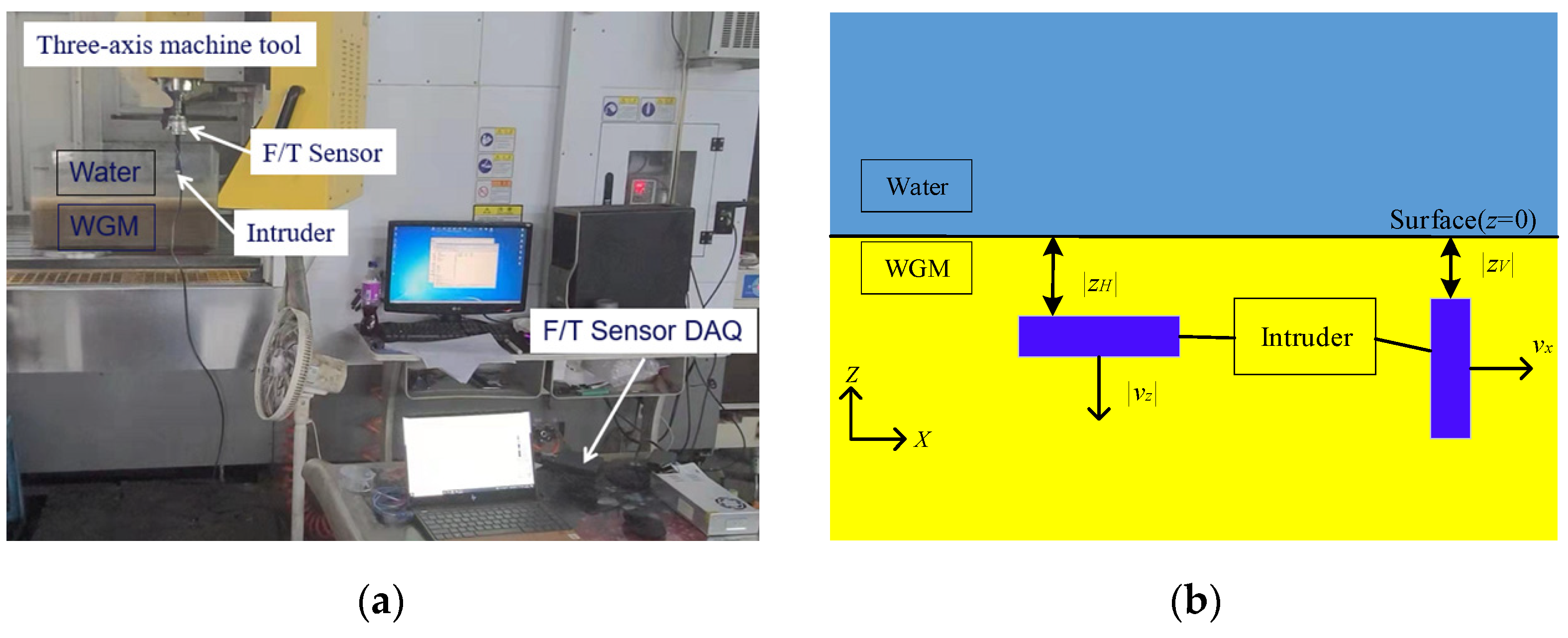
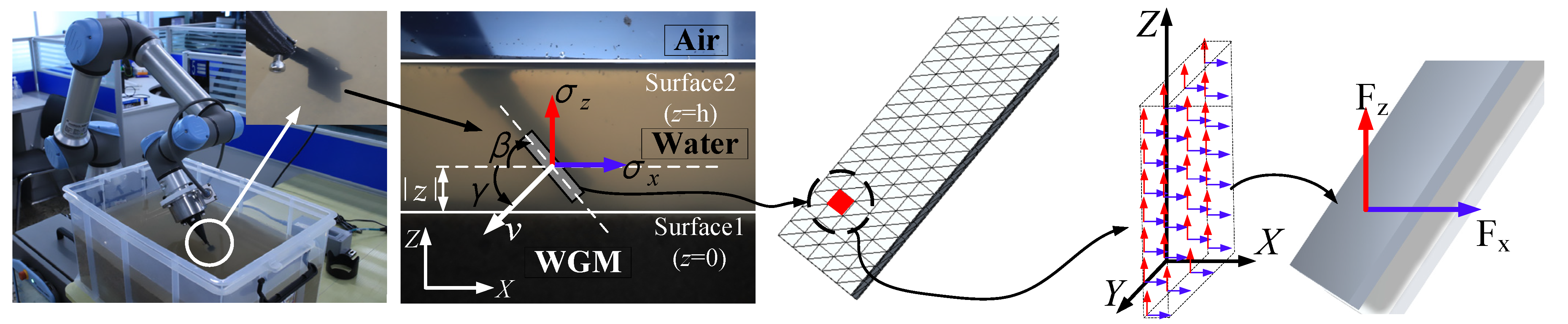


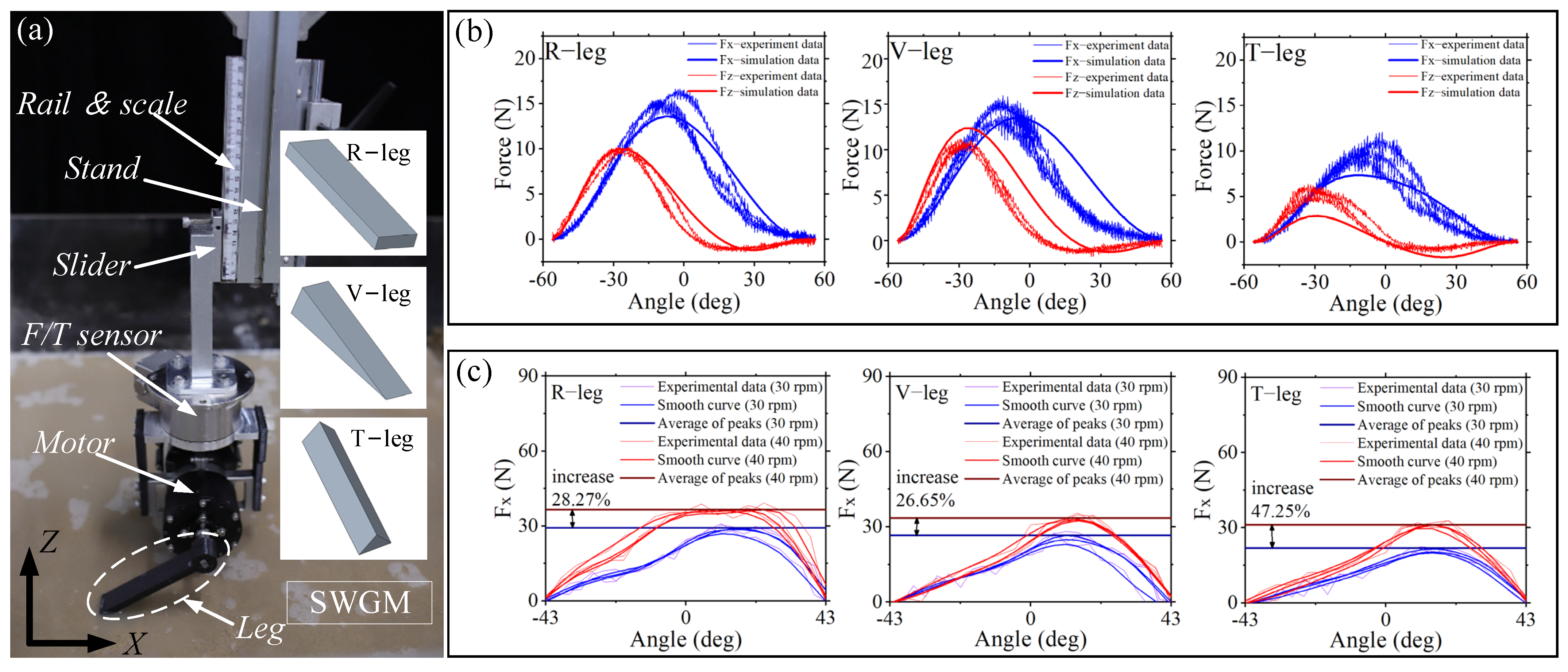

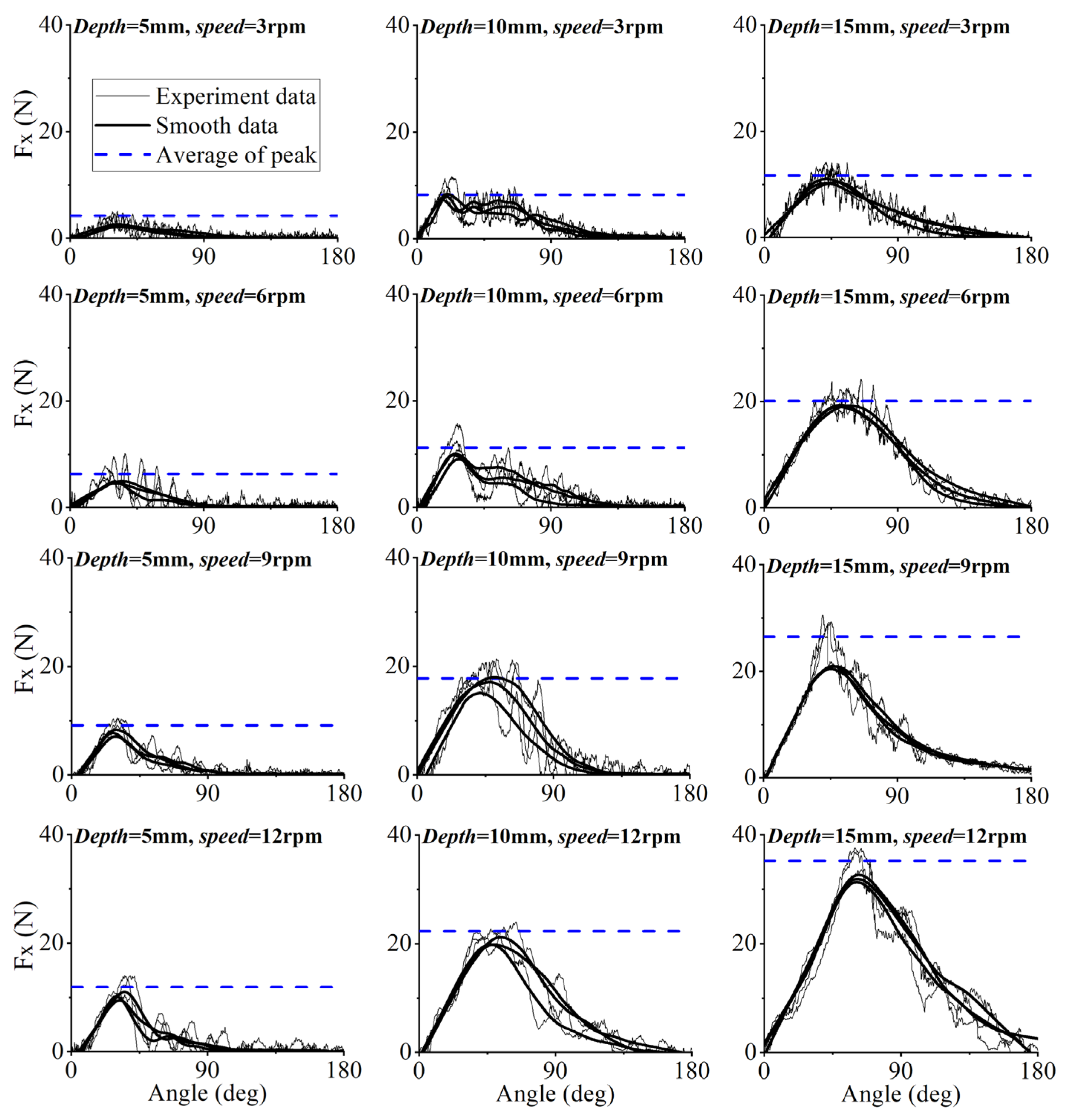

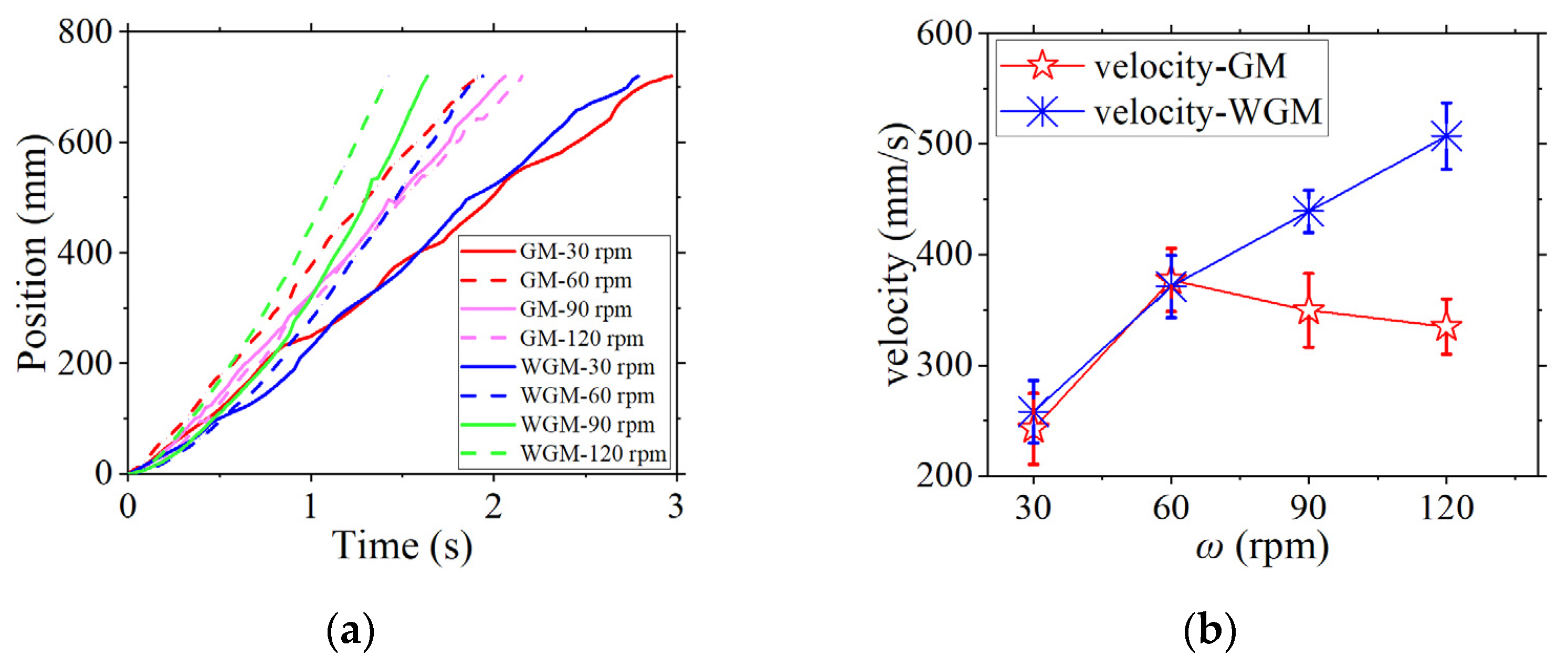
| Equipment | Model or Material | Key Parameters | |
|---|---|---|---|
| 1 | Machine center | NINGBO KAIBO CNC, DC-1317 | Position accuracy: ≤0.01 mm |
| 2 | F/T sensor | SRI-M4325k1 | Range: Fx = Fy = Fz ≤ 200 N, Mx = My = Mz ≤ 20 Nm |
| 3 | Intruder | Aluminum alloy 7075 | Projected area in the direction of v: 20 mm × 20 mm Thickness: 2 mm |
| 5 | Granular media | Sea sand | Particle diameter: ≤1 mm |
| 6 | Box | Plexiglass | Length × width × height = 800 mm × 800 mm × 400 mm |
| Parameter | Definition | |
|---|---|---|
| 1 | β | angle of attack |
| 2 | γ | angle of intrusion |
| 3 | z | the distance from the center of intruder to the surface |
| 4 | area of intruder’s leading face | |
| 5 | S | area of leg’s leading face |
| 6 | vertical and horizontal stress, σz,x = Fz,x/A | |
| 7 | Fz,x | vertical and horizontal force |
| 8 | αz,x | vertical and horizontal stresses per unit depth αz,x/|z| |
| 9 | stress (per unit depth) at the speed of v | |
| 10 | vertical and horizontal stresses at the speed of v | |
| 11 | velocity coefficient | |
| 12 | the basic stress obtained by testing |
| Coefficient | Average Value | ||
|---|---|---|---|
| 1 | 0.16 | 0.952 | |
| 2 | 0.23 | 0.940, 0.977, 0.968 | |
| 3 | 0.37 | 0.941, 0.965, 0.961 | |
| 4 | 0.47 | 0.933, 0.959, 0.970 |
| Force Properties | GM | SWGM |
|---|---|---|
| Sensitivity to speed | × | √ |
| Linearly related to depth | √ | √ |
| The stresses per unit depth | Fixed | Linearly related to speed |
| The force distribution is asymmetric | √ | √ |
| Equipment | Model |
|---|---|
| F/T sensor | ATI Gamma IP68 |
| Motor | KOLLMORGEN TBM(S)-6013-A |
| Encoder | RLS MRA029BC010DSE00 |
| Driver | G-SOLTWI15/100EE1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Wang, G.; Liu, K.; Chen, X.; Wang, J.; Pan, B.; Wang, L. Granular Resistive Force Theory Extension for Saturated Wet Sand Ground. Machines 2022, 10, 721. https://doi.org/10.3390/machines10090721
Ma X, Wang G, Liu K, Chen X, Wang J, Pan B, Wang L. Granular Resistive Force Theory Extension for Saturated Wet Sand Ground. Machines. 2022; 10(9):721. https://doi.org/10.3390/machines10090721
Chicago/Turabian StyleMa, Xinmeng, Gang Wang, Kaixin Liu, Xi Chen, Jixin Wang, Biye Pan, and Liquan Wang. 2022. "Granular Resistive Force Theory Extension for Saturated Wet Sand Ground" Machines 10, no. 9: 721. https://doi.org/10.3390/machines10090721
APA StyleMa, X., Wang, G., Liu, K., Chen, X., Wang, J., Pan, B., & Wang, L. (2022). Granular Resistive Force Theory Extension for Saturated Wet Sand Ground. Machines, 10(9), 721. https://doi.org/10.3390/machines10090721






