Research on Path Planning and Trajectory Tracking of an Unmanned Electric Shovel Based on Improved APF and Preview Deviation Fuzzy Control
Abstract
:1. Introduction
- (1)
- Based on the improved APF method and combined with the actual working conditions of the shovel, an obstacle-free path that meets the requirements of the shovel movement is planned;
- (2)
- Real-time control of ES preview distance and centroid deviation in trajectory tracking based on a fuzzy control method. An ES can quickly adjust the heading angle direction and track the preset trajectory in real-time.
2. ES Walking Condition
3. Motion Path Planning Method
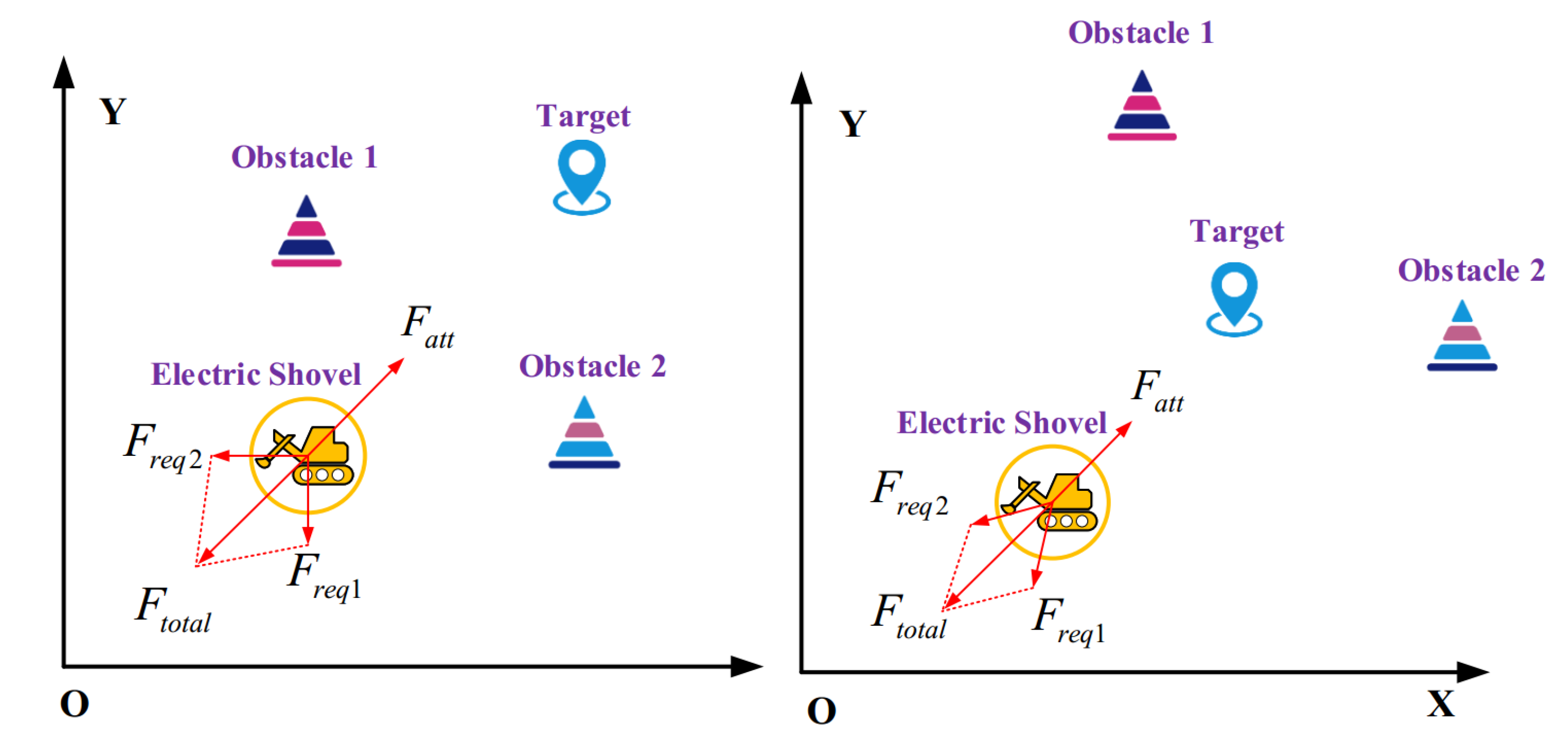
3.1. APF Method
3.2. Improved APF Method
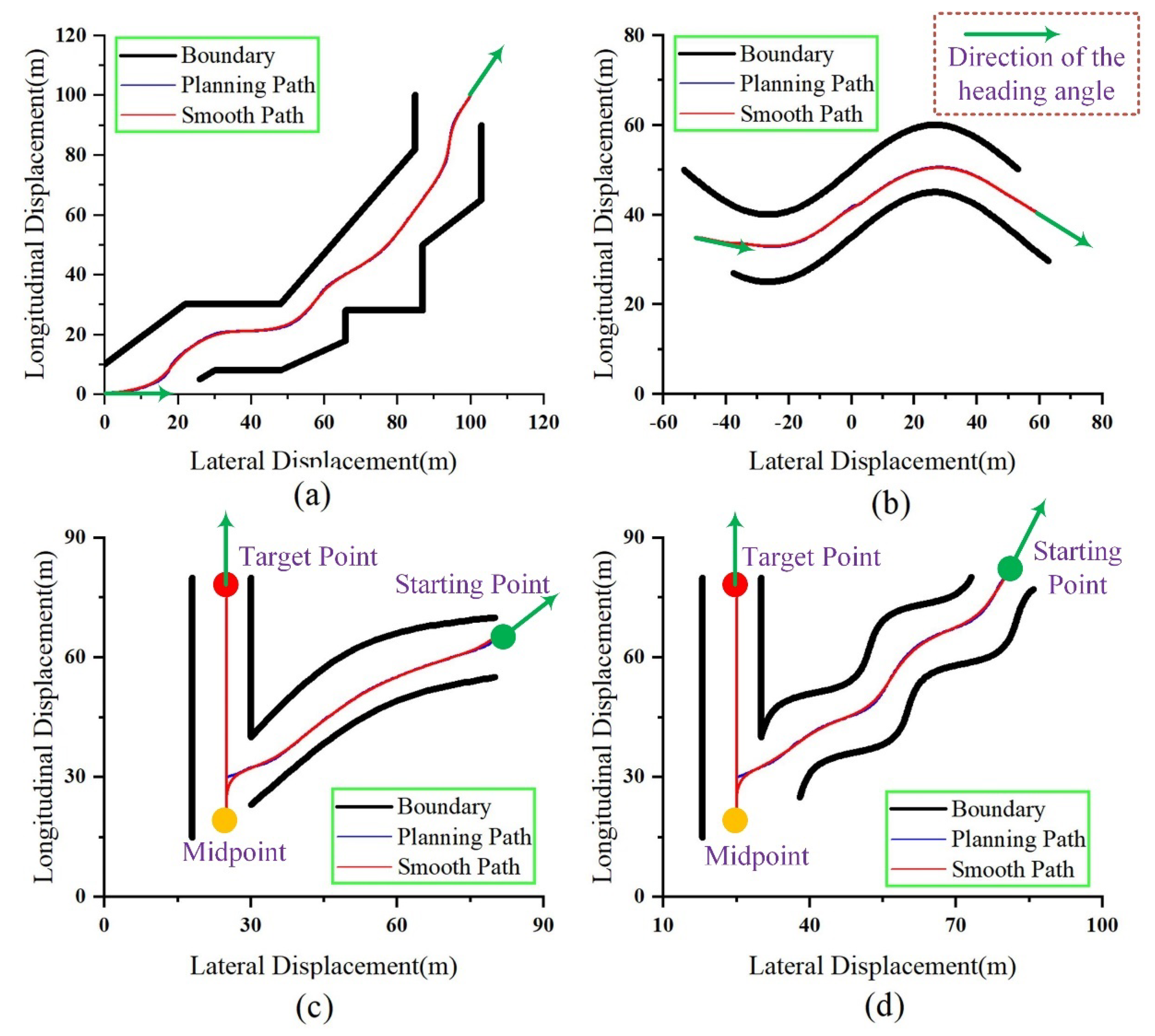
3.3. Simulation
4. Trajectory Tracking Method
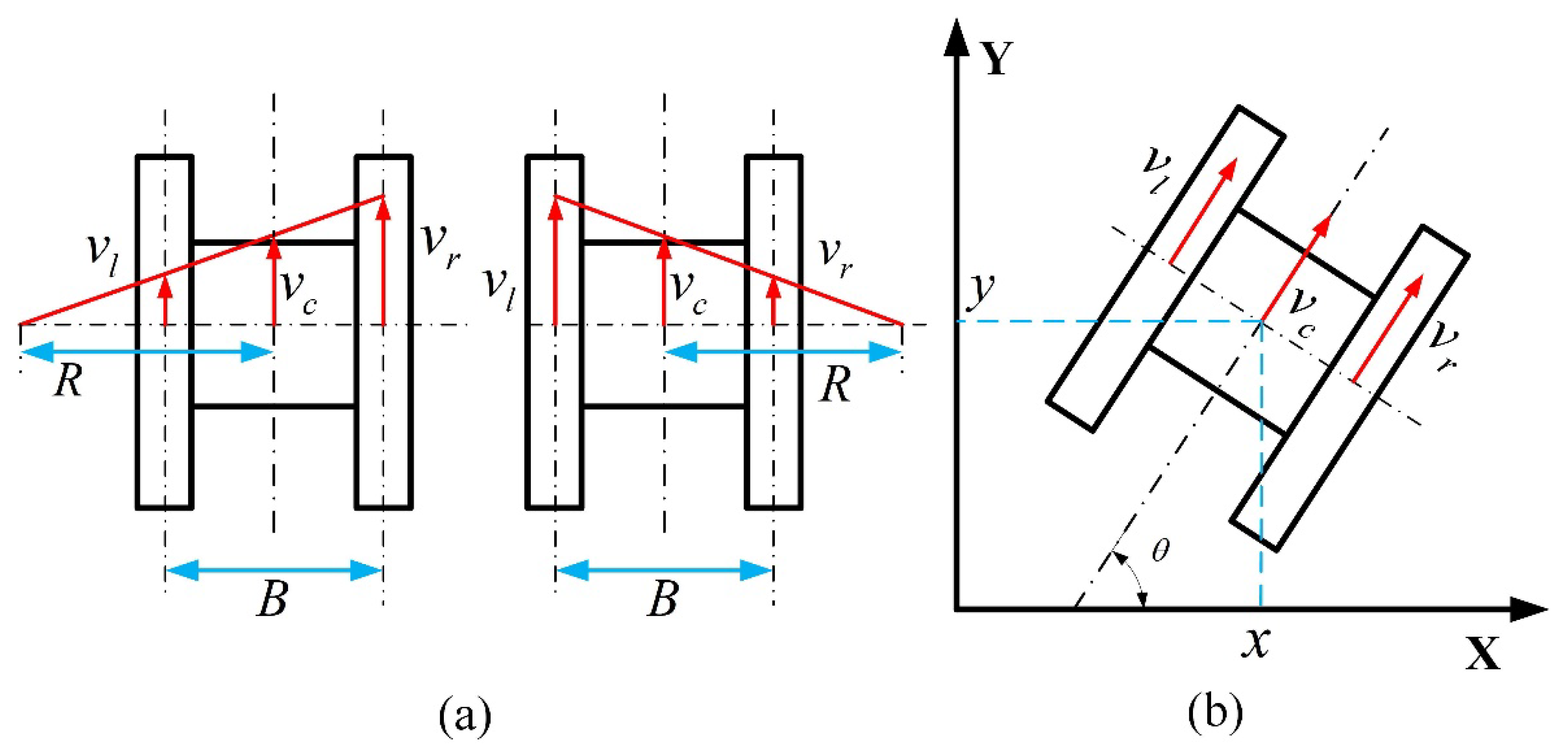
4.1. Kinematics Model of an ES
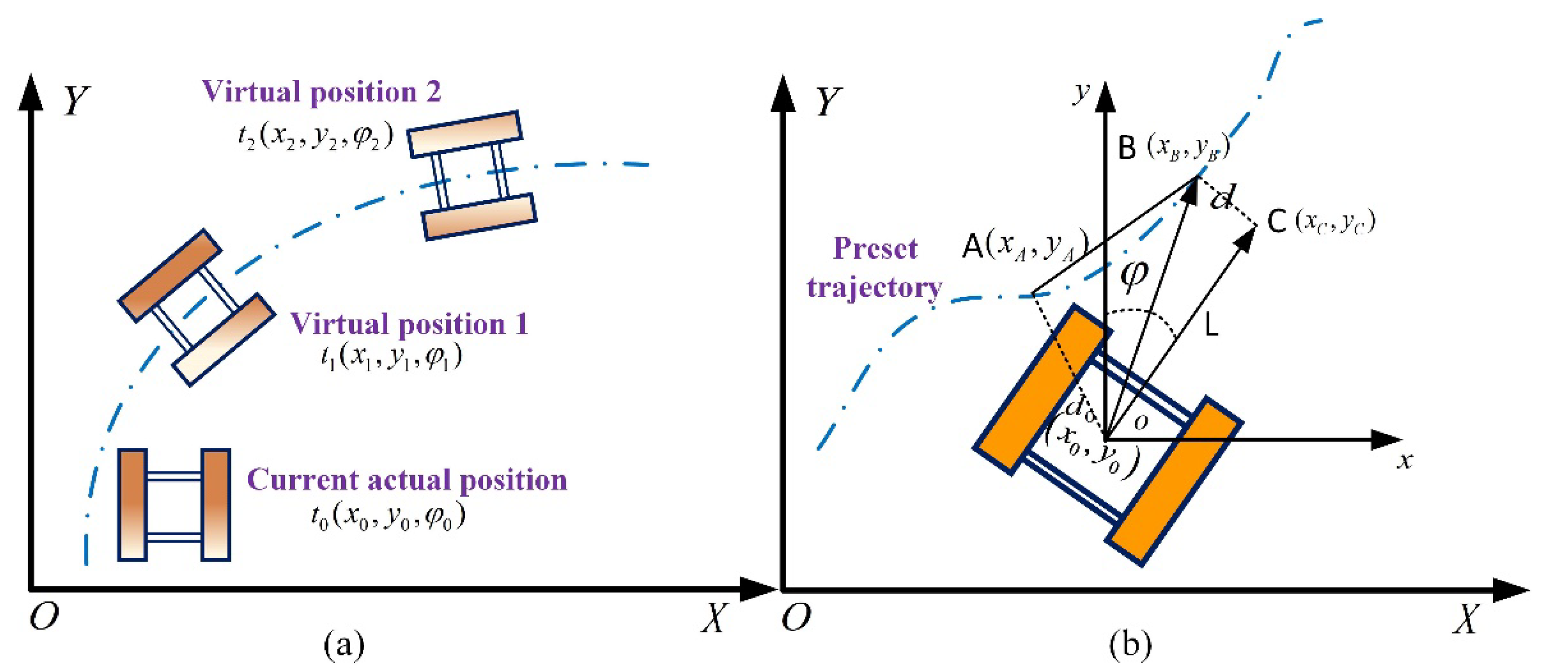
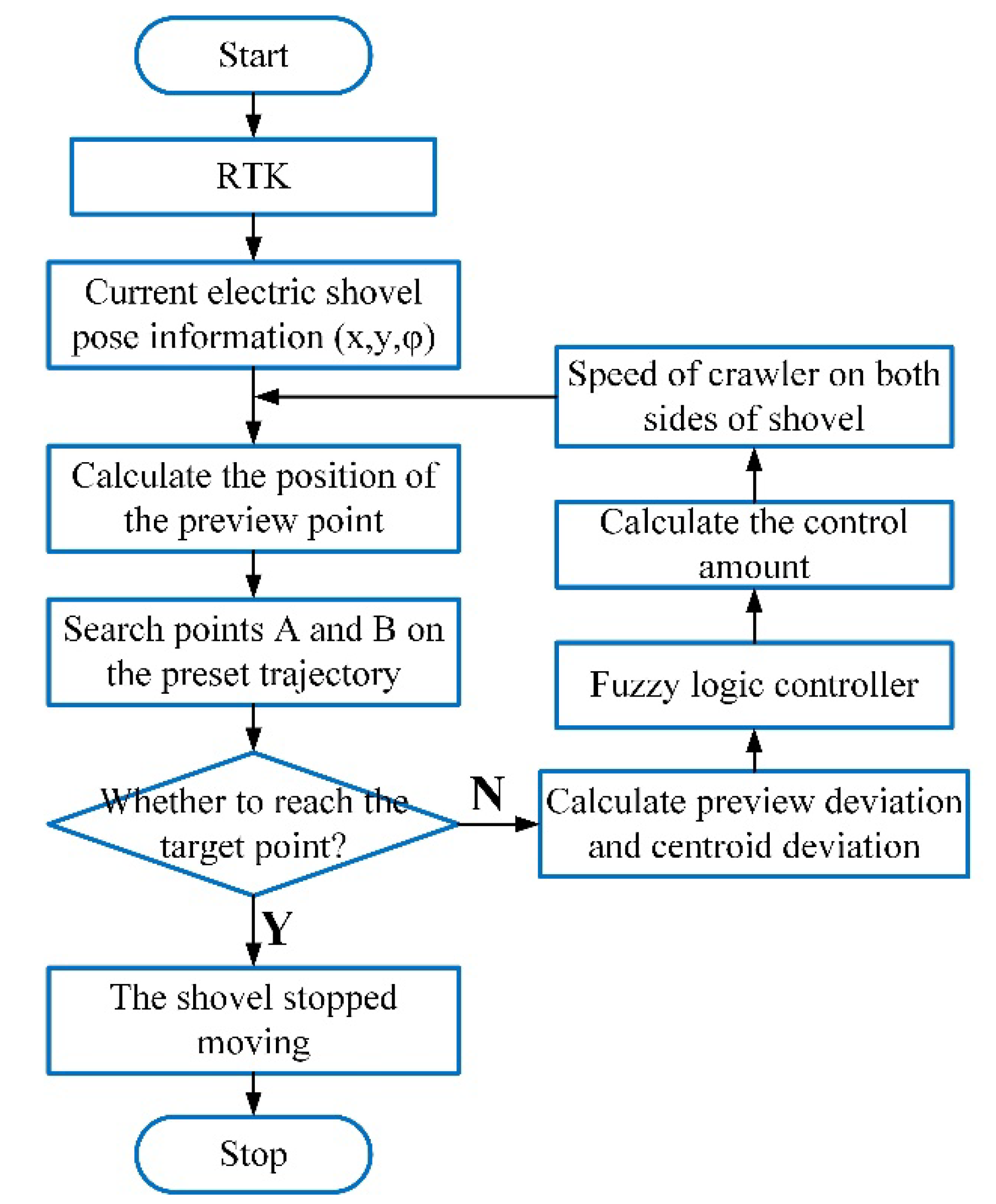
4.2. Trajectory Tracking Strategy
4.3. Fuzzy Logic Controller
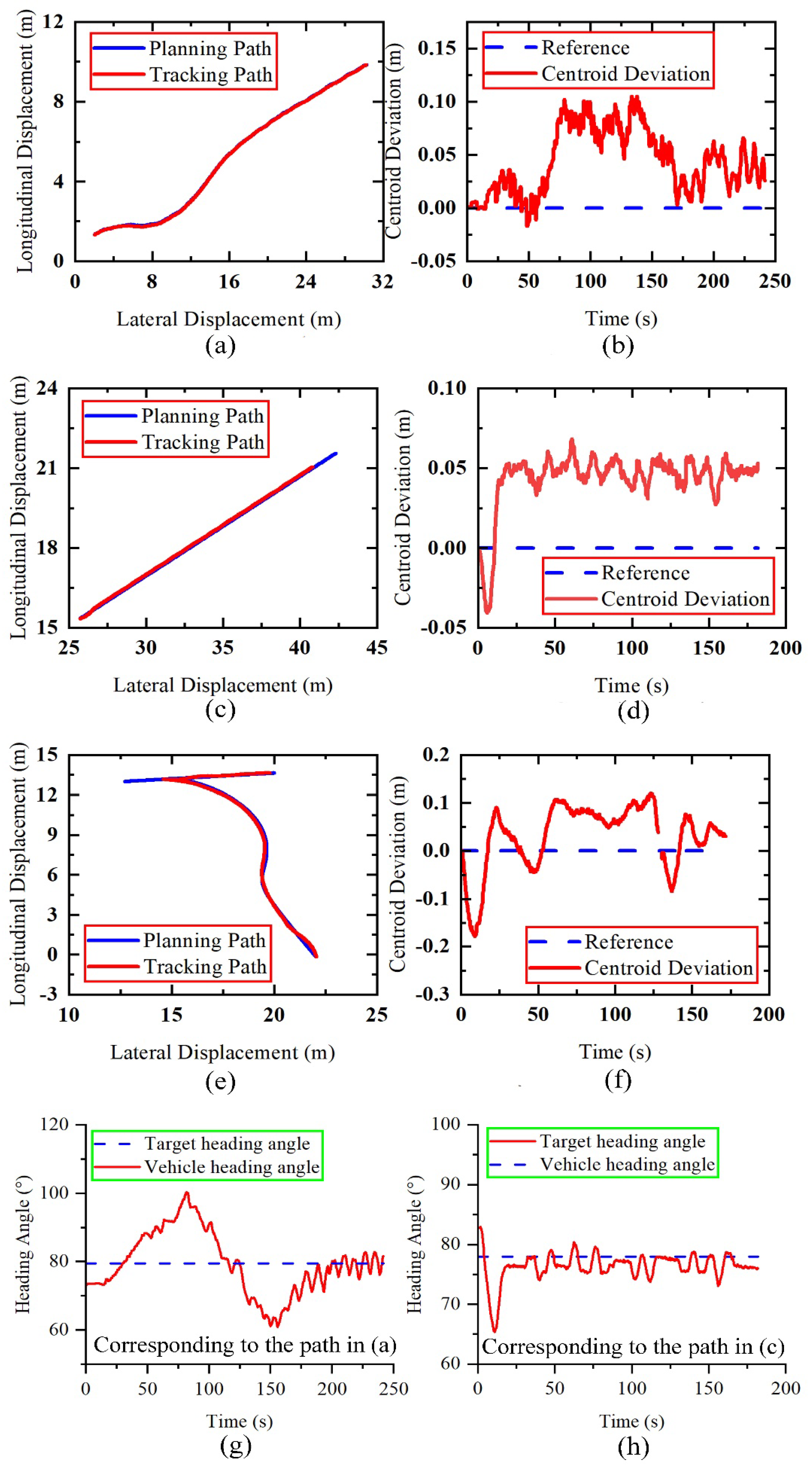
5. Experiment and Discussion
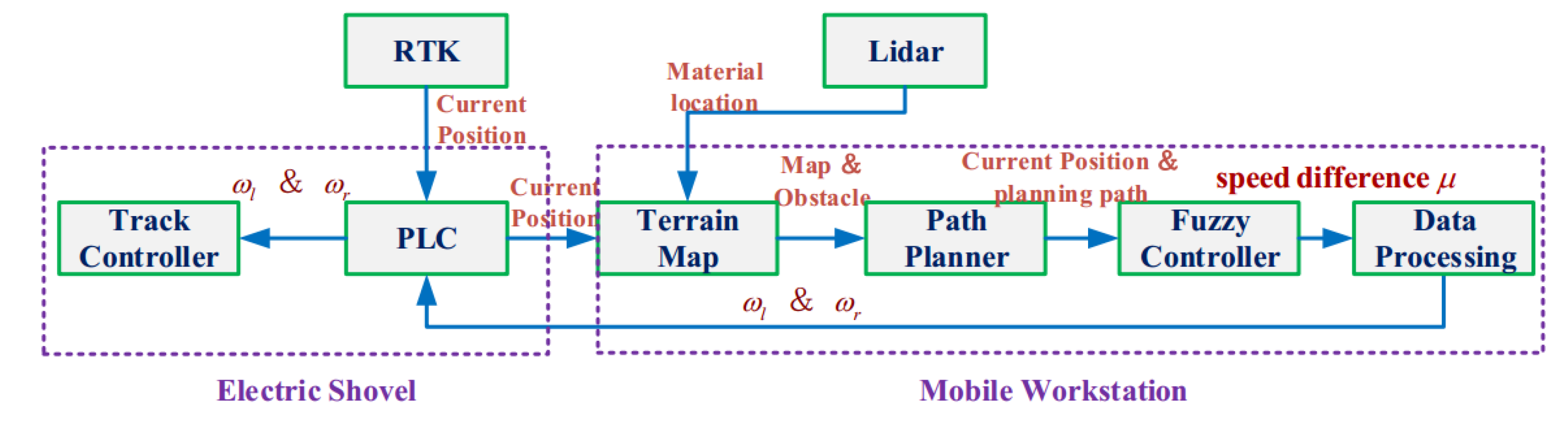
5.1. Experimental Setup
5.2. Communication
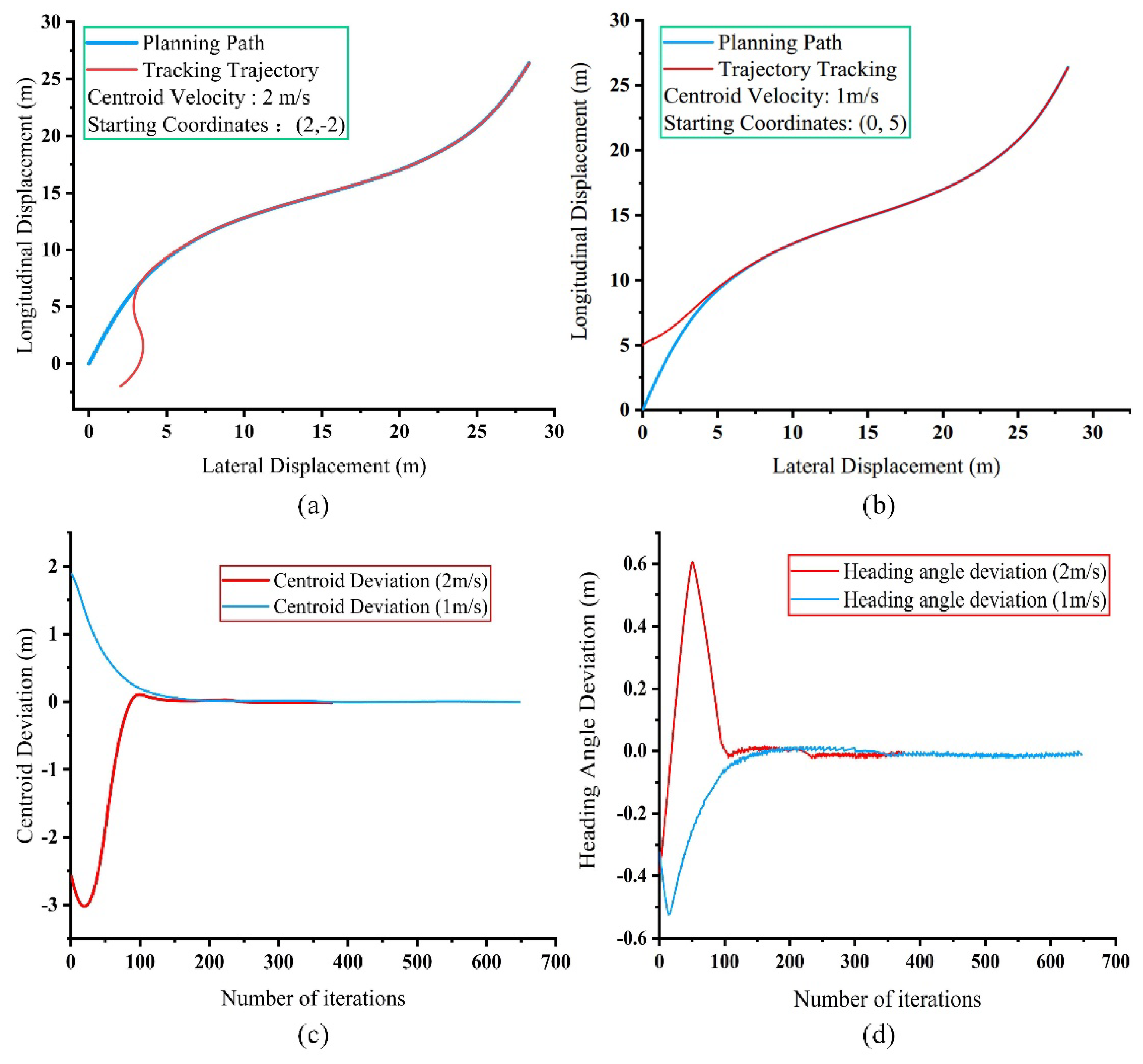
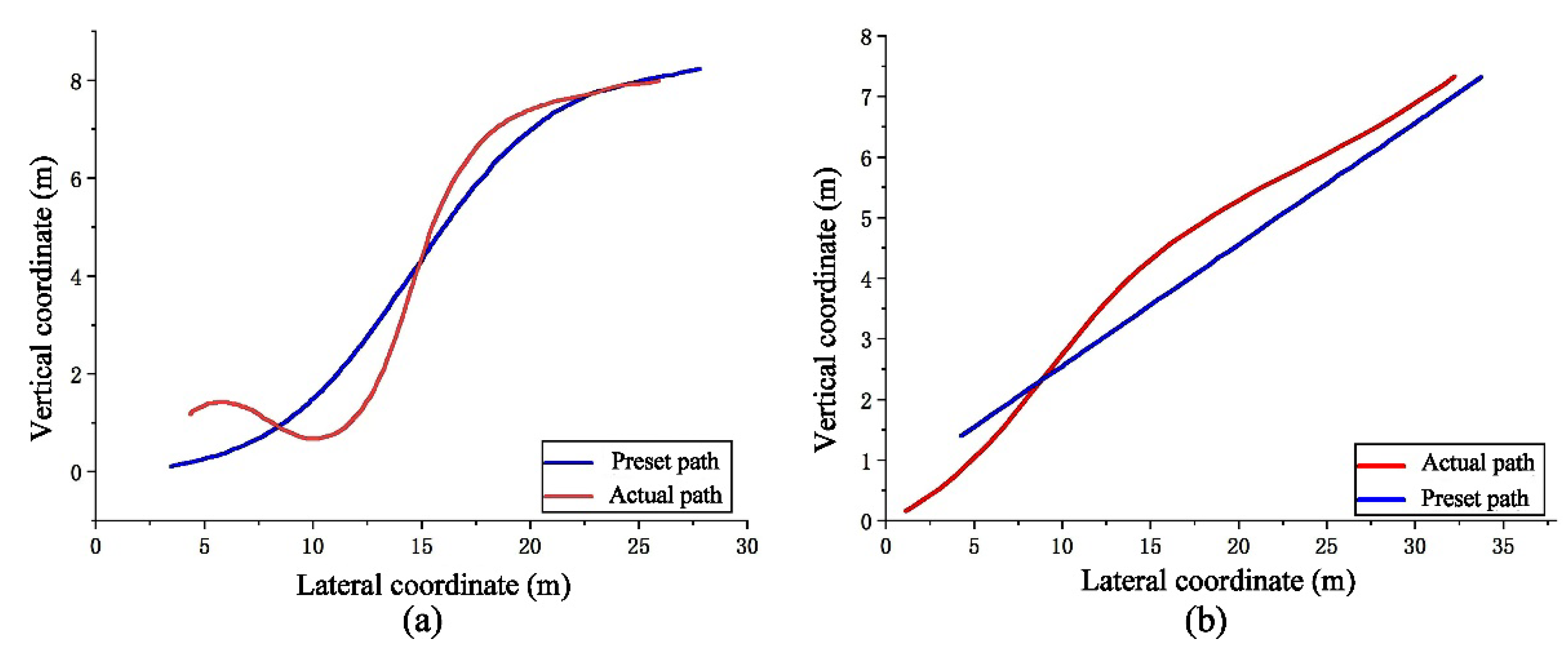
5.3. Discussion
5.4. Method Comparison
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bi, Q.; Wang, G.; Wang, Y.; Yao, Z.; Hall, R. Digging Trajectory Optimization for Cable Shovel Robotic Excavation Based on a Multi-Objective Genetic Algorithm. Energies 2020, 13, 3118. [Google Scholar] [CrossRef]
- Ghodrati, B.; Hoseinie, S.H.; Garmabaki, A.H.S. Reliability considerations in automated mining systems. Int. J. Min. Reclam. Environ. 2015, 29, 404–418. [Google Scholar] [CrossRef]
- Valenzuela Guzman, M.; Anibal Valenzuela, M. Integrated Mechanical-Electrical Modeling of an AC Electric Mining Shovel and Evaluation of Power Requirements During a Truck Loading Cycle. IEEE Trans. Ind. Appl. 2015, 51, 2590–2599. [Google Scholar] [CrossRef]
- Tubis, A.A.; Werbińska-Wojciechowska, S.; Góralczyk, M.; Wróblewski, A.; Ziętek, B. Cyber-Attacks Risk Analysis Method for Different Levels of Automation of Mining Processes in Mines Based on Fuzzy Theory Use. Sensors 2020, 20, 7210. [Google Scholar] [CrossRef]
- Li, X.; Liu, C.; Li, J.; Baghdadi, M.; Liu, Y. A Multi-Sensor Environmental Perception System for an Automatic Electric Shovel Platform. Sensors 2021, 21, 4355. [Google Scholar] [CrossRef]
- Sebastian, B.; Ben-Tzvi, P. Physics Based Path Planning for Autonomous Tracked Vehicle in Challenging Terrain. J. Intell. Robot. Syst. 2019, 95, 511–526. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D.-e.; Seo, J. Task Planning Strategy and Path Similarity Analysis for An Autonomous Excavator. Autom. Constr. 2020, 112, 103108. [Google Scholar] [CrossRef]
- Guan, T.; He, Z.; Manocha, D.; Zhang, L. TTM: Terrain Traversability Mapping for Autonomous Excavator Navigation in Unstructured Environments. arXiv 2021. [CrossRef]
- Hu, J.; Wang, M.; Zhao, C.; Pan, Q.; Du, C. Formation control and collision avoidance for multi-UAV systems based on Voronoi partition. Sci. China-Technol. Sci. 2020, 63, 65–72. [Google Scholar] [CrossRef]
- Huang, Y.; Ding, H.; Zhang, Y.; Wang, H.; Cao, D.; Xu, N.; Hu, C. A Motion Planning and Tracking Framework for Autonomous Vehicles Based on Artificial Potential Field Elaborated Resistance Network Approach. IEEE Trans. Ind. Electron. 2020, 67, 1376–1386. [Google Scholar] [CrossRef]
- Lin, P.; Choi, W.Y.; Yang, J.H.; Chung, C.C. Waypoint Tracking for Collision Avoidance Using Artificial Potential Field. In Proceedings of the 39th Chinese Control Conference (CCC), Shenyang, China, 27 July 2020. [Google Scholar]
- Lin, P.; Choi, W.Y.; Chung, C.C. Local Path Planning Using Artificial Potential Field for Waypoint Tracking with Collision Avoidance. In Proceedings of the 2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC), Rhodes, Greece, 20–23 September 2020; pp. 1–7. [Google Scholar]
- Nazarahari, M.; Khanmirza, E.; Doostie, S. Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm. Expert Syst. Appl. 2019, 115, 106–120. [Google Scholar] [CrossRef]
- Huang, Q.M.; Chen, Y.H.; Cheng, A.G. Adaptive Robust Control for Fuzzy Mechanical Systems: Constraint-Following and Redundancy in Constraints. IEEE Trans. Fuzzy Syst. 2015, 23, 1113–1126. [Google Scholar] [CrossRef]
- Wang, D.; Lin, X.; Zhang, Y. Fuzzy logic control for a parallel hybrid hydraulic excavator using genetic algorithm. Autom. Constr. 2011, 20, 581–587. [Google Scholar] [CrossRef]
- Hanh, L.D.; Ahn, K.K.; Kha, N.B.; Jo, W.K. Trajectory control of electro-hydraulic excavator using fuzzy self tuning algorithm with neural network. J. Mech. Sci. Technol. 2009, 23, 149–160. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, M.; Rogers, E. Trajectory Tracking Control for Autonomous Underwater Vehicles Based on Fuzzy Re-Planning of a Local Desired Trajectory. IEEE Trans. Veh. Technol. 2019, 68, 11657–11667. [Google Scholar] [CrossRef]
- Zhang, T.; Fu, T.; Song, X.; Qu, F. Multi-objective excavation trajectory optimization for unmanned electric shovels based on pseudospectral method. Autom. Constr. 2022, 136, 104176. [Google Scholar] [CrossRef]
- Tota, A.; Velardocchia, M.; Rota, E.; Novara, A. Steering Behavior of an Articulated Amphibious All-Terrain Tracked Vehicle. In Proceedings of the WCX SAE World Congress Experience, Detroit, MI, USA, 21–23 April 2020. [Google Scholar]
- Tota, A.; Galvagno, E.; Velardocchia, M. Analytical Study on the Cornering Behavior of an Articulated Tracked Vehicle. Machines 2021, 9, 38. [Google Scholar] [CrossRef]
- Sharma, K.; Doriya, R. Coordination of multi-robot path planning for warehouse application using smart approach for identifying destinations. Intell. Serv. Robot. 2021, 14, 313–325. [Google Scholar] [CrossRef]
- Dunbabin, M.; Corke, P. Autonomous excavation using a rope shovel. J. Field Robot. 2006, 23, 379–394. [Google Scholar] [CrossRef]
- Kathib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots; Springer: New York, NY, USA, 1986. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, J.; Zhu, Z.; Yang, D.; Wu, J. Tangent navigated robot path planning strategy using particle swarm optimized artificial potential field. Optik 2018, 158, 639–651. [Google Scholar] [CrossRef]
- Wang, S.; Ge, H.; Ma, R.; Cui, D.; Liu, X.; Zhang, S. Study on the visual tracking control technology of six-crawler machine. Proc. Inst. Mech. Eng. Part C-J. Mech. Eng. Sci. 2019, 233, 6051–6075. [Google Scholar] [CrossRef]


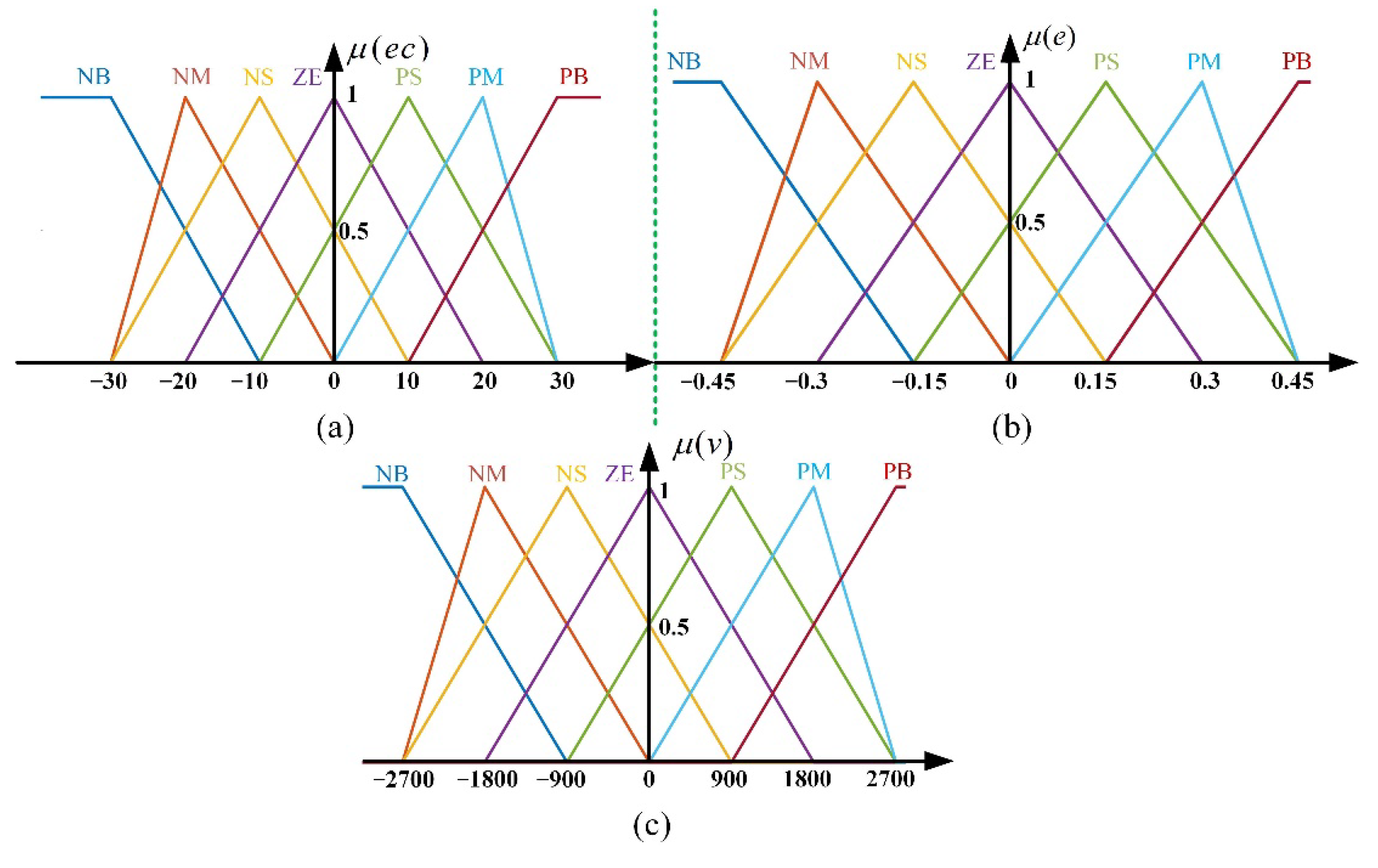


| NB | NM | NS | ZE | PS | PM | PB | ||
|---|---|---|---|---|---|---|---|---|
| NB | NB | NB | NM | NM | NS | NS | ZE | |
| NM | NB | NM | NM | NS | NS | ZE | PS | |
| NS | NM | NM | NS | NS | ZE | PS | PS | |
| ZE | NM | NS | NS | ZE | PS | PS | PM | |
| PS | NS | NS | ZE | PS | PS | PM | PM | |
| PM | NS | ZE | PS | PS | PM | PM | PB | |
| PB | ZE | PS | PS | PM | PM | PB | PB | |
| Sensor Name | Sensor Model | Sensor Accuracy | Frequency |
|---|---|---|---|
| RTK | P3-DU Beidou GNSS | Positioning accuracy: centimeter level Direction finding accuracy ≤ 0.2° | 10 Hz |
| Lidar | RoboSense: Number of lines: 80 | Horizontal angular resolution 0.2°/0.4° Vertical angular resolution Up to 0.1° Accuracy (typical value) Up to ±3 cm | 20 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Wang, S.; Bi, Q.; Wu, G.; Guan, W.; Wang, Y.; Yan, C. Research on Path Planning and Trajectory Tracking of an Unmanned Electric Shovel Based on Improved APF and Preview Deviation Fuzzy Control. Machines 2022, 10, 707. https://doi.org/10.3390/machines10080707
Fang Y, Wang S, Bi Q, Wu G, Guan W, Wang Y, Yan C. Research on Path Planning and Trajectory Tracking of an Unmanned Electric Shovel Based on Improved APF and Preview Deviation Fuzzy Control. Machines. 2022; 10(8):707. https://doi.org/10.3390/machines10080707
Chicago/Turabian StyleFang, Yi, Shuai Wang, Qiushi Bi, Guohua Wu, Wei Guan, Yongpeng Wang, and Chuliang Yan. 2022. "Research on Path Planning and Trajectory Tracking of an Unmanned Electric Shovel Based on Improved APF and Preview Deviation Fuzzy Control" Machines 10, no. 8: 707. https://doi.org/10.3390/machines10080707
APA StyleFang, Y., Wang, S., Bi, Q., Wu, G., Guan, W., Wang, Y., & Yan, C. (2022). Research on Path Planning and Trajectory Tracking of an Unmanned Electric Shovel Based on Improved APF and Preview Deviation Fuzzy Control. Machines, 10(8), 707. https://doi.org/10.3390/machines10080707





