CLOVER Robot: A Minimally Actuated Jumping Robotic Platform
Abstract
:1. Introduction
1.1. Design Goals
- Design for minimal actuation of main-drive jump linkage (thrust force vectoring is not considered at this stage)
- Focus on linkage mechanism potential-kinetic energy conversion efficiency
- Design for reduced linkage mechanism maintenance
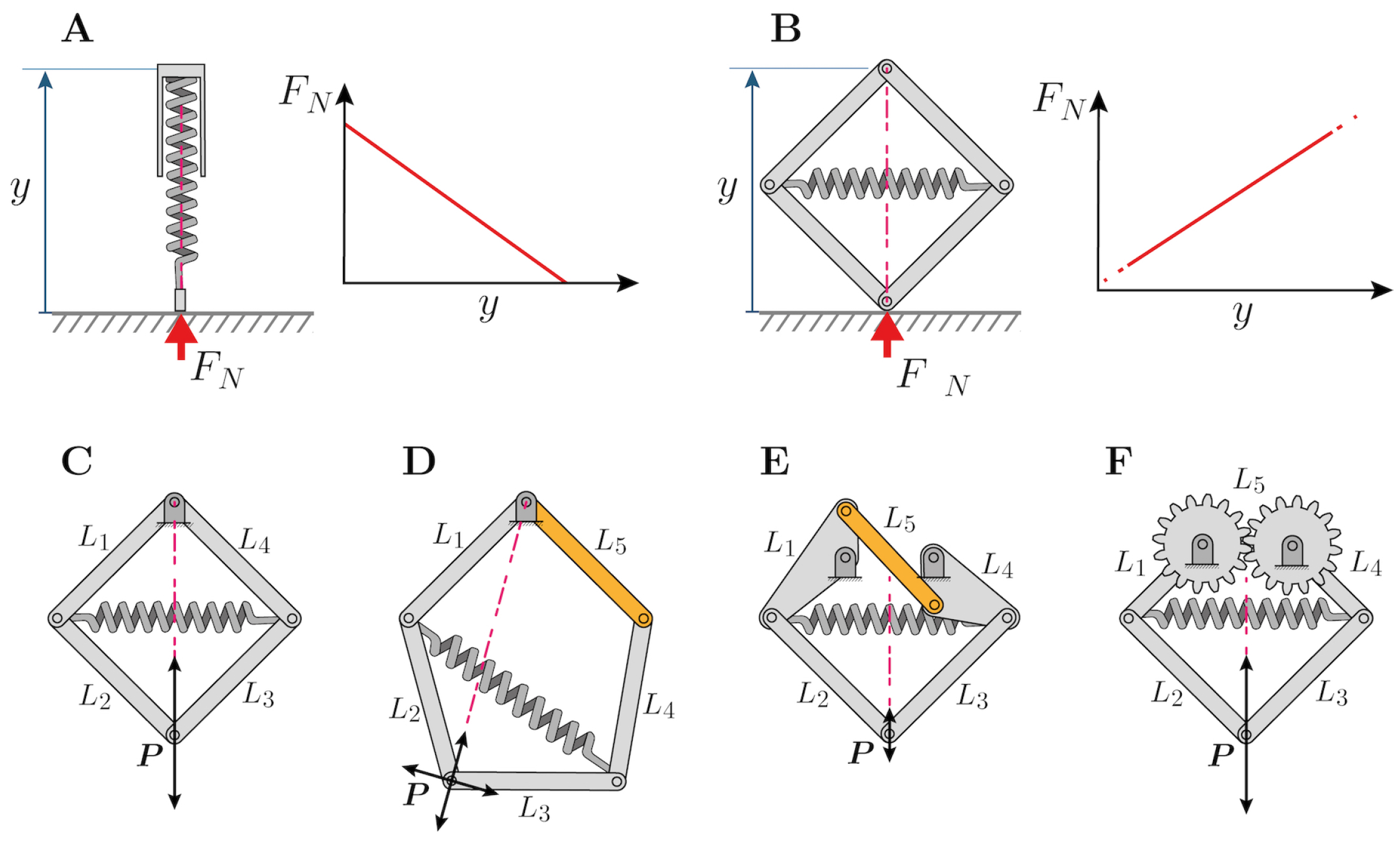
2. Mechanism Design
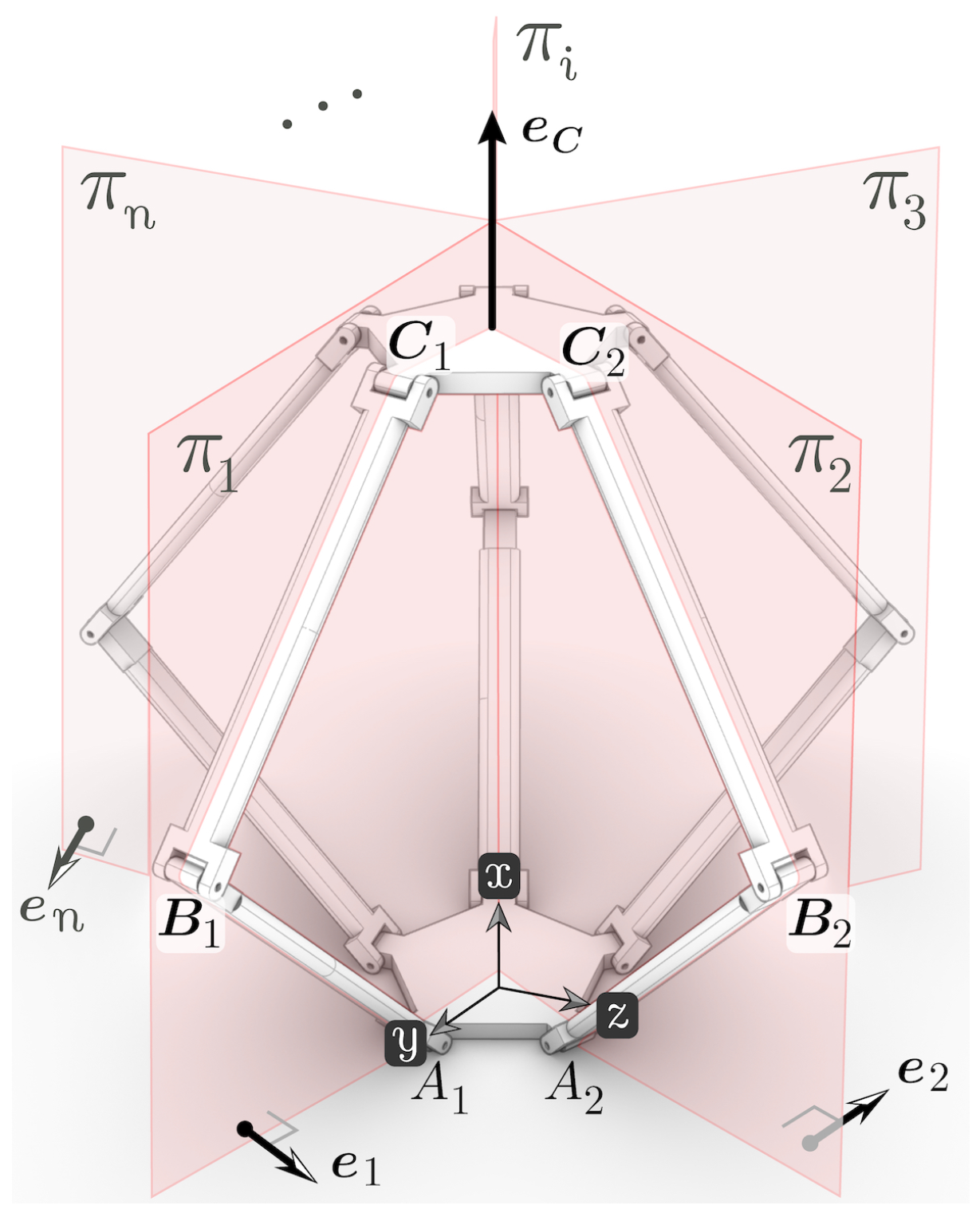
2.1. Kinematic Chains and Mobility Analysis
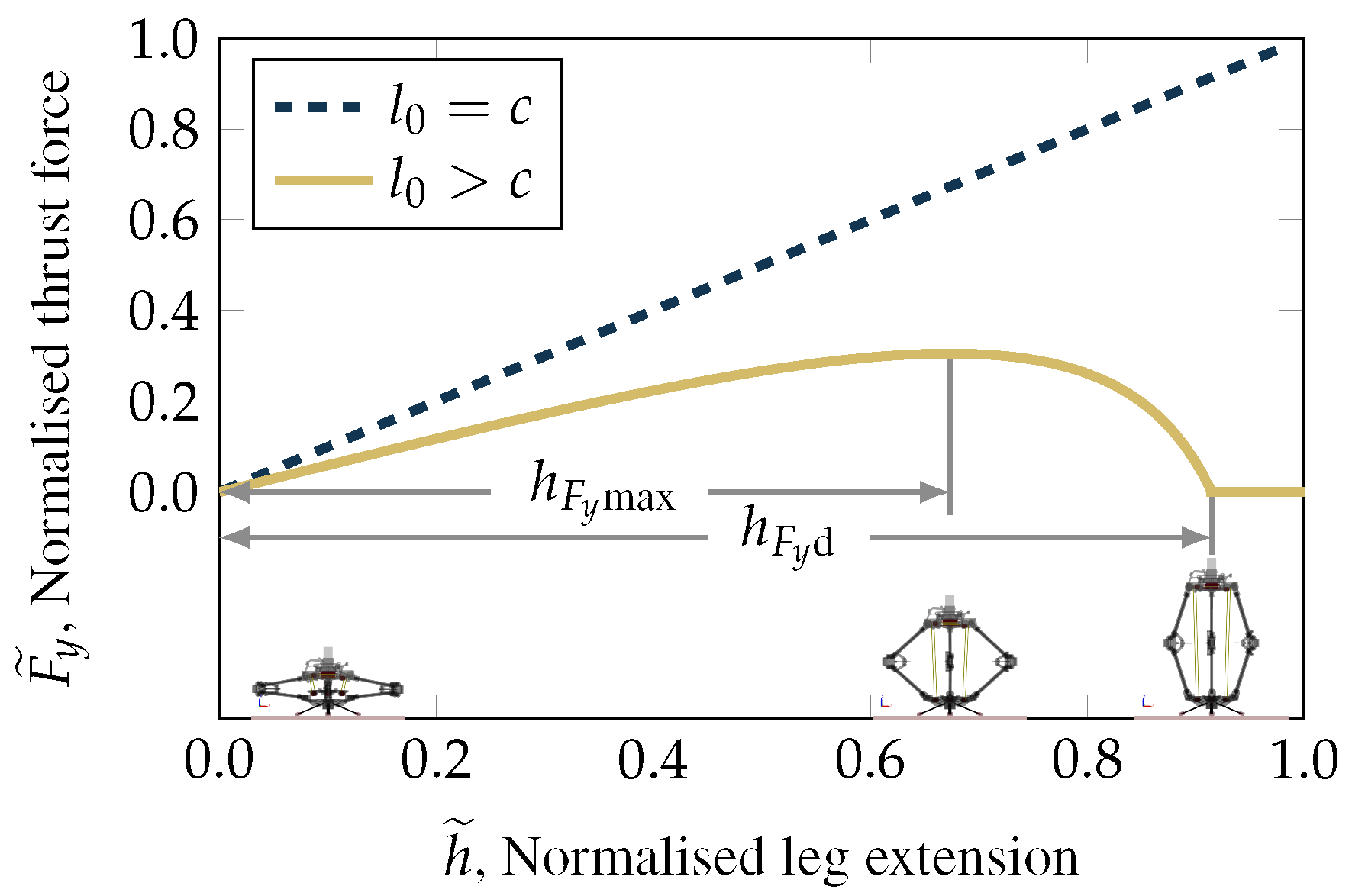
2.2. Thrust Force
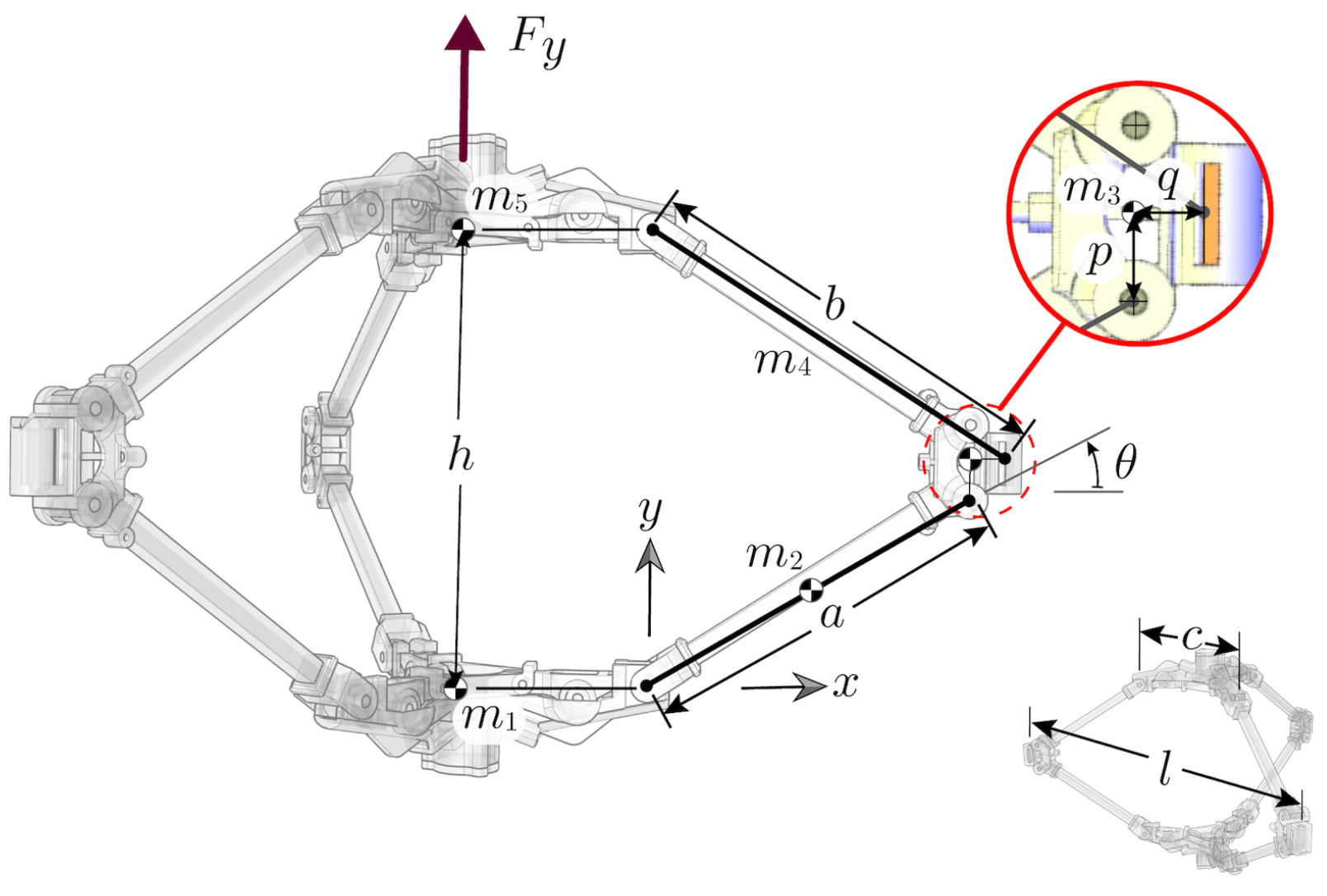
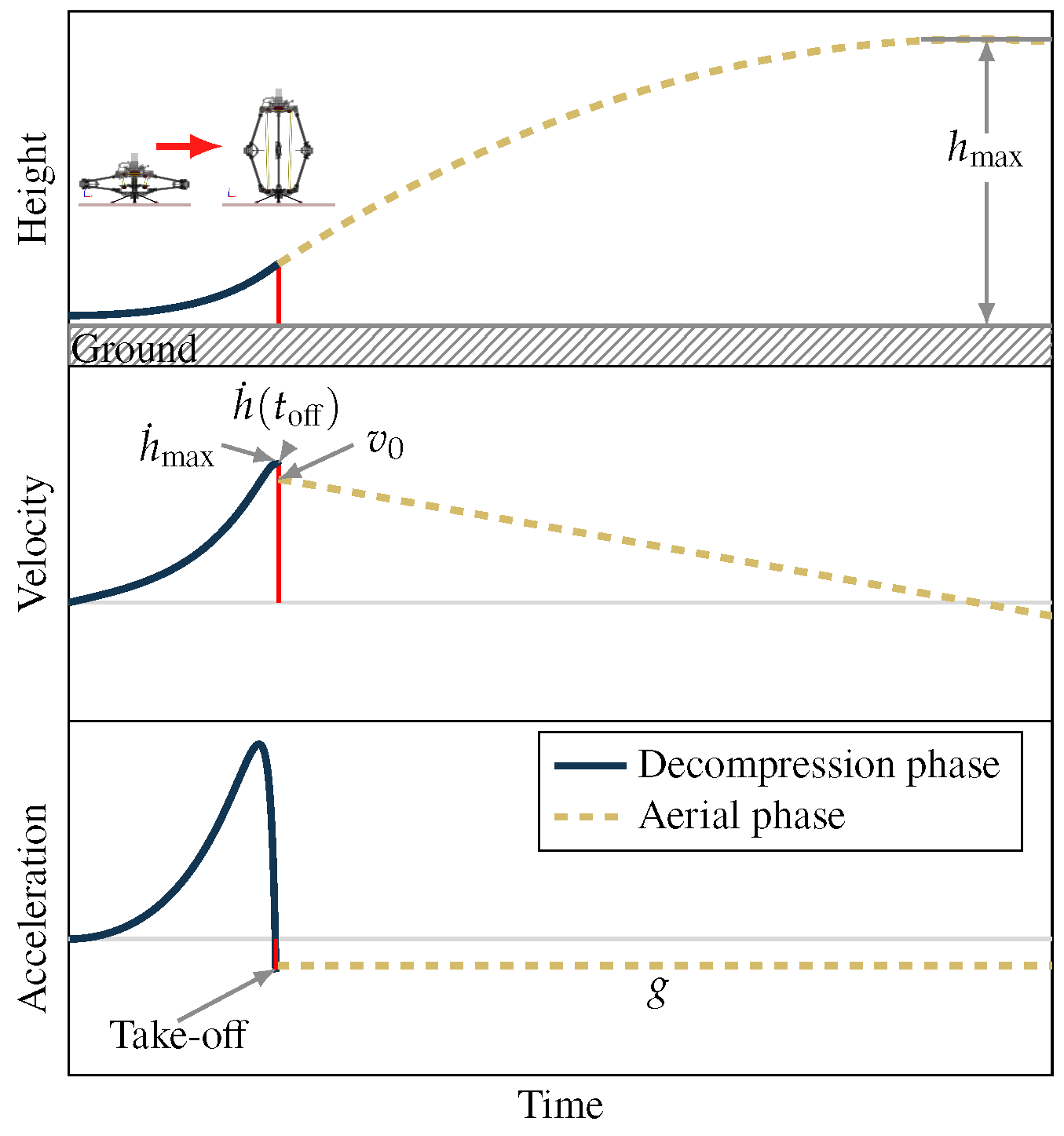
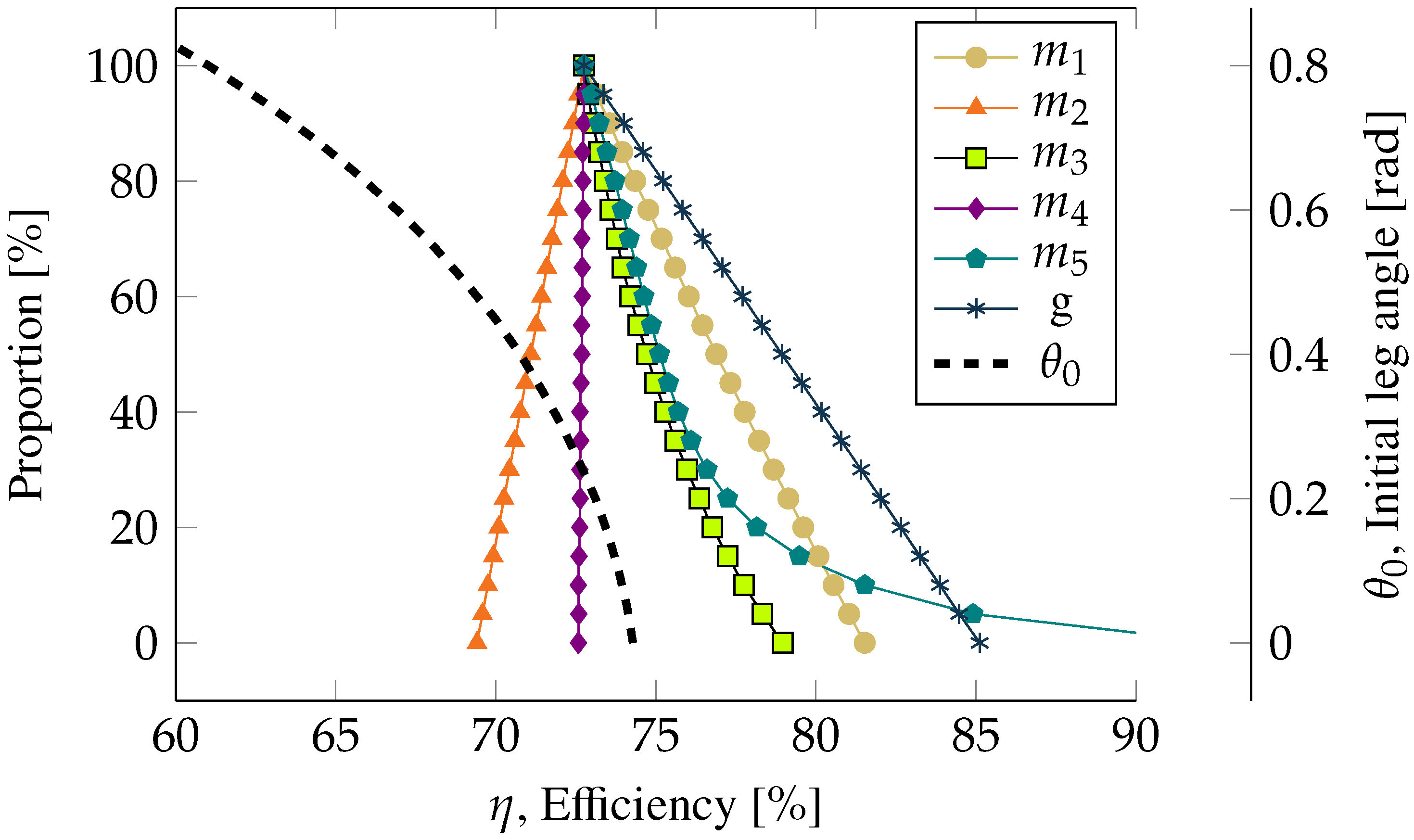
2.3. Dynamic Modelling
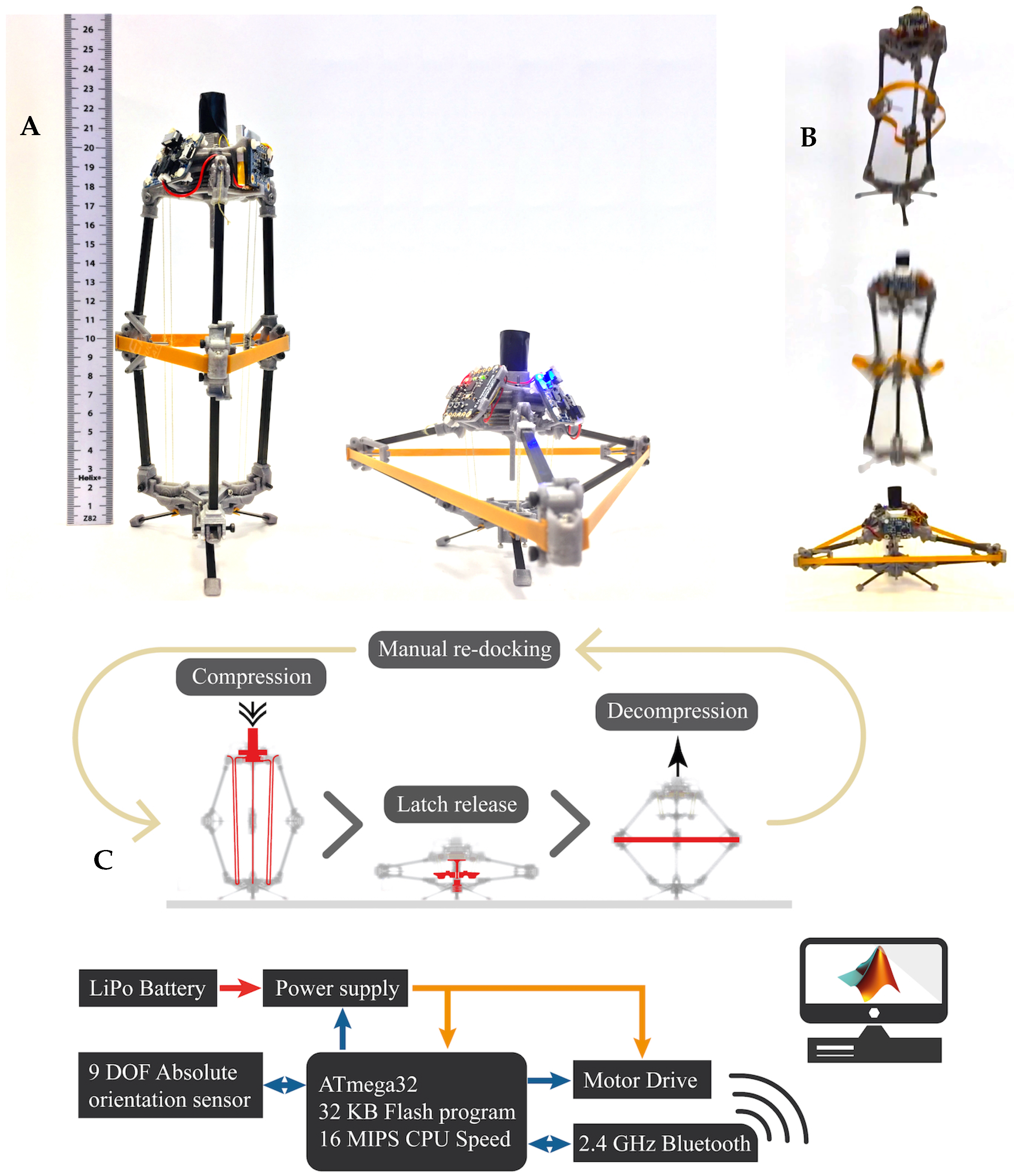
3. Laboratory Demonstrator Design
3.1. Compression Mechanism Design Approach
3.2. Docking Mechanism Design Approach
4. Assessment of Laboratory Demonstrator
Laboratory Demonstrator Experimental Jumping Performance
5. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
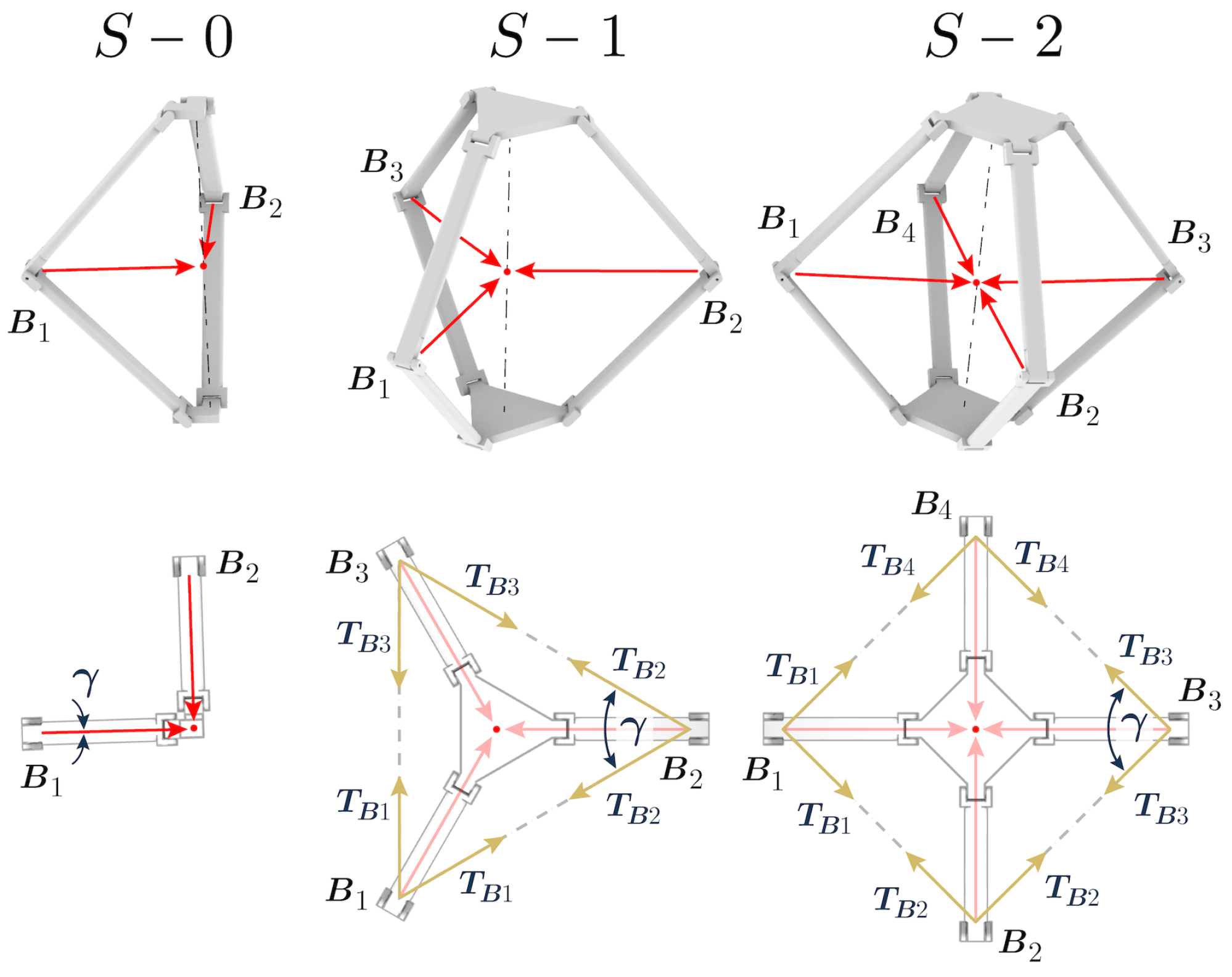
Appendix A. The n-Sided Sarrus Linkage

References
- Chignoli, M.; Kim, D.; Stanger-Jones, E.; Kim, S. The MIT Humanoid Robot: Design, Motion Planning, and Control For Acrobatic Behaviors. arXiv 2021, arXiv:2104.09025. [Google Scholar]
- Liljeback, P.; Pettersen, K.Y.; Stavdahl, Ø.; Gravdahl, J.T. Controllability and stability analysis of planar snake robot locomotion. IEEE Trans. Autom. Control 2010, 56, 1365–1380. [Google Scholar] [CrossRef] [Green Version]
- Wakabayashi, S.; Sato, H.; Nishida, S.I. Design and mobility evaluation of tracked lunar vehicle. J. Terramech. 2009, 46, 105–114. [Google Scholar] [CrossRef]
- Maimone, M.; Biesiadecki, J.; Tunstel, E.; Cheng, Y.; Leger, C. Surface navigation and mobility intelligence on the Mars Exploration Rovers. Intell. Space Robot. 2006, 1, 45–69. [Google Scholar]
- Seeni, A.; Schäfer, B.; Hirzinger, G. Robot mobility systems for planetary surface exploration–state-of-the-art and future outlook: A literature survey. Aerosp. Technol. Adv. 2010, 492, 189–208. [Google Scholar]
- Harvey, B. Russian Planetary Exploration: History, Development, Legacy and Prospects; Springer Science & Business Media: Berlin, Germany, 2007. [Google Scholar]
- Ulamec, S.; Kucherenko, V.; Biele, J.; Bogatchev, A.; Makurin, A.; Matrossov, S. Hopper concepts for small body landers. Adv. Space Res. 2011, 47, 428–439. [Google Scholar] [CrossRef]
- Kim, K.; Spieler, P.; Lupu, E.S.; Ramezani, A.; Chung, S.J. A bipedal walking robot that can fly, slackline, and skateboard. Sci. Robot. 2021, 6, eabf8136. [Google Scholar] [CrossRef] [PubMed]
- Haldane, D.W.; Plecnik, M.M.; Yim, J.K.; Fearing, R.S. Robotic vertical jumping agility via series-elastic power modulation. Sci. Robot. 2016, 1, eaag2048. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Niiyama, R.; Nagakubo, A.; Kuniyoshi, Y. A bipedal jumping and landing robot with an artificial musculoskeletal system. In Proceedings of the IEEE International Conference on Robotics and Automation, Rome, Italy, 10–14 April 2007; Volume 2007. [Google Scholar]
- Plecnik, M.M.; Haldane, D.W.; Yim, J.K.; Fearing, R.S. Design exploration and kinematic tuning of a power modulating jumping monopod. J. Mech. Robot. 2017, 9, 011009. [Google Scholar] [CrossRef]
- Zhang, C.; Zou, W.; Ma, L.; Wang, Z. Biologically inspired jumping robots: A comprehensive review. Robot. Auton. Syst. 2020, 124, 103362. [Google Scholar] [CrossRef]
- Ellery, A. Planetary Rovers: Robotic Exploration of the Solar System; Springer: Berlin, Germany, 2016. [Google Scholar]
- Watanabe, S.I.; Tsuda, Y.; Yoshikawa, M.; Tanaka, S.; Saiki, T.; Nakazawa, S. Hayabusa2 mission overview. Space Sci. Rev. 2017, 208, 3–16. [Google Scholar] [CrossRef]
- Ho, T.M.; Baturkin, V.; Grimm, C.; Grundmann, J.T.; Hobbie, C.; Ksenik, E.; Lange, C.; Sasaki, K.; Schlotterer, M.; Talapina, M.; et al. MASCOT—The mobile asteroid surface scout onboard the HAYABUSA2 mission. Space Sci. Rev. 2017, 208, 339–374. [Google Scholar] [CrossRef]
- Parslew, B.; Sivalingam, G.; Crowther, W. A dynamics and stability framework for avian jumping take-off. R. Soc. Open Sci. 2018, 5, 181544. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, Y.; Smith, K.; Macario-Rojas, A.; Zhang, H. Simulation of the Landing Buffer of a Three-Legged Jumping Robot. Machines 2022, 10, 299. [Google Scholar] [CrossRef]
- University of Manchester, RAIN Hub. Robotics and Artificial Intelligence for Nuclear. 2022. Available online: https://rainhub.org.uk (accessed on 26 July 2022).
- Smith, M.; Craig, D.; Herrmann, N.; Mahoney, E.; Krezel, J.; McIntyre, N.; Goodliff, K. The Artemis program: An overview of NASA’s activities to return humans to the moon. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–10. [Google Scholar]
- ESA. Preparing for the Future: ESA Plans Mission to Explore Lunar Caves. 2022. Available online: https://www.esa.int/Enabling_Support/Preparing_for_the_Future/Discovery_and_Preparation/ESA_plans_mission_to_explore_lunar_caves (accessed on 26 July 2022).
- Bayliss, C.; Langley, K. Nuclear Decommissioning, Waste Management, and Environmental Site Remediation; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Ellery, A. Environment robot interaction the basis for mobility in planetary micro-rovers. Robot. Auton. Syst. 2005, 51, 29–39. [Google Scholar] [CrossRef]
- Batts, Z.; Kim, J.; Yamane, K. Untethered one-legged hopping in 3D using linear elastic actuator in parallel (LEAP). In International Symposium on Experimental Robotics; Springer: Cham, Denmark, 2016; pp. 103–112. [Google Scholar]
- Carpi, F.; De Rossi, D.; Kornbluh, R.; Pelrine, R.E.; Sommer-Larsen, P. Dielectric Elastomers as Electromechanical Transducers: Fundamentals, Materials, Devices, Models and Applications of an Emerging Electroactive Polymer Technology; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Zhao, J.; Xu, J.; Gao, B.; Xi, N.; Cintron, F.J.; Mutka, M.W.; Xiao, L. MSU jumper: A single-motor-actuated miniature steerable jumping robot. IEEE Trans. Robot. 2013, 29, 602–614. [Google Scholar] [CrossRef]
- Hale, E.; Schara, N.; Burdick, J.; Fiorini, P. A minimally actuated hopping rover for exploration of celestial bodies. In Proceedings of the 2000 ICRA, Millennium Conference, IEEE International Conference on Robotics and Automation. Symposia Proceedings (Cat. No. 00CH37065), San Francisco, CA, USA, 24–28 April 2000; Volume 1, pp. 420–427. [Google Scholar]
- Truong, N.T.; Phan, H.V.; Park, H.C. Design and demonstration of a bio-inspired flapping-wing-assisted jumping robot. Bioinspir. Biomim. 2019, 14, 036010. [Google Scholar] [CrossRef]
- Jung, G.P.; Casarez, C.S.; Jung, S.P.; Fearing, R.S.; Cho, K.J. An integrated jumping-crawling robot using height-adjustable jumping module. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4680–4685. [Google Scholar]
- Bai, L.; Zheng, F.; Chen, X.; Sun, Y.; Hou, J. Design and experimental evaluation of a single-actuator continuous hopping robot using the geared symmetric multi-bar mechanism. Appl. Sci. 2019, 9, 13. [Google Scholar] [CrossRef] [Green Version]
- Budynas, R.G.; Nisbett, J.K.; Tangchaichit, K. Shigley’s Mechanical Engineering Design; McGraw Hill New York: New York, NY, USA, 2005. [Google Scholar]
- Huang, Z.; Li, Q.; Ding, H. Mobility analysis part-1. In Theory of Parallel Mechanisms; Springer: Berlin, Germany, 2013; pp. 47–70. [Google Scholar]
- Armour, R.; Paskins, K.; Bowyer, A.; Vincent, J.; Megill, W. Jumping robots: A biomimetic solution to locomotion across rough terrain. Bioinspir. Biomim. 2007, 2, S65–S82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Armour, R.H. A Biologically Inspired Jumping and Rolling Robot. Ph.D. Thesis, University of Bath, Bath, UK, 2010. [Google Scholar]
- Patterson, R.M.; Stegink Jansen, C.W.; Hogan, H.A.; Nassif, M.D. Material properties of Thera-Band tubing. Phys. Ther. 2001, 81, 1437–1445. [Google Scholar] [CrossRef]
- Pellicer, J.; Manzanares, J.A.; Zúñiga, J.; Utrillas, P.; Fernández, J. Thermodynamics of rubber elasticity. J. Chem. Educ. 2001, 78, 263. [Google Scholar] [CrossRef]
- Zhao, J.; Feng, Z.; Chu, F.; Ma, N. Advanced Theory of Constraint and Motion Analysis for Robot Mechanisms; Academic Press: Oxford, UK, 2013. [Google Scholar]



| Coefficient | Value |
|---|---|
| Value | Units | |
|---|---|---|
| a | ||
| c | ||
| g | ||
| * | ||
| * | ||
| p | ||
| q |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Macario-Rojas, A.; Parslew, B.; Weightman, A.; Smith, K.L. CLOVER Robot: A Minimally Actuated Jumping Robotic Platform. Machines 2022, 10, 640. https://doi.org/10.3390/machines10080640
Macario-Rojas A, Parslew B, Weightman A, Smith KL. CLOVER Robot: A Minimally Actuated Jumping Robotic Platform. Machines. 2022; 10(8):640. https://doi.org/10.3390/machines10080640
Chicago/Turabian StyleMacario-Rojas, Alejandro, Ben Parslew, Andrew Weightman, and Katharine Lucy Smith. 2022. "CLOVER Robot: A Minimally Actuated Jumping Robotic Platform" Machines 10, no. 8: 640. https://doi.org/10.3390/machines10080640
APA StyleMacario-Rojas, A., Parslew, B., Weightman, A., & Smith, K. L. (2022). CLOVER Robot: A Minimally Actuated Jumping Robotic Platform. Machines, 10(8), 640. https://doi.org/10.3390/machines10080640







