A New Method of Bearing Remaining Useful Life Based on Life Evolution and SE-ConvLSTM Neural Network
Abstract
:1. Introduction
2. Basic Theory
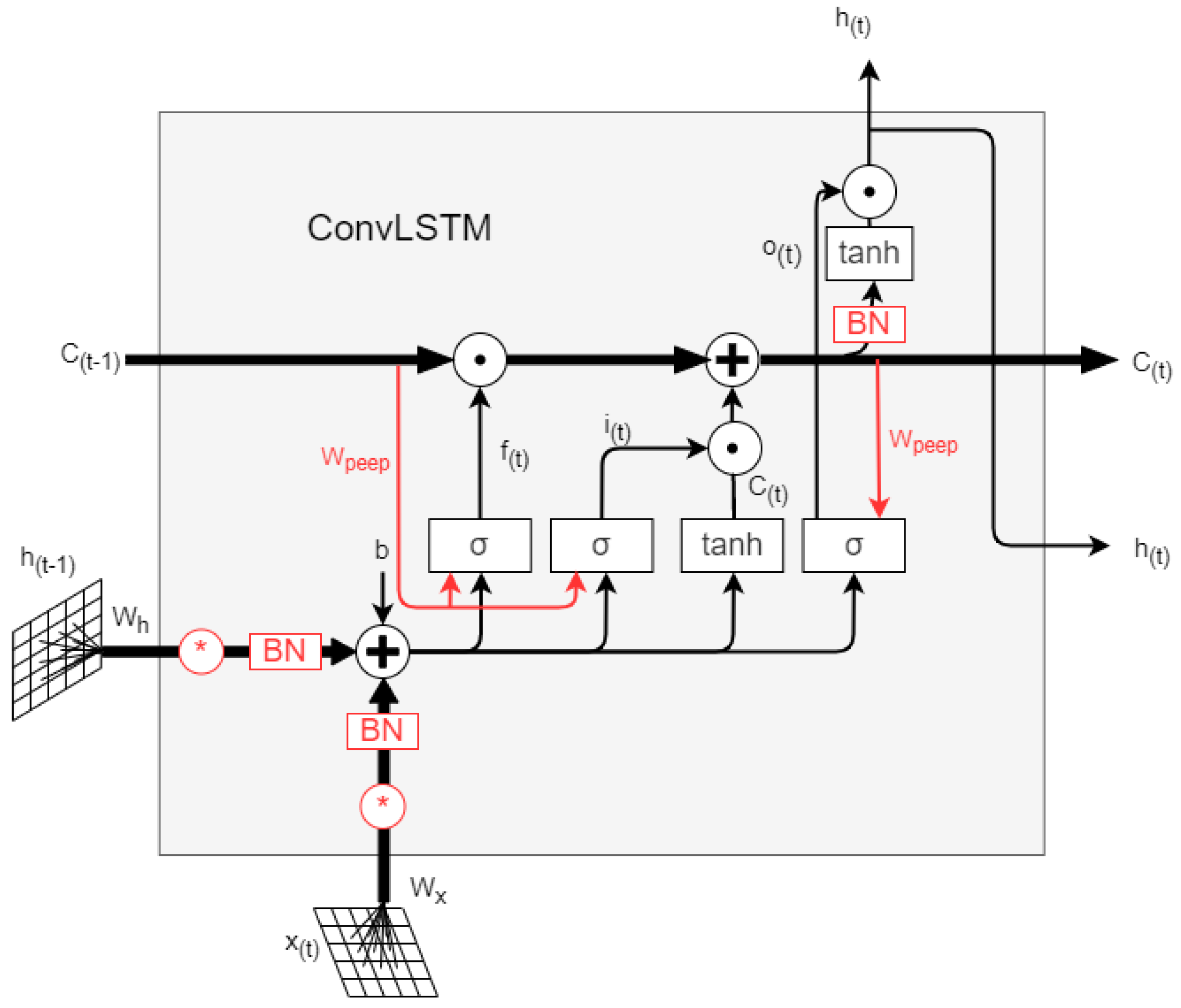
2.1. SE-ConvLSTM Neural Network
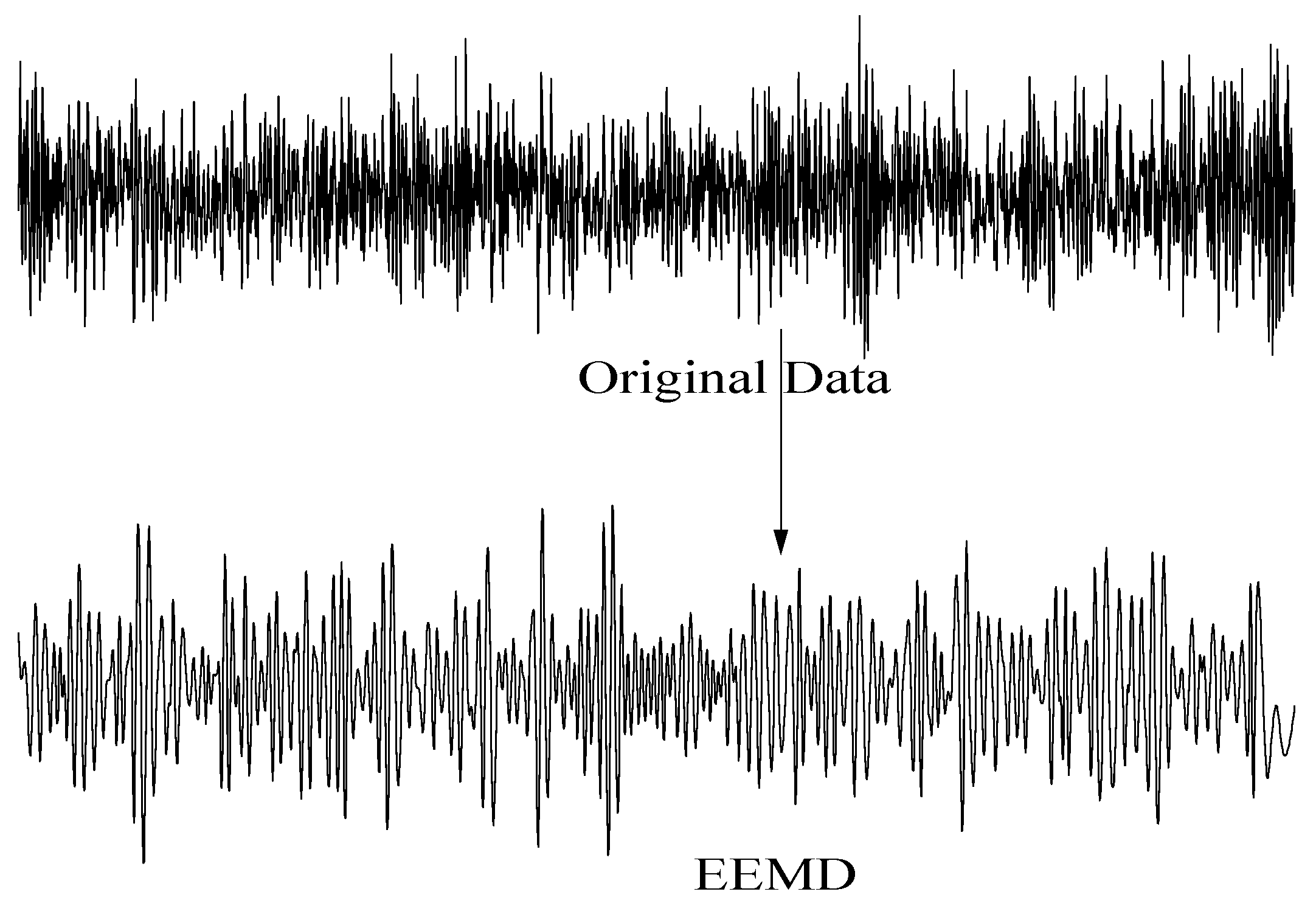
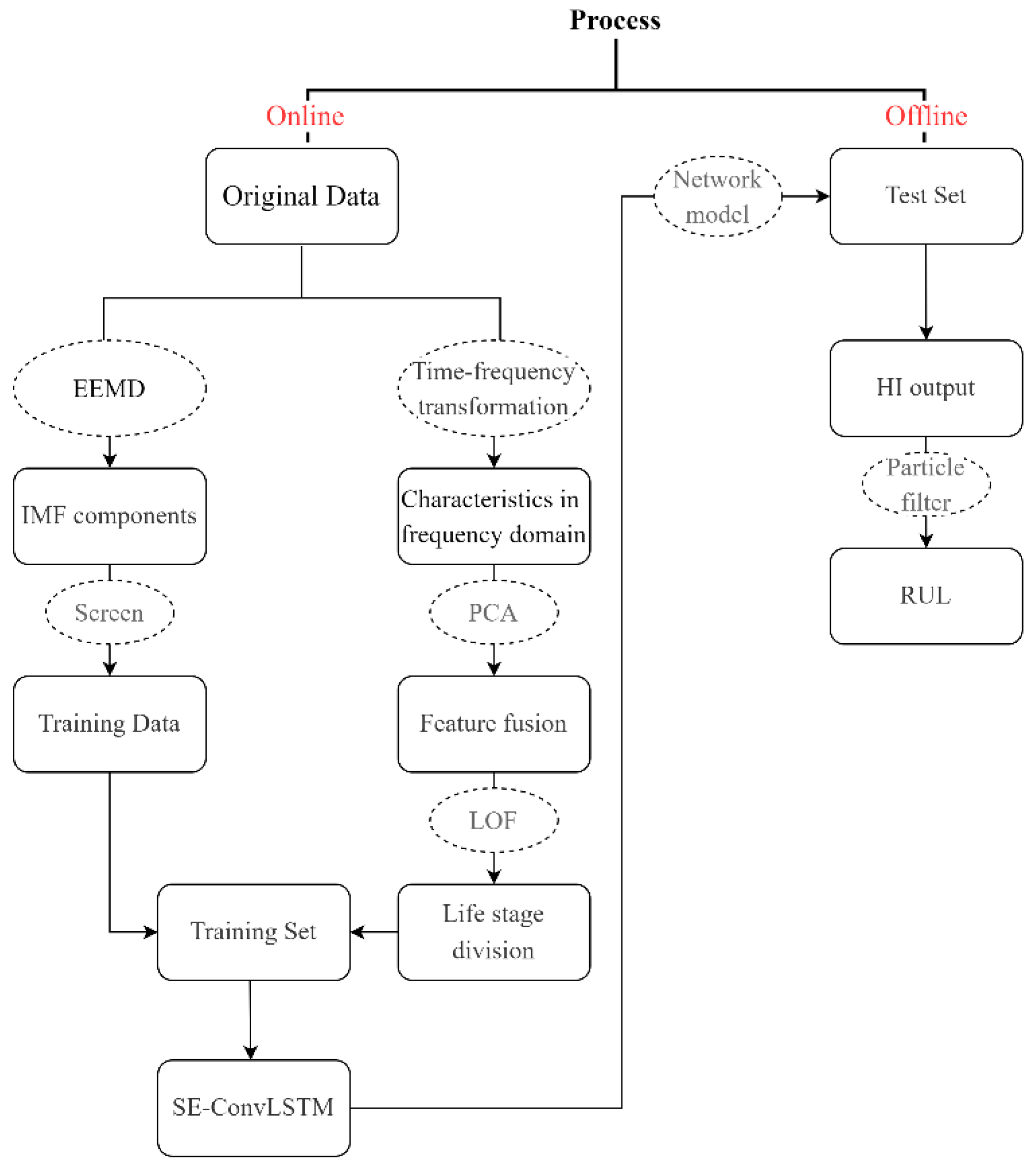
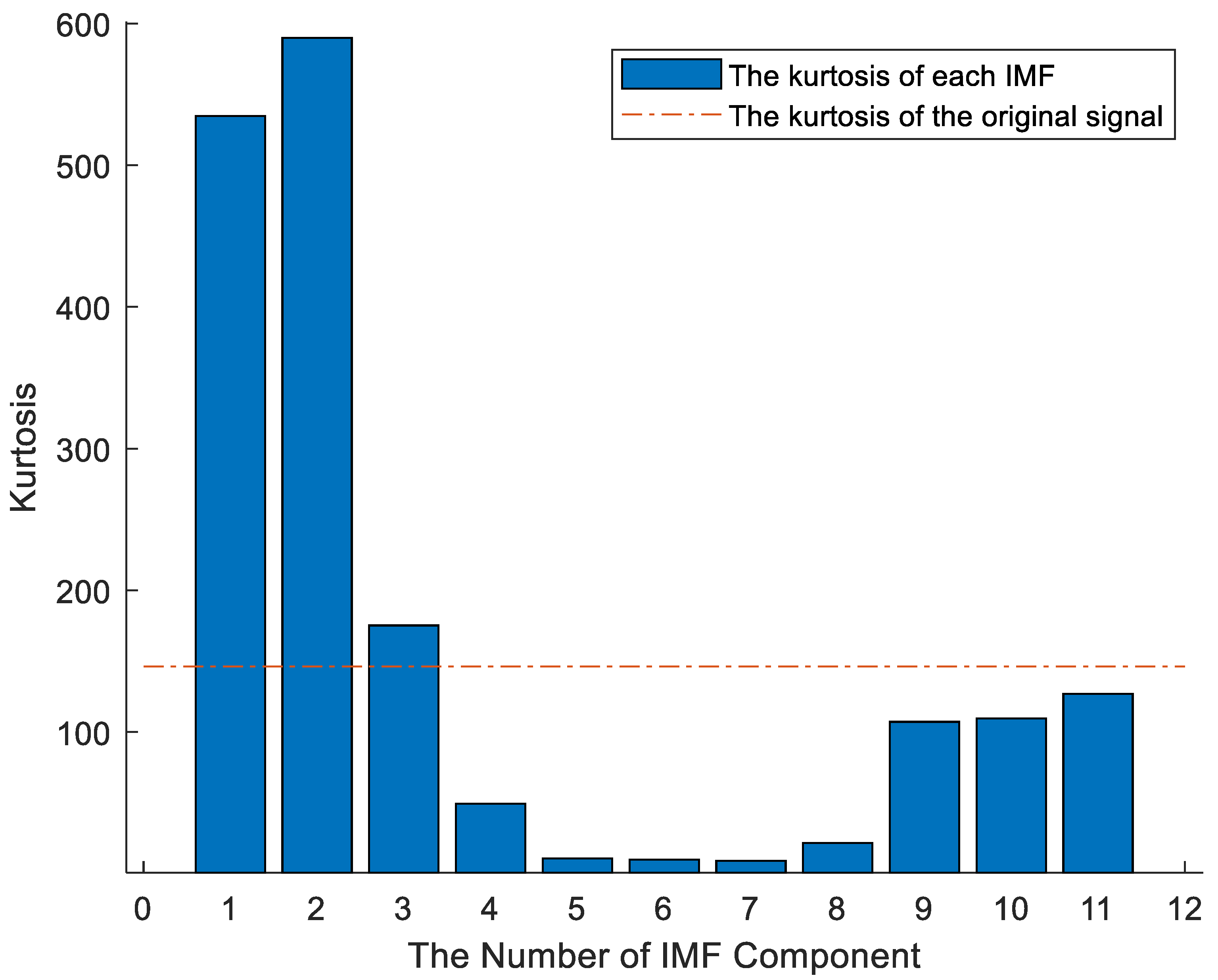
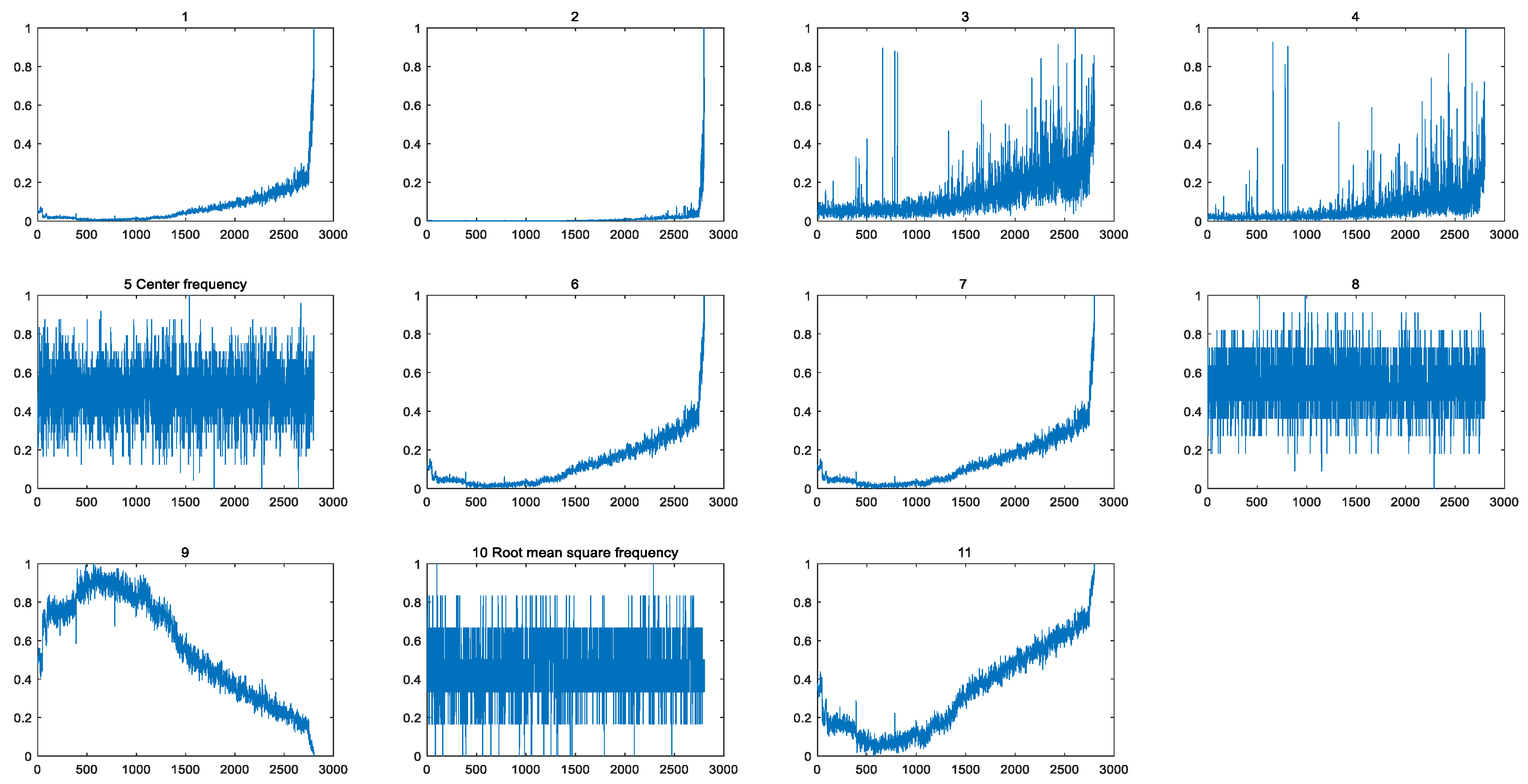
2.2. Data Processing and Characteristic Index Construction
- (1)
- Set the original signal processing times n.
- (2)
- Add Gaussian noise to n group of signals randomly to obtain a new signal.
- (3)
- The IMF components were obtained by EEMD decomposition of the new signal.
- (4)
- The mean value of IMF components of corresponding modes was calculated to obtain the decomposition result of EEMD.
3. Health Indicator Model Based on SE-ConvLSTM
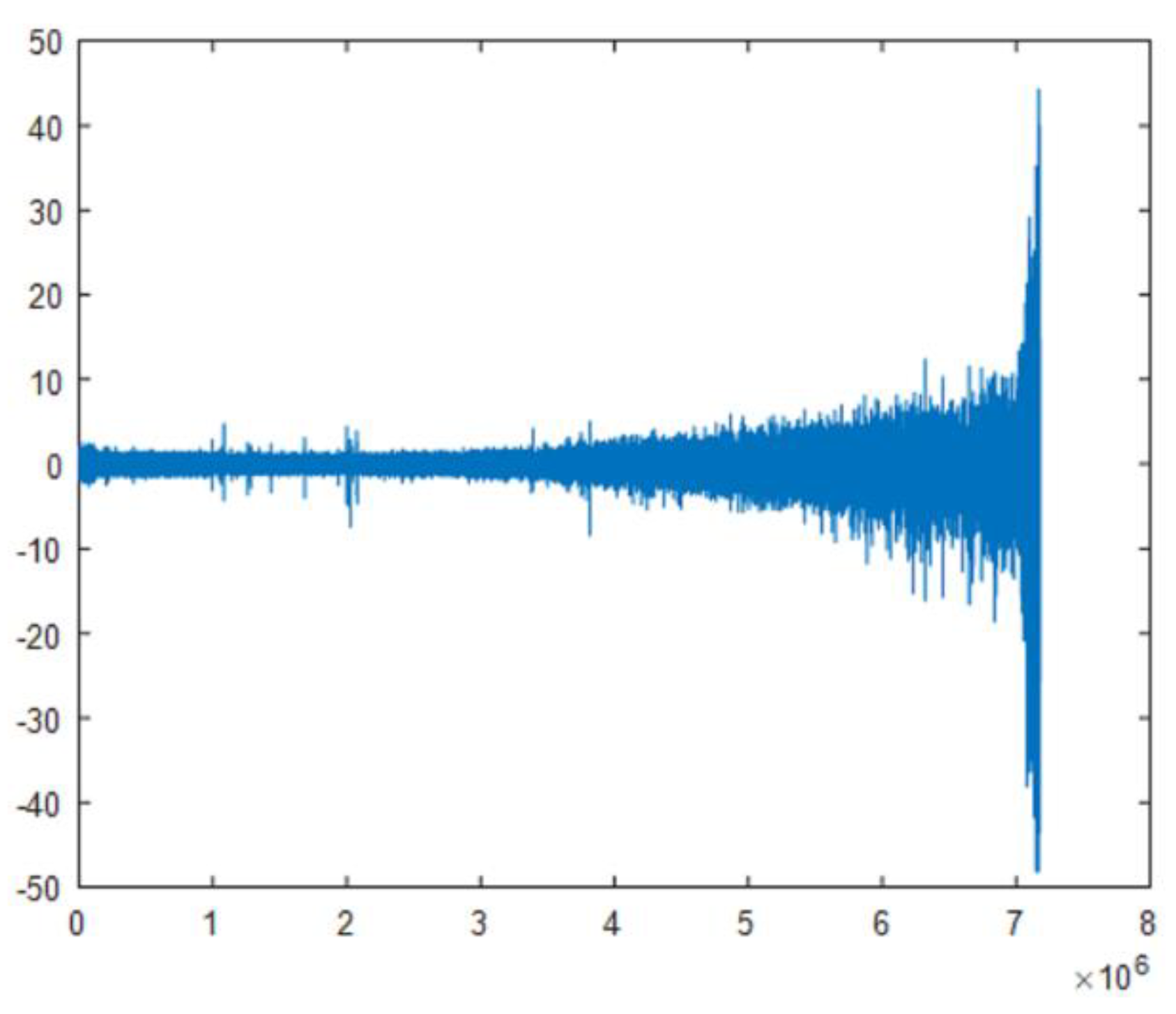
4. Test Verification
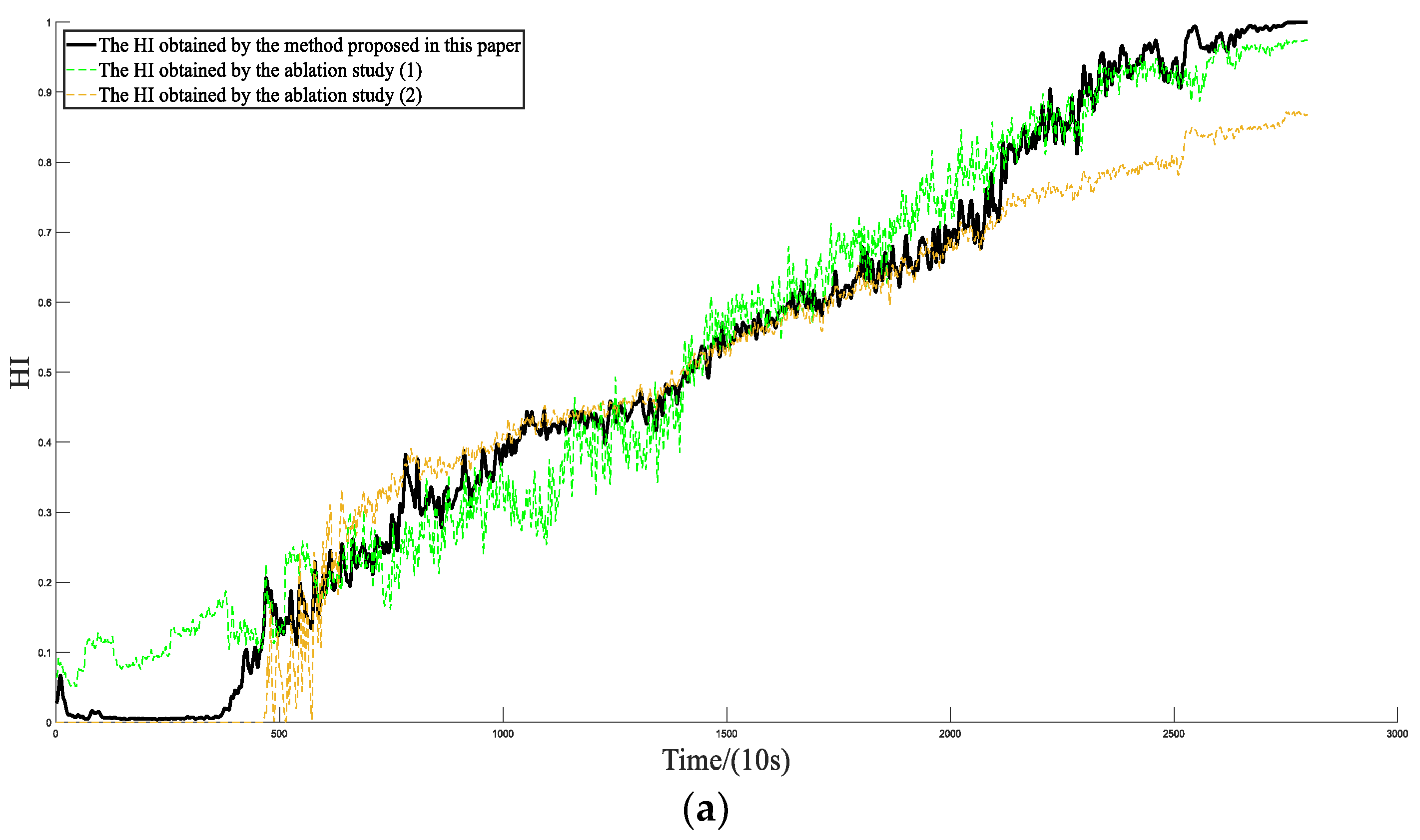
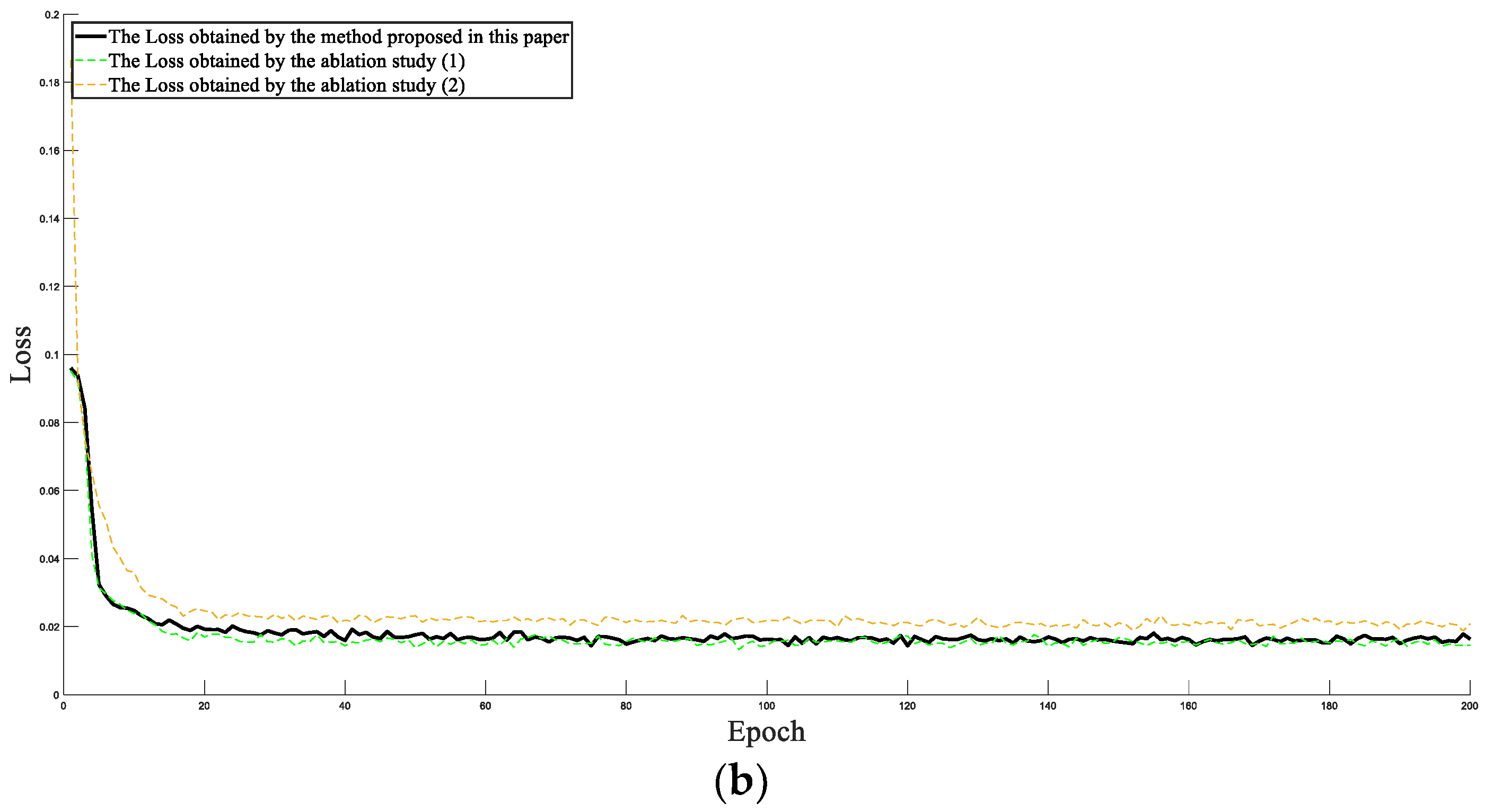
- (1)
- Original data and SE-ConvLSTM neural network were used for training.
- (2)
- Processed data and ConvLSTM neural networks without the SE module were used for training.
- (3)
- Processed data and the SE-ConvLSTM neural network were used for training.
5. Conclusions
- (1)
- Proposed the SE-ConvLSTM health index construction model, which realized the bearing health index output by utilizing the time and space characteristics of the convolutional long short-term memory neural network and attention mechanism of the SE Block.
- (2)
- Machine learning algorithms including EEMD and LOF were used to divide the bearing degradation interval, and then we constructed a health indicator in line with the bearing degradation process. By comparison, it was concluded that the three-stage performance indicator proposed in this paper predicted the bearing’s remaining useful life with higher accuracy and had important reference significance for bearing health evaluations.
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lei, Y.; Li, N.; Gontarz, S.; Lin, J.; Radkowski, S.; Dybala, J. A Model-Based Method for Remaining Useful Life Prediction of Machinery. IEEE Trans. Reliab. 2016, 65, 1314–1326. [Google Scholar] [CrossRef]
- Qiao, W.; Zhang, P.; Chow, M.Y. Condition Monitoring, Diagnosis, Prognosis, and Health Management for Wind Energy Conversion Systems. IEEE Trans. Ind. Electron. 2015, 62, 6533–6535. [Google Scholar] [CrossRef]
- Lei, Y.; Li, N.; Guo, L.; Li, N.; Yan, T.; Lin, J. Machinery health prognostics: A systematic review from data acquisition to RUL prediction. Mech. Syst. Signal. Process. 2018, 104, 799–834. [Google Scholar] [CrossRef]
- Wang, J.; Wen, G.; Yang, S.; Liu, Y. Remaining Useful Life Estimation in Prognostics Using Deep Bidirectional LSTM Neural Network. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018. [Google Scholar]
- Dong, S.; Wen, G.; Lei, Z.; Zhang, Z. Transfer learning for bearing performance degradation assessment based on deep hierarchical features. ISA Trans. 2020, 108, 343–355. [Google Scholar] [CrossRef]
- Zhang, J. Bearing Remaining Useful Life Prediction Based on a Scaled Health Indicator and a LSTM Model with Attention Mechanism. Machines 2021, 9, 238. [Google Scholar]
- Zhao, H.; Liu, H.; Jin, Y.; Dang, X.; Deng, W. Feature Extraction for Data-driven Remaining Useful Life Prediction of Rolling Bearings. IEEE Trans. Instrum. Meas. 2021, 99, 1. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, X. Convolutional neural network based on attention mechanism and Bi-LSTM for bearing remaining life prediction. Appl. Intell. 2021, 52, 1076–1091. [Google Scholar] [CrossRef]
- Pavle, B.; Matej, G.; Dejan, P.; Juričić, D. Bearing fault prognostics using Rényi entropy based features and Gaussian process models. Mech. Syst. Signal. Process. 2015, 52–53, 327–337. [Google Scholar]
- Deng, F.; Bi, Y.; Liu, Y.; Yang, S. Deep-Learning-Based Remaining Useful Life Prediction Based on a Multi-Scale Dilated Convolution Network. Mathematics 2021, 9, 3035. [Google Scholar] [CrossRef]
- Guo, L.; Li, N.; Jia, F.; Jing, F. A recurrent neural network based health indicator for remaining useful life prediction of bearings. Neurocomputing 2017, 240, 98–109. [Google Scholar] [CrossRef]
- Zhang, A.; Wang, H.; Li, S.; Cui, Y.; Liu, Z.; Yang, G.; Hu, J. Transfer Learning with Deep Recurrent Neural Networks for Remaining Useful Life Estimation. Appl. Sci. 2018, 8, 2416. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Jia, M.; Ding, P.; Ding, Y. Transfer learning for remaining useful life prediction of multi-conditions bearings based on bidirectional-GRU network. Measurement 2021, 178, 109287. [Google Scholar] [CrossRef]
- Mao, W.; He, J.; Zuo, M.J. Predicting Remaining Useful Life of Rolling Bearings Based on Deep Feature Representation and Transfer Learning. IEEE Trans. Instrum. Meas. 2019, 99, 1. [Google Scholar] [CrossRef]
- Sun, C.; Ma, M.; Zhao, Z.; Tian, S.; Yan, R.; Chen, X. Deep transfer learning based on sparse autoencoder for remaining useful life prediction of tool in manufacturing. IEEE Trans. Ind. Inform. 2018, 15, 2416–2425. [Google Scholar] [CrossRef]
- Zhang, S.; Ye, F.; Wang, B.; Habetler, T. Few-shot bearing fault diagnosis based on model-agnostic meta-learning. IEEE Trans. Ind. Appl. 2021, 57, 4754–4764. [Google Scholar] [CrossRef]
- Li, C.; Li, S.; Zhang, A.; He, Q.; Liao, Z.; Hu, J. Meta-learning for few-shot bearing fault diagnosis under complex working conditions. Neurocomputing 2021, 439, 197–211. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2011–2023. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2019, 1, 1–41. [Google Scholar] [CrossRef]
- Chen, J.; Li, X. Application of ensemble empirical mode decomposition to noise reduction of fatigue signal. J. Vib. Meas. Diagn. 2011, 31, 15–19. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Nectoux, P.; Gouriveau, R.; Medjaher, K.; Ramasso, E.; Chebel-Morello, B.; Zerhouni, N.; Varnier, C. PRONOSTIA: An experimental platform for bearings accelerated degradation tests. In Proceedings of the IEEE International Conference on Prognostics and Health Management, PHM’12, Denver, CO, USA, 18–21 June 2012. [Google Scholar]
- Tang, G.; Zhou, Y.; Wang, H.; Li, G. Prediction of bearing performance degradation with bottleneck feature based on LSTM network. In Proceedings of the 2018 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Houston, TX, USA, 14–17 May 2018. [Google Scholar]
- Zhang, B.; Zhang, L.; Xu, J. Degradation Feature Selection for Remaining Useful Life Prediction of Rolling Element Bearings. Qual. Reliab. Eng. Int. 2016, 32, 547–554. [Google Scholar] [CrossRef]
- Laurens, V.D.M.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Guo, R.; Wang, Y.; Zhang, H.; Zhang, G. Remaining useful life prediction for rolling bearings using EMD-RISI-LSTM. IEEE Trans. Instrum. Meas. 2021, 70, 1–12. [Google Scholar] [CrossRef]





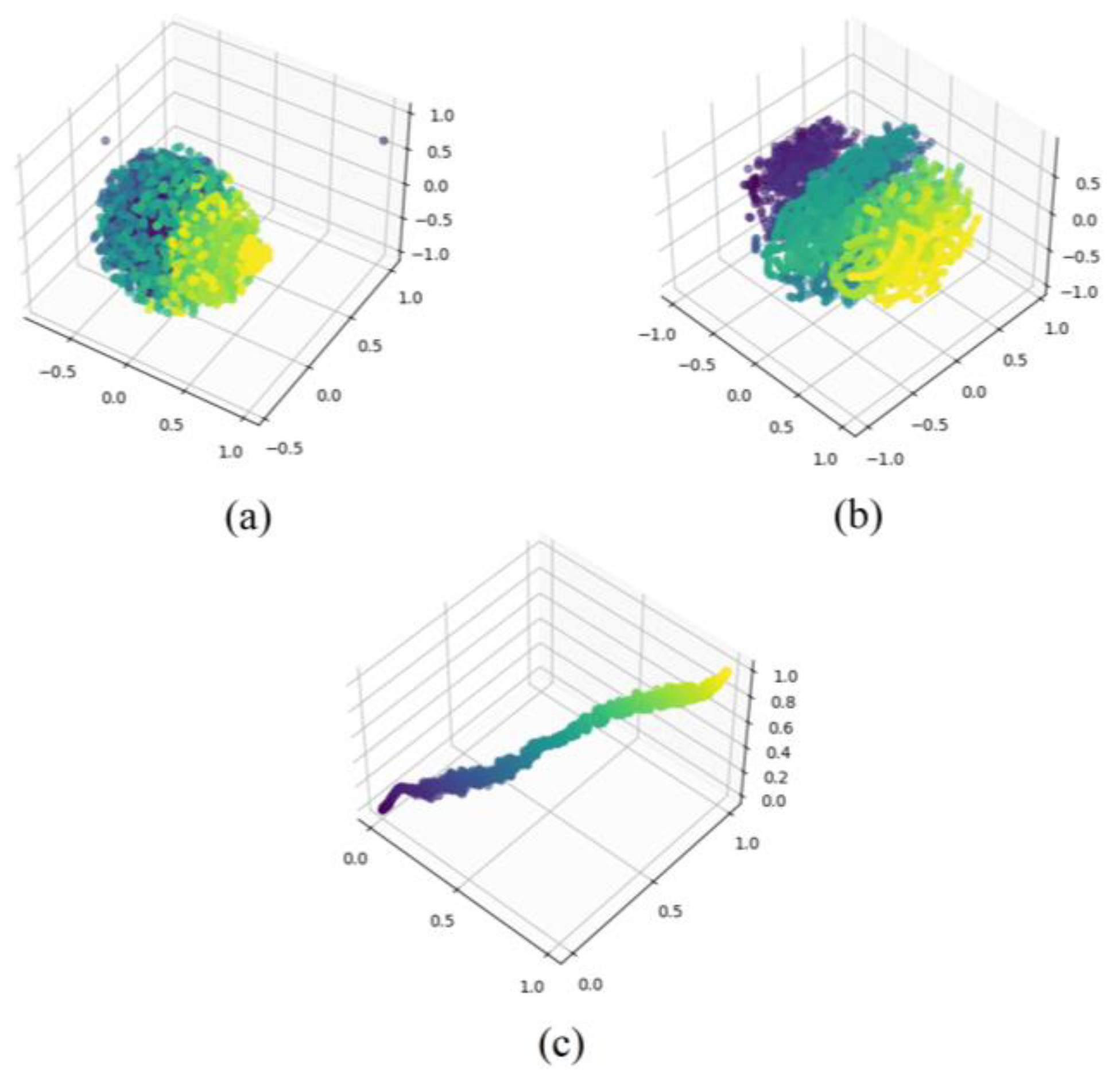

| Layer | Parameters | |
|---|---|---|
| ConvLSTM_1 | Filters = 20, kernel size = (64, 1). | |
| ConvLSTM_2 | Filters = 20, kernel size = (3, 1) | |
| ConvLSTM_3 | Filters = 1, kernel size = (1, 1) | |
| Maxpooling_1 | Pool size = (8,1,1) | |
| Maxpooling_2 | Pool size = (2,1,1) | |
| Flatten | None | |
| Dense_1 | Units = 3 | |
| Dense_2 | Units = 1, activation = sigmoid | |
| Dropout | Rate = 0.5 | |
| SE module | Global Average Pooling | None |
| Dense | Units = 4 | |
| RELU | None | |
| Dense | Passed by RELU | |
| Sigmoid | None | |
| Equation | Equation | ||
|---|---|---|---|
| 1 | 7 | ||
| 2 | 8 | ||
| 3 | 9 | ||
| 4 | 10 | ||
| 5 | 11 | ||
| 6 |
| Condition | Condition 1 | Condition 2 | Condition 3 |
|---|---|---|---|
| Training Data | Bearing1_1 | Bearing2_1 | Bearing3_1 |
| Bearing1_2 | Bearing2_2 | Bearing3_2 | |
| Test Data | Bearing1_3 | Bearing2_3 | Bearing3_3 |
| Bearing1_4 | Bearing2_4 | ||
| Bearing1_5 | Bearing2_5 | ||
| Bearing1_6 | Bearing2_6 | ||
| Bearing1_7 | Bearing2_7 |
| Proposed Method | LSTM | CNN | |
|---|---|---|---|
| Mon | 0.976 | 0.887 | 0.892 |
| Corr | 0.981 | 0.973 | 0.962 |
| Test Data | Current Time | True RUL | Prediction RUL | Proposed Method | Reference [28] | Reference [11] | LSTM | CNN |
|---|---|---|---|---|---|---|---|---|
| (10 s) | (10 s) | (10 s) | (%) | (%) | (%) | (%) | (%) | |
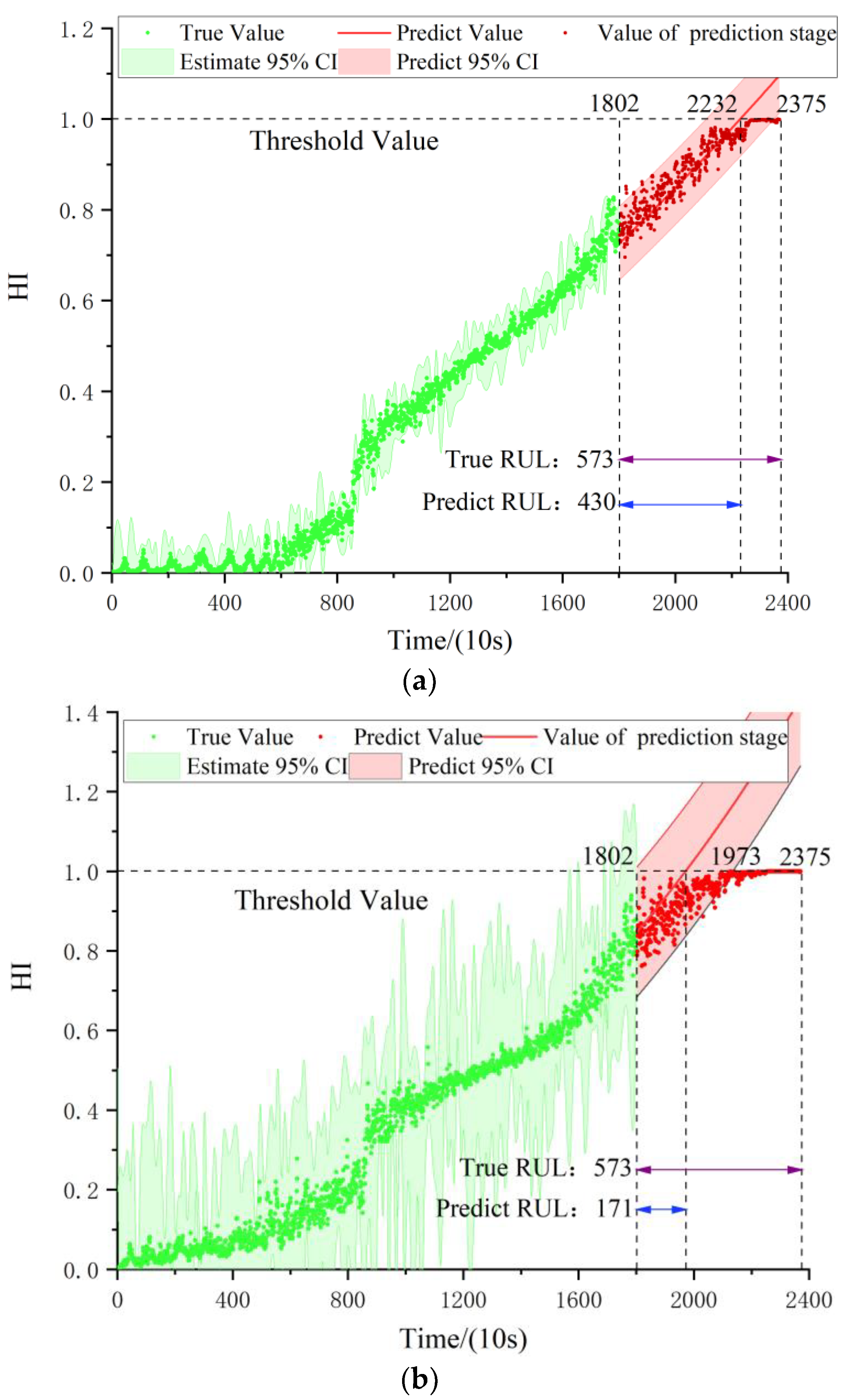
| Bearing1_3 | 1802 | 573 | 430 | 33.86 | 17.28 | 43.28 | 77.31 | 49.74 |
| Bearing1_4 | 1139 | 289 | 330 | −14.19 | 40.34 | 67.55 | 61.08 | 57.85 |
| Bearing1_5 | 2302 | 161 | 134 | 16.77 | −27.33 | −22.98 | −25.33 | −39.91 |
| Bearing1_6 | 2302 | 146 | 122 | 16.44 | −34.25 | 21.23 | 16.26 | 22.46 |
| Bearing1_7 | 1502 | 757 | 701 | 7.40 | 5.15 | 17.83 | 20.74 | 18.47 |
| Bearing2_3 | 1202 | 753 | 485 | 35.59 | −11.69 | 37.84 | 40.17 | 38.08 |
| Bearing2_4 | 612 | 139 | 162 | −16.55 | −31.65 | −19.42 | 38.47 | −30.26 |
| Bearing2_5 | 2002 | 309 | 90 | 70.87 | −9.06 | 54.37 | 49.27 | 55.25 |
| Bearing2_6 | 572 | 129 | 130 | −0.78 | −13.95 | −13.95 | 24.91 | −20.65 |
| Bearing2_7 | 172 | 58 | 70 | −20.69 | 50.00 | −55.17 | −40.12 | −69.47 |
| Bearing3_3 | 351 | 83 | 74 | 10.85 | None | 3.66 | 12.84 | 12.54 |
| Er | 21.37 | 22.10 | 32.48 | 36.98 | 37.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, S.; Liu, Y.; Liao, Y.; Su, K. A New Method of Bearing Remaining Useful Life Based on Life Evolution and SE-ConvLSTM Neural Network. Machines 2022, 10, 639. https://doi.org/10.3390/machines10080639
Yang S, Liu Y, Liao Y, Su K. A New Method of Bearing Remaining Useful Life Based on Life Evolution and SE-ConvLSTM Neural Network. Machines. 2022; 10(8):639. https://doi.org/10.3390/machines10080639
Chicago/Turabian StyleYang, Shuai, Yongqiang Liu, Yingying Liao, and Kang Su. 2022. "A New Method of Bearing Remaining Useful Life Based on Life Evolution and SE-ConvLSTM Neural Network" Machines 10, no. 8: 639. https://doi.org/10.3390/machines10080639
APA StyleYang, S., Liu, Y., Liao, Y., & Su, K. (2022). A New Method of Bearing Remaining Useful Life Based on Life Evolution and SE-ConvLSTM Neural Network. Machines, 10(8), 639. https://doi.org/10.3390/machines10080639






