Abstract
Bolted connections are the main method of connecting the components of an aero-engine low pressure rotor. Due to the influence of the elastic interaction relationship, it is easy to cause uneven distribution of the preload force of the bolt group, although it can meet the stiffness needs; however, it may lead to the deflection of the spatial relative position of the components, which is can easily cause coaxiality overrun. In view of the contradictory problem of optimization between coaxiality and stiffness of rotor assembly, this paper proposes a semi-physical simulation optimization method for the bolt tightening process based on reinforcement learning. Firstly, by studying the elastic interaction mechanism between the bolts, the elastic interaction matrix was established using finite element simulation data. On this basis, a coaxiality prediction model for the bolt tightening process was established using a GRU (gate recurrent unit) network to realize the prediction of coaxiality in the bolt tightening process. Then, through the analysis of the bolt connection stiffness, a stiffness calculation model containing the bolt stiffness, the stiffness of the connected parts, and the contact stiffness of the joint surface in series was constructed to realize the calculation of the stiffness during the bolt tightening process. Finally, with the bolt preload force as the optimization variable, coaxiality and stiffness as the optimization target, and the tightening torque and preload force of the installed bolts in the actual assembly process as the constraints, a semi-physical simulation optimization model of the bolt tightening process was established using reinforcement learning to realize the optimization of the bolt tightening process. Moreover, through the semi-physical simulation optimization method, the bolt tightening process can be installed and adjusted at the same time.
1. Introduction
The low-pressure rotor is an important component of the aero-engine [1] and is mainly made up of a stack of multi-stage disc drums with stops and bolted connections, with bolting being its most common fastening connection [2]. The bolted connection ensures on the one hand the precision of the fit of the discs and drums and on the other hand the tight connection between the discs and drums and the transmission of torque during operation. This therefore requires that the bolt preload is as uniform as possible to avoid stress concentrations. However, due to the elastic interaction between the bolts [3], the bolts that are tightened later have an effect on the bolts that are tightened first, resulting in the actual preload being far from the expected one. The discrete distribution of the preload in the bolt set further affects the complete aero-engine. Too much preload on the bolts may cause the threads to yield and reduce the load carrying capacity of the bolted structure, while too little preload can reduce the stiffness of the bolted connection to the point of loosening, leading to serious rotor failure. At the same time, each time the bolt is tightened, the rotor is deflected, and all the deflections are added up in space, causing the upper and lower rotor stages to deflect relative to each other in space, resulting in poor rotor coaxiality.
In view of the above problems, this paper takes the aero-engine rotor as the research object and proposes a semi-physical simulation optimization method for the bolt tightening process based on reinforcement learning. Firstly, by studying the elastic interaction mechanism between the bolts, the elastic interaction matrix was established using finite element simulation data. On this basis, a coaxiality prediction model for the bolt tightening process was established using GRU (gate recurrent unit) network to realize the prediction of coaxiality in the bolt tightening process. Then, through the analysis of the bolt connection stiffness, a stiffness calculation model containing the bolt stiffness, the stiffness of the connected parts, and the contact stiffness of the joint surface in series was constructed to realize the calculation of the stiffness during the bolt tightening process. Finally, with the bolt preload force as the optimization variable, coaxiality and stiffness as the optimization target, and the tightening torque and preload force of the installed bolts in the actual assembly process as the constraints, a semi-physical simulation optimization model of the bolt tightening process is established using reinforcement learning to realize the optimization of the bolt tightening process. Moreover, through the semi-physical simulation optimization method, the bolt tightening process can be installed and adjusted at the same time.
2. Literature Review
This section discusses the current state of research at home and abroad in terms of both rotor assembly quality and methods for optimising the bolt tightening process.
2.1. Status of Domestic and International Research on Rotor Assembly Quality
(1) Current status of rotor assembly coaxiality research
In recent years, scholars at home and abroad have made many achievements in the study of rotor coaxiality. Li Hong et al. [4] constructed a finite element model of the flange-fixed bolt connection of the accelerator alignment assembly and investigated the relationship between the preload force and the coaxiality on the basis of the high coaxiality requirement of the linear induction accelerator, taking into account the influence of flanges, bolts, and gaskets. Xinming [5] used finite element and MATLAB software, using the least squares method to fit the circle center, analyzing the changes caused by the bolt preload force, bolt positioning deviation, and the number of bolts on the coaxiality of the magazine after assembly, and the article concluded that when the bolt preload force changes according to the normal rule, the coaxiality of the magazine will also change, and the bolt positioning deviation will cause a large impact on the coaxiality, obtaining the influence law of multi-bolt positioning error and preload force on the change of coaxiality. Zhang Dongmei [6] constructed a calculation method for engine coaxiality based on the theory of form tolerance and studied the influence of structural features on the coaxiality of the assembly from both theory and simulation, respectively. The results showed that end runout and mounting angle would be two important causes of coaxiality overrun, and at the same time proposed a method to improve the accuracy of coaxiality. Bo Shusheng et al. [7] built a finite element simulation model of the compressor magazine under multi-bolt conditions, simulated the bolt preload force action using ANSYS, and studied the coaxiality in terms of the number of bolts, tightening sequence, and preload force distribution, and the results showed that using symmetric multiple tightening could improve the coaxiality accuracy. Ye Yongsong [8] constructed a simplified finite element model of the rotor; simulated the deformation of the mounting edge and the stop during rotor assembly; and investigated the effects of parallelism, interference size, and size and fastening sequence on the coaxiality.
(2) Status of rotor assembly stiffness research
In recent years, a large number of domestic and foreign scholars have conducted research on bolted connections. Zhao Guang [9] obtained the variation law of the intrinsic frequency and preload force using bolted connection experiments, and combined with the stress distribution on the bolts, the relationship between the intrinsic frequency of the bolts and the elastic model was obtained using the double thin-layer unit method, and the established stiffness model was applied to the disc-drum bolted connection. Brecher [10] calculated the contact stiffness and damping coefficients of bolted connections and then introduced the structural and empirical parameters into the commonly used structural parametric analysis methods. Qin et al. [11] obtained more consistent results by comparing the established analytical model of bolted connections with the data from finite element simulations, and then introduced this analytical model into the model of rotor dynamics.
In summary, although relevant studies have been conducted at home and abroad on the coaxiality and stiffness of the rotor after assembly, most of the above-mentioned literature proves that the bolt connection has an effect on the coaxiality and stiffness, and no accurate quantitative analysis of the bolt tightening process has been formed to provide guidance on the actual assembly process. Moreover, the effect of bolt tightening process on coaxiality and stiffness is not studied at the same time, which tends to make the coaxiality and stiffness of the assembly unbalanced. This paper intends to carry out research on the optimization method of aero-engine low-pressure rotor tightening process from the perspective of coaxiality and stiffness at the same time, in order to achieve simultaneous optimization of coaxiality and stiffness.
2.2. Status of Research on the Optimization Method of the Bolt Tightening Process
Hirokazu et al. [12] conducted bolt tightening experiments using the ASME method and the CW method, and the results showed that the CW method not only ensures the uniformity of the bolt preload force but is also simpler compared to the ASME method, except that the ASME method has limited improvement in the uniform distribution of the preload force after increasing the number of tightening rounds to a certain degree. Susumu et al. [13] stated that although the CW method reduces the cost and simplifies the specification of the tightening process to a certain extent, it may cause inconsistent gaps in the contact surface, which will cause the contact surface to tilt during tightening, thus leading to variations in the tightening torque, resulting in large deviations between the actual preload force and the design value. Susumu proposes tightening only part of one of the bolts when tightening, and there will be no inconsistent gaps between the upper and lower contact surfaces using this method. Shi Gang [14] relied on the instrumentation to conduct monitoring tests on the deformation of the bolts and analyzed the variation law of deformation with time. At the same time, he also conducted experiments on eight bolt sets with three types of fastening sequences. It was found that the tightening sequence from the center to the diagonal on both sides was the best. Takaki [15] used the finite element method to analyze the variation law of preload force versus time during bolt tightening and obtained the elastic interaction matrix used to set the initial preload force magnitude on the basis of the simulation data to achieve a uniform distribution of the bolt preload force. Chen Chengjun [16] proposed a digital design method of the bolt tightening process for the requirements of contact surface sealing performance in order to design a bolt tightening process that meets the requirements of sealing performance in the design phase; analyzed the laws of bolt tightening sequence, preload force size, and contact surface connection performance; and established a relationship model between preload force size and contact surface pressure, on the basis of which the bolt tightening process can be optimized according to the requirements of sealing performance.
In the optimization of bolt tightening process, the current research on the impact of the bolt tightening process on coaxiality is less, and there is no corresponding optimization method of the bolt tightening process. Considering that the low-pressure rotor of the aero-engine, which is the subject of this paper, often works at ultra-high speed, the coaxiality, which is an important index, occupies a crucial position. Therefore, in this paper, when optimizing the tightening process, the coaxiality and stiffness of the bolted connection are considered at the same time to improve the comprehensive quality of the rotor after assembly.
3. Semi-Physical Simulation Framework for Tightening Process Optimization
Aero-engine rotors are generally bolted together. The low-pressure rotor is assembled from three disks, and the disks are connected to each other by a certain number of bolts. Since the tightening sequence, tightening starting point, and number of tightening passes in the tightening process, which are important factors affecting rotor coaxiality and stiffness, are often used in textual form for recording, it is not easy to enter the network. Therefore, this paper converted the combined effect of the above tightening process into the change of preload force by establishing the elastic interaction matrix, which completely characterizes the different tightening processes and also reflects the characteristic that the preload force always changes. The change of preload is the fundamental reason for the change of coaxiality and stiffness.
Since the assembly structure and the number of bolts and contact surface roughness vary from application to application, the focus of this paper is on how to use a data-driven approach to solve the optimization problem of the tightening process during rotor assembly. Therefore, the following assumptions exist in this paper: (1) the simplified model of the low-pressure rotor involved is the subject of this paper, as shown in Figure 1 and Figure 2; (2) the errors arising from the conversion of the tightening torque into the preload force are not considered; (3) the influence of the sensor accuracy on the data accuracy is not considered; (4) the influence of other factors (such as contact surface roughness, parallelism, etc.) on the elastic interaction matrix is not considered.
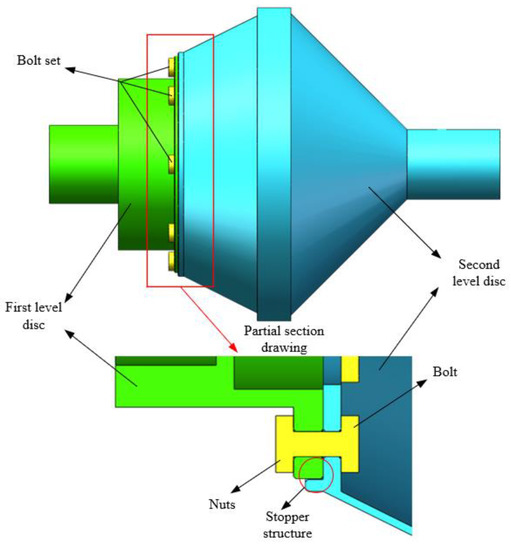
Figure 1.
Simplified model of low-pressure rotor.

Figure 2.
Simplified experimental parts.
During the tightening of low-pressure rotor bolts, the preload force after the tightening of each bolt is not only related to the current tightening process, but also to the tightening result of the previous bolt. Moreover, due to the elastic interaction, the preload force of the bolt is also influenced by the subsequent bolt tightening process. Each bolt tightening will affect the coaxiality and stiffness of the rotor. To ensure that the final rotor coaxiality and stiffness meet the design requirements and are as optimal as possible, as well as to avoid coaxiality and stiffness overruns caused by human installation errors and other factors, the bolt tightening process needs to be monitored. Since the final overall coaxiality and stiffness are formed after the bolt tightening process is fully completed and the subsequent bolts have not been tightened during the assembly process, the actual measured data of the subsequent bolt preload force cannot be obtained. Therefore, this paper constructed a semi-physical simulation model of bolt tightening, combined the measured preload data of the tightened bolts with the theoretical preload data of the untightened bolts, and calculated the overall coaxiality and stiffness of the rotor. As shown in Figure 3. The implementation process is as follows.
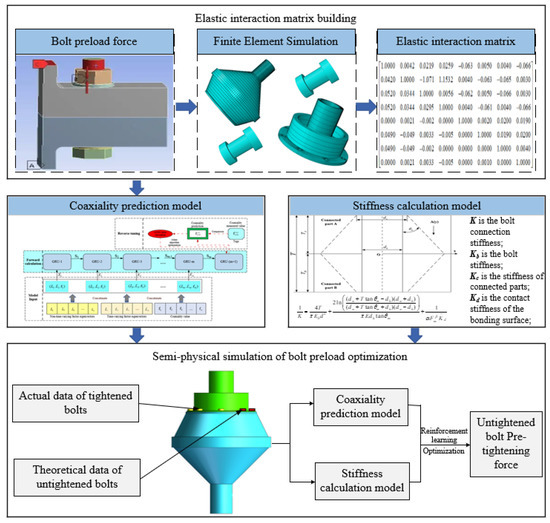
Figure 3.
Semi-physical simulation framework for the tightening process optimization.
1. Building the coaxiality prediction model. In order to realize the prediction of rotor coaxiality during the tightening process while loading, this paper proposes a real-time coaxiality prediction method for the bolt tightening process with the fusion of mechanism and data drive. Firstly, the elastic interaction mechanism between the bolts was studied, and the elastic interaction model was established on the basis of the finite element simulation data to realize the dynamic calculation of the preload force of the bolts during the tightening process. Then, a coaxiality prediction model for the bolt tightening process was constructed by using GRU (gate recurrent unit) neural network for the temporal correlation between preload force and coaxiality, and the accurate prediction of coaxiality was achieved by using the “long time memory” capability of the model.
2. Establishing the stiffness calculation model. Stiffness as a measure of the performance of bolted parts is one of the important indicators, especially for low-pressure rotors such as high-speed rotating parts; the greater the stiffness that can be withstood, the greater the load capacity, effectively improving the reliability of the rotor. In addition to the bolt stiffness and the stiffness of the connected parts, the contact stiffness of the bonding surface was added to the bolt connection stiffness calculation model in this paper, as shown in Equation (1).
In the formula, is the bolted connection stiffness; is the bolt stiffness; is the stiffness of the connected parts; and is the contact stiffness of the bonding surface.
3. Calculation of coaxiality and stiffness during bolt tightening. When the tth bolt was tightened, the previous t-1 bolts were already tightened, so the actual bolt preload data were used for the t-1 bolts, and the design data were used for the remaining untightened bolts instead. Moreover, the final coaxiality and stiffness at this point were calculated by the coaxiality prediction model and the stiffness calculation model.
4. Semi-physical simulation of bolt preload force optimization. Monitoring of bolt tightening process on the basis of real-time calculation of coaxiality and stiffness during bolt tightening. Reinforcement learning was used to optimize the preload of subsequent untightened bolts to ensure that the coaxiality and stiffness of the rotor were always balanced during the bolt tightening process. It was also possible to make the rotor coaxiality and stiffness meet the design requirements by optimizing the preload of subsequent untightened bolts in the case of coaxiality and stiffness overruns.
4. Modeling of Bolt Tightening Process Optimization
The coaxiality and stiffness of the assembled aero-engine rotor are the main indicators in the evaluation of the engine performance. The low-pressure rotor of the aero-engine studied in this paper is made of multi-stage discs stacked by bolting. The coaxiality of the rotor after assembly is mainly due to the change of the relative position of the upper and lower rotor stages in space caused by the bolt preload, while the stiffness of the rotor after assembly is mainly caused by the change of the bonding surface pressure by the bolt preload. Both coaxiality and stiffness are attributed to the bolt preload, and the way in which to ensure the optimal coaxiality and stiffness during the assembly process is the goal of this research. As shown in Figure 4, when the bolt tightening operation was performed, the difference in the bolt preload force led to deflection of the upper and lower disc, which eventually led to a change in the coaxiality of the assembly, as well as a change in the stiffness of the bolt connection. The essence of coaxiality and stiffness optimization is to adjust the bolt preload so that the two rotors assembled to each other are as coaxial as possible in space while maintaining the assembly stiffness.
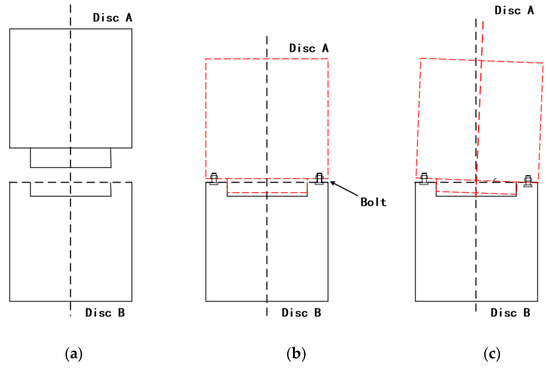
Figure 4.
Rotor assembly diagram. (a) Before assembly; (b) Before bolt tightening; (c) After bolt tightening.
4.1. Coaxiality Prediction Modeling
Due to the influence of the elastic interaction between the bolts, the actual preload force of the bolts is in error with the design requirements. The accumulation of tightening errors in all bolts causes a change in the relative position of the rotor in space, resulting in coaxiality overruns. Therefore, this paper used the finite element simulation method combined with the bolt elastic deformation principle to establish an elastic interaction model to realize the calculation of the actual preload force in the bolt tightening process. Then, the GRU (gate recurrent unit) network was used to establish the coaxiality prediction model to realize the prediction of coaxiality in the assembly process. The coaxiality prediction model has been implemented and has resulted in a related paper under expert review, so only the implementation steps and results are presented here. The specific implementation process consisted of the following three steps.
Step 1: The assembly process, machining quality, assembly accuracy, environmental parameters, material properties, and coaxiality after each tightening operation were collected during the rotor assembly process. The coaxiality was collected by the coaxiality measurement device designed in this paper, and the device is shown in Figure 5.

Figure 5.
Coaxiality acquisition device.
Step 2: The bolt tightening process was simulated using the finite element method, and the elastic interaction matrix was established on the basis of the simulation data to obtain the dynamic changes of the preload force. The elastic interaction matrix is different for different tightening methods. In this paper, the cross-tightening method of eight bolts was used as an example to simulate the bolt tightening process. The material properties in the finite element simulation were defined as parameters related to cast aluminum alloy (AlSi10 Mg). The first stage disk and the second stage disk were meshed by sweeping the grid center axis method. As the key fit parts used fine mesh division, the rest of the non-critical location used coarse mesh division. Figure 6a shows the first-stage disk finite element model with a total number of cells of 11780. Figure 6b shows the second-stage disk finite element model with a total number of cells of 14085. The preload force was increased from 1500 N to 2500 N in increments of 100 N. The elastic interaction matrix was calculated on the basis of the remaining preload force of the bolt, and the results are as follows.
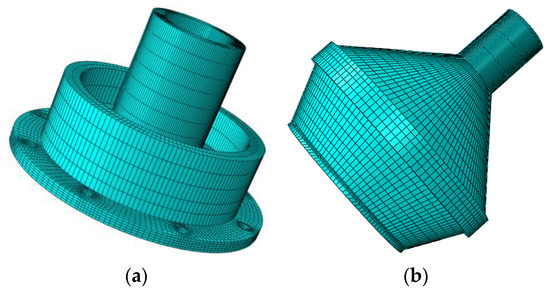
Figure 6.
Rotor finite element model. (a) First-stage disc finite element model. (b) Second-stage disc finite element model.
Step 3: The GRU (gate recurrent unit) network was used to build a coaxiality prediction model in the bolt tightening process. Divided into n time steps according to the number of bolts, when the tth bolt is tightened, the actual preload force of t bolts and the theoretical preload force of n-t bolts and the assembly influence factors collected in stpe1 are taken as input, and the final coaxiality is taken as output to realize the prediction of coaxiality during bolt tightening. The coaxiality prediction model is shown in Figure 7.
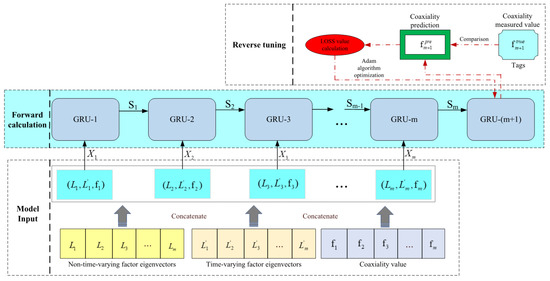
Figure 7.
Coaxiality prediction model.
4.2. Modeling of Stiffness Calculation
Stiffness is one of the most important indicators of the performance of bolted joints, especially for low-pressure rotors, which are high-speed rotating parts; the greater the stiffness, the greater the load it can withstand, which can effectively improve the reliability of the rotor. In addition to the bolt stiffness and the stiffness of the connected parts, the contact stiffness of the bonding surface was added to the bolt connection stiffness calculation model in this paper.
The bolted joint stiffness is mainly composed of three parts in series: the bolt stiffness, the stiffness of the connected parts, and the contact stiffness of the bonding surface [17].
In the formula, is the bolt connection stiffness; is the bolt stiffness; is the stiffness of the connected parts; and is the contact stiffness of the bonding surface.
According to the German (VDI) standard, the bolt stiffness is generally calculated by considering the bolt as a uniform cylinder [18].
In the formula, is the material modulus of elasticity of the bolt; is the diameter of the bolt; and is the total thickness of the connected parts.
If the stresses in the connected parts under bolt compression show a uniform distribution along the radial direction, then the shape of the compressed layer exhibits a cone [19], as shown in Figure 8.
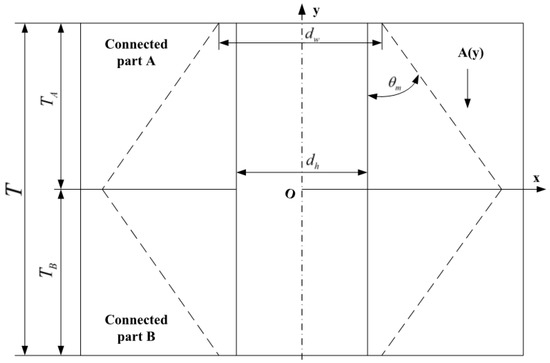
Figure 8.
Axial variation of the area of the pressurized layer of the connected parts.
The stiffness of the connected member changes with the area of the compressed layer, which is mainly determined by the elastic modulus of the material and the thickness affecting the cone angle , and the equation fitted in the joint literature [20] establishes the relationship between the elastic modulus and the thickness causing the cone angle change, as in Equation (5).
In the formula, denotes the equivalent modulus of elasticity of the upper and lower connected member materials [21].
The area of the pressurized layer of the connected parts is shown in Equation (9).
In the formula, indicates the clamping outside diameter of the bolt, and indicates the inner diameter of the threaded hole.
According to the Hooke’s law relationship, the stiffness of the connected member is
Considering that the bond surface stiffness will be mainly influenced by the contact pressure, it is necessary to obtain the contact pressure of the bond surface before calculating the bond surface stiffness value. For the connected parts with the same thickness, the outer diameter . If there is no shim between the connected parts, then the distribution of the contact pressure can be considered as a fourth-order polynomial [22] with respect to the radius shown in Figure 9, where is the half-top angle assumed for the cylinder, then
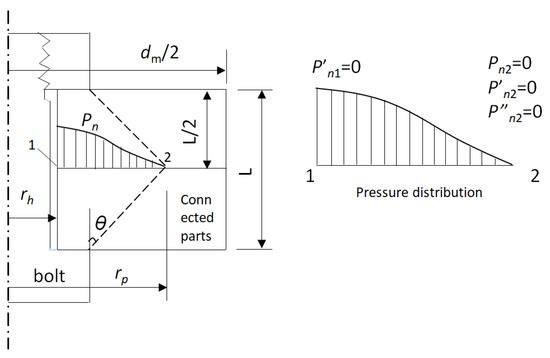
Figure 9.
Assumption of contact pressure distribution of connected parts.
In the formula, is the coefficient to be determined.
According to the literature [23], the contact stiffness of the bond surface is obtained as
In the formula, is the applied preload force, and is the pressure distribution after applying a unit load.
Make , then
Combining Equations (3)–(13), the stiffness of the bolted connection is
4.3. Bolt Tightening Process Optimization Model
In this paper, the coaxiality and stiffness of the rotor are taken as the optimization objectives, the tightening torque and preload force equalization limit in the actual assembly process are taken as the constraints, and the dual-objective optimization model of the low-pressure rotor is established by combining the coaxiality prediction model and stiffness calculation model. The tightening process is optimized under the premise of ensuring the coaxiality and stiffness to meet the requirements as much as possible. Integrating the coaxiality prediction model and the stiffness calculation model, the objective function of the bolt tightening process optimization model is
In the formula, is the weight parameter of the ith objective function.; is the coaxiality of the assembled low-pressure rotor; is the low pressure rotor bolt connection stiffness; is the bolt preload force vector; and is the preload force of the ith bolt.
The preload force of the bolt is not arbitrarily selected in order to ensure the stability of the rotor connection and can withstand a certain amount of tension, torsion, and bending, according to the general steel connection bolt preload force formula.
In the formula, is the yield limit (in this paper ). is the cross-sectional area of the small diameter of the thread.
Substituting into this paper, we obtained by calculation .
Considering that the minimum accuracy of the torque wrench in the example verification of this paper was 1.5 N·m and the minimum preload force was 1500 N by calculation, then the value of the bolt preload force was taken between 1500 and 2600 N.
In order to avoid the problem of stress concentration in the rotor after tightening of the bolts, the maximum preload and the minimum preload of the individual bolts were not more than 20% between them. Then, the multi-stage rotor bi-objective optimization constraint is shown in Equation (17).
In the formula, is the maximum coaxiality allowed after tightening the bolt; is the minimum allowable stiffness of the bolt after tightening; is the maximum preload force for a single bolt; and is the minimum preload force for a single bolt.
5. Optimization Model of Bolt Tightening Process Based on Reinforcement Learning
In this section, the Q-learning learning algorithm is used to solve the bolt tightening process optimization model. Reinforcement learning addresses the entire bolt tightening process optimization problem and is global in nature. Q-learning learning algorithms can converge faster than ordinary reinforcement learning algorithms, being able to improve the efficiency of bolt tightening process optimization.
5.1. Reward and Punishment Function Design
The objective of the reinforcement learning of the bolt tightening process optimization model is to be able to find a bolt tightening process strategy that optimizes the coaxiality and stiffness of the rotor. The design of the reward and punishment function determines not only whether the model can obtain long-term payoffs, but also whether the model can learn the bolt tightening process strategy as quickly as possible.
The optimization objective considered in this paper is to optimize the rotor coaxiality and stiffness, so the reward and punishment function is set as follows:
5.2. Q-Value Update Strategy
R is the immediate reward for each action of the model and considers the long-term impact of each action. We set the matrix to be the knowledge learned from experience, where h represents the number of bolts, the rows of the matrix Q represent the current state and the columns represent the possible actions to reach the next state, and the matrix Q is initialized to 0.
Every time the model is trained, the elements of the matrix Q are updated by the following equation:
In the formula, s is the current state; a is the action; R is the immediate reward; and is the learning variable.
The value of the elements in the matrix Q is then equal to the sum of the immediate reward R under the current state s and action a and the learning variable multiplied by the maximum reward value for all possible actions to reach the next state. The parameter takes a value between 0 and 1, . If is closer to 0, the model tends to consider only the immediate reward; if is closer to 1, the model will consider the overall reward with a greater weight.
The bolt tightening process optimization model learns from experience using the algorithm described above, with each experience being equivalent to a training session. During each training, the model continuously selects the bolt tightening force and inputs the selected tightening force for the first t steps and the unselected theoretical preload force for the next n-t steps, the initial coaxiality, and the collected assembly influences into the coaxiality prediction model and the stiffness calculation model to calculate the final coaxiality and stiffness of the rotor. Once the target state is reached, the bonus value is obtained. The purpose of training is to enhance the experience of the model, represented by the matrix Q. More training results will result in a more accurate matrix Q.
During the actual bolt tightening process, the rotor stiffness is calculated from the actual data of the tightened bolts and the theoretical data of the untightened bolts. The change of rotor coaxiality is monitored by the coaxiality acquisition device, so that the preload force of the untightened bolts is adjusted in real time to keep the rotor coaxiality and stiffness optimal, and the Q value is updated according to the real time adjustment result. If the matrix Q has been trained and updated several times, the model will not explore blindly during the bolt tightening process but will reach the target state the fastest.
6. Experimental Verification
In order to verify the reliability of the reinforcement learning-based semi-physical simulation optimization method for the bolt tightening process, a simplified model of the rotor was used to experimentally validate the experimental parts machined according to 1:1.
6.1. Rotor Assembly Experiment Preparation
Coaxiality acquisition using a laser sensor was used, as shown in Figure 10; the model was a Panasonic HG-C1030 miniature laser displacement sensor, with an accuracy of 10nm and sampling frequency of 800 Hz. An ordinary lathe was used to provide a rotary reference for measurement, a model CS6150 of Baoji Machine Tool Factory, with spindle speed from 9 to 1600 rpm and spindle power of 7.5 KW. A three-jaw centering chuck was used for clamping the measured parts.

Figure 10.
Experimental sample coaxiality measuring device.
The geometric parameters of the simplified experimental part of the low-pressure rotor are shown in Table 1.

Table 1.
Geometric parameters of experimental parts.
In the actual assembly, the tightening torque is generally used instead of the preload force. The specific operation is to set the parameters in the torque wrench and use the torque wrench to tighten the bolt, so as to control the preload force size. The relationship between the bolt tightening torque and the preload force is shown below [24].
Considering the maximum tightening torque that the nominal diameter 4 mm bolt can withstand, the maximum tightening torque of 2 N·m was selected in this paper, and the maximum preload force of 2500 N can be obtained by using the formula.
The preload force of the rotor bolt set was applied using the Yarick digital electronic torque wrench, as shown in Figure 11. Torque wrench alarm range was 1.5~30 N·m, and accuracy was ±2%. During the experiment, the preload force to be applied was converted into the tightening torque by Equation (20), and the tightening torque to be applied was set before applying the force; the torque wrench would beep and stop applying the force when the set value was reached during the tightening process.

Figure 11.
Digital display electronic torque wrench.
6.2. Optimization of Bolt Tightening Process
(1) Coaxiality prediction
For the reliability of the model, tightening experiments were conducted on the basis of the experimental low-pressure rotor parts, with bolt 1 as the starting point of tightening each time, and the tightening sequence was cross-tightening. In other words, the tightening sequence was 1-5-3-7-2-6-4-8, and the bolt tightening torque varied from 1.5 to 2.0 N·m. The specific tightening process parameters are shown in Table 2. Using the above device, the coaxiality of the experimental part assembly can be collected in real time, and the measured coaxiality and the bolt preload were used as input to predict the future coaxiality of the assembly using the coaxiality prediction model that has been studied by the authors.

Table 2.
Bolt tightening torque parameters (unit:N·m).
Laser sensors were used to measure the runout at the position of the disk rotation axis after each tightening step. The least squares method was used to fit the runout values collected at several points to a circle, and the average of the horizontal and vertical coordinates of all points on the circle was defined as the circle center of the circle, with the offset between the position of the fitted circle and the standard circle center being used as the coaxiality of the rotor after assembly. A circle fitted using the least squares method is shown in Figure 12.
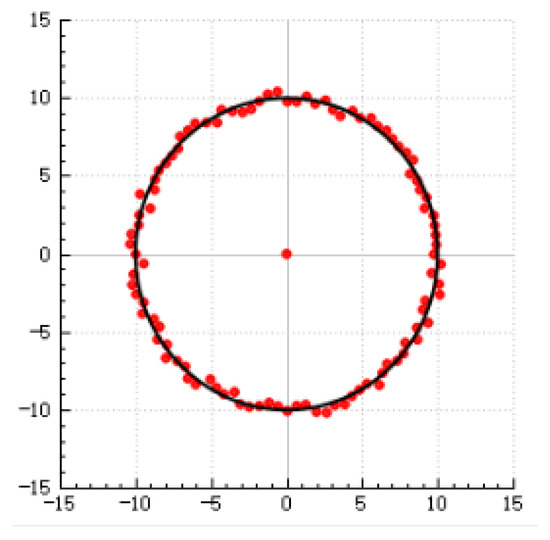
Figure 12.
Least squares fitting of the circle center.
The actual preload force during the tightening process can be obtained by processing the bolt preload force using the previously established elastic interaction matrix. The preload force of experiment number 1 in Table 2 is demonstrated as shown in Table 3 below.

Table 3.
Variation of bolt preload during assembly (unit: N).
A fourfold cross-validation method was used to train 36 sets of experimental samples. The model training process was set with a learning rate of 0.001, a batch size of 32, and a training iteration count of 200, and the gradient descent process was optimized using the Adam algorithm. Twelve groups of samples were randomly selected to test the coaxiality prediction model trained by the fourfold cross-validation method, and the test results are shown in Figure 13, where the red fold is the true value and the black fold is the predicted value.
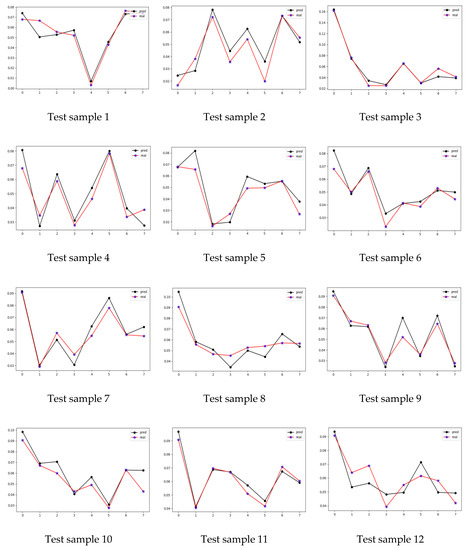
Figure 13.
Coaxiality prediction network prediction effect graph.
The four sets of data from the test sample are presented in a table, and the results are shown in Table 4.

Table 4.
Comparison of the predicted and true values of the 4 groups.
To better evaluate the prediction effectiveness of the coaxiality prediction model, the Nash efficiency coefficient (NSEC) values were calculated for 12 test groups of samples. The smaller the error between the predicted and true values of the coaxiality, the closer the NSEC value is to 1. The NSEC calculation results for the 12 test groups of samples are shown in Table 5 below.

Table 5.
Test sample predicted value vs. true value results.
From Figure 13, it can be seen that the difference between the predicted and true values of coaxiality in 12 test samples was not large, and the prediction accuracy was relatively good, accurately reflecting the trend of coaxiality change and verifying the validity of the model. As can be seen from Table 5, the NSEC values of the 12 test samples were very close to 1. The prediction model can generally achieve the prediction of low-pressure rotor coaxiality under the action of multi-bolt tightening.
(2) Stiffness calculation
During the experiment, the bolt tightening torque parameters were designed in advance, as shown in Table 2. Therefore, after converting the bolt tightening torque to preload force, the actual preload force for each group of experiments can be calculated according to the elastic interaction matrix, and the equivalent stiffness of the rotor bolt connection after the assembly is completed and can be calculated according to the actual preload force by Equation (14). The results of the stiffness calculation are shown in the Table 6 below.

Table 6.
Stiffness calculation results (unit: N·m).
(3) Optimization of bolt tightening process
On the basis of the above coaxiality and stiffness calculation results, the reinforcement learning was used to solve the bolt tightening process optimization model. Within the design range of bolt tightening torque, multiple sets of optimization results were obtained by setting different tightening torques for the first bolt, and the results with extreme values of rotor coaxiality less than 26 μm and extreme values of stiffness greater than 1.3 × 108 N/m were selected, as shown in Table 7 below.

Table 7.
Optimization results of bolt tightening process (unit: N).
According to the table, the coaxiality and stiffness of the non-inferior solution bolt set under the preload force were calculated, and the calculated coaxiality and stiffness were taken as shown in Figure 14. It can be seen from Figure 14 that the coaxiality can reach a minimum of 22.1 μm by using the inverse result of the tightening torque under the preload of the third group of bolts, and the selection of this group of bolts’ preload can make the coaxiality value after tightening reach a minimum. The preload force of the second group of bolts achieved a maximum stiffness of 1.87 × 108 N/m. The preload force of this group of bolts was selected to achieve the highest stiffness after assembly. The coaxiality and stiffness under the preload of the sixth group of bolts were maintained at good values of 22.9 μm and 1.7 × 108 N/m, respectively, which can make the coaxiality and stiffness more balanced if the preload of this group of bolts is chosen.
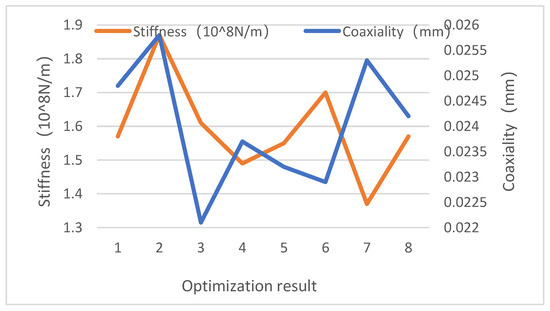
Figure 14.
Optimization results.
6.3. Semi-Physical Simulation of Bolt Tightening Process Optimization
In order to verify the validity of the semi-physical simulation model, the bolt preload force of group 6 in Table 7 was selected for verification, and the bolts were tightened according to the crossover method: bolt 1–bolt 5–bolt 3–bolt 7–bolt 2–bolt 6–bolt 4–bolt 8. To make the verification results more significant, the design incorrectly set the preload force of bolt 3 to 2125 N, or a tightening torque of 1.7 N·m, during the installation process.
The coaxiality of the third bolt after assembly was 0.068 mm by using the coaxiality acquisition device and fitting by least squares method. As shown in Figure 15 below, the red point is the center of the fitted circle, the black point is the center of the standard circle, and the distance between the two points is the coaxiality.
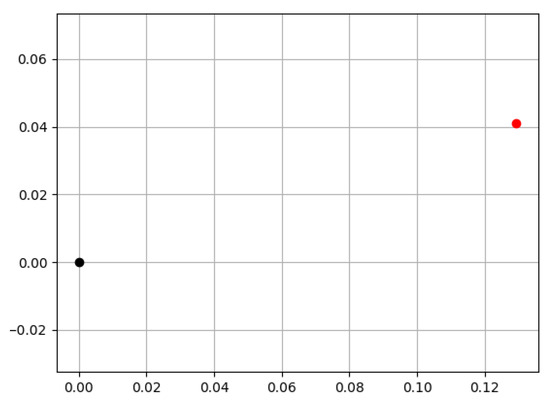
Figure 15.
Fitting results.
Using the currently measured coaxiality, the actual preload force of the tightened bolts, and the theoretical preload force of the untightened bolts as inputs, the coaxiality prediction model was used to predict the final coaxiality of 0.0258. The final stiffness of 1.89×108 N/m was obtained using the stiffness calculation model. The result was not optimal, although it met the design requirements. Therefore, the bolt tightening process optimization model was used to optimize the preload force of the subsequent five bolts so as to optimize the coaxiality and stiffness. The comparison before and after the optimized adjustment of the bolt preload is shown in Table 8 below.

Table 8.
Bolt preload comparison (unit: N).
After calculation, in the case of incorrect setting of bolt 3 preload force, when the assembly was carried out according to the originally designed bolt tightening process scheme, the coaxiality of the completed assembly was 0.0258 mm and the stiffness was 1.89 × 108 N/m. In addition, when assembled according to the scheme optimized by the bolt tightening process optimization model, the coaxiality of the completed assembly was 0.0237 and the stiffness was 1.74 × 108 N/m. Although the result of assembly according to the optimized scheme was worse than the result of the scheme without errors in bolt 3, bolt disassembly was largely avoided and assembly efficiency was improved. The effectiveness of the semi-physical simulation model constructed in this paper for the optimization of bolt tightening process was proven.
7. Conclusions
This paper proposes a semi-physical simulation optimization method for the bolt tightening process on the basis of reinforcement learning. Firstly, by studying the elastic interaction mechanism between the bolts, the elastic interaction matrix was established using finite element simulation data. On this basis, a coaxiality prediction model for the bolt tightening process was established using the GRU (gate recurrent unit) network to realize the prediction of coaxiality in the bolt tightening process. Then, through the analysis of the bolt connection stiffness, a stiffness calculation model containing the bolt stiffness, the stiffness of the connected parts, and the contact stiffness of the joint surface in series was constructed to realize the calculation of the stiffness during the bolt tightening process. Finally, with the bolt preload force as the optimization variable, coaxiality and stiffness as the optimization target, and the tightening torque and preload force of the installed bolts in the actual assembly process as the constraints, a semi-physical simulation optimization model of the bolt tightening process was established using reinforcement learning to realize the optimization of the bolt tightening process. Moreover, through the semi-physical simulation optimization method, the bolt tightening process can be installed and adjusted at the same time.
However, the objects selected for study in this paper were only primary and secondary disc assemblies, and the error transmission path after rotor assembly was short. Actual aero-engine high-pressure rotors are commonly assembled from rotors of nine or more stages, with long error transfer paths. Moreover, the optimization results in this paper only provide the values of preload force after assembly, but do not provide specific guidance on the specific tightening strategy on the basis of the preload optimization results. Therefore, future optimization of the model is also needed to consider the coaxiality and stiffness optimization under multi-stage rotor assembly.
Author Contributions
H.Z. has made contributions to the analysis of blade sorting problems, the determination of solutions to blade sorting problems, experimental design, experimental data processing, and paper writing. M.W. (Mingwei Wang) and J.Z. (Jingtao Zhou) gave guidance on the overall methodology of the paper; W.D., J.Z. (Jianhua Zhao), X.M. and L.Y. contributed to the figures, tables, and English translation of the paper; M.W. (Manxian Wang) provided the 3D model of the rotor. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key R&D Program of China (No. 2019YFB1703802).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw/processed data needed to reproduce these findings cannot be shared at this time because they are confidential.
Acknowledgments
Thanks to Enming Li and Changsen Yang for compiling the experimental data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shi, H. Aero-Engine Assembly Process Technology; Beihang University Press: Beijing, China, 2015. [Google Scholar]
- Zhang, Y.; Li, L.; Chen, J.; Shi, X.; Zhuo, S. Research Current Status and Prospect on Aero-Engine Assembly Process Technology. Aeronaut. Manuf. Technol. 2019, 62, 14–21. [Google Scholar]
- Bibel, G.D.; Ezell, R.M. An improved flange bolt-up procedure using experimentally determined elastic interaction coefficients. J. Press. Vessel. Technol. 1992, 114, 439. [Google Scholar] [CrossRef]
- Li, H.; Huang, J.; Zhang, Q.; Liu, Y.; Yao, J. The influence of Bolted-flange connection on the coaxial tolerance in accelerator centering assembling. J. Sichuan Univ. (Eng. Sci. Ed.) 2007, 22, 155–159. [Google Scholar]
- Xin, M. Characteristics of the Casing Is Installed in the Gas Side and Axial Forces Acting; Shenyang Aerospace University: Shenyang, China, 2016. [Google Scholar]
- Zhang, D. Analysis of the Influence and Control of Structural Characteristic Parameters Effect on Pivot Concentricity for Aero-engine. Aeronaut. Sci. Technol. 2015, 26, 22–26. [Google Scholar]
- Bai, S.; Zhai, X.; Ai, Y.; Ma, W. The Influence of Bolted Connection on the Coaxial Tolerance and Dynamic Analysis in Aero-engine Casing. Aeronaut. Sci. Technol. 2010, 35–37. [Google Scholar]
- Ye, Y. Study on Pre-tightening Force and Deformation of Bolted Connection with rabbet Considering Actual Contact; Dalian University of Technology: Dalian, China, 2020. [Google Scholar]
- Zhao, G.; Wang, Y.; Zhao, X.; Li, S.; Teng, G. Modeling and application test of contact stiffness of bolt connection structure of disk and drum. J. Aerosp. Power 2022, 37, 76–86. [Google Scholar]
- Brecher, C.; Fey, M.; BUmler, S. Damping models for machine tool components of linear axes. CIRP Ann.-Manuf. Technol. 2013, 62, 399–402. [Google Scholar] [CrossRef]
- Qin, Z.; Han, Q.; Chu, F. Bolt loosening at rotating joint interface and its influence on rotor dynamics. Eng. Fail. Anal. 2016, 59, 456–466. [Google Scholar] [CrossRef]
- Tsuji, H. Bolt Preload Control for Bolted Flange Joint. In Proceedings of the PVP2002 2002 ASME Pressure Vessels and Piping Conference, Vancouver, BC, Canada, 5–9 August 2002; pp. 163–170. [Google Scholar]
- Kumakura, S.; Saito, K. Tightening Sequence for Bolted Flange Joint Assembly. In Proceedings of the ASME Pressure Vessels & Piping Conference, Cleveland, OH, USA, 20–24 July 2003. [Google Scholar]
- Shi, G.; Shi, Y.; Wang, Y. Comparison of tightening sequences of high strength bolts in end-plate connections. Sichuan Build. Sci. 2005, 31, 3. [Google Scholar]
- Takaki, T.; Fukuoka, T. Effective Bolting Up Procedure Using Finite Element Analysis and Elastic Interaction Coefficient Method. In Proceedings of the ASME/JSME 2004 Pressure Vessels and Piping Conference, San Diego, CA, USA, 25–29 July 2004. [Google Scholar]
- Chen, C.; Yang, G.; Chang, D.; Hong, J. Assembly Connection Design Orienting to Sealing Performance of Joint Surface. J. Xi’an Jiaotong Univ. 2012, 46, 9. [Google Scholar]
- Liu, F.; Zhao, L.; Mehmood, S.; Zhang, J.; Fei, B. A modified failure envelope method for failure prediction of multi-bolt composite joints. Compos. Sci. Technol. 2013, 83, 54–63. [Google Scholar] [CrossRef]
- Ingenieure, V.D. Systematic Calculation of High Duty Bolted Joints Joints with One Cylindrical Bolt; Oak Ridge National Lab.: Oak Ridge, TN, USA, 2003. [Google Scholar]
- CRC Press. Introduction to the Design and Behavior of Bolted Joints, 4th ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Ma, Y.; Liu, G.; Wei, J.; Li, C.; Liang, C. Improvement of Bolt Connection Stiffness Model Based on Finite Element Method. Modul. Mach. Tool Autom. Manuf. Tech. 2021, 45–48. [Google Scholar]
- Budynas, R.G.; Nisbett, K.J. Shigley’s Mechanical Engineering Design; McGraw-Hill Education (Asia): Singapore, 2014. [Google Scholar]
- Hu, J.W.; Leon, R.T.; Park, T. Mechanical modeling of bolted T-stub connections under cyclic loads Part I: Stiffness Modeling. J. Constr. Steel Res. 2011, 67, 1710–1718. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J. Contact of nominally flat surfaces. Proc. R. Soc. Lond. 1966, 295, 300–319. [Google Scholar]
- Huan, G. Analysis of Finite Element and Control of Preloading Force Based on the Bolt Connection Between the Key Missile Parts. Master’s Thesis, Xidian University, Xi’an, China, 2014. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).