Abstract
In order to find a suitable designer team for the collaborative design crowdsourcing task of a product, we consider the matching problem between collaborative design crowdsourcing task network graph and the designer network graph. Due to the difference in the nodes and edges of the two types of graphs, we propose a graph matching model based on a similar structure. The model first uses the Graph Convolutional Network to extract features of the graph structure to obtain the node-level embeddings. Secondly, an attention mechanism considering the differences in the importance of different nodes in the graph assigns different weights to different nodes to aggregate node-level embeddings into graph-level embeddings. Finally, the graph-level embeddings of the two graphs to be matched are input into a multi-layer fully connected neural network to obtain the similarity score of the graph pair after they are obtained from the concat operation. We compare our model with the basic model based on four evaluation metrics in two datasets. The experimental results show that our model can more accurately find graph pairs based on a similar structure. The crankshaft linkage mechanism produced by the enterprise is taken as an example to verify the practicality and applicability of our model and method.
1. Introduction
The traditional method of product innovation is to conduct market research first, then design new products according to market feedback, and finally produce new products according to market demand. However, this mode is high-cost and low-reward. With the continuous innovation of science and technology, the diversified development of market demand, and the increasing complexity of products, more and more companies are aware of the need to use social resources for the innovative development of new products in social manufacturing. Crowdsourcing mode [1] emerges as the times require. This kind of open product design mode can make full use of social manpower, software and hardware resources, shorten the product development cycle, and improve product design quality. Crowdsourcing tasks are generally selected and completed by individuals based on crowdsourcing platforms, but as the complexity of product design increases, multi-person collaborative design is needed, so as to achieve design results that are both partially and overall satisfactory. Therefore, how to find a suitable designer team has become a key problem that needs to be resolved.
To solve this problem, we describe the product design task under the crowdsourcing mode as a graph, which is called the collaborative design crowdsourcing task network graph. The nodes represent the tasks in the crowdsourcing design, and the edges represent the relationships between the tasks. The designer team is also described as a graph, called the designer network graph. The nodes represent the designers, and the edges represent the connections between the designers. Therefore, we can consider the matching problem between the collaborative design crowdsourcing task network graph and the designer network graph to find a suitable designer team. However, due to the difference in the nodes and edges of the two types of graphs, we can only consider graph matching based on graph structure similarity. The problem to be studied is transformed into a graph similarity matching problem [2,3]. Graph similarity matching takes similarity of the query graph as the query criterion. In the target graph dataset, all graphs or subgraphs that are similar to the query graph are searched.
On the basis of viewpoints mentioned above, we propose a graph matching model based on graph structure similarity to calculate the similarity score between the collaborative design crowdsourcing task network graph and the designer network graph in this paper. The model first uses the Graph Convolutional Network (GCN) to extract features of the graph structure to obtain the node-level embeddings. Secondly, an attention mechanism considering the differences in the importance of different nodes in the graph assigns different weights to different nodes to aggregate node-level embeddings into graph-level embeddings. Finally, the two graph vectors are input into a multilayer fully connected neural network for feature extraction after they are obtained from the concat operation, and the binary cross-entropy loss function is used to predict the similarity score of the graph pair. The main contributions of this paper are summarized as follows:
- We regard the graph similarity calculation problem as a learning problem, i.e., to learn a function based on GNN. When the structure of the two graphs is input, the function outputs the similarity score (between 0~1) of the two graphs;
- We construct sample labels to train the model. The construction method of the sample label is innovative;
- The improved model and the basic model in this paper are compared and tested based on the accuracy ratio, precision ratio, recall ratio, and AUC index on two real graph datasets to verify the effectiveness of the improved model;
- We conduct a case study to prove the practical application of the improved model.
The sections of this paper are organized as follows. Section 2 is the related work that introduces the literature review. Section 3 is related materials and methods to describe in detail the graph matching model based on the graph structure similarity proposed in this paper. In Section 4, we compare the improved model and the basic model based on four evaluation metrics in two graph datasets to perform experiments. Section 5 is the case study. Section 6 gives the conclusions.
2. Related Work
Graph similarity calculation is a calculation method to predict the similarity score between one pair of graphs, including classification and clustering of graphs [4], social group network similarity recognition [5], object recognition in computer vision [6], biomolecular similarity search [7,8], etc. In graph deep learning, the models for graph similarity calculation can generally be divided into two categories. These two types of models use the GCN to learn embeddings and use embeddings to calculate the similarity score of the graph pairs [9]. One is the graph embedding model. This type of model mainly encodes each graph directly into a vector representation and then calculates the similarity score between one pair of graphs by calculating the similarity of the vectors, avoiding the difficulty of direct calculation on the graph. For example, Ktena et al. used a GCN to learn graph embedding, input the obtained graph embedding into a fully connected layer, and trained the fully connected layer to calculate the similarity score of the graph pairs [10]. Although this method has high time efficiency for graph similarity calculation, it is easy to ignore a lot of node information in the graph, which makes the results less accurate. The other one is the graph matching model. This type of model encodes each node in the graph as a vector representation, which contains not only the state information of the node itself, but also the state information of neighboring nodes, and uses different interaction strategies to calculate the similarity score of the graph pairs. For example, Riba et al. used a GCN to obtain node-level embeddings for the graph and calculated the similarity score of the graph pairs by calculating the similarity of the node-level embeddings [11]. This method is more suitable for graph similarity calculation on small graphs. Since this method considers each node in the graph, it still has the problem of low time efficiency for the similarity calculation on large graphs. It only uses node-level embeddings for graph similarity calculation, making the results less comprehensive.
In addition, there are methods that combine graph embedding models and graph matching models to calculate the similarity scores of the graph pairs. Xu et al. first divided two graphs to be matched into a set of smaller subgraphs, used a network model that combined an attention mechanism with a Graph Neural Network (GNN) [12,13] to learn the node-level embeddings and graph-level embeddings of these subgraphs, and calculated the similarity score of the graph pairs by comprehensively considering node-level embedding similarity and graph-level embedding similarity between subgraphs [14]. Although this method comprehensively considers node-level embeddings and graph-level embeddings for graph similarity calculation, it performs well only on small graphs, and it is too complicated with a low time efficiency for large graphs. Li et al. first interacted the nodes in the two graphs with each other by introducing a cross-graph attention layer and then calculated the similarity of the graph pairs by calculating the similarity of the graph embeddings [15]. Compared with the methods mentioned above, although this method improves the performance of graph similarity calculation on large graphs, it still has the problem of a high computation cost. That is, since each cross-graph matching step requires the computation of the full attention matrices, this is expensive for large graphs. As the matching model operates on graph pairs, it cannot be directly used for indexing and searching through large graph databases. Bai et al. first used a GCN to obtain node-level embeddings and proposed a new attention mechanism to aggregate node-level embeddings into graph-level embeddings. Secondly, a Neural Tensor Network (NTN) [16] was used to calculate the similarity of two graph-level embeddings. When bypassing the NTN module, the node-level similarity could be directly calculated. That is, the similarity score of the graph pairs was calculated by comprehensively considering graph-level embedding similarity and node-level embedding similarity [17,18]. This method not only considers node-level embeddings and graph-level embeddings for graph similarity computation, but an attention mechanism is also added for node aggregation, making it perform better on large graphs compared to the methods mentioned above. In addition, it can handle graphs with node types but cannot process edge features. There are also methods that combine a GCN with traditional neural networks to calculate the similarity scores of the graph pair. For example, Xiu et al. used the Earth Mover Distance (EMD) to obtain the one-to-one mapping between nodes of two graphs at each stage and obtained the correlation matrix according to the node-level embeddings in the two graphs, and the correlation matrices of all stages were input into a convolutional neural network, and the similarity score of the graph pairs was predicted by minimizing the mean squared error [19]. Although this method does not have high time efficiency for graph similarity calculation on large graphs, it improves the accuracy of the calculation by using a small increase in complexity, so as to achieve a reasonable trade-off between accuracy and efficiency. Bai et al. used a GCN with different layers to construct multiple correlation matrices between nodes of two graphs and used the correlation matrices based on a convolutional neural network to predict the similarity scores of the graph pairs [20]. This method achieved the state-of-the-art performance on four real-world graph datasets compared to existing popular methods for graph similarity calculation, but it still has high computational complexity problems on large graphs.
3. Materials and Methods
Referring to the literature review and the proposed idea of problem-solving in this paper, we define an undirected and unweighted graph , where is a set of nodes and is a set of edges. represents the features of nodes, where is the number of nodes in graph (or ) and is the dimension of the node feature vectors. Our goal is to learn a function based on a GNN that takes the structure of two graphs as input and outputs the similarity score of the two graphs.
3.1. Materials
In this section, we introduce the related materials of our graph matching model based on graph structure similarity.
3.1.1. Graph Convolutional Network (GCN)
We use a GCN to obtain the node representations of the graphs. Traditional Convolutional Neural Networks (CNNs) [21] can only process Euclidean spatial data, such as images, text, and speech. As non-Euclidean spatial data, graph data do not satisfy translation invariance and cannot be studied using traditional CNNs. The GCN is a variant proposed on the basis of a CNN and graph embedding [22]. The main idea of the GCN is to generate the node representation in the graph by aggregating the characteristics of the node itself and the characteristics of its neighboring nodes and to use a fixed number of layers (each layer has a different weight value) to deal with cyclic interdependence in the architecture.
The GCN mainly includes two categories, one is frequency domain convolution [23], which mainly uses Fourier transform to achieve convolution. The Fourier transform can not only be used to separate noise points from normal points but also to speed up convolution. The other one is spatial convolution [23]; the core is to aggregate neighbor node information. The general framework is the Message Passing Neural Network (MPNN) [11]. The MPNN mainly includes two phases: a message passing phase and a readout phase. In the message passing phase, the state information of the node is aggregated and updated. In the readout phase, the feature vector of the whole graph is read out.
3.1.2. Graph Embedding
The GCN is usually used to map the graph data, i.e., convert a high-dimensional dense matrix into a low-dimensional dense vector. This process is usually called graph embedding. It is also called network embedding or graph representation learning. It can solve the problem that graph data are difficult to efficiently input into machine learning algorithms. Graph embedding mainly includes node-level embeddings and graph-level embeddings. Node-level embedding means that each node in the graph is encoded as a vector. In the graph similarity matching problem, node-level embedding is suitable for calculating node similarity. Graph-level embedding means that the whole graph is encoded as a vector and is often used to predict, compare, or visualize the whole graph at the graph level. In the graph similarity matching problem, graph-level embeddings are suitable for the similarity calculation of graph pairs. Figure 1 is the process of graph data being represented as graph embedding. Graph data are represented as vectors, and the dimension of each vector is . Therefore, the graph embedding is a vector, and each row of the graph embedding is a node-level embedding, which represents the state information of the node in the graph.
Figure 1.
Graph embedding process.
For node-level embedding learning, there are currently several types of methods, including matrix factorization-based methods (NetMF [24]), skip-gram-based methods (DeepWalk [25], Node2Vec [26], LINE [27]), autoencoder-based methods (SDNE [28]), and neighbor aggregation-based methods (GCN, GraphSAGE [29]). Among them, the most popular method is based on neighbor aggregation. In this method, the GCN is the most widely used.
For graph-level embedding learning, the classic methods such as Graph2vec [30], which also use the skip-gram idea [31], encode the whole graph into a vector representation. In addition, methods such as Patchy-san [32], sub2vec (embed subgraphs) [33], and Deep WL kernels are also commonly used for learning graph-level embeddings.
Node-level embeddings can be transformed into graph-level embeddings through aggregation. The aggregation method is usually simple average aggregation, weighted average aggregation, and maximum aggregation, where the simple average and weighted average aggregation methods are also called “sum-based” methods [10].
The current method of aggregating nodes is either “sum-based” methods or maximum aggregation. Although these aggregation methods consider the importance of nodes, they do not consider the differences in the importance of different nodes in a graph, for example, the GMN model [15]. Aiming at this problem, we propose an attention mechanism that assigns different weights to different nodes in aggregate node-level embeddings.
3.1.3. Graph Edit Distance (GED)
The Maximum Common Subgraph (MCS) [34] and the GED [35] are usually the criteria for measuring the similarity of graph structure, and the MCS is equivalent to the GED under the same cost function. Therefore, in this paper, we use the GED to measure the structural similarity between two graphs.
The GED that measures the similarity between two graphs is defined as the smallest editing operation for mutual transformation between two graphs. The GED is the operation required to transform graph into graph including an edge insertion or deletion in the graph, an isolated node insertion or deletion in the graph, and the label modification of the node or edge. However, the calculation of the GED is usually regarded as an NP-Hard problem, so we cannot calculate the exact value of the GED every time. Sometimes we can only use some heuristic algorithms to calculate the approximate value of the GED.
3.2. Methods
We establish a graph matching model based on graph structure similarity. Aiming at the problem that the basic model (gcn-pool) does not consider the difference of the importance of different nodes, we propose an attention mechanism to aggregate nodes to improve the basic model, called gcn-attention (gcn-attn). Gcn-attn is mainly composed of 3 parts: (1) The GCN obtains the feature vector of the graph structure, i.e., GCN extracts node-level embeddings based on the graph structure; (2) An attention mechanism aggregates node-level embeddings into graph-level embeddings; (3) The two graph vectors are input into the multilayer fully connected neural network for feature extraction to predict the similarity score. The framework of the graph matching model is shown in Figure 2.
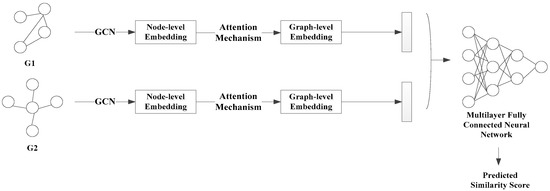
Figure 2.
The framework of the graph matching model.
The difference between the basic model and the improved model is the process of aggregating node-level embeddings into graph-level embeddings. The aggregation method is average aggregation or maximum aggregation in the basic model. The aggregation method is to use the attention mechanism for aggregation in the improved model. The detailed formula description of each part is as follows.
3.2.1. Node Embedding
We use 2 identical GCNs to obtain the node representations of the two graphs independently and in parallel, and the model parameters of each layer are not shared. The GCN updates the node state of the whole graph referring to Equation (1):
where is the activation function such as , is the adjacency matrix of graph . denotes the adjacency matrix with an inserted self-loop. The degree matrix is a diagonal matrix, . is the normalized adjacency matrix. is equivalent to a linear transformation for all node embeddings in the layer. Each node is left multiplied by the adjacency matrix to show that the features of the nodes are the result of adding the feature of the neighbor node, where is a learnable mapping matrix, and is the dimension of the embedding for .
The node-level embeddings in the graph can be described as Equation (2):
where the node-level embedding of node is equivalent to the row in the whole graph embedding . represents the neighbor node of node . represents the number of neighbor nodes of node . represents bias. Intuitively, the graph convolution operation aggregates the first-order neighbor features of the node.
3.2.2. Attention Mechanism
In the step of aggregating nodes, we consider the differences in the importance of different nodes and propose an attention mechanism. The principle of the attention mechanism is briefly described as follows: the average value of the states of all nodes in the graph is calculated, and the inner product of the average value and the state of each node in the graph is used as the attention weight. The attention weight is used to aggregate node-level embeddings into graph-level embeddings.
Firstly, the averaging method is used to obtain the representation characteristics of the information of the whole graph referring to Equation (3):
where is a learnable weight matrix.
Secondly, the result of the inner product of the whole graph information and the node information is used as the attention coefficient of each node referring to Equation (4):
where is a sigmoid activation function, ensures that the attention coefficient is between 0 and 1.
Finally, after obtaining the attention weight of each node, the graph-level embedding is described as Equation (5):
where represents the graph-level vector of the whole graph.
3.2.3. Loss Function
After obtaining the graph-level embeddings, the two graph-level embeddings are input into a multilayer fully connected neural network to obtain the similarity score of the graph pairs after performing the concat operation. In order to enable the model to accurately calculate the similarity score of the graph pairs, we need to train the model. We construct sample labels for training, and the specific construction method is as follows: we randomly split 80% and 20% of all graphs in the dataset as training set and testing set, respectively. The data are generated by sampling and are controlled by the sample parameter. For example, sample = 50 means that 50 graphs are randomly selected to match each graph in the training set to form a training sample.
In order to train the model, firstly, the GED function in the Pytorch framework is used to calculate the GED of the graph pairs in the training samples of the dataset. Secondly, the median function in the framework is directly called to obtain the median of the GED of the graph pairs, and the median is used as the threshold for classification. If the GED is greater than the threshold, it is classified as 0, which means that the two graphs are not similar; if the GED is less than the threshold, it is classified as 1, which means that the two graphs are similar. Therefore, it can be regarded as a binary classification problem.
We use the binary cross-entropy loss function BCELoss to predict the similarity score of the graph pairs. This function is used to calculate the binary cross entropy loss between the output value (predicted value) of the graph matching model and the true value. It can be used directly by calling the F.binary_cross_entropy in the Pytorch framework, and the function form is simplified referring to Equation (6):
where is the probability that the model predicts that the two graphs are similar and the value of is between 0 and 1. is the constructed sample label. If the two graphs are similar in the training sample, the value of is 1, otherwise the value of is 0.
3.2.4. The Complexity Analysis
The model proposed in this paper is used to predict whether graph pairs are similar. The analysis of time complexity mainly includes two parts: (1) node-level embedding and graph-level embedding calculation steps; (2) graph-pair similarity score calculation steps.
In the simplest case, we only visit each edge once and perform two calculation operations on the two nodes it connects for the embedding model, so that the time complexity of the process of forming local topological features is usually , where is the number of edges in the larger graph in the two graphs [14]. For the node-level embedding and graph-level embedding calculation steps, the time complexity is . For calculating the graph pair similarity score, since the two graph-level vectors are input into a multilayer fully connected neural network after the concat operation, no time complexity analysis is performed in this step. Only the vector dimension changes from to . To sum up, the time complexity of the whole model is .
4. Experiments
In this section, we mainly compare the basic model (gcn-pool) and the improved model (gcn-attn) based on four evaluation metrics on two graph datasets to verify the advancement and effectiveness of the improved model.
4.1. Datasets
We perform experiments on two real graph datasets. These two datasets have been applied to the graph similarity matching problem many times to verify the effectiveness of the method. The specific information is shown in Table 1.

Table 1.
Introduction to datasets.
4.2. Parameter Settings
For the model construction, we set the number of GCN layers to 3, and use the ReLU as the activation function. For the initial node representations, we adopt a one-hot encoding strategy for the AIDS dataset to reflect the node type and a constant encoding strategy for the LINUX dataset because the nodes in the LINUX dataset have no labels. The output dimensions of the first layer, second layer, and third layer of the GCN are set to 64, 32, and 16, respectively. We use five fully connected layers to build a fully connected neural network, which are a linear combination layer with 96 inputs and 256 outputs; a nonlinear activation layer with ReLU as the activation function; a linear combination layer with 256 inputs and 256 outputs; a linear combination layer with 256 inputs and 16 outputs; and a linear combination layer with 16 inputs and 1 output to predict the graph pair similarity score. The details are shown in Table 2.

Table 2.
Construction of the graph matching model.
According to Table 2, firstly, the graph node feature extraction is performed based on the graph structure through the three-layer GCN. Secondly, each node in the graph is aggregated into a composite vector of the graph. Finally, the torch.nn.Sequential class in Pytorch is used to build a fully connected neural network. The graph vectors of the two graphs are input into the fully connected neural network after the concat operation to calculate the similarity score of the graph pairs.
All experiments are run on a PC, using Nvidia GeForce GTX 1660 Super GPU, 16 G, RAM. The excellent Pytorch Geometric framework to implement our model in Python is used. As for training, we set the batch size to 64, dropout to 0.2, use the Adam algorithm for optimization, and set the initial learning rate to 0.01. We set the number of iterations to 100 and select the best model based on the lowest validation loss.
4.3. Evaluation Metrics
For the binary classification problem, the commonly used evaluation metrics include the accuracy ratio, precision ratio, recall ratio, and AUC index. Before introducing these metrics, some definitions are described. The prediction results of the binary classification problem include four categories according to the situation: True Positive (TP): the predicted value is 1, the true value is 1; False Positive (FP): the predicted value is 1, the true value is 0; True Negative (TN): the predicted value is 0, the true value is 0; False Negative (FN): the predicted value is 0, the true value is 1. Thus the total number of positive samples T = TP + FN, and the total number of negative samples F = FP + TN, as shown in Table 3.

Table 3.
Prediction results of the binary classification problem.
The accuracy ratio is the ratio of the number of samples that the predicted value of the model is the same as the true value to the total number of samples, referring to Equation (7):
There is a problem with using the accuracy ratio to evaluate algorithms, i.e., when there are extremely biased data in the dataset, the accuracy ratio cannot objectively evaluate the pros and cons of the algorithm.
The precision ratio is the ratio of the number of true positive samples of the model to the number of true samples, referring to Equation (8):
The recall ratio is the ratio of the number of true positive samples to the total number of all positive samples, referring to Equation (9):
The precision ratio and the recall ratio are trade-offs, i.e., the higher the precision ratio, the lower the recall ratio. In some cases, these two metrics need to be taken into account at the same time, so the AUC index is proposed.
The AUC index represents the area enclosed by the ROC (Receiver Operating Characteristic) curve, which is used to comprehensively evaluate the accuracy ratio and the recall ratio. The reason for using the AUC value as the evaluation standard is that in many cases the ROC curve cannot clearly indicate which classifier performs better, and the AUC value range is generally between 0.5~1, and the classification effect corresponding to a larger AUC value is better.
4.4. Results
We run the basic model (gcn-pool) and the improved model (gcn-attn) 100 times based on the accuracy ratio, precision ratio, recall ratio as well as the AUC index on the AIDS and LINUX datasets. The results of 100 calculations for each metric are averaged to obtain a comparison of the average results of each metric of the two models on the AIDS and LINUX datasets, as shown in Table 4 and Table 5.

Table 4.
Average results of four evaluation metrics based on the AIDS dataset.

Table 5.
Average results of four evaluation metrics based on the LINUX dataset.
It can be seen from the experimental data that in the AIDS dataset, compared to the basic model (gcn-pool), the accuracy ratio of the improved model (gcn-attn) has increased by 10.7%, the precision ratio has increased by 17.6%, the recall ratio has increased by 8.4%, and the AUC index has increased by 11.5%.
In the LINUX dataset, compared to the basic model (gcn-pool), the accuracy ratio of the improved model (gcn-attn) has increased by 8.9%, the precision ratio has increased by 13.1%, the recall ratio has increased by 7.4%, and the AUC index has increased by 11.5%.
In order to more intuitively see the comparison effect of the two models based on the four evaluation metrics, a curve comparison chart is shown in Figure 3.
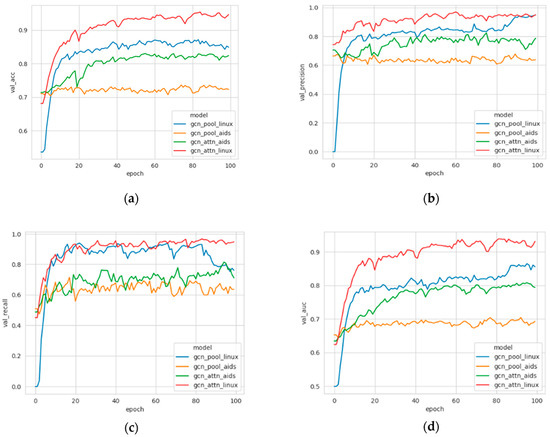
Figure 3.
The curve comparison chart of the two models based on four evaluation metrics for the AIDS and LINUX datasets. (a) Accuracy ratio, (b) Precision ratio, (c) Recall ratio, (d) AUC index.
It can be seen from the curve comparison chart that the accuracy ratio, the precision ratio, the recall ratio, and the AUC index of the improved model (gcn-attn) are higher than those of the basic model (gcn-pool) for both the AIDS dataset and the LINUX dataset. The larger these evaluation metrics, the better the effect of the model.
Therefore, it can be concluded that the gcn-attn model is more advanced and effective than the gcn-pool model regarding the graph matching problem based on graph structure similarity, i.e., the improved model is able to more accurately find graph pairs based on a similar structure.
5. Case Study
In order to verify that the model proposed in this paper can be accurately applied to the matching problem between the collaborative design crowdsourcing task network graph and the designer network graph, we conduct a case study. At the same time, the Pytorch-Geometric framework is used for visualization.
5.1. Case Description
We take the crankshaft linkage mechanism produced by one enterprise as an example, where the mechanical analysis of the crankshaft linkage mechanism requires a design team. We first use a graph to describe the tasks involved in the mechanical analysis of the crankshaft linkage mechanism, then establish a designer community candidate set with several designer teams, and finally use the method proposed in this paper to find the most suitable designer team.
5.2. Use of Method Proposed
The mechanical analysis of the crankshaft linkage mechanism includes force analysis (including stress, bearing force, and crankshaft torque analyses), material analysis (including toughness and strength analyses), and motion analysis [36]. After the nine tasks are numbered, the collaborative design crowdsourcing task network graph is constructed according to their dependencies, as shown in Figure 4.
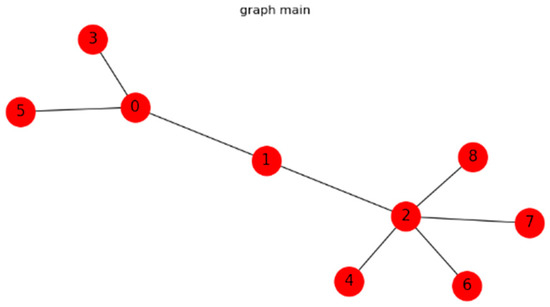
Figure 4.
The collaborative design crowdsourcing task network graph.
In order to construct the designer community candidate set, five WeChat groups are studied. The members of these five WeChat groups are all designers who joined the crowdsourcing design. By collecting the conversational communication data within the WeChat group as the analysis text and numbering the designers, the data are preprocessed into a network structure, so as to construct the designer community candidate set that includes five designer network graphs, as shown in Figure 5.
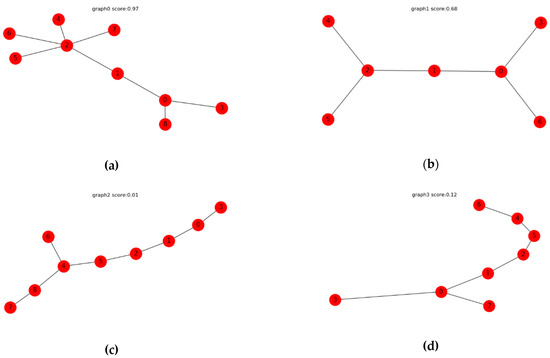
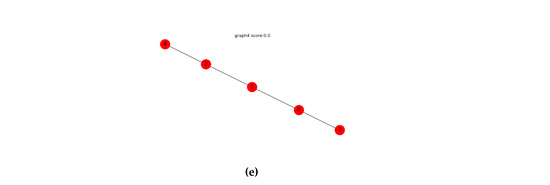
Figure 5.
The designer community candidate set. (a) Designer network graph 1, (b) Designer network graph 2, (c) Designer network graph 3, (d) Designer network graph 4, (e) Designer network graph 5.
As shown in the framework of the graph matching model in Figure 2, we take the collaborative design crowdsourcing task network graph in Figure 4 is as . Five designer network graphs in Figure 5 are successively taken as . and are input into the graph matching model independently and in parallel. Since the graph matching model has been trained, it already has the best model parameters for calculating the similarity score of the graph pairs. Therefore, after and are input into the model, two identical GCNs first extract the node-level embeddings of and based on graph structure in parallel. Secondly, the node-level embedding are aggregated into graph-level embedding by the attention mechanism proposed in this paper. Finally, the similarity score between and is output through the calculation of the multi-layer fully connected neural network after the two graph-level embeddings are obtained using concat operation.
In summary, we take the collaborative design crowdsourcing task network graph in Figure 4 as the query graph, the designer community candidate set in Figure 5 as the target graph set, and use the improved graph matching model in this paper to find the target graph most similar in structure to the query graph from the target graph set.
5.3. Case Results and Discussion
It can be seen that the value above each graph in the designer community candidate set represents the matching similarity score between the collaborative design crowdsourcing task network graph in Figure 4 and the designer network graph in Figure 5. The larger the value, the more similar the two graphs are based on the graph structure. The matching similarity scores between the designer network graph and the collaborative design crowdsourcing task network graph are 0.97, 0.68, 0.01, 0.12, and 0.00. Therefore, the designer network graph 1 has the highest similarity to the collaborative design crowdsourcing network graph, so we have found the most suitable designer team for the collaborative design crowdsourcing task.
The case study describes the mechanical analysis of the crankshaft linkage mechanism as a collaborative design crowdsourcing task network graph and uses this graph as a query graph to find the designer network graph based on similar graph structure, which is actually a graph similarity matching problem. The traditional acceleration strategies of graph similarity algorithms are all at the cost of increased memory consumption, i.e., space is exchanged for time, and the efficiency is low. Therefore, the graph matching model combined with GNN proposed in this paper is more innovative. The experimental data and case results also reflect the rationality and practicality of the method and model in this paper. On the basis of finding a suitable designer team, the relevant indicators of tasks and designers can be considered for task assignment in the future, thus making up for the problem of node similarity not considered in graph matching in this paper.
6. Conclusions
Graph structures are widely used in various fields to describe complex relationships between things, such as the World Wide Web, social networks, protein interaction networks, chemical molecular structures, power grids, and road networks. With the development of these fields and the increase in data, the size and number of graphs are also increasing. How to perform efficient graph matching operations on a large number of accumulated graphs has become a new research goal of academia and industry. As a research method of artificial intelligence, deep learning is changing the world at an unprecedented speed, and it plays an important role in the field of education, image recognition, speech technology, and unmanned driving.
The increase in the scale and complexity of product design often involves tasks that require multiple people to design collaboratively, so it is necessary to find a suitable designer team. Aiming at this problem, we propose a graph similarity matching method to find a designer team suitable for the collaborative design crowdsourcing task of the product. Compared with the traditional method, this paper introduces the matching problem between the collaborative design crowdsourcing task and the designer team into the field of graph theory research and combines deep learning knowledge to make the research method more innovative and researchable. The model and method in this paper are suitable for matching between undirected and unweighted network graphs based on a similar graph structure, such as social relationship query, social security analysis, recommendation system, network attack detection, and biological data analysis.
Although the model and method proposed in this paper are feasible and practical, there are still some shortcomings. The experiments in Section 3 are performed on the public AIDS dataset and the LINUX dataset, and the graph data in these two datasets are small in scale. The graph matching model proposed in this paper performs well on small-scale graph data, but still does not perform well on large-scale graph data. The improved graph matching model in this paper is simple. In the future, we will design a more complex graph matching model for large-scale graph matching.
Author Contributions
Conceptualization, supervision, project administration, funding acquisition and methodology, D.L.; software, formal analysis, data curation, writing—original draft preparation, writing—review and editing, and visualization, D.W.; investigation and resources, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 71961005, and Natural Science Foundation of Guangxi Zhuang Autonomous Region, grant number 2020GXNSFAA297024.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author Danling Wu (1020190643@glut.edu.cn) upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Qiu, D.Y. Product Design Task Recommendation Based on Crowdsourcing Mode. J. Mach. Des. 2017, 34, 48–52. [Google Scholar]
- Xiang, Y.Z.; Tan, J.X.; Han, J.S.; Shi, H. Survey of Graph Matching Algorithms. Comput. Sci. 2018, 45, 27–45. [Google Scholar]
- Yu, J.; Liu, Y.B.; Zhang, Y.; Liu, M.Y. Survey on Large-scale Graph Pattern Matching. J. Comput. Res. Dev. 2015, 52, 391–409. [Google Scholar]
- Neuhaus, M.; Bunke, H. Edit Distance-based Kernel Functions for Structural Pattern Classification. Pattern Recognit. 2006, 39, 1852–1863. [Google Scholar] [CrossRef]
- Ogaard, K.; Roy, H.; Kase, S.; Nagi, R.; Sambhoos, K.; Sudit, M. Discovering Patterns in Social Networks with Graph Matching Algorithms. In Proceedings of the 6th International Conference on Social Computing, Behavioral-Cultural Modeling, and Prediction, Washington, DC, USA, 2–5 April 2013. [Google Scholar]
- Aghasi, A.; Romberg, J. Convex Cardinal Shape Composition and Object Recognition in Computer Vision. In Proceedings of the 49th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 8–11 November 2015. [Google Scholar]
- Suzuki, H.; Kawabata, T.; Nakamura, H. Omokage Search: Shape Similarity Search Service for Biomolecular Structures in Both the PDB and EMDB. Bioinformatics 2016, 4, 619–620. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Mceachin, R.C.; Santos, C.; States, D.J.; Patel, J.M. Saga: A Subgraph Matching Tool for Biological Graphs. Bioinformatics 2007, 23, 232–239. [Google Scholar] [CrossRef]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Ktena, S.I.; Parisot, S.; Ferrante, E. Distance Metric Learning using Graph Convolutional Networks: Application to Functional Brain Networks. In Proceedings of the 20th International Conference on Medical Image Computing and Computer-Assisted Intervention, Quebec City, QC, Canada, 11–13 September 2017. [Google Scholar]
- Riba, P.; Fischer, A.; Llado’s, J. Learning Graph Distances with Message Passing Neural Networks. In Proceedings of the 24th International Conference on Pattern Recognition, Beijing, China, 20–24 August 2018. [Google Scholar]
- William, L.H. Graph Representation Learning. Synth. Lect. Artif. Intell. Mach. Learn. 2020, 14, 1–159. [Google Scholar]
- Zhou, J.; Cui, G.Q.; Hu, S.D. Graph Neural Networks: A Review of Methods and Applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Xu, H.; Duan, Z.; Feng, J. Graph Partitioning and Graph Neural Network based Hierarchical Graph Matching for Graph Similarity Computation. Neurocomputing 2020, 439, 348–362. [Google Scholar] [CrossRef]
- Li, Y.; Gu, C.; Dullien, T. Graph Matching Networks for Learning the Similarity of Graph Structured Objects. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019. [Google Scholar]
- Socher, R.; Chen, D.; Manning, C.D. Reasoning with Neural Tensor Networks for Knowledge Base Completion. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe Nevada, CA, USA, 5–10 December 2013. [Google Scholar]
- Bai, Y.; Ding, H.; Bian, S. SimGNN: A Neural Network Approach to Fast Graph Similarity Computation. In Proceedings of the 12th ACM International Conference on Web Search and Data Mining, Melbourne, Australia, 11–15 February 2019. [Google Scholar]
- Bai, Y.; Ding, H.; Sun, Y. Convolutional Set Matching for Graph Similarity. In Proceedings of the 32th Conference and Workshop on Neural Information Processing, Montreal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Xiu., H.; Yan, X.; Wang, X. Hierarchical Graph Matching Network for Graph Similarity Computation. arXiv 2020. [Google Scholar] [CrossRef]
- Bai, Y.; Ding, H.; Sun, Y. Learning-based Efficient Graph Similarity Computation via Multi-Scale Convolutional Set Matching. In Proceedings of the 32th AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Kim, P. Convolutional Neural Network. In MATLAB Deep Learning; George, R., Ed.; Apress: Berkeley, CA, USA, 2017; pp. 121–147. [Google Scholar]
- Goyal, P.; Ferrara, E. Graph Embedding Techniques, Applications, and Performance: A Survey. Knowl-Based Syst. 2018, 151, 78–94. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.B.; Cen, K.T.; Huang, J.J. A Survey on Graph Convolutional Neural Network. Chin. J. Comput. 2020, 43, 755–780. [Google Scholar]
- Qiu, J.Z.; Dong, Y.X.; Ma, H.; Li, J.; Wang, K.S.; Tang, J. Network Embedding as Matrix Factorization: Unifying Deepwalk, Line, Pte, and Node2vec. In Proceedings of the 11th ACM International Conference on Web Search and Data Mining, New York, NY, USA, 5–9 February 2018. [Google Scholar]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online Learning of Social Representations. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014. [Google Scholar]
- Grover, A.; Leskovec, J. Node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Jian, T.; Meng, Q.; Wang, M. Line: Large-scale Information Network Embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015. [Google Scholar]
- Wang, D.; Peng, C.; Zhu, W. Structural Deep Network Embedding. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive Representation Learning on Large Graphs. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Narayanan, A.; Chandramohan, M.; Venkatesan, R. Graph2vec: Learning Distributed Representations of Graphs. In Proceedings of the 13th International Workshop on Mining and Learning with Graphs, Halifax, NS, Canada, 14 August 2017. [Google Scholar]
- Lazaridou, A.; Pham, N.T.; Baroni, M. Combining Language and Vision with a Multimodal Skip-gram Model. In Proceedings of the 2015 Conference of the North American Chapter of the Association for Computational Linguistics, Denver, CO, USA, 31 May–5 June 2015. [Google Scholar]
- Niepert, M.; Ahmed, M.; Kutzkov, K. Learning Convolutional Neural Networks for Graphs. In Proceedings of the 33rd International Conference on International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Adhikari, B.; Zhang, Y.; Ramakrishnan, N. Sub2Vec: Feature Learning for Subgraphs. In Proceedings of the 22nd Pacific-Asia Conference on Knowledge Discovery and Data Mining, Melbourne, Australia, 15–18 May 2018. [Google Scholar]
- Horst, B.; Kim, S. A Graph Distance Metric Based on the Maximal Common Subgraph. Pattern Recognit. Lett. 1998, 19, 255–259. [Google Scholar]
- Bunke, H. What is the distance between graphs. Bull. EATCS 1983, 20, 35–39. [Google Scholar]
- Chen, Y.; Zuo, L.; Niu, Y. Task Assignment Method of Product Development Based on Knowledge Similarity. J. Comput. Appl. 2019, 39, 323–329. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).