Study on Plant Crushing and Soil Throwing Performance of Bionic Rotary Blades in Cyperus esculentus Harvesting
Abstract
:1. Introduction
2. Materials and Methods
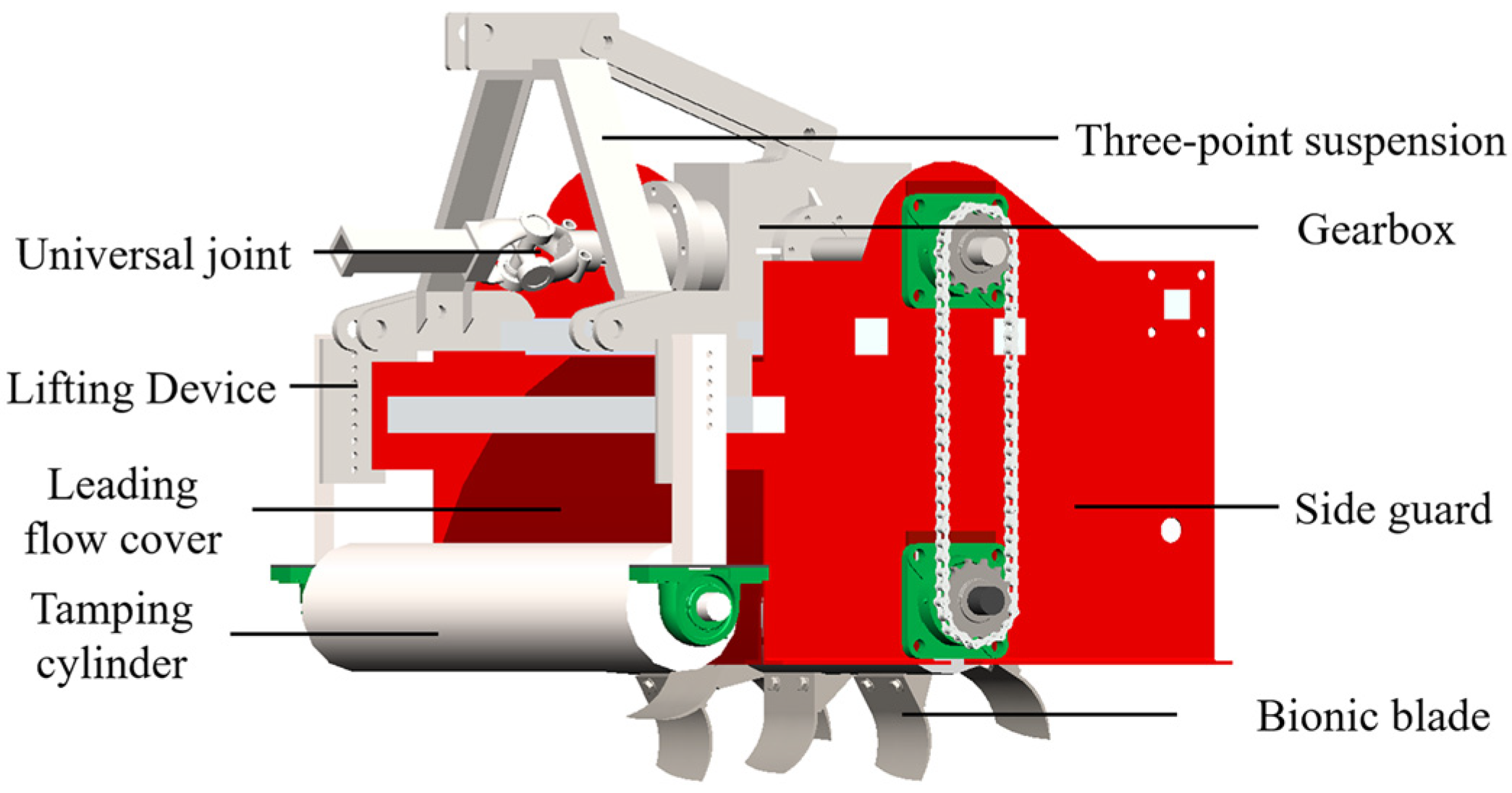
2.1. General Structure
2.2. Design and Analysis of Bionic Rotary Blade
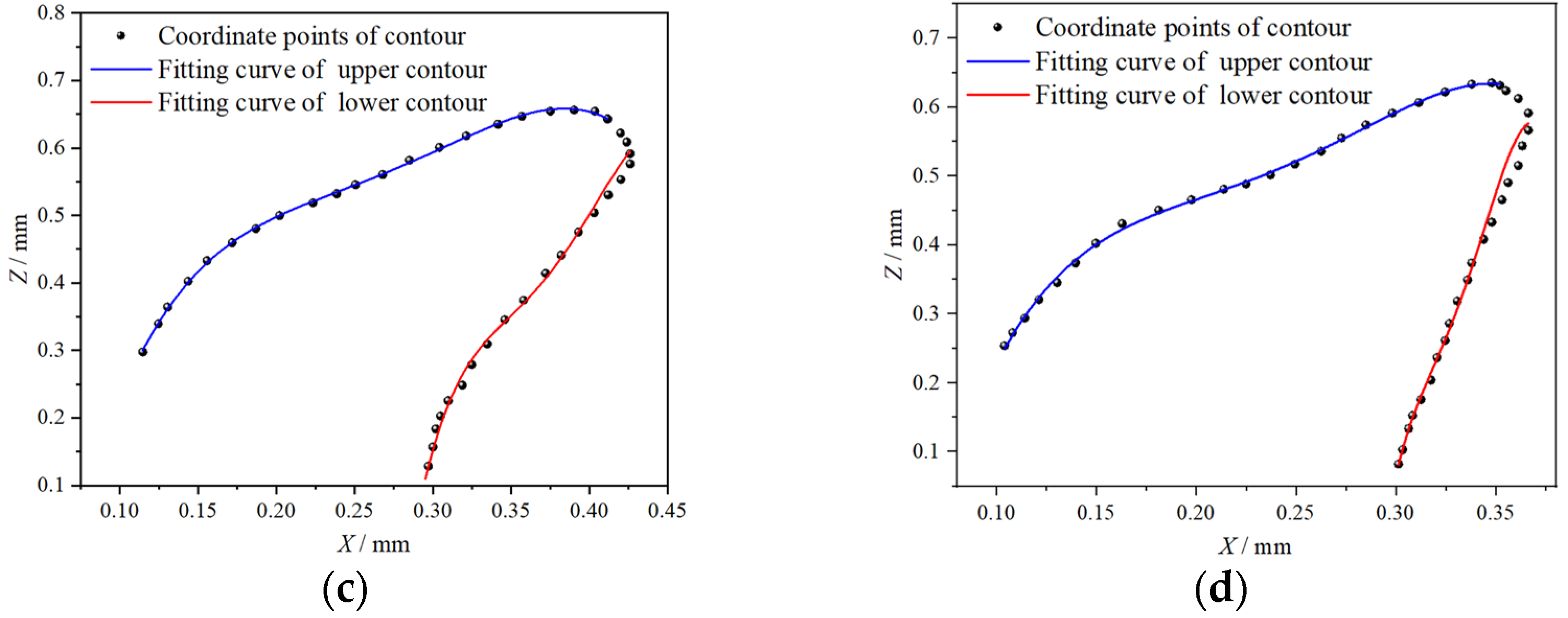
2.2.1. Excavation Edge Contour Curve Fitting of Bionic Rotary Blade
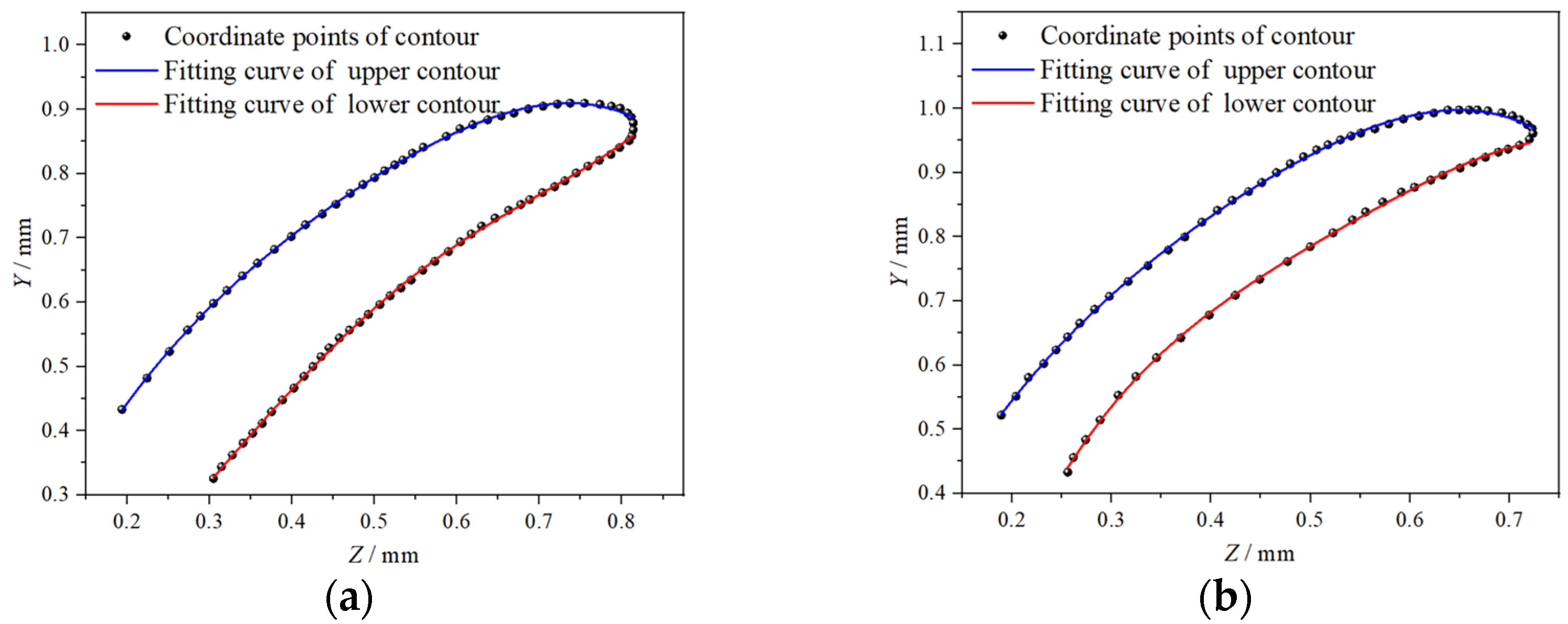
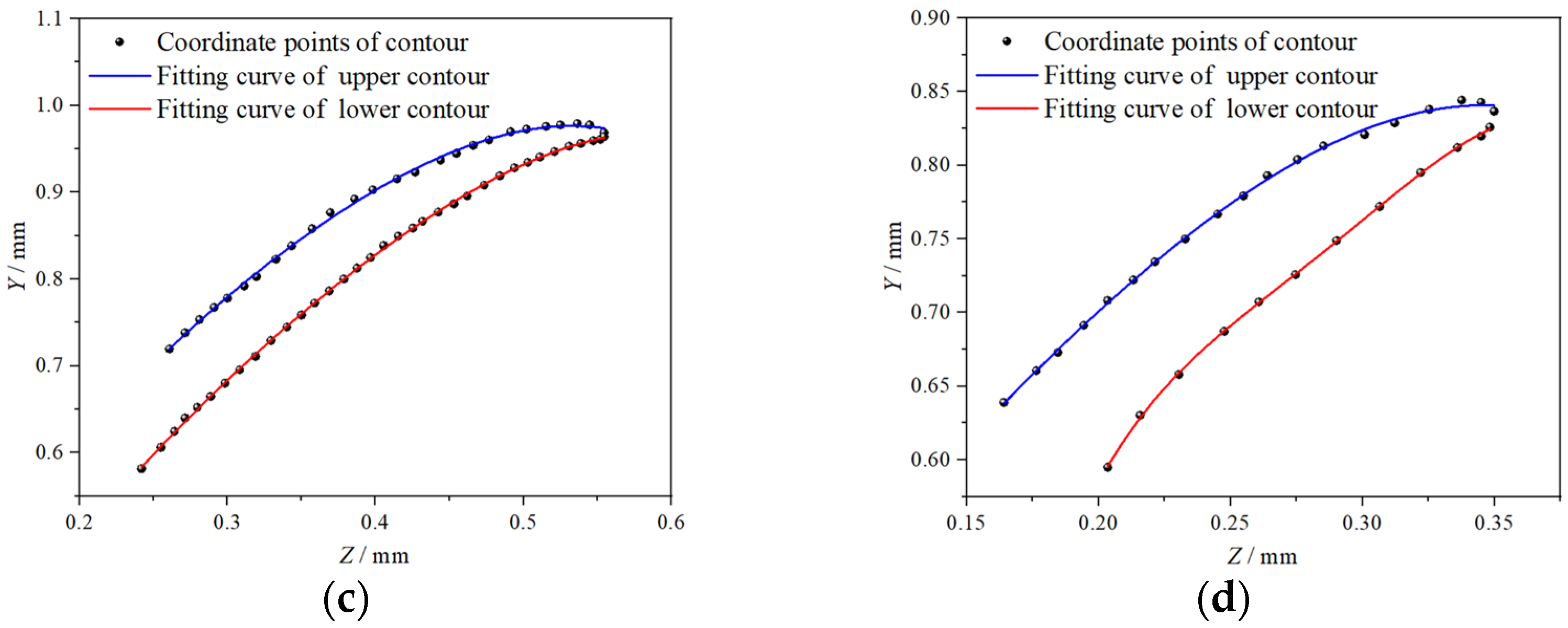
2.2.2. Excavation Surface Contour Curve Fitting of Bionic Rotary Blade
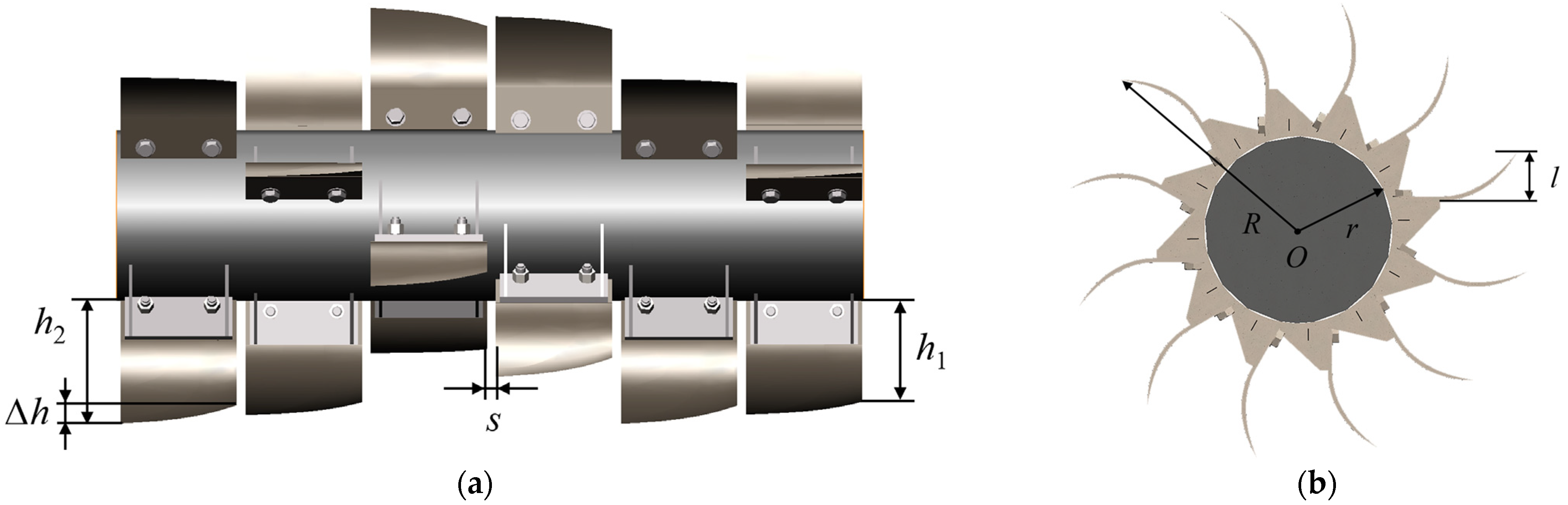
2.2.3. Parameter Design of Bionic Rotary Blade
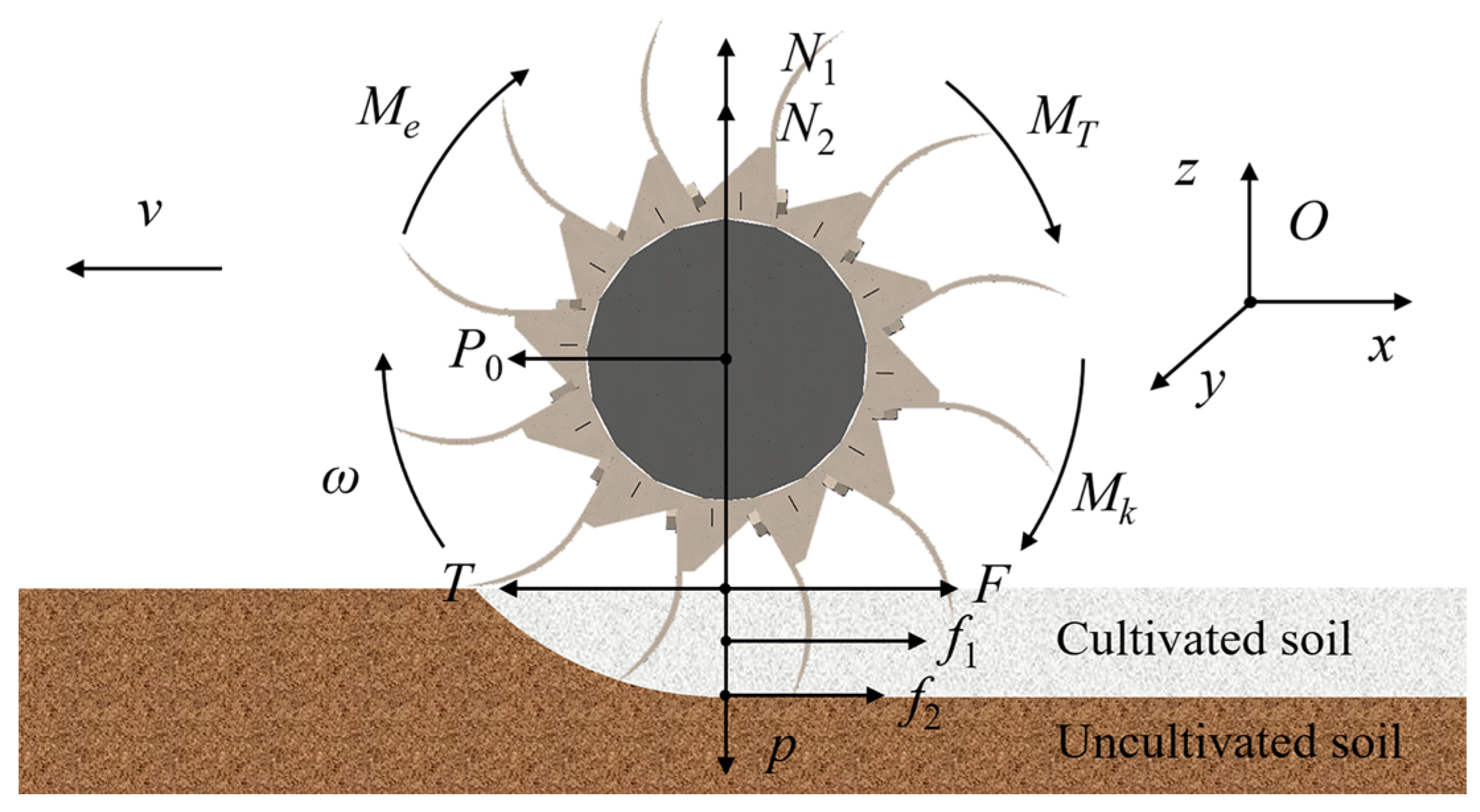
2.3. Cutting Mechanics Analysis
2.3.1. Force Analysis of the Soil Unit
2.3.2. Critical Conditions for Shear Damage in Cyperus esculentus Plants
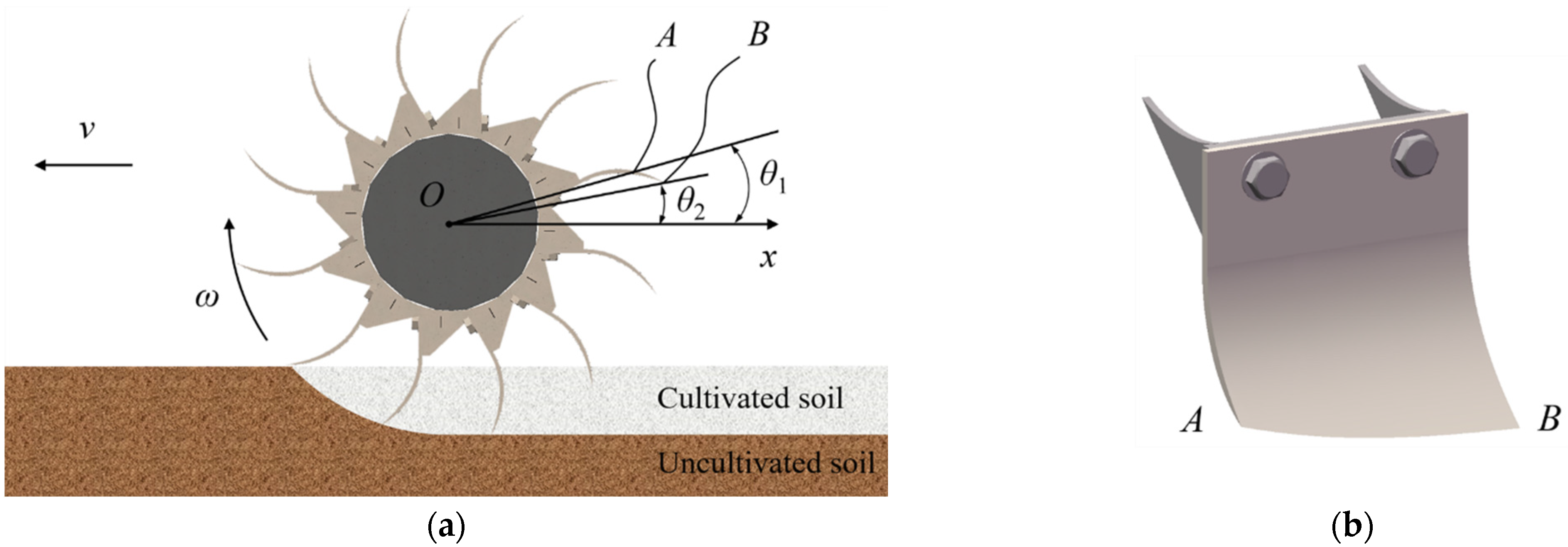
2.4. Kinematic Analysis
2.4.1. Kinematic Analysis of Bionic Rotary Blade
2.4.2. Kinematic Analysis of the Soil Unit
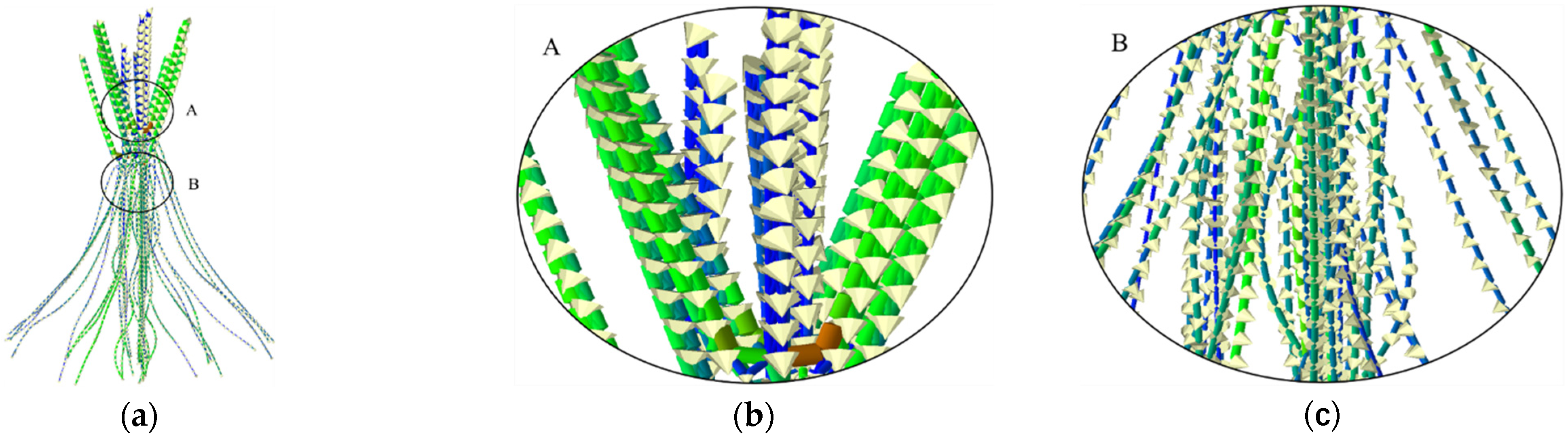
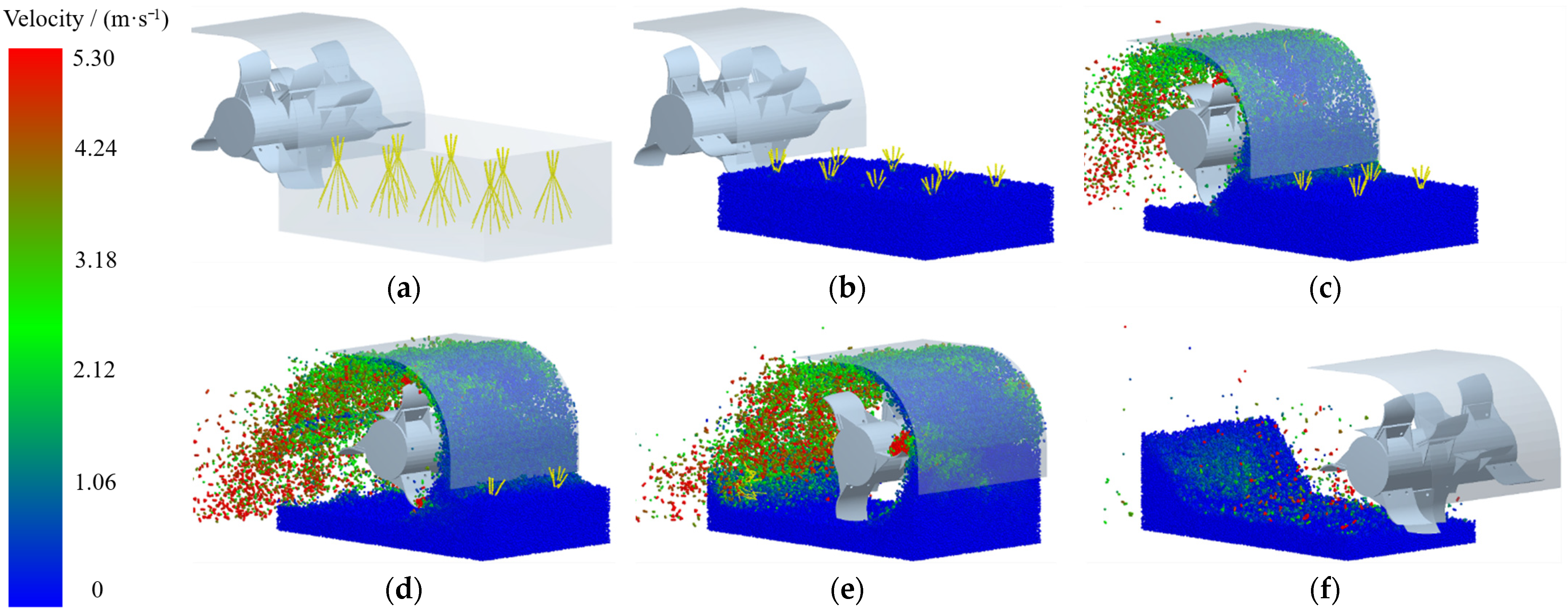
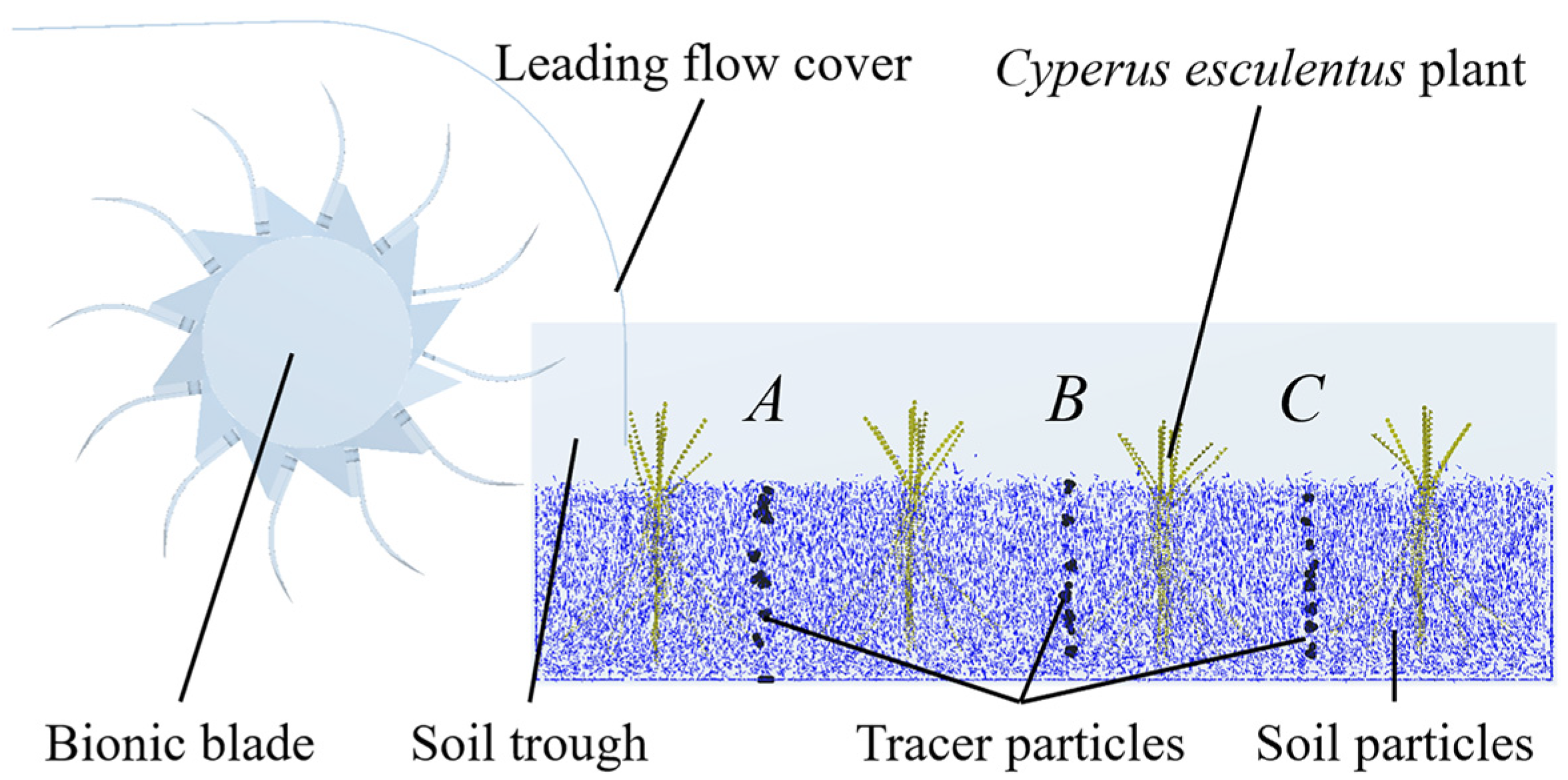
2.5. Discrete Element Simulation
2.6. Evaluation Index of Cyperus esculentus Harvesting
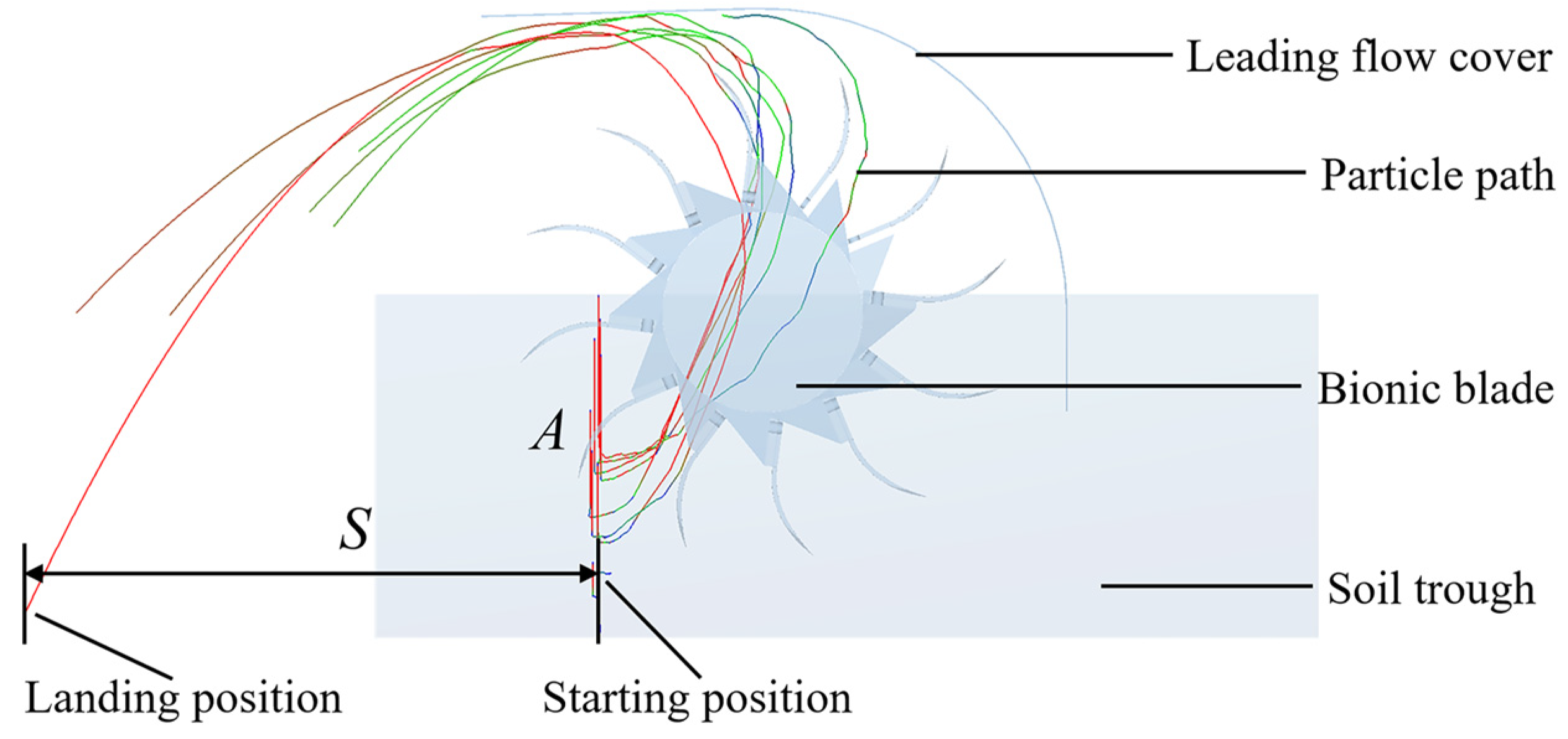
2.6.1. Soil Throwing Performance
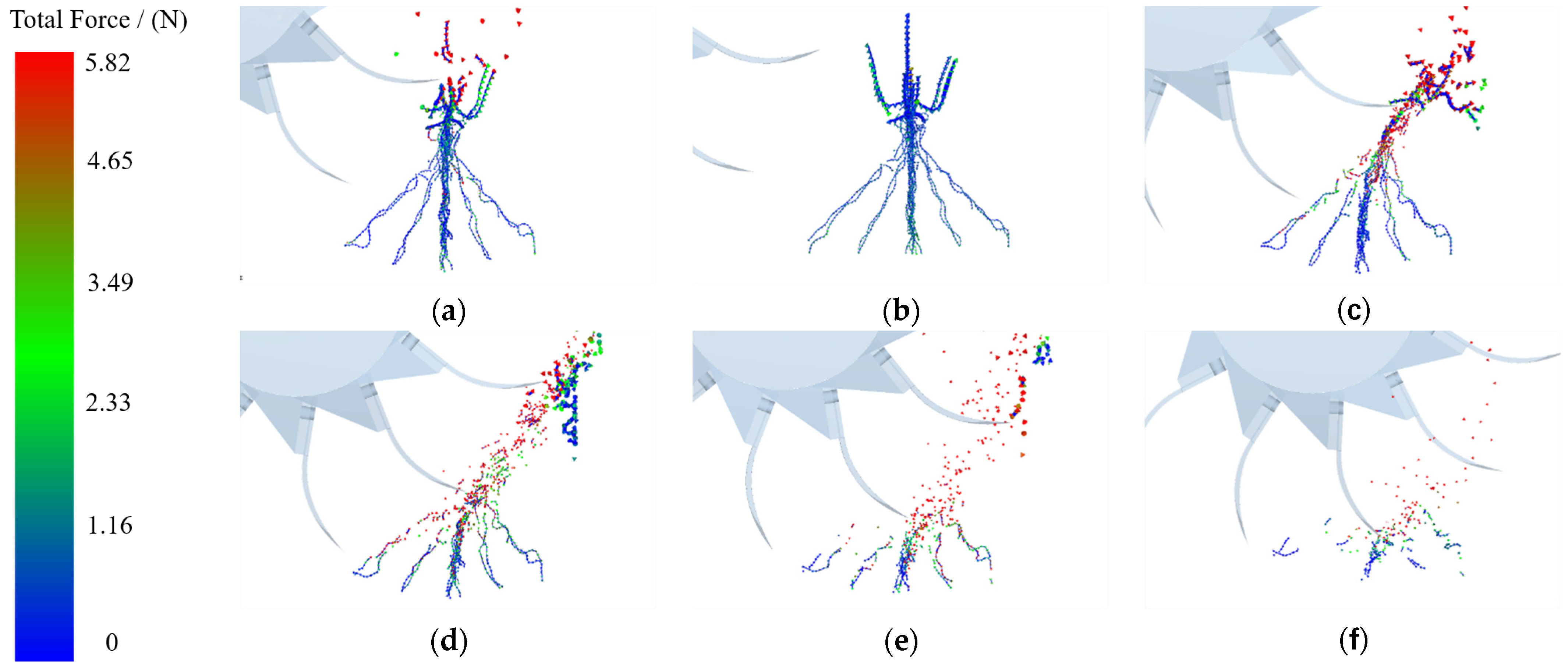
2.6.2. Plant Crushing Performance
2.7. Field Experiment
3. Results and Analysis
3.1. Single Factor Experiment
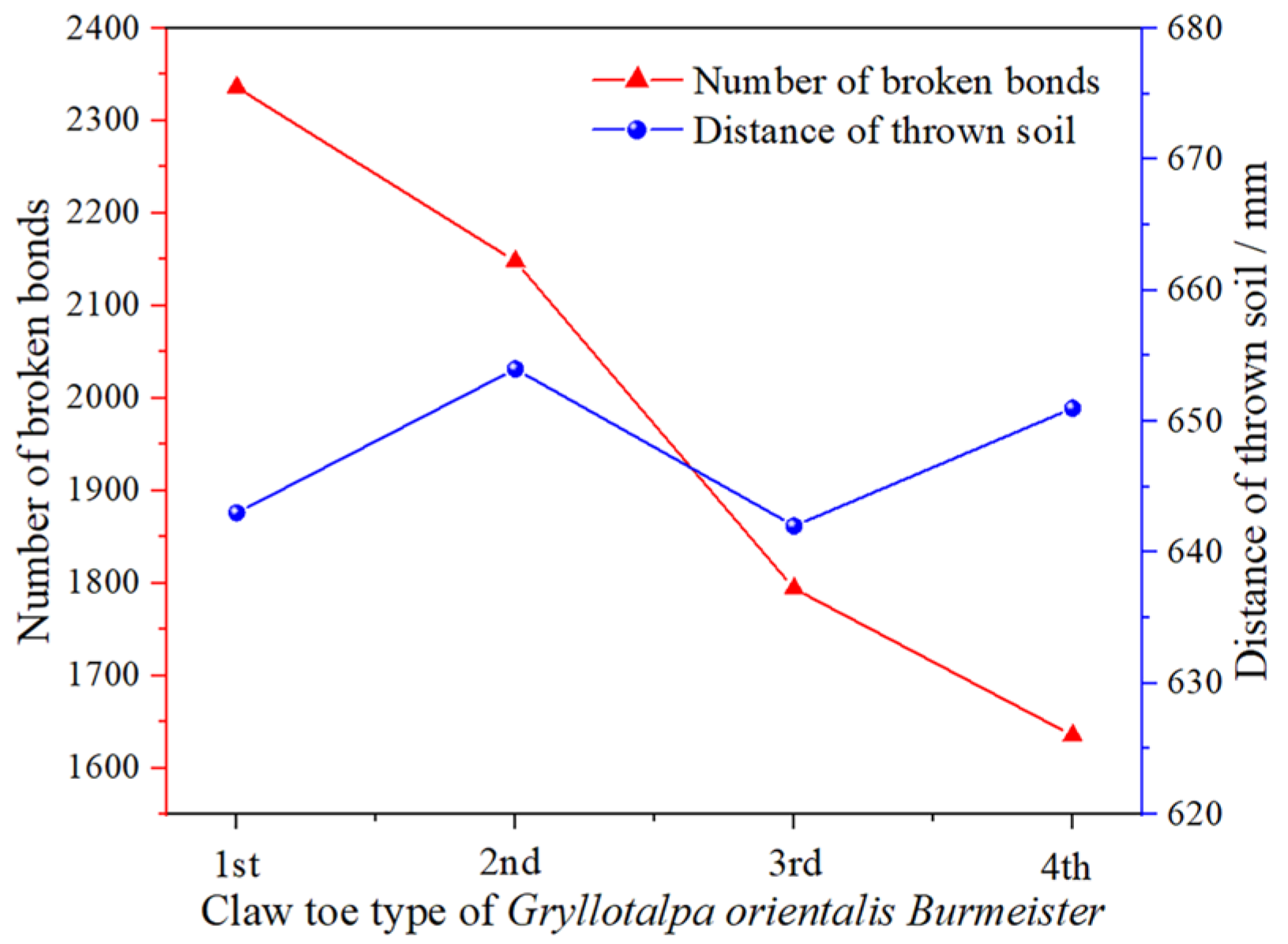
3.1.1. Effect of Bionic Rotary Blade Edge Curve on Operation Quality
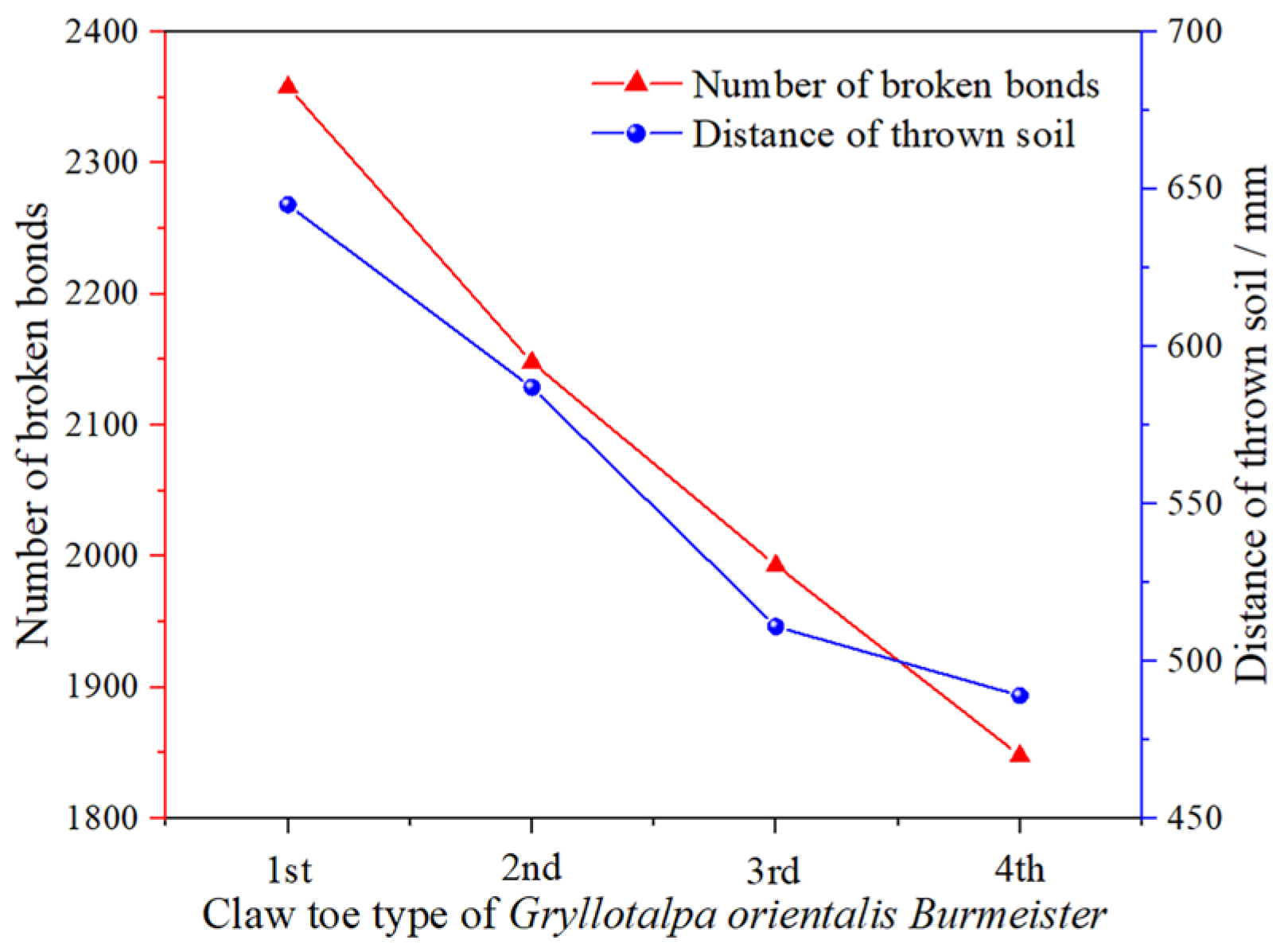
3.1.2. Effect of Bionic Rotary Blade Curved Surface on Operation Quality
3.2. Results of Quadratic Regression Orthogonal Rotational Combination Design
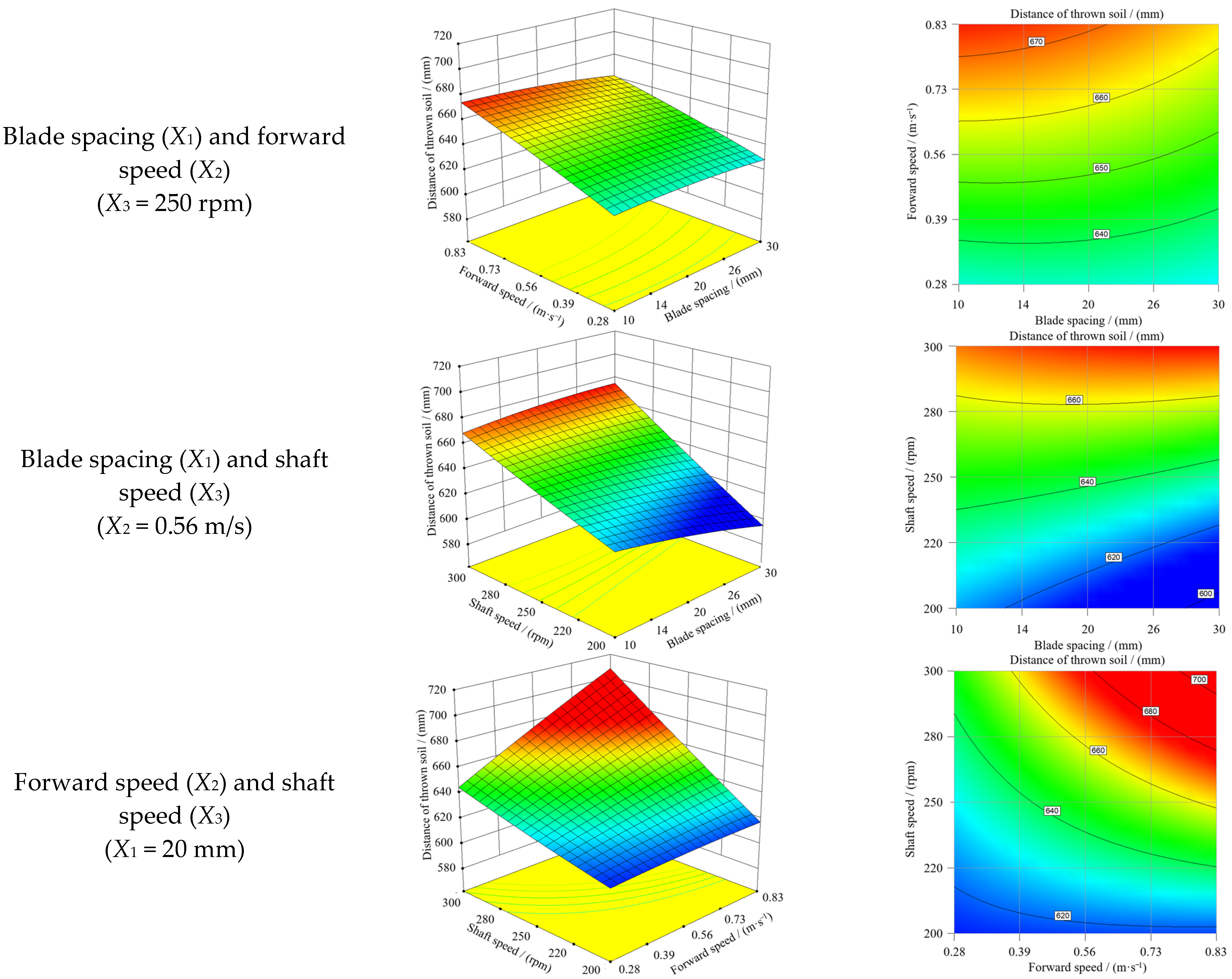
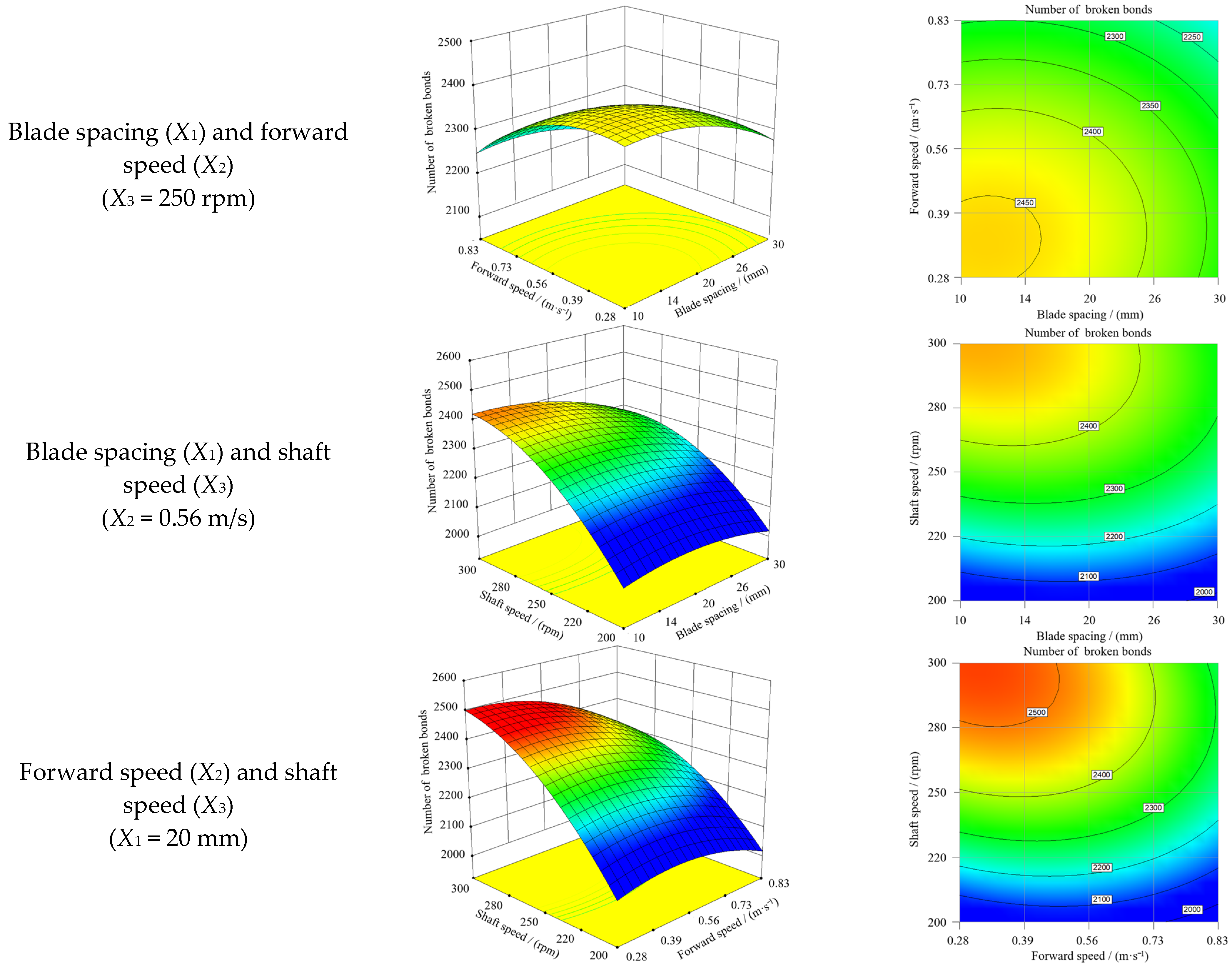
3.3. Response Surface Analysis
3.4. Parameter Optimization
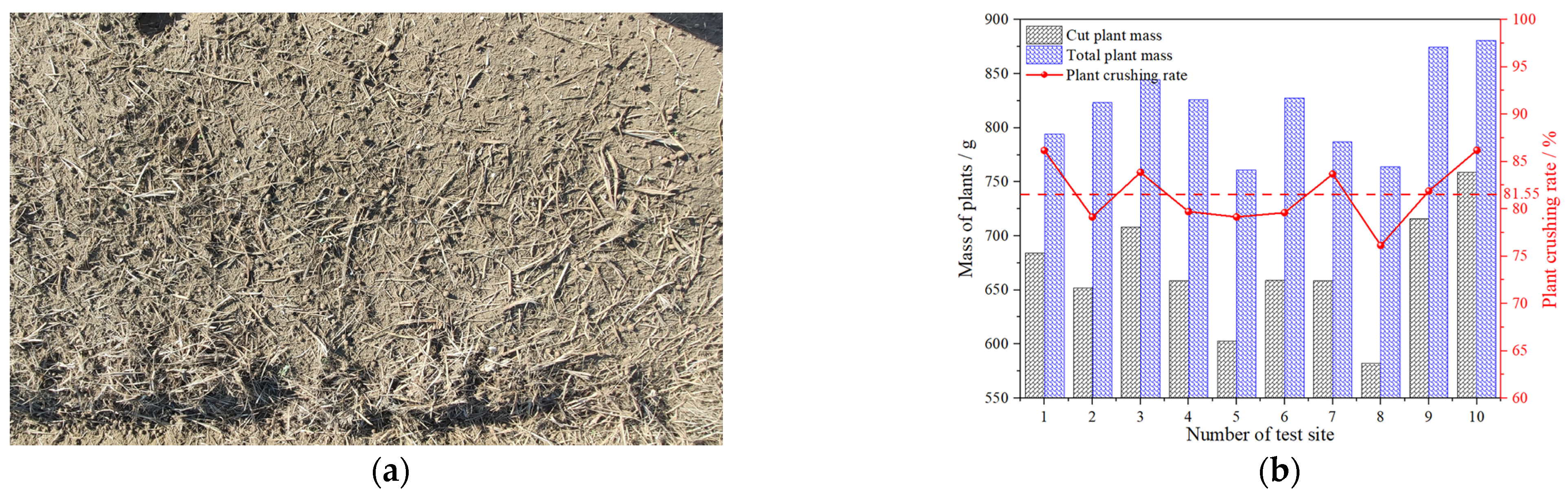
3.5. Results and Analysis of Field Experiment
4. Discussion
5. Conclusions
- (1)
- A bionic rotary blade was designed to address the problems of severe soil congestion and easy plant entanglement in the harvesting and excavation of Cyperus esculentus. Based on the unique combination of longitudinal soil cutting and lateral soil throwing of Gryllotalpa orientalis Burmeister, the edge curve and curved surface of the bionic rotary blade were designed using the excavation edge curve and excavation surface curvature of the toes of the mole cricket. Mechanical and kinematic analyses of the bionic rotary blade during the harvesting process of Cyperus esculentus were conducted. The parameters affecting the digging quality of Cyperus esculentus were determined to be the blade spacing, forward speed, and shaft speed.
- (2)
- A discrete element model of the flexible plant soil bionic rotary blade was established. A single factor experiment and a quadratic regression orthogonal rotational combination design were conducted, with the soil throwing distance and the number of broken bonds of Cyperus esculentus plants as evaluation indices. The results showed that the bionic rotary blade, designed with excavation edge and excavation surface based on the first claw toe of the mole cricket had the best operational performance. The best combination of the bionic rotary blade parameters were 11.16 mm for blade spacing, 0.66 m/s for forward speed, and 300 rpm for shaft speed.
- (3)
- The prototype was produced, and a field experiment was conducted according to the best parameters combination. The results showed that the bionic rotary blade’s average soil throwing distance and plant crushing rate were 632.3 mm and 81.55%, respectively. The soil throwing and plant crushing performance of the bionic rotary blade were good, which could effectively solve the problems of severe soil congestion and low plant crushing rate. The operation performance of the bionic rotary blade was superior to that of the Chinese standard rotary blade IT245 and the rotary blade IT245P. The results of this study can enrich the bionic configuration design method and provide bionic design ideas and methods for the design of the soil-engaging components of tillage machinery, such as the rotary blade and the returning blade.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, S.B.; Cui, G.F.; Wang, C.L. A new high-yield oil crop Cyperus esculentus. Xinjiang Agric. Sci. Technol. 2001, 4, 40. [Google Scholar]
- Guo, T.T.; Wan, C.J.; Huang, F.H.; Wei, C.L.; Hu, Z.H. Research Progress on main nutritional components and physiological functions of Cyperus esculentus. Chin. J. Oil Crop Sci. 2021, 43, 1174–1180. [Google Scholar]
- Hou, Z.H.; Mu, Z.J.; Zhao, J.L.; Bao, J.W.; Zhao, X.Q.; Wang, J.G.; Lu, Z.Y. Construction of evaluation index system for the windbreak and sand-fixing technology model of Cyperus esculentus guided by ecology, life and production integration concepts in windy and sandy areas in northern China. J. North. Agric. 2021, 49, 127–134. [Google Scholar]
- Yang, Z.L. Characteristics and research progress of Cyperus esculentus. North. Hortic. 2017, 17, 192–201. [Google Scholar]
- Wang, Z.C.; Li, S.S.; Liang, X.; Xu, L.J.; Zou, X.J. Development status and prospect of Cyperus esculentus industry in China. Sci. Technol. India 2022, 22, 62–67. [Google Scholar]
- Zhu, H.B.; Qian, C.; Bai, L.Z.; Zhao, H.R.; Ma, S.W.; Zhang, X.; Li, H. Design and experiment of forward and reverse power type corn stubble cutting anti-blocking device. Trans. Chin. Soc. Agric. Eng. 2022, 38, 1–11. [Google Scholar]
- Jiang, R.; Chen, Y.; Yu, C.X.; Wang, X.F.; Zhu, D.Q. Design and experimentation of stubble elimination blades with reduced resistance by imitation cricket cutting tooth blades. J. Eng. Des. 2018, 25, 409–419. [Google Scholar]
- Chen, Y. Design and Experiment of Bionic Stubble Elimination Knife Based on the Characteristics of Cricket Cutting Teeth Leaves. Master’s Thesis, Anhui Agricultural University, Hefei, China, 2018. [Google Scholar]
- Qi, H. Optimal Design and Experimental Research of Imitation Rotary Tillage Knives. Master’s Thesis, Anhui Agricultural University, Hefei, China, 2017. [Google Scholar]
- Zhang, Y.; Qiao, C.X.; Wang, T.Q.; Cao, J.F.; Wang, P.F.; Shi, L. Three-dimensional geometric conformation of the forefoot and toe of the mole cricket. Trans. Chin. Soc. Agric. Eng. 2021, 37, 309–315. [Google Scholar]
- Zhang, J.X.; Zhang, K.K.; Zhang, Y.; Zhu, Y.Y. Design of soil excavation mechanism with imitation of mole crickets’ motion characteristics. Mach. Des. Manuf. 2020, 8, 180–183, 187. [Google Scholar]
- Xiao, M.H.; Wang, K.X.; Yang, W.; Wang, W.C.; Jiang, F. Design and experimentation of a bionic rotary tillage knife based on the claw-toe of the Oriental mole cricket. Trans. Chin. Soc. Agric. Mach. 2021, 52, 55–63. [Google Scholar]
- Guan, C.S.; Fu, J.J.; Xu, L.; Jiang, X.Z.; Wang, L.; Cui, Z.C. Study on the reduction of soil adhesion and tillage force of bionic cutter teeth in secondary soil crushing. Biosyst. Eng. 2022, 213, 133–147. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Q.Y.; Muhammad, S.M.; Ji, C.Y.; Zhao, Z. Design and experimentation of rototill-straw crushing serrated blade with imitation mole toe arrangement. Trans. Chin. Soc. Agric. Eng. 2017, 33, 43–50. [Google Scholar]
- Yang, Y.W. Research on Soil Cutting Performance of Mole Forefoot Multi-Toe Combination Structure and Bionic Rotary Tillage Knife Design. Ph.D. Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Guo, C.F.; Li, Y.; Yao, D.Y.; Wei, S.L.; Wu, Z.H.; Li, Y. Optimization and experimentation of key components operating parameters of a bionic banana straw crushing device. J. Agric. Mech. Res. 2022, 43, 93–100. [Google Scholar]
- He, X.N.; Zhang, X.J.; Zhao, Z.; Shang, S.Q.; Wang, D.W.; Yuan, X.W. Design and test of resistance reducing excavation device for Cyperus esculentus based on discrete element method. Trans. Chin. Soc. Agric. Mach. 2021, 52, 124–133. [Google Scholar]
- Ma, H.L.; Gao, H.W.; Li, H.W.; Wei, S.Y. Design and Experimentation of No-Till Seeder with Tilt Drive Disc. Trans. Chin. Soc. Agric. Mach. 2016, 5, 45–47, 66. [Google Scholar]
- Cao, X.P.; Wang, Q.J.; Li, H.W.; He, J.; Lu, C.Y. Study on the combination of side cutter and stubble disc stubble clearing device for corn no-till planter. Trans. Chin. Soc. Agric. Mach. 2021, 52, 36–44. [Google Scholar]
- Magalhães, P.S.G.; Bianchini, A.; Braunbeck, O.A. Simulated and Experimental Analyses of a Toothed Rolling Coulter for Cutting Crop Residues. Biosyst. Eng. 2007, 96, 193–200. [Google Scholar] [CrossRef]
- Zhu, J.P.; Yuan, D.; Ding, Y.; Peng, Z.M.; Xia, M.; Yao, K.H. Research on soil throwing characteristics of oversized disc openers and parameter selection. J. Agric. Mech. Res. 2012, 34, 46–50, 57. [Google Scholar]
- Yang, W.; Zhao, J.F.; Liu, X.Y.; Xi, L.Q.; Liao, J.A. Simulation and Test of “Separated Burying Device” of Green Manure Returning Machine Based on the EDEM Software. Agriculture 2022, 12, 569. [Google Scholar] [CrossRef]
- Xu, G.M.; Xie, Y.X.; Matin, M.A.; He, R.Y.; Ding, Q.S. Effect of Straw Length, Stubble Height and Rotary Speed on Residue Incorporation by Rotary Tillage in Intensive Rice–Wheat Rotation System. Agriculture 2022, 12, 222. [Google Scholar] [CrossRef]
- Hu, M.J.; Xia, J.; Zhou, Y.; Luo, C.; Zhou, M.; Liu, Z. Measurement and calibration of the discrete element parameters of coated delinted cotton seeds. Agriculture 2020, 12, 286. [Google Scholar] [CrossRef]
- Han, L.J.; Yuan, W.; Yu, J.J.; Jin, J.J.; Xie, D.S. Simulation and Experiment of Spiral Soil Separation Mechanism of Compound Planter Based on Discrete Element Method (DEM). Agriculture 2022, 12, 511. [Google Scholar] [CrossRef]
- Shi, G.K.; Ding, L.P.; Zhang, Z.Y.; Ding, H.Z.; Kan, Z. Calibration and Tests for the Discrete Element Simulation Parameters of Fallen Jujube Fruit. Agriculture 2022, 12, 38. [Google Scholar] [CrossRef]
- Liu, X.M.; Sang, Z.Z.; Wang, J.F. Experimental Study on Submerged Soil Rotation (2)—Experimental Study on Reversing Rotating and Throwing Blades. J. Jiamusi Eng. Coll. 1998, 1, 1–6. [Google Scholar]
- Liu, X.M.; Sang, Z.Z.; Wang, J.F. Experimental Study on Submerged Soil Rotation (3)—Experimental Study on Reversing Rotating and Throwing Blades. J. Jiamusi Eng. Coll. 1998, 3, 283–287. [Google Scholar]
- Zhu, H.; He, X.; Shang, S.; Zhao, Z.; Wang, H.; Tan, Y.; Li, C.; Wang, D. Evaluation of Soil-Cutting and Plant-Crushing Performance of Rotary Blades with Double-Eccentric Circular-Edge Curve for Harvesting Cyperus esculentus. Agriculture 2022, 12, 862. [Google Scholar] [CrossRef]
- Wang, J.F.; Zhang, X.; Tang, H.; Wang, J.W.; Weng, W.X.; Yang, D.Z. Optimal design and test of rice straw counter rotating deep buried sliding cutting and returning knife. Trans. Chin. Soc. Agric. Mach. 2021, 52, 28–39. [Google Scholar]
- Cao, X.L.; Li, Z.H.; Li, H.W.; Wang, X.C.; Ma, X. Measurement and Calibration of the Parameters for Discrete Element Method Modeling of Rapeseed. Processes 2021, 9, 605. [Google Scholar] [CrossRef]
- Liu, B.L. Research on Extracting Movement Information of Thrown Soil Based on High-Speed Camera. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2005. [Google Scholar]
- Lu, Z.C. Design and Experimental Research of a Test Device for Cutting Corn Root Stubble Movement Characteristics of Disc Stubble-Breaking Knife. Master’s Thesis, Shenyang Agricultural University, Shenyang, China, 2016. [Google Scholar]
- Liu, X.M.; Sang, Z.Z. Research on submerged soil reversal rotary tillage. Trans. Chin. Soc. Agric. Mach. 1996, 4, 41–45. [Google Scholar]
- Ren, S.G.; Wu, M.L.; Guan, C.Y.; Liu, X.G. Research on soil throwing performance of no-till direct seeding combine for rape. J. Hunan Agric. Univ. 2013, 39, 543–548. [Google Scholar] [CrossRef]
- Qi, H.D. Development and Experiment of Oblique Submerged Soil Reversing Deep Rotary Tiller. Master’s Thesis, Jiangsu University, Zhenjiang, China, 2018. [Google Scholar]
- Gao, J.M.; Liu, X.D.; Qi, H.D.; Lakhiar, I.A. Simulation and experiments on reversing rotary tillage by inclined submerged soil. Trans. Chin. Soc. Agric. Eng. 2019, 35, 54–63. [Google Scholar] [CrossRef]
- Zhang, C.L. Design and Experiment of Key Components of Six-Headed Spiral Straw Return Tiller. Ph.D. Thesis, Huazhong Agricultural University, Wuhan, China, 2019. [Google Scholar]
- Zhang, C.L.; Xia, J.F.; Zhang, J.M.; Zhou, H.; Zhu, Y.H.; Wang, J.W. Design and test of cutter roller of six head spiral straw returning tillage machine. Trans. Chin. Soc. Agric. Mach. 2019, 50, 25–34. [Google Scholar]
- Wang, J.Y.; Zhao, S.H.; Gao, L.L.; Yuan, Y.Y.; Yang, Y.Q. Design and test of passive disc stubble cutter with self-adjusting blade angle for corn ridge farming. Trans. Chin. Soc. Agric. Mach. 2021, 52, 59–67. [Google Scholar]
- Wang, Q. Design and Experimental Research of Rice Whole Stalk Deep Buried Returning Device. Master’s Thesis, Northeast Agricultural University, Harbin, China, 2016. [Google Scholar]







| Coefficients | 1st Claw Toe | 2nd Claw Toe | 3rd Claw Toe | 4th Claw Toe |
|---|---|---|---|---|
| a | −0.5581 | 8.557 | −0.9531 | 824.9 |
| b | 0.775 | −77.55 | 20.33 | 9979 |
| c | 7.97 | 254.5 | −110 | −45,250 |
| d | −13.65 | −353.5 | 273.2 | 91,120 |
| e | 6.599 | 179.6 | −250.2 | −68,700 |
| R2 | 0.9996 | 0.9985 | 0.9910 | 0.9909 |
| Coefficients | 1st Claw Toe | 2nd Claw Toe | 3rd Claw Toe | 4th Claw Toe |
|---|---|---|---|---|
| a | 0.1142 | −1.032 | −0.07473 | −5.031 |
| b | −0.9333 | 10.65 | 4.085 | 77.29 |
| c | 8.84 | 26.44 | −8.222 | −401 |
| d | −13.42 | −32.42 | 13.01 | 938.9 |
| e | 6.579 | −15.2 | −9.705 | −821.6 |
| R2 | 0.9997 | 0.9996 | 0.9998 | 0.9997 |
| Claw Toe | h1 | h2 | ∆h | l |
|---|---|---|---|---|
| 1st | 130.00 | 117.64 | 12.36 | 24.74 |
| 2nd | 130.00 | 111.60 | 18.40 | 17.39 |
| 3rd | 130.00 | 120.53 | 9.47 | 13.46 |
| 4th | 130.00 | 123.11 | 6.89 | 8.38 |
| Parameter | Value | ||
|---|---|---|---|
| Intrinsic parameter | Soil | Density/(kg·m−3) | 2679 |
| Shear Modulus/(Pa) | 1.2 × 105 | ||
| Poisson’s Ratio | 0.36 | ||
| Plant | Density/(kg·m−3) | 470 | |
| Shear Modulus/(Pa) | 1.7 × 106 | ||
| Poisson’s Ratio | 0.40 | ||
| 65 Mn | Density/(kg·m−3) | 7850 | |
| Shear Modulus/(Pa) | 7.9 × 1010 | ||
| Poisson’s Ratio | 0.30 | ||
| Contact Parameter | Soil-Soil | Restitution Coefficient | 0.55 |
| Static Friction Coefficient | 0.15 | ||
| Rolling friction Coefficient | 0.43 | ||
| Plant-Plant | Restitution Coefficient | 0.34 | |
| Static Friction Coefficient | 0.08 | ||
| Rolling friction Coefficient | 0.35 | ||
| Soil-Plant | Restitution Coefficient | 0.48 | |
| Static Friction Coefficient | 0.05 | ||
| Rolling friction Coefficient | 0.32 | ||
| Soil-65 Mn | Restitution Coefficient | 0.52 | |
| Static Friction Coefficient | 0.12 | ||
| Rolling friction Coefficient | 0.20 | ||
| Plant-65 Mn | Restitution Coefficient | 0.33 | |
| Static Friction Coefficient | 0.10 | ||
| Rolling friction Coefficient | 0.30 | ||
| Contact Model | Normal Contact Stiffness/(N·m−3) | 1.723 × 108 | |
| Tangential Contact Stiffness/(N·m−3) | 9.075 × 107 | ||
| Normal Critical Stress/(Pa) | 2.215 × 105 | ||
| Tangential Critical Stress/(Pa) | 2.215 × 105 | ||
| Group | Test Factor | Constant Factor | |||
|---|---|---|---|---|---|
| Edge Curve | Curved Surface | Blade Spacing /(mm) | Forward Speed /(m·s−1) | Shaft Speed /(r·min−1) | |
| 1 | Excavation edge of 1st/2nd/3rd/4th claw toe | Excavation surface of 2nd claw toe | 20 | 0.56 | 250 |
| 2 | Excavation edge of 2nd claw toe | Excavation surface of 1st/2nd/3rd/4th claw toe | 20 | 0.56 | 250 |
| Code | Blade Spacing/(mm) | Forward Speed/(m·s−1) | Shaft Speed/(r·min−1) |
|---|---|---|---|
| 1.682 | 30 | 0.83 | 300 |
| 1 | 26 | 0.73 | 280 |
| 0 | 20 | 0.56 | 250 |
| −1 | 14 | 0.39 | 220 |
| −1.682 | 10 | 0.28 | 200 |
| ∆j | 6 | 0.17 | 30 |
| No. | Test Factor | Evaluation Index | |||
|---|---|---|---|---|---|
| Blade Spacing X1 | Forward Speed X2 | Shaft Speed X3 | Soil Throwing Distance Y1/mm | Number of Broken Bonds Y2 | |
| 1 | −1 | −1 | −1 | 623.01 | 2233 |
| 2 | 1 | −1 | −1 | 613.65 | 2201 |
| 3 | −1 | 1 | −1 | 660.18 | 2196 |
| 4 | 1 | 1 | −1 | 623.68 | 2189 |
| 5 | −1 | −1 | 1 | 649.01 | 2438 |
| 6 | 1 | −1 | 1 | 653.68 | 2398 |
| 7 | −1 | 1 | 1 | 676.45 | 2386 |
| 8 | 1 | 1 | 1 | 673.57 | 2334 |
| 9 | −1.682 | 0 | 0 | 652.74 | 2398 |
| 10 | 1.682 | 0 | 0 | 637.30 | 2297 |
| 11 | 0 | −1.682 | 0 | 633.70 | 2406 |
| 12 | 0 | 1.682 | 0 | 657.73 | 2265 |
| 13 | 0 | 0 | −1.682 | 626.74 | 2174 |
| 14 | 0 | 0 | 1.682 | 667.81 | 2458 |
| 15 | 0 | 0 | 0 | 645.44 | 2347 |
| 16 | 0 | 0 | 0 | 642.61 | 2349 |
| 17 | 0 | 0 | 0 | 644.98 | 2355 |
| 18 | 0 | 0 | 0 | 642.85 | 2354 |
| 10 | 0 | 0 | 0 | 644.05 | 2361 |
| 20 | 0 | 0 | 0 | 644.10 | 2349 |
| 21 | 0 | 0 | 0 | 648.18 | 2357 |
| 22 | 0 | 0 | 0 | 648.56 | 2366 |
| 23 | 0 | 0 | 0 | 641.33 | 2336 |
| Source | Soil Throwing Distance | Number of Broken Bonds | ||||||
|---|---|---|---|---|---|---|---|---|
| Sum of Squares | Mean Square | F Value | p-Value | Sum of Squares | Mean Square | F Value | p-Value | |
| Model | 5114.31 | 568.26 | 31.66 | <0.01 ** | 137,917.50 | 15,324.16 | 28.47 | <0.01 ** |
| X1 | 359.17 | 359.17 | 20.01 | <0.01 ** | 6627.98 | 6627.98 | 12.31 | <0.01 ** |
| X2 | 1333.38 | 1333.38 | 74.28 | <0.01 ** | 11,840.99 | 11,840.99 | 21.99 | <0.01 ** |
| X3 | 2965.99 | 2965.99 | 165.23 | <0.01 ** | 108,028.09 | 108,028.09 | 200.70 | <0.01 ** |
| X1X2 | 150.42 | 150.42 | 8.38 | 0.0125 * | 21.12 | 21.13 | 0.04 | 0.8460 |
| X1X3 | 283.82 | 283.82 | 15.81 | <0.01 ** | 351.12 | 351.13 | 0.65 | 0.4338 |
| X2X3 | 0.002 | 0.002 | 0.0002 | 0.9915 | 561.12 | 561.13 | 1.04 | 0.3259 |
| X12 | 0.91 | 0.91 | 0.051 | 0.8254 | 1307.13 | 1307.14 | 2.43 | 0.1431 |
| X22 | 3.74 | 3.74 | 0.21 | 0.6558 | 2816.01 | 2816.01 | 5.23 | 0.0396 * |
| X32 | 17.07 | 17.07 | 0.95 | 0.3473 | 6487.94 | 6487.95 | 12.05 | <0.01 ** |
| Residual | 233.36 | 17.95 | 6997.10 | 538.23 | ||||
| Lack of Fit | 185.80 | 37.16 | 6.25 | 0.0119 | 6387.10 | 1277.42 | 16.75 | 0.0005 |
| Pure Error | 47.56 | 5.95 | 609.99 | 76.24 | ||||
| R2 = 0.9564; C.V. = 0.66% | R2 = 0.9517; C.V. = 1.00% | |||||||
| Rotary Blade IT245 | Rotary Blade IT245 | Bionic Rotary Blade | |
|---|---|---|---|
| Cost (RMB) | 15 | 17 | 20 |
| Number of Broken Bonds | 1575 | 1762 | 2440 |
| Power Consumption/(kW) | 43.90 | 38.82 | 37.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, H.; Wang, D.; He, X.; Shang, S.; Zhao, Z.; Wang, H.; Tan, Y.; Shi, Y. Study on Plant Crushing and Soil Throwing Performance of Bionic Rotary Blades in Cyperus esculentus Harvesting. Machines 2022, 10, 562. https://doi.org/10.3390/machines10070562
Zhu H, Wang D, He X, Shang S, Zhao Z, Wang H, Tan Y, Shi Y. Study on Plant Crushing and Soil Throwing Performance of Bionic Rotary Blades in Cyperus esculentus Harvesting. Machines. 2022; 10(7):562. https://doi.org/10.3390/machines10070562
Chicago/Turabian StyleZhu, Hao, Dongwei Wang, Xiaoning He, Shuqi Shang, Zhuang Zhao, Haiqing Wang, Ying Tan, and Yanxin Shi. 2022. "Study on Plant Crushing and Soil Throwing Performance of Bionic Rotary Blades in Cyperus esculentus Harvesting" Machines 10, no. 7: 562. https://doi.org/10.3390/machines10070562
APA StyleZhu, H., Wang, D., He, X., Shang, S., Zhao, Z., Wang, H., Tan, Y., & Shi, Y. (2022). Study on Plant Crushing and Soil Throwing Performance of Bionic Rotary Blades in Cyperus esculentus Harvesting. Machines, 10(7), 562. https://doi.org/10.3390/machines10070562






