A Quantile Dependency Model for Predicting Optimal Centrifugal Pump Operating Strategies
Abstract
1. Introduction
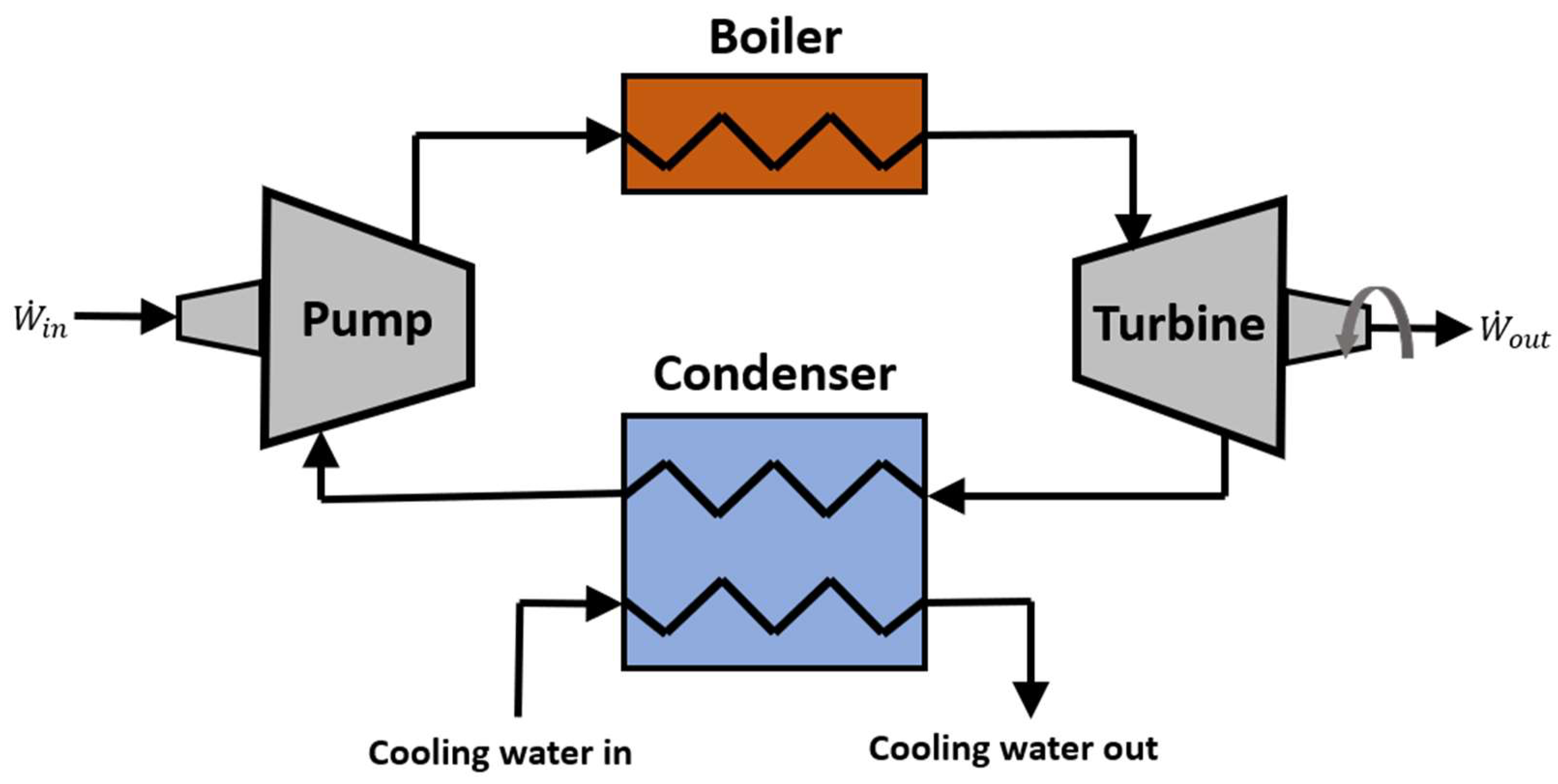
2. Centrifugal Pumps: Principles of Operation and Industrial Application
Case Study: AGR Main Boiler Feed Pumps
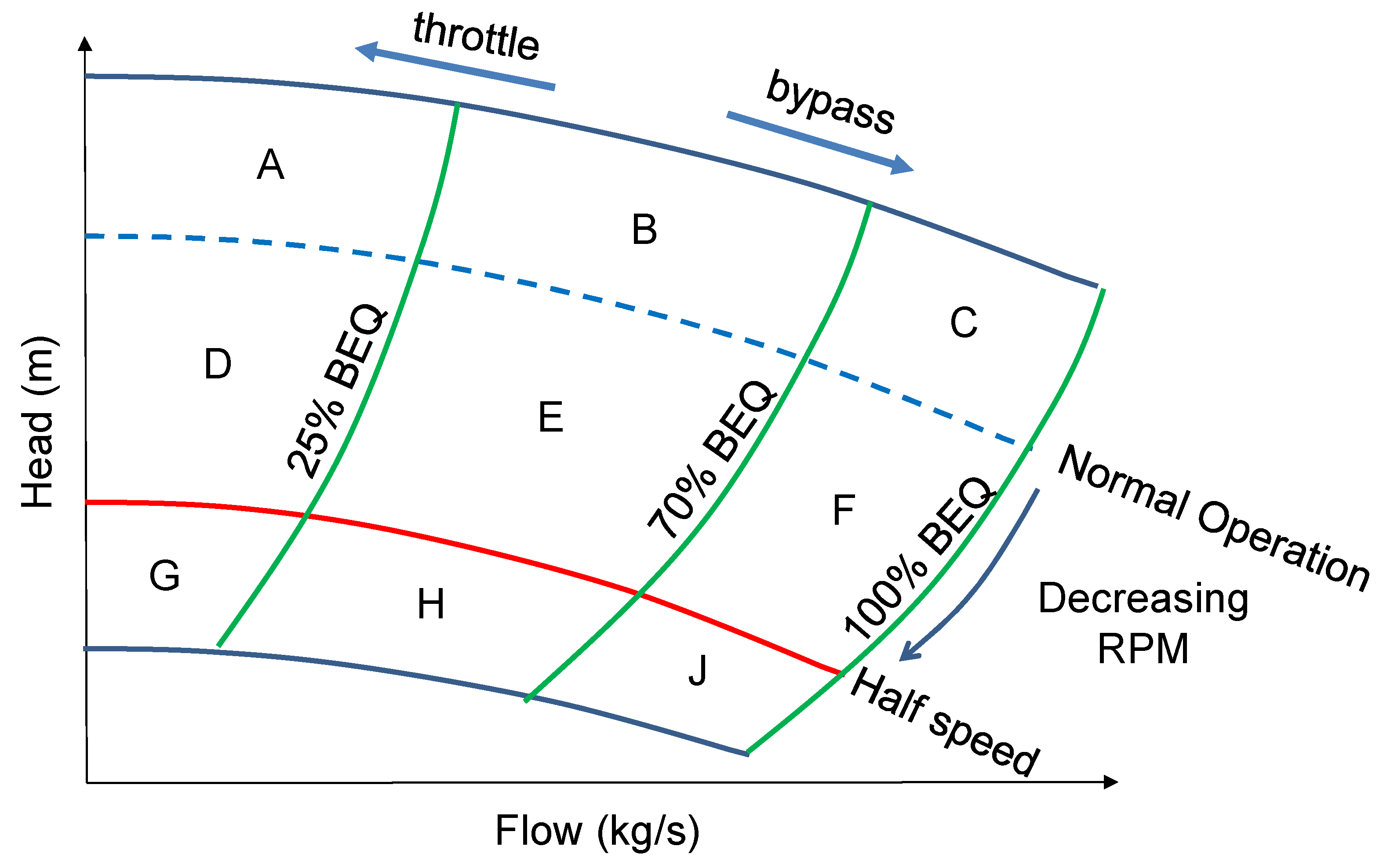
3. Pump Curve Quantile Characterization
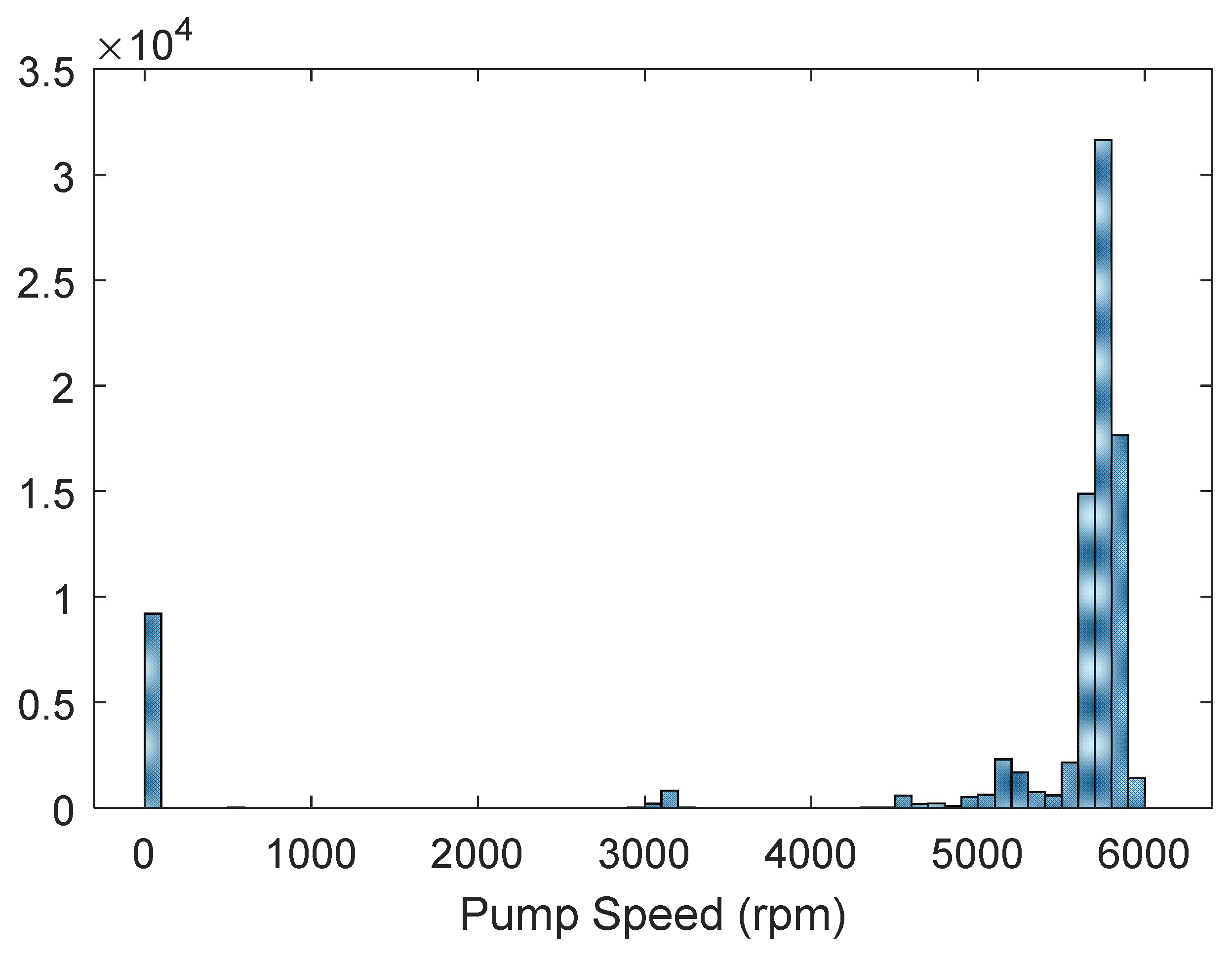
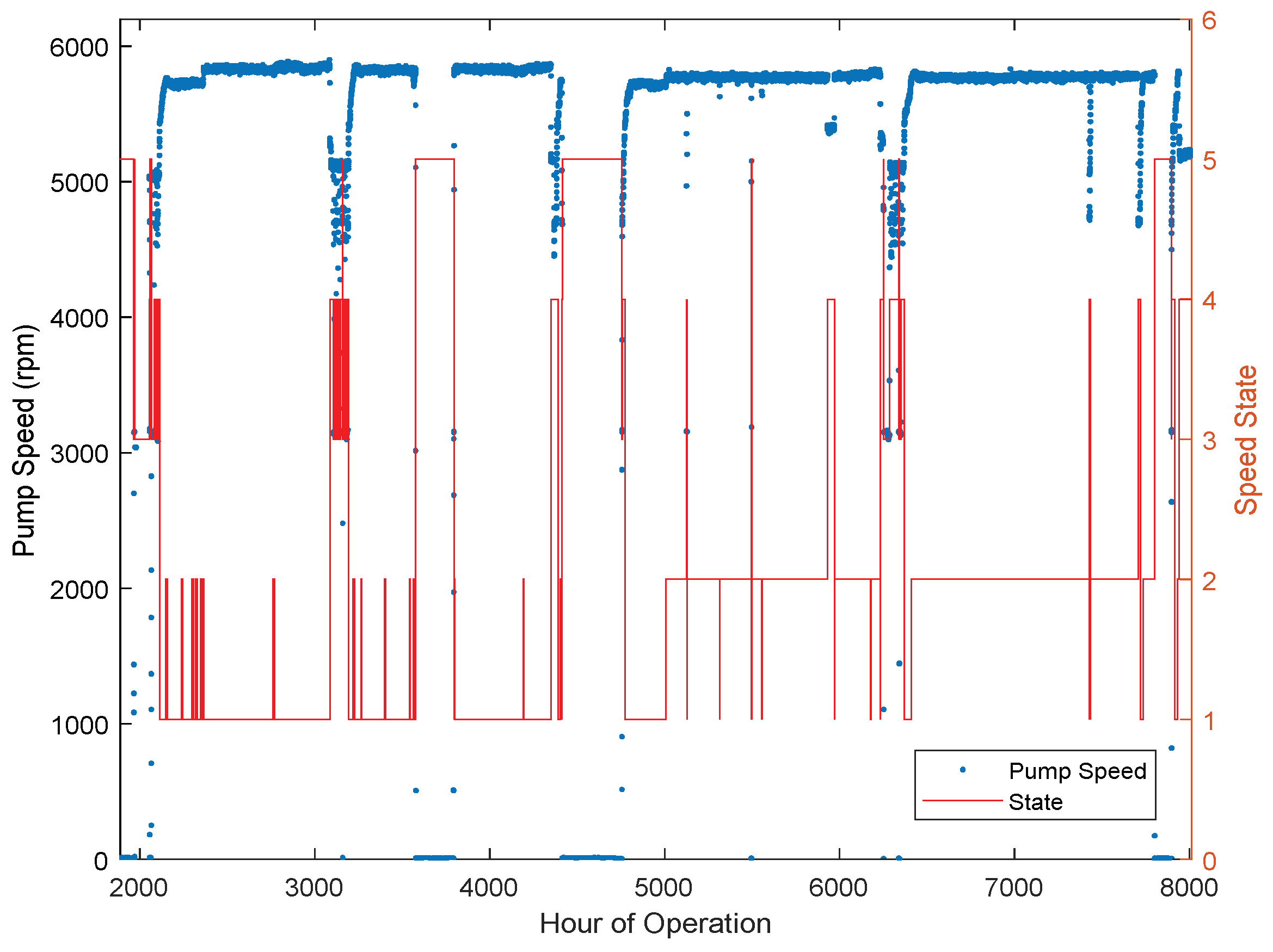
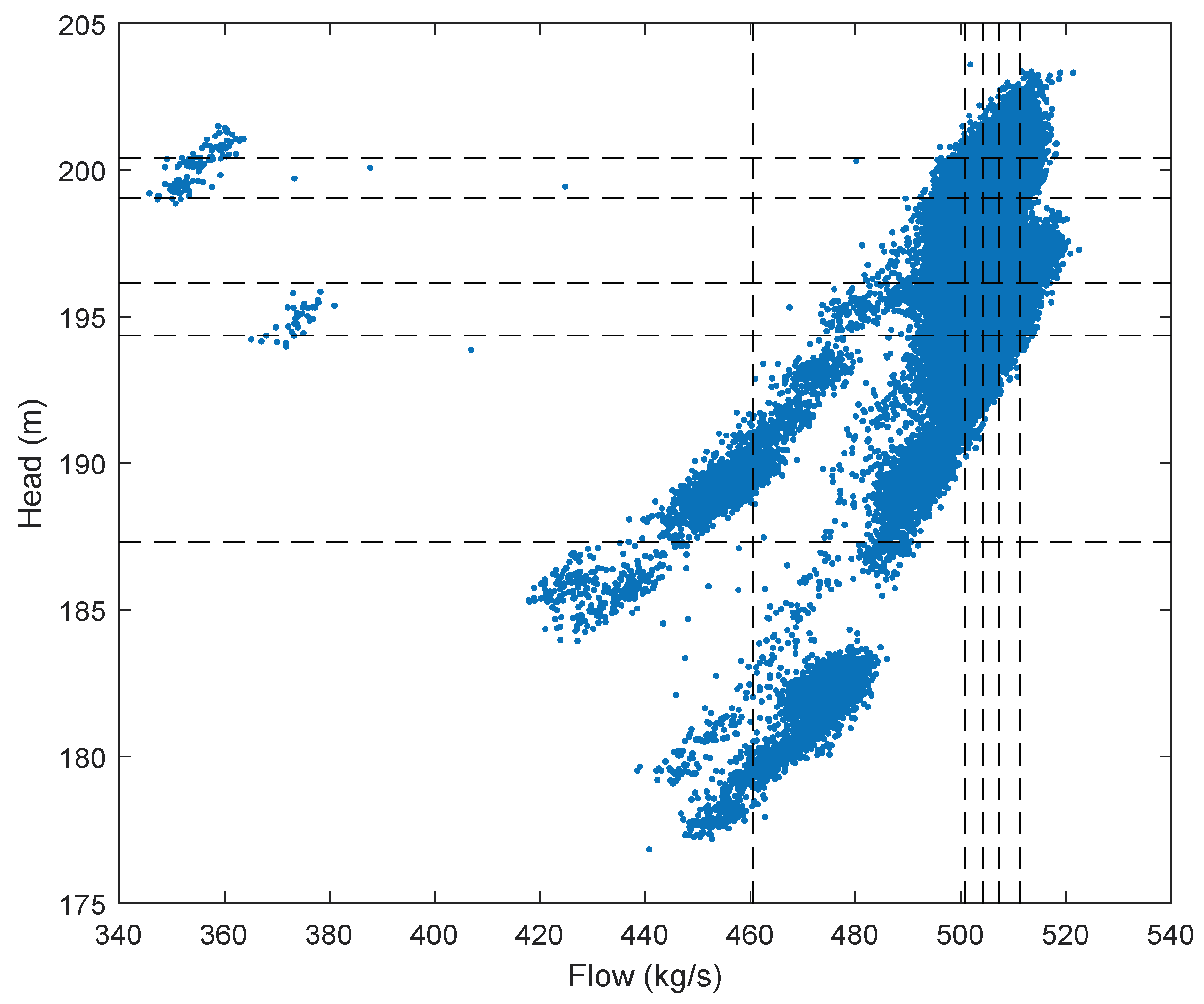
3.1. Automatic Operating Zone Delineation
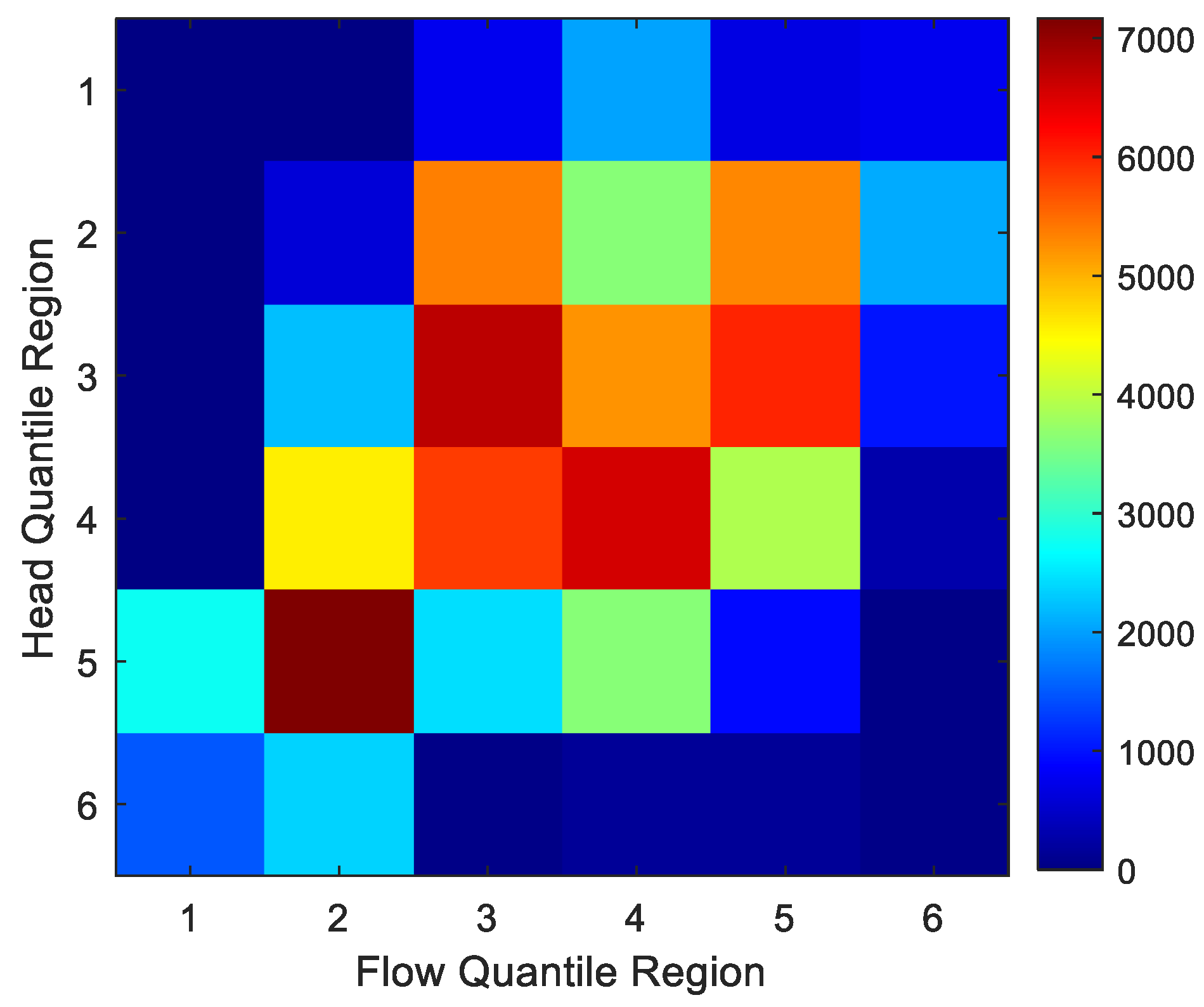
3.2. Empirical Bivariate Quantile Partition: Quantification of Preferred Operation Adherence
3.3. Measuring Operational Consequence: Choice of Degradation Metric
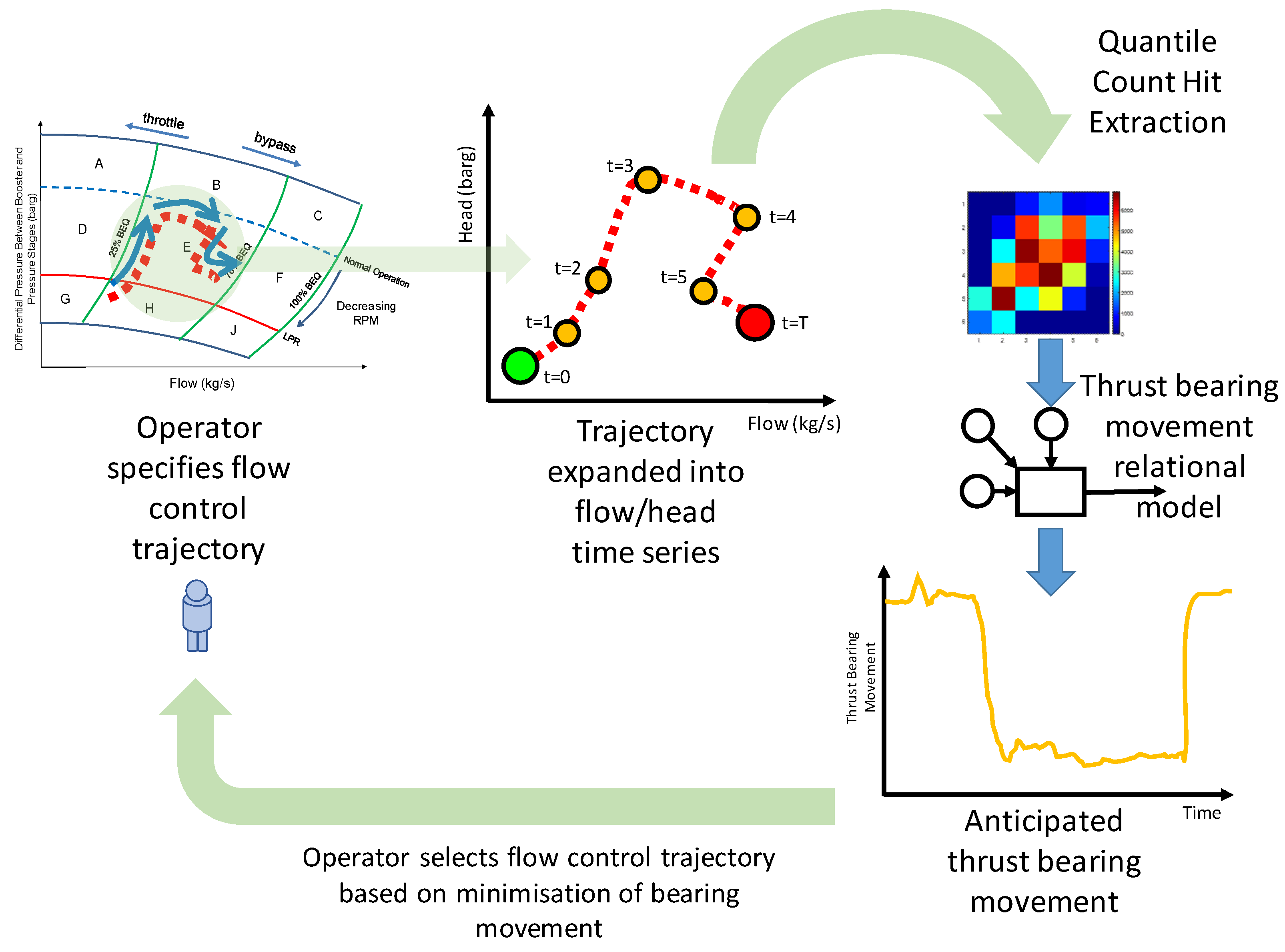
4. Pump Performance Response Quantification
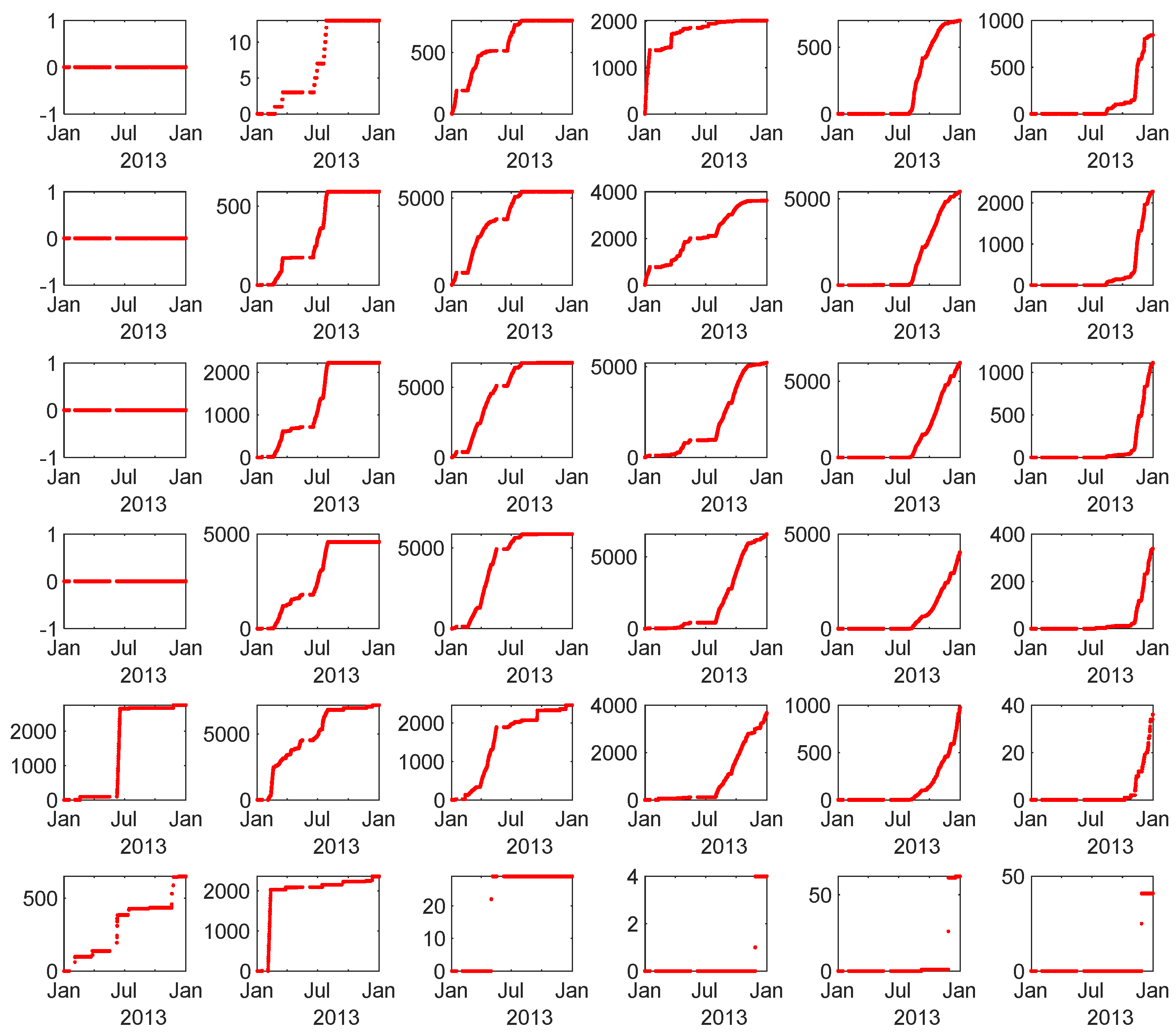
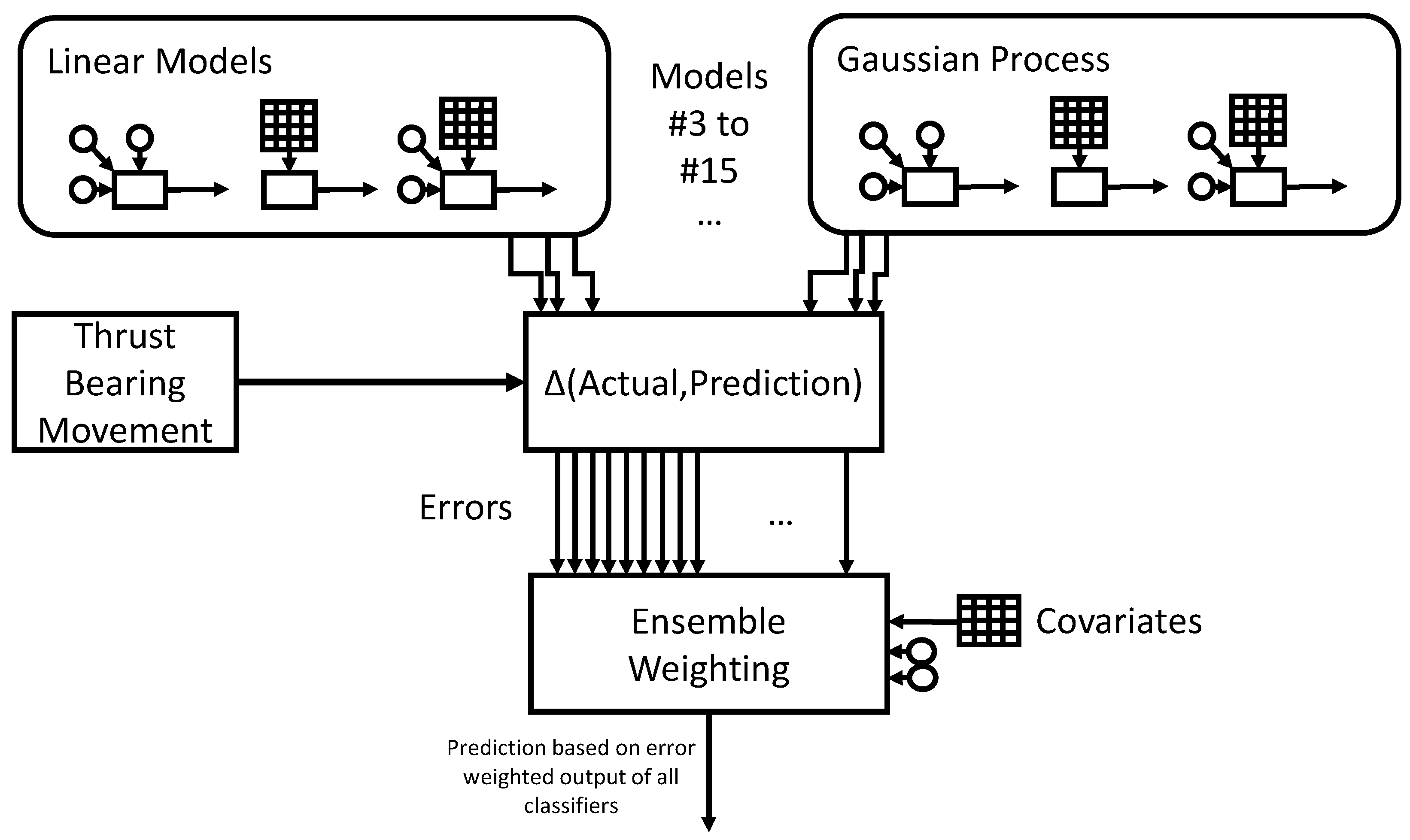
4.1. Relational Model—Operation/Thrust Bearing Movement
- Ordinary Least Squares linear regression (Models 1–3)
- Least Squares and Absolute Shrinkage Selection Operator (LASSO) (Models 4–6)
- Random Forest Regression, learning rate 1.0, LSBoost, 100 tree learners, (Models 7–9)
- Tree Regression with pruning and leaf merging (Models 10–12)
- Support Vector Regression with linear kernel (Models 13–15)
- Gaussian Process Regression with a squared exponential kernel with parameters set to be the lengthscale and the standard deviation of the training data (Models 16–18)
4.2. Candidate Inputs
4.3. Ensemble Predictions
4.4. Performance Measures
5. Evaluation of Proposed Operations by Predicting Resultant Degradation
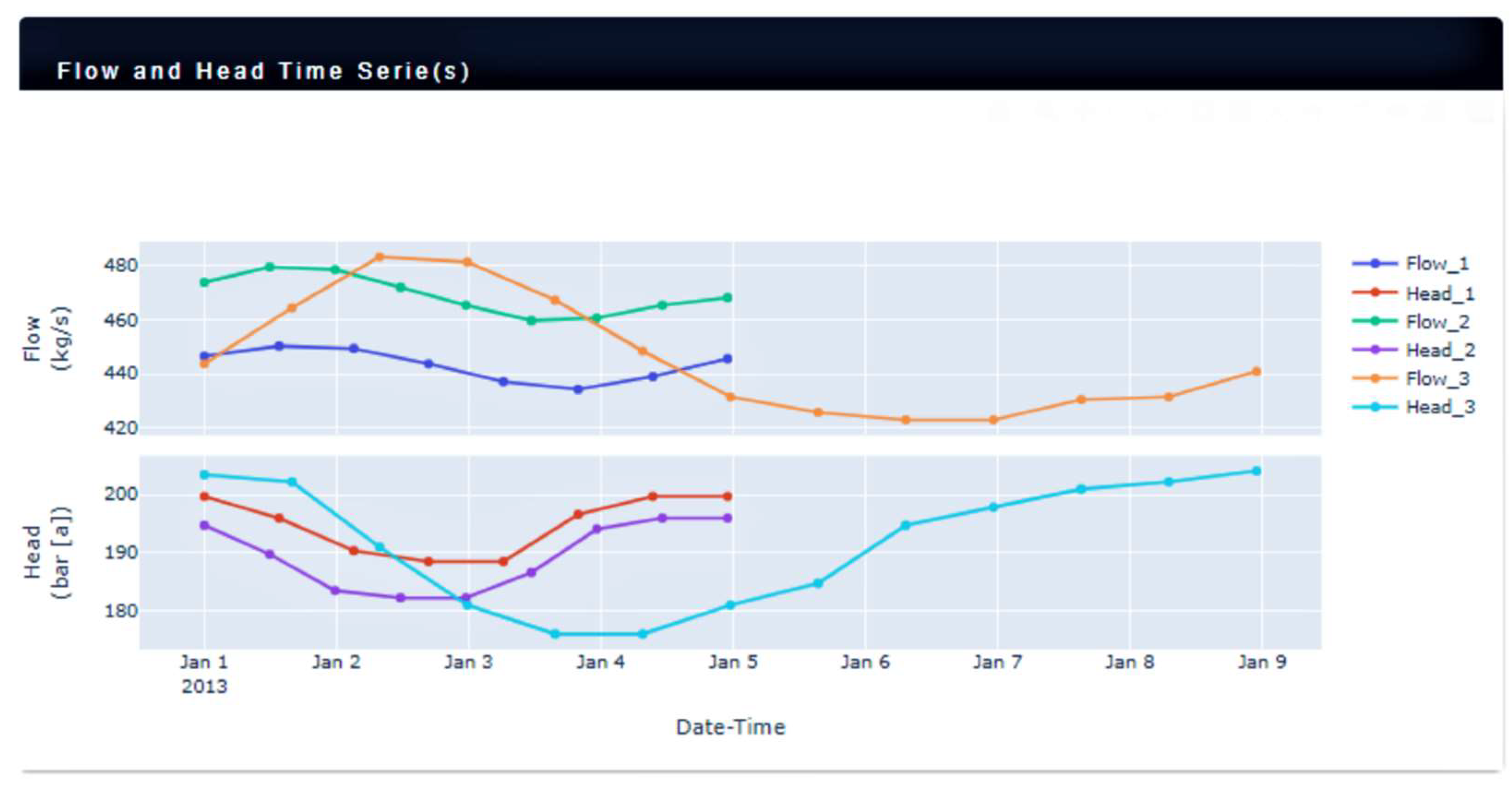
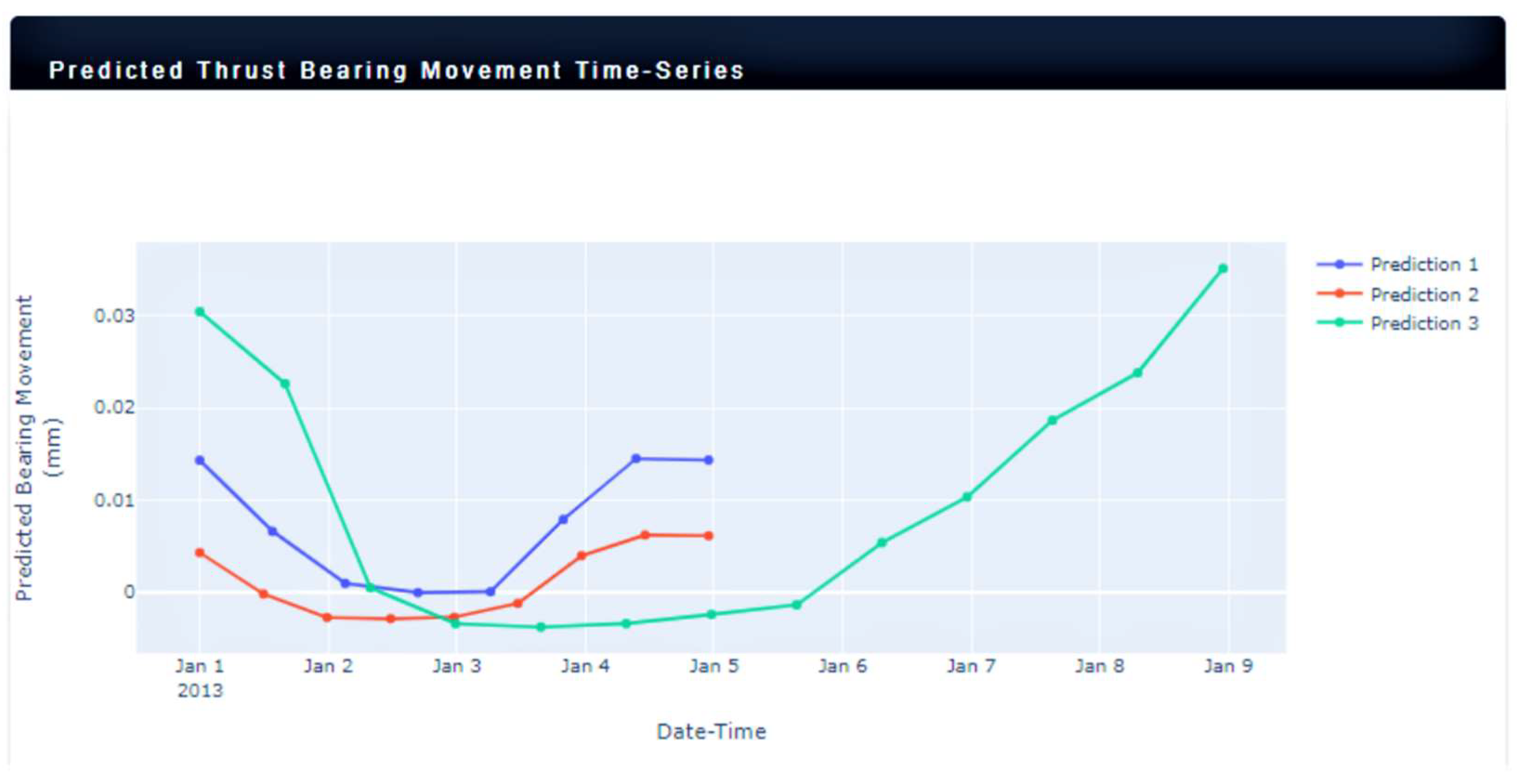
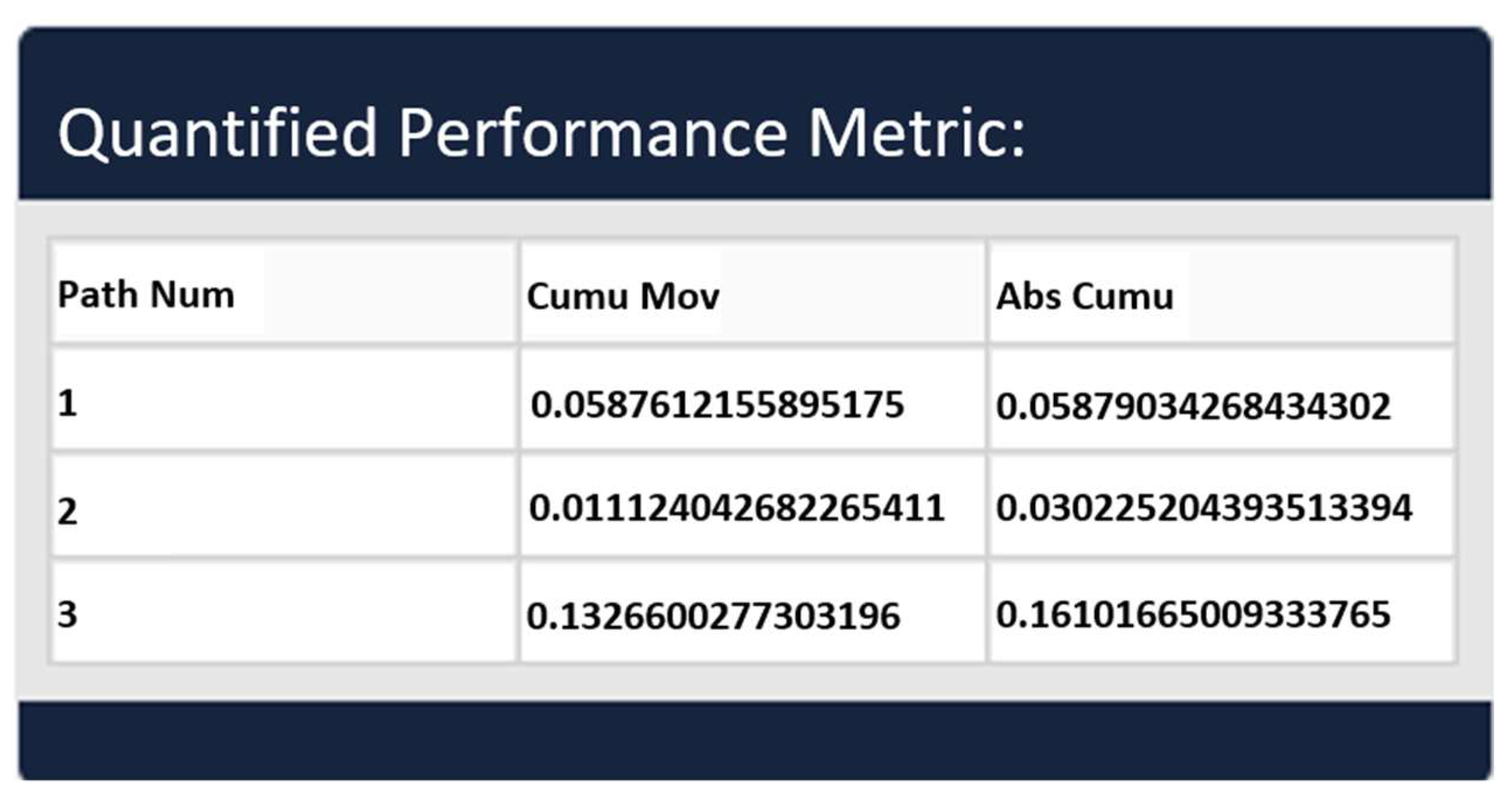
6. Operational Use Case
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Garvey, J.; Garvey, D.; Seibert, R.; Hines, J.W. Validation of on-line monitoring techniques to nuclear plant data. Nucl. Eng. Technol. 2007, 39, 149–158. [Google Scholar] [CrossRef]
- Coble, J.; Ramuhalli, P.; Bond, L.J.; Hines, J.; Ipadhyaya, B. A review of prognostics and health management applications in nuclear power plants. Int. J. Progn. Health Manag. 2015, 6, 16. [Google Scholar]
- La Roche-Carrier, N.; Dituba Ngoma, G.; Ghie, W. Numerical Investigation of a first stage of a multistage centrifugal pump: Impeller, diffuser with return vanes, and casing. Int. Sch. Res. Not. 2013, 2013, 578072. [Google Scholar] [CrossRef]
- Bergs, C.; Heizmann, M.; Hartmann, D.; Carillo, G.L. Novel method for online wear estimation of centrifugal pumps using multi-fidelity modeling. In Proceedings of the 2019 IEEE International Conference on Industrial Cyber Physical Systems (ICPS), Taipei, Taiwan, 6–9 May 2019; pp. 185–190. [Google Scholar] [CrossRef]
- Gribok, A.V.; Attieh, I.K.; Hines, J.W.; Uhrig, R.E. Regularization of feedwater flow rate evaluation for venturi meter fouling problem in nuclear power plants. Nucl. Technol. 2001, 134, 3–14. [Google Scholar] [CrossRef][Green Version]
- Okoh, C.; Roy, R.; Mehnen, J. Predictive maintenance modelling for through-life engineering services. Procedia CIRP 2017, 59, 196–201. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J. Unsupervised Adversarial Adaptation Network for Intelligent Fault Diagnosis. IEEE Trans. Ind. Electron. 2019, 67, 9904–9913. [Google Scholar] [CrossRef]
- Jiao, J.; Zhao, M.; Lin, J.; Ding, C. Classifier Inconsistency-Based Domain Adaptation Network for Partial Transfer Intelligent Diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 5965–5974. [Google Scholar] [CrossRef]
- Hines, J.W.; Rasmussen, B. Online sensor calibration monitoring uncertainty estimation. Nucl. Technol. 2005, 151, 281–288. [Google Scholar] [CrossRef]
- Cheng, F.; Qu, L.; Qiao, W.; Hao, L. Enhanced particle filtering for bearing remaining useful life prediction of wind turbine drivetrain gearboxes. IEEE Trans. Ind. Electron. 2018, 66, 4738–4748. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble methods in machine learning. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Zio, E.; Baraldi, P.; Gola, G. Feature-based classifier ensembles for diagnosing multiple faults in rotating machinery. Appl. Soft Comput. 2008, 8, 1365–1380. [Google Scholar] [CrossRef]
- Dragunov, A.; Saltanov, E.; Pioro, I.; Kirillov, P.; Duffey, R. Power Cycles of Generation III and III+ Nuclear Power Plants. J. Nucl. Eng. Radiat. Sci. 2015, 1, 021006. [Google Scholar] [CrossRef]
- Borkowf, C.B.; Gail, M.H.; Carroll, R.J.; Gill, R.D. Analyzing bivariate continuous data grouped into categories defined by empirical quantiles of marginal distributions. Biometrics 1997, 53, 1054–1069. [Google Scholar] [CrossRef] [PubMed]
- Improving Pumping System Performance: A Sourcebook for Industry, 2nd ed.; National Renewable Energy Laboratory: Golden, CO, USA, 2006.
- Simpson, A.R.; Marchi, A. Evaluating the approximation of the affinity laws and improving the efficiency estimate for variable speed pumps. J. Hydraul. Eng. 2013, 139, 1314–1317. [Google Scholar] [CrossRef]
- Nonbøl, E. Description of the Advanced Gas Cooled Type of Reactor (AGR); No. NKS-RAK--2 (96) TR-C2; Nordisk Kernesikkerhedsforskning: Roskilde, Denmark, 1996. [Google Scholar]
- Charcharos, A.N.; Wood, M.B.; Glasgow, J.R. Heysham II/Torness AGR Steam Generator (IWGGCR--15); International Atomic Energy Agency (IAEA): Vienna, Austria, 1988. [Google Scholar]
- Lee, J.; Wu, F.; Zhao, W.; Ghaffari, M.; Liao, L.; Siegel, D. Prognostics and health management design for rotary machine systems—Reviews, methodologies and applications. Mech. Syst. Signal Process. 2014, 42, 314–334. [Google Scholar] [CrossRef]
- Costello, J.J.; West, G.M.; McArthur, S.D. Machine learning model for event-based prognostics in gas circulator condition monitoring. IEEE Trans. Reliab. 2017, 66, 1048–1057. [Google Scholar] [CrossRef]
- Penny, W.D.; Roberts, S.J. Dynamic models for nonstationary signal segmentation. Comput. Biomed. Res. 1999, 32, 483–502. [Google Scholar] [CrossRef] [PubMed]
- Yu, J. Health Condition Monitoring of Machines Based on Hidden Markov Model and Contribution Analysis. IEEE Trans. Instrum. Meas. 2012, 61, 2200–2211. [Google Scholar] [CrossRef]
- Forney, G.D. The viterbi algorithm. Proc. IEEE 1973, 61, 268–278. [Google Scholar] [CrossRef]
- Bilmes, J. A Gentle Tutorial of the EM algorithm and its application to Parameter Estimation for Gaussian Mixture and Hidden Markov Models; Technical Report TR-97-021; ICSI: New Delhi, India, 1997. [Google Scholar]
- Steele, R.J.; Raftery, A.E. Performance of Bayesian model selection criteria for Gaussian mixture models. Front. Stat. Decis. Mak. Bayesian Anal. 2010, 2, 113–130. [Google Scholar]
- Genest, C.; Nešlehová, J. A Primer on Copulas for Count Data. ASTIN Bull. 2007, 37, 475–515. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, H.; Hu, L.; He, H. Fault diagnosis and failure prediction by thrust load analysis for a turbocharger thrust bearing. In ASME Turbo Expo 2010: Power for Land, Sea, and Air; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2010; pp. 491–498. [Google Scholar]
- Lüddecke, B.; Nitschke, P.; Dietrich, M.; Filsinger, D.; Bargende, M. Unsteady Thrust Force Loading of a Turbocharger Rotor During Engine Operation. J. Eng. Gas Turbines Power 2016, 138, 012301. [Google Scholar] [CrossRef]
- Gjika, K.; LaRue, G.D. Axial load control on high-speed turbochargers: Test and prediction. In ASME Turbo Expo 2008: Power for Land, Sea, and Air; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2008; pp. 705–712. [Google Scholar]
- Yao, Y.; Vehtari, A.; Simpson, D.; Gelman, A. Using stacking to average Bayesian predictive distributions (with discussion). Bayesian Anal. 2018, 13, 917–1007. [Google Scholar] [CrossRef]


| Set | Variables |
|---|---|
| A | Flow |
| Head | |
| B | Quantile Region Counts |
| C | data |
| data | |
| A and B Combined | |
| data |
| Model | Benchmark | Quantile | Combined |
|---|---|---|---|
| OLS | 0.014 | 0.008 | 0.010 |
| Elastic Net | 0.013 | 0.014 | 0.008 |
| SVM | 0.073 | 0.009 | 0.015 |
| RF | 0.008 | 0.019 | 0.009 |
| Tree | 0.008 | 0.009 | 0.008 |
| GP | 0.024 | 0.006 | 0.024 |
| Ensemble | 0.011 | 0.011 | 0.004 |
| PB Ensemble | 0.005 | 0.011 | 0.004 |
| Stacking | 0.007 | 0.007 | 0.011 |
| Model | Benchmark | Quantile | Combined |
|---|---|---|---|
| OLS | 0.013 | 0.020 | 0.010 |
| Elastic Net | 0.015 | 0.019 | 0.004 |
| SVM | 0.013 | 0.028 | 0.010 |
| RF | 0.006 | 0.022 | 0.011 |
| Tree | 0.008 | 0.003 | 0.008 |
| GP | 0.020 | 0.008 | 0.007 |
| Ensemble | 0.005 | 0.015 | 0.007 |
| PB Ensemble | 0.005 | 0.014 | 0.007 |
| Stacking | 0.007 | 0.027 | 0.008 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stephen, B.; Brown, B.; Young, A.; Duncan, A.; Helfer-Hoeltgebaum, H.; West, G.; Michie, C.; McArthur, S.D.J. A Quantile Dependency Model for Predicting Optimal Centrifugal Pump Operating Strategies. Machines 2022, 10, 557. https://doi.org/10.3390/machines10070557
Stephen B, Brown B, Young A, Duncan A, Helfer-Hoeltgebaum H, West G, Michie C, McArthur SDJ. A Quantile Dependency Model for Predicting Optimal Centrifugal Pump Operating Strategies. Machines. 2022; 10(7):557. https://doi.org/10.3390/machines10070557
Chicago/Turabian StyleStephen, Bruce, Blair Brown, Andrew Young, Andrew Duncan, Henrique Helfer-Hoeltgebaum, Graeme West, Craig Michie, and Stephen D. J. McArthur. 2022. "A Quantile Dependency Model for Predicting Optimal Centrifugal Pump Operating Strategies" Machines 10, no. 7: 557. https://doi.org/10.3390/machines10070557
APA StyleStephen, B., Brown, B., Young, A., Duncan, A., Helfer-Hoeltgebaum, H., West, G., Michie, C., & McArthur, S. D. J. (2022). A Quantile Dependency Model for Predicting Optimal Centrifugal Pump Operating Strategies. Machines, 10(7), 557. https://doi.org/10.3390/machines10070557







