Semi-Supervised Transfer Learning Method for Bearing Fault Diagnosis with Imbalanced Data
Abstract
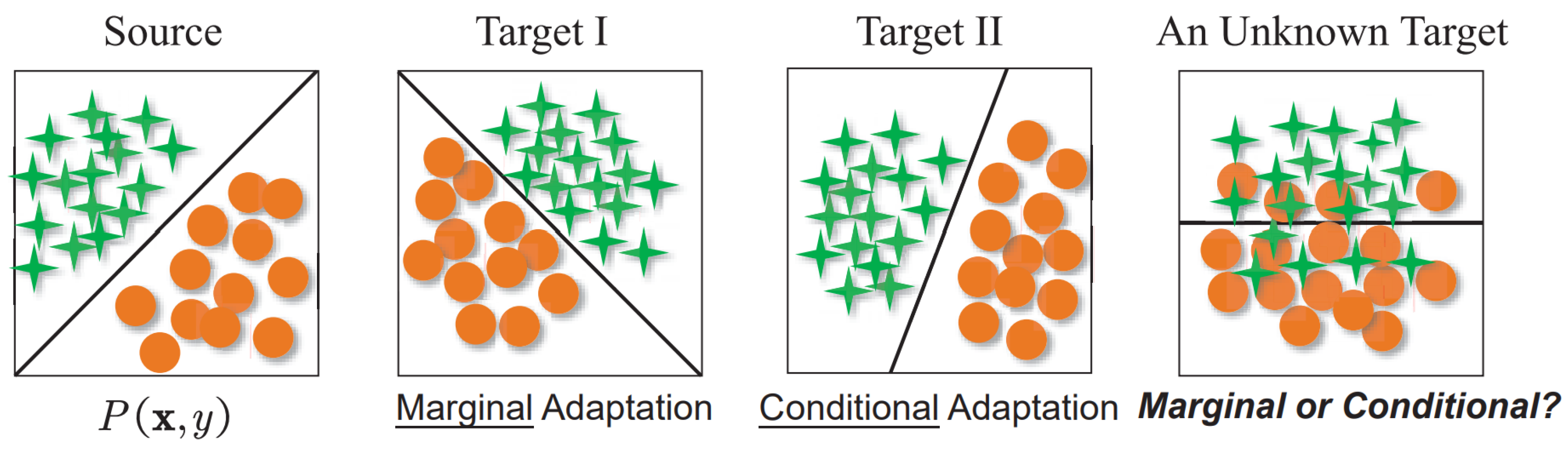
:1. Introduction
- 1.
- A hybrid UPS model with a DANN is proposed with a variable ratio to improve accuracy and robustness;
- 2.
- Unlabeled data are labeled with pseudo-labels to enlarge the labeled target dataset;
- 3.
- The proposed method is successfully verified in the analysis of the bearing fault diagnosis task on the Case Western Reserve University (CWRU) dataset and Xi’an Jiaotong University-Sumyoung (XJTU-SY) dataset, where the diagnosis accuracy is proven to be higher than other well-known fault diagnosis methods.
2. Materials and Methods
2.1. Data Preprocessing
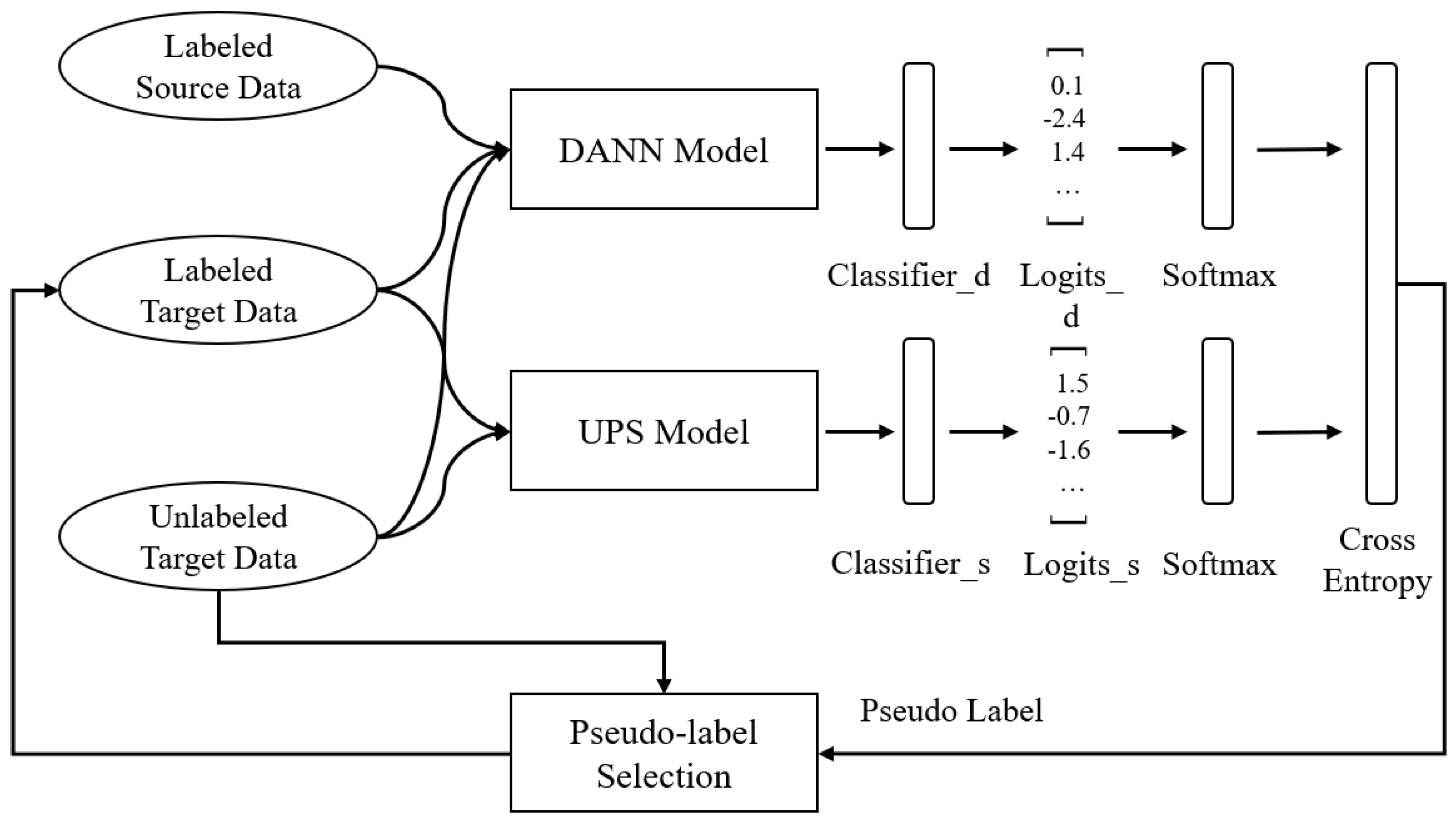
2.2. Proposed Method Based on UPS and a DANN
2.2.1. Negative Learning
2.2.2. Uncertainty Estimation
2.2.3. Model Structure
3. Experiment and Result Analysis
3.1. Experiment Set-Up
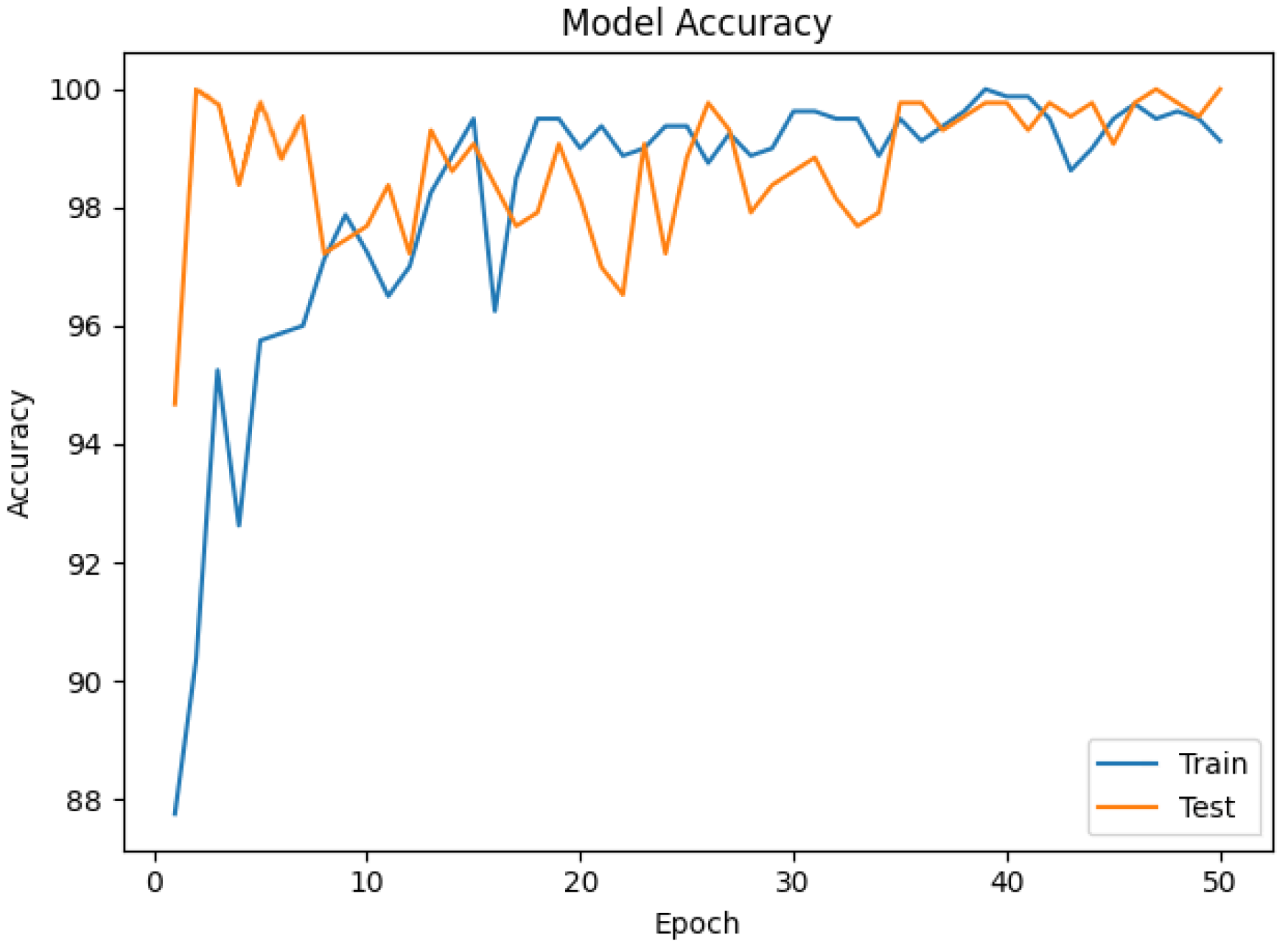
3.2. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Yang, R.; Huang, M.; Han, Y.; Wang, Y.; Di, Y.; Su, D.; Lu, Q. A simultaneous fault diagnosis method based on cohesion evaluation and improved BP-MLL for rotating machinery. Shock Vib. 2021, 2021, 7469691. [Google Scholar] [CrossRef]
- Wu, L.; Yao, B.; Peng, Z.; Guan, Y. Fault diagnosis of roller bearings based on a wavelet neural network and manifold learning. Appl. Sci. 2017, 7, 158. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.; Zhong, M. Machine Learning-Based Fault Diagnosis for Industrial Engineering Systems; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Lu, Q.; Yang, R.; Zhong, M.; Wang, Y. An improved fault diagnosis method of rotating machinery using sensitive features and RLS-BP neural network. IEEE Trans. Instrum. Meas. 2019, 69, 1585–1593. [Google Scholar] [CrossRef]
- Wang, D. K-nearest neighbors based methods for identification of different gear crack levels under different motor speeds and loads: Revisited. Mech. Syst. Signal Process. 2016, 70, 201–208. [Google Scholar] [CrossRef]
- Baraldi, P.; Podofillini, L.; Mkrtchyan, L.; Zio, E.; Dang, V.N. Comparing the treatment of uncertainty in Bayesian networks and fuzzy expert systems used for a human reliability analysis application. Reliab. Eng. Syst. Saf. 2015, 138, 176–193. [Google Scholar] [CrossRef] [Green Version]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An intelligent fault diagnosis method using unsupervised feature learning towards mechanical big data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Liu, R.; Yang, B.; Zio, E.; Chen, X. Artificial intelligence for fault diagnosis of rotating machinery: A review. Mech. Syst. Signal Process. 2018, 108, 33–47. [Google Scholar] [CrossRef]
- LeCun, Y.; Boser, B.; Denker, J.; Henderson, D.; Howard, R.; Hubbard, W.; Jackel, L. Handwritten digit recognition with a back-propagation network. In Advances in Neural Information Processing Systems 2 (NIPS 1989); Neural Information Processing Systems: San Diego, CA, USA, 1989; pp. 396–404. [Google Scholar]
- You, W.; Shen, C.; Guo, X.; Jiang, X.; Shi, J.; Zhu, Z. A hybrid technique based on convolutional neural network and support vector regression for intelligent diagnosis of rotating machinery. Adv. Mech. Eng. 2017, 9, 1687814017704146. [Google Scholar] [CrossRef] [Green Version]
- Ouali, Y.; Hudelot, C.; Tami, M. An overview of deep semi-supervised learning. arXiv 2020, arXiv:2006.05278. [Google Scholar]
- Lee, D.H. Pseudo-label: The simple and efficient semi-supervised learning method for deep neural networks. Workshop Challenges Represent. Learn. ICML 2013, 3, 896. [Google Scholar]
- Rizve, M.N.; Duarte, K.; Rawat, Y.S.; Shah, M. In defense of pseudo-labeling: An uncertainty-aware pseudo-label selection framework for semi-supervised learning. arXiv 2021, arXiv:2101.06329. [Google Scholar]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Wan, Z.; Yang, R.; Huang, M.; Zeng, N.; Liu, X. A review on transfer learning in EEG signal analysis. Neurocomputing 2021, 421, 1–14. [Google Scholar] [CrossRef]
- Wan, Z.; Yang, R.; Huang, M. Deep transfer learning-based fault diagnosis for gearbox under complex working conditions. Shock Vib. 2020, 2020, 8884179. [Google Scholar] [CrossRef]
- Wan, Z.; Yang, R.; Huang, M.; Liu, W.; Zeng, N. EEG fading data classification based on improved manifold learning with adaptive neighborhood selection. Neurocomputing 2022, 482, 186–196. [Google Scholar] [CrossRef]
- Mao, W.; Liu, Y.; Ding, L.; Safian, A.; Liang, X. A new structured domain adversarial neural network for transfer fault diagnosis of rolling bearings under different working conditions. IEEE Trans. Instrum. Meas. 2020, 70, 1–13. [Google Scholar] [CrossRef]
- Wang, X.; Yang, R.; Huang, M. An unsupervised deep-transfer-learning-based motor imagery EEG classification scheme for brain-computer interface. Sensors 2022, 22, 2241. [Google Scholar] [CrossRef]
- Pan, S.J.; Yang, Q. A survey on transfer learning. IEEE Trans. Knowl. Data Eng. 2009, 22, 1345–1359. [Google Scholar] [CrossRef]
- Yang, R.; Huang, M.; Lu, Q.; Zhong, M. Rotating machinery fault diagnosis using long-short-term memory recurrent neural network. IFAC-PapersOnLine 2018, 51, 228–232. [Google Scholar] [CrossRef]
- Ganin, Y.; Ustinova, E.; Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M.; Lempitsky, V. Domain-adversarial training of neural networks. J. Mach. Learn. Res. 2016, 17, 2030–2096. [Google Scholar]
- Yu, C.; Wang, J.; Chen, Y.; Huang, M. Transfer learning with dynamic adversarial adaptation network. In Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM), Beijing, China, 8–11 November 2019; pp. 778–786. [Google Scholar]
- Chen, S.; Yang, R.; Zhong, M. Graph-based semi-supervised random forest for rotating machinery gearbox fault diagnosis. Control Eng. Pract. 2021, 117, 104952. [Google Scholar] [CrossRef]
- Yang, Z.; Yang, R.; Huang, M. Rolling bearing incipient fault diagnosis method based on improved transfer learning with hybrid feature extraction. Sensors 2021, 21, 7894. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Lee, Y.; Tama, B.; Lee, S. Reliability-enhanced camera lens module classification using semi-supervised regression method. Appl. Sci. 2020, 10, 3832. [Google Scholar] [CrossRef]
- Naeini, M.P.; Cooper, G.; Hauskrecht, M. Obtaining well calibrated probabilities using Bayesian binning. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015. [Google Scholar]
- Case Western Reserve University Bearing Data CenterWebsite. Available online: https://engineering.case.edu/bearingdatacenter (accessed on 5 May 2022).
- Wang, B.; Lei, Y.; Li, N.; Li, N. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings. IEEE Trans. Reliab. 2018, 69, 401–412. [Google Scholar] [CrossRef]
- Kim, Y.; Yim, J.; Yun, J.; Kim, J. Nlnl: Negative learning for noisy labels. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 101–110. [Google Scholar]
- Zhang, R.; Tao, H.; Wu, L.; Guan, Y. Transfer learning with neural networks for bearing fault diagnosis in changing working conditions. IEEE Access 2017, 5, 14347–14357. [Google Scholar] [CrossRef]

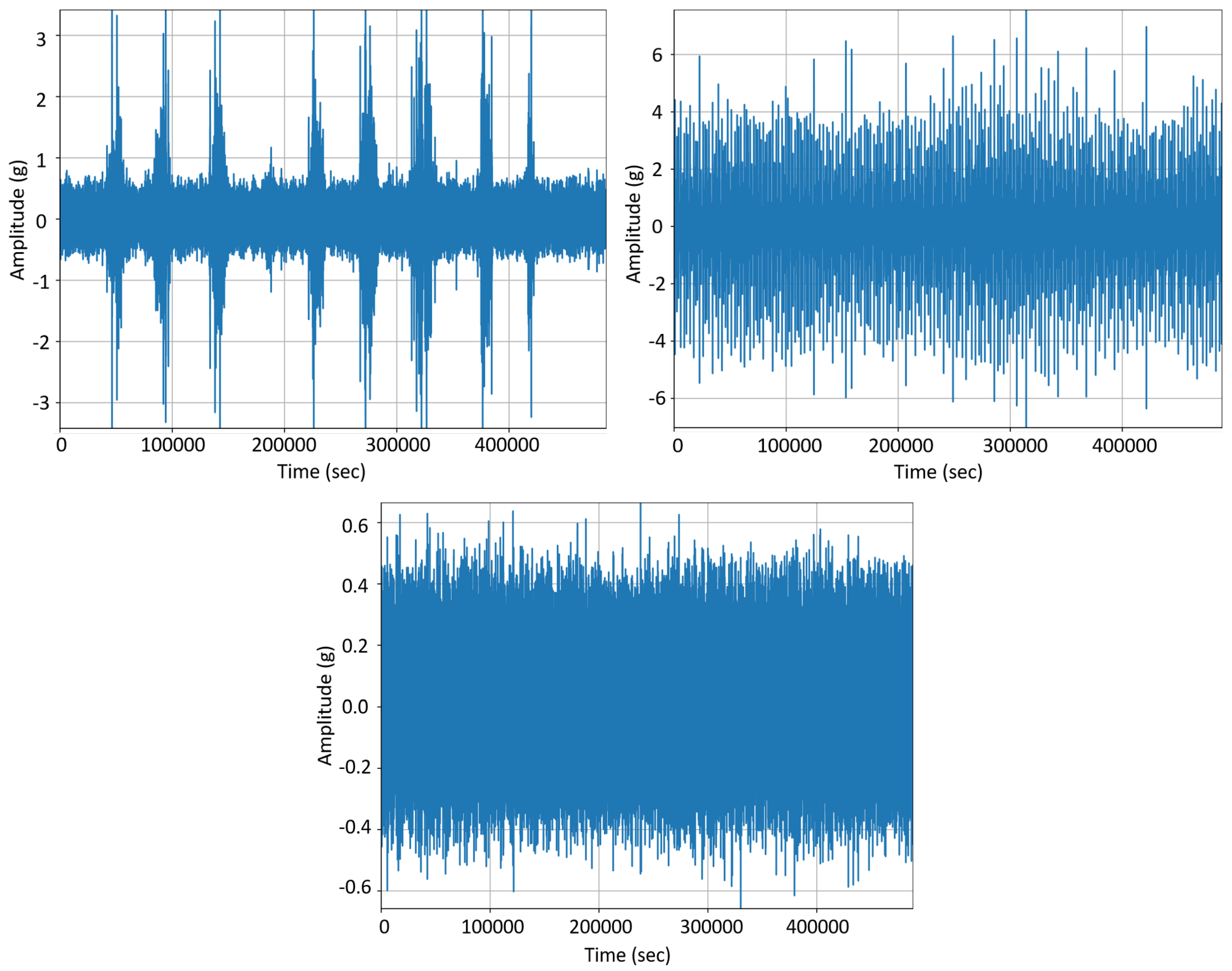
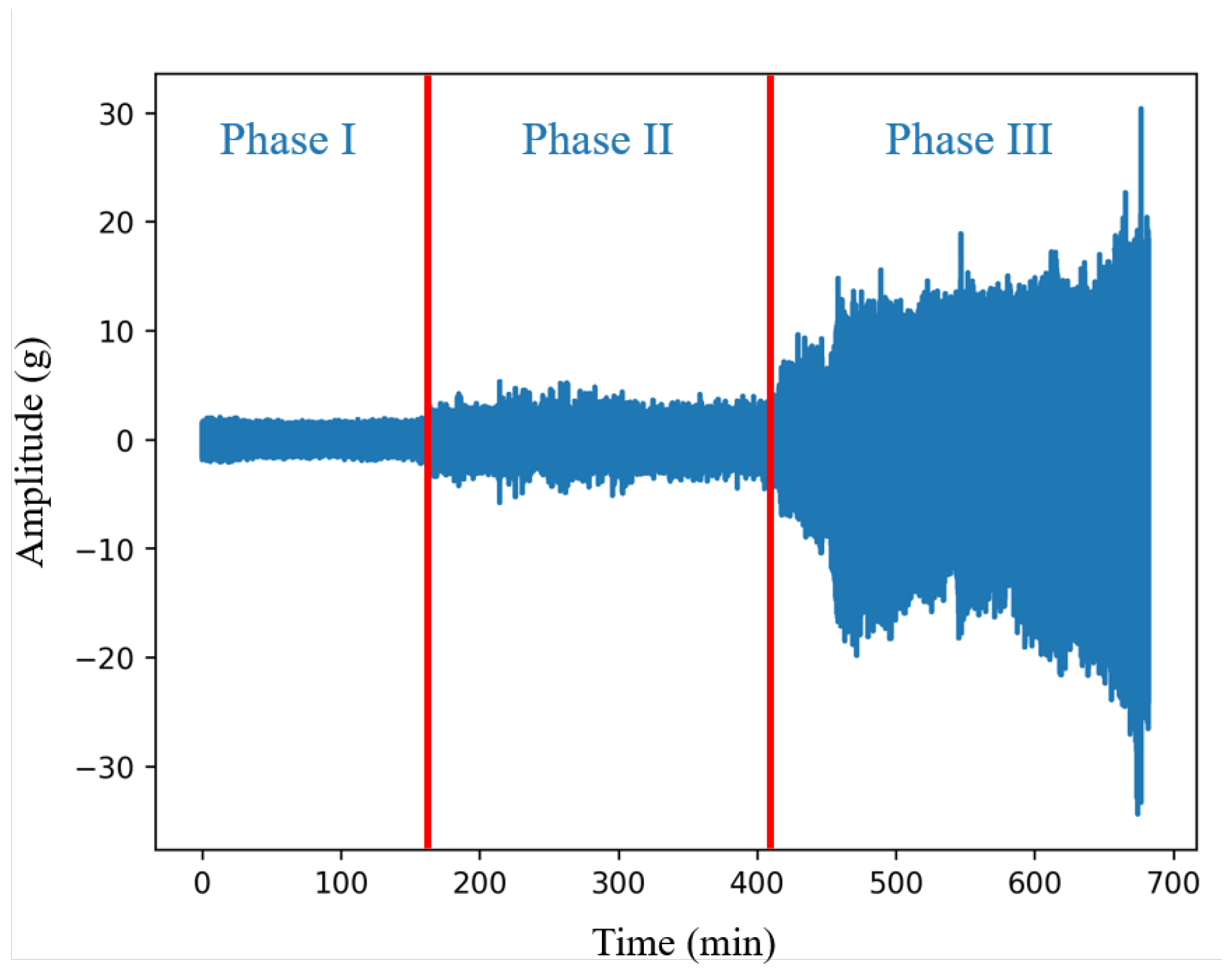

| CWRU | XJTU-SY | |
|---|---|---|
| Working Condition | (1) 1797 rpm (2) 1772 rpm (3) 1750 rpm (4) 1730 rpm | (1) 2100 rpm (35 Hz) and 12 kN (2) 2250 rpm (37.5 Hz) and 11 kN (3) 2400 rpm (40 Hz) and 10 kN |
| Degeneration Process | No | Yes |
| Sample Frequency | 12 kHz 48 kHz | 25.6 kHz |
| Vibration Signals in Each Sample | Around 122,000 | Depends on bearing’s lifetime |
| Fault Element | Inner race, ball, outer race | Inner race, ball, cage, and outer race |
| Fault type | Single fault element | Multiple fault elements |
| Class | Class Label | Source/Target | Labeled or Unlabeled | Data Size |
|---|---|---|---|---|
| Inner Race | 0 | Source Target | Labeled Labeled Unlabeled | 480,000 120,000 552,000 |
| Outer Race | 1 | Source Target | Labeled Labeled Unlabeled | 480,000 120,000 552,000 |
| Normal | 2 | Source Target | Labeled Labeled Unlabeled | 480,000 120,000 552,000 |
| Diameter | Load (HP) | Motor Speed (rpm) | File Name | Fault Element |
|---|---|---|---|---|
| 0.007 | 3 | 1730 | IR007_3 | Inner Race |
| 0.014 | 3 | 1730 | IR014_3 | Inner Race |
| 0.021 | 3 | 1730 | IR021_3 | Inner Race |
| 0.007 | 3 | 1730 | OR007@6_3 | Outer Race |
| 0.014 | 3 | 1730 | OR014@6_3 | Outer Race |
| 0.021 | 3 | 1730 | OR021@6_3 | Outer Race |
| - | - | - | Normal_1 | - |
| - | - | - | Normal_2 | - |
| - | - | - | Normal_3 | - |
| Bearing | Fault Element | Normal Range | Fault Range |
|---|---|---|---|
| Bearing 2_1_37.5 Hz | Inner | 1-452 | 454-484 |
| Bearing 2_2_37.5 Hz | Outer | 1–50 | 51–159 |
| Bearing 2_4_37.5 Hz | Outer | 1–30 | 31–40 |
| Bearing 2_5_37.5 Hz | Outer | 1–120 | 121–337 |
| Bearing 3_1_40 Hz | Outer | 1–2463 | 2464–2536 |
| Bearing 3_3_40 Hz | Inner | 1–340 | 341–369 |
| Bearing 3_4_40 Hz | Inner | 1–1416 | 1417–1514 |
| Bearing 3_5_40 Hz | Outer | 1–10 | 11–110 |
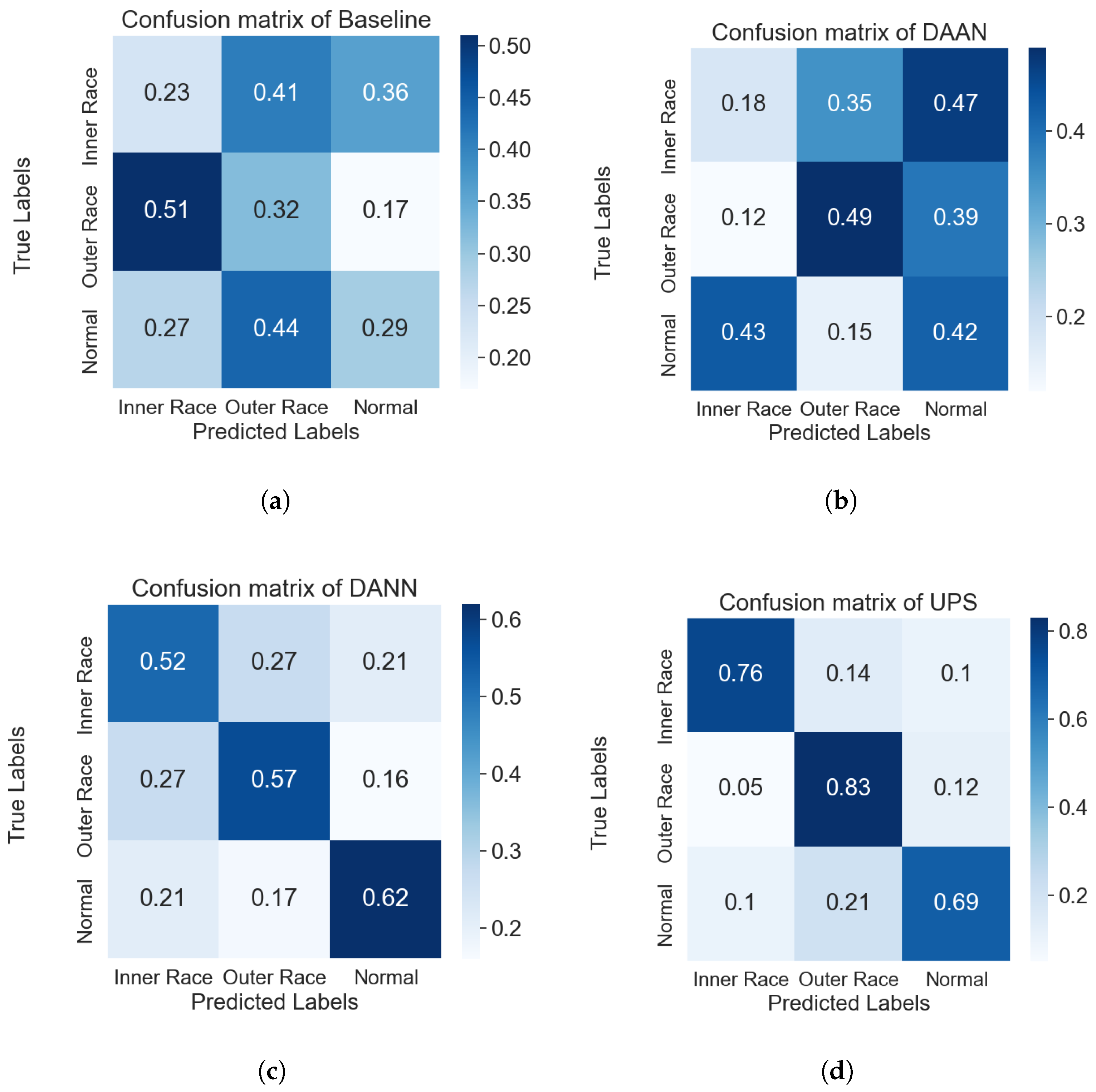
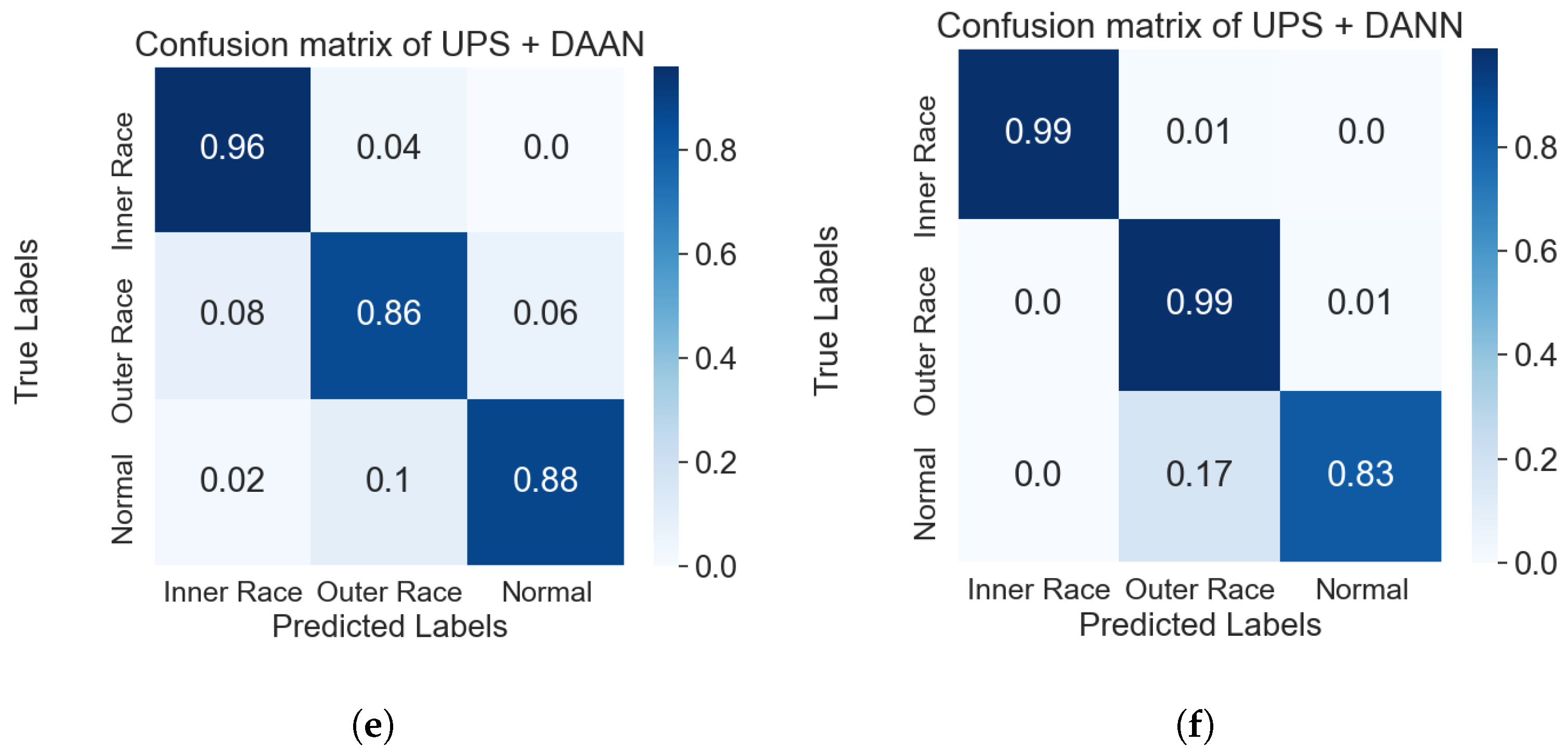
| Model | Best Test Acc. | Average Test Acc. |
|---|---|---|
| Baseline | 29.84% | 23.45% |
| DAAN | 45.67% | 42.33% |
| DANN | 60.72% | 56.88% |
| UPS | 84.21% | 76.35% |
| UPS + DAAN | 96.43% | 90.20% |
| UPS + DANN | 99.63% | 96.77% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zong, X.; Yang, R.; Wang, H.; Du, M.; You, P.; Wang, S.; Su, H. Semi-Supervised Transfer Learning Method for Bearing Fault Diagnosis with Imbalanced Data. Machines 2022, 10, 515. https://doi.org/10.3390/machines10070515
Zong X, Yang R, Wang H, Du M, You P, Wang S, Su H. Semi-Supervised Transfer Learning Method for Bearing Fault Diagnosis with Imbalanced Data. Machines. 2022; 10(7):515. https://doi.org/10.3390/machines10070515
Chicago/Turabian StyleZong, Xia, Rui Yang, Hongshu Wang, Minghao Du, Pengfei You, Su Wang, and Hao Su. 2022. "Semi-Supervised Transfer Learning Method for Bearing Fault Diagnosis with Imbalanced Data" Machines 10, no. 7: 515. https://doi.org/10.3390/machines10070515
APA StyleZong, X., Yang, R., Wang, H., Du, M., You, P., Wang, S., & Su, H. (2022). Semi-Supervised Transfer Learning Method for Bearing Fault Diagnosis with Imbalanced Data. Machines, 10(7), 515. https://doi.org/10.3390/machines10070515







