Vibration Control of Disturbed All-Clamped Plate with an Inertial Actuator Based on Cascade Active Disturbance Rejection Control
Abstract
:1. Introduction
2. Preliminaries
2.1. Linear Dynamics of All-Clamped Plate
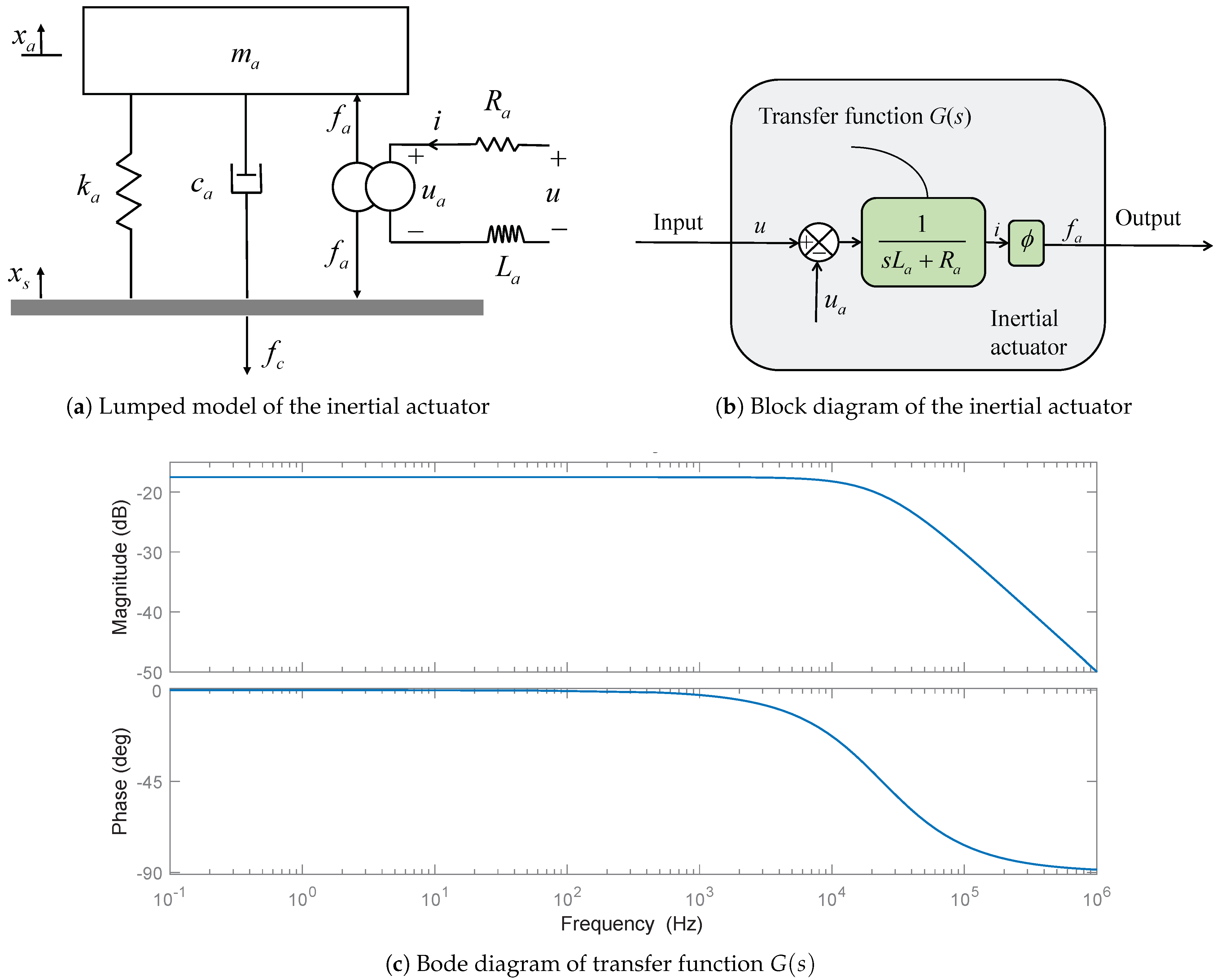
2.2. Linear Dynamics of Inertial Actuator
2.3. Nonlinear Dynamics of the System
3. Control Scheme
3.1. System Re-Modeling
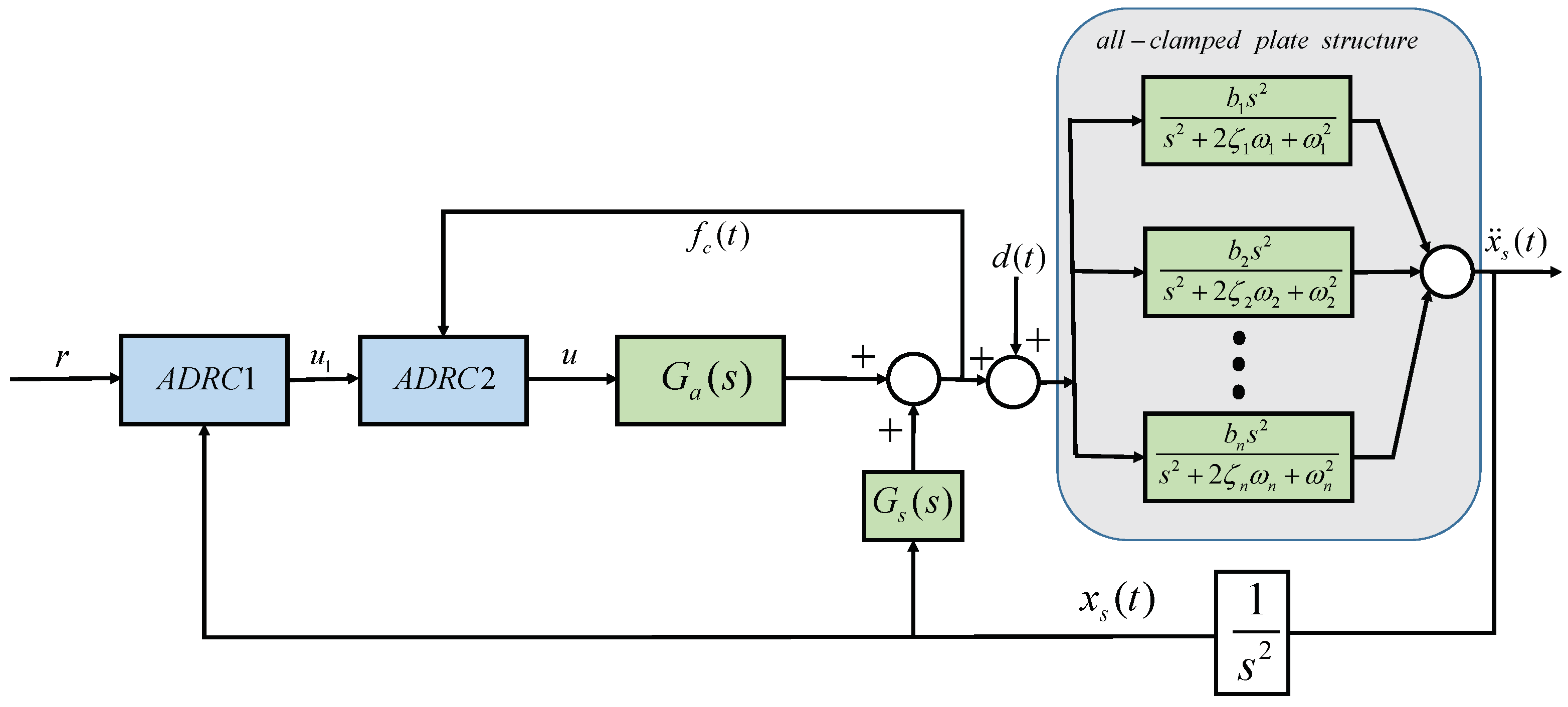
3.2. Cascade Active Disturbance Rejection Vibration Controller
3.3. Parameter Selection Guidelines
3.4. Stability Analysis
4. Experimental Verification
4.1. Experimental Set Up
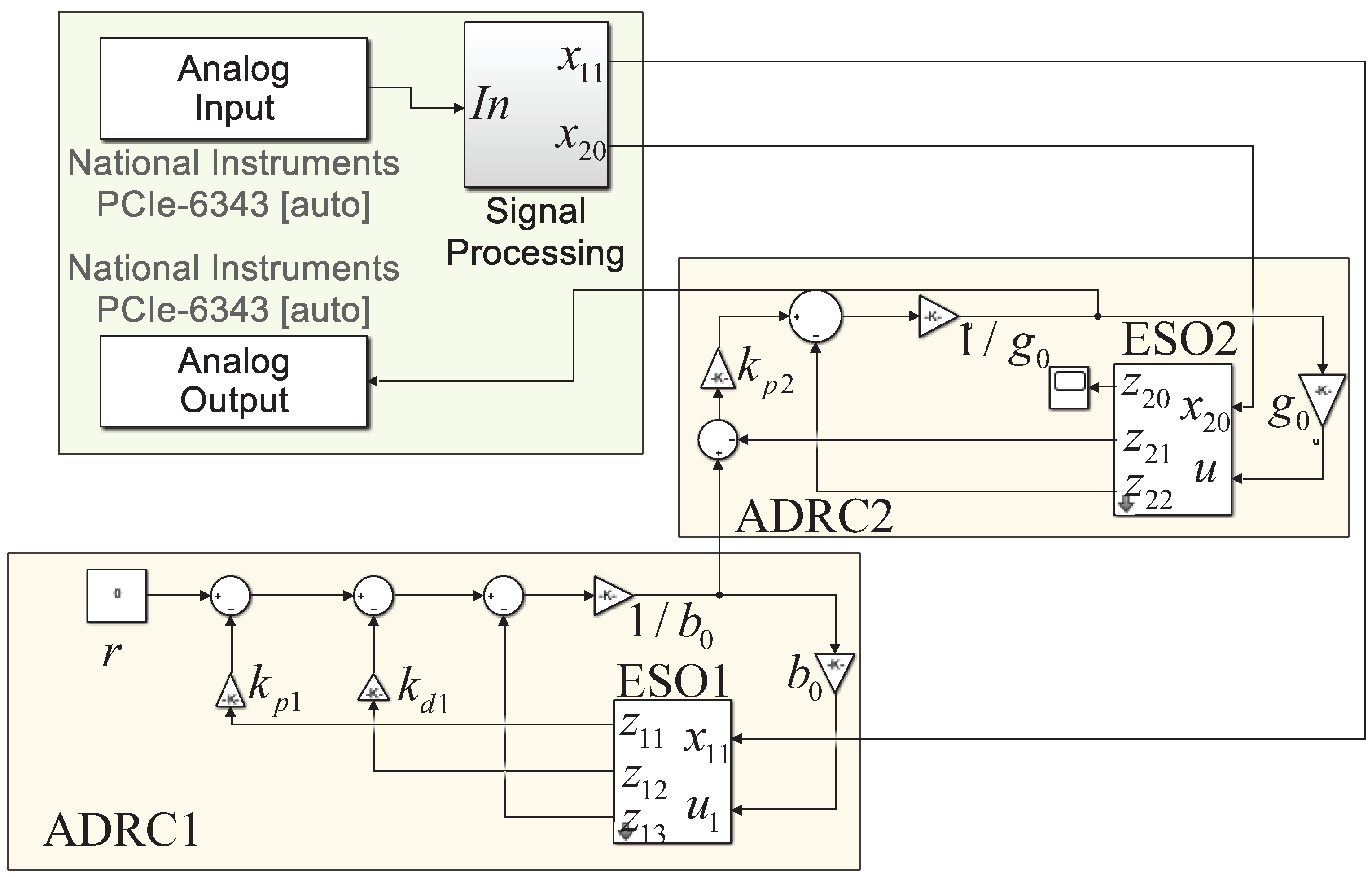
4.1.1. Design of the Hardware Components
4.1.2. Software System Development
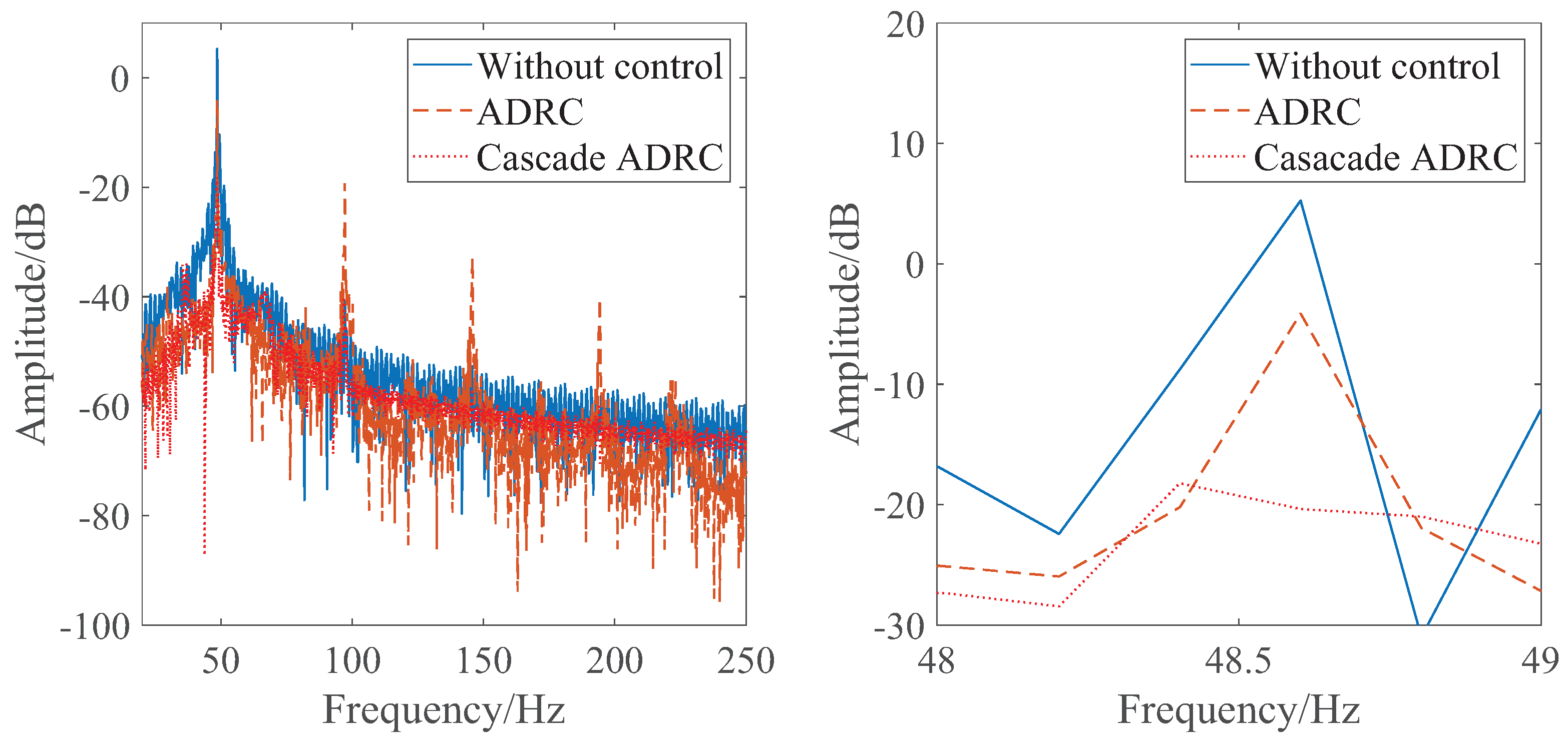
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Borgo, M.; Tehrani, M.; Elliott, S. Active nonlinear control of a stroke limited inertial actuator: Theory and experiment. J. Sound Vib. 2020, 465, 115009. [Google Scholar] [CrossRef]
- Camperi, S.; Tehrani, M.; Elliott, S. Parametric study on the optimal tuning of an inertial actuator for vibration control of a plate: Theory and experiments. J. Sound Vib. 2018, 435, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Boulandet, R.; Michau, M.; Micheau, P.; Berry, A. Aircraft panel with sensorless active sound power reduction capabilities through virtual mechanical impedances. J. Sound Vib. 2016, 361, 2–19. [Google Scholar] [CrossRef]
- Camperi, S.; Tehrani, M.; Elliott, S. Local tuning and power requirements of a multi-input multi-output decentralised velocity feedback with inertial actuators. Mech. Syst. Signal Process. 2019, 117, 689–708. [Google Scholar] [CrossRef] [Green Version]
- Dáz, C.G.; Gardonio, P. Feedback control laws for proof-mass electrodynamic actuators. Smart Mater. Struct. 2007, 16, 1766–1783. [Google Scholar]
- Airimitoaie, T.; Landau, I. Robust and Adaptive Active Vibration Control Using an Inertial Actuator. IEEE Trans. Ind. Electron. 2016, 63, 6482–6489. [Google Scholar] [CrossRef] [Green Version]
- Cao, T.; Chen, L.; He, F.; Summut, K. Adaptive integral sliding mode control for active vibration absorber design. In Proceedings of the 39th IEEE Conference Decision and Control, Sydney, Australia, 12–15 December 2000; pp. 2436–2437. [Google Scholar]
- Zhang, L.; Li, S.; Zhu, C.; Li, J. Eso-based vibration control for all-clamped plate using an electrodynamic inertial actuator. Int. J. Struct. Stab. Dyn. 2022, 22, 2250013. [Google Scholar] [CrossRef]
- Borgo, M.; Tehrani, M.; Elliott, S. Identification and analysis of nonlinear dynamics of inertial actuators. Mech. Syst. Signal Process. 2019, 115, 338–360. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Zhang, L.; Zhu, C.; Su, J.; Li, J. Nonlinear eso-based vibration control for an all-clamped piezoelectric plate with disturbances and time delay: Design and hardware implementation. J. Intell. Mater. Syst. Struct. 2022. [Google Scholar] [CrossRef]
- Chi, R.; Li, H.; Shen, D.; Hou, Z.; Huang, B. Enhanced P-type Control: Indirect Adaptive Learning from Set-point Updates. IEEE Trans. Autom. Control 2022. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J.; Wu, H.; Kang, S. Robust precision motion control of piezoelectric actuators using fast nonsingular terminal sliding mode with time delay estimation. Meas. Control 2018, 52, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Yang, J.; Guo, L.; Li, S. Disturbance-observer-based control and related methods—An overview. IEEE Trans. Ind. Electron. 2016, 63, 1083–1095. [Google Scholar] [CrossRef] [Green Version]
- Wei, W.; Duan, B.; Zuo, M. Active disturbance rejection control for a piezoelectric nano-positioning system: A U-model approach. Meas. Control 2021, 54, 506–518. [Google Scholar] [CrossRef]
- Han, J. From PID to Active Disturbance Rejection Control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Guo, B.; Bacha, S.; Alamir, M.; Hably, A.; Boudinet, C. Generalized Integrator-Extended State Observer with Applications to Grid-Connected Converters in the Presence of Disturbances. IEEE Trans. Control. Syst. Technol. 2021, 29, 744–755. [Google Scholar] [CrossRef]
- Abdul-Adheem, W.; Ibraheem, I.; Humaidi, A.; Azar, A. Model-free active input-output feedback linearization of a single-link flexible joint manipulator: An improved active disturbance rejection control approach. Meas. Control 2021, 54, 856–871. [Google Scholar] [CrossRef]
- Madonski, R.; Shao, S.; Zhang, H.; Gao, Z.; Yang, J.; Li, S. General error-based active disturbance rejection control for swift industrial implementations. Control Eng. Pract. 2019, 84, 218–229. [Google Scholar] [CrossRef]
- Zhang, F.; Hou, J.; Ning, D.; Gong, Y. Depth Control of an Oil Bladder Type Deep-Sea AUV Based on Fuzzy Adaptive Linear Active Disturbance Rejection Control. Machines 2022, 10, 163. [Google Scholar] [CrossRef]
- Roman, R.; Precup, R.; Petriu, E. Hybrid Data-Driven Fuzzy Active Disturbance Rejection Control for Tower Crane Systems. Eur. J. Control 2021, 58, 373–387. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Y.; Li, Z.; Zhao, C.; Gao, F.; Xu, F.; Wang, P. Extended-state-observer based model predictive control of a hybrid modular dc transformer. IEEE Trans. Ind. Electron. 2022, 69, 1561–1572. [Google Scholar] [CrossRef]
- Baz, A. Active acoustic metamaterial with tunable effective density using a disturbance rejection controller. J. Appl. Phys. 2019, 125, 074503. [Google Scholar] [CrossRef]
- Li, S.Q.; Zhu, C.W.; Mao, Q.B.; Su, J.Y.; Li, J. Active disturbance rejection vibration control for an all-clamped piezoelectric plate with delay. Control Eng. Pract. 2021, 108, 104719. [Google Scholar]
- Hezzi, A.; Elghali, S.; Bensalem, Y.; Zhou, Z.; Benbouzid, M.; Abdelkrim, M. ADRC-Based Robust and Resilient Control of a 5-Phase PMSM Driven Electric Vehicle. Machines 2020, 8, 17. [Google Scholar] [CrossRef]
- Díaz, I.; Pereira, E.; Hudson, M.; Reynolds, P. Enhancing active vibration control of pedestrian structures using inertial actuators with local feedback control. Eng. Struct. 2012, 41, 157–166. [Google Scholar] [CrossRef]
- Huyanan, S.; Sims, N. Vibration control strategies for proof-mass actuators. J. Vib. Control 2007, 13, 1785–1806. [Google Scholar] [CrossRef] [Green Version]
- Madonski, R.; Herman, P. Method of sensor noise attenuation in high-gain observers; Experimental verification on two laboratory systems. In Proceedings of the 2012 IEEE International Symposium on Robotic and Sensors Environments Proceedings, Magdeburg, Germany, 16–18 November 2012; pp. 121–126. [Google Scholar]
- Xue, W.; Huang, Y. Performance analysis of 2-DOF tracking for a class of nonlinear uncertain systems with discontinuous disturbances. Int. J. Robust Nonlinear Control 2018, 28, 1456–1473. [Google Scholar] [CrossRef]




| The dimensions of the plate | 0.5 × 0.5 m |
| The thickness of the plate | 0.001 m |
| The mass density of the plate | 2700 kg/m |
| The Young’s modulus of the plate E | 7.1 × N/m |
| The Poisson ratio of the plate | 0.33 |
| First resonant frequency f | 48.6 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Li, J.; Li, S.; Gu, R. Vibration Control of Disturbed All-Clamped Plate with an Inertial Actuator Based on Cascade Active Disturbance Rejection Control. Machines 2022, 10, 528. https://doi.org/10.3390/machines10070528
Zhang L, Li J, Li S, Gu R. Vibration Control of Disturbed All-Clamped Plate with an Inertial Actuator Based on Cascade Active Disturbance Rejection Control. Machines. 2022; 10(7):528. https://doi.org/10.3390/machines10070528
Chicago/Turabian StyleZhang, Luyao, Juan Li, Shengquan Li, and Renjing Gu. 2022. "Vibration Control of Disturbed All-Clamped Plate with an Inertial Actuator Based on Cascade Active Disturbance Rejection Control" Machines 10, no. 7: 528. https://doi.org/10.3390/machines10070528
APA StyleZhang, L., Li, J., Li, S., & Gu, R. (2022). Vibration Control of Disturbed All-Clamped Plate with an Inertial Actuator Based on Cascade Active Disturbance Rejection Control. Machines, 10(7), 528. https://doi.org/10.3390/machines10070528







