The Unsteady-State Response of Tires to Slip Angle and Vertical Load Variations
Abstract
:1. Introduction
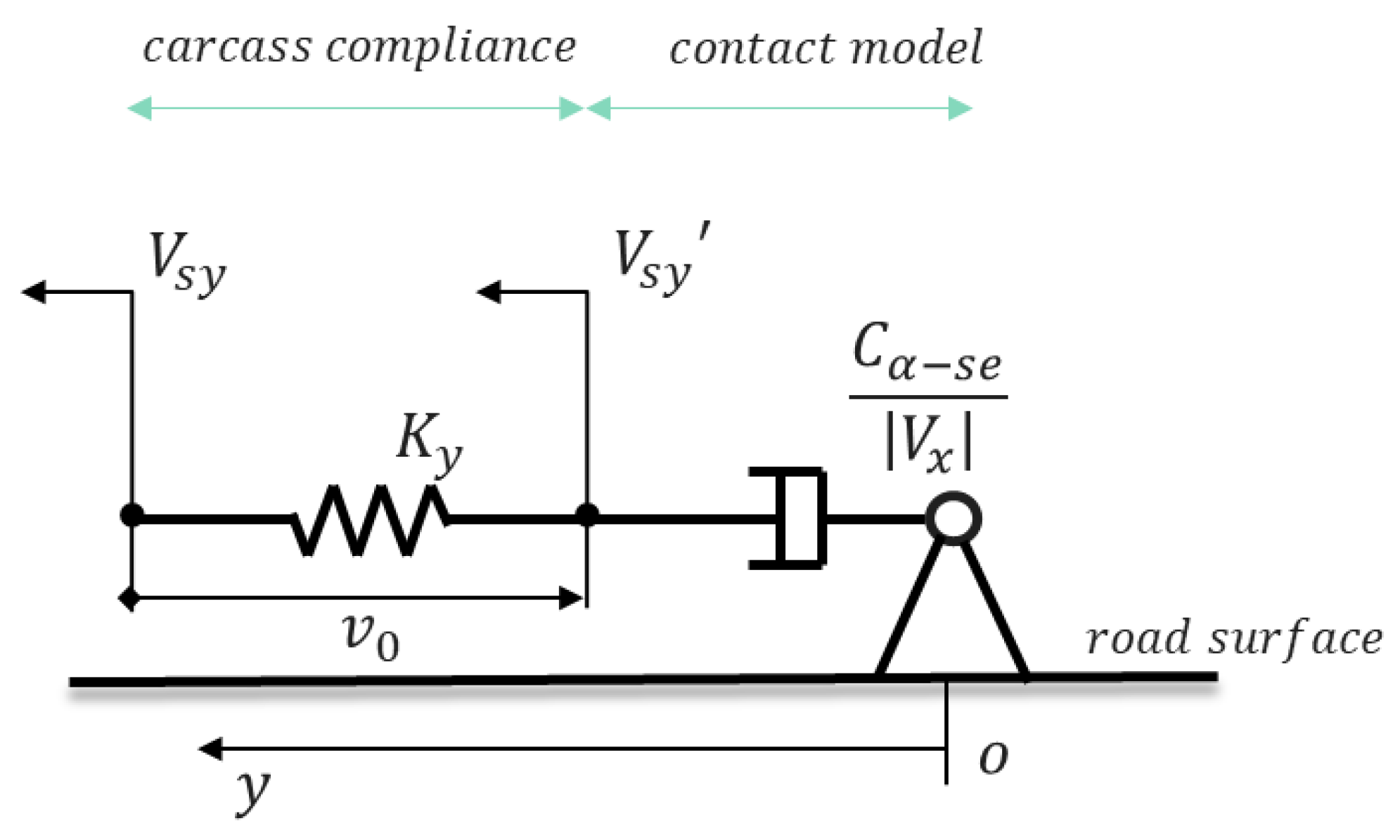
2. Unsteady Cornering Theoretical Model Considering Complex Deformation of Carcass
- (1)
- The complex deformation (lateral) of the carcass is expressed by the superposition of three deformations of translation, torsion, and bending;
- (2)
- It is used for side deviation analysis without considering the influence of tire width;
- (3)
- For cornering analysis, only the lateral deformation of the tread is considered;
- (4)
- Inertia factors, such as tire mass and gyroscopic effect, are not considered, and it is assumed to be a steady system;
- (5)
- In the initial state (), each state parameter and variable starts from 0 (displacement, deformation, etc.);
- (6)
- For small movements near any slip angle, the slip between the tread end point and the road surface is considered, but the input conditions for small movements of local linearization are still satisfied;
- (7)
- The stiffness and deformation of the tire carcass and tread are not considered;
- (8)
- The pressure distribution of the grounding trace is assumed not to consider the width;
- (9)
- Only pure cornering conditions are considered, and the imprint update speed is consistent with the longitudinal translation speed of the tire;
3. Nonlinear Unsteady Dynamic Load Sideslip Semi-Physical Model
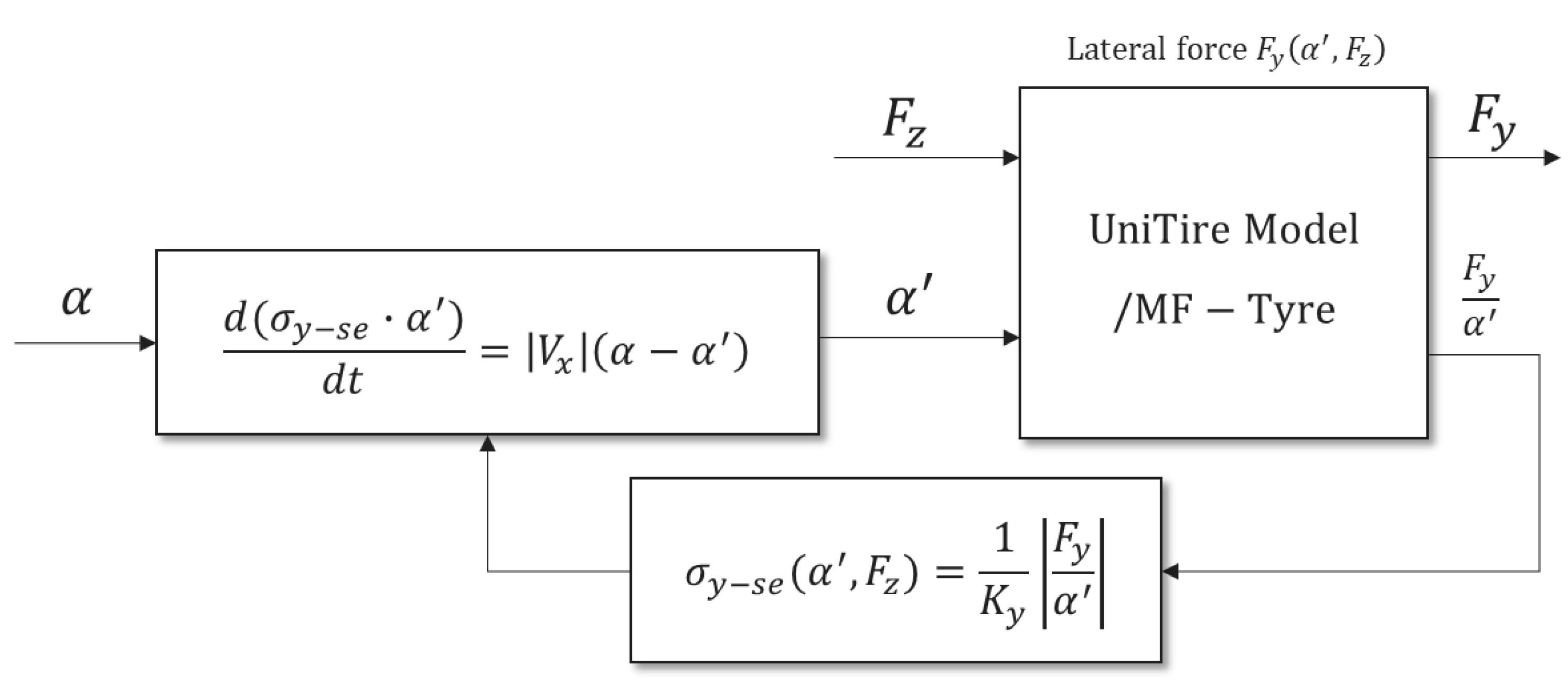
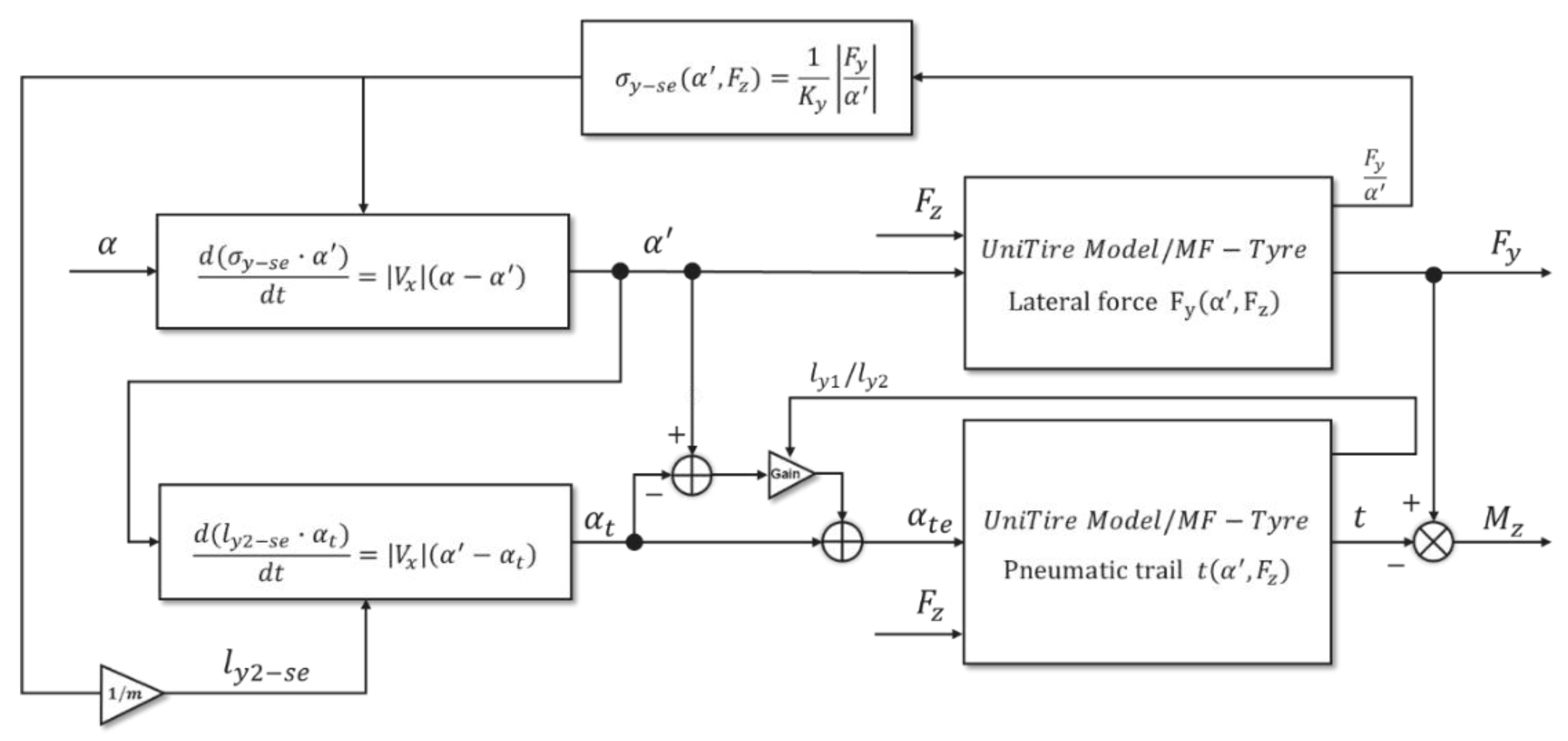
3.1. Nonlinear Unsteady Semi-Physical Model of Tire Lateral Force
3.2. Nonlinear Unsteady Semi-Physical Model of Tire Aligning Torque
4. Results and Discussion
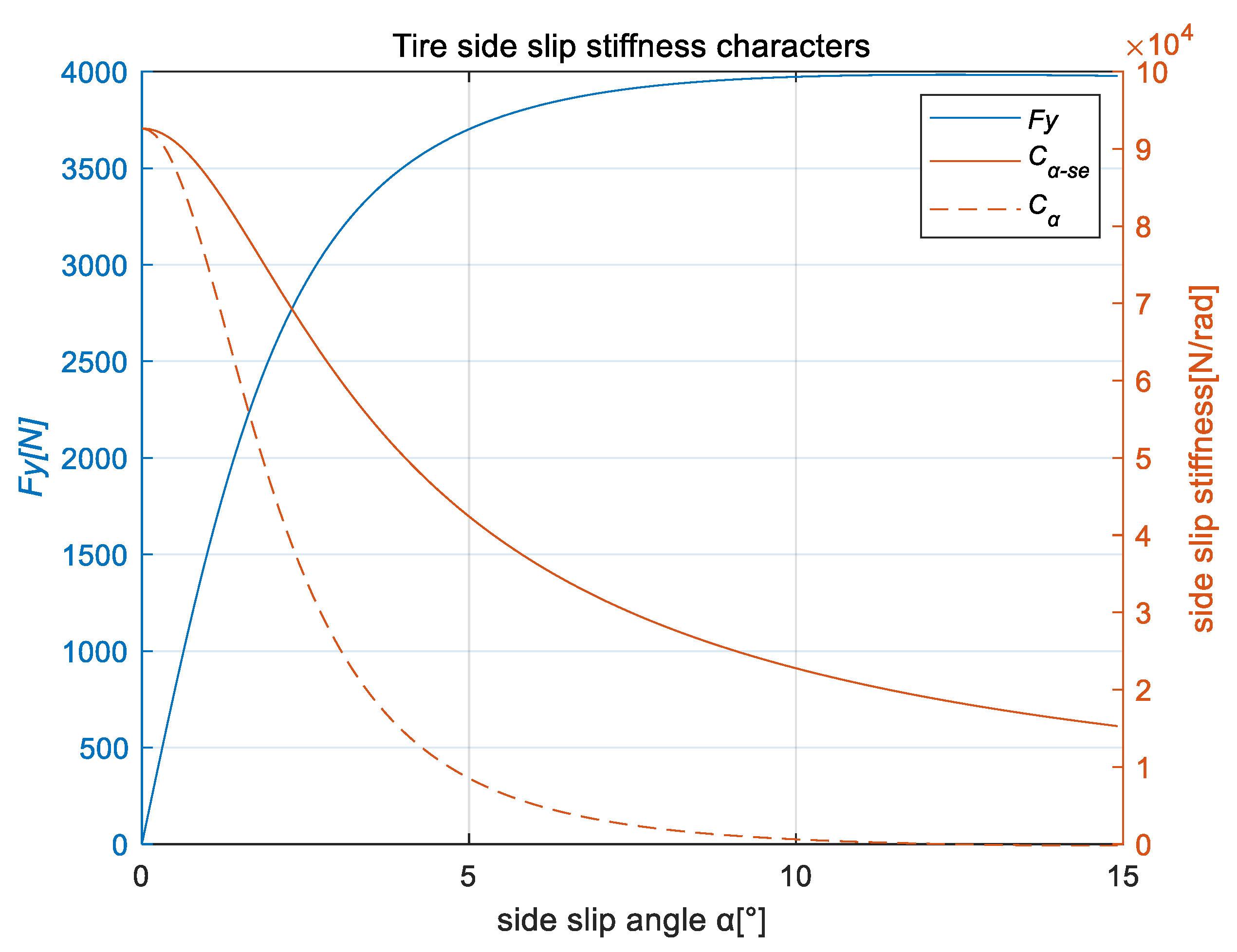
4.1. Characteristic Identification of Tire Steady-State Cornering Lateral Force and Realigning Moment for Dynamic Load Research
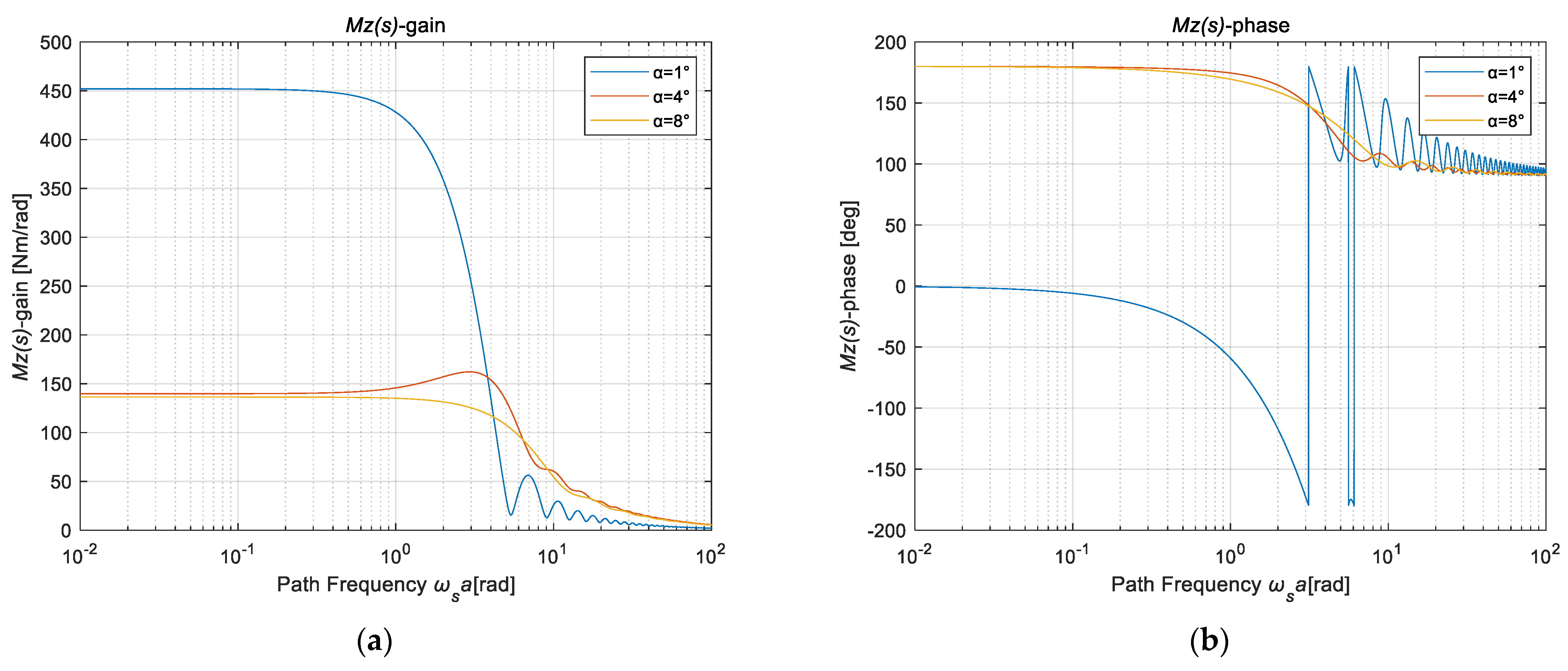
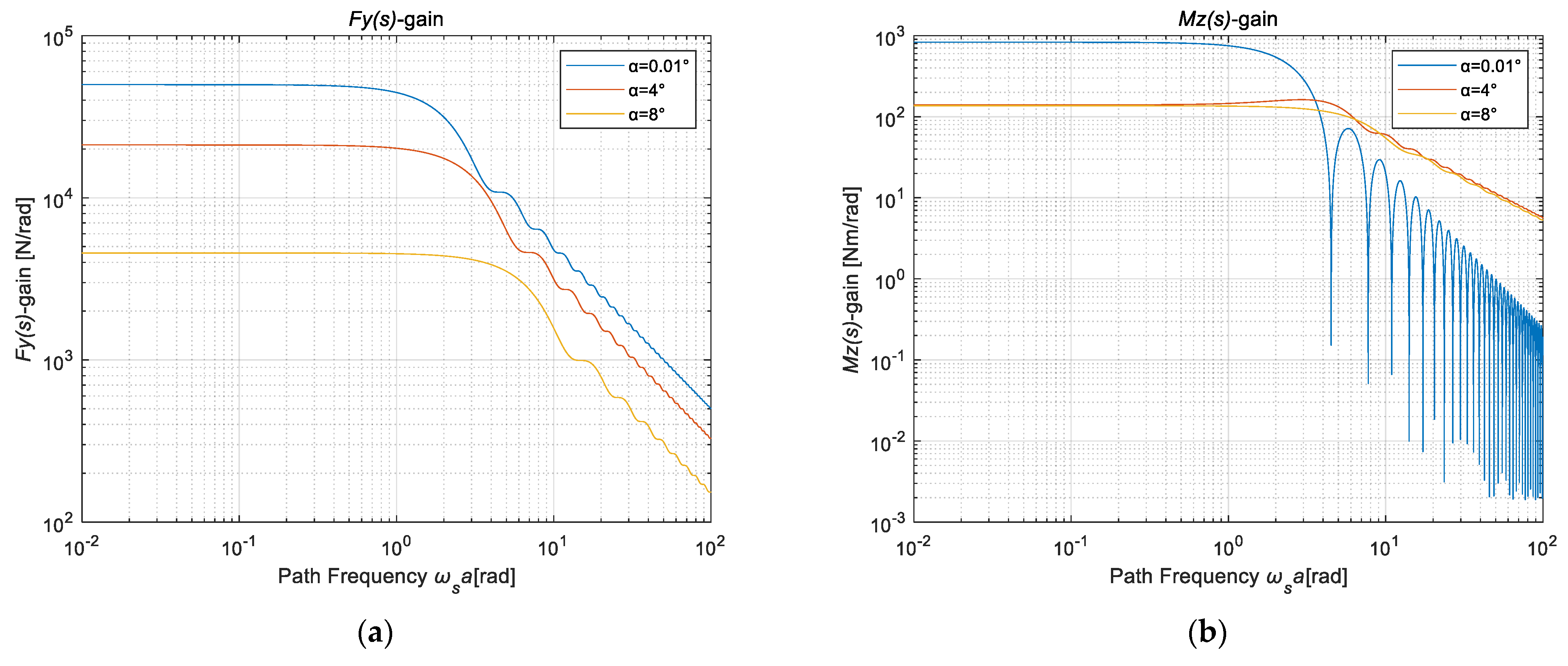
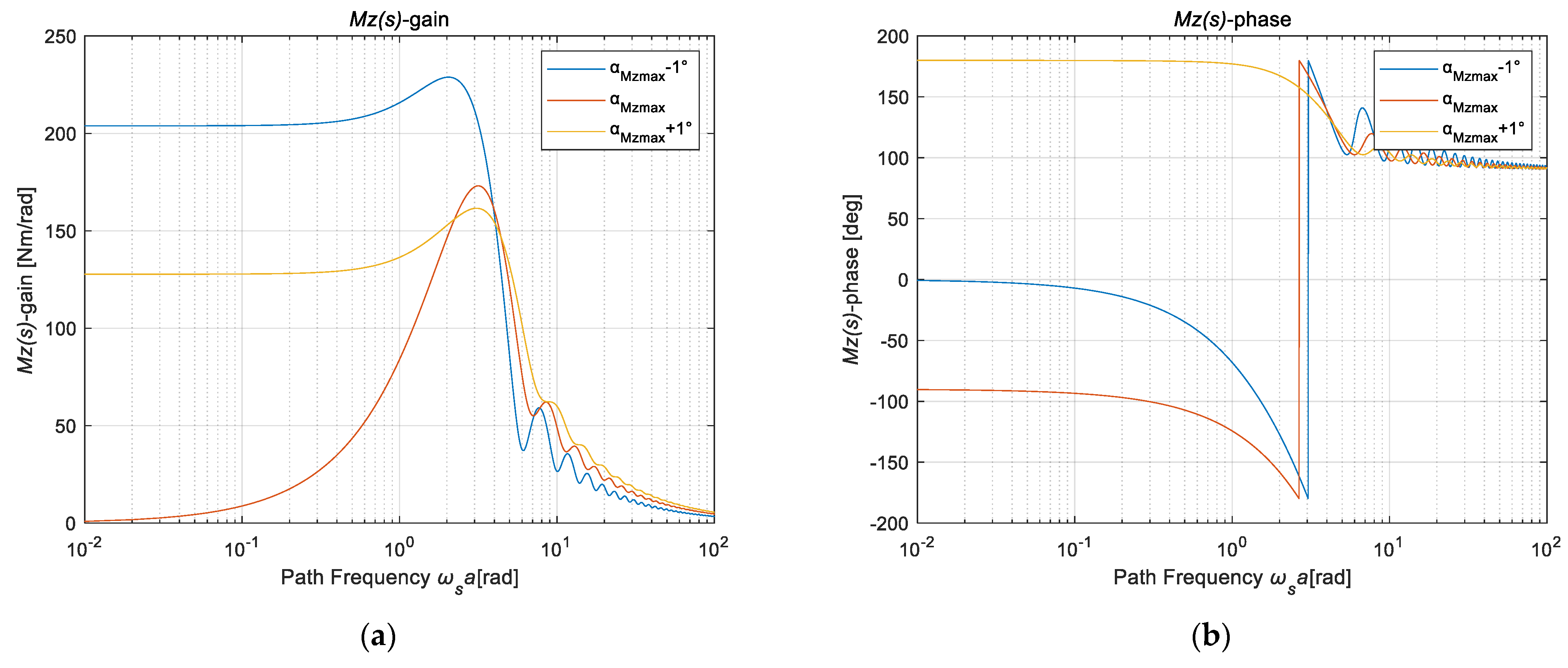
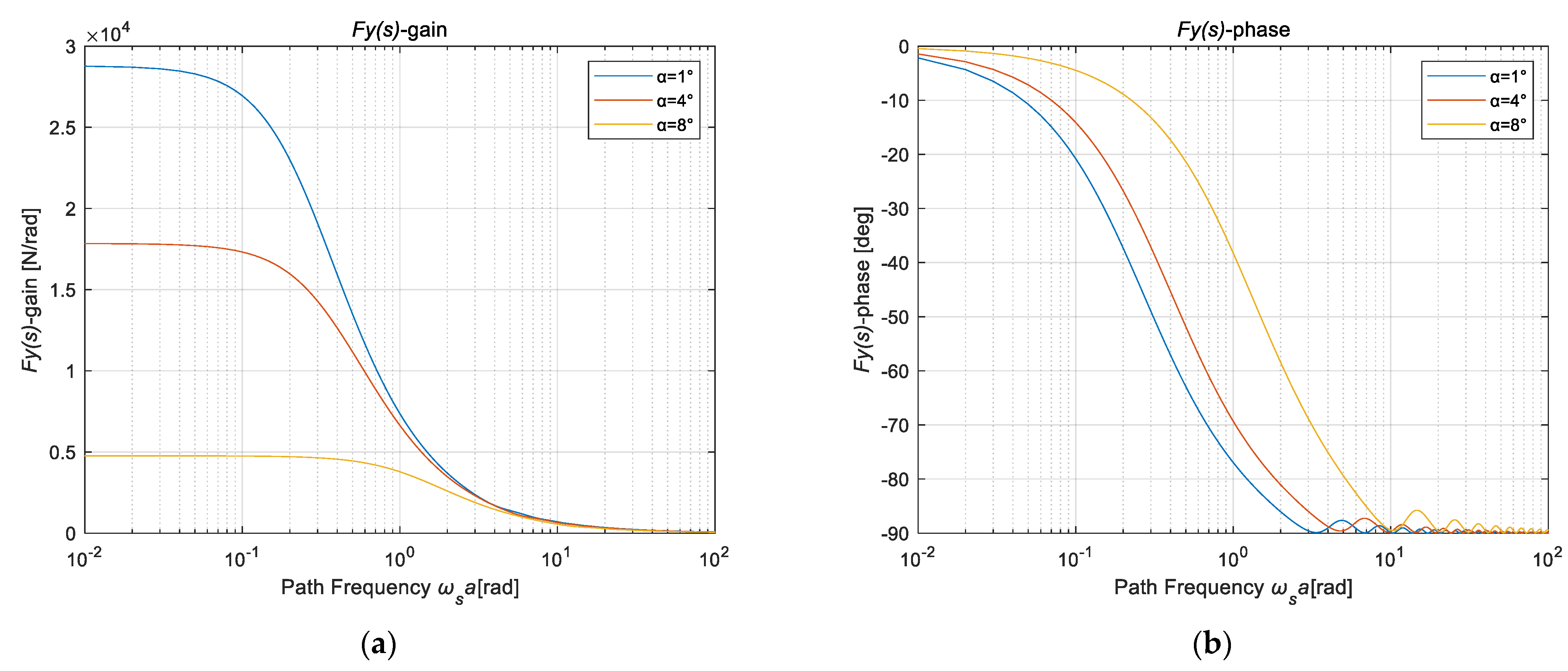
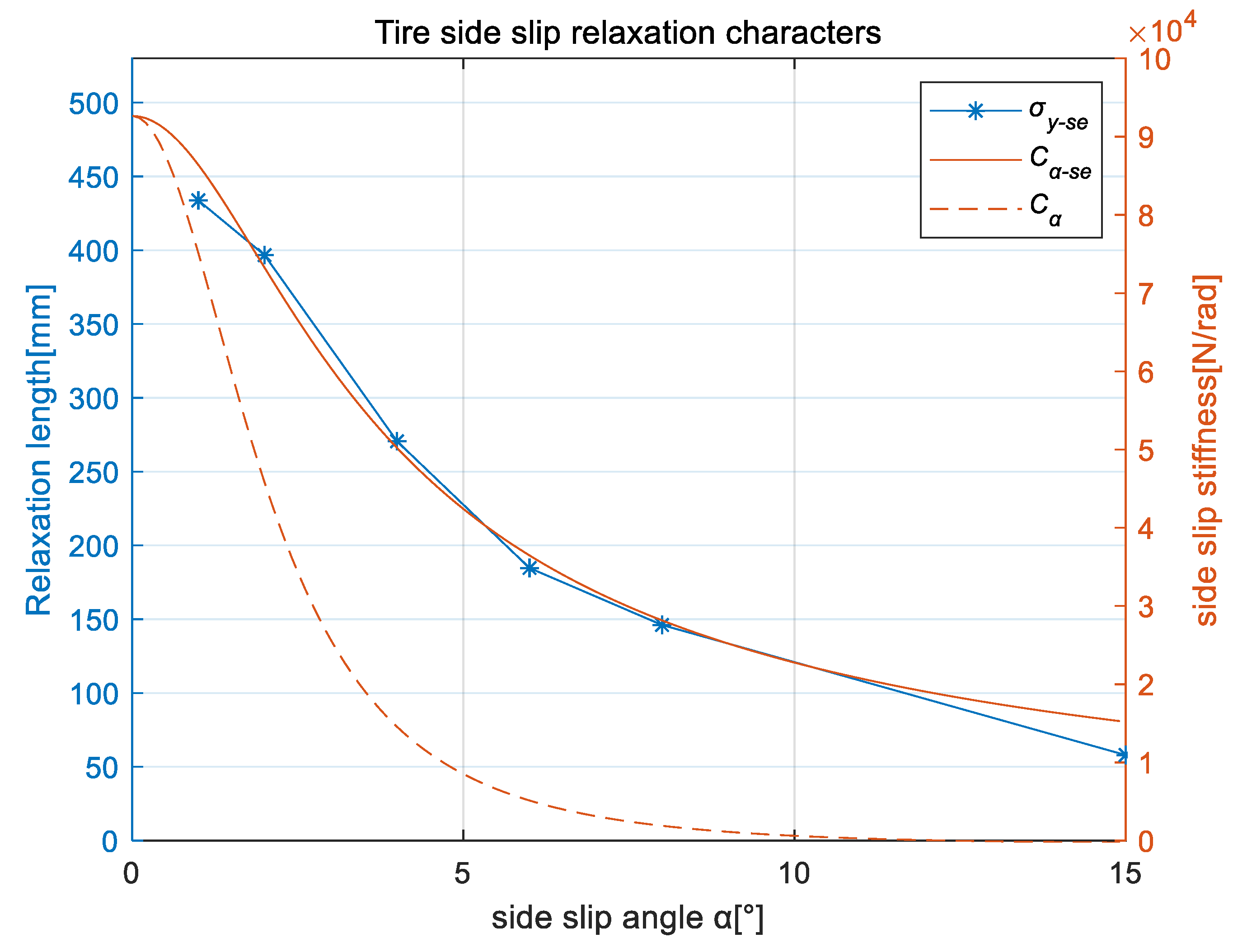
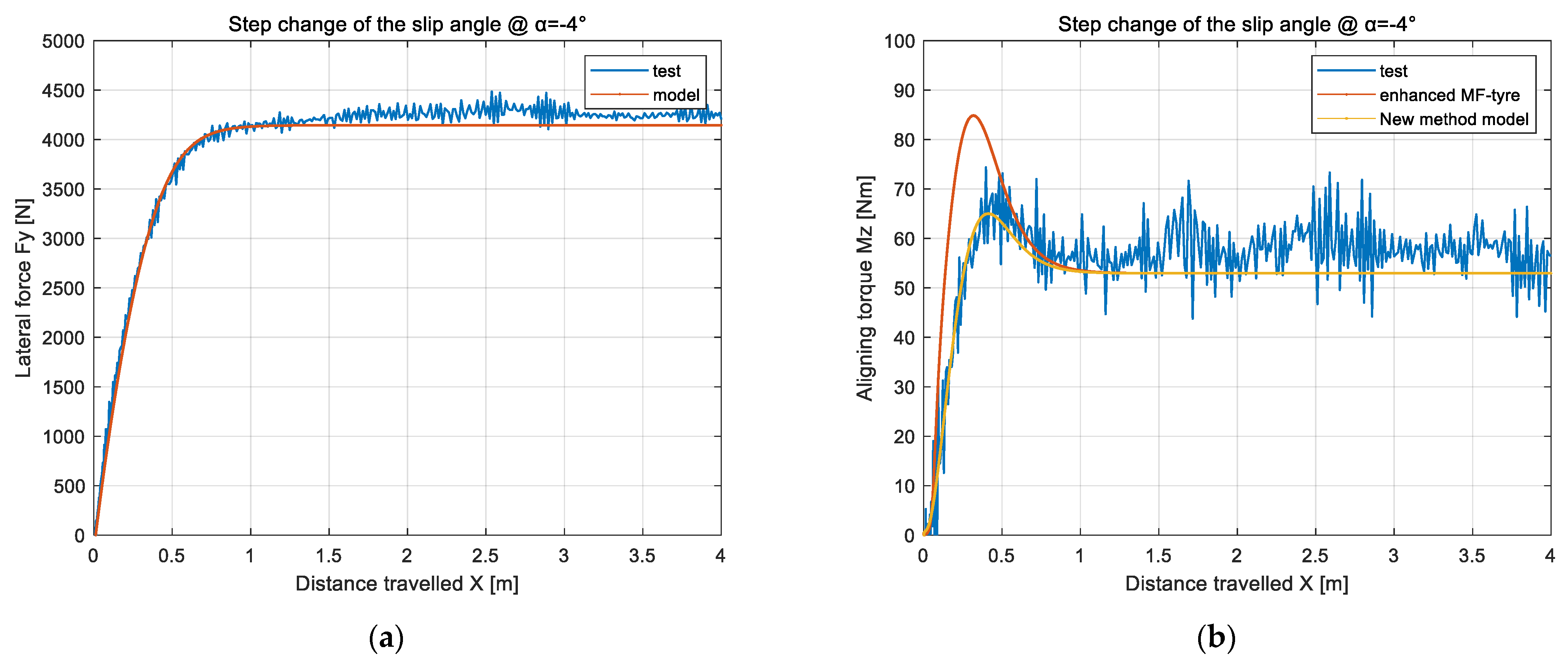
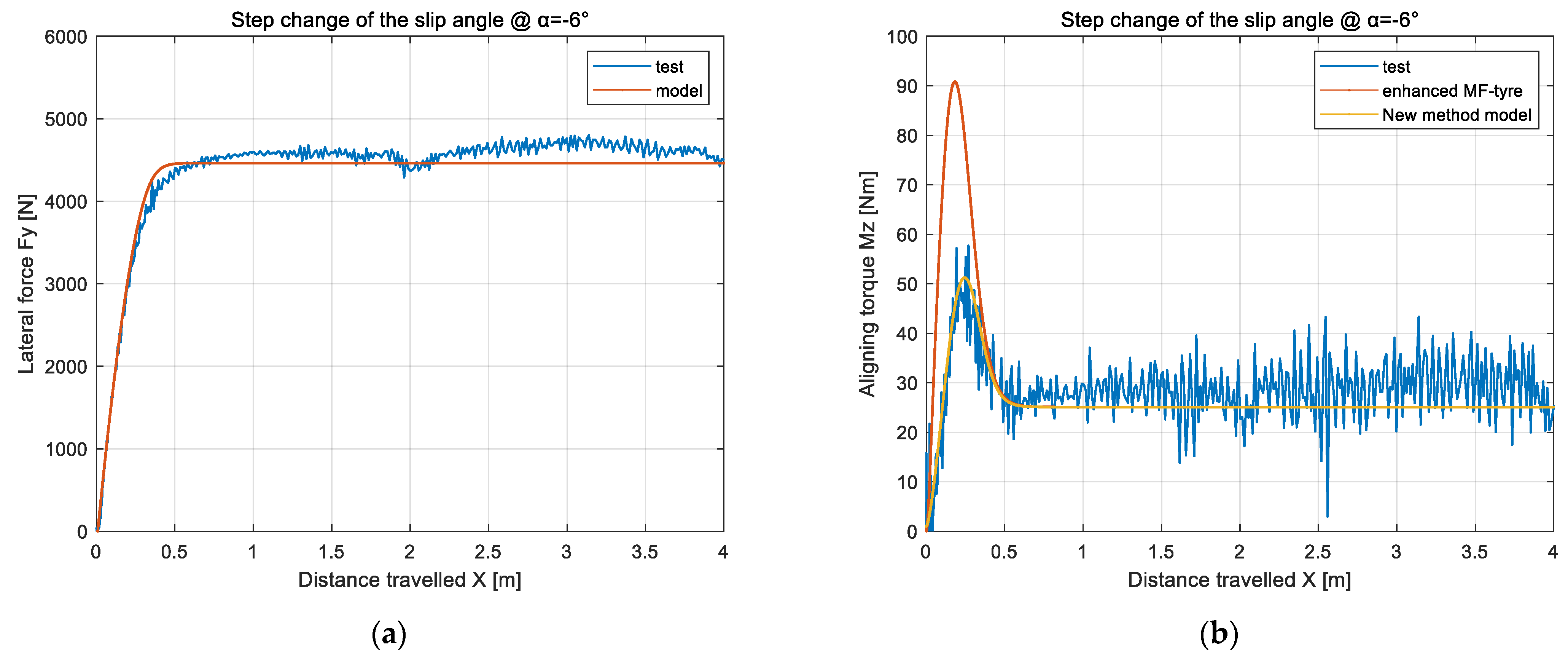
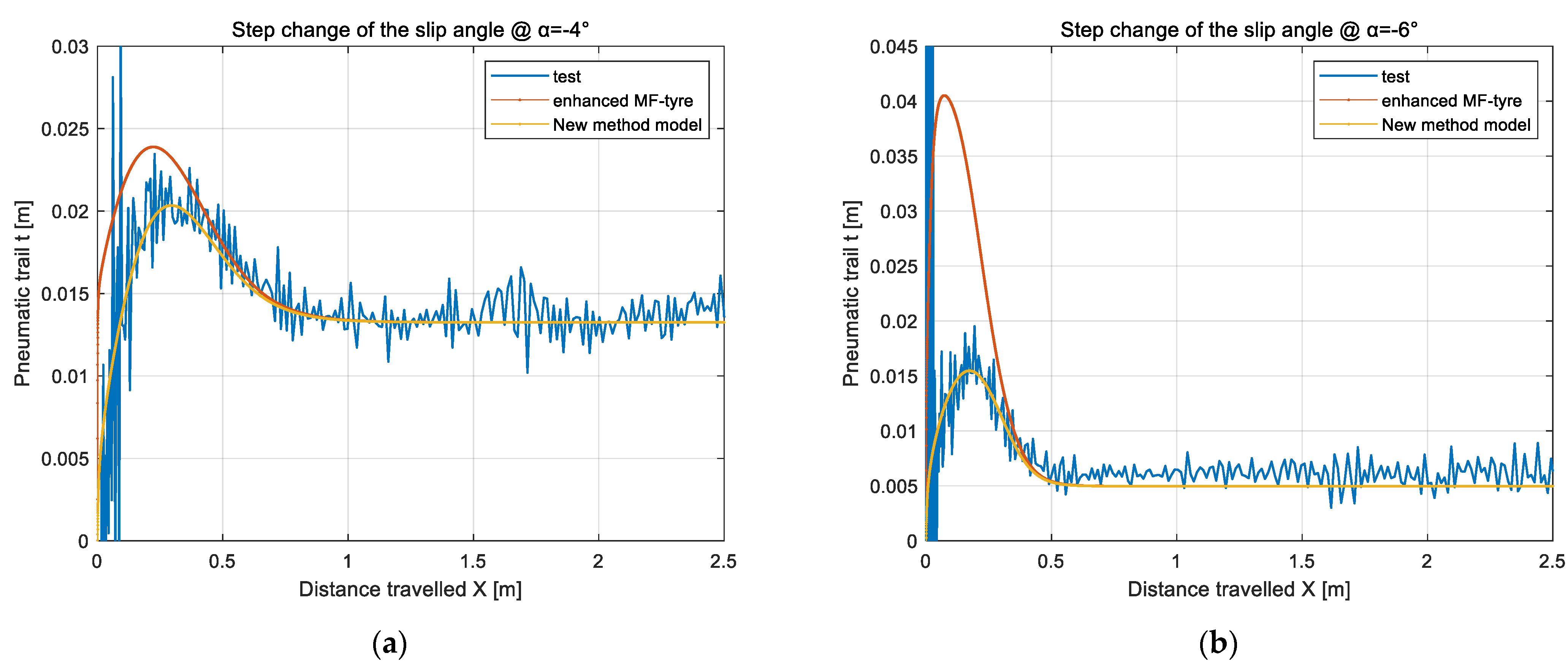
4.2. Characteristic Identification of Nonlinear Unsteady Sideslip Lateral Force and Aligning Torque
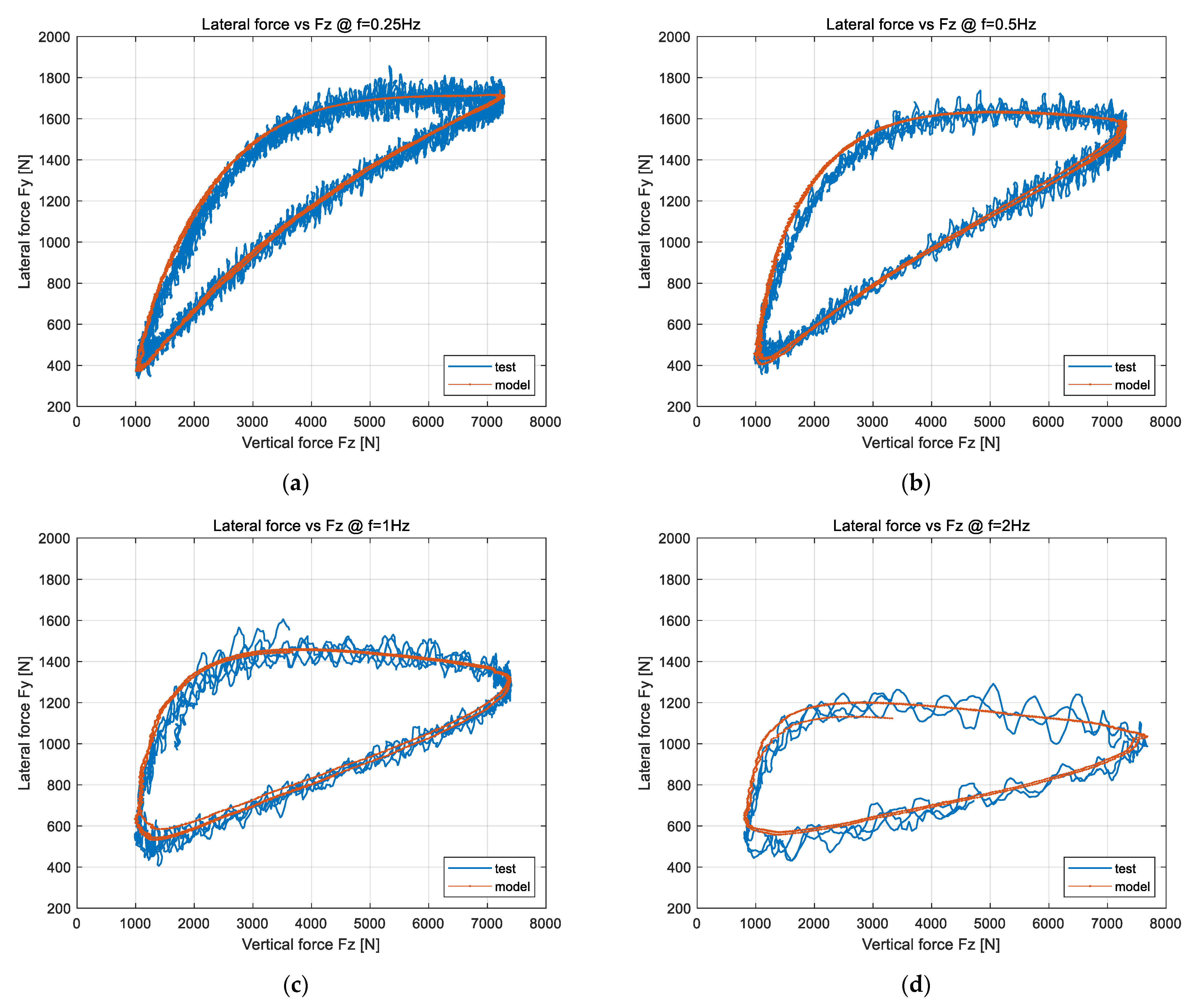
4.3. Characteristic Identification of Dynamic Load Sideslip Conditions Lateral Force and Aligning Torque (Linear Region and Nonlinear Region)
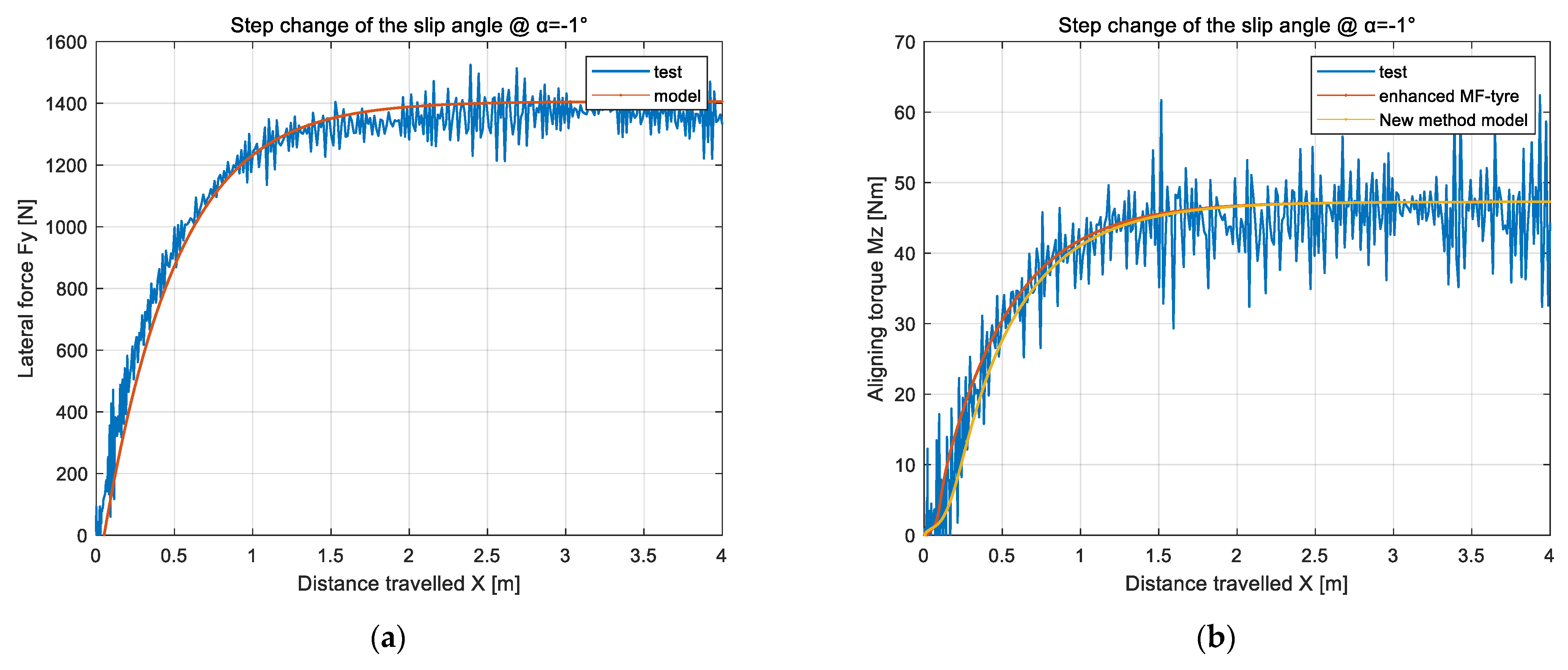
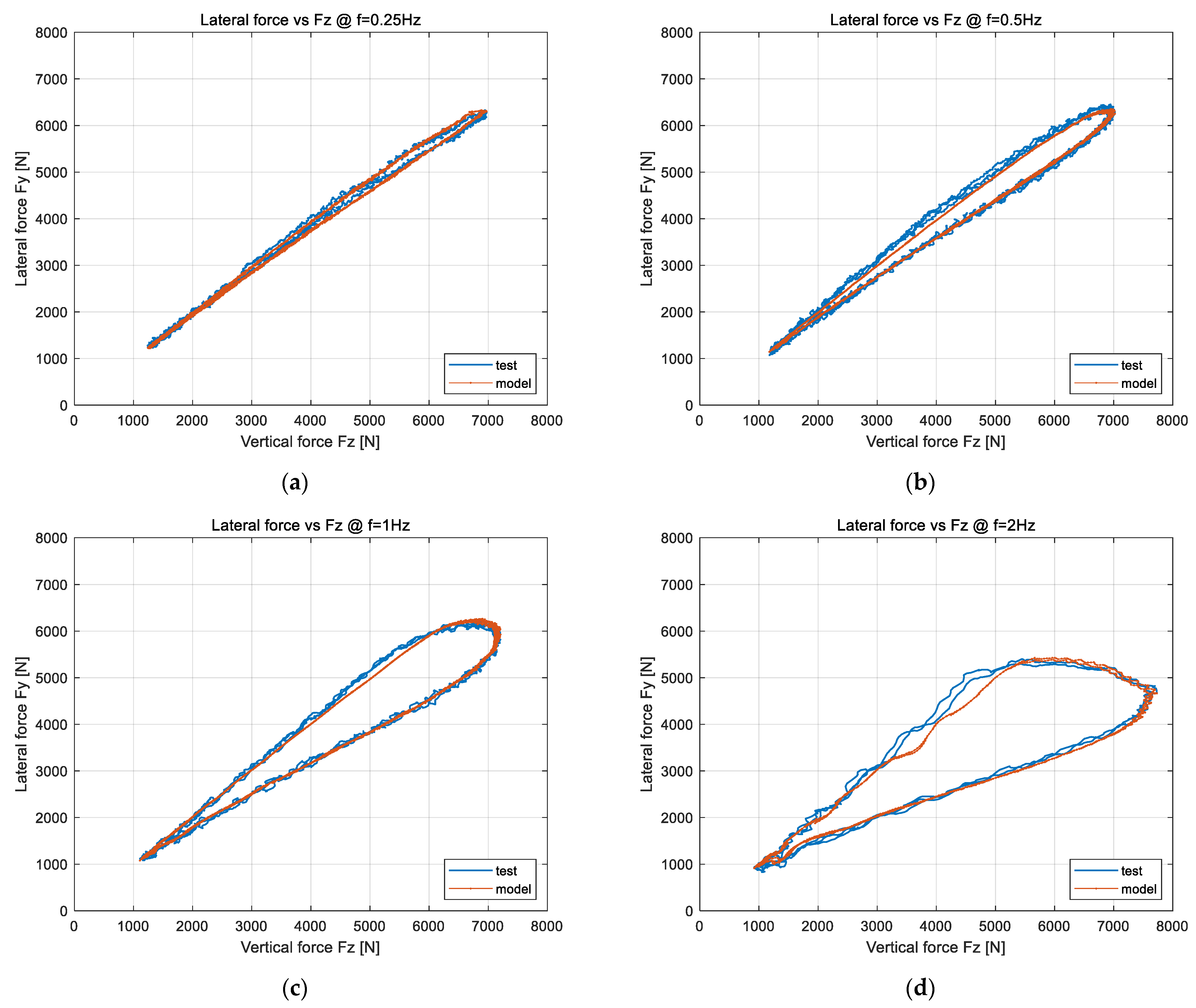
4.3.1. Verification of Dynamic Load Cornering Lateral Force and Aligning Torque in Linear Region
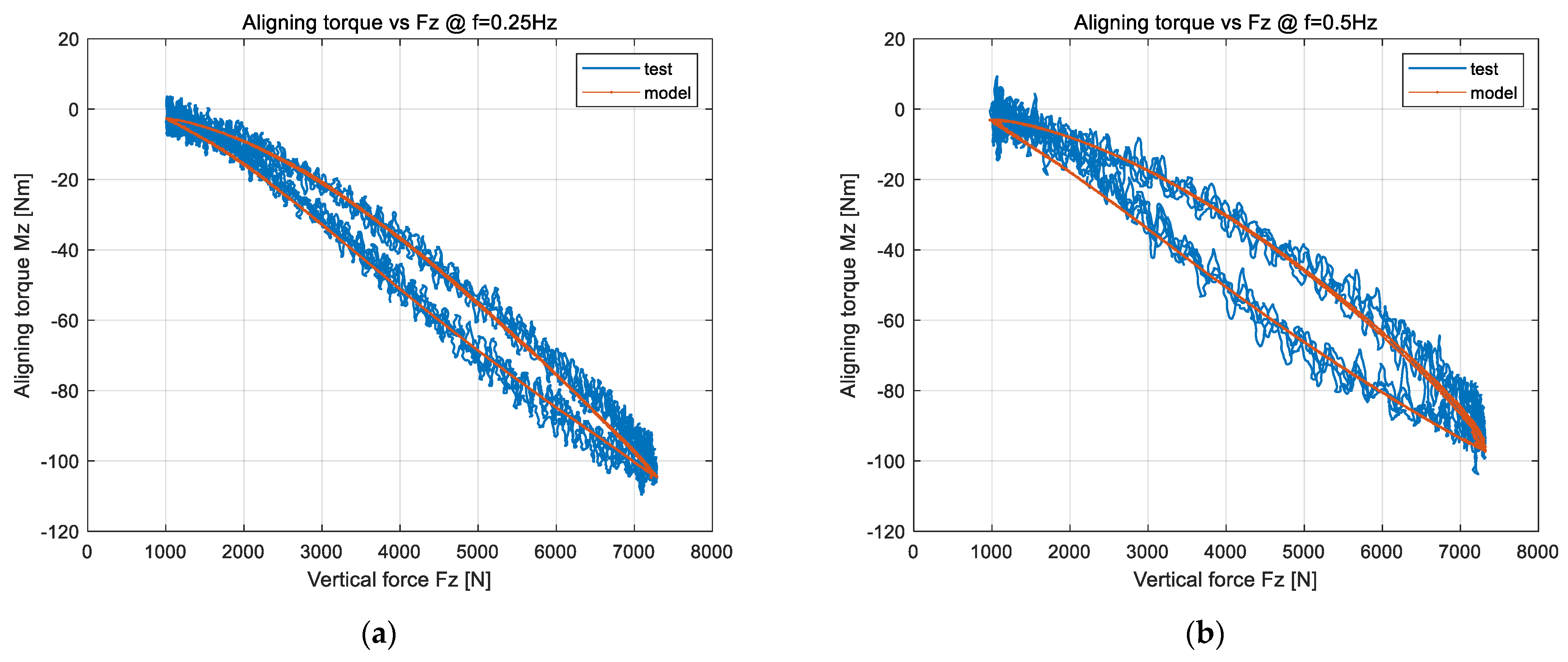
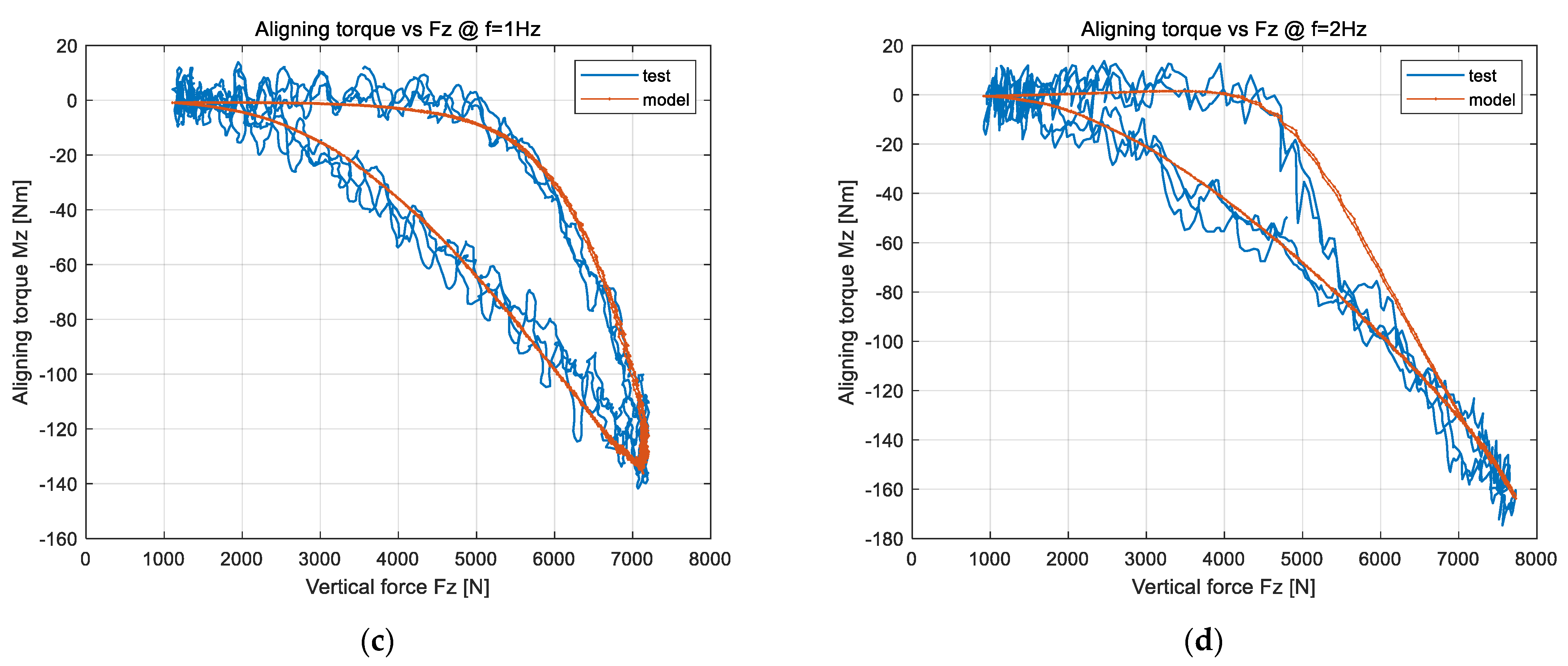
4.3.2. Verification of Dynamic Load Cornering Lateral Force and Aligning Torque in Nonlinear Region
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Description |
| lateral coordinate position of the lower end point of the tread | |
| lateral coordinate position of the lower end point of the carcass | |
| tire lateral force | |
| tire aligning torque | |
| pneumatic trail, time | |
| half contact length | |
| tread element lateral stiffness per unit of length | |
| lateral translational deformation of the carcass | |
| lateral bending deformation of the carcass | |
| lateral torsional deformation of the carcass | |
| lateral translational stiffness of the carcass | |
| lateral bending stiffness of the carcass | |
| lateral torsional stiffness of the carcass | |
| translation deformation feature ratio | |
| bending deformation feature ratio | |
| torsional deformation feature ratio | |
| tire carcass lateral deformation | |
| lateral slip velocity | |
| longitudinal velocity | |
| rolling velocity | |
| sideslip angle | |
| lateral slip velocity on the ground | |
| accumulated time of tread unit movement within contact | |
| longitudinal coordinate of transition from adhesion to sliding | |
| where adhesion occurs | |
| tire parameter of the brush model | |
| path frequency | |
| adhesion parameter | |
| lateral relaxation length | |
| varying part (very small) of sideslip angle | |
| transient tire slip angle | |
| cornering stiffness (tangent) | |
| cornering stiffness (secant) | |
| lateral relaxation length (secant) | |
| pneumatic trail distance constant 1 | |
| pneumatic trail distance constant 2 | |
| pneumatic trail distance constant 2 (secant) | |
| pneumatic trail transient parameter n | |
| pneumatic trail transient parameter m |
References
- Arslan, M.S.; Sever, M. Vehicle stability enhancement and rollover prevention by a nonlinear predictive control method. Trans. Inst. Meas. Control 2019, 41, 2135–2149. [Google Scholar] [CrossRef]
- Van Zanten, A.; Erhardt, R.; Lutz, A. Measurement and Simulation of Transient in Longitudinal and Lateral Tire Forces; SAE Technical Paper 900210; SAE International: Warrendale, PA, USA, 1990; pp. 300–318. [Google Scholar]
- Van Zanten, A.; Erhardt, R.; Landesfeind, K.; Pfaff, G. VDC Systems Development and Perspective. SAE Trans. 1998, 107, 424–444. [Google Scholar]
- Van Zanten, A. Evolution of electronic control systems for improving the vehicle dynamic behavior. In Proceedings of the 6th International Symposium on Advanced Vehicle Control, Hiroshima, Japan, 9–12 September 2002. [Google Scholar]
- Madhusudhanan, A.K.; Corno, M.; Holweg, E. Vehicle yaw rate control using tyre force measurements. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015. [Google Scholar]
- Corno, M.; Gerard, M.; Verhaegen, M.; Holweg, E. Hybrid ABS control using force measurement. IEEE Trans. Control Syst. Technol. 2011, 20, 1223–1235. [Google Scholar] [CrossRef]
- Madhusudhanan, A.K.; Corno, M.; Holweg, E. Lateral vehicle dynamics control based on tyre utilization coefficients and tyre force measurements. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013. [Google Scholar]
- Schieschke, R. The importance of tire dynamics in vehicle simulation. In Proceedings of the Tire Society. 9th Annual Meeting and Conference on Tire Science and Technology, Akron, OH, USA, 20–21 March 1990. [Google Scholar]
- Schieschke, R.; Hiemenz, R. The relevance of tire dynamics in vehicle simulation. In Proceedings of the XXIII FISITA Congress, Torino, Italy, 7–11 May 1990. [Google Scholar]
- Luty, W. Simulation research of the tire Basic Relaxation Model in conditions of the wheel cornering angle oscillations. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Bangalore, India, 14–16 July 2016. [Google Scholar]
- Luty, W. Influence of the tire relaxation on the simulation results of the vehicle lateral dynamics in aspect of the vehicle driving safety. J. KONES 2015, 22, 185–192. [Google Scholar] [CrossRef]
- Lozia, Z. Is the representation of transient states of tyres a matter of practical importance in the simulations of vehicle motion? Arch. Automot. Eng.—Arch. Motoryz. 2017, 77, 63–84. [Google Scholar]
- Segel, L. Force and moment response of pneumatic tires to lateral motion inputs. J. Manuf. Sci. Eng. 1966, 88, 37–44. [Google Scholar] [CrossRef]
- Pacejka, H.B. Tire and Vehicle Dynamics, 3rd ed.; Elsevier: Oxford, UK, 2012. [Google Scholar]
- Gong, S. Study of In-Plane Dynamics of Tires. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1993. [Google Scholar]
- Higuchi, A. Transient Response of Tyres at Large Wheel Slip and Camber. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1997. [Google Scholar]
- Zegelaar, P.W.A. The Dynamic Response of Tyres to Brake Torque Variations and Road Unevennesses. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1998. [Google Scholar]
- Maurice, J.P. Short Wavelength and Dynamic Tyre Behaviour under Lateral and Combined Slip Conditions. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2000. [Google Scholar]
- Schmeitz, A.J.C. A Semi-Empirical Three-Dimensional Model of the Pneumatic Tyre Rolling Over Arbitrarily Uneven Road Surfaces. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2004. [Google Scholar]
- Besselink, I.J.M. Tire characteristics and modeling. In Vehicle Dynamics of Modern Passenger Cars; Lugner, P., Ed.; Springer: Cham, Switzerland, 2019; Volume 582, pp. 47–108. [Google Scholar]
- Guo, K.; Liu, Q. Modelling and simulation of non-steady state cornering properties and identification of structure parameters of tyres. Veh. Syst. Dyn. 1997, 27 (Suppl. 1), 80–93. [Google Scholar] [CrossRef]
- Pandey, A.; Shaju, A. Modelling transient response using PAC 2002-based tyre model. Veh. Syst. Dyn. 2020, 60, 20–46. [Google Scholar]
- Gipser, M. FTire: A physically based application-oriented tyre model for use with detailed MBS and finite-element suspension models. Veh. Syst. Dyn. 2005, 43 (Suppl. 1), 76–91. [Google Scholar] [CrossRef]
- Février, P.; Blanco Hague, O.; Schick, B.; Miquet, C. Advantages of a thermomechanical tire model for vehicle dynamics. ATZ Worldw. 2010, 112, 33–37. [Google Scholar] [CrossRef]
- Farroni, F.; Giordano, D.; Russo, M.; Timpone, F. TRT: Thermo racing tyre a physical model topredict the tyre temperature distribution. Meccanica 2014, 49, 707–723. [Google Scholar] [CrossRef] [Green Version]
- Sorniotti, A. Tire Thermal Model for Enhanced Vehicle Dynamics Simulation; SAE Technical Paper (No. 2009-01-0441); SAE International: Warrendale, PA, USA, 2009. [Google Scholar]
- Farroni, F.; Sakhnevych, A.; Timpone, F. An evolved version of thermo racing tyre for real time applications. In Lecture Notes in Engineering and Computer Science. In Proceedings of the World Congress on Engineering (WCE), London, UK, 15–17 July 2015. [Google Scholar]
- Beregi, S.; Takacs, D.; Gyebroszki, G.; Stepan, G. Theoretical and experimental study on the nonlinear dynamics of wheel-shimmy. Nonlinear Dyn. 2019, 98, 2581–2593. [Google Scholar] [CrossRef] [Green Version]
- Beregi, S.; Takacs, D.; Stepan, G. Bifurcation analysis of wheel shimmy with non-smooth effects and time delay in the tyre–ground contact. Nonlinear Dyn. 2019, 98, 841–858. [Google Scholar] [CrossRef] [Green Version]
- Beregi, S.; Takács, D. Analysis of the tyre–road interaction with a non-smooth delayed contact model. Multibody Syst. Dyn. 2019, 45, 185–201. [Google Scholar] [CrossRef] [Green Version]
- Romano, L. Advanced Brush Tyre Modelling; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Romano, L.; Sakhnevych, A.; Strano, S.; Timpone, F. A novel brush-model with flexible carcass for transient interactions. Meccanica 2019, 54, 1663–1679. [Google Scholar] [CrossRef] [Green Version]
- Romano, L.; Bruzelius, F.; Jacobson, B. Unsteady-state brush theory. Veh. Syst. Dyn. 2021, 59, 1643–1671. [Google Scholar] [CrossRef]
- Canudas-de-Wit, C.; Tsiotras, P.; Velenis, E.; Basset, M.; Gissinger, G. Dynamic friction models for road/tire longitudinal interaction. Veh. Syst. Dyn. 2003, 39, 189–226. [Google Scholar] [CrossRef]
- Tsiotras, P.; Velenis, E.; Sorine, M. A LuGre tire friction model with exact aggregate dynamics. Veh. Syst. Dyn. 2004, 42, 195–210. [Google Scholar] [CrossRef]
- Velenis, E.; Tsiotras, P.; Canudas-De-Wit, C.; Sorine, M. Dynamic tyre friction models for combined longitudinal and lateral vehicle motion. Veh. Syst. Dyn. 2005, 43, 3–29. [Google Scholar] [CrossRef]


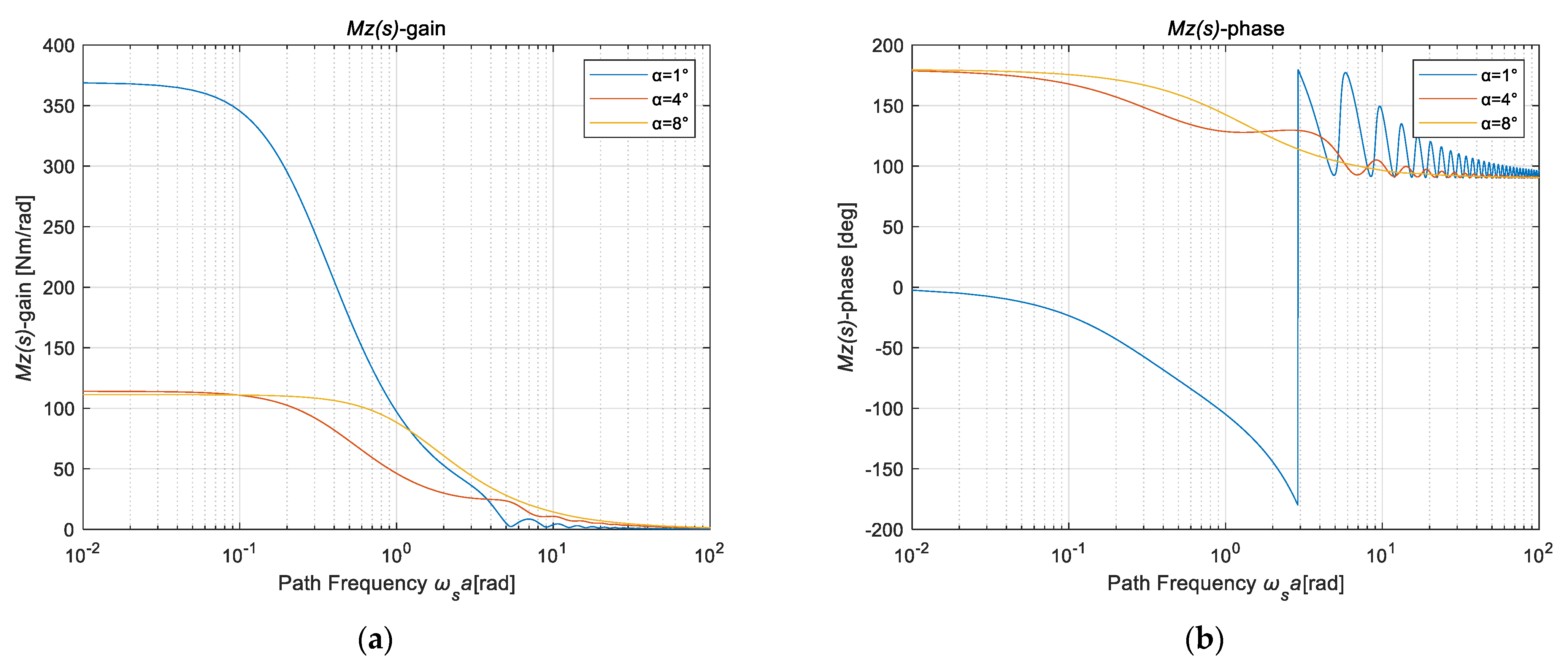
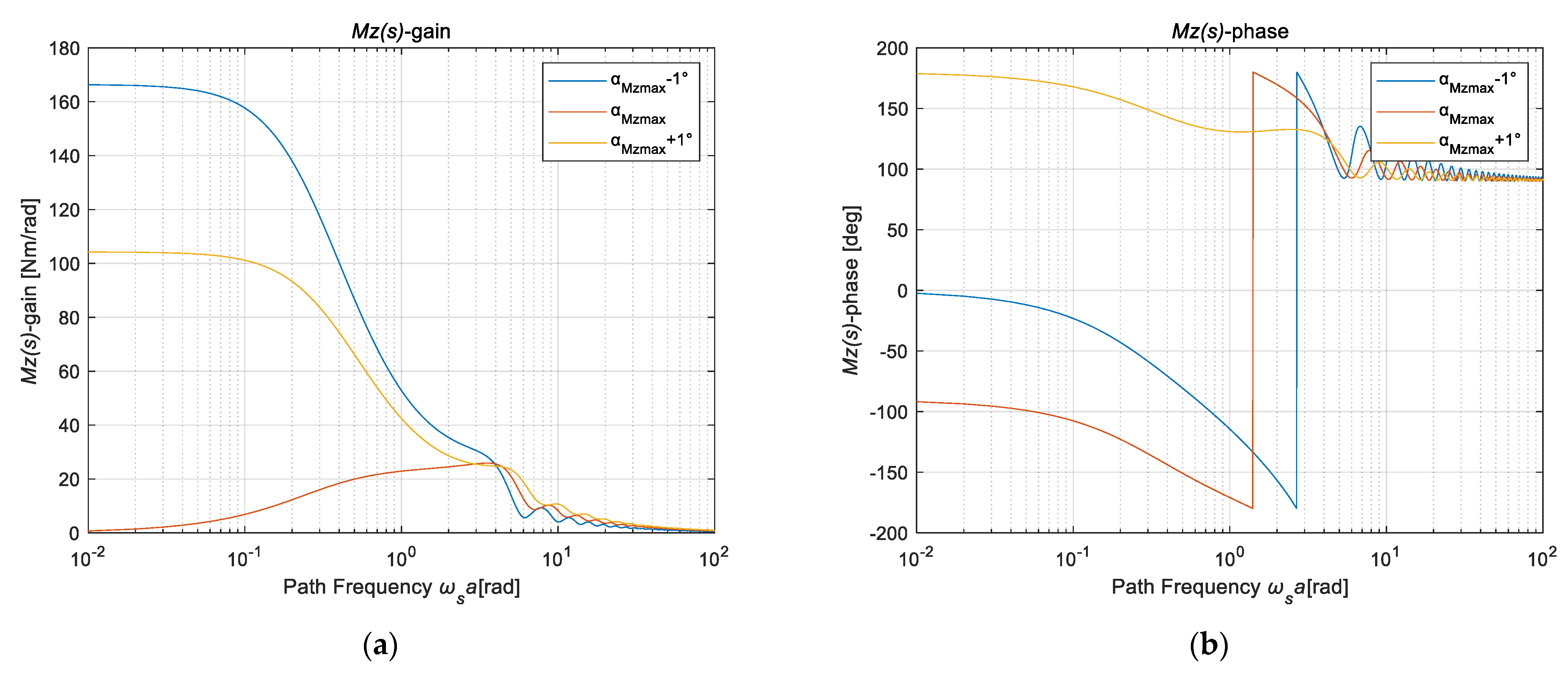
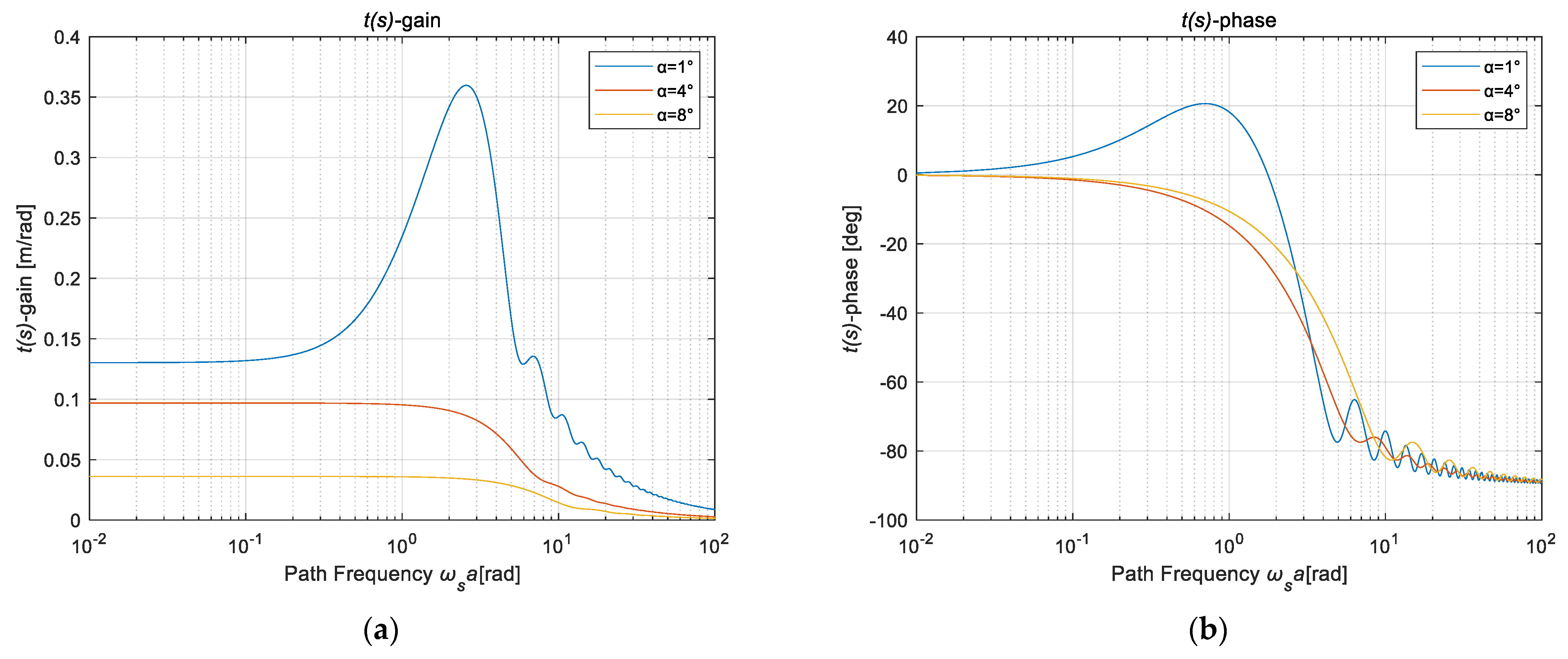
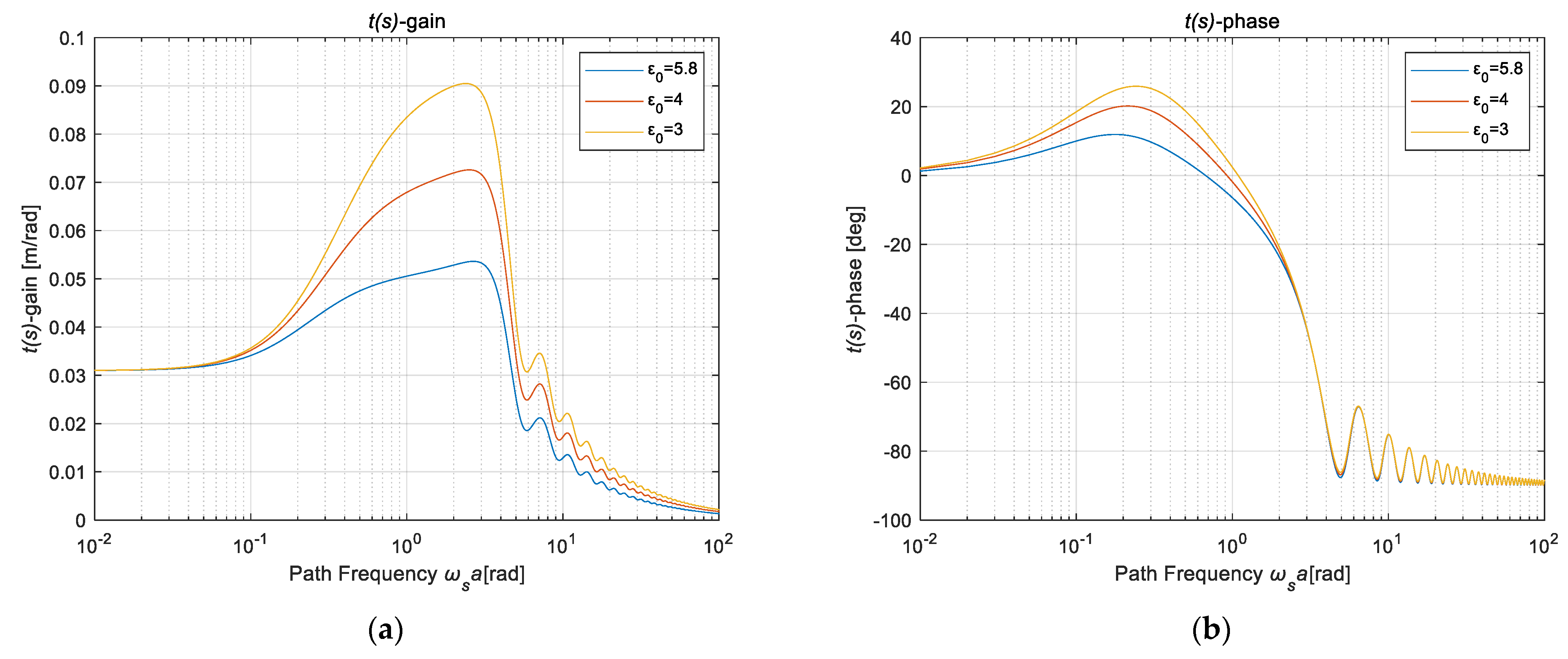

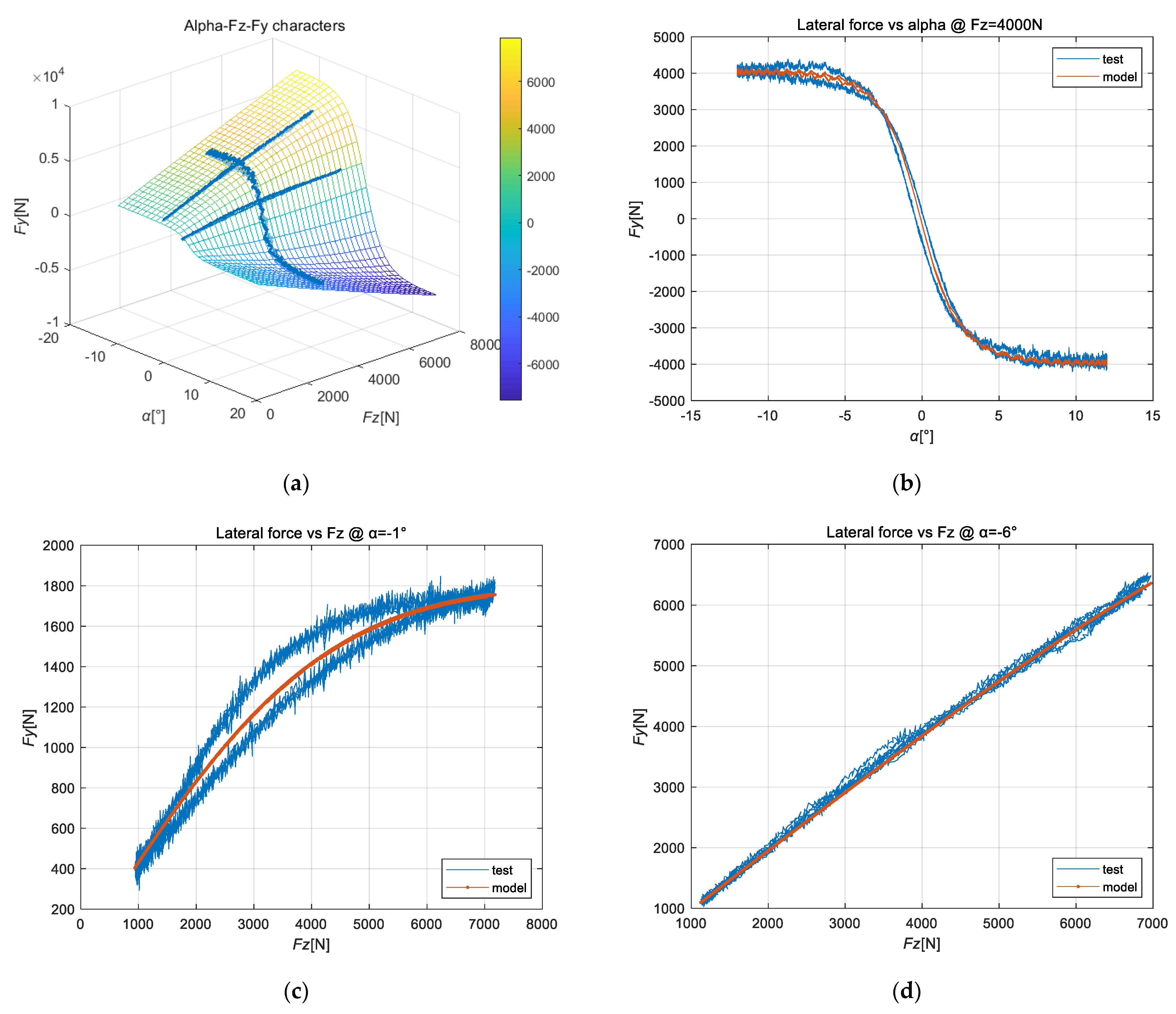


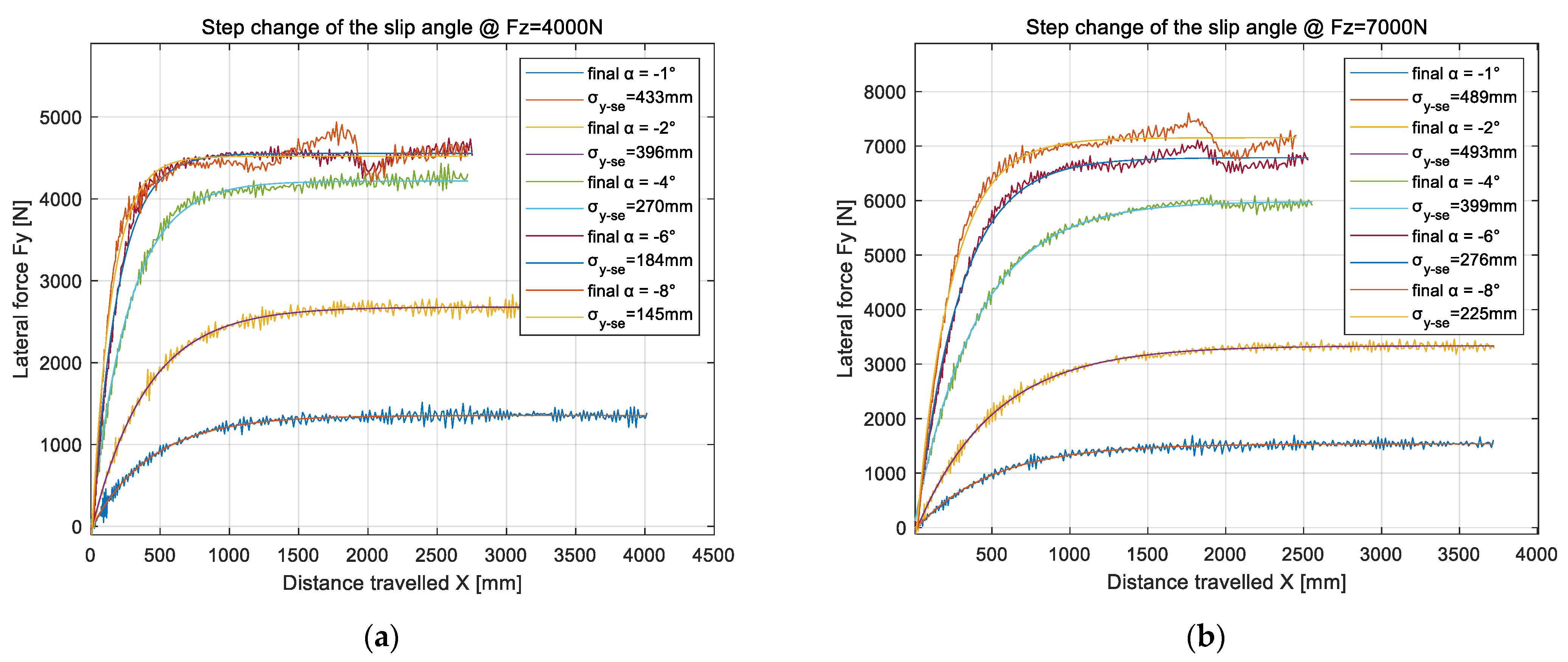




| Inflation Pressure | Road Speed | Load Method | Slip Angle | Load Cycle | Vertical Load |
|---|---|---|---|---|---|
| 230 kPa | 5 km/h | Sideslip sweep | −12~12° | 100 s | 4000 N |
| 230 kPa | 5 km/h | Vertical load sweep | −1° | 10 s | 1000~7000 N |
| 230 kPa | 5 km/h | Vertical load sweep | −6° | 10 s | 1000~7000 N |
| Inflation Pressure | Road Speed | Load Method | Slip Angle | Vertical Load |
|---|---|---|---|---|
| 230 kPa | 0→5 km/h | slip angle step | −1° | 3000\4000\5000\7000 N |
| 230 kPa | 0→5 km/h | slip angle step | −2° | 3000\4000\5000\7000 N |
| 230 kPa | 0→5 km/h | slip angle step | −4° | 3000\4000\5000\7000 N |
| 230 kPa | 0→5 km/h | slip angle step | −6° | 3000\4000\5000\7000 N |
| 230 kPa | 0→5 km/h | slip angle step | −8° | 3000\4000\5000\7000 N |
| Inflation Pressure | Road Speed | Load Method | Slip Angle | Load Frequency | Vertical Load |
|---|---|---|---|---|---|
| 230 kPa | 5 km/h | Vertical load sweep | −1°, −6° | 0.10 Hz | 1000~7000 N |
| 230 kPa | 5 km/h | Vertical load sweep | −1°, −6° | 0.25 Hz | 1000~7000 N |
| 230 kPa | 5 km/h | Vertical load sweep | −1°, −6° | 0.50 Hz | 1000~7000 N |
| 230 kPa | 5 km/h | Vertical load sweep | −1°, −6° | 0.10 Hz | 1000~7000 N |
| 230 kPa | 5 km/h | Vertical load sweep | −1°, −6° | 0.25 Hz | 1000~7000 N |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Lu, D.; Yin, H.; Li, L.; Lv, M.; Wang, W. The Unsteady-State Response of Tires to Slip Angle and Vertical Load Variations. Machines 2022, 10, 527. https://doi.org/10.3390/machines10070527
Ma Y, Lu D, Yin H, Li L, Lv M, Wang W. The Unsteady-State Response of Tires to Slip Angle and Vertical Load Variations. Machines. 2022; 10(7):527. https://doi.org/10.3390/machines10070527
Chicago/Turabian StyleMa, Yao, Dang Lu, Hengfeng Yin, Lun Li, Manyi Lv, and Wei Wang. 2022. "The Unsteady-State Response of Tires to Slip Angle and Vertical Load Variations" Machines 10, no. 7: 527. https://doi.org/10.3390/machines10070527
APA StyleMa, Y., Lu, D., Yin, H., Li, L., Lv, M., & Wang, W. (2022). The Unsteady-State Response of Tires to Slip Angle and Vertical Load Variations. Machines, 10(7), 527. https://doi.org/10.3390/machines10070527





