Review on the Selection of Health Indicator for Lithium Ion Batteries
Abstract
:1. Introduction
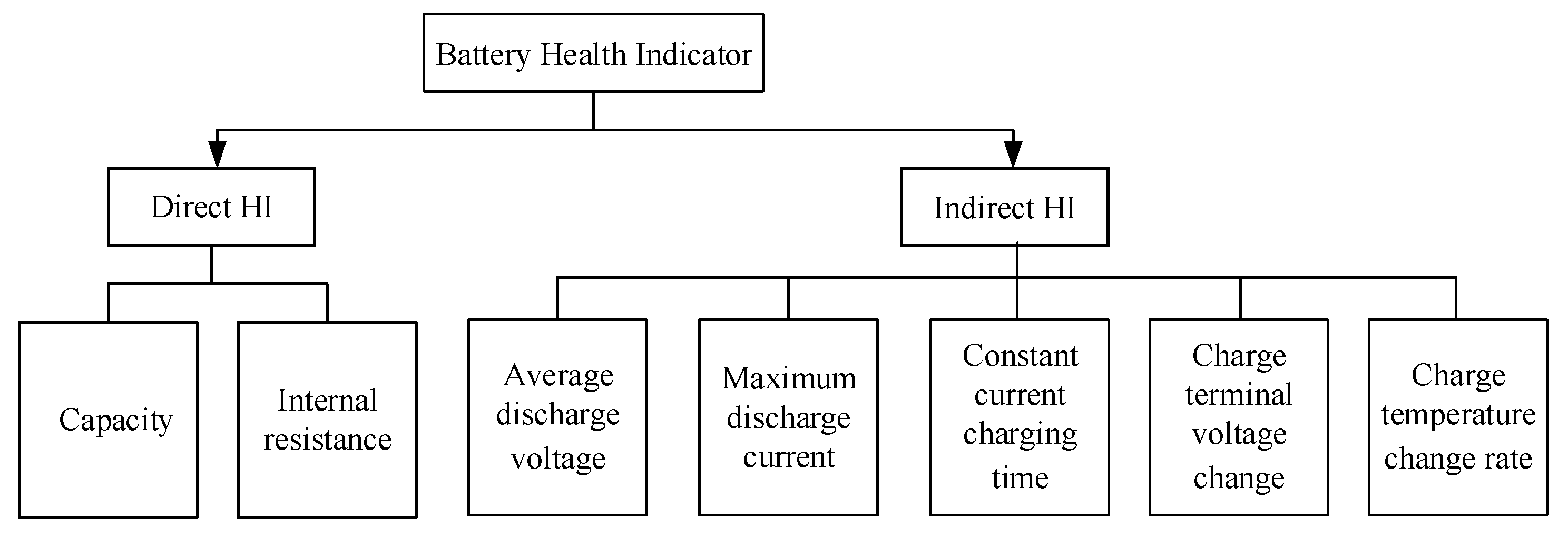
2. Lithium-Ion Battery Health Indicator
2.1. Direct Health Indicator
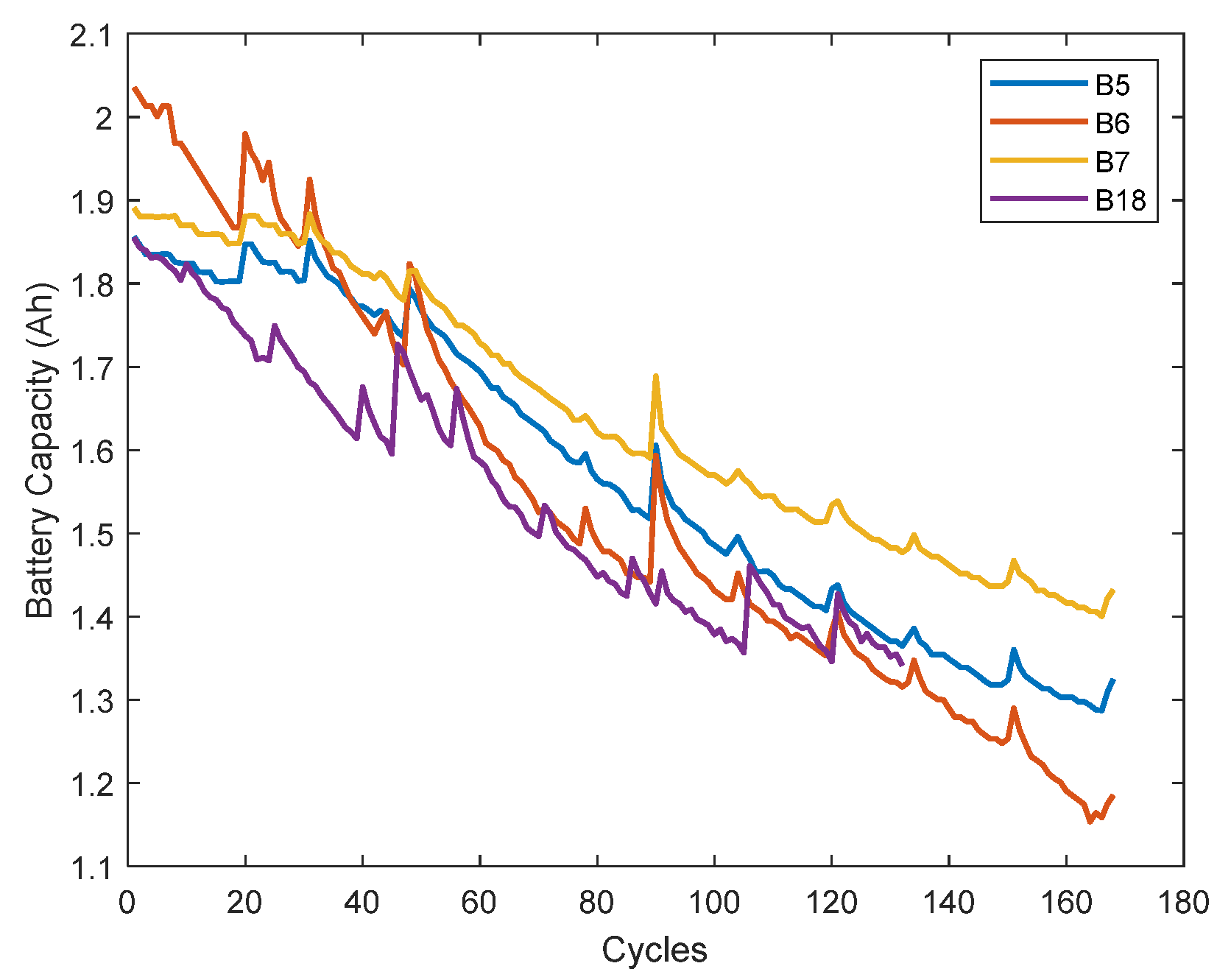
2.1.1. Battery Capacity
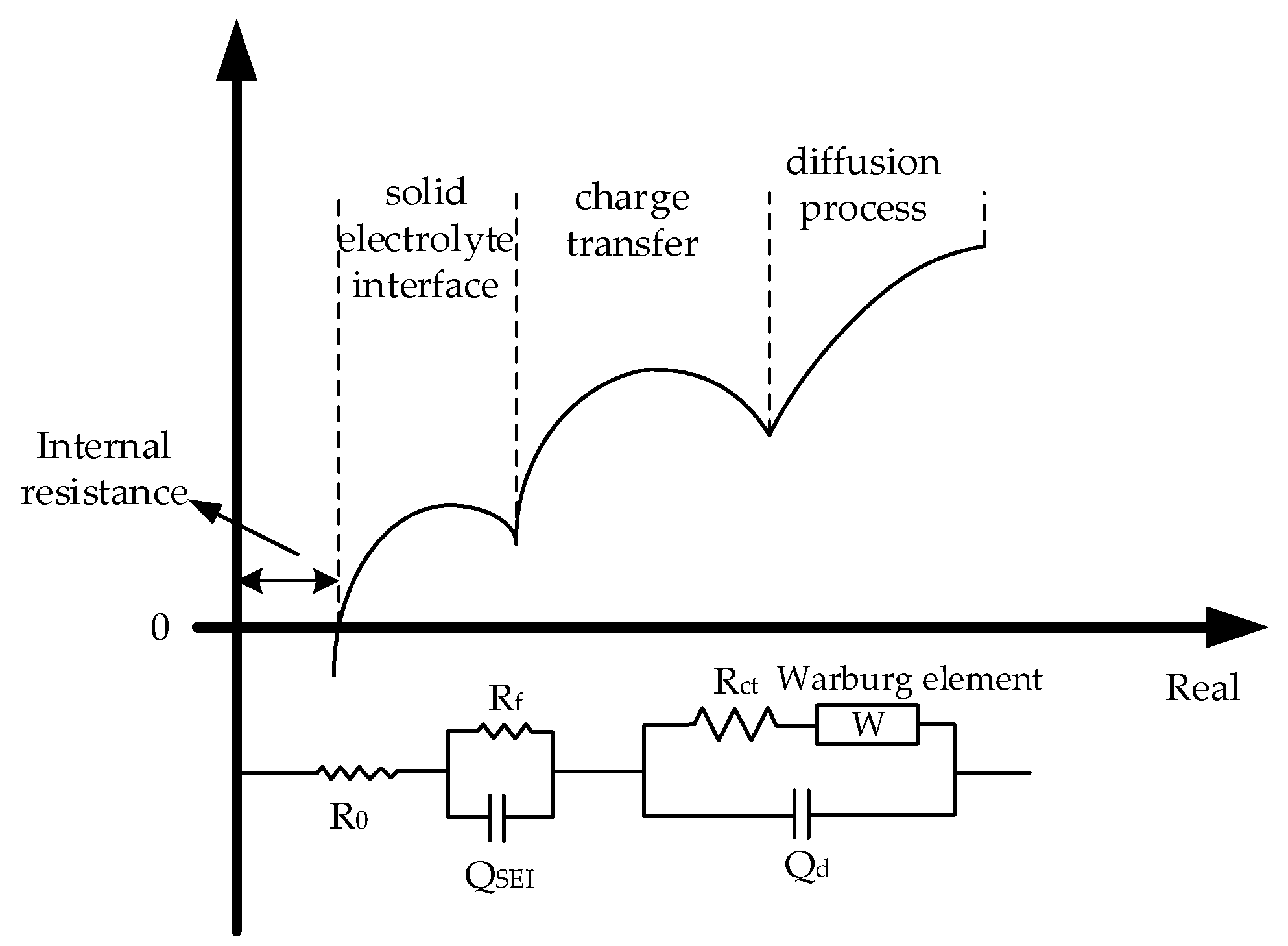
2.1.2. Battery Internal Resistance
2.2. Indirect Health Indicator
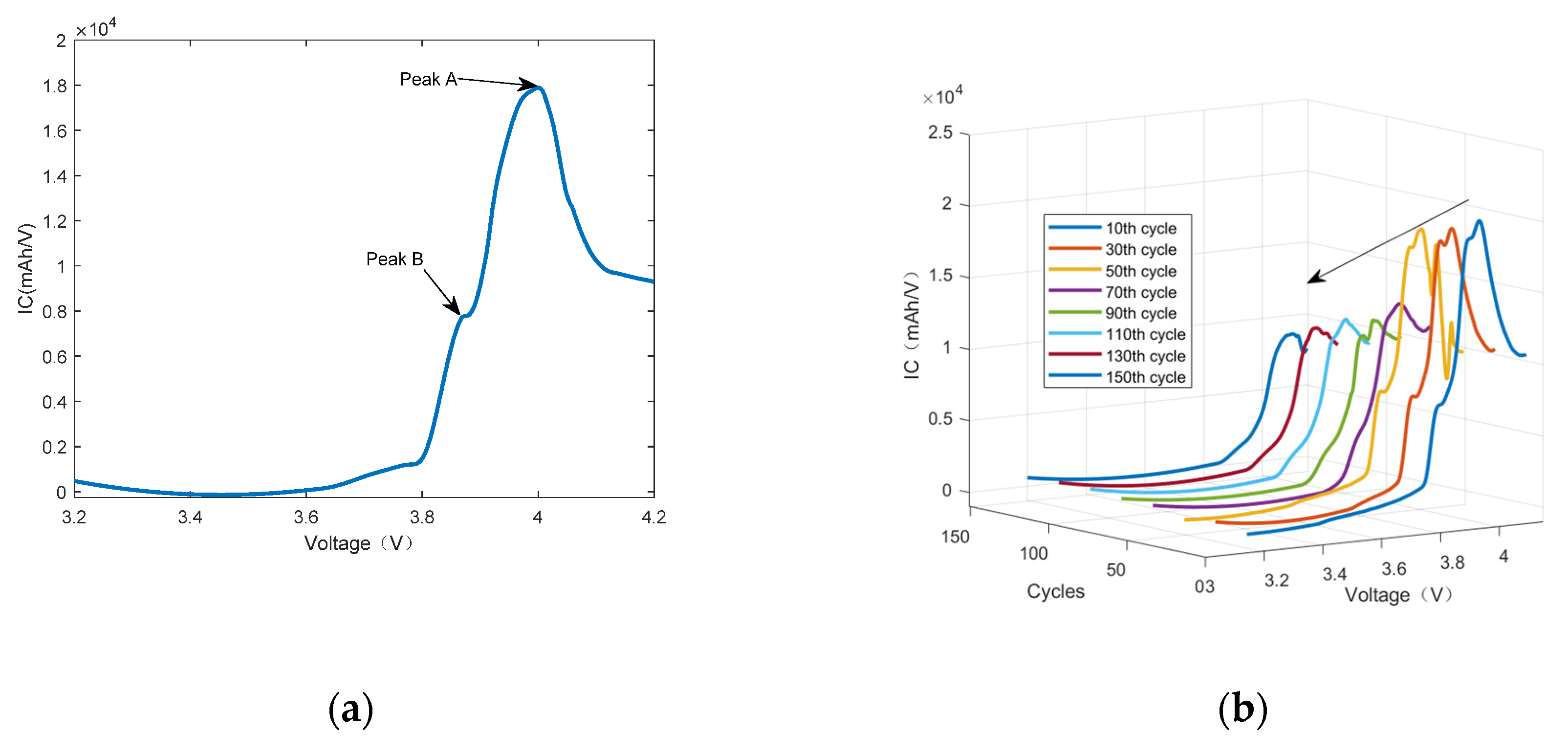
2.2.1. Indirect HI Based on Discharge Process
2.2.2. Indirect HI Based on Charging Process
2.2.3. Fusion of HIs
3. Summary
4. Future Development
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tucki, K.; Orynycz, O.; Świć, A.; Mitoraj-Wojtanek, M. The Development of Electromobility in Poland and EU States as a Tool for Management of CO2 Emissions. Energies 2019, 12, 2942. [Google Scholar] [CrossRef] [Green Version]
- Gomes, E. Sustainable Population Growth in Low-Density Areas in a New Technological Era: Prospective Thinking on How to Support Planning Policies Using Complex Spatial Models. Land 2020, 9, 221. [Google Scholar] [CrossRef]
- Zang, P.; Dong, W.; Ma, B. Overview of research on echelon utilization of electric vehicle power batteries. In Proceedings of the 3rd Smart Grid Conference-Smart Power Consumption, Beijing, China, 27–30 October 2019; pp. 484–486. [Google Scholar]
- Jiang, J.; Gao, Y.; Zhang, C. On-line diagnosis method of electric vehicle lithium-ion power battery health status. Chin. J. Mech. Eng. 2019, 55, 60–72. [Google Scholar]
- Yao, J.; Li, Z.; Wang, M. Automobile active tilt control based on active suspension. Adv. Mech. Eng. 2018, 10, 168781401880145. [Google Scholar] [CrossRef] [Green Version]
- Jiao, Z.; Fan, X.; Zhang, X. State Tracking and Remaining Service Life Prediction Method of Li-ion Battery Based on Improved Particle Filter Algorithm. Chin. J. Electrotech. Technol. 2020, 35, 3979–3993. [Google Scholar]
- Lin, C.P.; Cabrera, J.; Yang, F.; Ling, M.H.; Tsui, K.L.; Bae, S.J. Battery state of health modeling and remaining useful life prediction through time series model. Appl. Energy 2020, 275, 115338. [Google Scholar] [CrossRef]
- Wu, L.; Fu, X.; Guan, Y. Review of the Remaining Useful Life Prognostics of Vehicle Lithium-Ion Batteries Using Data-Driven Methodologies. Appl. Sci. 2016, 6, 166. [Google Scholar] [CrossRef] [Green Version]
- Noura, N.; Boulon, L.; Jemeï, S. A Review of Battery State of Health Estimation Methods: Hybrid Electric Vehicle Challenges. World Electr. Veh. J. 2020, 11, 66. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Song, D. Lithium Battery State of Health Assessment Based on Surface Temperature Characteristics. Master’s Thesis, Xidian University, Xi’an, China, 2021. [Google Scholar]
- Li, W.; Jiao, Z.; Du, L.; Fan, W.; Zhu, Y. An indirect RUL prognosis for lithium-ion battery under vibration stress using Elman neural network. Int. J. Hydrogen Energy 2019, 44, 12270–12276. [Google Scholar] [CrossRef]
- Wang, R. Prediction of the Remaining Life of Lithium Batteries Based on New Health Indicators. Master’s Thesis, Xidian University, Xi’an, China, 2020. [Google Scholar]
- Tian, J.; Xiong, R.; Yu, Q. Fractional order model based incremental capacityanalysis for degradation state recognition of lithium-ion batteries. IEEE Trans. Ind. Electron. 2019, 66, 1576–1584. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Briat, O.; Delétage, J.Y.; Martin, C.; Chadourne, N.; Vinassa, J.M. Efficient state of health estimation of Li-ion battery under several ageing types for aeronautic applications. Microelectron. Reliab. 2018, 88, 1231–1235. [Google Scholar] [CrossRef]
- Tang, J.; Liu, Q.; Liu, S.; Xie, X.; Zhou, J.; Li, Z. A health monitoring method based on multiple indicators to eliminateinfluences of estimation dispersion for lithium-ion batteries. IEEE Access 2019, 7, 122302–122314. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, W. Capacity estimation of lithium-ion batteries based on new health indicators. Electron. Meas. Technol. 2020, 43, 10–15. [Google Scholar] [CrossRef]
- Khumprom, P.; Yodo, N. A Data-Driven Predictive Prognostic Model for Lithium-ion Batteries based on a Deep Learning Algorithm. Energies 2019, 12, 660. [Google Scholar] [CrossRef] [Green Version]
- Nieto, P.G.; García-Gonzalo, E.; Lasheras, F.S.; de Cos Juez, F.J. Hybrid PSO-SVM-based method for forecasting of the remaining useful life for aircraft engines and evaluation of its reliability. Reliab. Eng. Syst. Saf. 2015, 138, 219–231. [Google Scholar] [CrossRef]
- Gao, L.; Xu, F.; Li, H. Recognition method of sheet surface defects based on deep learning features and nonlinear support vector machine. Chin. J. For. Eng. 2019, 4, 99–106. [Google Scholar]
- Sun, S. A new stress field intensity model and its application in component high cycle fatigue research. PLoS ONE 2020, 15, e0235323. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.; Kong, C. Prediction of the remaining service life of lithium batteries based on GWO-SVR. J/OL J. Power Supply. 2021. Available online: http://kns.cnki.net/kcms/detail/12.1420.TM.20210520.1300.002.html.
- Wang, Y.; Ni, Y.; Zheng, Y. Prediction of the remaining service life of lithium-ion batteries based on ALO-SVR. Chin. J. Electr. Eng. 2021, 41, 1445–1457. [Google Scholar]
- Duong, P.; Raghavan, N. Heuristic Kalman optimized particle filter for remaining useful life prediction of lithium-ion battery. Microelectron. Reliab. 2018, 81, 232–243. [Google Scholar] [CrossRef]
- Guha, A.; Patra, A. State of Health Estimation of Lithium-Ion Batteries Using Capacity Fade and Internal Resistance Growth Models. IEEE Trans. Transp. Electrif. 2018, 4, 135–146. [Google Scholar] [CrossRef]
- Pan, C.; Huang, A.; He, Z. Prediction of remaining useful life for lithium-ion battery based on particle filter with residual resampling. Energy Sci. Eng. 2021, 9, 1115–1133. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, Z.; Sun, C. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Exponential Model and Particle Filter. IEEE Access 2018, 6, 17729–17740. [Google Scholar] [CrossRef]
- Li, Y.; Lin, S.; Yuan, X. Research on RUL Prediction of Lithium Batteries Based on New Capacity Degradation Model. Comput. Simul. 2020, 37, 120–124. [Google Scholar] [CrossRef]
- Jouin, M.; Gouriveau, R.; Hissel, D. Particle filter-based prognostics: Review, discussion and perspectives. Mech. Syst. Signal Process. 2016, 72, 2–31. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, Y.; Zhang, F. Power battery life prediction method based on extended H_∞ particle filter algorithm. Chin. J. Mech. Eng. 2019, 55, 36–43. [Google Scholar]
- Zhang, H.; Miao, Q.; Zhang, X. An improved unscented particle filter approach for lithium-ion battery remaining useful life prediction. Microelectron. Reliab. 2018, 81, 288–298. [Google Scholar] [CrossRef]
- Wei, H.; An, J.; Cheng, J. Realization of RUL prediction of lithium-ion battery based on improved particle filter algorithm. Automot. Eng. 2019, 41, 1377–1383. [Google Scholar]
- Wang, R.; Feng, H. Lithium-ion batteries remaining useful life prediction using Wiener process and unscented particle filter. J. Power Electron. 2020, 20, 270–278. [Google Scholar] [CrossRef]
- Cheng, W.; Cai, Y.; Su, Y. Remaining life prediction of lithium-ion battery based on improved particle filter. China Test 2021, 47, 148–153. [Google Scholar]
- Tai, Y.; Li, P.; Zheng, Y. Entropy Generation and Thermoelastic Damping in the In-plane Vibration of Microring Resonators. Entropy 2019, 21, 631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, Q. Research on Li-ion Battery State of Health Estimation Based on Multi-feature Variable Extraction. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2021. [Google Scholar]
- Choi, W.; Shin, H.-C.; Kim, J.M. Modeling and Applications of Electrochemical Impedance Spectroscopy (EIS) for Lithium-ion Batteries. J. Electrochem. Sci. Technol. 2020, 11, 786–812. [Google Scholar] [CrossRef] [Green Version]
- Yao, L.; Xu, S.; Tang, A.; Zhou, F.; Hou, J.; Xiao, Y.; Fu, Z. Prediction of remaining life of lithium-ion battery based on charge transfer resistance. Chin. J. Mech. Eng. 2021, 57, 105–117. [Google Scholar]
- Tian, Y.; Zeng, G.; Rutt, A.; Shi, T.; Kim, H.; Wang, J.; Ceder, G. Estimation of charge transfer resistance of lithium-ion batteries at different temperatures and states of charge. Automot. Eng. 2020, 42, 445–453. [Google Scholar]
- Mingant, R.; Bernard, J.; Sauvant-Moynot, V. Novel state-of-health diagnostic method for Li-ion battery in service. Appl. Energy 2016, 183, 390–398. [Google Scholar] [CrossRef] [Green Version]
- Saha, B.; Goebel, K.; Christophersen, J. Comparison of prognostic algorithms for estimating remaining useful life of batteries. Trans. Inst. Meas. Control 2009, 31, 293–308. [Google Scholar] [CrossRef]
- Ma, Z.; Chen, Y.; Wu, J. Ecological optimization for a combined diesel-organic Rankine cycle. AIP Adv. 2019, 9, 015320. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wei, X.; Dai, H. Estimation of state of health of lithium-ion batteries based on charge transfer resistance considering different temperature and state of charge. J. Energy Storage 2019, 21, 618–631. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M.; Chen, Y.; Tao, Y. A novel health indicator for on—line lithium—ion batteries remaining useful life prediction. J. Power Sources 2016, 321, 1–10. [Google Scholar] [CrossRef]
- He, Z.; Wei, T.; Pan, C.; Zhou, H.; Li, Y. An indirect prediction method of lithium-ion battery remaining life based on particle filter and polynomial regression. J. Chongqing Univ. Technol. 2020, 34, 27–33. [Google Scholar]
- Wang, R.; Feng, H. Remaining useful life prediction of lithium-ion battery using a novel health indicator. Qual. Reliab. Eng. Int. 2021, 37, 1232–1243. [Google Scholar] [CrossRef]
- Xiao, G.; Zhang, H.; Sun, N. Cooperative link scheduling for RSU-assisted dissemination of basic safety messages. Wirel. Netw. 2021, 27, 1335–1351. [Google Scholar] [CrossRef]
- Zhao, Q.; Cai, Y.; Wang, X. Prediction of the remaining service life of lithium-ion batteries in their entire life cycle. J/OL J. Power Supply 2021, 2095, 1–14. [Google Scholar]
- Liu, D.; Zhou, J.; Liao, H. A Health Indicator Extraction and Optimization Framework for Lithium-Ion Battery Degradation Modeling and Prognostics. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 915–928. [Google Scholar]
- Wang, F.-K.; Mamo, T. A hybrid model based on support vector regression and differential evolution for remaining useful lifetime prediction of lithium-ion batteries. J. Power Sources 2018, 401, 49–54. [Google Scholar] [CrossRef]
- Su, C.; Chen, H.; Wen, Z. Prediction of remaining useful life for lithium-ion battery with multiple health indicators. Eksploatacja I Niezawodnosc-Maint. Realib. 2021, 23, 176–183. [Google Scholar] [CrossRef]
- Liang, D.; Gao, J.; Xi, J. RUL prediction of power battery based on multi-feature fusion. China Test 2021, 47, 149–156. [Google Scholar]
- Chen, L.; Zhang, Y.; Zheng, Y. Remaining useful life prediction of lithium-ion battery with optimal input sequence selection and error compensation. Neurocomputing 2020, 414, 245–254. [Google Scholar] [CrossRef]
- Cheng, Z.; Lu, Z. Research on Load Disturbance Based Variable Speed PID Control and a Novel Denoising Method Based Effect Evaluation of HST for Agricultural Machinery. Agriculture 2021, 11, 960. [Google Scholar] [CrossRef]
- Tian, J.; Wang, Q.; Ding, J. Integrated Control With DYC and DSS for 4WID Electric Vehicles. IEEE Access 2019, 7, 124077–124086. [Google Scholar] [CrossRef]
- Sun, Y.; Hao, X.; Pecht, M.; Zhou, Y. Remaining useful life prediction for lithium-ion batteries based on an integrated health indicator. Microelectron. Reliab. 2018, 88, 1189–1194. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.; Chen, Z. An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks. Appl. Energy 2016, 173, 134–140. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, P.; Chen, Z. Joint estimation of SOC-SOH-RUL for lithium-ion batteries based on charging voltage segment and fusion method. Power Grid Technol. 2022, 46, 1063–1072. [Google Scholar]
- Chen, W.; Cai, Y.; Su, Y. Research on Indirect Prediction Method of Remaining Life of Li-ion Battery. Power Technol. 2021, 45, 719–722. [Google Scholar]
- Xu, X.; Lin, P. Parameter identification of sound absorption model of porous materials based on modified particle swarm optimization algorithm. PLoS ONE 2021, 16, e0250950. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Z.; Zheng, M. Performance Analysis and Optimization of a High-Temperature PEMFC Vehicle Based on Particle Swarm Optimization Algorithm. Membranes 2021, 11, 691. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.; Zhang, X. A novel state of health estimation method of Li-ion battery using group method of data handling. J. Power Sources 2016, 327, 457–464. [Google Scholar] [CrossRef]
- Agudelo, B.O.; Zamboni, W.; Monmasson, E. Application domain extension of incremental capacity-based battery SoH indicators. Energy 2021, 234, 121224. [Google Scholar] [CrossRef]
- Guo, P.; Zhang, C.; Gao, X. State-of-health estimation method for ternary lithium-ion battery based on capacity increment curve. Glob. Energy Internet 2018, 1, 180–187. [Google Scholar]
- Fly, A.; Chen, R. Rate dependency of incremental capacity analysis (dQ/dV) as a diagnostic tool for lithium—ion batteries. J. Energy Storage 2020, 29, 101329. [Google Scholar] [CrossRef]
- Pan, W.; Luo, X.; Zhu, M. A health indicator extraction and optimization for capacity estimation of Li-ion battery using incremental capacity curves. J. Energy Storage 2021, 42, 469–502. [Google Scholar] [CrossRef]
- Li, H. Capacity Estimation and Consistency Screening of Decommissioned Batteries Based on IC Curves. Master’s Thesis, Dalian University of Technology, Dalian, China, 2021. [Google Scholar]
- Yang, S.; Luo, B.; Wang, J. Estimation of Lithium-ion Battery State of Health Based on Characteristic Parameters of Capacity Increment Curve Peak Interval. Chin. J. Electrotech. Technol. 2021, 36, 2277–2287. [Google Scholar]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]
- Tang, X.; Zou, C.; Yao, K. A fast estimation algorithm for lithium-ion battery state of health. J. Power Sources 2018, 396, 453–458. [Google Scholar] [CrossRef]
- Pang, X.; Liu, X.; Jia, J. A lithium-ion battery remaining useful life prediction method based on the incremental capacity analysis and Gaussian process regression. Microelectron. Reliab. 2021, 127, 114405. [Google Scholar] [CrossRef]
- Feng, H.; Zhang, X. Estimation of State of Health and Remaining Life Prediction of Lithium Batteries Based on New Health Factors. J. Nanjing Univ. 2021, 57, 660–670. [Google Scholar]
- Zhu, R. Research on the Remaining Life of Lithium Batteries with Multi-Indicator Fusion under the Charging Curve. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Jiang, Y. Aging mechanisms under different state-of-charge ranges and the multi-indicators system of state-of-health for lithium-ion battery with Li(NiMnCo)O2 cathode. J. Power Sources 2018, 400, 641–651. [Google Scholar] [CrossRef]
- Feng, H.; Song, D. A health indicator extraction based on surface temperature for lithium-ion batteries remaining useful life prediction. J. Energy Storage 2021, 34, 102118. [Google Scholar] [CrossRef]
- Afshari, S.S.; Cui, S.; Xu, X. Remaining Useful Life Early Prediction of Batteries Based on the Differential Voltage and Differential Capacity Curves. IEEE Trans. Instrum. Meas. 2022, 71, 3117631. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhou, H.; Lu, Z. A Novel 10-Parameter Motor Efficiency Model Based on I-SA and Its Comparative Application of Energy Utilization Efficiency in Different Driving Modes for Electric Tractor. Agriculture 2022, 12, 362. [Google Scholar] [CrossRef]
- Li, X.; Deng, T.; Wang, M. Improvement of Linear Location Algorithm of Wood Acoustic Emission Source Based on Wavelet and Correlation Analysis. Chin. J. For. Eng. 2020, 5, 138–143. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H. Lithium-Ion Battery Remaining Useful Life Prediction With Box-Cox Transformation and Monte Carlo Simulation. IEEE Trans. Ind. Electron. 2019, 66, 1585–1597. [Google Scholar] [CrossRef]
- Shu, X.; Liu, Y.; Shen, J. Prediction of Li-ion Battery Capacity Based on Improved Least Squares Support Vector Machine and Box-Cox Transform. Chin. J. Mech. Eng. 2021, 57, 118–128. [Google Scholar]
- Bingchen, H.; Xueming, Y.; Jinsong, W.; Xu, Z.; Zongjie, H.; Qiang, L. Remaining service life prediction of lithium-ion battery based on PCA-GPR. J. Sol. Energy 2022, 43, 484–491. [Google Scholar] [CrossRef]
- Pang, X.Q.; Wang, Z.Q.; Zeng, J.C.; Jia, J.F.; Shi, Y.H.; Wen, J. Prediction of Remaining Service Life of Li-ion Batteries Based on PCA-NARX. J. Beijing Inst. Technol. 2019, 39, 406–412. [Google Scholar] [CrossRef]
- Shi, Y.; Shi, M.; Ding, E. Remaining life prediction of lithium-ion battery based on multiple degradation characteristics. Power Technol. 2020, 44, 836–840. [Google Scholar]
- Wang, Z.; Pang, X.; Huang, R. RUL prediction of lithium-ion battery based on KPCA-ANFIS. J. Electron. Meas. Instrum. 2018, 32, 26–32. [Google Scholar]
- Liu, J.; Chen, Z. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Health Indicator and Gaussian Process Regression Model. IEEE Access 2019, 7, 39474–39484. [Google Scholar] [CrossRef]
- Venugopal, P.; Shankar, S.S.; Jebakumar, C.P. Analysis of Optimal Machine Learning Approach for Battery Life Estimation of Li-Ion Cell. IEEE Access 2021, 9, 159616–159626. [Google Scholar] [CrossRef]


| References | HI | HI Equations and Description | Correlation |
|---|---|---|---|
| [11] | Constant current charging time X1 | Among them, t(k) represents the time when the constant current charging mode ends; A(k) represents the measured current value; k is the current number of cycles; n is the sample size. | 0.8763 |
| Average rate of change in voltage during constant current charging X2 | Among them, v(k) and V(k) represent the initial voltage value of theconstant current charging process and the voltage value at the end of the constant current charging process, respectively; t(k) is the charging time of the constant current charging process; k is the current number of cycles; n is the sample size. | 0.6223 | |
| Constant voltage charging time X3 | Among them, t(k) represents the moment when the measured voltage rises to 4.2 V, that is, the moment when the constant current charging ends; T(k) represents the moment when the charging process ends; V(k) represents the measured voltage value; k is the current cycle number; n is the sample size. | 0.7104 | |
| Average rate of change in current during constant voltage charging X4 | Among them, i(k) and I(k) represent the current value at the beginning and end of the constant voltage charging mode, respectively; t(k) represents the time of constant voltage charging, k is the current number of cycles; n is the sample size. | 0.9399 | |
| The time for the surface temperature to rise to the highest during charging X5 | Among them, t(k) represents the time when the surface temperature rises to the highest during the charging process, T(k) represents the measured surface temperature value, k is the current number of cycles, and n is the sample size. | 0.9116 | |
| [12] | the time of equal discharge voltage tk | Among them, tk represents the equal discharge voltage time of the kth cycle, Tvmin represents the time to reach the lower voltage value, and tvmax represents the time to reach the upper voltage value. | 0.8309 |
| [13] | Current rate of change during constant current charging ICCCR_CV | Among them, Bk is the charging current change rate of the kth cycle, and n is the sample size. k is the current number of cycles, and n is the sample size. | 0.9776 |
| [14,15] | The peak intensity of IC curve (IC_peak) | IC_peak is the normalized intensity of the IC peak | high correlation |
| [16] | The peak area of IC curve (IC_area) | where w is the value of dQ/dV; wk is the discrete values of w corresponding to different voltage interval, k is the current number of cycles, and n is the sample size. | high correlation |
| [17] | Average charge voltage rise (ACVR) | Among them, Vj is the voltage within the charging time from 1000 to 1500 s, VT is the cut-off voltage, k is the current cycle number, and n is the sample size. | 0.9940 |
| discharge process | total voltage at the beginning of discharge, total voltage at the end of discharge, time interval of equal voltage drop, voltage difference at the same time interval, sample entropy of discharge voltage, rate of temperature change during discharge, battery capacity increment, depth of discharge, maximum discharge current, average voltage, average current, maximum feedback current, capacity increment curve in discharge stage. |
| charging process | terminal voltage change, time of constant current charging process, time of constant voltage charging process, total time of charging stage, maximum slope of charging voltage curve, maximum slope of charging current curve, slope at the turning point of constant current charging mode, temperature change in charging stage, equal voltage rise charging time, equal time interval charging voltage rise, equal time interval charging current drop, average voltage decay, battery capacity increment, arc length, normal and curvature changes in the constant current charging phase. |
| HI | Classification | Advantage | Disadvantage |
|---|---|---|---|
| Direct HI | Battery Capacity | Directly characterize battery aging with high accuracy for battery SOH estimation and RUL prediction | It is impossible to realize online monitoring and real-time acquisition; it is calculated by the –integral method, which is time-consuming and has accumulated errors |
| Battery Internal Resistance | Strong correlation with battery aging | Measuring battery internal resistance with EISEIS is complex and time-consuming | |
| Indirect HI | HIs Extracted Based on The Discharge Process | The aging state of the battery can be monitored online | Affected by external factors, the collected data are not objective enough |
| HIs Extracted Based on The Charging Process | Less affected by external factors, the collected data are relatively accurate | Unable to monitor battery aging status while the car is in motion | |
| Fusion of multiple HIs | Considering multiple factors that affect the aging of battery performance, fully including the aging information of the battery | The amount of calculation increases and there is redundant information between multiple health indicators, which requires preprocessing |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Lu, Q.; Zheng, Y. Review on the Selection of Health Indicator for Lithium Ion Batteries. Machines 2022, 10, 512. https://doi.org/10.3390/machines10070512
Zhou W, Lu Q, Zheng Y. Review on the Selection of Health Indicator for Lithium Ion Batteries. Machines. 2022; 10(7):512. https://doi.org/10.3390/machines10070512
Chicago/Turabian StyleZhou, Wenlu, Qiang Lu, and Yanping Zheng. 2022. "Review on the Selection of Health Indicator for Lithium Ion Batteries" Machines 10, no. 7: 512. https://doi.org/10.3390/machines10070512
APA StyleZhou, W., Lu, Q., & Zheng, Y. (2022). Review on the Selection of Health Indicator for Lithium Ion Batteries. Machines, 10(7), 512. https://doi.org/10.3390/machines10070512






