1. Introduction
Finite element analysis, which has been widely used in machine tools, aircraft, automobiles, and other industrial designs, can greatly shorten the design period of products and improve their competitiveness of products. The key factor of finite element analysis is to establish an accurate digital model which could reflect the performance of the structure. Nowadays, commercial finite element software such as ANSYS and Nastran could treat single mechanical parts with high accuracy, but the modeling of large mechanical systems is somewhat unsatisfactory. One of the main barriers lies in the modeling of connected joints. The dynamic modeling and parameter identification of joints have attracted much attention from researchers from all over the world.
The bolt joint is almost the most common connection in mechanical systems, and various models are proposed around the modeling of this joint. The commonly used model includes the classic spring-damping model [
1,
2,
3,
4], the zero-thickness model [
5,
6,
7], the eight-nodes-hexahedron-element model [
8,
9], the elastic contact stiffness model [
10,
11], and the virtual material model [
12,
13,
14,
15]. The spring-damping model is simple and convenient, and therefore, it has been widely used in engineering structures. However, this kind of model ignores the coupling effect between the joints, and the distribution of springs is closely related to the connected structure [
14], which limited the accuracy of this model. The zero-thickness model and the eight-nodes-hexahedron model reflect the coupling effect between the joints and the degree of freedom which could give high modeling precision, but the parameters of this kind of model are too much, which makes the modeling process complex, and makes the iterative optimization design time-consuming. The virtual material model treats the joint as a layer of material that can be easily combined with the general finite element software for engineering applications. However, the testing results of pressure distribution of the bolted connection showed that the practical contact scope is limited to the bolt-related area [
16,
17,
18,
19], while the common virtual material model does not consider these local features.
The parameter identification methods of the joint can be classified as direct method and indirect method. The direct method includes the direct measurement of force and displacement which is used in the spring model [
20,
21], the Hertz contact theory [
22,
23,
24], or the fractal theory used in the virtual material model [
14,
25,
26,
27]. Nowadays, the virtual material model is usually carried out by using the Hertz contact theory and the fractal theory to deduce the elastic modulus and Poisson’s ratio. However, this kind of parameter identification method faces the challenge to determine the thickness of virtual material, whose value changes from 0.031–0.131 mm and has a great influence on the dynamic property of the virtual material model [
28].
For the indirect method, the dynamics characteristics of the overall structure are tested first, and then the model updating or the inverse method is used for model parameter identification. The commonly used indirect methods contain the frequency-response-function-based method and model-parameters-based method. In the frequency-response-function-based methods, the dynamic matrices of the sub-structures are calculated theoretically and the FRF of the whole structure is obtained experimentally, and then the joint parameters are calculated by inverse methods [
29,
30,
31,
32]. The difference with this kind of method lies in the way to treat the inverse problem. As the joint parameters are usually sensitive to the FRF near the resonance, the FRFs near the resonance are usually used in parameter identification. However, a slightly offset modal frequency could introduce huge errors to the experimental FRF, which makes this kind of parameter identification method sensitive to noise, especially for lightly damped systems. Due to the effort of lots of researchers, the sensitivity analysis of eigenproblems including the undamped systems [
33], damped systems [
34,
35,
36], and repeated root systems [
37,
38,
39,
40,
41] have been developed maturely, which lay the foundation for parameter identification based on modal parameters. However, due to the imperfection of the test modes, the result of parameter identification may appear to be static uncertainty. A suitable parameter identification method of joint with high accuracy is still the pursuit of researchers.
In this paper, a three-dimensional transition interface model for bolt joints is proposed. In
Section 2, the existing problems of modeling bolt joints are stated, and therefore, a transition interface model of bolt joint which contains the geometrical and physical parameters is proposed.
Section 3 introduced the geometric parameter identification method and then established the geometric parameter database of bolt joints for machine tools. In
Section 4, the model updating method with left- and right-weighted matrix is developed for physical parameters identification, while the accuracy of the parameter’s identification method and the joint model is verified. The database of the transition interface model for bolted joints is then constructed. In
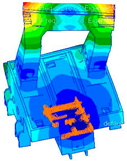
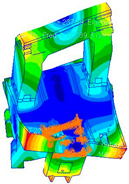
Section 5, the application of the engraving machine tool is used as an engineering example to check the practicability of the proposed transition interface model and the constructed model database.
2. Problem Statement and a Transition Interface Model of Bolt Joint
In the bolt-connected structure, two substructures are bolted together as a whole system under the action of preloads. The essence of bolt connection can be thought of as
a contact problem. One of the widely-used models is the zero-thickness model [
5,
6,
7], which states that the contact zone of the contacting bodies can be modeled using an interface whose thickness is zero.
When the plane elements are adopted in the zero-thickness model, the internal moment between contacting bodies in the zero-thickness plane model cannot be allowed to exist due to the neglected flexural rigidity in nature. If a shell element is used for constructing the zero-thickness model, there exists the traction discontinuity problem [
42]:
where the operator ⟦•⟧ in this study denotes the discrepancy of
of the upper and lower contacting interface. That is,
with subscript “+” denoting the upper surface and “
” denoting the lower surface; here,
is the stress tensor, and
is the unit normal of the interface. The traction discontinuity problem can result in computational difficulties. Additionally, due to the two-dimensional setting, the physical or material properties are not consistent with those of three-dimensional contacting bodies. To overcome these issues, we model the bolt connections using a three-dimensional setting.
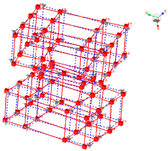
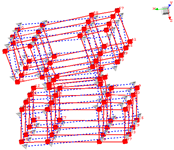
Furthermore, the size of contact area is ambiguity. Often the geometric interface, instead of the ‘real’ physical interface, is used for modeling bolt connections. It must be noted that the influence zone of the bolt connections is not infinite but finite. To illustrate the phenomenon of the finite influence zone, a finite element contact analysis, as an example, is used to study the contact characteristics of bolt connection structures. The contact analysis is performed. The finite element model is constructed by two plates connected with a bolt, which is shown in
Figure 1a, the contact element are added between the two plates, the gasket plate, and the bolt head-plate. The element meshing of the whole structure is shown in
Figure 1b. It should be mentioned that, due to the axial symmetry of contact pressure, the element size along the R-axis is set small to reduce the influence of element size on the results, and the element size in the other direction is somewhat coarse to reduce the computational cost.
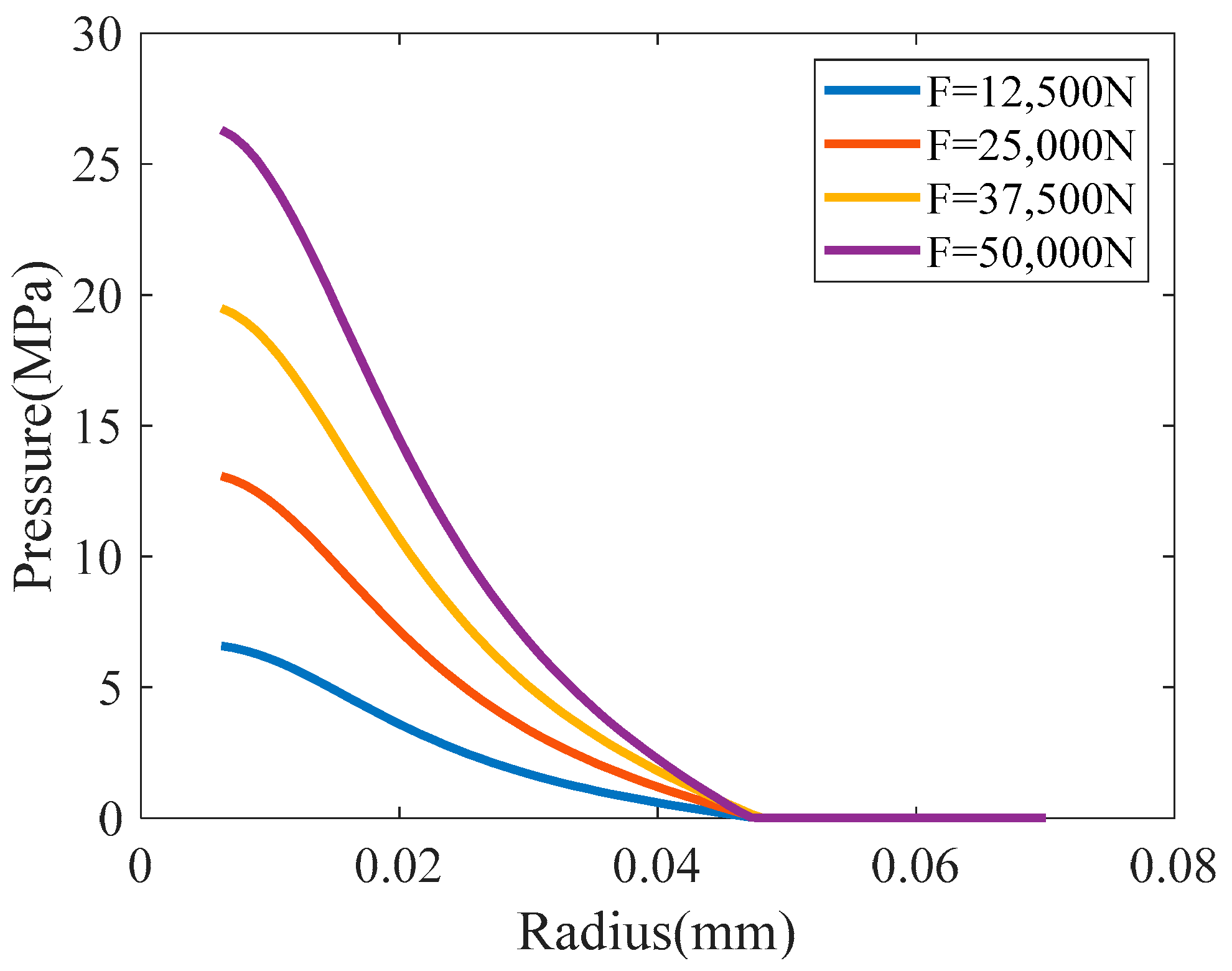
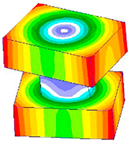
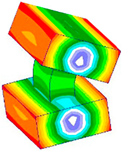
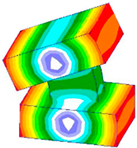
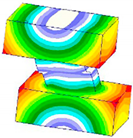
The results of contact analysis can be seen in
Figure 2a. As can be seen from the analytical results, the influence of bolted joints on structure exhibits strong local characteristics. To obtain the distribution of the contact pressure between the plates, the values of contact pressure along the R-axis are extracted and drawn in
Figure 2b.
It is clear that the influence zone of the bolt connections is finite. For the static connection using bolts, we assume that both the displacement field and the traction satisfy the continuity conditions, which require
Here,
is the displacement field. As defined before, the operator ⟦•⟧ denotes the discrepancy of
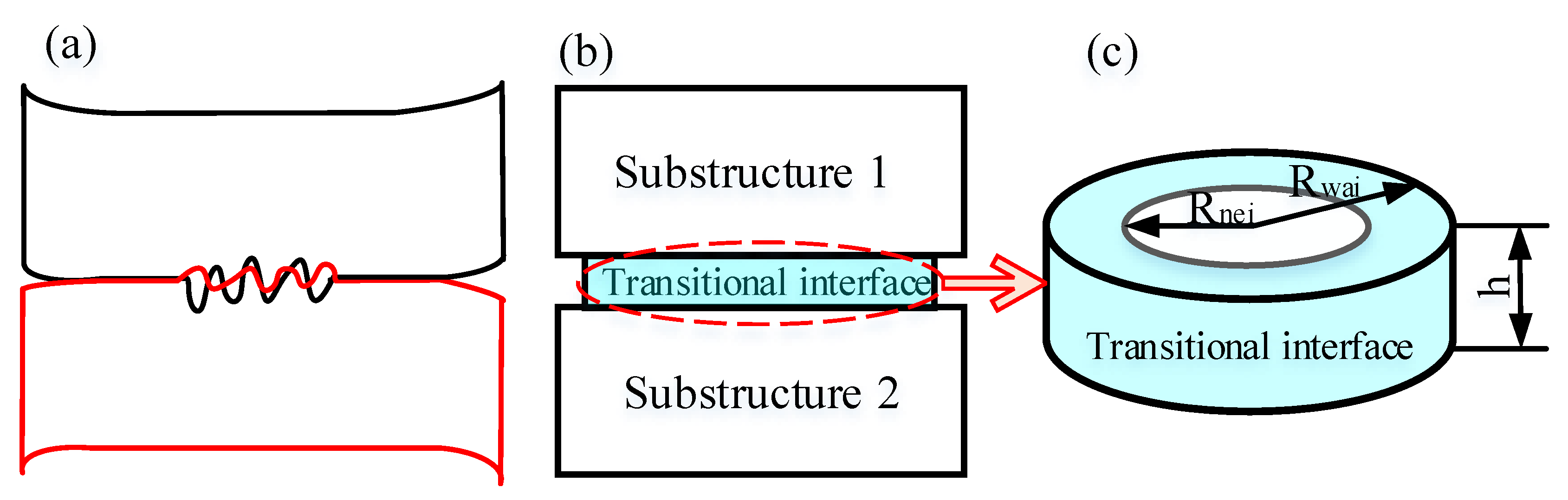
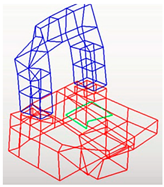
. These two conditions mean that there is no discrepancy of the upper and lower contacting interface for displacement field and the traction. With these assumptions, we propose the transitional interface model, as shown in
Figure 3a. As the bolt-connected structure can be treated as two substructures bolted together under the action of preloads, the ‘real’ physical contact area is a key factor that affects the connection performance. That is, the essence of bolt connection can be alternatively viewed as a
local (finite) interface problem. Regarding this, the joint is modeled as a piece of the transition interface material with geometric parameters shown in
Figure 3b. The geometric parameters of the transition interface material reflect the actual contact area and the thickness of the transition interface material. The geometric parameters can be calibrated based on experimental data.
As the connecting area of the bolt joint usually acts as circles, the geometric parameters of the virtual material can be modeled as a concentric ring with a certain thickness
h, which is shown in
Figure 3c. The inner diameter of the concentric ring
is related to the diameter of the bolt hole. According to the contact analysis results, the actual contact area of the concentric ring is related to the thickness of the connecting plate and the bolt tightening force. So, the outside diameter of the concentric ring
, which is related to the thickness
b of the connected substructure and the tightening force
F of the bolt, is defined as Equation (5). The thickness of the concentric ring
h is related to the material properties and surface roughness of the connected substructure, as well as the normal load, which can be defined as
Here, D means the diameter of the bolt hole, b means the thickness of the connected substructure, F means the tightening force of the bolt, and E1 and E2 mean the elastic modulus of the connected substructure, respectively. and mean the Poisson’s ratio of the connected substructures. and mean the surface roughness of the connected substructures. is the normal pressure between the bolt joint and the connected substructure.
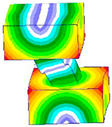
As mentioned above, the transition interface material is an interface problem, thus the physical or material properties shall be different to those of its connecting bodies. To explore the feature of the transition interface material, we use the control variable method to clarify the affection of different contact conditions. To illustrate the affection of thickness, the bolt diameter and the tightening force are set as M12 and 25,000 N, respectively. The contact pressure under the thickness value of 10 mm, 20 mm, 30 mm, and 40 mm is analyzed. The contact pressure distribution between the plates modeled using different thicknesses is shown in
Figure 4. Clearly, the physical properties of the transition interface material shall change smoothly through its thickness as a gradient way.
To clarify the affection of tightening force, the bolt diameter and thickness are constant, and the contact pressure distribution between the plates under different tightening forces is drawn in
Figure 5. The same process is performed to clarify the affection of bolt diameter, material, and roughness. The result shows that the affection of bolt diameter on the contact pressure distribution of joint bolt connection structures is not significant.
However, modeling the transition interface material using gradient properties is difficult to implement for engineering applications (using common finite element software). For the sake of simplification, the physical properties of the transition interface material are assumed to be uniform. This simplification is mainly aiming at significantly cutting down the complexity of the problem of concern while retaining its most important features. For these reasons, we assume that the transition interface material is isotropic and its property is uniform (only two independent parameters, that is, the elastic modulus and the Poisson’s ratio ).
The physical parameters of the transition interface model are reflected mechanical properties of the contact area, which describe the contact stiffness of the surface. Those parameters are mainly determined by the contact pressure. As the contact pressure is related to normal pressure between the joint, the material of contact structure, and the surface roughness. So, the physical parameters of the transition interface material can be defined as
Additionally, the density expressed in Equation (9) can be set to zero. This is because the density of the connecting bodies is assumed to unchanged.
The geometric parameters of the transition interface reflect the actual contact area and the thickness of the transition interface material. The physical parameters of the transition interface material reflect the mechanical properties caused by the contact pressure of the contact area. The transition interface material is fixedly connected with the substructure in the contact surface and the material properties changes at the connection part. The connected bolt structure and the transition interface model are shown in
Figure 3a,b, respectively.
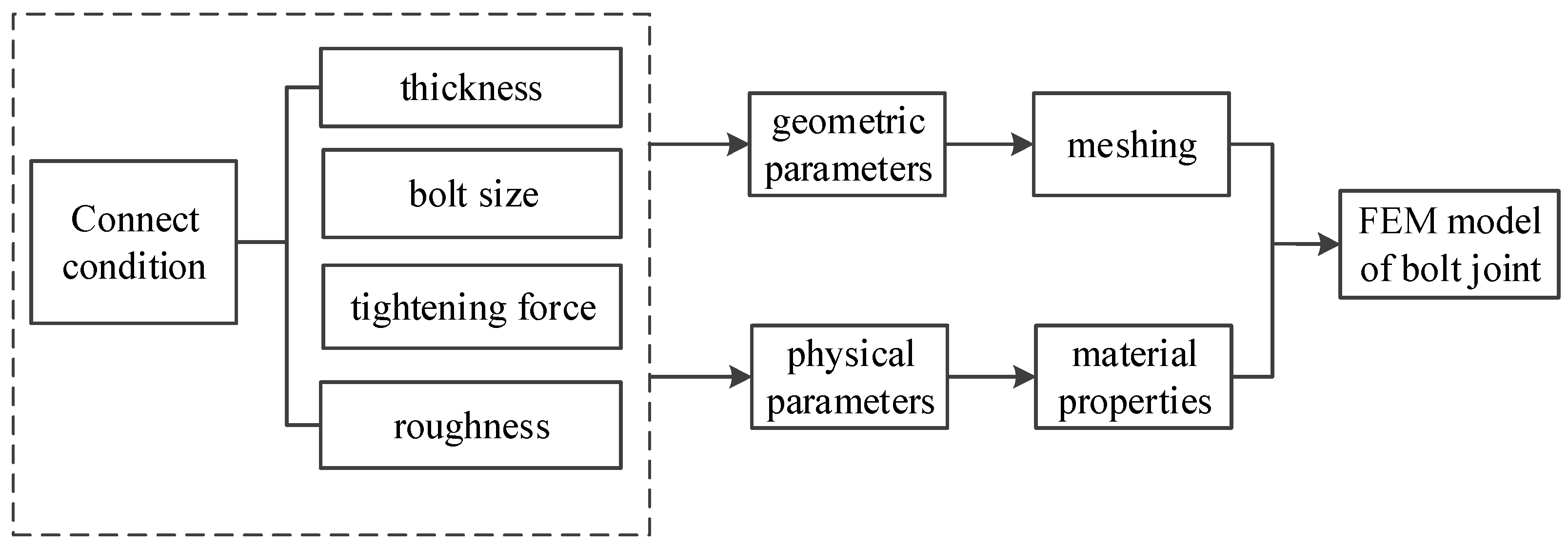
The sizes of the contact area and the contact pressure on this area are the main factors affecting the connection performance. Clarifying the affection of contact conditions (material, thickness, bolt diameter, tightening force, and so on) on the contact characteristics is the basis of joint modeling.
The transition interface model of the bolt joint proposed in this part has geometric parameters and physical parameters. The geometric parameters describe the geometric dimensions of the actual contact area of the joint, and the physical parameters describe the mechanical properties of the contact area. The application of this model can be shown in
Figure 6 According to the surface condition parameters, the geometric and physical parameters of the combined surface are determined. After that, the model is meshed according to the geometric parameters and the physical parameters are given to the mesh. Then, the finite element model of the joint is developed.
As can be seen from
Figure 6, the transition interface model takes full consideration of the actual contact situation of the joint in the modeling so that this model is universal. The transition interface model consists of geometric parameters and physical parameters, which can be easily connected with the general finite element software. Moreover, the mesh size of the joint can be conveniently controlled to meet the analysis requirements of different precision.
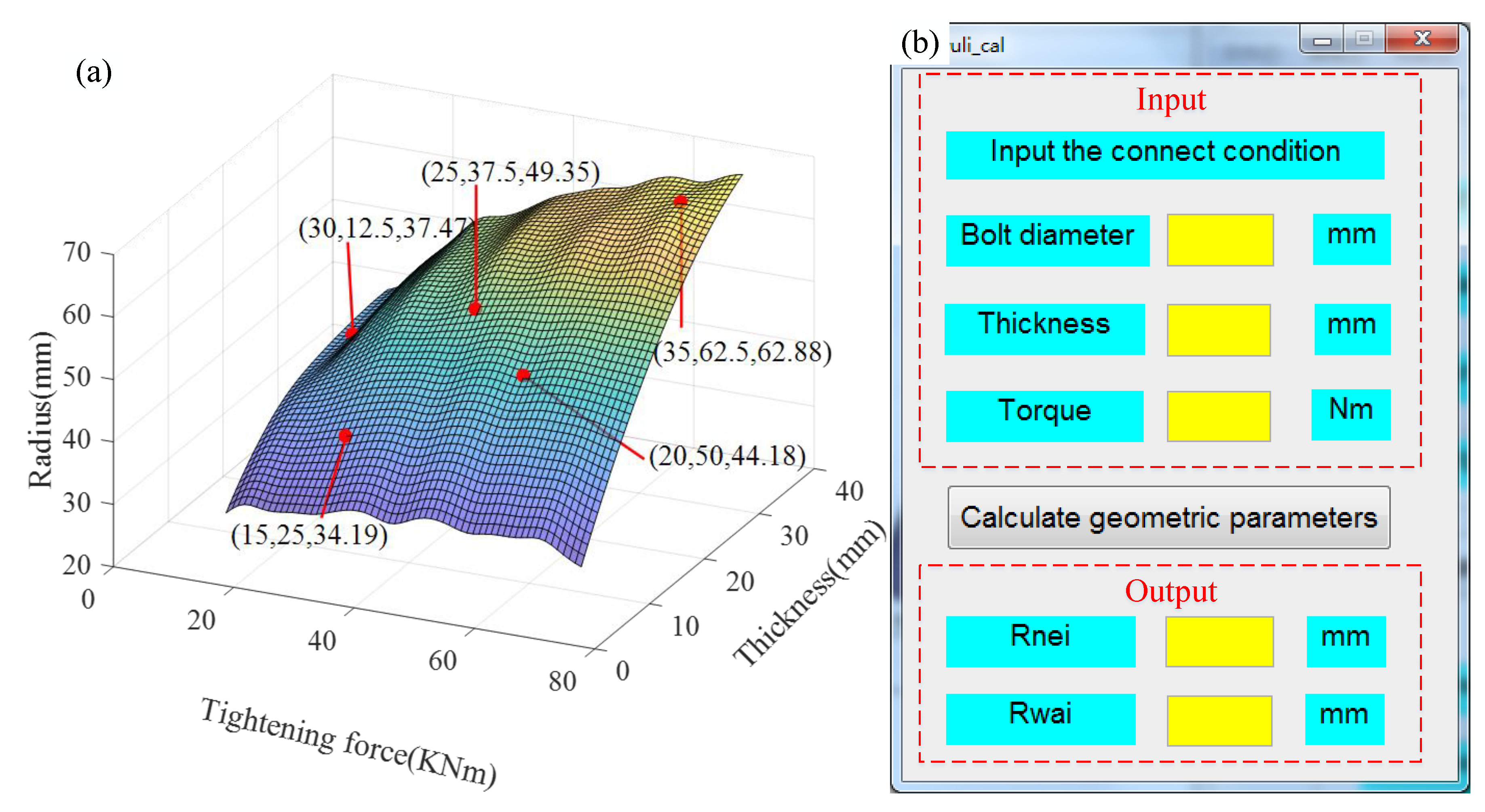
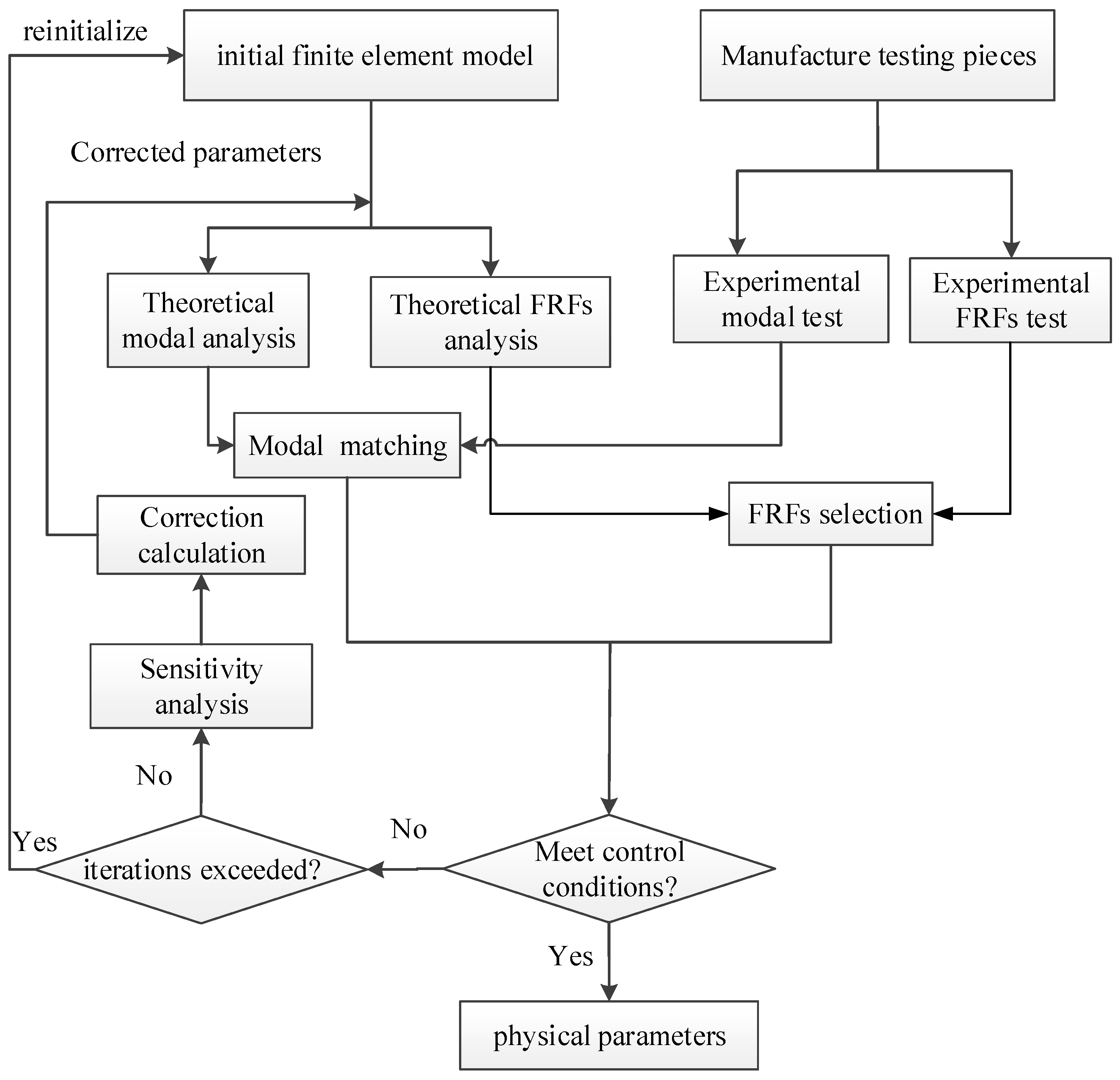
The application of the proposed transition interface model requires the determination of geometric parameters and physical parameters. As can be given by the connection condition of bolt diameter, the density of virtual can be determined by the average density of the contact plates. The parameters which need to be determined are the geometric parameters Rwai and h, as well as the physical parameters E and . The next two sections introduce the parameter identification of transition interface model mode. The contact analysis is conducted to determine the geometric parameters and the average normal pressures of the contact area. After that, the physical parameters are identified by the model updating method because the joint significantly affects the dynamic characteristics of the whole structure.
6. Conclusions
This paper aimed at the dynamic modeling and parameter identification of bolt joints. The main work can be concluded as follows:
(1) Based on the fact that the characteristics of bolt joints rely on the contact area and contact pressure of the surface, and assuming there is no discrepancy of the upper and lower contacting interfaces for displacement field and the traction, a transition interface model of bolt joints containing geometric and physical parameters is proposed.
(2) The contact radius of the bolt joint is calculated based on the contact analysis, and the geometric parameter database of bolt joint on machine tools is established by the Kriging interpolation method. The error of contact radius estimated by the testing point is less than 2%, which verified the accuracy of the established geometric parameter database.
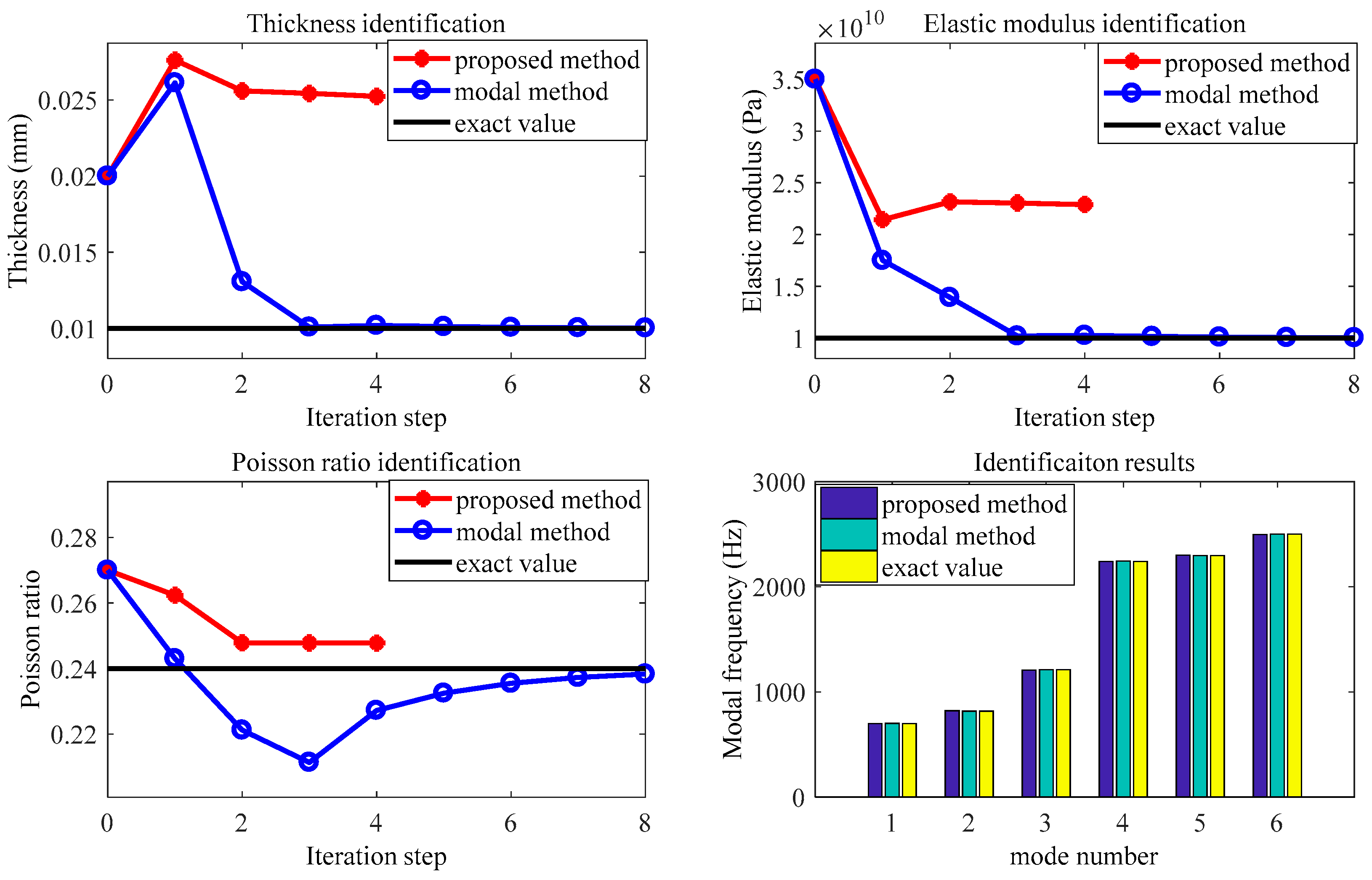
(3) The model updating method, which is constructed by the combination of modal parameters and FRFs, is proposed for physical parameter identification of the transition interface model. Additionally, a numerical example is used to check the validity of the proposed identification method. The results show that once the FRFs are added and weighted with the left and right weight matrix to the identification process, the proposed method is accurate for parameter identification of the transition interface model.
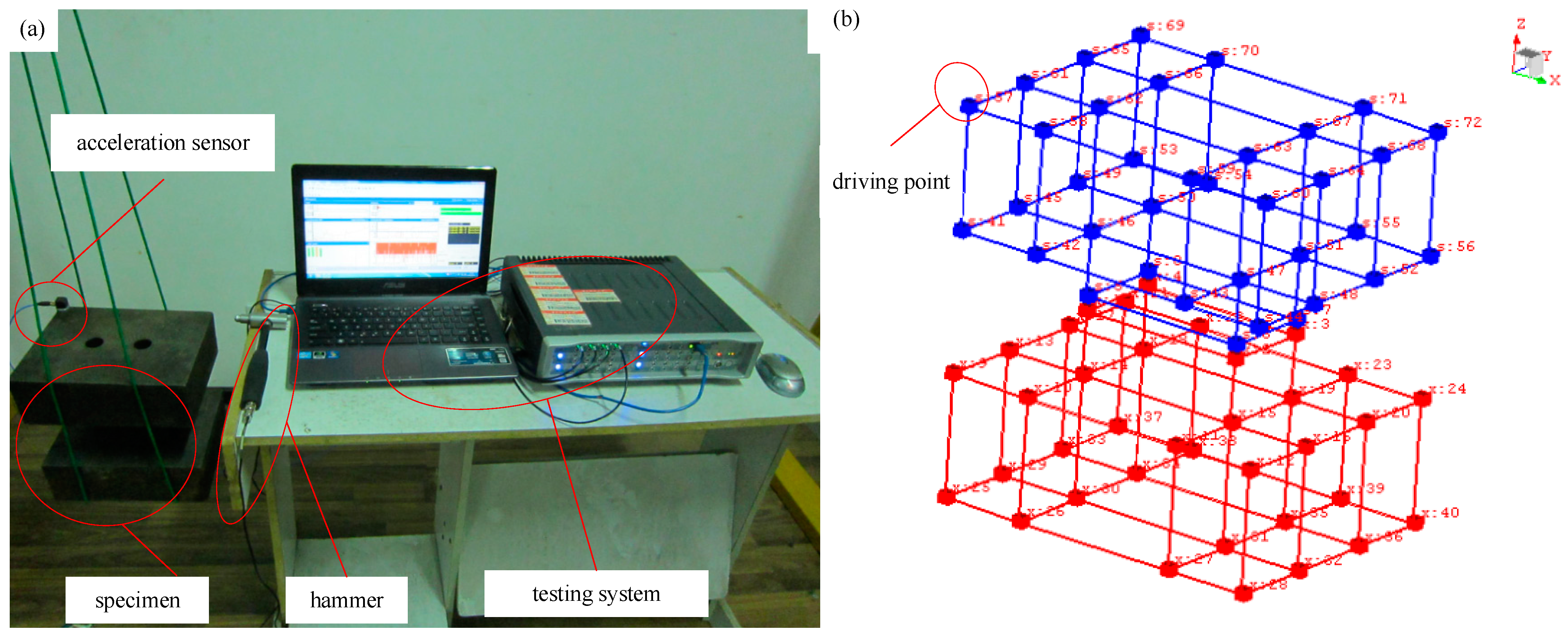
(4) A dumbbell-like experimental system containing the bolt joints is designed and manufactured for joint parameter identification and joint model validation. The difference in the first six order modal frequencies between the theoretical model analysis and the experimental results is less than 7.5%, which means that the proposed joint model is accurate.
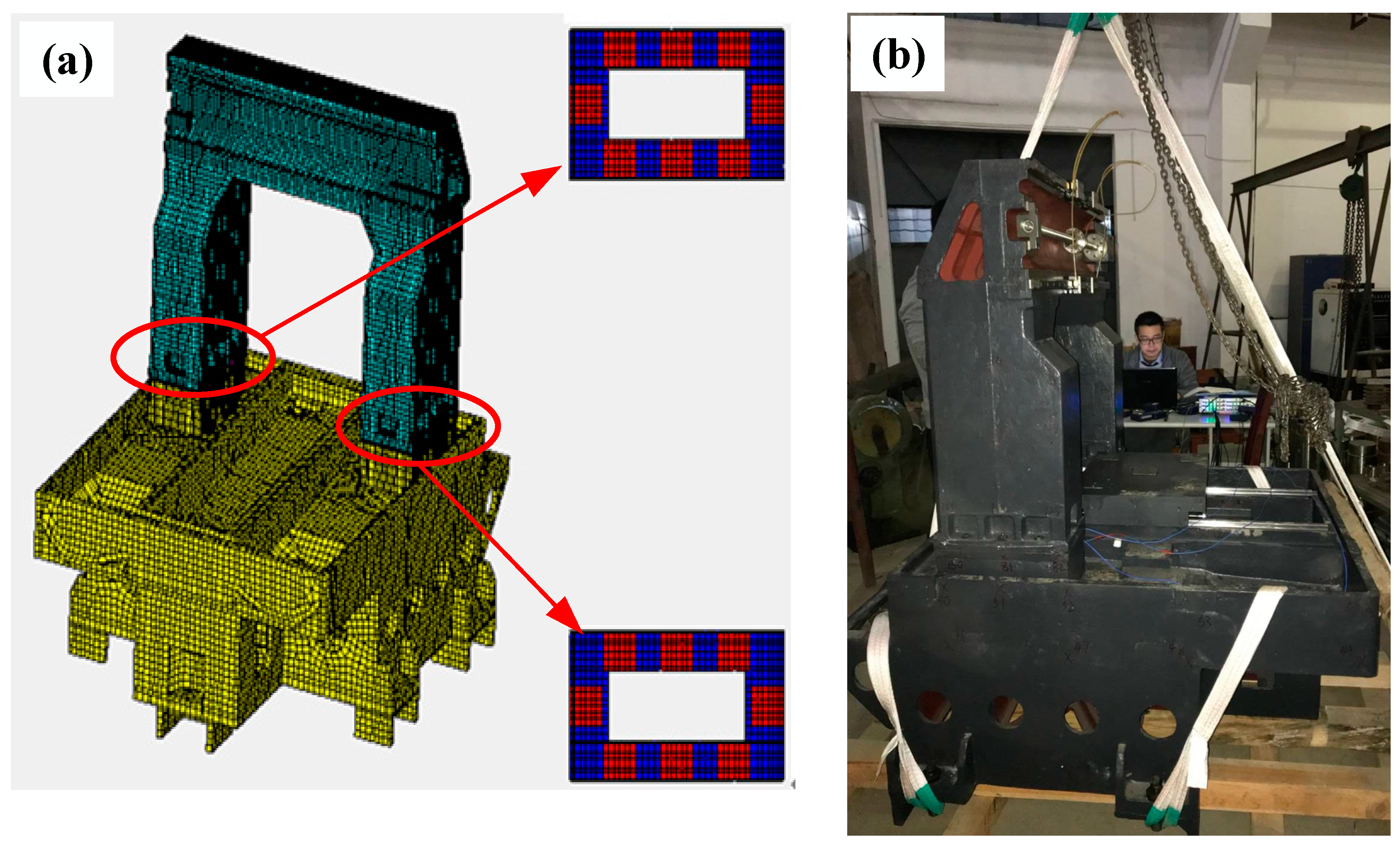
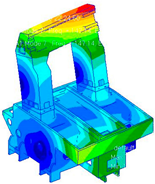
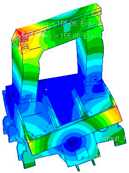
(5) The frame of the engraving machine tool is used to check the effectiveness of the proposed transition interface model and the good agreement of the analysis modal frequency, and the experimental results demonstrated that the proposed model can be used for engineering applications such as structural optimization design and structural health monitoring.