Optimal Synthesis of Loader Drive Mechanisms: A Group Robust Decision-Making Rule Generation Approach

Abstract

The objective of this paper is to present a novel, hybrid group multi-criteria decision approach that can be used to evaluate alternatives for the optimal synthesis of loader drive mechanisms. In most product design engineering groups, experts have expertise in different areas and robust decision-making is necessary to integrate a number of opposing opinions, attitudes, and solutions. This study presents the application of an integrated approach for decision-making, i.e., the generation of a robust decision-making rule for group decision-making (RDMR-G) by combining different multi-criteria decision-making (MCDM) methods and Taguchi’s robust quality engineering principles. The basic idea behind this article was to create an approach that enables the comprehensive and robust consideration of expert opinions given the existence of numerous objective and subjective methods for determining the criteria weights, which are crucial to the final ranking of alternatives in any decision-making problem. In order to set the optimal configuration of a loader drive mechanism, five experts, all with a high level of experience and knowledge in this field, considered twenty-six different kinematic chain construction solutions, i.e., alternatives, and evaluated them with respect to six criteria. The obtained results and rankings provided by each expert and each criteria weighting method were compared using Kendall’s τ_b and Spearman’s ρ tests. As an example, this paper demonstrates the practical application of a RDMR-G approach and in doing so contributes to the literature in the fields of product design engineering and decision-making.

1. Introduction

Structural engineering design optimization, evaluation, and decision-making are very important in product development. Engineering design is the process of configuring an artefact so that the performance attributes of the chosen solution meet functional requirements [1]. As structural engineering design problems are usually of a multi-objective nature, they require a trade-off between several conflicting objectives. In such a process, numerous design solutions can be generated, and multi-criteria decision-making (MCDM) has been recognized as an appropriate approach for selecting the “best” design concept from a set of alternative variants [2,3]. MCDM methods are used for the generation of a decision rule based on which set of given alternatives are evaluated according to different criteria with corresponding criteria weights [4]. Design engineers have to consider different criteria, such as those related to functionality, quality, economy, ergonomy, manufacturability, maintainability, reliability, etc., and to determine their relative importance levels, i.e., via by establishing criteria weights through the use of subjective or objective approaches. The assessment of an expert can greatly influence the alternative product design solution. Therefore, during the conceptual engineering design phase of product development, solving structural design problems involves the adoption of collaborative decision-making processes by engineering groups. In such engineering groups, experts have expertise in different areas and robust group decision-making is necessary to integrate opposite opinions, attitudes, and solutions. Such an approach requires the application of mathematical aggregators for obtaining an aggregated initial decision-making matrix or criteria weights. To the best of the authors’ knowledge, some widely used traditional aggregators are the arithmetic mean operator [5], geometric mean operator [6], Dombi aggregators [7], Bonferroni aggregators [8], Einstein and Hamacher operators [9], power aggregation operators [10], and Heronian aggregation operators [11].

The determination of criteria weights is one of the key problems that arises in MCDM models of mechanical systems evaluation. Defining the criteria weights is not an easy task, and, in essence, depends on the subjective attitudes of design engineers. Depending on the method of solving the MCDM problem, the influence of criteria weights on the obtained solution also changes, and even a small change in their values can lead to a change in the ranking of alternative product design solutions. In addition to the fact that there is no single definition of the term criteria weights, the problem of their determination is further complicated by insufficient knowledge of the possible methods for their determination in a specific decision-making situation. Different approaches for determining criteria weights have been the subject of research and scientific discussions for years. It is possible to find more developed approaches for their determination in the literature [12,13,14,15,16,17,18,19]. Put simply, most approaches are either subjective or objective. Subjective approaches determine criteria weights based on information obtained from the decision-maker or from the experts involved in the group decision-making process. This approach reflects the subjective opinion, knowledge, and expertise of the decision-maker and thus the decision-maker directly influences the outcome of the decision-making process. Objective approaches determine criteria weights based on the information contained in the decision matrix, specifically considering only attribute values, using certain mathematical methods, and, therefore, objective approaches ignore the opinion of the decision-maker.

Several industrial case studies for assessing the efficiency of multi-criteria decision-making-based conceptual engineering design models have been presented in the literature. Among them, different multi-criteria decision-making approaches have been employed: the fuzzy analytic hierarchy process (F-AHP), the fuzzy technique for order of preference by similarity to ideal solution (F-TOPSIS), decision-matrix logic, the fuzzy weighted average (FWA) approach, and the fuzzy grey relational analysis (F-GRA), etc.

In research undertaken by Sreeram and Katti [20], a MCDM model using the AHP and trade off solutions such as Nash, Kalai–Somordinsky solution was proposed in the context of machine structure design. Also, in research undertaken by Renzi and Leali, the application of a MCDM-based design platform was demonstrated in a context of group selection of the most suitable conceptual design of mechanical components [21]. The proposed platform integrated F-TOPSIS and multiple objective particle swarm optimization for solving problems related to the conceptual design. An industrial case study of the conceptual design of heel tips for women’s shoes was used to highlight the efficiency of this modelling platform. Oladejo et al. [22] developed a computer-based model for the evaluation of design concept using decision-matrix logic. They presented a model as a logical procedure for the evaluation of design concepts considering specified attributes and their relative importance. The computer model was developed using the Visual Basic platform that runs in the Microsoft Windows environment, and the implementation of the package was demonstrated on the evaluation of concepts in the design of a low-cost simple gearbox for a special purpose machine. Similarly, Hung et al. [2] presented a computer-based information system called the performance assessing decision support system (PSDSS), which uses an enhanced FWA approach to handle linguistic as well as ordinary quantitative information in engineering design processes. The leading-in device of a button-sewing machine in a costume-machine factory was used as an example to demonstrate the efficiency of the developed MCDM approach. The FWA approach coupled with F-AHP was used by Olabanji and Mpofu [23] to develop a novel hybridized model for the identification of an optimal design for a reconfigurable assembly fixture from a set of alternative design concepts. The same authors, one year later, presented a model for the identification of optimal conceptual designs by hybridizing the F-AHP and F-GRA methods [24]. In both papers, the F-AHP method was used for the determination of design features and sub-features weights, and FWA/F-GRE were used for the ranking of design concept.

Moreover, in the literature, other decision support techniques for structural engineering design evaluations can be found, such as feasibility judgment, the principle of maximum entropy, pairwise comparisons, and prototype testing.

Considering the above literature review, it is obvious that researchers and engineers attempted to apply different hybrid MCDM approaches in order to analyze the ranking stability and sensitivity of criteria weight changes. In recent years, special attention has been paid to hybrid approaches which combine the application of different methods for solving a decision-making problem in order to take advantage of the strengths of each single particular method and minimize their weaknesses [25]. One instance of this idea can be found in research undertaken by Brauers and Zavadskas [26], where it was indicated that “the use of two different MCDM methods is more robust than the use of a single method; the use of three methods is more robust than the use of two, etc”. This idea was further elaborated by Petrovic et al. [4] through the development of an approach to generating a robust decision-making rule (RDMR) for solving different transport and logistics decision making problems. In that paper, the authors concluded that no single MCDM method can be hailed as a superior method for all decision-making problems and no method can be considered as being the most insensitive to criteria weight changes. They suggested that a combination of several theoretical backgrounds behind MCDM methods could provide a more comprehensive and robust decision rule.

Based on these research findings, the application of an integrated approach to decision-making, i.e., the generation of a robust decision-making rule for group decision-making (RDMR-G) by combining different MCDM methods and Taguchi’s robust quality engineering principles, is presented in this paper. The validation of the proposed RDMR-G approach was realized through the evaluation of alternatives for the optimal synthesis of loader drive mechanisms, so that the selected alternative satisfied the basic goal function, i.e., maximum performance with minimal loss of power during the operation of the loader.

Mobile machines of all sizes are characterized by several manipulators that consist of kinematic chains with linkage elements connected by rotating kinematic pairs, i.e., fifth-class joints [27]. Manipulator drive mechanisms chines are comprised of manipulator kinematic pairs linked directly or indirectly to two-way hydraulic cylinders.

A very important and complex class of mobile machines are loaders, with their basic function being to transport bulk material by performing repetitive loading cycles. The basic loader cycle consists of the following operations: the loading and digging of material, transfer, unloading, and returning to a new position. Several configurations of the kinematic chains of the loader mechanism have been developed to perform the basic functions, but concept which employs Z kinematics in the drive mechanisms has been distinguished among them as the most dominant model existing in the construction industry. Z kinematics mechanisms consist of the arm mechanism and the bucket mechanism being interconnected with hydraulic cylinders and levers. The bucket mechanism usually consists of one hydro-cylinder, which on one side is connected via a direct link to the frame of loader and on the other side is connected to the bucket via a two-arm lever and rod. The whole structure forms a configuration in the shape of the letter Z, from which the kinematics of the mechanism takes its name. A mathematical model of the Z kinematics manipulator for dynamic analysis and kinematic parameter optimization of the drive mechanisms, with the aim of minimizing the power consumption during the material loading operation, was presented in paper [28]. The concept of optimal synthesis in relation to loader drive manipulator mechanisms is presented in papers [27,29]. The first paper, [27], presents an optimal synthesis procedure using multi-objective optimization via the application of a genetic algorithm. The authors defined three conflict objective functions and a set of optimization constraints, based on which a Pareto set of solutions was obtained, but how to choose the unique configuration of the manipulator mechanism was not demonstrated. In the second paper, [29], the authors used a single objective optimization approach to optimize loader drive mechanisms. They developed the mathematical model that defines the cycle time criterion as one of the possible criteria for optimization. Similarly, Shen et al. [30] suggested the weighted total objective function as an approach to encompass six sub-objective functions.

All these approaches can be classified as a priori techniques where compromise between conflicting requirements has to be made according to (pre-defined) preferences of criteria. These approaches include the preferences involved in the optimization process, usually by transforming the multi-objective problem into a single-objective problem. On the other hand, RDMR-G can be used as a posteriori decision making tool, where each Pareto solution represents an alternative in MCDM. Through the application of the RDMR approach, a robust differentiation between loader drive manipulator mechanisms can be made based on the preferences which are considered during a-posteriori analyses of the optimization results.

The rest of paper is structured as follows: In Section 2, the three-phase process of the multi-criteria synthesis of loader manipulator drive mechanisms is presented; Section 3 describes the applied methods and the proposed RDMR-G approach in a decision-making context. Section 4, named “Results and discussion”, explains the main finding of this research and the final robust ranking that was determined using the proposed RDMR-G approach. Finally, Section 5 provides concluding remarks as well the advantages and limitations of the study.

2. The Process of Optimal Synthesis of Loader Manipulator Drive Mechanisms

The process of the synthesis of loader manipulator drive mechanisms implies the multi-criteria synthesis approach because of the complexity of the functions and structure of drive mechanisms. In principle, the synthesis determines the transmission and executive parameters and the parameters of the mechanism’s structure on the basis of the given operating conditions parameters (the input parameters) and performance parameters (the output parameters of the mechanisms).

The process of the multi-criteria synthesis of loader manipulator drive mechanisms has three phases:

• Phase 1: generation of variant solutions for mechanisms;
• Phase 2: the definition of the synthesis criteria;
• Phase 3: the evaluation and selection of the variant solutions for mechanisms using the proposed RDMR approach.

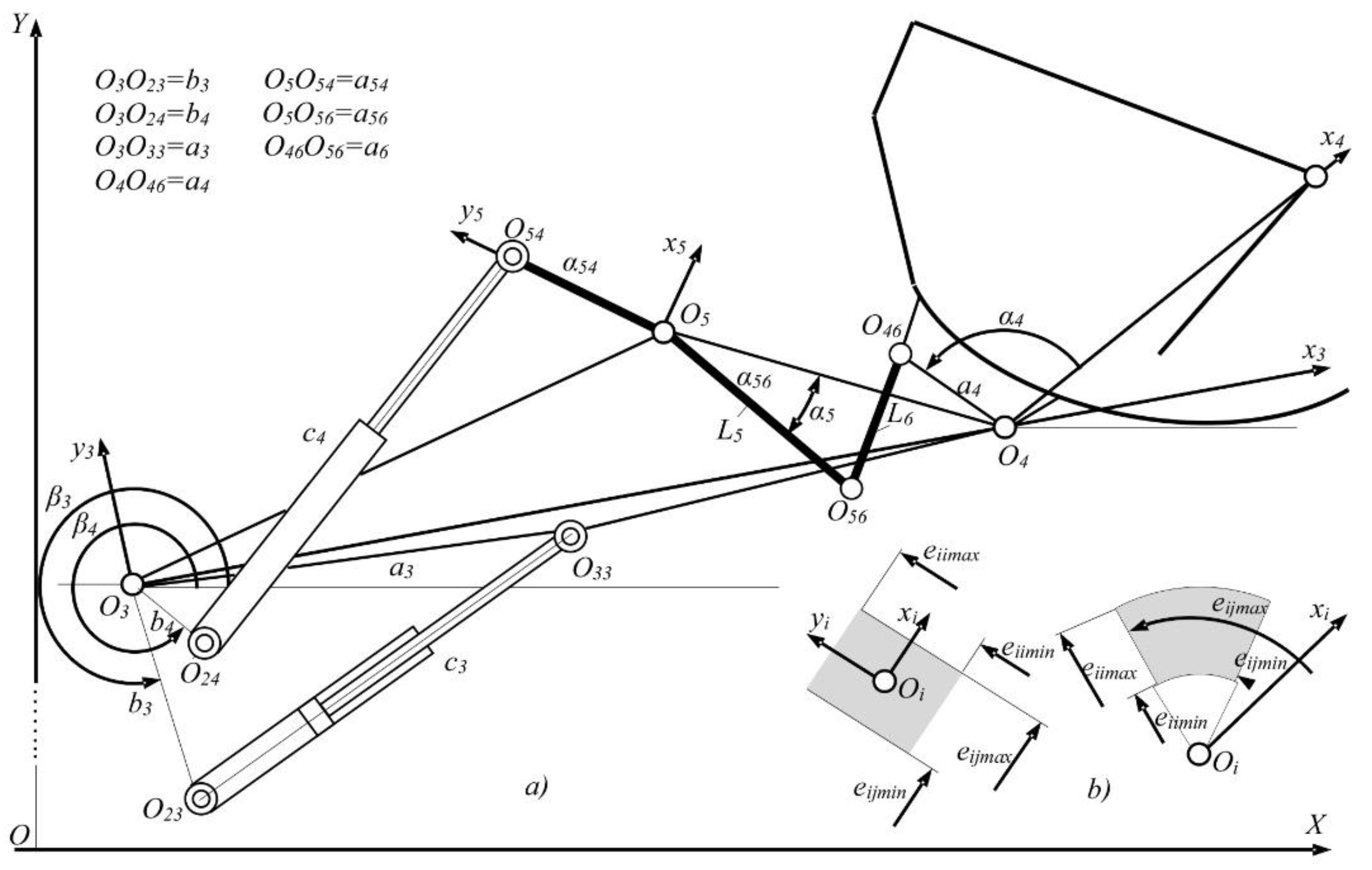
2.1. Generation of Variant Mechanism Solutions

During the first phase of mechanism synthesis, a mathematical model, an algorithm, and software for the generation of possible variant solutions for Z kinematics manipulator drive mechanisms were developed. The search area includes transmission parameters, namely the coordinates of joints and the lengths of the transmission levers of mechanisms, and executive parameters: the sizes of hydraulic cylinders of mechanisms.

The developed program first generates the transmission parameters of the mechanisms using a genetic algorithm. It then generates the executive parameters of the mechanisms by sequentially searching the file of available discrete standard cylinder sizes (generate and test method). The transmission parameters are generated based on the objective function defined according to the requirement for the maximum functional dependence of the manipulator mechanisms.

Variants of mechanisms are generated with limitations related to the kinematics of mechanisms in manipulator limit positions, the allowed characteristics of the hydraulic cylinders of manipulator mechanisms, the required driving moments of mechanisms, and the given declared bucket breaking force.

At the beginning of the process of generating variant solutions, a set of parameters is given (Equation (1) and Figure 1):

$$P_m=\left|V,X_i,Y_i,{\alpha }_i,Y_d,Y_t,{\alpha }_t,t_p,t_i,t_s,F_d,p_{max}\right|$$

(1)

where $V$ is the bucket volume, $X_i,Y_i,Y_d,Y_t$ are the working area of the manipulator, ${\alpha }_t, {\alpha }_i$ are angles of the bucket position during transport and unloading, $t_p,t_i,t_s$ is the time of operation for the manipulation task, $F_d$ is the declared bucket breaking force, and $p_{max}$ is the maximum pressure of the manipulator hydrostatic drive system.

According to the given input set of parameters, based on the developed mathematical model of the loader, a set of possible variant solutions for manipulator drive mechanisms is generated:

$$E_v=\left|E_{3v},E_{4v}\right|\forall v=1,\dots {\mathrm{n}}_v$$

(2)

where $E_{3v}$–is the possible variant of the arm mechanism, $E_{4v}$ is the possible variant of the bucket mechanism, and $n_v$ is the number of the possible variants.

The variants of the loader manipulator mechanisms are generated, according to the defined mathematical model of the loader, by searching the possible range of parameter changes (optimization areas) and selecting the possible variant solutions according to certain generation constraints.

2.1.1. Generation of Searching Area

Two types of variables occur in the synthesis of manipulator drive mechanisms:

• Continuous variables (transmission parameters): the coordinates of joints and lengths of mechanisms levers, which are included in the following sets:

$$E_{3vp}=\left\{e_{3j}\right\}\forall j=1,\dots ,4; E_{4vp}=\left\{e_{4j}\right\}\forall j=1,\dots ,10$$

(3)

• Discrete variables (executive parameters): the diameters of pistons and rods of hydraulic cylinders of manipulator drive mechanisms:

$$E_{3vt}=\left\{e_{3j}\right\}\forall j=5,6; E_{4vt}=\left\{e_{4j}\right\}\forall j=11,12$$

(4)

The area of generation (optimization) is the possible changes in the transmission parameters of mechanisms in the range:

$$e_{3j min}\le e_{3j}\le e_{3j max}\forall j=1,\dots ,4; e_{4j min}\le e_{4j}\le e_{4j max}\forall j=1,\dots ,10$$

(5)

And executive parameters that belong to the file Dc of available hydraulic cylinders with standard piston and connecting rod diameters:

$$e_{3j}\in D_c\forall j=5,6 ; e_{4j}\in D_c\forall j=11,12$$

(6)

where $e_{3j min}$, $e_{4j min}$, $e_{3j max}$, $e_{4j max}$ are minimum and maximum values of the transmission parameters the mechanisms that are given according to the possible installation space and undisturbed relative movement of the members of the manipulator drive mechanisms in relation to the members of the loader kinematic chain.

2.1.2. The Procedure of Variant Solutions Generation

In the first part of the program, the transmission part of the mechanisms is generated (the coordinates of the joints and the kinematic length of the mechanism members) using a genetic algorithm by searching the given optimization area. The possible variant solutions for the mechanism’s transmission part are selected by the set of geometric constraints considering the relative position of the mechanism’s members in certain positions of the manipulator and by the defined objective functions related to the transmission functions of the mechanisms.

In the second part of the program, the transmission part of the mechanisms is added to the executive part by the choice of the actuators (hydraulic cylinders) using a discrete search of the available sizes of hydraulic cylinders with standard diameters with regard to the piston and connecting rod. The constraints that are set when the executive part of the mechanisms is being chosen, and these refer to the allowed characteristics and possibilities of the hydraulic cylinders: the given declared breaking force and the required driving moments of the mechanisms.

As an example, using the developed program, possible variant solutions for the drive mechanisms of a loader manipulator with Z kinematics, with a mass $m=15,000 \left[\mathrm{kg}\right]$ and bucket volume $V=2.7 \left[{\mathrm{m}}^3\right]$, were generated. The initial solution corresponds to the physical model of the wheel loader WA320 (manufactured by Komatsu company), according to which the search areas for the variable transmission parameters of the mechanisms were determined. The file $D_c$ of hydraulic cylinders that was used for searching the executive parameters of the mechanisms was formed according to the available hydraulic cylinders from Bosch Rexroth and Liebherr companies.

2.1.3. Analysis of Generated Variant Solutions

The generated set of possible variants of Z kinematics manipulator mechanisms shows that arm and bucket mechanisms (

Table 1. Variant solutions for the arm drive mechanism.

${\mathit{E}}_{3\mathit{v}}$	Transmission Parameters 1–4				Executive Parameters 5,6		Additional Parameters
	${\mathit{b}}_3,$	${\mathit{\beta }}_3$	${\mathit{a}}_{3\mathit{x}}$	${\mathit{a}}_{3\mathit{y}}$	${\mathit{D}}_3$	${\mathit{d}}_3$	${\mathit{c}}_{3 \mathit{m}\mathit{i}\mathit{n}}$	${\mathit{c}}_{3 \mathit{m}\mathit{a}\mathit{x}}$	${\mathit{n}}_{\mathit{c}3}$
	[mm]	[°]	[mm]	[mm]	[mm]	[mm]	[mm]	[mm]	[-]
3.001	524	269.7	1655	−129	125	90	1340	2058	2
3.014	495	259.7	1498	55	125	80	1335	1945
3.020	482	262.6	1614	−15	125	80	1402	2028
3.026	575	262.6	1602	−28	110	80	1361	2097
3.028	583	263.5	1682	−81	110	80	1410	2172
3.033	380	261.9	1604	−16	140	90	1431	1930
3.036	1633	262.3	512	−109	125	90	1330	2031
3.051	343	262.1	1612	−26	150	100	1449	1904
3.053	481	262.8	1655	−23	125	90	1438	2066
3.064	367	262.5	1662	0	140	90	1491	1976
3.095	498	262.6	1628	−16	125	90	1410	2056
3.108	362	267.4	1360	−86	150	100	1179	1618
3.111	621	263.5	1691	−91	110	80	1404	2213
3.117	413	262.7	1667	0	140	90	1474	2018
3.135	524	285.2	1764	−115	125	90	1340	2073
3.147	370	262,4	1658	0	140	90	1487	1974
3.150	486	262.6	1633	−19	125	90	1418	2049
3.178	335	284.7	1434	−78	150	100	1183	1629
3.223	449	260.5	1538	27	125	80	1366	1936
3.236	595	263,1	1657	−7	110	80	1390	2161
3.245	338	262.4	1668	12	150	100	1511	1958
3.267	482	260,3	1526	36	125	80	1353	1956
3.271	614	263,4	1686	−95	110	80	1401	2202
3.278	587	263.3	1689	−78	110	80	1418	2184
3.290	475	262.5	1750	−150	125	90	1508	2145
3.295	475	262.5	1750	150	125	90	1585	2182

and

Table 2. Variant solutions for the bucket drive mechanism.

${\mathit{E}}_{4\mathit{v}}$	Transmission Parameters 1–10							Executive Parameters 11,12		Additional Parameters
	${\mathit{b}}_4/{\mathit{\beta }}_4$	${\mathit{x}}_{35}$	${\mathit{y}}_{35}$	${\mathit{a}}_4/{\mathit{\alpha }}_4$	${\mathit{a}}_{54}$	${\mathit{a}}_{56}/{\mathit{\alpha }}_5$	${\mathit{a}}_6$	${\mathit{D}}_4$	${\mathit{d}}_4$	${\mathit{c}}_{4 \mathit{m}\mathit{i}\mathit{n}}$	${\mathit{c}}_{4 \mathit{m}\mathit{a}\mathit{x}}$	${\mathit{n}}_{\mathit{c}4}$
	[mm/°]	[mm]	[mm]	[mm/°]	[mm]	[mm/°]	[mm]	[mm]	[mm]	[mm]	[mm]	[-]
4.001	293/314.6	1703	577	369/88	720	751/15.1	756	150	100	1340	1897	1
4.014	252/341.3	1742	632	270/84.2	764	784/10.7	643	160	100	1440	1815
4.020	325/342.8	1748	614	348/85.8	700	735/16.2	757	140	90	1349	1818
4.026	259/340.7	1739	631	287/84.1	763	814/10.9	631	170	115	1412	1798
4.028	235/350.1	1622	657	253/86.4	834	849/11.7	676	180	115	1329	1688
4.033	251/347.9	1627	637	267/86.3	839	853/11.8	675	160	110	1299	1675
4.036	300/342.5	1750	633	320/85	749	779/13.7	690	150	100	1385	1822
4.051	250/342.5	1725	633	270/85	763	793/10	650	170	110	1433	1803
4.053	275/342.5	1650	527	295/90	720	750/10	730	150	100	1241	1647
4.064	300/342.5	1700	607	320/90	820	850/11.8	650	150	100	1297	1736
4.095	325/342.5	1775	620	345/85	706	736/15.6	730	140	100	1379	1849
4.108	250/340.6	1703	577	300/95	647	840/6.1	637	180	125	1397	1727
4.111	250/342.5	1675	633	270/85	806	836/10	650	170	115	1372	1742
4.117	400/342.5	1675	607	445/85	763	793/11.8	850	125	90	1258	1840
4.135	293/314.6	1703	577	355/88	720	751/15.1	756	150	100	1393	1862
4.147	250/342.5	1650	567	270/90	791	821/11.8	650	160	100	1238	1615
4.150	275/342.5	1650	553	295/90	791	821/10	670	160	100	1231	1640
4.178	295/325	1695	570	360/88	740	850/15.1	663	150	100	1411	1706
4.223	300/342.5	1675	607	320/85	763	793/15.6	730	150	100	1258	1699
4.236	263/347.9	1635	626	278/86	826	858/11.9	667	170	110	1271	1656
4.245	345/342.2	1750	608	366/86.3	718	746/16.1	759	140	90	1326	1825
4.267	250/351.6	1600	660	270/85	806	836/11.8	730	170	115	1314	1687
4.271	350/351.6	1675	660	370/90	806	836/19.3	750	140	100	1212	1719
4.278	275/342.5	1775	647	295/85	734	764/17.5	670	160	100	1406	1813
4.290	250/351.6	1600	687	270/85	820	850/17.5	730	160	100	1271	1648
4.295	275/342.5	1675	567	295/90	777	807/13.7	670	150	100	1232	1642

) have different transmission and executive parameters.

The generated parameters of the arm mechanism are given in Table 1, and shown in Figure 2, where $b_3,{\beta }_3$ are the coordinates of the joint O₂₃, where the arm hydraulic cylinder is connected to the front member, L₂, of the moving mechanism, defined in the local coordinate system of the member L₂; $a_{3x},a_{3y}$ are the coordinates of the joint O₃₃, where arm hydraulic cylinder is connected to the arm L₃, defined in the local arm coordinate system; $D_3,d_3$ are the diameter of the piston and connecting rod of the arm hydraulic cylinder; $c_{3 min}$ is the minimum (initial) length of the arm hydraulic cylinder; $c_{3 max}$ is the maximum (final) length of the arm hydraulic cylinder; and $n_{c3}=2$ (in all variants), i.e., the number of arm hydraulic cylinders.

The generated parameters of the bucket mechanism are given in Table 2, where: $b_4,{\beta }_4$ are the coordinates of the joint O₂₄, where the bucket hydraulic cylinder is connected to the front member, L₂, of the moving mechanism defined in the local coordinate system of the member L₂; $x_{35},y_{35}$ are the coordinates of joint O₅, where the arm is connected to the two-arm lever defined in the local coordinate system of the arm L₃; $a_4,{\alpha }_4$ are the coordinates of the joint O₄₆, where lever L₆ is connected to the bucket; $a_{54}$ is the length of the arm of the two-arm lever, L₅, which is connected to the bucket hydraulic cylinder C₄; $a_{56}$ is the length of the arm of the two-arm lever, L₅, which is connected to the arm L₆; ${\alpha }_5$ the angle between the arms of the two-arm lever L₅; $a_6$ is the length of the arm L₆; $D_4, d_4$ is the diameter of the piston and connecting rod of the bucket hydraulic cylinder C₄; $c_{4 min}$ is the minimum (initial) length of the bucket hydraulic cylinder; $c_{4 max}$ is the maximum (final) length of the bucket hydraulic cylinder; and $n_{c4}=1$ (in all variants), i.e., the number of bucket hydraulic cylinders.

2.2. Definition of Synthesis Criteria

In the different stages of a product lifecycle (PLC) there are numerous criteria by which the products are evaluated. In the case of the development of an actual product, a number of criteria related to technical issues, economy, ergonomics, controllability, and environmental issues must be considered. Among these, some criteria might be specific for a particular PLC stage, while others may be relevant across several stages. In this study, the focus was on the first (design) phase of product development, considering only technical criteria. Those criteria were defined according to the conditions of the problem being considered. Based on the literature review [27,28,29], the authors’ knowledge of the field of the design of mobile machines design and the experts’ attitudes obtained through a survey, a kinematic criterion, a criterion of directed digging force, a tribological criterion, a time criterion, a mass criterion, and a dynamic criterion were singled out as relevant for the optimal synthesis of loader drive mechanisms. The defined criteria are independent of each other because they reflect different aspects of the engineering design process (kinematics, dynamics, power, mass, tribological aspect, etc.).

• The kinematic criterion, C₁, was defined with the aim of ensuring that during the operation of material transfer, when a full bucket with material is lifting from the transport to the unloading position, the bucket back angle in relation to the ground base deviates minimally from the given transport angle to prevent the spillage of bucket loaded material.
• The criterion of directed digging force, C₂, was defined with the aim of achieving maximum digging forces in the zone of the manipulator working area harmonized with potential loader stability. As an indicator of the criteria, the directed digging force was defined based on the possible digging forces determined in the entire working area of the manipulator corrected by the loading position factor and direction factor of the digging force in relation to the cutting edge of the bucket.
• The tribological criterion, C₃, is defined with the aim of minimizing energy losses caused by friction in the kinematic chain joints and manipulator drive mechanisms. It reflects the energy efficiency of the manipulator drive mechanisms. The indicator of the criterion is determined according to the power losses caused by the manipulation tasks of the loader in the entire working area of the manipulator.
• The time criterion, C₄: The duration of the operation of the loading, transport, and unloading of material with a bucket is determined as an indicator of the criteria in order to achieve the maximum technical performance of the loader with the manipulator drive mechanisms. It is assumed that the hydraulic cylinders of the drive mechanisms of the manipulator are supplied by a hydraulic pump of variable specific flow with regulation of the hydraulic flow according to the criterion of constant hydraulic power.
• The manipulator mass criterion C₅ was determined with the aim of ensuring that the mass of the members of the kinematic chain and the drive mechanisms of the manipulator are minimal. The indicators of the criteria are the relative mass of the actuators of the drive mechanisms and the nominal mass of the arm and the levers of the manipulator bucket mechanism, as determined by the transmission and executive parameters of the mechanisms.
• The dynamic criterion C₆ refers to the influence of the parameters of the drive mechanisms of the manipulator on the dynamic stability of the loader. As an indicator of the criterion, the vertical movement of the support-moving member of the kinematic chain of the loader caused by the movement of the kinematic chain members of the manipulator in the loader dynamic model is taken. The hydraulic cylinders of the manipulator drive mechanisms are modeled as elastic-damping elements since they act as “hydraulic springs” under load.

3. Applied Methods and Proposed RDMR-G Approach

A number of hybrid MCDM approaches have been developed in recent years to make choices more objective and rational. Approaches which combine several MCDM methods are distinguished among them. In this paper, an approach to the determination of criteria weights via the integration of different MCDM methods using Taguchi’s robust quality engineering principles is presented. A short description of the MCDM methods used for generation of the proposed RDMR-G approach is provided in this section.

3.1. Applied Methods to Criteria Weights Determination

3.1.1. Fuzzy Analytic Hierarchy Process

The analytic hierarchy process (AHP) method, proposed by Saaty [31], has certainly become one of the most widely used MCDM methods in recent years. It is characterized by its ease of use and its ability to structure problems systematically and calculate both criteria weights and alternative priorities [13]. The fuzzy analytic hierarchy process (F-AHP), as an extension of the conventional AHP in the form of the integration of the fuzzy number and AHP method, was introduced by Van Laarhoven and Pedrycz [32], Buckley [33], and Chang [34]. Today, examples of the application of F-AHP are numerous. According to the electronic database Elsevier’s Science Direct, there has been a significant increase in the applications of the F-AHP method in scientific journal papers and books over the last ten years (86 references in 2010 and 423 references in 2021). A number of interesting reviews of the F-AHP method have been published by Liu et al. [13] and Mardani [35]. The algorithm of a particular application of the fuzzy AHP method follows the defining of the comparison matrix, the aggregation of multiple judgements, the measuring of the consistency, and the defuzzifying of the fuzzy weights. In this study, algorithm presented by Zavadskas et al. [36] was adopted.

3.1.2. Fuzzy Pivot Pairwise Relative Criteria Importance Assessment

The original pivot pairwise relative criteria importance assessment (PIPRECIA) was proposed by Stanujkic et al. [37] by upgrading the SWARA method while solving a case study of selecting the most appropriate traditional Serbian restaurant. It is a subjective weighting method based on decision makers’ judgments and is particularly beneficial for group decisions involving a large number of experts. The method has been extended to deal with fuzzy numbers and to handle uncertainties in decision makers’ judgments by Stević et al. [15]. In that paper, the fuzzy pivot pairwise relative criteria importance assessment (F-PIPRECIA) method was introduced for the evaluation of the conditions for the implementation of barcode technology in a warehouse system. The F-PIPRECIA method consists of eleven steps, fully defined in study [15], and was adopted for application in this study.

3.1.3. Fuzzy Full Consistency Method

The full consistency method (FUCOM) is one of the most recent subjective methods proposed for the determination of criteria weights. The FUCOM method, developed by Pamučar et al., [16], is based on of the pairwise comparisons of criteria and the validation of results throughout a deviation from maximum consistency. According to Pamucar et al. [38], the main advantages are reflected in the fact that the FUCOM method:

(1)

allows for the pairwise comparison of the evaluation criteria not only through the use of integers but also by utilizing decimal values,

(2)

uses a simple algorithm to determine the criteria weights,

(3)

and needs a smaller number of pairwise comparisons for deciding criteria weights.

Potential applications for the FUCOM method in group decision-making were presented by Fazlollahtabar et al. [39] and Durmić et al. [40]. The extension of the FUCOM method for solving decision-making problems with fuzzy numbers (F-FUCOM) was developed by Pamučar et al. [41]. In this study, the original algorithm developed by Pamucar and Ecer [42] was adopted.

3.1.4. Entropy Weighting Method

The entropy weight method (EWM) is an objective weighting method that measures value dispersion in decision-making based on probability theory and the attribute values in the decision matrix. Originally proposed by Shannon [43] and further developed by Zeleny [44], the EWM works on the principle that a higher degree of dispersion of the measured values (the greater the difference between the values of the elements in the column in the decision matrix) provides less entropy and a higher criterion weight.

Significant applications of the EWM method have been observed in the last five years. In this study, the algorithm presented by Mukhametzyanov [17] was adopted.

3.1.5. Criteria Importance through Intercriteria Correlation Method

The criteria importance through intercriteria correlation (CRITIC) methods is one of the most widely used objective criteria weighting methods. The CRITIC method, which was originally proposed by Diakoulaki et al. [45], uses correlation analysis and standard deviation of the normalized criterion values by columns to determine the contrasts between criteria [46]. In the original CRITIC method algorithm, seven steps were proposed, by which final criteria weights are obtained based on the multiplication of the standard deviation of each column and the sum of the linear correlation coefficients of the column vectors. In this study, the CRITIC-M method (a modification of the CRITIC method proposed by Žižović et al. [18]) was used. In the CRITIC-M method, two modifications are performed: (1) the modification of normalizing data in the initial decision matrix and (2) the modification of expressions for determining the final values of criteria weights.

3.1.6. Method based on the Removal Effects of Criteria

The method based on the removal effects of criteria (MEREC) is a new method developed by Keshavarz-Ghorabaee et al. [19]. The basic goal of the MEREC method is the determination of criteria weights by the assessment of each criterion’s removal effect on the performance of alternatives. For that purpose, the MEREC method uses the absolute deviation measure to reflect the difference between the overall alternative’s performance and its performance in removing a criterion. Higher weights are allocated to the criteria that have higher effects on the performance of alternatives.

3.2. MCDM Method Used to Rank Alternatives of Loader Mechanisms

There are dozens of methods available for solving alternatives ranking in MCDM problems. According to the original RDMR approach [4], it is believed that a combination of different MCDM methods creates a more robust and objective basis for decision-making. Nevertheless, only one MCDM method was applied in this paper for the alternative ranking of loader mechanisms (TOPSIS) in order to clearly highlight the impact of different approaches in determining the criteria weights. Additional methods for the ranking of alternatives could easily be integrated in a new comprehensive model, but in this study, such an approach would have blurred and hidden differences between criteria weighting methods.

The technique for the order preference by similarity to ideal solution (TOPSIS) method, is the most well-known and widely used MCDM method for the ranking of alternatives and was developed by Hwang and Yoon [47]. The TOPSIS method is based on the concept that the chosen alternative must have the closest Euclidian distance from the positive ideal solution and at the same time the longest distance from the negative ideal solution [48]. As the popularity of the method grew, some modifications to the TOPSIS method, extending it to a group decision environment using grey numbers [49] and fuzzy numbers [50].

3.3. The Proposed Approach for Generating a Robust Decision Rule

In this paper, the idea proposed by Petrovic et al. [4] for robust decision-making rule (RDMR) generation is adopted and extended for group decisioning (RDMR-G). Considering that different decision-making rules, obtained for different vectors of criteria weights, may yield a different ranking of alternatives, the objective was to generate a RDMR-G by the integration of rankings obtained by solving the same decision-making problem but with different criteria importance levels and weights. This novel approach combines the theoretical foundations of different methods for criteria weight calculations, based on Taguchi’s signal to noise (S/N) ratios, with aim of the final result being a more robust and objective complete ranking of the alternatives. Taguchi’s ideas on quality improvement using the quality loss function (signal to noise (S/N) ratios) to measure the performance characteristics [51] were recognized as a powerful robust design technique for the generation of a RDMR-G using the rankings of the alternatives obtained with the application of different criteria weighting methods, both objective and subjective. In this study, a form of expression, “smaller-the-better” is adopted for the S/N ratio because in decision-making processes, the alternative with the smallest rank is the best alternative [4].

The practical implementation of the proposed RDMR-G approach was performed through the evaluation of alternatives for the optimal synthesis of loader mechanisms of a hydraulic excavator. The schematic algorithm of the proposed approach is shown in Figure 3. Noted acronyms of MCDM methods in Figure 3 include: SWARA, stepwise weight assessment ratio analysis; BWM, best-worst method; FANMA, named after its authors Ma, Fan, and Huang; SD, standard deviation; WASPAS, weighted aggregates sum product assessment; COPRAS, complex proportional assessment; MOORA, multi-objective optimization method on the basis of ratio analysis,; VIKOR, visekriterijumska optimizacija i kompromisno resenje (in Serbian); ROV, range of value; and PSI, preference selection index.

Any decision-making problem can be described using a decision matrix consisting of m alternatives, n criteria, and $m\times n$ attributes, with $x_{ij}$ representing the performance of i-th alternative relative to the j-th criterion. In this case study, which concerned the optimal synthesis of loader mechanisms of hydraulic excavators, the decision matrix was obtained after the first two phases (Section 2).

The third phase, i.e., the optimal synthesis, evaluation, and selection of mechanisms using the RDMR-G, can be defined as presented in the following steps:

Step 1: The selection of the group of experts ($e=1,2,\dots ,b$), where b represents the number of experts which will evaluate criteria.

Step 2: The evaluation of criteria based on expert preferences. Every expert has to evaluate criteria according to the requirements of each individual subjective method. In total, $s·b$ vectors of criteria weights will be determined by this way, where s denotes the number of applied criteria weighting methods.

Step 3: The calculation of criteria weights based on o objective methods and the previously defined decision matrix. In this way, o vectors of criteria weights will be determined.

Step 4: The determination of design alternative complete rankings for the defined decision matrix and each of $n=s·b+o$ vectors of criteria weights.

Step 5: The calculation of signal-to-noise (S/N) ratios according to Equation (7) as:

$$S/N_j=-10log\left(\frac{1}{n}{\displaystyle \sum }_{k=1}^n{y}_k^2\right)$$

(7)

where values $y_k$ represent ranks of an alternative j obtained using different vectors of criteria weights ($k=1÷n$).

Step 6: The final step in generating an RDMR-G is the ranking of $S/N_j$ ratios so that the largest $S/N_j$ value represents the best alternative and the smallest $S/N_j$ value determines the worst alternative.

Using proposed integrated approach, a more robust, comprehensive, and objective rank of alternatives can be generated.

4. Results and Discussion

In this section, the RDMR-G approach is applied for the optimal synthesis of loader drive mechanisms according to the six criteria. In the first phase of this process, twenty-six different construction solutions for the kinematic chain (alternatives) are defined. In the next phase, criteria based on which the alternatives performances are evaluated are specified: Kinematic criterion, C₁; criterion of directed digging force, C₂; tribological criterion, C₃; time criterion, C₄; manipulator mass criterion, C₅; dynamic criterion, C₆. The criteria C₁, C₃, C₄, C₅, and C₆ are non-beneficial (cost) criteria, with the smaller attribute values being superior. C₂, meanwhile, is the beneficial criterion, with greater values being superior. For all considered criteria, mathematical models and simulation software were developed, and the ratings of each alternative against specific criterion were calculated. For some criteria, the developed simulation software was validated by experimental measurements on a loader. The ratings of alternatives with respect to each criterion are given in a decision matrix (

Table 3. Loader mechanisms performance–decision-matrix.

Alternative-Variants of the Drive Mechanisms Ev	C1 [°]	C2 [kN]	C3 [W]	C4 [s]	C5 [kg]	C6 [m]
	Min	Max	Min	Min	Min	Min
V.001	4.089	22.652	425.137	8.504	971.621	0.0142
V.014	0.183	22.653	541.580	8.113	1085.811	0.0120
V.020	0.734	22.591	446.604	7.828	900.815	0.0123
V.026	1.368	21.718	473.667	8.003	1048.561	0.0103
V.028	0.155	21.974	513.465	8.523	1099.590	0.0102
V.033	0.108	22.553	634.874	7.910	1218.694	0.0162
V.036	0.332	23.658	424.215	7.910	1084.033	0.0115
V.051	0.154	23.217	708.934	8.227	1319.761	0.0156
V.053	0.538	22.580	498.660	7.899	912.036	0.0148
V.064	0.385	22.055	598.755	7.794	1101.295	0.0153
V.095	0.416	22.909	448.396	7.648	952.286	0.0117
V.108	3.429	23.416	674.644	7.832	1391.960	0.0165
V.111	0.254	22.709	470.975	8.063	974.863	0.0095
V.117	0.495	23.036	476.138	7.578	904.988	0.0142
V.135	3.979	22.732	425.254	8.105	903.912	0.0130
V.147	0.458	22.227	641.743	8.112	1064.816	0.0162
V.150	0.408	22.861	515.947	8.155	1075.259	0.0125
V.178	2.260	21.535	602.219	7.749	1122.245	0.0154
V.223	0.227	21.484	509.715	7.853	971.883	0.0134
V.236	0.487	22.054	476.795	8.187	967.528	0.0134
V.245	0.441	22.777	615.591	7.885	1092.325	0.0144
V.267	0.288	22.455	559.207	8.196	1172.175	0.0124
V.271	0.414	22.478	372.014	7.750	812.676	0.0086
V.278	0.474	22.064	444.064	8.131	1008.867	0.0100
V.290	0.300	22.587	524.807	8.196	1071.200	0.0128
V.295	0.520	22.247	516.179	7.821	961.929	0.0135

).

At the beginning of phase 3, five experts, each with substantial experience in research and development in the field of mechanical engineering and mobile machines, were selected to evaluate different levels of criteria priority. Six different methods for determination criteria weights were combined in the process of the evaluation of alternatives for the optimal synthesis of loader mechanisms. For the better perception of subjective opinions, i.e., the knowledge and expertise of the decision-makers in group decisioning, three fuzzy subjective criteria weighting methods ($s=3$) were adopted: F-AHP, F-PIPRECIA, and F-FUCOM. This way, experts were given the opportunity to express their own assessments in a wider range of intervals, in accordance with their conviction, to a certain degree. This is especially relevant in the field of mechanical systems where design can be characterized by imprecise or vague requirements. Fuzzy set theory and fuzzy logic have emerged as powerful ways of representing uncertainty in subjective judgments and imprecision in the selections of alternatives [5]. Also, three objective criteria weighting methods, EWM, CRITIC, and MEREC ($o=3$), were adopted with aim of obtaining a more robust decision-making rule. As five experts ($b=5$) were involved in the criteria evaluation, in total $n=18$ different vectors of criteria weights were obtained (

Table 4. Criteria weights of considered criteria.

Criteria Weights			W1	W2	W3	W4	W5	W6
F-AHP	Expert 1		0.108	0.087	0.178	0.146	0.258	0.224
	Expert 2		0.295	0.363	0.117	0.117	0.107	0.000
	Expert 3		0.084	0.099	0.243	0.287	0.178	0.109
	Expert 4		0.208	0.256	0.215	0.215	0.106	0.000
	Expert 5		0.270	0.258	0.210	0.129	0.062	0.071
F-PIPRECIA	Expert 1	l	0.081	0.081	0.127	0.106	0.162	0.196
		m	0.095	0.095	0.162	0.150	0.249	0.249
		u	0.121	0.114	0.247	0.192	0.356	0.377
		d	0.097	0.096	0.171	0.149	0.253	0.262
	Expert 2	l	0.153	0.182	0.131	0.131	0.107	0.093
		m	0.212	0.227	0.145	0.145	0.135	0.135
		u	0.269	0.345	0.196	0.190	0.149	0.129
		d	0.211	0.239	0.151	0.151	0.133	0.127
	Expert 3	l	0.083	0.083	0.139	0.163	0.137	0.137
		m	0.105	0.105	0.205	0.205	0.190	0.190
		u	0.128	0.128	0.294	0.335	0.261	0.248
		d	0.105	0.105	0.209	0.220	0.193	0.191
	Expert 4	l	0.165	0.165	0.160	0.123	0.087	0.059
		m	0.216	0.216	0.198	0.167	0.122	0.081
		u	0.382	0.368	0.311	0.214	0.141	0.080
		d	0.235	0.233	0.210	0.167	0.119	0.077
	Expert 5	l	0.202	0.202	0.151	0.123	0.090	0.110
		m	0.215	0.215	0.172	0.158	0.115	0.125
		u	0.289	0.275	0.204	0.160	0.106	0.136
		d	0.225	0.223	0.174	0.153	0.109	0.124
F-FUCOM	Expert 1	l	0.043	0.051	0.091	0.039	0.124	0.122
		m	0.136	0.106	0.209	0.135	0.246	0.268
		u	0.169	0.106	0.209	0.135	0.246	0.268
		d	0.126	0.097	0.189	0.119	0.226	0.244
	Expert 2	l	0.141	0.194	0.151	0.053	0.049	0.048
		m	0.246	0.194	0.246	0.133	0.149	0.101
		u	0.246	0.194	0.251	0.133	0.164	0.101
		d	0.229	0.194	0.231	0.120	0.135	0.092
	Expert 3	l	0.049	0.048	0.141	0.194	0.151	0.053
		m	0.149	0.101	0.246	0.194	0.246	0.133
		u	0.164	0.101	0.246	0.194	0.251	0.133
		d	0.135	0.092	0.229	0.194	0.231	0.120
	Expert 4	l	0.194	0.141	0.151	0.053	0.049	0.048
		m	0.194	0.246	0.246	0.133	0.149	0.101
		u	0.194	0.246	0.251	0.133	0.164	0.101
		d	0.194	0.229	0.231	0.120	0.135	0.092
	Expert 5	l	0.181	0.120	0.118	0.088	0.030	0.038
		m	0.181	0.238	0.241	0.202	0.088	0.130
		u	0.181	0.238	0.259	0.202	0.098	0.130
		d	0.181	0.218	0.223	0.183	0.080	0.115
EWM			0.125	0.191	0.154	0.153	0.111	0.268
CRITIC			0.353	0.126	0.131	0.153	0.134	0.102
MEREC			0.702	0.014	0.099	0.020	0.090	0.074

l, m, u— the lower, the medium, and the upper limit value of the triangular fuzzy number respectively. D—crisp values obtained using defuzzification of fuzzy weights $d=\left(l+4m+u\right)/6$.

).

The obtained values of the criteria weights, in the case of subjective methods (experts’ evaluations), show that the weights of the first three criteria, C₁–C₃, are quite similar, whereby the tribological criterion, C₃, has the highest values. The lowest values are characteristic of criterion C₆, the criterion of the dynamic stability of loader movement.

It is important to note that the objective methods provided significantly different results, whereby the MEREC method stood out with criteria weights values which are unrealistically different from the values obtained using other approaches. For example, the MEREC method gave weight to the first criterion ($w_1=0.702)$, while other criteria had negligible impact ($w_2=0.014$ or $w_4=0.002$). In such cases, the application of the proposed RDMR-G approach (Figure 3) provides the decision maker with the opportunity to exclude from consideration a method that gives realistically unacceptable results for a particular class of problems.

The fourth step of the third phase of the proposed RDMR-G approach requires the application of a MCDM method for the alternative ranking of loader mechanisms. The TOPSIS method, as a well-known and widely used for solving many real-life case studies, was chosen for that purpose. The complete rankings of the design variant solutions according to different criteria weights are shown in

Table 5. Complete rankings of the alternatives according to different criteria weights.

Alternatives-Variants of the Drive Mechanisms Ev	F-AHP					F-PIPECIA					F-FUCOM					EWM	CRITIC	MEREC	S/N Ratio	RDMR-G
	E1	E2	E3	E4	E5	E1	E2	E3	E4	E5	E1	E2	E3	E4	E5
V.001	25	26	25	25	26	25	26	25	25	26	25	25	25	25	25	25	26	26	−28.075	25
V.014	9	2	15	9	7	8	6	10	10	6	8	8	14	10	8	7	4	2	−18.696	8
V.020	7	21	6	16	19	7	19	7	7	19	7	16	8	16	16	10	21	21	−23.330	14
V.026	17	22	16	22	22	15	22	17	17	22	17	22	21	22	22	17	22	22	−26.025	20
V.028	6	3	11	6	4	5	4	6	6	4	6	5	10	6	6	4	2	1	−15.236	5
V.033	21	10	20	18	16	21	17	20	20	16	20	18	19	18	18	20	11	4	−24.911	18
V.036	5	5	5	2	2	6	3	5	5	3	5	3	5	3	2	5	5	9	−13.358	3
V.051	22	15	22	21	20	22	21	22	22	20	22	21	22	21	21	21	16	6	−26.111	21
V.053	15	19	10	13	15	17	15	15	15	15	16	14	11	13	15	16	19	20	−23.734	16
V.064	19	13	18	17	17	19	16	19	19	17	19	17	17	17	17	19	14	10	−24.636	17
V.095	4	8	2	4	6	4	5	4	4	5	4	4	3	4	4	6	9	13	−15.178	4
V.108	26	24	26	26	24	26	24	26	26	24	26	26	26	26	26	26	24	24	−28.080	26
V.111	2	1	3	3	1	2	1	2	2	1	2	2	2	2	3	2	1	5	−7.132	1
V.117	11	14	7	8	13	14	13	11	11	13	13	11	6	8	11	15	15	18	−21.696	12
V.135	24	25	24	24	25	24	25	24	24	25	24	24	24	24	24	24	25	25	−27.726	24
V.147	20	20	21	20	21	20	20	21	21	21	21	20	20	20	20	22	20	16	−26.131	22
V.150	13	11	13	12	10	11	10	12	12	10	11	12	15	12	12	8	10	12	−21.246	11
V.178	23	23	23	23	23	23	23	23	23	23	23	23	23	23	23	23	23	23	−27.235	23
V.223	8	4	9	5	5	9	8	8	8	7	9	7	7	7	7	12	3	3	−17.324	7
V.236	10	16	8	11	12	10	12	9	9	12	10	10	9	9	10	13	13	17	−21.110	10
V.245	18	17	19	19	18	18	18	18	18	18	18	19	18	19	19	18	17	14	−25.096	19
V.267	16	9	17	14	11	16	11	16	16	11	15	13	16	15	13	11	8	7	−22.541	13
V.271	1	7	1	1	3	1	2	1	1	2	1	1	1	1	1	1	6	11	−11.158	2
V.278	3	12	4	7	9	3	7	3	3	8	3	6	4	5	5	3	12	15	−17.123	6
V.290	12	6	14	10	8	12	9	13	13	9	12	9	13	11	9	9	7	8	−20.401	9
V.295	14	18	12	15	14	13	14	14	14	14	14	15	12	14	14	14	18	19	−23.331	15

.

According to the last two steps of phase 3, each alternative (S/N) ratio was calculated using Equation (7), and a robust complete ranking was determined. In that way, the highest S/N ratio (−7.132) was calculated for a loader drive manipulator mechanism marked as alternative V.111, and therefore it should be chosen as the best alternative. Mechanism V.108 had the smallest S/N ratio (−28.080), so it has the lowest ranking. In the last column of Table 5, the complete rankings of the alternatives obtained with the proposed RDMR-G approach are provided.

It is characteristic that the decision-making process singled out variant solutions of mechanisms (V.111, V.271, etc.) which, according to the concept described in Section 2, belong to mechanisms with smaller executive parameters, i.e., smaller piston/connecting rod diameters of hydraulic cylinders, and larger transmission parameters, i.e., longer transmission lever lengths and coordinates of hydraulic cylinder connection joints for mechanism members. Such conceptions of mechanisms were in the group of the best solutions, compared to other variant solutions, because they performed significantly better with respect to criteria with a higher level of priority, in particular the tribological, C₃, and manipulator mass, C₅, criteria.

The best rated variant of the V.111 mechanism has the following parameters: $D_3=110 \left[\mathrm{mm}\right]$, $d_3=80 \left[\mathrm{mm}\right]$, $b_3=621 \left[\mathrm{mm}\right]$, ${\beta }_3=263.5 [°]$, $a_{3x}=1691 \left[\mathrm{mm}\right]$, $a_{3y}=-91 \left[\mathrm{mm}\right]$, $D_4=170 \left[\mathrm{mm}\right]$, $d_4=115 \left[\mathrm{mm}\right]$, $b_4=250 \left[\mathrm{mm}\right]$, ${\beta }_4=342.5 [°]$, $x_{35}=1675 \left[\mathrm{mm}\right]$, $y_{35}=633 \left[\mathrm{mm}\right]$, $a_4=270 \left[\mathrm{mm}\right]$, $a_4=85 \left[°\right]$, $a_{54}=806 \left[\mathrm{mm}\right]$, $a_{56}=836 \left[\mathrm{mm}\right]$, ${\alpha }_5=10 [°]$, $a_6=650 \left[\mathrm{mm}\right]$.

Statistical Comparison of Complete Rankings using Kendall’s Tau-b and Spearman’s Rho Tests

In this paper, while all the complete rankings of alternatives, i.e., loader drive manipulator mechanisms variants, were obtained using different vectors of criteria weights, they have different levels of similarities. In order to analyze the similarities of the complete rankings, the Kendall’s tau-b (${\tau }_b$) and Spearman’s rho ($\rho$) tests were selected. These two non-parametric statistical tests were conducted to measure correlations of the ranks obtained using eighteen vectors of criteria weights. The Kendall’s tau-b represents the similarities in the ordering of ranked alternatives (the number of concordances and discordances in paired observations), and the Spearman’s rho test shows the strength of the linear relationship of two complete rankings obtained based on different criteria weights vectors. The results of the Kendall’s tau-b and Spearman’s rho tests are shown in

Table 6. Performance test results–Kendall’s and Spearman’s rank correlation coefficients.

			F-AHP					F-PIPECIA					F-FUCOM					EWM	CRITIC	MEREC	RDMR-G
			E1	E2	E3	E4	E5	E1	E2	E3	E4	E5	E1	E2	E3	E4	E5
F-AHP	E1	${\tau }_b$	1.00	0.53	0.85	0.82	0.74	0.94	0.77	0.98	0.98	0.75	0.96	0.84	0.85	0.85	0.85	0.86	0.57	0.33	0.85
		$\rho$	1.00	0.72	0.96	0.94	0.88	0.99	0.90	1.00	1.00	0.90	1.00	0.95	0.96	0.95	0.95	0.96	0.75	0.46	0.96
	E2	${\tau }_b$	0.53	1.00	0.43	0.66	0.80	0.54	0.77	0.53	0.53	0.78	0.56	0.68	0.50	0.64	0.67	0.61	0.95	0.77	0.68
		$\rho$	0.72	1.00	0.59	0.85	0.93	0.72	0.91	0.72	0.72	0.92	0.74	0.86	0.67	0.82	0.86	0.80	0.99	0.91	0.86
	E3	${\tau }_b$	0.85	0.43	1.00	0.75	0.62	0.82	0.65	0.86	0.86	0.63	0.83	0.74	0.93	0.78	0.73	0.74	0.45	0.21	0.74
		$\rho$	0.96	0.59	1.00	0.90	0.80	0.93	0.82	0.96	0.96	0.81	0.94	0.89	0.98	0.92	0.89	0.87	0.61	0.30	0.89
	E4	${\tau }_b$	0.82	0.66	0.75	1.00	0.85	0.77	0.87	0.82	0.82	0.86	0.80	0.96	0.83	0.96	0.95	0.77	0.69	0.45	0.91
		$\rho$	0.94	0.85	0.90	1.00	0.97	0.91	0.97	0.94	0.94	0.97	0.93	0.99	0.94	0.99	0.99	0.91	0.86	0.60	0.98
	E5	${\tau }_b$	0.74	0.80	0.62	0.85	1.00	0.72	0.96	0.73	0.73	0.98	0.75	0.88	0.69	0.83	0.88	0.78	0.83	0.59	0.88
		$\rho$	0.88	0.93	0.80	0.97	1.00	0.88	0.99	0.88	0.88	1.00	0.89	0.98	0.85	0.95	0.97	0.92	0.95	0.72	0.97
F-PIPECIA	E1	${\tau }_b$	0.94	0.54	0.82	0.77	0.72	1.00	0.76	0.94	0.94	0.74	0.97	0.81	0.79	0.80	0.82	0.90	0.56	0.34	0.83
		$\rho$	0.99	0.72	0.93	0.91	0.88	1.00	0.90	0.99	0.99	0.89	1.00	0.93	0.92	0.92	0.93	0.97	0.75	0.47	0.95
	E2	${\tau }_b$	0.77	0.77	0.65	0.87	0.96	0.76	1.00	0.76	0.76	0.98	0.79	0.91	0.72	0.86	0.91	0.82	0.79	0.56	0.90
		$\rho$	0.90	0.91	0.82	0.97	0.99	0.90	1.00	0.90	0.90	1.00	0.91	0.98	0.86	0.96	0.98	0.94	0.93	0.69	0.98
	E3	${\tau }_b$	0.98	0.53	0.86	0.82	0.73	0.94	0.76	1.00	1.00	0.74	0.97	0.83	0.85	0.86	0.84	0.87	0.56	0.32	0.85
		$\rho$	1.00	0.72	0.96	0.94	0.88	0.99	0.90	1.00	1.00	0.89	1.00	0.94	0.96	0.95	0.94	0.95	0.74	0.46	0.96
	E4	${\tau }_b$	0.98	0.53	0.86	0.82	0.73	0.94	0.76	1.00	1.00	0.74	0.97	0.83	0.85	0.86	0.84	0.87	0.56	0.32	0.85
		$\rho$	1.00	0.72	0.96	0.94	0.88	0.99	0.90	1.00	1.00	0.89	1.00	0.94	0.96	0.95	0.94	0.95	0.74	0.46	0.96
	E5	${\tau }_b$	0.75	0.78	0.63	0.86	0.98	0.74	0.98	0.74	0.74	1.00	0.77	0.90	0.70	0.85	0.89	0.81	0.81	0.58	0.90
		$\rho$	0.90	0.92	0.81	0.97	1.00	0.89	1.00	0.89	0.89	1.00	0.91	0.98	0.86	0.96	0.98	0.93	0.94	0.71	0.98
F-FUCOM	E1	${\tau }_b$	0.96	0.56	0.83	0.80	0.75	0.97	0.79	0.97	0.97	0.77	1.00	0.84	0.82	0.83	0.85	0.90	0.58	0.35	0.86
		$\rho$	1.00	0.74	0.94	0.93	0.89	1.00	0.91	1.00	1.00	0.91	1.00	0.95	0.94	0.94	0.95	0.97	0.77	0.49	0.96
	E2	${\tau }_b$	0.84	0.68	0.74	0.96	0.88	0.81	0.91	0.83	0.83	0.90	0.84	1.00	0.81	0.95	0.98	0.82	0.72	0.48	0.95
		$\rho$	0.95	0.86	0.89	0.99	0.98	0.93	0.98	0.94	0.94	0.98	0.95	1.00	0.93	0.99	1.00	0.94	0.88	0.62	0.99
	E3	${\tau }_b$	0.85	0.50	0.93	0.83	0.69	0.79	0.72	0.85	0.85	0.70	0.82	0.81	1.00	0.86	0.80	0.72	0.53	0.29	0.80
		$\rho$	0.96	0.67	0.98	0.94	0.85	0.92	0.86	0.96	0.96	0.86	0.94	0.93	1.00	0.95	0.93	0.87	0.69	0.39	0.92
	E4	${\tau }_b$	0.85	0.64	0.78	0.96	0.83	0.80	0.86	0.86	0.86	0.85	0.83	0.95	0.86	1.00	0.94	0.78	0.67	0.43	0.90
		$\rho$	0.95	0.82	0.92	0.99	0.95	0.92	0.96	0.95	0.95	0.96	0.94	0.99	0.95	1.00	0.99	0.92	0.84	0.56	0.98
	E5	${\tau }_b$	0.85	0.67	0.73	0.95	0.88	0.82	0.91	0.84	0.84	0.89	0.85	0.98	0.80	0.94	1.00	0.82	0.71	0.47	0.94
		$\rho$	0.95	0.86	0.89	0.99	0.97	0.93	0.98	0.94	0.94	0.98	0.95	1.00	0.93	0.99	1.00	0.94	0.87	0.61	0.99
EWM		${\tau }_b$	0.86	0.61	0.74	0.77	0.78	0.90	0.82	0.87	0.87	0.81	0.90	0.82	0.72	0.78	0.82	1.00	0.63	0.40	0.85
		$\rho$	0.96	0.80	0.87	0.91	0.92	0.97	0.94	0.95	0.95	0.93	0.97	0.94	0.87	0.92	0.94	1.00	0.82	0.56	0.96
CRITIC		${\tau }_b$	0.57	0.95	0.45	0.69	0.83	0.56	0.79	0.56	0.56	0.81	0.58	0.72	0.53	0.67	0.71	0.63	1.00	0.76	0.72
		$\rho$	0.75	0.99	0.61	0.86	0.95	0.75	0.93	0.74	0.74	0.94	0.77	0.88	0.69	0.84	0.87	0.82	1.00	0.89	0.88
MEREC		${\tau }_b$	0.33	0.77	0.21	0.45	0.59	0.34	0.56	0.32	0.32	0.58	0.35	0.48	0.29	0.43	0.47	0.40	0.76	1.00	0.48
		$\rho$	0.46	0.91	0.30	0.60	0.72	0.47	0.69	0.46	0.46	0.71	0.49	0.62	0.39	0.56	0.61	0.56	0.89	1.00	0.62
RDMR-G		${\tau }_b$	0.85	0.68	0.74	0.91	0.88	0.83	0.90	0.85	0.85	0.90	0.86	0.95	0.80	0.90	0.94	0.85	0.72	0.48	1.00
		$\rho$	0.96	0.86	0.89	0.98	0.97	0.95	0.98	0.96	0.96	0.98	0.96	0.99	0.92	0.98	0.99	0.96	0.88	0.62	1.00
Sum		${\tau }_b$	15.3	12.6	13.6	15.5	15.2	15.0	15.5	15.3	15.3	15.4	15.4	15.9	14.3	15.7	15.9	15.0	13.1	9.1	15.9
		$\rho$	17.2	15.6	16.0	17.6	17.4	17.0	17.5	17.2	17.2	17.5	17.3	17.8	16.6	17.6	17.7	17.2	15.9	11.5	17.8

.

Taking into account that the Kendall’s tau-b and Spearman’s rho tests results can have values in intervals [−1,+1], where a value of 1 indicates that there is a complete 100% positive association between two complete rankings and, a value of −1 indicates 100% negative association, and a value 0 indicates that there is no association between the compared groups of ranks, it can be concluded that greater values of Sum(${\tau }_b$) and Sum($\rho$) show the smallest variation in ranking orders. It is obvious that the RDMR-G, derived using the proposed approach, has the greatest sum value of the Kendall’s tau-b (15.9) and Spearman’s rho (17.8), so it can provide a more robust and comprehensive decision rule and be very useful in solving real-life decision-making problems. Also, the general characteristic of this case study, the optimal synthesis of loader drive mechanisms, is that the wide dispersion of ranking orders obtained using eighteen vectors of criteria weights is not noted, which is confirmed by high values of Sum(${\tau }_b$) and Sum($\rho$) (maximum values are 18). Only in the case of the application of the MEREC objective criteria weighting method was there some discordance in the ordering of ranked alternatives compared to other approaches.

5. Conclusions

The optimization of the structural design of a mechanical system is an important stage in product development. The designing process is very complex and usually features incomplete data or data gaps and opposing opinions, attitudes, and solutions. In view of this, an efficient decision-making system is necessary for identifying an optimal variant solution from a set of alternatives. The present study introduced a new hybrid multi-criteria decision approach for RDMR-G using different criteria weights, MCDM methods, and Taguchi’s S/N ratios. The basic motive for the proposed approach was the fact that ranks of alternatives can be very sensitive to the different vectors of criteria weights obtained based on the different theoretical backgrounds of weighting methods. The proposed RDMR-G approach was verified by solving the case study of the optimal synthesis of loader drive mechanisms. For that purpose, the algorithm with three phases is presented. Five experts were interviewed, and their attitudes were transformed into criteria weights vectors using three subjective fuzzy weighting methods. Also, three objective weighting methods were applied in order to involve information contained in the decision matrix without the direct influences of the decision-makers. Twenty-six design variant solutions for drive mechanisms were evaluated according to the six criteria and the optimal solution was selected. In addition, a statistical comparison of the complete rankings using Kendall’s tau-b and Spearman’s rho tests was performed with aim of analyzing the similarities of the complete rankings.

Based on previous considerations, the following conclusions can be summarized:

• The proposed integrated RDMR-G approach was found to be very useful in the aggregation of different attitudes in decision-making processes by engineering groups. The RDMR-G approach is particularly applicable to cases where there is certain degree of inconsistency in the alternative final rankings obtained using different weighting methods.
• The conducted statistical comparison of complete rankings using Kendall’s tau-b and Spearman’s rho tests shows that the application of the RDMR-G approach provided the highest overall summary values, which indicates that this approach enables the highest level of stability of the final complete rankings.
• The process of the optimal synthesis of loader drive mechanisms using a three phase algorithm and the RDMR-G approach showed that the dominant characteristics of the best-rated variants of the mechanism are smaller pistons/connecting rod diameters of hydraulic cylinders and larger transmission lever lengths and coordinates of hydraulic cylinder connection joints.
• The proposed three phase algorithm has a general character and can be used for the synthesis of the lever mechanisms of manipulators and other mobile machines.
• Also, proposed RDMR-G approach has a general character and can be applied to any MCDM problem with group decisioning.

The study presented in this paper has some limitations. The major limitation of this approach is that it requires significant computational efforts to compute a number of decision rules from different criteria weighting and ranking methods. The main direction in future research should be development of an expert software system based on the RDMR-G approach presented in this study. The practical application of the proposed approach can be enhanced through the development of expert and intelligent decision-making systems, which could greatly simplify the decisioning process. Historical data collected from numerous other machines can also provide a strong starting point for such an expert system. The expert system could recognize and propose to the decision maker those MCDM methods in the RDMR-G approach that provide the highest level of stability in terms of the final complete rankings for a specific class of decision-making problems.

In this paper, we mainly considered technical criteria for decision-making, so another future extension of this study may include other criteria for the evaluation of loader drive mechanisms design variants, for example in the fields of controllability, economics, or sustainable development. Such criteria can have a significant influence on the energy efficiency of the machine and a reductions in fuel consumption, prices, and environmental pollution, or on other key performance indicators. Further research will certainly continue to analyze the drive mechanisms of mobile machines, particularly in case of hybrid drive systems or innovative energy recovery systems.