Optimization Procedure and Toolchain for Roll Dynamic Geometry

Abstract

In rolls manufactured from first bent and then welded sheets of steel, the asymmetric distribution of mass due to the weld seam as well as imperfections of the geometry due to the bending may cause the roll cross-section roundness profiles to deform due to centrifugal forces when the roll is accelerated to rotate at its operating speed. This effect is known as the dynamic geometry of the roll. In previous research, it has been shown that it is possible to measure the dynamic geometry in operating speed and compensate for the deformation by grinding a suitable opposite geometry on the roll. This direct approach may work when only little material is removed. Such conditions apply especially for polymer coated rolls, where the dynamic geometry is mostly dependent on the geometry of the much stronger and denser steel body under the roll cover. This paper goes further to investigate the possibilities for compensating the dynamic geometry in cases where the amount of removed material is significant enough to have an effect on the dynamic geometry itself due to altered mass and stiffness. The paper presents a toolchain consisting of a parametric roll CAD model, finite element simulation of the dynamic geometry and a geometry optimization procedure based on minimizing a target function describing roundness errors in cross-sections of the roll. Results of simulation experiments for a case example indicate that the presented optimization procedure can be used to eliminate roundness errors related to dynamic geometry of the roll. Finally, the paper discusses the application of such a toolchain in the manufacturing of rolls.

1. Introduction

Rolls are an essential part of many industrial processes, such as paper and cardboard making, printing, or the rolling of metals. In these processes, accurate roll geometry and dynamic behaviour is essential since the manufacturing processes utilize the roll body to transfer and form thin materials with strict requirements for thickness variation.

To manufacture rolls for such operating conditions, several industrial solutions exist. For example, to ensure the roundness (and further, cylindricity) of rolls in operation measurement with multi-probe roundness, measurement methods [1,2,3,4,5,6] and compensation machining (turning or grinding) [1,4,5,7] can be used to reduce roll geometry errors. In addition to roundness and cylindricity of the rolls, it is also important to consider the dynamic balancing to minimize run-out of the rolls in operation. For balancing of rolls, offset-centre turning has been known to be used since the 1970s [8] and later also with systems utilizing ultrasonic measurement [9].

The body of a roll may be manufactured from first bent and then welded steel sheets [5], after which the outside surface can be turned and ground to finish the roll surface. The resulting asymmetric and varying wall thickness and distribution of mass may cause the roundness profiles of the roll cross-section to deform due to centrifugal forces when the roll is accelerated to rotate at its operating speed. This effect, investigated in detail by Juhanko [5], is referred to as the dynamic geometry of the roll. In this previous study, the removed material was assumed to be so minor that it will not have an effect on the measured roundness error and that the deflection can simply be inverted and then ground on the roll surface [5].

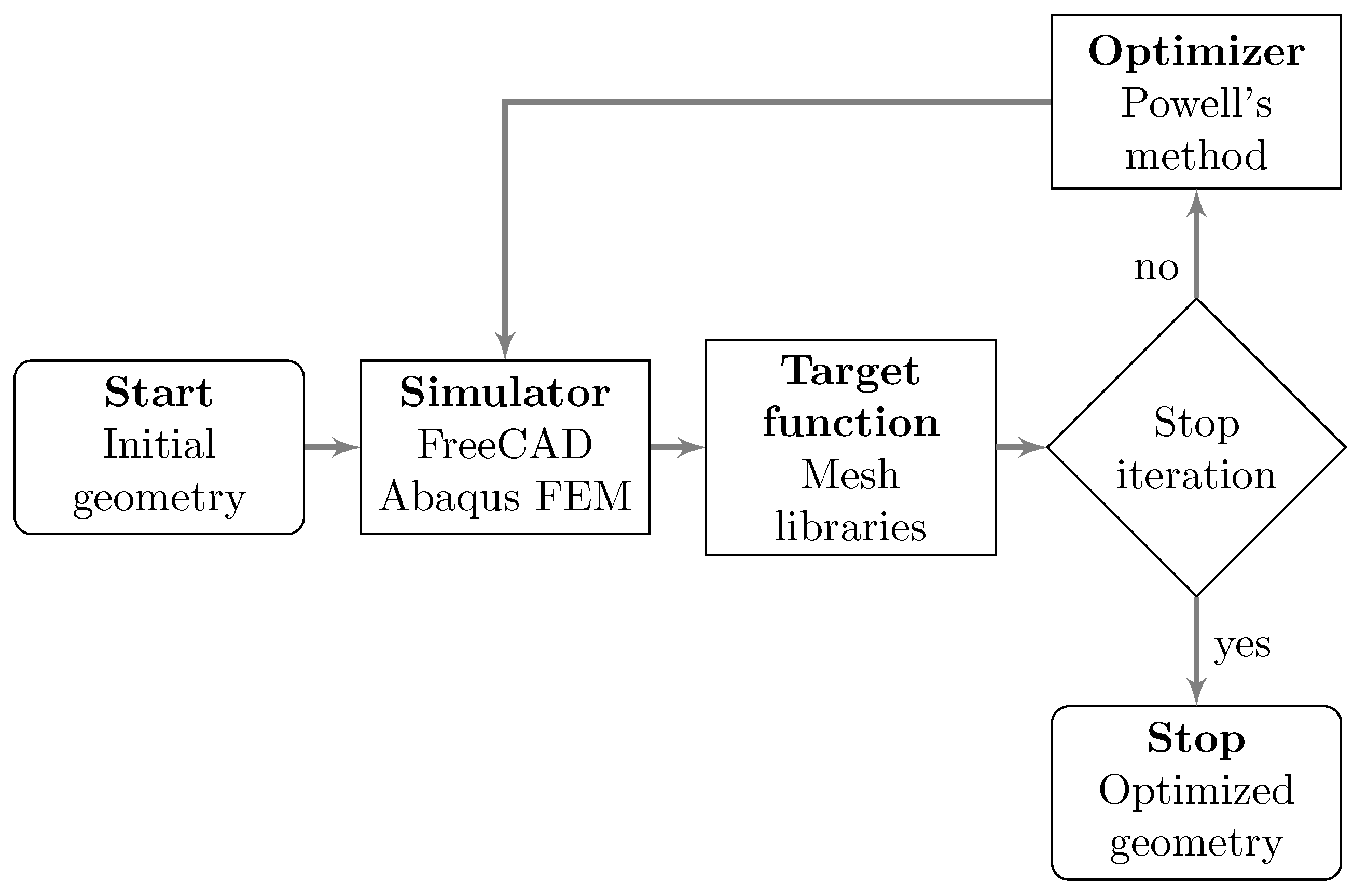
This article goes further to investigate the possibilities for compensating the dynamic geometry in such cases, where the amount of removed material is significant enough to have an effect on the dynamic geometry itself due to altered mass and stiffness. A toolchain consisting of a parametric roll CAD model, finite element simulation of the dynamic geometry and a geometry optimization procedure (Figure 1) based on minimizing a target function is presented. The target function (shown in Figure 2) is defined as the mean the RMS (root-mean-square) roundness error defined in the ISO 12181-1 standard [10] in cross-sections of the roll. To reduce the complexity of the problem, the undeformed geometry of the roll is controlled with a set number of control points that define the boundaries of the roll model.

Specifically, this article aims to answer the following question: can the dynamic geometry change be compensated for with an iterative optimization approach based on a target function describing the mean roundness error in the roll cross-sections? To demonstrate a successful elimination of the roundness error caused by the dynamic geometry phenomenon, this article presents results of applying the optimization procedure on a case example with a cylindrical workpiece with wall thickness variations.

Increasing computation power has enabled computing many previously unsolvable problems with standard equipment. The approach used in this paper is a computational design optimization based on an iterative scheme, where a numerical optimization algorithm is used to refine locations of control points to reach a minimum of a target function calculated based on simulated deformations. Many different approaches of performing such optimization have been studied previously [11]. More advanced methods that do not require re-meshing at every iteration have also been developed [12], but these were not considered in this study. This research is restricted to a numerical simulation study with the main aim to investigate the feasibility of structuring and successfully solving the optimization problem.

2. Methods

This section presents the optimization problem and the toolchain consisting of several software components. After the optimization problem and toolchain have been presented, a case example is shown where the toolchain is applied to obtain a compensative geometry for a roll with variable shell thickness.

2.1. Optimization Procedure

The optimization procedure is shown in Figure 1. The procedure consists of three distinct software components, the simulator, target function evaluator and the optimizer itself. Detailed descriptions of each of the components follow in this section.

2.2. Simulator

Simulation is used to obtain the dynamic geometry of the roll for a given input. The simulator operates by programmatically operating a computer aided design (CAD) and a finite element method (FEM) software, in this case FreeCAD and ABAQUS FEM, respectively. The Python interfaces of FreeCAD and ABAQUS are utilized to operate the simulator, which receives new control point values from the optimizer as input and outputs a deformed mesh for the evaluation of the target function, which is used to obtain updated control point values.

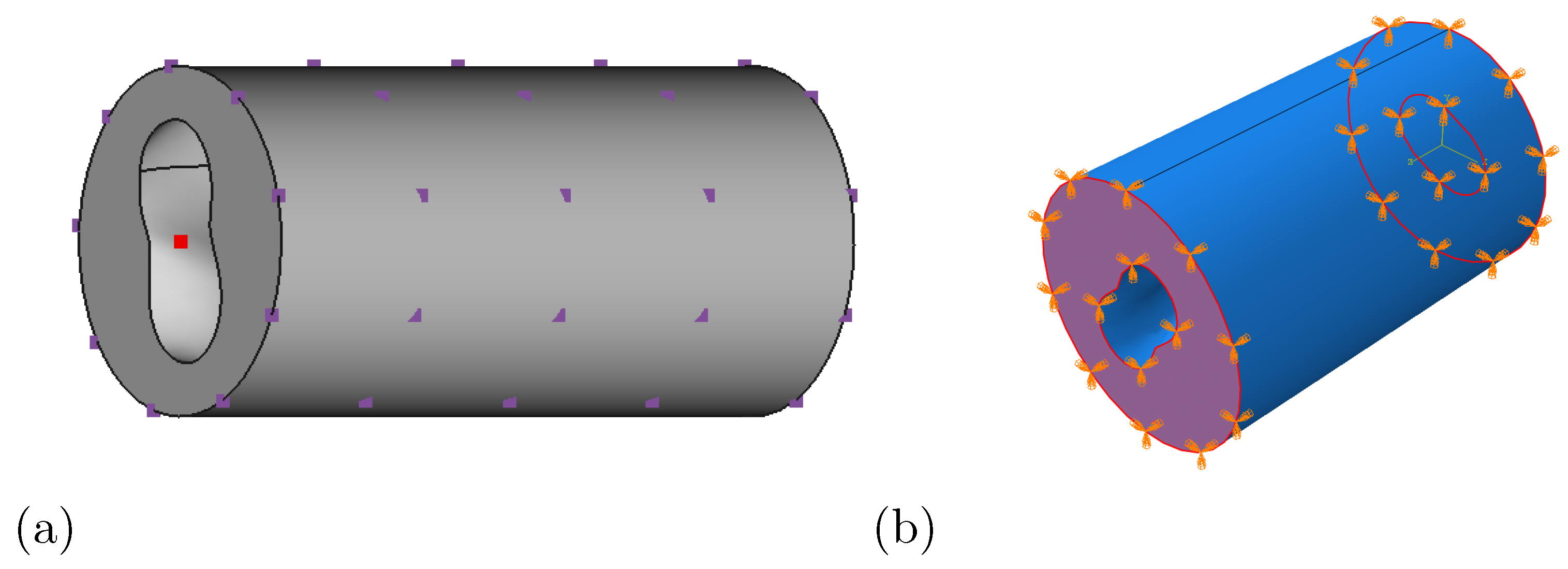
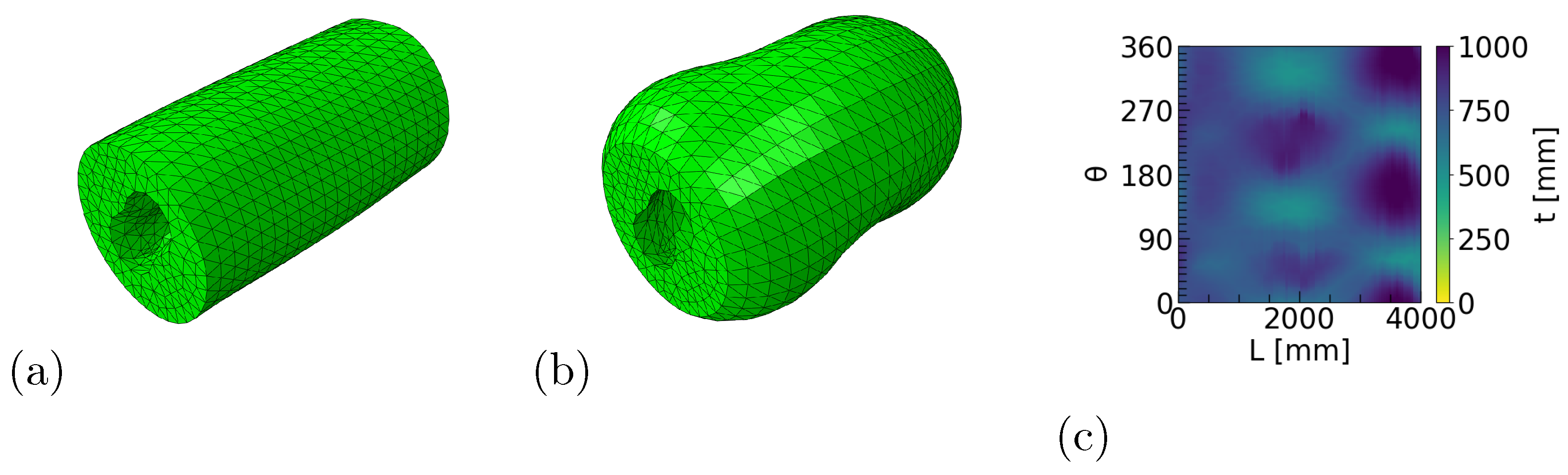
A parametric scripted roll model in the FreeCAD software is used (Figure 3a). The outer shell of the roll model is defined as a loft between several B-splines describing the geometry of the cross-sections with a set number of control points placed on planes perpendicular to the length axis (z direction in Figure 2) of the roll. A polar coordinate system is used for the control points, the point locations described by radii from the axis of the roll. Based on the given control points, the CAD software generates a new model with the specified input and generates a model file in STEP format, which is passed to ABAQUS for meshing and simulation of the dynamic geometry. ABAQUS is scripted to mesh the given roll model, apply the loads and boundary conditions and output the nodes and their displacements to files.

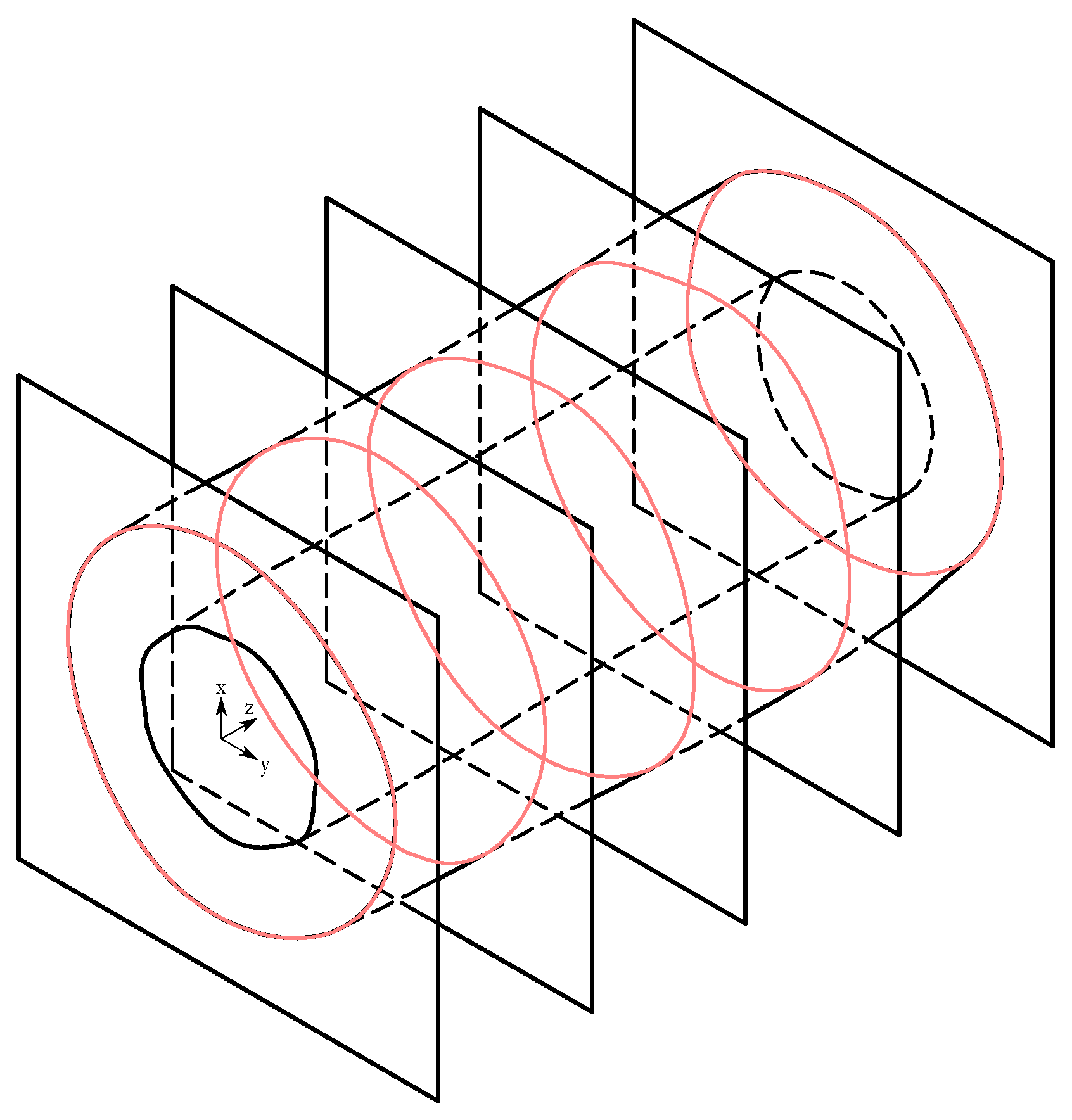
2.3. Target Function

A target function to describe the deviation from the desired geometry is presented. The target function is defined as the mean RMS roundness error (relative to the least-squares centre as defined in the ISO 12181-1 standard [10]) of a number of equally spaced roll cross-sections. A schematic picture of the target function is shown in Figure 2.

To obtain the roundness profiles, the deformed mesh obtained from the simulation is first intersected with a set number of planes. Of the obtained intersection curves, the outer one is selected and the least squares circle centre point is calculated. From their respective centre points, the profiles are resampled to consist of 1024 points per revolution. The profiles are then filtered according to ISO 12181-2 [13] with a cutoff frequency of the desired UPR (undulations per revolution). The output of the target function is the mean of the RMS roundness values of the profiles in the selected number of evenly spaced cross-sections of the roll.

According to the ISO 12181-1 standard, roundness can be evaluated in several different ways, for example relative to different centre-points. Of these methods, the RMS roundness relative to the least-squares centre was viewed to be the most stable for this particular optimization problem due to its assumed continuous nature.

The target function f can be formulated for roll geometry defined with n control points and roundness evaluated in N cross-sections as follows:

$$f(p_1,\cdots p_n)=\frac{1}{N}{\mathrm{RONq}}_N$$

(1)

where ${\mathrm{RONq}}_N$ is the root-mean-square roundness error in the Nth cross-section, calculated according to ISO 12181-1 [10]. The optimization problem is to find suitable control point radii $p_n$ that minimize the target function.

2.4. Optimizer

Based on the target function values it receives, the optimizer searches for suitable combination of input parameters to minimize the target function.

Some optimization methods rely on assumptions about the independence of the input variables or other behaviour of the target function. For a complex target function, this kind of information is not readily available. In general, an optimization method should be selected depending on the nature of the target function. In the case presented, the target function is complex, probably has many local minima and is costly to evaluate.

Powell’s conjugate direction method was used as the optimization algorithm [14]. The method is based on searching for new value in conjugate directions in the parameter space. It has been shown to find the minimum for functions with quadratic behaviour [14]. Powell’s method does not require knowledge of the derivatives of the variables, which would be extremely difficult to obtain in this kind of target function based on simulated geometry errors.

2.5. Case Example

A roll with round outer shell cross-sections and uniform diameter (in stationary conditions), but a varying inside geometry is used as a case example. The used roll model is shown in Figure 3. The outer surface was defined with 9 control points in 5 cross-sections resulting in a total of 45 control points. The locations of the control points are altered by moving them along a corresponding radius from the center axis of the roll.

The simulated roll has a length of 4 $\mathrm{m}$ and in the initial state, the control points are all placed at a radius of 1.3 $\mathrm{m}$ from the roll axis. In this initial undeformed state, the outer cross-sections of the roll have no roundness error (Figures 5a and 8a). The internal structure of the roll exhibits some randomly selected varying thickness variations, which can be seen in detail in Figure 5c.

The material properties and key parameters used in the simulation are shown in

Table 1. Material properties and parameters used in the simulation.

Parameter	Value
Density	7800 $\frac{\mathrm{kg}}{{\mathrm{m}}^3}$
Young’s modulus	215 $\mathrm{GPa}$
Poisson’s ratio	0.3
Rotating speed	1200 $\mathrm{rad}/\mathrm{s}$
Initial control point radius	1.3 $\mathrm{m}$
Upper boundary for control point radius	1.3 $\mathrm{m}$
Lower boundary for control point radius	1.05 $\mathrm{m}$

. As a boundary condition for the simulation, the displacements of nodes in the end cross-sections of the roll were fixed (shown in Figure 3b).

Twenty planes spaced evenly between the ends were used for the evaluation of the target function (Figure 2). To simulate grinding and thus removal of material, the initial control point values (radii of 1.3 $\mathrm{m}$) were given as upper constraints for the optimization algorithm, only allowing the control points to move nearer to the longitudinal axis of the roll. Radii of 1.05 $\mathrm{m}$ were used as lower constraints to prevent the optimizer from trying values that would cause the shell to become too thin.

The case example was not chosen to resemble a realistic paper machine roll made from steel sheets, but created as an example of a geometry that would demonstrate the capability of the toolchain in solving the dynamic geometry problem, firstly, exhibiting significant dynamic geometry change and secondly, exhibiting shell thickness variations in the order of the material to be removed by the optimization.

3. Results

This section presents the results of optimization for the case example described in Section 2.5. To summarize the results, the optimization procedure was successfully used to reduce the thickness of the workpiece in selected areas to obtain a geometry in which the cross-sections are not round in the initial stationary conditions, but the roundness errors are eliminated when the roll is accelerated to a selected rotating speed.

The progress of the optimization is shown in Figure 4. As can be seen, initially the target function decreases fast and then reaches a region where the improvement of the target function becomes slower. The decrease of the target function value is not steady: single steps in the input parameter space in any direction may lead to a significantly worsened value of the target function, which is evidence of the instability of the target function. In other simulation runs, repeating patterns were observed in the target function output values during optimization.

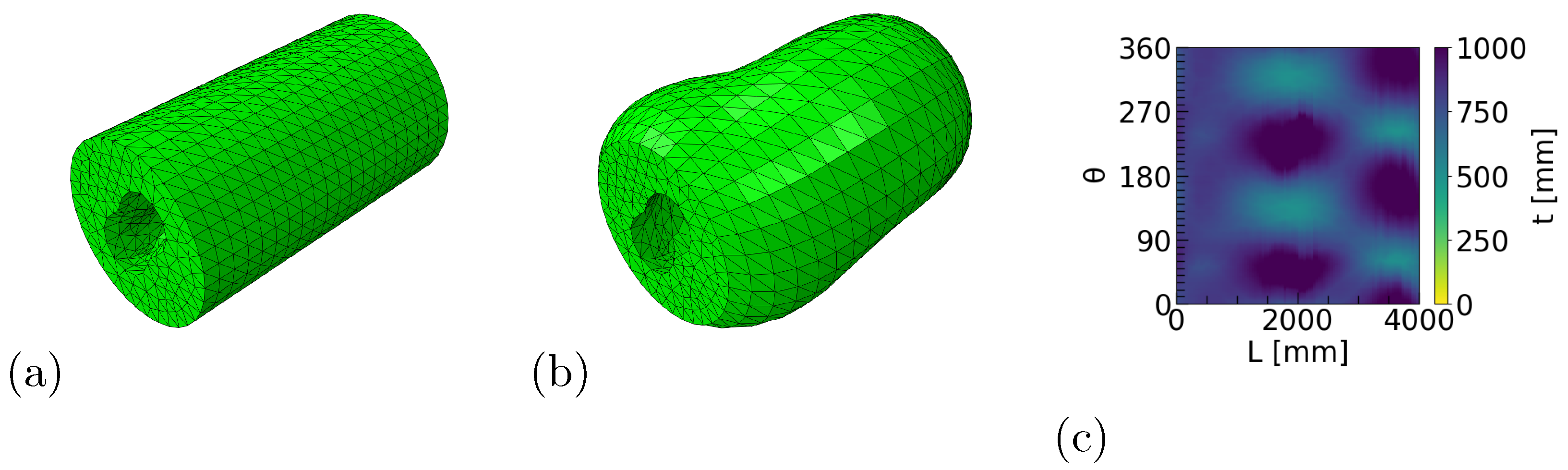
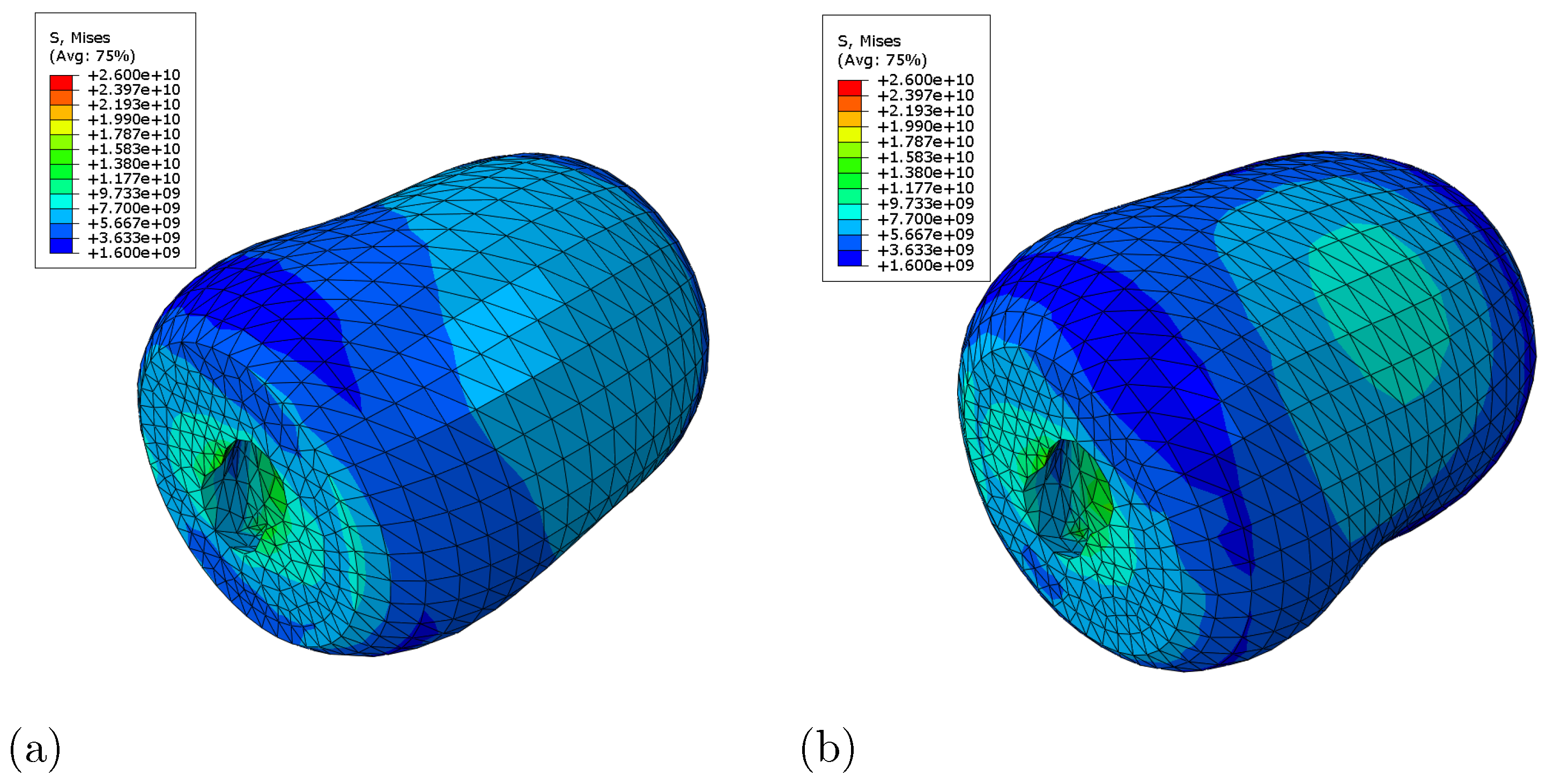
Figure 5 and Figure 6 present the initial and final geometries of the roll (with 2-factor magnification) and their shell thickness variations. Additionally, the von Mises stresses in the initial and optimized situations are shown in Figure 7. By comparing Figure 5c and Figure 6c, it can be observed how the optimization procedure changes the shell thickness to compensate for the dynamic geometry. The most significant changes in the shell thickness are observed in areas near the middle cross-sections (around 2000 mm and 300 to 360 degrees) of the roll, which are also the areas furthest away from the roll ends, which are fixed as boundary conditions.

The optimized geometry features some diameter variation along the length axis of the roll, which can be observed from Figure 6. The result is expected, since the target function only considers the average root-mean-square roundness errors in the cross-sections. Other parameters related to cylindricity, such as the diameter variation or straightness errors of the centre axis, are not considered in the target function.

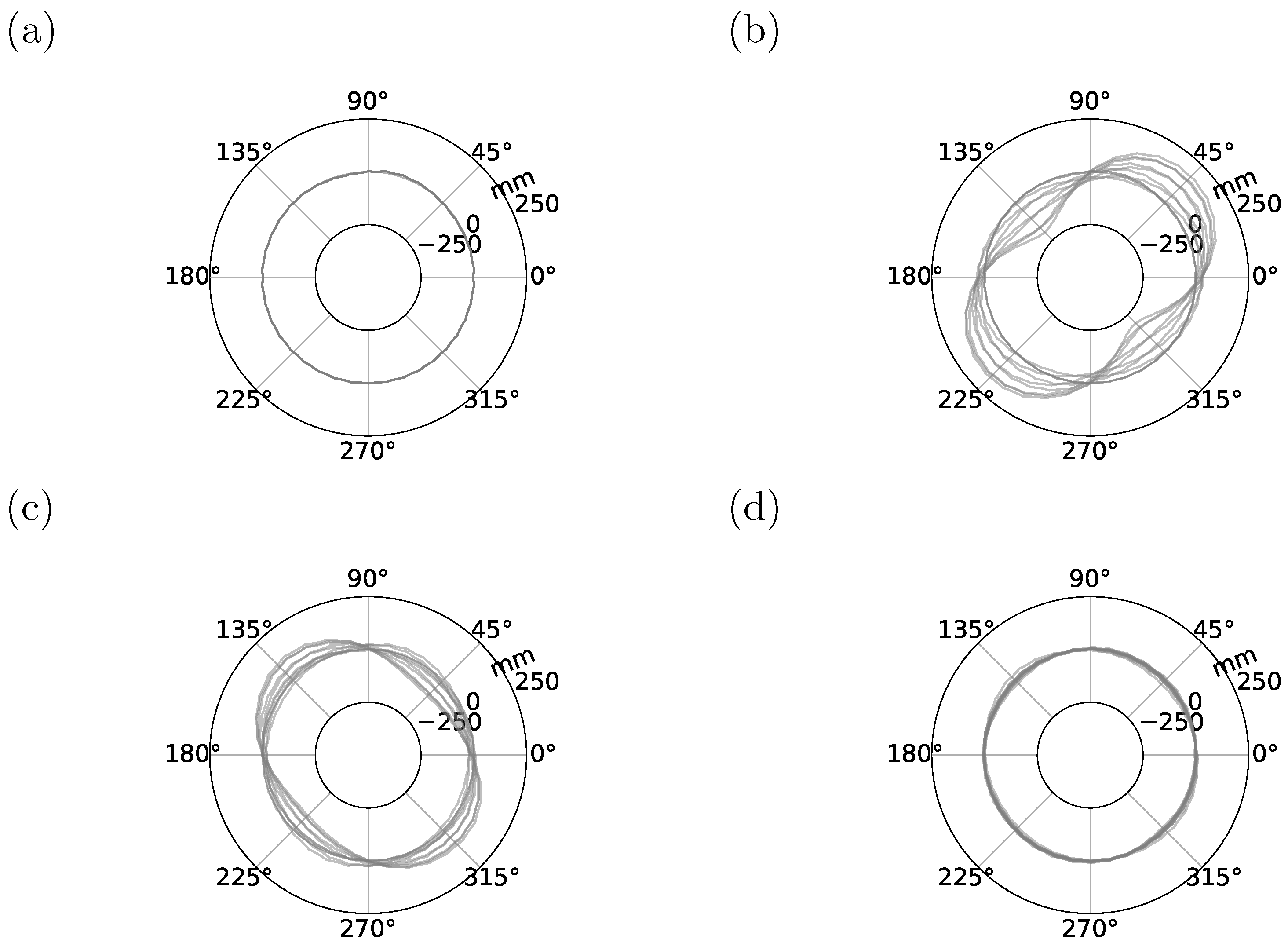
Figure 8 presents roundness profiles of 10 cross-sections evenly spaced along the length of the roll for both the unoptimized and optimized geometry, both stationary and rotating. It can be observed that the optimization procedure almost completely eliminates the remaining roundness error when the workpiece is rotating. Figure 8a,c show the roundness profiles of the unoptimized and optimized roll geometry in stationary conditions. It can be observed that, in terms of cross-section roundness profiles, the resulting optimized geometry is not directly the initial deformed geometry inverted.

The simulator re-meshed the model for each iteration of the finite element simulation. In the case example shown here, the roll was meshed to consist roughly of between 10,000 and 20,000 tetrahedra (examples of the resulting mesh are visible in Figure 5 and Figure 6). For computing time, one iteration of the optimization took roughly 35 s when run on a standard desktop workstation PC with 16 GB of RAM and an Intel Xeon E3-1230 processor.

During the testing and development of the software, the simulator was run with different parameters, material parameters and rotating speeds. With some parameter combinations, simulation and calculation of the target function failed due to self-intersection nodes in the mesh. This condition could probably have been fixed with a denser mesh or different boundary conditions for the optimizer. Similar results as the run presented in the results of this article were obtained during the testing runs.

4. Discussion

In the shown case example, the toolchain was successfully used to obtain an optimized geometry to eliminate the roundness errors due to the dynamic geometry change caused by the rotational body forces and the uneven shell thickness of the roll.

As can be interpreted from the rather unpredictable behaviour of the target function in Figure 4 during the optimization, the target function seems to be highly non-linear in nature, which is certainly understandable, especially when larger deformations are encountered. Furthermore, the optimization did not completely eliminate the roundness error. This may be due to limitations due to the level of detail in the simulation, or further, it may not even be possible to compensate, since any change in any point of the geometry potentially has an effect on the whole deformed geometry of the roll.

Returning to the original research question: can the roll be used in cases where the removed material itself has an effect on the deformations? It is not evident that the removed material at one location in the roll will cause the roll surface to be less deflected at that area of the roll. A comparison of the roundness profiles of the optimized and inverse geometries shows that the optimized geometry is not simply the initial deformed geometry inverted. However, there may be many different solutions to the optimization problem.

The authors view that defining the target function as the mean of the RMS roundness errors will cause the target function to exhibit a clearer gradient when compared to other the roundness or cylindricity metrics. No attempts were made to further characterize the target function, which was observed to behave rather unpredictably. The selected optimization algorithm works optimally for functions which exhibit quadratic behaviour [14]. Furthermore, the selection of the initial guess may have a significant effect on the needed number of iterations; the initial guess need not correspond to the measured geometry.

One must be aware of some potential drawbacks of the presented approach. Firstly, the selected target function is one with probably many local minima and the used initial parameter values may have a effect on the result of the optimization. Considering only roundness, the target function does not aim for a constant diameter or straightness along the length of the roll. Using a function with specified cylindricity metrics such as the root-mean-square cylindricity deviation specified in ISO 12180-1 [15] could lead to a more cylindrical result with less thickness variation and straightness deviation of the centre line. However, the authors speculate that this kind of target function may be more difficult to optimize.

The simplification for the control of the geometry was implemented with control points of B-splines, which is an approach where the resulting geometry can suffer from overfitting-type errors [16]. The constraints for the optimization algorithm do not ensure that material will only be removed from the roll. In practice, this does not seem to be the case, and the grinding simulation reduced the wall as can be seen from Figure 5c and Figure 6c. There is a trade-off between the number of control points and the required number of iterations to reach a satisfactory optimization result. These are values that need to be selected case-by case, depend on factors such as workpiece geometry and the desired amount of control. The filtering applied to the roundness profiles has a similar effect: it may be important (and often only possible, due to limitations in manufacturing methods) to correct the low-order harmonic errors in large workpieces.

Although challenges will certainly arise, the authors view that the presented optimization procedure could be implemented in roll production, in practice. Data is already available for the roundness errors, straightness errors and approximate diameters from from ulti-probe roundness measurement systems [6,7] and ultrasonic systems can be used to determine the shell thickness variations [9,17]. This measurement data can be used to determine the initial locations of the control points for the simulation. Fitting of actual measurement data into the initial values for the simulator should not pose a significant problem.

However, there are several sources of uncertainty when applying such methods in practice. In many cases, the deformations can be quite small, and challenges may rise related to measurement and manufacturing accuracies. Furthermore, the results of the optimization may suffer due to inaccuracies that are not considered in the measurement and simulation, such as residual stresses in weld seams, the varying strength or other inhomogeneities of the material. Such unknown variables will cause the simulated deformations to differ from the real deformations.

The effects of these types of uncertainties could be reduced not only by altering the optimization scheme, but also by altering the manufacturing and measurement procedures. For example, non-uniformities in stresses caused by welding seams could be reduced by heat treatments or completely avoiding welding by using a different manufacturing procedure. Similarly, other material inhomogeneities could be overcome by using different materials or improved measurement procedures which would enable taking them into account in the optimization.

5. Conclusions

This article presented method and a toolchain for optimizing roll dynamic geometry. In paper machine rolls, the dynamic geometry is a relevant phenomenon when centrifugal forces in the system are significant, i.e., for rolls operating at higher speeds, especially with larger diameter and thinner (but varying) wall thicknesses. The authors view that the presented iterative optimization procedure could be successfully utilized to eliminate the dynamic geometry. Furthermore, it may suitable for cases where the material removed from the roll itself has an effect on the dynamic geometry. With minor modifications, the toolchain is suitable for many other geometry optimization problems. Further considerations related to material inhomogeneities their measurement as well as accurate measurement of geometries would be required when applying such an optimization procedure in practice.