Comprehensive and Simplified Fault Diagnosis for Three-Phase Induction Motor Using Parity Equation Approach in Stator Current Reference Frame
Abstract
:1. Introduction
2. Motivation
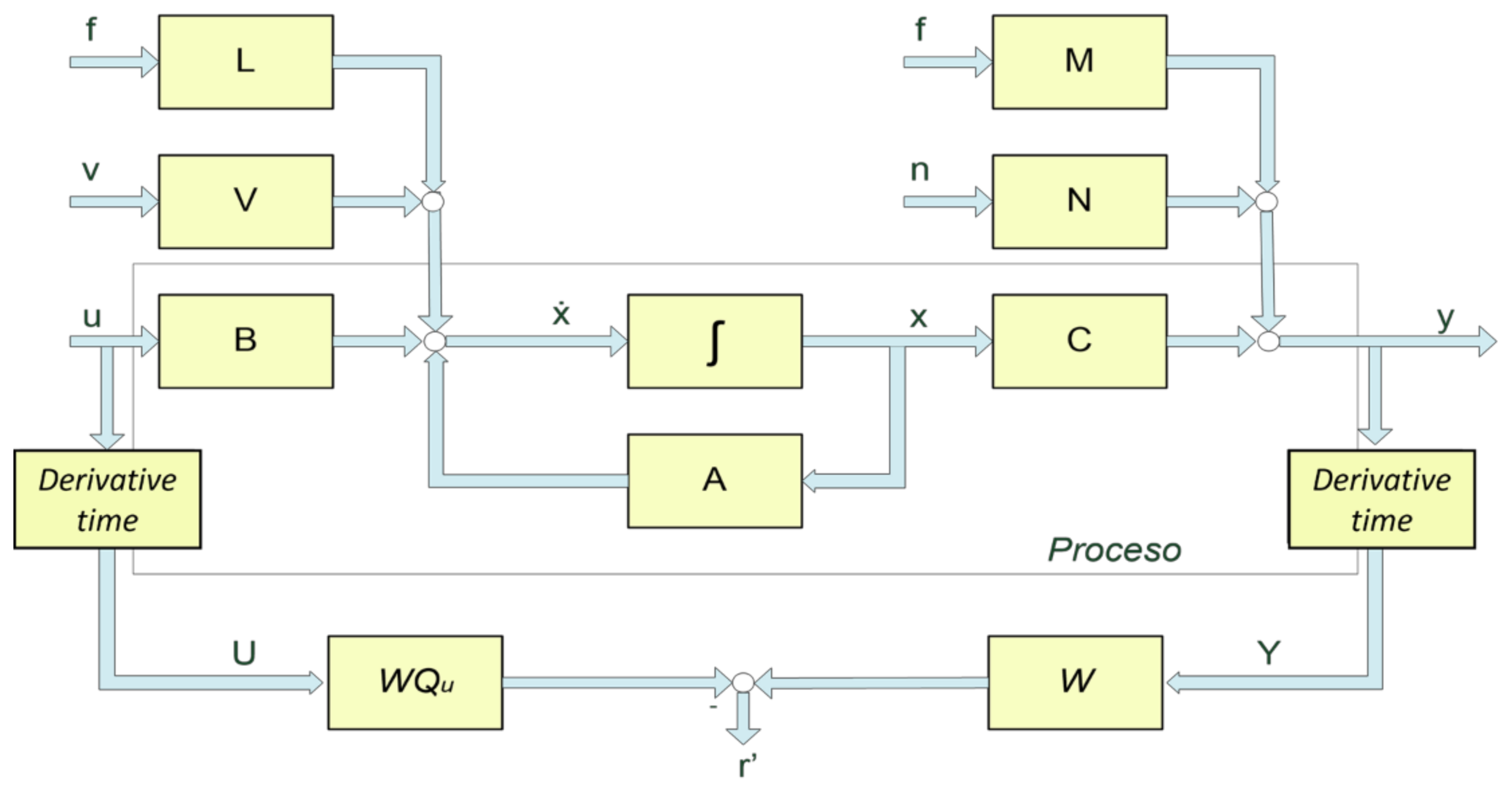
2.1. Parity Equations for Fault Diagnostic
- is a vector
- is a vector
- is a matrix
- is a matrix
- is a matrix
2.2. Fault Diagnosis Using DQ Reference Frame for Induction Motor
3. Three-Phase Induction Motor Model Based on Stator Current Reference Frame
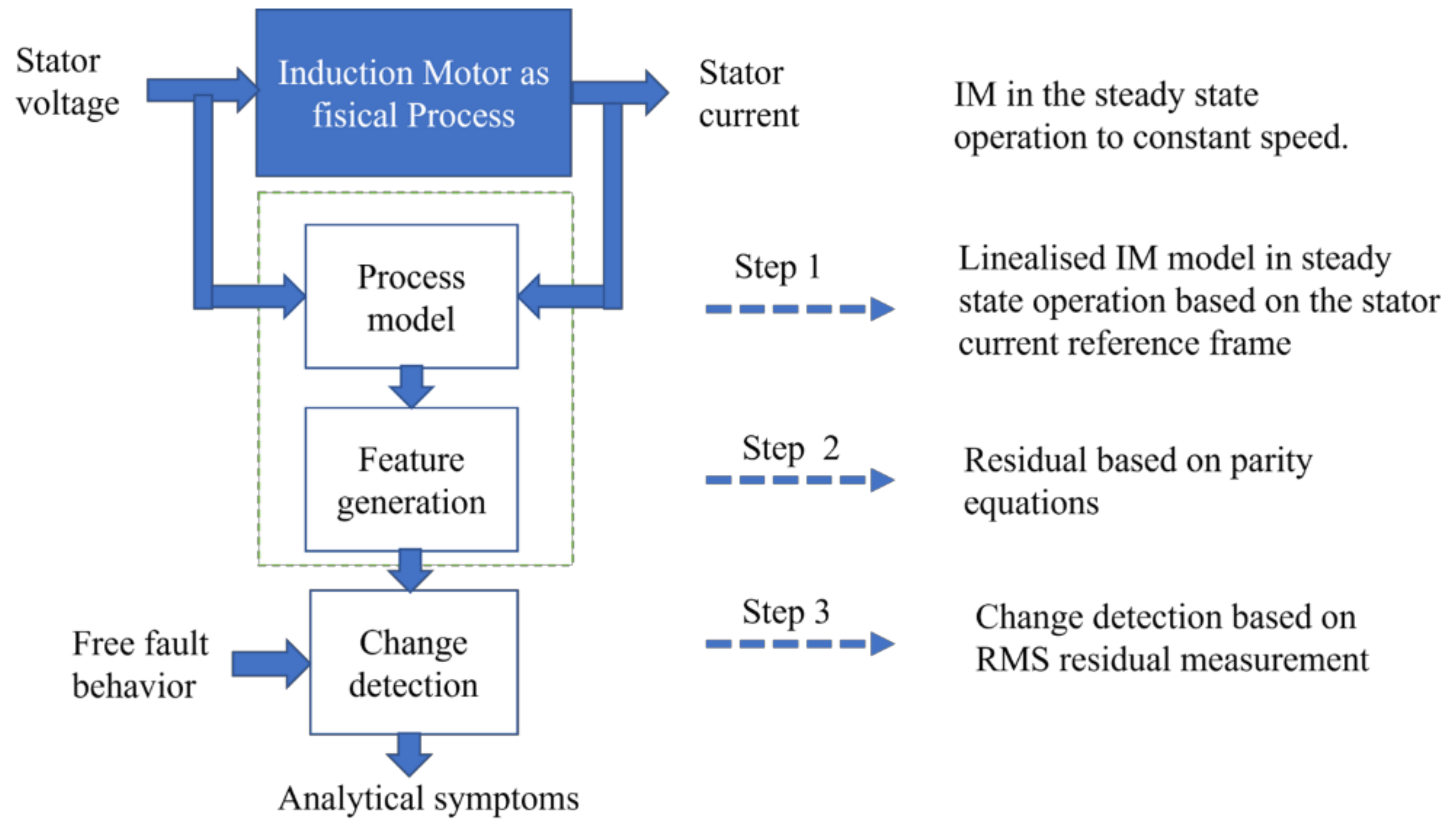
4. Fault Diagnosis Based on Stator Current Reference Frame
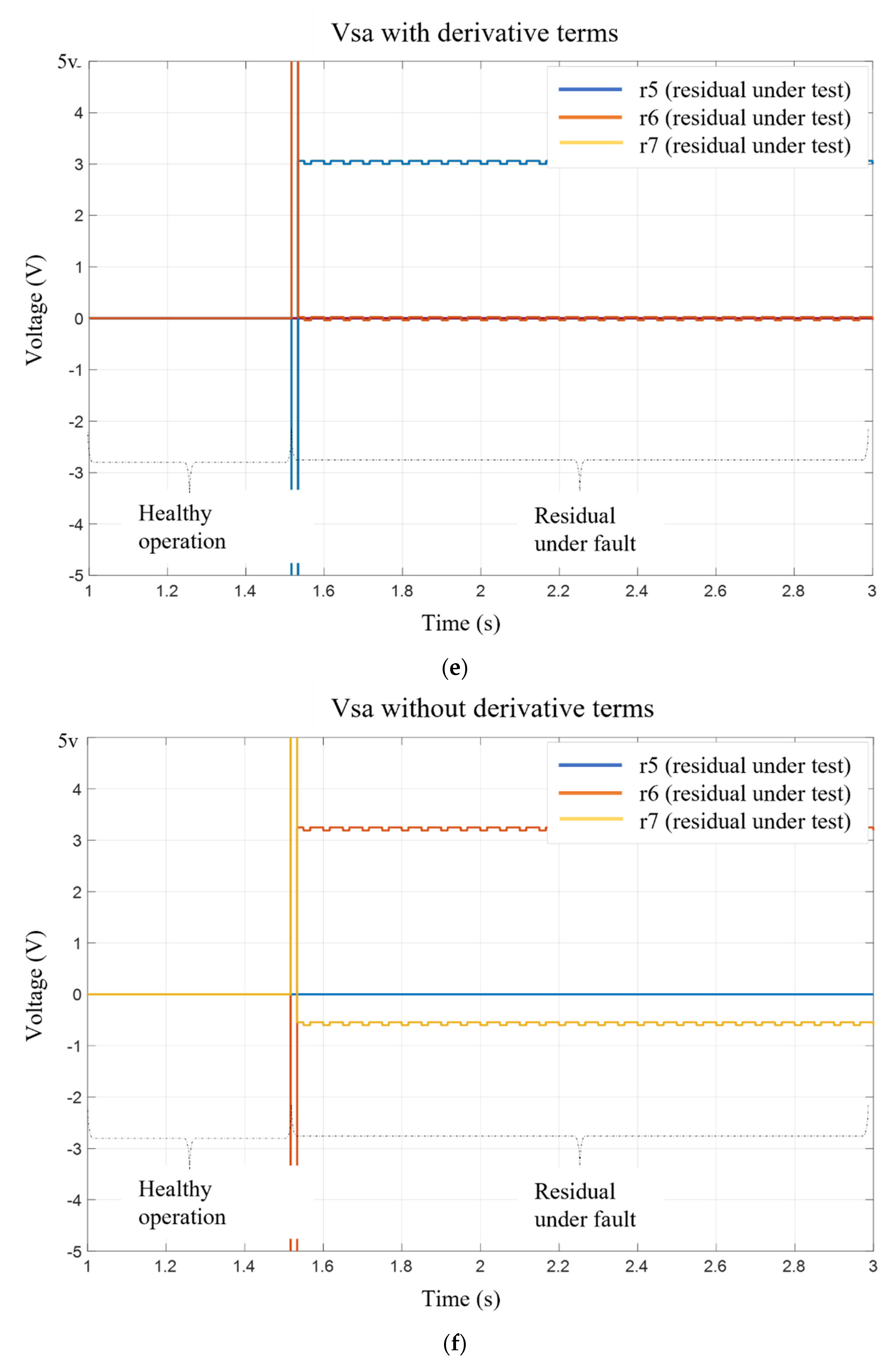
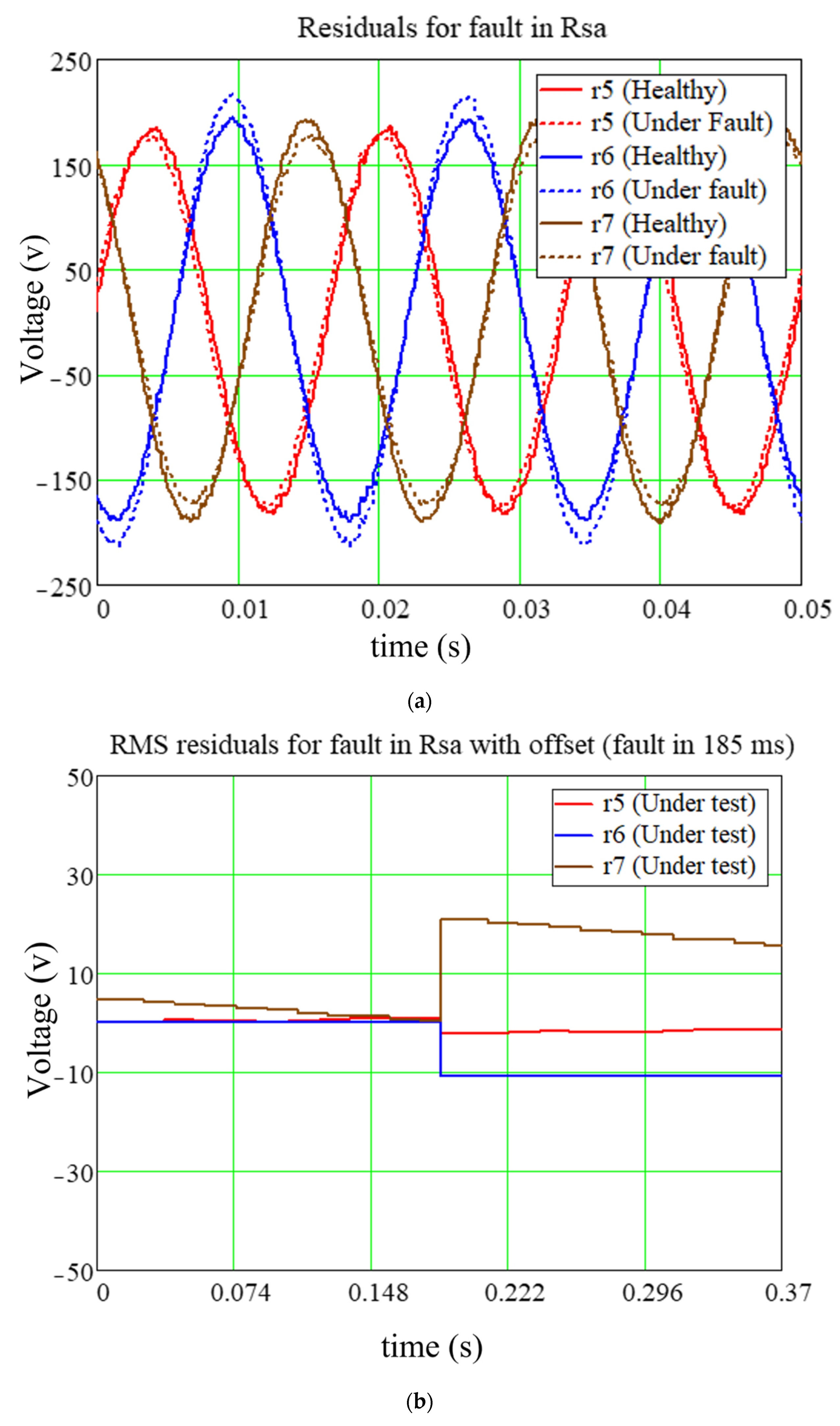
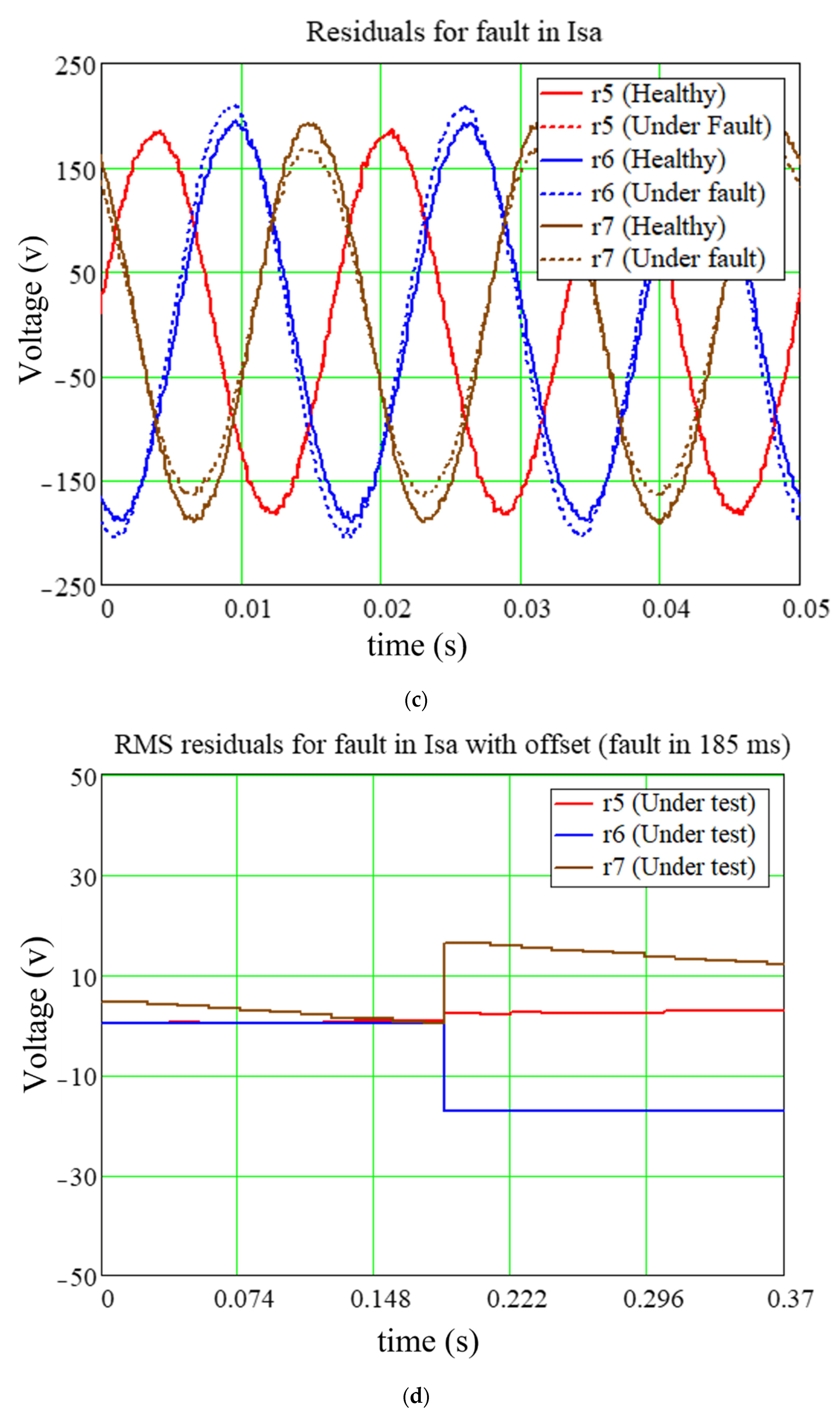
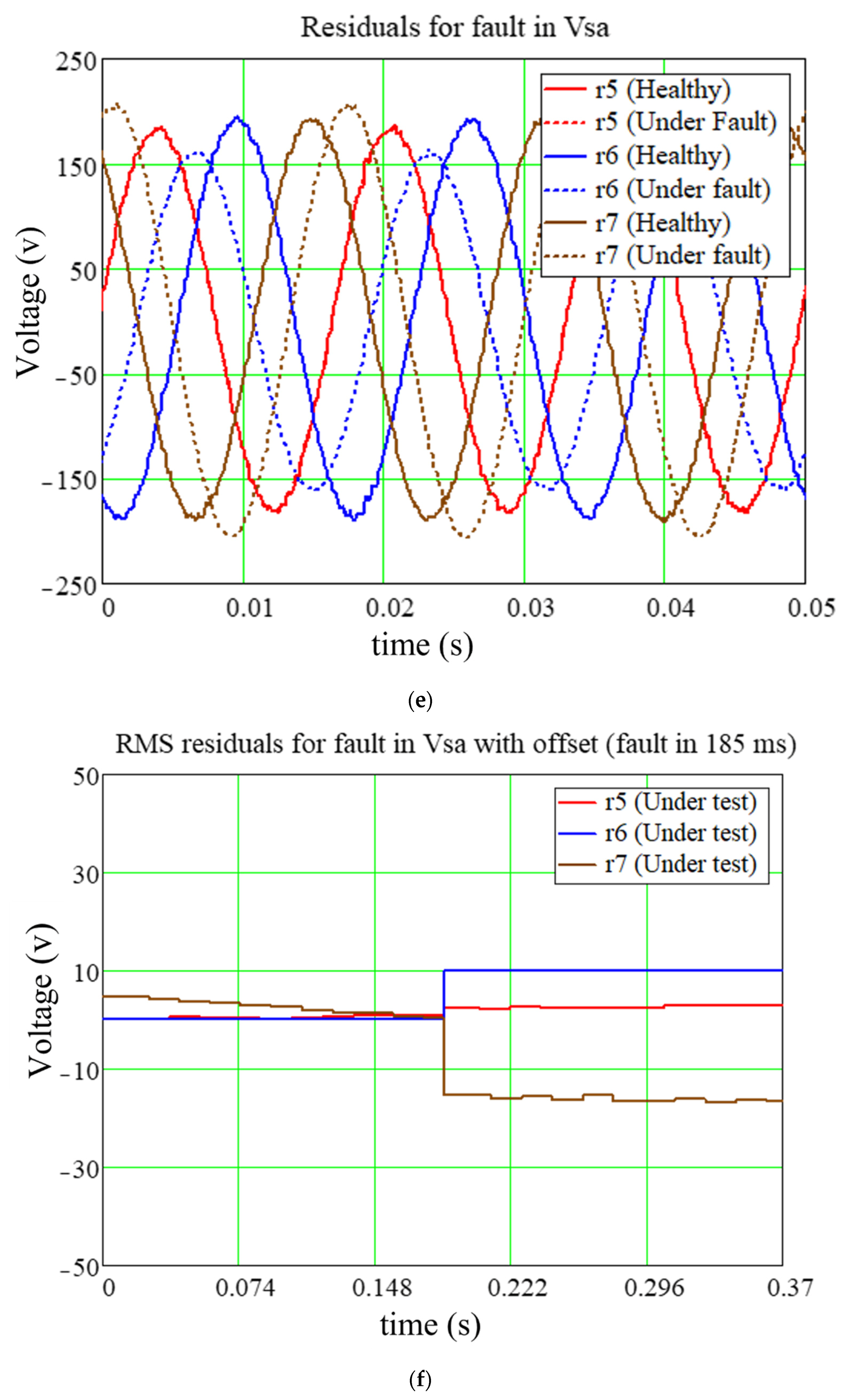
5. Discussion and Results
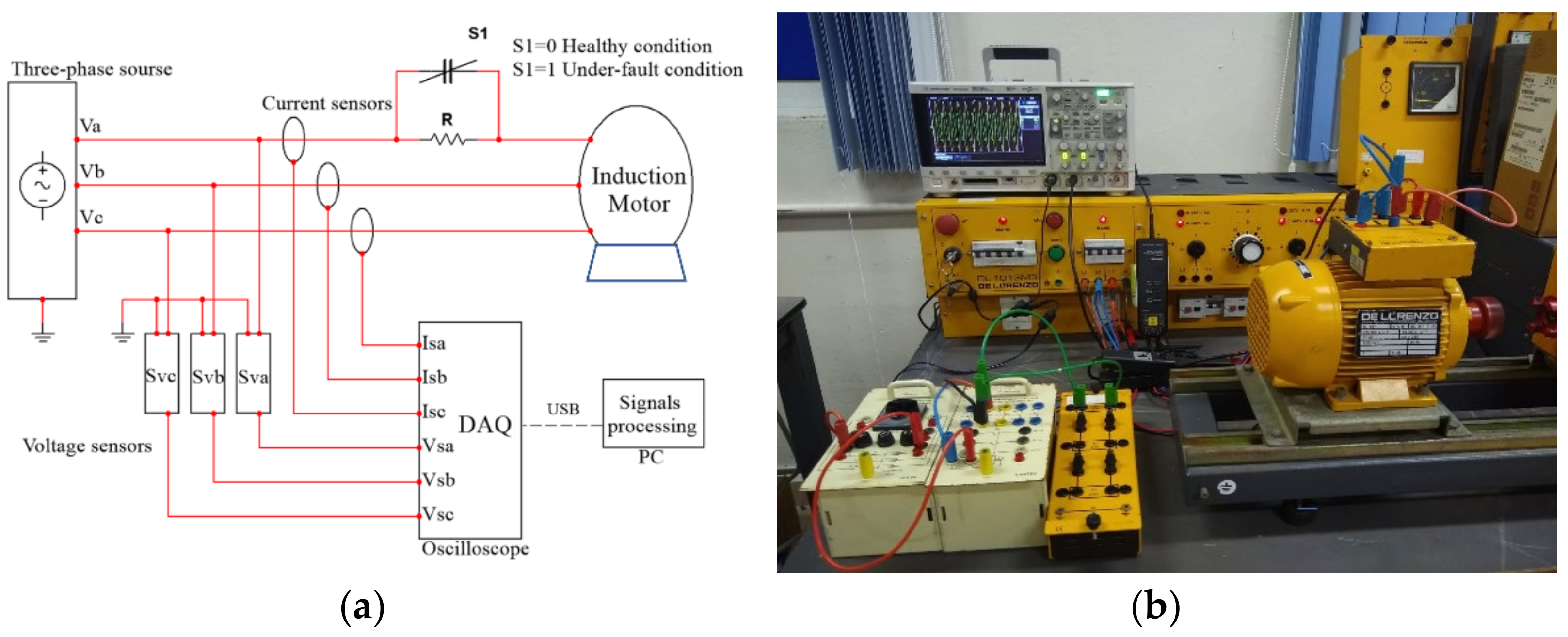
5.1. Fault Detection Scheme for Experimental and Simulation Setup
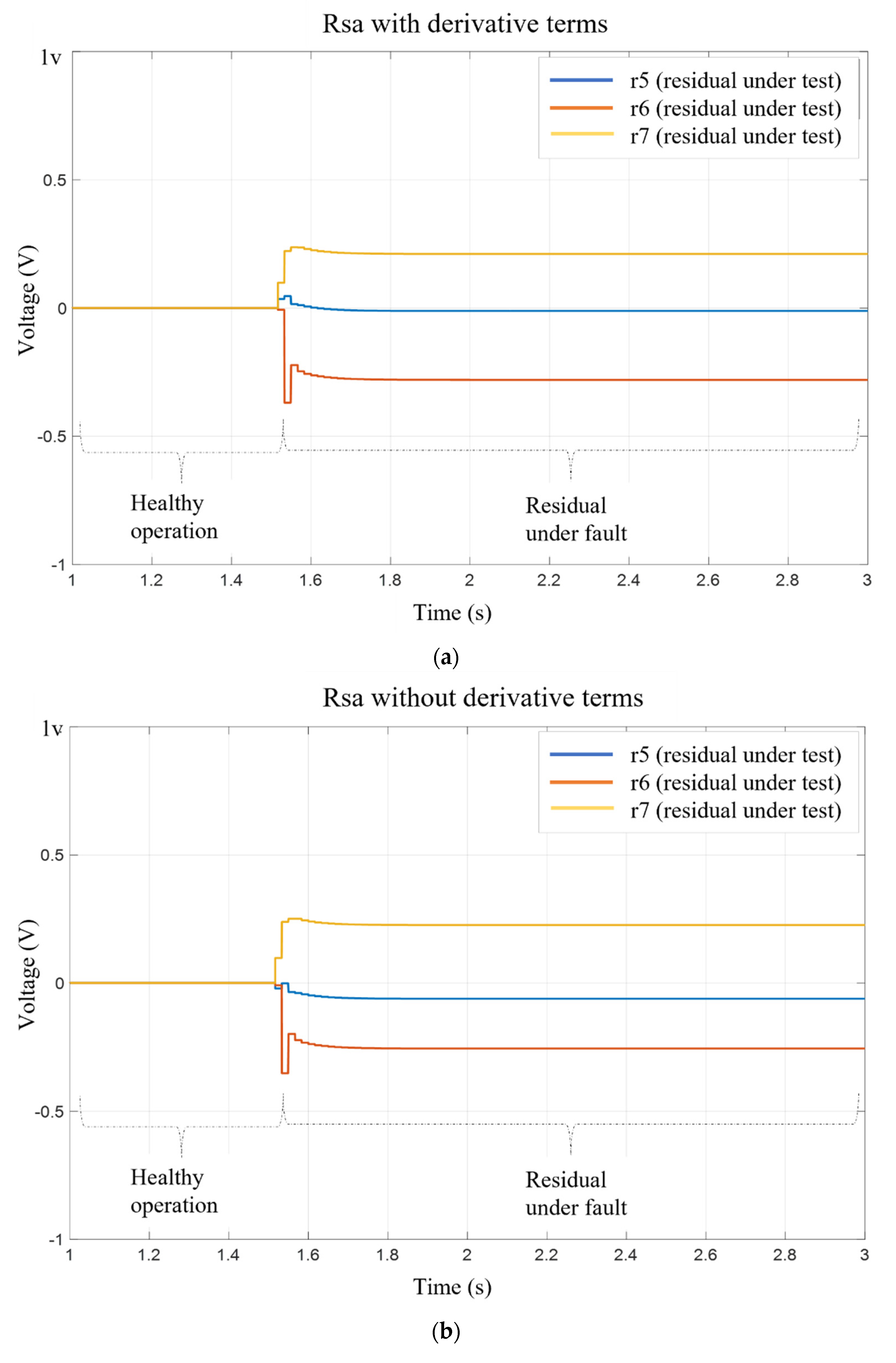
5.2. Fault Analysis for Experimental and Simulation Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bianchini, C.; Immovilli, F.; Cocconcelli, M.; Rubini, R.; Bellini, A. Fault Detection of Linear Bearings in Brushless AC Linear Motors by Vibration Analysis. IEEE Trans. Ind. Electron. 2011, 58, 1684–1694. [Google Scholar] [CrossRef]
- Kolla, S.; Varatharasa, L. Identifying three-phase induction motor faults using artificial neural networks. ISA Trans. 2000, 39, 433–439. [Google Scholar] [CrossRef]
- Nandi, S.; Toliyat, H.A.; Li, X. Condition Monitoring and Fault Diagnosis of Electrical Motors—A Review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]
- Loparo, K.; Adams, M.; Lin, W.; Abdel-Magied, M.; Afshari, N. Fault detection and diagnosis of rotating machinery. IEEE Trans. Ind. Electron. 2000, 47, 1005–1014. [Google Scholar] [CrossRef]
- Mendes, A.; Cardoso, A.J.M. Fault-Tolerant Operating Strategies Applied to Three-Phase Induction-Motor Drives. IEEE Trans. Ind. Electron. 2006, 53, 1807–1817. [Google Scholar] [CrossRef]
- Cash, M.; Habetler, T.; Kliman, G. Insulation failure prediction in AC machines using line-neutral voltages. IEEE Trans. Ind. Appl. 1998, 34, 1234–1239. [Google Scholar] [CrossRef]
- Klima, J. Analytical investigation of an induction motor drive under inverter fault mode operations. IEE Proc.-Electr. Power Appl. 2003, 150, 255–262. [Google Scholar] [CrossRef]
- Chan, C.; Hua, S.; Hong-Yue, Z. Application of Fully Decoupled Parity Equation in Fault Detection and Identification of DC Motors. IEEE Trans. Ind. Electron. 2006, 53, 1277–1284. [Google Scholar] [CrossRef] [Green Version]
- Bouattour, J. Diagnosing Parametric Faults in Induction Motors with Nonlinear Parity Relations. IFAC Proc. Vol. 2000, 33, 971–976. [Google Scholar] [CrossRef]
- Isermann, R. Model base fault detection and diagnosis methods. In Proceedings of the American Control Conference, Seattle, WA, USA, 21–23 June 1995; Volume 3. [Google Scholar] [CrossRef]
- Isermann, R. Supervision, fault-detection and fault-diagnosis methods—An introduction. Control Eng. Pract. 1997, 5, 639–652. [Google Scholar] [CrossRef]
- Rodriguez, M.; Hernandez, M.; Mendez, F.; Sibaja, P.; Hernandez, L. A simple fault detection of induction motor by using parity equations. In Proceedings of the SDEMPED 2011-8th IEEE Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives, Bologna, Italy, 5–8 September 2011; pp. 573–579. [Google Scholar] [CrossRef]
- Chulines, E.; Rodríguez, M.A.; Duran, I.; Sánchez, R. Simplified Model of a Three-Phase Induction Motor for Fault Diagnostic Using the Synchronous Reference Frame DQ and Parity Equations. In Proceedings of the 2nd IFAC Conference on Modelling, Identification and Control of Nonlinear Systems MICNON 2018, Jalisco, Mexico, 20–22 June 2018; Volume 51. [Google Scholar] [CrossRef]
- El Khil, S.K.; Jlassi, I.; Estima, J.; Mrabet-Bellaaj, N.; Cardoso, A.M. Current sensor fault detection and isolation method for PMSM drives, using average normalised currents. Electron. Lett. 2016, 52, 1434–1436. [Google Scholar] [CrossRef]
- Gertler, J.J. Fault Detection and Diagnosis in Engineering Systems, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017; Volume 1. [Google Scholar] [CrossRef]
- Isermann, R. Fault-Diagnosis Systems: An Introduction from Fault Detection to Fault Tolerance, 1st ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2006; ISBN 978-3-540-24112-6. [Google Scholar]
- Kazmierkowski, M.P. Electric motor drives: Modeling, analysis and control. Int. J. Robust Nonlinear Control 2004, 14, 767–769. [Google Scholar] [CrossRef]
- Höfling, T.; Isermann, R. Fault detection based on adaptive parity equations and single-parameter tracking. Control Eng. Pract. 1996, 4, 1361–1369. [Google Scholar] [CrossRef]
- Rodríguez, M.A.; Hernandez, M.; Golikov, V.; Martínez, G. Fault Diagnostic Based on Parity Equations Applied to Induction Motor. In Proceedings of the XXI Congreso de la Asociación Chilena de Control Automático ACCA, Santiago, Chile, 5–7 November 2014; pp. 65–71. [Google Scholar]
- Krause, P.; Wasynczuk, O.; Sudhoff, S.; Pekarek, S. Analysis of Electric Machinery and Drive Systems, 1st ed.; IEEE: New York, NY, USA, 2013; Volume 1, ISBN 9781118024294. [Google Scholar] [CrossRef]


| Faults | |||||
|---|---|---|---|---|---|
| Parametric | I | 0 | 0 | I | |
| I | 0 | 0 | I | ||
| I | 0 | I | I | ||
| I | I | I | I | ||
| 0 | I | I | I | ||
| 0 | I | I | I | ||
| Additive | I | I | I | 0 | |
| I | I | 0 | I | ||
| I | 0 | I | I | ||
| (a) | |||||
|---|---|---|---|---|---|
| Faults | |||||
| Parametric | Rs | Rsa | 0 | I | I |
| Rsb | I | 0 | I | ||
| Rsc | I | I | 0 | ||
| Ls | Lsa | 0 | I | I | |
| Lsb | I | 0 | I | ||
| Lsc | I | I | 0 | ||
| msr | I | I | I | ||
| Additive | Is | Isa | I | I | I |
| Isb | I | I | I | ||
| Isc | I | I | I | ||
| Vs | Vsa | 0 | I | I | |
| Vsb | I | 0 | I | ||
| Vsc | I | I | 0 | ||
| (b) | |||||
| Faults | |||||
| Parametric | Rs | Rsa | 0 | I | I |
| Rsb | I | 0 | I | ||
| Rsc | I | I | 0 | ||
| Ls | Lsa | 0 | 0 | 0 | |
| Lsb | 0 | 0 | 0 | ||
| Lsc | 0 | 0 | 0 | ||
| msr | 0 | 0 | 0 | ||
| Additive | Is | Isa | 0 | I | I |
| Isb | I | 0 | I | ||
| Isc | I | I | 0 | ||
| Vs | Vsa | 0 | I | I | |
| Vsb | I | 0 | I | ||
| Vsc | I | I | 0 | ||
| DQ Model | Three-Phase Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Fault | |||||||||
| Parametric | I | 0 | 0 | I | 0 | I | I | ||
| I | 0 | 0 | I | I | 0 | I | |||
| I | 0 | 0 | I | I | I | 0 | |||
| I | 0 | 0 | I | 0 | I | I | |||
| I | 0 | I | I | I | I | I | |||
| I | 0 | I | I | I | I | I | |||
| I | 0 | I | I | I | I | I | |||
| I | I | I | I | I | I | 0 | |||
| 0 | I | I | I | 0 | 0 | 0 | |||
| 0 | I | I | I | 0 | 0 | 0 | |||
| Additive | I | I | I | 0 | 0 | I | I | ||
| I | I | I | 0 | I | 0 | I | |||
| I | I | I | 0 | I | I | 0 | |||
| I | I | 0 | I | 0 | 0 | 0 | |||
| I | 0 | I | I | 0 | I | I | |||
| I | 0 | I | I | I | 0 | I | |||
| I | 0 | I | I | I | I | 0 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez-Blanco, M.A.; Golikov, V.; Vazquez-Avila, J.L.; Samovarov, O.; Sanchez-Lara, R.; Osorio-Sánchez, R.; Pérez-Ramírez, A. Comprehensive and Simplified Fault Diagnosis for Three-Phase Induction Motor Using Parity Equation Approach in Stator Current Reference Frame. Machines 2022, 10, 379. https://doi.org/10.3390/machines10050379
Rodriguez-Blanco MA, Golikov V, Vazquez-Avila JL, Samovarov O, Sanchez-Lara R, Osorio-Sánchez R, Pérez-Ramírez A. Comprehensive and Simplified Fault Diagnosis for Three-Phase Induction Motor Using Parity Equation Approach in Stator Current Reference Frame. Machines. 2022; 10(5):379. https://doi.org/10.3390/machines10050379
Chicago/Turabian StyleRodriguez-Blanco, Marco Antonio, Victor Golikov, Jose Luis Vazquez-Avila, Oleg Samovarov, Rafael Sanchez-Lara, René Osorio-Sánchez, and Agustín Pérez-Ramírez. 2022. "Comprehensive and Simplified Fault Diagnosis for Three-Phase Induction Motor Using Parity Equation Approach in Stator Current Reference Frame" Machines 10, no. 5: 379. https://doi.org/10.3390/machines10050379
APA StyleRodriguez-Blanco, M. A., Golikov, V., Vazquez-Avila, J. L., Samovarov, O., Sanchez-Lara, R., Osorio-Sánchez, R., & Pérez-Ramírez, A. (2022). Comprehensive and Simplified Fault Diagnosis for Three-Phase Induction Motor Using Parity Equation Approach in Stator Current Reference Frame. Machines, 10(5), 379. https://doi.org/10.3390/machines10050379







