Thermal Field and Stress Analysis of Induction Motor with Stator Inter-Turn Fault
Abstract
:1. Introduction
2. Prototype Parameters and Simulation Model
2.1. Parameters and Material Properties of Prototype
2.2. Simulation Model
2.2.1. Basic Equations and Model of Thermal Field
2.2.2. Heat Dissipation Boundaries
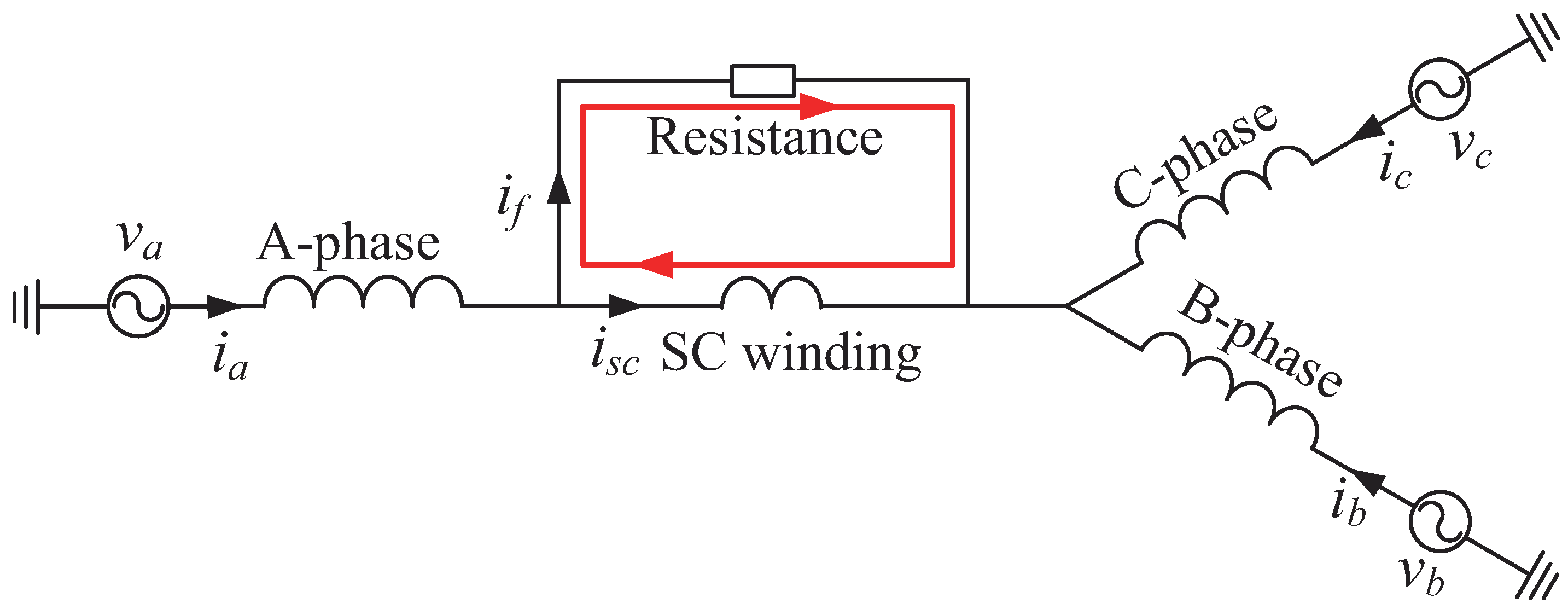
3. Experimental Platform
4. Heat Source Analysis
5. Thermal Field Analysis
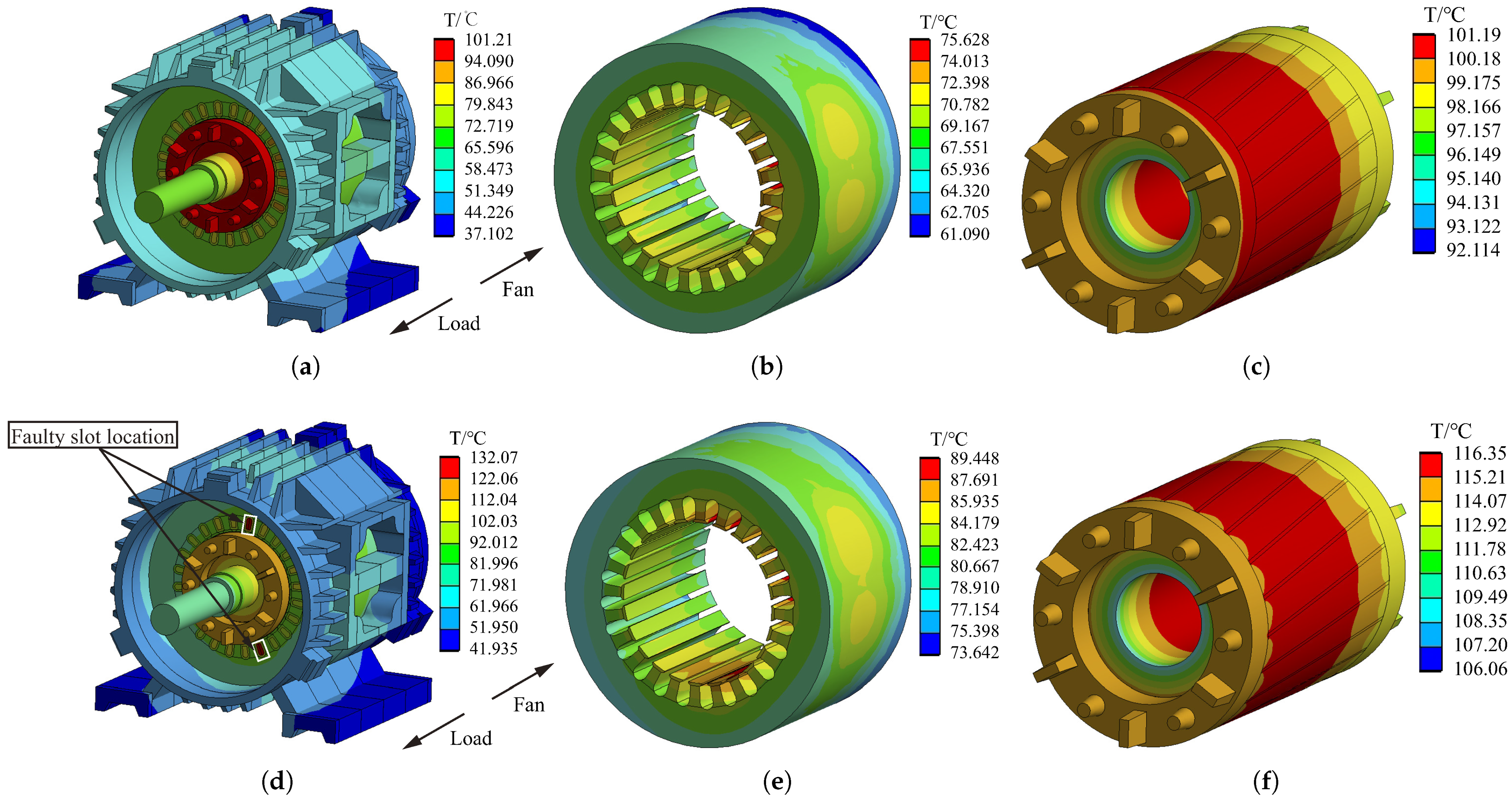
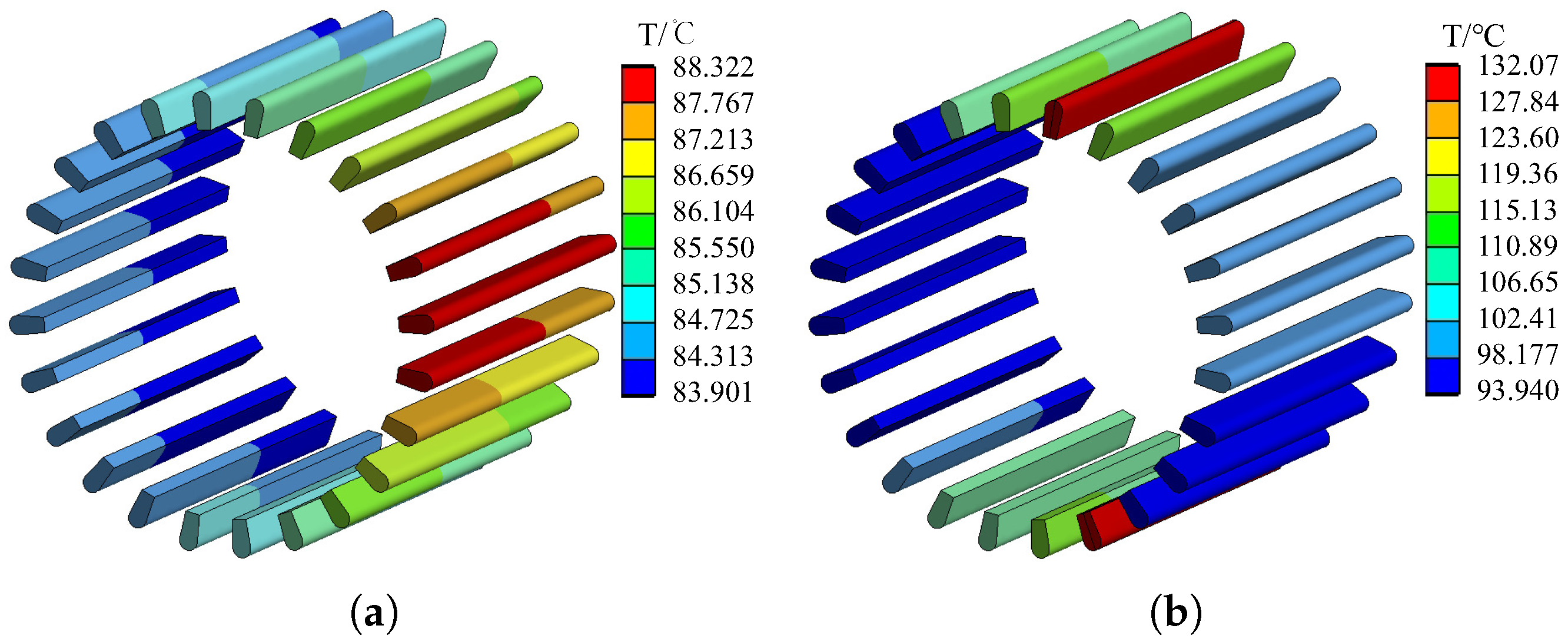
5.1. Thermal Field Distribution before and after Fault
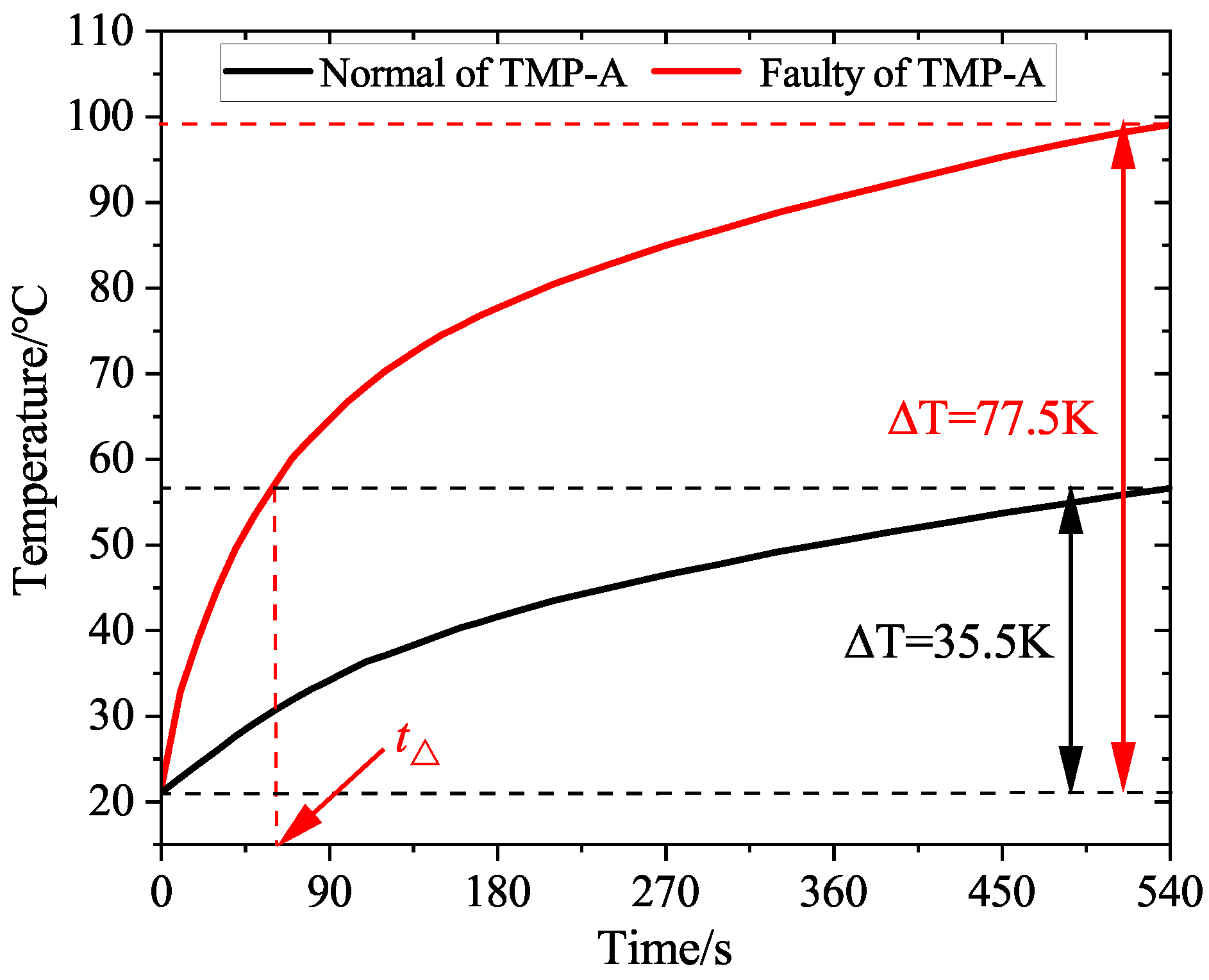
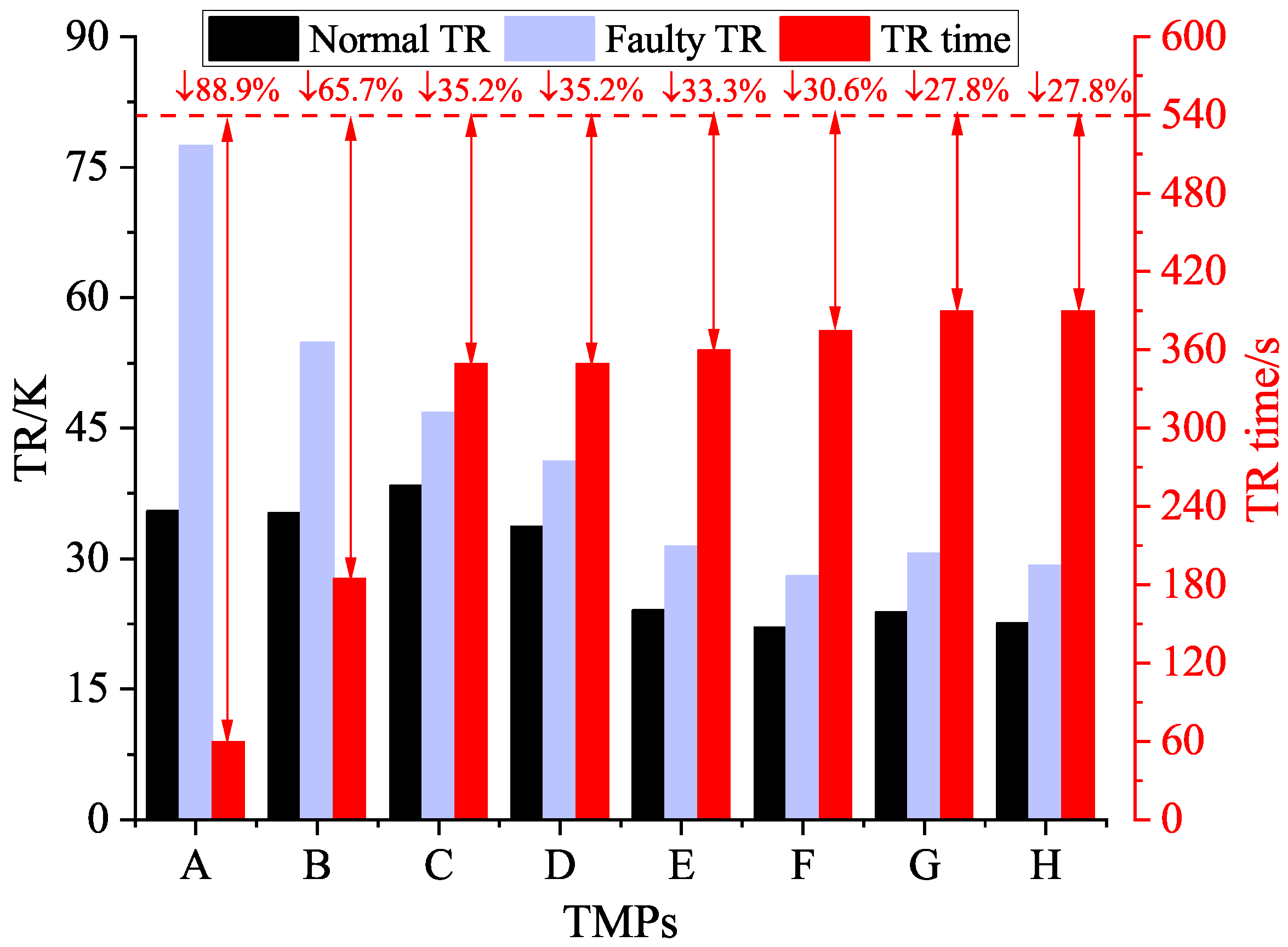
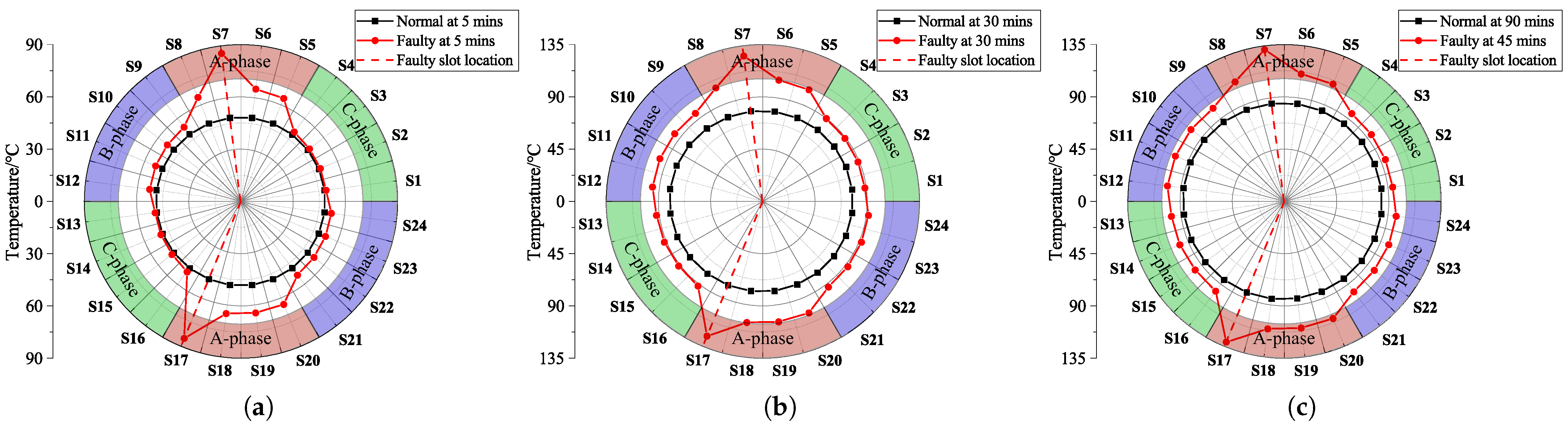
5.2. Thermal Characteristics Caused by Fault
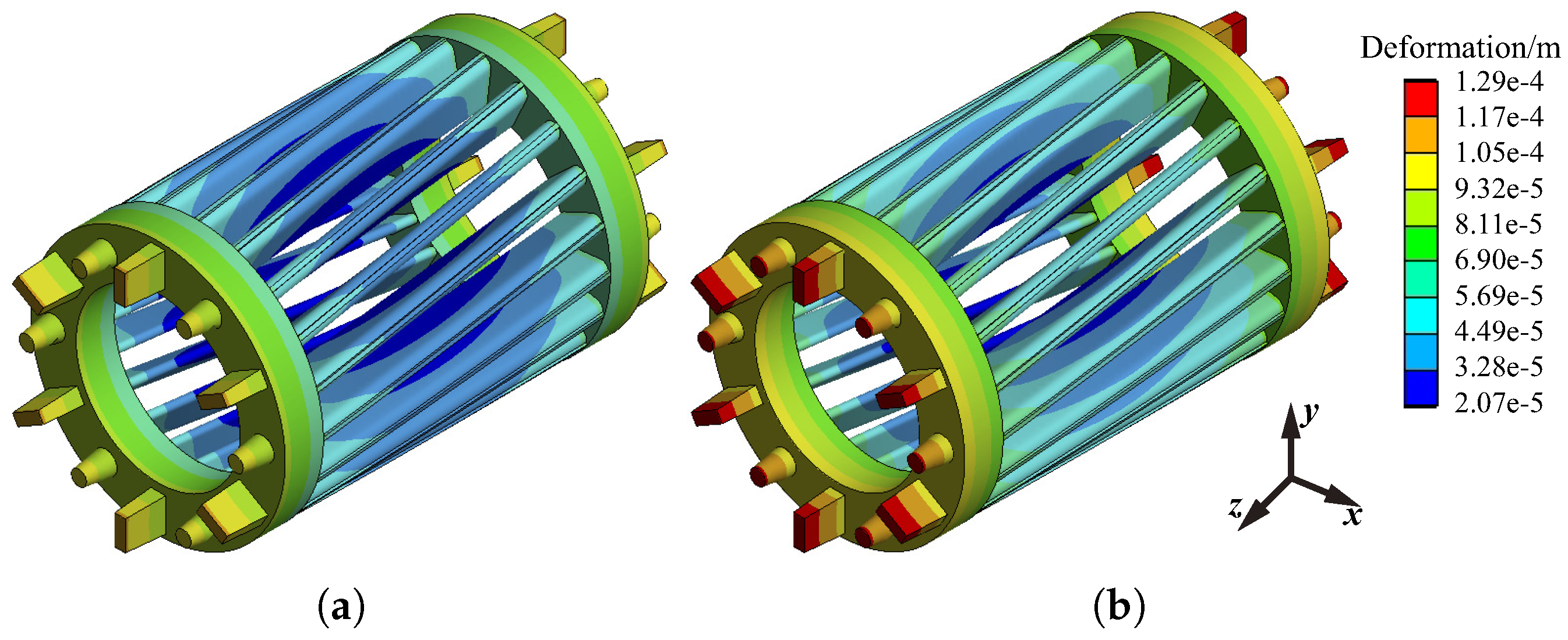
6. Thermal Stress Analysis of Rotor
6.1. Basic Equations of Thermal Stress Calculation
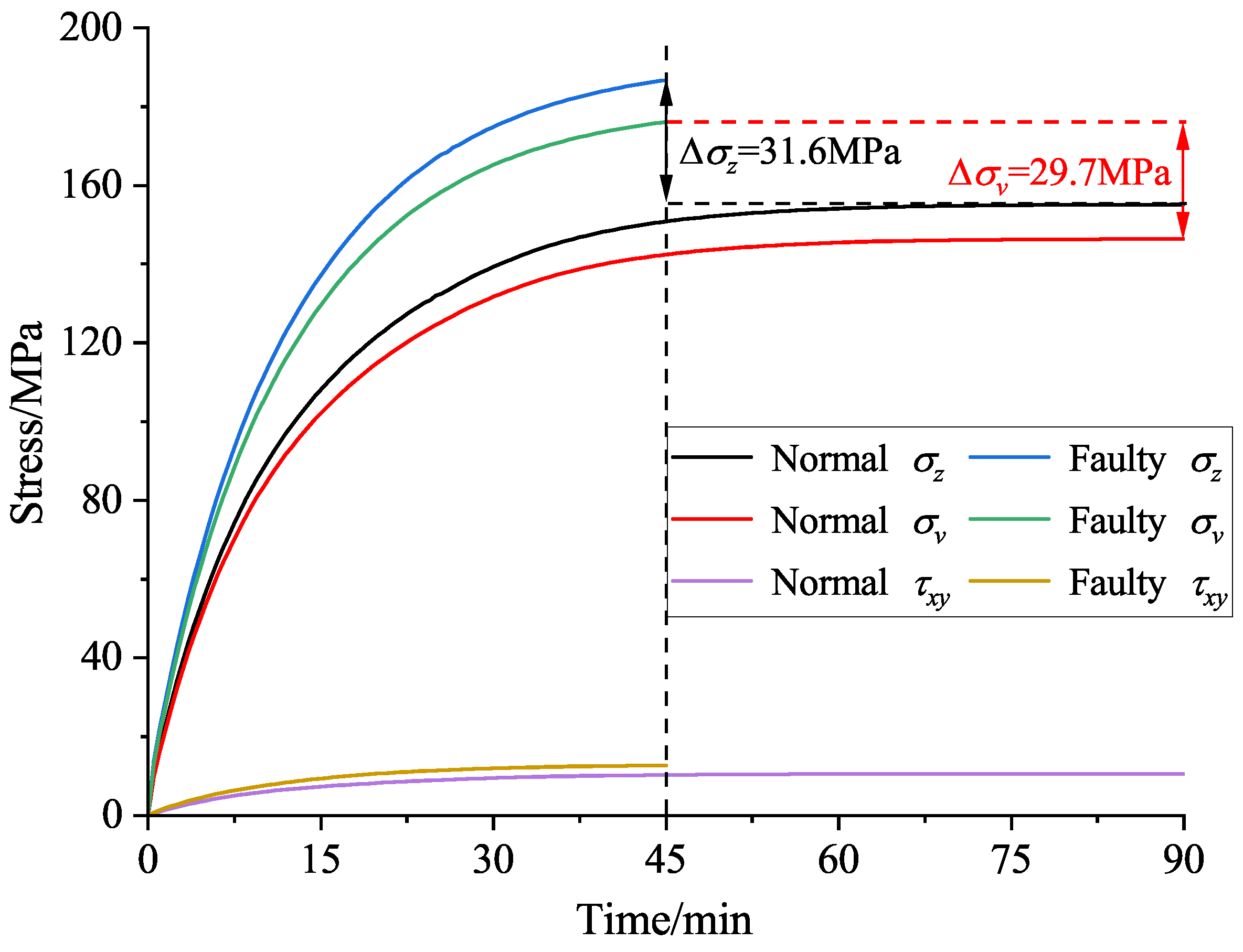
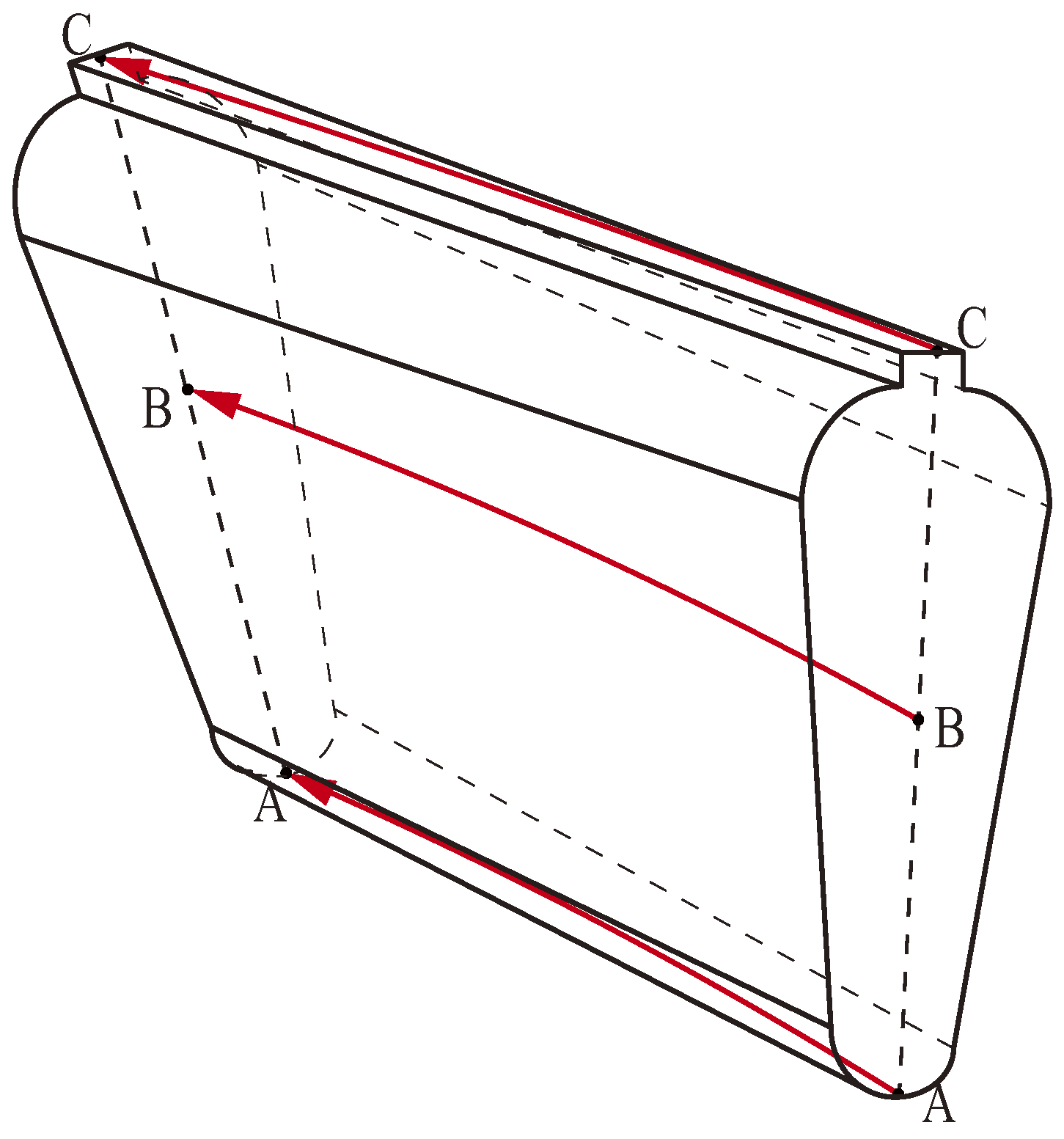
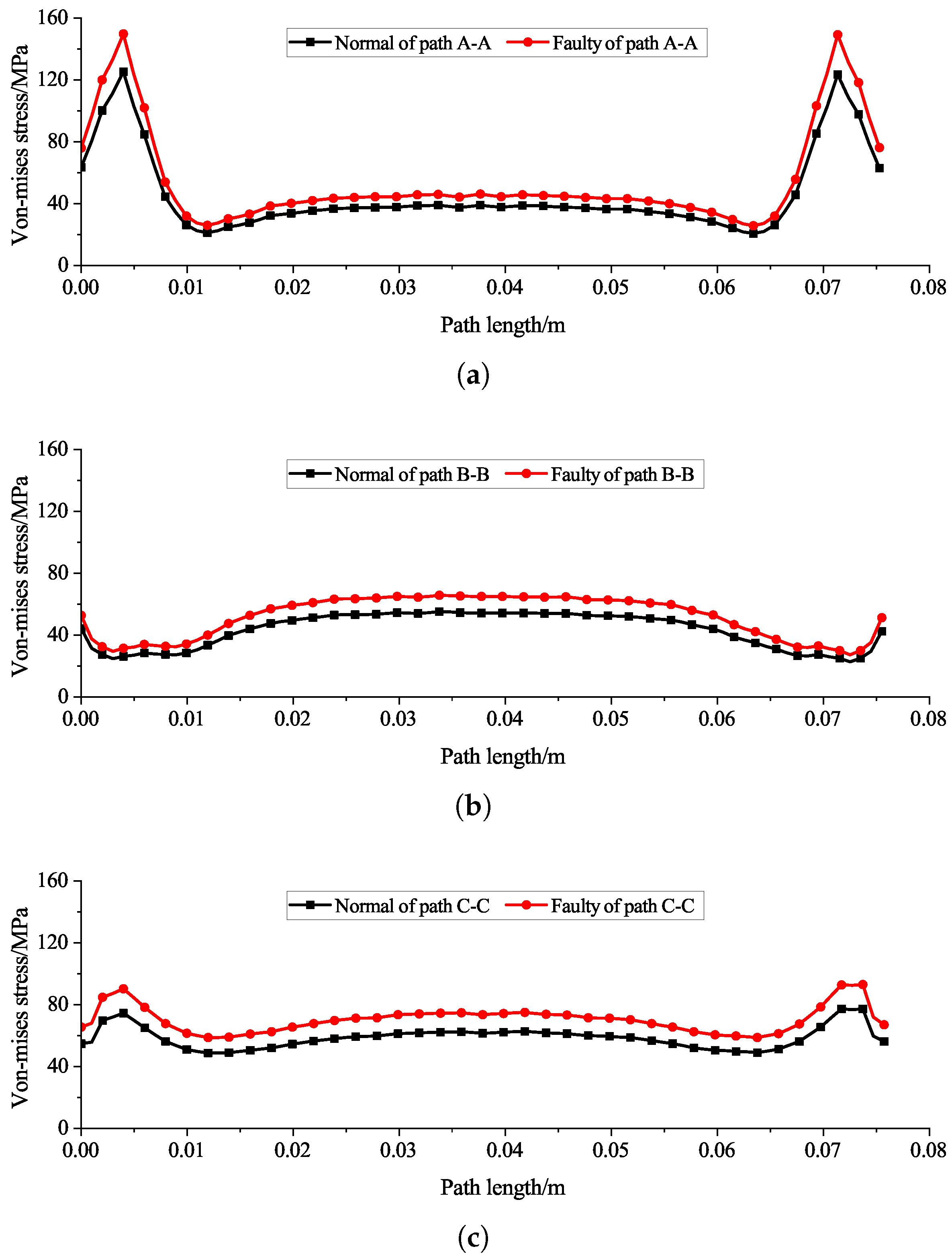
6.2. Analysis of Thermal Stress
7. Conclusions
- (1)
- The original temperature distribution law of the motor is broken after ITF, and the hotspot of the motor is transferred from the rotor to the faulty slot winding. The TR of each part of the motor is higher than that under normal conditions, and the difference in space and time characteristics of temperature distribution is further increased due to the different TR values and TR rates of each part.
- (2)
- The significant thermal characteristic of ITF is the difference in winding temperature distribution. Taking the TR of normal winding in the first nine minutes as the standard, the TR value and TR time of winding in the faulty slot are 2.2 times and 11.1%, respectively, of those of the normal motor. The statistical variance data of winding temperature show that the fault causes the discrete distribution of winding temperature, and the variance value can provide a reference for fault diagnosis.
- (3)
- The rotor thermal stress analysis is introduced for the first time in studying the stator ITF in induction motors. The maximum thermal stress of the squirrel cage rotor occurs at the bottom of the bar near the joint of the end-ring. After the fault, due to the increase in rotor temperature, the thermal stress value at this place further increases (20.7% higher than that under normal conditions), which intensifies the risk of broken bar fault.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karmakar, S.; Chattopadhyay, S.; Mitra, M.; Sengupta, S. Induction Motor Fault Diagnosis: Approach through Current Signature Analysis; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Zhang, P.; Du, Y.; Habetler, T.G.; Lu, B. A survey of condition monitoring and protection methods for medium-voltage induction motors. IEEE Trans. Ind. Appl. 2010, 47, 34–46. [Google Scholar] [CrossRef]
- Qiu, H.; Yu, W.; Tang, B.; Yang, C.; Zhao, H. Research on the influence of inter-turn short circuit fault on the temperature field of permanent magnet synchronous motor. J. Electr. Eng. Technol. 2017, 12, 1566–1574. [Google Scholar]
- Bento, F.; Adouni, A.; Muxiri, A.C.; Fonseca, D.S.; Marques Cardoso, A.J. On the risk of failure to prevent induction motors permanent damage, due to the short available time-to-diagnosis of inter-turn short-circuit faults. IET Electr. Power Appl. 2021, 15, 51–62. [Google Scholar] [CrossRef]
- Adouni, A.; Cardoso, A.J.M. Thermal analysis of low-power three-phase induction motors operating under voltage unbalance and inter-turn short circuit faults. Machines 2020, 9, 2. [Google Scholar] [CrossRef]
- He, Y.; Zhang, W.; Xu, M.; Tao, W.; Liu, H.; Dou, L.; Wan, S.; Li, J.; Gerada, D. Rotor loss and temperature variation under single and combined faults composed of static air-gap eccentricity and rotor inter-turn short circuit in synchronous generators. IET Electr. Power. Appl. 2021, 15, 1529–1546. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, J.; Wang, B. Electromagnetic-thermal coupled simulation under various fault conditions of a triple redundant 9-phase PMASynRM. IEEE Trans. Ind. Appl. 2019, 56, 128–137. [Google Scholar] [CrossRef]
- Li, G.; Ojeda, J.; Hoang, E.; Gabsi, M. Thermal-electromagnetic analysis of a fault-tolerant dual-star flux-switching permanent magnet motor for critical applications. IET Electr. Power. Appl. 2011, 5, 503–513. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Wang, J.; Wang, B. Transient 3-D lumped parameter and 3-D FE thermal models of a PMASynRM under fault conditions with asymmetric temperature distribution. IEEE Trans. Ind. Electron. 2020, 68, 4623–4633. [Google Scholar] [CrossRef]
- Wan, Y.; Wu, S.; Cui, S. Choice of pole spacer materials for a high-speed PMSM based on the temperature rise and thermal stress. IEEE Trans. Appl. Supercond. 2016, 26, 0608405. [Google Scholar] [CrossRef]
- Chen, G.; Di, C.; Bao, X.; Xu, W. Calculation and Optimization of Thermal Stress in Induction Motor with Double-Skewed Rotor. In Proceedings of the 2021 24th International Conference on Electrical Machines and Systems (ICEMS), Gyeongju, Korea, 31 October–3 November 2021; pp. 1445–1449. [Google Scholar]
- Li, J.; Wang, L. Calculation and analysis of rotor thermal static field for inter-turn short circuit of large hydro-generator excitation winding. Energies 2019, 12, 1252. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y.; Wang, Z.; Shan, X.; Li, Y. Investigation of rotor thermal stress in squirrel cage induction motor with broken bar faults. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 1865–1886. [Google Scholar] [CrossRef]
- Climente-Alarcon, V.; Arkkio, A.; Antonino-Daviu, J. Study of thermal stresses developed during a fatigue test on an electrical motor rotor cage. Int. J. Fatigue 2019, 120, 56–64. [Google Scholar] [CrossRef] [Green Version]
- Xie, Y. Performance evaluation and thermal fields analysis of induction motor with brok bars located at different relative positions. IEEE Trans. Magn. 2010, 46, 1243–1250. [Google Scholar]
- Boglietti, A.; Cossale, M.; Vaschetto, S.; Dutra, T. Thermal conductivity evaluation of fractional-slot concentrated-winding machines. IEEE Trans. Ind. Appl. 2017, 53, 2059–2065. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, Y. 3D temperature field analysis of the induction motors with broken bar fault. Appl. Therm. Eng. 2014, 66, 25–34. [Google Scholar] [CrossRef]
- Huang, G.; Fu, F. Small and Medium-Sized Rotating Motor Design Handbook; China Electric Power Press: Beijing, China, 2007. [Google Scholar]
- Chen, P.; Xie, Y.; Hu, S. Electromagnetic Performance and Diagnosis of Induction Motors With Stator Interturn Fault. IEEE Trans. Ind. Appl. 2020, 57, 1354–1364. [Google Scholar] [CrossRef]
- Li, W.; Huang, B.; Bi, Z. Thermal Stress Theory Analysis and Application; China Electric Power Press: Beijing, China, 2004. [Google Scholar]

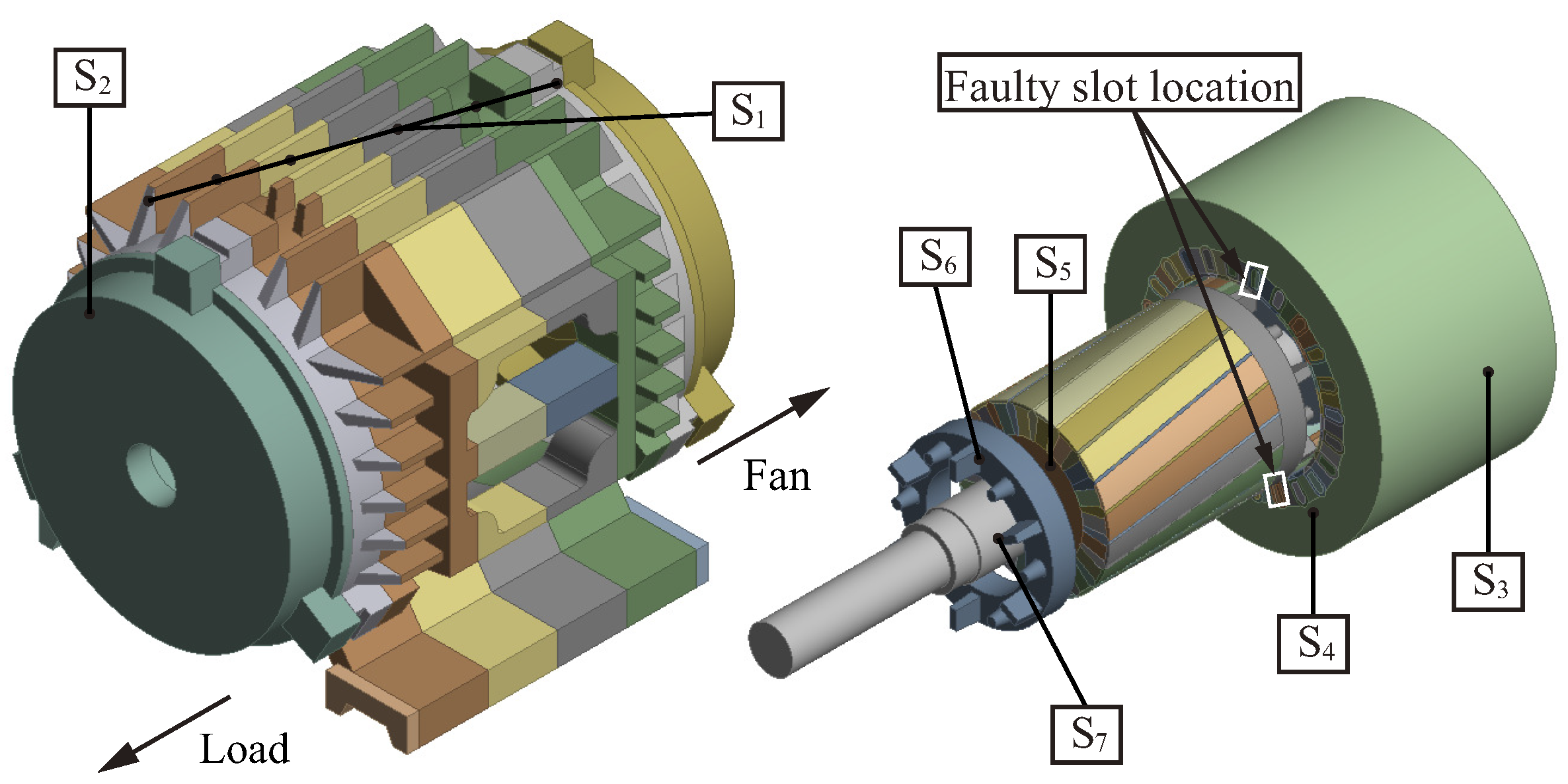




| Parameters | Units | Value |
|---|---|---|
| Cooling type | - | TEFC |
| Insulation class | - | F |
| Pole pairs | - | 1 |
| Stator/rotor slot number | - | 24/20 |
| Number of turns in series per phase | - | 256 |
| Rated power | kW | 1.1 |
| Rated speed | rpm | 2850 |
| Outer/inner diameter of stator | mm | 120/67 |
| Air-gap length | mm | 0.3 |
| Inner diameter of rotor | mm | 26 |
| Core length | mm | 75 |
| Motor Parts | Material | Thermal Conductivity W/(m·K) | Density kg/m | Specific Heat Capacity J/(kg·K) |
|---|---|---|---|---|
| Stator and rotor core | Silicon steel sheet | 39 (radial), 4 (axial) | 7700 | 470 |
| Stator coil | Copper | 386 | 8900 | 385 |
| Equivalent insulation in slot | Insulation material | 0.14 | 1200 | 1000 |
| Equivalent air-gap | Air | 0.03 | 1.164 | 1013 |
| Rotor cage | Cast aluminium | 221 | 2689 | 950 |
| Housing and end cap | Cast iron | 48 | 7350 | 460 |
| Shaft | 45# steel | 50.2 | 7850 | 434 |
| Bearing | Bearing steel | 35 | 7810 | 450 |
| Wedge | Wood | 0.5 | 1900 | 1150 |
| Heat Dissipation Surface | Calculation Formula | Variable Description | Value/W/(mK) |
|---|---|---|---|
| —Housing outer surface | v is the wind velocity on the housing surface. | 29.2–65.9 | |
| —End cap outer surface | represents the fan side and represents the load side; is half of the circumferential velocity at the outer diameter of the fan. | 28.9, 69 | |
| —Contact surface between stator core and housing | is the equivalent conduction thermal resistance, and it is assumed that the equivalent heat transfer resistance is equal to it; and are the air-gap length and the heat conduction area between stator core and housing. | 500 | |
| —End face of stator core | is the linear speed of the rotor surface; is the outer diameter of the rotor; n is the rotor speed. | 48.5 | |
| —End face of rotor core | is the Nusselt number; is the thermal conductivity of air; is the Reynolds number of the air at the rotor end face; is the kinematic viscosity of air. | 73.8 | |
| —Rotor end-ring surface | is the Nusselt number; is the Reynolds number of the air at the rotor end-ring surface; is rotor blade height. | 128.7 | |
| —Shaft surface | is 75% of circumferential velocity of shaft. | 18.4 |
| A | B | C | SC | Total | |
|---|---|---|---|---|---|
| Normal/W | 54.19 | 54.19 | 54.19 | 0 | 162.57 |
| Fault/W | 78.89 | 72.94 | 59.88 | 23.57 | 235.28 |
| Amplification | 45.6% | 34.6% | 10.5% | - | 44.7% |
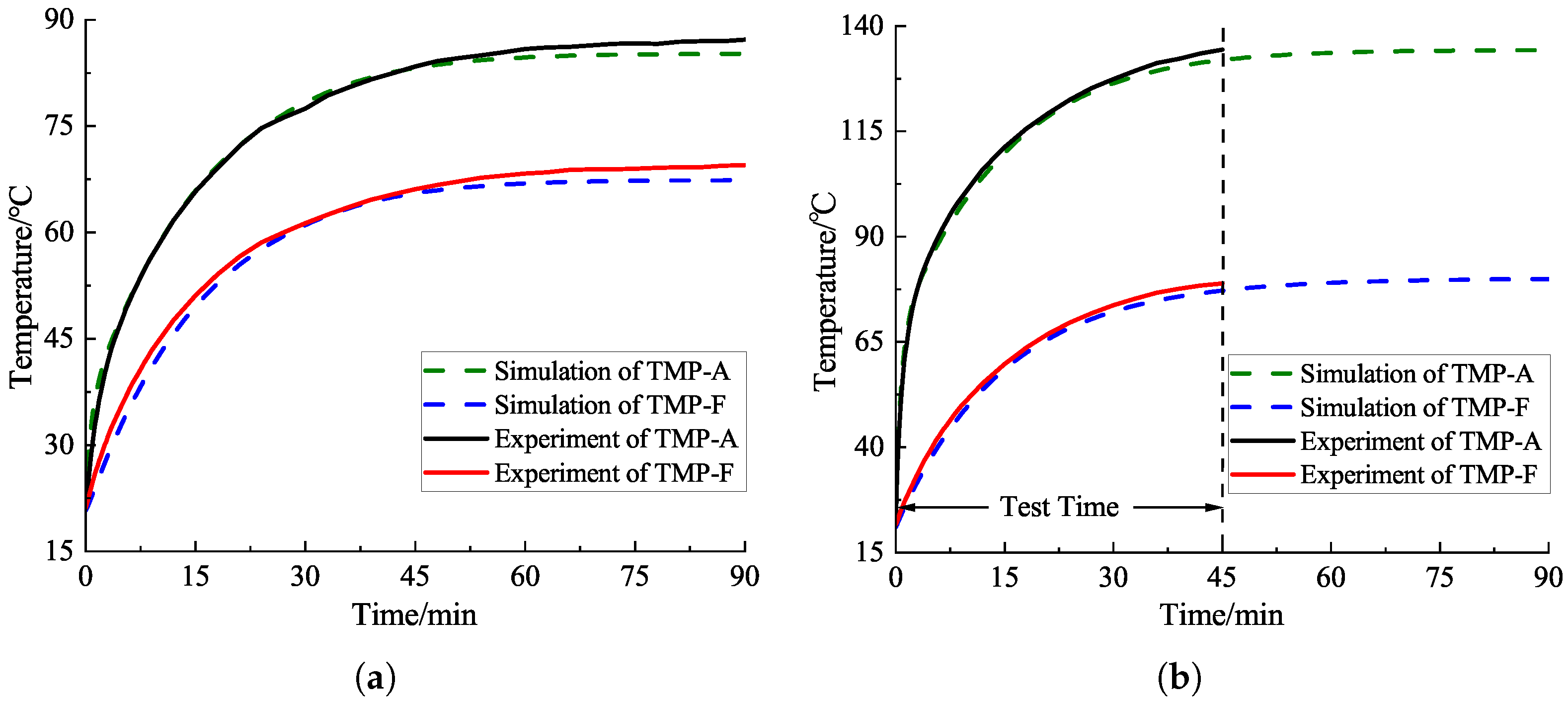
| Normal Condition | Measured Temperature | Simulated Temperature | Measured TR | Simulated TR |
|---|---|---|---|---|
| TMP-A | 87.2 | 85.2 | 66.1 | 64.4 |
| TMP-B | 85.3 | 84.6 | 65.4 | 63.8 |
| TMP-C | 91.7 | 88.2 | 70.5 | 67.4 |
| TMP-D | 83.2 | 84.4 | 63 | 63.6 |
| TMP-E | 75.4 | 72.5 | 55.1 | 51.7 |
| TMP-F | 69.7 | 67.4 | 48.5 | 46.6 |
| TMP-G | 75.6 | 76.9 | 56.1 | 56.1 |
| TMP-H | 72.4 | 72.5 | 52.5 | 51.7 |
| Faulty Condition | Measured Temperature | Simulated Temperature | Measured TR | Simulated TR |
| TMP-A | 134.4 | 131.95 | 112.8 | 110.95 |
| TMP-B | 107.9 | 110.1 | 87.5 | 89.1 |
| TMP-C | 103.5 | 102.1 | 81.8 | 81.1 |
| TMP-D | 93.8 | 97.3 | 73.1 | 76.3 |
| TMP-E | 86.5 | 86.1 | 65.7 | 65.1 |
| TMP-F | 78.9 | 77.8 | 57.2 | 56.8 |
| TMP-G | 87.1 | 90.5 | 67.1 | 69.5 |
| TMP-H | 83.2 | 82.9 | 62.8 | 61.9 |
| 5 min | 30 min | Final | ||||
|---|---|---|---|---|---|---|
| Normal | Faulty | Normal | Faulty | Normal | Faulty | |
| 0.03 | 102.05 | 1.02 | 101.66 | 1.61 | 101.93 | |
| 0.08 | 39.28 | 1.52 | 42.62 | 2.30 | 43.65 | |
| 0.06 | 263.52 | 1.47 | 260.44 | 2.26 | 260.45 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.; Xie, Y.; Li, D. Thermal Field and Stress Analysis of Induction Motor with Stator Inter-Turn Fault. Machines 2022, 10, 504. https://doi.org/10.3390/machines10070504
Chen P, Xie Y, Li D. Thermal Field and Stress Analysis of Induction Motor with Stator Inter-Turn Fault. Machines. 2022; 10(7):504. https://doi.org/10.3390/machines10070504
Chicago/Turabian StyleChen, Peng, Ying Xie, and Daolu Li. 2022. "Thermal Field and Stress Analysis of Induction Motor with Stator Inter-Turn Fault" Machines 10, no. 7: 504. https://doi.org/10.3390/machines10070504
APA StyleChen, P., Xie, Y., & Li, D. (2022). Thermal Field and Stress Analysis of Induction Motor with Stator Inter-Turn Fault. Machines, 10(7), 504. https://doi.org/10.3390/machines10070504






