A New Piecewise Nonlinear Asymmetry Bistable Stochastic Resonance Model for Weak Fault Extraction
Abstract
:1. Introduction
2. Piecewise Nonlinear Asymmetric Bistable Stochastic Resonance Model
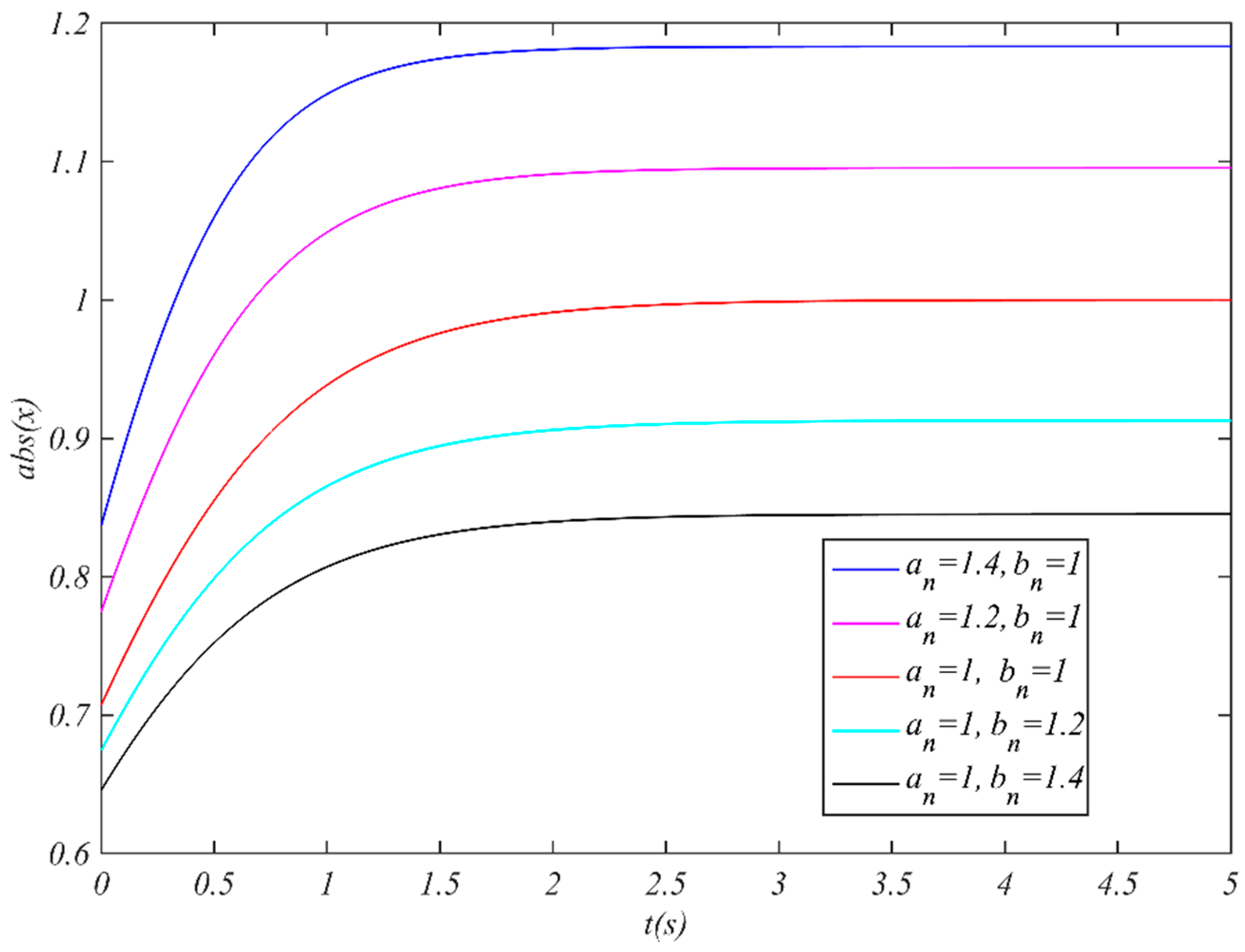
2.1. The Saturation Phenomena of CBSR Model
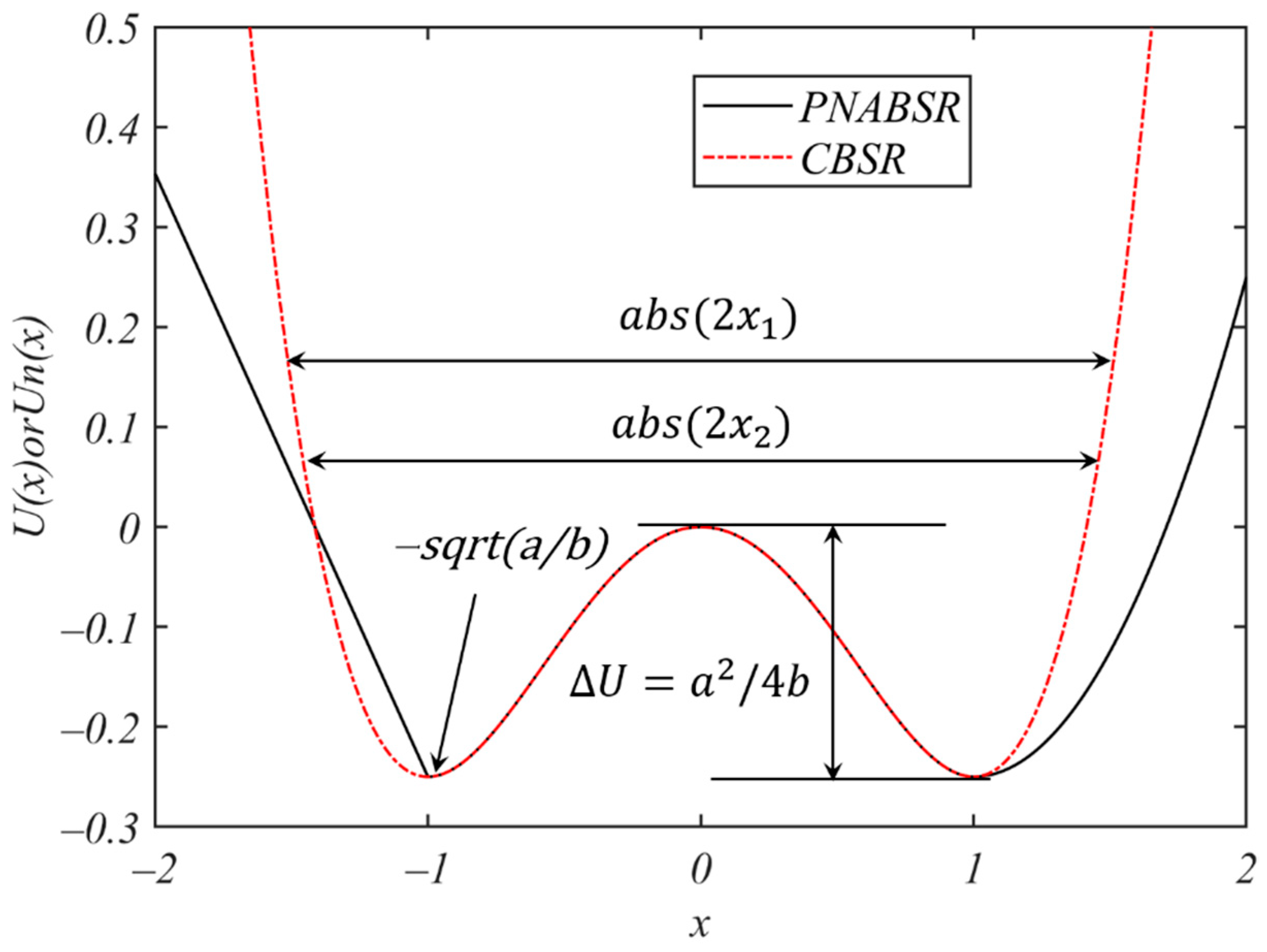
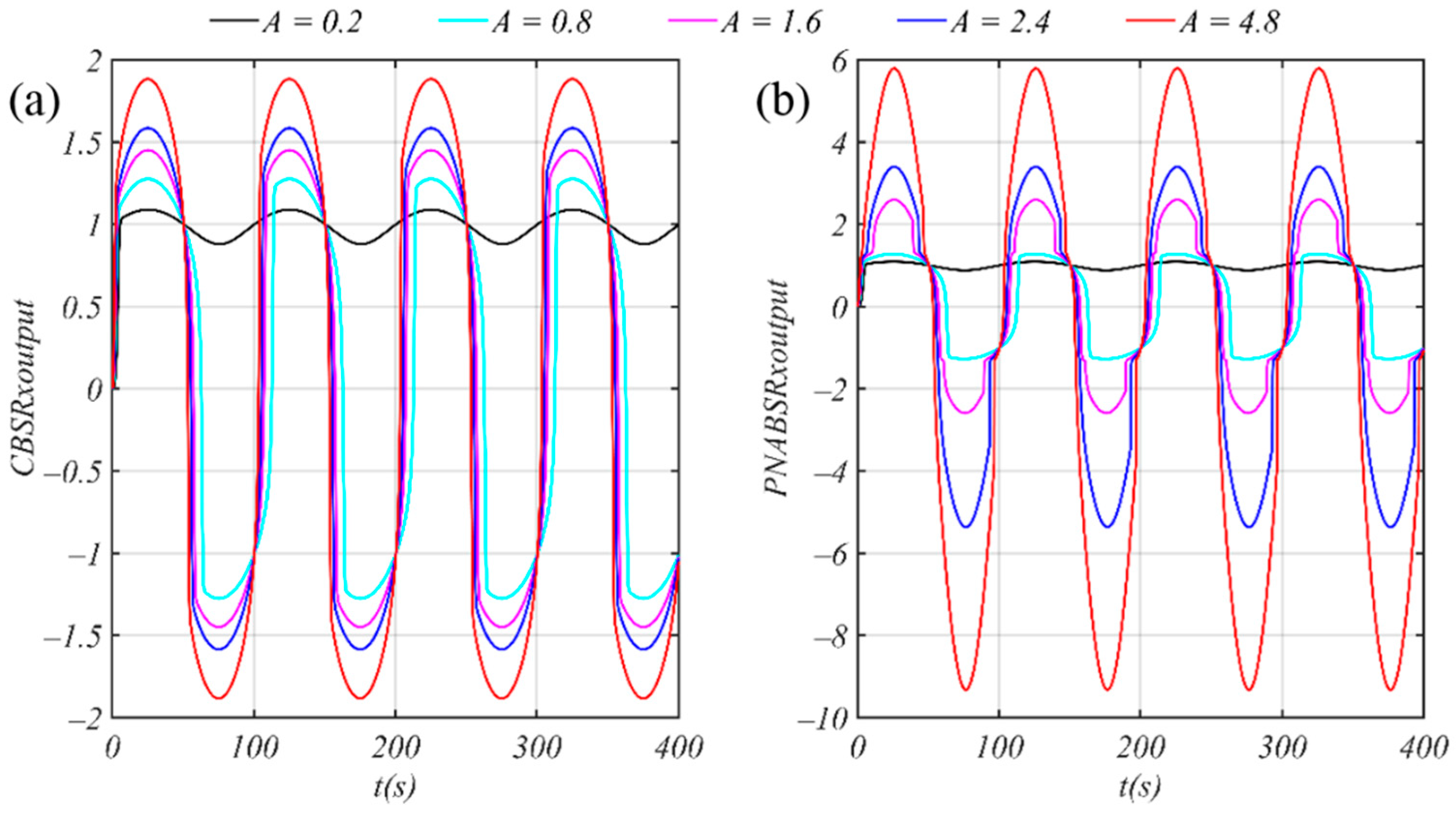
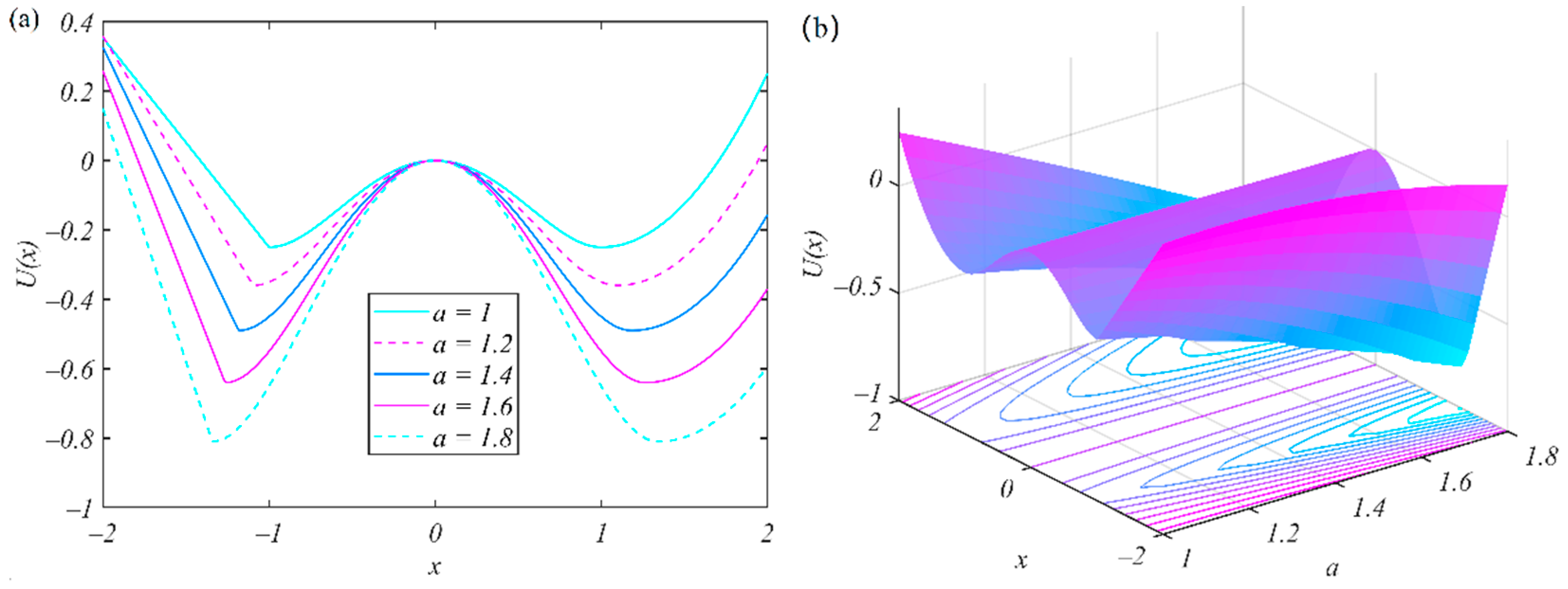
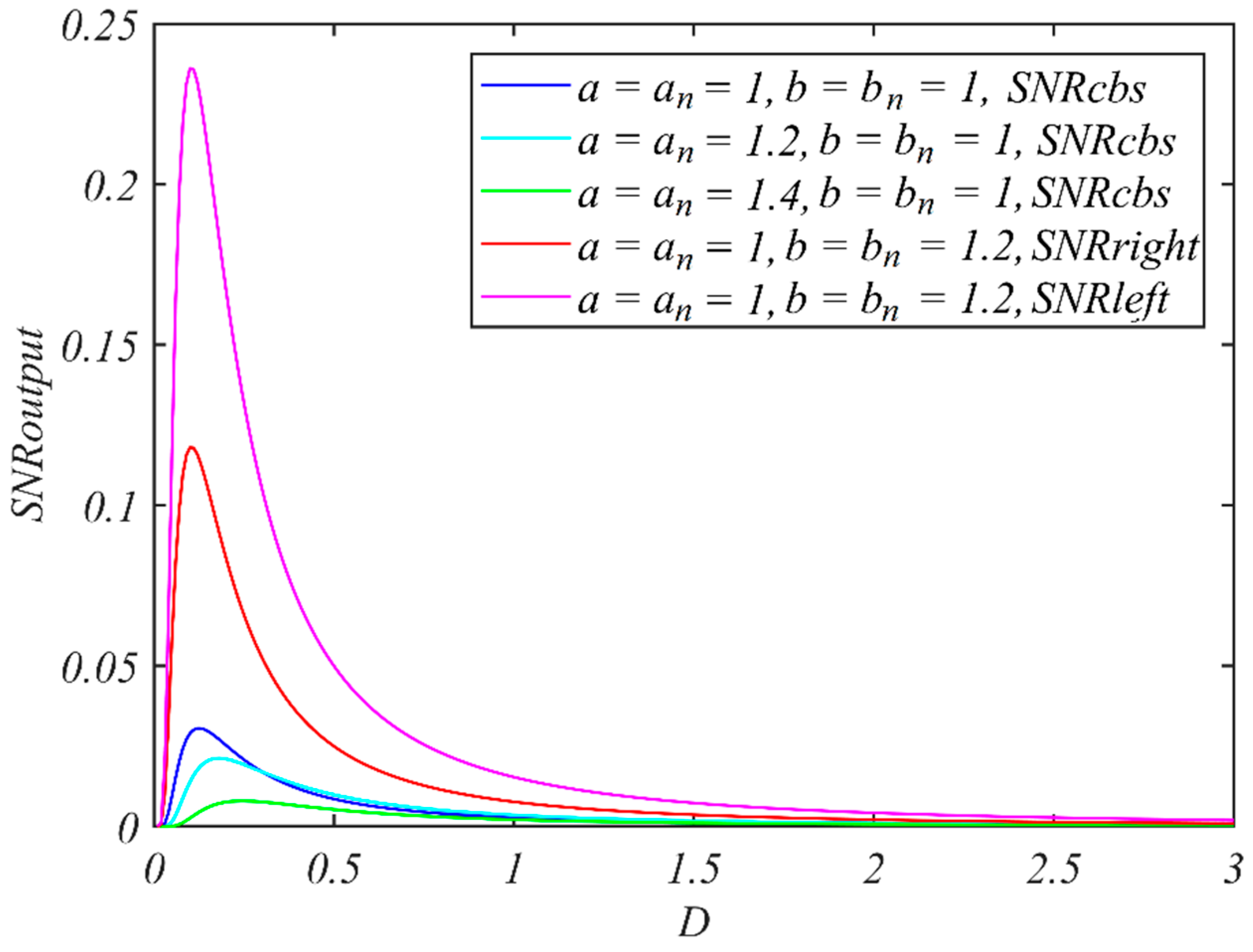
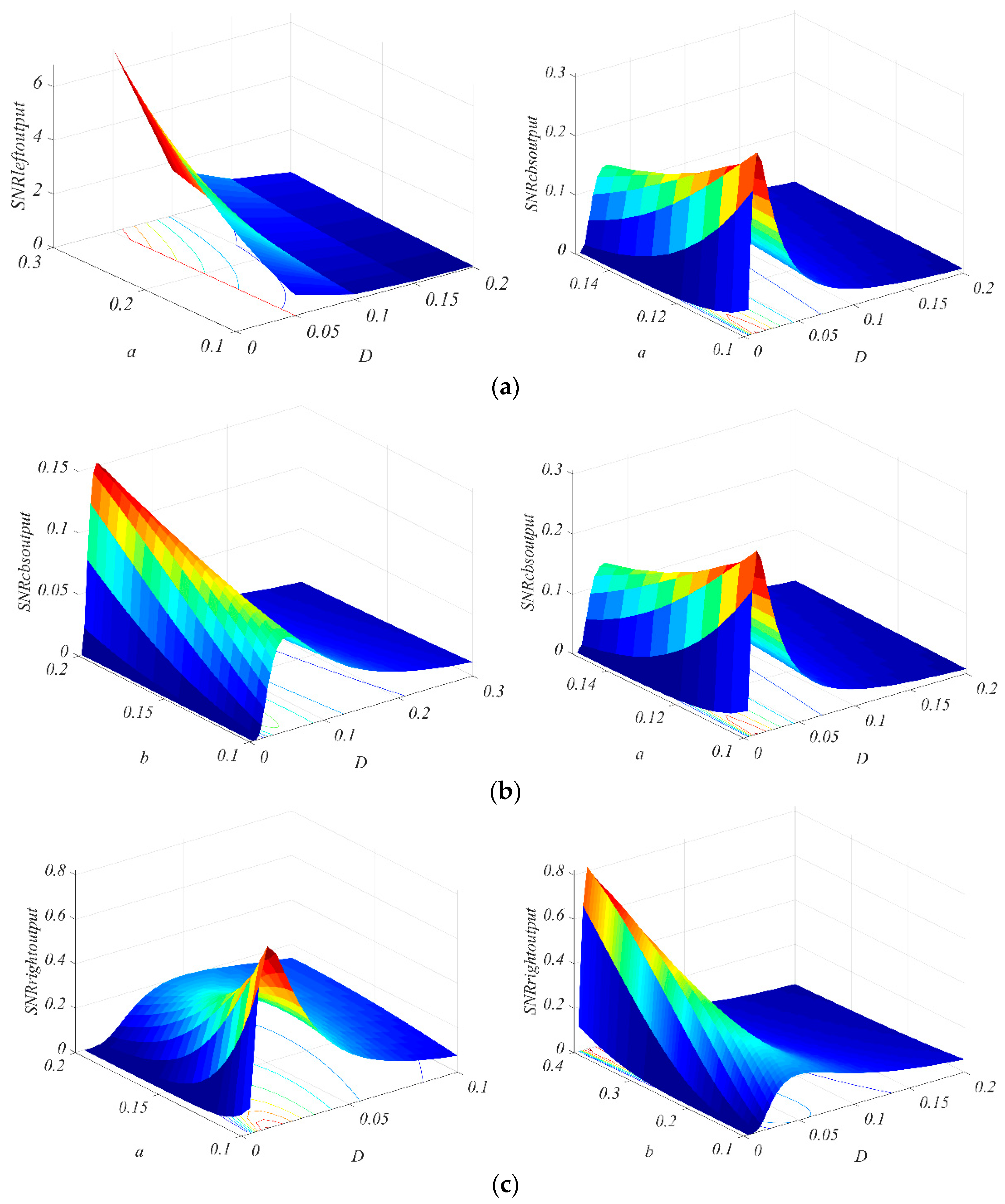
2.2. PNABSR Model and Its Performances
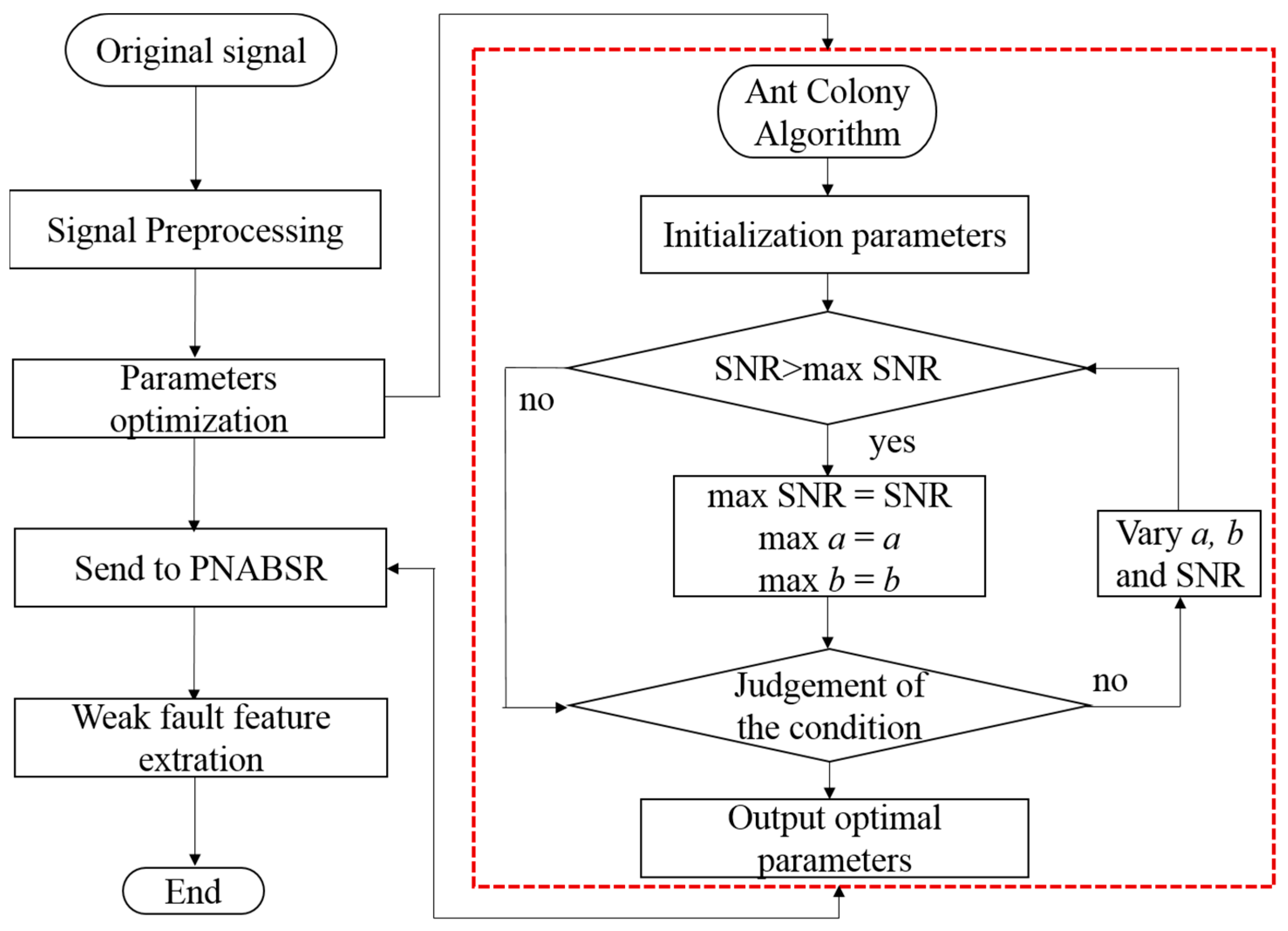
2.3. Optimization of PNABSR Parameters
3. Analysis and Discussion
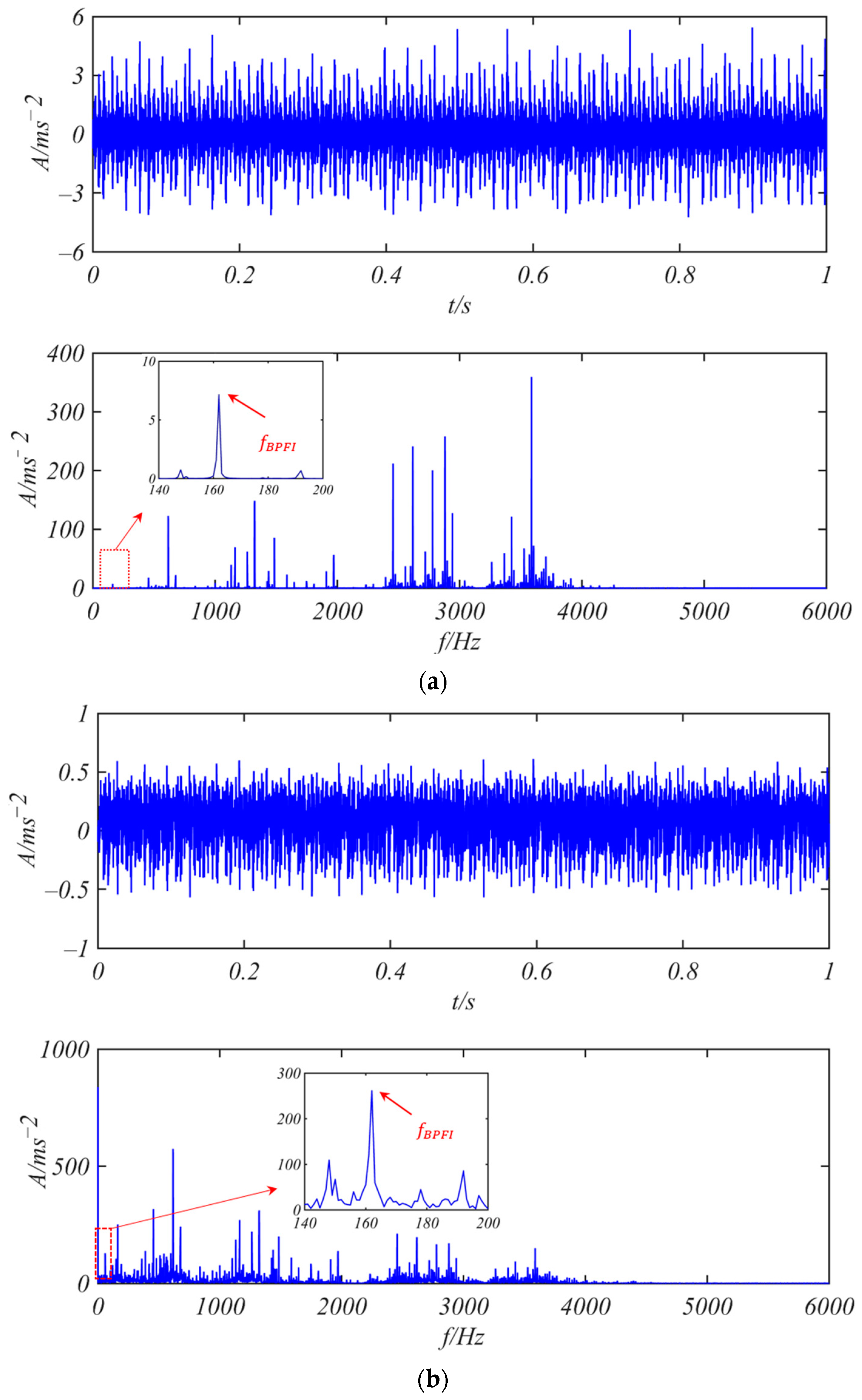
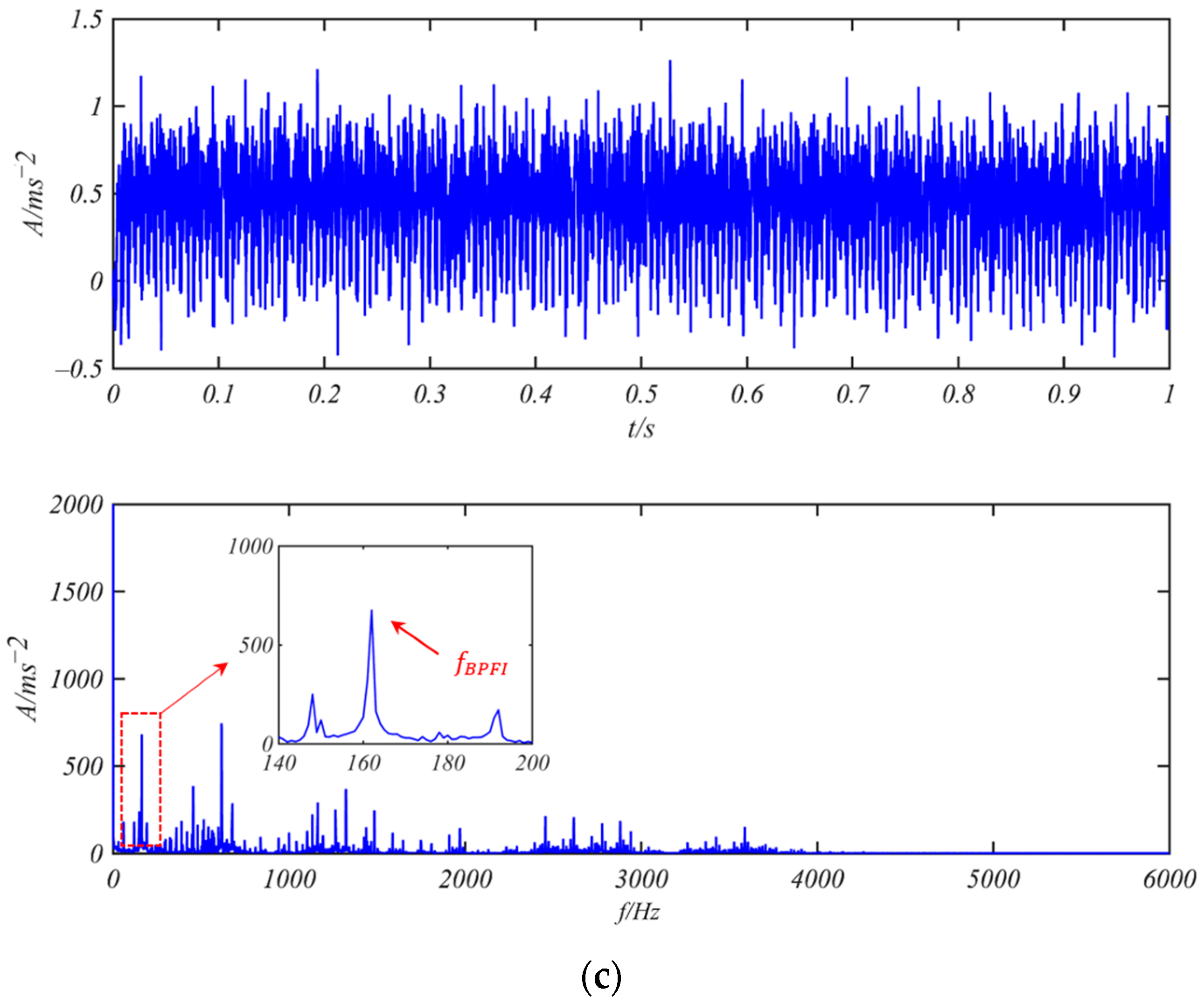
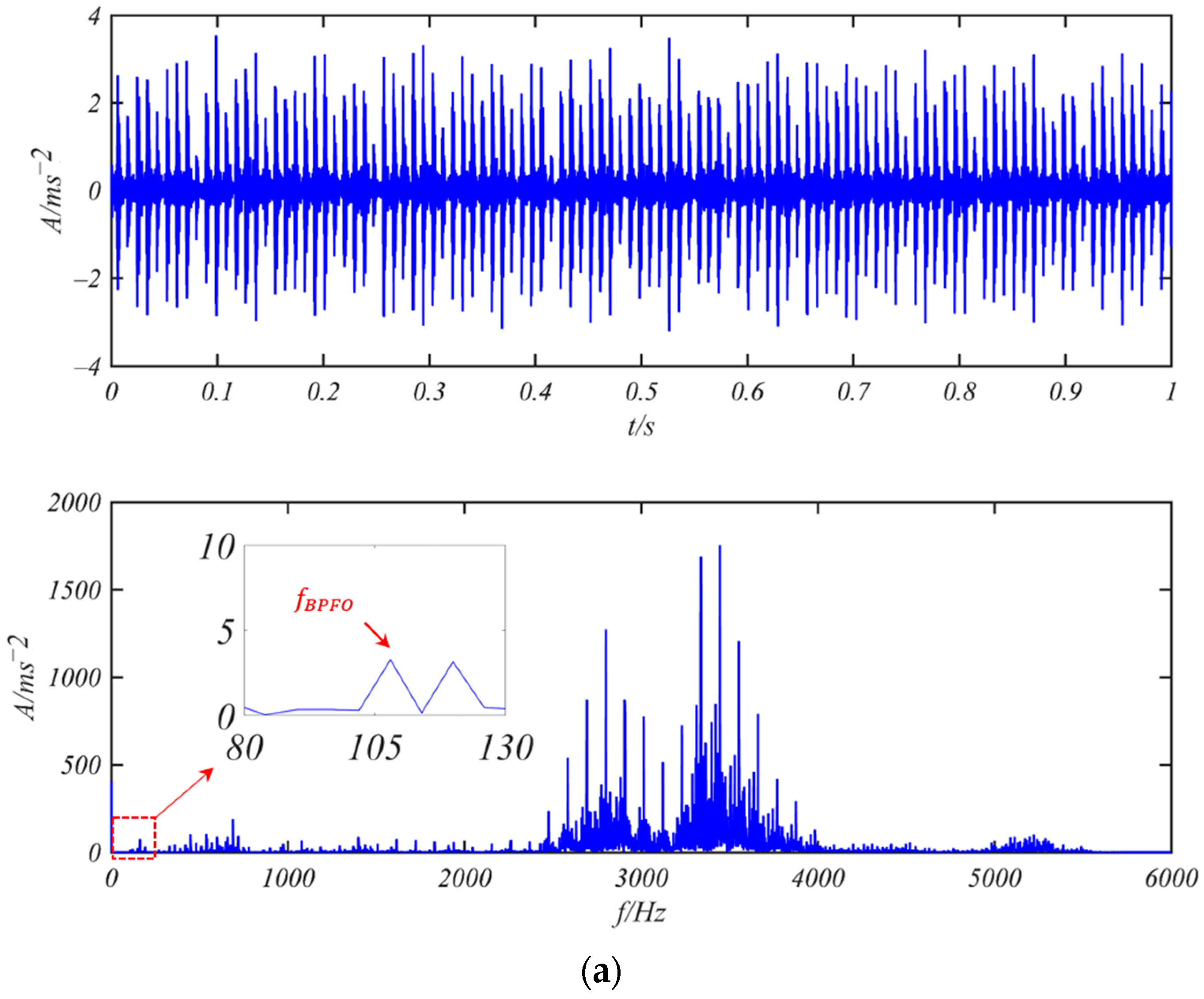
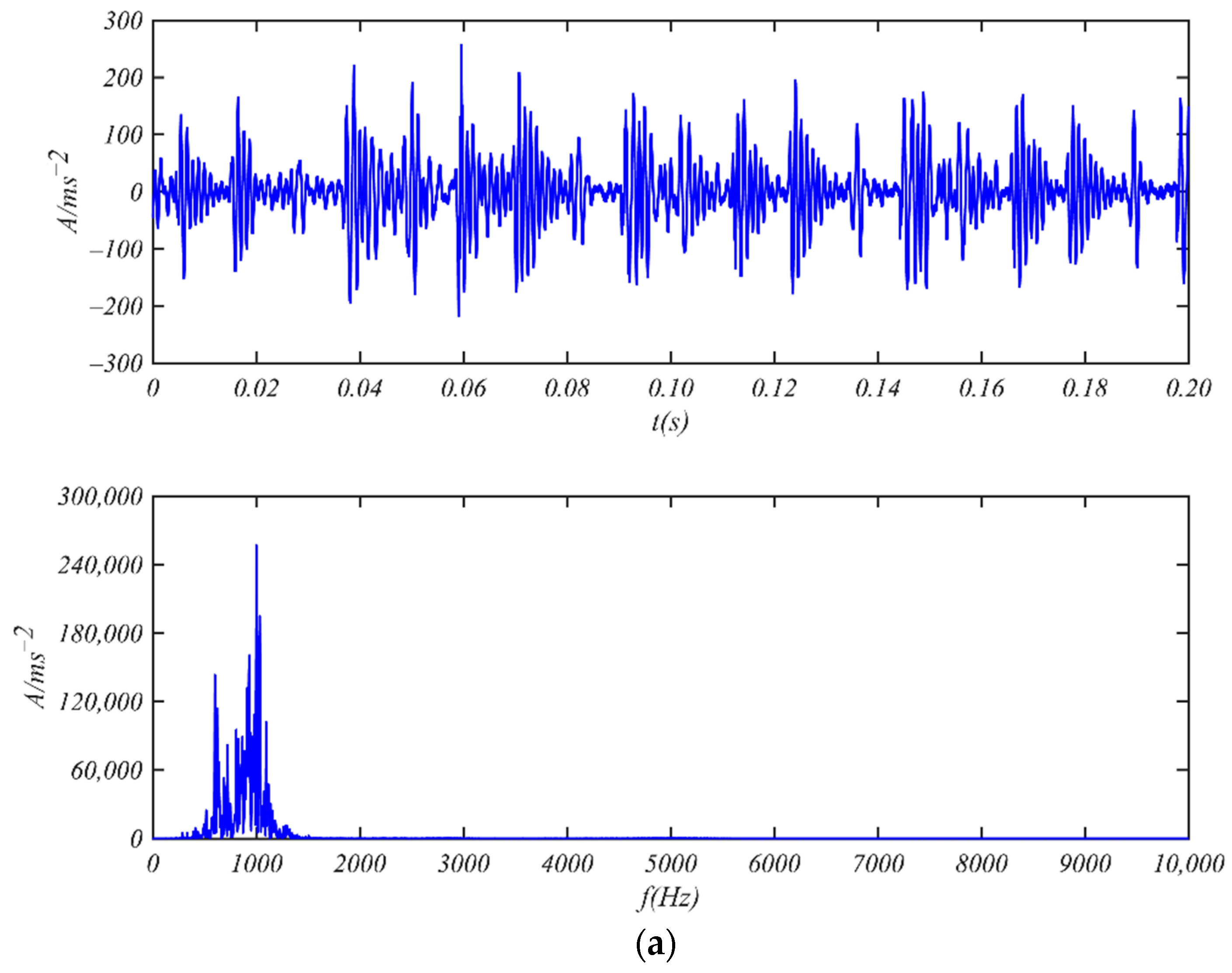
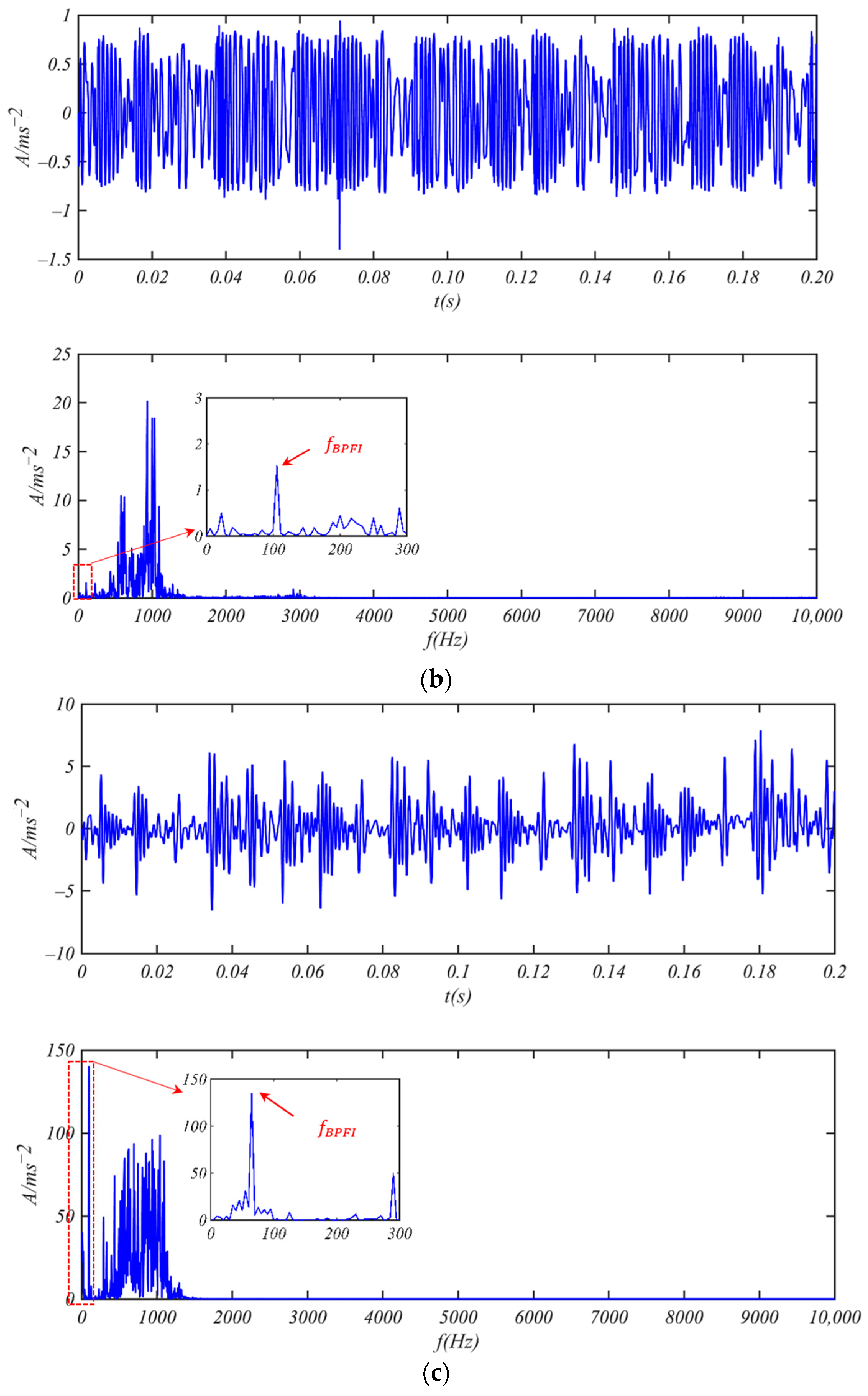
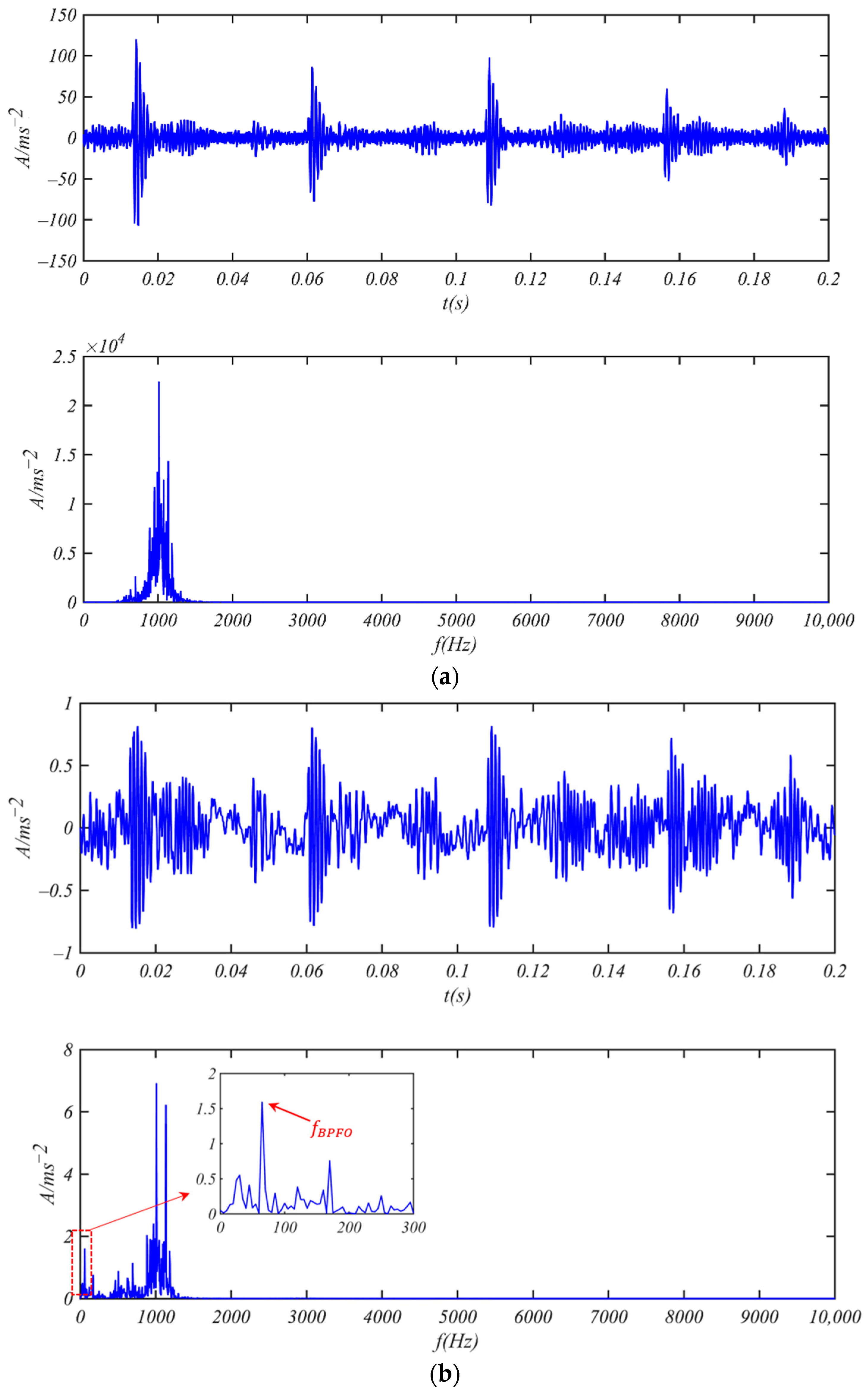
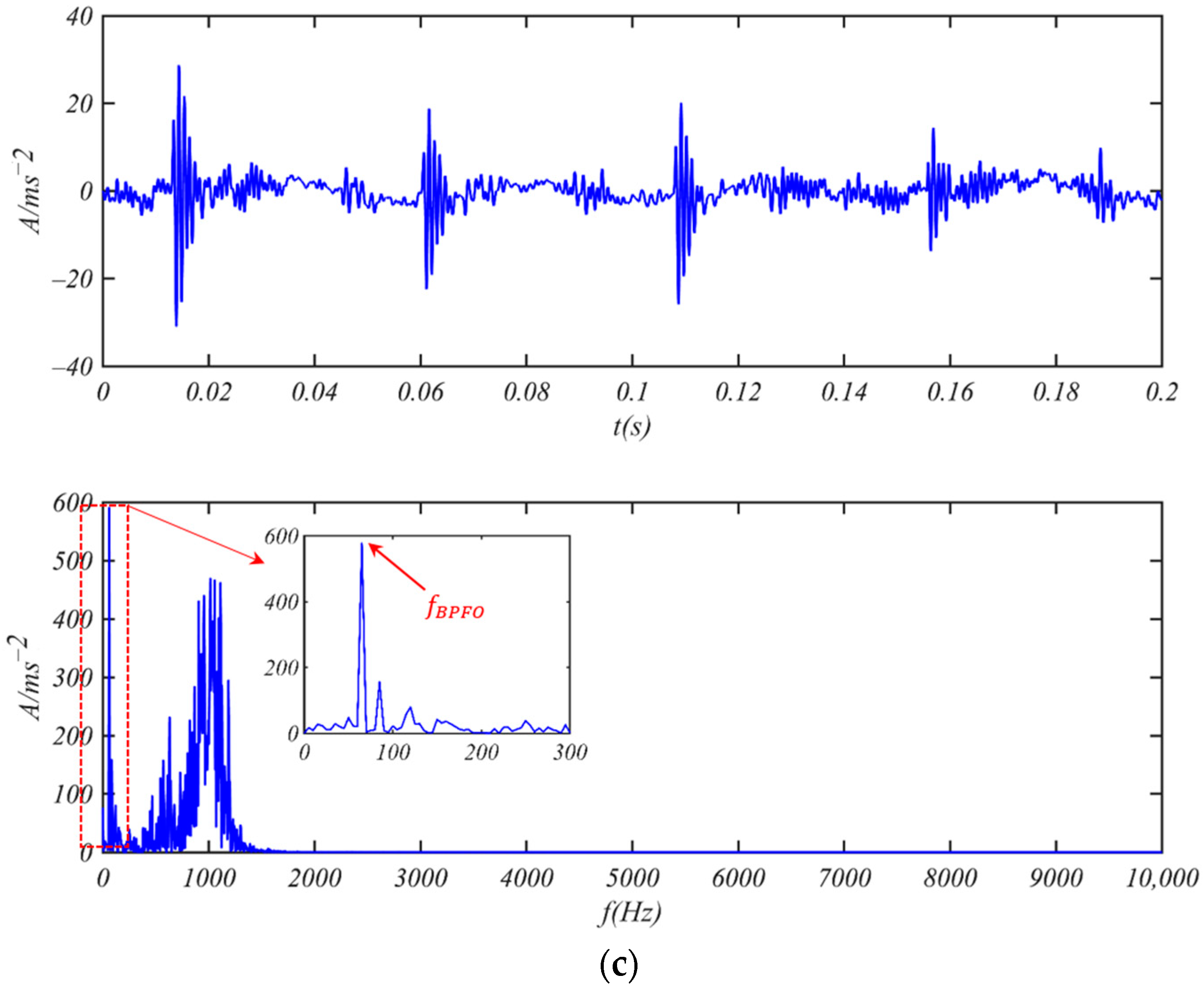
3.1. Fault Detection of Bearing SKF 6205-2RS
- (1)
- Bearing 6205-2RS JEM SKF with Weak Inner Ring Fault
- (2)
- Bearing 6205-2RS JEM SKF with Weak Outer Ring Fault
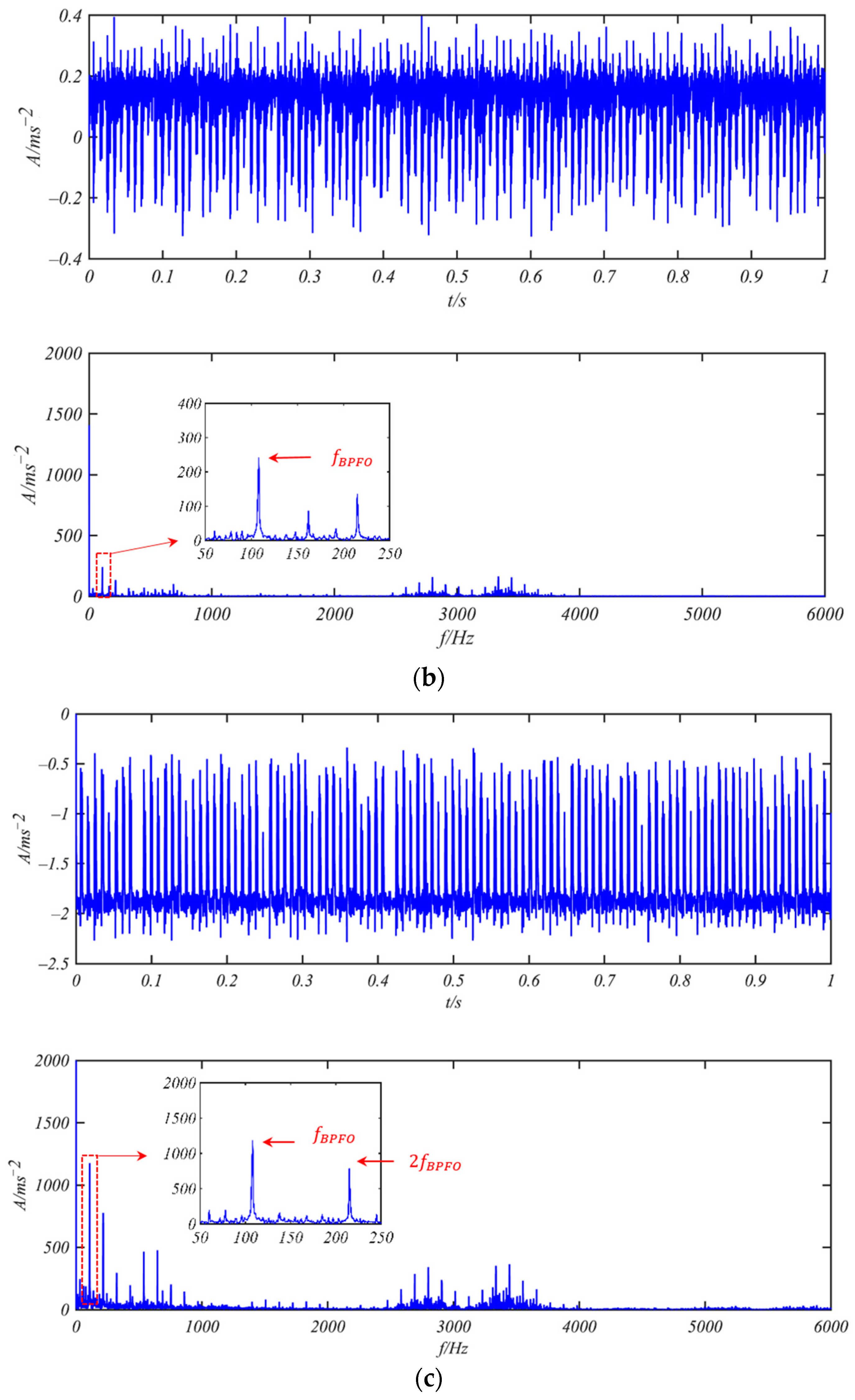
3.2. Weak Fault Detection Experiments of Bearing 6200-NR NSK
- (1)
- 6200-NR NSK Bearing with Weak Inner Ring Fault
- (2)
- 6200-NR NSK Bearing with Weak Outer Ring Fault
4. Conclusions
- In this paper, a coupled piecewise nonlinear asymmetric bistable stochastic resonance system is proposed, and the signal-to-noise ratio equation is derived.
- Using the ant colony intelligent algorithm to optimize parameters a and b, the signal-to-noise ratio of the PNABSR model can be 45% higher than that of the traditional CBSR model. It is easier for the PNABSR model to induce stochastic resonance.
- The test results show that the PNABSR model can observe the fault feature more clearly in practical applications. By comparing the experimental results of the CBSR and PNABSR models, it was found that the PNABSR system has outstanding advantages in terms of the amplitude amplification of weak fault characteristics and in improving the signal-to-noise ratio.
- The PNABSR model is suitable for weak fault extraction, especially under the conditions of strong background noise. Because the effectiveness of this model depends on parameter optimization, there is a certain time delay for real-time fault diagnosis.
- The extraction of the weak fault features is the first step of fault diagnosis. However, fault classification, fault degree evaluation, and prediction are also very important for the operation and maintenance of engineering equipment. We intend to discuss these problems in our future work.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benzi, R.; Sutera, A.; Vulpiani, A. The mechanism of stochastic resonance. J. Phys. A Math. Gen. 1981, 14, 453. [Google Scholar] [CrossRef]
- Chen, H.; Varshney, P.K.; Kay, S.M.; Michels, J.H. Theory of the Stochastic Resonance Effect in Signal Detection: Part I-Fixed Detectors. IEEE Trans. Signal Process. 2007, 55, 3172–3184. [Google Scholar] [CrossRef]
- Chen, H.; Varshney, L.R.; Varshney, P.K. Noise-enhanced information systems. Proc. IEEE 2014, 102, 1607–1621. [Google Scholar] [CrossRef] [Green Version]
- Fauve, S.; Heslot, F. Stochastic resonance in a bistable system. Phys. Lett. A 1983, 97, 5–7. [Google Scholar] [CrossRef]
- McNamara, B.; Wiesenfeld, K. Theory of stochastic resonance. Phys. Rev. Let. 1988, 60, 2626–2629. [Google Scholar] [CrossRef]
- Kang, Y.M.; Wang, M.; Xie, Y. Stochastic resonance in coupled weakly-damped bistable oscillators subjected to additive and multiplicative noises. Acta Mech. Sin. 2012, 28, 505–510. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics-A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Antoni, J.; Randall, R.B. Unsupervised noise cancellation for vibration signals: Part II-a novel frequency-domain algorithm. Mech. Syst. Signal Process. 2004, 18, 103–117. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, W. A new piecewise-linear stochastic resonance model. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 5209–5214. [Google Scholar]
- Qiao, Z.; Lei, Y.; Lin, J.; Jia, F. An adaptive unsaturated bistable stochastic resonance method and its application in mechanical fault diagnosis. Mech. Syst. Signal Process. 2017, 84, 731–746. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, D.; Zhang, T. Stochastic resonance in unsaturated piecewise nonlinear bistable system under multiplicative and additive noise for bearing fault diagnosis. IEEE Access 2019, 7, 58435–58448. [Google Scholar] [CrossRef]
- Tang, J.; Shi, B.; Bao, H.; Li, Z. A new method for weak fault feature extraction based on piecewise mixed stochastic resonance. Chin. J. Phys. 2020, 68, 87–99. [Google Scholar] [CrossRef]
- Zhao, S.; Shi, P.; Han, D. A novel mechanical fault signal feature extraction method based on unsaturated piecewise tri-stable stochastic resonance. Measurement 2021, 168, 108374. [Google Scholar] [CrossRef]
- Huang, X. Stochastic resonance in a piecewise bistable energy harvesting model driven by harmonic excitation and additive Gaussian white noise. Appl. Math. Model. 2021, 90, 505–526. [Google Scholar] [CrossRef]
- Xu, P.; Jin, Y. Stochastic resonance in an asymmetric tristable system driven by correlated noises. Appl. Math. Model. 2020, 77, 408–425. [Google Scholar] [CrossRef]
- Liu, X.; Liu, H.; Yang, J.; Litak, G.; Cheng, G.; Han, S. Improving the bearing fault diagnosis efficiency by the adaptive stochastic resonance in a new nonlinear system. Mech. Syst. Signal Process. 2017, 96, 58–76. [Google Scholar] [CrossRef]
- Leng, Y.G.; Leng, Y.S.; Wang, T.Y.; Guo, Y. Numerical analysis and engineering application of large parameter stochastic resonance. J. Sound Vib. 2006, 292, 788–801. [Google Scholar] [CrossRef]
- Cheng, W.; Xu, X.; Ding, Y.; Sun, K.; Li, Q.; Dong, L. An adaptive smooth unsaturated bistable stochastic resonance system and its application in rolling bearing fault diagnosis. Chin. J. Phys. 2020, 65, 629–641. [Google Scholar] [CrossRef]
- Casado-Pascual, J.; Gómez-Ordóñez, J.; Morillo, M. Stochastic resonance: Theory and numerics. Chaos Interdiscip. J. Nonlinear Sci. 2005, 15, 026115. [Google Scholar] [CrossRef]
- Di Paola, M.; Sofi, A. Approximate solution of the Fokker–Planck–Kolmogorov equation. Probabilistic Eng. Mech. 2002, 17, 369–384. [Google Scholar] [CrossRef]
- Wang, J.; He, Q.; Kong, F. An improved multiscale noise tuning of stochastic resonance for identifying multiple transient faults in rolling element bearings. J. Sound Vib. 2014, 333, 7401–7421. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.; Li, M.; Zhang, Y. A novel adaptive stochastic resonance method based on coupled bistable systems and its application in rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2019, 114, 128–145. [Google Scholar] [CrossRef]

| Inside Diameter (mm) | Outside Diameter (mm) | Width (mm) | Ball Diameter (mm) | Pitch Diameter (mm) | Ball Number |
|---|---|---|---|---|---|
| 25 | 52 | 15 | 7.938 | 39 | 9 |
| Inside Diameter (mm) | Outside Diameter (mm) | Width (mm) | Ball Diameter (mm) | Pitch Diameter (mm) | Ball Number |
|---|---|---|---|---|---|
| 10 | 30 | 9 | 5.5 | 20 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, L.; Xu, W. A New Piecewise Nonlinear Asymmetry Bistable Stochastic Resonance Model for Weak Fault Extraction. Machines 2022, 10, 373. https://doi.org/10.3390/machines10050373
Cui L, Xu W. A New Piecewise Nonlinear Asymmetry Bistable Stochastic Resonance Model for Weak Fault Extraction. Machines. 2022; 10(5):373. https://doi.org/10.3390/machines10050373
Chicago/Turabian StyleCui, Li, and Wuzhen Xu. 2022. "A New Piecewise Nonlinear Asymmetry Bistable Stochastic Resonance Model for Weak Fault Extraction" Machines 10, no. 5: 373. https://doi.org/10.3390/machines10050373
APA StyleCui, L., & Xu, W. (2022). A New Piecewise Nonlinear Asymmetry Bistable Stochastic Resonance Model for Weak Fault Extraction. Machines, 10(5), 373. https://doi.org/10.3390/machines10050373






