Reliability Assessment Method Based on Condition Information by Using Improved Proportional Covariate Model
Abstract
:1. Introduction
- It does not require the assumption that the independent variables and their errors conform to normal distribution. The application scope of the model is greatly expanded.
- Assuming that the degradation of equipment can be interpreted by a series of state characteristic parameters, the LRM can give the failure probability of the equipment. It increases the flexibility of the model application.
- The variables can be continuous variables, discrete variables, or dummy variables. Nor does it need to assume the existence of multivariate normal distribution between these variables. There is a complete set of test criteria for regression model parameter estimation.
2. Proportional Covariate Model and Logistic Regression Model
2.1. Proportional Covariate Model
- Polynomial function
- Power function
- Exponential functionwhere and are the function parameters that need to be estimated. The above functions can be used alone or combined. They can be estimated by linearization techniques referring to the literature [22].
2.2. Logistic Regression Model
3. The Improved Reliability Estimation Method
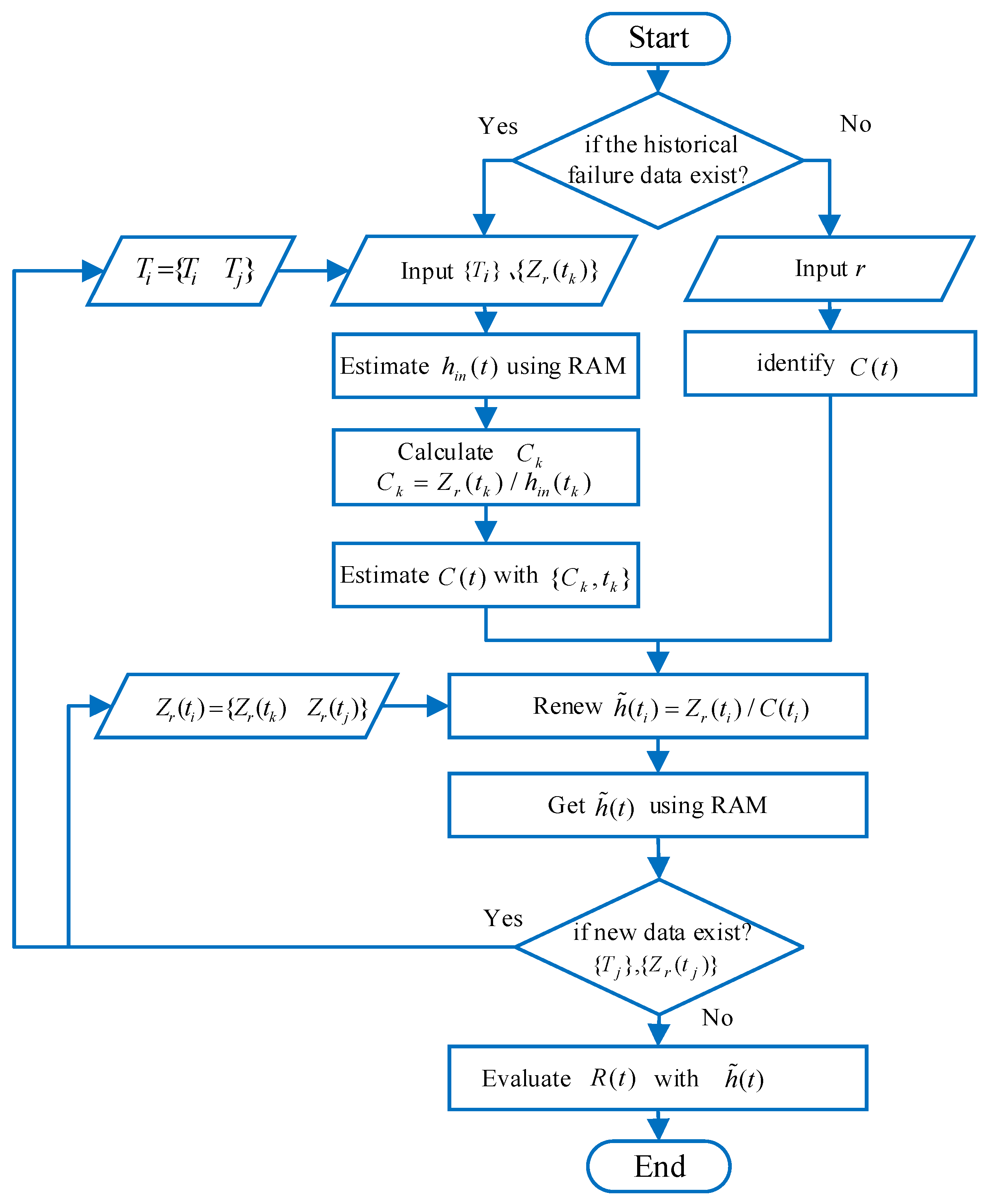
3.1. The PCM Reliability Estimation Method
- If the historical failure life data exist, the failure distribution parameters of the system are estimated to identify the system initial hazard function . Where is the number of failure sample.
- Calculate the discrete baseline covariate function using initial hazard function and covariates extracted from the condition monitoring signals.where is the number of conditional monitoring sample. Estimate the mathematical expression of the baseline covariate function by using the regression analysis method (RAM).
- If there are no historical failure life data, is identified by the linear proportional factor r between the covariate and hazard rate based on the experience of the operator or other supplementary information.
- Update the system hazard function by adding some new covariates and . is the number of the new conditional monitoring samples.Estimate the mathematical expression of the system hazard function by using RAM.
- Repeat the above process to update and if there are new failure data and condition data are obtained.
- Calculate the reliability function of the system through .
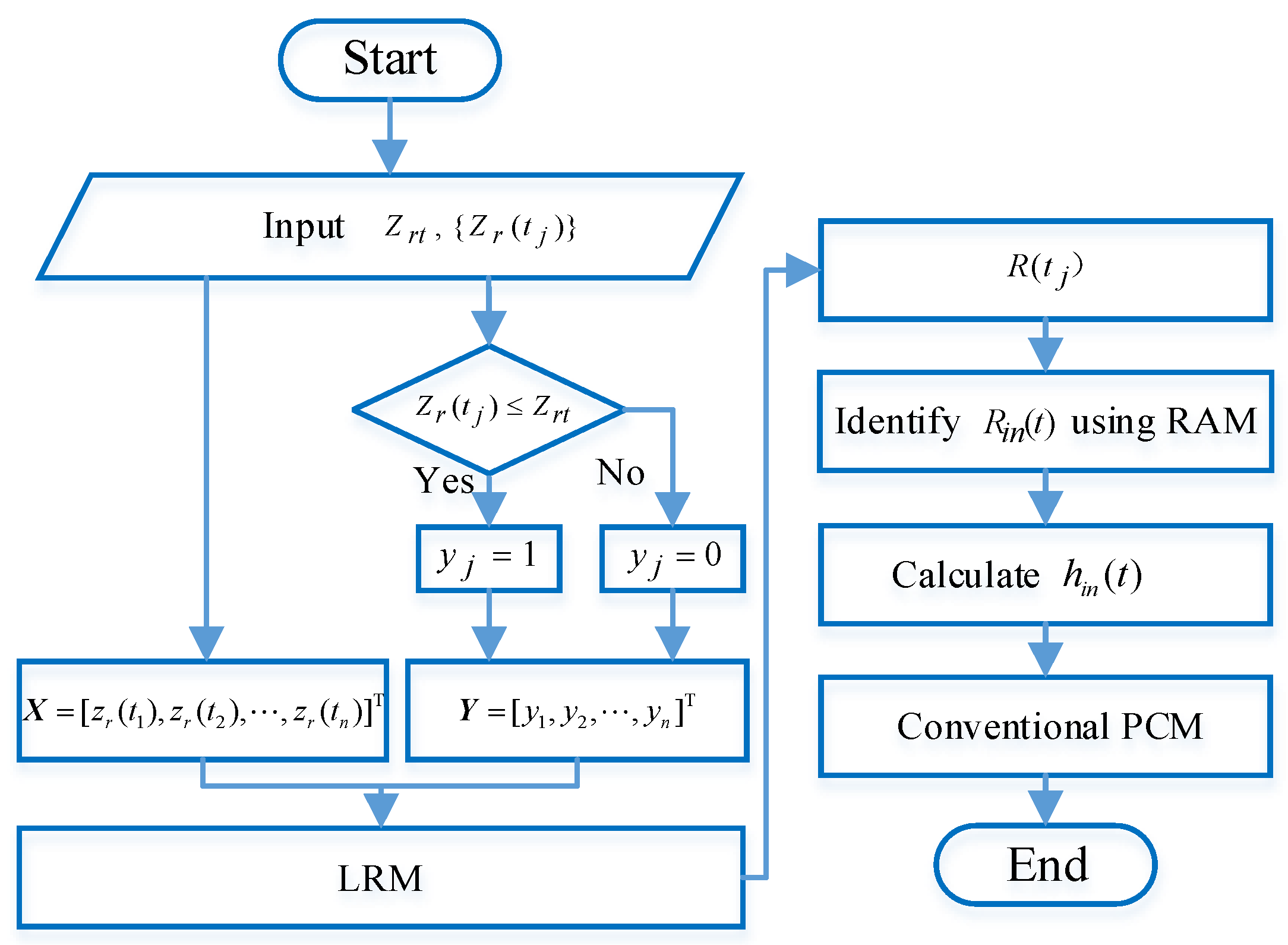
3.2. The IPCM Reliability Estimation Method
- (1)
- Input and , is the failure threshold of the response covariate and is the response covariate dataset extracted from the monitoring data;
- (2)
- Identify the input vector and the output vector of LRM, and , if , (under the normal state), otherwise ;
- (3)
- Estimate the parameters of LRM and calculate the concrete reliability corresponding to by using Equation (10);
- (4)
- Identify the expression of by using the regression analysis method (RAM).
- (5)
- Calculate the hazard function by equation and implement the remaining reliability assessment procedures (4)~(6) of conventional PCM mentioned in Section 3.1, where is the failure probability density function(PDF).
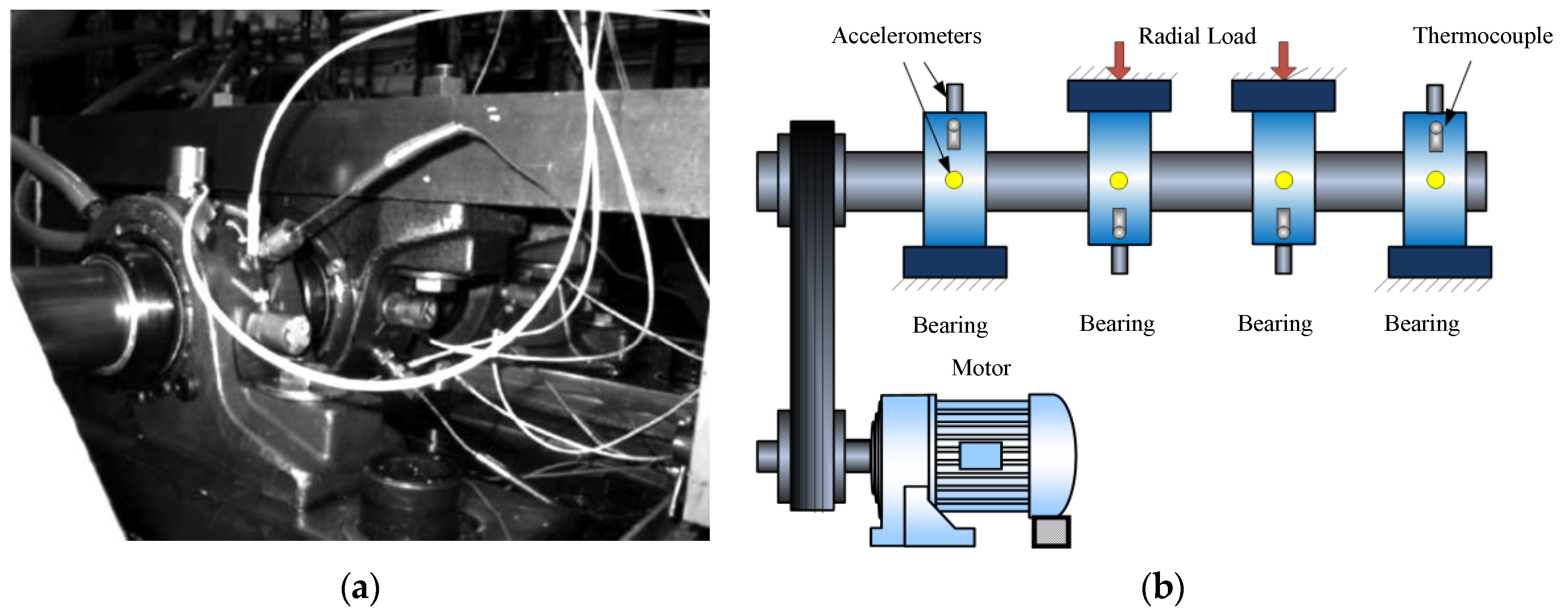
4. Case Study of Aero Engine Rolling Bearing
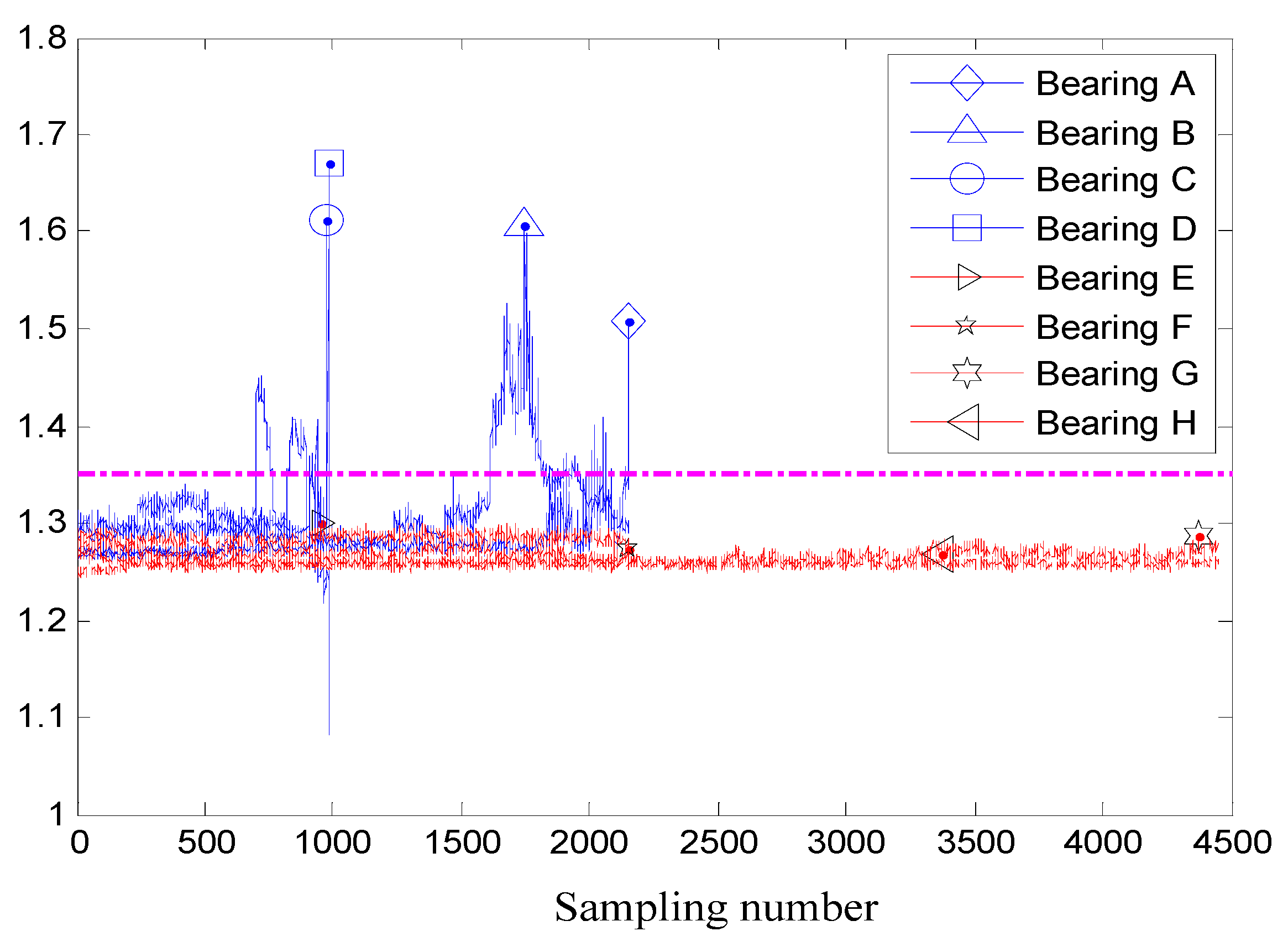
4.1. Data Description
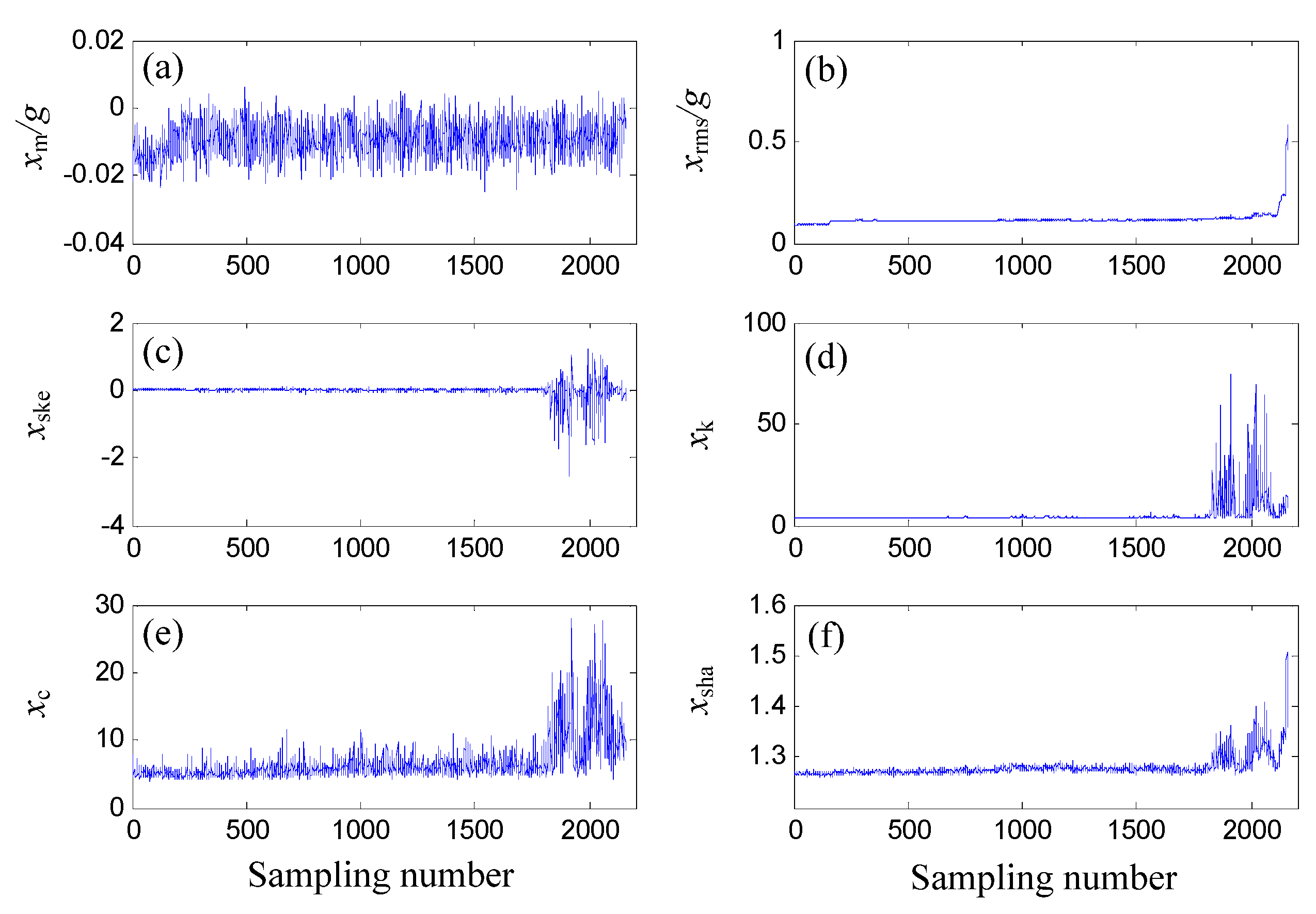
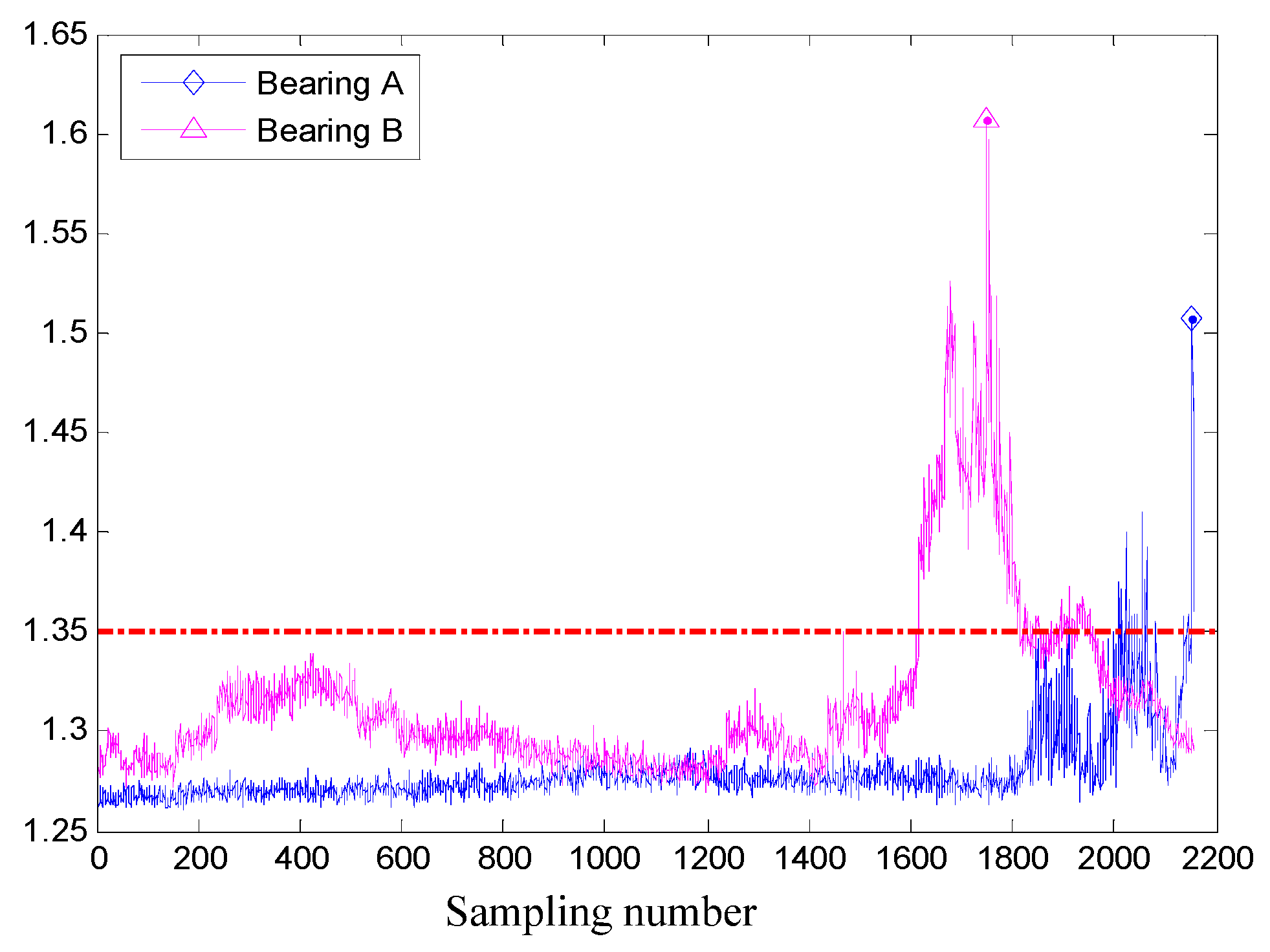
4.2. Data Analysis and Covariate Selection
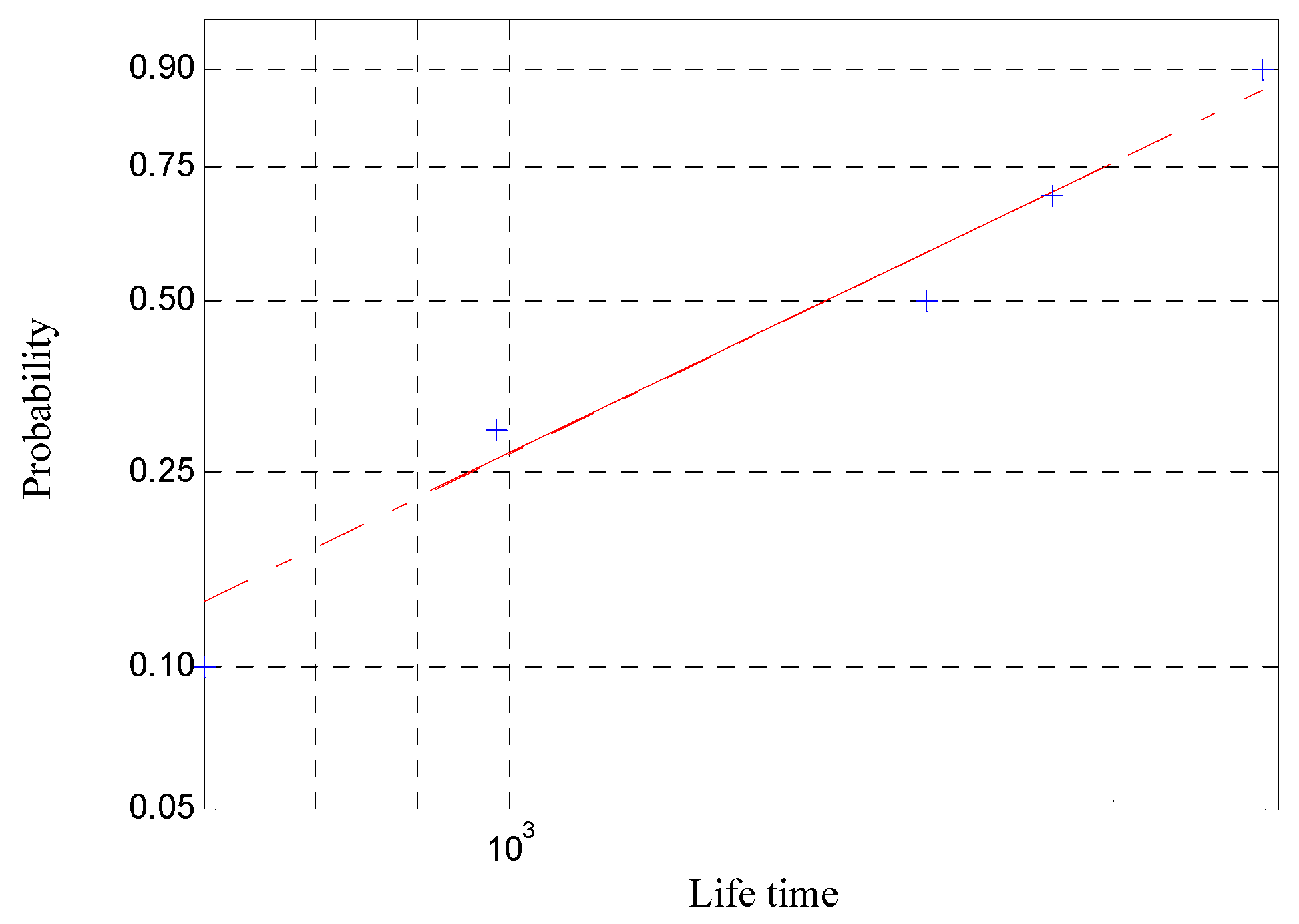
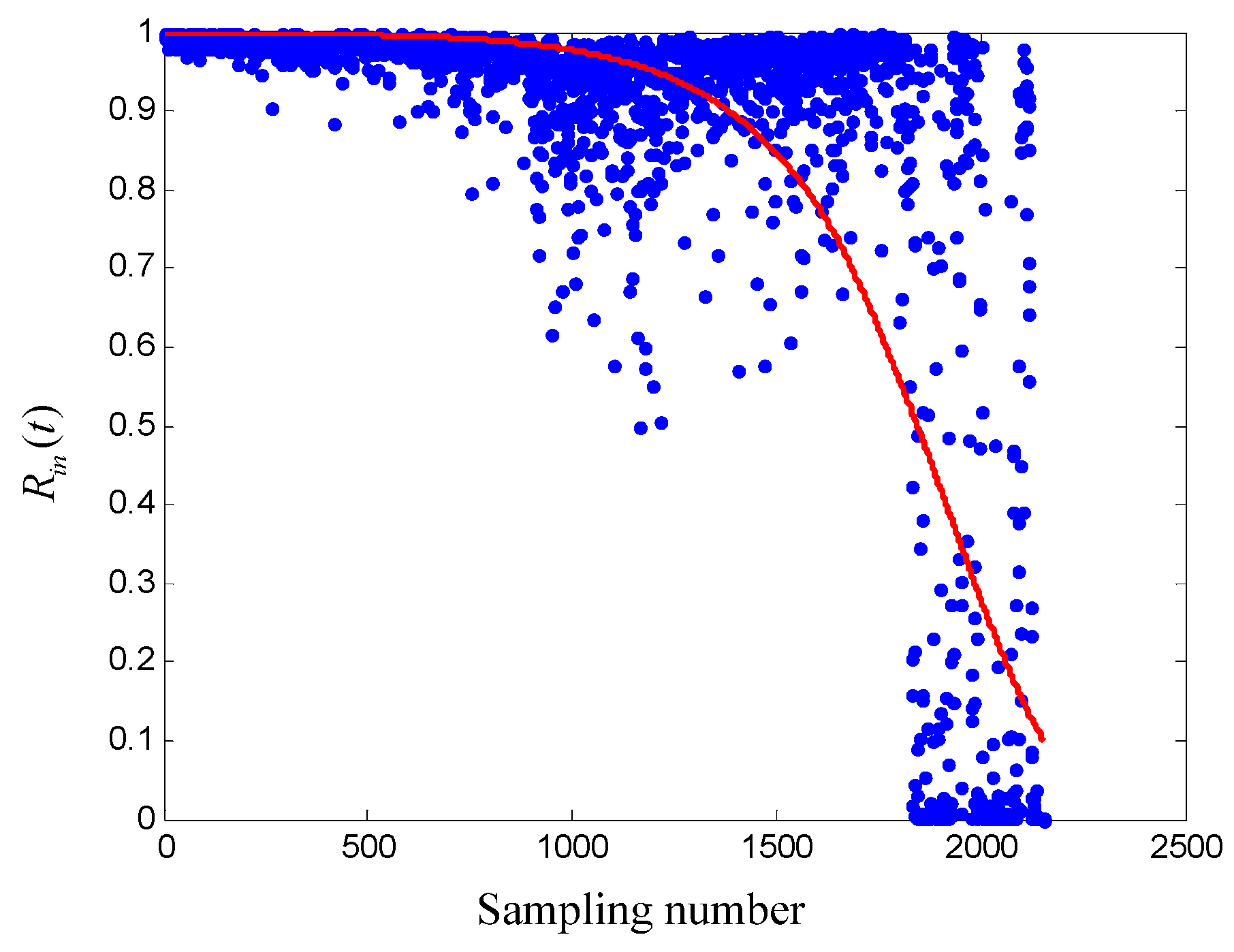
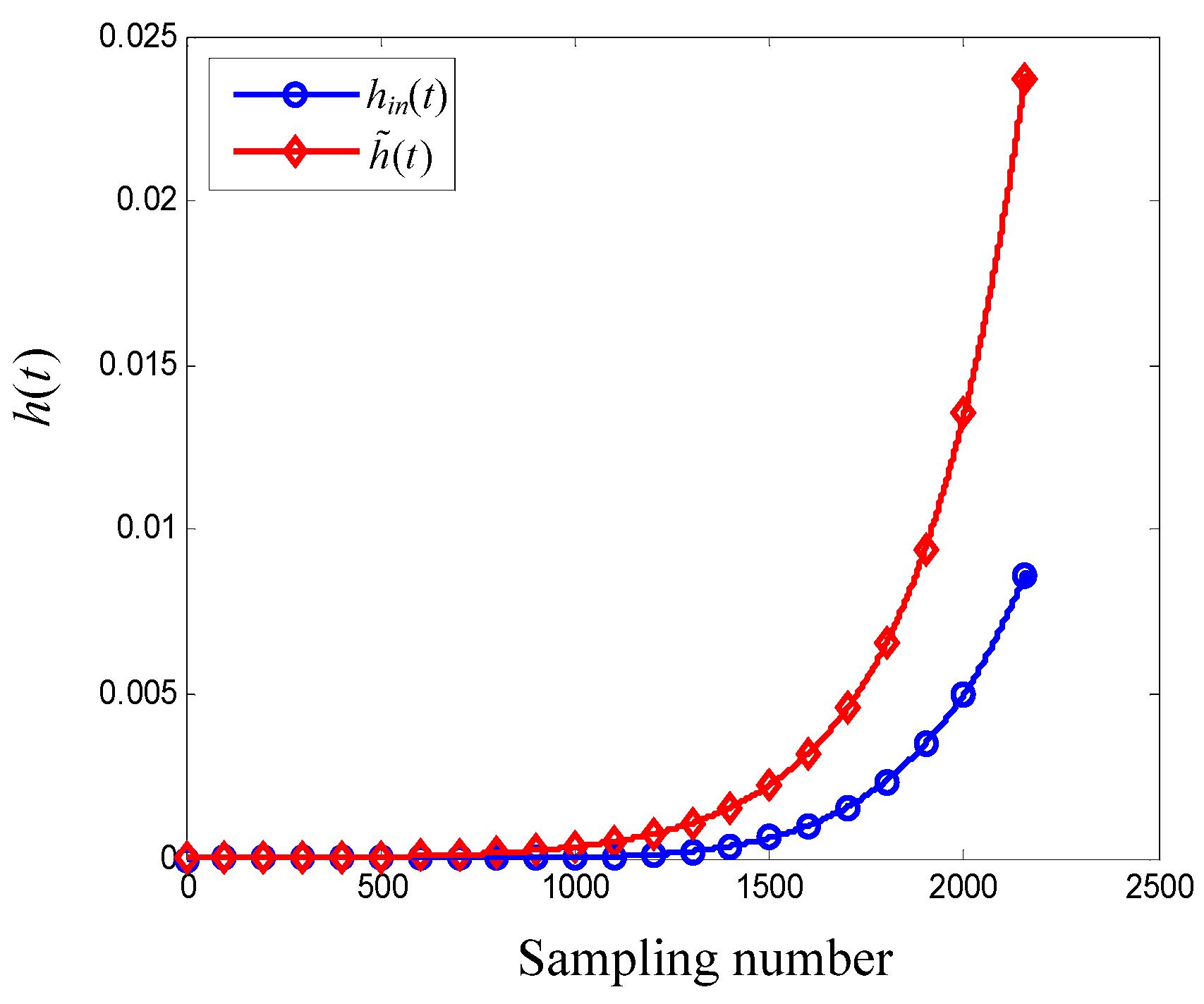
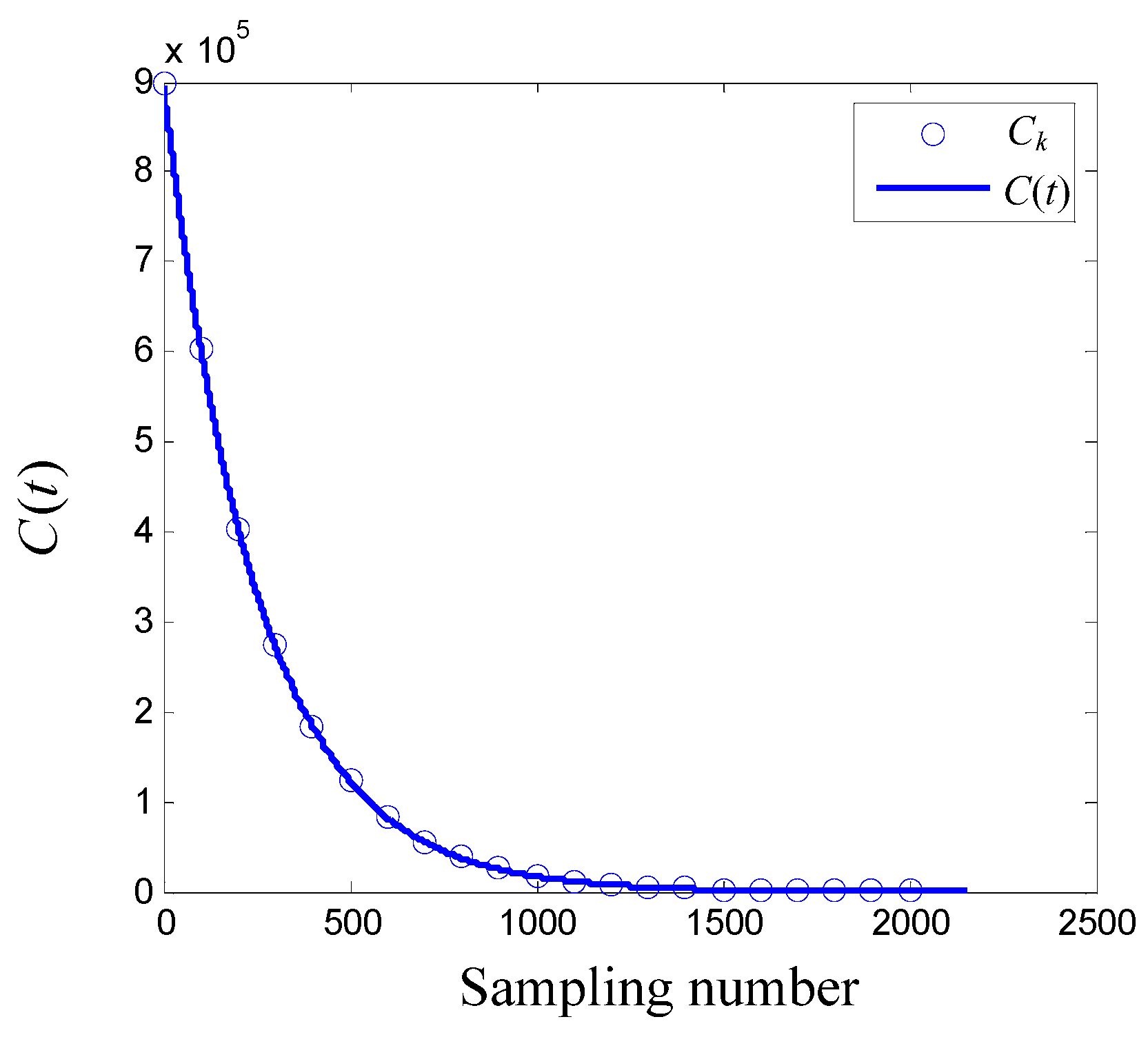
4.3. Reliability Estimation Based on Conventional PCM
4.4. Reliability Estimation Based on IPCM
5. Conclusions
- (1)
- The LRM-based estimation method only needs acquiring the equipment’s response covariate vectors and their corresponding states without requiring specific mechanical knowledge or making many assumptions about the PDFs of variables. It passes the process of the proportional factor identification between covariate and hazard rate so that it can avoid the influence of the subjective deviation.
- (2)
- The salient features extracted and selected from conditional monitoring data during the equipment operation process are more suitable for the equipment degradation evaluation. The assessing accuracy of IPCM is superior to conventional PCM for a small failure sample, which verifies the plausibility and effectiveness of the proposed method. The method reveals the equipment performance from the conditional monitoring data and provides a new method for reliability assessment under sparse or zero failure data conditions.
- (3)
- This paper only studies the evaluation method and results of IPCM in the case of univariate. Some suggestions are given for the multivariable. The specific operation process and effectiveness need to be tested in future work.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cerrada, M.; Sánchez, R.; Li, C.; Pacheco, F.; Cabrera, D.; de Oliveira, J.V.; Vásquez, R.E. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar] [CrossRef]
- Li, H.; Zuo, H.; Su, Y.; Xu, J.; Yin, Y. Study on segmented distribution for reliability evaluation. Chin. J. Aeronaut. 2017, 30, 310–329. [Google Scholar] [CrossRef]
- Baussaron, J.; Mihaela, B.; Léo, G.; Fabrice, G.; Paul, S. Reliability assessment based on degradation measurements: How to compare some models? Reliab. Eng. Syst. Saf. 2014, 131, 236–241. [Google Scholar] [CrossRef] [Green Version]
- Bhuyan, P.; Sengupta, D. Estimation of reliability with semi-parametric modeling of degradation. Comput. Stat. Data Anal. 2017, 115, 172–185. [Google Scholar] [CrossRef]
- O’Connor, P.D. Commentary: Reliability-past, present, and future. IEEE Trans. Reliab. 2000, 49, 335–341. [Google Scholar] [CrossRef]
- Zio, E. Reliability engineering: Old problems and new challenges. Reliab. Eng. Syst. Saf. 2009, 94, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Li, N.; Xu, P.; Lei, Y.; Cai, X.; Kong, D. A self-data-driven method for remaining useful life prediction of wind turbines considering continuously varying speeds. Mech. Syst. Signal Process. 2022, 165, 108315. [Google Scholar] [CrossRef]
- Yan, T.; Lei, Y.; Li, N.; Wang, B.; Wang, W. Degradation Modeling and Remaining Useful Life Prediction for Dependent Competing Failure Processes. Reliab. Eng. Syst. Saf. 2021, 212, 107638. [Google Scholar] [CrossRef]
- Chen, B.; Chen, X.; Li, B.; He, Z.; Cao, H.; Cai, G. Reliability estimation for cutting tools based on logistic regression model using vibration signals. Mech. Syst. Signal Process. 2011, 25, 2526–2537. [Google Scholar] [CrossRef]
- Sy, J.P.; Taylor, J.M. Estimation in a Cox proportional hazards cure model. Biometrics 2000, 56, 227–236. [Google Scholar] [CrossRef]
- Kumar, D.; Klefsjö, B. Proportional hazards model: A review. Reliab. Eng. Syst. Saf. 1994, 44, 177–188. [Google Scholar] [CrossRef]
- Lin, D.; Banjevic, D.; Jardine, A.K. Using principal components in a proportional hazards model with applications in condition-based maintenance. J. Oper. Res. Soc. 2006, 57, 910–919. [Google Scholar] [CrossRef]
- Zhang, Q.; Hua, C.; Xu, G. A mixture Weibull proportional hazard model for mechanical system failure prediction utilising lifetime and monitoring data. Mech. Syst. Signal Process. 2014, 43, 103–112. [Google Scholar] [CrossRef]
- Banjevic, D.; Jardine, A.; Makis, V.; Ennis, M. A control-limit policy and software for condition-based maintenance optimization. INFOR Inf. Syst. Oper. Res. 2001, 39, 32–50. [Google Scholar] [CrossRef]
- Ding, F.; He, Z. Cutting tool wear monitoring for reliability analysis using proportional hazards model. Int. J. Adv. Manuf. Technol. 2011, 57, 565–574. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, L.; Mathew, J.; Wang, W.; Zhang, S. Mechanical systems hazard estimation using condition monitoring. Mech. Syst. Signal Process. 2006, 20, 1189–1201. [Google Scholar] [CrossRef]
- Cai, G.; Chen, X.; Li, B.; Chen, B.; He, Z. Operation reliability assessment for cutting tools by applying a proportional covariate model to condition monitoring information. Sensors 2012, 12, 12964–12987. [Google Scholar] [CrossRef] [Green Version]
- Rabbani, M.; Manavizadeh, N.; Balali, S. A stochastic model for indirect condition monitoring using Proportional Covariate model. IJE Trans. A Basics 2008, 21, 45–56. [Google Scholar]
- Yan, J.; Lee, J. Degradation assessment and fault modes classification using logistic regression. J. Manuf. Sci. Eng. 2005, 127, 912–914. [Google Scholar] [CrossRef]
- Liao, H.; Zhao, W.; Guo, H. Predicting remaining useful life of an individual unit using proportional hazards model and logistic regression model. In Proceedings of the RAMS’06 Annual Reliability and Maintainability Symposium, Newport Beach, CA, USA, 23–26 January 2006; pp. 127–132. [Google Scholar]
- Wang, F.; Wang, B.; Dun, B.; Chen, X.; Yan, D.; Zhu, H. Remaining life prediction of rolling bearing based on PCA and improved logistic regression model. J. Vibroeng. 2016, 18, 5192–5203. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Vining, G.G.; Robinson, T.J. Generalized Linear Models: With Applications in Engineering and the Sciences; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 0470556978. [Google Scholar]
- Menard, S. Applied Logistic Regression Analysis; Sage: Thousand Oaks, CA, USA, 2002; ISBN 0761922083. [Google Scholar]
- Xuewen, M.; Cong, N.; Yun, Y.; Lei, H.; Jie, H. Grade-lfe prognostic model of aircraft engine bearing. Trans. Nanjing Univ. Aeronaut. Astronaut. 2012, 29, 171–178. [Google Scholar]
- Lee, J.; Qiu, H.; Yu, G.; Lin, J. Bearing Data Set’, IMS; University of Cincinnati: Cincinnati, OH, USA, 2007. [Google Scholar]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Robust performance degradation assessment methods for enhanced rolling element bearing prognostics. Adv. Eng. Inform. 2003, 17, 127–140. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; Zuo, M.J.; He, Z. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
- He, Q.; Ding, X. Sparse representation based on local time–frequency template matching for bearing transient fault feature extraction. J. Sound Vib. 2016, 370, 424–443. [Google Scholar] [CrossRef]
- Xue, X.; Zhou, J. A hybrid fault diagnosis approach based on mixed-domain state features for rotating machinery. ISA Trans. 2017, 66, 284–295. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y.; Hu, Q. Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAs. Mech. Syst. Signal Process. 2007, 21, 2280–2294. [Google Scholar] [CrossRef]
- Gorjian, N.; Ma, L.; Mittinty, M.; Yarlagadda, P.; Sun, Y. A review on degradation models in reliability analysis. In Engineering asset Lifecycle Management; Springer: Berlin/Heidelberg, Germany, 2010; pp. 369–384. [Google Scholar]
- Jiang, R.; Jardine, A.K. Health state evaluation of an item: A general framework and graphical representation. Reliab. Eng. Syst. Saf. 2008, 93, 89–99. [Google Scholar] [CrossRef]
- Li, Z.; He, Z.; Zi, Y.; Chen, X. Bearing condition monitoring based on shock pulse method and improved redundant lifting scheme. Math. Comput. Simul. 2008, 79, 318–338. [Google Scholar]
- Gebraeel, N.Z.; Lawley, M.A. A neural network degradation model for computing and updating residual life distributions. IEEE Trans. Autom. Sci. Eng. 2008, 5, 154–163. [Google Scholar] [CrossRef]
- Jiang, R. Optimization of alarm threshold and sequential inspection scheme. Reliab. Eng. Syst. Saf. 2010, 95, 208–215. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, X.; Zhang, W. Remaining useful life prediction based on health index similarity. Reliab. Eng. Syst. Saf. 2019, 185, 502–510. [Google Scholar] [CrossRef]
- Chen, B.; Shen, B.; Zhang, F.; Xiao, W.; Chen, F.; Tian, H.; Chen, S. Operation reliability evaluation of cutting tools based on singular value decomposition transform and support vector space. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2019, 233, 175–185. [Google Scholar] [CrossRef]
- Thangavel, K.; Pethalakshmi, A. Dimensionality reduction based on rough set theory: A review. Appl. Soft Comput. 2009, 9, 1–12. [Google Scholar] [CrossRef]


| Bearing Model | Pitch Diameter | Roller Diameter | Number of Rolling Element | Tapered Contact Angle |
|---|---|---|---|---|
| ZA-2115 | 2.815 in | 0.331 in | 16 | 15.17° |
| No. | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| similar relationships | xm | xrms,xra,xstd,xp | xske | xk | xc,xi,xmar | xsha |
| Model | ||
|---|---|---|
| Parameters | a = 7.809 × 10−27 b = 7.212 | a = 2.354 × 10−6 b = 0.003822 |
| Goodness of fit: | ||
| SSE: | 7.989 × 10−6 | 2.922 × 10−6 |
| R-square: | 0.999 | 0.9996 |
| RMSE: | 0.999 | 0.9996 |
| Adjusted R-square: | 6.091 × 10−5 | 3.684 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, B.; Chen, Z.; Chen, F.; Xiao, W.; Xiao, N.; Fu, W.; Li, G. Reliability Assessment Method Based on Condition Information by Using Improved Proportional Covariate Model. Machines 2022, 10, 337. https://doi.org/10.3390/machines10050337
Chen B, Chen Z, Chen F, Xiao W, Xiao N, Fu W, Li G. Reliability Assessment Method Based on Condition Information by Using Improved Proportional Covariate Model. Machines. 2022; 10(5):337. https://doi.org/10.3390/machines10050337
Chicago/Turabian StyleChen, Baojia, Zhengkun Chen, Fafa Chen, Wenrong Xiao, Nengqi Xiao, Wenlong Fu, and Gongfa Li. 2022. "Reliability Assessment Method Based on Condition Information by Using Improved Proportional Covariate Model" Machines 10, no. 5: 337. https://doi.org/10.3390/machines10050337
APA StyleChen, B., Chen, Z., Chen, F., Xiao, W., Xiao, N., Fu, W., & Li, G. (2022). Reliability Assessment Method Based on Condition Information by Using Improved Proportional Covariate Model. Machines, 10(5), 337. https://doi.org/10.3390/machines10050337






