Improved DBSCAN Spindle Bearing Condition Monitoring Method Based on Kurtosis and Sample Entropy
Abstract
:1. Introduction
2. Algorithm Design
2.1. Feature Extraction Method Based on Kurtosis and Sample Entropy
2.1.1. Kurtosis
2.1.2. Sample Entropy
- (1)
- Given a sequence of m-dimensional vectorswhere .
- (2)
- As indicated in Equation (3), we can define the maximum difference between the elements corresponding to the vector and vector as the distance z between them, that is:where, is the distance between vector and vector .
- (3)
- Expand the value of m, and repeat steps: (1)~(3), the result is shown in Equation (6):
- (4)
- Therefore, the sample entropy of the sequence is calculated as shown in Equation (7):
2.2. IDBSCAN Clustering Algorithm
2.2.1. The List about Parameter Eps and MinPts
- (1)
- Create a list of Eps files
- For dataset Y, calculate the Euler distance distribution matrix , as shown in Equation (10):where is a real symmetric matrix, n is the number of sampling points, is the distance between the i-th sample point and the j-th sample point in the data set Y.
- Based on the matrix , n column vectors can be obtained by arranging the elements of each row in ascending order, recorded as: . According to the closeness of the relationship between the sample points, the first column is the Euclidean distance from the sample point to itself, which is all zero. The Y of the elements of the Kth column constitutes the K-nearest neighbor distance vector for all data points.
- Calculate the average value of each column element of the matrix . A vector of K-averaged nearest-neighbor distances is obtained, which is then noted as the candidate set of Eps. The calculation for the vector is shown in Equation (11):
- (2)
- Create a list of MinPts files
- (3)
- Parametric analysis
2.2.2. The Procedure for Identifying Parameters
- (1)
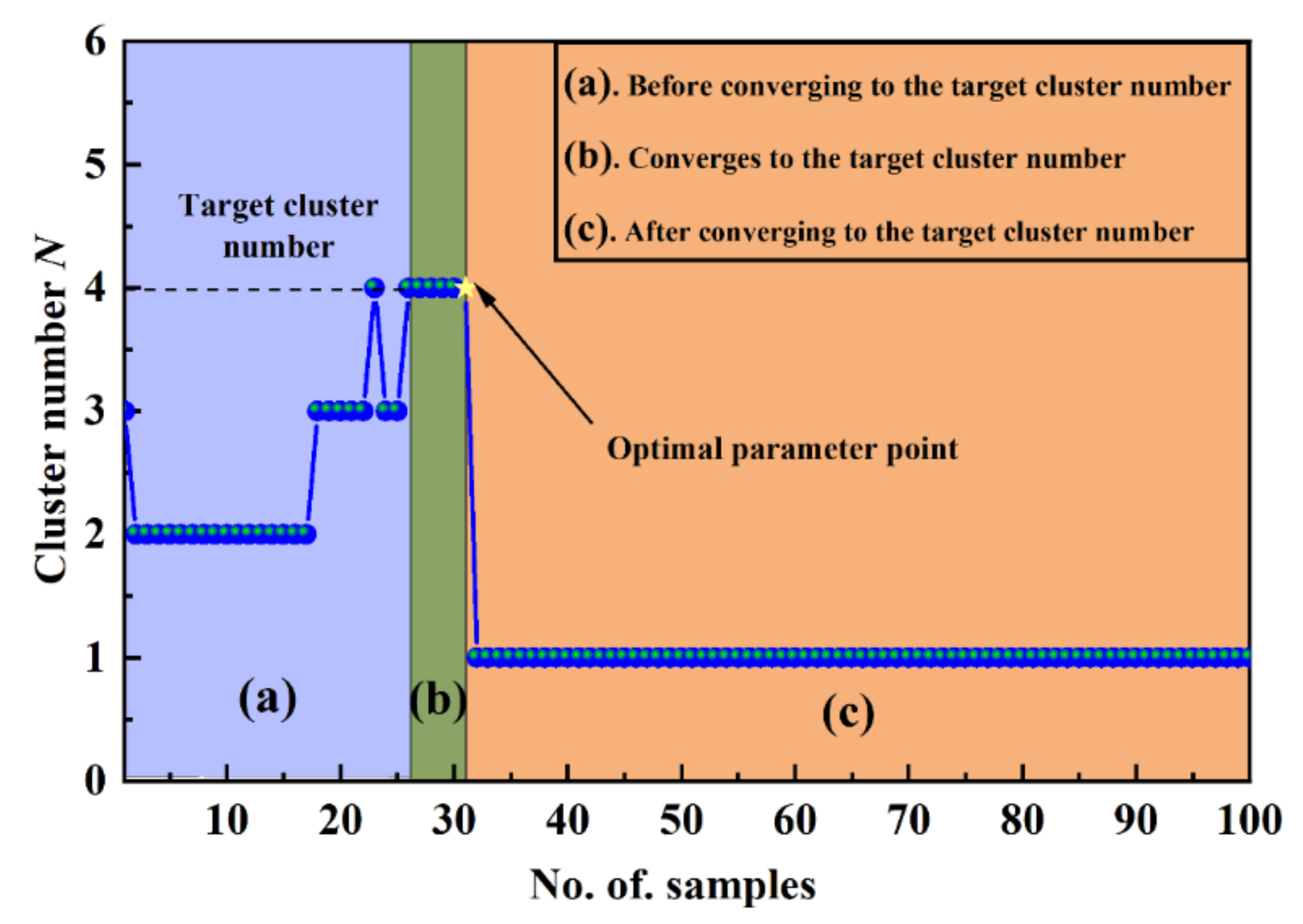
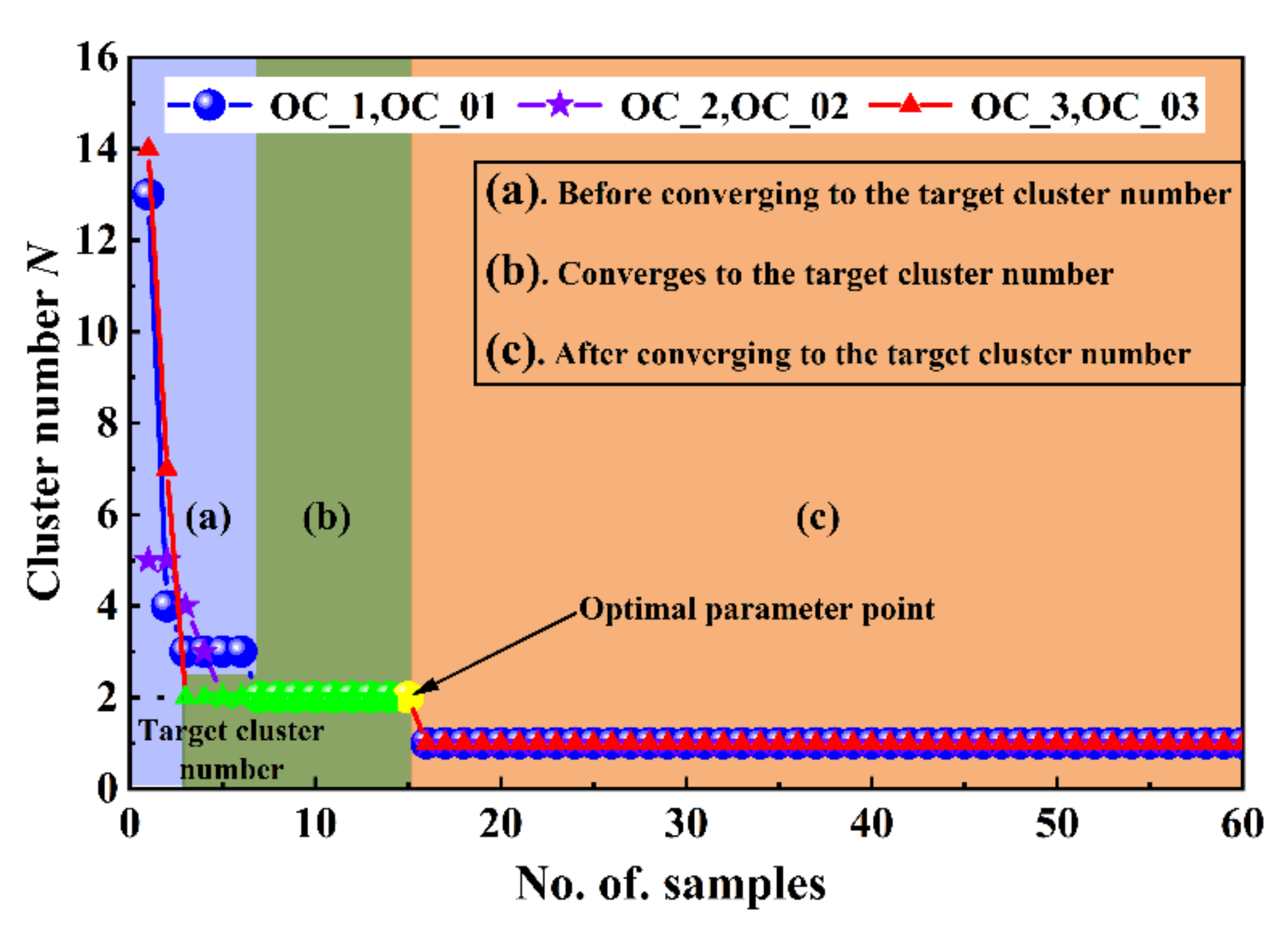
- The DBSCAN clustering analysis is performed sequentially on the already obtained Eps and MinPts parameter values, and the obtained clustering results are analyzed to obtain the corresponding number of clusters, noted as CNK (K = 1,2…,n). If the CNK does not reach the target number of clusters N, continue the clustering analysis by changing the parameter values.
- (2)
- The clustering result is optimal when the number of clusters generated converges continuously to the target number of clusters, and therefore the corresponding optimal Eps and MinPts parameters can be obtained.
- (3)
- The outliers of each cluster shape are recognized, the form of the cluster corresponding to each state is determined, and the classification effect error is validated in the cluster analysis findings of the optimum Eps and MinPts parameters.
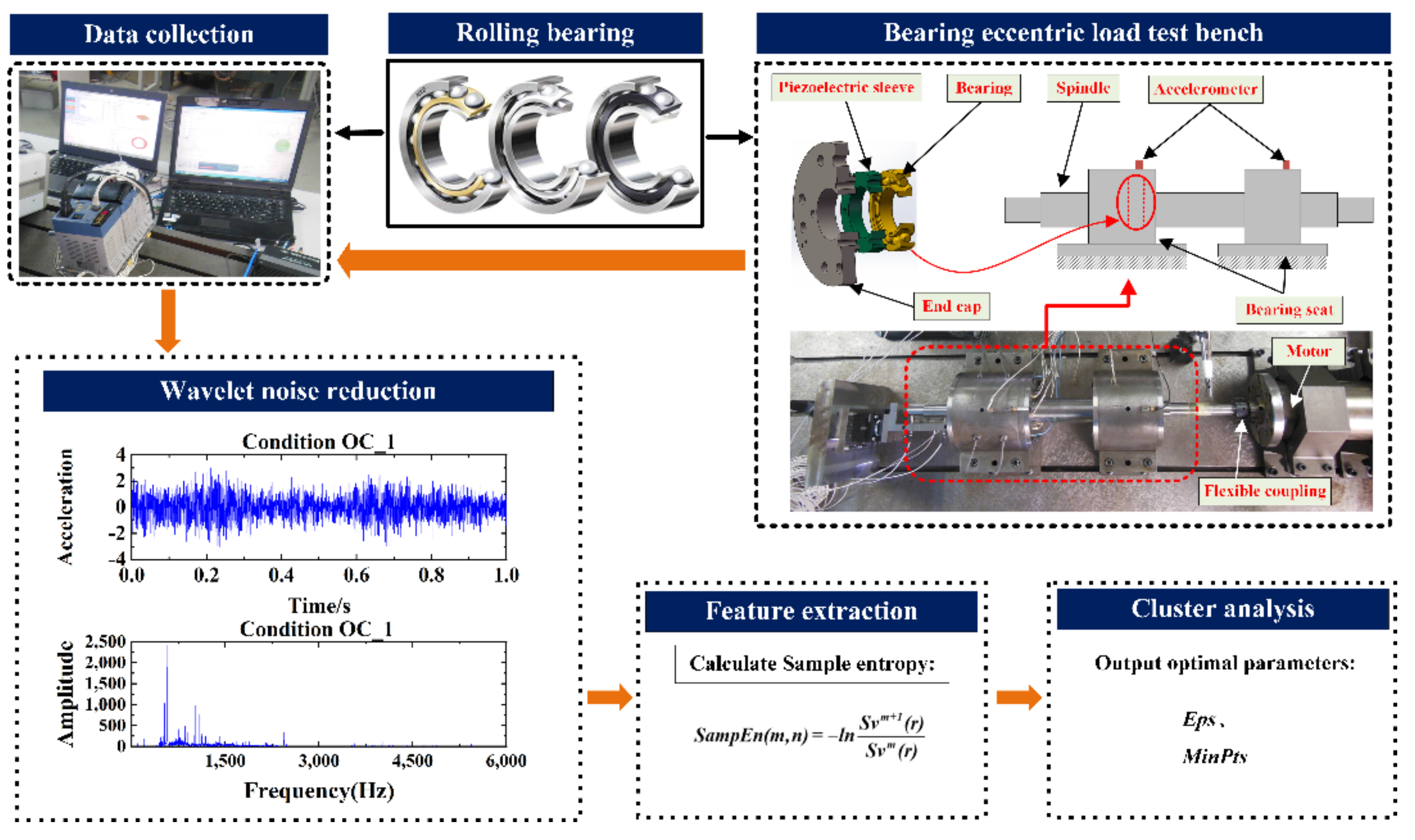
- It was built to collect vibration signals from rolling bearings under various deflection conditions.
- Wavelet noise reduction is used to preprocess the original vibration signal before extracting kurtosis and sample entropy eigenvalues and building the Eigenvector dataset from the original vibration signal.
- IDBSCAN clustering analyses are parameter-seeking, with the optimal parameters MinPts and Eps selected to utilize in the clustering analysis in the final monitoring results.
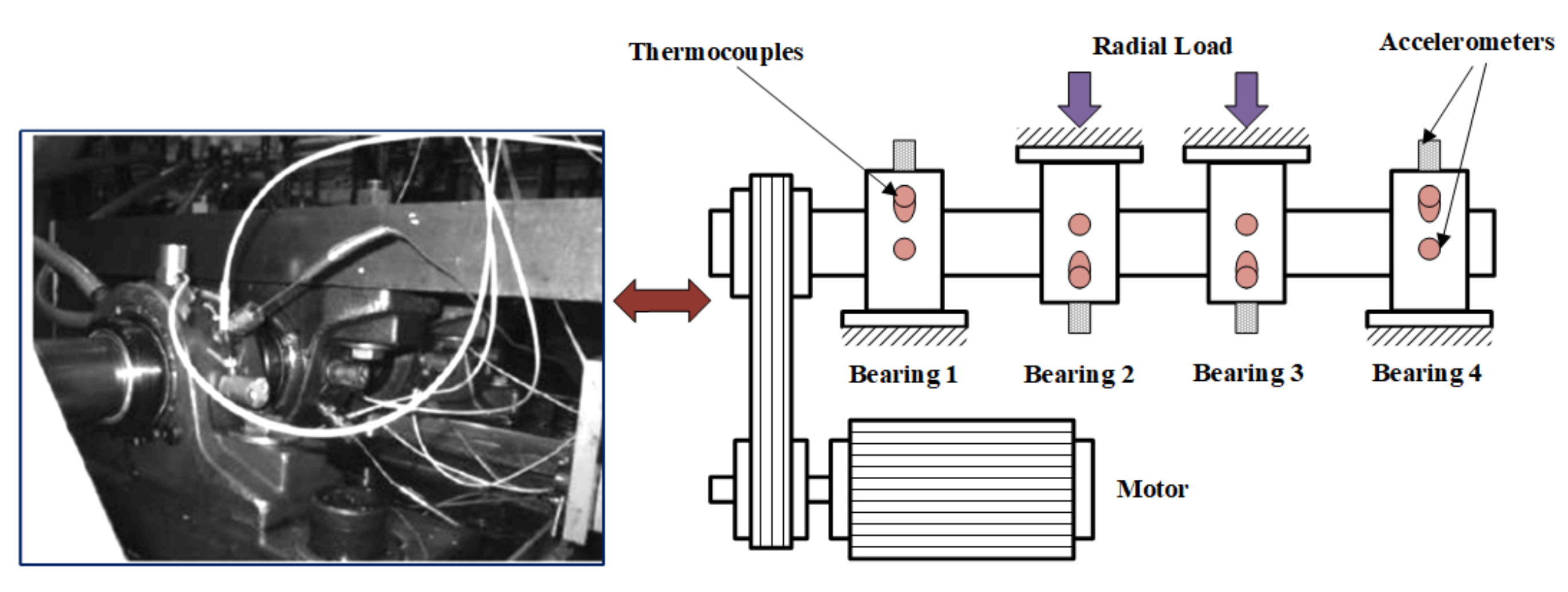
3. Algorithm Verification Based on IMS Bearing Test Bench
3.1. Data Collection
3.2. Feature Extraction
3.3. Cluster Analysis
4. Algorithm Verification Based on Unbalanced Bearing’s Load Test Bench
4.1. Data Collection
4.2. Feature Extraction
4.3. Cluster Analysis
5. Conclusions
- Weak bearing characteristics may be effectively extracted using the proposed kurtosis and frequency domain sample entropy-based feature extraction method.
- An updated DBSCAN method enables automatic cluster analysis by determining the optimal values of the Eps and MinPts parameters, as well as the position of the optimal parameters, using a more precise optimization strategy.
- Using the condition monitoring approach proposed in the paper, the experimental results reveal that both bearings in fault conditions and bearings under varying loading conditions can be identified, and the condition detection rate is extremely high, reaching 96% in all cases.
- Although this work demonstrates that the operating condition of a bearing may be recognized under both unbalanced and uniform load situations, the recognition effect of operating the bearing under diverse load conditions is not clearly demonstrated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, J.; Li, Z.; Li, C.; Zhan, L.; Zhang, G. Rolling Bearing crack Diagnosis Based on Refined Composite Multi-Scale Approximate Entropy and Optimized Probabilistic Neural Network. Entropy 2021, 23, 259. [Google Scholar] [CrossRef] [PubMed]
- Gu, R.; Chen, J.; Hong, R.; Wang, H.; Wu, W. Incipient fault diagnosis of rolling bearings based on adaptive vibrational mode decomposition and Teager energy operator. Measurement 2020, 149, 106941. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Y.; Li, C.; Li, Z. Nonlinear dynamic analysis of CNC lathe spindle-bearing system considering thermal effect. Nonlinear Dyn. 2021, 105, 131–166. [Google Scholar] [CrossRef]
- Tian, S.; Zhao, X.; Dong, S. Dynamic support stiffness of motorized spindle bearings under high-speed rotation. Int. J. Adv. Manuf. Technol. 2021, 117, 2359–2367. [Google Scholar] [CrossRef]
- Zhao, H.; Yang, Z.; Chen, C.; Tian, H.; Chen, L.; Ying, J.; Jia, X. Development of Reliability Test System Based on Working Principle and Fault Analysis of Motorized Spindle. In Proceedings of the 2018 3rd International Conference on System Reliability and Safety (ICSRS), Barcelona, Spain, 23–25 November 2018; pp. 299–307. [Google Scholar]
- Yi, J.; Pang, B.; Liu, H.; Wang, F.; Ji, B.; Jing, M. Influence of Misalignment on Nonlinear Dynamic Characteristics for Matched Bearings-Rotor System. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2014, 228, 172–181. [Google Scholar] [CrossRef]
- Lin, J.L.; Liu, J.Y.C.; Li, C.W.; Tsai, L.F.; Chung, H.Y. Motor shaft misalignment detection using multiscale entropy with wavelet denoising. Expert Syst. Appl. 2010, 37, 7200–7204. [Google Scholar] [CrossRef]
- Xing, Y.; Xu, H.; Pei, S.; Zhang, X.; Chang, W. Mechanical Analysis of Spherical Roller Bearings Due to Misalignments between Inner and Outer Rings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 231, 3250–3262. [Google Scholar] [CrossRef]
- Li, L.; Zhang, D.; Xie, Y. Effect of misalignment on the dynamic characteristic of MEMS gas bearing considering rarefaction effect. Tribol. Int. 2019, 139, 22–35. [Google Scholar] [CrossRef]
- Tong, V.C.; Kwon, S.W.; Hong, S.W. Fatigue Life of Cylindrical Roller Bearings. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2017, 231, 623–636. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Li, M. Nonlinear Dynamics of Unsymmetrical Rotor-Bearing System with Fault of Parallel Misalignment. Adv. Mech. Eng. 2018, 10, 1687814018772908. [Google Scholar] [CrossRef] [Green Version]
- Xie, Z.; Shen, N.; Zhu, W.; Tian, W.; Hao, L. Theoretical and experimental investigation on the influences of misalignment on the lubrication performances and lubrication regimes transition of water lubricated bearing. Mech. Syst. Signal Process. 2021, 149, 107211. [Google Scholar] [CrossRef]
- Rai, A.; Upadhyay, S.H. A review on signal processing techniques utilized in the fault diagnosis of rolling element bearings. Tribol. Int. 2016, 96, 289–306. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Application of EEMD and improved frequency band entropy in bearing crack feature extraction. ISA Trans. 2019, 88, 170–185. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Tang, G.; He, M. Peak-Based Mode Decomposition for Weak Fault Feature Enhancement and Detection of Rolling Element Bearing. Shock. Vib. 2020, 2020, 8901794. [Google Scholar] [CrossRef]
- Ding, C.; Feng, F.; Zhang, B.; Wu, S. Improved multi-scale symbolic dynamics information entropy and its application in feature extraction of planetary gearboxes. Vib. Shock. 2020, 39, 97–102. [Google Scholar]
- Castellani, F.; Garibaldi, L.; Daga, A.P.; Astolfi, D.; Natili, F. Diagnosis of Faulty Wind Turbine Bearings Using Tower Vibration Measurements. Energies 2020, 13, 1474. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Yan, Z.; Chen, W. Defect Detection for Wheel-Bearings with Time-Spectral Kurtosis and Entropy. Entropy 2014, 16, 607–626. [Google Scholar] [CrossRef] [Green Version]
- Rohani Bastami, A.; Bashari, A. Rolling element bearing diagnosis using spectral kurtosis based on optimized impulse response wavelet. J. Vib. Control 2020, 26, 175–185. [Google Scholar] [CrossRef]
- Tian, J.; Morillo, C.; Azarian, M.H.; Pecht, M. Motor Bearing crack Detection Using Spectral Kurtosis-Based Feature Extraction Coupled With K-Nearest Neighbor Distance Analysis. IEEE Trans. Ind. Electron. 2016, 63, 1793–1803. [Google Scholar] [CrossRef]
- Zhong, J.; Wang, D.; Guo, J.; Cabrera, D.; Li, C. Theoretical Investigations on Kurtosis and Entropy and Their Improvements for System Health Monitoring. IEEE Trans. Instrum. Meas. 2021, 70, 3503710. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, G.; Kang, Y.; Zhou, Z.; Duan, B.; Zhang, C. A multi-fault diagnosis method based on modified Sample Entropy for lithium-ion battery strings. J. Power Sources 2020, 446, 227275. [Google Scholar] [CrossRef]
- Lin, T.-K.; Chien, Y.-H. Performance Evaluation of an Entropy-Based Structural Health Monitoring System Utilizing Composite Multiscale Cross-Sample Entropy. Entropy 2019, 21, 41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sandoval, D.; Leturiondo, U.; Vidal, Y.; Pozo, F. Entropy Indicators: An Approach for Low-Speed Bearing Diagnosis. Sensors 2021, 21, 849. [Google Scholar] [CrossRef] [PubMed]
- Delgado-Bonal, A.; Marshak, A. Approximate Entropy and Sample Entropy: A Comprehensive Tutorial. Entropy 2019, 21, 541. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, M.; Pan, J. A fault diagnosis method combined with LMD, sample entropy and energy ratio for roller bearings. Measurement 2015, 76, 7–19. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, L.; Cai, Y. Rolling bearing crack diagnosis using generalized refined composite multiscale sample entropy and optimized support vector machine. Measurement 2020, 156, 107574. [Google Scholar] [CrossRef]
- Mouchaweh, M.S. Advanced Pattern Recognition method for the Monitoring of Dynamic Systems. IFAC Proc. Vol. 2009, 42, 510–515. [Google Scholar] [CrossRef]
- Kankar, P.K.; Sharma, S.C.; Harsha, S.P. Fault diagnosis of ball bearings using machine learning methods. Expert Syst. Appl. 2011, 38, 1876–1886. [Google Scholar] [CrossRef]
- Dong, L.; Shi, R.; Zeng, Z. Fault diagnosis of hoist spindle system based on complex network clustering. Vib. Test Diagn. 2016, 36, 688–693, 809. [Google Scholar]
- Li, C.; Cabrera, D.; De Oliveira, J.V.; Sanchez, R.V.; Cerrada, M.; Zurita, G. Extracting repetitive transients for rotating machinery diagnosis using multiscale clustered grey infogram. Mech. Syst. Signal Process. 2016, 76–77, 157–173. [Google Scholar] [CrossRef]
- Shi, J.; Deng, Y.; Wang, Z.; Guo, X. An adaptive new state recognition method based on density peak clustering and voting probabilistic neural network. Appl. Soft Comput. 2020, 97, 1876–1886. [Google Scholar] [CrossRef]
- Du, M.; Ding, S.; Jia, H. Study on density peaks clustering based on k-nearest neighbors and principal component analysis. Knowl. -Based Syst. 2016, 99, 135–145. [Google Scholar] [CrossRef]
- Kerroumi, S.; Rasolofondraibe, L.; Chiementin, X. Dynamic Pattern Recognition Method for Bearing Monitoring. Proceedings of ISMA 2014; Katholieke Universiteit Leuven: Leuven, Belgium, 2014; pp. 2809–2820. [Google Scholar]
- Li, H.; Wang, W.; Huang, P.; Li, Q. Fault diagnosis of rolling bearing using symmetrized dot pattern and density-based clustering. Measurement 2020, 152, 107293. [Google Scholar] [CrossRef]
- Li, W.; Yan, S.; Jiang, Y.; Zhang, S.; Wang, C. Research on adaptively determining DBSCAN algorithm parameters. Comput. Eng. Appl. 2019, 55, 1–7. [Google Scholar]
- Caesarendra, W.; Tjahjowidodo, T. A Review of Feature Extraction Methods in Vibration-Based Condition Monitoring and Its Application for Degradation Trend Estimation of Low-Speed Slew Bearing. Machines 2017, 5, 21. [Google Scholar] [CrossRef]



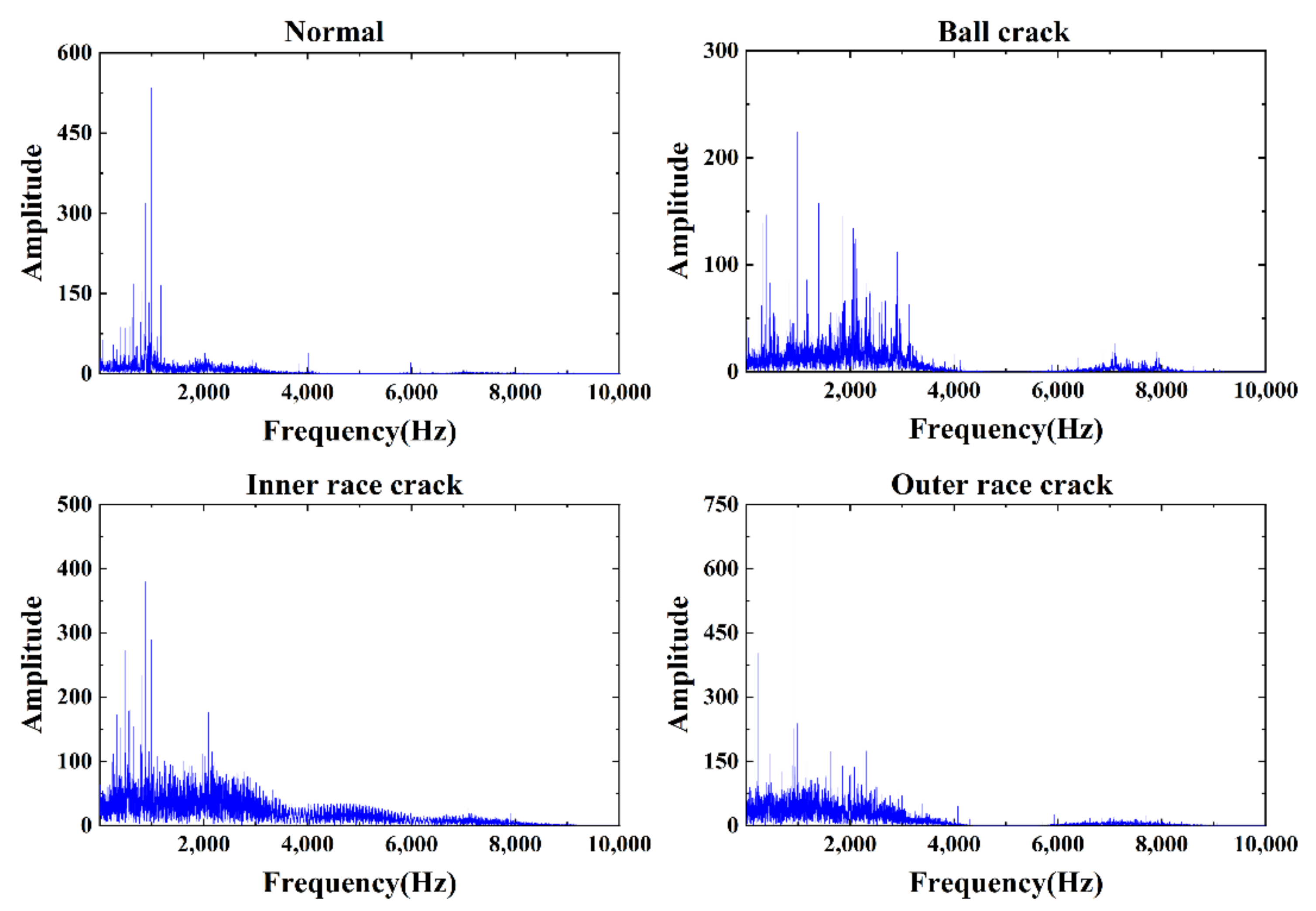



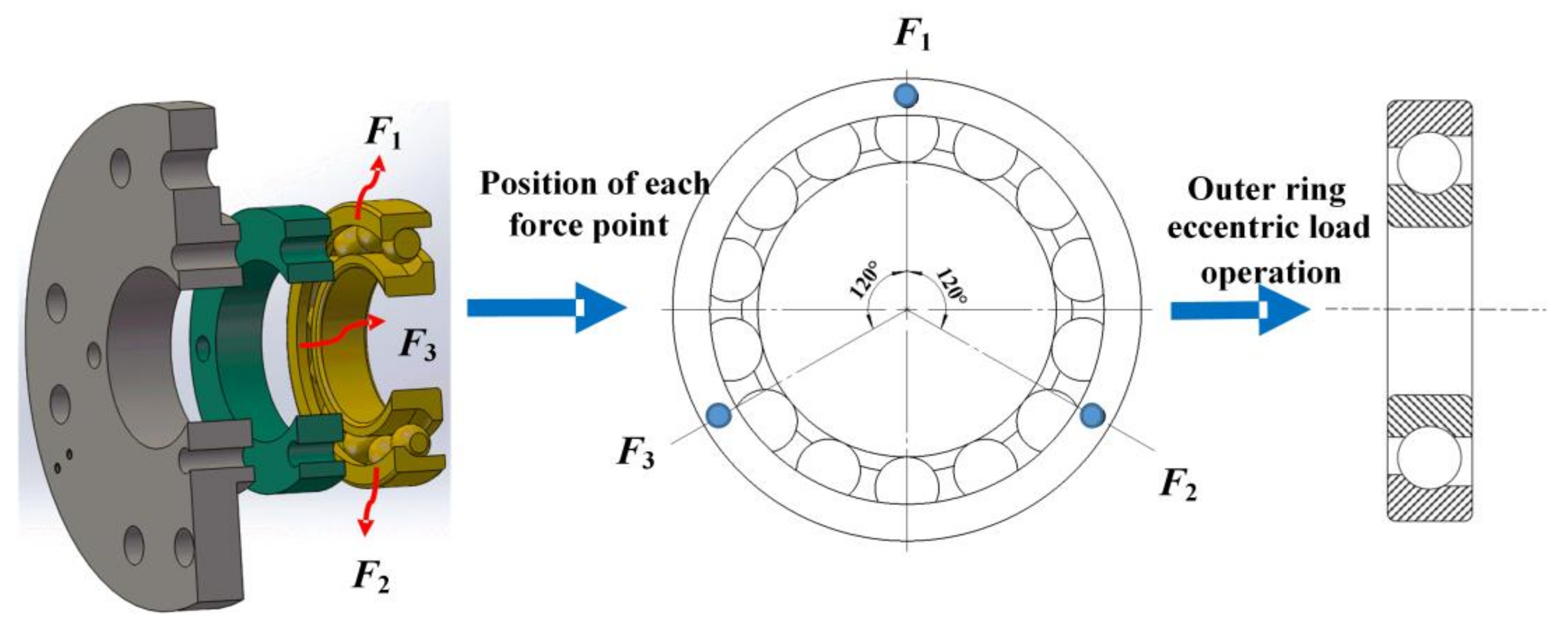
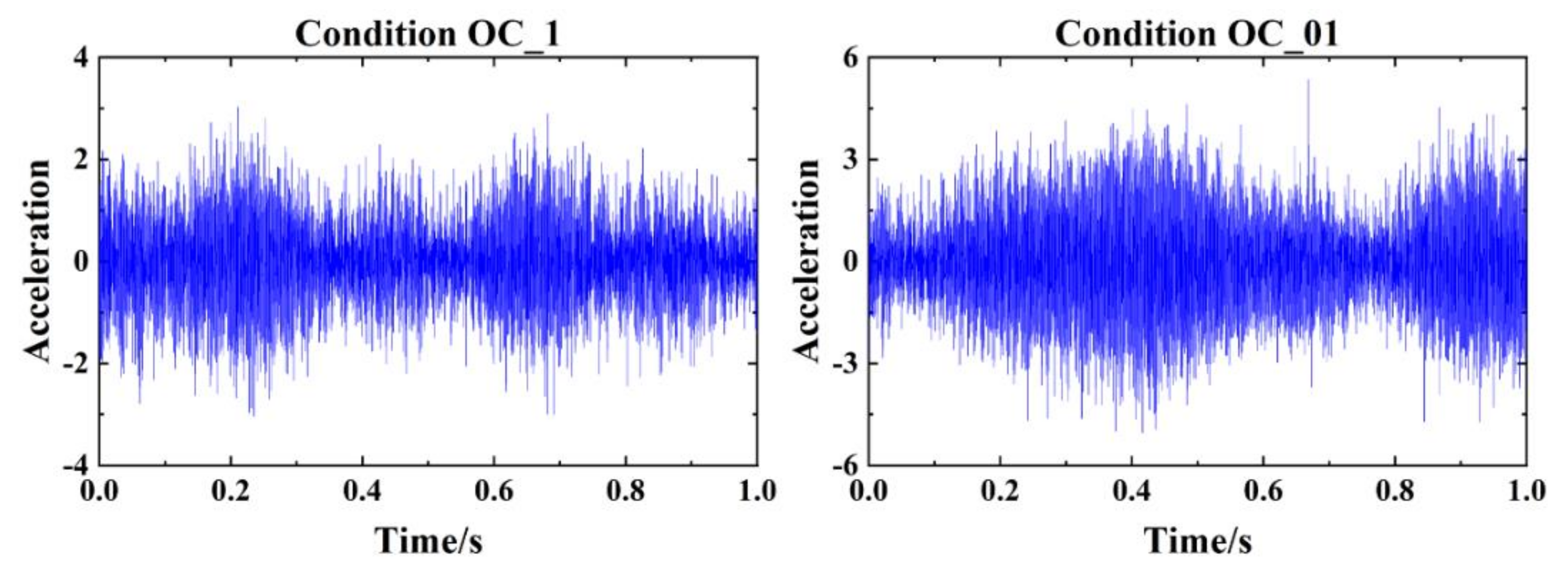
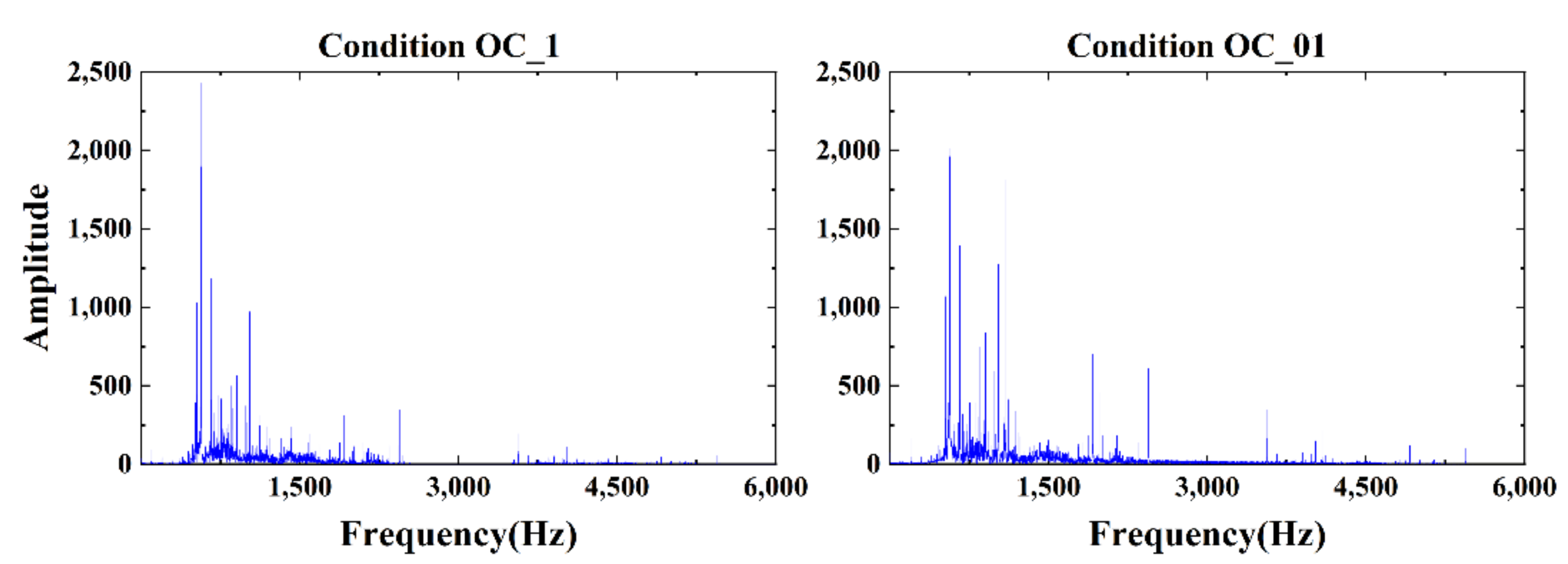
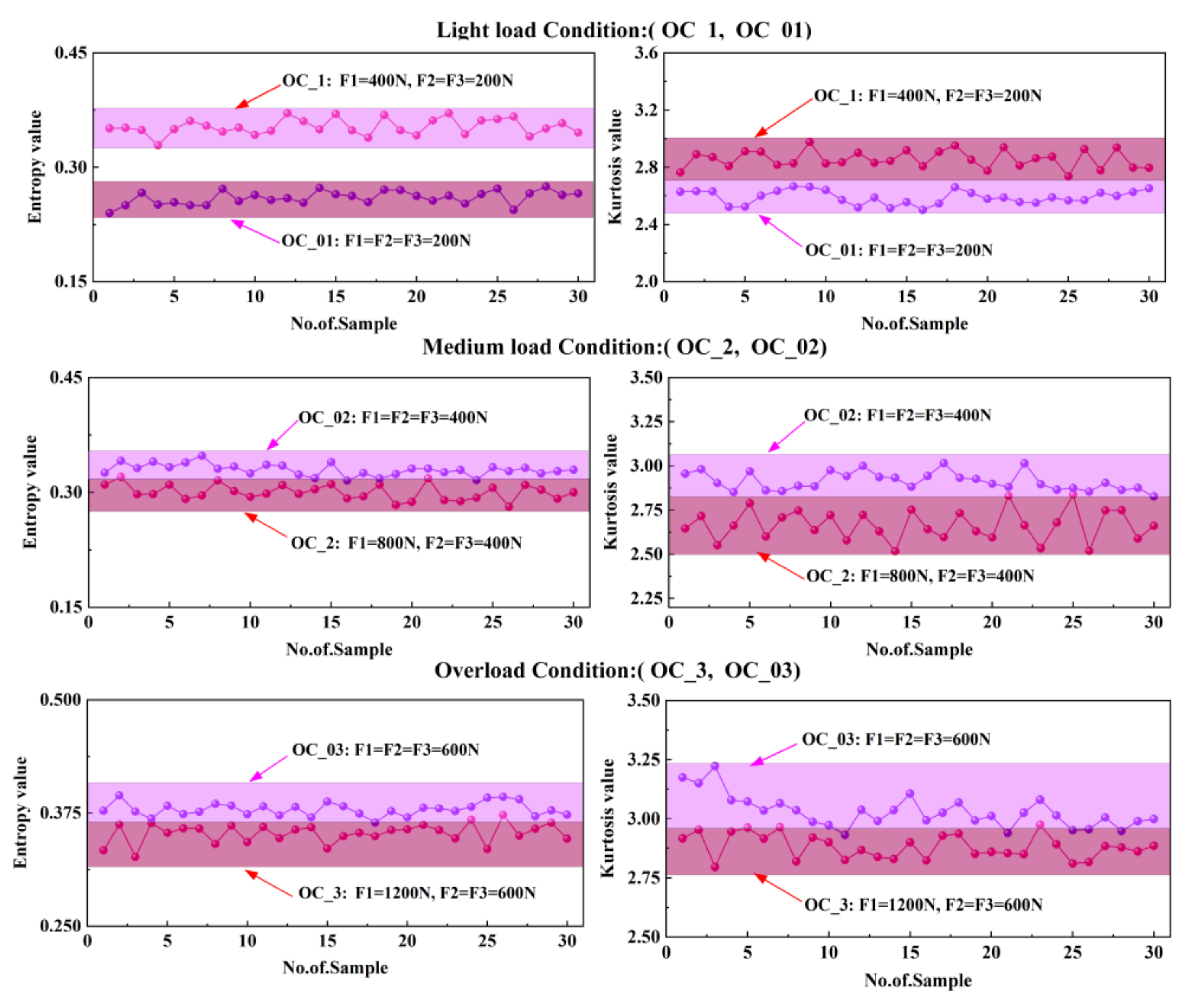

| Data Set Number | Fault Type | Sampling Length |
|---|---|---|
| Data set 1-bearing 1 | Normal | 81,920 |
| Data set 1-bearing 3 | Inner ring crack | 81,920 |
| Data set 1-bearing 4 | Boll crack | 81,920 |
| Data set 3-bearing 3 | Outer ring crack | 81,920 |
| Inner Ring Diameter/mm | Outer Ring Diameter/mm | Thickness/mm | Dynamic Load/KN | Static Load/mm |
|---|---|---|---|---|
| 70 | 100 | 20 | 47 | 43 |
| Operational State | F1/N | F2/N | F3/N |
|---|---|---|---|
| OC_1 | 400 | 200 | 200 |
| OC_2 | 800 | 400 | 400 |
| OC_3 | 1200 | 600 | 600 |
| OC_01 | 200 | 200 | 200 |
| OC_02 | 400 | 400 | 400 |
| OC_03 | 600 | 600 | 600 |
| Loaded Conditions | Eps | MinPts |
|---|---|---|
| (OC_1,OC_01) | 0.1682 | 17 |
| (OC_2,OC_02) | 0.2241 | 16 |
| (OC_3,OC_03) | 0.2412 | 17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, Y.; Kong, L.; Niu, Q.; Bai, Y. Improved DBSCAN Spindle Bearing Condition Monitoring Method Based on Kurtosis and Sample Entropy. Machines 2022, 10, 363. https://doi.org/10.3390/machines10050363
Zhang Y, Li Y, Kong L, Niu Q, Bai Y. Improved DBSCAN Spindle Bearing Condition Monitoring Method Based on Kurtosis and Sample Entropy. Machines. 2022; 10(5):363. https://doi.org/10.3390/machines10050363
Chicago/Turabian StyleZhang, Yanfei, Yunhao Li, Lingfei Kong, Qingbo Niu, and Yu Bai. 2022. "Improved DBSCAN Spindle Bearing Condition Monitoring Method Based on Kurtosis and Sample Entropy" Machines 10, no. 5: 363. https://doi.org/10.3390/machines10050363
APA StyleZhang, Y., Li, Y., Kong, L., Niu, Q., & Bai, Y. (2022). Improved DBSCAN Spindle Bearing Condition Monitoring Method Based on Kurtosis and Sample Entropy. Machines, 10(5), 363. https://doi.org/10.3390/machines10050363






