Abstract
The hydro-mechanical continuously variable transmission (HMCVT) has complicated transmission characteristics. To analyze the influences of various factors on HMCVT’s efficiency characteristics and build a more precise HMCVT efficiency characteristic model, the paper conducted a full factorial simulation test for and a modeling study on a novel five-stage HMCVT’s efficiency characteristics. The full factorial test considered four factors with a total of 160 groups of test samples and used a range analysis method. Moreover, we proposed a piecewise modeling method for HMCVT efficiency characteristics based on the improved genetic algorithm (I-GA) and compared the precision of seven models. Research results showed that the working stage with the power output from the planet carrier had relatively higher efficiency. The variable pump’s displacement ratio had the greatest influence, and the HMCVT’s efficiency characteristics presented two variation laws with the boundary that the displacement ratio is 0. The load power and the engine speed showed a positive correlation and a negative correlation with the efficiency characteristics, respectively, and the influences decreased as the factor values increased. The modeling method proposed had high modeling precision and the mean absolute percentage error (MAPE) of seven models was in the range of 1.6884~3.1375%. The estimation precision greatly could be improved (the MAPE reduced by 7.7024% and the R2 increased by 9.2943%) by introducing the first-order term of engine speed on the basis of a two-factor model (in which the factors were the displacement ratio and the load power). The paper aimed to offer direct reference information on parameters of the mechanical design and control strategy development of HMCVT from an energy-saving perspective in the design stage.
1. Introduction
The power transmission system is one of the important subsystems of vehicles. There is a great variety of vehicles which can be divided into electric vehicles (uses power batteries [1] and driving motor [2] as the main power system) and fuel-engine vehicles in terms of energy. Most vehicles have a transmission which gives the vehicle a better chance of working in a stage with the best dynamic or economical property by changing its transmission ratio to fit the engine [3]. Theoretically, the more transmission ratio series the transmission has (i.e., the more gear shifts the transmission has) and the bigger the variation range of transmission ratio is, the better service characteristics the vehicle has. Moreover, the automatically intelligent control of the transmission system helps the development of intelligent vehicles [4] and the sustainable development of environment and ecology to some extent.
The hydro-mechanical continuously variable transmission (HMCVT) [5,6] as a power-split continuously variable speed system [7,8] (the power output from the engine is split into the hydraulic power flow and the mechanical power flow) can meet the requirements above effectively (i.e., the more transmission series the transmission has, the larger the variation range of transmission ratio is; automatically intelligent control). The HMCVT has been researched and applied to the fields of agriculture and forestry work vehicles, military vehicles, and some commercial vehicles [9], especially for agriculture and forestry work vehicles (such as tractors) working in poor environments with complicated and variable load conditions [10,11]. Therefore, the application of HMCVT to vehicles such as tractors has great significance for the improvement in the automation and the intelligence and operational performance (mainly referring to the power performance and economic efficiency) of full vehicles.
A reasonable design and control of HMCVT is the key to engineering applications. Currently, there are some studies on the design and control of HMCVT. For instance, Ni et al. [12] and He et al. [13] designed the HMCVT of tractors with the equal-ratio principle. Volpe et al. [14] analyzed the transmission characteristics and researched the optimized design for the power-split continuously variable transmission. In the study, they used methods including the differential evolution algorithm for the optimized design of different types of power-split continuously variable transmissions. Macor and Rossetti [15] proposed a multi-objective optimized design method for CVT (one of the optimization objects was the minimum fuel consumption, considering the integral mean loss between the zero-speed vehicle and the maximum design speed of vehicle as the objective function). The method combined software MATLAB and AMESim, and was based on the multi-objective particle swarm optimizer (MOPSO). Xiao et al. [16] proposed a HMCVT speed ratio matching method based on the tractor’s fuel economy and mainly adopted the simulation test to study the effective specific fuel consumption of the tractor in different working conditions. Ahn et al. [17] proposed a mixed transmission control strategy for tractors considering engine characteristics and HMCVT’s transmission efficiency, and built a co-simulation model for tractors based on AMESim and MATLAB/simulink (without the PTO) to analyze the full vehicle system’s fuel efficiency. Ince and Guler [18] conducted a comparative study on the performance of the power-split continuously variable transmission and the conventional transmission in terms of fuel consumption. The study simulated two different control strategies based on MATLAB. Zhang et al. [19] analyzed the fuel consumption rate of the engine and the efficiency variation characteristics of HMCVT, calculated and obtained the optimal gear ratio of tractors in different working conditions using the parameter round-robin algorithm, compared the characteristics of tractors in unitary and binary coordinated regulations, and verified the energy-saving effect of the proposed binary regulation variable speed control strategy. It showed that grasping the efficiency characteristics of the CVT system is the key to the reasonable transmission design and control strategy development. However, currently, some studies introduce a fixed value to the efficiency of the power-split CVT system, some studies neglect the influence of working conditions in the efficiency models used, and some studies describe the variation laws of power-split CVT efficiency using mathematical models with few independent variables.
Currently, there are few studies on HMCVT’s efficiency characteristics. Li et al. [20], basing on the plunger-pump-motor system efficiency model with few parameters and the engaging power method, assessed the HMCVT of amphibian tractors. Xia and Sun [21] set the single-stage external meshing gear transmission efficiency as a fixed value (0.97) when researching the working efficiency of CVT, and considered the energy loss of HMCVT’s gear shift, pump-motor system, and planetary row in the research process. Liu et al. [22] split the hydro-mechanical transmission efficiency into a mechanical part and a hydraulic part, calculated the efficiency of the two parts and then the efficiency of the whole transmission system according to the proportions of two parts of efficiency, and made a torque-rotating-speed-efficiency map. Cheng et al. [23] built an efficiency characteristic model by using an improved simulated annealing algorithm with a few test data. This study used a stage of multi-stage HMCVT as an example and calculated the power-split proportions of HMCVT (combining the calculation of mechanical transmission ratio’s variation characteristics and the calculation of the pressure difference between inlet and outlet oil circuits of a constant motor). To summarize, current studies on the HMCVT efficiency characteristic model generally use purely theoretical calculation models based on analyses of the energy transmission characteristics of parts in the system. The HMCVT’s efficiency characteristics are affected by working conditions (i.e., the working speed, load power, displacement ratio, and other factors affect the HMCVT’s working efficiency). Therefore, it is difficult to build an efficiency model with certain reliable precision in the design stage. It is also possible to obtain efficiency characteristics by producing a HMCVT prototype and making a practical test. However, it may have an excessive cost and require a heavy workload. Wang et al. [24] built a HMCVT efficiency characteristic model with the Simulation X and verified the precision of the simulation model through a comparison with the measured value of the practical test. However, it is difficult to optimize HMCVT’s design parameters and develop control strategies through the simulation model of Simulation X alone in the design stage. The model with specific mathematical expressions can be applied to the optimized design and control strategy development of HMCVT effectively.
To solve the above problems, we proposed a piecewise modeling method for HMCVT efficiency characteristics considering HMCVT’s working stage characteristics, engine working speed, load power, and variable pump’s displacement ratio in the design stage. We built a simulation model of efficiency characteristics specific for a novel five-stage HMCVT transmission scheme using software Simulation X. We conducted an efficiency characteristic test using a full factorial test, obtained 160 groups of simulation test samples, and explored the influences of various factors on HMCVT’s efficiency characteristics using a range analysis. Test results showed that the variable pump’s displacement ratio had the greatest influence, and HMCVT’s efficiency characteristics presented two variation laws with the boundary that the displacement ratio is 0. On this basis, we proposed a piecewise model to describe the variation laws of HMCVT’s efficiency characteristics. According to all test samples, we used an improve genetic algorithm (I-GA) to build seven efficiency characteristic mathematical models (which were all piecewise models). Additionally, we compared the results of seven models using the mean absolute percentage error (MAPE) and the coefficient of determination (R2) as evaluation indexes. This paper offers valuable reference information for the optimized design of HMCVT’s structure and parameters, and also offers reliable mathematical models of efficiency characteristics that can be used directly for the development of control strategies in the design stage. Moreover, the paper offers an evaluation method for HMCVT efficiency.
2. Materials and Methods
2.1. A Novel 5-Stage HMCVT
The research in this paper was specific for a novel 5-stage HMCVT composed of the variable pump, the constant motor, the planetary gears, the wet clutch, the brake, and the shaft gear. The 5-stage HMCVT studied in this paper had 5 working stages (named stage H0, HM1, HM2, HM3, and HM4, respectively). Each working stage realized stepless change of the transmission ratio within a certain range. The transmission ratio range of the adjacent working stage was continuous. See Figure 1 for the system’s transmission scheme.
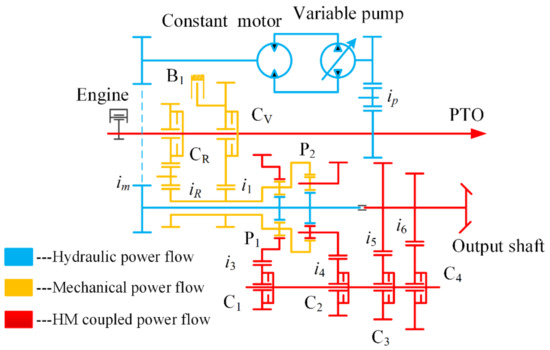
Figure 1.
Transmission scheme of a novel 5-stage hydro-mechanical continuously variable transmission (HMCVT).
In Figure 1, the blue full line represents the hydraulic power flow’s transmission route. In this route, a part of the engine’s output power is fed into the sun gear of planetary gear P1 or P2 through ip, the variable pump, the constant motor, and im. The yellow full line represents the mechanical power flow’s transmission route. In this route, a part of the engine’s output power is fed into planetary gear P1 or gear ring P2 through i1 or iR. The red full line represents the transmission route of the engine total output power flow and the hydro-mechanical (HM) coupled power flow. In this route, the power of the hydraulic power flow and the mechanical power flow converge and then is output by gear ring P1 or planet carrier P2. Finally, the power is transmitted to the output end through i3 or i4 and i5 or i6. The 5-stage HMCVT uses clutch CR and clutch CV to make the vehicle move forward and backward, respectively. Moreover, for the opposite rotation direction, when clutch CR or clutch CV works, the HMCVT has the following five consistent working stages: (1) one purely hydraulic working stage (stage H0) in which brake B1 and clutches C1 and C3 work; (2) four HM power coupled working stages including stage HM1 (in which clutches C2 and C3 work), stage HM2 (in which clutches C1 and C3 work), stage HM3 (in which clutches C2 and C4 work), and stage HM4 (in which clutches C1 and C4 work).
The HMCVT used in this study was designed by the principle of equal ratio. That is, except for the initial working stage (H0 stage), the ratios of the maximum and minimum transmission ratios of HM1~HM4 stages are approximately equal (note: the transmission ratio of HMCVT is defined by the effective working range of the displacement ratio). In this study, the common ratio was 1.81, the maximum transmission ratio of HMCVT was 7.52, and the minimum transmission ratio was 0.72. The design values of transmission system parameters obtained by calculation are shown in Table 1.

Table 1.
Design values of transmission system parameters.
Figure 2 shows the variation characteristics of the 5-stage HMCVT’s transmission ratio (use the forward pattern as an example).
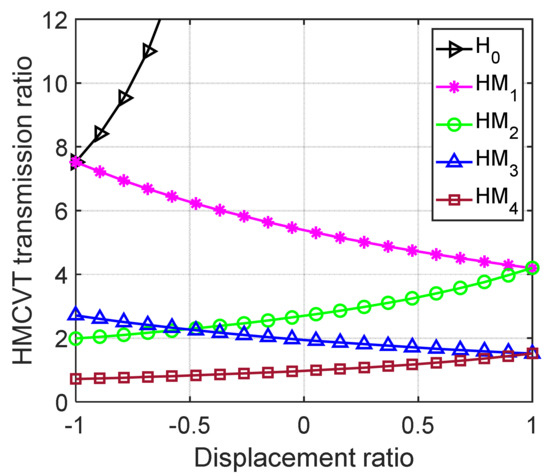
Figure 2.
Variation characteristics of HMCVT’s transmission ratio.
2.2. Build a Simulation Test Platform for Efficiency Characteristics Based on Simulation X
Simulation X has been applied widely in the research on power transmission systems, and its modularized modeling method is applicable to the research objective in this paper. We built a 5-stage HMCVT simulation model (see Figure 3) with the inbuilt variable pump, constant motor model, various types of valve models, planetary gear model, fixed-shaft gear model, and clutch model of the software.
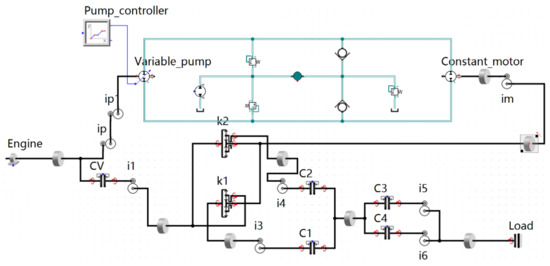
Figure 3.
HMCVT efficiency characteristic simulation model based on Simulation X.
We measured the load end power and the engine power and then divided the two values to obtain the total transmission efficiency of the whole transmission system based on the simulation test system. In this research, the transmission efficiency of shaft gear was set as 0.98. Planetaries took into account stiffness and damping of contact (the power loss mainly includes power dissipated due to damping). Hydro-mechanical efficiency (maximum efficiency was set to 0.9, mainly including sticking friction torque and coulomb friction torque) was considered in both the variable pump and the constant motor system. Because the research work was oriented to the conceptual design stage, the leakage of hydraulic system, friction loss of bearing, and hydraulic loss of gear and shaft dipped into oil were ignored.
2.3. The Full Factorial Test Design for Four Efficiency Characteristic Factors
According to reference document [23], HMCVT’s efficiency characteristics may vary in different working conditions. The engine speed, the load power, the variable pump’s displacement ratio, and the working stage of HMCVT (HMCVT’s working parts are different in different working stages) are the variable factors related to the HMCVT during the running of the vehicle. We used a full factorial test method to explore the variation characteristics of HMCVT’s transmission efficiency when the four factors were in different cases.
The vehicles with HMCVT generally use the diesel engine. This paper uses the diesel engine of model LR6105ZWT3 as an example. The diesel engine has a working speed range of 800~2200 rpm and a rated power of 132 kW. The research sets the engine speed and load power to be divided into three levels equally into the ranges of 800~2200 rpm and 10~132 kW, respectively. The variable pump’s displacement ratio has a positive mode and the negative mode. The paper sets three levels evenly in each mode (including the levels of 800 rpm, 1500 rpm, and 2200 rpm and the levels of 10 kW, 71 kW, and 132 kW). Additionally, the two modes both have the state that the displacement ratio is 0 (i.e., the variable pump does not output the displacement in which case the constant motor’s output speed is 0). Merging the states when the displacement ratio is 0, the variable pump’s displacement ratio can be equally divided into five levels (including levels −1, −0.5, 0, 0.5, and 1). The HMCVT has a total of five working stages, while the purely hydraulic working stage generally works in the starting stage of the vehicle and has a relatively simple transmission route. This paper only explored the HMCVT efficiency characteristics in HM power coupled working stages. Therefore, the HMCVT’s working stages were divided into four levels (representing stages HM1~HM4, respectively). Then, Table 2 shows the full designed factorial test.

Table 2.
Range calculation results.
We used a range analysis method to explore each factor’s influence on HMCVT’s efficiency characteristics. We calculated four factors’ (the engine speed, the load power, the variable pump’s displacement ratio, and the HMCVT working stage) range of mean efficiency of all levels (i.e., the difference between the maximum and the minimum of mean efficiency of all levels in the full factorial test results of each factor). The following is the calculation formula:
where is the range of the ith factor and is the set of mean efficiency of all levels of the ith factor.
We compared the range of each factor to analyze the influence on efficiency characteristics. For a factor, a positive range means the factor has a positive correlation with efficiency characteristics, while a negative range means the factor has a negative correlation with efficiency characteristics. Moreover, the bigger the range is, the greater influence the factor has on efficiency characteristics.
2.4. An I-GA-Based Piecewise Modeling Method for Efficiency Characteristics
According to reference documents [3,23], the HMCVT’s efficiency characteristics present two significantly different variation laws in different working ranges of the variable pump’s displacement ratio. Specifically, the HMCVT’s efficiency characteristics are significantly different when the displacement ratio is in the ranges of −1~0 and 0~1. It was also supported by the test results of this paper (see Section 3).
On this basis, we used the form of a piecewise function (with the displacement ratio in the ranges of −1~0 and 0~1, respectively) to build the HMCVT efficiency characteristic model. Because the variation laws of efficiency characteristics had some similarity in the two ranges (see Section 3), for the convenience of HMCVT efficiency characteristic model’s modeling and applications, we used the same form of the model to describe two kinds of characteristics in the two ranges.
We proposed an I-GA-based piecewise modeling method for efficiency characteristics. The piecewise model is, essentially, the combination of two sub-models, so the traditional modeling method uses a series mode to build the sub-models of the piecewise mode one by one. To improve the efficiency of modeling (i.e., the speed, convenience, and precision of modeling), the proposed method considers all unknown parameters in the HMCVT efficiency characteristic piecewise model as the decision variables of I-GA. Moreover, the method sets the fitness function as the highest total precision of two sub-models in the piecewise model, resulting in the HMCVT efficiency characteristic model built synchronously in a parallel way.
In the optimization algorithm, the decision variables are:
where is the number of decision variables in the single sub-model of piecewise model, are the decision variables of the first sub-model of piecewise model, and are the decision variables of the second sub-model of piecewise model.
The proposed method considers the MAPE between the test value and estimation value as the index to evaluate the precision of the efficiency characteristic model. Then, the objective function is:
where is the number of samples in each range after the range division of efficiency characteristics, is the estimated value of sub-model 1, is the measured value in the working stages of sub-model 1, is the estimated value of sub-model 2, and is the measured value in the working stages of sub-model 2.
Figure 4 shows the flow chart of the proposed modeling method.
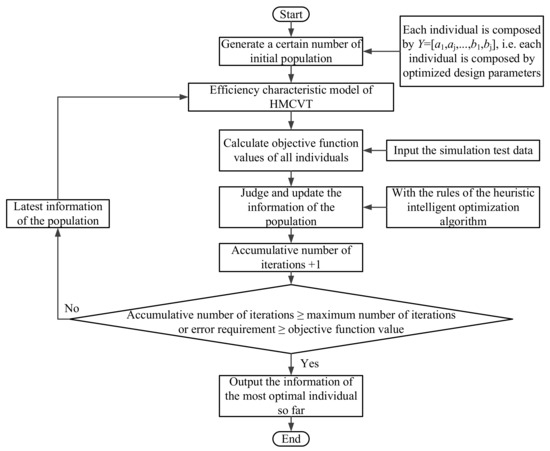
Figure 4.
The flow chart of the proposed modeling method.
The proposed HMCVT efficiency characteristic piecewise model has many variables to be optimized (see Section 2.5; the three piecewise models have 4, 12, and 14 unknown parameters, respectively). The algorithm’s objective function is nonlinear. The heuristic optimization algorithm plays an important role in solving complicated engineering problems. For example, the research studies in references [25,26,27,28] can be reflected to a certain extent. Considering that the research object has two nonlinear objectives and two sub-models searching the optimum synchronously (which causes relatively more decision variables), we used the genetic algorithm (GA) to solve the unknown parameters in sub-models to build the HMCVT efficiency characteristic piecewise model. To further improve the modeling result of the efficiency characteristic piecewise model, we used the I-GA proposed in previous research and verified for engineering applications [29]. The I-GA improves the convergence rate and precision through the following steps: (1) judging and screening the super individual in the population, (2) adaptive changes of the population size, and (3) adaptive changes of the crossover and mutation probabilities.
2.5. Types of Piecewise Models and Accuracy Evaluation Indexes Studied in the Paper
The 5-stage HMCVT researched has four HM power coupled working stages (i.e., stages HM1~HM4). We explored the laws of efficiency characteristics of each working stage varying with three factors (including the engine speed, the load power, and the variable pump’s displacement ratio). We proposed a method to build the efficiency characteristic piecewise model according to the influences of the three factors. According to the range analysis results (see Section 3.2), we built the efficiency characteristic piecewise models of HMCVT’s single working stage with a single factor, two factors, and three factors as independent variables, respectively. The single-factor model uses the factor with the greats influence on efficiency characteristics. The two-factor model uses the two factors with greater influences on efficiency characteristics. The three-factor model use all the three factors researched in the paper. The polynomial model can contain both the single-factor higher order term and the multi-factor interaction term, so it generally has good estimation precision in engineering applications [30].
Through the range analysis, we set the factors as x1 (with a relatively greater influence), x2, and x3 (with relatively smaller influences) according to their influences on efficiency characteristics.
The single-factor polynomial model built considers the first-order term of a single factor and its expression is as follows:
where is the HMCVT efficiency characteristic piecewise model built with the polynomial, and is variable pump’s displacement ratio.
The two-factor polynomial model built considers the first-order term, second-order term, and interaction term of two factors and its expression is as follows:
x3 has the smallest influence on efficiency characteristics comparatively. If we introduce the parameter in the same way as introducing x1 and x2, it may cause too many unknown parameters to be solved in the model, and consequently may result in an overfitting phenomenon. Therefore, we only introduced an independent variable containing x3, , to correct the original two-factor model. The following is the expression of new model:
For the multiple independent variable forms with x3 (we considered x3’s first-order term, second-order term, and interaction term with other factors), we proposed an enumeration method for the comparison to determine the relatively optimal new independent variable . Specifically, (1) introducing different forms of one by one to form a new three-factor model; (2) completing the three-factor model with the I-GA-based method proposed in Section 2.3; and (3) comparing different forms of three-factor models one by one in terms of precision to select the relatively optimal .
We used the MAPE and coefficient of determination as the indexes to compare and evaluate the precision of different efficiency characteristic piecewise models. The following is the calculation formula of :
where is the total number of samples at one HM stage of HMCVT and represents all test values at one HM stage of HMCVT.
3. Results and Discussion
3.1. Results of Full Factorial Test
Figure 5 presents the full factorial test results of the 5-stage HMCVT efficiency characteristics research. Because the engine in the research output high power with the speed of 800 rpm, we neglected the test combination of engine speed of 800 rpm and load power of 132 kW. Finally, the research obtained a total of 160 groups of test data using the simulation platform built on the basis of Simulation X.
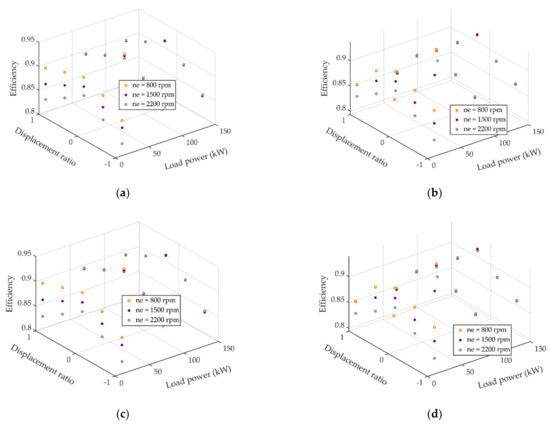
Figure 5.
Measurement results of full factorial test for HMCVT transmission efficiency. (a) Stage HM1; (b) stage HM2; (c) stage HM3; and (d) stage HM4.
All efficiency data at different stages of HMCVT with the same level of displacement ratio of variable pump were counted and the averages were calculated (see the results in Figure 6).
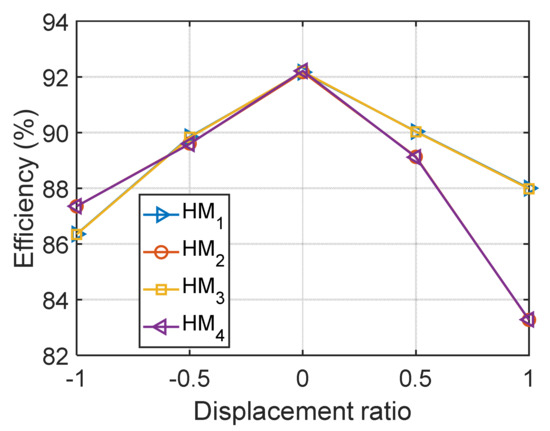
Figure 6.
Mean efficiency of different displacement ratios at the stages.
According to Figure 6, the efficiency characteristics of HMCVT working stages presented two variation laws with the boundary of . In order to further observe the change in efficiency characteristics, the efficiencies of different HMCVT working stages under the same working conditions (i.e., the engine speed, the load power, and the displacement ratio are consistent) were compared (see Figure 7).
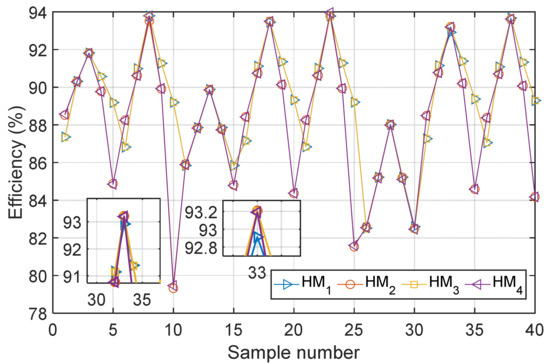
Figure 7.
Transmission efficiency of HMCVT stages in the same working conditions.
According to Figure 5, Figure 6 and Figure 7 stage HM1 and stage HM3 had similar efficiency characteristics, while stage HM2 and stage HM4 had similar efficiency characteristics. However, stages HM1 and HM3 showed significantly different efficiency characteristics compared with stages HM2 and HM4. Stages HM1 and HM3 showed relatively low efficiency when the displacement ratio was smaller than 0, while stages HM2 and HM4 showed opposite efficiency characteristics (i.e., the two stages showed relatively low efficiency when the displacement ratio was bigger than 0).
3.2. Range Analysis Results
The averages of four factors (including the HMCVT working stage, the engine speed, the load power, and the variable pump’s displacement ratio) on different levels were calculated used the range analysis method (see Figure 8 for the results). The four factors’ range results are shown in Table 2.
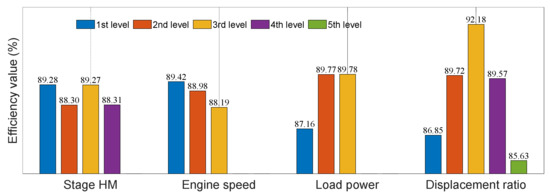
Figure 8.
Range calculation results.
According to Figure 6 and Table 2, stages HM1 and HM3 had higher efficiency compared with stages HM2 and HM4. Stages HM1 and HM3 were both the working stages of planetary row P2 (output from the planet carrier) and stages HM2 and HM4 were both the working stages of planetary row P1 (output from the gear ring). The efficiency characteristics of different HMCVT working stages had relatively small differences. The four factors listed in descending order by the influence on efficiency characteristics are displacement ratio > load power > engine speed > stage HM. With the boundary of , the HMCVT’s efficiency characteristics presented two variation laws. The load power was positively correlated to the efficiency while the engine speed was negatively correlated to the efficiency. Therefore, the single-factor model should choose the displacement ratio as the independent variable, while the two-factor model should choose the displacement ratio and the load power as independent variables.
3.3. Modeling Result of I-GA-Based Efficiency Characteristic Piecewise Model
According to Section 3.1 and Section 3.2, the HMCVT working stage has less influence on efficiency characteristics, and the variation laws of efficiency of different stages show certain similarity. Using stage HM1 as an example, we compared different models in terms of precision to choose the optimal form of the efficiency characteristic model.
Table 3 shows the parameter identification results of the single-factor model, the two-factor model, and the three-factor model (including five forms). The single-factor model is model 1. The two-factor model is model 2. The three-factor model is divided into models 3~7 according to the type of (including the first-order term of engine speed, the second-order term of engine speed, the interaction term of engine speed and load power, the interaction term of engine speed and displacement ratio, and the interaction term of three factors).

Table 3.
Parameter identification results of I-GA-based models.
According to Table 3, the seven models based on I-GA after parameter identification all had high precision. Model 3 had the highest R2 and minimum objective function value. Therefore, introducing the engine speed’s first-order term on the basis of the two-factor model could improve the efficiency characteristic model’s precision significantly. Moreover, the two-factor model (model 2) also had a relatively smaller objective function value and a higher R2. Additionally, the two-factor model neglects the influence of engine speed and thus was easy comparatively. Therefore, it was appropriate to use the two-factor model from the perspective of reducing test quantity and workload.
Figure 9 shows the comparison between the estimated values of three-factor models with the first-order term of engine speed and the measured values in a simulation test.
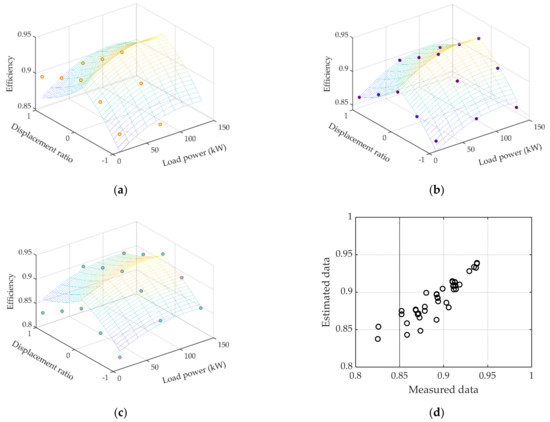
Figure 9.
The comparison between estimated values and measured values. (a) Engine speed of 800 rpm; (b) engine speed of 1500 rpm; (c) engine speed of 2200 rpm; and (d) scatter diagram.
According to Figure 9, the estimated value of model 3 (modified two-factor model with the first-order term of engine speed) was highly consistent with the measured value. Specifically, the measured and estimated values of the 40 groups of data were distributed along a diagonal line as shown in Figure 9d. This shows two aspects: (1) introducing the first-order term of engine speed to modify the original two-factor model could effectively improve the accuracy of the original two-factor model, the R2 increased by 9.29% and MAPE increased by 7.70%. (2) The I-GA algorithm was effective in parameter identification of the model. In the identification process of Model 3, the algorithm objective function finally converged to 1.6884 (this value is the mean absolute percentage error between the measured value and the estimated value). The iterative evolution curves of the I-GA (7 models) are shown in Figure 10.
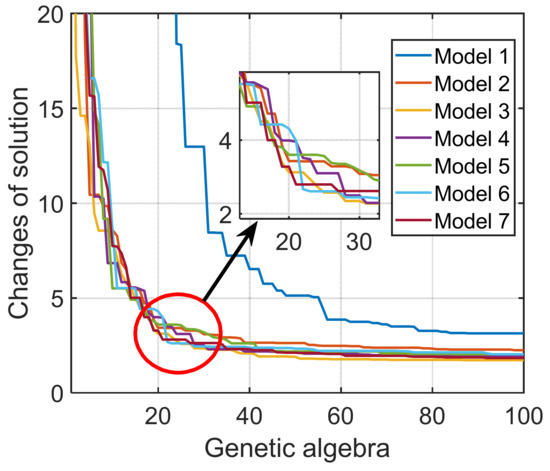
Figure 10.
Iterative evolution curve of I-GA (seven models).
4. Conclusions
We explored the efficiency characteristics of a new 5-stage HMCVT. According to the full factorial test results (with a total of 160 groups of sample data), the working stages using the same planetary row had similar efficiency characteristics. Moreover, when the hydraulic power flow and the mechanical power flow were input from the sun gear and the planet carrier (output from the planetary row), respectively, the working efficiency was slightly higher than that in the case where the hydraulic power flow and the mechanical power flow were input from the sun gear and the planet carrier (output from the gear ring), respectively. The efficiency characteristics of HMCVT at different working stages showed two variation laws with the boundary of .
The range analysis results showed that the factors’ ranking by the influence on efficiency characteristics was displacement ratio > load power > engine speed > stage HM. The influences of load power and engine speed on efficiency characteristics were the positive correlation and the negative correlation, respectively. The influences decreased as the load power and the engine speed increased.
The proposed I-GA-based piecewise modeling method for HMCVT efficiency characteristics had a good modeling result. The MAPE of all models (a total of seven models) had an error range of 1.6884~3.1375% used the stage HM1 as an example. The two-factor model considered the displacement ratio and the load power as independent variables and could be applied to the case with less test data. The two-factor model could be corrected by introducing the first-order term of engine speed, in which case the MAPE was reduced by 7.7024% and the R2 was improved by 9.2943%.
Author Contributions
Methodology, Z.C.; software, Z.C., J.L. and Y.C.; validation, Z.C.; investigation, Z.C., W.L., L.L., P.Z. and W.C.; resources, Z.C. and Z.L.; writing—original draft preparation, Z.C.; writing—review and editing, Z.C. and Z.L.; supervision, Z.L.; and project administration, Z.C. and Z.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant number: 52105063), National Key Research and Development Plan (2016YFD0701103) and Metasequoia teacher research start-up fund of Nanjing Forestry University (163106061).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on demand from the corresponding authors at (luzx@njau.edu.cn or chengzhun38@163.com).
Acknowledgments
The authors thank the National Natural Science Foundation of China (grant number: 52105063), National Key Research and Development Plan (2016YFD0701103) and Metasequoia teacher research start-up fund of Nanjing Forestry University (163106061) for funding. We also thank the anonymous reviewers for providing critical comments and suggestions that improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| HMCVT | Hydro-mechanical continuously variable transmission |
| I-GA | Improved genetic algorithm |
| MAPE | Mean absolute percentage error |
| R2 | Coefficient of determination |
| CR, CV, C1~C4 | Clutch in HMCVT system |
| ip, im, iR, i1~i6 | Gear ratio in HMCVT system |
| P1, P2 | Planetary gears in HMCVT system |
| B1 | Brake in HMCVT system |
| H0 | Purely hydraulic working stage |
| HM1~HM4 | Power coupled working stages |
| PTO | Power take-off |
| The range of the ith factor | |
| The set of mean efficiency of all levels of the ith factor | |
| a1~aj | The decision variables of the first sub-model of piecewise model |
| b1~bj | The decision variables of the second sub-model of piecewise model |
| The objective function | |
| The number of samples in each range after the range division of efficiency characteristics | |
| The estimated value of sub-model 1 | |
| The measured value in the working stages of sub-model 1 | |
| The estimated value of sub-model 2 | |
| The measured value in the working stages of sub-model 2 | |
| x1~ x3 | The factors ranked by range analysis |
| The HMCVT efficiency characteristic piecewise model built with the polynomial | |
| Variable pump’s displacement ratio | |
| The new independent variable in order to correct the original two-factor model | |
| The total number of samples at one HM stage of HMCVT | |
| All test values at one HM stage of HMCVT | |
| ne | Engine speed |
References
- Tian, J.; Wang, Q.; Ding, J.; Wang, Y.Q.; Ma, Z.S. Integrated control with DYC and DSS for 4WID electric vehicles. IEEE Access 2019, 7, 124077–124086. [Google Scholar] [CrossRef]
- Zhou, W.L.; Zheng, Y.P.; Pan, Z.J.; Lu, Q. Review on the Battery Model and SOC Estimation Method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Cheng, Z.; Zheng, S.; Qian, Y.; Lu, Z.; Zhang, H. Based on improved SA and GA a new method for optimizing transmission parameters of automotive HMCVT. J. Mech. Strength 2020, 42, 61–66. [Google Scholar]
- Xiao, G.B.; Zhang, H.B.; Sun, N.; Zhang, Y. Cooperative link scheduling for RSU-assisted dissemination of basic safety messages. Wirel. Netw. 2021, 27, 1335–1351. [Google Scholar] [CrossRef]
- Macor, A.; Rossetti, A. Optimization of hydro-mechanical power split transmissions. Mech. Mach. Theory 2011, 46, 1901–1919. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Zhang, H.T.; Ge, Y.Y.; Qiu, W.; Xiao, M.H.; Xu, X.M.; Zhou, M.H. Mechanical Efficiency of HMCVT under Steady-State Conditions. Shock Vib. 2021, 2021, 4275922. [Google Scholar] [CrossRef]
- Wu, W.; Luo, J.L.; Wei, C.H.; Liu, H.; Yuan, S.H. Design and control of a hydro-mechanical transmission for all-terrain vehicle. Mech. Mach. Theory 2020, 153, 104052. [Google Scholar] [CrossRef]
- Fussner, D.R.; Singh, Y.P. Design of input coupled split power transmissions, arrangements, and their characteristics. J. Mech. Des. 2004, 126, 542–550. [Google Scholar] [CrossRef]
- Du, J.Y.; Yuan, S.H.; Guo, Z.Z. Study on the Characteristics of Hydro-mechanical Transmissions for Vehicle. J. Mech. Transm. 2008, 32, 51–53, 131. [Google Scholar]
- Lu, L.; Zhou, Y.; Li, H.; Wang, Y.; Yin, Y.; Zhao, J. Electro-hydraulic Shift Quality of Power Shift Transmission of Heavy Duty Tractor. Trans. Chin. Soc. Agric. Mach. 2020, 51 (Suppl. 1), 550–556, 602. [Google Scholar]
- Xi, Z.; Zhou, Z.; Zhang, M.; Cao, Q. Shift Characteristics and Control Strategy of Powershift Transmission on Tractor. Trans. Chin. Soc. Agric. Mach. 2016, 47, 350–357. [Google Scholar]
- Ni, X.D.; Zhu, S.H.; Ouyang, D.Y.; Chang, Y.L.; Wang, G.M.; Nguyen, W.T. Design and experiment of hydro-mechanical CVT speed ratio for tractor. Trans. Chin. Soc. Agric. Mach. 2013, 44, 15–20. [Google Scholar]
- He, C.; Lang, P.; Kang, M.; Zhang, H. Transmission design and force analysis of HMCVT for high power tractor. J. Mech. Transm. 2018, 42, 54–59. [Google Scholar]
- Volpe, S.S.; Carbone, G.; Napolitano, M.; Sedoni, E. Design optimization of input and output coupled power split infinitely variable transmissions. J. Mech. Des. 2009, 131, 111002. [Google Scholar] [CrossRef]
- Rossetti, A.; Macor, A. Multi-objective optimization of hydro-mechanical power split transmissions. Mech. Mach. Theory 2013, 62, 112–128. [Google Scholar] [CrossRef]
- Xiao, M.H.; Zhao, J.; Wang, Y.W.; Zhang, H.J.; Lu, Z.X.; Wei, W.H. Fuel economy of multiple conditions self-adaptive tractors with hydro-mechanical CVT. Int. J. Agric. Biol. Eng. 2018, 11, 102–109. [Google Scholar] [CrossRef]
- Ahn, S.; Choi, J.; Kim, S.; Lee, J.; Choi, C.; Kim, H. Development of an integrated engine-hydro-mechanical transmission control algorithm for a tractor. Adv. Mech. Eng. 2015, 7, 1687814015593870. [Google Scholar] [CrossRef]
- Ince, E.; Guler, M.A. On the advantages of the new power-split infinitely variable transmission over conventional mechanical transmissions based on fuel consumption analysis. J. Clean. Prod. 2020, 244, 118795. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, J.; Wang, J.; Guo, Z.; Guo, F.; Xi, Z.; Xu, J. Speed changing control strategy for improving tractor fuel economy. Trans. Chin. Soc. Agric. Eng. 2020, 36, 82–89. [Google Scholar]
- Li, J.; Liu, L.; Xiao, M.; Wang, T.; Wang, X.; Zhang, H. Research on dynamic characteristics of hydro-mechanical continuously variable transmission. J. Mech. Strength 2017, 39, 14–19. [Google Scholar]
- Xia, Y.; Sun, D. Characteristic analysis on a new hydro-mechanical continuously variable transmission system. Mech. Mach. Theory 2018, 126, 457–467. [Google Scholar] [CrossRef]
- Liu, F.; Wu, W.; Hu, J.; Yuan, S. Design of multi-range hydro-mechanical transmission using modular method. Mech. Syst. Signal Process. 2019, 126, 1–20. [Google Scholar] [CrossRef]
- Cheng, Z.; Lu, Z.; Dai, F. Research on HMCVT Efficiency Model Based on the Improved SA Algorithm. Math. Probl. Eng. 2019, 2019, 2856908. [Google Scholar] [CrossRef]
- Wang, G.; Zhu, S.; Shi, L.; Ni, X.; Ruan, W.; Ouyang, D. Simulation and experiment on efficiency characteristics of hydraulic mechanical continuously variable transmission for tractor. Trans. Chin. Soc. Agric. Eng. 2013, 29, 42–48. [Google Scholar]
- Xu, X.M.; Lin, P. Parameter identification of sound absorption model of porous materials based on modified particle swarm optimization algorithm. PLoS ONE 2021, 16, e0250950. [Google Scholar] [CrossRef]
- Chang, C.C.; Zheng, Y.P.; Yu, Y. Estimation for battery state of charge based on temperature effect and fractional extended kalman filter. Energies 2020, 13, 5947. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, Y.P.; Yu, Y. Joint estimation of soc of lithium battery based on dual kalman filter. Processes 2021, 9, 1412. [Google Scholar] [CrossRef]
- Li, Y.J.; Ma, Z.S.; Zheng, M.; Li, D.X.; Lu, Z.H.; Xu, B. Performance analysis and optimization of a high-temperature PEMFC vehicle based on particle swarm optimization algorithm. Membranes 2021, 11, 691. [Google Scholar] [CrossRef]
- Cheng, Z.; Lu, Z.X.; Qian, J. A new non-geometric transmission parameter optimization design method for HMCVT based on improved GA and maximum transmission efficiency. Comput. Electron. Agric. 2019, 167, 105034. [Google Scholar] [CrossRef]
- Cheng, Z.; Zhou, H.D.; Lu, Z.X. A Novel 10-parameter motor efficiency model based on I-SA and its comparative application of energy utilization efficiency in different driving modes for electric tractor. Agriculture 2022, 12, 362. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).