Study on Structural Vibration Characteristics of L-Shaped Flexible Ring Gear and Establishment of System Coupling Vibration Model
Abstract
:1. Introduction
2. Modeling of Planetary Transmission System Coupled with Vibration of L-Shaped Flexible Structure and Rigid System
2.1. Steps for Building a Coupled Vibration Planetary Transmission System Model
- (a)
- Determine the meshing line position of each internal and external meshing pairs
- (b)
- Set the time varying meshing unit and function relation
- (c)
- Errors, loaded transmission errors and meshing impact are included
- (d)
- Other components
- (e)
- Create flexible body of ring gear
2.2. Flexible Body Theory
2.3. Comparison of Coupled Model and Lump Mass Method
3. Structural Vibration Characteristics of L-Shaped Flexible Ring Gear and Its Influence on System Dynamic Characteristics
3.1. Type of Structural Vibration
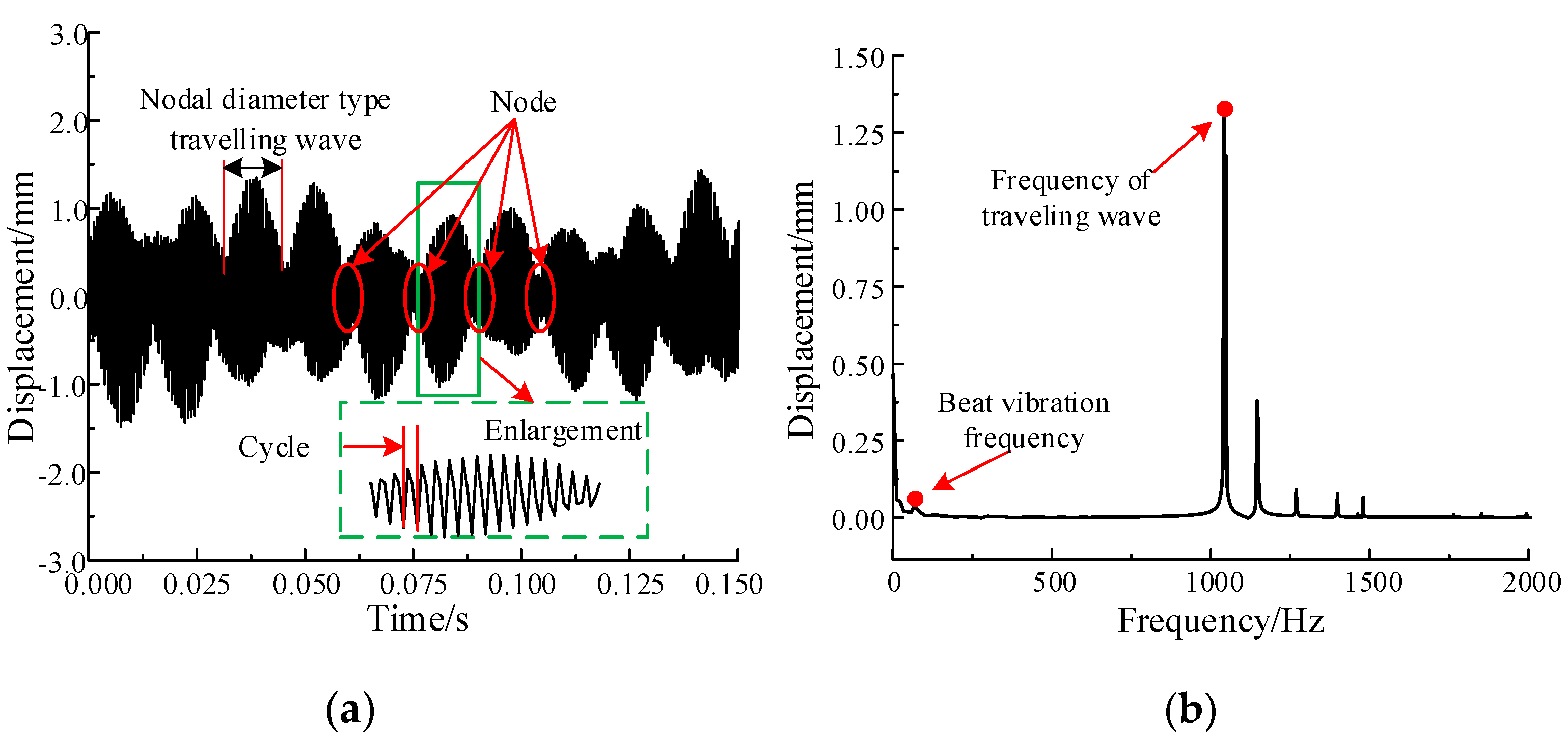
3.2. Characteristics of Nodal Diameter Vibration
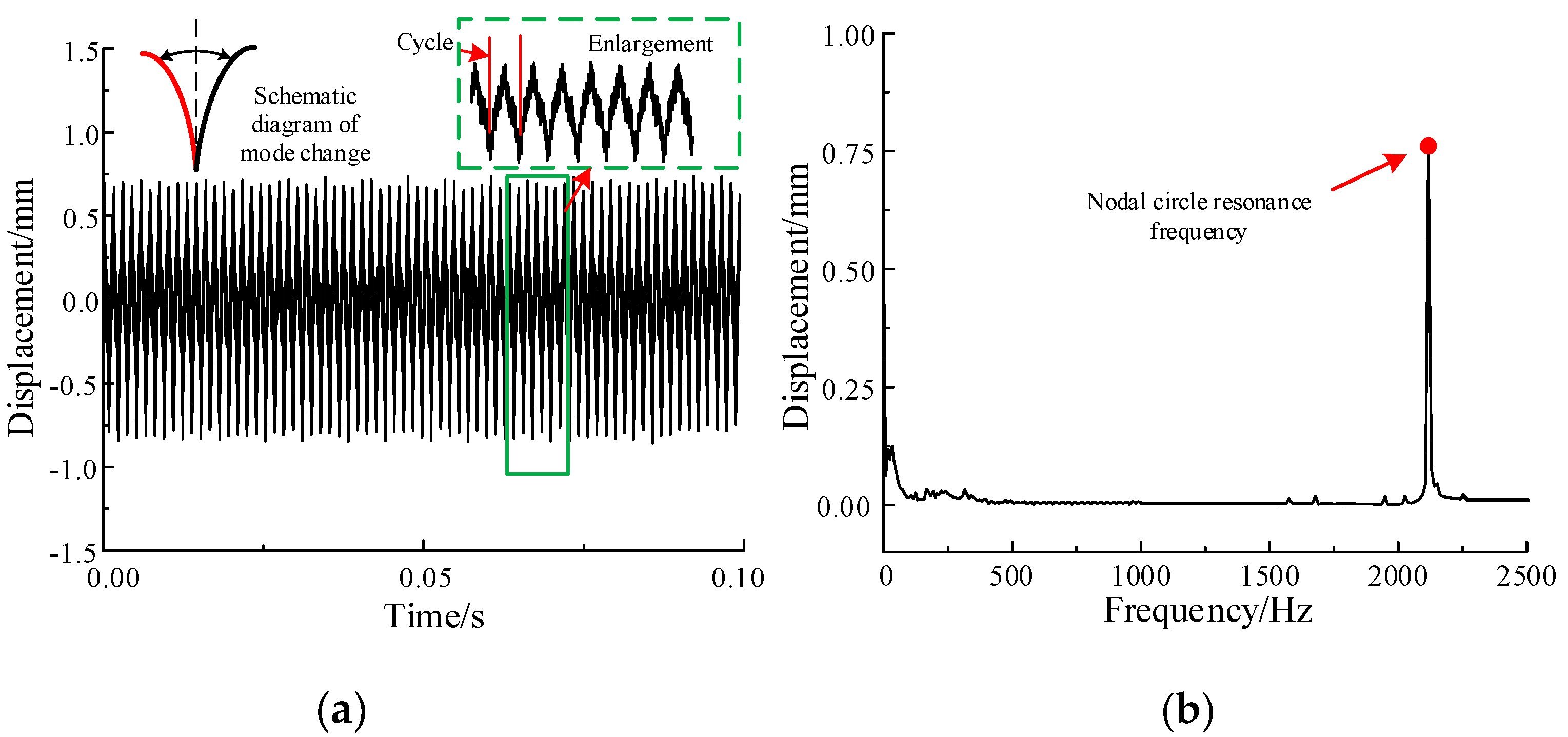
3.3. Analysis of Nodal Circle Vibration Characteristics
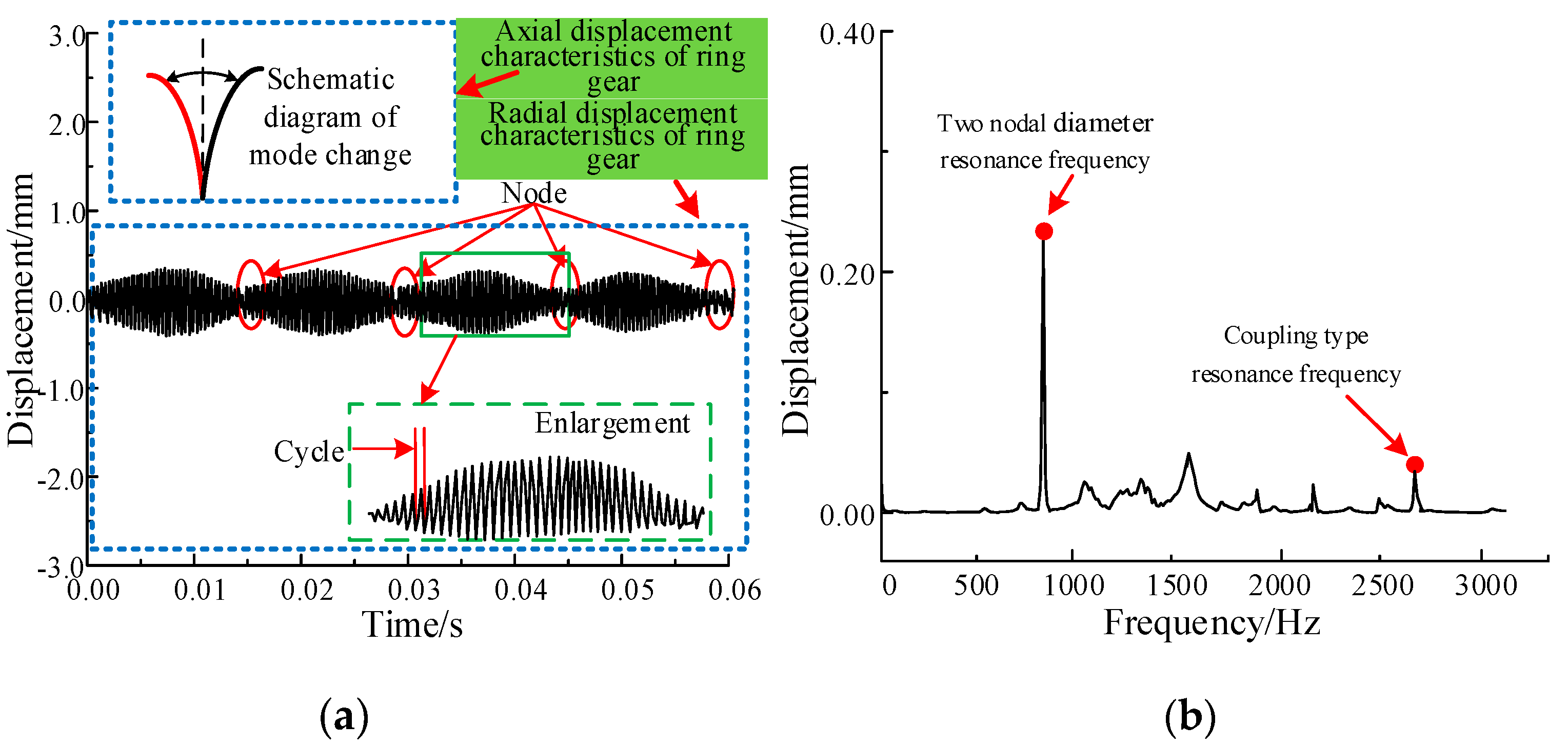
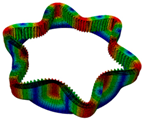
3.4. Analysis of Coupling Nodal Diameter and Nodal Circle Vibration Characteristics
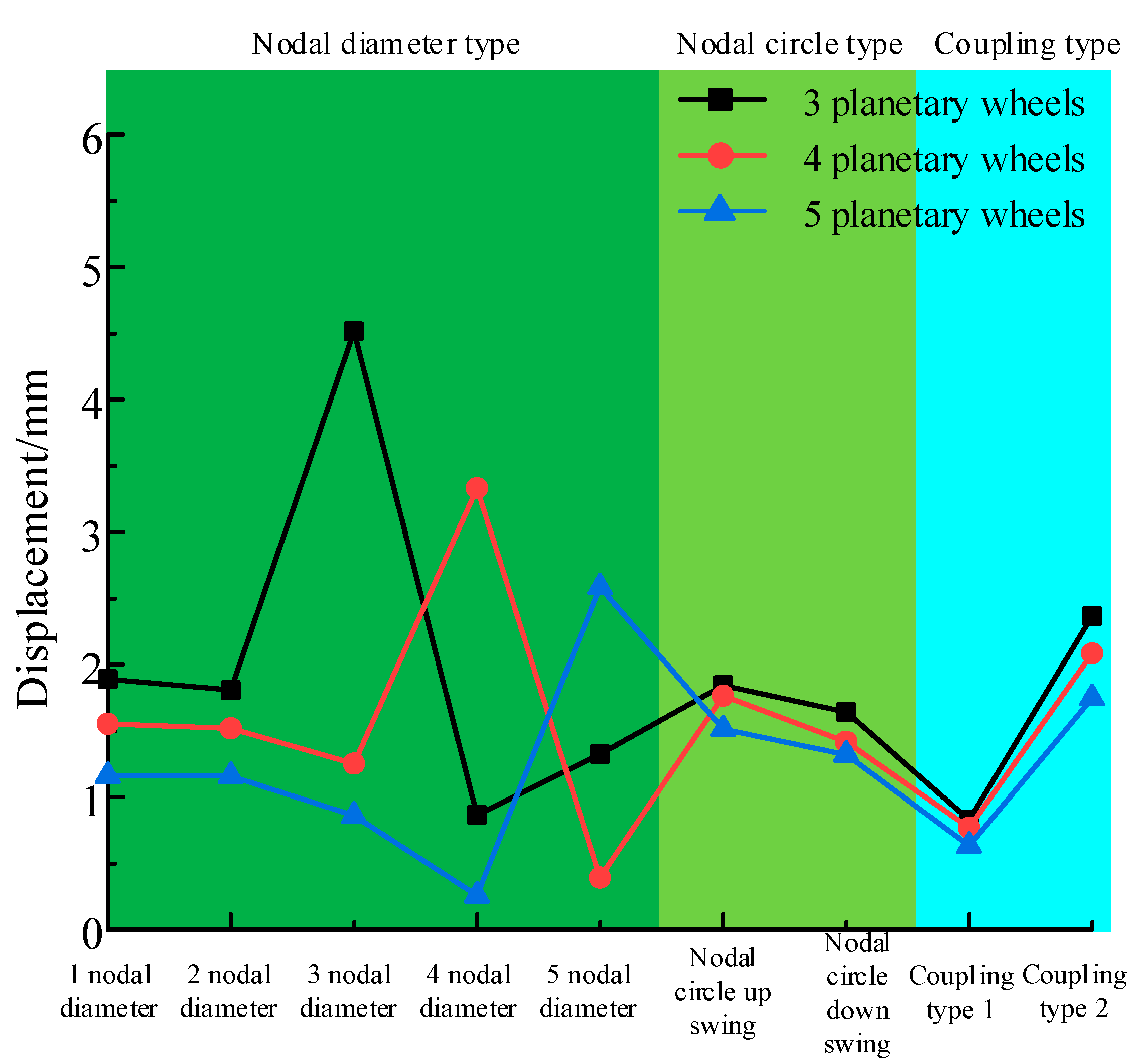
3.5. Relationship between Structural Modes and the Number of Planetary Wheels
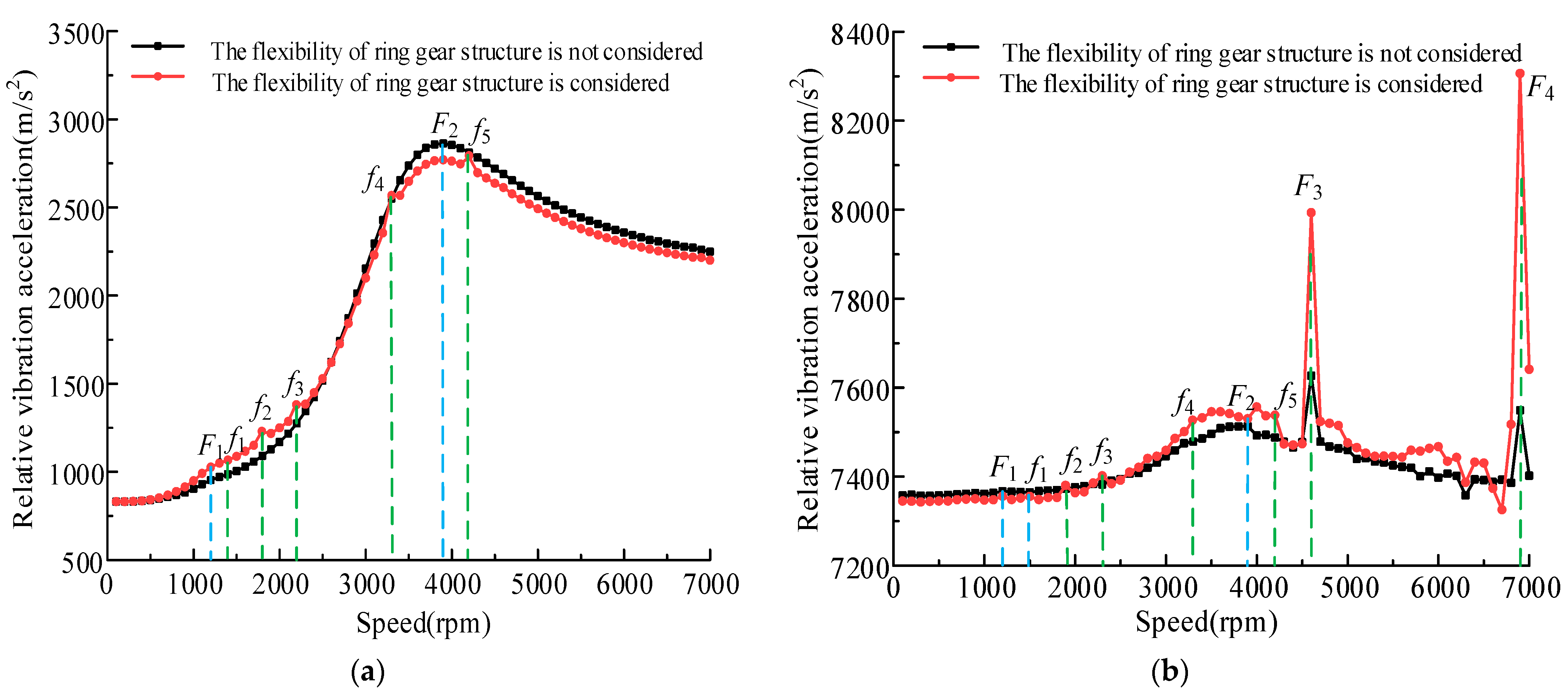
3.6. Influence of L-Shaped Flexible Ring Gear on Dynamic Response of Planetary Transmission System under All Working Conditions
4. Conclusions
- (1)
- When the nodal diameter traveling wave vibration is generated, the displacement response presents obvious periodic envelope vibration, which has the characteristics of beat vibration, the displacement response amplitude is significantly enhanced, and the unbalance loading effect of L-shaped flexible ring gear will be further increased.
- (2)
- When the nodal circle type resonance occurs, the displacement response on the rim does not show periodic envelope vibration. Compared with the nodal diameter traveling wave vibration, the resonance amplitude is smaller, resulting in the continuous change of the unbalance loading position on the tooth surface of L-shaped flexible ring gear. The coupling mode is a high order mode, which has the least influence on the structural vibration.
- (3)
- When the number of nodal diameters is equal to the number of planetary gears, the vibration displacement response of the structure is the largest. In addition, the vibration displacement response of traveling wave with low nodal diameter is stronger than that with high nodal diameter.
- (4)
- The low order mode and nodal diameter mode are not conducive to the load sharing performance of the system, and the nodal circle shaking mode will make the load sharing and dynamic load performance of the system worse.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Xu, H.C.; Qin, D.T. Vibration response of flexible spur ring gear with elastic foundation under internal excitation. J. Mech. Eng. 2008, 9, 161–167. [Google Scholar] [CrossRef]
- Qin, D.T. International gear transmission research status. J. Chongqing Univ. 2014, 8, 1–10. [Google Scholar]
- Hidaka, T.; Terauchi, Y.; Nagamura, K. Dynamic behavior of planetary gear: 7th report, influence of the thickness of the ring gear. Bull. JSME 1979, 22, 1142–1149. [Google Scholar] [CrossRef]
- Kahraman, A.; Ligata, H.; Singh, A. Influence of ring gear rim thickness on planetary gear set behavior. J. Mech. Des. 2012, 132, 021002. [Google Scholar] [CrossRef]
- Kahraman, A.; Vijayakar, S. Effect of internal gear flexibility on the quasi-static behavior of a planetary gear set. J. Mech. Des. 2001, 123, 408–415. [Google Scholar] [CrossRef]
- Kahraman, A.; Kharazi, A.A.; Umrani, M. A deformable body dynamic analysis of planetary gears with thin rims. J. Sound Vib. 2003, 262, 752–768. [Google Scholar] [CrossRef]
- Wang, L.X.; Wu, S.M.; Liu, J.H.; Chen, L.K. Dynamic characteristics analysis of the planetary gear system with the flexible ring. Mach. Des. Manuf. 2018, 1, 40–43. [Google Scholar]
- Bao, H.Y.; Zhou, X.J.; Zhu, R.P.; Lu, F.X. Load sharing analysis of planetary gear train with meshing beyond pitch point considering flexible deformable ring. J. Cent. South Univ. (Nat. Sci.) 2016, 47, 3005–3010. [Google Scholar]
- Li, L. Research on load-sharing design technology of flexible gear ring of planetary gear train. Xi’an Univ. Technol. 2019, 24, 286–289. [Google Scholar] [CrossRef]
- Hu, S.; Fang, Z.; Xu, Y.; Guan, Y.; Shen, R. Characteristics analysis of the new flexible ring gear for helicopter reducer. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2021, 235, 353–374. [Google Scholar] [CrossRef]
- Hu, S.Y.; Fang, Z.D.; Xu, Y.Q.; Shen, R. Analysis and comparison of the flexible and load sharing and dynamic characteristics load factor of the structure type of ring gear. J. Chongqing Univ. 2020, 12, 1–16. [Google Scholar]
- Ren, C.; Cui, B.Z.; Wang, B. Simulation research of Planetary wheel wear Fault based on ADAMS. Manuf. Technol. Mach. Tools 2019, 8, 113–116. [Google Scholar]
- Ma, C.Y.; Yi, J.D.; Xu, Y.G. Dynamic simulation analysis of planetary gearbox based on rigid-flexible coupling model. J. Beijing Univ. Technol. 2019, 45, 719–726. [Google Scholar] [CrossRef]
- Guo, H.Z.; Tang, C.J.; Chen, J.F. Dynamic simulation of planetary gear Train based on ADAMS. J. Mech. Transm. 2013, 5, 86–89. [Google Scholar]
- Lu, Y.; Ma, X.G.; Shu, Q.L. Planetary Gear Train dynamics Simulation based on RecurDyn. J. Shenyang Li Gong Univ. 2008, 27, 76–79. [Google Scholar]
- Ma, X.G.; Yang, W.; You, X.M. Multi-body dynamical analysis on rigid-flexible coupling for planetary gear system. Chin. J. Constr. Mach. 2009, 7, 24–30. [Google Scholar]
- Jia, X.P.; Fan, S.G.; Yu, K.L. Dynamical simulation of planetary coupling mechanism based on RecurDyn. J. Hunan Inst. Sci. Technol. (Nat. Sci. Ed.) 2014, 1, 43–46. [Google Scholar]
- Xu, H.B.; Xu, T.J.; Huang, Y.P. Analysis of Load Sharing of Planetary Gear Train Considering the Flexibility of Planet Carrier. J. Mech. Transm. 2016, 3, 107–111. [Google Scholar]
- Huang, X.C. Dynamics characteristic analysis of a multistage gear transmission mechanism based on SIMPACK. J. Mech. Transm. 2014, 38, 148–150. [Google Scholar]
- Chen, X.H.; Huang, Z.H.; Pu, J.L. Dynamics Simulation Analysis of Flexible Wheel set Based on ANSYS and SIMPACK. Electr. Drive Locomot. 2014, 1, 41–45. [Google Scholar]
- Miu, B.R.; Fang, X.H.; Fu, X.T. SIMPACK Dynamics Analysis Basics Tutorial; Southwest Jiao Tong University Press: Chengdu, China, 2008. [Google Scholar]
- Hu, S.Y.; Fang, Z.D.; Xu, Y.Q.; Guan, Y.B.; Shen, R. Meshing impact analysis of planetary transmission system considering the influence of multiple errors and its effect on the load sharing and dynamic load factor characteristics of the system. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2020, 235, 57–74. [Google Scholar] [CrossRef]
- Yan, L.T.; Zhu, Z.G.; Li, Q.H. Vibration of High-Speed Rotating Machinery; National Defense Industry Press: Beijing, China, 1994. [Google Scholar]
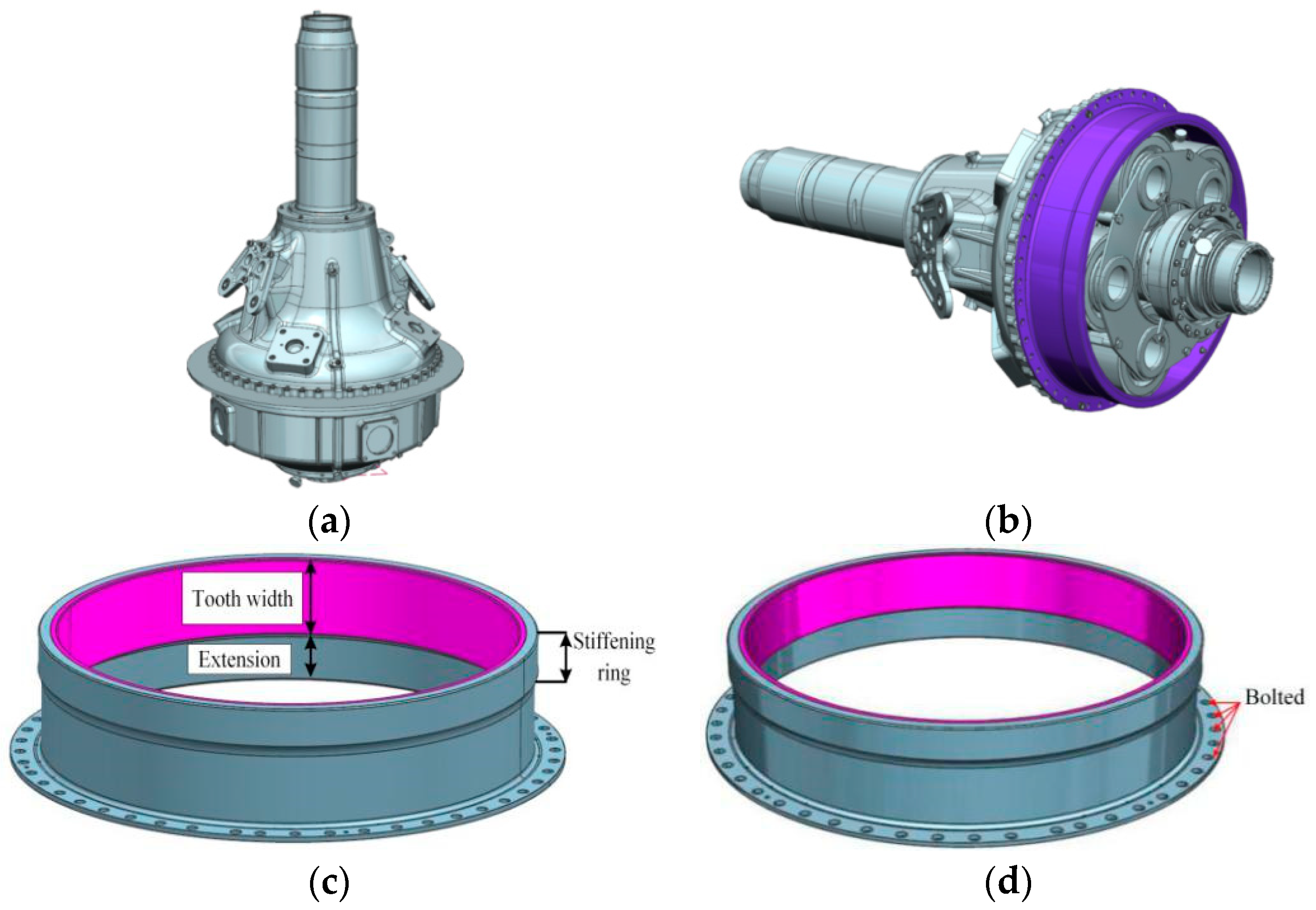
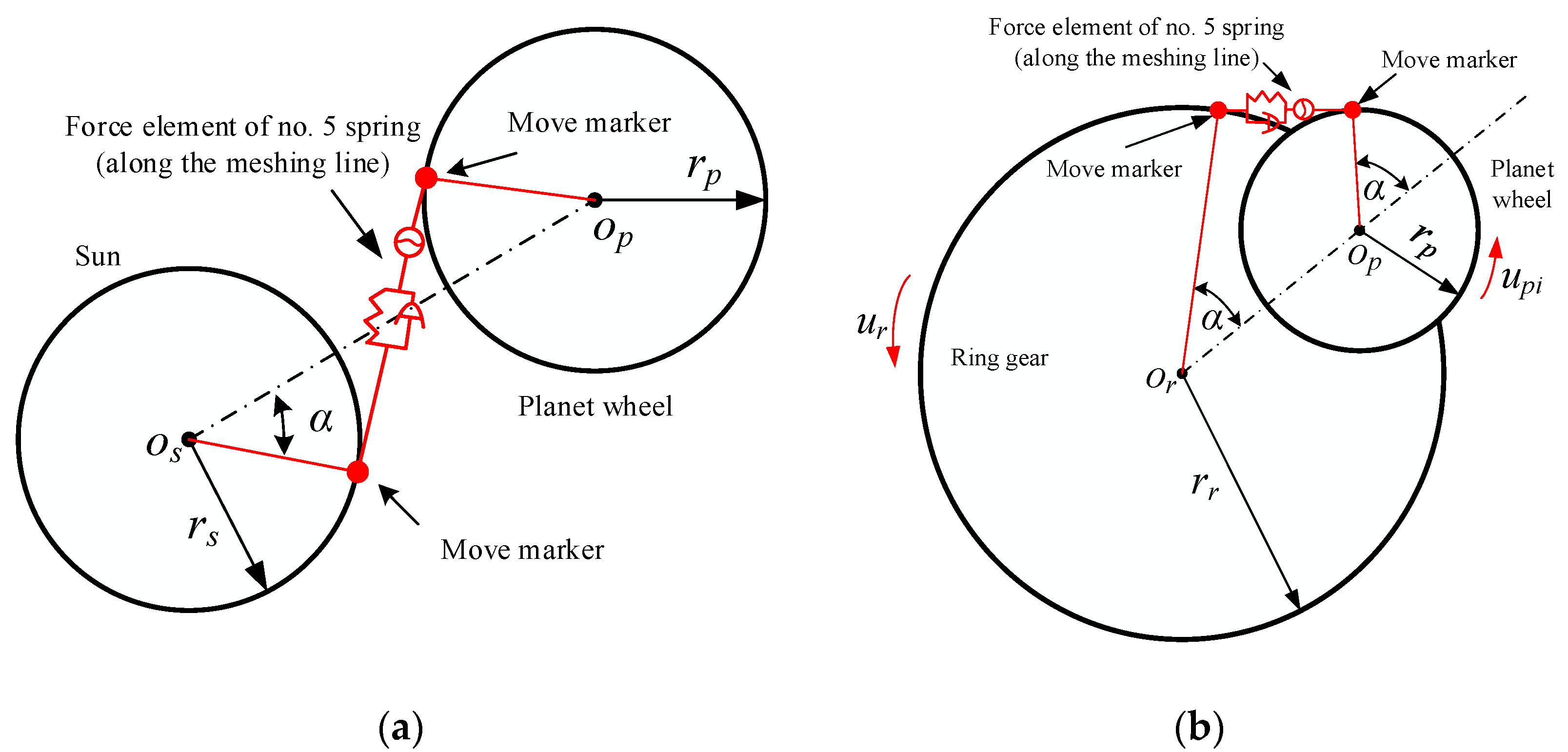



| Parameters | Unit | Sun | Planetary Gear | L-Shaped Flexible Ring Gear |
|---|---|---|---|---|
| Tooth number Z1 and Z2 | — | 48 | 55 | 162 |
| Normal module mn | mm | 3.8 | ||
| Normal pressure angle αn | deg | 22.5 | ||
| Face width B | mm | 88 | ||
| Addendum ha | mm | 6.6 | 6.6 | 3.35 |
| Dedendum hf | mm | 2.05 | 2.05 | 4.825 |
| Elastic modulus E | GPa | 210 | ||
| Density ρ | g/cm3 | 7.85 | ||
| Speed v | rpm | 1128 | ||
| Power | kW | 2958.8 | ||
| Order | Frequency/Hz | Order | Frequency/Hz | Order | Frequency/Hz | Order | Frequency/Hz |
|---|---|---|---|---|---|---|---|
| 1 | 645.37 | 6 | 863.00 | 11 | 1558.70 | 16 | 2206.70 |
| 2 | 645.62 | 7 | 1081.60 | 12 | 1559.00 | 17 | 2207.40 |
| 3 | 742.58 | 8 | 1081.90 | 13 | 2069.00 | 18 | 2238.50 |
| 4 | 744.32 | 9 | 1388.10 | 14 | 2128.10 | 19 | 2430.20 |
| 5 | 862.68 | 10 | 1388.40 | 15 | 2131.10 | 20 | 2567.80 |
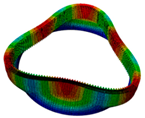 | 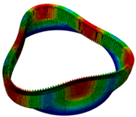 | 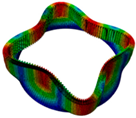 | 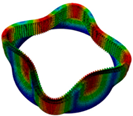 | 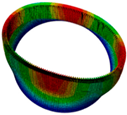 |
| Three nodal diameter | Three nodal diameter | Four nodal diameter | Four nodal diameter | Two nodal diameter |
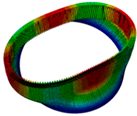 | 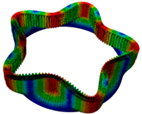 | 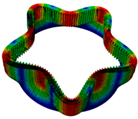 |  |  |
| Two nodal diameter | Five nodal diameter | Five nodal diameter | One nodal diameter | One nodal diameter |
 |  | 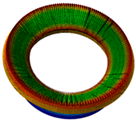 | 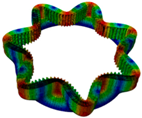 | 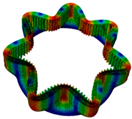 |
| Six nodal diameter | Six nodal diameter | Nodal circle up swing | Seven nodal diameter | Seven nodal diameter |
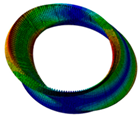 |  |  |  |  |
| Coupling type 1 | Coupling type 1 | Nodal circle down swing | Nodal circle up swing | Coupling type 2 |
| Type | Three Nodal Diameter | Four Nodal Diameter | Two Nodal Diameter | Five Nodal Diameter | One Nodal Diameter | Six Nodal Diameter | Seven Nodal Diameter |
|---|---|---|---|---|---|---|---|
| Resonance speed (rpm) | 1045.73 | 1203.25 | 1397.86 | 1752.59 | 2249.24 | 2525.67 | 3448.31 |
| Resonance frequency (Hz) | 645.37 | 742.58 | 862.68 | 1081.60 | 1388.10 | 1558.70 | 2128.10 |
| Type | Resonance Speed (rpm) | 3 Wheels/mm | 4 Wheels/mm | 5 Wheels/mm |
|---|---|---|---|---|
| One nodal diameter | 2249.24 | 1.8892 | 1.5538 | 1.1610 |
| Two nodal diameter | 1397.86 | 1.8083 | 1.5200 | 1.1600 |
| Three nodal diameter | 1045.73 | 4.5142 | 1.2537 | 0.8600 |
| Four nodal diameter | 1203.25 | 0.8658 | 3.3312 | 0.2585 |
| Five nodal diameter | 1752.59 | 1.3250 | 0.3919 | 2.5865 |
| Nodal circle up swing | 3352.54 | 1.8442 | 1.7662 | 1.5120 |
| Nodal circle down swing | 3627.19 | 1.642 | 1.4181 | 1.3210 |
| Coupling type 1 | 3575.67 | 0.8283 | 0.7688 | 0.6340 |
| Coupling type 2 | 4160.78 | 2.3667 | 2.0844 | 1.7485 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Fang, Z.; Guan, Y.; Hou, X.; Liu, C. Study on Structural Vibration Characteristics of L-Shaped Flexible Ring Gear and Establishment of System Coupling Vibration Model. Machines 2022, 10, 339. https://doi.org/10.3390/machines10050339
Hu S, Fang Z, Guan Y, Hou X, Liu C. Study on Structural Vibration Characteristics of L-Shaped Flexible Ring Gear and Establishment of System Coupling Vibration Model. Machines. 2022; 10(5):339. https://doi.org/10.3390/machines10050339
Chicago/Turabian StyleHu, Shengyang, Zongde Fang, Yabin Guan, Xiangying Hou, and Chao Liu. 2022. "Study on Structural Vibration Characteristics of L-Shaped Flexible Ring Gear and Establishment of System Coupling Vibration Model" Machines 10, no. 5: 339. https://doi.org/10.3390/machines10050339
APA StyleHu, S., Fang, Z., Guan, Y., Hou, X., & Liu, C. (2022). Study on Structural Vibration Characteristics of L-Shaped Flexible Ring Gear and Establishment of System Coupling Vibration Model. Machines, 10(5), 339. https://doi.org/10.3390/machines10050339






