Bearing Fault Diagnosis via Incremental Learning Based on the Repeated Replay Using Memory Indexing (R-REMIND) Method
Abstract
:1. Introduction
2. Theoretical Background
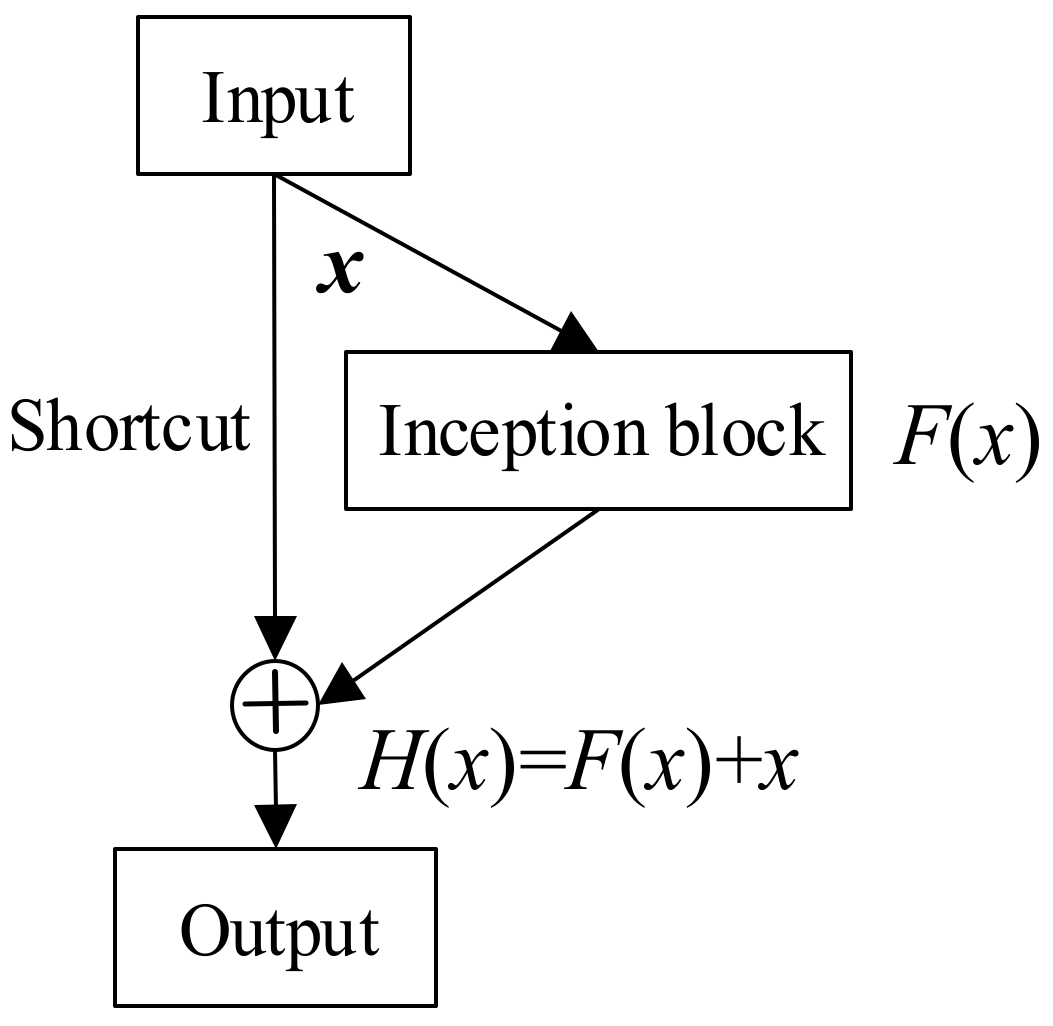
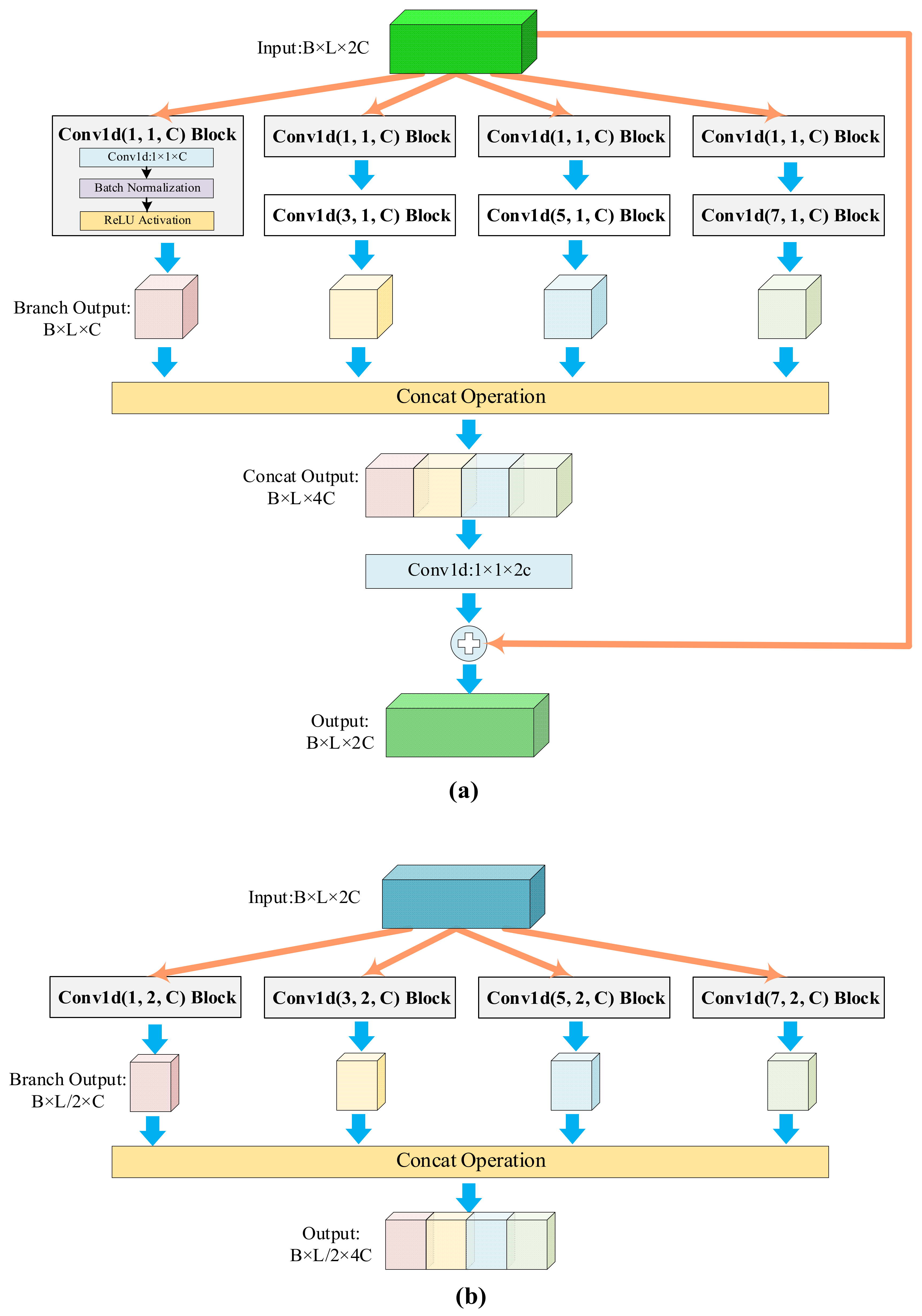
2.1. Inception-ResNet Module
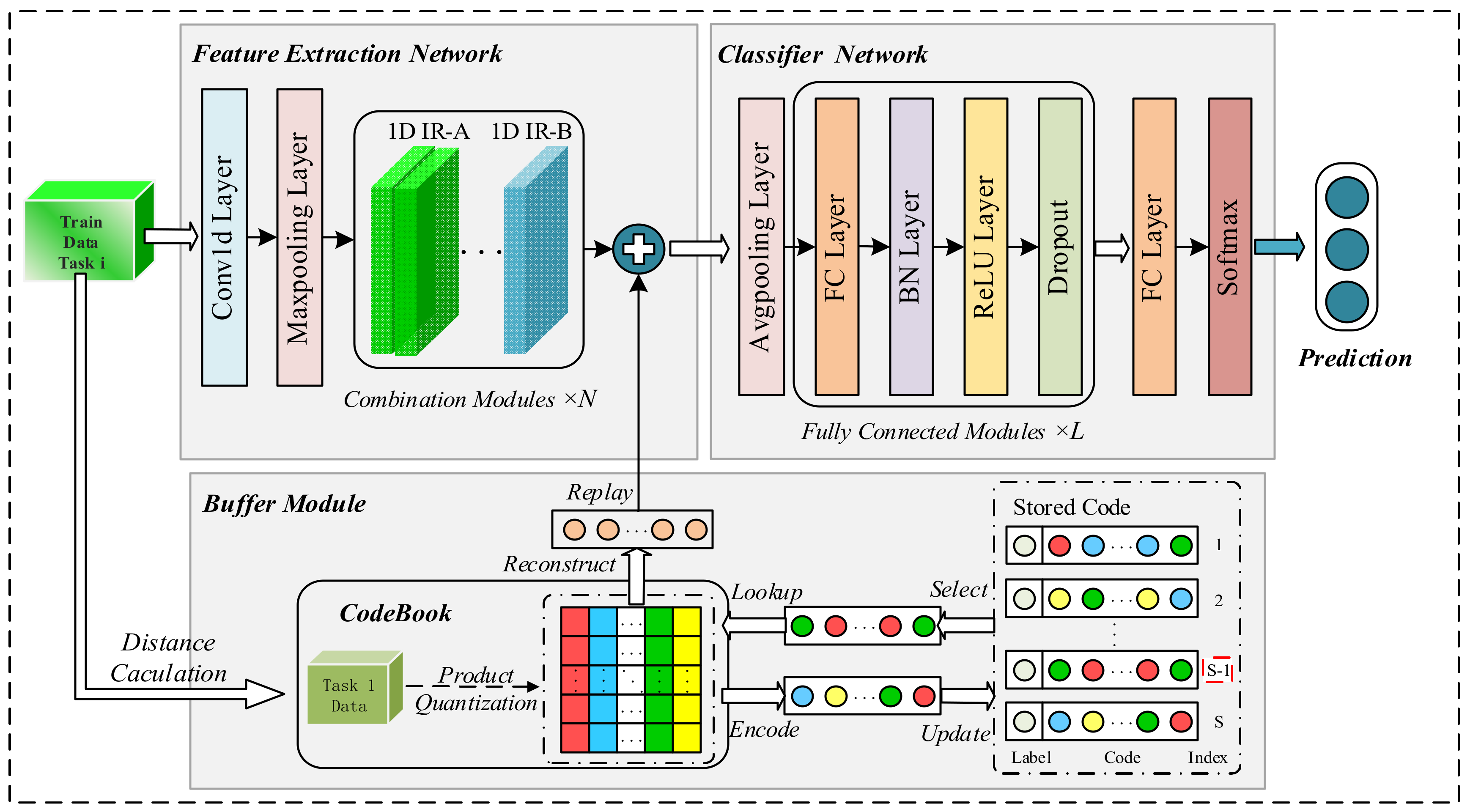
2.2. Product Quantization
3. The Proposed Method
3.1. The R-REMIND Model
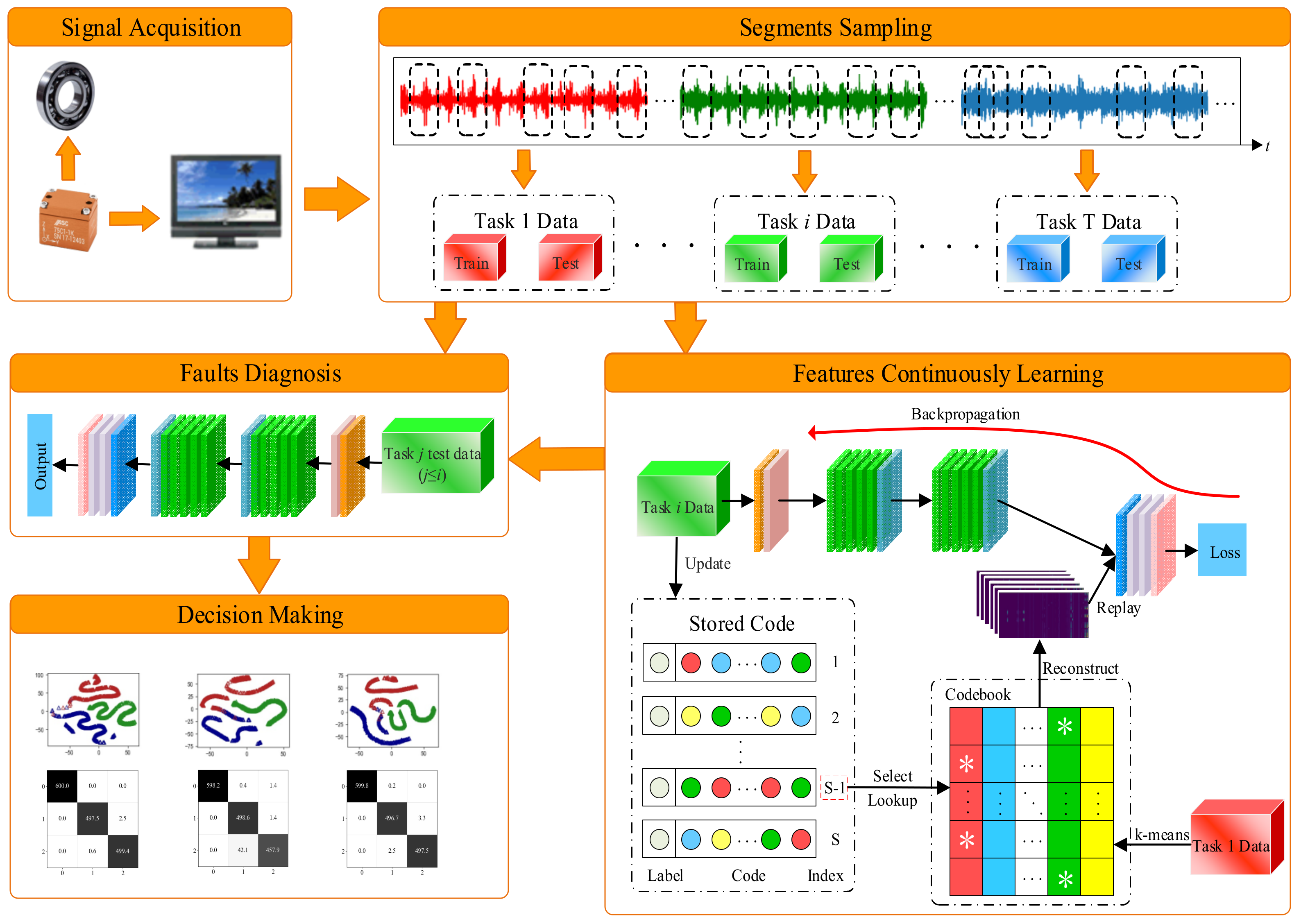
3.2. Diagnostic Framework
- Step 1: Signal acquisition. Under different loads, vibration signals and bearing status data are collected and processed.
- Step 2: Segmental sampling. The collected raw vibration signals are randomly sampled using a fixed-length sliding window. The sampled segments are divided into training and test datasets under various working conditions.
- Step 3: Continuous learning. The training data for different tasks are sequentially learned by R-REMIND. The buffer module is updated using the features of the current task after learning is complete.
- Step 4: Fault diagnosis. The data of previous tasks are diagnosed by the current R-REMIND model to verify the effectiveness of the method.
- Step 5: Decision-making. The model reviews the bearing status and developmental trend, and then makes a decision.
4. Experiments and Results
4.1. The Dataset
4.2. Experimental Setup
4.3. Evaluation Metrics
4.4. Results and Analysis
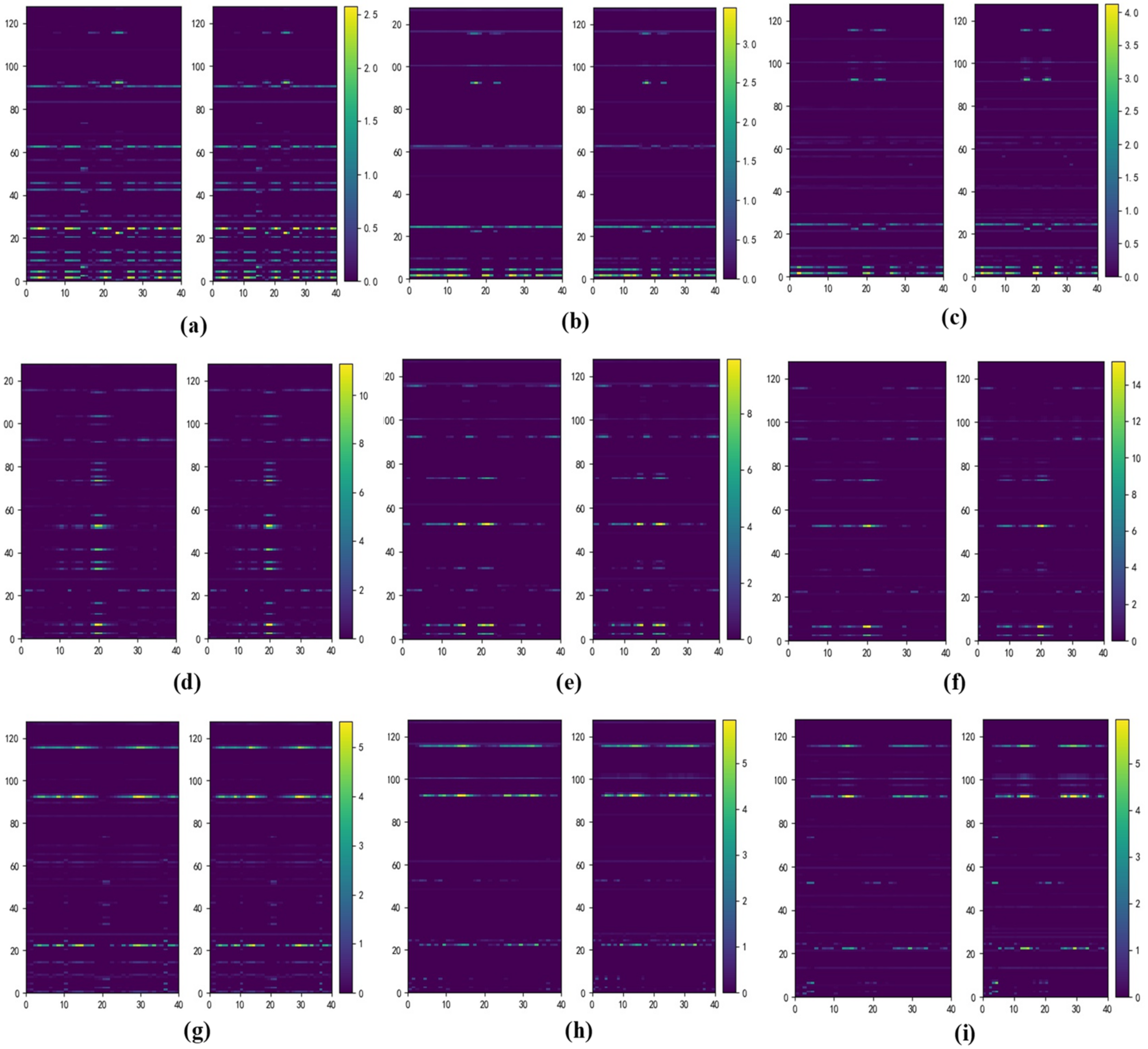
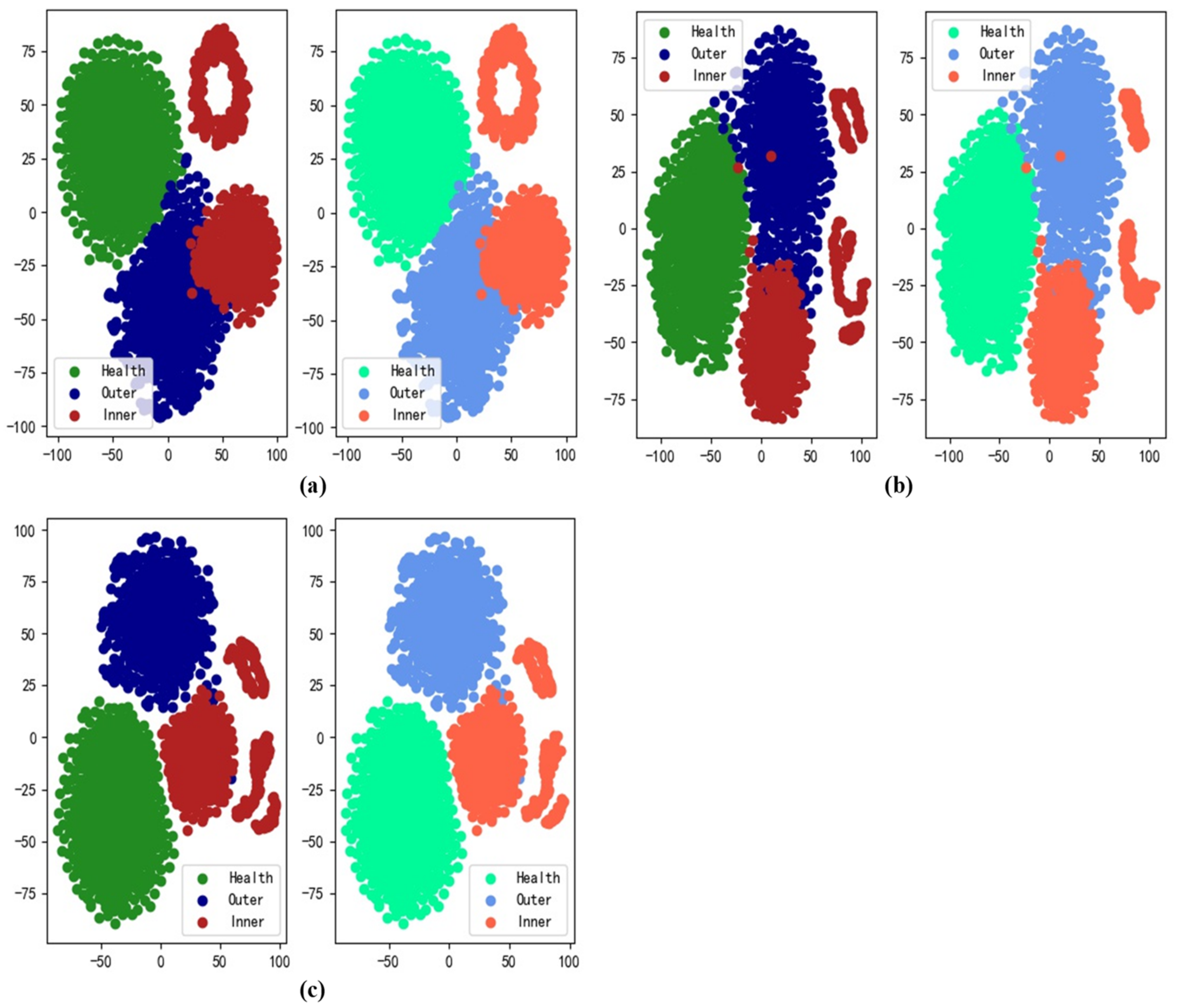
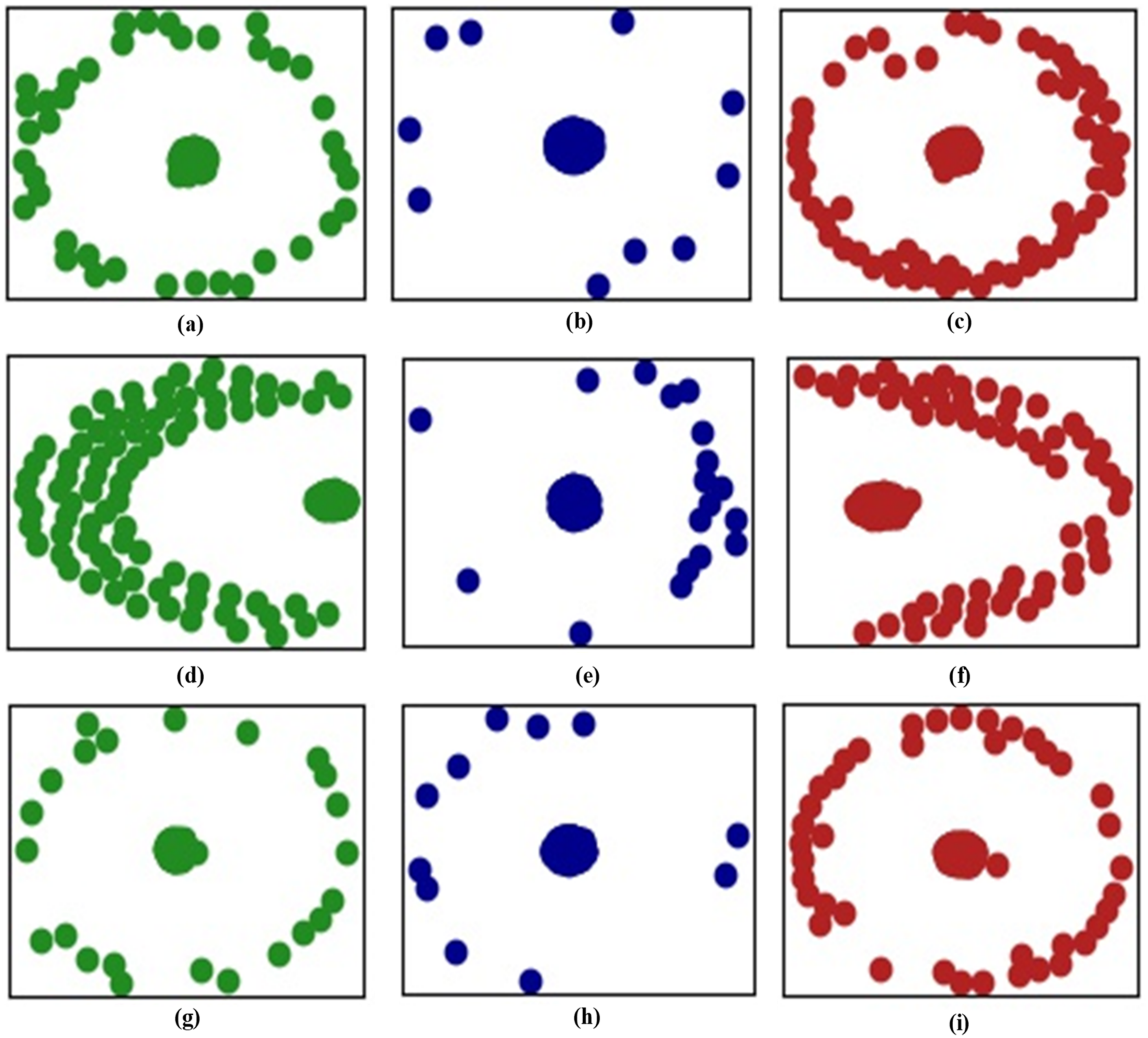
4.4.1. Visualization of Reconstructed Features
4.4.2. Visualization of Training
4.4.3. Model Results
4.4.4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shahriar, M.R.; Borghesani, P.; Tan, A.C.C. Electrical signature analysis-based detection of external bearing faults in electromechanical drivetrains. IEEE Trans. Ind. Electron. 2018, 65, 5941–5950. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, M.; Li, Y.; Xu, Z.; Wang, J.; Fang, X. A multi-input and multi-task convolutional neural network for fault diagnosis based on bearing vibration signal. IEEE Sens. J. 2021, 21, 10946–10956. [Google Scholar] [CrossRef]
- Kudelina, K.; Baraškova, T.; Shirokova, V.; Vaimann, T.; Rassõlkin, A. Fault detecting accuracy of mechanical damages in rolling bearings. Machines 2022, 10, 86. [Google Scholar] [CrossRef]
- Yuan, H.; Wu, N.; Chen, X.; Wang, Y. Fault diagnosis of rolling bearing based on shift invariant sparse feature and optimized support vector machine. Machines 2021, 9, 98. [Google Scholar] [CrossRef]
- Nguyen, V.C.; Hoang, D.T.; Tran, X.T.; Van, M.; Kang, H.J. A bearing fault diagnosis method using multi-branch deep neural network. Machines 2021, 9, 345. [Google Scholar] [CrossRef]
- Ni, Q.; Ji, J.C.; Feng, K.; Halkon, B. A novel correntropy-based band selection method for the fault diagnosis of bearings under fault-irrelevant impulsive and cyclostationary interferences. Mech. Syst. Signal Process. 2021, 153, 107498. [Google Scholar] [CrossRef]
- Ni, Q.; Ji, J.C.; Feng, K.; Halkon, B. A fault information-guided variational mode decomposition (FIVMD) method for rolling element bearings diagnosis. Mech. Syst. Signal Process. 2022, 164, 108216. [Google Scholar] [CrossRef]
- Sabir, R.; Rosato, D.; Hartmann, S.; Guehmann, C. LSTM based bearing fault diagnosis of electrical machines using motor current signal. In Proceedings of the 2019 18th IEEE International Conference on Machine Learning and Applications (ICMLA), Boca Raton, FL, USA, 16–19 December 2019; pp. 613–618. [Google Scholar]
- Hoang, D.T.; Kang, H.J. A motor current signal-based bearing fault diagnosis using deep learning and information fusion. IEEE Trans. Instrum. Meas. 2020, 69, 3325–3333. [Google Scholar] [CrossRef]
- Elforjani, M.; Shanbr, S. Prognosis of bearing acoustic emission signals using supervised machine learning. IEEE Trans. Ind. Electron. 2018, 65, 5864–5871. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Wang, X.; Zhang, L. Fault diagnosis of industrial wind turbine blade bearing using acoustic emission analysis. IEEE Trans. Instrum. Meas. 2020, 69, 6630–6639. [Google Scholar] [CrossRef]
- Shao, H.; Xia, M.; Han, G.; Zhang, Y.; Wan, J. Intelligent fault diagnosis of rotor-bearing system under varying working conditions with modified transfer convolutional neural network and thermal images. IEEE Trans. Ind. Inform. 2021, 17, 3488–3496. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Y.; Zheng, Y.; Gao, R.X.; Zhang, F. An integrated fault diagnosis and prognosis approach for predictive maintenance of wind turbine bearing with limited samples. Renew. Energy 2020, 145, 642–650. [Google Scholar] [CrossRef]
- Liang, T.; Wu, S.; Duan, W.; Zhang, R. Bearing fault diagnosis based on improved ensemble learning and deep belief network. J. Phys. Conf. Ser. 2018, 1074, 012154. [Google Scholar] [CrossRef]
- Jiang, H.; Li, X.; Shao, H.; Zhao, K. Intelligent fault diagnosis of rolling bearings using an improved deep recurrent neural network. Meas. Sci. Technol. 2018, 29, 065107. [Google Scholar] [CrossRef]
- Hoang, D.T.; Kang, H.J. Rolling element bearing fault diagnosis using convolutional neural network and vibration image. Cogn. Syst. Res. 2019, 53, 42–50. [Google Scholar] [CrossRef]
- Pham, M.T.; Kim, J.M.; Kim, C.H. 2D CNN-based multi-output diagnosis for compound bearing faults under variable rotational speeds. Machines 2021, 9, 199. [Google Scholar] [CrossRef]
- He, J.; Li, X.; Chen, Y.; Chen, D.; Guo, J.; Zhou, Y. Deep transfer learning method based on 1d-cnn for bearing fault diagnosis. Shock Vib. 2021, 2021, 1–16. [Google Scholar] [CrossRef]
- Han, T.; Liu, C.; Wu, L.; Sarkar, S.; Jiang, D. An adaptive spatiotemporal feature learning approach for fault diagnosis in complex systems. Mech. Syst. Signal Process. 2019, 117, 170–187. [Google Scholar] [CrossRef]
- Razavi-Far, R.; Farajzadeh-Zanjani, M.; Saif, M.; Palade, V. A hybrid ensemble scheme for diagnosing new class defects under non-stationary and class imbalance conditions. In Proceedings of the 2017 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Shanghai, China, 16–18 August 2017; pp. 355–360. [Google Scholar]
- Razavi-Far, R.; Saif, M.; Palade, V.; Zio, E. Adaptive incremental ensemble of extreme learning machines for fault diagnosis in induction motors. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1615–1622. [Google Scholar]
- Kang, J.; Liu, Z.; Sun, W.; Zuo, M.J.; Qin, Y. A class incremental learning approach based on autoencoder without manual feature extraction for rail vehicle fault diagnosis. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018; pp. 45–49. [Google Scholar]
- Yang, Z.; Long, J.; Zi, Y.; Zhang, S.; Li, C. Incremental novelty identification from initially one-class learning to unknown abnormality classification. IEEE Trans. Ind. Electron. 2022, 69, 7394–7404. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, L.; Ding, X.; Wang, L.; Shao, Y. Incremental learning of bearing fault diagnosis via style-based generative adversarial network. In Proceedings of the 2020 International Conference on Sensing, Measurement & Data Analytics in the era of Artificial Intelligence (ICSMD), Xi’an, China, 15–17 October 2020; pp. 512–517. [Google Scholar]
- Wang, Y.; Zeng, L.; Wang, L.; Shao, Y.; Zhang, Y.; Ding, X. An efficient incremental learning of bearing fault imbalanced data set via filter styleGAN. IEEE Trans. Instrum. Meas. 2021, 70, 107498. [Google Scholar] [CrossRef]
- Li, F.; Chen, J.; He, S.; Zhou, Z. Layer regeneration network with parameter transfer and knowledge distillation for intelligent fault diagnosis of bearing using class unbalanced sample. IEEE Trans. Instrum. Meas. 2021, 70, 3522210. [Google Scholar] [CrossRef]
- Hayes, T.L.; Kafle, K.; Shrestha, R.; Acharya, M.; Kanan, C. REMIND your neural network to prevent catastrophic forgetting. In Proceedings of the 16th European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 466–483. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, Inception-ResNet and the impact of residual connections on learning. In Proceedings of the 31st AAAI Conference on Artificial Intelligence(AAAI), San Francisco, CA, USA, 4–9 February 2017; pp. 4278–4284. [Google Scholar]
- Jégou, H.; Douze, M.; Schmid, C. Product quantization for nearest neighbor search. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 117–128. [Google Scholar] [CrossRef] [Green Version]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. Available online: https://arxiv.org/abs/1409.1556 (accessed on 3 April 2022).
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification. In Proceedings of the European Conference of the Prognostics and Health Management Society(PHME16), Bilbao, Spain, 5–8 July 2016; pp. 5–8. [Google Scholar]
- Song, Y.; Li, Y.; Jia, L.; Qiu, M. Retraining strategy-based domain adaption network for intelligent fault diagnosis. IEEE Trans. Ind. Inform. 2020, 16, 6163–6171. [Google Scholar] [CrossRef]





| Task | Rotation Speed (r/min) | Load Torque (N·m) | Radial Force (N) |
|---|---|---|---|
| 1 | 1500 | 0.1 | 1000 |
| 2 | 1500 | 0.7 | 400 |
| 3 | 1500 | 0.7 | 1000 |
| Healthy | Inner Race Fault | Outer Race Fault |
|---|---|---|
| K001, K002, K003 K004, K005, K006 | KI04, KI14, KI17, KI18 KI21 | KA04, KA15, KA16, KA22, KA30 |
| Parameter | Symbol | Value |
|---|---|---|
| Kernel size of the large convolutional layer | ks | 9 × 1 |
| Stride of the large convolutional layer | s | 8 |
| Number of channels of the large convolutional layer | c | 32 |
| Structure of the combination module | blocks | 000001000001 |
| Output feature dimensions of the average pooling layer | na | 8 |
| Number of neurons in the fully connected layer | fcs | (64, 128) |
| Dropout ratio of the fully connected layer | drs | (0.5, 0.5) |
| Number of codebooks | m | 32 |
| Size of codebooks | k | 256 |
| Buffer size | BS | 10,000 |
| Replay ratio | rr | 0.5 |
| Batch size | bs | 128 |
| Training times | epoch | 300 |
| Weight decay ratio | wd | 10−5 |
| Learning rate | lr | 0.01 |
| Network | Module | Parameter | Output Size | No. | |
|---|---|---|---|---|---|
| Feature extraction network | Large convolutional layer | Conv (9, 8, 4, 32) | 320 × 1 × 32 | 1 | |
| Pooling layer #1 | Maxpool (2, 2, 0, 32) | 160 × 1 × 32 | 1 | ||
| 1D IR-A #1 | Conv (1, 1, 0, 16) + BN + ReLU | Conv (1, 1, 0, 32) | 160 × 1 × 32 | 5 | |
| Conv (1, 1, 0, 16) + BN + ReLU Conv (3, 1, 1, 16) + BN + ReLU | |||||
| Conv (1, 1, 0, 16) + BN + ReLU Conv (5, 1, 2, 16) + BN + ReLU | |||||
| Conv (1, 1, 0, 16) + BN + ReLU Conv (7, 1, 3, 16) + BN + ReLU | |||||
| 1D IR-B #1 | Conv (1, 2, 0, 16) + BN + ReLU | 80 × 1 × 64 | 1 | ||
| Conv (3, 2, 1, 16) + BN + ReLU | |||||
| Conv (5, 2, 2, 16) + BN + ReLU | |||||
| Conv (7, 2, 3, 16) + BN + ReLU | |||||
| 1D IR-A #2 | Conv (1, 1, 0, 32) + BN + ReLU | Conv (1, 1, 0, 64) | 80 × 1 × 64 | 5 | |
| Conv (1, 1, 0, 32) + BN + ReLU Conv (3, 1, 1, 32) + BN + ReLU | |||||
| Conv (1, 1, 0, 32) + BN + ReLU Conv (5, 1, 2, 32) + BN + ReLU | |||||
| Conv (1, 1, 0, 32) + BN + ReLU Conv (7, 1, 3, 32) + BN + ReLU | |||||
| 1D IR-B #2 | Conv (1, 2, 0, 32) + BN + ReLU | 40 × 1 × 128 | 1 | ||
| Conv (3, 2, 1, 32) + BN + ReLU | |||||
| Conv (5, 2, 2, 32) + BN + ReLU | |||||
| Conv (7, 2, 3, 32) + BN + ReLU | |||||
| Classification network | Pooling layer #2 | Avgpool (8) | 8 × 1 × 128 | 1 | |
| Fully connected module #1 | FC(64) + BN + ReLU + Dropout (0.5) | 64 | 1 | ||
| Fully connected module #2 | FC(128) + BN + ReLU + Dropout (0.5) | 128 | 1 | ||
| Fully connected layer | FC(3) | 3 | 1 | ||
| Object | Experiment Number | Average | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| Task 1 | 99.88 | 99.63 | 99.75 | 99.88 | 99.94 | 99.81 | 99.81 | 99.81 | 99.63 | 99.88 | 99.8 |
| 98 | 97 | 97 | 97.81 | 96 | 95.19 | 94.44 | 97.69 | 96.56 | 98.06 | 96.78 | |
| 96.75 | 99.25 | 99.75 | 99.75 | 99.31 | 99.63 | 99.75 | 98.88 | 99.06 | 99.5 | 99.16 | |
| Task 2 | 100 | 99.88 | 100 | 99.94 | 99.88 | 99.94 | 99.63 | 99.81 | 99.94 | 99.81 | 99.88 |
| 91.38 | 95.56 | 93.94 | 95.31 | 98.5 | 89.38 | 88.75 | 92.13 | 87.63 | 94.75 | 92.73 | |
| Task 3 | 99.94 | 99.94 | 99.94 | 99.88 | 99.69 | 100 | 99.94 | 100 | 100 | 99.94 | 99.93 |
| ACC | 97.66 | 98.54 | 98.4 | 98.76 | 98.89 | 97.33 | 97.05 | 98.05 | 97.14 | 98.66 | 98.05 |
| BWT | −5.88 | −2.35 | −3.03 | −2.38 | −1.01 | −5.37 | −5.47 | −4.31 | −6.44 | −2.72 | −3.89 |
| Model | Methods | Acc | BWT |
|---|---|---|---|
| R-REMIND | R-REMIND (our model) | 98.05 ± 0.70 | −3.89 ± 1.84 |
| Model 1 | CNN-based feature extraction network | 97.66 ± 0.77 | −4.74 ± 2.01 |
| Model 2 | ResNet-based feature extraction network | 96.38 ± 0.72 | −6.82 ± 2.21 |
| Model 3 | Feature-based buffer module | 97.28 ± 0.81 | −6.11 ± 2.07 |
| Model 4 | Without the 1D IR-A module | 97.29 ± 0.80 | −5.09 ± 2.39 |
| Model 5 | Without the 1D IR-B module | 97.33 ± 0.68 | −5.80 ± 1.95 |
| Model 6 | Without the fully connected module | 96.69 ± 0.60 | −7.46 ± 1.77 |
| Model 7 | Without the buffer module | 97.25 ± 0.49 | −6.20 ± 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Xiong, H.; Zhang, Y.; Su, K.; Hu, Z. Bearing Fault Diagnosis via Incremental Learning Based on the Repeated Replay Using Memory Indexing (R-REMIND) Method. Machines 2022, 10, 338. https://doi.org/10.3390/machines10050338
Zheng J, Xiong H, Zhang Y, Su K, Hu Z. Bearing Fault Diagnosis via Incremental Learning Based on the Repeated Replay Using Memory Indexing (R-REMIND) Method. Machines. 2022; 10(5):338. https://doi.org/10.3390/machines10050338
Chicago/Turabian StyleZheng, Junhui, Hui Xiong, Yuchang Zhang, Kaige Su, and Zheyuan Hu. 2022. "Bearing Fault Diagnosis via Incremental Learning Based on the Repeated Replay Using Memory Indexing (R-REMIND) Method" Machines 10, no. 5: 338. https://doi.org/10.3390/machines10050338
APA StyleZheng, J., Xiong, H., Zhang, Y., Su, K., & Hu, Z. (2022). Bearing Fault Diagnosis via Incremental Learning Based on the Repeated Replay Using Memory Indexing (R-REMIND) Method. Machines, 10(5), 338. https://doi.org/10.3390/machines10050338





