Abstract
This paper studies operator and fractional order nonlinear robust control for a spiral counter-flow heat exchanger with uncertainties and disturbances. First, preliminary concepts are presented concerning fractional order derivative and calculus, fractional order operator theory. Then, the problem statement about nonlinear fractional order derivative equation with uncertainties is described. Third, the design of an operator fractional order controller and fractional order PID controller and determination of several related parameters is described. Simulations were performed to verify tracking and anti-disturbance performance by comparison to different control cases; verification is described and concluding remarks provided.
1. Introduction
Heat exchangers which transfer heat energy from one fluid to another have been used widely in industrial applications such as refineries, chemical and petrochemical plants, and sewage treatment [1]. Heat exchangers help to minimize energy consumption and reduce waste heat emission. In industry, there are many different application types for heat exchangers. A spiral heat exchanger, for instance, is suitable for dirty fluids and viscous fluids and has the additional advantages of small size, high heat transfer efficiency, and ease of maintenance, among others. In industrial processes, the output temperature of the heated or cooled fluid often has certain requirements due to industry safety or product quality [2,3,4,5]. Thus, it is important to control output temperature on the heated or cooled fluid side in real-world applications. However, because the flow rate and fluid temperature often change, it is very difficult to control the output temperature.
Fractional order derivatives as an extension of integer order derivatives have been widely used to describe practical application objects following their first being proposed by Leibniz in 1695 [6]. Although the use of integer order derivatives to describe dynamic systems applications using traditional methods has a clear physical geometric interpretation, in certain real-world applications dynamic systems described by fractional order derivatives can be more accurate than those described by integer order derivatives; examples include viscoelastic systems, liquids, heat diffusion and dielectric polarization, electrode-electrolyte polarization, nonlinear thermoelastic system etc. [7,8,9,10,11]. Thus, a heat exchanger is suitable for description by fractional order derivative [12,13]. In a feedback control system, a proportion integral derivative (PID) control with only three parameters to tune is widely used thanks to its simple structure and high robustness. For nonlinear control systems with large delay times and disturbances, it is difficult to achieve good control performance. Fractional order PID (FOPID) control extends the conventional PID controller, having five parameters to tune and being more flexible than the traditional PID controller. FOPID control has better control performance in applications, as proven by many studies in recent years [14,15,16,17].
Nonlinear robust control is a problem that has been considered by many researchers in many different fields. In [18,19], the authors consider the right coprime factorization needed to compensate for the nonlinearity of the system and provide robust control performance in an improved system. The right coprime factorization suit is required for both linear feedback control and nonlinear feedback control. This provides a convenient approach to study the input–output stability of nonlinear feedback control systems. In [20,21,22,23], the authors studied robustness using right coprime factorization of a nonlinear system with perturbations. Operator-based nonlinear robust control is a simple method to improve stability and anti-disturbance using only the output signal of the plant.
A spiral heat exchanger (See Appendix A) is a nonlinear system with several uncertainties and many disturbances in the changes in the flow rate, fluid temperature, fluid density, fluid pressure on the two fluids side, etc., as well as a large delay time. It is very difficult to control under complex operating conditions. In application, the spiral heat exchanger mathematical model described via fractional order differential equation is more accurate than other methods [24,25,26,27]. Therefore, motivated by the above references, this paper presents a mathematical model of a spiral heat exchanger using a fractional order derivative system. Operator-based fractional order control is employed to improve robustness in a nonlinear system with uncertainties, disturbances, and a high delay time. A fractional order operator controller and fractional order PID controller are designed to account for uncertainties and disturbance, and the different control cases in tracking performance and stability are analyzed. Finally, the proposed control schemes are simulated and analyzed. This paper focuses on verifying operator and fractional order nonlinear robust control for a spiral counter-flow heat exchanger with uncertainties and disturbances by simulation (See Appendix A). In the future, we intend to study operator and fractional order nonlinear robust control for a spiral counter-flow heat exchanger with uncertainties and disturbances using experimental equipment (See Appendix A), to determine the optimal parameters for fractional order PID control, and to study MIMO control problems using fractional order derivatives [28,29].
The rest of this paper is constructed as follows. In Section 2, preliminaries regarding fractional order calculus and derivative and fractional order operator theory are described, and a problem statement concerning fractional order equations for a spiral-plate heat exchanger is presented. In Section 3, a fractional order operator controller is designed and the different control cases are analyzed in terms of tracking performance and stability. Simulations verifying operator and fractional order-based robust nonlinear control for a spiral counter-flow heat exchanger with uncertainties and disturbances are reviewed in Section 4. Finally, conclusions are provided in the final section.
2. Preliminaries and Problem Statement
A basic overview of fractional order integral and operator theory are presented in this section.
Definition 1
(The definition of Caputo’s fractional order calculus [6]).
where is Gamma function, .
Definition 2
(The definition of Caputo’s fractional order derivative [6]).
where n is a integer that is equal to or greater than q. If n = 1, then .
2.1. Lipschitz Operators Theory
Definition 3
([30]). Let and be two extended linear spaces which are associated, respectively, with two Banch spaces, X and Y, of measurable functions defined on the time domain , and let D be a subset of . A nonlinear operator is called a generalized Lipschitz operator on D if there exists a constant L such that
for all and for all .
Note that the least such constant L is provided by
which is a semi-norm for general nonlinear operators and is the actual norm for linear operator A. The actual norm for a nonlinear operator A is provided by
for any fixed .
Theorem 1.
Let and be two extended linear spaces which are associated, respectively, with two Banch spaces, X and Y, of measurable functions defined on the time domain , and let D be a subset of . A nonlinear operator fractional order operation, defined in [30], is a generalized Lipschitz operator on D.
Proof.
Let , meaning mapping from , where is a fractional order operation. For any ; however, extended linear space.
Because , , then
Therefore,
Obviously there exists which is the least constant of H.
Proof completed. □
Right Coprime Factorization
Operator P + P:V → Y denotes a nonlinear system with uncertainties. Where P is the nominal object, P means the uncertainties of object V and Y stands for the input and output space of the object.
Right factorization:
By appling an intermediate variable w ∈ W, W is called a quasi-state space of P and the input and output of the operator P are described as y = N(w) and v = D(w), respectively. If D is invertible, w(t) = D(v)(t), then P(v(t)) = N(w(t)) = ND(v)(t); if, furthermore, N and D are two stable operators, the operator P is said to have a right factorization, as shown in Figure 1.
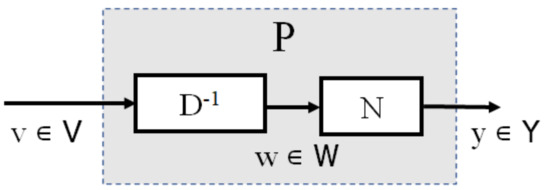
Figure 1.
Right factorization of a nonlinear object.
Right coprime factorization:
After right factorization of a object P into (N, D), if two operators R and S satisfy the following Bezout identity, the factorization is said to be right coprime factorization:
where R is invertible and M is a unimodular operator. The block diagram of the right coprime factorization of a nonlinear system P is shown in Figure 2. Figure 2 shows an operator-based feedback controller for a nonlinear plant P, with the operators R and S serving as the controller.
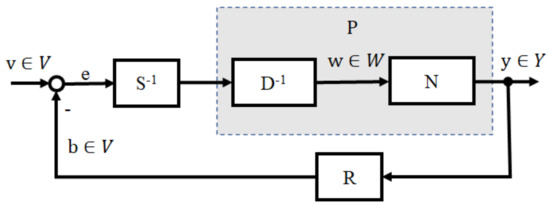
Figure 2.
Right coprime factorization of a nonlinear system.
For a nonlinear real object , it can be represented as a nominal object P with bounded uncertainty and . The right factorization of the nominal object P and the overall object are
and
where N, , and D are stable operators, D is invertible, and is unknown while the upper and lower bounds are known. If the following Bezout identity is satisfied and if is a unimodular operator, then the nonlinear feedback control system is said to be BIBO stable.
With the operators S and R determined, if they further satisfy the following condition then the robustness of the uncertain system is guaranteed:
where is a Lipschitz operator norm. The robust operator-based feedback control system with uncertainty is shown in Figure 3.
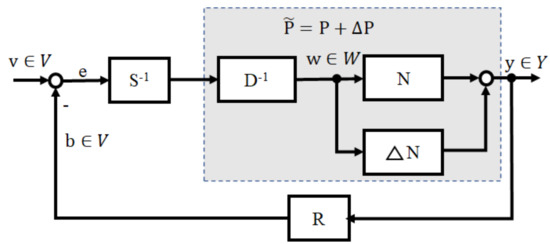
Figure 3.
Nonlinear operator-based feedback control system with uncertainty.
Theorem 2
([30]). Let be a linear subspace of the extended linear space associated with a given Banach space , and let . Let the Bezout identity of the nominal plant and the exact plant be , , respectively. If
then the system shown in Figure 3 is robust stable for .
Theorem 3
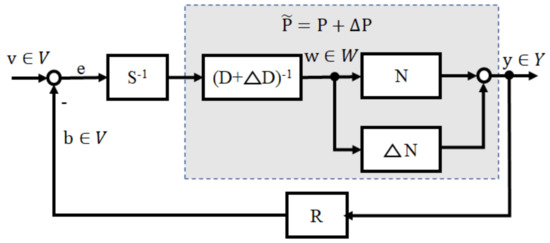
([30]). Let be a linear subspace of the extended linear space associated with a given Banach space , and let . Let the Bezout identity of the nominal plant and the exact plant be , , respectively. If
then the system shown in Figure 4 is robust stable for .

Figure 4.
Nonlinear operator-based feedback control system with uncertainties.
Theorem 4.
Let be a linear subspace of the extended linear space associated with a given Banach space , and let . Let the Bezout identity of the nominal plant and the exact plant be , , respectively. If
then the system shown in Figure 3 is robust stable for .
Proof.
If
then
According to Theorem 2, the system shown in Figure 3 is robust stable for .
Proof completed. □
Theorem 5.
Let be a linear subspace of the extended linear space associated with a given Banach space , and let . Let the Bezout identity of the nominal plant and the exact plant be , , respectively. If the condition
is satisfied, then the system shown in Figure 4 is robustly stable for , .
Proof.
In the same method with Theorem 4, this theorem was proved. □
2.2. Problem Statement
According to the law of heat-energy balance of two fluids, the fractional order derivative model for a spiral-plate parallel flow heat exchanger is derived as follows [13]:
Let , , then,
Thus,
where , , = , = , and = . and = , which is related to the plant of the spiral-plate heat exchanger; and are the densities of the cold fluid and the heat fluid, respectively; and are the specific heat capacities of the cold fluid and the heat fluid, respectively; and are the input temperatures of the cold fluid and the heat fluid, respectively; and are the output temperatures of the cold fluid and the heat fluid, respectively; and are fractional orders of the hot fluid and the cold fluid, respectively; and and are the volume flow rate of the hot fluid and the cold fluid, respectively.
where = , = , = , = . is the initial condition of the fractional order integral.
3. Fractional Order Operator Controller Design and Tracking Controller Design
3.1. Operator-Based Fractional Order Controller Design
As shown in Figure 4, provided a nonlinear operator control system, operators V and Y are the input and output space of this plant. Let (N, D) be the right factorization of P. The feedback nonlinear control system shown in Figure 4 is BIBO stable if there exist two stable operators R: Y → V, S: V → V (S being invertible as well) that satisfy the Bezout identity equation:
where M is a unimodular operator to consider the uncertain term in the nonlinear system. With the designed operators S and R in Figure 4, the following equation can be satisfied:
where is a Lipschitz norm. Then, the nonlinear feedback control system is robustly stable where M is an unimodular operator. The mathematical modeling of P considering the uncertain term can be provided for the the spiral heat exchanger system as follows:
where = , = , = , = . The plant can be right coprime factorized as follows:
The operator-based feedback control system is shown in Figure 2. The operators R and S are designed as follows:
where = .
Operators R and are designed to satisfy the Bezout identity:
thus, if
is satisfied according to Therom 5, then the system is BIBO stable.
3.2. Fractional Order Operator-Based Control Stability Analysis
In this section, the stability of the fractional order operator-based control system for a spiral-plate exchanger with uncertainties is presented.
thus,
According to the stability conditions of the fractional order operator-based control system, if
that is,
Here,
thus,
is a BIBO stable condition.
From Table A1, . . Let, , then, the nonlinear control system is BIBO stable.
The fractional order operator-based control system is stable under condition (44), however, the track precision is bad because of model error and disturbances. Therefore, it is rarely used alone. In order to improve the robustness, anti-interference, and tracking performance of the control system, we designed a feedback control system for the tracking controller.
3.3. Tracking Controller Design
The differential equation of fractional order controller is described by
If , it is a conventional PID control. It is obvious that the fractional order controller needs to design the three parameters , , and as well as the orders , of the integral and derivative controllers. The orders , need not necessarily be integers, and can be any real numbers. As shown in Figure 5, the FOPID (fractional order PID) controller generalizes the conventional integer order PID controller and expands it from point to plane. This expansion can provide a great deal more flexibility in PID control design.
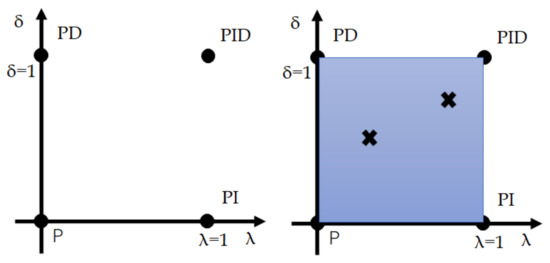
Figure 5.
FOPID controller.
3.4. Operator-Based Fractional Order Robust Control for Spiral-Plate Heat Exchanger with Uncertainties and Disturbances
As a spiral heat exchanger is a nonlinear system with uncertainties, disturbances, and a long delay time, it is difficult to improve the tracking performance of the output temperature. While operator-based control is a nonlinear control method to improve stability, tracking performance remains poor. PID feedback control is widely used in application due to its simple form and because it only required three parameters to be adjusted. FOPID, with its five parameters, is an extension of conventional PID. Thus, FOPID is more flexible than the conventional PID. The five cases for output temperature control of the presented spiral heat exchanger were designed to compare tracking performance and stablity for uncertanities and disturbance, as shown Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10.
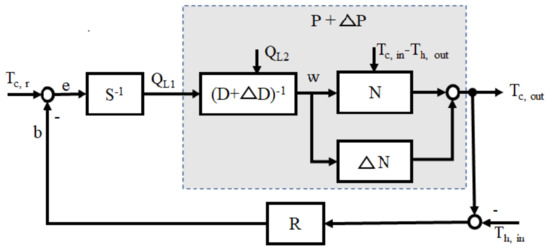
Figure 6.
Operator-based fractional order robust control.
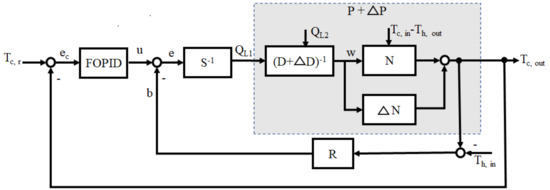
Figure 7.
Operator-based fractional order robust control with FOPID.
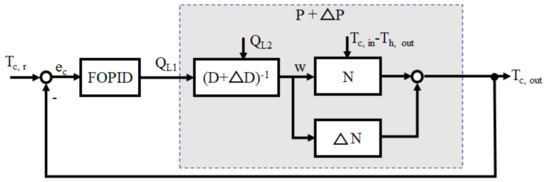
Figure 8.
Fractional order robust control with FOPID.
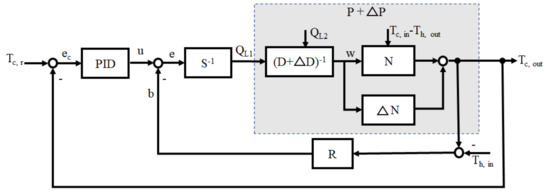
Figure 9.
Operator-based fractional order robust control with PID.
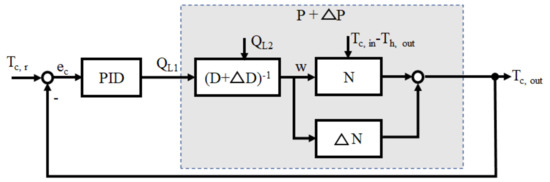
Figure 10.
Fractional order robust control with PID.
4. Simulation and Analysis
In this section, the five different cases are simulated and analysed in Matlab with the same uncertainties and disturbances.
4.1. Simulation Conditions
Here, Table 1 shows the simulation parameters for the spiral-plate heat exchanger. Table 2 denotes the simulation condition for the spiral-plate heat exchanger. The reference output temperature is the output temperature of the cold fluid. The volume flow rate on the cold fluid side is the disturbance signal; is changed from 1 L/Min to 7 L/Min in time 8 s, and are the uncertainties of the spiral heat exchanger’s shape and the heat transfer coefficient, respectively. The volume flow rate on the hot fluid side is the control signal. Considering the actual condition, the maximum input volume flow rate is 10 L/Min.

Table 1.
Simulation parameters of the spiral-plate heat exchanger.

Table 2.
Simulation condition of the spiral-plate heat exchanger.
4.2. Simulation and Analysis
The spiral counter-flow heat exchanger with uncertainties and disturbances described by the special fractional order equation is both a first order or norm fractional order system and a nonlinear system. Thus, the parameters of fractional order PID control cannot be tuned using the conventional tuning method. The parameters of both the conventional and fractional order PID control are tuned using a trial-and-error method. The first proportion is adjusted, then derivative integrals are adjusted in turn until the best parameters are derived. In the future, the parameters of fractional order PID is optimized by particle swarm optimum algorithm. Table 3, Table 4, Table 5, Table 6 and Table 7 are the best controller parameters to tune and the parameters of the operator controller.

Table 3.
Tuning parameters for operator controller.

Table 4.
Tuning parameters for FOPID Controller with operator controller.

Table 5.
Tuning parameters for FOPID Controller without operator controller.

Table 6.
Tuning parameters for PID Controller with operator controller.

Table 7.
Tuning parameters for PID Controller without operator controller.
It is obvious that the fractional order PID control with operator controller has the best tracking performance compared to the others, as shown in Figure 11. The overshoot and settle times for the fractional order PID control with operator controller are shorter than for the fractional order PID control without operator controller. The overshoot and settle times for the conventional PID control with operator controller are smaller than for the conventional PID control without operator controller.
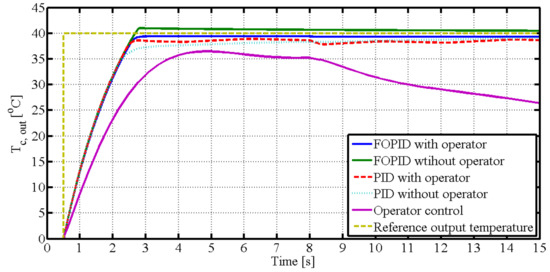
Figure 11.
Comparison of different control schemes.
Figure 12 shows that fractional order operator control can improve the stability when uncertainties and disturbances are present, although the tracking performance and anti-disturbance are bad.Figure 13, Figure 14, Figure 15 and Figure 16 show the control performance, control signals, and tracking performance in the control process for the five different control schemes with uncertainties and disturbance; , d, u, and are the reference output temperature of the cold fluid side, disturbance signal of the volume flow rate in the cold fluid side, control signal of the volume flow rate on the hot fluid side, and output temperature on the cold fluid side, respectively. The performance with operator-based fractional order PID control is the best in terms of anti-disturbance and stability compared to the other control schemes.
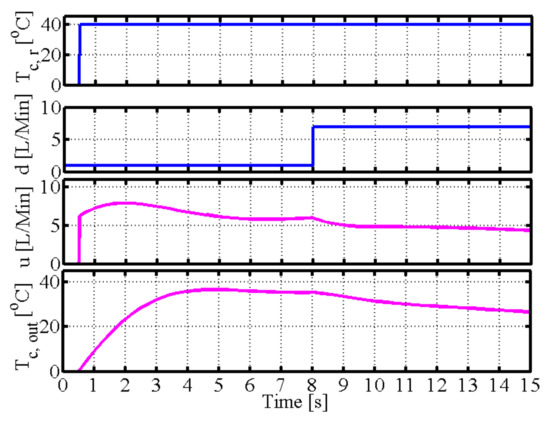
Figure 12.
Simulation of operator control.
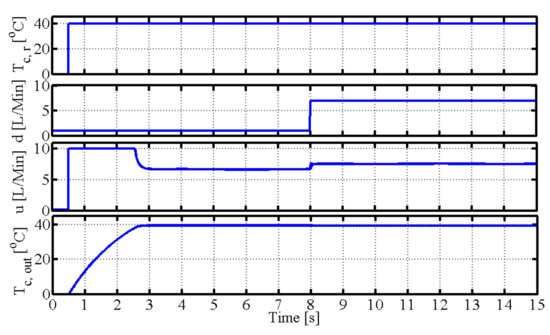
Figure 13.
Simulation of FOPID with operator.
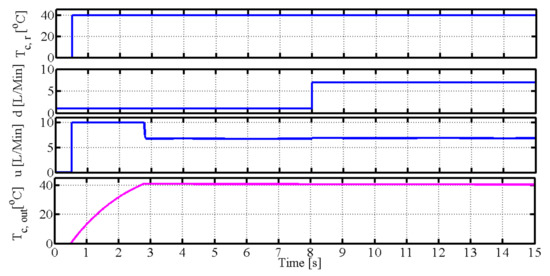
Figure 14.
Simulation of FOPID without operator.
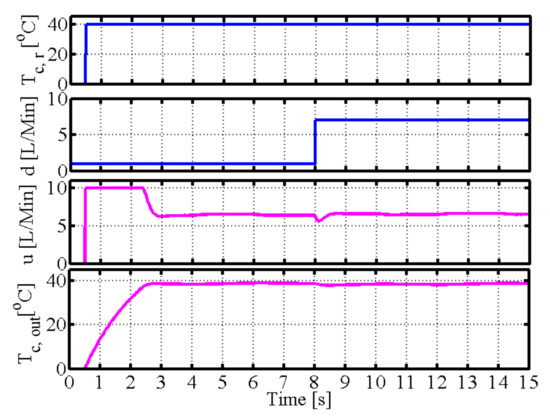
Figure 15.
Simulation of PID with operator.
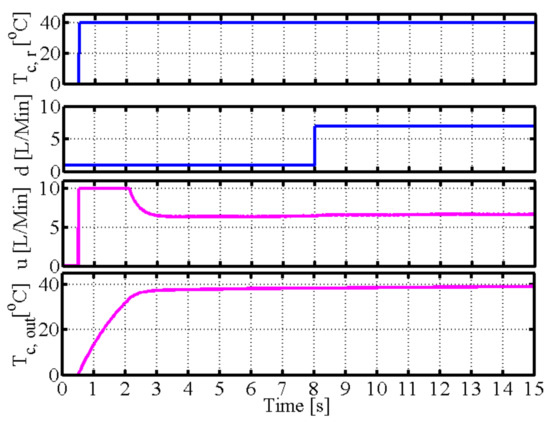
Figure 16.
Simulation of PID without operator.
5. Conclusions
In this paper, we have proposed operator-based fractional order PID nonlinear robust control with uncertainties and disturbance. First, we introduced the concepts of fractional order and the preliminaries of operator theory as extended to fractional order and nonlinear fractional order equations. Then, operator-based nonlinear fractional order controller design and fractional order PID tracking controller design were covered and the parameters of the operator controller and fractional order PID controller were determined. Finally, the robust stability and tracking performance of the operator-based nonlinear robust control system with uncertainties and disturbance were analyzed via simulation in Matlab. However, the tuning parameters of the fractional order controller continue to require adjustment offline or by hand, and robust control performance requires continued research as well.
Author Contributions
M.D. supervised the work; G.D. finished the simulation, and wrote the rest of the work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. A Spiral Heat Exchanger Plant
A spiral heat exchanger is shown in Figure A1. This design has many merits, such as a highly efficient heat transfer, small size in comparison to other heat exchangers, and self-cleaning capability thanks to the unique spiral structure.

Figure A1.
A spiral heat exchanger plant.
The spiral heat exchanger is an piece of excellent heat transfer equipment; however, its complex inner structure makes it difficult to built an accurate mathematical model. Generally, the logarithmic mean temperature difference method is used, however, control performance is bad. We considered using a fractional order derivative equation to describe a spiral heat exchanger. Figure A2 shows a cross-section of the inner structure of the spiral-plate heat exchanger, where , , and represent the width of hot fluid, the width of cold fluid and the width of solid wall, respectively. In this paper, the inner cold fluid, as shown in Figure A2, is divided into a micro-volume. A fractional order derivative equation is constructed by considering the heat balance of the two fluids.
The geometric parameters of the spiral-plate heat exchanger are denoted in Table A1.

Table A1.
Parameters of the spiral-plate heat exchanger.
Table A1.
Parameters of the spiral-plate heat exchanger.
| Meaning | Symbol | Value |
|---|---|---|
| Geometric parameter of a spiral function | a | m/rad |
| Initial radius of hot fluid side | b | 0.08 m |
| Spiral function angle of the spiral-plate heat exchanger | ||
| The width of hot flow channel | 0.005 m | |
| The width of cold flow channel | 0.005 m | |
| The width of solid wall | 0.0018 m | |
| The height of the spiral-plate heat exchanger | Z | 0.011 m |
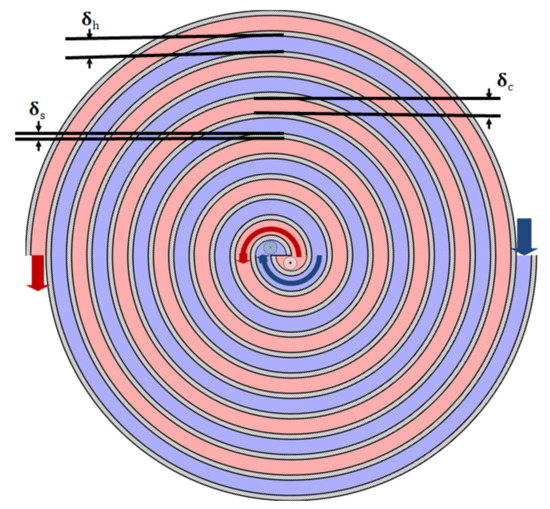
Figure A2.
Cross-section of the inner structure of the spiral-plate heat exchanger.
Heat exchangers are typically classified into parallel-flow and count-flow types based on their arrangement. In the parallel-flow type, both the input and the output of the two directional fluids (one a hot fluid, the other a cold fluid) flow in the same direction. In a counter-flow heat exchanger, the hot fluid and cold fluid flow in opposite directions. In this paper, we study a fractional order derivative model of a spiral counter-flow type heat exchanger.
References
- Tapre, R.W.; Kaware, J.P. Review on heat transfer in spiral heat exchanger. Int. J. Sci. Res. 2015, 5, 1–5. [Google Scholar]
- Metta, V.R.; Konijeti, R.; Dasore, A. Thermal design of spiral plate heat exchanger through numerical modelling. Int. J. Mech. Eng. Technol. 2018, 9, 736–745. [Google Scholar]
- Khorshidi, J.; Heidari, S. Design and construction of a spiral heat exchanger. Adv. Chem. Eng. Sci. 2016, 6, 201–298. [Google Scholar] [CrossRef] [Green Version]
- Sathiyan, S.; Rangarajan, M. An experimental study of spiral-plate heat exchanger for nitrobenzene-water two-phase system. Bulg. Chem. Commun. 2010, 42, 205–209. [Google Scholar]
- Memon, S.; Gadhe, P.; Kulkarni, S. Design and testing of a spiral plate heat exchanger for textile industry. Int. J. Sci. Eng. Res. 2019, 10, 149–157. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Challamel, N.; Zorica, D.; Atanacković, T.M.; Spasić, D.T. On the fractional generalization of Eringen’s nonlocal elasticity for wave propagation. Comptes Rendus MéCanique 2013, 341, 298–303. [Google Scholar] [CrossRef]
- Magin, R.L.; Ovadia, M. Modeling the cardiac tissue electrode interface using fractional calculus. J. Vib. Control 2008, 14, 1431–1442. [Google Scholar] [CrossRef]
- Sumelka, W. Thermoelasticity in the Framework of the Fractional Continuum Mechanics. J. Therm. Stress. 2014, 37, 678–706. [Google Scholar] [CrossRef]
- Sidhardh, S.; Patnaik, S.; Semperlotti, F. Thermodynamics of fractional-order nonlocal continua and its application to the thermoelastic response of beams. Eur. J. Mech. A/Solids 2021, 88, 104238. [Google Scholar] [CrossRef]
- Patnaik, S.; Sidhardh, S.; Semperlotti, F. Nonlinear thermoelastic fractional-order model of nonlocal plates: Application to postbuckling and bending response. Thin-Walled Struct. 2021, 164, 107809. [Google Scholar] [CrossRef]
- Dong, G.; Deng, M. GPU Based Modelling and Analysis for Parallel Fractional Order Derivative Model of the Spiral-Plate Heat Exchanger. Axioms 2021, 10, 344. [Google Scholar] [CrossRef]
- Dong, G.; Deng, M. Operator Based Fractional Order Control System for a Spiral Heat Exchanger with Uncertainties. In Proceedings of the 2021 International Conference on Advanced Mechatronic Systems (ICAMechS), Tokyo, Japan, 9–12 December 2021; pp. 242–247. [Google Scholar]
- Sandhya, A.; Sandhya, R.; Prameela, M. An overview of Fractional order PID Controllers and its Industrial applications. Int. J. Innov. Eng. Technol. 2016, 6, 534–546. [Google Scholar]
- Shekher, V.; Rai, P.; Prakash, O. Tuning and Analysis of Fractional Order PID Controller. Int. J. Electron. Electr. Eng. 2012, 5, 11–21. [Google Scholar]
- Swati, S.; Yogesh, H. Fractional Order Controller and its Applications: A Review. In Proceedings of the IASTED Asian Conference, Phuket, Thailand, 2–4 April 2012; pp. 1–6. [Google Scholar]
- Ranganayakulu, R.; Babu, G.U.B.; Rao, A.S.; Patle, D.S. A comparative study of fractional order PIλ/PIλDμ tuning rules for stablefirst order plus time delay processes. Resour. Effic. Technol. 2016, 2, S136–S152. [Google Scholar]
- Wen, S.; Deng, M. Operator-based robust nonlinear control and fault detection for a Peltier actuated thermal process. Math. Comput. Model. 2012, 57, 16–29. [Google Scholar] [CrossRef]
- Deng, M.; Wen, S.; Inoue, A. Operator-based robust nonlinear control for a Peltier actuated process. Meas. Control J. Inst. Meas. Control 2011, 44, 116–120. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A.; Goto, S. Operator based thermal control of an aluminum plate with a Peltier device. Int. J. Innov. Comput. Inf. Control 2008, 4, 3219–3229. [Google Scholar]
- Bi, S.; Deng, M.; Xiao, Y. Robust Stability and Tracking for Operator-Based Nonlinear Uncertain Systems. IEEE Trans. Autom. Sci. Eng. 2015, 12, 1059–1066. [Google Scholar] [CrossRef]
- Deng, M.; Kawashima, T. Adaptive Nonlinear Sensorless Control for an Uncertain Miniature Pneumatic Curling Rubber Actuator Using Passivity and Robust Right Coprime Factorization. IEEE Trans. Control Syst. Technol. 2016, 24, 318–324. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A.; Zhu, Q. An integrated study procedure on real time estimation of time varying multijoint human arm viscoelasticity. Trans. Inst. Meas. Control 2011, 33, 919–941. [Google Scholar] [CrossRef]
- Caponetto, R.; Dongola, G.; Fortuna, L.; Petras, I. Fractional Order Systems: Modeling and Control Applications; World Scientific: Singapore, 2010. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional Order Systems and Controls: Fundamentals and Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Fujii, R.; Deng, M.; Wakitani, S. Nonlinear remote temperature control of a spiral plate heat exchanger. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems, Beijing, China, 22–24 August 2015; pp. 533–537. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Wen, S.; Deng, M.; Inoue, A. Operator-based robust nonlinear control for gantry crane system with soft measurement of swing angle. Int. J. Model. Identif. Control 2012, 16, 86–96. [Google Scholar] [CrossRef]
- Wang, A.; Deng, M. Robust nonlinear multivariable tracking control design to a manipulator with unknown uncertainties using operator-based robust right coprime factorization. Trans. Inst. Meas. Control 2013, 35, 788–797. [Google Scholar] [CrossRef]
- Deng, M. Operator-Based Nonlinear Control Systems: Design and Applications; Wiley-IEEE Press: Singapore, 2014. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).